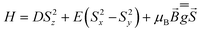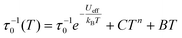Magnetic anisotropy and structural flexibility in the field-induced single ion magnets [Co{(OPPh₂)(EPPh₂)N}₂], E = S, Se, explored by experimental and computational methods

Abstract

During the last few years, a large number of mononuclear Co(II) complexes of various coordination geometries have been explored as potential single ion magnets (SIMs). In the work presented herein, the Co(II) S = 3/2 tetrahedral [Co{(OPPh₂)(EPPh₂)N}₂], E = S, Se, complexes (abbreviated as CoO₂E₂), bearing chalcogenated mixed donor-atom imidodiphosphinato ligands, were studied by both experimental and computational techniques. Specifically, direct current (DC) magnetometry provided estimations of their zero-field splitting (zfs) axial (D) and rhombic (E) parameter values, which were more accurately determined by a combination of far-infrared magnetic spectroscopy and high-frequency and -field EPR spectroscopy studies. The latter combination of techniques was also implemented for the S = 3/2 tetrahedral [Co{(EPⁱPr₂)₂N}₂], E = S, Se, complexes, confirming the previously determined magnitude of their zfs parameters. For both pairs of complexes (E = S, Se), it is concluded that the identity of the E donor atom does not significantly affect their zfs parameters. High-resolution multifrequency EPR studies of CoO₂E₂ provided evidence of multiple conformations, which are more clearly observed for CoO₂Se₂, in agreement with the structural disorder previously established for this complex by X-ray crystallography. The CoO₂E₂ complexes were shown to be field-induced SIMs, i.e., they exhibit slow relaxation of magnetization in the presence of an external DC magnetic field. Advanced quantum-chemical calculations on CoO₂E₂ provided additional insight into their electronic and structural properties.

---

Introduction

Extensive studies are currently being carried out, with an aim of investigating in depth the role of unpaired electrons in assuring specific functions in homogeneous or heterogeneous catalysts,^1,2 the active sites of metalloproteins,³ as well as molecular magnetic materials.^4,5 A major achievement related to the latter was the discovery, in the early 1990s, of single molecule magnets (SMMs), i.e., multinuclear metal complexes that exhibit magnetic bistability, and hence slow relaxation of magnetization owing to an energy barrier, whose magnitude depends on their total spin S and their magnetic anisotropy.^6–8 The latter, conventionally expressed via the zero-field splitting (zfs) axial D component, has been shown to acquire much larger values for mononuclear than for multinuclear metal complexes.^9–11 Thus, currently there is an increased interest in exploring slow relaxing mononuclear metal complexes, which are referred to either as mononuclear SMMs or as single ion magnets (SIMs).^12–15 Along these lines, intense research efforts have been devoted to mononuclear complexes of lanthanides^16–21 and actinides,²² exhibiting large magnetic anisotropy. Potential applications of these materials include information-storage or molecular devices that could be employed for the design of quantum computers.^23–25 However, it should be stressed that the slow magnetization relaxation of SMMs and SIMs is limited to temperatures lower than the corresponding blocking temperature (T_B),²⁰ setting a target of increasing this limit to technologically manageable values. To that end, major breakthroughs have been reported during the last five years concerning lanthanide complexes, the T_B value of which approaches,^26–28 or even surpasses,^29,30 that of liquid nitrogen (77 K).

In parallel to the development of lanthanide/actinide SIMs, there has been an increased interest in exploring mononuclear 3d-metal-based complexes.^{12,13,15,31–39} For these systems, it is of paramount importance to reliably and accurately determine the sign and magnitude of their zfs D component, as well as their rhombicity E/D (E is the rhombic component of the zfs).⁴⁰ The experimental methods that are employed for this - rather demanding - task, have been recently reviewed,⁴¹ and mainly include DC magnetometry,⁴⁰ high-frequency and -field EPR spectroscopy (HFEPR),^42–44 far-infrared magnetic spectroscopy (FIRMS),^45–47 inelastic neutron scattering,^48–50 magnetic circular dichroism^51–53 and Mössbauer spectroscopy.^54–57 Each experimental method has its advantages and limitations.⁴¹ Among these methods, direct current (DC) magnetometry has been a conventional method of estimating the magnitude of the zfs D and E components. However, to this end, DC magnetometry cannot compete with the significantly improved accuracy of resonance spectroscopic methods. For that reason, some of the above specific spectroscopic methods, either separate, or in combination, are currently employed for this task⁴¹ (vide infra). In that respect, it should be noted that, in combination with other physicochemical methods, FIRMS has been recently employed to probe the magnetic properties of various Co(II) complexes.^58–64

The vast majority of 3d-based SIMs involve Co(II) complexes of various coordination spheres and geometries,^13,65 including the seminal tetrahedral complex [Co(SPh)₄]²⁻,^66,67 and its O- and Se- congeners,⁶⁷ as well as some outstanding examples of SIMs bearing four-⁶⁸ or two-^69,70 coordinate Co(II) centers. Accordingly, the main target of the present work was the investigation of the tetrahedral Co(II) complexes [Co{(OPPh₂)(EPPh₂)N}₂], E = S,⁷¹ Se,⁷² (abbreviated as CoO₂E₂), bearing chalcogenated mixed donor-atom imidodiphosphinato ligands.⁷³ The crystal structure of these complexes is shown in Fig. S1 in the ESI.† The zfs parameters originally estimated by DC magnetometry^71,72 were not replicated by FIRMS/HFEPR. Therefore, these complexes were re-investigated by DC magnetometry in the present study. Their dynamic magnetic properties were also explored by alternating current (AC) susceptometry. Comparisons are thus made between the DC magnetometry- and FIRMS/HFEPR-derived zfs parameters of CoO₂E₂, as well as between the dynamic magnetic properties of CoO₂E₂ and CoE₄.

Recently, some of us investigated the S = 3/2 tetrahedral Co(II) complexes [Co{(EPⁱPr₂)₂N}₂], E = S, Se, bearing two chelating chalcogenated imidodiphosphinato ligands⁷⁴ (in the following abbreviated as CoE₄), by DC and AC magnetic investigations, as well as by HFEPR. These slow-relaxing complexes exhibit D values of −30.5 cm⁻¹ and −30.4 cm⁻¹, as deduced by DC magnetometry, since HFEPR cannot be fully implemented for these complexes, due to the magnitude of D and their negligible rhombicity.⁷⁴ In the work presented herein, these complexes were studied by FIRMS, providing accurate zfs data, in good agreement with the magnetometry-derived ones.

In the past, some of us carried out high-resolution multifrequency EPR spectroscopy studies on single crystals of the S = 2 tetrahedral Fe(II) complex [Fe{(SPPh₂)(SPPh₂)N}₂] bearing the disulfido analogue of the above ligands.⁷⁵ This study (at 9, 95 and 275 GHz) showed EPR signals attributed to distinct S = 2 centers and therefore provided evidence for the existence of multiple structural conformations of the compound. The zfs parameters of two such conformations were accurately determined. Since X-ray crystallography has shown that the crystal structure of CoO₂Se₂ exhibits structural disorder,⁷² similar studies were performed on the CoO₂E₂, E = S, Se, complexes, which indeed revealed two conformations of CoO₂Se₂. Furthermore, the CoO₂E₂ complexes were investigated by advanced quantum-chemical methods. Overall, our combined experimental and computational work provides a coherent picture of the structural, electronic and magnetic properties of this sub-family of tetrahedral Co(II) complexes, probing both their magnetic anisotropy and structural flexibility.

Results and discussion

DC magnetometry: static magnetic properties

The large discrepancy between the zfs values of the CoO₂E₂ complexes determined by FIRMS/HFEPR (vide infra) and those reported in the literature based on DC magnetometry (E = S,⁷¹ Se,⁷²), prompted us to reinvestigate them by the latter method. The χ_MT product of CoO₂E₂, E = S, Se, as a function of temperature, is presented in Fig. 1.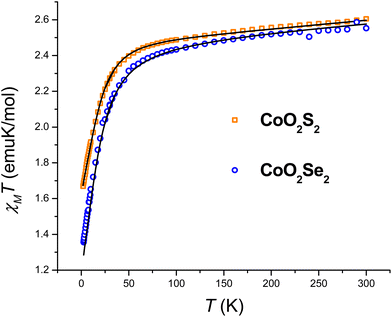

Fig. 1 Temperature dependence of the χ_MT product of CoO₂S₂ and CoO₂Se₂, along with the best fitting lines calculated as described in the text.

The investigated systems displayed a room temperature χ_MT value of 2.60 and 2.55 emu K mol⁻¹, respectively, higher than the one expected for a spin-only S = 3/2 system (1.875 emu K mol⁻¹), suggesting the presence of an unquenched orbital magnetic moment. On cooling down to 100 K, both systems undergo a linear decrease in their χ_MT product, which is interpreted as arising from a temperature-independent paramagnetism (TIP), previously found for tetrahedral S = 3/2 Co(II) complexes.^71,76 Upon further lowering of the temperature, the magnitude of χ_MT plot decreases more rapidly, to reach 1.67 and 1.35 emu K mol⁻¹ at 2.5 K for CoO₂S₂ and CoO₂Se₂, respectively, indicating the presence of magnetic anisotropy and/or antiferromagnetic interactions between neighboring Co(II) sites in their crystal lattice. The shortest distance between these sites in both CoO₂S₂⁷¹ and CoO₂Se₂⁷² is quite large (9.8 Å), and hence antiferromagnetic interactions are expected to be negligible. The zfs parameters D and E and Landé (g) factors were extracted from a fit of the χ_MT and isothermal magnetization plots shown in Fig. S2 (E = S) and S3 (E = Se) in the ESI,† using the following spin Hamiltonian:

The resulting best fitting parameters were obtained using the PHI software⁷⁷ and are reported in Table 1, and describe both systems as possessing a negative D parameter exceeding the 20 cm⁻¹ value, in much better agreement with the FIRMS/HFEPR-derived values, (D ∼ −21 cm⁻¹, Table 2, vide infra), than the previously reported |D| values by DC magnetometry (11.9 cm⁻¹,⁷¹ and 10.4 cm⁻¹,⁷² for the E = S and Se, respectively). However, the magnitude of the rhombicity E/D estimated by DC magnetometry (Table 1) differs significantly from that derived by FIRMS/HFEPR, especially for CoO₂Se₂ (4.2 × 10^–4 and 0.08 cm⁻¹, respectively, vide infra), again revealing the limitations of DC magnetometry in the accurate determination of the zfs D and E values.

Table 1 DC magnetometry data for CoO₂E₂, E = S, Se

	CoO2S2	CoO2Se2
g x	2.21(3)	2.20(1)
g y	2.20(1)	2.52(1)
g z	2.41(1)	2.13(1)
D (cm^−1)	−23.9(1)	−20.4(1)
E (cm^−1)	−0.9(4)	−0.01(18)
E/D	0.04(2)	4.2(8) × 10^–4
TIP (emu mol^−1)	5.5 × 10^–4	4.2 × 10^–4

---

Table 2 Spin Hamiltonian parameters of the CoO₂E₂ and CoE₄, E = S, Se, complexes determined by FIRMS/HFEPR

Complex	D (cm^−1)	E/D	g ⊥	g ||
a Assumed per analogy with CoO2Se2. b From Sottini et al.^74 c Assumed isotropic.
CoO2S2	∼ −20.8	∼ 0.1	2.2^a	2.4
CoO2Se2	–20.9	0.08	2.2	2.4
CoS4	–32.5	0.023^b	2.29^b^,^c
CoSe4	–33.3	0.0016^b	2.38^b^,^c

---

FIRMS and HFEPR studies

CoO₂E₂ complexes. The two CoO₂E₂, E = S, Se, complexes were subjected to spectroscopic examination using FIRMS and HFEPR techniques. Fig. 2 displays the results, presenting FIRMS color maps of normalized transmittance as a function of magnetic field and transition energy (or frequency). The transmission spectrum (single beam) and simulation of the magnetic resonance absorption are shown in Fig. S4 in the ESI.† Each of the CoO₂E₂ complexes shows a single magnetic transition in zero field at 41.6 ± 0.5 and 42.2 ± 0.5 cm⁻¹ for E = S and Se, respectively, corresponding to the energy gap between the two lowest-lying Kramers doublets in these compounds. These values amount therefore to 2|D*|, where D* = (D² + 3E²)^1/2, which is approximately equal to 2D, unless the zfs tensor is extremely rhombic. This means that, to a first approximation, for both systems |D| ∼ 21 cm⁻¹, as compared with the significantly different values of 11.9 cm⁻¹ (E = S)⁷¹ and 10.4 cm⁻¹ (E = Se),⁷² derived previously by DC magnetometry studies.

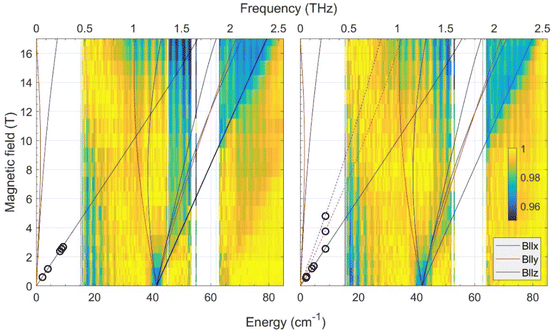Fig. 2 Joint FIRMS and HFEPR plots of magnetic resonances vs. transition energy (frequency) for the CoO₂E₂ complexes: E = S (left) and E = Se (right.) The color maps represent the magnitude of field-induced changes in the far-IR transmission spectrum (blue: most intense; yellow: least intense). White areas: the data are excluded due to large experimental error. The vertical stripes pattern stems from instrumental artifacts. The circles are observed HFEPR turning points. The lines represent turning points in the powder spectra and were calculated using spin Hamiltonian parameters as in Table 2. Solid lines originating from zero frequency at zero field correspond to the ground (M_s = ±3/2), and dashed lines in the right panel to the excited (M_s = ±1/2) intra-Kramers transitions.

In addition to the FIRMS color maps, resonances detected in the HFEPR spectra of each complex are shown as superimposed circles. In both complexes, the dominant resonance was identified as the B₀||z turning point belonging to the intra-Kramers (nominally: ΔM_s = ±3) transition within the M_s = ±3/2 doublet. This means that the M_s = ± 3/2 doublet is the ground state, i.e., the sign of D by convention is negative. At elevated temperatures (20–40 K), resonances originating from the excited M_s = ± 1/2 doublet also showed up (Fig. S5† in the ESI†). However, only for CoO₂Se₂, signals at the perpendicular (B₀||x, y) turning points of the ΔM_s = ±1 transition within the excited Kramers doublet were strong enough to be used for analysis. These points allowed us to estimate the rhombicity of the zfs tensor for CoO₂Se₂, which turned out to be impossible for CoO₂S₂.

By combining the FIRMS and HFEPR data of CoO₂Se₂, the spin Hamiltonian parameters were determined to be:

D = −20.9 cm⁻¹, E = −1.7 cm⁻¹, E/D = 0.08, g_⊥ = 2.2; g_|| = 2.4.

It should be mentioned that the above values assume an axial symmetry of the g-tensor. Simulations show, however, that if the observed splitting of the perpendicular turning points in the HFEPR originated from rhombic g-values, these values would be unphysical, such as one of the perpendicular g-values equal to about 1.85.

Since the HFEPR response of CoO₂S₂ was weaker than that of CoO₂Se₂, we could not reliably identify the perpendicular turning points like we did in the latter system. Hence, we could only determine the g_z value as 2.4, which is the same as for CoO₂Se₂. For the other spin Hamiltonian parameters, we thus had to rely on FIRMS results to deliver them. According to FIRMS/HFEPR, D = –20.9 cm⁻¹ and E/D = 0.08 for CoO₂Se₂ (Table 2). Previous DC magnetometry/HFEPR⁷⁴ and current FIRMS studies (vide infra) on the tetrahedral CoE₄ complexes showed that the nature of E (either S or Se) has a little bearing on the zfs components of the two complexes (Table 2). Based on this observation, we assume that the rhombicity of the zfs in CoO₂S₂ is similarly small (∼ 0.1) as for CoO₂Se₂ (0.08). This assumption was confirmed by the observation of the complete powder pattern belonging to the intra-Kramers transition within the M_s = ±3/2 doublet by high-resolution EPR (Fig. S7,† for text vide infra), owing to the unusual setup of that instrument (combination of an X-band frequency with a superconducting magnet). In particular the resolution of the two perpendicular turning points indicates a rhombicity of the zfs tensor similar to that of CoO₂Se₂. Based on the above, the D value of CoO₂S₂ is very close to the corresponding D*, i.e., about 41.6/2 = ∼ 20.8 cm⁻¹, thus the two CoO₂E₂ complexes have remarkably similar D parameters (Table 2). In addition, the fact that the combination of an X-band frequency and relatively high magnetic field (high-resolution EPR studies, vide infra) at low temperature detects exclusively the intra-Kramers transition within the M_S = ±3/2 doublet means that the sign of D is negative.

CoE₄ complexes. The two CoE₄, E = S, Se, complexes were previously investigated by DC magnetometry, AC susceptometry and HFEPR.⁷⁴ The latter revealed for CoS₄ exclusively the branch of resonances belonging to the parallel turning point of the intra-Kramers (nominally: ΔM_s = ±3) transition between the M_s = ±3/2 levels, analogously to CoO₂S₂ described above. This allowed some of us to determine the g_z value, but not the other spin Hamiltonian parameters, which were delivered (quite accurately in this case, vide infra) by DC magnetometry. The CoSe₄ complex was in turn EPR-silent, which was attributed to the negligible rhombicity of its zfs tensor, in which case the ΔM_s = ± 3 transition is forbidden.⁷⁴

In the current work, we revisited the two CoE₄ complexes by employing FIRMS. The results are shown in Fig. 3 as color maps. The transmission spectrum (single beam) and simulation of the magnetic resonance absorption are shown in Fig. S6 in the ESI.† The CoS₄ and CoSe₄ complexes each show a zero-field transition at 65.0 ± 0.5 and 66.6 ± 0.5 cm⁻¹, respectively. Given the very small rhombicity of the zfs tensor, as established previously,⁷⁴ these values represent twice the parameter D, which is therefore −32.5 and −33.3 cm⁻¹ for the E = S and Se complexes, respectively. These values are in good agreement (within 8% and 11%, respectively) with the corresponding ones previously derived by DC magnetometry (−30.5 cm⁻¹ and −30.4 cm⁻¹, respectively).⁷⁴ The previous HFEPR results for CoS₄ are plotted in the same Fig. 3 (left panel) as circles. The other spin Hamiltonian parameters, such as E/D and the g-values used to simulate the turning point branches, were taken from the HFEPR investigation of the CoE₄ complexes.⁷⁴

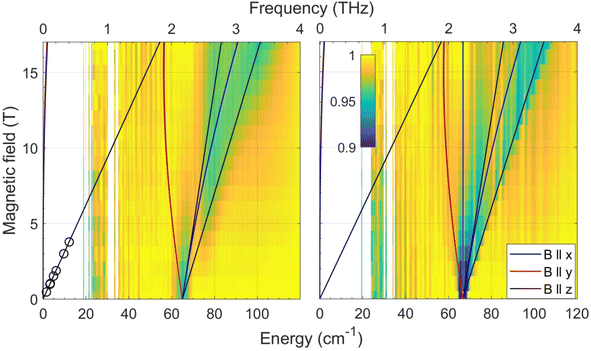Fig. 3 Joint FIRMS and HFEPR plots of magnetic resonances vs. transition energy (frequency) for the CoE₄ complexes: E = S (left) and E = Se (right.) The circles in the left panel represent the single turning point branch with B₀||z within the M_S = ±3/2 Kramers doublet observed by HFEPR in CoS₄. No corresponding turning point was detected for CoSe₄. The lines represent turning points in the powder spectra and were simulated using the spin Hamiltonian parameters in Table 2.

It should be noted that for both CoE₄ and CoO₂E₂ complexes, the small effect of the nature of the E donor atom (either S or Se) on the magnitude of D in these Co(II) systems is consistent with similar findings for other 3d-metal-based complexes, such as tetrahedral Fe(II) S = 2 FeE₄, E = S, Se,⁵⁵ and [Fe{(EPPh₂)₂N}₂], E = S,⁷⁵ Se,⁷⁸ as well as octahedral Ni(II) (S = 1) [Ni{(OPPh₂)(EPPh₂)N}₂(sol)₂], E = S, Se; sol = dmf, thf,⁷⁹ dmso.⁸⁰

High-resolution EPR spectroscopy at 9, 95, and 275 GHz

CoO₂S₂ complex. Fig. S7 in the ESI† shows the EPR spectrum at 9 GHz of a powder of the CoO₂S₂ complex at 5 K, with two relatively narrow lines at a magnetic field around 0.1 T, corresponding to effective g (in the following denoted as g′) values of about 6.5 and 4.2. The spectrum quickly broadens at temperatures above 10 K and the relative intensity of the lines around 0.1 T changes with temperature (Fig. S8†).

The spectrum of a single crystal of CoO₂S₂ offers higher resolution. The crystal, free to move in the EPR tube, was found to orient itself in a magnetic field of 1.5 T (as previously observed for the [Co{(SPPh₂)(SPⁱPr₂)N}₂] complex of the same sub-family).⁸¹Fig. 4 (top) shows the EPR spectrum at 9 GHz of such an oriented crystal of CoO₂S₂ at 5 K between 0.02 and 0.40 T. It reveals a narrow line around 0.1 T, which shows a structure that points to the overlap of two EPR transitions of comparable intensity. This structure is maintained upon temperature increase, while the relative intensity of the two transitions changes with temperature.

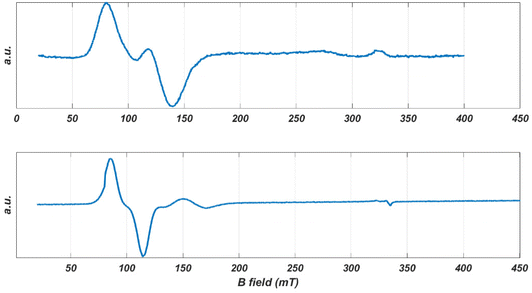Fig. 4 The EPR spectra of oriented single crystals of CoO₂S₂ (top) and CoO₂Se₂ (bottom) at 9 GHz and 5 K.

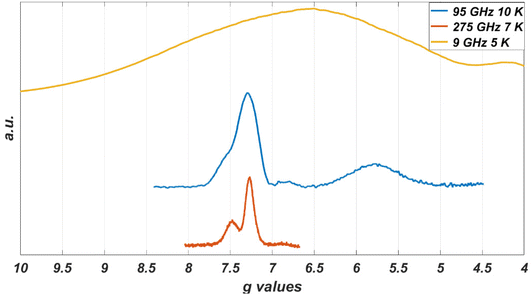
While the EPR spectrum at 9 GHz of the CoO₂S₂ powder did not resolve the two contributions to the low-field line, the spectra at higher microwave frequencies clearly do, owing to the enhanced g′ resolution. Fig. 5 represents the EPR spectra of the CoO₂S₂ powder at 9, 95, and 275 GHz on a common g′ axis. The line width at 9 GHz is determined by hyperfine interaction. This interaction is magnetic-field independent, and, at higher microwave frequencies and magnetic fields, transitions characterized by small differences in g′, hidden under the hyperfine-broadened line at low microwave frequency, become resolved.

Fig. 5 Low-field part of the EPR spectra of a powder sample of CoO₂S₂ at different microwave frequencies: 9 GHz (upper), 95 GHz (middle), and 275 GHz (lower). The spectrum at 9 GHz covers the magnetic-field range from 10 to 170 mT, the spectrum at 95 GHz from 0.8 to 1.5 T, and the spectrum at 275 GHz from 2.45 to 2.95 T.

CoO₂Se₂ complex. Fig. S9 in the ESI† shows the EPR spectrum at 9 GHz of a powder of the CoO₂Se₂ complex at 5 K, with two relatively narrow lines around 0.1 T corresponding to g′ values of about 7.1 and 4.9. As for the CoO₂S₂ analogue, the spectrum quickly broadens at temperatures above 10 K.

A single crystal of CoO₂Se₂ free to move in the EPR tube orients itself in a high magnetic field, as illustrated in Fig. S10 in the ESI.† The first scan from 0 to 1.5 T shows the spectrum for an arbitrary orientation of the crystal with respect to the magnetic field, the second one for the oriented crystal for which virtually only intensity in the low-field range is left. The latter spectrum is shown in Fig. 4 (bottom). It consists of a narrow line at 0.097 T and a second one of much lower intensity at 0.16 T.

The powder EPR spectra of the CoO₂S₂ and CoO₂Se₂ complexes reveal transitions corresponding to g′ values up to 7 and below 1. Such a combination of g′ values points to a negative sign of D, i.e., the M_s = ±3/2 doublet is lowest in energy, and a value of E/D = 0.10 ± 0.05. For CoO₂S₂, the transitions in the lower doublet show up at g′_z ∼ 6.5, g′_y ∼ 0.8 and g′_x ∼ 0.45, and the transitions in the upper doublet at g′_z ∼ 2 and g′ ∼ 4.2. For CoO₂Se₂, the transitions in the lower doublet show up at g′_z ∼ 7.1, g′_y ∼ 1 and g′_x ∼ 0.5, and the transitions in the upper doublet at g′_z ∼ 2 and g′ ∼ 4.9.

Based on the analysis of FIRMS data (vide supra), the value of D for both complexes was determined to be about −21 cm⁻¹ (Table 2). The interpretation of the 9 GHz EPR spectra of both CoO₂E₂ complexes is compatible with this value of D and a value of about 0.1 for E/D. A more quantitative analysis of the 9 GHz spectra is prohibited by the fact that they depend on too many spin Hamiltonian parameters. The large magnitude of D implies that inter-doublet transitions are not observable at the highest microwave frequency (275 GHz) and magnetic field (13 T) of our EPR experiments.

Subsequently, we consider the EPR data for the single crystals. Both the CoO₂S₂⁷¹ and the CoO₂Se₂⁷² complex crystallize in the P21/c space group, with four molecules in the unit cell. The inversion center connects the molecules two by two, which results in two magnetically inequivalent molecules in the unit cell.

After orientation in the magnetic field, the 9 GHz EPR spectrum of a single crystal of CoO₂Se₂ becomes easy to interpret. It shows a single narrow line at g′_z = 7.09, Fig. 4 (bottom). For this direction of the magnetic field with respect to the crystal, apparently parallel to the principal z axis of the g′ tensor, the signals of the two magnetically inequivalent molecules coincide, which means that the principal g′_z axes of the magnetically inequivalent molecules are parallel. In addition, the EPR spectrum contains a small feature at g′ = 3.95, the origin of which will be discussed below.

For the CoO₂S₂ complex, the single-crystal EPR spectrum of the oriented crystal consists of two lines that strongly overlap corresponding to g′ = 6.81 and g′ = 5.55, Fig. 4 (top). The relative intensity of these lines varies from crystal to crystal, which indicates that the two signals do not refer to the two magnetically inequivalent molecules in the unit cell. Most probably these signals refer to two distinct structures of the CoO₂S₂ complex with slightly different spin Hamiltonian parameters. In this case, the direction of the magnetic field with respect to the crystal will not be parallel to the principal g′_z axis of either of the two structures, and the g′ values of the observed lines will thus be a little smaller than the principal g′_z values.

Similarly, we interpret the small signal observed for the oriented CoO₂Se₂ crystal as to derive from a second conformation of this complex. The g′ value of 3.95 deviates significantly from the g′_z value of 7.09 corresponding to the large signal, Fig. 4 (bottom), which indicates that the direction of the magnetic field with respect to the oriented crystal, which is about parallel to the principal g′_z axis of the first structure, makes an angle of about 70° with the principal g′_z axis of the second structure.

In the EPR spectra at 9 GHz of the powders, the subtleties related to structural variation of the Co(II) coordination are hidden under the broad lines, but they do show up in the powder spectra of the CoO₂S₂ complex at 95 and 275 GHz (Fig. 5), where the low-field signal splits into two.

The X-ray diffraction study of the CoO₂Se₂ complex reveals the presence of distinct conformations of this complex. Structural disorder has been observed for one of the two (O, Se) chelates concerning the position of the O and the Se donor atoms (Fig. S1 in the ESI†). Interestingly, this is also the case for the analogous tetrahedral MO₂Se₂, M = Ni,⁷² Zn,⁸² complexes. Although such distinct conformations have not been detected by single-crystal X-ray diffraction for the CoO₂S₂ complex,⁷¹ we speculate that such distinct arrangements of the O and S/Se atoms are responsible for the ‘extra’ signals in the EPR spectra of the single crystals for both complexes. The EPR spectra are sensitive to the electronic structure, while the X-ray diffraction pattern reflects the geometric structure of the complexes. Apparently, the difference in the geometric structure of the two conformations is too small for the CoO₂S₂ complex to be discernible in the X-ray diffraction pattern. This conclusion is supported by the EPR spectra of the crystals. The directions of the principal g′_z axes of the distinct structures are found to (nearly) coincide for the CoO₂S₂ complex, while these directions differ significantly for the CoO₂Se₂ complex.

AC susceptometry: dynamic magnetic properties

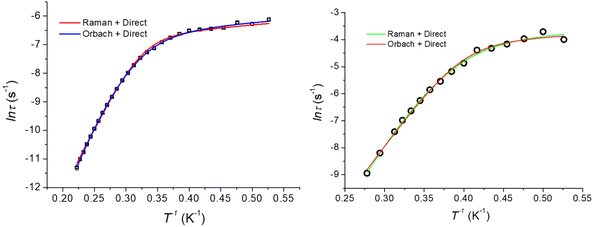
The dynamics of the magnetic moment of the two complexes CoO₂E₂, E = S, Se, were probed by AC susceptometry. With no static applied field, both CoO₂S₂ and CoO₂Se₂ did not display any out-of-phase susceptibility signal (Fig. S11 in the ESI†). This finding may be ascribed to the presence of a significant tunneling relaxation pathway, which may be triggered by the presence of dipolar magnetic interactions in the solid state, as observed for the structurally related CoE₄ complexes, E = S, Se.⁷⁴ An isothermal field scan of both complexes revealed the onset of slow relaxation upon the application of a static field, and in both cases 120 mT was chosen as the field inducing the slowest magnetization dynamics (Fig. S12†). The temperature dependence of χ_M′ and χ_M′′ is shown in Fig. S13† and reports, for both systems, a set of frequency and temperature dependent peaks in the χ_M′′, highlighting a slow relaxing magnetic moment.

The temperature dependence of the magnetic relaxation times τ, represented in Fig. 6, shows a nonlinear behavior: in the low temperature region the relaxation times showed a tiny dependence, while bigger variations appeared upon heating the systems. Fitting of these plots using a mixed relaxation model involving an Orbach/direct mechanism of relaxation¹² satisfactorily reproduced the experimental data, with an effective barrier to the reorientation of the magnetic moment (U_eff, Table 3), in line with what is expected on the basis of the static magnetic analysis (Table 1). A mixed Raman/direct relaxation mechanism yielded fits of similar quality, but for parameter values in an unphysical range,⁸³ and were thus discarded. The observed relaxation barriers suggest the presence of additional relaxation pathways lowering the magnetic reorientation barrier with respect to the one observed by FIRMS/HFEPR. When compared with the structurally related CoS₄ complex, featuring a barrier of about 54 cm⁻¹ with a D value of −30.5 cm⁻¹ and an E/D value of 0.0023,⁷⁴ the decrease in the barrier to the Orbach relaxation of CoO₂E₂, E = S, Se, correlates well with their less negative D and increased E/D values (Table 2). It should be noted that the relaxation of CoSe₄ has been shown to take place exclusively through a Raman mechanism, instead of an Orbach one.⁷⁴

Fig. 6 Temperature dependence of the magnetic relaxation times (Arrhenius plot) for CoO₂S₂ (left) and CoO₂Se₂ (right), along with the best fitting lines for the two mixed relaxation mechanisms described in the text.

Table 3 AC susceptometry data for CoO₂E₂, E = S, Se

	CoO2S2		CoO2Se2
τ 0 (s)	8(1) × 10^–10	—	3(1) × 10^–9	—
U eff (cm^−1)	30.5(5)	—	27(1)	—
C (s^−1 K^−n)	—	1.9(2) × 10^–3	—	5(1)
n	—	11.68(6)	—	12.9(4)
B (s^−1)	274(6)	251(3)	25(1)	23(1)
R ^2	0.9998	0.9993	0.9956	0.9969

---

Computational studies

The electronic structure of the crystal structure geometries of CoO₂S₂⁷¹ and CoO₂Se₂⁷² was calculated at the state-average complete active space self-consistent field/N-electron valence perturbation theory 2nd order (SA-CASSCF/NEVPT2) methodology. An active space of seven electrons in five 3d-orbitals, was used, and the orbitals were optimized for 10 quartet and 40 doublet roots. Furthermore, additional calculations were carried out where the orbitals were optimized for 7 quartets and 14 doublets. The spin Hamiltonian properties (zfs parameter D, g-factors) were computed using the effective Hamiltonian approach (HEFF)⁸⁴ and via the computation of the 2nd order contribution of the hyperfine coupling tensor (HFC) from spin–orbit coupling (SOC), namely SOC-2nd order. For the CoO₂Se₂ complex, two geometries (a, 88%) and (b, 12%) are experimentally found, see Fig. 1, where the structure (a) in the crystal is more stable than structure (b) by 46.7 kcal mol⁻¹ at NEVPT2. The geometries of the CoO₂E₂, E = S, Se, complexes were energetically optimized, as described in the Experimental section (vide infra). The lowest in energy structures are shown in Fig. 7. Full geometry optimization of the (a) and (b) structures significantly stabilized both of them and the two structures become almost degenerate, with (b) being lower in energy only by 0.24 kcal mol⁻¹ than (a) (Table S1 in the ESI†). Details about the energetics and the electronic structures of the 50 calculated structures are presented in the ESI.† The main CASSCF electronic configurations of all calculated states are given in Table S3,† the NEVPT2 and NEVPT2-LFT vertical transition energies from the ground state to the excited states are depicted in Fig. S15,† while the NEVPT2-LFT d-orbital splitting and the corresponding field matrix are listed in Table S4.† Finally, the geometries of the CoO₂E₂, E = S, Se, complexes were energetically optimized, as described in the Computational studies section (vide infra), to investigate the experimental observation of two geometries for CoO₂Se₂, and, in addition, to examine whether this can also happen in the case of CoO₂S₂, even though this has not – up to now – been observed experimentally. Moreover, it was checked how the geometry optimization affects the properties of the complexes, including the zfs parameters

Fig. 7 The lowest in energy isomers of the CoO₂E₂, E = S, Se complexes. Color coding: Co (light blue), O (red), S (yellow), Se (light brown), P (brown), N (blue), C (gray).

Comparing the geometries of the crystal structures with those of the optimized structures, it is found that the former are more distorted than the latter. Specifically, regarding the [Co(OENP₂)(O′E′N′P′₂)] core, in the lowest-energy optimized structures, the Co–O, Co–S and Co–Se bond distances are similar, i.e., Co–O: ∼1.96 Å, Co–S: 2.37 Å, and Co–Se: ∼2.43 Å. On the contrary, in the crystal structures, only the two Co–S distances are similar at ∼2.33 Å, while the Co–O and Co–Se bond distances are different, i.e., Co–O: 1.95–2.13 Å and Co–Se: 2.38–2.46 Å, see Table S1.† Regarding the phenyl groups, in the optimized structures, the planes of two phenyl groups are approximately parallel to each quasi-plane of the CoOENP₂ ring, while in the crystal structures this occurs only for one CoOENP₂ ring. Moreover, the PSOP and P′S′O′P′ dihedral angles are similar and about 40° in the optimized structures, while in the crystal geometries they are not equal (33° and 17°, respectively). In addition, the dihedral angle θ between the OCoS and S′CoO′ planes is 88.3°, while in the crystal structure this dihedral angle is 86.3°. Thus, the symmetry is distorted in the experimental crystal structures. The (a) and (b) structures of CoO₂Se₂ differ in the position of the CoOSe plane with respect to the CoO′Se′plane, see Fig. 7. The OCoEO′ is about −120° for CoO₂S₂ and CoO₂Se₂ (b structure), while it is about 120° for CoO₂Se₂ (a structure), see Table S1.† This distortion is responsible for the energy difference between structure (a) and (b), where (a) is more stable than structure (b) by 46.7 kcal mol⁻¹ at NEVPT2, while in the full geometry-optimized (a) and (b) structures, they become almost energetically degenerate, with (b) being lower in energy only by 0.24 kcal mol⁻¹ than (a) (Table S1 in the ESI†). Finally, it should be noted that concerning the CoO₂S₂ complex, geometry optimization of the (a) and (b) structures in which Se was replaced by S resulted in the same structure.

The electric dipole moment of the complexes in their crystal structure geometries is 3.74 Debye for CoO₂S₂, and for the (a) and (b) structures of CoO₂Se₂ 3.57 and 5.46 Debye, respectively (Table S2†). In the energy-optimized geometries, the dipole moments become almost half of the previous values, i.e., the value is 1.90 Debye for CoO₂S₂, and 1.95 Debye (a) and 2.38 Debye (b) for CoO₂Se₂, showing that the optimized molecular structures become less polar and more symmetrical than the corresponding crystal structures.^71,72

The two complexes have similar g-factors calculated in their crystal geometries and the energy-optimized ones (Table 4). However, regarding the zfs parameters, there are differences in the NEVPT2 values obtained for the crystal and the energy-optimized geometries for the CoO₂S₂ and CoO₂Se₂ (a) structures. Finally, comparing the NEVPT2 D values obtained via the HEFF and via the SOC-2nd approach, we observe that the effective Hamiltonian approach results in good agreement with the experimental values derived by FIRMS/HFEPR (Table 2) (vide infra), while the second methodology overestimates the D values by up to 5 cm⁻¹.

Table 4 NEVPT2 relative energies ΔE₁ (cm⁻¹), dihedral angle θ, zfs parameter D (cm⁻¹), E/D, and g-factors for different structures of the CoO₂E₂, E = S, Se, complexes. Our best calculated values are shown in bold

E	Geom.	ΔE1	θ	g x	g y	g z	g iso
S		0	88.31	2.19	2.24	2.56	2.33
		509	88.74	2.20	2.25	2.58	2.34
			86.28	2.22	2.25	2.46	2.31
Se (a)		84	95.21	2.19	2.24	2.49	2.31
		107	88.05	2.19	2.26	2.59	2.35
			85.71	2.21	2.26	2.26	2.32
Se (b)		0	90.01	2.20	2.24	2.51	2.32
			93.30	2.18	2.29	2.53	2.33

---

E	Geom.	D SOC ^b	D SSC ^c	D	E/DSOC ^b	E/D^c
a θ: (OCoS)/(S′CoO′). b SOC-HEFF [SOC-2nd order]. c HEFF. d NEVPT2/ZORA-def2-TZVPCo,Se,S,OZORA-def2-SVPP,N,C,H//B3LYP/6-31G(d,p). e NEVPT2/ZORA-def2-TZVPCo,Se,S,OZORA-def2-SVPP,N,C,H//B3LYP/def2-SVP. f NEVPT2/ZORA-def2-TZVPCo,Se,S,OZORA-def2-SVPP,N,C,H//Experimental crystal geometries, E = S,^71 Se.^72. g NEVPT2/ZORA-def2-TZVPCo,Se,S,OZORA-def2-SVPP,N,C,H//Experimental crystal geometries; roots = 7 (quartets) & 14 (doublets). h NEVPT2/ZORA-def2-TZVPCo,S(-f)OZORA-def2-SVPP,N,C,H//Experimental crystal geometries.
S		−29.7 [−34.2]	−0.18	−29.85	0.07 [0.07]	0.08
		−30.6 [−35.4]	−0.20	−30.78	0.07 [0.07]	0.07
		−19.4 [−21.9]; −19.9^g; −19.1^h	−0.21	−19.57	0.08 [0.08]	0.08
Se (a)		−23.8 [−26.9]	−0.30	−24.09	0.09 [0.09]	0.09
		−31.6 [−36.7]	−0.25	−31.81	0.10 [0.09]	0.10
		−21.7 [−24.6]	−0.28	−22.00	0.10 [0.11]	0.10
Se (b)		−25.0 [−28.6]	−0.20	−25.20	0.07 [0.07]	0.08
		−25.8 [−29.8]	−0.33	−26.10	0.22 [0.22]	0.22

---

For CoO₂S₂, the NEVPT2 D parameter (including only SOC) was computed using the effective Hamiltonian approach, and for the crystal geometry, values between −19.1 and −19.9 cm⁻¹ were obtained depending on the number of the calculated roots (Table 4). These values are in good agreement with those derived by FIRMS (Table 2), as well as with the value of −19.1 cm⁻¹ reported recently by Sarkar et al.⁸⁵ For the geometry-optimized structure of CoO₂S₂, the D value (including only SOC) is increased to −29.7 cm⁻¹, most likely due to the significant structural differences compared to the crystal structure (vide supra).

For CoO₂Se₂, as mentioned above, the (a) geometry, which is the dominant one found in the crystal, is lower in energy by 46.7 kcal mol⁻¹ than the (b) geometry at NEVPT2 (Table S2†). However, full energy optimization results in energetically degenerate (a) and (b) structures. Regarding the (a) structure, the dihedral angle θ between the two planes of OCoSe and Se′CoO′ deviates by about 5° from the orthogonal angle in both calculated and experimental crystal structures. The NEVPT2 calculation yields a D value, including SOC and SSC, of −22.0 cm⁻¹ for the crystal geometry (again in good agreement with the FIRMS/HFEPR-derived value), and −24.1 cm⁻¹ for the energy-optimized structure. Regarding the (b) structure, the NEVPT2 calculations yield values of D for the crystal geometry (−26.1 cm⁻¹) and for the energy-optimized structure (−25.2 cm⁻¹) (Table 4). Our best calculated D values in the crystal structure geometry of CoO₂Se₂ are −22.0 (a) and −26.1 cm⁻¹ (b) (Table 4), and therefore their average value, considering their corresponding % population, is −22.4 cm⁻¹, in good agreement with the experimental FIRMS/HFEPR-derived value of −20.9 cm⁻¹. Thus, our calculations in the crystal structure geometry confirm the fact that the (a) structure of CoO₂Se₂ is the favored one.⁷² Moreover, for CoO₂Se₂, our calculations support the experimental finding by X-ray crystallography⁷² - and herein confirmed by EPR spectroscopy (vide supra) - of two different conformations.

It should also be stressed that for both CoO₂E₂, E = S, Se, the spin–spin coupling (SSC) interactions contribute to the magnitude of D by, approximately, only −0.2 to −0.3 cm⁻¹, which is clearly a minor contribution as compared to that of the corresponding SOC interactions (Table 4).

Regarding the NEVPT2-LFT d-orbital splitting diagram of the calculated complexes, there are differences between the experimental crystal structures and the minimum calculated ones, see Fig. 8, which is expected given that the minimum calculated structures are more symmetrical than the crystallographic ones. Moreover, there are differences between the (a) and (b) structures of CoO₂Se₂: the lowest doubly occupied orbitals are the d_z² (m_{[small script l]} = 0) in (a), while in (b) are the d_xy and d_x²−y² (m_{[small script l]} = ± 2). Note also that the CoO₂S₂ and the (b) structure of CoO₂Se₂, which have similar relative position of the rings, i.e., similar OCoEE′, OCoEO′, O′CoE′E, and O′CoE′O dihedral angles, have both the d_xy and d_x²−y² (m_{[small script l]} = ± 2) as the lowest occupied orbitals. Finally, the splitting between the doubly occupied d orbitals and single occupied d orbitals, is 1625, 1832 and 1704 cm⁻¹ for CoO₂S₂, (a) structure of CoO₂Se₂ and (b) structure of CoO₂Se₂, respectively, for the energy-minimized structures; while, in the geometry of the crystal structures the splitting is significantly larger up to 400 cm⁻¹, and becomes 2218, 2119 and 2065 cm⁻¹, respectively.

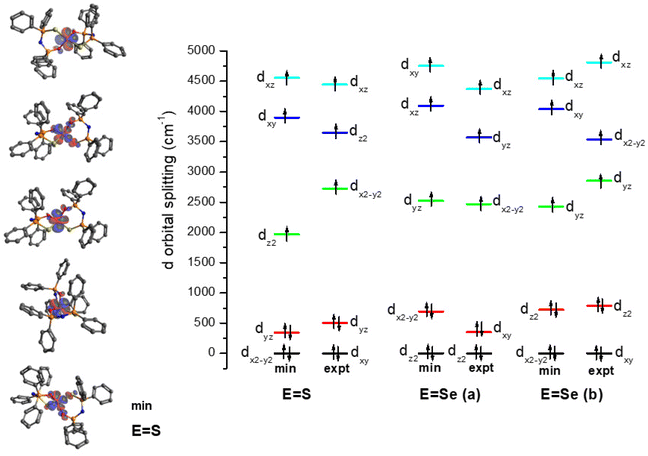Fig. 8 NEVPT2-LFT d-orbital splitting diagram of the calculated structures of CoO₂E₂, E = S, Se. The structures (a) and (b) correspond to 88 and 12% population, respectively, in the crystal structure of CoO₂Se₂.⁷²

Finally, the contribution of the calculated thirty-nine excited states to D and E is presented in Table S5 of ESI.† The three lowest excited states are quartet states, they are lying up to 5 × 10³ cm⁻¹ (0.6 eV) above the ground state and have the highest contribution to the D and E parameters, see Table 5 and cf. Table S5.†

Table 5 NEVPT2 vertical transition energies T_e (cm⁻¹) and state contribution to the zfs D and E parameters (cm⁻¹) for the lowest three calculated states of the CoO₂E₂, E = S, Se complexes. All states are quartets

	T e	T e ^a	D	E	T e	T e ^a	D	E
	NEVPT2^b				NEVPT2^c
a NEVPT2-LFT. b NEVPT2/ZORA-def2-TZVPCo,Se,S,OZORA-def2-SVPP,N,C, H//B3LYP/6-31G(d,p). c NEVPT2/ZORA-def2-TZVPCo,Se,S,OZORA-def2-SVPP,N,C, H//Experimental crystal geometries.^71,72
E = S
GS	0	0	0.00	0.00	0	0	0.00	0.00
1	2218	1815	26.30	25.84	2863	2307	20.94	20.20
2	4726	3686	−23.86	−0.09	4388	3412	−19.85	−0.88
3	5218	4065	9.77	−9.28	4993	3904	6.62	−8.59
E = Se (a)
GS	0	0	0.00	0.00	0	0	0.00	0.00
1	2750	2154	22.20	21.51	2775	2170	21.87	20.96
2	4380	3444	−12.34	−2.63	4283	3291	−23.51	−0.13
3	5283	4073	−1.01	−5.78	4847	3767	9.36	−8.79
E = Se (b)
GS	0	0	0.000	0.00	0	0	0.000	0.00
1	2444	1952	23.61	23.13	2436	1887	22.92	21.02
2	4775	3694	−19.53	−0.86	4251	3202	−24.04	−0.15
3	4976	3855	6.52	−8.67	4678	3500	8.02	−5.09

---

To sum up, the computed D and E/D values of both Co₂E₂ complexes are in good agreement with the ones derived by FIRMS/HFEPR. Additionally, for CoO₂Se₂, our calculations support the experimental finding by X-ray crystallography⁷² - and herein confirmed by EPR spectroscopy (vide supra) - of two different conformations.⁷² Finally, the energetically geometry optimization of the complexes results in more symmetrical structures, with similar g-factors and E/D values.

Conclusions

In this work, the tetrahedral CoO₂E₂, E = S, Se, complexes were studied by experimental (DC magnetometry and AC susceptometry, as well as FIRMS, high-resolution multifrequency EPR, and HFEPR spectroscopy) and computational methods. In addition, the CoE₄, E = S, Se, complexes were studied by FIRMS. One of the main aims of this work was to reliably determine the D and E/D values of all the above S = 3/2 Co(II) tetrahedral complexes. The experimentally determined zfs values, along with the calculated ones better matching the former, are listed in Table 6, and lead to the following conclusions: (i) The combination of FIRMS and HFEPR data on CoO₂Se₂, exhibiting a non-negligible rhombicity (E/D = 0.08), allowed to reliably determine both zfs components, (ii) A rhombicity E/D ∼ 0.1 is compatible with the high-resolution multifrequency X-band spectra of both CoO₂E₂ complexes, (iii) Our work has revealed certain limitations of DC magnetometry in providing accurate zfs data, (iv) The computed zfs values of CoO₂E₂ derived by the NEVPT2 method based on the corresponding crystal structures are in very good agreement with the FIRMS/HFEPR-derived ones. The magnitude of D of both complexes is shaped almost exclusively by SOC interactions, whereas the SSC contribution is negligible.

Table 6 The values of D (cm⁻¹) and E/D for complexes CoO₂E₂ and CoE₄, E = S, Se, determined by experimental and computational methods

Complex	D HFEPR/FIRMS	E/DHFEPR/FIRMS	E/DHREPR	D magn	E/Dmagn	D calc	E/Dcalc
a Calculated by taking into account the 88 and 12% populations of the (a) and (b) structure of CoO2Se2,^72 as described in the text.
CoO2S2	∼ −20.8		∼ 0.1	–23.9	0.04	−19.6	0.08
						−19.1^85	0.08^85
CoO2Se2	–20.9	0.08	∼ 0.1	–20.4	0.0004	−22.4^a	0.11^a
CoS4	–32.5			–30.5^74	0.023^74	−28.8^85	0.00^85
CoSe4	–33.3			–30.4^74	0.0016^74	−25.7^85	0.02^85

---

Moreover, high-resolution multifrequency EPR on powder and single crystal samples of CoO₂E₂ revealed the existence of multiple conformations, in accordance with the structural disorder observed previously in the crystal structure of CoO₂Se₂. Analysis of the EPR data indicate that the structural difference between the conformations is larger for the CoO₂Se₂ than for the CoO₂S₂ complex, confirming the crystallographic observations. The existence of two conformations of CoO₂Se₂ is also supported by advanced quantum chemical calculations.

The second aim of this work was to probe the dynamic magnetic properties of the CoO₂E₂ complexes, following the previous analogous investigation of the CoE₄ complexes. Our AC susceptometry studies reveal a dependence of the barrier to the Orbach relaxation of both CoO₂E₂, as well as of the previously studied CoS₄, on the corresponding D and E/D values.

In more general terms, this work shows that the reliable determination of the zfs D and E components is not an easy task, and points to the necessity of combining as many different experimental methods as possible. In parallel, this work highlights the capacity of a spectroscopic method, namely high-resolution multifrequency EPR spectroscopy, to probe the existence of multiple conformations in a paramagnetic metal complex. In that respect, such high-resolution spectroscopic techniques can be invaluable companions to X-ray crystallography when subtle structural features are investigated.

Experimental

Synthesis of complexes

Complexes CoO₂E₂, E = S,⁷¹ Se⁷² and CoE₄, E = S, Se,^74,86 were synthesized following the procedures reported in the literature, in which the corresponding X-ray crystal structures are also reported.

DC magnetometry

Samples employed for DC and AC susceptometry analyses consisted of pressed microcrystalline powders of CoO₂E₂, E = S, Se, wrapped in Teflon (TM) tape. The DC magnetic characterization was performed on Quantum Design MPMS (Magnetic Properties Measurement System) equipment provided with a 5 T magnet. The magnetization (M) dependence on the absolute temperature was investigated between 300 and 35 K using a magnetic field (B) of 1 T, and between 35 and 2 K with a field of 0.1 T to prevent magnetic saturation. Magnetic susceptibility per mole (χ_M) was then evaluated as χ_M = M_M/B.

FIRMS

Far infrared transmission measurements were performed at the National High Magnetic Field Laboratory using a Bruker Vertex 80v FT-IR spectrometer coupled with a 17 T vertical-bore superconducting magnet in a Voigt configuration (light propagation perpendicular to the external magnetic field). The experimental setup employs a mercury arc lamp as a broad-band terahertz radiation source. The radiation transmitted through the sample was detected by a composite silicon bolometer (Infrared Laboratories) mounted at the end of the quasioptical transmission line. Both the sample and bolometer were cooled by a low-pressure helium gas to the temperature of about 5 K. The transmission spectra of the microcrystalline powder sample (∼2 mg) bonded by n-eicosane were measured in the spectral region between 14 and 730 cm⁻¹ (0.42–22 THz) with an instrumental resolution of 0.3 cm⁻¹ (9 GHz). To discern the magnetic absorptions, the transmission spectrum measured at each magnetic field was divided by the reference spectrum, which is the mean of spectra at all magnetic fields, computed after removing the outlier points at each frequency. Such normalized transmittance spectra indicate the small-amplitude changes in the intensity induced by the magnetic field and exclude a strong nonmagnetic contribution due to vibrational absorptions and an instrumental function. All data analysis routine was implemented by an in-house written MATLAB code based on the EPR simulation software package EasySpin.⁸⁷

HFEPR spectroscopy

HFEPR spectra were recorded on polycrystalline samples (20–25 mg), using a homodyne spectrometer at the EMR facility associated with a 15/17-T superconducting magnet and a frequency range from 52 to 426 GHz.⁸⁸

Detection was provided with an InSb hot electron bolometer (QMC Ltd, Cardiff, UK). The magnetic field was modulated at 50 kHz for detection purposes. A Stanford Research Systems SR830 lock-in amplifier converted the modulated signal to dc voltage. The single-frequency spectra as well as their dependencies on frequency were simulated with the SPIN software from A. Ozarowski.

High-resolution EPR spectroscopy at 9, 95, and 275 GHz

These EPR experiments were performed at Leiden University. For the measurements at 9 GHz (X-band) and 95 GHz (W-band) a Bruker Elexsys E680 spectrometer was used. The X-band spectra were obtained using 100 kHz field modulation, with an amplitude of 0.5 to 1.5 mT, depending on the line width. The W-band spectra were obtained at a modulation frequency of 90 kHz, with an amplitude of 1 mT.

The X-band spectra of polycrystalline powders were recorded with the sample in the superconducting magnet, belonging to the W-band part of the spectrometer, in combination with the X-band bridge for microwave generation and detection. In this way, X-band spectra have been acquired up to fields of 3 T. Use was made of the dielectric resonator (Flexline, frequency about 9.7 GHz). The probe-head support was modified to position the resonator active volume in the center of the magnet homogeneity zone and to fit into the cryostat of the W-band probe-head.

Temperature calibration was performed as follows: a Lake Shore Carbon-Glass™ sensor (CGR-1 series) was calibrated in a commercial Quantum Design physical properties measurement system (PPMS) and subsequently placed at the sample position in the cryostat. The Oxford temperature unit was then calibrated against this sensor.

The 275 GHz spectrum of polycrystalline powder was measured on a homebuilt spectrometer, using 1.2 kHz field modulation of about 0.2 mT amplitude. In order to avoid self-orientation of the micro-crystals in the high magnetic field (up to 12 T), the powder was pressed into the sample tube using a tiny amount of cotton.

AC susceptometry

Alternating current magnetic susceptibility analyses were performed with a PPMS (Physical Properties Measurement System) platform, also from Quantum Design, with oscillating field frequencies ranging from 10 to 10⁴ Hz, and using static magnetic fields of zero and 0.1 T. The resulting magnetic data were corrected for the diamagnetic contributions of the ligands calculated from Pascal constants,⁸⁹ together with those measured for the sample container and the wrapping Teflon tape.

The isothermal frequency dependence of the out-of-phase magnetic susceptibility (χ′′) data were analyzed within the extended Debye model,^90,91 in which a maximum in the out-of-phase component χ_M′′ of the complex susceptibility is observed when the relaxation time τ equals (2πν)⁻¹:

χ_M′′ (ω) = (χ_T − χ_S)[(ωτ)^1−αcos (απ/2)]/[1 + 2(ωτ)^1−αsin (απ/2) + (ωτ)^2−2α

where ω = 2πν, χ_T and χ_S are the isothermal and adiabatic susceptibilities, i.e., the susceptibilities observed in the two limiting cases ν → 0 and ν → ∞, respectively, and α is a parameter, which accounts for a distribution of relaxation times.

The temperature dependence of the magnetic relaxation times τ has been fitted using the following equation:

where the terms represent an Orbach, Raman and direct relaxation mechanism, respectively. In order to reduce overparameterization, Orbach and Raman terms have been used alternatively.

Computational studies

The crystal structure of the CoO₂E₂, E = S,⁷¹ Se,⁷² complexes was calculated using the CASSCF/NEVPT2 methodologies as implemented in ORCA 4.2.1 suit of codes.⁹² Additionally, the complexes were optimized energetically optimized using the B3LYP^93,94 functional, in conjunction with the 6-31G(d,p)⁹⁵ and def2-SVP⁹⁶ basis sets. Additionally, for these optimized structures single point calculations were carried out at the CASSCF/NEVPT2 level of theory. The scalar relativistic Hamiltonian was considered using the ZORA (zeroth-order regular approximation) method.⁹⁷ The ZORA contracted versions of basis sets ZORA-def2-TZVP were used for Co, Se, S, O and ZORA-def2-SVP(-f) for P, N, C and H.⁹⁶ For the SA-CASSCF (state-average complete active space self-consistent field) calculations, an active space of seven electrons in five 3d-orbitals, i.e., CAS(7,5) was used; the orbitals were optimized for 10 quartet and 40 doublet roots. Additional calculations were also carried out where the orbitals were optimized for 7 quartets and 14 doublets. Furthermore, the NEVPT2 (N-electron valence perturbation theory 2nd order) methodology was used which incorporates the dynamic correlation additionally to the static of the CASSCF methodology. The SOC was calculated using the spin–orbit mean field SOMF(1×) method,⁹⁸ while the spin-state mixing was obtained by employing the quasi-degenerate perturbation theory (QDPT) method.⁹⁹ The spin Hamiltonian properties (zfs parameter D, g-factors) were computed using the effective Hamiltonian approach (HEFF).⁸⁴ Finally, the contribution of SSC and SOC to the magnitude of D was calculated.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to the Special Account for Research Grants of the National and Kapodistrian University of Athens (P. K.), FAPERJ through grants E-26/202.912/2019, SEI-260003/001167/2020 and E-26/010.000978/2019 (G. P.), and The Netherlands Organization for Scientific Research (NWO) (E. J. J. G) for financial support. Part of this work was performed at the National High Magnetic Field Laboratory, which is supported by National Science Foundation Cooperative Agreement No. DMR-1644779 and the State of Florida. E. F. has been awarded a State Scholarship Foundation (IKY) fellowship, by the act “Support for Postdoctoral Researchers”, from the operational program “Human Power Development, Education and Lifelong Learning” (6, 8, 9 priority axes), co-funded by the European Social Fund and the Greek State. K. K.-L. acknowledges the National Science Centre NCN, Poland (ETIUDA 6, no. 2018/28/T/ST5/00120) for financial support during her internship at NHMFL. The Fulbright Foundation in Greece and the NHMFL via its Visiting Scientist Program supported a scientific extended visit of P. K. to the latter. Dr A. Ozarowski (NHMFL) is acknowledged for his EPR fit and simulation software SPIN. We would like to thank the Reviewers of our manuscript for their very constructive comments.

References

1. A. Brueckner, Chem. Soc. Rev., 2010, 39, 4673–4684.
2. S. Van Doorslaer and D. M. Murphy, EPR Spectroscopy: Applications in Chemistry and Biology, ed. M. Drescher and G. Jeschke, 2012, vol. 321, pp. 1–39.
3. J. Telser, J. Krzystek and A. Ozarowski, J. Biol. Inorg. Chem., 2014, 19, 297–318.
4. K. R. Dunbar, Inorg. Chem., 2012, 51, 12055–12058.
5. J. Ferrando-Soria, J. Vallejo, M. Castellano, J. Martinez-Lillo, E. Pardo, J. Cano, I. Castro, F. Lloret, R. Ruiz-Garcia and M. Julve, Coord. Chem. Rev., 2017, 339, 17–103.
6. R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141–143.
7. R. Bagai and G. Christou, Chem. Soc. Rev., 2009, 38, 1011–1026.
8. C. J. Milios and R. E. P. Winpenny, Molecular Nanomagnets and Related Phenomena, ed. S. Gao, 2015, vol. 164, pp. 1–109.
9. F. Neese and D. A. Pantazis, Faraday Discuss., 2010, 148, 229–238.
10. S. Gomez-Coca, D. Aravena, R. Morales and E. Ruiz, Coord. Chem. Rev., 2015, 289, 379–392.
11. E. Ruiz, J. Cirera, J. Cano, S. Alvarez, C. Loose and J. Kortus, Chem. Commun., 2008, 52–54.
12. J. M. Frost, K. L. M. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470–2491.
13. M. Feng and M. L. Tong, Chem. – Eur. J., 2018, 24, 7574–7594.
14. Y. S. Meng, S. D. Jiang, B. W. Wang and S. Gao, Acc. Chem. Res., 2016, 49, 2381–2389.
15. A. Zabala-Lekuona, J. M. Seco and E. Colacio, Coord. Chem. Rev., 2021, 441, 213984.
16. D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148.
17. B. M. Day, F. S. Guo and R. A. Layfield, Acc. Chem. Res., 2018, 51, 1880–1889.
18. Z. H. Zhu, M. Guo, X. L. Li and J. K. Tang, Coord. Chem. Rev., 2019, 378, 350–364.
19. K. L. M. Harriman, D. Errulat and M. Murugesu, Trends Chem., 2019, 1, 425–439.
20. C. A. P. Goodwin, F. Ortu and D. Reta, Int. J. Quantum Chem., 2020, 120, e26248.
21. T. G. Ashebr, H. Li, X. Ying, X. L. Li, C. Zhao, S. T. Liu and J. K. Tang, ACS Mater. Lett., 2022, 4, 307–319.
22. K. R. Meihaus and J. R. Long, Dalton Trans., 2015, 44, 2517–2528.
23. L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179–186.
24. P. C. E. Stamp and A. Gaita-Arino, J. Mater. Chem., 2009, 19, 1718–1730.
25. E. Coronado, Nat. Rev. Mater., 2020, 5, 87–104.
26. C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442.
27. F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamaki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445–11449.
28. K. R. McClain, C. A. Gould, K. Chakarawet, S. J. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, Chem. Sci., 2018, 9, 8492–8503.
29. F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamaki and R. A. Layfield, Science, 2018, 362, 1400–1403.
30. C. A. Gould, K. R. McClain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E. S. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Science, 2022, 375, 198–202.
31. A. Sarkar, S. Dey and G. Rajaraman, Chem. – Eur. J., 2020, 26, 14036–14058.
32. M. Feng, Z. Y. Ruan, Y. C. Chen and M. L. Tong, Chem. Commun., 2020, 56, 13702–13718.
33. P. S. Perlepe, D. Maniaki, E. Pilichos, E. Katsoulakou and S. P. Perlepes, Inorganics, 2020, 8, 39.
34. R. Boča and C. Rajnak, Coord. Chem. Rev., 2021, 430, 213657.
35. C. Rajnak and R. Boča, Coord. Chem. Rev., 2021, 436, 213808.
36. J. P. Sutter, V. Bereau, V. Jubault, K. Bretosh, C. Pichon and C. Duhayon, Chem. Soc. Rev., 2022, 51, 3280–3313.
37. A. K. Bar, C. Pichon and J. P. Sutter, Coord. Chem. Rev., 2016, 308, 346–380.
38. M. Atanasov, D. Aravena, E. Suturina, E. Bill, D. Maganas and F. Neese, Coord. Chem. Rev., 2015, 279, 177–214.
39. G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135–2147.
40. R. Boča, Coord. Chem. Rev., 2004, 248, 757–815.
41. J. Krzystek and J. Telser, Dalton Trans., 2016, 45, 16751–16763.
42. J. Telser, A. Ozarowski and J. Krzystek, Specialist Periodical Reviews of the Royal Chemical Society: Electron Paramagnetic Resonance, ed. B. C. Gilbert, D. M. Murphy and V. Chechik, 2012, 23, 209–263.
43. J. Krzystek, A. Ozarowski and J. Telser, Coord. Chem. Rev., 2006, 250, 2308–2324.
44. B. Cahier, M. Perfetti, G. Zakhia, D. Naoufal, F. El-Khatib, R. Guillot, E. Riviere, R. Sessoli, A. L. Barra, N. Guihery and T. Mallah, Chem. – Eur. J., 2017, 23, 3648–3657.
45. J. van Slageren, S. Vongtragool, B. Gorshunov, A. A. Mukhin, N. Karl, J. Krzystek, J. Telser, A. Muller, C. Sangregorio, D. Gatteschi and M. Dressel, Phys. Chem. Chem. Phys., 2003, 5, 3837–3843.
46. P. M. Champion and A. J. Sievers, J. Chem. Phys., 1977, 66, 1819–1825.
47. S. D. Jiang, D. Maganas, N. Levesanos, E. Ferentinos, S. Haas, K. Thirunavukkuarasu, J. Krzystek, M. Dressel, L. Bogani, F. Neese and P. Kyritsis, J. Am. Chem. Soc., 2015, 137, 12923–12928.
48. M. A. Dunstan, R. A. Mole and C. Boskovic, Eur. J. Inorg. Chem., 2019, 1090–1105.
49. S. E. Stavretis, Y. Q. Cheng, L. L. Daemen, C. M. Brown, D. H. Moseley, E. Bill, M. Atanasov, A. J. Ramirez-Cuesta, F. Neese and Z. L. Xue, Eur. J. Inorg. Chem., 2019, 1119–1127.
50. L. Chen, H. H. Cui, S. E. Stavretis, S. C. Hunter, Y. Q. Zhang, X. T. Chen, Y. C. Sun, Z. X. Wang, Y. Song, A. A. Podlesnyak, Z. W. Ouyang and Z. L. Xue, Inorg. Chem., 2016, 55, 12603–12617.
51. E. I. Solomon, T. C. Brunold, M. I. Davis, J. N. Kemsley, S. K. Lee, N. Lehnert, F. Neese, A. J. Skulan, Y. S. Yang and J. Zhou, Chem. Rev., 2000, 100, 235–349.
52. S. Ostrovsky, Z. Tomkowicz, S. Foro, J. Reedijk and W. Haase, Polyhedron, 2020, 187, 114630.
53. J. Krzystek, S. Zvyagin, A. Ozarowski, A. T. Fiedler, T. C. Brunold and J. Telser, J. Am. Chem. Soc., 2004, 126, 2148–2155.
54. B. M. Hakey, D. C. Leary, J. Xiong, C. F. Harris, J. M. Darmon, J. L. Petersen, J. F. Berry, Y. S. Guo and C. Milsmann, Inorg. Chem., 2021, 60, 18575–18588.
55. S. A. Stoian, M. Moshari, E. Ferentinos, A. Grigoropoulos, J. Krzystek, J. Telser and P. Kyritsis, Inorg. Chem., 2021, 60, 10990–11005.
56. M. E. Pascualini, N. V. Di Russo, A. E. Thuijs, A. Ozarowski, S. A. Stoian, K. A. Abboud, G. Christou and A. S. Veige, Chem. Sci., 2015, 6, 608–612.
57. V. V. Vrajmasu, E. L. Bominaar, J. Meyer and E. Münck, Inorg. Chem., 2002, 41, 6358–6371.
58. P. Kumar, D. J. SantaLucia, K. Kaniewska-Laskowska, S. V. Lindeman, A. Ozarowski, J. Krzystek, M. Ozerov, J. Telser, J. F. Berry and A. T. Fiedler, Inorg. Chem., 2020, 59, 16178–16193.
59. A. A. Pavlov, D. Y. Aleshin, S. A. Savkina, A. S. Belov, N. N. Efimov, J. Nehrkorn, M. Ozerov, Y. Z. Voloshin, Y. V. Nelyubina and V. V. Novikov, ChemPhysChem., 2019, 20, 1001–1005.
60. A. N. Bone, C. N. Widener, D. H. Moseley, Z. M. Liu, Z. G. Lu, Y. Q. Cheng, L. L. Daemen, M. Ozerov, J. Telser, K. Thirunavukkuarasu, D. Smirnov, S. M. Greer, S. Hill, J. Krzystek, K. Holldack, A. Aliabadi, A. Schnegg, K. R. Dunbar and Z. L. Xue, Chem. – Eur. J., 2021, 27, 11110–11125.
61. J. Vallejo, M. Viciano-Chumillas, F. Lloret, M. Julve, I. Castro, J. Krzystek, M. Ozerov, D. Armentano, G. De Munno and J. Cano, Inorg. Chem., 2019, 58, 15726–15740.
62. E. Y. Misochko, A. V. Akimov, D. V. Korchagin, J. Nehrkorn, M. Ozerov, A. V. Palii, J. M. Clemente-Juan and S. M. Aldoshin, Inorg. Chem., 2019, 58, 16434–16444.
63. A. Landart-Gereka, M. M. Quesada-Moreno, I. F. Díaz-Ortega, H. Nojiri, M. Ozerov, J. Krzystek, M. A. Palacios and E. Colacio, Inorg. Chem. Front., 2022, 9, 2810–2831.
64. D. H. Moseley, S. E. Stavretis, K. Thirunavukkuarasu, M. Ozerov, Y. Q. Cheng, L. L. Daemen, J. Ludwig, Z. G. Lu, D. Smirnov, C. M. Brown, A. Pandey, A. J. Ramirez-Cuesta, A. C. Lamb, M. Atanasov, E. Bill, F. Neese and Z. L. Xue, Nat. Commun., 2018, 9, 2572.
65. S. Tripathi, A. Dey, M. Shanmugam, R. S. Narayanan and V. Chandrasekhar, Organometallic Magnets, ed. V. Chandrasekhar and F. Pointillart, 2019, vol. 64, pp. 35–75.
66. (a) J. M. Zadrozny and J. R. Long, J. Am. Chem. Soc., 2011, 133, 20732–20734; (b) E. A. Suturina, J. Nehrkorn, J. M. Zadrozny, J. Liu, M. Atanasov, T. Weyhermuller, D. Maganas, S. Hill, A. Schnegg, E. Bill, J. R. Long and F. Neese, Inorg. Chem., 2017, 56, 3102–3118.
67. J. M. Zadrozny, J. Telser and J. R. Long, Polyhedron, 2013, 64, 209–217.
68. Y. Rechkemmer, F. D. Breitgoff, M. van der Meer, M. Atanasov, M. Hakl, M. Orlita, P. Neugebauer, F. Neese, B. Sarkar and J. van Slageren, Nat. Commun., 2016, 7, 10467.
69. X. N. Yao, J. Z. Du, Y. Q. Zhang, X. B. Leng, M. W. Yang, S. D. Jiang, Z. X. Wang, Z. W. Ouyang, L. Deng, B. W. Wang and S. Gao, J. Am. Chem. Soc., 2017, 139, 373–380.
70. P. C. Bunting, M. Atanasov, E. Damgaard-Moller, M. Perfetti, I. Crassee, M. Orlita, J. Overgaard, J. van Slageren, F. Neese and J. R. Long, Science, 2018, 362, eaat7319.
71. M. C. Aragoni, M. Arca, M. B. Carrea, A. Garau, F. A. Devillanova, F. Isaia, V. Lippolis, G. L. Abbati, F. Demartin, C. Silvestru, S. Demeshko and F. Meyer, Eur. J. Inorg. Chem., 2007, 4607–4614.
72. E. Ferentinos, D. Maganas, C. P. Raptopoulou, A. Terzis, V. Psycharis, N. Robertson and P. Kyritsis, Dalton Trans., 2011, 40, 169–180.
73. C. Silvestru and J. E. Drake, Coord. Chem. Rev., 2001, 223, 117–216.
74. S. Sottini, G. Poneti, S. Ciattini, N. Levesanos, E. Ferentinos, J. Krzystek, L. Sorace and P. Kyritsis, Inorg. Chem., 2016, 55, 9537–9548.
75. G. Mathies, S. D. Chatziefthimiou, D. Maganas, Y. Sanakis, S. Sottini, P. Kyritsis and E. J. J. Groenen, J. Magn. Reson., 2012, 224, 94–100.
76. R. L. Carlin, Magnetochemistry, Springer, Berlin, Heidelberg, 1986.
77. N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175.
78. E. Ferentinos, S. Chatziefthimiou, A. K. Boudalis, M. Pissas, G. Mathies, P. Gast, E. J. J. Groenen, Y. Sanakis and P. Kyritsis, Eur. J. Inorg.Chem., 2018, 713–721.
79. D. Maganas, J. Krzystek, E. Ferentinos, A. M. Whyte, N. Robertson, V. Psycharis, A. Terzis, F. Neese and P. Kyritsis, Inorg. Chem., 2012, 51, 7218–7231.
80. E. Ferentinos, C. P. Raptopoulou, V. Psycharis, A. Terzis, J. Krzystek and P. Kyritsis, Polyhedron, 2018, 151, 177–184.
81. D. Maganas, S. Milikisyants, J. M. A. Rijnbeek, S. Sottini, N. Levesanos, P. Kyritsis and E. J. J. Groenen, Inorg. Chem., 2010, 49, 595–605.
82. E. Ferentinos, A. B. Tsoupras, M. Roulia, S. D. Chatziefthimiou, C. A. Demopoulos and P. Kyritsis, Inorg. Chim. Acta, 2011, 378, 102–108.
83. A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Oxford University Press, Oxford, U.K., 2012.
84. R. Maurice, R. Bastardis, C. de Graaf, N. Suaud, T. Mallah and N. Guihery, J. Chem. Theory Comput., 2009, 5, 2977–2984.
85. A. Sarkar, S. Tewary, S. Sinkar and G. Rajaraman, Chem. – Asian J., 2019, 14, 4696–4704.
86. L. M. Gilby and B. Piggott, Polyhedron, 1999, 18, 1077–1082.
87. J. Nehrkorn, J. Telser, K. Holldack, S. Stoll and A. Schnegg, J. Phys. Chem. B, 2015, 119, 13816–13824.
88. A. K. Hassan, L. A. Pardi, J. Krzystek, A. Sienkiewicz, P. Goy, M. Rohrer and L. C. Brunel, J. Magn. Reson., 2000, 142, 300–312.
89. G. A. Bain and J. F. J. Berry, J. Chem. Educ., 2008, 85, 532–536.
90. C. Dekker, A. F. M. Arts, H. W. Dewijn, A. J. Vanduyneveldt and J. A. Mydosh, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 11243–11251.
91. K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341–351.
92. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
93. C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
94. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
95. L. A. Curtiss, M. P. McGrath, J. P. Blaudeau, N. E. Davis, R. C. Binning and L. Radom, J. Chem. Phys., 1995, 103, 6104–6113.
96. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3330.
97. C. V. Wüllen, J. Chem. Phys., 1998, 109, 392–399.
98. F. Neese, J. Chem. Phys., 2005, 122, 034107.
99. H. Nakano, J. Chem. Phys., 1993, 99, 7983–7992.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2dt03335f

---