Structural insight into halide-coordinated [Fe₄S₄X_nY_4−n]²⁻ clusters (X, Y = Cl, Br, I) by XRD and Mössbauer spectroscopy

Abstract

Iron sulphur halide clusters [Fe₄S₄Br₄]²⁻ and [Fe₄S₄X₂Y₂]²⁻ (X, Y = Cl, Br, I) were obtained in excellent yields (77 to 78%) and purity from [Fe(CO)₅], elemental sulphur, I₂ and benzyltrimethylammonium (BTMA⁺) iodide, bromide and chloride. Single crystals of (BTMA)₂[Fe₄S₄Br₄] (1), (BTMA)₂[Fe₄S₄Br₂Cl₂] (2), (BTMA)₂[Fe₄S₄Cl₂I₂] (3), and (BTMA)₂[Fe₄S₄Br₂I₂] (4) were isostructural to the previously reported (BTMA)₂[Fe₄S₄I₄] (5) (monoclinic, Cc). Instead of the chloride cubane cluster [Fe₄S₄Cl₄]²⁻, we found the prismane-shaped cluster (BTMA)₃[Fe₆S₆Cl₆] (6) (P1̄). ⁵⁷Fe Mössbauer spectroscopy indicates complete delocalisation with Fe^2.5+ oxidation states for all iron atoms. Magnetic measurements showed small χ_MT values at 298 K ranging from 1.12 to 1.54 cm³ K mol⁻¹, indicating the dominant antiferromagnetic exchange interactions. With decreasing temperature, the χ_MT values decreased to reach a plateau at around 100 K. From about 20 K, the values drop significantly. Fitting the data in the Heisenberg–Dirac–van Vleck (HDvV) as well as the Heisenberg Double Exchange (HDE) formalism confirmed the delocalisation and antiferromagnetic coupling assumed from Mössbauer spectroscopy.

---

Introduction

Cubane-shaped [Fe₄S₄] clusters represent a very interesting class of cofactors in biology and are involved in various functions in a cell's life cycle.^1–10 Due to their mixed valence character with formally two ferric (Fe³⁺) and two ferrous (Fe²⁺) iron atoms, [Fe₄S₄]²⁺ clusters show extraordinary electrochemical properties which are crucial for their biological functions in electron transfer and redox catalysis reactions.^1–10 During the last 40 years, numerous [Fe₄S₄]²⁺ clusters with terminal thiolate ligands have been prepared in order to model the structural, electronic and electrochemical properties as well as the reactivity of the naturally occurring clusters.^5–26 Moreover, the fascinating nature of [Fe₄S₄] clusters has triggered their use as precursors for electrocatalytic materials.^27–33 Halide-based [Fe₄S₄X₄]²⁻ with X = Cl, Br, or I are known to be useful precursors because halides can be easily exchanged with thiolate or other ligands by salt metathesis reactions. Homoleptic halide clusters have thus been studied previously and a couple of preparation methods have been published (Scheme 1).^{12,14,15,32–48}

Scheme 1 Reported preparation pathways for the [Fe₄S₄X₄]²⁻ clusters. (1) Müller et al.,³⁷ (2) Kanatzidis et al.,³² (3) Pohl et al.,^38–40 (4) Holm et al.,^36,41 Henderson et al. for X = Cl,^43–45 Tuczek et al. for X = Cl or Br,⁴⁶ (5) Holm et al. for X = Cl,⁴¹ and (6) Holm et al. for X = Cl, Br, I,³⁶ Tuczek et al. for X = I.⁴⁶

We have recently contributed to this very versatile method (3) starting from [Fe(CO)₅] and (BTMA)X (BTMA = benzyltrimethylammonium), (Ph₄P)X, and halogens or interhalogens obtaining excellent yields for the compounds (BTMA)₂[Fe₄S₄I₄] and (Ph₄P)₂[Fe₄S₄Br₄] containing the homoleptic [Fe₄S₄X₄]²⁻ clusters.⁴⁸ By the same method, we obtained the mixed-halide cluster compounds (BTMA)₂[Fe₄S₄BrI₃], (BTMA)₂[Fe₄S₄ClI₃], and (BTMA)₂[Fe₄S₄Cl₂I₂]. Using [Fe(CO)₅], sulphur, ferrous halides FeX₂ and (BTMA)X and adopting method (2), we obtained (BTMA)₂[Fe₄S₄Cl₄], (BTMA)₂[Fe₄S₄Br₄], (BTMA)₂[Fe₄S₄Cl₂I₂], (BTMA)₂[Fe₄S₄Br₂Cl₂] and (BTMA)₂[Fe₄S₄Br₂I₂]. By replacing the halide FeX₂ with tetrahalido ferrates (Ph₄P)[FeX₄] or (Et₄P)[FeX₄], we obtained (Et₄N)₂[Fe₄S₄Cl₄] and (Ph₄P)₂[Fe₄S₄Br₄]. The compounds were obtained in the pure form as microcrystalline solids, while single crystals were not obtained in this study.⁴⁸ A careful study of species in solution by UHR-ESI-MS(−) showed that the mixed halide clusters [Fe₄S₄X₂Y₂]²⁻ and [Fe₄S₄XY₃]²⁻ scramble their halide ligands in a coordinative disproportionation in THF solution, yielding all possible species [Fe₄S₄X_4−nY_n]²⁻ (X/Y = Cl, Br, I). The same was concluded from the UV-vis-NIR absorption spectroscopy results in MeCN solution. Powder X-ray diffraction (PXRD) indicated that the compounds (BTMA)₂[Fe₄S₄Br₄], (BTMA)₂[Fe₄S₄Br₂Cl₂], (BTMA)₂[Fe₄S₄Cl₂I₂] and (BTMA)₂[Fe₄S₄Br₂I₂] were isostructural to the previously reported (BTMA)₂[Fe₄S₄I₄] (monoclinic, Cc).⁴⁰

The lack of precise structural information from single crystal XRD was unfortunate since the crystal structures of the [Fe₄S₄X₄]²⁻ clusters are quite interesting due to the frequent observation that the symmetry of [Fe₄S₄L₄]ⁿ⁻ clusters strongly depends on the packing in the solid state. Frequently, distortion of the idealised cluster symmetry T_d towards D_2d was observed (Table 1).²² For the mixed-halide [Fe₄S₄X₂Y₂]²⁻ clusters belonging to the vast group of heteroleptic [Fe₄S₄L₂L′₂]^m− clusters, the T_d → C_2v symmetry reduction is immanent in the molecular symmetry of the cluster as is the T_d → C_3v symmetry reduction for [Fe₄S₄L₃L′₁]^m− clusters. At the same time, the packing in the crystal and thus the size and shape of the counter cation can cause lowering of the cluster symmetry and for all three types even lower symmetry caused by crystal packing was reported (Table 1).^37–61 Importantly, with these changes in cluster symmetry, essential properties such as the redox potentials, spin states, magnetic properties, and ligand exchange kinetics vary markedly.^{1,6,8,13,14,20–23,37–40,47,50,56,62–84}

Table 1 Selected structural features of [Fe₄S₄L₄]ⁿ⁻ [Fe₄S₄L₃L′]ⁿ⁻, and [Fe₄S₄L₂L′₂]ⁿ⁻ clusters

Cation	Ligand set	Crystal system	Space group	Cluster symmetry^a	Ref.
a Approximate symmetry of the cluster. b Approaches C3v symmetry as one Cl ligand shows strong H bonding to nBu3NH^+. c BTMA^+ = benzyltrimethylammonium. d Et2Dtc^− = N,N-diethyldithiocarbamate. e Selenium clusters [Fe4Se4X4]^2−. f Me2Tu = N,N-dimethylthiourea. g tBu2Tu = N,N-di-tert-butyl-thiourea. h R = 2,4,6-(iPr)3C6H2, Et2Tu = N,N-diethylthiourea.
Et4N^+	Cl	Monoclinic	P21/c	D 2d	36 and 42
nPr4N^+	Cl	Monoclinic	P21/n	C 1	41
Ph4P^+	Cl	Monoclinic	C2/c	D 2d	37
nBu3NH^+	Cl	Monoclinic	P21/n	C 3v	70
[K4[FeCl4](C12H24O6)4]^2+	Cl	Cubic	F23	T d	52
[Fe(MeCN)2[(P(OMe)3]4]^2+	Cl	Monoclinic	P21/c	D 2d	85
Ph4P^+	Br	Monoclinic	C2/c	D 2d	37
Et4N^+	Br^e	Monoclinic	P21/c	S 4	87
[(nBu4N)2[Fe(DMF)6]]^4+	Br	Monoclinic	P21/n	T d	86
Ph4P^+	I	Tetragonal	I41/a	S 4	40
BTMA^+^c	I	Monoclinic	Cc	C 1	40
nBu4N^+	I^e	Monoclinic	P21/n	C 3v	89
[(Et4N)6[Fe2S2I4]]^4+	I	Tetragonal	P42bc	T d	60
nBu4N^+	SMe	Orthorhombic	Pba2	T d	83
HnBu3N^+	SPh	Triclinic	P1̄	C 2v	70
HEt3N^+	SPh	Monoclinic	P21/n	D 2d	70
BTMA^+^c	StBu	Monoclinic	P21/c	C 1	82
Et4N^+	StBu	Tetragonal	I4̄2m	D 2d	82
Ph4P^+	2 Br 2 Cl	Monoclinic	C2/c	D 2d	37
Ph4P^+	2 Cl 2 SPh	Orthorhombic	Pbcn	D 2d	88
Ph4P^+	2 Cl 2 OPh	Orthorhombic	Pbcn	D 2d	89
Ph4P^+	2 SPh 2 OpTol	Orthorhombic	P212121	C 1	89
Ph4P^+	2 Cl 2 S Et2Dtc^d	Monoclinic	C2/c	C 2	91
Ph4P^+	2 SPh 2 S Et2Dtc^d	Monoclinic	C2/c	C 2	91
Ph4P^+	3 Cl 1 S Et2Dtc^d	Monoclinic	P21/c	C s	91
[FeIL3]^+	3 I 1 S Me2Tu^f	Triclinic	P1̄	C 3v	90
None	2 I 2 S tBu2Tu^g	Monoclinic	P21/n	C 2v	90
None	2 SR 2 S Et2Tu^h	Triclinic	P1	D 2d	57

---

Herein, we report the synthesis and detailed study of the materials (BTMA)₂[Fe₄S₄Br₄] (1), (BTMA)₂[Fe₄S₄Br₂Cl₂] (2), (BTMA)₂[Fe₄S₄Cl₂I₂] (3), (BTMA)₂[Fe₄S₄Br₂I₂] (4), and (BTMA)₂[Fe₄S₄I₄] (5) containing cubane type Fe₄S₄ clusters alongside with (BTMA)₃[Fe₆S₆Cl₆] (6) containing the prismane [Fe₆S₆Cl₆]³⁻ structure. After preparation in solution, the compounds were isolated as single crystals and we can provide full structural information from single crystal and PXRD analyses. Additionally, resonance Raman, ⁵⁷Fe Mössbauer and magnetic data were recorded for the first time on such mixed-halide clusters, with the exception of (Ph₄P)₂[Fe₄S₄Br₂Cl₂] for which the structure and Mössbauer data have previously been reported.³⁷

Results and discussion

Preparations

The materials were prepared as recently described (for details and analyses, see the ESI†). As in our previous study,⁴⁸ UHR-ESI-MS(−) showed that the mixed halide clusters [Fe₄S₄X₂Y₂]²⁻ scramble their halide ligands leading to coordinative disproportionation in solution yielding all possible species [Fe₄S₄X_4−nY_n]²⁻ (X/Y = Cl, Br, and I) (see the Experimental data in the ESI†). The elemental analyses of the crystallised products clearly show a 2 : 2 ratio for X : Y. Of course this does not rule out contributions from the 3 : 1 and 1 : 3 cluster species, but then both must contribute with the same amount. The same is true for the 4 : 0 and 0 : 4 species. Using methods such as resonance Raman, single crystal XRD, PXRD, magnetic measurements and Mössbauer spectroscopy we not only tried to study the local cluster symmetry but also tried to trace other species than the 2 : 2 complexes [Fe₄S₄X₂Y₂]²⁻.

Resonance Raman spectroscopy

The resonance Raman spectra of (BTMA)₂[Fe₄S₄Br₄] (1), (BTMA)₂[Fe₄S₄Br₂Cl₂] (2), (BTMA)₂[Fe₄S₄Cl₂I₂] (3), and (BTMA)₂[Fe₄S₄Br₂I₂] (4) were recorded at 458 and 514 nm excitation wavelengths (Fig S1, ESI†). Four bands can be distinguished in the NIR range from 180 to 580 cm⁻¹. Unfortunately, these bands are quite invariant on the first view which is expectable, as their main contributions come from the Fe–S bridging modes.^{46–48,92–94} This is in line with our previous FIR studies and confirms that the absorption bands observed around 500 nm (ε of about 2000 cm⁻¹ M⁻¹) in the UV-vis-NIR absorption spectra in solution have their origin essentially in the Fe₄S₄ cubane (S → Fe LMCT).⁴⁸ Unfortunately, direct irradiation of the X → Fe LMCT band at around 700 nm (ε ∼ 1500 cm⁻¹ M⁻¹) was technically not feasible. Nevertheless, two trends were observed. The introduction of the light Cl⁻ led to a slight high-energy shift of all bands and decreased symmetry led to detectable wavelength dependence for all four bands. In homoleptic compound 1, only the bands at about 500 and 400 cm⁻¹ vary with the excitation wavelength, while the bands at 283 and 219 cm⁻¹ are completely invariant. The bands which were most sensitive to variation in the halides and wavelength were ranging from 285 to 276 cm⁻¹ and were assigned to the T^b₁ mode in T_d symmetry while the resonances from 404 to 398 cm⁻¹ probably fit to T^b₂ mode in T_d symmetry.^46,47,93,94 These modes indicate already a distortion below D_2d.⁴⁶ The intense bands at 220 to 216 cm⁻¹ have clearly their origin in the symmetry reduction lower than D_2d for the homoleptic cluster in 1 or lower than C_2v for the heteroleptic derivatives 2, 3, and 4.

X-ray crystal structures

Single crystals of high quality were obtained for 1 to 4 and (BTMA)₃[Fe₆S₆Cl₆] (6) directly from the synthesis procedure or were obtained through the slow diffusion of diethyl ether into saturated MeCN solutions. The crystal structures of 1 to 4 were solved and refined in the monoclinic space group Cc, while that of 5 was found to crystallise in the triclinic space group P1̄ (details in Fig. S2 to S6 and Tables S1–S9 in the ESI†). The Fe₄S₄ compounds are thus isostructural to (BTMA)₂[Fe₄S₄I₄] (5),⁴⁰ regardless if they are pure clusters like 1 or mixed halide species like 2, 3, and 4.

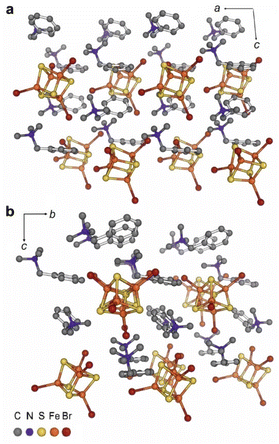
Like in (BTMA)₂[Fe₄S₄I₄] (5),⁴⁰ the iron sulphur clusters in (BTMA)₂[Fe₄S₄Br₄] (1) are arranged in planes at the [110] direction packed with the BTMA⁺ cation in between. The planes are rotated by 90° around the c axis direction (Fig. 1).

Fig. 1 Crystal structure of (BTMA)₂[Fe₄S₄Br₄] (1) viewed along the [110] direction (a) and rotated by 90° around the crystallographic c axis to show segregated columns of anions and cations (b). The bottom inset shows atom colouring: H atoms are omitted for clarity.

The intermolecular C–H⋯S and C–H⋯Br hydrogen bonds with the CH₃ and CH₂ groups of the BTMA⁺ cations (Fig. 2) exceed 3 Å than the H⋯X distance and are thus weak.⁹⁵ Br⋯Br interactions between the cluster ions form a chain-like infinite motif along the [110] direction (Fig. 1 and 2) occurring between Br3 and Br4 are 3.814(2) Å long and thus slightly exceed the sum of the van der Waals radii.^96,97

Fig. 2 Intermolecular C–H⋯S, C–H⋯Br, and Br⋯Br interactions in (BTMA)₂[Fe₄S₄Br₄] (1); distances are in Å and angles are in °.

The idealised T_d symmetry of the cubane-shaped [Fe₄S₄Br₄]²⁻ dianion is significantly decreased. The Fe₄ cluster core is compressed along the Fe3⋯Fe4 edge with an extraordinarily short distance of 2.717(2) Å (Tables S2, S5 and S6†). This is 0.048 Å shorter than the average of the other Fe⋯Fe distances (2.765 Å). The Fe–S bond lengths vary from 2.249(2) to 2.305(2) Å showing four markedly decreased values, one for each Fe atom (Table S2†). The analysis of the Br–Fe–Fe and S–Fe–Br angles revealing the asymmetrical distortion of the clusters is connected to the intermolecular Br⋯Br interactions between Br3 and Br4 (Fig. 2). The Br3–Fe3–Fe4 (138.53(10)°) and the Br4–Fe4–Fe3 (138.03(10)°) angles are smaller than all other Br–Fe–Fe angles (between 140.06(10)° and 151.03(10)°), whereas the opposite S4–Fe3–Br3 (119.66(12)°) and S2–Fe4–Br4 (120.03(12)°) angles are larger compared with 108.30(11) to 118.87(12)°.

The lengths of the other two terminal Fe–Br bonds are not affected by the compression and the values between 2.332(2) and 2.354(2) Å coincide with those observed for the Ph₄P⁺ structure.³⁷ We thus suspect that the Br⋯Br interactions are rather repulsive in the packing. In contrast to this, the I⋯I interactions in (BTMA)₂[Fe₄S₄I₄] (5) seem to be favorable as the I⋯I distance of 3.917 Å is below the sum of the van der Waals radii (4.3 Å).⁴⁰ In contrast to this, in the PPh₄⁺ derivative, the I⋯I distances are longer which contradicts the idea that the I⋯I interactions might govern the cluster distortion.⁴⁰

For the mixed-cluster compounds, crystalline material was obtained from (BTMA)₂[Fe₄S₄Br₂Cl₂] (2), (BTMA)₂[Fe₄S₄Cl₂I₂] (3), and (BTMA)₂[Fe₄S₄Br₂I₂] (4) and single crystal XRD data were collected at 293 K and 173 K. All three compounds crystallise isostructural (Cc) to the homoleptic 1 and 5 ⁴⁰ and no phase transition was observed on going from 293 to 173 K. The heteroleptic clusters [Fe₄S₄X₂Y₂]²⁻ show mixed occupancies of both halides on each position as reported before for (Ph₄P)₂[Fe₄S₄Br₂Cl₂],³⁷ and we refined the data of the compounds 2, 3, and 4 using the SUMP command (details and data in the ESI†).

In our previous study, we found that in solution and therefore also during synthesis, all possible cubane species [Fe₄S₄X_4−xY_x]²⁻ (x = 0 to 4) are present with [Fe₄S₄X₂Y₂]²⁻ as the dominating one.⁴⁸ Since the here reported materials were obtained through slow crystallisation by ether diffusion at −18 °C in the presence of BTMA⁺ cations, slight deviations of x from the ideal value of 2 in mixed halide clusters [Fe₄S₄X_xY_y]²⁻ might be expected.³⁷ But only when we were freely refining the data recorded at 173 K for compound 3 (Cl : I), we obtained a halide ratio of 1.76 : 2.24 deviating from the ideal 2 : 2 (Table S10†). Unfortunately, the quality of the data did not allow satisfying refinement. The same problems were reported for the structure solution and refinement of (Ph₄P)₂[Fe₄S₄Br₂Cl₂].³⁷

In line with earlier assumptions, we believe that the cluster composition and thus the cluster symmetry have no effect on the packing and the clusters arrange randomly in the structures.

A comparison of the unit cell volumes of the mixed-ligand compounds (BTMA)₂[Fe₄S₄X₂Y₂] (2 to 4) with those of the homoleptic derivatives 1 and 5 and the calculated cluster volumes using the so-called Solvent Excluded Volume,⁹⁸ including the Cl₄ cluster derivative (Fig. 3 and Table 2), showed that by exchanging smaller halides with larger ones, the cell volumes and the cluster volumes increase along the series Cl₄ < Cl₂Br₂ < Br₄ < Cl₂I₂ < Br₂I₂ < I₄ in line with the increasing ionic radii⁹⁹ (Cl⁻: 1.81 Å, Br⁻: 1.96 Å, I⁻: 2.20 Å).

Fig. 3 Comparison of unit cell and the calculated cluster volumes (A) of [Fe₄S₄X_4−xY_x]²⁻ (x = 0 or 2). The calculated so-called solvent excluded volumes (V_SE) (B).⁹⁸ Note that the values for 1 to 4 are from data at 173 K, while 5 and “Cl₄” are from 298 K data.

Table 2 Cell volumes and calculated cluster volumes of [Fe₄S₄X_4−xY_x]²⁻ clusters (x = 0 or 2)^a

	Cell volume 298 K^b	Cell volume 173 K^b	Cluster volume 298 K^c	Cluster volume 173 K^c
a Values in Å^3. b From single crystal structures of (BTMA) salts. c Calculated solvent excluded volume (VSE).^98 d Data not available for BTMA salts; values for other salts are not comparable. e Derived from the (Et4N)2[Fe4S4Cl4] structure determined at 213 K.^36,42 f From ref. 49, at 150 K. g BzEt3N^+ salt at 150 K, from ref. 100. h From ref. 40. i BzEt3N^+ salt at 173 K, from ref. 101.
Cl4	—^d	—^d	221.71^e	221.78^f
Cl2Br2	3269.0(2)	3201.6(1)	242.51	232.65
Br4	3340.8(4)	—^d	244.35	244.38^g
Cl2I2	3389.6(1)	3323.3(2)	325.62	277.02
Br2I2	3440.5(2)	3342.6(1)	326.00	286.03
I4	3514.8(2)^h	—^d	328.66^h	328.94^i

---

This underlines that potential contributions from cluster species with 1 : 3 and 3 : 1 ratios cannot be detected if they are present in equal amounts or make only minor contributions. So, we cannot exclude mixed-clusters with 3 : 1 and 1 : 3 halide ratios to contribute to the mixed-halide cluster compounds, but we have also no evidence for them.

Due to this, the Fe–X bond distances of the mixed-halide clusters do not allow a straightforward comparison with literature data from (BTMA)₂[Fe₄S₄I₄] (5),⁴⁰ (Ph₄P)₂[Fe₄S₄I₄],⁴⁰ (Ph₄P)₂[Fe₄S₄X₄] (X = Br, Cl),³⁷ (Et₄N)₂[Fe₄S₄Cl₄],^36,42 (nPr₄N)₂[Fe₄S₄Cl₄]⁴¹ (Table S7†).

The Fe₄S₄ cluster cores in the mixed-halide compounds 2 to 4 showed that the characteristic distortion of the [Fe₄S₄] core is lower than the D_2d symmetry (Fig. S5 and S6†). For all three clusters, a significant shortening of the Fe3⋯Fe4 distance (Tables S5 and S6†) and distortion of the X_3/4–Fe_3/4–Fe_4/3 angles and their opposite S–Fe_3/4–Br_3/4 angles (Table S2†) were found. As for the homoleptic compound 1, the intermolecular halide⋯halide interactions (Table S5†) were observed parallel to the compressions of the cluster core along the Fe3⋯Fe4 axis, while at the same time the Fe1⋯Fe2 axis is slightly elongated (Tables S5 and S6†). For interactions with iodide contribution (i.e. I⋯I, Br⋯I and Cl⋯I), the observed distances are always below the sum of the van der Waal radii pointing to an attractive interaction whereas the Br⋯Br distances are larger as in the homoleptic 1. Br⋯Cl and Cl⋯Cl interactions are not observed.

On the other hand, in [Fe₄S₄X₄]²⁻ (X = Br or I) derivatives containing R₄N⁺ and Ph₄P⁺ cations,^{9,10,29,30,40,56,69} both Br⋯Br and I⋯I interactions are longer than in the BTMA⁺ structures by least 0.24 Å (Br) and 0.45 Å (I), respectively (Tables S6 and S7†). The halide⋯halide distances in the homoleptic compounds 1 and 5 ⁴⁰ are also shorter compared with the published Ph₄P⁺ structures.^37,40 This is also in line with the higher density of the BTMA⁺ structures (Tables S5 and S6†). As a consequence of these shorter halide⋯halide interactions, the BTMA⁺ structures show markedly higher Fe⋯Fe distortions for both the homoleptic and the mixed-halide clusters. When taking the difference between the largest and the smallest Fe⋯Fe distances, the BTMA⁺ structures lie at around 0.05 Å (Table S6†), while the Ph₄P⁺ derivatives show values around 0.02 Å (Table S7†). Within the BTMA⁺ structures, the homoleptic Br₄ and I₄ show the largest deviations and both these two homoleptic structures and the three mixed-halide structures were found to have the same distortion pattern: two shortened and four extended Fe⋯Fe distances with overall very low cluster symmetry and very similar cluster shapes (Fig. S5 and S6†).

Attempts to crystallise [Fe₄S₄Cl₄]²⁻ with BTMA⁺ by the same method led to the formation of a prismane structure (BTMA)₃[Fe₆S₆Cl₆] (6) which crystallised in the triclinic P1̄ space group. The prismane cluster [Fe₆S₆Cl₆]³⁻ is positioned on the inversion centre and is surrounded by three BTMA⁺ cations (Fig. S2†). Based on this structural feature, the asymmetric unit is represented by two halves of the clusters and three counter ions which can be combined to get two units of 6 per unit cell (Fig. S3†). Pronounced intermolecular H bonding interactions are absent (Fig. S4†). The prismane structure can be described as two alternating layered [Fe₃S₃] rings in a chair conformation. Its D_3d symmetry is only slightly perturbed. The Fe–Cl and Fe⋯Fe distances are found to be very similar (Table S9†) and comparable to bromide and chloride prismanes with Et₄N⁺.^87–91 The Cl–Fe–S angles ranging from 108.26(4)° to 115.96(5)° are quite close to an ideal tetrahedral angle. The bulk material of 6 is not completely phase pure but does definitely not contain the (BTMA)₂[Fe₄S₄Cl₄] phase isostructural to (BTMA)₂[Fe₄S₄Br₄] (1) (see Powder XRD). The [Fe₄S₄Cl₄]²⁻ cluster was previously crystallised with a number of cations, such as Et₄N⁺,^36,42nPr₄N⁺,⁴¹ or Ph₄P⁺.³⁷ We were unable to detect even traces of (BTMA)₂[Fe₄S₄Cl₄] (see powder XRD, Mössbauer, or magnetic measurement). At the moment, we have no explanation other than a superior crystallisation of prismane 6.

Powder XRD studies

In previous investigations,⁴⁸ we have already shown that the Fe₄S₄ cluster compounds (1 to 5) are obtained as homogeneous materials with no signs of phase separation. Very weak additional reflections point to some minor impurities of unknown identity. No significant differences between the crystal structures obtained at 170 K and RT are visible excluding the possible phase transitions upon cooling. The diffraction pattern of the Fe₆S₆ prismane (Fig. S7†) shows that 6 is only a minority phase in the reaction product. It was speculated that the main product could be the still unknown chloride (BTMA)₂[Fe₄S₄Cl₄]. The simulated diffraction pattern of (BTMA)₂[Fe₄S₄Br₄] (1) is provided for comparison. Assuming that 1 and the unknown chloride crystallise in the isotypic crystal structures, the pattern of the chloride should be shifted to higher 2θ values thus completely excluding this assumption. However, it should be noted that the formation of the chloride (BTMA)₂[Fe₄S₄Cl₄] crystallising in another crystal structure cannot completely be ruled out at this point. In addition, another modification of (BTMA)₃[Fe₆S₆Cl₆] can possibly make up the majority of the studied material.

⁵⁷Fe Mössbauer spectroscopy

For (BTMA)₂[Fe₄S₄Br₄] (1) a symmetric doublet with an isomer shift δ = 0.48 mm s⁻¹ was recorded (Fig. S8A†). Analysis by fitting using a Lorentzian line shape also reveals a quadrupole splitting ΔE_Q of 1.77 mm s⁻¹ and a line width at half maximum Γ of 0.42 mm s⁻¹ (Table 3).

Table 3 Mössbauer parameters at 77 K of the complexes obtained from spectra fitting analysis^a

	n	δ	ΔEQ	Γ	Fe
a Contribution n/%, isomer shift δ/mm s^−1, quadrupole splitting ΔEQ/mm s^−1, line width at half maximum Γ/mm s^−1. Iron oxidation state Fe. b Two species simulated in a 50 : 50 ratio. c Minor species of 11% (see text and Fig. S8†).
1	100	0.48 ± 0.01	1.07 ± 0.02	0.42 ± 0.01	2.5+
2	100	0.48 ± 0.01	1.07 ± 0.03	0.35 ± 0.01	2.5+
3	A: 50	0.48 ± 0.02	1.16 ± 0.02	0.37 ± 0.02	2.5+
	B: 50	0.46 ± 0.01	0.80 ± 0.01	0.47 ± 0.02	2.5+
4	100	0.48 ± 0.01	1.05 ± 0.02	0.35 ± 0.01	2.5+
5	89	0.48 ± 0.02	1.02 ± 0.02	0.35 ± 0.01	2.5+
6	A: 96	0.48 ± 0.02	0.88 ± 0.02	0.35 ± 0.01	2.5+

---

An isomer shift of 0.48 mm s⁻¹ is in keeping with the previously reported [Fe₄S₄Br₄]²⁻ clusters with different counter ions.^86,87 It is also in the range observed for [4Fe–4S]²⁺ centres occurring in 4Fe–4S proteins. These clusters exhibit complete delocalisation of one electron in the Fe²⁺–Fe³⁺ spin pairs. The ferromagnetic double exchange between the iron spins formally leads to Fe^2.5+–Fe^2.5+ pairs with the pair spin S_p = 9/2.⁶ In turn, antiparallel (antiferromagnetic) coupling of the pair spins leads to the clusters’ diamagnetic ground state.^{6,71,75,102,103} The Mössbauer spectrum of 5 was fitted alongside a singlet signal (11%) which can be assigned to monomeric (NEt₄)[FeI₄]⁸⁹ (Fig. S8B†). Besides this, the behaviour is the same as for 1. Correspondingly, all Fe atoms in the homoleptic 1 and 5 (Fig. S8†) have an oxidation state of 2.5+.

For both heteroleptic compounds (BTMA)₂[Fe₄S₄Br₂Cl₂] (2) and (BTMA)₂[Fe₄S₄Br₂I₂] (4), symmetric Lorentzian-type doublets with δ values of 0.48 mm s⁻¹ were recorded (Fig. S9†). Thus, the average oxidation state of iron in both mixed-halide-clusters is 2.5+ with complete delocalisation.

In contrast, (BTMA)₂[Fe₄S₄Cl₂I₂] (3) exhibited a slightly asymmetric Mössbauer doublet whose analysis reveals the equal contributions of the two species (Fig. 4).

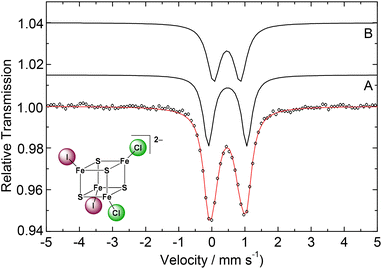Fig. 4 ⁵⁷Fe Mössbauer spectrum of (BTMA)₂[Fe₄S₄Cl₂I₂] (3) at 77 K (dots: collected data, parameters for the simulated species A and B in Table 3).

Species A causes a doublet with δ₁ = 0.48 mm s⁻¹ and ΔE_Q1 = 1.16 mm s⁻¹. Species B causes an isomer shift with δ₂ = 0.46 mm s⁻¹ which is within the experimental error identical to that of species B. Thus, 3 also has all irons in the 2.5+ oxidation state (Table 3). The different values of ΔE_Q may be a result of the large differences in the EN of Cl and I.

It should be noted that in contrast to the analysis with two “nested” doublets presented above, the Mössbauer spectrum of 3 can alternatively be fitted with two “crossed” doublets (Fig. S11†). This leads to δ_A = 0.54 and δ_B = 0.37 mm s⁻¹ which may indicate electron localisation. However, high spin Fe³⁺ and Fe²⁺ sites have significantly different ΔE_Q values, and the analysis with two “crossed” doublets shows almost identical ΔE_Q values of 1.0 mm s⁻¹ (Fig. S11†) which contradicts electron localisation. Therefore, we conclude that indeed 3 has all irons in the 2.5+ state.

Such a situation has also been observed for [Fe₄S₄X₂Y₂]²⁻ clusters with monodentate ligands X, Y = Cl, OPh and SPh show δ values between 0.46 and 0.50 mm s⁻¹ for both coordination sites.⁵⁶

For (Ph₄P)₂[Fe₄S₄Br₄], δ = 0.488 mm s⁻¹ and ΔE_Q = 0.662 mm s⁻¹ were reported at 77 K.³⁷ A crude measurement of the mixed-halide compound (Ph₄P)₂[Fe₄S₄Br₂Cl₂] was reported with a shift of about 0.00 mm s⁻¹ and significant line-broadening³⁷ similar to that observed for 3.

The high similarity of all clusters in the BMTA⁺ containing materials in their Mössbauer spectra is in line with the very similar distortion of the clusters from T_d to very low symmetry (see the XRD section).

For (BTMA)₃[Fe₆S₆Cl₆] (6), an isomer shift of 0.48 mm s⁻¹ was recorded and the oxidation state of each iron inside the prismane core can be assigned to 2.5+. Like the previous prismane cluster, the core of 6 consists of three Fe²⁺–Fe³⁺ spin pairs coupling ferromagnetically and resulting in Fe^+2.5 on average.⁸⁶ The observed ΔE_Q of 0.88 mm s⁻¹ is smaller than those reported for other prismanes,^{12,38,85–90,102–108} but overall, the isomer shift and the quadrupole splitting for 6 are very similar to those of the (Et₄N)₃[Fe₆S₆Cl₆] prismane with δ = 0.495 mm s⁻¹ and ΔE_Q = 1.085 mm s⁻¹ at 125 K.⁸⁶

For fitting the collected data, a second species with a contribution of 4% was necessary. This second doublet was fitted with δ = 1.40, ΔE_Q = 1.01, and Γ = 0.40 mm s⁻¹ and is due to the FeCl₂ impurities from the starting material (Fig. S10†). For (Ph₄P)₂[Fe₄S₄Cl₄], a δ value of 0.49 mm s⁻¹ was reported at 77 K with a ΔE_Q of 0.67 mm s⁻¹.^56,86 Although PXRD showed that the crystal structure of (BTMA)₃[Fe₆S₆Cl₆] is only the minor phase in the isolated material, the Mössbauer results provide good evidence that the major component of the material contains the [Fe₆S₆Cl₆]³⁻ prismanes. At the same time, the Mössbauer results do not completely rule out the occurrence of the compound (BTMA)₄[Fe₄S₄Cl₄] as the reported data for (Ph₄P)₂[Fe₄S₄Cl₄] is not very different from our data for 6.

Magnetic measurements

The molar magnetic susceptibilities of all four compounds are shown in Fig. 5 as χ_MT vs. T plots. All compounds show quite similar magnetic behaviour (Fig. 4 and Fig. S12–S14, ESI†).

Fig. 5 Temperature dependence of the molar magnetic susceptibility depicted as χ_MT vs. T of the homoleptic cluster (BTMA)₂[Fe₄S₄Br₄] (1, black) and the heteroleptic clusters (BTMA)₂[Fe₄S₄Br₂Cl₂] (2, green), (BTMA)₂[Fe₄S₄Cl₂I₂] (3, red), and (BTMA)₂[Fe₄S₄Br₂I₂] (4, blue).

At 298 K, the observed χ_MT values are 1.17 cm³ K mol⁻¹, 1.41 cm³ K mol⁻¹, 1.54 cm³ K mol⁻¹ and 1.12 cm³ K mol⁻¹ for 1 to 4, respectively, far below the expected spin-only value of 14.75 cm³ K mol⁻¹ for four uncoupled spins with S₁ = S₂ = 4/2 (ferrous) and S₃ = S₄ = 5/2 (ferric).

Upon lowering the temperature, a steady decrease in the χ_MT-products is observed for all compounds, indicating strong dominant antiferromagnetic interactions between the iron ions. Further cooling below 100 K initially leads to no significant change in the values. However, upon cooling only below 20 K, the χ_MT values decrease significantly.

For cluster systems with four antiferromagnetically coupled spin centres, an HDvV (Heisenberg–Dirac–van Vleck) spin Hamiltonian, , with one single exchange interaction parameter J leads to a highly degenerated spin ground state. However, this assumption is incompatible with the results of the Mössbauer investigations and especially with the observed temperature-dependent magnetic moments for the four compounds (Fig. 5).

The application of a full HDdV with two exchange interactions, which includes a stronger antiferromagnetic exchange interaction J₁, within the two Fe²⁺–Fe³⁺ dimers, and an exchange interaction, J₂, accounting for the inter-dimer interaction, allows quite satisfactory simulations for the curves for all four compounds (Fig. 5 and Table 4).

Table 4 Fitting parameter obtained by applying HDvV and HDE^a

	HDvV			HDE
	J 1/cm^−1	J 2/cm^−1	g	J/cm^−1	B/cm^−1	g
a HDvV = Heisenberg–Dirac–van Vleck; HDE = Heisenberg double exchange.
1	−129 (3)	−2.6 (3)	1.775 (16)	−257 (10)	462.2 (5)	1.66 (5)
2	−135 (7)	−3.2 (3)	2.09 (5)	−256 (10)	462.5 (5)	1.91 (6)
3	−115 (2)	−2.0 (2)	1.853 (11)	−274 (13)	554.6 (9)	1.74 (8)
4	−132 (1)	−2.8 (2)	1.759 (6)	−291 (13)	552.1 (7)	1.65 (6)

---

However, in three of the four fits, a g value considerably below 2.0 was obtained. For the Fe₄S₄ cluster, this phenomenon is well-known⁶ and assigned to the presence of spin-dependent delocalisation which is related to the double exchange theory devolved by Anderson and Hasewaga.¹⁰⁹ They have shown that resonance delocalisation in a mixed-valence dimer leads to additional splitting ±B(S + 1/2) of the energy-split spin ladder JS(S + 1) for the exchange coupled spin system.

To estimate the double exchange parameter B in the present Fe₄S₄ tetramers, we followed the approach recently reported by Henthorn, Cutsail et al.¹¹⁰ and applied the solved Bleaney–Bowers equation for dimers of high spin d⁵–d⁶ mixed-valence centres (Table 4, eqn (S1), (S2), and Fig. S14†). Note that the data at low temperatures were not taken into account for fitting to E = −JS(S + 1) ± B(S + 1/2). This is in accordance with the literature and the interested reader is referred to the publication and the references therein for further information.¹¹⁰ The values obtained for B are consistent with the reported values^6,111–113 in all cases and clearly show the presence of electron delocalisation, which is also evident from the Mössbauer data, showing only a single doublet assigned to a mixed valence state. Most importantly, the ratio |B/J| is relatively small, so the spin ground state of S = 1/2 can be taken as given for the dimers. This justifies the application of the HDdV formalism, which in analogy leads to an S = 1/2 ground state for the antiferromagnetically coupled Fe²⁺–Fe³⁺ dimers. Furthermore, with the HDvV-formalism, we are now able to take the inter-dimer interaction into account. Although the values for J₂ are almost two orders of magnitude smaller than J₁, the resulting final ground states for the Fe₄S₄²⁺-clusters are diamagnetic with S = 0, which matches perfectly with the decrease in the χ_MT values at low temperature.

In the temperature-dependent magnetisation measurements for (Et₄N)₂[Fe₄S₄Cl₄], the magnetic moment μ increased from 0.45 to 2.48 μB upon increasing the temperature from 50 to 338 K,³⁶ which is in good agreement with the behaviour in our compounds.

Conclusions

The iron sulphur halide clusters [Fe₄S₄Br₄]²⁻ and [Fe₄S₄X₂Y₂]²⁻ (X, Y = Cl, Br, I) were synthesised in excellent yields and purity on a gram scale using a recently refined method starting from [Fe(CO)₅], elemental sulphur, I₂ and benzyltrimethylammonium (BTMA⁺) iodide, bromide and chloride. Through crystallisation, we obtained materials showing a clear 1 : 1 ratio of X : Y for the mixed-halide cluster compounds. Single crystals of (BTMA)₂[Fe₄S₄Br₄] (1), (BTMA)₂[Fe₄S₄Br₂Cl₂] (2), (BTMA)₂[Fe₄S₄Cl₂I₂] (3) and (BTMA)₂[Fe₄S₄Br₂I₂] (4) were isostructural to the previously reported (BTMA)₂[Fe₄S₄I₄] (5) (monoclinic, Cc). In the same way, we tried to synthesise the previously unknown chloride cubane cluster compound (BTMA)₂[Fe₄S₄Cl₄]. But we obtained the prismane-shaped cluster (BTMA)₃[Fe₆S₆Cl₆] (6) (P1̄) instead.

No phase transitions were observed for the mixed-halide cluster containing materials from powder XRD at 298 or 170 K or single crystal XRD at 293 and 173 K. Although in solution four different clusters [Fe₄S₄X_4−xY_x]²⁻ (x = 0 to 4) might occur for the mixed-halide compounds, the structure refinements gave no indication for the X : Y ratio deviating from 2 : 2. Also, a closer look on the cluster volumes (solvent excluded volumes, the unit cell volumes and the cluster distortions) gave evidence for other species than X₂Y₂. On the other hand, our XRD data do not rule out X₁Y₃ species if they were present in the same amount as X₃Y₁ species and all cluster species arrange randomly in the structures.

However, Mössbauer spectroscopy rules out larger amounts of such X₃Y₁ species. For the homoleptic 1 and 5 and the mixed-halide clusters 2, 3, and 4, Lorentzian-type doublets were observed in ⁵⁷Fe Mössbauer spectroscopy in line with a complete delocalisation with Fe^2.5+ oxidation states for all iron atoms.

Magnetic measurements for 1 to 4 showed small χ_MT values at 298 K ranging from 1.12 to 1.54 cm³ K mol⁻¹. From about 20 K, the values drop significantly. Fitting the data in the Heisenberg–Dirac–van Vleck (HDvV) formalism gave g values markedly below 2 and confirmed the complete delocalisation and antiferromagnetic coupling assumed from Mössbauer spectroscopy.

Thus, the herein described synthesis is reliable and robust and allows the production of mixed-halide clusters [Fe₄S₄X₂Y₂]²⁻ (X, Y = Cl, Br, I) on a gram scale and with high purity. In particular, the [Fe₄S₄Cl₂I₂]²⁻ derivative might be interesting for further studies as the very different halide ligands might allow the selective substitution of two halide ligands to form new mixed ligand [Fe₄S₄] clusters.

Experimental section

Materials

The compounds were prepared and crystallised following already published procedures⁴⁸ by diffusion techniques from layered MeCN/diethyl ether mixtures at −18 °C over a period of 3 weeks. After filtration, washing with diethyl ether and drying under anaerobic and dry atmosphere (argon) using Schlenck techniques the opaque black rod shape crystals were stored and prepared for analyses in an argon-filled glove box at room temperature. The details and analytics are available in the ESI.†

Instrumentation

The resonance Raman spectra were recorded either with 457 nm or 514 nm excitation (13 mW, Coherent Innova 70c) in backscattering geometry using a confocal microscope coupled to a single stage spectrograph (Jobin Yvon XY 800) equipped with a CCD detector.

For (BTMA)₂[Fe₄S₄Br₄] (1), (BTMA)₂[Fe₄S₄Br₂Cl₂] (2), (BTMA)₂[Fe₄S₄Br₂I₂] (4) and (BTMA)₃[Fe₆S₆Cl₆] (6), single crystal data collection at 293(2) K was performed using STOE-IPDS (I, II or IIT) diffractometers using graphite-monochromated Mo-K_α radiation (λ = 0.71073 Å). The samples have been measured in capillaries sealed under an argon atmosphere (0.2 mm diameter). The structures were solved by direct methods using the WinGX¹¹⁴ package and/or Olex2.¹¹⁵ For some of them, first structure proposals were obtained with Sir2014.¹¹⁶ Model refinement was carried out with SHELXL2018/1^117,118 by employing full-matrix least-squares methods on F². All non-hydrogen atoms were treated anisotropic and the hydrogen atoms were included by using appropriate riding models. Numeric absorption correction was performed using X-Red¹¹⁹ and X-Shape¹²⁰ packages. CCDC Deposition Numbers are 2048374 for (BTMA)₂[Fe₄S₄Br₄] (1), 2048953 for (BTMA)₂[Fe₄S₄Br₂Cl₂] (2), 2055695 for (BTMA)₂[Fe₄S₄Br₂I₂] (4), and 2048377 for (BTMA)₃[Fe₆S₆Cl₆] (6), respectively.†

For (BTMA)₂[Fe₄S₄Br₂Cl₂] (2), (BTMA)₂[Fe₄S₄Cl₂I₂] (3) and (BTMA)₂[Fe₄S₄Br₂I₂] (4), LT single crystal data were collected at 173(2) K and for (BTMA)₂[Fe₄S₄Cl₂I₂] (3) at 293(2) K using an Oxford Diffraction Xcalibur Gemini Eos diffractometer using graphite-monochromated Mo-K_α radiation (λ = 0.71073 Å). The crystals were transferred under argon to Paratone oil and mounted on a nylon loop. For cooling, cold dry air was provided by an Oxford Cryosystems Desktop Cooler. CrysAlis Pro,¹²¹ from Oxford Diffraction, was used to collect the initial frames for determination of the unit cell. Subsequently, the program was used to plan a data collection. In most cases, a full sphere of data were collected. After collection, data reduction was carried out with the Crysalis Pro suite and multiscan absorption correction was carried out (SCALE3 ABSPACK scaling algorithm).¹²² The space group selection was made using the inbuilt program, GRAL, which selected the monoclinic space group Cc for all structures. The output files were used for initial structure solution using SHELXle¹²³ or Olex2.¹¹⁵ Subsequently, the structures were refined using SHELXL 2018/1.^117,118 The mixed-halide clusters showed signs of disorder and this was modelled at first by allowing the occupancies for the halide ligands to refine freely. In the final refinement, the occupancies of the disordered pairs of halides, i.e., bromide and chloride, iodide and chloride, or bromide and iodide, were restrained using the SUMP command (SHELXL).^117,118 In all cases, this strategy resulted to be more adequate to treat the data and obtain better quality refinement indicators and realistic Fe–X and X⋯Y distances. The CCDC Deposition Numbers are 2048376, 2048378, 2048375 (173 K) and 2048954 (293 K) for (BTMA)₂[Fe₄S₄Br₂Cl₂] (2), (BTMA)₂[Fe₄S₄Cl₂I₂] (3), and (BTMA)₂[Fe₄S₄Br₂I₂] (4), respectively.†

The selected bond lengths and angles of the compounds were calculated using the PLATON software.¹²⁴ The graphical representations were done by Mercury¹²⁵ and PyMOL,¹²⁶ and the editing of CIF files was performed using the PublCif¹²⁷ software.

Synchrotron X-ray powder diffraction data collection was performed at DESY (Hamburg, beamline P02.1, storage ring Petra III with λ = 0.207203 Å and a PerkinElmer XRD 1621 flat panel detector). The samples were measured in capillaries sealed under an argon atmosphere (0.5 mm diameter). The collected data was transformed with Fit2d¹²⁸ and analysed with WinXPow.¹²⁹

The ⁵⁷Fe Mössbauer data were recorded in the transmission geometry using a constant acceleration spectrometer operated in conjunction with a 512-channel analyser in the time-scale mode (WissEl GmbH) using Wissoft 2003. The detector consisted of a proportional counter and the source contained ⁵⁷Co diffused in Rh with an activity of 1.4 GBq. The spectrometer was calibrated against α-iron at room temperature. Sample cooling to 77 K was achieved by placing the samples in a continuous flow cryostat from Oxford Instruments. The spectral data were transferred from the multi-channel analyser to a PC for further analysis employing the public domain program Vinda¹³⁰ running on the Microsoft Excel 2003® platform. The spectra were analysed by least-squares fits using Lorentzian line shapes.

The magnetic measurements were performed with a Quantum Design MPMS-XL-7 SQUID magnetometer using powdered microcrystalline samples. The variable temperature susceptibility data were collected in the temperature range of 2 to 300 K under an applied field of 0.1 Tesla. The experimental susceptibility data were corrected for the temperature-dependent magnetic contribution of the holder and the underlying diamagnetism using Pascal's constants.

Author contributions

AOS: investigation, data curation, visualisation, writing – original draft, and funding acquisition. BMR: investigation, data curation, and visualisation. FDS: data curation, visualisation, and supervision. LC: investigation, data curation, validation, and visualisation. VKG: investigation, data curation, and visualisation. FD: methodology, validation, project administration, supervision, and funding acquisition. ERE: methodology, validation, and supervision. VS: methodology, validation, and supervision. UR: methodology, validation, project administration, supervision, funding acquisition, and writing – review and editing. AK: methodology, validation, project administration, supervision, and writing – review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful to Peter Kliesen, Malgorzata Smolarek and Silke Kremer (Department of Chemistry, University of Cologne) for single crystal X-ray diffraction, IR spectroscopy and microanalysis data collection. We are indebted to HASYLAB at DESY (Hamburg, Germany) for the kind support with synchrotron radiation. AOS acknowledges the German Academic Exchange Programme (DAAD) for traveling grants (EuroBIC 10 Thessaloniki, Greece & EuroBIC 11 Granada, Spain) and CONICET for financial support (Código de Beca: 105 201301 00912 CO).

References

1. W. Kaim, B. Schwederski and A. Klein, Bioinorganic Chemistry: Inorganic Elements in the Chemistry of Life, Wiley Chichester, 2nd edn, 2013.
2. R. Lill and S.-A. Freibert, Mechanisms of Mitochondrial Iron-Sulfur Protein Biogenesis, Annu. Rev. Biochem., 2020, 89, 471–499.
3. C. C. Lee, M. T. Stiebritz and Y. Hu, Reactivity of [Fe₄S₄] Clusters toward C1 Substrates: Mechanism, Implications, and Potential Applications, Acc. Chem. Res., 2019, 52, 1168–1176.
4. M. K. Johnson and A. D. Smith, in Encyclopedia of Inorganic and Bioinorganic Chemistry, John Wiley & Sons, Ltd, Hoboken NJ, USA, 2011, pp. 2589–2619.
5. C. Greco, M. Bruschi, P. Fantucci, U. Ryde and L. De Gioia, Mechanistic and Physiological Implications of the Interplay among Iron–Sulfur Clusters in [FeFe]-Hydrogenases. A QM/MM Perspective, J. Am. Chem. Soc., 2011, 133, 18742–18749.
6. H. Beinert, R. H. Holm and E. Münck, Iron-Sulfur Clusters: Nature's Modular, Multipurpose Structures, Science, 1997, 277, 653–659.
7. D. C. Johnson, D. R. Dean, A. D. Smith and M. K. Johnson, Structure, Function, and Formation of Biological Iron-Sulfur Clusters, Annu. Rev. Biochem., 2005, 74, 247–281.
8. H. Beinert, Iron-sulfur proteins: ancient structures, still full of surprises, J. Biol. Inorg. Chem., 2000, 5, 2–15.
9. B. Srour, S. Gervason, B. Monfort and B. D'Autréaux, Mechanism of Iron–Sulfur Cluster Assembly: In the Intimacy of Iron and Sulfur Encounter, Inorganics, 2020, 8, 55.
10. S. J. Mayr, R.-R. Mendel and G. Schwarz, Molybdenum cofactor biology, evolution and deficiency, Biochim. Biophys. Acta, Mol. Cell Res., 2021, 1868, 118883.
11. Y. Bai, T. Chen, T. Happe, Y. Lu and A. Sawyer, Iron–sulphur cluster biogenesis via the SUF pathway, Metallomics, 2018, 10, 1038–1052.
12. A. McSkimming and D. L. M. Suess, Selective Synthesis of Site-Differentiated Fe₄S₄ and Fe₆S₆ Clusters, Inorg. Chem., 2018, 57, 14904–14912.
13. S. Ohta and Y. Ohki, Impact of Ligands and Media on the Structure and Properties of Biological and Biomimetic Iron-Sulfur Clusters, Coord. Chem. Rev., 2017, 338, 207–225.
14. R. H. Holm and W. Lo, Structural Conversions of Synthetic and Protein-Bound Iron−Sulfur Clusters, Chem. Rev., 2016, 116, 13685–13713.
15. S. C. Lee, W. Lo and R. H. Holm, Developments in the Biomimetic Chemistry of Cubane-Type and Higher Nuclearity Iron–Sulfur Clusters, Chem. Rev., 2014, 114, 3579–3600.
16. K. Tanifuji, N. Yamada, T. Tajima, T. Sasamori, N. Tokitoh, T. Matsuo, K. Tamao, Y. Ohki and K. Tatsumi, A Convenient Route to Synthetic Analogues of the Oxidized Form of High-Potential Iron–Sulfur Proteins, Inorg. Chem., 2014, 53, 4000–4009.
17. A. Alwaaly, I. Dance and R. A. Henderson, Unexpected explanation for the enigmatic acid-catalysed reactivity of [Fe₄S₄X₄]²⁻ clusters, Chem. Commun., 2014, 50, 4799–4802.
18. I. Dance and R. A. Henderson, Large structural changes upon protonation of Fe₄S₄ clusters: the consequences for reactivity, Dalton Trans., 2014, 43, 16213–16226.
19. I. Span, K. Wang, W. Wang, J. Jauch, W. Eisenreich, A. Bacher, E. Oldfield and M. Groll, Structures of Fluoro, Amino, and Thiol Inhibitors Bound to the [Fe₄S₄] Protein IspH, Angew. Chem., Int. Ed., 2013, 52, 2118–2121.
20. D. L. Gerlach, D. Coucouvanis and N. Lehnert, Connecting [4Fe–4S] Clusters and Hemes – Towards Modeling the Active Site of Sulfite Reductase, Eur. J. Inorg. Chem., 2013, 2013, 3883–3890.
21. D. L. Gerlach, D. Coucouvanis, J. Kampf and N. Lehnert, Isolation and Characterization of Single and Sulfide-Bridged Double [4Fe–4S] Cubane Clusters with 4-Pyridinethiolato Ligands, Eur. J. Inorg. Chem., 2013, 2013, 5253–5264.
22. P. V. Rao and R. H. Holm, Synthetic Analogues of the Active Sites of Iron-Sulfur Proteins, Chem. Rev., 2004, 104, 527–559.
23. R. H. Holm, in Comprehensive Coordination Chemistry II, Pergamon, Oxford, 2003, 61–90.
24. R. H. Holm, [1:3] Site-differentiated and sulfide-bridged cubane clusters in chemistry and biology, Pure Appl. Chem., 1998, 70, 931–938.
25. T. D. P. Stack, J. A. Weigel and R. H. Holm, The Cavitand Concept in the Synthesis of Subsite-Differentiated Analogues of Biological [4Fe-4S/Se]²⁺ Clusters: Cluster Capture Reactions, Ligand Conformational Analysis, and the Structure of a Trigonal [4Fe-4Se]²⁺ Analogue, Inorg. Chem., 1990, 29, 3745–3760.
26. R. H. Holm, Synthetic approaches to the active sites of iron-sulfur proteins, Acc. Chem. Res., 1977, 10, 427–434.
27. Y. Shim, R. M. Young, A. P. Douvalis, S. M. Dyar, B. D. Yuhas, T. Bakas, M. R. Wasielewski and M. G. Kanatzidis, Enhanced Photochemical Hydrogen Evolution from Fe₄S₄-Based Biomimetic Chalcogels Containing M²⁺ (M = Pt, Zn, Co, Ni, Sn) Centers, J. Am. Chem. Soc., 2014, 136, 13371–13380.
28. Y. Shim, B. D. Yuhas, S. M. Dyar, A. L. Smeigh, A. P. Douvalis, M. R. Wasielewski and M. G. Kanatzidis, Tunable Biomimetic Chalcogels with Fe₄S₄ Cores and [Sn_nS_2n+2]⁴⁻ (n = 1, 2, 4) Building Blocks for Solar Fuel Catalysis, J. Am. Chem. Soc., 2013, 135, 2330–2337.
29. J. B. Varley, H. A. Hansen, N. L. Ammitzøll, L. C. Grabow, J. Rossmeisl and J. K. Nørskov, Ni−Fe−S Cubanes in CO₂ Reduction Electrocatalysis: A DFT Study, ACS Catal., 2013, 3, 2640–2643.
30. J. Liu, M. S. Kelley, W. Wu, A. Banerjee, A. P. Douvalis, J. Wu, Y. Zhang, G. C. Schatz and M. G. Kanatzidis, Nitrogenase-mimic iron-containing chalcogels for photochemical reduction of dinitrogen to ammonia, Proc. Natl. Acad. Sci. U. S. A., 2016, 133, 5530–5535.
31. V. C.-C. Wang, M. Can, E. Pierce, S. W. Ragsdale and F. A. Armstrong, A Unified Electrocatalytic Description of the Action of Inhibitors of Nickel Carbon Monoxide Dehydrogenase, J. Am. Chem. Soc., 2013, 135, 2198–2206.
32. B. D. Yuhas, A. L. Smeigh, A. P. Samuel, Y. Shim, S. Bag, A. P. Douvalis, M. R. Wasielewski and M. G. Kanatzidis, Biomimetic Multifunctional Porous Chalcogels as Solar Fuel Catalysts, J. Am. Chem. Soc., 2011, 133, 7252–7255.
33. C. J. Pickett, S. K. Ibrahim and D. L. Hughes, Polyferredoxin-based electrode materials, Faraday Discuss., 2000, 116, 235–244.
34. M. Akhtar, J. Akhter, M. A. Malik, P. O'Brien, F. Tuna, J. Raftery and M. Helliwell, Deposition of iron sulfide nanocrystals from single source precursors, J. Mater. Chem., 2011, 21, 9737–9745.
35. P. V. Vanitha and P. O'Brien, Phase Control in the Synthesis of Magnetic Iron Sulfide Nanocrystals From a Cubane-Type Fe−S Cluster, J. Am. Chem. Soc., 2008, 130, 17256–17257.
36. G. B. Wong, M. A. Bobrik and R. H. Holm, Inorganic Derivatives of Iron Sulfide Thiolate Dimers and Tetramers: Synthesis and Properties of the Halide Series [Fe₂S₂X₄]²⁻ and [Fe₄S₄X₄]²⁻ (X = Cl, Br, I), Inorg. Chem., 1978, 17, 578–584.
37. A. Müller, N. H. Schladerbeck, E. Krickemeyer, H. Bögge, K. Schmitz, E. Bill and A. X. Trautwein, Darstellung von Metall-Schwefel-Clustern durch einfache Reaktion von Metallsalzen mit H₂S: R₂(NH₄)[Cu₃S₁₂], R₂[Cu₄S₁₂].CH₃CN, R₂[Cu₄S_12.8], R₂[Fe₂S₂(S₅)₂], R₂[Fe₄S₄Br₄], R₂[Fe₄S₄Br₂Cl₂], R₂[Fe₄S₄Cl₄], R₂[Fe₂S₂Cl₄] (R = PPh₄) und [Fe(DMF)₆][Fe₂S₂Cl₄], Z. Anorg. Allg. Chem., 1989, 570, 7–36.
38. W. Saak and S. Pohl, Iodine Substituted Iron-Sulfur-Clusters: Novel Syntheses, Formation and Stability of Fe₂S₂I₄²⁻, Fe₄S₄I₄²⁻ and Fe₆S₆I₆²⁻. The Crystal Structure of (Et₄N)₆(Fe₄S₄I₄)₂Fe₂S₂I₄, Z. Naturforsch., B: Anorg. Chem., Org. Chem., 1985, 40b, 1105–1112.
39. W. Saak and S. Pohl, Fe₄S₄I₂(SPPh₃)₂: a Neutral, Mixed Terminal Ligand Iron-Sulfur Cluster, Z. Naturforsch., B: J. Chem. Sci., 1988, 43b, 813–817.
40. S. Pohl and W. Saak, Structural Distortion of Fe₄S₄I₄²⁻ Clusters through Iodine-Iodine Contacts: Crystal Structures of (Ph₄P)₂Fe₄S₄I₄ and (Me₃NCH₂Ph)₂Fe₄S₄I₄, Z. Naturforsch., B: J. Chem. Sci., 1988, 43b, 457–462.
41. B. M. Segal, H. R. Hoveyda and R. H. Holm, Terminal Ligand Assignments Based on Trends in Metal-Ligand Bond Lengths of Cubane-Type [Fe₄S₄]^2+,+ Clusters, Inorg. Chem., 1998, 37, 3440–3443.
42. M. A. Bobrik, K. O. Hodgson and R. H. Holm, Inorganic Derivatives of Iron-Sulfide-Thiolate Dimers and Tetramers. Structures of Tetrachloro-p-disulfido-diferrate(III) and Tetrakis(chloro-μ₃-sulfido-iron) Dianions, Inorg. Chem., 1977, 16, 1851–1858.
43. K. Bates, L. Johnson and R. A. Henderson, Mechanism of the Reactions of Synthetic Fe-S-Based Clusters with PhCOCl: Parallel Pathways Involving Free and Coordinated Thiolate as Nucleophiles, Inorg. Chem., 2006, 45, 9423–9433.
44. K. Bates, M. Wouldhave and R. A. Henderson, Involvement of thiolate ligands in binding substrates to Fe–S clusters, Dalton Trans., 2008, 2008, 6527–6529.
45. K. Bates and R. A. Henderson, Binding Nucleophiles to [Fe4Y4Cl4]2⁻ (Y = S or Se) can Increase or Suppress the Rate of Proton Transfer to the Cluster, Inorg. Chem., 2008, 47, 5850–5858.
46. A. Kern, C. Näther and F. Tuczek, Application of a Universal Force Field to Mixed Fe/Mo-S/Se Cubane and Heterocubane Clusters. 1. Substitution of Sulfur by Selenium in the Series [Fe₄X₄(YCH₃)₄]²⁻; X = S/Se and Y = S/Se, Inorg. Chem., 2004, 43, 5003–5010.
47. A. Kern, C. Näther and F. Tuczek, Application of a Universal Force Field to Mixed Fe/Mo-S/Se Cubane and Heterocubane Clusters. 2. Substitution of Iron by Molybdenum in Fe₄(S/Se)₄ Clusters with Terminal Halide and Thiolate Ligands, Inorg. Chem., 2004, 43, 5011–5020.
48. A. O. Schüren, V. K. Gramm, M. Dürr, A. Foi, I. Ivanović-Burmazović, F. Doctorovich, U. Ruschewitz and A. Klein, Halide coordinated homoleptic [Fe₄S₄X₄]²⁻ and heteroleptic [Fe₄S₄X₂Y₂]²⁻ clusters (X, Y = Cl, Br, I)—alternative preparations, structural analogies and spectroscopic properties in solution and solid state, Dalton Trans., 2016, 45, 361–375.
49. T. M. M. Al-Rammahi, P. G. Waddell and R. A. Henderson, X-ray crystal structures of [NHR₃]₂[Fe₄S₄X₄] (X = PhS, R = Et or ⁿBu; X = Cl, R = ⁿBu): implications for sites of protonation in Fe–S clusters, Transition Met. Chem., 2016, 41, 1–7.
50. P. K. Mascharak, K. S. Hagen, J. T. Spence and R. H. Holm, Structural Distortions of the [Fe₄S₄]²⁺ Core of [Fe₄S₄(S-t-C₄H₉)₄]²⁻ in Different Crystalline Environments and Detection and Instability of Oxidized ([Fe₄S₄]³⁺) Clusters, Inorg. Chim. Acta, 1983, 80, 157–170.
51. K. S. Hagen, J. G. Reynolds and R. H. Holm, Definition of Reaction Sequences Resulting in Self-Assembly of [Fe₄S₄(SR)₄]²⁻ Clusters from Simple Reactants, J. Am. Chem. Soc., 1981, 103, 4054–4063.
52. J. B. Willems and M. Köckerling, Synthesis and structure of an unprecedented high-symmetry [Fe₄S₄Cl₄] cubane-type unit in supramolecular [K₄(FeCl₄)(C₁₂H₂₄O₆)₄][Fe₄S₄Cl₄], Chem. Commun., 2001, 2001, 1380–1381.
53. M. Kawano, C. Hoshino, K. Sakai and K. Matsumoto, Crystal Structure of cis-Bis(acetonitrile)tetrakis(trimethylphosphite)iron(II) Tetrachlorotetrakis(μ³-sulfido)tetra-ferrate (2II, 2III), Anal. Sci., 1991, 7, 829–830.
54. A. C. M. Young, M. A. Walters and J. C. Dewan, Structure of [N(C₄H₉)₄]₂[Fe(C₃H₇NO)₆][Fe₄Br₄S₄]₂, Acta Crystallogr., Sect. C: Struct. Chem., 1989, 45, 1733–1736.
55. D. Coucouvanis, M. G. Kanatzidis, E. Simhon and N. C. Baenziger, Synthesis, Molecular Structure, and Reactions of Bis(tetraphenylphosphonium) Hexakis(μ-thiophenolato)-tetrachlorotetraferrate(II), (Ph₄P)₂[Fe₄(SPh)₆Cl₄]. Its Reactions with Dibenzyl Trisulfide and the Synthesis of the [Fe₄S₄Cl₄]²⁻ and [Fe₄S₄(Cl)₂(SC₆H₅)₂]²⁻ “Cubane”-Type Clusters, J. Am. Chem. Soc., 1982, 104, 1874–1882.
56. M. G. Kanatzidis, N. C. Baenziger, D. Coucouvanis, A. Simopoulos and A. Kostikas, Synthesis, Structural -Characterization, and Electronic Structures of the “Mixed” Terminal Ligand Cubanes [Fe₄S₄Cl₂(XC₆H₅)₂]²⁻ (X = S, O) and [Fe₄S₄(SC₆H₅)₂(OC₆H₄-p-CH₃)₂]²⁻. The First Examples of [Fe₄S₄]²⁺ Cores with a Noncompressed D_2d Idealized Geometry, J. Am. Chem. Soc., 1984, 106, 4500–4511.
57. M. G. Kanatzidis, D. Coucouvanis, A. Simopoulos, A. Kostikas and V. Papaefthymiou, Synthesis, Structural Characterization, and Electronic Properties of the Ph₄P⁺ Salts of the Mixed Terminal Ligand Cubanes Fe₄S₄(Et₂Dtc)_n(X)_4−n²⁻ (X = Cl⁻, PhS⁻) (n = 1, 2). Two Different Modes of Ligation on the [Fe₄S₄]²⁺ Core, J. Am. Chem. Soc., 1985, 107, 4925–4935.
58. M. Kanatzidis, M. Ryan, D. Coucouvanis, A. Simopoulos and A. Kostikas, Synthesis and Structural Characterization of Bis(tetraphenylphosphonium) Bis(diethyldithiocarbamato)bis(thiophenolato)tetrakis(μ₃-sulfido)tetraferrate(2II,2III), (Ph₄P)₂[Fe₄S₄(SPh)₂(Et₂dtc)₂]. A “Cubane” Type Cluster with Mixed Terminal Ligands and Two Different Modes of Ligation on the Fe₄S₄ Core, Inorg. Chem., 1983, 22, 179–181.
59. S. Rutchik, S. Kim and M. A. Walters, Facile One-Step Synthesis of Fe₄Q₄²⁺ (Q = S, Se) Cubane-like Centers, Inorg. Chem., 1988, 27, 1513–1516.
60. S. Pohl and U. Bierbach, [Fe₄S₄]²⁺-Clusters with Thiourea Ligands: [Fe_IL₃][Fe₄S₄I₃L] (L = (Me₂N)₂CS) and [Fe₄S₄I₂L’₂] (L′ = (C₄H₉NH)₂CS), Z. Naturforsch., B: J. Chem. Sci., 1991, 46b, 68–74.
61. U. Bierbach, W. Saak, D. Haase and S. Pohl, Neutral and Cationic Iron-Sulfur Complexes and Clusters - Syntheses and Crystal Structures of [Fe(SR)₂L₂]·PhMe and [Fe₄S₄(SR)₂L₂], and on the Formation of [Fe(SR)L₃]⁺, [FeL₄]²⁺, [Fe₄S₄(SR)L₃]⁺ and [Fe₄S₄L₄]²⁺ (R = 2,4,6-i-Pr₃C₆H₂; L = SC(NMe₂)₂), Z. Naturforsch., B: J. Chem. Sci., 1991, 46b, 1629–1634.
62. P. Zanello, The competition between chemistry and biology in assembling iron–sulfur derivatives. Molecular structures and electrochemistry. Part V. {[Fe₄S₄](S^γCys)₄} proteins, Coord. Chem. Rev., 2017, 335, 172–227.
63. T. Terada, K. Hirabayashi, D. Liu, T. Nakamura, T. Wakimoto, T. Matsumoto and K. Tatsumi, [3:1] Site-Differentiated [4Fe−4S] Clusters Having One Carboxylate and Three Thiolates, Inorg. Chem., 2013, 52, 11997–12004.
64. L. Deng, A. Majumdar, W. Lo and R. H. Holm, Stabilization of 3:1 Site-Differentiated Cubane-Type Clusters in the [Fe₄S₄]¹⁺ Core Oxidation State by Tertiary Phosphine Ligation: Synthesis, Core Structural Diversity, and S = 1/2 Ground States, Inorg. Chem., 2010, 49, 11118–11126.
65. E. P. L. van der Geer, Q. Li, G. van Koten, R. J. M. Klein Gebbink and B. Hessen, N-Substituted indole-3-thiolate [4Fe–4S] clusters with a unique and tunable combination of spectral and redox properties, Inorg. Chim. Acta, 2008, 361, 1811–1818.
66. C. Walsdorff, W. Saak and S. Pohl, A new preorganized tridentate ligand bearing three indolethiolategroups. Preparation of 3:1 subsite-differentiated Fe₄S₄ clusters, J. Chem. Soc., Dalton Trans., 1997, 1857–1861.
67. C. Zhou and R. H. Holm, Comparative Isotropic Shifts, Redox Potentials, and Ligand Binding Propensities of [1:3] Site-Differentiated Cubane-Type [Fe₄Q₄]²⁺ Clusters (Q=S, Se), Inorg. Chem., 1997, 36, 4066–4077.
68. J. Zhou, Z. Hu, E. Münck and R. H. Holm, The Cuboidal Fe₃S₄ Cluster: Synthesis, Stability, and Geometric and Electronic Structures in a Non-Protein Environment, J. Am. Chem. Soc., 1996, 118, 1966–1980.
69. F. Osterloh, W. Saak and S. Pohl, Unidentate and Bidentate Binding of Nickel(II) Complexes to an Fe₄S₄ Cluster Via Bridging Thiolates: Synthesis, Crystal Structures, and Electrochemical Properties of Model Compounds for the Active Sites of Nickel Containing CO Dehydrogenase/Acetyl-CoA Synthase, J. Am. Chem. Soc., 1997, 119, 5648–5656.
70. C. Goh, J. A. Weigel and R. H. Holm, The [2:2] Site-Differentiated Clusters [Fe₄S₄L₂(RNC)₆] Containing Two Low-Spin Iron(II) Sites, Inorg. Chem., 1994, 33, 4861–4868.
71. J. A. Weigel, K. K. P. Srivastava, E. P. Day, E. Münck and R. H. Holm, Isonitrile Binding to a Site-Differentiated Synthetic Analogue of Biological [4Fe-4S] Clusters: Equilibria, Magnetic Interactions and the Spin-Isolated [3Fe-4S] Cluster Fragment, and the Structure of a Low-Spin Iron(II) Subsite, J. Am. Chem. Soc., 1990, 112, 8015–8023.
72. J.-M. Mouesca and B. Lamotte, Iron–sulfur clusters and their electronic and magnetic properties, Coord. Chem. Rev., 1998, 178–180, 1573–1614.
73. R. E. Johnson, G. C. Papaefthymiou, R. B. Frankel and R. H. Holm, Effects of Secondary Bonding Interactions on the [Fe₄S₄]²⁺ Core of Ferredoxin Site Analogues: [Fe₄S₄(SC₆H₄-o-OH)₄]²⁻, a Distorted Cubane-Type Cluster with One Five-Coordinate Iron Atom, J. Am. Chem. Soc., 1983, 105, 7280–7287.
74. W. E. Cleland, D. A. Holtman, M. Sabat, J. A. Ibers, G. C. DeFotis and B. A. Averill, Effects of Phenoxide Ligation on Iron-Sulfur Clusters. Preparation and Properties of [Fe₄S₄(OAr)₄]²⁻ Ions and the Structure of [(C₂H₅)₄N]₂[Fe₄S₄(OC₆H₅)₄], J. Am. Chem. Soc., 1983, 105, 6021–6031.
75. S. J. Yoo, Z. Hu, C. Goh, E. L. Bominaar, R. H. Holm and E. Münck, Determination of the Exchange-Coupling Constant of an Fe³⁺-Fe³⁺ Pair in a Cubane-Type Iron-Sulfur Cluster, J. Am. Chem. Soc., 1997, 119, 8732–8733.
76. E. L. Bominaar, S. A. Borshch and J.-J. Girerd, Double-Exchange and Vibronic Coupling in Mixed-Valence Systems. Electronic Structure of [Fe₄S₄]³⁺ Clusters in High-Potential Iron Protein and Related Models, J. Am. Chem. Soc., 1994, 116, 5362–5312.
77. G. C. Papaefthymiou, E. J. Laskowski, S. Frota-Pessoa, R. B. Frankel and R. H. Holm, Antiferromagnetic Exchange Interactions in [Fe₄S₄(SR)₄]₂ Clusters, Inorg. Chem., 1982, 21, 1723–1728.
78. L. M. Lawson Daku, J. Pecaut, A. Lenormand-Foucaut, B. Vieux-Melchior, P. Iveson and J. Jordanov, Investigation of the Reduced High-Potential Iron−Sulfur Protein from Chromatium vinosum and Relevant Model Compounds: A Unified Picture of the Electronic Structure of [Fe₄S₄]²⁺ Systems through Magnetic and Optical Studies, Inorg. Chem., 2003, 42, 6824–6850.
79. K. Kimura, H. Inokuchi, H. Nanami and T. Yagi, Magnetic Susceptibility of Hydrogenase from Desulfovibrio vulgaris, J. Biochem., 1985, 97, 1831–1833.
80. M. Belinskii, Spin coupling model for tetrameric iron clusters in ferredoxins. II. Hyperfine interactions, magnetism, high-spin systems, Chem. Phys., 1993, 172, 213–238.
81. T. D. P. Stack and R. H. Holm, Subsite-Specific Functionalization of the [4Fe-4S]²⁺ Analogue of Iron-Sulfur Protein Clusters, J. Am. Chem. Soc., 1987, 109, 2546–2547.
82. E. Victor and S. J. Lippard, A Tetranitrosyl [4Fe−4S] Cluster Forms En Route to Roussin's Black Anion: Nitric Oxide Reactivity of [Fe₄S₄(LS₃)L′]²⁻, Inorg. Chem., 2014, 53, 5311–5320.
83. C. Walsdorff, W. Saak, D. Haase and S. Pohl, A preorganised doubly tripodal hexathiol: syntheses and crystal structures of complexes with two 3:1 subsite-differentiated Fe₄S₄ clusters, Chem. Commun., 1997, 1997, 1931–1932.
84. K. S. Hagen and M. Uddin, A Continuous Symmetry Measure of [4Fe-4S]⁺ Core Distortions and Analysis of Supramolecular Synthons in Crystal Structures of (Et₄N)₃[Fe₄S₄Cl₄]·Et₄NCl at 100 and 295 K, Inorg. Chem., 2008, 47, 11807–11815.
85. M. G. Kanatzidis, A. Salifoglou and D. Coucouvanis, Chemistry of [Fe₆S₆]³⁺ Prismatic Cages. Synthesis, Structural Characterization, and Electronic Structures of the [Et₄N]₃[Fe₆S₆L₆] Clusters (L = p-CH₃C₆H₄O⁻,Br⁻), Inorg. Chem., 1986, 25, 2460–2468.
86. M. G. Kanatzidis, W. R. Hagen, W. R. Dunham, R. K. Lester and D. Coucouvanis, Metastable Fe/S Clusters. The Synthesis, Electronic Structure, and Transformations of the [Fe₆S₆(L)₆]³⁻ Clusters (L=Cl⁻, Br⁻, I⁻, RS⁻, RO⁻) and the Structure of [(C₂H₅)₄N]₃[Fe₆S₆Cl₆], J. Am. Chem. Soc., 1985, 107, 953–961.
87. D. Coucouvanis, M. G. Kanatzidis, A. Salifoglou and W. R. Dunham, Spectroscopic and Structural Evidence of Temperature Dependent Charge Localization and Structural Differentiation of the Fe Sites within the [Fe₆S₆X₆]²⁻ Clusters (X = Cl, Br), J. Am. Chem. Soc., 1987, 109, 6863–6865.
88. M. G. Kanatzidis, W. R. Dunham, W. R. Hagen and D. Coucouvanis, A New Iron-Sulphide Cluster containing the ‘Prismane’ [Fe₆(μ-S)₆]³⁺ Core. Synthesis, Structure, and Properties of [Et₄N]₃[Fe₆S₆Cl₆], J. Chem. Soc., Chem. Commun., 1984, 1984, 356–358.
89. D. J. Evans, G. García, M. D. Santana and M. C. Torralba, About the synthesis of the prismane [NEt₄]₂[Fe₆S₆I₆], Inorg. Chim. Acta, 1999, 284, 296–299.
90. D. Coucouvanis, M. G. Kanatzidis, W. R. Dunham and W. R. Hagen, Oxidative Transformation of the [Fe₄S₄X₄]²⁻ “Cubanes” to the [Fe₆S₆X₆]²⁻ “Prismane” Clusters (X = Cl, Br). The Crystal and Molecular Structure of [(C₆H₅)₄P]₂Fe₆S₆Cl₆], J. Am. Chem. Soc., 1984, 106, 7998–7999.
91. W. Saak and S. Pohl, Spontaneous Self Assembly of an Octanuclear Iron-Nickel Cluster by Reaction of [Fe₆S₆I₆]²⁻ with [NiI₄]²⁻, Angew. Chem., Int. Ed. Engl., 1991, 30, 881–883.
92. K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds: Applications in Coordination, Organometallic, and Bioinorganic Chemistry, Part B, John Wiley & Sons, 5. edn, 1997.
93. D. Mitra, S. J. George, Y. Guo, S. Kamali, S. Keable, J. W. Peters, V. Pelmenschikov, D. A. Case and S. P. Cramer, Characterization of [4Fe-4S] Cluster Vibrations and Structure in Nitrogenase Fe Protein at Three Oxidation Levels via Combined NRVS, EXAFS, and DFT Analyses, J. Am. Chem. Soc., 2013, 135, 2530–2543.
94. Y. Xiao, M. Koutmos, D. A. Case, D. Coucouvanis, H. Wang and S. P. Cramer, Dynamics of an [Fe₄S₄(SPh)₄]²⁻ cluster explored via IR, Raman, and nuclear resonance vibrational spectroscopy (NRVS)-analysis using ³⁶S substitution, DFT calculations, and empirical force fields, J. Chem. Soc., Dalton Trans., 2006, 2192–2201.
95. T. Steiner, The hydrogen bond in the solid state, Angew. Chem., Int. Ed., 2002, 41, 48–76.
96. A. Bondi, van der Waals Volumes and Radii, J. Phys. Chem., 1964, 68, 441–451.
97. R. S. Rowland and R. Taylor, Intermolecular Nonbonded Contact Distances in Organic Crystal Structures: Comparison with Distances Expected from van der Waals Radii, J. Phys. Chem., 1996, 100, 7384–7391.
98. M. L. Connolly, Computation of molecular volume, J. Am. Chem. Soc., 1985, 107, 1118–1124.
99. R. D. Shannon, Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides, Acta Crystallogr., Sect. A: Found. Adv., 1976, 32, 751–767.
100. U. Flörke , CSD Communication 2013 (Private Communication), ID code: ZIXBAL.
101. U. Flörke, M. Ayaz and G. Henkel, CSD Communication 2016 (Private Communication). ID code: KABKUW01.
102. V. Schünemann, From Small Molecules to Complex Systems: A Survey of Chemical and Biological Applications of the Mössbauer Effect, Top. Appl. Phys., 2021, 137, 173–219.
103. A. X. Trautwein, E. Bill, E. L. Bominaar and H. Winkler, Iron-containing proteins and related analogs—complementary Mössbauer, EPR and magnetic susceptibility studies, Struct. Bonding, 1991, 78, 1–95.
104. M. Kröckel, A. X. Trautwein, H. Winkler, D. Coucouvanis, A. Kostikas and V. Papaefthymiou, A synthetic iron-containing prismane complex: peculiar electron-delocalization and spin-coupling properties deduced from Mössbauer and magnetization studies, Inorg. Chim. Acta, 1998, 283, 111–117.
105. G. P. F. van Strijdonck, J. A. E. H. van Haare, P. J. M. Honen, R. C. G. M. van den Schoor, M. C. Feiters, J. G. M. van der Linden, J. J. Steggerda and R. J. M. Nolte, Cyclotriveratrylene models for [4Fe–4S] proteins: 3:1 subsite differentiation and modulation of the redox potential, J. Chem. Soc., Dalton Trans., 1997, 1997, 449–462.
106. S. Ciurli, M. Carrié, J. A. Weigel, M. J. Carney, T. D. P. Stack, G. C. Papaefthymiou and R. H. Holm, Subsite-Differentiated Analogues of Native [4Fe-4S]²⁺ Clusters: Preparation of Clusters with Five- and Six-Coordinate Subsites and Modulation of Redox Potentials and Charge Distributions, J. Am. Chem. Soc., 1990, 112, 2654–2664.
107. F. Osterloh, B. M. Segal, C. Achim and R. H. Holm, Reduced Mono-, Di-, and Tetracubane-Type Clusters Containing the [MoFe₃S₄]²⁺Core Stabilized by Tertiary Phosphine Ligation, Inorg. Chem., 2000, 39, 980–989.
108. D. Coucouvanis, A. Salifoglou, M. G. Kanatzidis, W. R. Dunham, A. Simopoulos and A. Kostikas, Synthesis, Structural Characterization, and Electronic Properties of the [Fe₆S₆X₆(M(CO)₃)₂]ⁿ⁻ Anions (M = Mo, W; n = 3, 4; X = Cl, Br, I). Heteronuclear Clusters of Possible Structural Relevance to the Fe/Mo/S Center in Nitrogenase, Inorg. Chem., 1988, 27, 4066–4077.
109. P. W. Anderson and H. Hasegawa, Considerations on double exchange, Phys. Rev., 1955, 100, 675–681.
110. J. T. Henthorn, G. E. Cutsail, T. Weyhermüller and S. DeBeer, Stabilization of intermediate spin states in mixed-valent diiron dichalcogenide complexes, Nat. Chem., 2022, 14, 328–333.
111. G. Blondin and J.-J. Girerd, Value of the β transfer integral in Fe-S clusters, JBIC, J. Biol. Inorg. Chem., 1996, 1, 170–172.
112. M. Kröckel, M. Grodzicki, V. Papaefthymiou, A. X. Trautwein and A. Kostikas, Tuning of electron delocalization in polynuclear mixed-valence clusters by super-exchange and double exchange, JBIC, J. Biol. Inorg. Chem., 1996, 1, 173–176.
113. L. Noodleman, D. A. Case, J.-M. Mouesca and B. Lamotte, Valence electron delocalization in polynuclear iron-sulfur clusters, JBIC, J. Biol. Inorg. Chem., 1996, 1, 177–182.
114. L. J. Farrugia, WinGX and ORTEP for Windows: an update, J. Appl. Crystallogr., 2012, 45, 849–854.
115. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, OLEX2 : A Complete Structure Solution, Refinement and Analysis Program, J. Appl. Crystallogr., 2009, 42, 339–341.
116. M. C. Burla, R. Caliandro, B. Carrozzini, G. L. Cascarano, C. Cuocci, C. Giacovazzo, M. Mallamo, A. Mazzone and G. Polidori, G. Crystal structure determination and refinement via SIR2014, J. Appl. Crystallogr., 2015, 48, 306–309.
117. G. M. Sheldrick, SHELXT – Integrated Space-Group and Crystal-Structure Determination, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
118. G. M. Sheldrick, Crystal structure refinement with SHELXL, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
119. STOE X-RED, Data Reduction Program, Version 1.31/Windows, STOE & Cie, Darmstadt, Germany, 2005.
120. STOE X-SHAPE, Crystal Optimisation for Numerical Absorption Correction, Version 1.06/Windows, STOE & Cie, Darmstadt, Germany, 1999.
121. CrysAlis: Agilent, CrysAlis PRO, Agilent Technologies Ltd Version 1.171.36.28, Oxfordshire, England, 2013.
122. Empirical absorption correction using spherical harmonics, implemented in SCALE3 ABSPACK scaling algorithm within CrysAlisPro software, Version 1.171.34.41, Oxford Diffraction Ltd.
123. C. B. Hübschle, ShelXle: a Qt graphical user interface for SHELXL, J. Appl. Cryst., 2011, 44, 1281–1284.
124. A. L. Spek, Single-crystal structure validation with the program PLATON, J. Appl. Crystallogr., 2003, 36, 7–13.
125. C. F. Macrae, P. R. Edgington, P. McCabe, E. Pidcock, G. P. Shields, R. Taylor, M. Towler and J. van de Streek, Mercury: visualization and analysis of crystal structures, J. Appl. Crystallogr., 2006, 39, 453–457.
126. The PyMOL Molecular Graphics System, Version 1.7.4 Schrödinger, LLC.
127. S. P. Westrip, publCIF: software for editing, validating andformatting crystallographic information files, J. Appl. Crystallogr., 2010, 43, 920–925.
128. A. P. Hammersley, FIT2D, V10.3, ESRF, Grenoble, France, 1998.
129. STOE WinXPow, version 3.01.03, STOE and Cie GmbH, Darmstadt, Germany, 2010.
130. H. P. Gunnlaugsson, Spreadsheet based analysis of Mössbauer spectra, Hyperfine Interact., 2016, 237, 79.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2048374, 2048953, 2055695, 2048377, 2048376, 2048378, 2048375 and 2048954. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2dt03203a

---