 Open Access Article
Open Access ArticleTheoretical study on the mechanism of the hydrogen evolution reaction catalyzed by platinum subnanoclusters†
Keita
Kuge
,
Kosei
Yamauchi
 and
Ken
Sakai
and
Ken
Sakai
 *
*
Department of Chemistry, Faculty of Science, Kyushu University, Motooka 744, Nishi-ku, Fukuoka 819-0395, Japan. E-mail: ksakai@chem.kyushu-univ.jp
First published on 24th November 2022
Abstract
The smallest subnanocluster models of platinum colloid (Ptn) are supposed to diffuse in aqueous media in order to examine their behaviors when they are subjected to the electrocatalytic hydrogen evolution reaction under zero overpotential conditions at pH 0. The DFT approach allows us to clarify the nature of individual proton transfer (PT) and electron transfer (ET) processes together with the importance of relying on concerted proton–electron transfer (CPET) pathways to promote the majority of H* adsorption processes by Ptn subnanoclusters. Although the CPET processes are closely correlated with the Volmer steps (Pt + H+ + e− → Pt–H*) described so far in electrochemistry, our study for the first time points out the essential capability of the Ptn clusters to promote the multiple PT steps without the need to transfer any electrons, revealing the fundamentally high basicity of the naked Ptn clusters (pKa = 27–28 for Pt4, Pt5, and Pt6). The discrete cluster models adopted herein avoid the structural constraints forced by the standard slab models and enable us to discuss the drastic alterations in the geometric and electronic structures of the intermediates given by the consecutive promotion of multiple CPET steps. The weakening of the Pt–H* bond strength with the increasing number of CPET steps is well rationalized by carefully examining the changes in the ν(Pt–H*) vibrational frequencies, the hydricity, and the H2 desorption energy. The behaviors are also correlated with the underpotential and overpotential deposited hydrogen atoms (HUPD and HOPD) discussed in electrochemical studies for many years.
Introduction
Platinum is one of the most highly active electrocatalysts for the hydrogen evolution reaction (HER),1,2 and has been extensively studied due to its activity dependency on the orientation of single-crystalline surfaces.3–7 The reports revealed that Pt(111), Pt(100), and Pt(110) facets exhibit completely different characteristics in hydrogen adsorption, known as a discharge step, as shown in eqn (1).| M + H+ + e− → M–H* (Volmer reaction) | (1) |
| M–H* + H+ + e− → M + H2 (Heyrovsky reaction) | (2) |
| 2M–H* → 2M + H2 (Tafel reaction) | (3) |
The structures of these facets by repeated scanning in the so-called underpotential domain (0.05–0.60 V vs. RHE) were ascertained to last even after tens of hydrogen adsorption–desorption cycles. Moreover, Marković et al. observed a difference in activation barriers together with the HER mechanisms exhibited by these facets (ΔH‡ = 18, 12, and 9.5 kJ mol−1 for Pt(111), Pt(100), and Pt(110), respectively).5 However, such facet-dependences were shown to be totally lost in the overpotential domain (below 0.05 V vs. RHE) where the HER is vigorously promoted, which was attributed to the reconstruction of surface structures.6 For all these facets, a common Tafel slope of 30 mV dec−1, consistent with the Volmer–Tafel mechanism, was evidenced for the HER in the overpotential domain.7 One can suppose that the HER-promoting surfaces afford some cluster-like domains with a non-uniform packing arrangement which deviates from that in the bulk crystal.
In spite of the above-mentioned highly changeable surface structures of platinum electrodes, an approach for examining the geometrical changes given at active sites while promoting the catalysis of the HER is still lacking. The earliest report using the DFT method examined the dissociative H2 adsorption over the Pt(100)-derived planar Pt5 platform with all the adjacent Pt–Pt distances frozen at 2.74 Å,8 and attempted to clarify the relationship between the Pt–H distances and the IR-active Pt–H stretching frequencies for the on-top HOPD atoms (i.e., overpotential deposited H* atoms). The theoretical approach widely accepted in recent years was originally developed by Nørskov et al.,9 in which a three-layered Pt(111)-derived slab was adopted with two surface layers relaxed in geometry and the bottom layer fixed to the crystallographic geometry. By computing the structures of H*-adsorbed metal surfaces, they demonstrated the method of estimating the free energy of H*-adsorption (ΔG(H*) in eV). They further demonstrated a gradual decrease in H* adsorption energy upon increasing the surface H* coverage.10 The ΔG(H*) values estimated using such a method have been widely adopted to reveal how the metals or alloys are suited for hydrogen evolution at enhanced rates.11,12 Vast experimental results so far evidenced that the underpotential deposited H* atoms (HUPD) are tightly bonded to the Pt atoms and suggested to be innocent to the actual H2 evolution.7 Actually, the stepwise H2 adsorption energies computed for small Pt clusters demonstrated a gradual decrease in energy upon increasing the coverage.13 The most recently advanced theoretical approach was made by Santos and Schmickler.1,2 They proposed some useful principles explaining the factors that govern the activity of each metal in the HER, and succeeded to estimate the activation barriers (Eact′s) for the Volmer process at various metal surfaces (H+ + e− → H*)1,2,14 together with the barriers when dihydrogen splits into protons during 2-electron oxidation coupled with H–H bond breaking (H–H → 2H+ + 2e−).15 Their remarkable finding lies in the realization that the Eact′s are largely lowered when the filled d-orbital-based bands (i.e., d bands) can have sufficient overlap in energy with either proton 1s or dihydrogen σ*(1s–1s) orbitals at either the capturing or releasing stage. While these 1s-derived orbitals are passing through the saddle point, the metals with a widely spanning d band near the Fermi level, such as Pt, were shown to greatly lower Eact for both hydrogen evolution and oxidation. The importance of the d band levels together with its spanning range below the Fermi level was suggested to be the key factor for the substantial acceleration in the rate of catalysis. Another important factor they could demonstrate is the long-range interaction between the d band and the hydrogen 1s orbital, which becomes true with third-row transition metals like Pt, Ir, and Re because of the spatially broad nature of the d orbital lobes.1,2 This is not the case for first-row transition metals like Co and Ni. However, what is still lacking in these approaches is the molecular level discussion on the mechanism of catalysis since the changes given in geometrical and electronic structures in local metal cluster domains have been little documented.
Here we attempt to develop the basic concepts required to better understand the structural and electronic alterations at local geometries of metal electrode surfaces based on the theoretical studies on relatively small metal clusters. The study also aims at clarifying the role of cluster domains which may be irregularly formed over the electrode surfaces in the overpotential domain. The basic catalytic properties of relatively small metal clusters can be investigated by treating them as homogeneous species diffusing in solution. This treatment allows us to examine Gibbs free energies, metal oxidation states (e.g., mixed-valence states), spin states, chemical bonding and solvation properties, redox potentials, molecular orbitals (MOs), and so forth. Moreover, the results of such studies can be directly compared with the behaviors of molecular HER catalysts known to exhibit HER activity by diffusing over the electrode surfaces without any physical contact. In particular, the catalytic behaviors of small platinum clusters can be discussed on the basis of the key factors that govern the catalytic activity of Pt(II)-based and other related (e.g., Co(I)- and Ni(II)-based) molecular HER catalysts extensively studied to date.16–20
As previously discussed,18–20 proton-coupled electron transfer (PCET) toward a molecular catalyst intermediate possessing a filled dz2 orbital is considered to afford a metal hydride intermediate owing to the increased basicity at the dz2 donor upon electron injection into the vacant MO in close proximity. By following the standard formalism widely accepted for the organometallic hydride formation reactions, this type of PCET-induced metal hydride formation, for instance by a Pt(II)L-based catalyst (L denotes the ligand), can be described using eqn (4).
| Pt(II)L + H+ + e− → Pt(III)L(H−) | (4) |
This is defined as an oxidative addition reaction as it supposes the formal one-electron oxidation at the Pt center to give a hydride donor upon the PCET event. However, this definition clearly fails to accurately describe the actual events concomitantly proceeding. As described elsewhere,18–20 such reactions may be much more rationally interpreted as protonation at the filled dz2 donor upon one-electron injection into the metal- or ligand-based vacant orbital, as expressed using eqn (5) and (6), where H+-dz2 denotes the protonation occurring at the filled dz2 orbital. The reactions falling into the intermediate category, in which the electron is injected into a metal–ligand hybrid orbital, may also take place.
| Pt(II)L + H+ + e− → Pt(I)L(H+-dz2) | (5) |
| Pt(II)L + H+ + e− → Pt(II)(L−)(H+-dz2) | (6) |
Based on the above considerations, it must be understood that the Volmer reactions at the Ptn clusters may be described in three different ways, as given using eqn (7)–(9).
| Ptn + H+ + e− → Ptn(H*) (classical) | (7) |
| Ptn + H+ + e− → Pt(0)n−1Pt(I)(H−) (formal) | (8) |
| Ptn + H+ + e− → Pt(0)n−1Pt(−I)(H+) (actual) | (9) |
In the above context, one can understand that eqn (9) is best suited to describe the actual phenomena that take place upon promoting PCET. As we describe in this paper, Ptn clusters are fundamentally made up of (6s)1(5d)9 metal centers and thereby both the 6s and 5d orbitals are responsible for the stabilization of metal–metal bonding together with the electron charging undertaken at H* adsorption steps. It should also be noted that eqn (9) may also fail in describing the actual electronic systems if there is any specific valence delocalization in clusters, as described for the so-called mixed-valence platinum blues having a nonintegral oxidation state like Pt(2.25+) (formally, Pt(II)3Pt(III)).21–24
In the present study, we first develop the concept of covalent bonding in Pt0n clusters (n < 14), demonstrating that each Pt0 center has a maximum capacity for accepting donors or electrons. We next generalize the basic structural aspects of the Pt0n clusters together with their simplest H*-adsorbed products. Variations in the Pt–Pt and Pt–H* bond distances are used to understand the strength of H* adsorption together with the flexibility in the electron acceptor capacity of the clusters. Finally, several multi-step H* adsorption steps for small Pt0n clusters (n = 1–3) are discussed by constructing the so-called square schemes (see Scheme 1), clarifying that the CPET (concerted proton–electron transfer) paths are primarily favored because of the following two major reasons. One is that ET paths are in general highly endergonic due to the electron rich character of the Ptn clusters. The other is that the PT paths giving Ptn(H+) are often too highly exergonic and the subsequent ET paths affording Ptn(H*) also suffer from the highly endergonic character. In such cases, either the CPET or further PT becomes the realistic pathway to promote. This realization further permits us to examine the involvement of intermediates with the number of protons higher than that of electrons, even though such intermediates have never been discussed to understand the electrode reactions in the past. The strength of Pt–H* bonds in such small models is also discussed in terms of the Pt–H* vibrational frequencies, which is also related to the behaviors of HUPD and HOPD atoms formed in the electrocatalytic HER by platinum electrodes. As demonstrated for the successive H2 adsorption by Ptn clusters,13 we further demonstrate that the feasibility of H2 release from the H*-adsorbed Ptn clusters drastically increases at a higher H* coverage, which is also consistent with the indications from the electrochemical studies.7 Moreover, the most remarkable approach here is to separately examine the transfer of protons and electrons, which has never been explored by others in the past. Electrochemistry indeed cannot handle simple protonation processes due to the lack of electrical responses, which probably led to the lack of awareness on the promotion of PT without ET. Thus, our study here for the first time unveils the highly basic characteristics of the Ptn clusters which themselves can get protonated without accompanying any electron transfer events.
 | ||
| Scheme 1 Three possible PCET pathways for H* adsorption, where PT, ET, and CPET denote proton transfer, electron transfer, and concerted proton–electron transfer, respectively. | ||
Computational methods
General methods
All DFT calculations were performed using either the Gaussian 09 or 16 package of programs.25,26 Geometry optimizations were conducted for various initial structures postulated using M06 hybrid functionals27–29 in combination with the SDD basis set for the Pt atom and the 6-31+G** basis set for the rest of the atoms. The effect of solvation in water was finally taken into consideration using the conductor-like polarizable continuum model (C-PCM) method.30,31 The reduction potentials and pKa values were calculated through Born–Haber thermodynamic cycles shown in Fig. 1A and B, respectively.32,33 In the present study, the structures determined in their gas phase were used to estimate their energies in the aqueous phase (C-PCM), as the validity of using gas-phase-optimized geometries in estimating reduction potentials and pKa values has been well documented in the literature.33–36 The free energies of all chemical species in solution are considered to be in a 1 M standard state, except for the solvent H2O treated to have a 55.6 M standard state. | ||
| Fig. 1 Born–Haber thermodynamic cycles used to compute Gibbs free energy changes upon (A) reduction and (B) proton dissociation. | ||
For the reduction processes, the free energy of reduction in aqueous media, 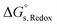 , is expressed using eqn (10), where
, is expressed using eqn (10), where  is the free energy of reduction in the gas phase, and
is the free energy of reduction in the gas phase, and  and
and  are the solvation free energies of the reduced and oxidized species, respectively.
are the solvation free energies of the reduced and oxidized species, respectively.
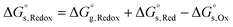 | (10) |
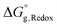 is also corrected for the enthalpy and entropy of electrons by adding −0.868 kcal mol−1 to the free energy of the oxidized species.33 By employing the computed value of
is also corrected for the enthalpy and entropy of electrons by adding −0.868 kcal mol−1 to the free energy of the oxidized species.33 By employing the computed value of  , the reduction potential, E°, is given using eqn (11), where F is the Faraday constant.
, the reduction potential, E°, is given using eqn (11), where F is the Faraday constant.
 | (11) |
The pKa values correlated with the proton dissociation constants Ka′s are similarly calculated as follows. The free energy of deprotonation of an acid in aqueous media,  , is expressed using eqn (12), where
, is expressed using eqn (12), where  is the free energy of deprotonation of the acid in the gas phase, while
is the free energy of deprotonation of the acid in the gas phase, while  ,
,  , and
, and  (265.9 kcal mol−1)35 are the solvation free energies of the acid (AH), the conjugate base (A−), and proton (H+), respectively.
(265.9 kcal mol−1)35 are the solvation free energies of the acid (AH), the conjugate base (A−), and proton (H+), respectively.
 | (12) |
The pKa values are then derived using eqn (13), where R is the gas constant and T is the temperature in Kelvin (298.15 K).
 | (13) |
All the energy diagrams, developed to predict the most likely reaction pathways, are derived from the computed free energy changes associated with (i) the protonation of intermediates due to proton transfer in acidic aqueous media at pH 0 and (ii) the reduction of intermediates at an electrode potential of 0.0 V vs. NHE (zero overpotential). Molecular orbital pictures were generated using GaussView 6.0.16.37
Benchmarking of pKa's and reduction potentials
In order to obtain the most reliable estimates in both calculated pKa values and reduction potentials, extensive efforts were made to judge the validity of our selection in the reference acids and redox couples whose experimental values are reported in the literature. In benchmarking the pKa values, cationic, neutral, and anionic acids were initially selected and their pKa values were computed using the same level of DFT calculations. Table S2† shows a summary of the pKa values of acids computed in this study together with the experimental values reported. As a result of our efforts, it was judged that the most realistic benchmarking results can be attained when the reference acids are limited to the cationic acids (i.e., pyridinium, triethylammonium, pyrrolidinium, guanidinium, and [Pt(NH3)2Cl(H2O)]+). As depicted in Fig. S1A,† six cationic acids were chosen to determine the correlation factor to relate the calculated and experimental pKa values. On the other hand, six redox couples, listed in Table S4,† were chosen to estimate the correlation between the computed and experimental reduction potentials. By assuming the linear correlation of the computed and experimental values with a slope of unity, the correlation factor was determined from the linear fit by using six redox couples (see Fig. S1B†).Results and discussion
Predominant forms of Ptn clusters in aqueous media
The gaseous platinum(0) atom is known to possess a triplet ground state described by [Xe](6s)1(5d)9. When metals are interacting within the clusters or in the crystal lattice, vacant 6s and 5d primarily serve as acceptors in order to form Pt–Pt bonding interactions. The major bonding scheme is known to be given by the sd-based (i.e., 6s,5d-based) hybridization.38,39 Lower contributions of 6p orbitals are well understood by their relatively high energy levels compared to those of 6s orbitals. In the same way, the sd-based orbitals with a vacancy play a major role in H* adsorption, as discussed below. The important new approach in this study is to model the structures of Ptn species under the solvated conditions in aqueous media. With this purpose, all the structures studied here are correlated with the species dissolved in water. Therefore, the first approach is to confirm whether each species accepts donation by water oxygens to give any aqua-coordinated species or not.Fig. 2 depicts the stablest form of each nuclearity system in water before promoting either reduction or protonation. Both the mono- and triplatinum systems stabilize a singlet ground state, while the remaining systems afford a triplet. Although the fundamental structural features are consistent with those computed by others in the literature,40–44 none of the reports carefully discuss the chemical bonding and reactions of such Ptn clusters in solution.
 | ||
| Fig. 2 The stablest forms realized for Ptn clusters (n = 1–5). The values in parentheses are the average Pt–Pt lengths (Table S5; Fig. S6, Tables S64 and S65†). | ||
As shown in Fig. 2 and 3 (see also Fig. S2†), only the monoplatinum can accept aqua ligands. The relative abundances of the naked, monoaqua, and diaqua species in water were estimated by using the equilibrium constants computed for the stepwise formation equilibria shown in Fig. 3. Only the naked Pt01 is a triplet with the 6s and one of the 5d orbitals half-filled (Fig. S2†). Fig. 3 indicates that diaquaplatinum(0) is the sole species in solution, supposing that no hydrolysis takes place in acidic media. This linear 2-coordinate structure has relevance to the linear structure of dichloroplatinum(0) previously supposed to be given prior to the aggregation to yield nanoparticles.45 The lack of ability to form a triaqua species clearly indicates that a single Pt(0) atom can only stabilize the covalent bonding of two aqua ligands. This is in sharp contrast with the 4-coordinate structures stabilized in various platinum(0) phosphine complexes. The linear Oaqua–Pt–Oaqua geometry of diaquaplatinum(0) is stabilized using the sd-hybrid orbital (Fig. S3†), by analogy to the bonding in Au(I) and Cu(I) complexes.38,39 The Pt–Oaqua distances (2.122 Å) in this species are roughly comparable to those in the standard square-planar Pt(II) complexes (e.g., 2.04–2.13 Å for [Pt(OH2)2(bpy)]2+, trans-[PtCl2(PPh3)(OH2)], etc.).46–49 It must be, however, noted that only a single filled bonding orbital contributes to the stabilization of the two Pt–Oaqua bonds (Fig. S3†), indicative of the 3-center 2-electron (3c–2e) bonding in this Oaqua–Pt–Oaqua geometry. This also reveals that a single Pt(0) atom roughly possesses the electron accepting capacity of about 2 electrons (2-e) presumably due to the specific stabilization given by the [Xe](6s)2(5d)10 configuration. The formal 2-e capacity of Pt(0) can be further correlated with the changes seen in the structures of Ptn clusters upon increasing the nuclearity. As discussed below, the electron injection into the clusters beyond this 2-e capacity per Pt can be further promoted as successive H* adsorption processes, in which the electron accepting capacity is tuned based on the relaxation or dissociation of the metal–metal (or metal–aqua) bonding associations and also by the partial hybridization of vacant 6p orbitals. However, there is a clear limitation in the total accepting capacity depending upon the cluster size, which is regarded as the fundamental basis rationalizing the reason why the Pt–HUPD bonds are observed to be stabler than the Pt–HOPD ones (see below).
 | ||
| Fig. 3 Possible aqua coordination equilibria for the Pt1 system in water at 25 °C, where the relative abundances estimated using [H2O] = 55.6 M are also shown. | ||
In the 3[Pt2] system, the Pt–Pt bond distance (2.396 Å) is the shortest distance among those observed in this study. This is roughly consistent with the value of 2.33 Å experimentally estimated by observing the Pt–Pt stretching vibration of Pt02 in the gas phase.50Fig. 4 (left) shows the MO diagram clarifying the manner in which the formal double bond is formed within the diplatinum entity. This double bond can be closely correlated with that achieved within the triplet dioxygen molecule. However, the σ(6s–6s) orbital is higher in energy than the π(5d–5d)/π*(5d–5d) orbitals since the σ(6s–6s) is formed in the outer shell, in sharp contrast with the orbital arrangement in dioxygen. Interestingly, this Pt0![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Pt0 double bond distance is quite close to the shortest PtIII–PtIII single bond distance (2.3906 Å) observed for the quadruply bridged PtIII2 dimer reported by Appleton et al.,51 although the relatively short distance in this PtIII2 dimer is partly responsible for the compressing effect caused by the short bite distances in the four acetate bridges. Nevertheless, when compared with the much purer PtIII–PtIII single bond distances reported for the amidated-bridged cis-diammineplatinum(III) dimers (e.g., 2.6235(13) Å),52 the value of 2.396 Å observed for 3[Pt2] appears quite reasonable as a Pt
Pt0 double bond distance is quite close to the shortest PtIII–PtIII single bond distance (2.3906 Å) observed for the quadruply bridged PtIII2 dimer reported by Appleton et al.,51 although the relatively short distance in this PtIII2 dimer is partly responsible for the compressing effect caused by the short bite distances in the four acetate bridges. Nevertheless, when compared with the much purer PtIII–PtIII single bond distances reported for the amidated-bridged cis-diammineplatinum(III) dimers (e.g., 2.6235(13) Å),52 the value of 2.396 Å observed for 3[Pt2] appears quite reasonable as a Pt![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Pt double bond. Note that such a multi-bonding character of platinum has not been well discussed in the literature.41 Importantly, it was ascertained that this Pt02 dimer cannot further accept any aqua donors (confirmed using DFT), consistent with the formal 2-e capacity per Pt(0) discussed above. Both Pt centers do satisfy the [Xe](6s)2(5d)10 configuration. In addition, the half-filled π*(5d–5d) orbitals have a clear mismatch in the orbital phase in forming a bond with an aqua ligand.
Pt double bond. Note that such a multi-bonding character of platinum has not been well discussed in the literature.41 Importantly, it was ascertained that this Pt02 dimer cannot further accept any aqua donors (confirmed using DFT), consistent with the formal 2-e capacity per Pt(0) discussed above. Both Pt centers do satisfy the [Xe](6s)2(5d)10 configuration. In addition, the half-filled π*(5d–5d) orbitals have a clear mismatch in the orbital phase in forming a bond with an aqua ligand.
 | ||
| Fig. 4 Schematic representations of the molecular orbitals correlated with the Pt–Pt bonding interaction in the 3[Pt2] system together with that for its one-electron reduced product 2[Pt2]−. | ||
On the other hand, Fig. 4 (right) further depicts the manner in which the Pt–Pt distance becomes longer (2.498 Å) upon one-electron reduction to afford 2[Pt2]−. This behavior correlates with a decrease in bond order from 2 to 1.5 by filling another electron into the π*(5d–5d) orbital. Moreover, 2[Pt2]− is defined as a highly delocalized mixed-valence Pt(−0.5)2 system (formally Pt(0)Pt(−I)), clearly belonging to the Robin–Day class III mixed-valence classification.53 For several higher nuclearity nanoclusters, we also confirmed that the corresponding 1-e-reduced systems similarly show elongation in the average Pt–Pt distance. It was further confirmed that such simple reduction processes (i.e., Pt0n + e− → [Pt0n−1Pt−I]−) are highly endergonic (see below), indicating that the Pt0n fragments cannot accept any more electrons beyond the maximum acceptor capacity unless PT proceeds either beforehand or concertedly. In other words, the initial Pt0n clusters are all stabilized by filling the available acceptor orbitals based on the mutual donor–acceptor interactions. Consequently, the initial H* adsorption on each Pt0n cluster cannot adopt the ET–PT route, as discussed below in detail.
As depicted in Fig. 2 and 5, the average Pt–Pt distance in the Pt0n cluster clearly increases with increasing nuclearity (see also Table S5†). This behavior can be rationally interpreted as bond weakening occurs as the nuclearity is increased because the number of adjacent Pt atoms at each Pt center increases. As discussed above, the electron accepting capacity of each Pt(0) center has a limitation and therefore the bond order at each Pt–Pt association must be diminished as the number of bonds on each Pt(0) center is increased. The structure of the Pt13 cluster used to make a plot, as shown in Fig. 5, was optimized under the constraint to preserve a highly symmetric cuboctahedral geometry equivalent to the partial domain in crystalline platinum. The common Pt–Pt distance applied to all distances in this Pt13 converged at Pt–Pt = 2.785 Å (Table S6†), consistent with the value of Pt–Pt = 2.775 Å determined for bulk Pt by X-ray diffraction at 20 °C.54 Each Pt(0) atom in the crystal lattice is surrounded by 12 Pt(0) atoms with an equivalent interaction mode so that the twelve Pt–Pt bonds are substantially lowered in the individual bond order, reflecting the highly soft character of pure metallic platinum due to weak metal–metal bonding (i.e., the bond strength on each Pt–Pt association is largely diluted).
 | ||
| Fig. 5 Variation in the average Pt–Pt distance as a function of the nuclearity for the Pt0n clusters. | ||
Structures of the 1st and 2nd CPET products
To model the H*-adsorbed species, this section exemplifies the structures of the first and second CPET products for the three smallest clusters; Pt1, Pt2, and Pt3. As shown in Fig. 6, the H* adsorption to [Pt0(OH2)2] results in the formation of [Pt−I(H+-dz2)(OH2)], which can also be expressed as [PtI(H−)(OH2)] based on eqn (8). The former is a more rational expression because the Pt–H bonding orbital is interpreted to consist of the filled dz2 orbital hybridized with a vacant 1s H orbital (see Fig. 6A), corresponding to the definition given using eqn (9). The Pt–Oaqua distance in this species (2.343 Å) is clearly longer than those in [Pt0(OH2)2], reflecting the decrease in electron acceptor capacity at the metal upon 1-e reduction. The increased electron density and negative charge clearly contribute to the increased basicity at the filled Pt dz2 donor in order to stabilize the protonated species. The second H* adsorption for this system similarly induces the elimination of the remaining aqua donors to afford a diprotonated intermediate [Pt(−II)(H+)2] (Fig. 6B) which has a [Xe](6s)2(5d)10 configuration with two protons attached in a cis fashion. As depicted in Fig. 6B, the filled 6s and 5dx2−y2-type orbitals contribute to the stabilization of two equivalent Pt–H single bonds.As shown in Fig. 6C and E, the first H* adsorption by the Pt2 and Pt3 clusters affords Pt2(μ2-H*) and Pt3(μ2-H*) bearing common features at the H*-bridged geometry. Two Pt–H*bridge distances (1.72–1.74 Å) are clearly longer than the Pt–H*ontop distances (1.51–1.57 Å). The remarkable feature is that the Hbridge atom is bitten by two dz2-derived orbitals with a σ-type Pt–Hbridge–Pt association in a 3c–2e bonding fashion, analogous to the bonding scheme in diborane (B2H6). Moreover, this Hbridge atom is further stabilized by employing a π-type Pt–Hbridge–Pt association (HOMO−9 and HOMO−7) shown in Fig. 6C, which rationalizes the reason why such bridging H* atoms behave as HUPD's with their binding strength substantially higher than the HOPD's. These bridging geometries can be described by either [Pt(−0.5)2(μ2-H+)] or [Pt(+0.5)2(μ2-H−)], where the electron injected, for example, goes into the π*(Pt–Pt)-type orbital depicted in Fig. 4. The triplatinum cluster behaves similarly using π*(Pt3) orbitals established in a trigonal fashion (see Fig. S8†). The two Pt atoms bridged by an H* atom are structurally and electronically equivalent because of the approximate mirror symmetry adopted by the Pt2(μ2-H*) and Pt3(μ2-H*) systems. As discussed later in detail, these bridging H*'s are quite strongly bonded and thereby assignable to the HUPD atoms which cannot directly participate in H2 evolution events. The dz2-bitten geometry together with the mixed-valent character (i.e., [Pt(−0.5)2(μ2-H+)]) contributes to the relatively high pKa values of these singly H*-adsorbed clusters (pKa = 16.3 and 23.3 respectively; see below).
As discussed above for Fig. 6C, due to the canting of the Pt–H* axis with regard to the axis perpendicular to the H*-bridged Pt–Pt vector, the proton can be more closely located to other filled d orbitals other than dz2, leading to gaining additional stabilization. Such bonding contributions are further recognized in other d-orbital-derived MOs (see Fig. S7 and S8†). These features can also be correlated with the reason why the HUPD atoms possess higher adsorption energy over the platinum electrode surfaces. In contrast, the Hontop atoms are much less canted and cannot form additional interactions with other filled d orbitals including those in adjacent Pt atoms. These realizations must have relevance to the fact that the surface adsorption energy of the HOPD atoms becomes lower than the HUPD atoms.
The second H* adsorption to the Pt2 and Pt3 clusters afford [Pt2(H*ontop)2] and [Pt3H*ontopH*bridge], respectively (Fig. 6D and F). The former can be regarded as comprised of two Pt(−I)(H+) units with an elongated Pt–Pt distance (2.546 Å) due to decreased electron acceptor capacity by the overall 2-e reduction. Furthermore, its Pt–H*ontop distances (1.521 Å) are the shortest among those exemplified in Fig. 6, which can be rationalized by the fact that the MOs contributing to the Pt–H*ontop bonding are most localized over the dz2 orbitals, leading to the higher electron density at the proton binding sites. In contrast, the H*ontop in the [Pt3H*ontopH*bridge] is more weakly attached to the Pt atom (Pt–H*ontop = 1.562 Å), attributable to the delocalization of the Pt–H bonding electron density over the triplatinum entity (see Fig. 6F). In the same manner, the similarly longer Pt–H*ontop distance in [Pt0(OH2)(H*)] (1.565 Å) is attributable to the partial transfer of the Pt–H bonding electron density to the 2pz(Oaqua) orbital hybridized with the dz2 orbital in an antibonding fashion (see HOMO−5 in Fig. 6A). It is important to note here that such weakly bound H* atoms show ν(Pt–H) vibrational frequencies attributable to the HOPD atoms (see below).
In the later sections, we will show that [Pt2(H*ontop)2] can further undertake several successive PT–ET or CPET steps until affording a 5-protonated 4-e-reduced species [(Hontop)3Pt–Pt(Hontop)2]+ by generating more or less similar HUPD and HOPD sites. The resulting H* adsorption capacity of about 2.5H*'s per Pt roughly coincides with the report on the Pt13 cluster by Roduner,55 which evidenced the capacity of about three H*s per Pt.
Square diagrams for possible PT, ET, and CPET steps
To the best of our knowledge, all the electrochemical studies have so far assumed that a PT process in the electrochemical HER always proceeds with the concomitant promotion of an ET process, as shown using eqn (1) and (2). It is obviously due to the fact that electrochemistry works along with the electrical responses. In other words, purely chemical events showing no electrode current cannot be handled in voltammetric analysis. In contrast, the individual electron and proton transfer steps can be separately investigated by theoretically developing the square diagrams for various possible PT and ET steps, which also provide insights into the requirements of CPET processes. It must be emphasized that this approach even allows us to postulate and examine the paths which have never been focused on in electrochemical studies. Successive promotion of PT steps without promoting ET can be even examined (see below).Actually, the results exemplified in Fig. 7, for the first time, demonstrate that the protonation of the initial Pt0n fragments is largely exergonic, revealing the highly basic character of naked platinum clusters. Indeed, such behaviors have never been revealed by the electrochemical technique. Moreover, the Pt2 and Pt3 clusters roughly show twice larger pKa values (pKa = 19–20) compared to the monoplatinum system (pKa = 12.1). This indicates that the basicity is drastically enhanced by the metal–metal interactions, indicative of the increased electron density due to the mutual donation among the metals. We also note that the high pKa values of the [Ptn(H+)] (i.e., [PtnH]+) clusters are similarly exhibited by the clusters with higher nuclearity (n > 3). For instance, [Pt4H]+, [Pt5H]+ and [Pt6H]+ have been computed to possess pKa values of 27.0, 26.5, and 28.4, respectively (see Table S7 and Fig. S13–S15†). Additionally, such high pKa values are preserved even after further H* adsorption, as exemplified by the values of pKa = 16.3 and 23.3 for 2[Pt2H2]+ and 2[Pt3H2]+, respectively. Even the triply H*-adsorbed Pt2 cluster (i.e., 2[Pt2H3]) preserves sufficiently high basicity; pKa = 14.6 for 2[Pt2H4]+ (see Fig. S10†).
On the other hand, the reduction of all the initial Pt0n species (E = −1.78 V for 1[Pt(OH2)2], −1.51 V for 3[Pt2], and −1.68 V for 1[Pt3]+; Fig. 7) is extremely uphill under the applied electrode potential of 0.0 V vs. NHE, which is close to the potential at which the HUPD deposition switches into the HOPD deposition (0.02 V vs. NHE).56 These behaviors confirm that the electron accepting capacity is nearly saturated in the Pt0n species, even though it changes upon protonation. Furthermore, the reduction of all the initial monoprotonated species is still disfavored when electrolyzed at 0.0 V (i.e., E = −0.47 V for 1[Pt(OH2)2H]+, −0.44 V for 3[Pt2H]+, and −0.85 V for 1[Pt3H]+; Fig. 7). The combined results reveal that the first steps of H* adsorption to these Pt0n species can only proceed via the CPET pathways only if the paths are reasonably feasible.
In this section, the discussion is limited to several initial H* adsorption steps in the Pt1–Pt3 systems. However, a much larger number of consecutive H* adsorption steps have been calculated in this study (see Fig. S9, S10, and S12†). All these results were used to create the free energy diagrams, shown in the Free energy diagrams for the Ptn-catalyzed H2 evolution section, in order to find out the pathways capable of promoting the electrocatalytic HER under zero overpotential conditions. We have also been making efforts to clarify the reaction paths for the higher nuclearity clusters (e.g., Pt4, Pt5, and Pt11), part of the results of which are supplied as Fig. S13–S16.†
The modes of H* adsorption and vibrational frequencies
The vibrational frequencies for the H+-added (i.e., protonated) and H*-adsorbed species can be compared with the values electrochemically observed by in situ SEIRAS (surface-enhanced infrared absorption spectroscopy),56,57 which successfully revealed the growth of Pt–HOPD stretching bands at ν(Pt–H) = 2080–2090 cm−1. The reports also pointed out the difficulty in observing the vibrational frequencies attributable to the (Pt–HUPD)-derived modes.Even though the Pt1 system possesses no metal–metal interactions, it is still considered as an attractive target of research because of the recent reports on the relatively high HER activity suggested for single-atom platinum catalysts.58 The most primitive intermediate affordable in the Pt1 system is the simply protonated intermediate 1[(H2O)2Pt(H)]+ shown in Fig. 7A. It shows the ν(Pt–H) frequency at 2422 (int. 45) cm−1 which is higher in energy than the value of ν(Pt–H) = 2108 (int. 613) cm−1 computed for its 1-e-reduced product 2[(H2O)Pt(H*)], where the value in parentheses with a prefix ‘int.’ corresponds to the oscillator strength proportional to the theoretical intensity. As shown in Fig. 8, the observed trend in ν(Pt–H) frequency is consistent with the trend in Pt–H bond strength deduced from the Pt–H distance (i.e., a lower frequency in 2[(H2O)Pt(H*)] is consistent with a longer Pt–H; Pt–H = 1.565 Å). Importantly, the ν(Pt–H) for 2[(H2O)Pt(H*)] is quite comparable to those electrochemically observed for the Pt–HOPD species (ca. 2080–2090 cm−1).56,57 In contrast, the higher ν(Pt–H) frequency of [(H2O)2Pt(H)]+ can be correlated with the HUPD atom. The ν(Pt–H) frequencies of 2344 (int. 36) and 2392 (int. 11) cm−1 computed for the next probable intermediate 2[PtH2]+ (Pt–H = 1.537 Å) similarly suggest that the H atoms are rather tightly bound HUPD-like atoms. Even for the next doubly H*-adsorbed species 1[PtH2], the Pt–H distances do not show meaningful elongation (Pt–H = 1.532 Å; Fig. S4†) and the ν(Pt–H) frequencies (2336 (int. 223) and 2401 (int. 82) cm−1) do not turn into those assignable to the Pt–HOPD species, presumably due to the highly localized electron density at the single Pt center. It is confirmed that the Pt(H*)3 species is not energetically accessible so the triple H* adsorption by the Pt1 system is ruled out. As a result, the most weakly bound H* atom with HOPD character is only achievable by the singly aqua-coordinated species 2[(H2O)Pt(H*)] in the Pt1 system. This finding may be correlated with the discussion given for the operando EXAFS study on a single-platinum HER catalyst which was suggested to yield a near-free Pt(0) liberating from the nitrogen–carbon substrate followed by aqua coordination in the overpotential domain,58 even though the report did not clarify whether its aggregation can be ruled out.
On the other hand, protonation of 3[Pt2] affords 3[Pt2(μ-H)]+ by accompanying elongation in the Pt–Pt distance (2.396 Å → 2.454 Å; Fig. S5†), revealing the partial transfer of the electron density from the metal–metal bonding site to the two bridging Pt–H bonds. The ν(Pt–H) frequencies for 3[Pt2(μ-H)]+ are computed as 631.7 (int. 311) and 1610 (int. 137) cm−1, corresponding to the sliding (ρ) and stretching (ν) modes, respectively. Upon reduction of 3[Pt2(μ-H)]+, the resulting 2[Pt2(μ-H*)] similarly shows vibrational frequencies at 680.9 (int. 2) and 1607 (int. 236) cm−1. The latter shows good agreement with that assigned to the Pt2(μ-H*) fragments (1679 cm−1) formed in the H*-adsorbed Pt13 cluster in a zeolite.55 The next intermediate 2[Pt2(Hontop)2]+ (Pt–H = 1.524 Å; see also Fig. S5†) possesses Hontop atoms with the ν(Pt–H) frequencies at 2394 (int. 181) cm−1, indicative of their HUPD character. A further reduction affords 2[Pt2(Hontop)2] (Pt–H = 1.521 Å, ν(Pt–H) = 2362 (int. 91) 2364 (int. 265); see also Fig. S5†), in which the H*′s still preserve their HUPD character. The details of other vibrational frequencies computed, including those for the Pt3 system, are supplied as Tables S8–S10.†
On the other hand, the structural changes induced by promoting successive PT–ET steps for both the Pt2 and Pt3 systems obey a common logic. For instance, the reduction of 3[Pt2(μ-H)]+ into 2[Pt2(μ-H*)] causes only a slight decrease in the Pt–H distance (1.759 Å → 1.729 Å). However, an obvious increase is given in the Pt–Pt distance (2.454 Å → 2.532 Å; Fig. S5†), revealing that the electron injection results in partial loss in the electron acceptor capacity required to reinforce the metal–metal bonding on each Pt atom. These behaviors clearly indicate that the Pt–Pt bonding associations possess the flexibility to serve as an electron-injection buffer, by analogy to the action made upon protonation (see above). Thus, the donor–acceptor interactions among the Pt centers are utilized to finely tune the overall balance in electron density within the clusters upon promoting either PT or ET. Quite similar behaviors are seen upon reduction of 2[Pt2(Hontop)2]+ (Pt–H = 1.524 Å, Pt–Pt = 2.478 Å) to 2[Pt2(Hontop)2] (Pt–H = 1.521 Å, Pt–Pt = 2.546 Å; Fig. S5†). The corresponding structural responses by the Pt3 cluster (Fig. S6†) are quite similar, even though the electron injection is buffered by the overall expansion in the triangular Pt3 unit. Additionally, another behavior commonly seen for both the Pt2 and Pt3 systems is the shortening of the Pt–Pt distance upon protonation only when the Pt2(μ-H*) unit converts into the non-H*-bridged (Hontop–Pt–Pt–Hontop)+ unit (Fig. S5 and S6†).
Fig. 9 shows the manner in which the ν(Pt–H) frequency changes by promoting successive PT–ET processes. The remarkable feature is the zig-zag behaviors for all nuclearity, revealing that the ν(Pt–H) frequency tends to increase by PT and decrease by ET. The PT-induced increase in frequency indicates that the density contributing to the Pt–H bonding is more strongly attracted by the positive charge introduced by protonation. In contrast, the ET-induced decrease in frequency is attributable to the weakening of attracting the electrons shared by either H* or H− (hydride) at the Hontop geometry.
As noted above for the Pt1 system, Fig. 9 shows that the HOPD-assignable H* atom is only given after promoting the first PT–ET or CPET step (i.e., Cat-2@Pt1). The highest thermodynamic hydricity, which corresponds to the lowest hydricity value in the vertical axis in Fig. 9, is also shown by the same species, reflecting the greatest weakening of the Pt–H* bonding association in Cat-2@Pt1. On the other hand, the ν(Pt–H) frequency for the Pt2 system suggests that the releasable H* atom only generates after promoting four sets of PT–ET (or CPET) processes (i.e., quadruple H* adsorption; Cat-8@Pt2). Nevertheless, the hydricity value rather suggests that the releasable H* atom is already evolved after promoting three sets of PT–ET processes (i.e., Cat-6@Pt2) with the hydricity value as low as that for the quadruply H*-adsorbed species (Cat-8@Pt2; Fig. 9), even though the ν(Pt–H) frequency for the Pt2(H*)3 species (2232 cm−1) is slightly higher than the standard values observed for the HOPD atoms (ca. 2080–2090 cm−1).56,57 The situation for the Pt3 system is a little more complicated since four releasable H* atoms with the ν(Pt–H) frequency lower than 2122 cm−1 appear four times while promoting six H*-adsorption processes. The hydricity value is also kept low after completing two H* adsorption steps (Fig. 9), indicating that the loss of electron density upon releasing a hydride can be more feasibly compensated in higher nuclearity clusters, presumably by more rationally/flexibly reinforcing the multiple metal–metal bonding associations. This realization highlights the important role of metal–metal interactions in feasible H* or H− elimination.
Importantly, three highly feasible H2 releasing steps (ΔGH2 < 4 kcal mol−1), which will be described in the subsequent section, are also illustrated in Fig. 9. Both the Pt2 and Pt3 models can evolve H2 by cycling the [Cat-9]/[Cat-5](@Pt2 or Pt3) couple with ΔGH2 = 1.0 and 2.1 kcal mol−1, respectively. Moreover, Pt3 can provide another feasible H2 evolution path based on the [Cat-12]/[Cat-8]@Pt3 couple with ΔGH2 = 1.7 kcal mol−1. These results imply that the H2 releasable Cat-axis (i.e., horizontal axis) domain gradually expands as the nuclearity increases.
An important conclusion derived from the above results is that the extended metal–metal interactions in higher nuclearity clusters greatly contribute to the higher flexibility and tunability in both geometric and electronic structures, leading to the higher opportunities to afford (i) a releasable H* having a lower ν(Pt–H) frequency, (ii) a H2-releasable step, and (iii) less endergonic hydride releasing characteristics (i.e., higher hydricity).
Additionally, we note that only Cat-9@Pt3 (i.e., [Pt3H5]+), corresponding to one of the H2-releasable intermediates, possesses a nearly H2-like moiety bearing a relatively short H–H distance (0.867 Å; see also Table S13†). This H2 is bonded to the Pt3 entity with the Pt–H distances ca. 1.73 Å (ν(Pt–H) = 1082.37 cm−1). Thus, Cat-9@Pt3 can be expressed as [Pt3(Hontop)2(μ-Hbridge)(H2)]+, and is classified as a so-called ‘true hydrogen complex’ which has only a trivial elongation in H–H, clearly due to the extremely small back donation to the σ*(H–H) orbital from the metal centers.59,60 All the rest of the H*-adsorbed sites realized in this study are formally classified either as ‘elongated hydrogen complexes’ or ‘metal hydrides’.
Free energy diagrams for Ptn-catalyzed H2 evolution
The free energy diagrams developed for the Pt1- and Pt2-catalyzed HER are shown in Fig. 10, where those for the Pt3-catalyzed one are supplied as Fig. S11.† The full details of square schemes showing all the calculated pKa values and reduction potentials are supplied as Fig. S9, S10, and S12.† Under the applied potential of 0.0 V vs. NHE at pH 0, the energy of the H2-releasing state is highly consistent with the energy of the catalyst leaving from H2 due to zero driving force conditions. In other words, the energy of the H2-releasing state in Fig. 10 must be, in principle, consistent with that of the state before accepting the set of 2H+/2e− to be evolved as H2. Fig. 10 shows that, in general, PT towards neutral clusters result in too severe lowering in energy, leading to making such protonation products difficult to climb back to the H2-releasing state. In fact, too much lowering in energy by such a PT step tends to cause difficulty in reducing the resulting protonated species by showing highly endergonic character for ET. In such a case, the CPET path is considered as the most favorable route to afford a H* adsorbed product. Thus, the neutral clusters often have a highly electron rich character so high pKa values are given to their protonated products. Some of the resulting protonated species even remain basic enough to stabilize the diprotonated species without promoting ET (see Fig. S11†). For clarity, the ET paths starting from neutral clusters are not drawn in the energy diagrams in Fig. 10. As a result, accessible catalytic pathways are judged to primarily consist of PT and CPET processes with only one exception of an exergonic ET path after the second aqua ligand dissociation in the Pt1 system. | ||
| Fig. 10 Energy diagrams for possible reaction steps for the Pt1 (A) and Pt2 (B) models when the electrocatalytic HER is driven by 0.0 V vs. NHE at pH 0. | ||
An important insight is further gained by carefully examining the manner in which the CPET-induced lowering in energy occurs in the Pt2-catalyzed system (Fig. 10B). It clearly shows that the excessive dropping down in energy undesirable for climbing up to the H2-releasing state is gradually diminished as the number of steps increases. After yielding 3[Pt2H]+ by initially promoting the PT in Fig. 10B, both the third and fourth CPET steps (i.e., 1[Pt2H3]+ → 2[Pt2H4]+ → 1[Pt2H5]+) require only a small change in energy so that the H2 release from 1[Pt2H5]+ becomes substantially feasible (ΔGH2 = 1.0 kcal mol−1). Although complexity increases, the Pt3-derived pathways also involve several such energetically desirable double CPET steps permitting a feasible H2 elimination (Fig. S11†).
To more rationally understand the complicated behaviors of all three nuclearity systems when they catalyze the HER, the schematic diagrams in Fig. 11 are developed by showing only accessible intermediates as colored spots. The blue spots are classified as the intermediates judged to undertake highly feasible H2 release with ΔGH2 < 6 kcal mol−1. The red spots are still classified as those sufficiently feasible in H2 release with 7 < ΔGH2 < 14 kcal mol−1. The classification adopted here is based on the TOF (turnover frequency) values of 26–65 s−1 reported for the single-atom platinum catalyst,61,62 which correspond to ΔGH2 = 14–15 kcal mol−1. It is also supposed that the H2 release is a barrierless step which limits the overall reaction rate of the HER (i.e., ΔGHER‡ = ΔGH2). The green spot corresponds to the intermediate which is unfeasible in H2 release (17.2 kcal mol−1). The yellow spots correspond to those which do not participate in H2 elimination. Importantly, the total number of blue and red spots increases as the nuclearity increases. Moreover, the ΔGH2 value indeed decreases as the number of CPET steps increases, consistent with the argument made by Conway and Bai in 1986.63 Their study clarified a nearly full coverage of HOPD atoms over the near-surface region of platinum at the most vigorously H2 evolving stage, by which they pointed out the importance of weakening of the M–H* adsorption energy leading to activating the H2 release by the Tafel mechanism.
Conclusions
Our approach establishes an important new basis to understand the characteristics of multi-step H+ and H* adsorption processes which could not be handled either by experimental studies or by theoretical studies on the slab models defined under periodic boundary conditions. Individual PT or ET events, which have never been independently discussed in the electrochemical studies on metal electrode reactions, are investigated in detail with an implication of their relevance to the electrochemical HER by platinum electrodes.By carefully examining the structural and electronic responses in several smallest subnanocluster models, some important basic concepts useful in elucidating the catalytic properties are successfully determined as follows:
(i) A Pt(0) atom can serve both as an electron acceptor and a donor with the accepting capacity (ca. 2-e) roughly equivalent to the donating capacity (ca. 2-e) when simply forming metal–metal bonding associations in the neutral Pt0n clusters having no adsorbed H* atoms. However, 2–3 electrons per Pt can be further accepted by the clusters as a result of 2–3H* adsorption per Pt. This is likely to be the fundamental basis for the reason why the platinum group metal (Ni, Pd, and Pt) exhibits the highest HER activity in each row, as shown by the periodicity in the HER activity clarified many years ago by Kita.64 It should be, however, noted that Pt exhibits outstanding performance, e.g., compared to Ni, due to the spatially broad nature of the d orbitals leading to facilitating CPET based on the long-range interaction with the proton for uptake, as previously described.2,14
(ii) The electron donating and accepting capacities can be synergetically increased in multinuclear Pt0n clusters so that the basicity of the clusters increases as the nuclearity increases. The overall electron accepting capacity also increases synergetically.
(iii) The Ptn clusters have high structural flexibility and undertake the overall changes in their Pt–Pt bond lengths and strengths in order to buffer the changes given in electron density upon promoting the PT, ET, or CPET processes. The PT generally results in partial transfer of the electron density to Pt–H bonding, leading to partial elongation in Pt–Pt distances. Similarly, ET and CPET cause expansion of the cluster size due to the ET-induced partial decrease in the accepting capacity required to reinforce the attractive interactions between the metals. These imply that the reconstruction of the surface structures of platinum electrodes during HER catalysis is inevitable due to the structural expansion upon successively promoting H* adsorption. Moreover, the highest barrier observed for the hexagonal close-packed Pt(111) facet by Marković et al.5 is also rationalized by the lowest mobility of the Pt atoms on the top layer, leading to hindering the structural deformation required to promote the successive H* adsorption.
(iv) The exception is the PT-induced shortening of the Pt–Pt distance which takes place when an H*-bridged geometry turns into a non-bridged (i.e., on top) geometry because of the increase in donating ability available for mutual Pt–Pt associations. This behavior does not support one of the past suppositions made by electrochemists on the preservation of HUPD atoms as spectators for the HER,7 because the HUPD atoms may turn into the HOPD atoms as the PT or CPET steps successively proceed.
(v) In general, the ν(Pt–Hontop) frequency increases upon PT and decreases upon ET, indicating that the Pt–Hontop bond strength increases upon introduction of a positive charge and vice versa. In other words, protonation increases the electrostatic attraction of the electron density residing in either H* or H− (hydride), while electron injection induces an inverse effect. Successive electron injection via ET or CPET fills up the available accepting capacity in the clusters, leading to evolving the HOPD-like sites ready for H2 release via the Tafel mechanism.
(vi) Extended metal–metal interactions in higher nuclearity clusters more favorably provide a catalytically active platform which can more flexibly make structural and electronic responses desired to promote the electrocatalytic HER.
The present study thus succeeds in relying on computational techniques to make an approach to the reactivities of relatively low nuclearity species when they are subjected to HER catalysis. The extended study dealing with the higher nuclearity clusters is now underway. Part of the results already ascertains the tendencies similar to those observed in the present study (Fig. S13–S16†). We therefore understand that the theoretical studies using such hypothetical models with a smaller number of metals indeed make sense and provide some useful piece of information that could not be well understood only by looking at the electrochemical responses. We thus believe the present study sheds new light on the mechanistic understanding of electrocatalysis by various metal electrodes by revealing the importance of paying much more precise attention to the highly structurally and electronically flexible characteristics of metal clusters while promoting HER catalysis. The studies on such subnanocluster models will become important new targets of research for any type of reaction over any metal or alloy surfaces.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by JSPS KAKENHI Grant Numbers JP18H01996, JP18H05171 and JP21H01952. K. K. acknowledges the support from the Kyushu University Program for Leading Graduate Schools: ‘Advanced Graduate Course on Molecular Systems for Devices. K. K. also acknowledges the support from the Faculty of Science, Kyushu University Program for Young Researchers (Reiwa No. 1).References
- E. Santos, P. Quaino and W. Schmickler, Phys. Chem. Chem. Phys., 2012, 14, 11224–11233 RSC.
- P. Quaino, F. Juarez, E. Santos and W. Schmickler, Beilstein J. Nanotechnol., 2014, 5, 846–854 CrossRef PubMed.
- J. Clavilier, R. Faure, G. Guinet and R. Durand, J. Electroanal. Chem., 1980, 107, 205–209 CrossRef CAS.
- M. A. Climent, M. J. Valls, J. M. Feliu, A. Aldaz and J. Clavilier, J. Electroanal. Chem., 1992, 326, 113–127 CrossRef CAS.
- N. M. Marković, B. N. Grgur and P. N. Ross, J. Phys. Chem. B, 1997, 101, 5405–5413 CrossRef.
- E. Yeager, J. Electrochem. Soc., 1981, 128, 160C–171C CrossRef.
- H. Kita, J. Mol. Catal. A: Chem., 2003, 199, 161–174 CrossRef CAS.
- X. Xu, D. Y. Wu, B. Ren, H. Xian and Z.-Q. Tian, Chem. Phys. Lett., 1999, 311, 193–201 CrossRef CAS.
- J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23–J26 CrossRef.
- A. G. S. Karlberg, T. F. Jaramillo, E. Skulason, J. Rossmeisl, T. Bligaard and J. K. Nørskov, Phys. Rev. Lett., 2007, 99, 126101 CrossRef.
- N. Dubouis and A. Grimaud, Chem. Sci., 2019, 10, 9165–9181 RSC.
- J. Zhu, L. Hu, P. Zhao, L. Y. S. Lee and K.-Y. Wong, Chem. Rev., 2020, 120, 851–918 CrossRef CAS PubMed.
- C. Zhou, J. Wu, A. Nie, R. C. Forrey, A. Tachibana and H. Cheng, J. Phys. Chem. C, 2007, 111, 12773–12778 CrossRef CAS.
- E. Santos, A. Lundin, K. Pötting, P. Quaino and W. Schmickler, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 235436 CrossRef.
- E. Santos and W. Schmickler, Angew. Chem., Int. Ed., 2007, 46, 8262 CrossRef CAS.
- K. Kawano, K. Yamauchi and K. Sakai, Chem. Commun., 2014, 50, 9872–9875 RSC.
- K. Yamauchi and K. Sakai, Dalton Trans., 2015, 44, 8685–8696 RSC.
- H. Ozawa and K. Sakai, Chem. Commun., 2011, 47, 2227–2242 RSC.
- M. Ogawa, G. Ajayakumar, S. Masaoka, H.-B. Kraatz and K. Sakai, Chem. – Eur. J., 2011, 17, 1148–1162 CrossRef CAS PubMed.
- K. Koshiba, K. Yamauchi and K. Sakai, ChemElectroChem, 2019, 6, 2273–2281 CrossRef CAS.
- T. V. O'Halloran, P. K. Mascharak, I. D. Williams, M. M. Roberts and S. J. Lippard, Inorg. Chem., 1987, 26(8), 1261–1270 CrossRef.
- K. Matsumoto and K. Sakai, Adv. Inorg. Chem., 1999, 49, 375–427 CrossRef.
- B. Lippert, Coord. Chem. Rev., 1999, 182, 263–295 CrossRef.
- C. H. Hendon, A. Walsh, N. Akiyama, Y. Konno, T. Kajiwara, T. Ito, H. Kitagawa and K. Sakai, Nat. Commun., 2016, 11950 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09 (Revision D.03), Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 (Revision C.01), Gaussian Inc., Wallingford, CT, 2016 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2008, 112, 1095–1099 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- B. H. Solis and S. Hammes-Schiffer, Inorg. Chem., 2011, 50, 11252–11262 CrossRef CAS PubMed.
- B. H. Solis and S. Hammes-Schiffer, Inorg. Chem., 2014, 53, 6427–6443 CrossRef CAS PubMed.
- M.-H. Baik and R. A. Friesner, J. Phys. Chem. A, 2002, 106, 7407–7412 CrossRef CAS.
- C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2007, 111, 408–422 CrossRef CAS.
- L. E. Roy, E. Jakubikova, M. Graham Guthrie and E. R. Batista, J. Phys. Chem. A, 2009, 113, 6745–6750 CrossRef CAS.
- R. Dennington, T. A. Keith and J. M. Millam, GaussView (Version 6.0.16), Semichem Inc., Shawnee Mission, KS, 2016 Search PubMed.
- H.-J. Zhai, C. Bürgel, V. Bonacic-Koutecky and L.-S. Wang, J. Am. Chem. Soc., 2008, 130, 9156–9167 CrossRef CAS.
- Y.-L. Wang, X.-B. Wang, X.-P. Xing, F. Wei, J. Li and L.-S. Wang, J. Phys. Chem. A, 2010, 114, 11244–11251 CrossRef CAS.
- Q. Cui, D. G. Musaev and K. Morokuma, J. Phys. Chem. A, 1998, 102, 6373–6384 CrossRef CAS.
- Q. Cui, D. G. Musaev and K. Morokuma, J. Chem. Phys., 1998, 108, 8418–8428 CrossRef CAS.
- L. Xiao and L. Wang, J. Phys. Chem. A, 2004, 108, 8605–8614 CrossRef CAS.
- M. N. Huda and L. Kleinman, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 195407 CrossRef.
- C. L. Heredia, V. Ferraresi-Curotto and M. B. López, Comput. Mater. Sci., 2012, 53, 18–24 CrossRef CAS.
- S. Chen, Q. Yang, H. Wang, S. Zhang, J. Li, Y. Wang, W. Chu, Q. Ye and L. Song, Nano Lett., 2015, 15, 5961–5968 CrossRef CAS.
- F. D. Rochon, P. C. Kong and R. Melanson, Inorg. Chem., 1990, 29, 2708–2712 CrossRef CAS.
- N. P. Rath, K. A. Fallis and G. K. Anderson, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1993, C49, 2079–2081 CrossRef CAS.
- W. Chen and K. Matsumoto, Bull. Chem. Soc. Jpn., 2002, 75, 1561–1562 CrossRef CAS.
- K. J. Bonnington, F. Zhang, M. M. A. R. Moustafa, B. F. T. Cooper, M. C. Jennings and R. J. Puddephatt, Organometallics, 2012, 31, 306–317 CrossRef CAS.
- M. B. Airola and M. D. Morse, J. Chem. Phys., 2002, 116, 1313–1317 CrossRef CAS.
- T. G. Appleton, K. A. Byriel, J. R. Hall, C. H. L. Kennard and M. T. Mathieson, J. Am. Chem. Soc., 1992, 114, 7305–7307 CrossRef CAS.
- K. Sakai, I. Sakai, T. Kajiwara and T. Ito, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2004, E60, m255–m258 CrossRef.
- M. B. Robin and P. Day, Adv. Inorg. Chem. Radiochem., 1967, 10, 247–422 CrossRef CAS.
- Y. Waseda, K. Hirata and M. Ohtani, High Temp. – High Pressures, 1975, 7, 221–226 CAS.
- C. Jensen, J. V. Slageren, P. Jakes, R.-A. Eichel and E. Roduner, J. Phys. Chem. C, 2013, 117, 22732–22745 CrossRef CAS.
- K. Kunimatsu, T. Senzaki, M. Tsushima and M. Osawa, Chem. Phys. Lett., 2005, 401, 451–454 CrossRef CAS.
- K. Kunimatsu, T. Senzaki, G. Samjeské, M. Tsushima and M. Osawa, Electrochim. Acta, 2007, 52, 5715–5724 CrossRef CAS.
- S. Fang, X. Zhu, X. Liu, J. Gu, W. Liu, D. Wang, W. Zhang, Y. Lin, J. Lu, S. Wei, Y. Li and T. Yao, Nat. Commun., 2020, 11, 1029 CrossRef CAS PubMed.
- G. J. Kubas, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6901–6907 CrossRef CAS.
- D. M. Heinekey, A. Lledós and J. M. Lluch, Chem. Soc. Rev., 2004, 33, 175–182 RSC.
- Q. Yang, H. Liu, P. Yuan, Y. Jia, L. Zhuang, H. Zhang, X. Yan, G. Liu, Y. Zhao, J. Liu, S. Wei, L. Song, Q. Wu, B. Ge, L. Zhang, K. Wang, X. Wang, C.-R. Chang and X. Yao, J. Am. Chem. Soc., 2022, 144, 2171–2178 CrossRef CAS PubMed.
- H. Zhang, P. An, W. Zhou, B. Y. Guan, P. Zhang, J. Dong and X. W. Lou, Sci. Adv., 2018, 4, eaao6657 CrossRef PubMed.
- B. E. Conway and L. Bai, J. Electroanal. Chem., 1986, 198, 149–175 CrossRef CAS.
- H. Kita, J. Electrochem. Soc., 1966, 113, 1095–1111 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2dt02645g |
| This journal is © The Royal Society of Chemistry 2023 |





