Driving school for self-driving labs

Abstract

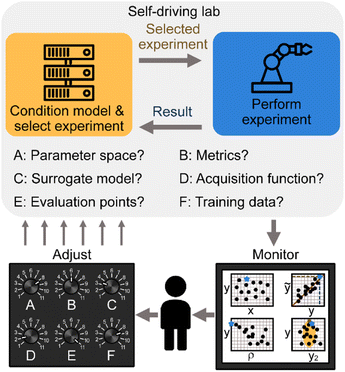
Self-driving labs (SDLs) have emerged as a strategy for accelerating materials and chemical research. While such systems autonomously select and perform physical experiments, this does not mean that the human experimenter has no role to play. Instead, the experimenter must monitor progress of the SDL and make adjustments to ensure that the SDL progresses towards the chosen goal. Unfortunately, researchers rarely receive training specific to the unique challenges inherent to operating SDLs. Here, we provide a heuristic framework for SDL operators. In analogy with how a human might operate a car or other complex system, this framework defines the knobs and the gauges, or the SDL settings that can be modified and the information that an experimenter can consider to change these settings. These lessons are discussed in the context of a common optimization strategy (Bayesian optimization using Gaussian process regression) but can be generalized to other models. Crucially, these adjustments constitute fine tunings that can occur at any point during an SDL campaign, allowing the experimenter to participate in this closed-loop process without being in the loop. As the framework introduced here is material-system agnostic, it can form a resource for researchers developing or using SDLs in any discipline.

---

1. Introduction

To fully take advantage of the effectively infinite number of possible materials and processing conditions, it is necessary to leverage every opportunity to accelerate the pace of progress. Advances in machine learning and artificial intelligence have shined a spotlight on the possibility of using these advanced computational methods to transform research. Unfortunately, many material properties can only be reliably determined by experiment, making experiments the gold standard and often the only method for generating high-fidelity data. These considerations have led to the development of self-driving labs (SDLs), which are research systems that iteratively select physical experiments using machine learning and automatically perform these experiments without human intervention.¹ While systems with closed-loop control over experimental conditions date back decades to self-optimizing chemical reactors,² the past five years have seen the rapid introduction of increasingly sophisticated SDLs that operate with a wide variety of material systems and form factors.^1,3–6 These SDLs have included those that study carbon nanotube synthesis,⁷ yeast genetics,⁸ catalyst composition,⁹ nanoparticle synthesis,^10–13 properties of thin films,^14–17 and the mechanics of additively manufactured structures.^18,19 SDLs have been found to reduce by 10–600 fold the number of experiments needed to reach a given performance level relative to grid-based searching,^18–23 to say nothing of their ability to perform experiments at a faster pace than what is possible with human experimentation. The value of these systems has been further proved through their discovery of new multi-component electrolytes,²⁴ previously unreported chemical compounds,²⁵ and structures with superlative mechanical performance.²⁶

The fact that SDLs are self driving does not mean that they cannot have input from people. Indeed, the construction and programming of SDLs is inherently a human process in which people have provided input, codifying their priorities and goals. This process itself can be complex and important as it involves turning the human domain knowledge into an algorithmic format that can be utilized by the SDL.²⁷ Nevertheless, for most SDL campaigns published to date, this initialization is the end of the meaningful human interaction outside of restocking reagents or other feedstock materials. In particular, the SDL iteratively selects and performs experiments based on the programming until the allotted number of experiments has been reached. While this “hands-off’” approach is reasonable when considering SDL campaigns that collect data over a few days, it is increasingly unrealistic as the timeframe of campaigns stretches into weeks and months. Under these conditions, it is very natural for the human experimenters to monitor the SDL and make adjustments. Indeed, there have been recent reports highlighting the importance of the human–machine collaboration and how this collaboration can be used as part of otherwise autonomous systems.^28,29 However, given that we are only now seeing the widespread adoption of SDLs, there do not yet exist resources to help experimenters know what to monitor and what to adjust.

Here, we present a take on driving school for SDLs based on our experience running the Bayesian experimental autonomous researcher (BEAR). In particular, we have recently concluded a campaign in which we performed >25 000 experiments using this SDL over the span of two years.²⁶ This campaign was a highly dynamic process in which many settings were adjusted based on feedback obtained by monitoring progress made by the SDL. In this manuscript, we detail our key learnings from this process and codify two important aspects, namely the choices an experimenter needs to make and the information that they should be monitoring to make these choices. We narrow these items down into six settings that must be chosen and four plots that should be monitored periodically throughout the campaign to adjust these settings. Despite our insights coming from a campaign based on studying the mechanical properties of additively manufactured structures, the lessons learned are largely system agnostic. We discuss these lessons using the commonly adopted framework of Bayesian optimization to aid in their adoption by others. While the heuristics presented herein cannot account for every situation faced when operating SDLs, we hope that the language, principles, and processes can provide experimenters with greater intuition and increase the adoption and effectiveness of SDLs across the materials space.

2. Overview of self-driving lab campaigns

While the details of materials research campaigns performed by SDLs vary considerably with the SDL architecture, materials system, and campaign goals, they share the need to sequentially select experiments based on the currently available data (Fig. 1). There are a number of algorithms that can perform this selection process.³⁰ However, we focus our discussion on Bayesian optimization (BO) as it is commonly used in SDLs and because BO separates the steps of amalgamating knowledge and choosing experiments in a manner that is heuristically useful.³¹ In particular, BO generally proceeds as a two-step process. For the sake of defining a consistent language, we consider the task of maximizing some experimentally measured property y across some multi-dimensional parameter space x⃑. The objective or ground truth function y = f(x⃑) is unknown and heteroskedastic (variance is not constant across parameter space). The first step of BO is to use the available knowledge to condition a surrogate model f(x⃑;[small theta, Greek, vector]), or a probabilistic approximation of the objective function that depends on hyperparameters [small theta, Greek, vector]. Available knowledge can include, for example, experimental data, physical knowledge about the system such as expected symmetries, or related prior knowledge such as simulation results. Second, the surrogate model is used as an input to an acquisition function a(x⃑;f̃) which quantifies the expected benefit of performing an experiment at any location in x⃑. The maximum of a across x⃑ is generally selected as the next experiment.

Fig. 1 Schematic showing the interactions between a human researcher and a self-driving lab (SDL). The SDL proceeds autonomously as an iterative process of performing experiments and then conditioning a model to select the next experiment. The human can monitor the progress of the individual experiments and campaigns as a whole using a series of plots to adjust settings that guide the operation of the SDL. Importantly, the human is not in the loop and any adjustments can happen asynchronously without slowing the pace of experimentation.

Each step of BO requires the experimenter to set a number of parameters whose values may not be obvious or physically intuitive. Crucially, the BO process, and the operation of the SDL more generally, need not be static, and the experimenter should continually revisit settings based on recent results to improve the chances of converging towards the best outcome. Below, we highlight the actions that the experimenter can take (Section 3) and then detail the feedback that forms the basis for how to choose which actions to perform (Section 4).

3. Actions to be taken – the knobs

Despite the use of the term self driving, in practice there are a number of deliberate choices that the human experimenter must make to productively guide an SDL to make efficient progress. In this section, we list six decisions that we have found to be most significant when running an SDL campaign.

A The range of parameters considered

The range of x⃑ that is considered as the parameter space is a non-trivial choice that can be crucial to the success of an SDL campaign. In physical experiments, each component of x⃑ corresponds to a tangible physical quantity such as the identity of a compound, a processing temperature, or the length of a geometric feature. As such, not all permutations of x⃑ correspond to valid experiments and there is no guarantee that the space of valid experiments is a convex region. In the simplest case, when each component of x⃑ is independent, the full parameter space can be considered a hypercube. Even in this case, determining the maximum and minimum values for each parameter is often a judgement call based on experimenter intuition. More generally, there exists some geometrically complicated domain in x⃑ that corresponds to valid experiments. If the boundary of valid experiments is known at the beginning of the campaign, invalid experiments can be avoided. In contrast, if the boundary is unknown but the system is such that invalid experiments can be attempted, the boundary of this domain can itself be learned during the campaign.³² In addition to the range of parameters considered, it can be useful to transform the parameter space such that correlations are easier to learn. For instance, monotonic transformations such as taking the logarithm of a parameter can facilitate learning if the parameter is positive definite (always greater than zero) and varies across several orders of magnitude.

B The metrics that define performance

As stated above, we are considering an SDL campaign whose goal is to maximize a metric y. Even when stated so simply, there are two additional considerations to mention. First, it is rare to conceive of a material that is only evaluated on a single axis. More often, multiple properties are considered important.^17,33–35 For example, a structural material can be evaluated based on its strength, stiffness, density, cost, or toughness. When multiple metrics are important, these metrics must be distilled into a single value to guide automated experiment selection. There are a number of techniques to do this that can be drawn from multi-objective optimization. Early work focused on combining the multiple objectives into a single scalar metric that embodies the user-defined relative importance of these objectives.³⁶ This relative importance can also be changed throughout a campaign, which has led to strategies such as adaptive weighted sum methods for multi-objective optimization.³⁷ More recently, it is common to base experiment selection on hypervolume optimization,^17,33,38 which converts each potential ỹ(x⃑) into the predicted amount of additional hypervolume in the output space that is expected to be enclosed from that experiment.

Even when only a single metric is important, there are impactful choices to make in how this variable is quantified. While linear transformations such as normalization should not affect SDL progress, provided that the numbers are not made so large or small such that they lead to numerical precision errors, non-linear transformations can also be used to compress or expand important domains in y. For example, when y has a finite range (say an efficiency that varies from 0 to 1), the model will often predict non-physical values (i.e. ỹ> 1 or ỹ< 0). Thus performing transformations that enforce these physical constraints can be helpful. For example, building a model to predict y′ = arctanh(2y − 1) both preserves the physical constraints on y while expanding the domains associated with high and low values.²⁶

C The surrogate model used to approximate the experimental response

A core decision in the BO process is deciding how to model y as defined in Section 2. In principle, any type of mathematical model can be used here, provided it can predict both the expectation value and uncertainty at any x⃑. The most commonly applied model is Gaussian process regression (GPR). This model is highly applicable in the low- to medium-data regimes and is relatively free of bias, despite only being able to model surfaces that are infinitely differentiable.

To gain intuition about the function of a GPR, it can be thought of as a tool for predicting the expectation ỹ(x⃑) at any x⃑ as the weighted average of the prior belief μ₀(x⃑) and the results of all prior experiments y_i(x⃑_i). Commonly, the prior is assumed to be constant and therefore usually considered uninformative, although more advanced methods can be used such as setting this prior using low-fidelity measurements including simulation-based approximations of the experimental function.¹⁹ The weighting used for this prior is based on a hyperparameter θ₀, which represents the total range of experimentally realizable values. More interesting are the weights chosen for each experimental measurement. The underlying assumption is that points closer to the sampling point are more highly correlated, although each dimension of x⃑ could feature correlations with different length scales. A common strategy is to define a kernel function that models how correlations vary in space with common choices being squared exponential or Matérn functions.³⁹ Such functions feature a set of hyperparameters [small theta, Greek, vector] that represent the distance in each dimension over which the output is expected to be highly correlated. This kernel function, together with the physical measurement uncertainty σ_y, together determine the weighting of each previously measured experiment. A similar process can be used to predict the uncertainty in ỹ(x⃑), termed [small sigma, Greek, tilde](x⃑). The hyperparameters [small theta, Greek, vector], θ₀, σ_y are crucial to GPR performance and these hyperparameters are typically set using maximum likelihood estimation. It is important to note that σ_y is an estimation of the measurement uncertainty used by the GPR and it can either be independently estimated by performing control experiments or it can be chosen using statistical methods such as maximum likelihood estimation. Either way, the decision to use a single value of σ_y across the whole parameters space is an approximation that deserves careful consideration. For a more nuanced look at GPRs, their mathematical underpinnings have been outlined in prior publications.^31,40

It should be noted that there are vastly more sophisticated approaches that can be taken than the simple GPR-based approach described above. For instance, rather than assuming that correlations between points are translationally invariant (that correlations depend solely on distance between points but not on their location in parameter space), one can define non-stationary kernel functions that allow correlations that capture nuances in the parameter space itself.^41–44 Additionally, there are hybrid methods such as deep kernel learning (DKL) in which a deep neural network is trained to transform the input data to a GPR.^45,46 This concatenation of models makes the system able to accommodate variable length-scale correlations and discontinuities in the input space.

In addition to data-driven methods to modify the expected correlations in space, there are considerable opportunities for the experimenter to bring physical intuition into the modeling effort. In particular, it is possible to transform the input space based on compound variables that are expected to more closely connect to the physical output. Simple examples of this process could include dividing the masses of reagents by their volumes to learn on concentrations or taking the ratio of geometric parameters to learn on aspect ratios.²⁶ While such anecdotes appeal to our intuition, the choice of how to represent the variables that define the parameter space is an underappreciated facet of SDL operation and deserves concerted study.⁴⁷

D The acquisition function used to evaluate the benefit of sampling at a given location

The second half of BO is choosing an acquisition function a. The goal of this function is to convert the predictions ỹ(x⃑) and [small sigma, Greek, tilde](x⃑) into a scalar quantity that relates to the predicted benefit of sampling at that location. A key consideration here is balancing the needs of exploration and exploitation.³¹ Exploration prioritizes sampling in regions with little prior information while exploitation prioritizes sampling in regions believed to be high performing as a means of optimizing this performance. One acquisition function that displays this dichotomy well is the upper confidence bound (UCB) in which a_UCB = ỹ(x⃑) + λ[small sigma, Greek, tilde]²(x⃑), where λ reflects a weighting in which λ = 0 would be considered pure exploitation while λ → ∞ would be considered pure exploration. Other commonly used acquisition functions are expected improvement (EI), in which a_EI is proportional to the amount by which the sampling point is expected to be above the highest previously observed point. Like surrogate modeling, there have been innovations in the development of advanced acquisition policies, such as those that incorporate simulation data^19,32 or expert knowledge.⁴⁸

Another consideration when choosing an acquisition function is whether experiments are performed individually or in batches.^49–52 When experiments are performed in batches, it is necessary to take action to make sure that each point will target a different region in x⃑. One approach, for instance, is to select the first experiment in the batch, then recondition the GPR assuming that the point was sampled and either returned the GPR mean (Kriging believer) or a constant value (constant liar), and use this updated GPR to predict the next point iteratively until all batch points have been selected.⁵⁰ Alternatively, a simple penalty can be applied after selecting each experiment to force subsequent experiments to be further away in x⃑.

E Finding the maximum of the acquisition function

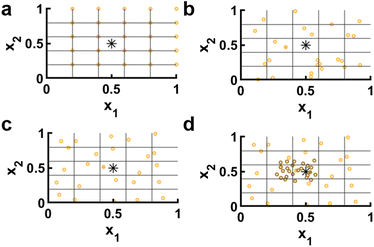
Once the surrogate model is conditioned and a decision policy selected, the maximum of the acquisition function must be determined. Because GPR models do not provide an equation where the maximum can be located in a closed form, it is necessary to choose discrete locations in x⃑ to evaluate as candidate experiments. Exhaustively evaluating every possible location is nearly always impractical, especially when dealing with continuous variables. Thus, it becomes necessary to choose a subset of points to sample.⁵³ Grid and random sampling are unfavorable for opposite reasons: Grid based search will fail to locate a maximum point if it is not on the grid, while random sampling fails to ensure evenly spaced sampling points (Fig. 2a and b). In contrast, Latin hypercube sampling (LHS) presents a way to cover all of parameter space while introducing some randomness that prevents the same precise point from being reconsidered multiple times in subsequent steps (Fig. 2c). In terms of how many points to select, the curse of dimensionality plays a major role. Specifically, if x⃑ has d dimensions, adding 10 conditions per d leads to ∼10^d points, which becomes intractable when d > 7 despite 10 conditions providing only a sparse sampling of space. Thus, in any reasonably high dimensional space, it becomes necessary to couple an initial sampling with a refinement or optimization process. For example, a second cluster of LHS points may be collected near the maximum observed during the first round (Fig. 2d). Alternatively. The maximum or maxima of the first round can be used as input points to other optimization algorithms such as gradient ascent or genetic algorithms to find local maxima of a.³³

Fig. 2 Selection methods for sampling points. (a), Grid based sampling (orange open circles) will sample the same points each time. The target maximum (black asterisk) and the closest point (solid orange circle) are also shown. (b) Random sampling is statistically likely to cluster in local regions, leaving other regions with no points. (c) Latin hypercube sampling (LHS) points are selected by dividing the space into a grid and selecting one point randomly in each domain of the resulting grid. (d) A second round of LHS points (dark orange open circles) can be used to further search in a promising region, finding a better point (dark solid orange circle) than the original selection points.

F Which experimental data points are used to condition the surrogate model

It may seem obvious that one should use all available data to improve the predictive power of the surrogate model, but as campaigns shift from exploration to exploitation, it is useful to focus on high performing regions. This counterintuitive approach has two rationales. First, as the number of experiments increases, the time to condition the model and predict the performance at the sampling points increases to the point where it can slow the progress of the SDL. By focusing on the experiments that are most likely to be relevant to the area of interest, the experiment selection process can avoid becoming a bottleneck. Second, focusing on the region of interest allows the hyperparameters to be tuned to the region of interest. This focusing may be necessary if the output space is inherently different on average than it is in the region of interest, e.g. it is a needle in a haystack. This challenge can also manifest if the density of experiments in the region of interest is higher than it is in the rest of the parameter space, allowing shorter length scale hyperparameters to be employed in a manner that increases prediction accuracy. The opportunities inherent in pruning the available data have been recently noted in both the chemical and material spaces.^54,55 There are several algorithms that have been developed to do this pruning including zooming memory-based initialization (ZoMBI)⁵⁶ and trust region Bayesian optimization (TuRBO).⁵⁷

An interesting related point is how to deal with outliers. Algorithmically rejecting outliers is a risky strategy as in a needle-in-a-haystack type search, the needle is likely to look like an outlier. For this reason, it is easier to justify including or excluding data based on its position in x⃑ rather than its measured value of y. That said, all available data and characterization should be used to assess whether a given experiment was conducted correctly and therefore whether the measured value can be trusted.

4. Sources of feedback to adjust the knobs – the gauges

Having outlined the main variables that the experimenter can adjust, now we turn to the ways in which the experimenter can determine when to make adjustments. In other words, we seek to identify the avenues for obtaining real-time information during a campaign that provides actionable feedback that can be used to change settings A–F listed above. Crucially, given the complexity of SDL campaigns and the opacity of many ML models, we seek to draw direct connections between graphical observables that exist in spaces of any dimensionality and each setting A–F. In this way, the experimenter can build intuition for the connections between these items and exercise their agency in fruitfully guiding the SDL. In particular, we have identified four sets of graphs that the experimenter should be examining and listed how features of these graphs can provide guidance when adjusting SDL settings.

Response scatter plots

After each additional experiment, a set of d plots should be generated that each feature y vs. a single dimension of x⃑ with the most recently added data highlighted. Older data points can be colored to illustrate the order in which they were collected (Fig. 3). Looking at one dimensional slices of a multidimensional space can only offer limited insight, but one thing that such plots can do quite well is illustrate whether top performing points are on a boundary. Such an observation would be an indication that the boundaries of x⃑ should be enlarged if possible to capture this trend, thus providing feedback on parameter range (A). We note that if boundaries are not independent, rather than plotting y vs. each component of x⃑, it may be more useful to plot y vs. the distance from the nearest boundary.

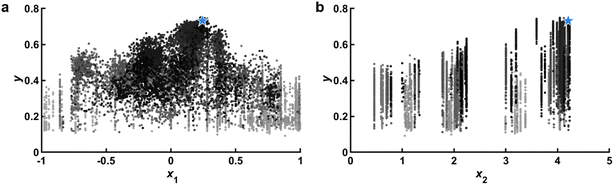Fig. 3 Response scatter points. (a) Observed response y vs. x₁. Points colored based on the order that they were tested (light gray to black), with the most recent test data shown as a blue star. In this panel, the peak of y is firmly within the boundaries of x₁, indicating that the range is likely appropriate. (b) Observed y vs. x₂. In contrast with x₁ which is a design variable that can be chosen continuously, x₂ corresponds to a material property and therefore only discrete values corresponding to known materials can be selected. In this panel, the peak of y is on the boundary that cannot be expanded due to material constraints, pointing to potential material development goals. Data corresponds to experiments and is adapted from ref. 26.

Parity plots

A crucial plot to consistently observe is the parity plot, or the plot of ỹvs. y (Fig. 4). Naturally, data on this plot should fall on the line ỹ= y, but imperfections in the model and experimental noise will prevent this from occurring. Of particular interest is the result of the most recent experiment and so the model that was used to select the last experiment should be the one used to compute ỹ. In this way, it is possible to assess the goal of the experiment (how good the point was predicted to be) as well as its accuracy (how close the experiment was to the prediction). The general appearance of this parity plot is a crucial metric in determining the acquisition function (D), namely to adjust the priority of the policy to more heavily lean towards exploration or exploitation. In brief, if the parity plot exhibits a very poor correlation, then any attempt at exploitation will likely fail and exploration should be prioritized. It should be noted that while some policies, namely UCB, feature a discrete knob that allows one to change the relative focus on exploration versus exploitation, not all policies have such a setting, so changing a entirely may be necessary.²² It is also possible to use combinations of multiple acquisition policies.^9,26,58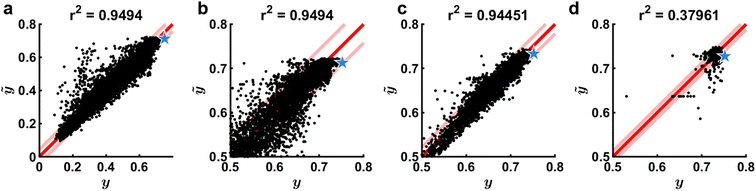

Fig. 4 Parity plots. (a) Predicted response ỹvs. y built from 13 250 data points. Red line represent ỹ= y and pink lines represent estimated measurement error σ_y. Blue star represents the latest experimental prediction and the subsequent result. (b) Same model as a, but zoomed in on the upper section of the data to highlight the flat plateau that occurs at ỹ≈ 0.7, leading to significant underprediction of performance for the latest experiment. (c) Model built from 4060 data points near max(y) shows improved performance at high values, which are the most important in a maximization problem. Predicted value of σ_y is also decreased. (d) Model built from 410 data points illustrating deteriorated performance and a very small estimated σ_y due to too little data. Data corresponds to experiments and is adapted from ref. 26.

The overall behavior of the parity plot is also crucial in validating the surrogate model (C). Two aspects of fit quality should be immediately apparent when examining the parity plot. First, the spread of the data about the trend line provides an excellent proxy for prediction accuracy and this can be quantified using the square of the Pearson's correlation coefficient r². Since these are in-training sample predictions, training conditions exist for a perfect match between model and data. However, it is important to remember that the model is Bayesian with the expectation that experimental data has uncertainty and thus the spread about the parity line should approach σ_y. As such, one would expect ∼65% of data points to fall between lines parallel to the parity line but spaced apart by ±σ_y, shown as light red lines in Fig. 4. If nearly all of the data falls between these lines, this is a signal that the model is overfitting. While generally r² will increase as the volume of data increases, it is also highly dependent upon the model hyperparameters θ and any transformations made to the input space. Thus, low r² reflects the need to pay careful attention to these terms. We recommend making decisions to set these terms based upon minimizing cross-validation error or through maximum likelihood estimation. In addition to spread about the parity line, if the residuals of the data are not uniformly distributed, it may reflect an incorrect bias in the model. As GPRs are nearly bias-free, they should not exhibit this phenomenon.

The parity plot can also clearly communicate what data should be included in the model (F). In particular, for maximization problems, the data that reflects the largest values of y are in many ways the most important. A common occurrence with GPRs is that they will effectively smooth out sharp peaks in parameter space due to their inability to model wide low-performing regions while also modeling narrow high-performing regions, or needles in a haystack. This problem is manifest in the parity plot through a flattening of ỹat the high end (Fig. 4b). Under these circumstances, it will be very challenging to tease out accurate predictions in high-performing regions. One solution is to adjust the data used to train the model (F). In particular, one can retrain the model using only the data in the proximity of the high-performing points, thus ensuring that the model accurately captures this region (Fig. 4c). Variations exist to this approach such as omitting data based on y (only including high performing experiments), the location in x⃑ relative to argmax(y) (only including experiments near the best performing experiment), or the location in x⃑ relative to argmax(ỹ) (only including experiments near the best predicted sampling point of an initial GPR model). However, if too few data points are included, the model performance can deteriorate (Fig. 4d).

Proximity plots

While hunting for extrema in complex and high dimensional parameter spaces, a crucial metric to examine is how close experiments are to one another. In order to readily visualize this metric as the campaign progresses, y should be plotted vs.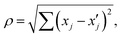 where 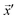is the location of the most recently sampled point (Fig. 5) and the subscript j corresponds to an iterator over each dimension in the parameter space. A virtue of plotting data in this way is that it makes it very clear the degree to which the SDL is prioritizing exploration vs. exploitation for the most recent experiment. Simply – the further the sampled point is from nearby points, the more exploration focused the choice of the policy. This makes such plots very useful for evaluating the behavior of the decision policy (D) and ensuring that it is behaving as expected. This is also very useful when using policies like EI that themselves balance exploration and exploitation. The distance of the nearest point is a clear indicator of how the policy is resolving this tradeoff. In addition to providing feedback into the acquisition function, proximity plots can be useful in helping select the data used to train the model (F). When training a model with some subsample of the available data, it is useful to indicate this data on the proximity plot to illustrate the complexity of the subspace under consideration.

Fig. 5 Proximity plots. Observed y vs. distance to selected point ρ. Black points represent previous experiments, while the blue star represents the selected experiment and its predicted performance ỹ. The distance of the point closest to the star is an indicator of the exploration/exploitation tradeoff. In this panels, this tradeoff is illustrated by selecting a point based on upper confidence bound with varied hyperparameter λ. (a) λ = 0, pure exploitation. (b) λ = 1, balance of exploration/exploitation. (c) λ = 5, focus on exploration. (d) λ = 25, nearly pure exploration. Data corresponds to experiments and is adapted from ref. 26.

Despite the utility of proximity plots, a question arises in how to normalize ρ to make the data most meaningful. For instance, considering a normalized d-dimensional parameter space, the furthest two points can be from one another is √d, making Euclidian distance in a normalized space a very useful way of thinking about distances. That said, the relevance of distances depends on the topography of the response surface and not just the chosen bounds. One way to take this into consideration when using a GPR is to normalize each dimension by the length scale hyperparameter θ_j associated with that dimension. In this way, the magnitude of ρ is closely connected to covariance with ρ ∼2 indicating that only 5% of the sample point's variance is captured by the neighbor. Unfortunately, this approach can be challenging as [small theta, Greek, vector] can change and in particular shrink as additional data becomes available that elucidates high-spatial-frequency variations. This makes it hard to track the performance of this plot over time. Interestingly, when using proximity plots normalized by GPR hyperparameters, the behavior of points ρ < 2 illustrates how well the GPR is performing in the experimental region. If y is spread widely despite being considered statistically close by the GPR, it is a signal that the model is not performing well in the region of interest and the surrogate model (C) needs to be reevaluated.

Performance gamut

Since the ultimate goal of the SDL, in at least this example application, is the optimization of performance y, a crucial piece of information is evaluating the full spectrum of y that has been observed thus far (Fig. 6). This plot is ultimately the main avenue for collecting feedback on the choice of the metric (B). Even though it is ultimately necessary to make decisions based on a single metric, this is not always the most useful for conceptualizing the response surface. Humans visualize information easily in two dimensions and thus, it is very useful to conceive of ways to define two dimensions to aid in visualization, even if they are not directly related to the SDL decision-making process. For a high dimensional y⃑, unsupervised approaches such as principle component analysis or autoencoders may be useful for reducing the performance space to two variables. When optimizing a scalar metric, it is useful to introduce another value that provides a second dimension for visualization. Ideally, this second metric would be related to the first, but not directly connected. For example, in a campaign to optimize toughness, material stiffness could be a useful second property for visualization as it would help distinguish tough but compliant materials from brittle but stiff materials, even if they both had the same toughness.

Fig. 6 Performance gamut. (a) Experimental data (black dots) are represented by two dimensions: y₁ and y₂. (b) To find the maximum of the acquisition function, LHS is used to evaluate sampling points (orange) using the zoomed-in GPR model from Fig. 4c. (c) A second pass of LHS (dark orange) is done with the same GPR model but in a smaller region to more closely locate the maximum of the aquisition function. Data corresponds to experiments and is adapted from ref. 26.

In addition to plotting the actual values of y, it is useful to plot on the same axis the ỹthat were in consideration for the most recent experiment as this can be useful for determining the number of sampling points used when finding the maximum of the acquisition function (D). The predicted points should be dense enough that they fill a reasonable region in the performance gamut with predicted points that ideally extend above the highest observed experiments. If the observed prediction space appears too sparse, one solution is to increase the number of sampling points. However, this is not the only consideration when deciding the number of points to sample. In particular, the process of training a model and selecting sampling points can take non-trivial amounts of time. The easiest way to modulate this time is by adjusting the number of sampling points (E). Given that the tempo of an SDL campaign is naturally set by the pace of collecting experimental data, one approach is to adjust the number of sampling points until the time required to perform experiments is commensurate with the time to choose subsequent samples. Further considerations are necessary when experiments are performed in batch or using asynchronous agents, but the availability of supercomputing clusters means that running prediction models in parallel can increase the prediction rate.

5. Concluding remarks

Collectively, the principles and heuristics presented here provide a blueprint for sustained operation of an SDL in which SDL-driven discoveries and human-led interventions together accelerate the research enterprise. The focus on two complementary aspects – the settings that govern SDL operation and data showing the SDL performance in real time – draws a close analogy with operating automobiles in which drivers have a clear idea of how to act on feedback from each gauge. While this work draws from our experience running SDLs, there are many other practitioners with valuable insight, and so it is expected that these methods will require updating as more sophisticated methods and tools become available. Indeed, we anticipate that this is a facet of human–machine interaction that is sure to become increasingly complex in the coming years. It should be noted that there are also opportunities for meta learning in which processes such as reinforcement learning are used to adjust the knobs discussed in this work, which could be further leveraged to increase the pace of learning.

Data availability statement

The data used in this work is available at: https://hdl.handle.net/2144/46687. The code used to create the plots used in the figures is available at: https://github.com/KelseyEng/DSSDL_Figures.

Conflicts of interest

The authors declare no conflict of interests.

Acknowledgements

The authors acknowledge Aldair Gongora, Kristofer Reyes, Patrick Riley, Tonio Buonassisi, Milad Abolhasani, Roman Garnett, Peter Frazier, Joshua Schrier, and Benji Maruyama for helpful discussions. This work was supported by Google LLC, the Boston University Rafik B. Hariri Institute for Computing and Computational Science & Engineering (2017-10-005), the National Science Foundation (CMMI-1661412), and the US Army CCDC Soldier Center (contract W911QY2020002). This work was funded by Honeywell Federal Manufacturing and Technologies through contract number N000471618. Honeywell Federal Manufacturing and Technologies, LLC operates the Kansas City National Security Campus for the United States Department of Energy/National Nuclear Security Administration under contract number DE-NA0002839.

References

1. E. Stach, B. DeCost, A. G. Kusne, J. Hattrick-Simpers, K. A. Brown, K. G. Reyes, J. Schrier, S. Billinge, T. Buonassisi, I. Foster, C. P. Gomes, J. M. Gregoire, A. Mehta, J. Montoya, E. Olivetti, C. Park, E. Rotenberg, S. K. Saikin, S. Smullin, V. Stanev and B. Maruyama, Matter, 2021, 4, 2702–2726.
2. H. Winicov, J. Schainbaum, J. Buckley, G. Longino, J. Hill and C. Berkoff, Anal. Chim. Acta, 1978, 103, 469–476.
3. R. Hickman, P. Bannigan, Z. Bao, A. Aspuru-Guzik and C. Allen, Matter, 2023, 6, 1071–1081.
4. M. Abolhasani and E. Kumacheva, Nature Synthesis, 2023, 2, 483–492.
5. M. L. Green, B. Maruyama and J. Schrier, Appl. Phys. Rev., 2022, 9, 030401.
6. J. A. Bennett and M. Abolhasani, Curr. Opin. Chem. Eng., 2022, 36, 100831.
7. P. Nikolaev, D. Hooper, F. Webber, R. Rao, K. Decker, M. Krein, J. Poleski, R. Barto and B. Maruyama, npj Comput. Mater., 2016, 2, 16031.
8. R. D. King, K. E. Whelan, F. M. Jones, P. G. Reiser, C. H. Bryant, S. H. Muggleton, D. B. Kell and S. G. Oliver, Nature, 2004, 427, 247.
9. B. Burger, P. M. Maffettone, V. V. Gusev, C. M. Aitchison, Y. Bai, X. Wang, X. Li, B. M. Alston, B. Li, R. Clowes, N. Rankin, B. Harris, R. S. Sprick and A. I. Cooper, Nature, 2020, 583, 237–241.
10. R. W. Epps, M. S. Bowen, A. A. Volk, K. Abdel-Latif, S. Han, K. G. Reyes, A. Amassian and M. Abolhasani, Adv. Mater., 2020, 2001626.
11. H. Zhao, W. Chen, H. Huang, Z. Sun, Z. Chen, L. Wu, B. Zhang, F. Lai, Z. Wang, M. L. Adam, C. H. Pang, P. K. Chu, Y. Lu, T. Wu, J. Jiang, Z. Yin and X.-F. Yu, Nature Synthesis, 2023, 2, 505–514.
12. A. A. Volk, R. W. Epps, D. T. Yonemoto, B. S. Masters, F. N. Castellano, K. G. Reyes and M. Abolhasani, Nat. Commun., 2023, 14, 1403.
13. Y. Jiang, D. Salley, A. Sharma, G. Keenan, M. Mullin and L. Cronin, Sci. Adv., 2022, 8, eabo2626.
14. B. P. MacLeod, F. G. Parlane, T. D. Morrissey, F. Häse, L. M. Roch, K. E. Dettelbach, R. Moreira, L. P. Yunker, M. B. Rooney, J. R. Deeth, V. Lai, J. G. Ng, H. Stiu, R. H. Zhang, M. S. Elliott, T. H. Haley, D. J. Dvorak, A. Aspuru-Guzik, J. E. Hein and C. P. Berlinguette, Sci. Adv., 2020, 6, eaaz8867.
15. Y. Liu, A. N. Morozovska, E. A. Eliseev, K. P. Kelley, R. Vasudevan, M. Ziatdinov and S. V. Kalinin, Patterns, 2023, 4, 100704.
16. M. B. Rooney, B. P. MacLeod, R. Oldford, Z. J. Thompson, K. L. White, J. Tungjunyatham, B. J. Stankiewicz and C. P. Berlinguette, Digital Discovery, 2022, 1, 382–389.
17. B. P. MacLeod, F. G. L. Parlane, C. C. Rupnow, K. E. Dettelbach, M. S. Elliott, T. D. Morrissey, T. H. Haley, O. Proskurin, M. B. Rooney, N. Taherimakhsousi, D. J. Dvorak, H. N. Chiu, C. E. B. Waizenegger, K. Ocean, M. Mokhtari and C. P. Berlinguette, Nat. Commun., 2022, 13, 995.
18. A. E. Gongora, B. Xu, W. Perry, C. Okoye, P. Riley, K. G. Reyes, E. F. Morgan and K. A. Brown, Sci. Adv., 2020, 6, eaaz1708.
19. A. E. Gongora, K. L. Snapp, E. Whiting, P. Riley, K. G. Reyes, E. F. Morgan and K. A. Brown, iScience, 2021, 24, 102262.
20. L. Kavalsky, V. I. Hegde, E. Muckley, M. S. Johnson, B. Meredig and V. Viswanathan, Digital Discovery, 2023, 2, 1112–1125.
21. E. Annevelink, R. Kurchin, E. Muckley, L. Kavalsky, V. I. Hegde, V. Sulzer, S. Zhu, J. Pu, D. Farina, M. Johnson, D. Gandhi, A. Dave, H. Lin, A. Edelman, B. Ramsundar, J. Saal, C. Rackauckas, V. Shah, B. Meredig and V. Viswanathan, MRS Bull., 2022, 47, 1036–1044.
22. Q. Liang, A. E. Gongora, Z. Ren, A. Tiihonen, Z. Liu, S. Sun, J. R. Deneault, D. Bash, F. Mekki-Berrada, S. A. Khan, K. Hippalgaonkar, B. Maruyama, K. A. Brown, J. Fisher III and T. Buonassisi, npj Comput. Mater., 2021, 7, 188.
23. B. Rohr, H. S. Stein, D. Guevarra, Y. Wang, J. A. Haber, M. Aykol, S. K. Suram and J. M. Gregoire, Chem. Sci., 2020, 11, 2696–2706.
24. S. Matsuda, G. Lambard and K. Sodeyama, Cell Rep. Phys. Sci., 2022, 3, 100832.
25. B. Koscher, R. B. Canty, M. A. McDonald, K. P. Greenman, C. J. McGill, C. L. Bilodeau, W. Jin, H. Wu, F. H. Vermeire, B. Jin, T. Hart, T. Kulesza, S.-C. Li, W. H. Green and K. F. Jensen, chemrxiv, 2023, preprint,  DOI:10.26434/chemrxiv-2023-r7b01.
26. K. L. Snapp, B. Verdier, A. Gongora, S. Silverman, A. D. Adesiji, E. F. Morgan, T. J. Lawton, E. Whiting and K. A. Brown, arXiv, 2023, preprint, arXiv:2308.02315,  DOI:10.48550/arXiv.2308.02315.
27. K. Hippalgaonkar, Q. Li, X. Wang, J. W. Fisher III, J. Kirkpatrick and T. Buonassisi, Nat. Rev. Mater., 2023, 8, 241–260.
28. F. Adams, A. McDannald, I. Takeuchi and A. G. Kusne, arXiv, 2023, preprint, arXiv:2306.10406,  DOI:10.48550/arXiv.2306.10406.
29. K. J. Kanarik, W. T. Osowiecki, Y. Lu, D. Talukder, N. Roschewsky, S. N. Park, M. Kamon, D. M. Fried and R. A. Gottscho, Nature, 2023, 616, 707–711.
30. D. A. Cohn, Z. Ghahramani and M. I. Jordan, J. Artif. Intell. Res., 1996, 4, 129–145.
31. P. I. Frazier, arXiv, 2018, preprint, arXiv:1807.02811,  DOI:10.48550/arXiv.1807.02811.
32. Z. Liu, N. Rolston, A. C. Flick, T. W. Colburn, Z. Ren, R. H. Dauskardt and T. Buonassisi, Joule, 2022, 6, 834–849.
33. T. Erps, M. Foshey, M. K. Luković, W. Shou, H. H. Goetzke, H. Dietsch, K. Stoll, B. von Vacano and W. Matusik, Sci. Adv., 2021, 7, eabf7435.
34. H. M. Sheikh and P. S. Marcus, Struct. Multidiscip. Optim., 2022, 65, 331.
35. K. Y. L. Andre, V.-G. Eleonore, L. Yee-Fun and H. Kedar, J. Mater. Inf., 2023, 3, 11.
36. S. Krishnadasan, R. Brown, A. Demello and J. DeMello, Lab Chip, 2007, 7, 1434–1441.
37. I. Y. Kim and O. L. de Weck, Struct. Multidiscip. Optim., 2006, 31, 105–116.
38. Y. Iwasaki, H. Jaekyun, Y. Sakuraba, M. Kotsugi and Y. Igarashi, Sci. Technol. Adv. Mater.: Methods, 2022, 2, 365–371.
39. E. Schulz, M. Speekenbrink and A. Krause, J. Math. Psychol., 2018, 85, 1–16.
40. C. K. Williams and C. E. Rasmussen, Gaussian Processes for Machine Learning, MIT press Cambridge, MA, 2006.
41. M. M. Noack, G. S. Doerk, R. Li, J. K. Streit, R. A. Vaia, K. G. Yager and M. Fukuto, Sci. Rep., 2020, 10, 17663.
42. M. M. Noack and K. G. Reyes, MRS Bull., 2023, 48, 153–163.
43. M. M. Noack, H. Krishnan, M. D. Risser and K. G. Reyes, Sci. Rep., 2023, 13, 3155.
44. Y. Xu, C. W. Farris, S. W. Anderson, X. Zhang and K. A. Brown, Sci. Rep., 2023, 13, 12527.
45. Y. Liu, M. Ziatdinov and S. V. Kalinin, ACS Nano, 2022, 16, 1250–1259.
46. M. Valleti, R. K. Vasudevan, M. A. Ziatdinov and S. V. Kalinin, arXiv, 2023, preprint, arXiv:2303.14554,  DOI:10.48550/arXiv.2303.14554.
47. S. Markovitch and D. Rosenstein, Mach. Learn., 2002, 49, 59–98.
48. F. Häse, M. Aldeghi, R. J. Hickman, L. M. Roch and A. Aspuru-Guzik, Appl. Phys. Rev., 2021, 8, 031406.
49. P. Honarmandi, V. Attari and R. Arroyave, Comput. Mater. Sci., 2022, 210, 111417.
50. C. Chevalier and D. Ginsbourger, International Conference on Learning and Intelligent Optimization, Springer, 2013.
51. R. Tamura, G. Deffrennes, K. Han, T. Abe, H. Morito, Y. Nakamura, M. Naito, R. Katsube, Y. Nose and K. Terayama, Sci. Technol. Adv. Mater.: Methods, 2022, 2, 153–161.
52. L. D. González and V. M. Zavala, Comput. Chem. Eng., 2023, 170, 108110.
53. N. Dige and U. Diwekar, Comput. Chem. Eng., 2018, 115, 431–454.
54. D. E. Graff, M. Aldeghi, J. A. Morrone, K. E. Jordan, E. O. Pyzer-Knapp and C. W. Coley, J. Chem. Inf. Model., 2022, 62, 3854–3862.
55. K. Li, D. Persaud, K. Choudhary, B. DeCost, M. Greenwood and J. Hattrick-Simpers, arXiv, 2023, preprint, arXiv:2304.13076,  DOI:10.48550/arXiv.2304.13076.
56. A. E. Siemenn, Z. Ren, Q. Li and T. Buonassisi, npj Comput. Mater., 2023, 9, 79.
57. D. Eriksson, M. Pearce, J. Gardner, R. D. Turner and M. Poloczek, Adv. Neural Inf. Process., 2019, 32 DOI:10.48550/arXiv.1910.01739.
58. C. C. Rupnow, B. P. MacLeod, M. Mokhtari, K. Ocean, K. E. Dettelbach, D. Lin, F. G. L. Parlane, H. N. Chiu, M. B. Rooney, C. E. B. Waizenegger, E. I. de Hoog, A. Soni and C. P. Berlinguette, Cell Rep. Phys. Sci., 2023, 4, 101411.

---