Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
CoPriNet: graph neural networks provide accurate and rapid compound price prediction for molecule prioritisation†
Ruben
Sanchez-Garcia
 *ab,
Dávid
Havasi
*ab,
Dávid
Havasi
 cd,
Gergely
Takács
cd,
Gergely
Takács
 cd,
Matthew C.
Robinson
e,
Alpha
Lee
cd,
Matthew C.
Robinson
e,
Alpha
Lee
 ef,
Frank
von Delft
ef,
Frank
von Delft
 *bgh and
Charlotte M.
Deane
*bgh and
Charlotte M.
Deane
 *a
*a
aDepartment of Statistics, University of Oxford, Oxford, OX1 3LB, UK. E-mail: deane@stats.ox.ac.uk; ruben.sanchez-garcia@stats.ox.ac.uk
bStructural Genomics Consortium (SGC), University of Oxford, Oxford OX3 7DQ, UK
cMcule.com Kft, Bartók Béla út 105-113, Budapest, 1115, Hungary
dDepartment of Chemical and Environmental Process Engineering, Budapest University of Technology and Economics, Műegyetem rakpart 3, Budapest, 1111, Hungary
ePostEra Inc., 1209 Orange Street, Wilmington, Delaware 19801, USA
fDepartment of Physics, University of Cambridge, Cambridge CB3 0HE, UK
gDiamond Light Source, Didcot OX11 0DE, UK
hDepartment of Biochemistry, University of Johannesburg, Johannesburg 2006, South Africa
First published on 28th November 2022
Abstract
Compound availability is a critical property for design prioritization across the drug discovery pipeline. Historically, and despite their multiple limitations, compound-oriented synthetic accessibility scores have been used as proxies for this problem. However, the size of the catalogues of commercially available molecules has dramatically increased over the last decade, redefining the problem of compound accessibility as a matter of budget. In this paper we show that if compound prices are the desired proxy for compound availability, then synthetic accessibility scores are not effective strategies for us in selection. Our approach, CoPriNet, is a retrosynthesis-free deep learning model trained on 2D graph representations of compounds alongside their prices extracted from the Mcule catalogue. We show that CoPriNet provides price predictions that correlate far better with actual compound prices than any synthetic accessibility score. Moreover, unlike standard retrosynthesis methods, CoPriNet is rapid, with execution times comparable to popular synthetic accessibility metrics, and thus is suitable for high-throughput experiments including virtual screening and de novo compound generation. While the Mcule catalogue is a proprietary dataset, the CoPriNet source code and the model trained on the proprietary data as well as the fraction of the catalogue (100 K compound/prices) used as test dataset have been made publicly available at https://github.com/oxpig/CoPriNet.
Introduction
The drug design process can be thought of as a multi-objective optimization problem in which potential drug compounds need to satisfy a wide set of properties from binding affinity and toxicity to selectivity and solubility.1 One property that is key when developing potential drug molecules is their availability, since no matter how promising a design might be, if it is not available, it is doomed to fail.In order to estimate compound availability, several computationally calculated synthetic accessibility (SA) scores have been developed. These approaches can be roughly classified as retrosynthesis-based predictions,2–6 binary classifiers,7–9 and complexity-based estimations.10–13
Retrosynthesis-based approaches aim to identify suitable synthetic routes for a given molecule using distinct types of search algorithms over databases of building blocks and chemical transformations. State-of-the-art methods,2,6,14,15 which are based on deep learning, are able to integrate information from millions of reactions and building blocks, suggesting feasible synthetic routes for the majority of the benchmarked compounds in a matter of seconds to minutes.2 However, their outputs strongly depend on the employed databases16 and they tend to suggest multiple solutions which are difficult to rank17 and more importantly, even the fastest are computationally demanding and therefore ill-suited for high-throughput computational pipelines.8
Binary classifiers are machine learning algorithms trained to distinguish between compounds that are easy or difficult to make. Although the available approaches may differ in terms of learning algorithms (support vector machine, neural network, etc.) and compound featurization (descriptors, fingerprints, etc.), it is the definition of the training set, consisting of compounds labelled as easy or difficult to make, that most impacts the behaviour of these methods. Some strategies for compiling training datasets include retrosynthesis,7,8 presence in commercial catalogues9 or virtually edited compounds.9 Although binary classifiers tend to be much faster than retrosynthesis-based methods, they are also less accurate9 and their performance is highly dependent on the training dataset.8 Binary classifiers also by definition cannot distinguish between different levels of difficulty.8,9
Complexity-based methods try to define an empirical metric under the assumption that complex molecules are more difficult to synthesize.13,18,19 Most methods define complexity as a function of the presence of features deemed to be complex or infrequent such as chiral centres, uncommon moieties, or unusual molecular fragments. One of the most popular measures of SA,20–24 SAscore10 is a complexity-based method that uses the rarity of fragments found in PubChem25 and a set of predefined properties such as the ring complexity or the number of stereo centres to calculate its score. Another commonly used SA score, SCScore11 employs an indirect estimation of complexity assuming that the complexity of the reactants is never larger than the complexity of the products.
Due primarily to their simplicity and speed, SAscore and SCScore have been used extensively in drug development pipelines including for compound screening,20–22,26 dataset preparation23,24 and molecule generation/optimization.27–30 SAScore is one of the most popular metrics for biasing or discarding potentially infeasible compounds in methods for computational generation of de novo molecules.27,31–34 However, as described above, SAscore and SCScore are simple approximations for SA and as such, present several limitations. For instance, it is well known that these scores tend to underestimate the SA of difficult compounds that can be synthesized from complex commercially available building blocks.35,36 It has also been shown that structurally similar compounds, which tend to have similar complexity-based scores, can require synthetic strategies of different difficulty levels,35 leading to incorrect SA estimations.
Independent of their nature, the aim of all the methods described above is to computationally filter compounds, ruling out those difficult to make or purchase. This suggests the need of an alternative metric that directly estimates the actual metric of compound availability, namely its price. This is after all what influences many of the decisions in drug discovery, particularly in the early stages when the cost of the compounds to be experimentally tested is often of central importance.
Current SA metrics exhibit poor correlation with prices, Fukunishi et al.37 found that the Pearson correlation coefficient (PCC) between their SA measurement and the logarithmic sales prices of the compound, in $ per mmol, was ∼0.3. Fernandez et al.38 observed only a weak correlation between prices and two complexity-based SA scores: ring complexity index39 and SAscore. This is perhaps not surprising, since SA scores were never intended to capture price information. Nevertheless, most methods for automatic compound design try to optimize their molecules against a SA metric, which leads to the suggestion of many feasible yet prohibitively expensive compounds.
For the hundreds of millions of compounds in the commercial catalogues, price estimation is merely a database search question that, in real situations can be severely delayed by the quotation process. However, the real challenge is estimating price for the rest of chemical space: the advent of machine learning-based molecular generation techniques and large virtual compound collections makes this problem increasingly acute.
Compound cost prediction has previously been addressed using QSAR-like methods38 or retrosynthesis-based approaches.40 Fernandez et al.38 developed the QS$R approach, a classical machine learning method aimed to learn the relationship between the structure of the compounds and their prices for QSAR-like setups. As a proof-of-concept, the QS$R model was trained on ∼4000 pairs of compound descriptors and prices, performing particularly well for compounds in the lower price range. Badowski et al.40 estimated the cost of a molecule as the cost of the cheapest retrosynthetic route considering the cost of the initial reactants, reactions yield, and fixed costs. While this formulation captures the different terms involved in the final price, it relies on the assumption that the cheapest retrosynthetic route is the one that determines the final cost, which does not necessary hold, and on estimations of reaction yields and fixed costs, information that is only available for a limited number of reactions and that, in many cases, is not in the public domain.
With the aim of overcoming these problems, in this manuscript we present CoPriNet, a retrosynthesis-free method to obtain price predictions using only the compound itself. Our method is based on a graph neural network (GNN) trained on a dataset of >6M pairs of molecules and their prices collected from the Mcule41 catalogue (https://mcule.com/) and can be directly employed to assess novel compounds. Our approach follows that of SA binary classifiers trained on retrosynthesis predictions: given enough data, machine learning methods should identify patterns in the input molecules that are relevant for the synthetic planning (or the price) without the need to explicitly undergo retrosynthetic decomposition. Although retrosynthesis-based computations tend to be more accurate, our predictions exhibit a far stronger correlation with catalogue prices than any SA metric, with comparable running times. Consequently, our approach can be employed as a complementary metric to fast SA estimations for high throughput assays and more importantly, for de novo molecule generation, in which the large number of required assessments prevents retrosynthetic-based approaches from being used.
Methods
Datasets
Two main sources of compounds were employed in this work. The first is the Mcule catalogue,41 that contains more than 40 million compounds and their up-to-date prices compiled from more than a hundred vendors. In order to avoid common errors that may arise from the integration of different catalogues (misdrawn and incorrect structures), the catalogue is curated using the Mcule Advanced Curation process (MAC) that involves a rigorous molecule registration system including structural checks, and various steps of standardization, preparation and correction, ensuring that the information contained in the catalogue is highly reliable. From this catalogue we extracted the subset of in-stock compounds (>6M), that was divided into train, validation, and test partitions randomly. The price of each compound was collected on March 2021 from the Mcule database as the best price for 1 g of compound. Prices were then converted from $ per g to $ per mmol because, as found by Fukunishi et al.,37 correlations with SA measurements were stronger.All statistics and figures included in this work are derived from the compounds in the test set except when explicitly stated. The test set is also referred to as the purchasable compounds dataset (PC) throughout this manuscript as it only contains purchasable compounds. For the generalizability study, a random subset of 100 K virtual compounds was also extracted from the Mcule catalogue as a separate independent test set.
The second source of compounds was the ZINC database42 from which we extracted a subset comprising only non-commercially available natural products, that we refer to as the NPNP (Non-Purchasable Natural Products) dataset. We use this dataset as an approximate set of non-synthesizable compounds.
We also employed two of the datasets compiled by Gao and Coley.35 These were their dataset of molecules compiled from five different sources: MOSES,43 ZINC,42 ChEMBL,44 Sheridan et al.,45 and GBD-17;46 and their dataset of de novo generated molecules comprising of two subsets of molecules optimized against multiple properties including or not the SAscore.
Synthetic accessibility calculations
Four distinct SA metrics were employed in this work: SAscore,10 SCScore,11 the AstraZeneca RAscore8 and SYBA.9 All of them were executed using default parameters. Additionally, the retrosynthesis-based score ManifoldSA was computed using the Postera Manifold API v1 (https://api.postera.ai/api/v1/docs/). ManifoldSA summarizes retrosynthesis results into a number between 0 (easy) and 1 (difficult) that estimates the synthetic accessibility of a compound. For Fig. 2, compounds were classified as synthesizable if their ManifoldSA < 0.5 and non-synthesizable otherwise.Manifold first performs a tree-search to compute possible retrosynthetic routes from the target molecule to purchasable starting materials, using Molecular Transformer14,47 to predict the probability of success of each step. The ManifoldSA is then computed by considering the feasibility and robustness of multiple routes to the molecule, taking into account probability of success at each step of a route. The Manifold algorithm has been used in synthesis-driven de novo design.48
Retrosynthesis calculations
Retrosynthesis prediction was carried out using the Postera Manifold API, that implements the molecular transformer approach.14,47 We employed the v1 retrosynthesis endpoint using a depth search of four and the Mcule catalogue as the source of building blocks.Comparison with other methods
Price estimation from retrosynthesis predictions was performed using a simple heuristic as a replacement for the non-publicly available method proposed by Badowski et al.40 This heuristic only considers the cost of the building blocks neglecting any additional cost. Thus, taking into account that the retrosynthesis results obtained for each compound tend to include several pathways, potentially involving multiple building blocks, we employed two simple strategies. The first one assumes ideal route ranking, thus overestimates the performance (ignoring non-reactant costs) by selecting the route that best matched our price records. The second strategy just reports the minimum price route and should provide an underestimation of the performance.The QS$R multilayer perceptron model was reimplemented as indicated in Fernandez et al.38 with the exception of descriptors calculation, that were computed using Rdkit.49 The model was retrained using the same training data as used for CoPriNet.
CoPriNet graph neural network
To create our price prediction GNN we represented compounds as 2D graphs with atoms corresponding to nodes and bonds to edges. Nodes are encoded using five features: atomic number, valence, formal charge, number of neighbours, and aromaticity. Edges are represented with four features: bond type, aromaticity, conjugation, and ring membership. Our GNN first embeds the node and edge features using a learnable linear transformation from dimension five and four to 75 and 50 respectively. After that, ten blocks consisting of a PNA layer,50 batch normalization51 and ReLU52 activation are applied one after another. Then, an embedding for the graph is obtained applying a Set2set layer.53 Finally, two dense layers with batch normalization and ReLU activation and one last linear layer with one single unit are applied to the graph embedding. A schematic of our GNN architecture is depicted in Fig. 1. The hyperparameters were selected by cross-validation over the validation dataset, exhibiting a robust behaviour. See ESI Section 9† for more details.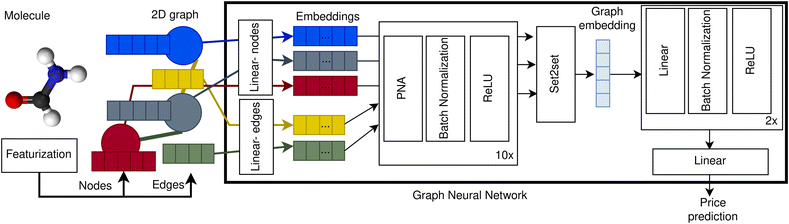 | ||
| Fig. 1 Price prediction graph neural network architecture. Molecules are represented as 2D graphs consisting of nodes (blue, grey, and red circles), encoded as node vectors of dimension five (blue, grey and red rectangles), and edges (yellow and green lines), encoded as vectors of dimension four (yellow and green rectangles). The node and edge vectors are projected into higher dimensionality embeddings (coloured rectangles within GNN box) using independent learnable weights for the nodes (linear-nodes) and for the edges (linear-edges). After that, the node and edge embeddings are processed by ten blocks of PNA layer, batch normalization and ReLU activation, updating the state of the node embeddings after each block. Then, the processed embeddings of all the nodes are combined into one single graph embedding using a Set2Set layer.53 Finally, the graph embedding is processed by two blocks of linear layer, batch normalization and ReLU activation from which the price prediction is obtained using a linear layer with one single unit. | ||
Our network was trained using the Adam optimizer54 with a batch size of 512 graphs. Initial learning rate was set to 10−5 and decreased by a factor of 0.1 when the validation loss did not improve during 25 epochs. The mean squared error was used as the loss function.
Evaluation metrics
The correlation between continuous variables was measured using the absolute value of the Pearson Correlation Coefficient (PCC, eqn (1)) and the Spearman's Rank Correlation Coefficient (SRCC, eqn (2)).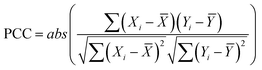 | (1) |
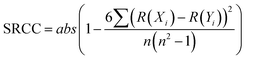 | (2) |
![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) is the average of variable X, R(Xi) is the ranking of the i-th observation of the variable X and n is the number of observations.
is the average of variable X, R(Xi) is the ranking of the i-th observation of the variable X and n is the number of observations.
Binary classification performance was evaluated using the Matthews Correlation Coefficient (MCC, eqn (3)) at the threshold that maximizes its value.
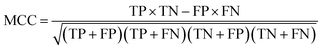 | (3) |
Results and discussion
Synthetic accessibility estimations present limitations
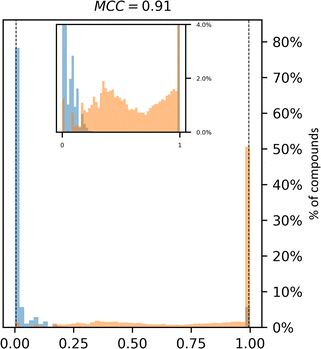
Historically, SA scores have been employed as proxies for compound accessibility assuming that synthesizability implies availability and ignoring other relevant aspects such as compound cost. In practice, SA scores have been used to classify compounds as synthesizable or non-synthesizable selecting different thresholds. We sought to test how this strategy performs on two sets of molecules, a dataset of purchasable compounds (PC) and a dataset of non-purchasable natural products (NPNP) using four different types of SA scores: SAscore,10 SCScore,11 SYBA,9 and RAscore8 (Fig. 2a–d). As a first approximation all the PC molecules should be classified as synthetically feasible, and most of them as highly accessible, whereas most of the NPNP compounds should be considered hard to synthesize. As Fig. 2a–e shows, none of the methods, including CoPriNet, which will be discussed later, perfectly separate the two compound sets. However, this is not surprising nor potentially even desired since not all NPNP are synthetically infeasible, nor are all purchasable compounds easy to make. In order to get a better estimation of the actual number of synthetically feasible NPNP compounds we computed ManifoldSA, a pure retrosynthesis-based score (see Methods for more details). Retrosynthesis-based approaches tend to be far more accurate than standard fast SA scores and as such, we can consider them as an (imperfect) ground truth when evaluating simple SA scores. For the NPNP, ManifoldSA estimates that ∼24% of the compounds are synthesizable, with 4.6% of those being easily synthesizable (see Fig. 3). Whereas for the PC dataset, ∼6% of the compounds were regarded as infeasible despite being commercially available. While these numbers also suggest that retrosynthesis predictions are not perfect, they are more accurate than fast SA scores. So, it is interesting to consider them as ground truth (Fig. 2f–j). The results obtained in this case, although worse for all methods, are similar to the ones of the previous experiment.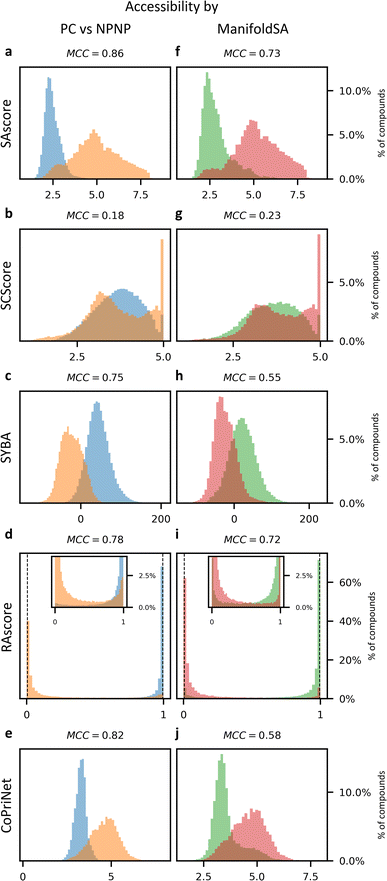 | ||
| Fig. 2 Synthetic accessibility scores are no better approximations for compound availability than CoPriNet, suggesting that CoPriNet generalizes beyond its training set of purchasable compounds. Left: score distributions for purchasable compounds (PC, blue) and non-purchasable natural products (NPNP, orange) computed with (a) SAscore,10 (b) SCScore,11 (c) SYBA,9 (d) RAscore,8 and (e) CoPriNet. This test the premise that NPNPs are synthetically less accessible and more expensive that PC compounds. Right: score distributions for PC and NPNP compounds labelled according to their predicted synthesizability (synthesizable, ManifoldSA < 0.5, green, non-synthesizable, ManifoldSA > 0.5, red), computed with (f) SAscore,10 (g) SCScore,11 (h) SYBA,9 (i) RAscore,8 and (j) CoPriNet. Note that compounds predicted as synthesizable can also have expensive prices. The Matthew's correlation coefficient for each score is displayed on top of each subplot. | ||
The reliability of the different approaches can be influenced by the dataset used. As such we also tested their behaviour on the datasets compiled by Gao and Coley35 that include typically used catalogues of compounds as well as de novo generated molecules for which retrosynthesis predictions were computed (see Methods). Overall, the SAscore and the RAscore better reproduced the retrosynthesis results (see ESI Section 4†), but the different data subsets show quite different results. One case of especial interest is the dataset of de novo generated molecules that were optimized against several multi-property objective functions (see ESI Fig. 9 and 10†). In this case, the RAscore score performance drops when the properties used to optimize the molecules do not account for SA. These results are in line with what would be expected for a machine learning approach, since the molecules that are obtained, although biased to replicate catalogue properties, do not necessarily represent viable instances.
The results for the PC and NPNP dataset and those from the Gao and Coley datasets suggest that the SAscore, with all its imperfections, is currently the best heuristic for retrosynthesis-based SA estimation. However, and leaving aside that synthesizability may not be the most useful proxy for compound availability, there are also several examples reported where SAscore severely underperforms (for visual examples see ESI Fig. 2†). Moreover, retrosynthesis-based methods, despite being computationally demanding, are not perfect at identifying synthetically accessible compounds. The high degree of variability and the fact that the agreement between the different estimations depends on the dataset used, suggests that all methods are far from perfect (see ESI Fig. 11†).
Price and synthetic accessibility have a complex relationship
Though synthetic accessibility is an important criterion, often particularly early in the drug discovery pipeline molecules to be tested are selected based on price, effective availability and ease of synthesis. Given that, we next examined the relationship between SA metrics and price. We compared the price in the Mcule catalogue for the compounds in the PC dataset to our set of SA scores. All SA metrics had only a weak correlation with price (see Fig. 4), with PCC values ranging from 0.16 to 0.35 and SRCC ranging from 0.16 to 0.41. Even a combination of all scores in the form of a linear regression model still performs poorly when trying to predict the price, with a PCC of 0.46 (see ESI Fig. 15†). These numbers agree with the value of 0.3 reported by Fukunishi et al.37 and suggest that the synthetic difficulty of a molecule may have only a small impact on the final cost of a compound.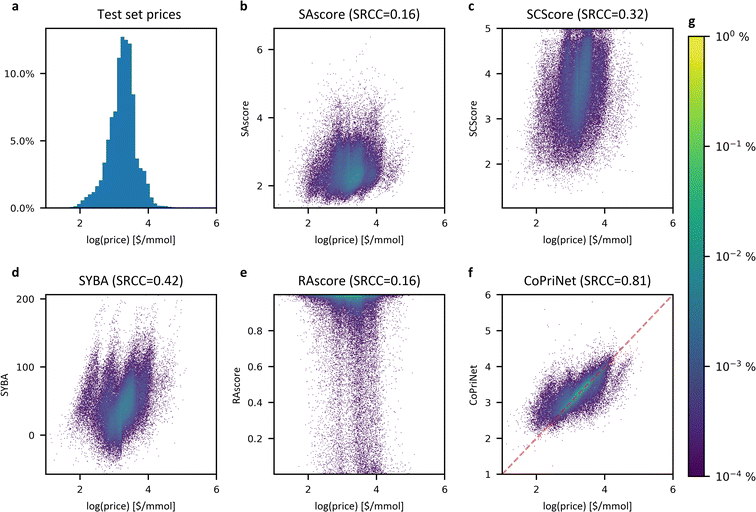 | ||
| Fig. 4 Synthetic accessibility scores correlate poorly with compound price whereas CoPriNet predictions are strongly correlated. (a) Histogram of the compound prices of the CoPriNet test set; (b–e) density heatmaps for CoPriNet test set compound prices against four different SA scores: SAscore,10 SCScore,11 SYBA9 and RAscore;8 (f) density heatmap for CoPriNet test set compound prices against CoPriNet predictions. Compound prices are displayed as natural logarithm of catalogue prices. The absolute value of the Spearman's Rank Correlation Coefficient is displayed in parenthesis (SRCC). (g) Colour bar for subplots (b–f) displaying the percentage of the PC dataset in each bucket. | ||
Although this conclusion seems counterintuitive, there are many reasons why this might be the case, for example, compounds that are in high demand will benefit from economies of scale, thus lowering their price regardless of their synthetic accessibility. For the same reasons, it is not unusual to find complicated building blocks at low prices in multiple catalogues, which allows the easy synthesis of otherwise difficult compounds. Nevertheless, while cheap compounds comprise both easy and difficult compounds, in general, expensive compounds tend to be less synthetically accessible than their cheaper counterparts (see Fig. 5).
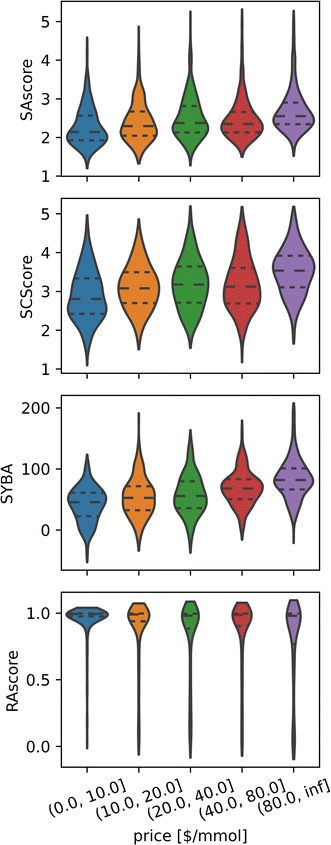 | ||
| Fig. 5 Expensive compounds tend to exhibit larger Synthetic Accessibility (SA), but SA metrics are unhelpful for price prediction as they correlate weakly across all price ranges. Distributions of different synthetic accessibility estimations (SAscore,10 SCScore,11 SYBA9 and RAscore8) for catalogue compounds of different price ranges. Last price range comprises all compounds with prices above 80 $ per mmol. | ||
CoPriNet predicts compound prices using a graph neural network
We hypothesised that a graph neural network (GNN) model should be able to detect patterns in molecules that indirectly reflect the drivers of pricing by automatically combining simple features such as the atomic number, aromaticity, or bond type across the different atoms of the molecules. Deep learning models are well suited to identify complex patterns in raw data providing enough data points are used during training, and GNNs are especially effective for molecular graphs, which are moreover fast to compute.We therefore built a model, CoPriNet, that can predict compound prices using as input molecular graphs. CoPriNet was trained as a regression model against catalogue prices and is able to produce far more accurate price predictions on our test set than any of the considered SA measurements (Fig. 4f): the PCC of 0.77 and SRCC of 0.80 are far higher than the best achieved by any of the other methods.
CoPriNet exhibits generalizability
The performance of all machine learning methods is dominated by their training set,8 so one of the most important questions for CoPriNet is to establish how well it generalises across different compounds. The specific challenge is that we can only obtain prices for the tiny fraction of the chemical space that is contained in the Mcule catalogue, and that prices for commercial catalogues are not generally in the public domain.We first tested that predictions are consistent independently of the random train/validation split. To do so, we trained CoPriNet on three distinct train/validation partitions, and found a high consistency, with mean PCC and SRCC of 0.73 and 0.74 with a standard deviation of 0.04 for PCC and 0.07 for SRCC.
Next, we tested generalisability by analysing a set of non-catalogue compounds, namely non-purchasable natural products (NPNP), that are both quite different from the training/validation set (see ESI Fig. 1† for dataset comparison), and which can be reasonably assumed to be in general more expensive than purchasable compounds (PC), as they are much more difficult to synthesize. Fig. 2e shows that CoPriNet tends to predict larger prices for the NPNP compounds than for the compounds of the PC dataset, suggesting that it generalises well beyond its training set.
In addition, we also studied CoPriNet performance using as test data the subset of compounds that were not present in the database snapshot used for training (March) but that were included in the next release (June). CoPriNet predictions exhibit a PCC of 0.65 (see ESI Fig. 16†), far better than any SA score. Although it is true that the PCC value obtained on the default test set is better, it is important to notice that prices fluctuate over time, thus affecting the performance of our method. Fortunately, this limitation could be easily addressed by retraining the model after each database release.
Finally, we tested generalizability with another set of molecules substantially different from those in the training set (see ESI Fig. 1† for dataset comparison), namely a set compiled from virtual compounds included in the Mcule catalogue. These are compounds likely to be easily synthesizable from accessible building blocks and for which prices are estimated by the providers according to expected synthetic routes and requirements; as a result, price distributions tend to be substantially different from the one of the training set. For these compounds, the correlations with price are poor for all SA scores CoPriNet predictions are also worse, as they systematically underestimate prices, leading to a poor linear correlation. This can be partially explained by vendor's differences in pricing strategies (see ESI Section 7†) as well as by the fact that virtual compounds tend to include additional “on-demand” fees that could hide the actual synthesis cost. Even so, the ranking performance (SRCC 0.56) is far better than that of the best performing SA metric (SCScore, SRCC of 0.32). This is important because in practice, prioritisation is generally conducted by selecting the top most promising compounds, so that a reliable ranking is even more important than accurate price prediction. Therefore, it is likely that CoPriNet predictions will be useful even across catalogues.
Comparison against other approaches
To the best of our knowledge neither of the two previously published methods for price prediction38,40 is publicly available, so we employed custom versions instead (see Methods).We first compared CoPriNet against a retrosynthesis-based implementation. While this approach is more accurate than CoPriNet by almost 0.1 in PCC (see ESI Table 3†), it is also 3 orders of magnitude slower (∼1–10 vs. ∼1000 compounds/s on a single GPU). Indeed, CoPriNet throughput is comparable to fast SA estimations such as RAscore or SYBA, and thus eminently suitable for high-throughput studies, overcoming one of the main limitations of retrosynthesis-based methods.
In the case of QS$R, we conducted two experiments. First, we computed CoPriNet scores on the QS$R testing dataset, that was collected before the year 2019 and as such, prices could have changed considerably. Even so, we found a f1-score > 0.8, inferior to the value reported in the QS$R publication, but still high, especially when considering the time difference between their test dataset and the CoPriNet training set. Next, we trained the QS$R Multilayer Perceptron (MLP) model on the CoPriNet dataset. For this experiment, we observed that the QS$R model learning curves saturate sooner, achieving worse performance than CoPriNet in both training and validation sets and showing signs of overfitting (see ESI Fig. 12†). The MLP model outperforms all the studied SA scores, achieving a PCC of 0.58. This PCC value, lower than the 0.77 measured for CoPriNet, suggest that although the simple MLP used in QS$R is able to capture some compound–price relationships, it is not able to exploit the massive amounts of data that we employed for CoPriNet training, and thus, its usage should be limited to QSAR-like situations.
Conclusions
Availability and ease of synthesises are crucial properties that all drug-like compounds should exhibit to be progressed in the drug discovery pipeline. Due to its importance, several approximations for these properties have been developed. In this manuscript we have illustrated some of the limitations of current synthetic accessibility (SA) estimations for use in estimating availability, including the poor correlation between SA estimations and compound price. The practical implications of this lack of correlation are far ranging, since SA estimations are commonly employed for compound prioritization and price is an important variable when deciding which compounds should be assayed. More importantly, most de novo methods for molecule generation are biased to or optimized against simple SA measurements such as SAscore, which significantly undermines their usefulness, as they will consistently suggest prohibitively expensive designs that will hardly ever be selected for progression.CoPriNet alleviates this problem, as it relies on a deep learning model trained to predict compound prices using only their molecular 2D graph. Our approach not only exhibits far better performance than existing alternatives, as evaluated on an independent test set, but also has excellent throughput, being able to process up to one thousand molecules per second. This speed means that CoPriNet can be deployed for high-throughput problems such as virtual screening or de novo compound generation/optimization, where more complex retrosynthesis-based approaches are too computationally demanding.
Data availability
CoPriNet source code, trained models and test dataset are available at https://github.com/oxpig/CoPriNet.Author contributions
Ruben Sanchez-Garcia: methodology, data curation, software, writing – original draft, Dávid Havasi: data curation, writing – review & editing, Gergely Takác: data curation, writing – review & editing, Matthew C. Robinson: resources, Alpha Lee: resources, writing – review & editing, Frank von Delft: funding acquisition, writing – review & editing, and Charlotte M. Deane: funding acquisition, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank https://Mcule.com for sharing their private data and their support and assistance. We thank PosteraAI for their support and assistance. This work has been economically supported by the Rosetrees Trust (Ref. M940).References
- C. A. Nicolaou and N. Brown, Drug Discovery Today: Technol., 2013, 10, e427–e435 CrossRef PubMed.
- S. Genheden, A. Thakkar, V. Chadimová, J.-L. Reymond, O. Engkvist and E. Bjerrum, J. Cheminf., 2020, 12(1), 1–9 Search PubMed.
- V. J. Gillet, G. Myatt, Z. Zsoldos and A. P. Johnson, Perspect. Drug Discovery Des., 1995, 3(1), 34–50 CrossRef CAS.
- Q. Huang, L.-L. Li and S.-Y. Yang, J. Chem. Inf. Model., 2011, 51, 2768–2777 CrossRef CAS PubMed.
- W.-D. Ihlenfeldt and J. Gasteiger, Angew. Chem., Int. Ed. Engl., 1996, 34, 2613–2633 CrossRef.
- C. W. Coley, D. A. Thomas, J. A. M. Lummiss, J. N. Jaworski, C. P. Breen, V. Schultz, T. Hart, J. S. Fishman, L. Rogers, H. Gao, R. W. Hicklin, P. P. Plehiers, J. Byington, J. S. Piotti, W. H. Green, A. John Hart, T. F. Jamison and K. F. Jensen, Science, 2019, 365(6453) DOI:10.1126/science.aax1566.
- Y. Podolyan, M. A. Walters and G. Karypis, J. Chem. Inf. Model., 2010, 50, 979–991 CrossRef CAS PubMed.
- A. Thakkar, V. Chadimová, E. J. Bjerrum, O. Engkvist and J. L. Reymond, Chem. Sci., 2021, 12, 3339–3349 RSC.
- M. Voršilák, M. Kolář, I. Čmelo and D. Svozil, J. Cheminf., 2020, 12(1), 1–13 Search PubMed.
- P. Ertl and A. Schuffenhauer, J. Cheminf., 2009, 1(1), 1–11 Search PubMed.
- C. W. Coley, L. Rogers, W. H. Green and K. F. Jensen, J. Chem. Inf. Model., 2018, 58, 252–261 CrossRef CAS PubMed.
- T. K. Allu and T. I. Oprea, J. Chem. Inf. Model., 2005, 45, 1237–1243 CrossRef CAS PubMed.
- R. Barone and M. Chanon, J. Chem. Inf. Comput. Sci., 2001, 41, 269–272 CrossRef CAS PubMed.
- P. Schwaller, T. Laino, T. Gaudin, P. Bolgar, C. A. Hunter, C. Bekas and A. A. Lee, ACS Cent. Sci., 2019, 5, 1572–1583 CrossRef CAS PubMed.
- H. Dai, C. Li, C. W. Coley, B. Dai and L. Song, Adv. Neural Inf. Process. Syst., 2019, 32 CAS , https://proceedings.neurips.cc/paper/2019/hash/0d2b2061826a5df3221116a5085a6052-Abstract.html.
- M. Voršilák and D. Svozil, J. Cheminf., 2017, 9(1), 1–7 Search PubMed.
- Y. Mo, Y. Guan, P. Verma, J. Guo, M. E. Fortunato, Z. Lu, C. W. Coley and K. F. Jensen, Chem. Sci., 2021, 12, 1469–1478 RSC.
- K. Boda, T. Seidel and J. Gasteiger, J. Comput.-Aided Mol. Des., 2007, 21(6), 311–325 CrossRef CAS PubMed.
- J. B. Hendrickson, P. Huang and A. G. Toczko, J. Chem. Inf. Comput. Sci., 1987, 27, 63–67 CrossRef CAS.
- K. F. Omolabi, E. A. Iwuchukwu, C. Agoni, F. A. Olotu and M. E. S. Soliman, J. Mol. Model., 2021, 27, 35 CrossRef CAS PubMed.
- S. Basu, B. Veeraraghavan, S. Ramaiah and A. Anbarasu, Microb. Pathog., 2020, 149, 104546 CrossRef CAS PubMed.
- Y. Lu and M. Li, Pharmaceuticals, 2021, 14, 141 CrossRef CAS PubMed.
- F. Imrie, A. R. Bradley and C. M. Deane, Bioinformatics, 2021, 37, 2134 CrossRef CAS PubMed.
- L. Humbeck, S. Weigang, T. Schäfer, P. Mutzel and O. Koch, ChemMedChem, 2018, 13, 532–539 CrossRef CAS PubMed.
- S. Kim, P. A. Thiessen, E. E. Bolton, J. Chen, G. Fu, A. Gindulyte, L. Han, J. He, S. He, B. A. Shoemaker, J. Wang, B. Yu, J. Zhang and S. H. Bryant, Nucleic Acids Res., 2016, 44, D1202 CrossRef CAS PubMed.
- Y. Huang, L. Wei, X. Han, H. Chen, Y. Ren, Y. Xu, R. Song, L. Rao, C. Su, C. Peng, L. Feng and J. Wan, Eur. J. Med. Chem., 2019, 184, 111749 CrossRef CAS PubMed.
- J. Leguy, T. Cauchy, M. Glavatskikh, B. Duval and B. da Mota, J. Cheminf., 2020, 12(1), 1–19 Search PubMed.
- Z. Zhou, S. Kearnes, L. Li, R. N. Zare and P. Riley, Sci. Rep., 2019, 9, 1–10 CrossRef PubMed.
- Y. Khemchandani, S. O'Hagan, S. Samanta, N. Swainston, T. J. Roberts, D. Bollegala and D. B. Kell, J. Cheminf., 2020, 12(1), 1–17 Search PubMed.
- D. V. S. Green, S. Pickett, C. Luscombe, S. Senger, D. Marcus, J. Meslamani, D. Brett, A. Powell and J. Masson, J. Comput.-Aided Mol. Des., 2020, 34, 747–765 CrossRef CAS PubMed.
- R. Yassine, M. Makrem and F. Farhat, Biomed. Res. Int., 2021, 2021, 6696012 Search PubMed.
- F. Imrie, A. R. Bradley, M. van der Schaar and C. M. Deane, J. Chem. Inf. Model., 2020, 60, 1983–1995 CrossRef CAS PubMed.
- O. Prykhodko, S. V. Johansson and P. C. Kotsias, et al., J. Cheminform., 2019, 11, 74 CrossRef PubMed.
- Y. Khemchandani, S. O′Hagan, S. Samanta, N. Swainston, T. J. Roberts, D. Bollegala and D. B. Kell, J. Cheminf., 2020, 12, 53 CAS.
- W. Gao and C. W. Coley, J. Chem. Inf. Model., 2020, 60, 5714–5723 CrossRef CAS PubMed.
- G. M. Makara, L. Kovács, I. Szabó and G. Pőcze, ACS Med. Chem. Lett., 2021, 12, 185–194 CrossRef CAS PubMed.
- Y. Fukunishi, T. Kurosawa, Y. Mikami and H. Nakamura, J. Chem. Inf. Model., 2014, 54, 3259–3267 CrossRef CAS PubMed.
- M. Fernandez, F. Ban, G. Woo, O. Isaev, C. Perez, V. Fokin, A. Tropsha and A. Cherkasov, J. Chem. Inf. Model., 2019, 59, 1306–1313 CrossRef CAS PubMed.
- J. Gasteiger and C. Jochum, J. Chem. Inf. Comput. Sci., 2002, 19, 43–48 CrossRef.
- T. Badowski, K. Molga and B. A. Grzybowski, Chem. Sci., 2019, 10, 4640–4651 RSC.
- R. Kiss, M. Sandor and F. A. Szalai, J. Cheminf., 2012, 4(1), 1 Search PubMed.
- T. Sterling and J. J. Irwin, J. Chem. Inf. Model., 2015, 55, 2324–2337 CrossRef CAS PubMed.
- D. Polykovskiy, A. Zhebrak, B. Sanchez-Lengeling, S. Golovanov, O. Tatanov, S. Belyaev, R. Kurbanov, A. Artamonov, V. Aladinskiy, M. Veselov, A. Kadurin, S. Johansson, H. Chen, S. Nikolenko, A. Aspuru-Guzik and A. Zhavoronkov, Front. Pharmacol., 2020, 1931 Search PubMed.
- A. Gaulton, L. J. Bellis, A. P. Bento, J. Chambers, M. Davies, A. Hersey, Y. Light, S. McGlinchey, D. Michalovich, B. Al-Lazikani and J. P. Overington, Nucleic Acids Res., 2012, 40, D1100 CrossRef CAS PubMed.
- R. P. Sheridan, N. Zorn, E. C. Sherer, L.-C. Campeau, C. Z. Chang, J. Cumming, M. L. Maddess, P. G. Nantermet, C. J. Sinz and P. D. O’Shea, J. Chem. Inf. Model., 2014, 54, 1604–1616 CrossRef CAS PubMed.
- L. Ruddigkeit, R. van Deursen, L. C. Blum and J.-L. Reymond, J. Chem. Inf. Model., 2012, 52, 2864–2875 CrossRef CAS PubMed.
- A. A. Lee, Q. Yang, V. Sresht, P. Bolgar, X. Hou, J. L. Klug-Mcleod and C. R. Butler, Chem. Commun., 2019, 55, 12152–12155 RSC.
- A. Morris, W. McCorkindale, N. Drayman, J. D. Chodera, S. Tay, N. London and A. A. Lee, Chem. Commun., 2021, 57, 5909–5912 RSC.
- RDKit, https://www.rdkit.org/.
- G. Corso, L. Cavalleri, D. Beaini, P. Liò and P. Veličković, Adv. Neural Inf. Process. Syst., 2020, 34, 13260–13271 Search PubMed.
- S. Ioffe and C. Szegedy, 32nd International Conference on Machine Learning, ICML 2015, 2015, vol. 1, pp. 448–456 Search PubMed.
- V. Nair and G. E. Hinton, in ICML 2010 – Proceedings, 27th International Conference on Machine Learning, 2010, pp. 807–814 Search PubMed.
- O. Vinyals, S. Bengio and M. Kudlur, in 4th International Conference on Learning Representations, ICLR 2016 – Conference Track Proceedings, International Conference on Learning Representations, ICLR, 2016 Search PubMed.
- D. P. Kingma and J. Ba 3rd, arXiv, 2014, preprint, arxiv:1412.6980, DOI:10.48550/arXiv.1412.6980.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2dd00071g |
| This journal is © The Royal Society of Chemistry 2023 |