Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Enhanced hydrogen evolution reaction performance of anatase–rutile TiO2 heterojunction via charge transfer from rutile to anatase†
Nurul Affiqah
Arzaee
 ab,
Nuttapon
Yodsin
c,
Habib
Ullah
ab,
Nuttapon
Yodsin
c,
Habib
Ullah
 *d,
Sabiha
Sultana
de,
Mohamad Firdaus
Mohamad Noh
ab,
Ahmad Wafi
Mahmood Zuhdi
*d,
Sabiha
Sultana
de,
Mohamad Firdaus
Mohamad Noh
ab,
Ahmad Wafi
Mahmood Zuhdi
 b,
Abd Rashid Bin
Mohd Yusoff
*f,
Siriporn
Jungsuttiwong
*c and
Mohd Asri
Mat Teridi
b,
Abd Rashid Bin
Mohd Yusoff
*f,
Siriporn
Jungsuttiwong
*c and
Mohd Asri
Mat Teridi
 *a
*a
aSolar Energy Research Institute, Universiti Kebangsaan Malaysia, 43600 Bangi, Selangor, Malaysia. E-mail: asri@ukm.edu.my; Tel: +603 8911 8580
bInstitute of Sustainable Energy (ISE), Universiti Tenaga Nasional (UNITEN), Jalan IKRAM-UNITEN, 43000 Kajang, Selangor, Malaysia
cCenter for Organic Electronics and Alternative Energy, Department of Chemistry and Center for Innovation in Chemistry, Faculty of Science, Ubon Ratchathani University, Ubon Ratchathani 34190, Thailand. E-mail: siriporn.j@ubu.ac.th; Tel: +66 8 1692 4610
dDepartment of Engineering, Faculty of Environment, Science and Economy, University of Exeter, Penryn Campus, Cornwall TR10 9FE, UK. E-mail: hu203@exeter.ac.uk
ePhysics Department, Faculty of Science, Universiti Teknologi Malaysia, 81310, Johor Bahru, Johor, Malaysia
fDepartment of Chemical Engineering, Pohang University of Science and Technology (POSTECH), 77 Cheongam-Ro, Nam-Gu, Pohang 37673, Republic of Korea. E-mail: abdr@khu.ac.kr
First published on 17th October 2023
Abstract
In light of recent doubts surrounding the industrial viability of photo(electro)catalysis technology for sustainable hydrogen production, it becomes imperative to align materials development with rationalized synthesis protocols. In this study, we present an innovative technique utilizing atmospheric-pressure chemical vapor deposition (APCVD) to rapidly produce TiO2 in just 5 minutes using pure TiCl4 as the sole reagent. The resulting photoanode exhibits exceptional photoelectrochemical (PEC) water-splitting performance, achieving a photocurrent density of 2.06 mA cm−2 at 1.23 V RHE. Moreover, the photoanode demonstrates sustained operation for 16 hours, leading to the successful collection of 138 μmol of H2 and 62 μmol of O2. These remarkable results are attributed to the controlled formation of an anatase–rutile phase-junction, the presence of well-balanced oxygen vacancies, and the bifrustum nanoparticle–nanoflake structure with a unique light trapping effect and large surface area. Density functional theory calculations confirm that the water-splitting reaction primarily occurs at undercoordinated Ti and O atoms in both anatase and rutile TiO2. Notably, the calculated Gibbs free energy values for the hydrogen evolution reaction (HER) differ significantly between rutile (−0.86 eV) and anatase TiO2 (0.22 eV). In the heterojunction, charge transfer enhances the HER performance through shared electronic density, resulting in a synergistic effect that surpasses the capabilities of individual surfaces and underscores the importance of electronic interactions within the junction.
Introduction
Photoelectrochemical (PEC) water splitting using semiconductors as photoelectrodes has been considered a promising route to generate renewable hydrogen fuel.1,2 To achieve sustainable production of hydrogen, it is critical to develop an energy-efficient fabrication process for the photoelectrode material. Specifically, the process must be designed in a way that production time and chemical use are minimized. TiO2 is chosen as a representative photoelectrode in this study due to the suitable band edge position, good stability and nontoxicity.3,4 Nonetheless, TiO2 still suffers from poor light absorption and high electron–hole recombination rate, which are responsible for the performance loss.5,6 It is well documented that these limitations can be alleviated using various strategies such as by introducing an anatase–rutile junction7–9 and oxygen vacancies in TiO2.7,10 The junction between the anatase and rutile phases is of particular interest in photocatalysis because it can facilitate the separation of photo-generated electron–hole pairs, leading to higher photocatalytic activity.11Nevertheless, the fabrication of the anatase–rutile junction is rather complex and time-consuming. For instance, Yang and Wu developed anatase–rutile nanostructures using several synthesis techniques including hydrothermal and solvothermal methods.12 TiO2 generated a photocurrent of 1.73 mA cm−2 at 1.23 VRHE, but more than 40 hours was required to prepare the photoanode. Sutiono et al. fabricated the anatase–rutile TiO2via a hydrothermal method by placing the FTO substrate at the bottom of a Teflon-liner instead of leaning the FTO against the liner's wall.13 Although a high photocurrent of 2.32 mA cm−2 at 1.23 VRHE was recorded, at least 18.5 hours were needed to complete the fabrication process. A more complicated preparation process of anatase–rutile was reported by Wei et al. through the combination of hydrothermal method and atomic layer deposition, which produced photocurrent of only 2.08 mA cm−2 at 1.23 VRHE.14
Meanwhile, introduction of oxygen vacancies in the TiO2 photoanode is favorable for PEC activity as the defect increases the concentration of free carrier density7 and provides high water adsorption sites.10 However, the formation and tuning of oxygen vacancies usually involve post-treatments on pre-deposited TiO2 films such as dipping in NaBH4 (ref. 15) and annealing in N2 or H2 atmosphere.14,16 The post-treatments have further extended the synthesis duration of pristine TiO2. This means that the development of high-performance TiO2 by combining the anatase–rutile and oxygen vacancy approaches is inefficient. Hence, a more realistic synthesis route is highly sought after to achieve a sustainable hydrogen generation via the TiO2 photoanode.
In response to this, atmospheric pressure chemical vapor deposition (APCVD) has been demonstrated as an efficient and rapid synthesis approach for photoelectrodes, which is also convenient for large-scale processes.17,18 Previous studies have successfully developed TiO2 films with various dopants like boron, nitrogen, and fluorine using the APCVD method and the time taken for depositing the films was not more than 210 s.18–20 However, the synthesized film consisted of only a single phase (either anatase or rutile) most likely due to the use of ethyl acetate as oxygen source and insufficient transformation temperature. The single phase is ineffective for charge separation in the photoelectrode. To partially convert the anatase phase to rutile phase, Kafizas et al. have applied an additional annealing process with a temperature of over 600 °C after preparing the TiO2 by APCVD,21 but this strategy defeats the purpose of developing a rapid fabrication method.
Here, we present for the first time the successful fabrication of a high-performance mixed-phase TiO2 photoanode via APCVD in a very short timescale (5 minutes) using pure TiCl4 as a sole reagent. A systematic parameter study for optimizing APCVD was performed to determine the optimum conditions to deposit TiO2 with exceptional properties. Along with the appropriate concentration of oxygen vacancies and well-tuned film morphology, it is found that the coexistence of anatase and rutile phases naturally forms a staggered junction in the photoanode, which effectively suppresses the recombination of charge carriers. As a result, an impressive photocurrent density of 2.06 mA cm−2 at 1.23 VRHE is obtained. Besides, the photoanode is highly reproducible with a small performance deviation and exhibits a stable photocurrent over at least 16 h of operation time. The experimental data are validated with first principle density functional theory (DFT) simulations and the results proved that the water splitting reaction mechanism occurs at the undercoordinated Ti and O atoms in both anatase and rutile TiO2. Overall, our findings provide one of the best solutions for the sustainable development of outstanding TiO2 photoanodes.
Experimental section
Preparation of TiO2 thin films
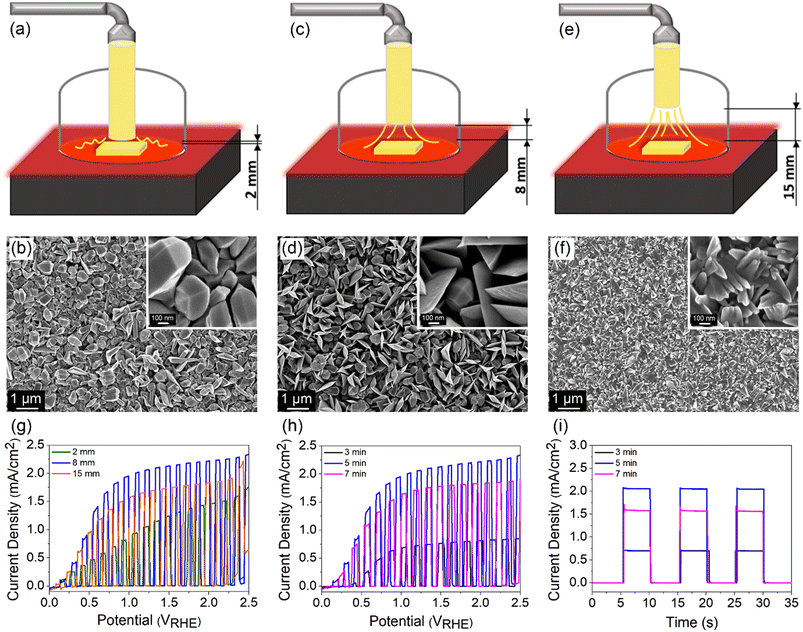
TiO2 films were grown on FTO (TEC 8, Pilkington) using a custom-built APCVD system (Fig. S1†). Briefly, 1 ml TiCl4 (99%, Merck) was inserted into the trap body of a two-piece glass cold trap and the trap body was capped with a trap finger. Two separate tubes were then connected to the joints of the trap finger, where the inner joint-sidearm was connected to an argon gas supply while the outer joint to a three-neck round-bottom flask (mixing chamber). The mixing chamber was also connected to a purified air supply and a glass tube connected to a covered hot plate (reaction chamber). Prior to the deposition process, FTO substrates were cleaned using an ultrasonic bath in acetone, methanol and 2-propanol (each for 10 min). The substrates were then rinsed under DI water and dried with a nitrogen stream. A substrate was placed on the preheated hot plate and the nozzle of the glass tube was positioned directly on top of the substrate. The deposition began by flowing argon and purified air at 90 and 1560 cm3 min−1, respectively. The process was carried out at 400, 500 and 600 °C for 5 min to investigate the phase changes. Correspondingly, the samples are denoted by TiO2-400, TiO2-500 and TiO2-600. The morphology of the samples was studied by varying the distance between the nozzle and the FTO surface (2, 8 and 15 mm) as well as by controlling the deposition time (3, 5 and 7 min).Characterization
The crystalline behavior of the films was explored using an X-ray diffractometer (XRD) (Bruker, D8 Advance). The mass fraction of anatase (Wa) and rutile (Wr) phases in each sample can be estimated from the XRD spectra using the following equations: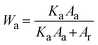 | (1) |
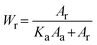 | (2) |
| ERHE = EAg/AgCl + 0.059pH + E0Ag/AgCl | (3) |
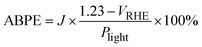 | (4) |
Density functional theory computations
The reaction mechanism of water splitting on the anatase TiO2 (101) and rutile TiO2 (110) was investigated using plane-wave based DFT calculations performed using the Vienna Ab initio Simulation Package (VASP). The projector-augmented wave (PAW)27 with a generalized gradient approximation (GGA) refined by Perdew, Burke and Ernzerhof (PBE)28 was used in the calculations. An energy convergence of 1 × 10−6 eV per cell, a force convergence of 1 × 10−2 eV Å−1 and an energy cut-off of 450 eV were employed in the calculations. A spin-unrestricted calculation was applied in all cases. An isolated gas molecule was calculated in a 15 Å × 15 Å × 15 Å box. A (2 × 2) slab of the anatase TiO2 (101) and rutile TiO2 (110) surfaces was separated from its replicas by 12 Å of vacuum. The anatase TiO2 (101) and rutile TiO2 (110) surfaces consist of 72 and 68 atoms with three Ti-layers, respectively. Monkhorst–Pack grids of 5 × 5 × 1 were used for all TiO2 systems. The electronic properties, i.e., the density of states (DOS), was analyzed to understand the changes in the electronic properties of anatase TiO2 (101) and rutile TiO2 (110) surfaces. The adsorption energy (Eads) was calculated from the following equation:| Eads = Esystem − Esurface − Eisolated water | (5) |
Results and discussion
Phase and defect modulation
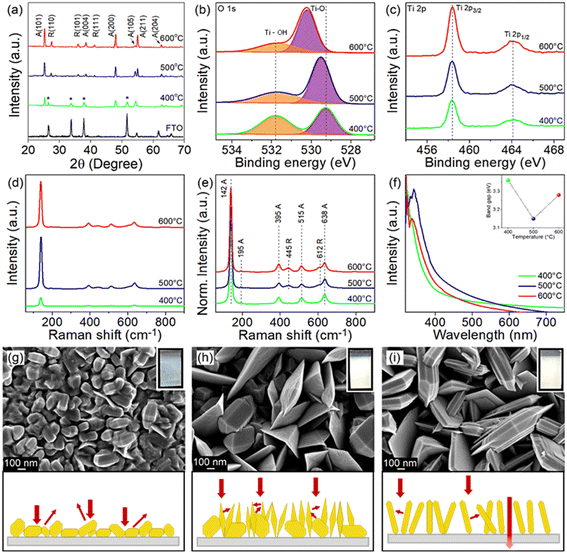
The crystal phase and crystallographic defect concentration of TiO2 films were tuned by annealing the films at 400, 500 and 600 °C. As shown by XRD analysis in Fig. 1a, TiO2-400 exhibits characteristic peaks corresponding to pure anatase phase (JCPDS No. 21-1272).29 Peaks belonging to FTO substrate are also identified in this sample, which might be due to the low film thickness. This could be correlated with the slow decomposition rate of TiCl4 at low temperature. As the deposition temperature increases to 500 and 600 °C, the FTO diffraction peaks disappear, indicating that the TiO2 film completely covers the underlying substrate.30 Meanwhile, similar anatase peaks are observed in the TiO2 deposited at higher temperatures. The intensity of XRD peaks also becomes stronger with the increase of temperature, suggesting that TiO2 films with higher crystallinity are formed. On a closer view, the peak intensity of the (105) crystal plane reduces, while that of the (211) plane enhances as the films were subjected to higher temperature, reflecting the switch of the growth orientation.Samples grown at 500 and 600 °C also exhibit new peaks, which are unambiguously assigned to the rutile phase (JCPDS No. 21-1276).31 Furthermore, the increasing trend in the peak intensity of rutile with respect to deposition temperature is identical to that of anatase. Table S1† clearly shows that the mass fraction of rutile increases with increasing deposition temperature (0, 24 and 28 wt% for TiO2 deposited at 400, 500 and 600 °C, respectively). In typical cases, the anatase phase starts to transform irreversibly to rutile phase in air at a temperature between 600 and 700 °C.32,33 However, the transition temperature could become lower depending on the raw materials and processing methods used for the fabrication of TiO2.34 Besides, the phase transformation process is not instantaneous but rather time-dependent.35 For these reasons, the TiO2 prepared by APCVD shows mixed-phase at lower temperature of 500 °C.
Considering the detection limitations of XRD, the concentration of crystallographic defects in the films was determined with XPS. The O 1s spectra in Fig. 1b show two peaks centered at 529.3 and 531.8 eV which are associated with the lattice oxygen bonded to Ti metal (Ti–O) and hydroxyl groups chemisorbed on Ti ions (Ti–OH) to reimburse the charge site of oxygen vacancies (VO), respectively.36 The peak intensity of Ti–OH obviously decreases when the deposition temperature increases from 400 to 600 °C, which indirectly indicates the suppressed VO formation at high temperature. This is verified by estimating the ratio of VO to lattice oxygen using Gaussian fitting on the Ti–OH and Ti–O peaks,37,38 where the ratios of 1.03, 0.53 and 0.43 have been acquired for samples prepared at 400, 500 and 600 °C, respectively. Meanwhile, the Ti 2p3/2 and Ti 2p1/2 peaks detected at 458.3 and 464.1 eV signify the existence of Ti4+ (Fig. 1c).7,39 Note that the electronic structure of Ti 2p does not change upon increasing the annealing temperature, despite the significant change of Ti–OH peaks (i.e., change of oxygen vacancies in the samples).39 Additionally, the broadening of the Raman peak in Fig. 1d particularly for TiO2-400 is ascribed to the non-stoichiometric behavior of TiO2. This result could confirm the presence of a high density of oxygen vacancies in the film.7,40 The intensity of the Raman peak was then normalized to investigate the phase transformation (Fig. 1e). The vibrational modes of the anatase phase of TiO2 peaked at 142, 395, 515 and 638 cm−1, which agree with the respective Raman active modes of Eg, B1g, A1g and Eg and can be clearly observed in all films.9,22,41 The Raman peak at 142 cm−1 is associated with the symmetric stretching vibration of the Ti–O–Ti bond, while peaks at 395 and 515 cm−1 are formed by the symmetric and anti-symmetric bending vibration of O–Ti–O in TiO2, respectively.22,42 In line with XRD, peaks attributed to rutile TiO2 located at 445 (Eg) and 612 cm−1 (A1g) appear only in TiO2-500 and TiO2-600, thereby substantiating the presence of mixed phase in TiO2 samples deposited at higher temperature.13,22
UV-vis absorption spectra of all films (Fig. 1f) demonstrate relatively strong absorption in the UV region, whereby the absorption edge is located at about 400 nm.7,8 The TiO2-400 spectrum reveals an obvious absorption tail in the visible region, which is attributable to the high density of oxygen vacancies43,44 and morphology-induced light scattering effect.45,46 Besides, the absorption edge of TiO2-400 also appears at a shorter wavelength due to the existence of pure anatase phase in the sample. An increase in annealing temperature of TiO2 leads to a red shift of the absorption edge, owing to an increase in rutile content as confirmed by XRD.7,9 Note that oxygen vacancies may also contribute to the narrowing of the band gap due to the involvement of shallow defect energy levels.43,47,48 As a result, TiO2-500 exhibits significantly red shifted absorption than TiO2-600 because of the synergistic effect between the mixed phase and the moderate number of oxygen vacancies. TiO2-500 also shows obvious improvement in absorption intensity most likely caused by the trapping of scattered light. The band gaps of TiO2-400, TiO2-500 and TiO2-600 estimated from the Tauc plot (Fig. S2†) are 3.36, 3.15, and 3.28 eV, respectively.
FESEM images in Fig. 1g–i depict that TiO2-400 forms nanoparticles with bifrustum structure having an average length between 150 and 200 nm. Besides, most of the nanoparticles fuse together, signifying poor crystallization degree. In contrast, TiO2-500 shows that some of the nanoparticles grow into larger and highly crystallized bifrustum structures, while some of the particles convert into nanoflake structures with an average length of 300–800 nm, enlarging the surface area for PEC reaction. The fragments of nanoparticles and nanoflakes can be observed in the TEM image in Fig. S3.† Further increase of the temperature to 600 °C completely converts the nanoparticles into nanoflakes. This transformation of structure can be explained in terms of the crystal growth direction. As elaborated in the XRD section, at the annealing temperature of 400 °C, the particles prefer to grow along the (105) crystal plane, therefore forming bifrustum structures. As the temperature increases, the growth rate of nanoparticles along the (105) plane becomes slower than that along the (211) plane, resulting in the transformation of nanoparticles into nanoflakes. The influence of morphology on the light behavior of the film is represented in the schematic diagram. The mixture of bifrustum nanoparticles and nanoflakes in TiO2-500 is beneficial for light absorption as the bifrustum nanoparticles increase the optical path length through multiple scattering while the nanoflakes effectively trap the scattered light.45,46 On the other hand, most of the scattered light in TiO2-400 is not effectively trapped, whereas a fraction of the light simply passes through the TiO2-600 sample, as supported by UV-vis spectra.
The corresponding photos of the samples are also displayed in the insets of Fig. 1g–i. The cloudy appearance of all samples looks homogeneous when observed from the surface, implying that the present deposition technique forms a uniform coating. However, the film synthesized at 400 °C appeared to be thinner compared to films subjected to higher temperature. As determined from the profilometer, the average thickness of sample deposited at 400 °C is 711 nm, which is lower than that of the TiO2 deposited at 500 (1120 nm) and 600 °C (1391 nm). As mentioned before, this is because the low annealing temperature weakly supports the growth of TiO2. AFM analysis in Fig. S4† depicts that the root mean square (RMS) roughness of the synthesized films increases with the deposition temperature, where the recorded values are 30.1, 75.7 and 85.9 nm for TiO2-400, TiO2-500 and TiO2-600, respectively. The change in roughness is more prominent between the samples that were fabricated at 400 and 500 °C due to the conversion of bifrustum nanoparticles into nanoflakes, which is congruous with the earlier observation.
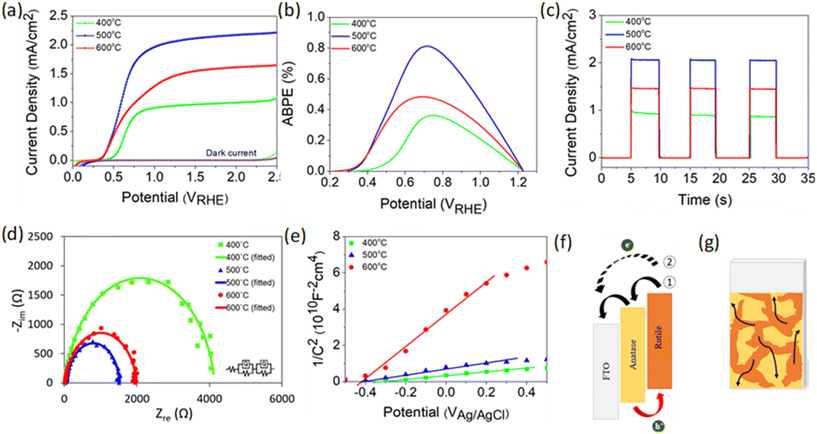
PEC performance obtained from linear sweep voltammetry (LSV) demonstrates that TiO2-400 has a relatively weak photocurrent density of 0.5 mA cm−2 at 1.23 VRHE (Fig. 2a). As the deposition temperature increases to 500 °C, a steep increase in photocurrent with respect to potential is observed and the performance remarkably enhances, reaching 2.06 mA cm−2. Moreover, the onset potential experiences a cathodic shift which is indicative of an effective charge carrier separation. In contrast, the photocurrent decreases by 0.6 mA cm−2 when the temperature is further increased to 600 °C. Note that the negative shift of the dark current onset potential of TiO2-400 might be due to the exposure of FTO to the electrolyte.49Fig. 2b shows that the ABPE of TiO2-500 reaches a maximum value of 0.81% at 0.72 VRHE, which is quite impressive for a photoanode with single material. A similar trend of photocurrent density is observed in the chronoamperometric scans under chopped illumination (Fig. 2c). The photocurrent spikes in this curve are associated with recombination behavior between electrons and holes. Fig. S5† provides a better view of the photocurrent spikes, where TiO2-400 shows the most obvious spike, implying the fastest charge recombination. Conversely, the spikes are not visible in TiO2-500. This observation is also supported by the evaluation of transient photocurrent decay (Fig. S6†), where longer transient time implies lower recombination rate. According to the calculation method described in our previous work,50 TiO2-500 reveals the longest transient decay time (0.086 s), followed by TiO2-600 (0.070 s) and TiO2-400 (0.054 s).
Fig. 2d presents the electrochemical impedance spectroscopy (EIS) results of TiO2 under illumination and the values of all resistances obtained from the fitted curves are compiled in Table S2.†R1 and R2 represent the charge transfer resistance in the bulk and at the semiconductor/electrolyte interface, respectively. It is apparent that R2 plays a significant role in the PEC reaction, whereby the resistance decreases in the order TiO2-400 > TiO2-600 > TiO2-500. Further study on the free-carrier density was conducted using Mott–Schottky analysis as depicted in Fig. 2e. The positive slope of the tangent line validates the n-type nature of the semiconductor.51,52 A steeper slope generally represents lower free carrier density ND as confirmed by the calculation in the ESI.† The ND value of TiO2 is primarily governed by the concentration of oxygen vacancies. Generally, the point defects associated with oxygen vacancies decrease the coordination number of the neighboring Ti4+ ions to Ti3+ ions. Each under-coordinated Ti atom consists of an unpaired electron and this electron causes an increase in the number of majority carriers in the bulk of TiO2.26 Based on the XPS O 1s spectra, the Ti–OH peak clearly reduces with increasing deposition temperature of TiO2. This observation clarifies the origin of the lower ND value of fabricated at higher temperature.
From the experimental data above, it is suggested that the enhanced performance of TiO2-500 is attributed to the synergistic effect between the anatase–rutile mixed phase, appropriate amount of oxygen vacancies and porous structure of the sample. A possible structure of energy band alignment is proposed as in Fig. 2f. Despite the fact that mixed-phase TiO2 shows better PEC performance than the individual phases, the direction of charge transfer across the phase junction has been controversial.9,53 This is attributed to the inconsistency of the reported arrangement of the electronic structure between anatase and rutile. Several studies found that the energy band of anatase is higher than that of rutile, whereas some others reported vice versa.8,48,54–57 In this work, the band structure of rutile was found to be higher than that of anatase (see Fig. S7† for more details on the construction of the electronic structure). While photogenerated holes are accumulated in the rutile phase, the electron transfer process may occur in two ways. Firstly, the presence of both phases in this film forms the phase junction or more specifically staggered (type II) heterojunction, which allows the effective transfer of photogenerated electrons from rutile to FTO via the anatase phase. Secondly, the electrons from rutile and anatase can also be directly transferred to FTO due to the random contact of both TiO2 phases with FTO, as shown in Fig. 2g.
Basically, the mixed phase can suppress the electron–hole recombination by driving the carriers in opposite directions.7–9,58 This is consistent with the smallest charge transfer resistance of TiO2-500 observed in EIS spectra. Note that the anatase phase does not only offer the separation path for electron–hole pairs, but the water splitting reaction also occurs at the surface of both anatase and rutile phases, as proven by the DFT calculation in a later section. The DFT analysis reveals that the presence of oxygen vacancies in the sample provides reactive sites for PEC activity. The appropriate amount of oxygen vacancies in TiO2-500 induces higher free carrier density which can facilitate the PEC activity of the photoanode. Along with the oxygen vacancies, the introduction of rutile in TiO2-500 leads to a narrow band gap which benefits the light absorption ability. Furthermore, the combination of bifrustum nanoparticles and nanoflakes enhances the light scattering and trapping effects. The high porosity of nanoflake structures of TiO2-500 also provides a large surface area for photocatalytic reaction and thereby increases the charge transfer rate between the TiO2 photoanode and the electrolyte.59
Meanwhile, the absence of an anatase–rutile mixed phase junction in TiO2-400 film is detrimental to the charge transfer of TiO2. Moreover, an excessive number of oxygen vacancies in TiO2-400 may serve as recombination centers which further deteriorate the charge transfer process.60 As proven by the calculation of transient decay time above, it is clearly seen that TiO2-400 suffers from the highest recombination rate. Besides that, from the viewpoint of morphological properties, the nanoparticle structure of TiO2-400 also reduces the available active sites. On the other hand, the PEC performance of TiO2-600 reduces again, despite the mixed phase and large surface area of the film. This could be ascribed to the poor light trapping induced by the morphology (see FESEM and UV-vis) and low free carrier density induced by low number of oxygen vacancies (see XPS and Mott–Schottky). The low carrier density causes a reduction of electrical conductivity and eventually increases the charge transfer resistance as detected by EIS measurement.61–63 Another possible reason for the decrease in photocurrent density may be the deterioration of FTO caused by high annealing temperature.64–66 However, Hall measurement in Table S3† shows negligible change in the electrical properties of FTO before and after annealing, implying that the performance degradation of TiO2-600 is not attributable to the damage of the substrate.
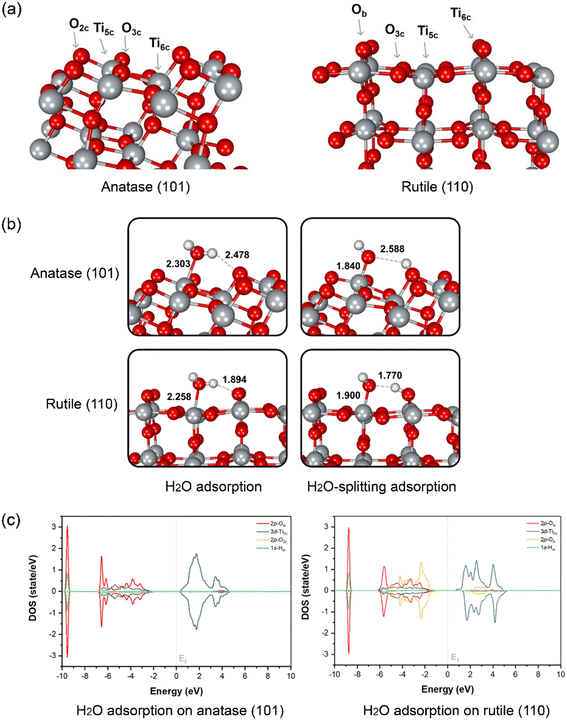
To evaluate the water splitting reaction on the surface of anatase and rutile, DFT calculation was performed on two main TiO2 surfaces as detected from XRD, namely anatase (101) and rutile (110). The optimized structures of the two surfaces and atom-type labeling are illustrated in Fig. 3a. Anatase (101) provides the characteristic of a terrace-like structure with surface edges constructed by 5-coordinated titanium atoms (Ti5c) and 2-coordinated oxygens (O2c). These undercoordinated atoms are revealed to the interface and it can interact directly with water. In addition, 3-coordinated oxygen (O3c) is found to be the surface interconnecting rows of Ti5c. At the bottom part of the ridges, the 6-coordinated titanium (Ti6c) is disclosed, interacting with O3c. Nevertheless, either O3c or Ti6c is less crucial for interaction with water due to its fully saturated chemical valences by bonding within the TiO2 structure. Another type of TiO2 obtained from our synthesis is rutile (110), which is thermodynamically more stable than the anatase form.67 This plane consists of O3c, Ti5c, and Ti6c atoms. Bridging oxygen atoms (Ob) are illustrated above the rows of bridging. In this case, Ti5c and Ob are reactive sites for water splitting on this surface.
The water and OH−/H+ adsorption on either anatase (101) or rutile (110) facets for PEC water splitting reaction were further investigated. In the molecular-adsorption calculations, there are three water adsorption types on the first hydration layer of the anatase (101) surface, which has a characteristic triple-peak pattern in its density profile.68 First, water hydrogen-bonding to two neighboring O2c by its Hw atoms has been recognized. The second type of water adsorption is that water is hydrogen-bonded via only one of its Hw to surface O2c while another Hw can interact with other water molecules in the interface region through H-bonding. Lastly, the most stable water adsorption type on the anatase (101) facet is that the water interacts with the surface by its Ow with the unsaturated surface Ti5c site, which is consistent with a previous work.67
The interaction between water and anatase is also confirmed via partial density of states (PDOS) plots. It is clearly shown that there is a strong hybridization between the 3d-orbital of Ti5c and the 2p-orbital of Ow. Moreover, water adsorption is slightly stabilized by hydrogen bonding between its Hw and the nearest O2c of the surface with a bond distance of 2.478 Å, as confirmed by the hybridization between the 1s-orbital of Hw and the 2p-orbital of O2c (Fig. 3c). The dissociation of a single water molecule has also been studied as depicted in the top panel of Fig. 3b. H2O-splitting adsorption occurs when the proton moves to form H-bonding with O2c while negatively charged hydroxyl (OH−) locates coordinated to Ti5c with a bond length of 1.840 Å above the Ti5c layer. In the case of rutile (110), the water molecular arrangement is presented in the bottom panel of Fig. 3b. The first hydration layer is composed of two main interactions, which are water coordinated by Ow to surface Ti5c and water hydrogen-bonded by Hw to bridging Ob atoms with bond distances of 2.258 and 1.894 Å, respectively. From the PDOS analysis, we found a strong hybridization between the 3d-orbital of Ti5c and the 2p-orbital of Ow. Remarkably, the 2p-orbital of Ob strongly hybridizes the 1s-orbital of Hw at the region of −6 to −2 eV, indicating the hydrogen-bonding between water and rutile (110). The Ti5c-coordinated water splitting is observed when the proton of water moves to the nearest bridging Ob. The bond length of adsorbed OH− on Ti5c is 1.900 Å, while that of H+ deposited on the Ob of rutile (110) surface is 1.770 Å. The mechanism of water dissociation and OH−/H+ adsorption at the surface is in good agreement with previous ReaxFF studies of titania surfaces.69–71
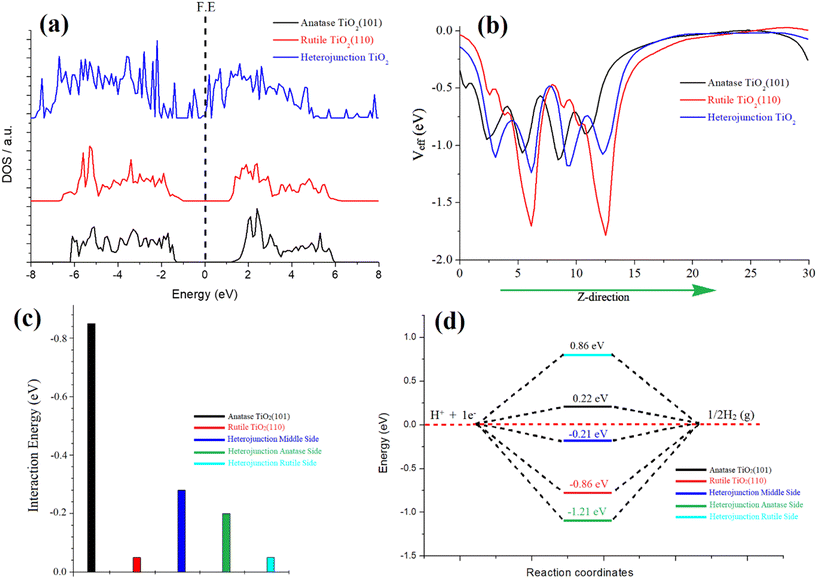
In our investigation, we focused on the anatase–rutile heterojunction, a composite material comprising anatase and rutile phases. This heterojunction possesses a type II band alignment, resulting in an amplified photocatalytic activity of TiO2. To elucidate the underlying reasons behind this enhanced activity, we conducted simulations of the density of states (DOS) for individual anatase and rutile and the heterojunction, as depicted in Fig. 4a. Notably, the DOS analysis revealed the emergence of additional bands near the Fermi energy within the heterojunction, indicating a pronounced hybridization between the atoms of rutile and anatase TiO2. This strong hybridization effect led to a reduction in the band gap, ultimately enhancing the catalytic activity of the heterojunction. Furthermore, we also simulated the optical spectra for these three species, revealing a narrower optical band gap specifically observed in the heterojunction, as depicted in Fig. S8 of the ESI.†
The phenomenon of charge transformation within the heterojunction is visually evident through the effective potential map, as depicted in Fig. 4b. The potential map reveals a transfer of charge from rutile TiO2 to anatase TiO2. This is manifested by the comparatively more negative red line representing rutile, in contrast to the black line representing anatase. The effective potential of the heterojunction reaches an optimum state, signifying electron transfer to anatase and resulting in an optimized species. Furthermore, this charge transformation is further supported by the electron localization function (ELF) and electron density difference (EDD) plots. The ELF and EDD plots demonstrate excellent interaction/hybridization of electron cloud densities between the atoms, as shown in Fig. S9 and S10 in the ESI.†
To evaluate the water adsorption energy over the surfaces of the three species, we considered the energies of the isolated water molecule, the clean surface, and the water-covered surface. This involved subtracting these energies according to eqn (5). For anatase TiO2(101), the calculated water adsorption energy is −0.85 eV, indicating a strong binding of water molecules to this surface. This suggests a robust interaction between water and the anatase surface. For rutile TiO2 (110), the calculated water adsorption energy is −0.5 eV, indicating a moderate binding of water molecules to this surface. Water exhibits a moderately strong interaction with the rutile surface. Regarding the anatase–rutile heterojunction, the analysis reveals three potential sites for water adsorption: anatase, rutile, and the middle sites, as depicted in Fig. S11 in the ESI.†
The water adsorption energies at the anatase, rutile, and middle sites of the heterojunction are found to be −0.20 eV, −0.05 eV, and −0.28 eV, respectively. These values indicate the strength of the water binding to the respective sites, with the middle site exhibiting the strongest interaction.
In the context of the hydrogen evolution reaction (HER), we conducted investigations on the properties of anatase, rutile, and the three possible sites of the heterojunction (rutile, anatase, and middle). Introduction of an H atom and subsequent optimization were performed for each case. The HER mechanism was analysed using a three-state diagram encompassing the initial H+ state, intermediate H* state, and 1/2H2 state. The free energy of the H* state (ΔGH*) was found to be a crucial factor in describing the HER activity of the catalyst. It is notable that Pt-based catalysts typically exhibit a ΔGH* value close to 0.09 eV, representing optimal HER performance.
To determine the ΔGH* value, we utilized eqn (6), which incorporates various factors. ΔE represents the total energy change obtained from density functional theory (DFT) simulations, T denotes the temperature (298.15 K for room temperature), and ΔEZPE and ΔS represent the changes in zero-point energy and entropy, respectively.
| ΔGH* = ΔEH* + ΔEZPE − TΔSH | (6) |
To simplify the theoretical analysis, we assumed a pH of 0, as the theoretical working potential does not depend on pH. The free energy of hydrogen at standard temperature and pressure (STP) was approximated as the energy of 1/2H2, and the entropy of H2 was obtained from the National Institute of Technology (NIST) database. In eqn (7), ΔEH* corresponds to the binding energy of the adsorbed hydrogen. E(H*) and E(*) represent the energies of the surface with and without H adsorption, respectively, while EH2 represents the DFT energy of molecular H2 in the gas phase.
| ΔEH* = E(H*) − E(*) − 1/2EH2 | (7) |
Eqn (8) can be employed to calculate the free energy of H:
| ΔGH* = ΔEH* + 0.37 eV | (8) |
The Gibbs free energy (ΔGH*) values were calculated for pristine anatase TiO2 (101) (0.22 eV) and rutile TiO2 (110) (−0.86 eV), as shown in Fig. 4d. Additionally, the heterojunction's anatase, rutile, and middle sites were considered (Fig. S11†). The calculated ΔGH* values for the heterojunction were −1.21 eV (anatase site), 0.86 eV (rutile site), and −0.21 eV (middle of the junction site). Notably, the heterojunction, particularly the middle site, demonstrated an optimal value for the hydrogen evolution reaction (HER). This indicates that the heterojunction's combined structure of anatase and rutile phases creates more favorable conditions for the HER process compared to individual anatase or rutile surfaces. The charge transfer from rutile to anatase plays a crucial role in enhancing the HER performance of the heterojunction.
Morphological control
The morphology and thickness of TiO2 films are further controlled by regulating (1) the distance between the nozzle tip and the FTO surface d and (2) the deposition time. The distance was varied between 2, 8 and 15 mm, while the deposition time and temperature were kept constant at 5 min and 500 °C, respectively. A schematic drawing of different nozzle-to-FTO distances and the corresponding FESEM images are shown in Fig. 5a–f. TiO2 fabricated at d = 2 mm forms nanoparticles with bifrustum structure having a wide range of sizes which are distributed over the entire substrate. As the distance was extended to 8 mm, a mixture of nanoparticles and nanoflakes are formed, resulting in an increase in the surface roughness and porosity. On the other hand, a compact surface composed of inhomogeneous shard-like particles is obtained when d = 15 mm. From the evaluation of PEC performance (Fig. 5g), the highest photocurrent density of 2.06 mA cm−2 at 1.23 VRHE was acquired for TiO2 deposited at d = 8 mm. Thus, it implies that a more porous surface results in a superior performance.At a fixed nozzle-to-FTO distance of 8 mm and temperature of 500 °C, a range of deposition times (3, 5 and 7 min) for fabricating TiO2 were further studied aiming to tune the thickness of the film. The average profilometer measurements of TiO2 deposited for 3, 5 and 7 min are 610, 1120 and 1362 nm, respectively, whereby TiO2 deposited for 5 min gives the best PEC performance (Fig. 5h). ABPE for every sample is shown in Fig. S12a and b.† It is known that the PEC activity is also governed by the light absorption and charge carrier diffusion length, both of which correlate strongly with the film thickness. A thin TiO2 layer deposited for 3 min ineffectively absorbs light which leads to a low number of photogenerated charge carriers. In contrast, excessive thickness obtained from a long deposition time of 7 min may suffer from high charge recombination owing to the limited charge carrier diffusion length. This is reflected in the obvious photocurrent spike in the chronoamperometric scan of the sample deposited for 7 min (Fig. 5i). A balance between the optical and electrical properties explains the origin of the high PEC performance for 5 min-deposited TiO2 photoanode.
Practicability of APCVD
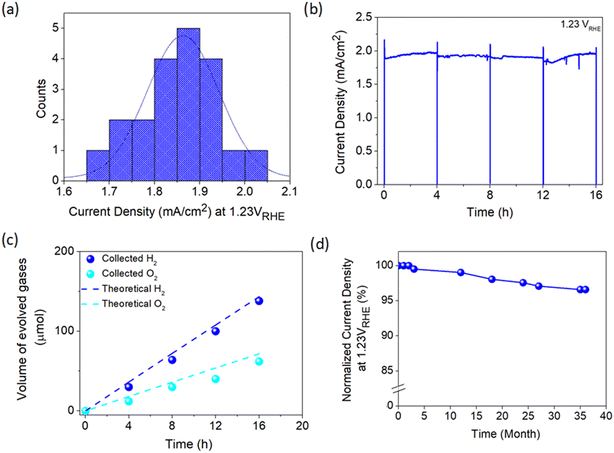
To move further towards practical implementation in solar hydrogen production, a fabrication process capable of producing an efficient photoelectrode with high consistency is imperative. Therefore, the consistency of the developed APCVD method for growing TiO2 in this work was further scrutinized by fabricating 20 photoanodes under optimized deposition parameters. As presented in Fig. 6a, the average current density measured at 1.23 VRHE is 1.86 mA cm−2, which is merely 10% deviation from the champion sample. Moreover, TiO2 demonstrates relatively stable performance with high photocurrent output over 16 h of continuous operation under irradiation (Fig. 6b). The PEC activity of the photoanode was also verified by measuring the generated hydrogen and oxygen gases during the stability test. Fig. 6c shows that approximately 138 μmol of H2 and 62 μmol of O2 are produced after 16 h of illumination, which are in close agreement with the theoretical values. The LSV curve of the champion TiO2 photoanode was also taken randomly from time to time. Surprisingly, the sample retains 97% of the initial photocurrent density at 1.23 VRHE even after 3 years of storage under ambient conditions (Fig. 6d), signifying the magnificent stability of the photoanode against standard environmental stress.Additionally, a variety of preparation approaches carried out for depositing TiO2 photoanode is summarized in Table S4† to provide a comparison between this work and the available fabrication methods. Most of the synthesis methods reported to date not only involved multiple deposition protocols but also used various types of chemicals. This may reduce the energy- and cost-effectiveness of photoelectrode production. Besides, those methods took several hours to obtain high-performance TiO2 which is basically unsuitable for industrial implementation of PEC technology in the future. On the other hand, the reasonable performance, excellent reproducibility and high stability of the TiO2 photoanode prepared in this work from a single reagent (i.e., TiCl4 only) using a single deposition technique (i.e., APCVD) under a very short time-scale (i.e., 5 min) offers a remarkable breakthrough in PEC water splitting application. A TiO2 photoanode with an area of l6 cm2 (4 × 4 cm) has also been developed, which is the largest area achievable using our laboratory system set-up. Despite the experimental limitation and mediocre film quality (Fig. S13a†), a photocurrent density of 0.77 mA cm−2 at 1.23 VRHE is still attainable (Fig. S13b†) which is around 40% of the 1 cm2-sized sample. This suggests the practicability of the present work, but further development is needed to enhance the performance of large-area photoanodes closer to the optimum value.
Conclusion
In summary, an efficient TiO2 photoanode was successfully developed using a rapid deposition technique (5 min) based on a custom-built APCVD system and by employing TiCl4 as a single reagent. The crystal phase, defect density, morphology and thickness of TiO2 films have been rationally tuned to acquire the optimum deposition conditions. The formation of a staggered junction between anatase and rutile phases in TiO2 significantly improves electron–hole separation and suppresses charge recombination. An appropriate number of oxygen vacancies provides high free carrier density and prevents the formation of undesirable recombination centers. DFT analysis also proves that the undercoordinated Ti and O atoms in both anatase and rutile phases serve as active sites for photocatalytic reaction. Furthermore, an intriguing observation reveals that the TiO2 heterojunction exhibits superior hydrogen evolution reaction (HER) performance, primarily attributed to its optimized Gibbs free energy compared to pure rutile and anatase. This enhancement can be attributed to the transfer of charges from rutile to anatase, resulting in an amplified HER performance within the heterojunction. Besides, the mixture of bifrustum nanoparticles and nanoflakes provide a unique light trapping effect and large active sites. Moreover, appropriate thickness ensures a balance between light absorption and charge diffusion length. The best photoanode not only reveals a high and stable photocurrent of 2.06 mA cm−2 at 1.23 VRHE but also yields 138 μmol of H2 and 62 μmol of O2 over 16 h of PEC operation. The discovery in this study may be a valuable guide for designing, developing and commercializing sustainable PEC technology.Author contributions
Nurul Affiqah Arzaee: investigation, writing – original draft, writing – review & editing. Nuttapon Yodsin, Siriporn Jungsuttiwong, Habib Ullah, and Sabiha Sultana: methodology, software. Mohamad Firdaus Mohamad Noh and Ahmad Wafi Mahmood Zuhdib: formal analysis, validation. Abd Rashid Bin Mohd Yusoff: resources: formal analysis, validation. Mohd Asri Mat Teridi: supervision, conceptualization, funding acquisition.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
M. A. M. Teridi would like to thank Universiti Kebangsaan Malaysia for financial support through grant GUP-2020-073. S. Jungsuttiwong thanks the Center of Excellence for Innovation in Chemistry (PERCH-CIC) and the Program Management Unit for Human Resources & Institutional Development, Research and Innovation [grant B05F630099]. N. Yodsin thanks the Human Resource Development in Science Project Science Achievement Scholarship of Thailand (SAST). We also acknowledge the Advanced Research Computing facilities of the University of Exeter for carrying out this work.References
- Z. Chen, A. J. Corkett, C. de Bruin-Dickason, J. Chen, A. Rokicińska, P. Kuśtrowski, R. Dronskowski and A. Slabon, Inorg. Chem., 2020, 59, 13589–13597 CrossRef CAS PubMed.
- N. A. Mohamed, J. Safaei, A. F. Ismail, M. F. Mohamad Noh, N. A. Arzaee, N. N. Mansor, M. A. Ibrahim, N. A. Ludin, J. S. Sagu and M. A. Mat Teridi, J. Alloys Compd., 2019, 818, 152916 CrossRef.
- H. Zheng, L. Zheng, X. Ye, X. Deng, Y. Wang, Y. Zhao and X. Shi, ACS Sustainable Chem. Eng., 2020, 8, 15906–15914 CrossRef.
- Z. Liang, H. Hou, Z. Fang, F. Gao, L. Wang, D. Chen and W. Yang, ACS Appl. Mater. Interfaces, 2019, 11, 19167–19175 CrossRef CAS PubMed.
- T. Zhou, J. Wang, S. Chen, J. Bai, J. Li, Y. Zhang, L. Li, L. Xia, M. Rahim, Q. Xu and B. Zhou, Appl. Catal., B, 2020, 267, 118599 CrossRef CAS.
- X. Cheng, Y. Zhang, H. Hu, M. Shang and Y. Bi, Nanoscale, 2018, 10, 3644–3649 RSC.
- J. Hu, S. Zhang, Y. Cao, H. Wang, H. Yu and F. Peng, ACS Sustainable Chem. Eng., 2018, 6, 10823–10832 CrossRef CAS.
- F. Cao, J. Xiong, F. Wu, Q. Liu, Z. Shi, Y. Yu, X. Wang and L. Li, ACS Appl. Mater. Interfaces, 2016, 8, 12239–12245 CrossRef CAS PubMed.
- A. Li, Z. Wang, H. Yin, S. Wang, P. Yan, B. Huang, X. Wang, R. Li, X. Zong, H. Han and C. Li, Chem. Sci., 2016, 7, 6076–6082 RSC.
- A. Ghobadi, T. G. Ulusoy, R. Garifullin, M. O. Guler and A. K. Okyay, Sci. Rep., 2016, 6, 30587 CrossRef CAS PubMed.
- S. Jia, X. Shu, H. Song, Z. An, X. Xiang, J. Zhang, Y. Zhu and J. He, Ind. Eng. Chem. Res., 2021, 60, 12282–12291 CrossRef CAS.
- J. S. Yang and J. J. Wu, ACS Appl. Mater. Interfaces, 2018, 10, 3714–3722 CrossRef CAS PubMed.
- H. Sutiono, A. M. Tripathi, H. M. Chen, C. H. Chen, W. N. Su, L. Y. Chen, H. Dai and B. J. Hwang, ACS Sustainable Chem. Eng., 2016, 4, 5963–5971 CrossRef CAS.
- N. Wei, Y. Liu, M. Feng, Z. Li, S. Chen, Y. Zheng and D. Wang, Appl. Catal., B, 2019, 244, 519–528 CrossRef CAS.
- Q. Kang, J. Cao, Y. Zhang, L. Liu, H. Xu and J. Ye, J. Mater. Chem. A, 2013, 1, 5766 RSC.
- X. Lv, L. Tao, M. Cao, X. Xiao, M. Wang and Y. Shen, Nano Energy, 2018, 44, 411–418 CrossRef CAS.
- I. Cesar, K. Sivula, A. Kay, R. Zboril and M. Grätzel, J. Phys. Chem. C, 2009, 113, 772–782 CrossRef CAS.
- P. Carmichael, D. Hazafy, D. S. Bhachu, A. Mills, J. A. Darr and I. P. Parkin, Phys. Chem. Chem. Phys., 2013, 15, 16788–16794 RSC.
- C. Sotelo-Vazquez, R. Quesada-Cabrera, J. A. Darr and I. P. Parkin, J. Mater. Chem. A, 2014, 2, 7082 RSC.
- A. Kafizas, N. Noor, P. Carmichael, D. O. Scanlon, C. J. Carmalt and I. P. Parkin, Adv. Funct. Mater., 2014, 24, 1758–1771 CrossRef CAS.
- A. Kafizas, X. Wang, S. R. Pendlebury, P. Barnes, M. Ling, C. Sotelo-Vazquez, R. Quesada-Cabrera, C. Li, I. P. Parkin and J. R. Durrant, J. Phys. Chem. A, 2016, 120, 715–723 CrossRef CAS PubMed.
- M. Chandra and D. Pradhan, ChemSusChem, 2020, 13, 3005–3016 CrossRef CAS PubMed.
- S. Wang, T. He, J. H. Yun, Y. Hu, M. Xiao, A. Du and L. Wang, Adv. Funct. Mater., 2018, 28, 1–10 Search PubMed.
- M. Kuang, P. Han, Q. Wang, J. Li and G. Zheng, Adv. Funct. Mater., 2016, 26, 8555–8561 CrossRef CAS.
- J. Safaei, H. Ullah, N. A. Mohamed, M. F. Mohamad Noh, M. F. Soh, A. A. Tahir, N. Ahmad Ludin, M. A. Ibrahim, W. N. R. Wan Isahak and M. A. Mat Teridi, Appl. Catal., B, 2018, 234, 296–310 CrossRef CAS.
- M. F. Mohamad Noh, H. Ullah, N. A. Arzaee, A. Ab Halim, M. A. F. Abdul Rahim, N. A. Mohamed, J. Safaei, S. N. F. Mohd Nasir, G. Wang and M. A. Mat Teridi, Dalton Trans., 2020, 49, 12037–12048 RSC.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. Paier, R. Hirschl, M. Marsman and G. Kresse, J. Chem. Phys., 2005, 122, 234102 CrossRef PubMed.
- S. Yu, B. Han, Y. Lou, G. Qian and Z. Wang, Inorg. Chem., 2020, 59, 3330–3339 CrossRef CAS PubMed.
- N. A. Arzaee, M. F. Mohamad Noh, A. Ab Halim, M. A. F. Abdul Rahim, N. A. Mohamed, J. Safaei, A. Aadenan, S. N. Syed Nasir, A. F. Ismail and M. A. Mat Teridi, Ceram. Int., 2019, 45, 16797–16802 CrossRef.
- J. Ding, L. Wang, Y. Zhao, X. Yu, L. Xing, G. Ding, J. Zhang and R. Che, ACS Appl. Mater. Interfaces, 2020, 12, 48140–48149 CrossRef CAS PubMed.
- C. Byrne, R. Fagan, S. Hinder, D. E. McCormack and S. C. Pillai, RSC Adv., 2016, 6, 95232–95238 RSC.
- M. G. Kim, J. M. Kang, J. E. Lee, K. S. Kim, K. H. Kim, M. Cho and S. G. Lee, ACS Omega, 2021, 6, 10668–10678 CrossRef CAS PubMed.
- C. Byrne, L. Moran, D. Hermosilla, N. Merayo, Á. Blanco, S. Rhatigan, S. Hinder, P. Ganguly, M. Nolan and S. C. Pillai, Appl. Catal., B, 2019, 246, 266–276 CrossRef CAS.
- D. A. H. Hanaor and C. C. Sorrell, J. Mater. Sci., 2011, 46, 855–874 CrossRef CAS.
- J. Huang, T. Chen, M. Zhao, P. Yi, F. Zhao, B. He, Y. Wang, Y. Chen, X. Liu and Z. Li, CrystEngComm, 2021, 23, 2952–2960 RSC.
- D. Yoon, S. Yu and J. Son, NPG Asia Mater., 2018, 10, 363–371 CrossRef CAS.
- C. A. Aggelopoulos, M. Dimitropoulos, A. Govatsi, L. Sygellou, C. D. Tsakiroglou and S. N. Yannopoulos, Appl. Catal., B, 2017, 205, 292–301 CrossRef CAS.
- X. Huang, X. Gao, Q. Xue, C. Wang, R. Zhang, Y. Gao and Z. Han, Dalton Trans., 2020, 49, 2184–2189 RSC.
- J. Li, M. Zhang, Z. Guan, Q. Li, C. He and J. Yang, Appl. Catal., B, 2017, 206, 300–307 CrossRef CAS.
- H. Cui, W. Zhao, C. Yang, H. Yin, T. Lin, Y. Shan, Y. Xie, H. Gu and F. Huang, J. Mater. Chem. A, 2014, 2, 8612–8616 RSC.
- H. Zhang, J. Cai, Y. Wang, M. Wu, M. Meng, Y. Tian, X. Li, J. Zhang, L. Zheng, Z. Jiang and J. Gong, Appl. Catal., B, 2018, 220, 126–136 CrossRef CAS.
- M. Kim, B. Lee, H. Ju, J. Y. Kim, J. Kim and S. W. Lee, Adv. Mater., 2019, 31, 1903316 CrossRef PubMed.
- M. F. Mohamad Noh, N. A. Arzaee, J. Safaei, N. A. Mohamed, H. P. Kim, A. R. Mohd Yusoff, J. Jang and M. A. Mat Teridi, J. Alloys Compd., 2019, 773, 997–1008 CrossRef CAS.
- Y. Chen, W. Zheng, S. Murcia-López, F. Lv, J. R. Morante, L. Vayssieres and C. Burda, J. Mater. Chem. C, 2021, 9, 3726–3748 RSC.
- Z. Wang, H. Zhu, W. Tu, X. Zhu, Y. Yao, Y. Zhou and Z. Zou, Adv. Sci., 2022, 9, 2103744 CrossRef CAS PubMed.
- X. Zhang, L. Luo, R. Yun, M. Pu, B. Zhang and X. Xiang, ACS Sustainable Chem. Eng., 2019, 7, 13856–13864 CrossRef CAS.
- C. Ai, P. Xie, X. Zhang, X. Zheng, J. Li, A. Kafizas and S. Lin, ACS Sustainable Chem. Eng., 2019, 7, 5274–5282 CrossRef CAS.
- P. Dias, T. Lopes, L. Meda, L. Andrade and A. Mendes, Phys. Chem. Chem. Phys., 2016, 18, 5232–5243 RSC.
- N. A. Arzaee, M. F. Mohamad Noh, N. S. H. Mohd Ita, N. A. Mohamed, S. N. F. Mohd Nasir, I. N. Nawas Mumthas, A. F. Ismail and M. A. Mat Teridi, Dalton Trans., 2020, 49, 11317–11328 RSC.
- L. Luo, T. Zhang, X. Zhang, R. Yun, Y. Lin, B. Zhang and X. Xiang, Catalysts, 2020, 10, 539 CrossRef CAS.
- N. A. Arzaee, M. F. Mohamad Noh, A. Aadenan, I. N. Nawas Mumthas, F. F. Ab Hamid, N. N. Kamarudin, N. A. Mohamed, M. A. Ibrahim, A. F. Ismail and M. A. Mat Teridi, Chem. Eng. Sci., 2021, 117294 Search PubMed.
- W. N. Zhao, S. C. Zhu, Y. F. Li and Z. P. Liu, Chem. Sci., 2015, 6, 3483–3494 RSC.
- D. Wang, X. Zhang, P. Sun, S. Lu, L. Wang, C. Wang and Y. Liu, Electrochim. Acta, 2014, 130, 290–295 CrossRef CAS.
- P. Sun, X. Zhang, C. Wang, Y. Wei, L. Wang and Y. Liu, J. Mater. Chem. A, 2013, 1, 3309 RSC.
- Z. Liu, X. Zhang, S. Nishimoto, M. Jin, D. A. Tryk, T. Murakami and A. Fujishima, Langmuir, 2007, 23, 10916–10919 CrossRef CAS PubMed.
- M. Meng, L. Yang, J. Yang, Y. Zhu, C. Li, H. Xia, H. Yuan, M. Zhang, Y. Zhao, F. Tian, J. Li, K. Liu, L. Wang and Z. Gan, J. Colloid Interface Sci., 2023, 648, 56–65 CrossRef CAS PubMed.
- J. S. Yang, W. P. Liao and J. J. Wu, ACS Appl. Mater. Interfaces, 2013, 5, 7425–7431 CrossRef CAS PubMed.
- S. N. F. Mohd Nasir, H. Ullah, M. Abd Mutalib, F. H. Saifuddin, N. A. Arzaee, A. A. Tahir, M. F. Mohamad Noh, M. A. Ibrahim, H. Moria, M. N. Alghamdi and M. A. Mat Teridi, J. Phys. Chem. C, 2021, 125, 27148–27158 CrossRef CAS.
- Y. Wang and J. M. Wu, Adv. Funct. Mater., 2020, 30, 1907619 CrossRef CAS.
- H. Meng, K. Fan, J. Low and J. Yu, Dalton Trans., 2016, 45, 13717–13725 RSC.
- T. Soltani and B.-K. Lee, Sci. Total Environ., 2020, 736, 138640 CrossRef CAS PubMed.
- N. A. Arzaee, M. F. Mohamad Noh, A. A. Halim, M. A. F. Abdul Rahim, N. S. H. Mohd Ita, N. A. Mohamed, S. N. F. Mohd Nasir, A. F. Ismail and M. A. Mat Teridi, J. Alloys Compd., 2021, 852, 156757 CrossRef CAS.
- D. Wang, Y. Chen, Y. Zhang, X. Zhang, N. Suzuki and C. Terashima, Appl. Surf. Sci., 2017, 422, 913–920 CrossRef CAS.
- E. S. Cho, M. J. Kang and Y. S. Kang, Phys. Chem. Chem. Phys., 2015, 17, 16145–16150 RSC.
- A. Annamalai, A. Subramanian, U. Kang, H. Park, S. H. Choi and J. S. Jang, J. Phys. Chem. C, 2015, 119, 3810–3817 CrossRef CAS.
- Z. Futera and N. J. English, J. Phys. Chem. C, 2017, 121, 6701–6711 CrossRef CAS.
- Z. Futera and N. J. English, J. Phys. Chem. C, 2016, 120, 19603–19612 CrossRef CAS.
- S.-Y. Kim, N. Kumar, P. Persson, J. Sofo, A. C. T. van Duin and J. D. Kubicki, Langmuir, 2013, 29, 7838–7846 CrossRef CAS PubMed.
- M. Raju, S.-Y. Kim, A. C. T. van Duin and K. A. Fichthorn, J. Phys. Chem. C, 2013, 117, 10558–10572 CrossRef CAS.
- L. Huang, K. E. Gubbins, L. Li and X. Lu, Langmuir, 2014, 30, 14832–14840 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cy00918a |
| This journal is © The Royal Society of Chemistry 2023 |