Exploring CO₂ hydrogenation to methanol at a CuZn–ZrO₂ interface via DFT calculations

Abstract

Multi-component heterogeneous catalysts are among the top candidates for converting greenhouse gases into valuable compounds. Combinations of Cu, Zn, and ZrO₂ (CZZ) have emerged as promisingly efficient catalysts for CO₂ hydrogenation to methanol. To explore the catalytic mechanism, density functional theory (DFT) calculations and the energetic span model (ESM) were used to study CO₂ conversion routes to methanol on CuZn–ZrO₂ interfaces with a varying Zn content. Our results demonstrate that the presence of Zn sites at the interface improves CO₂ binding. However, the adsorption and activation energies are insensitive to Zn concentration. The calculations also show that the hydrogenation of adsorbate oxygen atoms at the interface is kinetically more favourable and requires hydrogen spillover from the metal to the zirconia. This leads to barriers that are lower than those reported on interface or metal-only sites in previous literature. While DFT calculations alone are unable to identify which one of the competing pathways is more favourable, the ESM model predicts that the carboxyl pathway has a higher turnover frequency than the formate route. Our findings also show the importance of considering effects such as hydrogen spillover which take place at a metal-oxide interface when modelling complex catalytic environments.

---

1 Introduction

Transforming CO₂ into value-added products such as methanol, hydrocarbon fuels, and other platform chemicals has gained attention as an attractive approach to reduce the negative impact carbon dioxide has on the climate.^1–4 Using renewable energy and sustainable hydrogen would allow us to establish a circular economy based on carbon recycling.^1,2,5–8 However, due to the stable nature of CO₂, highly active, selective, and deactivation-resistant catalysts are required to make large-scale adaptation feasible.⁵ Various catalytic systems with different combinations of active metal and supporting metal oxide have been prepared and characterised to maximise catalytic activity and selectivity for CO₂ conversion to methanol (CTM):^3,9–18

CO₂(g) + 3H₂(g) → CH₃OH(g) + H₂O(g). (R1)

Oxide-supported Cu nanoparticles have been extensively studied for catalysing CTM due to their promising methanol selectivity, which can be upwards of 60%.^3,19 Several experimental^3,20–24 and computational^3,21,23–26 studies have associated the catalytic activity with active sites at the metal-oxide interface. The type of oxide support can substantially influence the activity and selectivity of the catalyst.^3,4,24 Common choices for suitable oxides include zinc oxide ZnO, zirconia ZrO₂, titania TiO₂, and alumina Al₂O₃. For example, the ternary system of Cu/ZnO/Al₂O₃ is already an industrially established CTM catalyst, but it displays relatively low conversion, typically below 20%, leading to efforts to develop more selective catalysts in addition to the continuous search for increased activity.^3,6,9,27 To this end, zirconia (ZrO₂) has been suggested as an alternative oxide support due to increased turnover rates and selectivity of ZrO₂-supported Cu.^3,24 Additionally, zirconia has been reported to offer enhanced thermal and mechanical stability and to prevent Cu particles from sintering and thus to hinder the deactivation of the catalyst.^3,24,28–33 Adding ZnO as another oxide into Cu/ZrO₂ has demonstrated higher methanol production rates and total conversion percentages than either Cu/ZnO or Cu/ZrO₂, often reaching a 20% conversion whereas a lower 5 to 10 percent conversion is typical for binary systems.^3,4,30,34

The precise function of ZnO in Cu/ZnO/ZrO₂ (CZZ) is still under debate.³³ The ZnO component is suggested to be able to temporarily store hydrogen,³³ and it may also act as an additional structural modifier, enhancing Cu dispersion and increasing its surface area.³⁰ The actual oxidation state of Zn and the mechanism of catalytic promoting remain somewhat controversial,^{3,9–11,13,20,22,23,35–39} and the question of whether or not a CuZn-alloy is involved as the active phase remains open. It is known that the strong interaction between the components may lead to partial ZnO coverage of a Cu surface.^11,20 Under certain conditions the ZnO component can partially reduce into metallic Zn which has two possible outcomes: either forming oxygen vacancies or creating surface alloys of Cu and Zn.^{9,10,13,40,41} The CuZn alloys formed at defect and edge sites of metal particles can then be partially reduced by the adsorbates and serve as the active sites of Cu/ZnO catalysts.⁹ Based on a combination of in situ analyses, it has been determined that the extent of the alloying varies largely based on the exact temperatures, the presence of CO₂ or other gaseous species i.e. the reducing quality of the conditions.^{13,22,23,41,42} Therefore the significance of the alloying remains controversial. A bulk alloy may oxidise and separate into Cu and oxidised Zn,²² or simply lose its ability to act as an efficient catalyst.⁴² Instead, an oxidised phase of Zn in the form of Zn formates has been suggested to be the active intermediate species that lead to methanol formation.^22,36 While the discussion is often centered around bulk alloying, the presence of metallic Zn impurities or dilute alloys at the metal-oxide interface acting as the active sites demand investigation.

In computational studies, a pristine Cu facet such as Cu(111) or Cu(211) has typically been chosen as the model to represent the Cu-containing catalyst system.^9,27,43 While simple to work with, these models obviously omit the effects of the supporting oxide. For example, when CO₂ is electronically activated upon adsorption, it takes a bent shape with an O–C–O angle of 123°, as if sp² hybridised. However, both at and stepped Cu surfaces bind CO₂ only in a linear fashion even though physisorption energies as large as −0.56 eV and −0.71 eV have been reported on Cu(111)^9,27,43,44 and Cu(211),^9,45,46 respectively. On the other hand, the copper-oxide interface has been reported to activate CO₂, which bends upon adsorption and the adsorption energy varies in the range of −0.4–1.8 eV, depending on the specific structure of the interface.^25,44,47 Therefore, binary systems where a metal cluster or nanorod is supported on an oxide slab are a common alternative to a purely metallic model.^25,44,47,48 In a recent study combining experiments and calculations, a single Cu atom catalyst on ZrO₂ was found to promote CTM with near 100% selectivity whereas additional active sites at larger Cu clusters and particles were shown to diminish this efficiency.¹⁴

As the precise role of the Zn promoter in CTM is unsettled,^35,41 the choice of how it should be included in computational models has varied. The density functional theory (DFT) studies on CZZ catalysts conducted so far have only considered one or two of the three components. For example, a CZZ system was recently modelled²¹ by depositing a small ZrO₂ cluster on a ZnO(112̄0) surface to better understand the catalytic behavior on oxide interfaces. Very recently, an inverse ZrZn₂O₃/Cu(111) system was used to model ZrO₂/Cu and ZnO/Cu interfaces.⁴⁹ Purely metallic Cu or CuZn models have also been used to mimic active sites at facets and edges of nanoparticles.^{9,23,27,46,50} Even though a CuZn(211) surface is unable to activate CO₂ and the intermediates bound to it are thermodynamically less stable than the gas-phase reagents,⁹ the hydrogenation intermediates are nevertheless more strongly bound to an alloyed CuZn surface than to a pure Cu surface.⁹

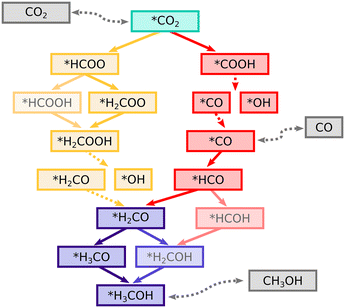
While the reaction mechanism of CTM has been studied for a variety of catalyst compositions, the views are not unanimous on the identity of the key intermediates, the main reaction pathway, and an active catalyst domain.^3,19,24 Generally, the plausible pathways have been narrowed down to two competing ones: one converting CO₂ to a formate (HCOO) which then reacts onwards to methanol, and the other, where CO₂ first breaks down to carbon monoxide (CO) through a reverse water–gas shift (RWGS) reaction and then hydrogenates to methanol via a formaldehyde intermediate. Different interpretations of computational and experimental results have led to differing opinions on the dominant reaction route. For example, a formate species bound to the zirconia surface has been both computationally and experimentally determined to be highly stable and could be considered a strong thermodynamic sink.^25,28,44,48 Therefore, formates have been suggested to accumulate at the zirconia and poison the active sites rather than acting as key intermediates in CTM. However, the barrier for HCOO conversion to dioxymethylene (H₂COO) has been computed to be only 0.66 eV on a ZrO₂/ZnO interface.²¹ This finding is supported by in situ diffuse reflectance infrared spectroscopy measurements, which have shown that the CZZ system can quickly convert formate to a methoxy (CH₃O) species.^21,25

Another key feature for a hydrogenation catalyst is the ability to efficiently dissociate molecular hydrogen, which, in a Cu-based system, is assumed to be take place on the metal component, where hydrogen readily adsorbs dissociatively.^{4,9,21,51–53} Hydrogen spillover from the metal to the ZrO₂ surface may take place and promote a zirconia-bound hydrogen to participate in the CTM reactions.^51,54,55 However, the efficiency and mechanism of the spillover on irreducible oxides, such as zirconia, has been a subject of debate^56–58 and the importance of the kinetic control of the spillover step is unclear.

In this work, we employ DFT calculations to examine the intermediate and transition states for the branched reaction network of CO₂ CTM by first discussing the reactant properties at the interface using supported CuZn nanorod models, then outlining the formate and RWGS route specifics, combining them to form the products, and finally evaluating the kinetic aspects of the catalytic cycle. We model the active interface by constructing mixed CuZn structures with varying concentration of Zn atoms at the Cu-monoclinic ZrO₂(1̄11) interface mimicking a diluted interface nanoalloy. The energetic span model is used to identify rate-controlling intermediates and to draw a simplified comparison between the optimal kinetics of competing mechanisms.

2 Computational methods

DFT calculations were carried out using the BEEF-vdW exchange–correlation functional⁵⁹ in the projector-augmented wave (PAW)⁶⁰ formalism as implemented in the GPAW⁶¹ package. The core electrons of all elements were described in the frozen-core approximation. A maximum spacing of 0.20 Å was used for the real-space grid basis, and the reciprocal space was sampled at the Γ point. A Hubbard U correction⁶² of 2.0 eV, determined using a self-consistent linear response method detailed in ref. 63, was applied to the d-orbitals of the zirconium atoms. A higher value of 4 eV is common in literature^64–67 but the difference is not unusual as the value of the U parameter is very sensitive to the specific DFT implementation used. The geometry optimisations were performed using the fast inertial relaxation engine (FIRE) algorithm as implemented in the atomic simulation environment (ASE).^68,69 During optimisations, the bottom layer of the ZrO₂ slab was kept frozen in its initial bulk geometry. All other atoms were allowed to relax until the maximum residual force was reduced below 0.02 eV Å⁻¹. The transition state searches were carried out using the climbing image nudged elastic band (CI-NEB)^70,71 method where the maximum residual force was set to 0.05 eV Å⁻¹ which keeps the computational cost feasible. Hydrogenation reactions were carried out such that the H atom was initially placed either on the metal side of the interface or on the oxide side, close to the molecule to be hydrogenated. The transition states were confirmed by calculating the vibrational modes using the Frederiksen method⁷² and verifying that only one mode with an imaginary frequency exists along the reaction coordinate. Partial charges on atoms were analysed with the Bader method⁷³ using code written by Tang et al.⁷⁴

For the metal-oxide interface, we utilise the oxide-supported metal nanorod concept consisting of a Cu rod with some edge Cu atoms replaced with Zn atoms at different concentrations (see Fig. 1 for the structures and denominations). The Cu–(m-ZrO₂(1̄11)) interface model was adopted from our previous study,⁴⁷ where the length of the nanorod is eight atoms and the thickness three atomic layers. A (111) plane is exposed towards the interface. The zirconia surface is described by a two-layer-thick slab model, built from a 3 × 2 m-ZrO₂(1̄11) supercell with periodic boundary conditions in the horizontal directions. While a Cu rod was found to be more stable on a tetragonal zirconia surface,⁴⁷ the monoclinic variety is thermodynamically favoured under reaction conditions⁷⁵ and has shown activity towards CO₂ activation and CTM in experiments.^34,76 Three different Zn concentrations were examined by replacing every fourth Cu atom, 3/4 of Cu atoms, or all Cu atoms on the nanorod edge with Zn. These models were named the Zn-dilute, the Zn-rich, and the Zn interface, respectively. This represents situations where Zn centres are dispersed to a varying degree, such as the case where atomic layer deposition has been used to prepare the catalyst.³⁴ In this instance we have chosen to place the Zn centers along the active interface instead of a more homogeneous alloying with Cu, allowing the use of a pure Cu interface model as a reference, assisting interpretation.

Fig. 1 The four metal/ZrO₂ interface systems with varying amounts of Zn in the Cu nanorod. A: Cu interface, B: Zn-dilute interface, C: Zn-rich interface, D: Zn interface. Red: O, white: H, dark grey: C, purple: Zn, turquoise: Zr, orange: Cu.

The simulation cell measures 20.67 × 14.79 × 24.0 in Å with angles of 90°/90°/116.5°. This unit cell size results in a minor compressive strain of −1.02% for the Cu atoms along the direction of the nanorod.⁴⁷ For the Zn interface, the strain is −4.2% as a result of the longer, 2.69 Å, Zn–Zn bulk distance. The strains experienced by the other interfaces are less clearly defined but are likely between the −1.02% of Cu and −4.2% of the Zn interface. A strain of this magnitude at the Cu interface⁴⁷ was found to enhance CO₂ binding by up to 0.4 eV. On the other hand, a computed lattice constant of 2.91 Å has been reported for a bulk β-CuZn,⁷⁷ corresponding to a shorter Cu–Zn distance of 2.52 Å. This could mean that the compressive strain of the Zn-dilute interface is slightly lower than that of the Cu interface. All three doped interfaces have a Zn atom at the site that binds CO₂ and many further reaction intermediates the strongest, so that they all measure the impact of Zn against the performance of the pure Cu interface. The relative strength of the adsorption at this site is likely due to a lower coordination caused by the interaction between the nanoparticle and the oxide. The models represent cases where the Zn atoms exist as single atom centers dispersed at the metallic interface or as more conjugated assemblies that span several Zn centers. The energy ΔE_def by which CO₂ adsorption deforms the interface was calculated as

where is the energy of a CuZn/ZrO₂ configuration after removal of CO₂ from an optimised adsorption geometry and E_CuZn/ZrO2 is the energy of the optimal interface without any adsorbate.

A graph theory-based energetic span model^78,79 (ESM) for complex reaction networks was utilised to assess the catalytic cycles. By summing together pairs of intermediate and transition state energies, it is possible to estimate turnover frequency of each mechanism,

where k_B is the Boltzmann constant, T is the temperature, h is the Planck constant, ΔG_r is the Gibbs energy of reaction, and T_i and I_j are the Gibbs energies of a given transition state and intermediate, respectively. Furthermore, a summation over all n possible mechanisms in the network gives an estimate of the total TOF.⁷⁹The delta term δG_i,j is defined as:⁷⁹The degree of turnover frequency control X_TOF is defined for intermediates and transition states according to eqn (5) and (6) (see ESI† section S3).The concept is similar to that of the degree of rate control. A value closer to 1 indicates that changes in the state's energy will affect the TOF more than the energies of states with X_TOF values close to 0. However, while the degree of rate control is often determined for elementary steps, here we define the degrees of TOF control separately for intermediates and transition states. This way the values of X_TOF can be maximal for two states that are not part of the same elementary step. We can show the direct influence of the energy of each intermediate of transition state as:which was estimated by using ∂T_i = ∂I_j = −0.001 eV. The DFT-computed adsorption and transition state energies were used as input. While the difference between free energies and DFT energies for gas-phase species can be in the order of 0.6 eV, we assume that the catalytic turnover frequencies (TOF) and the degree of TOF control values (X_TOF) can be compared between different reaction pathways that mainly take place on the surface, even though no free energy corrections were included. The TOF values were computed at a temperature of 500 K, which corresponds to experimental reaction conditions.⁸⁰

The ESM analysis was originally developed for studying homogeneous catalysis⁷⁸ but it has also been successfully applied for heterogeneous systems including CO₂ hydrogenation to methanol on Cu(111).⁸¹ The basic assumptions of the ESM include that: (i) Eyring's transition state theory is valid, (ii) a steady-state regime is applicable, and (iii) the intermediates undergo fast relaxation to the thermodynamic equilibrium described by the Boltzmann distribution.⁷⁸ While the reaction kinetics for heterogeneous catalyst systems is often studied via microkinetic modelling or kinetic Monte Carlo simulations,^{23,26–28,48,49,82} the ESM offers a simplified way to estimate which pathway is optimal. We used the gTOFfee software,^81,83 which was slightly modified to improve the performance for the present reaction network. Additionally, an extension was made to the code for calculating the degrees of TOF control, see ESI† for details.

3 Results and discussion

3.1 CO₂ and H₂ activation

The CO₂ adsorption properties of the interfaces were determined first since the CO₂ reduction pathways start with the adsorption of the reactants on the catalyst surface. All the interface atoms were first considered as potential sites for the CO₂ adsorption. Subsequent hydrogenation steps are then performed for the most stable CO₂ adsorption geometry, which is similar to the one for the Cu interface.⁴⁷ CO₂ binds to the CuZn–ZrO₂ interface in a conformation where the carbon atom resides on top of a Zn atom (C–Zn bond length 2.1 Å) and the two oxygen atoms bind on two Zr cations close to the interface (see Fig. S6†). Upon adsorption, CO₂ takes a bent shape, which resembles a carbonate anion^25,47 and indicates the activation of the molecule with a partial charge of 1.3|e|.⁴⁷ The interaction of CO₂ with the CuZn–ZrO₂ interface leads to a local deformation of the rod such that the metal atom in contact with the C atom is pulled out from the (111) plane.

The CO₂ adsorption is exothermic by −1.17 eV, −1.13 eV, and −1.30 eV at the Zn-dilute, Zn-rich and Zn interfaces, respectively. The Cu interface exhibits significantly weaker binding with an adsorption energy of −0.64 eV.⁴⁷ The difference can be rationalised by examining the energy penalty of deformation ΔE_def, calculated using eqn (1), which is +1.7 eV for the Cu interface and +1.1 eV for the Zn-dilute interface. The ΔE_def is consistent with the difference in adsorption energies: the stronger binding at the Zn-containing interface is due to smaller deformation energy. No energy penalty is seen for the Zn-rich and Zn interfaces, as their intrinsic strain already favours a deformed structure. CO₂ adsorption at the Zn-rich interface is a kinetically activated process with a barrier of 0.16 eV, which is 0.22 eV lower than the barrier computed for the Cu interface.⁴⁷ Similarly to the more negative adsorption energies, the lower barrier is likely due to the increased mobility of the Zn. Adsorption of CO₂ on the low-coordinated oxygen atoms of the ZrO₂ surface, without the involvement of the interface, is also possible in a trigonal carbonate-like geometry where the carbon atom of the CO₂ binds the lattice oxygen and one of its oxygens rests on a Zr cation. With an adsorption energy of −0.59 eV, this binding is likely in competition with the adsorption at the interface. In addition to adsorption, we considered dissociative adsorption of CO₂ into CO and O, as studied previously.^84–86 However, the reaction is endothermic with a barrier of 1.7 eV, see ESI† section 1.1 for details, and therefore this pathway was omitted from further evaluation.

The dissociative adsorption of H₂ was considered at the CuZn–ZrO₂ interface at various positions. The dissociation can be homolytic, where both H atoms adsorb on Cu/Zn sites on the rod and have similar small charges of ca. −0.3 e, regardless of if they are in the vicinity of a Zn site. Alternatively, it can happen across the interface either homolytically, where one H binds on the surface of the rod and the other on top of a Zr, or heterolytically, where a hydride binds to the surface of the metal rod and a proton to an oxide anion. These sites are illustrated in Fig. S7.† Hydrides and protons on the zirconia have charges of −0.6 e and +0.6 e, respectively. The heterolytic dissociation is endothermic by ca. +1 eV and has a kinetic barrier of 1.4 eV, while the homolytic path on the rod is endothermic only by +0.4 eV with a slightly smaller activation energy of 1.1 eV. The spillover of hydrogen from the metal to the oxide surface is endothermic by ca. +0.6 eV depending slightly on the interface site. The kinetic barrier for hydride migration from the metal to the Zr on-top site of the oxide is 0.8 eV. However, the presence of CO₂ or further reaction intermediates can stabilise the oxide-bound H, up to the point where it becomes thermodynamically favourable compared to the metal-bound H atom.

3.2 The formate and RWGS routes

The two most commonly proposed CTM reaction mechanisms are considered here: the formate pathway with intermediates labeled F_i, and the RWGS pathway with labels R_i, Fig. 2 displaying the detailed reaction network. The elementary steps along the formate and RWGS pathways were examined at both the Zn-dilute and Zn-rich interfaces, as well as examining selected steps at the Zn interface. We highlight the differences between the systems when they are relevant but in many cases they behave very similarly. In these situations, we use the Zn-dilute interface as an example. The computed adsorption and activation energies for all interfaces are summarised in the ESI† in Table S2 and the corresponding atomic structures are shown in Fig. S8–S13.†

Fig. 2 The CO₂ the two most common reaction routes for the CTM reaction network. The formate route is given in yellow whereas the RWGS route is displayed in pink. Solid lines imply hydrogenation and dashed lines stand for dissociation or ad-/desorption of the intermediate. Less favourable intermediates/paths are more faintly coloured.

CO₂ to HCOO. Formate, HCOO, is formed across the interface from co-adsorbed CO₂ and H. The CO₂ is initially in its most stable geometry and the hydrogen is positioned on the metal, close to the reaction site. The diffusion of the hydrogen from its optimal geometry on surface of the Cu particle is not included in the calculations. Formate (F₀₁) binds on the ZrO₂via O–Zr bonds and, unlike the CO₂, interacts only with the support as demonstrated by the long Zn–C distance of 3.8 Å. The reaction is exothermic by −1.2 eV and the activation energy is +1.2 eV. The energies are similar across the interface models (see Table S2†). Fig. 3 shows the atomic geometries for the initial, final, and transition states. At the transition state (TS₀₁), the hydrogen atom has migrated from the Cu–Cu bridge geometry to a Zn-top position while the C atom is still in contact with the Zn atom with a mildly elongated C–Zn bond length of 2.2 Å. The activation and reaction energies at CuZn interfaces are not significantly different compared to a Cu interface (Table S2†). The slightly lower activation energy of +1.0 eV at the Cu interface is likely due to the Cu–H interaction at the transition state being stronger than that between Zn and H. The binding geometries of CO₂ and HCOO as well as reaction energies for formate formation are similar to those reported in literature for a variety of different interfaces, i.e., Cu clusters or rods on zirconia,^25,44 zirconia clusters on Cu(111),²⁸ and other metal–zirconia interfaces.⁴⁸ The differences can be rationalised by the structural similarities of the interfaces. In all cases, the reaction energy varies only from −0.6 to −0.7 eV. Previously reported activation energies are in the order of +0.7 eV (ref. 25 and 48) with the exception of the inverse ZrO₂ cluster on Cu(111) model²⁸ where the barrier was reported to be only +0.14 eV.

Fig. 3 Initial, transition and final state geometries for formate formation at the Zn-dilute interface. Light red: lattice O, dark red: adsorbate O, white: H, dark grey: C, purple: Zn, turquoise: Zr, orange: Cu.

HCOO to H₂COO. The next reaction step in the formate route is formate hydrogenation to a dioxymethylene species (H₂COO). In this step, the hydrogen again reacts with the carbon from the metal side. To this end, the HCOO has to still be relatively close to the interface. This reaction is shown in Fig. 4. The reaction is endothermic by +0.2 eV with activation energies around +0.5 eV. In the transition state (TS₀₂), the C–H distance is around 1.5 Å, which is shorter compared to the 2.0 Å observed during formate formation (TS₀₁). The activation energies are comparable to the value of +0.5 eV that was previously computed at a Cu–ZrO₂(2̄12) interface.²⁶ The transition state geometry is also similar with a C–H distance of 1.58 Å. A study of a zirconia-supported Cu₃₈ cluster reported a slightly higher barrier of ca. +0.7 eV (ref. 25) still suggesting a fast interconversion between the HCOO and H₂COO. Interestingly, at a model ZrO₂/ZnO interface,²¹ the reaction energy for H₂COO formation is exothermic by −1.27 eV, but the activation energy of +0.66 eV is close to our values. Low activation energies reported for Cu/ZnO, Cu/ZrO₂, and ZnO/ZrO₂ interfaces are in strong contrast to the high activation energies on bare Cu surfaces. For example, the barrier on a Cu(111) surface has been reported to be 1.59 eV²⁷ or 0.97 eV.⁴³ On a stepped Cu(533) surface, the activation energy was determined to be 1.42 eV. Consequently, several computational studies^{9,23,27,28,45,46} on metal surfaces and inverse oxide-on-metal models have suggested that HCOO hydrogenation leads to formic acid (HCOOH) instead. In these cases, an oxygen atom of the adsorbate and the reacting H are connected to the same component, e.g. the metal surface. Thus it is sensible that the formation of an O–H bond to create formic acid is more facile than the reaction with the carbon atom of the formate, which points away from the surface. We find, however, that on CuZn/ZrO₂ the reaction to HCOOH is thermodynamically and kinetically significantly less favourable than the reaction to H₂COO with an activation energy that is over 1 eV higher, as apparent in Fig. S2 and S4 (see ESI† section 1.2 for the full discussion). The difference can be explained simply by the fact that the structure of a metal-oxide interface is able to bring the reacting H and the carbon centre of the HCOO species closer together to create a more favourable pathway.

Fig. 4 Initial, transition and final state geometries for HCOO hydrogenation to H₂COO, at the Zn-dilute interface. Light red: lattice O, dark red: adsorbate O, white: H, dark grey: C, purple: Zn, turquoise: Zr, orange: Cu.

H₂COO reduction to H₂COOH and splitting into H₂CO. During the conversion of H₂COO to a hydroxymethoxy species (H₂COOH), both the H₂COO and the H₂COOH intermediates stay on the zirconia, attached by their oxygens to Zr top positions but disconnected from the interface. The reacting H atom is initially bound to a zirconia lattice oxygen near the dioxymethylene intermediate. The reaction of H₂COO to H₂COOH is exothermic in the range of −0.1 eV to −0.5 eV with moderate activation energies of ca. 0.5 eV at the mixed interfaces. Previous computational studies^21,25 on cluster systems (ZrO₂ on ZnO, Cu₃₈ on ZrO₂) have found comparable activation energies for this step but reported the reaction to be slightly endothermic, likely due to a stabilising effect of the zirconia surface.

The next step on is the dissociation of H₂COOH into hydroxyl (OH) and formaldehyde (H₂CO). This reaction shows significant energetic variation depending on the interface, being practically thermoneutral at the Zn-dilute and Zn interfaces, and slightly endothermic by +0.2 eV at the Zn-rich interface. At the Cu interface, the reaction is more endothermic by ∼+0.4 eV, due to the weaker adsorption of the formaldehyde. The activation barriers are in the order of +0.2 to +0.5 eV. A previous study⁸⁰ found the reaction and activation energies on a Zn-decorated Cu(211) surface to be similarly slightly endothermic with a low barrier. When the C–O bond is broken, the OH part remains bound to a Zr-top site whereas the H₂CO (F₀₆), while still attached to an oxide cation via its oxygen, tilts toward the nearby interface and binds to a Zn via its C atom. The resulting C–Zn distance of 2.17 Å is similar to that of activated CO₂. The Zn atom is again slightly pulled out from the ideal position and there is no significant energy difference regarding which of the two neighbouring Zr atoms the oxygen atom binds to. Alternatively, H₂COOH may hydrogenate to methanediol H₂COHOH (F₀₇). However, we found the activation energy of +0.9 eV to be clearly higher than that of the dissociation. Therefore, the pathway was not considered further.

The full potential energy diagram of CTM through the formate mechanism is shown in Fig. 5. The final steps from H₂CO to methanol are shared between both the formate and the RWGS route.

Fig. 5 Potential energy diagrams of the formate route for CO₂ hydrogenation to methanol. Dissociative adsorption steps of hydrogens are not included as they are assumed to be available.

CO₂ to COOH. The RWGS route begins with the formation and subsequent dissociation of a carboxyl intermediate (COOH) at the metal-oxide interface. Starting from the adsorbed CO₂ and dissociated H, the reacting H atom must be spilled from the metal to the oxide surface, from where it reacts with an oxygen atom of the CO₂ molecule (see Fig. 6).Attempts to make the H react directly from the metallic component to the CO₂ oxygen were not successful. The resulting COOH intermediate (R₀₁) binds to the metal via the C atom and to the oxide via both O atoms the same way as CO₂ does. This is in contrast to the formate, which detaches from the interface. The formation of COOH at the CuZn interfaces is endothermic by approximately 0.4 eV, and has a moderate +0.7 eV barrier (see ESI,† Table S2, TS₁₁ onward). In contrast, the reaction barrier is 1.8 eV for a CuZn-bound H, which would severely hinder the RWGS mechanism. Employing the oxide-bound H also minimises the distance that the H atom needs to move to form the new O–H bond.

Fig. 6 CO₂ hydrogenation to COOH at the Zn-dilute interface. Light red: lattice O, dark red: adsorbate O, white: H, dark grey: C, purple: Zn, turquoise: Zr, orange: Cu.

The COOH is thermodynamically less stable by ca. 1.5 eV compared to the HCOO intermediate but the activation energy for COOH formation is 0.5 eV lower. A similar 1.4 eV difference in adsorption was found at a Cu₃₈/ZrO₂ interface.²⁵ However, in that case the H reacted directly from the Cu₃₈ cluster which corresponds to an activation energy of around +2 eV which is 1.2 eV higher than that of the formate formation. These activation energies and their differences are in line with our results but the case where H reacts from the oxide was not previously included.

COOH dissociation. The COOH species dissociates into carbon monoxide (CO) and an OH group that end up bound to adjacent Zr atoms (see R₀₂ in Fig. S9–S13†). In the transition state, the CO is bound to a Zr cation via its O atom while having a 2.2 Å C–Zn distance and a 1.8 Å C–OH distance. After the reaction is complete, the CO can stay physisorbed on the zirconia surface at a C–Zr distance of 2.8 Å or diffuse to bind at the interface. In both cases the CO adsorption energy is very similar and in the order of −0.5 eV. Bader analysis gives the OH group a charge of ≃0.7 e, pointing to it having an anionic character, while the CO adsorbed at the interface is neutral. The COOH splitting reaction is exothermic by ≃0.1 eV and its activation energy is ca. 0.2 eV at the mixed interfaces. At the Cu interface, the reaction energy increases to −0.4 eV due to the CO binding more strongly to Cu than to Zn. A previous study on Cu(111)²⁷ shows a +0.42 eV activation energy for the dissociation of COOH, while the reaction energy remains slightly exothermic by −0.14 eV.

CO to HCO. To produce a formyl (HCO) intermediate, a H atom moves in from the metal component to the C atom of a CO adsorbed at the interface (TS₁₃ and R₀₃ in Fig. S9–S13†). During the reaction, the C–Zn distance shortens to ∼2.1 Å, from the initial values ranging between 2.5 Å at the Zn-rich interface and 4.1 Å at the Zn-dilute. The reaction is exothermic by −0.4 eV, on average, and is accompanied by barriers ranging from 0.32 eV at the Zn-rich interface to 0.67 eV at the Zn interface. We note that these results were obtained in the presence of a bystander OH. We explored COH formation as an alternative but found it endothermic by +0.65 eV—that is—more than 1 eV less stable compared to HCO. Therefore this option was not explored further.

In some previous studies, the formation of HCO has had a different character compared to our CuZn/ZrO₂ results. Namely, on a Cu(111) surface,²⁷ the reaction is endothermic by +0.78 eV and has an activation energy of almost +1 eV. Furthermore, on an inverse ZnO/Cu model, the reaction is endothermic by +0.39 eV and the barrier is +0.88 eV.²³ These differences point to HCO adsorbing less strongly to Cu surfaces, and to the stabilising effect of the interface.

HCO to H₂CO. We start the reaction of HCO hydrogenation to H₂CO from a position where the molecule is connected to the interface via a C–Zn bond its oxygen rests on a Zr cation. Once again, the H preferably reacts from the metal side of the interface to the C atom rather than from the oxide. Both the intermediates and the transition state (TS₁₄) keep contact to the metal via a C–Zn bond while the OH group, if kept in the vicinity, remains a spectator. The reaction is exothermic by −0.9 eV to −1.2 eV on CuZn interfaces. At the Cu interface, the reaction energy is −0.7 eV, due to the slightly weaker binding of HCO compared to the CuZn interfaces. The reaction has an activation energy of +0.3–0.5 eV. This is close to the inverse ZnO/Cu model,²³ where the activation energy is +0.25 eV. The other reaction that HCO could participate in is the formation of hydroxymethylene (HCOH, R₀₆), which we found to be endothermic with a 0.9 eV kinetic barrier (visible in Fig. S5†), similar to the results on Cu(111).²⁷ See section 1.3 in ESI† for full discussion. The full potential energy diagram of the RWGS route for the Zn-dilute interface is shown in Fig. 7.

Fig. 7 Potential energy diagrams of the RWGS path. States from H₂CO forward include an OH on the zirconia surface.

3.3 Formaldehyde hydrogenation to methanol

The formate and RWGS pathways discussed above merge after the formation of formaldehyde (H₂CO). This species is stable, as the adsorption energy of H₂CO relative to formaldehyde in the gas phase is −1.4 eV. Next, we address two different ways to progress from H₂CO onward by considering the options of removing and keeping the ZrO₂-bound OH group produced during the previous reaction steps. This is done to investigate the influence of OH on reaction energetics, as it could have a co-catalysing effect via hydrogen bonds or due to its Lewis acidity. The removal of the OH from the zirconia can take place via H₂O formation and desorption, which is endothermic by +0.7 eV on average. A previous study⁴⁸ showed no kinetic barriers for the dissociative adsorption of water on ZrO₂ and therefore its desorption likely does not have a kinetic barrier either. For brevity, these two routes are shown in the PES diagrams of the previously discussed formate and RWGS pathways. The case where OH has been removed is shown in the diagram of the formate route (Fig. 5) whereas the OH is kept on the surface at the end of the RWGS path in Fig. 7.

H₂CO to H₃CO. Formaldehyde preferably adsorbs at the interface with its carbon attached to the Zn site and the oxygen on a Zr top site. The hydrogens of the H₂CO are bent away from the interface leaving the carbon with an sp³-like geometry which shows that the formaldehyde is electronically activated. The reacting H is again sitting on the metal component.

Upon hydrogenation to methoxy (H₃CO), the bond between the product and the metal at the interface is broken and the methoxy binds solely to ZrO₂via its O atom. The reaction is exothermic by −1 eV and requires an activation energy of 0.4–0.6 eV. In this case, the influence of the ZrO₂-bound OH is rather insignificant as the reaction and activation energies are similar to those without OH. In previous studies, the reaction was practically thermoneutral on Cu(111)²⁷ and exothermic by −0.67 eV on an inverse ZnO/Cu system.²³ The kinetic barriers at the CuZn interfaces are higher than those found on the Cu(111) and inverse ZnO/Cu surfaces where in both cases an activation energy ∼+0.2 eV was reported. This may simply be due to more favourable adsorption and transition state geometries. We also studied the alternative pathway forward via the formation and hydrogenation of hydroxymethyl (H₂COH) but found that it is significantly less favourable due to its relative instability and high activation barriers as seen in Fig. S2–S5.† Discussion of this pathway can be found in the ESI† section 1.3.

H₃CO to H₃COH. In the final step of both pathways, the reacting hydrogen transfers from the support oxide to the methoxy to form methanol. The reaction energy is practically thermoneutral and in all cases there is likely a fast interconversion between the methoxy and methanol species. The influence of surface OH on the reaction barrier is minor as the activation energy is ca. 0.1 eV with OH present and only a slightly higher ∼0.2 eV without (TS₁₉vs. TS₀₉). The methanol product binds solely to the ZrO₂ surface, on a Zr top site via its oxygen atom. The desorption of methanol into the gas phase does not have an activation barrier but requires a desorption energy of ∼1.3 eV. Alternatively, methanol can decompose into a methyl (H₃C) and an OH species with an activation energy quite close to the desorption energy. However, the splitting is clearly endothermic at most interfaces and thus unlikely, although small amounts of methane are observed in experiments.^3,34 A complete discussion of the splitting can be found in section 1.4 of the ESI.† The desorption of both methanol and water is endothermic by +2.2 eV, which leads to an overall reaction energy of −0.53 eV for the completed reaction cycle. Because of the stability of dissociated water on the zirconia surface, some of it will accumulate on the surface as the reaction cycles.

3.4 Potential energy landscape

Fig. 8 shows the potential energy profiles for the formate and RWGS pathways. At the Zn-dilute interface, the formate pathway exhibits lower energies and thus appears thermodynamically more stable as compared to the RWGS pathway. However, accessibility of the formate pathway is limited by the major barrier (TS₀₁) for HCOO formation which is energetically well in line with previous computational studies that have considered CuZn surfaces or Cu cluster models.^23,25 Despite the strong binding of formate, it does not severely poison the CuZn/ZrO₂ interface. This is because it readily reacts onward to H₂COO with a barrier around +0.4 eV. After a further hydrogenation to H₂COOH, the reaction proceeds via decomposition into H₂CO and a surface-bound OH group, which is removed to the gas phase as water. According to activation energies, the formation of H₂COH is favoured over H₃CO. However, the activation energy required for the final hydrogenation step from H₂COH to methanol is considerably larger than that from methoxy, which in turn favours the path through the H₃CO intermediate. Therefore, the methoxy intermediate is likely the dominant one, similar to what previous computational studies have suggested on both cluster and surface models.^23,25,27 In general, intermediates along the formate pathway tend to be slightly more stable at the Zn interface than the Zn-dilute and the Zn-rich interfaces (see Fig. 5). Overall, the variation in energy is modest with the largest difference being 0.25 eV in the case of the formate species.

Fig. 8 Potential energy diagram of both the formate and the RWGS paths (Zn-dilute interface). States from H₂CO forward include an OH on the zirconia surface.

Along the RWGS pathway, the activation energies are in general lower than those of the formate route. The carboxyl intermediate readily dissociates into OH and CO. At the interface, CO prefers to bind to a Cu site over a geometrically equivalent Zn site and can easily diffuse to a neighbouring Cu or even onto the ZrO₂ surface with no energy penalty. CO converts to HCO and H₂CO at a low energy cost. From this point, the reactions proceed similarly to the formate pathway. Again, the nearly non-existent barrier from H₃CO to methanol would suggest that the methoxy intermediate is dominant over H₂COH. In the case of the RWGS pathway, we often see the Zn-dilute interface with the most stable intermediates. The largest difference occurs for the COOH species with 0.27 eV energy difference between the Zn-dilute and Zn-rich interface. A possible explanation for these small trends between different Zn concentrations could lie in the increased mobility of Zn atoms going from Zn-dilute to the full-Zn interface.

The CuZn interfaces bind several intermediates stronger than the Cu interface does, including CO₂, COOH, HCO, HCOH, H₂CO, and H₂COH. The commonality between these intermediates is that they are bound at the interface, connected to the metal component via a Zn–C bond, and most of them are found along the RWGS pathway. Zn centers bind these adsorbates, on average, 0.4 eV stronger than geometrically equivalent adsorption sites at the Cu interface. The important exception to this is carbon monoxide, CO, which is adsorbed 0.1 to 0.3 eV stronger to Cu sites. We also note that a hydrogen placed in the immediate vicinity of the Zn center weakens the adsorption of all aforementioned intermediates and brings the adsorption energies roughly 0.3 eV closer to those at the Cu interface. Intermediates that preferably bind to the support are largely unaffected by the presence of Zn and its concentration.

3.5 Energetic span analysis

The results given by the energetic span model allow us to compare the competing formate and RWGS mechanisms. We note that the predicted turnover frequencies are unlikely directly comparable to experimental numbers.^78,79,81 They are, however, representative of the relative kinetics of the two pathways. The analysis was done separately for the Zn-dilute and Zn-rich interfaces. The relative energies in Table S2 were used as inputs and the model was run at 500 K. To obtain reliable results and to avoid problems with coverage effects, we limit the ESM analysis to competing pathways with the same number of atoms. Therefore the model can not be used to assess if the presence of OH groups speeds up latter reaction steps and they are left out of the following discussion. The endothermicity of the CO production and release also prevents its examination using the computational code of Garay-Ruiz and Bo⁸¹ as an endothermic (endergonic) cycle would lead to a negative TOF.^78,79 Nevertheless, CO is observed in most real-world CTM systems.^3,19 The production of CO is likely controlled, to some extent, by its endothermic nature and the fact that typical reaction conditions include high pressures.

In the terminology of the ESM, the formate and RWGS pathways are competing catalytic cycles. Both pathways are combined and presented as a network graph in Fig. 9a), labelling each intermediate state as a node and each transition state as a line. Starting from the left by adsorption of CO₂, the network is simplified and categorised by ignoring side branches or processes such as CO desorption. The four cycles given in Fig. 9b) feature the mechanisms with the highest turnover frequencies. The analogous Fig. S14 in the ESI† represents the Zn-rich interface. Cycles 1 and 2 follow the RWGS pathway, while Cycles 3 and 4 progress along the formate route. Furthermore, cycles 1 and 3 progress via the H₂COH intermediate while cycles 2 and 4 go through the formation of H₃CO instead.

Fig. 9 a) The simplified network used in the energetic span analysis. b) The catalytic cycles in the simplified network with their corresponding turnover frequencies on the Zn-dilute interface.

Cycle 2, i.e. the RWGS route with methanol formed from H₃CO, yields the highest TOF of the four cycles. Accordingly, the energetic span is lowest, being 1.89 eV at the Zn-dilute interface and 1.81 eV at the Zn-rich. The corresponding calculated turnover frequencies are 5.6 × 10⁻⁵ s⁻¹ and 2.9 × 10⁻⁴ s⁻¹, respectively, showing a relatively high degree of sensitivity to the change in δE. The next highest TOF belongs to cycle 4 representing the formate/H₃CO pathway where the effective energetic span is 0.48 eV higher. Cycles 1 and 3 which go through H₂COH have to pass a very high transition state, which becomes TOF-determining, and thus have significantly higher energetic spans and lower turnover frequencies.

A degree of turnover frequency control X_TOF analysis (detailed in the ESI† section 3) confirms that the formate acts as a thermodynamic sink. The X_TOF for HCOO is practically 1 in all unique cycles of the network (Fig. 9), indicating a large degree of turnover frequency control. Near the calculated formate energy, its effect on the TOF of cycle 2 (eqn (8)) is 1.2 × 10⁻³ s⁻¹ eV⁻¹. Note that, as described earlier, the presence of Zn sites at the interface does not affect the stability of the formate. Assigning the TOF-limiting transition states depends on the cycle. The transition state from H₂COH to CH₃OH (TS₁₀), present only in cycles 1 and 3, has the highest degree of TOF control owing to its significantly high activation energy. In cycles 2 and 4 the transition state from H₂CO to H₃CO (TS₀₇) takes dominance. In cycle 4, corresponding to a formate mechanism, the TS₀₁ from CO₂ to HCOO also has some TOF-controlling character with a 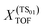of 0.32. The influence of TS₁₀ on cycle 1 (eqn (7)) is −9.0 × 10⁻¹¹ s⁻¹ eV⁻¹ and the influence of TS₀₇ on cycle 2 is −1.2 × 10⁻³ s⁻¹ eV⁻¹ near the calculated energies. Interestingly, all these elementary steps take place at the interface. Based on the energetic span analysis, we can conclude that the RWGS pathway is more favourable compared to the formate pathway, and that the last steps clearly involve the methoxy intermediate.

4 Conclusions

We have employed DFT calculations to obtain a thermodynamic and kinetic view of CO₂ hydrogenation to methanol using a Cu/Zn/ZrO₂ catalyst. To this end, we constructed a mixed CuZn/ZrO₂ interface model using Cu nanorods with a varying Zn concentration at the interface. Our results show that intermediates binding to metal atoms at the interface adsorb stronger to Zn sites than to geometrically equivalent Cu sites. Enhanced binding is visible for all the studied Zn configurations and most pronounced on the interface where the Zn solute is the most dispersed. CO is the one exception to this trend as it preferentially binds to Cu sites. The addition of Zn at the interface has minimal effect on intermediates that do not bind to the metallic component, including some key intermediates such as the formate and methoxy species. Comparison between the four considered interface models shows that the reaction steps are not very sensitive to the concentration and arrangement of Zn at the interface. Zinc centers are active regardless of the identity of their surrounding atoms.

A graph-based energetic span analysis can provide estimates for turnover frequencies to compare the competing mechanisms. Analysing the catalytic cycle as a whole allows us to identify the TOF-determining intermediates and transition states. The results support the RWGS route being the main CTM pathway. This can be explained by smaller reaction barriers along the RWGS mechanisms. Considering hydrogen spillover from the metal component to the support oxide is necessary as it facilitates the protonation of the surface-bound oxygen atoms of the intermediates. By including spillover, the barriers for the formation of several intermediates, notably carboxyl (COOH), become much lower than previously reported making the RWGS route more accessible.

Incorporating a Zn promoter into the interface structure selectively stabilises some intermediates, highlighting the importance of the effort to identify key intermediates and transition states. As Zn binds H less strongly, the role of the Cu is in hydrogen dissociation, storage, and spillover as well as enhancing CO binding. An increased understanding of promoter–adsorbate interactions allows tailoring of catalyst properties to influence adsorbate binding, which is important for selectivity and yield.

Conflicts of interest

The authors have no conflicts to declare.

Acknowledgements

The work was funded by Academy of Finland (project 329977). The electronic structure calculations were made possible by computational resources provided by the CSC – IT Center for Science, Espoo, Finland (https://www.csc.fi/en/) and computer capacity from the Finnish Grid and Cloud Infrastructure (urn:nbn:fi:research-infras-2016072533). Dr Minttu Kauppinen is acknowledged for carefully reading the manuscript.

References

1. G. A. Olah, G. K. S. Prakash and A. Goeppert, J. Am. Chem. Soc., 2011, 133, 12881–12898.
2. G. A. Olah, Angew. Chem., Int. Ed., 2013, 52, 104–107.
3. S. Kattel, P. Liu and J. G. Chen, J. Am. Chem. Soc., 2017, 139, 9739–9754.
4. K. Li and J. G. Chen, ACS Catal., 2019, 9, 7840–7861.
5. S. Roy, A. Cherevotan and S. C. Peter, ACS Energy Lett., 2018, 3, 1938–1966.
6. B. M. Tackett, E. Gomez and J. G. Chen, Nat. Catal., 2019, 2, 381–386.
7. R. P. Ye, J. Ding, W. Gong, M. D. Argyle, Q. Zhong, Y. Wang, C. K. Russell, Z. Xu, A. G. Russell, Q. Li, M. Fan and Y. G. Yao, Nat. Commun., 2019, 10, 5698.
8. J. Artz, T. E. Müller, K. Thenert, J. Kleinekorte, R. Meys, A. Sternberg, A. Bardow and W. Leitner, Chem. Rev., 2018, 118, 434–504.
9. M. Behrens, F. Studt, I. Kasatkin, S. Kühl, M. Hävecker, F. Abild-Pedersen, S. Zander, F. Girgsdies, P. Kurr, B.-L. Kniep, M. Tovar, R. W. Fischer, J. K. Nørskov and R. Schlögl, Science, 2012, 336, 893–897.
10. S. Kuld, M. Thorhauge, H. Falsig, C. F. Elkjær, S. Helveg, I. Chorkendorff and J. Sehested, Science, 2016, 352, 969–974.
11. S. Zander, E. L. Kunkes, M. E. Schuster, J. Schumann, G. Weinberg, D. Teschner, N. Jacobsen, R. Schlögl and M. Behrens, Angew. Chem., Int. Ed., 2013, 52, 6536–6540.
12. P. L. Hansen, J. B. Wagner, S. Helveg, J. R. Rostrup-Nielsen, B. S. Clausen and H. Topsøe, Science, 2002, 295, 2053–2055.
13. J. D. Grunwaldt, A. M. Molenbroek, N. Y. Topsøe, H. Topsøe and B. S. Clausen, J. Catal., 2000, 194, 452–460.
14. H. Zhao, R. Yu, S. Ma, K. Xu, Y. Chen, K. Jiang, Y. Fang, C. Zhu, X. Liu, Y. Tang, L. Wu, Y. Wu, Q. Jiang, P. He, Z. Liu and L. Tan, Nat. Catal., 2022, 5, 818–831.
15. O. Martin, A. J. Martín, C. Mondelli, S. Mitchell, T. F. Segawa, R. Hauert, C. Drouilly, D. Curulla-Ferré and J. Pérez-Ramírez, Angew. Chem., Int. Ed., 2016, 55, 6261–6265.
16. A. Bavykina, I. Yarulina, A. J. Al Abdulghani, L. Gevers, M. N. Hedhili, X. Miao, A. R. Galilea, A. Pustovarenko, A. Dikhtiarenko, A. Cadiau, A. Aguilar-Tapia, J. L. Hazemann, S. M. Kozlov, S. Oud-Chikh, L. Cavallo and J. Gascon, ACS Catal., 2019, 9, 6910–6918.
17. S. Kattel, W. Yu, X. Yang, B. Yan, Y. Huang, W. Wan, P. Liu and J. G. Chen, Angew. Chem., Int. Ed., 2016, 55, 7968–7973.
18. M. R. Gogate and R. J. Davis, Catal. Commun., 2010, 11, 901–906.
19. X. Jiang, X. Nie, X. Guo, C. Song and J. G. Chen, Chem. Rev., 2020, 120, 7984–8034.
20. T. Lunkenbein, J. Schumann, M. Behrens, R. Schlögl and M. G. Willinger, Angew. Chem., Int. Ed., 2015, 54, 4544–4548.
21. Y. Wang, S. Kattel, W. Gao, K. Li, P. Liu, J. G. Chen and H. Wang, Nat. Commun., 2019, 10, 1166.
22. M. Zabilskiy, V. L. Sushkevich, D. Palagin, M. A. Newton, F. Krumeich and J. A. van Bokhoven, Nat. Commun., 2020, 11, 2409.
23. S. Kattel, P. J. Ramírez, J. G. Chen, J. A. Rodriguez and P. Liu, Science, 2017, 355, 1296–1299.
24. N. Scotti, F. Bossola, F. Zaccheria and N. Ravasio, Catalysts, 2020, 10, 168.
25. K. Larmier, W.-C. C. Liao, S. Tada, E. Lam, R. Verel, A. Bansode, A. Urakawa, A. Comas-Vives and C. Copéret, Angew. Chem., Int. Ed., 2017, 56, 2318–2323.
26. Q.-L. Tang, Q.-J. Hong and Z.-P. Liu, J. Catal., 2009, 263, 114–122.
27. L. C. Grabow and M. Mavrikakis, ACS Catal., 2011, 1, 365–384.
28. S. Kattel, B. Yan, Y. Yang, J. G. Chen and P. Liu, J. Am. Chem. Soc., 2016, 138, 12440–12450.
29. T. Witoon, J. Chalorngtham, P. Dumrongbunditkul, M. Chareonpanich and J. Limtrakul, Chem. Eng. J., 2016, 293, 327–336.
30. Y. Nitta, O. Suwata, Y. Ikeda, Y. Okamoto and T. Imanaka, Catal. Lett., 1994, 26, 345–354.
31. D. Gasser and A. Baiker, Appl. Catal., 1989, 48, 279–294.
32. J. Weigel, R. A. Koeppel, A. Baiker and A. Wokaun, Langmuir, 1996, 12, 5319–5329.
33. I. Abbas, H. Kim, C. H. Shin, S. Yoon and K. D. Jung, Appl. Catal., B, 2019, 258, 117971.
34. A. Arandia, J. Yim, H. Warraich, E. Leppäkangas, R. Bes, A. Lempelto, L. Gell, H. Jiang, K. Meinander, T. Viinikainen, S. Huotari, K. Honkala and R. L. Puurunen, Appl. Catal., B, 2023, 321, 122046.
35. J. Sehested, J. Catal., 2019, 371, 368–375.
36. J. Nakamura, I. Nakamura, T. Uchijima, T. Watanabe and T. Fujitani, Stud. Surf. Sci. Catal., 1996, 101 B, 1389–1399.
37. S. Kattel, P. J. Ramírez, J. G. Chen, J. A. Rodriguez and P. Liu, Science, 2017, 357, eaan8210.
38. J. Nakamura, Y. Choi and T. Fujitani, Top. Catal., 2003, 22, 277–285.
39. J. Nakamura, T. Fujitani, S. Kuld, S. Helveg, I. Chorkendorff and J. Sehested, Science, 2017, 357, eaan8074.
40. N. Y. Topsøe and H. Topsøe, Top. Catal., 1999, 8, 267–270.
41. P. Amann, B. Klötzer, D. Degerman, N. Köpfle, T. Götsch, P. Lömker, C. Rameshan, K. Ploner, D. Bikaljevic, H.-Y. Wang, M. Soldemo, M. Shipilin, C. M. Goodwin, J. Gladh, J. H. Stenlid, M. Börner, C. Schlueter and A. Nilsson, Science, 2022, 376, 603–608.
42. E. Frei, A. Gaur, H. Lichtenberg, L. Zwiener, M. Scherzer, F. Girgsdies, T. Lunkenbein and R. Schlögl, ChemCatChem, 2020, 12, 4029–4033.
43. D. Kopač, B. Likozar and M. Huš, Appl. Surf. Sci., 2019, 497, 143783.
44. S. Polierer, J. Jelic, S. Pitter and F. Studt, J. Phys. Chem. C, 2019, 123, 26904–26911.
45. A. Cao, Z. Wang, H. Li, A. O. Elnabawy and J. K. Nørskov, J. Catal., 2021, 400, 325–331.
46. M. Kauppinen, A. Posada-Borbón and H. Grönbeck, J. Phys. Chem. C, 2022, 126, 15235–15246.
47. L. Gell, A. Lempelto, T. Kiljunen and K. Honkala, J. Chem. Phys., 2021, 154, 214707.
48. M. M. Kauppinen, M. M. Melander, A. S. Bazhenov and K. Honkala, ACS Catal., 2018, 8, 11633–11647.
49. B. C. Dharmalingam, A. V. Koushik, M. Mureddu, L. Atzori, S. Lai, A. Pettinau, N. S. Kaisare, P. Aghalayam and J. J. Varghese, Appl. Catal., B, 2023, 332, 122743.
50. X. Liu, J. Luo, H. Wang, L. Huang, S. Wang, S. Li, Z. Sun, F. Sun, Z. Jiang, S. Wei, W. Li and J. Lu, Angew. Chem., 2022, 61, e202202330.
51. E. L. Fornero, A. L. Bonivardi and M. A. Baltanás, J. Catal., 2015, 330, 302–310.
52. J. M. Campbell and C. T. Campbell, Surf. Sci., 1991, 259, 1–17.
53. S. Sakong and A. Groß, Surf. Sci., 2003, 525, 107–118.
54. K. D. Jung and A. T. Bell, J. Catal., 2000, 193, 207–223.
55. M. D. Rhodes, K. A. Pokrovski and A. T. Bell, J. Catal., 2005, 233, 210–220.
56. R. Prins, Chem. Rev., 2012, 112, 2714–2738.
57. H. Y. T. Chen, S. Tosoni and G. Pacchioni, ACS Catal., 2015, 5, 5486–5495.
58. M. M. Bettahar, Catal. Rev.: Sci. Eng., 2022, 64, 87–125.
59. J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149.
60. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
61. J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola, H. A. Hansen, H. H. Kristoffersen, M. Kuisma, A. H. Larsen, L. Lehtovaara, M. Ljungberg, O. Lopez-Acevedo, P. G. Moses, J. Ojanen, T. Olsen, V. Petzold, N. A. Romero, J. Stausholm-Møller, M. Strange, G. A. Tritsaris, M. Vanin, M. Walter, B. Hammer, H. Häkkinen, G. K. H. Madsen, R. M. Nieminen, J. K. Nørskov, M. Puska, T. T. Rantala, J. Schiøtz, K. S. Thygesen and K. W. Jacobsen, J. Phys.: Condens. Matter, 2010, 22, 253202.
62. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
63. V. Korpelin, M. M. Melander and K. Honkala, J. Phys. Chem. C, 2022, 126, 933–945.
64. A. R. Puigdollers, F. Illas and G. Pacchioni, J. Phys. Chem. C, 2016, 120, 17604–17612.
65. J.-H. Lan, L. Wang, S. Li, L.-Y. Yuan, Y.-X. Feng, W. Sun, Y.-L. Zhao, Z.-F. Chai and W.-Q. Shi, J. Appl. Phys., 2013, 113, 183514.
66. H. Koga, A. Hayashi, Y. Ato, K. Tada, S. Hosokawa, T. Tanaka and M. Okumura, Appl. Surf. Sci., 2020, 508, 145252.
67. O. A. Syzgantseva, M. Calatayud and C. Minot, J. Phys. Chem. C, 2012, 116, 6636–6644.
68. A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002.
69. E. Bitzek, P. Koskinen, F. Gähler, M. Moseler and P. Gumbsch, Phys. Rev. Lett., 2006, 97, 170201.
70. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
71. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985.
72. T. Frederiksen, M. Paulsson, M. Brandbyge and A.-P. Jauho, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 205413.
73. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990.
74. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
75. M. Rühle, Adv. Mater., 1997, 9, 195–217.
76. K. T. Jung and A. T. Bell, Catal. Lett., 2002, 80, 63–68.
77. J. S. Faulkner, Y. Wang and G. M. Stocks, Phys. Rev. Lett., 1998, 81, 1905–1908.
78. S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101–110.
79. S. Kozuch, ACS Catal., 2015, 5, 5242–5255.
80. F. Studt, M. Behrens, E. L. Kunkes, N. Thomas, S. Zander, A. Tarasov, J. Schumann, E. Frei, J. B. Varley, F. Abild-Pedersen, J. K. Nørskov and R. Schlögl, ChemCatChem, 2015, 7, 1105–1111.
81. D. Garay-Ruiz and C. Bo, ACS Catal., 2020, 10, 12627–12635.
82. H.-J. Chun, V. Apaja, A. Clayborne, K. Honkala and J. Greeley, ACS Catal., 2017, 7, 3869–3882.
83. D. Garay-Ruiz, gTOFfee, https://gitlab.com/dgarayr/gtoffee, (Feb. 2022).
84. A. Posada-Borbón, B. Hagman, A. Schaefer, C. Zhang, M. Shipilin, A. Hellman, J. Gustafson and H. Grönbeck, Surf. Sci., 2018, 675, 64–69.
85. B. Hagman, A. Posada-Borbón, A. Schaefer, M. Shipilin, C. Zhang, L. R. Merte, A. Hellman, E. Lundgren, H. Grönbeck and J. Gustafson, J. Am. Chem. Soc., 2018, 140, 12974–12979.
86. B. Eren, R. S. Weatherup, N. Liakakos, G. A. Somorjai and M. Salmeron, J. Am. Chem. Soc., 2016, 138, 8207–8211.

---

Footnote

† Electronic supplementary information (ESI) available: See ESI for the structures and energies of all adsorbed intermediates, potential energy diagrams, and details of the ESM analysis. See DOI: https://doi.org/10.1039/d3cy00549f

---