Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A computational study of CO2 hydrogenation on single atoms of Pt, Pd, Ni and Rh on In2O3(111)†
Francesco
Cannizzaro
 ,
Sjoerd
Kurstjens
,
Tom
van den Berg
,
Emiel J. M.
Hensen
,
Sjoerd
Kurstjens
,
Tom
van den Berg
,
Emiel J. M.
Hensen
 * and
Ivo A. W.
Filot
* and
Ivo A. W.
Filot
 *
*
Laboratory of Inorganic Materials and Catalysis, Department of Chemical Engineering and Chemistry, Eindhoven University of Technology, 5600 MB Eindhoven, The Netherlands. E-mail: i.a.w.filot@tue.nl
First published on 25th July 2023
Abstract
Metal promoted indium oxide (In2O3) catalysts are promising materials for CO2 hydrogenation to products such as methanol and carbon monoxide. The influence of the dispersion of the promoting metal on the methanol selectivity of In2O3 catalysts is a matter of debate, which centers around the role of atomically dispersed single metal atoms vs. metal clusters as catalysts for methanol formation. In this study, we used density functional theory calculations to compare the role of single atoms (SAs) of Ni, Pd, Pt and Rh placed on the In2O3(111) surface to study CO2 hydrogenation to CO and methanol. Direct and hydrogen-assisted CO2 dissociation pathways leading to CO as well as methanol formation via either formate or CO intermediates are explicitly considered. Microkinetic simulations show that all SA models mainly catalyze CO formation via a redox pathway involving oxygen vacancies where adsorbed CO2 dissociates followed by CO desorption and water formation. The higher barriers for hydrogenation of formate intermediates compared to the overall barrier for the rWGS reaction explain the negligible CH3OH selectivity.
Introduction
The reduction of CO2 emissions has become a crucial technological challenge because of the negative impact on the climate.1–3 To address this challenge, the conversion of CO2 captured from combustion processes and, in the future, directly from the air into liquid fuels and chemicals presents a viable solution, thereby reducing emissions and closing the carbon cycle. One of the most promising pathways for obtaining valuable products from CO2 is via its hydrogenation, provided that the required hydrogen is obtained from renewable resources.4–6 Not only does the large-scale hydrogenation of CO2 into fuels offer an opportunity to decrease our reliance on fossil fuels for energy, this technology can also be leveraged to obtain chemical intermediates.7–10 In this context, methanol is particularly attractive, because it can be used as a fuel or chemical building block.11–13Currently, large-scale methanol production is achieved by converting synthesis gas (CO/CO2/H2) over a Cu/ZnO/Al2O3 catalyst at temperatures of 473–573 K and pressures of 50–100 bar.14 Challenges arise however when CO2 is hydrogenated instead of CO. The Cu-based catalyst shows significant activity for the reverse water-gas-shift reaction (rWGS), leading to the formation of unwanted CO.15 Moreover, the catalyst suffers from sintering, resulting in slow deactivation.16,17 Many efforts have been made to identify new catalyst formulations with improved performance for the hydrogenation of CO2 to CH3OH.18 Recently, indium oxide (In2O3) has emerged as a promising catalyst for CO2 hydrogenation to methanol.19,20 Several density functional theory (DFT) studies emphasize the role of oxygen vacancies in the mechanism of CO2 hydrogenation to methanol on In2O3.19,21–25 Although such catalysts enable high selectivity to methanol by suppressing the competitive rWGS reaction, CO2 conversion is limited by the intrinsically low activity in H2 activation. To improve this, the use of metal promoters has been investigated. Recently, we reported by microkinetic modelling that small Ni clusters on In2O3 mainly catalyse methanol formation, whereas single atoms of Ni either doped in or adsorbed on In2O3 mainly catalyse CO.26,27 In a recent study, Pinheiro Araújo et al. reported that, atomically dispersed metal atoms (Pd, Pt, Rh, Ni, Co, Au, Ir) on the In2O3 surface promote hydrogen activation and methanol production while hindering CO formation.28 Frei et al. suggested by DFT calculations that single Ni atoms on In2O3 could catalyse the rWGS reaction but not methanol synthesis.29 The same authors proposed that single atoms of Pd doped in In2O3 can stabilize Pd clusters on the In2O3 surface, which can enhance H2 activation and, therefore, CH3OH productivity.30 Han et al. suggested that single atom (SA) of Pt doped in In2O3 would result in high methanol selectivity, whereas Pt nanoparticles on In2O3 would improve the rWGS reaction.31 Sun et al. showed by DFT calculations that the energetically most favourable pathway for methanol synthesis on a Pt4/In2O3 model occurs via hydrogenation of a CO intermediate.32 Wang et al. reported that highly dispersed Rh phases on In2O3 can enhance dissociative H2 adsorption and oxygen vacancy formation.33 Dostagir et al. found that Rh doped into In2O3 catalyzes CO2 hydrogenation to formate species.34 Furthermore, earlier DFT works pointed out that SAs on the In2O3 surface do not catalyze the formation of CH4.28–30,35,36 In nearly all these studies, the formation of atomically dispersed metal atoms was effective in shifting the selectivity towards the desired product. Although the role of supported clusters in metal-promoted In2O3 catalysts has been clarified for many cases,32,37 generic understanding about the role of SAs is still lacking. Gaining a comprehensive understanding of the reaction pathways involved in the hydrogenation of CO2 to synthesize methanol requires a thorough investigation of the role of SAs in In2O3.
In the present work, we study the reaction mechanism of CO2 hydrogenation to CH3OH and CO on SA-In2O3 model catalysts. Considering relevant literature, we have identified Ni, Pd, Pt, and Rh as potential promoters.28–31,34 The reaction pathways explored in our DFT studies include a direct route for CO2 hydrogenation to methanol (formate pathway), a pathway to methanol via CO hydrogenation and the competing rWGS reaction (both direct and hydrogen-assisted). We performed DFT calculations to determine the reaction energetics for all elementary reaction steps, which serve as input for microkinetic modelling. Microkinetic simulations show that the SA-In2O3 model surfaces produce CO as the main product with a very low methanol selectivity. The observed outcome can be primarily attributed to the presence of oxygen vacancies, which enable the adsorption of CO2 and prompt activation towards facile direct C–O bond scission. In contrast, the formation of methanol is hampered by to the high activation energies associated with the hydrogenation of formate intermediates, resulting in relatively low rates for the preferred methanol product.
Computational methods
Density functional theory calculations
The calculations reported in this work were done in the same manner as reported before.26,27 All DFT calculations were conducted using the projector augmented wave (PAW) method38 and the Perdew–Burke–Ernzerhof (PBE)39 exchange-correlation functional as implemented in the Vienna ab initio simulation package (VASP) code.40,41 The valence 5s and 5p states of In were treated explicitly as valence states within the scalar-relativistic PAW approach. By using a plane-wave basis set with a cut-off energy of 400 eV solutions to the Kohn-Sham equations were calculated. All calculations were spin-polarized. The Brillouin zone was sampled using a 3 × 3 × 1 Monkhorst-Pack grid. By using Gaussian smearing with a smearing width (σ) of 0.1 eV electron smearing was employed. The stoichiometric In2O3(111) surface was modelled as a 2D slab with periodic boundary conditions. To avoid the spurious interaction with neighbouring super cells, a 15.0 Å vacuum region was introduced in the c-direction. It was verified that the electron density approached zero at the edges of the periodic super cell in the c-direction. The bottom two layers were frozen, while the top two layers were allowed to perturb in all calculations. The supercell has dimensions of 14.57 Å × 14.57 Å × 26.01 Å. The In2O3(111) slab consisted of 96 O atoms and 64 In atoms, distributed in four atomic layers on top of which the SA species were placed.The stable states of the elementary reaction steps pertaining to CO2 hydrogenation were calculated using the conjugate-gradient algorithm. Eqn (1) defines the adsorption energies of adsorbates (ΔEadsX):
| ΔEadsX = EX+In2O3(111) − EIn2O3(111) − EX. | (1) |
The influence of oxygen vacancies on the reaction energetics was investigated by removing oxygen atoms from the In2O3(111) lattice. Since oxygen vacancies in chemical reactors are formed via surface reduction by H2, the energy required to remove an oxygen from In2O3 (ΔEOv) was calculated using H2O as reference, according to the following equation
| ΔEOv = Edefective slab − Estoichiometric slab + EH2O − EH2, | (2) |
Transition states were determined using the climbing-image nudged elastic band (CI-NEB) method.42 A frequency analysis was performed to all states to verify that that stable states have no imaginary frequencies and transition states have a single imaginary frequency aligned with the reaction coordinate.43 The Hessian matrix in this frequency analysis was constructed using a finite difference approach with a step size of 0.015 Å for displacement of individual atoms along each Cartesian coordinate. The normal mode vibrations found with these calculations were used to evaluate the zero-point energy (ZPE) correction and the vibrational partition functions.
Partial density of state (pDOS) analysis are conducted to analyze the electronic structure of each SA-In2O3 model using the Lobster package.44,45 The atomic charges were calculated using the Bader charge method.46
Microkinetic simulations
Microkinetic simulations were carried out based on the DFT-calculated activation and reaction energies. The kinetic network was modelled using a set of ordinary differential equations involving rate constants, surface coverages and partial pressures of gas-phase species. To integrate the differential equations with respect to time the linear multistep backwards differential formula method was employed with a relative and absolute tolerance of 10−8.47–49The net rate of the adsorption process of a gas-phase species i was calculated as:
| ri = ki,adsθ*Pi − ki,desθi | (3) |
To model adsorption processes, we assumed that the adsorbate loses one translational degree of freedom in the transition state with respect to the initial state. As a result of this, the rate of adsorption derived from transition state theory is:
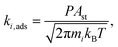 | (4) |
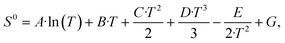 | (5) |
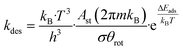 | (6) |
The rate constant (k) of an elementary reaction step is given by the Eyring equation:
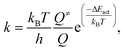 | (7) |
We employed the concepts of the degree of rate control (DRC) developed by Kozuch and Shaik52,53 and popularized by Campbell54 as well as the degree of selectivity control (DSC)54–56 to identify the steps that control the CO2 consumption rate and the product distribution.
Herein, the degree of rate control coefficient is defined as
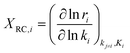 | (8) |
Results and discussion
Structure of SA-In2O3 models
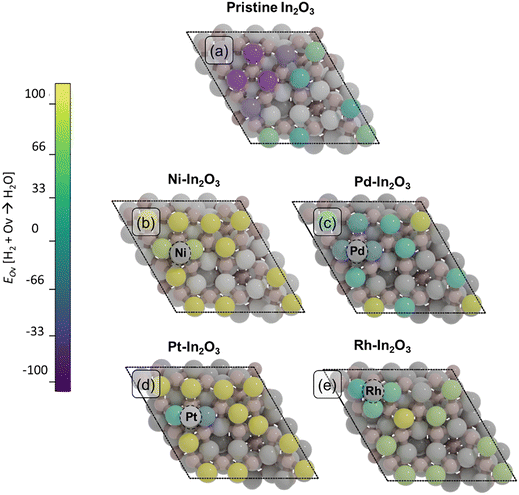
To study the catalytic properties of single atoms (SAs) of Ni, Pd, Pt and Rh, we constructed four models in which the SA was placed on the In2O3(111) surface, which is the most stable termination of In2O3.57 We first determined the most stable location of the SA on the In2O3(111) surface. For this, we calculated the adsorption energies of the SA in different positions (Table S1†). The most stable adsorption sites are depicted in Fig. 1. Single Ni, Pd and Pt atoms preferentially adsorb in bridge sites between two oxygen atoms, in agreement with previous theoretical studies (Fig. 1a–c).30,58 The Rh SA prefers to coordinate to three oxygens (Fig. 1d). A partial density of states (pDOS) analysis of the SA-In2O3 models shows that the bonding is mainly through interactions of the SA metal d orbitals and O 2p orbitals (Fig. S2†). The supported Ni, Pd, Pt and Rh SAs possess positive charges of +0.56, +0.35, +0.30 and +1.03, respectively. The energy needed to remove the SA atom to infinite distance from the surface is reported in Table S1.† Ni is most strongly bound to the surface (Eads = −512 kJ mol−1), followed by Pt (Eads = −481 kJ mol−1), Rh (Eads = −425 kJ mol−1) and Pd (Eads = −339 kJ mol−1). To understand the mobility of SAs on the In2O3(111) surface, we determined the barrier for migration between stable adsorption sites (Table S2†). Surface migration of SAs is associated with relatively high barriers for Ni, Ph and Rh (Ea > 100 kJ mol−1), whereas much lower barriers are found for Pd (Ea < 50 kJ mol−1). This is in line with the weaker binding energy of Pd with the In2O3(111) surface compared to Pt, Ni and Rh.Oxygen vacancy formation
Oxygen vacancies (Ov) in the In2O3 surface have been identified as the active sites for CO2 hydrogenation.19,21,22 Here, we determine the effect of surface SAs on the formation of such vacancies. To this purpose, we calculate the energy required to remove an oxygen atom on each SA-In2O3 model and compare the results with data for bare In2O3 (Fig. 2, Table S3 and Fig. S3†). Since oxygen vacancies during CO2 hydrogenation are formed via surface reduction by H2, the computed energies are referenced to gaseous H2O. For the bare In2O3(111) surface (Fig. 2a), the energy needed to remove an oxygen atom (EOv) ranges between −61 and 8 kJ mol−1, in line with previous theoretical calculations.59 The presence of a Ni atom on In2O3 (Fig. 2b) significantly increases the oxygen vacancy formation energy, resulting in EOv values between 139 and 190 kJ mol−1. The effect of a Pd SA is much less pronounced, resulting in values for EOv comparable to those for the bare In2O3(111) surface, namely between −77 and 80 kJ mol−1. For the Pt-In2O3 case (Fig. 2d), EOv assumes higher values than for Pd ranging between −35 and 217 kJ mol−1. The Rh-In2O3 model (Fig. 2e) has intermediate values for EOv ranging between 39 and 170 kJ mol−1. Overall, the removal of an oxygen atom on the bare In2O3(111) surface is less energetically demanding in comparison to SA-In2O3 models, except for Pd, where the oxygen formation energy is very similar.Further inspection of Fig. 2b–d shows that, for each of the SA-promoted surfaces, formation of vacancies is easier for lattice oxygen atoms directly bonding to the SA than for O atoms bonding only to In atoms. Comparing the H2O-referenced EOv values for O binding to the SA, we computed as lowest lowest EOv values of 141, −71, −35 and 39 kJ mol−1 for Ni-, Pd-, Pd- and Rh-In2O3, respectivley (Table S4†). On bare In2O3, the lowest EOv value is −61 kJ mol−1. The relatively more endothermic EOv values for Ni–, Pt– and Rh–In2O3 are in line with the strong adsorption energy of the SA on the surface (Table S1†). Because Pd binds to the surface less strongly, EOv is relatively speaking more exothermic than for the other SAs. To understand whether oxygen vacancies will be formed on these models under reaction conditions and what role they play in CO2 hydrogenation, we study the mechanism of oxygen vacancy formation via surface reduction by H2 as well as the CO2 hydrogenation reaction pathways by means of microkinetic simulations (vide infra).
Reaction mechanism
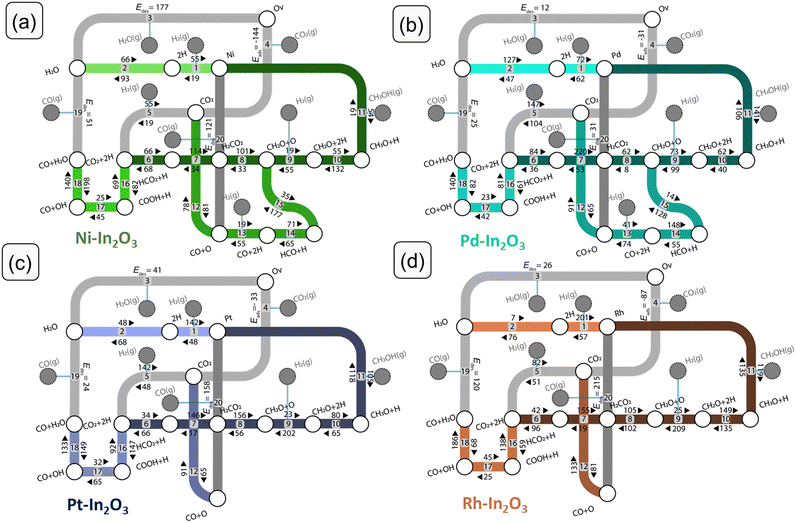
We performed DFT calculations to determine the reaction mechanism of CO2 hydrogenation to methanol (CH3OH), carbon monoxide (CO) and water (H2O). Hydrogenation of CO2 to methane (CH4) was not included, because methane formation was not observed in experiments with low-loaded metal-promoted In2O3 catalysts.28,32,34 Furthermore, earlier DFT works pointed out that SAs on the In2O3 surface do not catalyse the formation of CH4.28–30,35 The mechanism is depicted in Fig. 3 in the form of a reaction network diagram. Following previous computational studies, we investigated the pathways for (i) the formation of oxygen vacancies through H2O formation, (ii) the formation of CH3OH via formate, and (iii) the reverse water-gas shift (rWGS) pathway leading to CO2.32,57,60–62 The latter rWGS reaction can take place via either direct C–O bond cleavage in adsorbed CO or an H-assisted pathway involving COOH intermediate. In addition to methanol formation via formate, we considered the direct hydrogenation pathway of CO intermediate into CH3OH. We included a comparison with the DFT results of Frei et al. on In2O3(111).57Fig. 4 depicts the potential energy diagrams (PED) for each of these routes.Next, we discuss the elementary reaction steps on each SA-In2O3 surface and highlight differences in activation energies and transition-state structures. The activation barriers are given with respect to the most stable adsorbed state for each intermediate.
The geometries corresponding to initial, transition and final states can be found in the ESI† (Tables S6–S9). The computed forward and backward barriers for all elementary reaction steps are given in Tables S10–S13.†
Oxygen vacancy formation
We first discuss the formation of oxygen vacancies (steps 1–3). On all SA-In2O3 surfaces, the oxygen corresponding to the lowest EOv value is removed. For Ni-, Pd and Pt-In2O3, this corresponds to forming an oxygen vacancy in position Ov3 (Table S2 and Fig. S3†). For Rh–In2O3 formation of an oxygen vacancy in position Ov2 is preferred. On all SA-In2O3 models, H2 is heterolytically dissociated into SA–H and O–H moieties (step 1). Hydrogen activation is facile on Ni-In2O3 (Eact,Ni = 19 kJ mol−1) and more difficult on Pd-, Pt- and Rh-In2O3 (Eact,Pd = 62 kJ mol−1, Eact,Pt = 48 kJ mol−1 and Eact,Rh = 57 kJ mol−1). Dissociative adsorption of H2 is more exothermic on Pt- and Rh-In2O3 (ΔEr,Pt = −94 kJ mol−1, ΔEr,Rh = −144 kJ mol−1) than on Ni- and Pd-In2O3 (ΔEr,Ni = −36 kJ mol−1, ΔEr,Pd = −10 kJ mol−1). Oxygen vacancy formation proceeds via proton migration from a SA–H to an O–H moiety, resulting in adsorbed H2O (step 2). This step has similar barriers for Ni-In2O3, Pt-In2O3 and Rh-In2O3 (Eact,Ni = 93 kJ mol−1, Eact,Pt = 68 kJ mol−1 and Eact,Rh = 76 kJ mol−1). On these models, this step is endothermic by 27, 69, and 27 kJ mol−1, respectively. The lowest barrier is obtained for Pd-In2O3 (Eact = 47 kJ mol−1; ΔEr = 80 kJ mol−1). H2O desorption completes the oxygen vacancy formation pathway (step 3). The highest desorption energy is computed on Ni-In2O3 (ΔEdes,Ni = 177 kJ mol−1), while this step is considerably easier on the other SA models (ΔEdes,Pd = 12 kJ mol−1, ΔEdes,Pt = 41 kJ mol−1 and ΔEdes,Rh = 26 kJ mol−1). The overall reaction energy for oxygen vacancy formation with respect to gas-phase H2 amounts to +150 kJ mol−1 (Ni), −72 kJ mol−1 (Pd), −41 kJ mol−1 (Pt) and +16 kJ mol−1 (Rh). The overall barriers with respect to gas-phase H2 are 150, 72, 48 and 57 kJ mol−1 for Ni-, Pd-, Pt-, and Rh-In2O3, respectively. Notably, the higher overall barrier for Ni is in line with the stronger Ni–O bond as compared to the more noble metals considered here (Table S14†). With respect to the same reference, the unpromoted In2O3(111) surface has an overall barrier for oxygen vacancy formation of 67 kJ mol−1.59,63 The adsorption configurations of the SA on the In2O3(111) surface after formation of an oxygen vacancy are reported in Fig. S4.†Methanol synthesis via formate
For CO2 hydrogenation, we first discuss the most stable adsorption configuration for CO2 on the SA-In2O3 models. We have explored different adsorption configurations of CO2 on the SA-In2O3 models. The results are reported in Table S5 and Fig. S5,† respectively. On Ni-, Pd- and Pt-In2O3 CO2 adsorbs near the SA with one of its O atoms occupying the oxygen vacancy and the C atom bonding to the SA. On Rh-In2O3, the C atom coordinates directly to a lattice O instead of the SA. The adsorption energies of CO2 are −144, −31, −33 and −87 kJ mol−1 for Ni-, Pd-, Pt- and Rh-In2O3, respectively. Thus, the interaction of CO2 with Ni and Rh is relatively strong compared to Pd and Pt. This is in line with trends found in a previous computational study for CO2 adsorption on low-index surfaces of transition metals.64Dissociative adsorption of H2 (step 5) is heterolytic on all SA-In2O3 models and leads to O–H and SA–H moieties adjacent to adsorbed CO2. Homolytic dissociation on top of the metal atom was also investigated but resulted in the formation of a SA–H and a O–H moiety. This state constitutes the initial configuration for CO2 hydrogenation. Dissociative adsorption is facile on Ni-In2O3 (Eact,Ni = 19 kJ mol−1), whereas higher barriers were computed for Pd-, Pt- and Rh-In2O3 (Eact,Pd = 104 kJ mol−1, Eact,Pt = 48 kJ mol−1, Eact,Rh = 51 kJ mol−1). Next, methanol can be obtained via a mechanism involving a formate intermediate (steps 6–11 in Fig. 3). The PEDs of the formate pathway for the SA-In2O3 models are reported in Fig. 4a. The C atom in CO2 is hydrogenated by a SA–H to HCO2 (step 6). The forward activation energies for Ni-, Pd- Pt, and Rh-In2O3 are respectively 66, 84, 34 and 42 kJ mol−1. This reaction is endothermic for Pd-, Pt- and Rh-In2O3 with reaction energies of 48, 32 and 54 kJ mol−1 and slightly exothermic for Ni-In2O3 (ΔEr = −2 kJ mol−1). The C atom in HCO2 is protonated again via migration of a O–H to a SA–H moiety, resulting in H2CO2 (step 7). Forming the H2CO2 intermediate from HCO2 is endothermic on all SA-In2O3 models and involves relatively high activation energies of 114, 220, 146, and 155 kJ mol−1 for Ni-, Pd- Pt- and Rh-In2O3, respectively. Notably, higher barriers are associated with migration from O–H to SA–H compared to direct hydrogenation of the C atom by a SA–A moiety. Furthermore, step 7 is the most difficult one in the formate pathway for all SAs. Direct migration of a O–H to hydrogenate the C atom in HCO2 was not considered, as it will lead to even higher barriers. Next, scission of one of the C–O bonds in the H2CO2 intermediate results in CH2O and O (step 8). This step leads to healing of the oxygen vacancy. This step is endothermic for Ni–, and Pd– and Pt-In2O3 surfaces with reaction energies of 68, 54 and 100 kJ mol−1, respectively, whereas it is slightly exothermic for Rh-In2O3 (ΔEr = −3 kJ mol−1). Furthermore, lower barriers are found for Pd– (Eact = 62 kJ mol−1) than for Ni– (Eact = 101 kJ mol−1), Pt– (Eact = 156 kJ mol−1) and Rh-In2O3 (Eact = 105 kJ mol−1). Another pathway preceding C–O bond scission involves hydrogenation of HCO2 to HCO2H. We could not find a TS for this reaction because of the very weak adsorption of HCO2H. A similar issue was encountered in investigating the hydrogenation of H2CO2 to H2CO2H. On all SA-In2O3 models, dissociative adsorption of another H2 leads to a SA–H and O–H moieties adsorbed next to CH2O (step 9). The CH2O moiety resulting from H2CO2 dissociation is then hydrogenated to CH3O by proton migration from a SA–H moiety (step 10). This step has an activation energy of 55, 62, 80 and 149 kJ mol−1 for Ni-, Pd- Pt, and Rh-In2O3, respectively. Furthermore, it is endothermic for Pd-, Pt and Rh-In2O3 (Eact,Pd = 18 kJ mol−1, Eact,Pt = 15 kJ mol−1, Eact,Rh = 14 kJ mol−1), exothermic for Ni-In2O3 (Eact,Ni = −77 kJ mol−1). Finally, CH3OH is obtained in a single concerted step from CH3O via proton migration from the OH (step 11). This elementary reaction step has activation energies of 61, 106, 118 and 135 kJ mol−1 for Ni-, Pd- Pt, and Rh-In2O3, respectively. Furthermore, it is moderately exothermic for Ni-, Pd- and Pt-In2O3 (ΔEr,Ni = −7 kJ mol−1, ΔEr,Pd = −35 kJ mol−1, ΔEr,Pt = −13 kJ mol−1), slightly endothermic for Rh-In2O3 (ΔEr,Rh = 16 kJ mol−1).
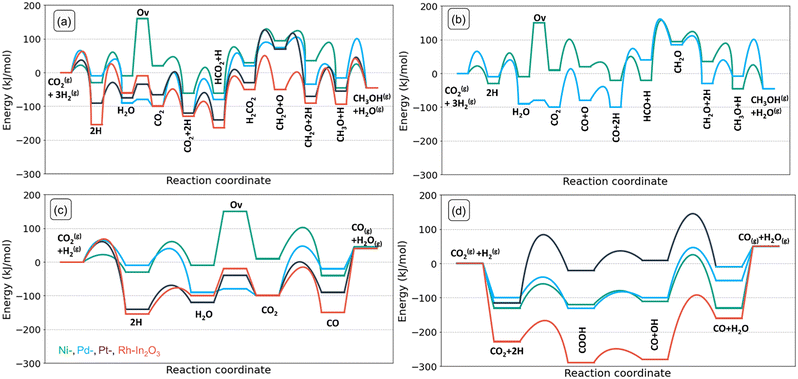 | ||
| Fig. 4 Potential energy diagrams of (a) formate pathway to CH3OH, (b) CO hydrogenation pathway to CH3OH and (c) redox pathway to CO and (d) carboxyl pathway to CO on different models. | ||
Frei et al. speculated based on potential energy diagrams that the most energetically favourable path to methanol involves three consecutive additions of hydrides and protons and features HCO2H and CH2(OH)2 as intermediates.57 However, as pointed out earlier, the very weak adsorption of HCO2H precludes this pathway on the SA-In2O3 models we investigated.
For Ni- and Pd-In2O3, H2 is heterolytically dissociated into a SA–H and an O–H moiety (step 13). Such mode of dissociative adsorption of H2 is more facile on Ni-In2O3 (Eact,Ni = 19 kJ mol−1) than on Pd-In2O3 (Eact,Pd = 41 kJ mol−1). Such state where CO is adsorbed next to a SA–H and a O–H moiety constitutes the initial state of the CO hydrogenation pathway. CO hydrogenation to HCO proceeds using the H adsorbed on the SA (step 14) with activation energies of 71 kJ mol−1 (Ni-In2O3) and 148 kJ mol−1 (Pd-In2O3). In line with this difference, the reaction is much more endothermic for Pd (ΔEr,Pd = 93 kJ mol−1) than for Ni (ΔEr,Ni = 6 kJ mol−1). Subsequently, HCO is hydrogenated to CH2O (step 15) with barriers of 177 kJ mol−1 (Ni-In2O3) and 128 kJ mol−1 (Pd-In2O3). We found that the preferential pathway involves migration of H from the OH moiety to the SA, followed by hydrogenation of HCO to CH2O. Direct migration of a OH to hydrogenate the C atom in HCO would face a higher barrier and was therefore not studied. This elementary step is endothermic for both SA-In2O3 models (ΔEr,Ni = 142, ΔEr,Pd = 114 kJ mol−1, respectively). The resulting CH2O intermediate also occurs in the formate pathway to methanol discussed above. Thus, further hydrogenation of CH2O to methanol will occur via steps 9 and 10.
CO formation via rWGS
On SA-In2O3 models, the formation of CO can occur either via direct C–O bond cleavage of CO2 (redox pathway, steps 4 and 20) or via a H-assisted pathway involving a COOH intermediate (carboxyl pathway, steps 16–19). In the redox pathway, after formation of H2O (steps 1–3) and CO2 adsorption (step 4) one of the C–O bonds in CO2 is cleaved (step 12). These steps have been previously discussed. The desorption of CO (step 20) closes the rWGS catalytic cycle. The highest barriers for CO desorption are found on Pt– (ΔEdes,Pt = 158 kJ mol−1) and Rh-In2O3 (ΔEdes,Rh = 215 kJ mol−1) whereas lower values are found on Ni– (ΔEdes,Ni = 121 kJ mol−1) and Pd-In2O3 (ΔEdes,Pd = 31 kJ mol−1). Concerning the unpromoted In2O3, Ye et al. reported that the process replenishing an oxygen vacancy by direct cleavage of the C–O bond in CO2 has a barrier of 134 kJ mol−1 on an In2O3(110) model surface.61The carboxyl pathway proceeds by protonation of adsorbed CO2 to form COOH by a SA–H moiety (step 16). The highest activation energies are computed for Ni-In2O3 (Eact = 82 kJ mol−1) and Pt-In2O3 (Eact = 147 kJ mol−1) followed by Pd-In2O3 (Eact = 61 kJ mol−1) and Rh-In2O3 (Eact = 59 kJ mol−1). Furthermore, this elementary step is endothermic for Ni- and Pt-In2O3 (ΔEr,Ni = 74 kJ mol−1, ΔEr,Pt = 55 kJ mol−1), whereas it is exothermic for Pd- and Rh-In2O3 (ΔEr,Pd = −20 kJ mol−1, Er,Rh = −78 kJ mol−1). Formation a COOH intermediate is associated with higher barriers compared to formation of HCOO, in line with an earlier study on In2O3.65 Next, COOH dissociates into CO and OH (step 17). This step features activation energies of 45, 42, 65, and 25 kJ mol−1 for Ni-, Pd-, Pt- and Rh-In2O3, respectively. Furthermore, it is endothermic for all SA-In2O3 surfaces (ΔEr,Ni = 17 kJ mol−1, ΔEr,Pd = 19 kJ mol−1, ΔEr,Pt = 33 kJ mol−1, and ΔEr,Rh = 20 kJ mol−1). Water is formed via proton transfer to the OH moiety obtained from COOH dissociation (step 18). This step features activation energies of 140, 140, 133 and 186 kJ mol−1 for Ni-, Pd-, Pt- and Rh-In2O3, respectively. Moreover, it is endothermic for Rh-, and Pd-In2O3 (ΔEr,Rh = 107 kJ mol−1, and ΔEr,Pd = 58 kJ mol−1), and exothermic for Ni– and Pt-In2O3 (ΔEr,Ni = −58 kJ mol−1, and ΔEr,Pt = −16 kJ mol−1). Notably, this step features the highest activation energy of the carboxyl pathway for all SA-In2O3. The elementary step of COOH dissociation on the bare In2O3(111) surface is associated with a relatively high barrier (146 kJ mol−1), similar to the ones found on our SA-In2O3 models. Desorption of CO (step 19) features a barrier of 51, 25, 24 and 120 kJ mol−1 for Ni-, Pd-, Pt- and Rh-In2O3, respectively, closing the carboxyl cycle.
Microkinetic simulations
The CO2 consumption rate and CH3OH selectivity as a function of temperature for each SA-In2O3 model are displayed in Fig. 5. The turnover frequencies (TOF) towards CH3OH and CO (TOFCH3OH and TOFCO, respectively) are reported in Fig. S6.† We also constructed a microkinetic model for unpromoted In2O3 based on the published DFT data of Frei et al.57Fig. 5a shows that the CO2 conversion rate decreases in the order Pd > Ni > Pt > Rh. Furthermore, none of the SA-In2O3 models show any appreciable methanol selectivity (Fig. 5b), which is due to the much lower TOFCH3OH in comparison to TOFCO (Fig. S6c and d†).
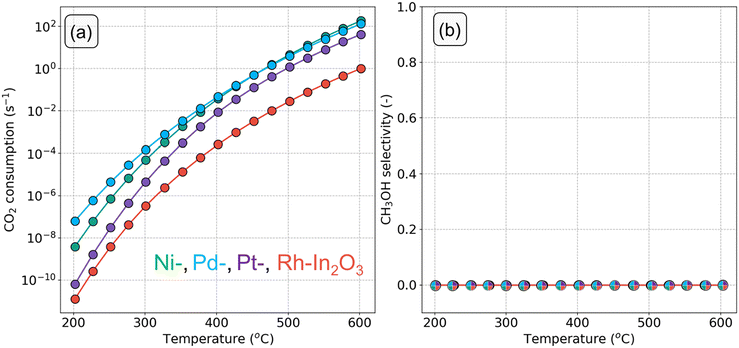 | ||
| Fig. 5 (a) CO2 consumption rate (s−1) and (b) CH3OH selectivity as a function of temperature on SA-In2O3 models (p = 50 bar, H2/CO2 ratio =5). | ||
Compared to bare In2O3, the adsorption of a SA on the In2O3(111) surface results in lower CO2 consumption rates (Fig. S6a†) and TOFCH3OH for T < 300 °C (Fig. S6c†). In the same range, the TOFCO decreases in the order Pd > Ni > bare In2O3 > Pt > Rh (Fig. S6d†).
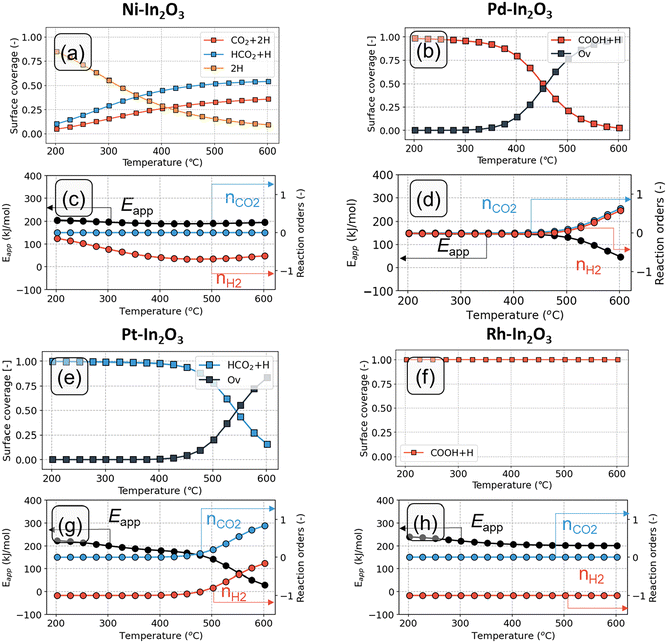
The analysis of the surface state, apparent activation energy and reaction orders as function of temperature is given in Fig. 6. The coverages in Fig. 6 should be interpreted as the fraction of time the system spends in a particular state (i.e., the time average). According to the ergodicity principle in statistical thermodynamics, this equals the fraction of active sites that is in a particular state (i.e., the ensemble average).
On the Ni-In2O3 surface (Fig. 6a), the dominant surface state at lower temperatures features two adsorbed H species (2H). The reason behind this can be understood from Fig. 3a. Activation of H2 and subsequent H2O formation (steps 1–2) are facile (Eact = 19 kJ mol−1 and Eact = 74 kJ mol−1, respectively), whereas water desorption (step 3) features a high barrier (ΔEdes = 177 kJ mol−1). The latter step is the most difficult one in the Ov formation pathway and limits the progress of the reaction. As water desorption is facilitated by a higher temperature, it leads to an increase in the number of oxygen vacancies and CO2 adsorption. Consequently, the coverage of the 2H state decreases and the coverage of intermediate states in the formate pathway to methanol (CO2 + 2H and HCO2 + H) increases. At T > 400 °C, the latter states become dominant. On the Ni-In2O3 model, hydrogenation of CO2 to HCO2 (step 6) has an activation energy of 66 kJ mol−1 and a reaction energy of −2 kJ mol−1. In contrast, subsequent hydrogenation to H2CO2 (step 7) has a considerably higher activation energy of 114 kJ mol−1 and is endothermic. As formation of H2CO2 is difficult and the previous two states are comparable in terms of energy, CO2 + 2H and HCO2 + H are the dominant states. At low temperature, the model predicts a reaction order of nearly zero in CO2 and H2 (Fig. 6c). Under these conditions, the reaction is limited by the rate of H2O removal, and an increase of the partial pressure of CO2 or H2 does not affect this process. Thus, the corresponding reaction orders in CO2 and H2 must be zero. At higher temperature, however, a negative reaction order in H2 is found. A higher partial pressure of H2 would lead to higher rates of H adsorption facilitating hydrogenation reactions. In turn, this pushes the reaction away from the CO product leading to a decrease in the overall rate. On the Ni-In2O3 model, the apparent activation energy (Eapp, Fig. 6c) has a constant value of at 175 kJ mol−1 between 200 °C and 400 °C. This value corresponds to the desorption energy of H2O. At higher temperature, a slight decrease in the Eapp is observed, indicating a change in the rate-limiting step. This aspect will be clarified with a DRC analysis (vide infra).
On the Pd-In2O3 model, the COOH + H is the dominant state at T < 450 °C (Fig. 6b). Fig. 3b shows that hydrogenation of CO2 to COOH (step 16) and its subsequent dissociation into CO and OH are facile (Eact = 61 kJ mol−1 and Eact = 42 kJ mol−1, respectively). However, the subsequent step of OH hydrogenation has a higher activation energy and is endothermic (Eact = 140 kJ mol−1 and ER = 58 kJ mol−1, respectively). This makes the conversion of the COOH + H state difficult. At high temperature (T > 450 °C), the barrier for OH hydrogenation (step 17) can be more easily overcome, resulting in formation of oxygen vacancies. As a result, the dominant state becomes the Pd-In2O3 surface with an oxygen vacancy (Ov). The model predicts a reaction order of zero in CO2 and H2 for T < 450 °C (Fig. 6d). As the dominant working state already corresponds to intermediates derived from H2 and CO2, a change in the partial pressure of these reactants does not impact the activity. For T > 450 °C, the reaction orders in CO2 and H2 are positive, indicating that hydrogenation reactions are controlling the reaction rate. The Eapp is approximately 150 kJ mol−1 at 200 °C and decreases with increasing temperature (Fig. 6d).
On the Pt-In2O3 model, the HCO2+H state is the dominant state for below 525 °C (Fig. 6e). Hydrogenation of CO2 to HCO2 (step 6 in Fig. 3c) is facile (Eact = 34 kJ mol−1), while the subsequent step of HCO2 hydrogenation to H2CO2 (step 7) is more difficult (Eact = 146 kJ mol−1, ER = +129 kJ mol−1). This hampers the conversion of the HCO2 + H state. At higher temperature, the surface coverage of the HCO2 + H state decreases in favor of oxygen vacancies (Ov). The Ov state becomes dominant for T > 525 °C. The reaction order in CO2 is zero at low temperature, because the surface is already covered with HCO2+H resulting from CO2 hydrogenation (Fig. 6g). At higher temperature (T > 475 °C), the reaction order in CO2 becomes positive indicating that CO2 activation reactions are controlling the rate. The reaction order in H2 is negative, as also found for Ni– and Pd-In2O3. The Eapp stays almost constant for temperature below 300 °C at 200 kJ mol−1 and decreases with increasing temperature (Fig. 6g).
Within the temperature range of 200 °C and 600 °C, the dominant state of Rh-In2O3 is the COOH+H state (Fig. 6f). The reason becomes apparent from inspection of Fig. 3d. Hydrogenation of CO2 to COOH and its further dissociation (step 16–17) are facile (Eact = 59 and Eact = 25 kJ mol−1, respectively). However, the subsequent step of OH hydrogenation is more difficult (Eact = 186 kJ mol−1) and hampers the conversion of the CO + OH state. With respect to the dominant COOH + H state, an overall barrier of 341 kJ mol−1 must be overcome to complete the H-assisted rWGS cycle (Fig. 4d). As a result, only for temperatures far above 600 °C, states other than COOH + H observed. The reaction order in CO2 is zero at low temperature, because the surface is already covered with COOH + H resulting from CO2 hydrogenation (Fig. 6h). The reaction order in H2 is negative, indicating that a higher partial pressure of H2 would push the reaction away from the dominant CO formation pathway. The apparent activation energy decreases from 260 kJ mol−1 to 220 kJ mol−1 between 200 and 400 °C (Fig. 6h).
Sensitivity analysis
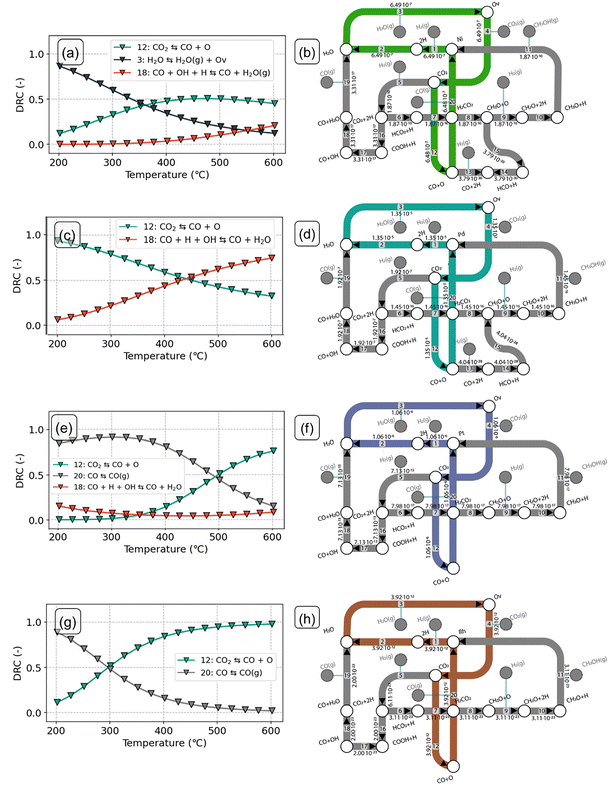
In this section, we analyse in more depth the steps that lead to CH3OH and CO during CO2 hydrogenation on the SA-promoted In2O3 models. We identify the elementary steps that control the overall CO2 consumption rate and the CH3OH selectivity and investigate how these steps change with reaction temperature. For this purpose, we conduct a sensitivity analysis based on the degree of rate control (DRC) analysis.54 At zero CO2 conversion, the sum of the DRC coefficients is conserved at unity.55The DRC analysis and reaction flux analysis for the Ni-In2O3 model are shown in Fig. 7a and b, respectively. At low temperature, the CO2 consumption rate is mostly controlled by water desorption (step 3) preceding oxygen vacancy formation (Fig. 7a). This result is in line with the dominant surface state being the 2H state, which precedes H2O formation (Fig. 6a). Furthermore, H2O desorption has the highest barrier in the oxygen vacancy formation pathway (ΔEdes = 177 kJ mol−1), making formation of an oxygen vacancy difficult. At higher temperature (T > 275 °C), water desorption results in oxygen vacancies and CO2 adsorption. As a result, the DRC coefficient of the H2O desorption step decreases, in favor of the CO2 dissociation step (step 12). At higher temperature, the latter becomes the main rate-limiting step. An increased rate of CO2 dissociation would result in a higher flux towards CO, benefiting the formation of this product. The dominant pathway (Fig. 7b) on the Ni-In2O3 model proceeds via formation of an oxygen vacancy followed by CO2 adsorption and direct dissociation. The carboxyl pathway to CO is not taken because OH removal (step 18) is associated with a higher barrier than direct CO2 dissociation (Eact = 140 kJ mol−1 and Eact = 81 kJ mol−1, respectively). Compared to the dominant pathway to CO, methanol formation pathways feature considerably lower molar fluxes. This is in keeping with our finding that Ni-In2O3 mainly produces CO. The formate pathway is not taken because the steps of H2CO hydrogenation to H2CO2 and its further dissociation into CH2O and O (steps 7–8) result in a combined reaction energy of +180 kJ mol−1. Hydrogenation of CO to methanol does not proceed because CH2O formation from HCO has a high activation energy and is endothermic (Eact = 177 kJ mol−1 and Er = 142 kJ mol−1, respectively).
For Pd-In2O3 (Fig. 7c), for T < 425 °C, the overall rate is mostly controlled by CO2 dissociation (step 12, Eact = 65 kJ mol−1). The dominant pathway on the Pd-In2O3 surface proceeds via formation of an oxygen vacancy and direct dissociation of CO2 (Fig. 7d). At higher temperature (T > 400 °C), a decrease in the DRC coefficient of step 12 is observed in favor of the step of OH removal in the carboxyl pathway (step 18, Eact = 140 kJ mol−1) which becomes the main rate limiting step. The change in rate limiting steps indicates a change in the dominant pathway. Indeed, for T > 425 C, the carboxyl pathway is the dominant pathway of CO formation (Fig. S7†). Furthermore, this is in line with the increasing reaction order in H2 with increasing temperature (Fig. 6d). Compared to the dominant pathway to CO, methanol formation pathways have considerably lower molar fluxes. The formate pathway is not taken because the step of HCO2 hydrogenation to H2CO2 has a high activation energy (Eact = 220 kJ mol−1) and is endothermic (Er = 167 kJ mol−1). Furthermore, hydrogenation of CO to CH3OH does not take place because the hydrogenation of CO to HCO has an activation energy of 148 kJ mol−1, significantly higher than the CO desorption energy (31 kJ mol−1). This makes further CO hydrogenation less favorable than its desorption.
The DRC analysis and reaction flux analysis for the Pt-In2O3 model are shown in Fig. 7e and f, respectively. At low temperature, the overall rate of is mainly controlled by CO desorption (step 20, ΔEdes = 158 kJ mol−1). OH hydrogenation (step 18, Eact = 133 kJ mol−1) controls the rate to a smaller extent as can be seen by its lower DRC coefficient. In line with Ni-In2O3, the dominant pathway proceeds via formation of an oxygen vacancy and direct dissociation of CO2 (Fig. 7f). The carboxyl pathway is not taken because COOH formation and OH removal are associated with high barriers (Eact = 147 kJ mol−1 and Eact = 133 kJ mol−1, respectively). With increasing temperature, the DRC coefficient of CO desorption decreases in favor of CO2 dissociation (step 12). This is in line with the positive reaction order in CO2 calculated at higher temperature (Fig. 6e). Compared to the dominant pathway to CO, hydrogenation of CO2 to methanol is associated with significantly lower molar fluxes. The formate pathway is not taken because the hydrogenation of HCO2 to H2CO2 has a high activation energy and is endothermic (Eact = 146 kJ mol−1, Er = 129 kJ mol−1).
On Rh-In2O3, for T < 300 °C, the rate of CO2 consumption is mainly controlled by CO desorption (step 20, ΔEdes = 215 kJ mol−1). At higher temperature, the DRC coefficient of this elementary step decreases in favour of CO2 dissociation (step 12, Eact = 81 kJ mol−1) that becomes the rate determining step (RDS) at T > 450 °C. In line with the other SA-In2O3 models, the dominant pathway proceeds via formation of an oxygen vacancy and direct dissociation of CO2 (Fig. 7h). The high barrier associated with OH hydrogenation (step 18, Eact = 186 kJ mol−1) hampers the carboxyl pathway. Compared to the dominant pathway to CO, methanol synthesis from CO2 is associated with significantly lower molar fluxes. The formate pathway is not taken because the hydrogenation of HCO2 to H2CO2 has a high activation energy and is endothermic (Eact = 155 kJ mol−1, Er = 136 kJ mol−1).
General discussion
The present study clarifies the role of single atoms of Pt, Pd, Ni and Rh adsorbed on the In2O3(111) surface in CO2 hydrogenation. The explored reaction mechanism includes a direct route for CO2 hydrogenation to methanol (formate pathway), a pathway to methanol via CO hydrogenation and the competing reverse water-gas shift (rWGS) reaction. Earlier studies pointed out that SAs on the In2O3 surface do not catalyse CH4 formation.29,30,35 A key result of this study is that CO is the dominant reaction product for all SA-In2O3 models. CO is obtained via a redox mechanism involving oxygen vacancy formation followed by CO2 adsorption and direct C–O bond cleavage. On all models, the CH3OH selectivity was found to be negligibly small, because barriers associated with the hydrogenation of formate intermediates to methanol are significantly higher than those for the dominant redox pathway to CO.Methanol formation on In2O3 involves the formation of oxygen vacancies and hydrogenation of formate intermediates.63,66 On the unpromoted In2O3(111) surface, oxygen vacancy formation has an overall barrier of 67 kJ mol−1 with respect to gas-phase H2.59,63 When a single Pd, Pt or Rh atom is adsorbed on In2O3, oxygen vacancy formation exhibits comparable overall barriers of respectively 62, 48 and 57 kJ mol−1. In contrast, a much higher overall barrier of 150 kJ mol−1 is computed for the single Ni atom on In2O3(111). Concerning the conversion of formate, HCO2 hydrogenation to H2CO2 on an In2O3(110) surface was earlier found to exhibit an activation energy of 55 kJ mol−1 and a reaction energy of +5 kJ mol−1.60 On In2O3(111), similar activation and reaction energies are found (98 and 15 kJ mol−1, respectively).57 All SA-In2O3 models show higher activation energies for this step (step 7 in Fig. 3), which is the main cause of the very low methanol formation rate. We performed a sensitivity analysis of the microkinetic simulations involving decreasing the activation energies of steps 7 by 10, 20, 30 and 40 kJ mol−1. The results given in Fig. S8† show that decreasing barriers result in a higher methanol selectivity for Ni-, Pt- and Rh-In2O3. Herein, we consider methanol selectivity of at least 1% as significant. Methanol formation is least improved for Pd-In2O3, because the activation energy associated with HCO2 hydrogenation (step 7) is very high (220 kJ mol−1). In this case, a decrease of at least 80 kJ mol−1 is required to obtain significant CH3OH selectivity. We extended the sensitivity analysis to include H2CO2 dissociation (step 8) and reported the results in Fig. S9.† Also in this case, decreasing barriers results in a higher methanol selectivity for Ni-, Pt- and Rh-In2O3, whereas methanol formation is less improved for Pd-In2O3 because the previous step has a higher barrier (220 kJ mol−1 and 62 kJ mol−1 for steps 7–8, respectively).
Our microkinetic simulations show that all SA-In2O3 have CO as the main product obtained via a redox mechanism. The activity for the rWGS reaction decreases in the order Pd > Ni > bare In2O3 > Pt > Rh (Fig. S6d†). We now explain this finding based on the DFT-computed activation energies and the analysis of the rate limiting steps. On all SA-In2O3 models, direct CO2 dissociation (step 12) and subsequent CO desorption (step 20) are the main rate-limiting steps towards CO formation. On Pd-In2O3, these steps have barriers of 65 and 31 kJ mol−1, respectively. On Ni-In2O3, direct CO2 dissociation and CO desorption are associated with barriers of 91 and 80 kJ mol−1, respectively. On bare-In2O3, CO is obtained via carboxyl pathway involving a COOH intermediate. This pathway is mainly limited by the rate of COOH dissociation which is associated with a high barrier (Eact = 150 kJ mol−1). Compared to Ni and Pd-In2O3, the barrier for CO2 dissociation on Pt-In2O3 is similar (Eact = 65 kJ mol−1), but CO desorption is associated with a higher barrier (ΔEdes = 158 kJ mol−1). On Rh-In2O3, desorption of CO is associated with a high desorption energy (ΔEdes = 215 kJ mol−1) hampering its formation. For this reason, this model shows the lowest activity to CO.
We know explain why the redox pathway is preferred over the carboxyl pathway for the formation of CO on our SA-In2O3 models. In the redox pathway, the C–O bond in CO2 is broken directly resulting in CO binding to the SA and the O healing the vacancy. This process is associated with relatively low barriers on all models, in line with the strong SA–O bond (Table S14†). Notably, on a bare In2O3(110) surface, where CH3OH is the main product, replenishing the oxygen vacancy by CO2 dissociation is associated with a reaction energy of 1.4 eV.60 This indicates that direct CO2 dissociation would have a barrier of at least 1.4 eV, making this elementary reaction step unlikely. In contrast with SA-promoted In2O3, on bare-In2O3, there is no active site available for accepting the CO molecule resulting from CO2 dissociation. On the SA-In2O3 models, breaking the C–O bond on a COOH intermediate is also possible, however the subsequent step of OH removal via H2O formation is associated with high barriers because it requires the migration of a OH moiety to the SA.
A fundamental assumption in this study was that each kinetic pathway features one oxygen vacancy, in line with previous DFT calculations on In2O3.19,21,22 To investigate whether the presence of a second oxygen vacancy could change the conclusions of this work, we calculated a few key elementary steps relevant to such a mechanism. The results are reported in Tables S15–S18† reveal that a second vacancy provides a lower activation energy for some elementary reaction steps. However, these deviations are not significant enough to impact the dominant pathway identified in our microkinetic simulations. Consequently, we deduce that the inclusion of a second oxygen vacancy does not change the conclusions put forth in this study.
We also compare our results to those recently reported in the literature. In line with the present work, Frei et al. concluded from DFT calculations that a Ni SA on In2O3 would be active for the rWGS, because it features lower barriers compared to CO2 hydrogenation to methanol.29 Furthermore, Millet et al. showed that isolated Ni atoms in a Ni1–Mg1−xO catalyst are active for the rWGS but are unable to catalyse CO2 hydrogenation to CH4 (or MeOH), for which Ni clusters are needed.67 Indeed, Shen et al. deployed DFT to compare various pathways of CO2 hydrogenation to methanol on a Ni4/In2O3(111) model and found that methanol can be obtained via CO intermediate obtained by rWGS.68 In an earlier computational work, we reported that single atoms of Ni either doped in or adsorbed on In2O3(111) surface would mainly catalyze CO formation, whereas small Ni clusters would mainly lead to methanol.27 In line with this earlier work, we indicate here that the Ni-In2O3 model features low-barrier CO2 dissociation resulting in a preference for CO formation over hydrogenation to methanol. Ye et al. reported that methanol is the main product of CO2 hydrogenation via formate on a Pd4/In2O3(111) model.62 Our Pd-In2O3 model features higher barriers for the formate pathway compared to direct CO2 dissociation precluding methanol formation in favor of CO. Liu et al. reported that methanol formation on a Pt4/In2O3(111) model takes place via hydrogenation of CO resulting from CO2 dissociation.32 Our Pt-In2O3 model does not allow a TS for the subsequent hydrogenation steps of CO to HCO and H2CO precluding methanol formation from CO hydrogenation. Clusters of Pd, Pt or Ni on the In2O3(111) surface catalyze the formation of methanol because hydrogenation of either formate or CO is favored over the rWGS reaction to CO. However, in the limit of a single atom of Pd, Pt or Ni on the In2O3(111) surface, pathways leading to methanol have higher barriers than the redox pathway to CO resulting in low methanol selectivity. In a recent theoretical study, Pinheiro Araújo et al. studied atomically dispersed metal atoms (Pd, Pt, Rh, Ni, Co, Au, Ir) on the In2O3 surface.28 They speculated on the basis of energy diagrams that CO2 hydrogenation to methanol via formate is favored over CO formation. Although this conclusion is at odds with our finding from microkinetic simulations that CO2 hydrogenation on SA-promoted In2O3 would mainly lead to CO, it can be understood from the fact that the study of Pinheiro Araújo et al. only considered the COOH pathway to CO, i.e., they omitted the redox pathway.
Conclusions
Using microkinetic models and DFT calculations, we clarified the role of single atoms (SA) on In2O3 in CO2 hydrogenation to CH3OH and CO. We investigated the role of single atoms of Pt, Pd, Ni and Rh on the (111) surface of In2O3 for the formation of methanol via formate and CO as well as the competing rWGS reaction via redox and carboxyl pathways. Compared to the pristine In2O3(111) surface, adsorbing a single Pd, Pt or Rh atom results in comparable overall barriers for oxygen vacancy formation. In contrast, the presence of a single Ni atom on the In2O3 surface increases the overall barrier for oxygen vacancy formation significantly. Microkinetic simulations reveal that all SA-In2O3 models mainly catalyze CO via formation of an oxygen vacancy followed by CO2 adsorption and direct C–O bond cleavage (redox pathway). The carboxyl pathway to CO is not taken, because OH removal resulting from COOH dissociation is associated with higher barriers compared to the dominant redox pathway. The model predicts that Pd is the preferred promoter for In2O3 model, achieving the highest activity among the transition metals considered due to a low barrier for CO2 dissociation and a relatively weak adsorption strength of the CO product. For all models, the CH3OH selectivity is negligibly low because high barriers are associated with the hydrogenation of HCO2 to H2CO2 and its subsequent dissociation into CH2O (formate pathway) compared to the dominant rWGS pathway.Author contributions
Francesco Cannizzaro: DFT calculations, microkinetic modelling, writing and visualization. Sjoerd Kurstjens and Tom van den Berg: DFT calculations. Emiel J.M. Hensen and Ivo Filot resources, conceptualization, supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge NWO and SurfSARA for providing access to computational resources used to carry out the DFT calculations reported in this work. This work was supported by the Netherlands Center for Multiscale Catalytic Energy Conversion (MCEC), an NWO Gravitation program funded by the Ministry of Education, Culture and Science of the government of the Netherlands. This project has received funding from the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No 801359.Notes and references
- A. González-Garay, M. S. Frei, A. Al-Qahtani, C. Mondelli, G. Guillén-Gosálbez and J. Pérez-Ramírez, Energy Environ. Sci., 2019, 12, 3425–3436 RSC.
- E. V. Kondratenko, G. Mul, J. Baltrusaitis, G. O. Larrazábal and J. Pérez-Ramírez, Energy Environ. Sci., 2013, 6, 3112 RSC.
- V. Dias, M. Pochet, F. Contino and H. Jeanmart, Front. Mech. Eng., 2020, 6, 21 CrossRef.
- A. Álvarez, A. Bansode, A. Urakawa, A. V. Bavykina, T. A. Wezendonk, M. Makkee, J. Gascon and F. Kapteijn, Chem. Rev., 2017, 117, 9804–9838 CrossRef PubMed.
- J. Zhong, X. Yang, Z. Wu, B. Liang, Y. Huang and T. Zhang, Chem. Soc. Rev., 2020, 49, 1385–1413 RSC.
- X. Jiang, X. Nie, X. Guo, C. Song and J. G. Chen, Chem. Rev., 2020, 120, 7984–8034 CrossRef CAS PubMed.
- J. Wang, G. Zhang, J. Zhu, X. Zhang, F. Ding, A. Zhang, X. Guo and C. Song, ACS Catal., 2021, 2020, 1406–1423 CrossRef.
- Y. A. Daza and J. N. Kuhn, RSC Adv., 2016, 6, 49675–49691 RSC.
- S. Saeidi, N. A. S. Amin and M. R. Rahimpour, J. CO2 Util., 2014, 5, 66–81 CrossRef CAS.
- W. Li, H. Wang, X. Jiang, J. Zhu, Z. Liu, X. Guo and C. Song, RSC Adv., 2018, 8, 7651–7669 RSC.
- S. Gumber and A. V. P. Gurumoorthy, Methanol Sci. Eng., 2018, pp. 661–674 Search PubMed.
- G. A. Olah, Angew. Chem., Int. Ed., 2005, 44, 2636–2639 CrossRef CAS PubMed.
- A. Goeppert, M. Czaun, J. P. Jones, G. K. Surya Prakash and G. A. Olah, Chem. Soc. Rev., 2014, 43, 7995–8048 RSC.
- C. Baltes, S. Vukojević and F. Schüth, J. Catal., 2008, 258, 334–344 CrossRef CAS.
- M. Behrens, Angew. Chem., Int. Ed., 2016, 55, 14906–14908 CrossRef CAS PubMed.
- J. Nakamura, Y. Choi and T. Fujitani, Top. Catal., 2003, 22, 277–285 CrossRef CAS.
- M. B. Fichtl, D. Schlereth, N. Jacobsen, I. Kasatkin, J. Schumann, M. Behrens, R. Schlögl and O. Hinrichsen, Appl. Catal., A, 2015, 502, 262–270 CrossRef CAS.
- X. Jiang, X. Nie, X. Guo, C. Song and J. G. Chen, Chem. Rev., 2020, 120, 7984–8034 CrossRef CAS PubMed.
- J. Ye, C. Liu and Q. Ge, J. Phys. Chem. C, 2012, 116, 7817–7825 CrossRef CAS.
- M. S. Frei, C. Mondelli, A. Cesarini, F. Krumeich, R. Hauert, J. A. Stewart, D. Curulla Ferré and J. Pérez-Ramírez, ACS Catal., 2020, 10, 1133–1145 CrossRef CAS.
- Q. Sun, J. Ye, C. Liu and Q. Ge, Greenhouse Gases: Sci. Technol., 2014, 4, 140–144 CrossRef CAS.
- J. Ye, C. Liu, D. Mei and Q. Ge, ACS Catal., 2013, 3, 1296–1306 CrossRef CAS.
- A. Cao, Z. Wang, H. Li and J. K. Nørskov, ACS Catal., 2021, 11, 1780–1786 CrossRef CAS.
- J. Wang, G. Zhang, J. Zhu, X. Zhang, F. Ding, A. Zhang, X. Guo and C. Song, ACS Catal., 2021, 11, 1406–1423 CrossRef CAS.
- A. Posada-Borbón and H. Grönbeck, ACS Catal., 2021, 11, 9996–10006 CrossRef.
- J. Zhu, F. Cannizzaro, L. Liu, H. Zhang, N. Kosinov, I. A. W. Filot, J. Rabeah, A. Brückner and E. J. M. Hensen, ACS Catal., 2021, 11, 11371–11384 CrossRef CAS PubMed.
- F. Cannizzaro, E. J. M. Hensen and I. A. W. Filot, ACS Catal., 2023, 13, 1875–1892 CrossRef CAS PubMed.
- T. Pinheiro Araújo, J. Morales-Vidal, T. Zou, R. García-Muelas, P. O. Willi, K. M. Engel, O. V. Safonova, D. Faust Akl, F. Krumeich, R. N. Grass, C. Mondelli, N. López and J. Pérez-Ramírez, Adv. Energy Mater., 2022, 12, 14 Search PubMed.
- M. S. Frei, C. Mondelli, R. García-Muelas, J. Morales-Vidal, M. Philipp, O. V. Safonova, N. López, J. A. Stewart, D. C. Ferré and J. Pérez-Ramírez, Nat. Commun., 2021, 12, 2–12 CrossRef PubMed.
- M. S. Frei, C. Mondelli, R. García-Muelas, K. S. Kley, B. Puértolas, N. López, O. V. Safonova, J. A. Stewart, D. Curulla Ferré and J. Pérez-Ramírez, Nat. Commun., 2019, 10, 1–11 CrossRef PubMed.
- Z. Han, C. Tang, J. Wang, L. Li and C. Li, J. Catal., 2021, 394, 236–244 CrossRef CAS.
- K. Sun, N. Rui, C. Shen and C. J. Liu, J. Phys. Chem. C, 2021, 125, 10926–10936 CrossRef CAS.
- J. Wang, K. Sun, X. Jia and C. J. Liu, Catal. Today, 2021, 365, 341–347 CrossRef CAS.
- N. H. M. Dostagir, C. Thompson, H. Kobayashi, A. M. Karim, A. Fukuoka and A. Shrotri, Catal. Sci. Technol., 2020, 10, 8196–8202 RSC.
- N. H. M. Dostagir, C. Thompson, H. Kobayashi, A. M. Karim, A. Fukuoka and A. Shrotri, Catal. Sci. Technol., 2020, 10, 8196–8202 RSC.
- X. Jia, K. Sun, J. Wang, C. Shen and C. J. Liu, J. Energy Chem., 2020, 50, 409–415 CrossRef.
- J. Ye, C. J. Liu, D. Mei and Q. Ge, J. Catal., 2014, 317, 453 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- D. Heidrich and W. Quapp, Theor. Chim. Acta, 1986, 70, 89–98 CrossRef CAS.
- R. Nelson, C. Ertural, J. George, V. L. Deringer, G. Hautier and R. Dronskowski, J. Comput. Chem., 2020, 41, 1931–1940 CrossRef CAS PubMed.
- S. Maintz, V. L. Deringer, A. L. Tchougr and R. Dronskowski, J. Comput. Chem., 2016, 37, 11–12 CrossRef PubMed.
- M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 134, 064111 CrossRef PubMed.
- P. N. Brown, G. D. Byrne and A. C. Hindmarsh, SIAM Journal on Scientific and Statistical Computing, 2006, 10, 1038–1051 CrossRef.
- G. D. Byrne and A. C. Hindmarsh, J. Comput. Phys., 1987, 70, 1–62 CrossRef.
- G. D. Byrne and A. C. Hindmarsh, ACM Trans. Math. Softw., 1975, 1, 71–96 CrossRef.
- C. H. Shomate, J. Phys. Chem., 2002, 58, 368–372 CrossRef.
- NIST Chemistry WebBook, https://webbook.nist.gov/chemistry/, (accessed 1 February 2022) Search PubMed.
- S. Kozuch and S. Shaik, J. Am. Chem. Soc., 2006, 128, 3355–3365 CrossRef CAS PubMed.
- S. Kozuch and S. Shaik, J. Phys. Chem. A, 2008, 112, 6032–6041 CrossRef CAS PubMed.
- C. T. Campbell, ACS Catal., 2017, 7, 2770–2779 CrossRef CAS.
- A. W. Filot, Introduction to Microkinetic Modeling, Technische Universiteit Eindhoven, 2017 Search PubMed.
- C. Stegelmann, N. C. Schiødt, C. T. Campbell and P. Stoltze, J. Catal., 2004, 221, 630–649 CrossRef CAS.
- M. S. Frei, M. Capdevila-Cortada, R. García-Muelas, C. Mondelli, N. López, J. A. Stewart, D. Curulla Ferré and J. Pérez-Ramírez, J. Catal., 2018, 361, 313–321 CrossRef CAS.
- M. S. Frei, C. Mondelli, R. García-Muelas, J. Morales-Vidal, M. Philipp, O. V. Safonova, N. López, J. A. Stewart, D. C. Ferré and J. Pérez-Ramírez, Nat. Commun., 2021, 12, 1–9 CrossRef PubMed.
- D. Albani, M. Capdevila-Cortada, G. Vilé, S. Mitchell, O. Martin, N. López and J. Pérez-Ramírez, Angew. Chem., Int. Ed., 2017, 56, 10755–10760 CrossRef CAS PubMed.
- J. Ye, C. Liu, D. Mei and Q. Ge, ACS Catal., 2013, 3, 1296–1306 CrossRef CAS.
- J. Ye, C. Liu and Q. Ge, J. Phys. Chem. C, 2012, 116, 7817–7825 CrossRef CAS.
- J. Ye, C. J. Liu, D. Mei and Q. Ge, J. Catal., 2014, 317, 44–53 CrossRef CAS.
- M. S. Frei, M. Capdevila-Cortada, R. García-Muelas, C. Mondelli, N. López, J. A. Stewart, D. Curulla Ferré and J. Pérez-Ramírez, J. Catal., 2018, 361, 313–321 CrossRef CAS.
- X. Liu, L. Sun and W. Q. Deng, J. Phys. Chem. C, 2018, 122, 8306–8314 CrossRef CAS.
- J. Ye, C. Liu, D. Mei and Q. Ge, ACS Catal., 2013, 3, 1296–1306 CrossRef CAS.
- J. Ye, C. Liu, D. Mei and Q. Ge, ACS Catal., 2013, 3, 1296–1306 CrossRef CAS.
- M. Millet, G. Algara-Siller, S. Wrabetz, A. Mazheika, F. Girgsdies, D. Teschner, F. Seitz, A. Tarasov, S. Levchenko, R. Schlögl and E. Frei, J. Am. Chem. Soc., 2019, 6, 2451–2461 CrossRef PubMed.
- C. Shen, Q. Bao, W. Xue, K. Sun, Z. Zhang, X. Jia, D. Mei and C. J. Liu, J. Energy Chem., 2022, 65, 623–629 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Description of the structure of SA-In2O3 models and oxygen vacancy formation (section S1–S3), geometries of elementary reaction steps (section S4–S7) full DFT dataset (section S8), and further microkinetic and DFT results (section S9 and S10). See DOI: https://doi.org/10.1039/d3cy00222e |
| This journal is © The Royal Society of Chemistry 2023 |