Application of statistical learning and mechanistic modelling towards mapping the substrate electronic space in a Cu-catalyzed Suzuki–Miyaura coupling

Abstract

Cu-catalyzed Suzuki–Miyaura coupling between highly fluorinated aryl boronate esters and aryl iodides has been studied with DFT calculations. The reaction mechanism proposed suggests that the oxidative addition of the aryl iodide onto the copper catalyst is the rate-determining step. Several alternative reactions, in which the initial substrates have been replaced by para- and meta-substituted reactants, have been computed to build a reaction barrier database that accounts for the electronic properties of a wide range of functional groups. Statistical learning techniques, based on multi linear regression (MLR) modeling, allow interpreting the electronic effects of both substrates onto the overall reaction barrier, indicating that both electron poor aryl boronate esters and aryl iodides produce lower reaction barriers. The reaction barrier database and the MLR models can be combined to generate an electronic substrate map that easily enables estimating the reaction outcome for analogous Suzuki–Miyaura reactions between aryl boronate esters and iodobenzenes.

---

Introduction

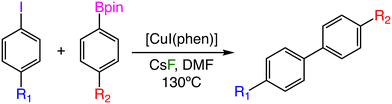
The use of homogeneous catalysts based on first-row (or base) transition metals (Mn, Fe, Co, Ni, and Cu) as a replacement for their precious metal analogs (Ru, Rh, Pd, Ir, Pt, Au) in cross coupling reactions has experienced a large increase in recent years.^1–3 This replacement obeys both environmental and economic factors; first-row transition metals are usually less toxic,⁴ cheaper, and more abundant⁵ than their precious second- and third-row transition metal counterparts, and if handled properly, they can provide equally active catalytic platforms. However, there are some important challenges to be addressed for base metals to be implemented as general catalysts, and these issues arise from their inherent reactivity, which can lead to problems with 1) the stability of the active species in presence of air, 2) the propensity to generate radical species through single-electron transfer processes (seriously affecting the selectivity of the reaction), and 3) the characterization of high-spin paramagnetic species, which requires less traditional techniques. The study of base metal-catalyzed cross-coupling reactions is experiencing a fast development and many classical reactions, usually carried out with precious metals, already showcase entire functional versions that employ base metal homogeneous species as catalysts. For instance, it is now possible to find classical cross-coupling reactions promoted by homogeneous catalysts based on manganese,^6–9 iron,^10–14 cobalt,^15–19 and nickel.^20–24 On the other hand, the study of copper-catalyzed homogeneous cross-coupling reactions is one of the most active research areas related to base metal catalysis.^25–27 Currently, it is possible to find a recent example for almost any of the classical coupling reactions such as Heck,²⁸ Sonogashira,²⁹ Stille,³⁰ Hiyama,³¹ and Buchwald–Hartwig.³² The Suzuki–Miyaura reaction, one of the most representative metal-catalyzed cross-couplings, has several versions in which the typical palladium catalysts have been replaced by analogous copper complexes.^33–39 Recently, a Cu-catalyzed Suzuki–Miyaura coupling of highly fluorinated aryl boronate esters with aryl iodides has been reported.⁴⁰ This procedure allows preparing polyfluorobiphenyl products that present a wide variety of potential applications in the fields of medicinal chemistry,^41,42 electron-transport materials,^43,44 and supramolecular chemistry.^45,46 The general experimental setup for this reaction showcases the coupling between 2,3,4,5,6-pentafluorophenylboronic acid pinacol ester (C₆F₅Bpin) and iodobenzene in the presence of the 1,10-phenanthroline (phen) ligand, the CsF base, and copper(I) iodide, which probably takes the shape of [CuI(phen)] as the initial catalyst (Scheme 1). One of the main interests of our group consists of computationally studying metal-catalyzed fluorination processes to find plausible reaction mechanisms that could allow to better understand the underlying chemistry in these systems.^47–52 Herein, we will study the reaction mechanism associated with the copper-catalyzed Suzuki–Miyaura shown in Scheme 1 and, afterward, we will explore the impact of electronic effects of both substrates, i.e., the aryl boronate ester and the aryl iodide, onto the activation barrier of the reaction. This procedure will be carried out by recomputing the catalytic cycle and hence creating a large activation barrier database for a varied range of para- and meta-substituted boronates and iodobenzenes. Finally, we will employ the reaction barrier database to explore the electronic substrate space with statistical learning techniques and to construct a substrate map, which will be able to relate the performance of each catalytic system with the electronic properties of both substrates.

Scheme 1 Cu-catalyzed Suzuki–Miyaura coupling between C₆F₅Bpin and iodobenzene, as described in ref. 40.

Computational details

All the structures have been fully optimized in N,N-dimethylformamide (DMF) using the Gaussian16⁵³ suite of programs with the B3LYP^54–57 functional. In the geometry optimization process, the 6-31G* basis set^58–60 was used to describe all atoms except for Cu and I, for which the Stuttgart double zeta basis set (SDD),^61–64 along with the associated ECP to describe the core electrons, was employed. Ultrafine integration grids have been used to ensure satisfactory convergence. This is necessary because some of the species under study present a number of low frequency vibrational modes (<100 cm⁻¹) that contribute significantly to the entropy and must be computed properly. In all cases, the solvation energies in N,N-dimethylformamide were computed with the (IEF-PCM)^65,66 continuum dielectric solvation model using the SMD⁶⁷ radii and non-electrostatic terms. Dispersion effects have been included in the optimization process using the D3 method of Grimme.⁶⁸ For some species, namely, I₆ and RETS (vide infra), additional features have to be included to produce the final geometries; in both cases, the maximum displacement step was set to 0.05 Bohr, and vibrational frequencies were computed during each optimization step. In all cases, frequency calculations are carried out to ensure the nature of stationary points and transition states. This computational scheme is named BS1.

Additional single point calculations on the optimized geometries have been employed to obtain improved Gibbs energy values with larger basis sets (scheme BS2). In these calculations, the B3LYP functional was kept and the 6-311+G** all-electron basis set^60,69,70 was employed for all the atoms except Cu and I, which were described with the aug-cc-pVTZ-PP basis set.^71,72 These single point calculations also include the solvation and dispersion effects. These computational settings have been used previously for studying similar copper-catalyzed reactions.^49,50,52

To improve the speed of calculations, the pinacolborane group (Bpin) was simplified to the corresponding [1,3,2]dioxaborolane analog. This approximation was validated by computing the initial reaction steps between PhI and C₆F₅Bpin with the full and simplified systems, which produced very similar relative Gibbs energies for the formation of intermediate I₃ (0.6 and 0.1 kcal mol⁻¹), and for the transmetalation transition state TMTS (8.1 and 7.4 kcal mol⁻¹). Therefore, all the references to the Bpin group throughout the manuscript refer to the [1,3,2]dioxaborolane moiety.

The NBO charges have been computed employing the NBO7 program⁷³ using the BS2 computational scheme.

The computed Gibbs energies were corrected to use a standard state corresponding to species in solution with a standard concentration of 1 M. The final Gibbs energies at a given temperature, based on the rigid rotor/harmonic oscillator approach to statistical mechanics, were obtained using the following formula

where E_BS2 is the electronic energy, including the solvent and dispersion terms, obtained with the large basis sets scheme (BS2). H_corr,BS1 is the thermal correction to enthalpy and contains the zero-point energy plus the vibrational, rotational, and translational energies computed with the BS1 scheme. Finally, TS_BS1 accounts for the entropic correction obtained from the BS1 scheme. Gibbs energies as output by Gaussian16, which refer to an ideal gas (P = 1 atm) standard state, were corrected to use a standard state, in which the species in the solution have a standard concentration of 1 M. This procedure was carried out by adding an additional term to the computed Gibbs energy of each species. This correction is computed as RT ln(C°/C^1atm), where C° is the standard reference state concentration (1 M), and C^1atm is the concentration of an ideal gas under the standard P = 1 atm conditions at a given temperature. Therefore, for an ideal gas at 1 atm and at 130 °C, C^1atm = 1/V_m = P/RT = 0.030 M; numerically, this correction term equals 2.80 kcal mol⁻¹ per molecule. The values of E_BS2, H_corr,BS1, TS_BS1, and G° at 130 °C can be found in Tables S1–S3.†

All the statistical analysis procedures—parameter correlations, construction of simple and multilinear regressions, external validation, and X-/Y-scrambling processes—have been performed with Excel.

Results and discussion

Determination of the reaction mechanism

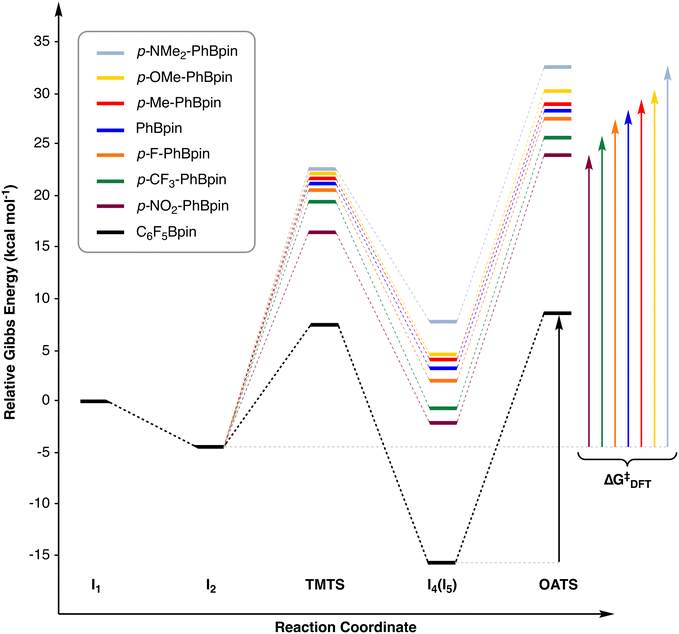
The first stage of this study consists of exploring the reaction shown in Scheme 1 to propose a plausible reaction sequence for the coupling of C₆F₅Bpin and iodobenzene (Scheme 2, the 3D representation of the species involved can be found in the ESI,† Fig. S1). In the process of finding a suitable mechanism, different reaction pathways have been considered and computed; finally, the pathway displaying the lowest energy requirements has been selected.

Scheme 2 Plausible reaction mechanism for the Cu-catalyzed Suzuki–Miyaura coupling between C₆F₅Bpin and PhI (top) and its corresponding Gibbs energy profile (bottom); in all cases, the bidentate phen ligand is represented as .

Recently, a catalytic system, reported by Lledós and Casares,⁷⁴ was reported to produce a similar pathway for the reaction between [Cu(bipy)(C₆F₅)] and aryl iodides, which generates biaryl products. Following this pathway, the reaction starts with the replacement of iodide by fluoride on the initial [CuI(phen)] catalyst (I₁) to produce intermediate I₂. This reaction stage is exergonic by 4.6 kcal mol⁻¹ and has been previously reported to proceed smoothly in similar reaction conditions;⁷⁵ hence, the transition state governing this transformation has not been sought. Then, C₆F₅Bpin comes in and attaches onto the fluoride ligand through the boron atom, delivering intermediate I₃, which is 4.7 kcal mol⁻¹ higher in energy than the previous species. Since fluoride is not sterically hindered, this addition is considered to be barrierless. The C₆F₅ group is transferred from boron to copper through the corresponding transmetalation transition state (TMTS), while fluoride detaches from the metal to form FBpin, which is released into the reaction mixture. This step requires further 7.4 kcal mol⁻¹, indicating that the overall barrier up to this point is 12.0 kcal mol⁻¹. After that, the organometallic complex [Cu(C₆F₅)(phen)] (I₄) is obtained, and the relative Gibbs energy goes down by 23 kcal mol⁻¹. Iodobenzene then reacts with I₄ to form an encounter complex (I₅), in which the incoming aryl ring exhibits a π-stacking interaction with the C₆F₅ group; this addition is almost thermoneutral. At this point, the oxidative addition takes place and the C–I bond is cleaved onto the copper; the most favorable transition state (OATS) adopts a square pyramid geometry in which both aryl rings are placed cis to each other, while one of the nitrogen donor atoms of phen occupies the axial coordination site. The oxidative addition step has an energy requirement of 24.2 kcal mol⁻¹. The trans oxidative addition transition state (trans-OATS) was also computed and found to require a slightly higher energy investment (25.4 kcal mol⁻¹). Alternative transition states with different ligand arrangements and trigonal bipyramidal geometries have been computed and found to produce the same cis and trans transition states described above.

Dinuclear oxidative addition transition states were not taken into consideration because of the low concentration of the initial catalytic species.⁷⁶ After the oxidative addition, intermediate I₆ should be formed; however, all the attempts to optimize this formally Cu(III) species with the regular computational settings, including different trigonal bipyramidal and square pyramidal complexes, have led to the formation of the final product (PhC₆F₅), indicating that the reductive elimination process seems to be barrierless. This behavior has been reported before by Bolm in a computational study of a copper-catalyzed Sonogashira coupling.⁷⁷ The stabilization of this structure as a local minimum was attempted by adding additional keywords during the geometry optimization procedure (vide supra) but they have not been able to produce the desired intermediate. Then, the angle between both aryl substituents on I₆ was frozen at different values and the complexes were optimized. These calculations produce the expected copper(III) intermediate as a local minimum (all vibrational frequencies positive) with a C_Ph–Cu–C_C6F5 angle of 93°; unfortunately, removing the angle constraint in a further reoptimization produces the reductive elimination of PhC₆F₅. Therefore, we decided to study the potential energy surface in the forward direction from I₆ by performing a relaxed potential energy surface scan of the C_Ph–Cu–C_C6F5 angle—starting at 93° with 5° decrements until the angle takes a value of 48°. The relaxed scan indicates that the energy smoothly decreases as the angle takes lower values, with no clear sign of an energy requirement to overcome the reductive elimination barrier, supporting the idea that intermediate I₆ is not stable and, whenever formed, automatically evolves into the final products (Fig. S2†). Nevertheless, intermediate I₆ could be considered a transient species in the reaction pathway and has been kept as such and further analyzed. This intermediate adopts a square pyramid geometry with one of the N atoms of the phen ligand taking the apical coordination position while both aryl rings are placed cis to each other in the equatorial plane. The relative Gibbs energy of I₆ is −3.4 kcal mol⁻¹, well below to that found for the trans-I₆ isomer (2.8 kcal mol⁻¹), in which the phenyl and the pentafluorophenyl rings are placed trans to each other in the equatorial plane of the complex. Intermediate I₆, which should formally be a copper(III) species, shows a certain ligand field inversion since its occupied frontier orbitals (HOMO, HOMO−1, etc., computed at the BS2 level) have mainly ligand character instead of showcasing the expected doubly occupied non-bonding d-orbitals of the copper center, which appear at lower energies (see ESI† and Fig. S3).⁷⁸ This particular electronic structure is probably responsible for the unstable nature of intermediate I₆, in which a certain oxidation state cannot be assigned to the copper center. Even so, NBO calculations state that the charge of copper increases from 0.68 to 1.07 when I₄ is transformed into I₆, indicating the oxidation of the metal during the oxidative addition stage. Other alternative pathways were computed to ascertain that the reaction proceeds through the sequence shown in Scheme 2. First, the outer-sphere electron transfer between I₄ and PhI to produce the corresponding [Cu(C₆F₅)(phen)]⁺ and PhI⁻ species has been computed to require an energy investment of more than 30 kcal mol⁻¹, which rules out the possibility of the reaction proceeding through this pathway. In addition, the reaction sequence from I₄ + PhI to I₁ + PhC₆F₅ does not correspond to a σ-complex-assisted metathesis. This can be observed from the IRC analysis^79,80 of the oxidative addition transition state, which produces the expected species close to the I₆ intermediate (Fig. S4†).

As stated above, I₆ is not stable and directly produces the final PhC₆F₅ product and the initial catalyst I₁. However, during the reviewing process of this manuscript, in particular from the relaxed potential energy surface scan from I₆, we were able to identify a plausible transition state for the reductive elimination stage (RETS). Although this transition state is not a “traditional” saddle point, we decided to keep it in the overall catalytic cycle for completeness. As expected from the relaxed potential energy surface scan described above, this transition state should be found at a Gibbs energy value slightly below that of I₆ (−4.3 kcal mol⁻¹). After RETS, the newly formed [CuI(phen)] (I₁) and PhC₆F₅ fragments do not strongly interact; thus, we consider that no significant intermediate is formed after this transition state. At this point, the reaction goes back to the starting point and a large amount of energy is released (ca. 55 kcal mol⁻¹) due to the C–C bond formation of PhC₆F₅. The overall energy barrier (ΔG^‡_DFT from now on), computed as the Gibbs energy difference between I₅ and OATS, corresponds to the oxidative addition step and spans over 24.2 kcal mol⁻¹.

Exploration of substrate electronic effects

The computed Gibbs energy profile, in which the oxidative addition is the rate-limiting stage, indicates that an electronic effect should be observed on the overall ΔG^‡_DFT value when iodobenzene is replaced by substrates bearing different substituents in the para position of the ring (Scheme 3). This possibility has been explored by computing the complete reaction mechanism for six additional para-substituted iodobenzenes (p-R₁-C₆H₄I, where R₁ = NO₂, CF₃, F, Me, OMe, and NMe₂) that cover almost all the range of electronic donation properties, with NO₂ as the most electron-withdrawing and NMe₂ as the most electron-donating substituents. Experimentally, the electronic effect for some of these substituents could not be observed clearly (reactions were reported for different p-R₁-C₆H₄I substrates with R₁ = F, CF₃, Me, and OMe substituents), probably because the reaction times were too long (18 hours) and all the aryl iodides produced almost quantitative isolated yields.⁴⁰ However, there are experimental data supporting the electronic effect of the iodobenzene substrate onto the overall performance of the reaction; competition experiments show that the reaction of a 1 : 1 mixture of p-Me–C₆H₄I and p-CF₃–C₆H₄I with C₆F₅Bpin produces a 1 : 3 product ratio, indicating that the latter substrate, which has an electron withdrawing substituent, generates a more efficient catalytic system. In fact, the authors state that “aryl halides bearing electron-withdrawing groups are more reactive and give better yields compared to aryl halides bearing electron-donating groups”, confirming the electronic effect of the iodobenzene substrate onto the reaction barrier.

Scheme 3 Cu-catalyzed Suzuki–Miyaura coupling between C₆F₅Bpin and different para-substituted iodobenzenes.

Computationally, the electronic effect of the para substituent can be clearly ascertained by the ΔG^‡_DFT values, which range between 22.2 and 27.4 kcal mol⁻¹ (Fig. 1), all of them low enough to produce operative reactions under the experimental conditions. In all cases, ΔG^‡_DFT is computed as the energy difference between OATS and (I₄ + p-R₁-C₆H₄I), indicating that these values also include the formation of intermediate I₅, which is always slightly higher in energy than the latter. As should be expected in an oxidative rate-determining step, the electron-withdrawing groups produce lower barriers than their electron-rich counterparts. As before, intermediate I₆ could not be computed for these reactions because it automatically reductively eliminates to deliver the final product and the initial catalyst (I₁); therefore, intermediate I₆ and RETS have not been further computed for any of these systems. At this point, we tried to correlate these computed ΔG^‡_DFT values with different electronic features of the para substituents of the aryl iodides. At first, and since the iodobenzene is accepting the electrons during the oxidative addition stage, we used the electrophilic conceptual density functional theory indices, namely, electrophilicity (ω)⁸¹ and electroaccepting power (ω⁺)⁸² of the p-R₁-C₆H₄I substrates. However, none of these parameters showed a good correlation with ΔG^‡_DFT. Then, we turned upon the classical Hammett para substituent constants (σ_p).⁸³ In this case, the correlation between σ_p and ΔG^‡_DFT is better (R² = 0.905, rmse = 0.53 kcal mol⁻¹, MAE = 0.43 kcal mol⁻¹) but the limited availability of σ_p values for more complex systems, e.g., the C₆F₅ ring or doubly substituted aryl rings, prompted us to search for a more general parameter to correlate with the DFT computed energy barriers.

Fig. 1 Computed ΔG^‡_DFT for reactions between different p-R₁-C₆H₄I species and C₆F₅Bpin.

Thus, we next explored the correlation of the ΔG^‡_DFT values with the electric properties of the carbon bound to iodide (C_ipso) in p-R₁-C₆H₄I, which is the main reactive point of these substrates toward the oxidative addition. The C_ipso electrostatic potential⁸⁴ shows just a moderate correlation with ΔG^‡_DFT (R² = 0.876, rmse = 0.60 kcal mol⁻¹, MAE = 0.54 kcal mol⁻¹). In addition, the Mulliken,⁸⁵ NBO,⁷³ and CM5 (ref. 86) charges were computed and correlated with the reaction barriers. The Mulliken and NBO charges did not show any relevant correlation; on the other hand, the CM5 charge of C_ipso (q_C from now on, Table S5†) showed a very good negative correlation with ΔG^‡_DFT (R² = 0.946, rmse = 0.40 kcal mol⁻¹, MAE = 0.34 kcal mol⁻¹, Fig. 2), indicating that the substrates displaying more positive q_C values, i.e., those bearing electron-withdrawing para-substituents, produce lower reaction barriers. This behavior allows the interpretation of the substrate effect on the reaction barrier; when an electron-withdrawing group is placed at the para position of the iodobenzene, the electron density of the ring is depleted toward that group. In this situation, the ipso carbon has a more positive charge that consequently produces an increased electrophilic character and a higher tendency for getting electrons from copper, thus lowering the oxidative addition transition state. The opposite behavior should be expected when an electron-donating group is placed in the para position of iodobenzene.

Fig. 2 ΔG^‡_LRvs. ΔG^‡_DFT for reactions between p-R₁-C₆H₄I and C₆F₅Bpin, and linear correlation between ΔG^‡_LRand the CM5 charge of the ipso carbon atom of p-R₁-C₆H₄I species (q_C).

Next, we sought whether the electronic effects of the aryl boronate ester could also play a role on the reaction outcome; this was done by replacing the C₆F₅ ring of the original substrate by para-substituted phenyl rings p-R₂-C₆H₄Bpin (R₂ = NO₂, CF₃, F, H, Me, OMe and NMe₂) that cover all the electron donating range, and then recomputing the complete reaction mechanism with iodobenzene as the counterpart (Scheme 4).

Scheme 4 Cu-catalyzed Suzuki–Miyaura coupling between iodobenzene and different para-substituted aryl ester boronates.

Experimentally, the substrate effect of the boronate onto the reaction barrier can be observed in the reaction between bromobenzene and C₆F₅Bpin, m,m′-(CF₃)₂C₆H₃Bpin and m,m′-Me₂–C₆H₃Bpin, which produce yields of 87%, 35%, and traces, respectively. These experiments again suggest that electron-poor aryl boronate esters produce more efficient reactions than their electron-rich counterparts.⁴⁰ Computationally, a clear electronic dependence on the identity of the R₂ substituent was observed for ΔG^‡_DFT, with electron-withdrawing groups producing lower barriers that increase as the electron donation ability of R₂ increases (Fig. 3). The computed ΔG^‡_DFT values for this series of reactions show a larger span than those from the aryl iodide substrates—from 24.2 kcal mol⁻¹ for C₆F₅Bpin to 37.0 kcal mol⁻¹ for p-NMe₂–C₆H₄Bpin. This electronic effect arises from how the Gibbs energy surface changes when the p-substituted phenyl ring replaces C₆F₅ on the aryl boronate ester. As stated above, ΔG^‡_DFT for the C₆F₅Bpin + PhI couple is computed as the energy difference between I₅ and OATS (for the other aryl iodides is the energy difference between I₄ + p-R₁-C₆H₄I and OATS). However, as soon as C₆F₅Bpin is replaced by para-R₂-C₆H₄Bpin, the Gibbs energy of all the species following the coordination of the aryl boronate ester (i.e., the formation of I₃) is much higher and the overall reaction barrier is found between OATS and I₂. This means that ΔG^‡_DFT must be computed as the Gibbs energy difference between (OATS + FBpin) − (I₂ + p-R₁-C₆H₄I + p-R₂-C₆H₄Bpin), as shown in Scheme 5. In this way, it seems obvious why the different p-R₂-C₆H₄Bpin substrates produce varying barriers and how the electronic effect of R₂ is projected onto ΔG^‡_DFT.

Fig. 3 Computed ΔG^‡_DFT for reactions between PhI and different p-R₂-C₆H₄Bpin species.

Scheme 5 Gibbs energy profiles for reactions between PhI and different p-R₂-C₆H₄Bpin species.

With the computed barriers of the eight p-R₂-C₆H₄Bpin substrates at hand, we tried to find a quantitative correlation with the electronic features of the para-R₂ substituents. As before, the Hammett para substituent constants (σ_p)⁸³ provide a quite good correlation (R² = 0.985, rmse = 0.33 kcal mol⁻¹, MAE = 0.28 kcal mol⁻¹) but the C₆F₅ ring must be excluded of this procedure since its σ_p value has not been experimentally determined. Again, we explored the atomic electrostatic potential⁸⁴ and the Mulliken,⁸⁵ NBO,⁷³ and CM5 (ref. 86) charges of the boron atom in the p-R₂-C₆H₄Bpin substrates. In this case, selecting the boron atom is favorable for various reasons: 1) boron is the anchoring point of the aryl boronate ester onto I₂ prior to transmetalation, 2) boron has a direct effect onto the para-R₂ group transfer in TMTS, and 3) the stability of the species formed after TMTS shows a trend with respect to the p-R₂-C₆H₄Bpin to FBpin transformation. As above, the Mulliken and NBO charges show very poor correlation with ΔG^‡_DFT. On the other hand, the electrostatic potential of the boron atom shows a very good correlation with the computed Gibbs energy barriers: R² = 0.984, rmse = 0.47 kcal mol⁻¹, and MAE = 0.43 kcal mol⁻¹. As in the case of aryl iodides, the CM5 charge of the boron atom in p-R₂-C₆H₄Bpin (q_B from here on, Table S4†) shows also a very good linear relationship with ΔG^‡_DFT (R² = 0.983, rmse = 0.49 kcal mol⁻¹, MAE = 0.40 kcal mol⁻¹) and was selected as the descriptor for quantitatively reproducing the overall reaction barrier with a simple linear regression for the studied set of p-R₂-C₆H₄Bpin substrates reacting with iodobenzene (Fig. 4). In principle, both the boron electrostatic potential and the q_B parameters could be employed, but the usage of an atomic charge seems to be more chemically intuitive.

Fig. 4 ΔG^‡_LRvs. ΔG^‡_DFT for reactions between PhI and p-R₂-C₆H₄Bpin, and linear correlation between ΔG^‡_LR and the CM5 charge of the boron atom of p-R₂-C₆H₄Bpin species (q_B).

The linear relationship described by q_B is negative with respect to this parameter, indicating that the substrates with more positive q_B values produce lower energy barriers. Since the aryl boronate ester is a Lewis acid, adding an electron withdrawing substituent to the para position of the ring produces a larger q_B value and enhances the possibility of coordinating to the fluoride ligand in I₂, hence increasing the overall reactivity of the system. The opposite behavior will be expected when an electron-donating group is placed in the para position of the aryl boronate ester.

Statistical learning for reaction barrier estimation

Up to this point, we have observed that the reaction barrier depends on the nature of both the aryl iodide and the aryl boronate ester substrates. In addition, we have stated that the activation barrier can be modeled from the CM5 charges of the key atoms of these substrates by linear regression methods. Therefore, we thought about building a quantitative structure–property relationship (QSPR) multilinear regression (MLR) mathematical model that allows estimating the overall barrier (ΔG^‡_MLR) for any pair of substrates directly from the computed q_C and q_B values. This kind of approach has been extensively employed by the group of Sigman in recent years.^87–89 The QSPR model will take the form shown is eqn (1)

ΔG^‡_MLR = a + b₁·q_C + b₂·q_B (1)

where a is the y-intercept of the regression and b_n are the regression coefficients of the CM5 charge descriptors. Of course, to do that, a relatively large and representative set of computed reaction barriers must be employed. Consequently, the reaction profiles (or at least the key intermediates and transition states) have been computed for a diverse range of reactions comprising different combinations of para-substituted substrate pairs that spread across the whole range of electronic donating properties (Scheme 6).

Scheme 6 Cu-catalyzed Suzuki–Miyaura coupling between para-substituted iodobenzenes and para-substituted aryl boronate esters.

We have computed the complete Gibbs energy profiles for 18 additional p-R₁-C₆H₄I/p-R₂-C₆H₄Bpin substrate pairs within three different series (see ESI†): 1) p-NO₂–C₆H₄I with p-R₂-C₆H₄Bpin, 2) p-NMe₂–C₆H₄I with p-R₂-C₆H₄Bpin, and 3) p-R₁-C₆H₄I with p-NMe₂–C₆H₄Bpin (where R₁ and R₂ = NO₂, CF₃, F, H, Me, OMe, and NMe₂). In principle, these series of substrate pairs contain the maximum variability on the electron-donating properties for R₁ and R₂. The computed energy profiles show that, in all cases, the highest energy stationary point is the oxidative addition transition state (OATS), and ΔG^‡_DFT must be computed as the energy difference between (OATS + FBpin) and (I₂ + p-R₁-C₆H₄I + p-R₂-C₆H₄Bpin), following the trend shown in Scheme 5. The only exceptions to this behavior are the p-R₁-C₆H₄I/C₆F₅Bpin pairs, where the overall barrier is found between OATS and I₄ + p-R₁-C₆H₄I. At this point, and to provide the database with a higher variability, new para-substituents were included in both p-R₁-C₆H₄I and p-R₂-C₆H₄Bpin substrates: R₁, R₂ = CN, COMe, Cl, tBu, OH, and NH₂. The electron-donating properties of these new substituents are in between those of the substituents employed before and, thus, these groups should produce activation barriers located in the range of 22–39 kcal mol⁻¹, which correspond to the most electron withdrawing (p-NO₂–C₆H₄I/C₆F₅Bpin) and most electron-donating (p-NMe₂–C₆H₄I/p-NMe₂–C₆H₄Bpin) pairs, respectively. Therefore, ΔG^‡_DFT was computed for several para-substituted substrate pairs (71) by computing only the species needed, i.e., p-R₁-C₆H₄I, p-R₂-C₆H₄Bpin and their corresponding OATS (I₂ and FBpin are also required but have been computed previously). At this point, 103 ΔG^‡_DFT values have been computed for p-R₁-C₆H₄I/p-R₂-C₆H₄Bpin substrate pairs (Table S6†), and the MLR model can be constructed. Usually, when building QSPR models, the dataset is randomly split into 80% for model selection (training set or tset) and 20% to validate the final model (prediction set or pset). In this case, the training set used for building the MLR model has been constructed to comprise a balanced amount of p-R₁ and p-R₂ substituents, i.e., each substituent appears 4 times as R₁ and R₂, except for R₁ = NMe₂, H, and NO₂, which are employed 5 times (Fig. S5†). Thereby, the tset used to build the MLR model includes 56 substrate pairs, which is ca. 50% of the dataset. All the other substrate pairs (47 points in the database) will be used as prediction set to validate the MLR as external predictors (Fig. S5†). The MLR model obtained, along with some of the relevant statistical parameters from both tset and pset, are shown in Table 1; the computed ΔG^‡_MLR values and the associated residual errors can be found in Table S7.† The cross-correlation coefficient between q_C and q_B for the reactions within the training set is as low as 0.002.

Table 1 Statistical parameters of the training and prediction sets for the constructed MLR

MLR equation	ΔG^‡MLR = 170.26 − 73.05qC − 349.77qB (2)
Standard MLR	ΔG^‡MLR = 31.27 − 1.23qC − 3.26qB (3)
	tset	pset
R ^2	0.965	0.971
R loo ^2	0.964	—
rmse (kcal mol^−1)	0.65	0.64
MAE (kcal mol^−1)	0.54	0.50

---

The statistical results of the MLR model are very good; for the training set, the correlation coefficient (R²) is 0.965 and the associated errors rmse and MAE are very low, 0.65 and 0.54 kcal mol⁻¹, respectively. Similar values are obtained for the prediction set, showing the robustness and the high prediction capacity of the model. Fig. 5 shows a plot of ΔG^‡_MLRvs. ΔG^‡_DFT for all the substrate pairs studied (including training and prediction sets). As in the previous linear regressions, both q_C and q_B showcase negative signs, indicating that larger charge values would produce lower activation barriers for both substrates. Hence, the physicochemical interpretation for both parameters remains the same as above. Adding an electron withdrawing substituent to the para position of the iodobenzene depletes the electron density of the ipso carbon, causing an increase of q_C and a higher tendency for the substrate to engage in the oxidative addition stage, which entails receiving electrons from the copper atom in I₄. On the other hand, adding an electron withdrawing group to the para position of the aryl boronate ester produces a stronger Lewis acid, which is more easily activated by I₂. In both cases, the presence of electron donating groups produce the opposite effect.

Fig. 5 ΔG^‡_MLRvs. ΔG^‡_DFT for the training and prediction sets of different substrate pairs.

The distribution of the predicted residual errors for the 103 barriers is shown in Fig. S6.† As may be observed, 89% of these values display an error lower than 1 kcal mol⁻¹, which is often considered as the chemical accuracy limit. The highest and lowest computed residual errors are 1.40 and −1.35 kcal mol⁻¹, respectively, well below three times the rmse of the MLR. In addition, only five substrate pairs have residual errors larger than twice the rmse (Table S7†), which indicates the goodness of the MLR model obtained. According to the regression coefficients found for the standardized MLR (in which both descriptors have been autoscaled to produce variables with zero mean and unit variance) shown in Table 1, q_B is ca. 2.75 times more important than q_C in the estimation of the reaction barrier, suggesting that the nature of the aryl boronate ester plays a major role in the expected reactivity of the system. Y-Randomization experiments were carried out to ensure that the good performance of the MLR model was not due to chance effects; the average R², rmse, and MAE values obtained for ten different scrambling procedures of the computed barriers are 0.022, 4.69 kcal mol⁻¹, and 3.68 kcal⁻¹, respectively, showing that chance correlation did not play any significant role in the resulting statistics. As an additional validation procedure, we have repeated the MLR modeling ten times by randomly varying the splitting of the whole dataset into training and prediction sets. The average statistical parameters obtained after this procedure are very similar to those reported above; tset: R² = 0.971, rmse = 0.64 kcal mol⁻¹, and MAE = 0.52 kcal mol⁻¹; pset: R² = 0.963, rmse = 0.65 kcal mol⁻¹, and MAE = 0.43 kcal mol⁻¹, demonstrating again the goodness of the proposed MLR model.

Since the electronic effect of the para-substituent on the computed barrier is transmitted through the q_C and q_B descriptors, it should be expected that the activation barrier of other substrates, for which the electronic properties are in between those employed to construct the MLR, could also be computed. At this point, we decided to use the MLR model to predict the activation barrier for substrate pairs bearing the substituents included in Fig. S5† in either para- or meta-positions. Thus, we built three different subsets of reactions between m-R₁-C₆H₄I/p-R₂-C₆H₄Bpin (m-R₁/p-R₂), p-R₁-C₆H₄I/m-R₂-C₆H₄Bpin (p-R₁/m-R₂), and m-R₁-C₆H₄I/m-R₂-C₆H₄Bpin (m-R₁/m-R₂) substrates, which contain 17, 16, and 17 substrate pairs respectively. The results obtained for these new external prediction sets are very good and the ΔG^‡_MLR derived values are quite close to those computed by DFT (Fig. 6 and Table S8†). As may be observed, the results for the m-R₁/p-R₂ and p-R₁/m-R₂ subsets are very close to those obtained for the original training and prediction sets both in terms of R² coefficients and error values. The correlation between ΔG^‡_MLR and ΔG^‡_DFT shows that the m-R₁/p-R₂ subset produces both positive and negative errors (points both above and below the perfect fit), while the p-R₁/m-R₂ substrate pairs mainly produce ΔG^‡_MLR values lower than their DFT counterparts (points below the diagonal in Fig. 6). This could be attributed to an incipient appearance of steric interactions between the meta substituent of the substrates with other parts of the catalytic system, mainly between both aryl rings in the oxidative addition transition state.

Fig. 6 ΔG^‡_MLRvs. ΔG^‡_DFT for reaction between substrate pairs that include para- and meta-substituted substrate pairs, and statistical parameters for these reaction subsets (* in kcal mol⁻¹).

This same behavior is stressed for the m-R₁/m-R₂ substrate pairs, which display the largest errors, probably because the steric interactions are becoming increasingly more important. Nevertheless, the statistical parameters of this reaction subset remain at a very good level, demonstrating that the MLR developed with only para-substituted substrates can also capture the electronic effects of meta-substituents. The deviation between ΔG^‡_MLR and ΔG^‡_DFT can be further observed for reactions where one of the substrates is doubly substituted at the meta-positions, i.e., m,m′-(R₁)₂-C₆H₃I or m,m′-(R₂)₂-C₆H₃Bpin. We have computed 10 additional systems comprising five m,m′-(R₁)₂-C₆H₃I/p-R₂-C₆H₄Bpin (m,m′-(R₁)₂/p-R₂) and five p-R₁-C₆H₄I/m,m′-(R₂)₂-C₆H₃Bpin (p-R₁/m,m′-(R₂)₂) substrate pairs and compared their MLR and DFT barriers (Fig. 7). Although the agreement found between the barriers is still quite good, both sets show larger errors and a clear deviation from the perfect fit can be observed (Table S9†), most probably because the electronic effects are starting to be blurred by the incipient appearance of steric interactions of the meta-substituents within the catalytic species. Obviously, ortho-substituted substrates produce even larger barrier differences because the steric hindrance introduced by the substituent is more pronounced; for this reason, substrate pairs including this substitution pattern have not been included in this study.

Fig. 7 ΔG^‡_MLRvs. ΔG^‡_DFT for reaction between substrate pairs that include one para- and one doubly substituted meta-substrate pairs, and statistical parameters for these reaction subsets (* in kcal mol⁻¹).

Mapping the substrate electronic space of the reaction

Finally, the computed barrier dataset can be employed to map the electronic chemical space of the substrates for the studied Suzuki–Miyaura reaction. To do this, a new MLR, similar to eqn (2), has been constructed employing all the single para- and meta-substituted iodobenzenes and aryl boronate esters (153 substrate pairs, eqn (4)).

ΔG^‡_MAP = 166.36 − 68.94q_C − 339.86q_B (4)

The computed regression parameters for eqn (4) are very similar to those found above: R² = 0.959, rmse = 0.65 kcal mol⁻¹, and MAE = 0.55 kcal mol⁻¹, providing a reliable way to compute the barrier of the reaction as a function of q_C and q_B. With these magnitudes at hand, the electronic map of the studied reaction can be constructed (Fig. 8); this map showcases the values of q_C and q_B (left and top axes, respectively), while the reaction barrier values take the bottom and right axes. The linear regression models corresponding to integer ΔG^‡_MAP values of eqn (4) have been added as black lines, and the surface of the map has been color-coded regarding these values (green for lower ΔG^‡_MAP, red for higher ΔG^‡_MAP). Moreover, the computed ΔG^‡_MAP values can be transformed into rate constants using the Eyring–Polanyi equation, which can then be employed to simulate the reaction yield at the desired reaction conditions. In this way, the estimated yield for each integer value of ΔG^‡_MAP, at 130 °C in 18 hours, has been added onto each regression line. Once constructed, the map can be easily employed to derive reaction barriers directly from q_C and q_B, for example, the coupling between p-CN-C₆H₄I (q_C = 0.078) and PhBpin (q_B = 0.385) should have a reaction barrier close to 31 kcal mol⁻¹ and would produce a yield of ca. 87%. Conversely, the map can be employed to find suitable or better counterparts for a given reaction; for instance, reactions with yields higher than 98% (ΔG^‡_MAP ≤ 27 kcal mol⁻¹) employing p-Cl–C₆H₄I (q_C = 0.060) as a substrate would need an aryl boronate ester with q_B ≥ 0.397, which could only be achieved by p-NO₂–C₆H₄Bpin and C₆F₅Bpin (q_B = 0.397 and 0.405, respectively). The map also reflects why the expected electronic effect for the reaction between C₆F₅Bpin and the different iodobenzenes could not be observed in 18 hour experimental runs. The q_B value for C₆F₅Bpin is 0.405, corresponding to the right axis of the map; thus, all the possible q_C values would produce nearly quantitative reactions, making it impossible to observe the electronic influence of the substituted iodobenzene on the overall reaction barrier. In addition, the computed data allows adapting the electronic map to different reaction conditions, i.e., temperature and reaction times with relative ease, thus allowing the prediction of the reaction barriers in different scenarios.

Fig. 8 Map of electronic substrate space for the Suzuki–Miyaura reaction between iodobenzenes and aryl boronate esters as a function of q_C and q_B. The black diagonal lines correspond to the representation of eqn (4) for the ΔG^‡_MAP values shown in the bottom and right axes. The computed 18-hour yield for each ΔG^‡_MAP value appears circled onto the corresponding regression line.

Conclusion

A plausible mechanism has been proposed for the copper-catalyzed Suzuki–Miyaura coupling between iodobenzenes (R₁-C₆H₄I) and aryl boronate esters (R₂-C₆H₄Bpin). The reaction seems to follow the typical transmetalation/oxidative addition/reductive elimination sequence for a copper-catalyzed process. The copper(III) intermediate, which should be formed after the oxidative addition, is unstable and automatically evolves into the final product through a low-energy reductive elimination barrier. This intermediate, with formal +3 oxidation state, shows a certain ligand field inversion that can be observed in its occupied frontier orbitals, which mainly display ligand contributions.

The reaction mechanism has been recomputed for different substrate pairs; in all cases, the highest energy transition state corresponds to the oxidative addition of the iodobenzene onto the copper(I) organometallic intermediate [Cu(C₆F₅)(phen)].

A large database of reaction barriers for several substrate pairs (153 different reactions) has been constructed by computational means. These reactions feature a wide variety of para- and meta-substituted iodobenzenes and aryl boronate esters, which cover the full range of electronic properties of both the substrates.

The electronic effects of both substrates on the reaction barrier are captured by the computed CM5 charges of the ipso carbon of the iodobenzene (q_C) and the boron atom of the aryl boronate ester (q_B), respectively. These parameters can be related with the propensity of both substrates to engage in the catalytic cycle. q_C modulates the ability of the aryl iodide to participate in the oxidative addition stage, with larger values producing lower activation barriers. q_B indicates the tendency of the aryl boronate ester to behave as Lewis acid and shows that electron-withdrawing substituents generate more reactive substrates and consequently lower activation barriers.

The q_C and q_B parameters, combined with the reaction barrier database, can be employed to derive multilinear regression (MLR) models that allow computing and predicting the activation energy in reactions between monosubstituted para- and meta-substituted reactants. The MLR equations show very small errors, typically lower than 1 kcal mol⁻¹, in all cases except for those in which one of the substrates has a double meta-substitution.

The MLR model comprising all the computed reactions allows building an electronic substrate map, based on q_C and q_B, which can be employed to easily allocate the activation barrier and the yield for any pair of substrates used in the studied Suzuki–Miyaura reaction.

Author contributions

FAGM was involved in the investigation and data curation of this manuscript. GA participated in the writing – review & editing procedure. JJ oversaw the conceptualization, formal analysis, visualization, and writing the original and revised version of this work.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support from MICINN (PGC2018-093863-B-C21) and the Spanish Structures of Excellence María de Maeztu program (MDM-2017-0767) is gratefully acknowledged. FAGM thanks the MICINN and the FSE program for the predoctoral grant PRE2019-091164.

Notes and references

1. P. Chirik and R. Morris, Getting Down to Earth: The Renaissance of Catalysis with Abundant Metals, Acc. Chem. Res., 2015, 48, 2495–2495.
2. M. Beller, Introduction: First Row Metals and Catalysis, Chem. Rev., 2019, 119, 2089–2089.
3. S. Shekhar, T. S. Ahmed, A. R. Ickes and M. C. Haibach, Recent Advances in Nonprecious Metal Catalysis, Org. Process Res. Dev., 2022, 26, 14–42.
4. K. S. Egorova and V. P. Ananikov, Which Metals are Green for Catalysis? Comparison of the Toxicities of Ni, Cu, Fe, Pd, Pt, Rh, and Au Salts, Angew. Chem., Int. Ed., 2016, 55, 12150–12162.
5. Mineral commodity summaries 2022, Reston, VA, 2022.
6. M. Rueping and W. Ieawsuwan, A Manganese-Catalyzed Cross-Coupling Reaction, Synlett, 2007, 2, 0247–0250.
7. T. C. Atack and S. P. Cook, Manganese-Catalyzed Borylation of Unactivated Alkyl Chlorides, J. Am. Chem. Soc., 2016, 138, 6139–6142.
8. B. E. Petel, M. Purak and E. M. Matson, Manganese-Catalyzed Kumada Cross-Coupling Reactions of Aliphatic Grignard Reagents with N-Heterocyclic Chlorides, Synlett, 2018, 29, 1700–1706.
9. K. Das, K. Sarkar and B. Maji, Manganese-Catalyzed Anti-Markovnikov Hydroamination of Allyl Alcohols via Hydrogen-Borrowing Catalysis, ACS Catal., 2021, 11, 7060–7069.
10. T. L. Mako and J. A. Byers, Recent advances in iron-catalysed cross coupling reactions and their mechanistic underpinning, Inorg. Chem. Front., 2016, 3, 766–790.
11. H. Xiong, Y. Li, B. Qian, R. Wei, E. V. Van der Eycken and H. Bao, Iron(II)-Catalyzed Heck-Type Coupling of Vinylarenes with Alkyl Iodides, Org. Lett., 2019, 21, 776–779.
12. M. P. Crockett, A. S. Wong, B. Li and J. A. Byers, Rational Design of an Iron-Based Catalyst for Suzuki–Miyaura Cross-Couplings Involving Heteroaromatic Boronic Esters and Tertiary Alkyl Electrophiles, Angew. Chem., Int. Ed., 2020, 59, 5392–5397.
13. J. Zhang, S. Wang, Y. Zhang and Z. Feng, Iron-Catalyzed Cross-Coupling Reactions for the Construction of Carbon-Heteroatom Bonds, Asian J. Org. Chem., 2020, 9, 1519–1531.
14. Q. Wang, Q. Sun, Y. Jiang, H. Zhang, L. Yu, C. Tian, G. Chen and M. J. Koh, Iron-catalysed reductive cross-coupling of glycosyl radicals for the stereoselective synthesis of C-glycosides, Nat. Synth., 2022, 1, 235–244.
15. S. Asghar, S. B. Tailor, D. Elorriaga and R. B. Bedford, Cobalt-Catalyzed Suzuki Biaryl Coupling of Aryl Halides, Angew. Chem., Int. Ed., 2017, 56, 16367–16370.
16. F. Kreyenschmidt, S. E. Meurer and K. Koszinowski, Mechanisms of Cobalt/Phosphine-Catalyzed Cross-Coupling Reactions, Chem. – Eur. J., 2019, 25, 5912–5921.
17. M.-Z. Lu, X. Ding, C. Shao, Z. Hu, H. Luo, S. Zhi, H. Hu, Y. Kan and T.-P. Loh, Direct Hiyama Cross-Coupling of (Hetero)arylsilanes with C(sp2)–H Bonds Enabled by Cobalt Catalysis, Org. Lett., 2020, 22, 2663–2668.
18. J. R. Ludwig, E. M. Simmons, S. R. Wisniewski and P. J. Chirik, Cobalt-Catalyzed C(sp2)–C(sp3) Suzuki–Miyaura Cross Coupling, Org. Lett., 2021, 23, 625–630.
19. L. R. Mills, D. Gygi, J. R. Ludwig, E. M. Simmons, S. R. Wisniewski, J. Kim and P. J. Chirik, Cobalt-Catalyzed C(sp2)–C(sp3) Suzuki–Miyaura Cross-Coupling Enabled by Well-Defined Precatalysts with L,X-Type Ligands, ACS Catal., 2022, 12, 1905–1918.
20. L. Guo, W. Srimontree, C. Zhu, B. Maity, X. Liu, L. Cavallo and M. Rueping, Nickel-catalyzed Suzuki–Miyaura cross-couplings of aldehydes, Nat. Commun., 2019, 10, 1957.
21. J. E. A. Russell, E. D. Entz, I. M. Joyce and S. R. Neufeldt, Nickel-Catalyzed Stille Cross Coupling of C–O Electrophiles, ACS Catal., 2019, 9, 3304–3310.
22. S. Bhakta and T. Ghosh, Emerging Nickel Catalysis in Heck Reactions: Recent Developments, Adv. Synth. Catal., 2020, 362, 5257–5274.
23. Y. Li, Y. Luo, L. Peng, Y. Li, B. Zhao, W. Wang, H. Pang, Y. Deng, R. Bai, Y. Lan and G. Yin, Reaction scope and mechanistic insights of nickel-catalyzed migratory Suzuki–Miyaura cross-coupling, Nat. Commun., 2020, 11, 417.
24. Q. Fan, H. Sun, S. Xie, Y. Dong, X. Li, O. Fuhr and D. Fenske, Nickel-Catalyzed Sonogashira Coupling Reactions of Nonactivated Alkyl Chlorides under Mild Conditions, Organometallics, 2021, 40, 2240–2245.
25. S. Thapa, B. Shrestha, S. K. Gurung and R. Giri, Copper-catalysed cross-coupling: an untapped potential, Org. Biomol. Chem., 2015, 13, 4816–4827.
26. S. Bhunia, G. G. Pawar, S. V. Kumar, Y. Jiang and D. Ma, Selected Copper-Based Reactions for C−N, C−O, C−S, and C−C Bond Formation, Angew. Chem., Int. Ed., 2017, 56, 16136–16179.
27. L.-J. Cheng and N. P. Mankad, C–C and C–X coupling reactions of unactivated alkyl electrophiles using copper catalysis, Chem. Soc. Rev., 2020, 49, 8036–8064.
28. C. Tang, R. Zhang, B. Zhu, J. Fu, Y. Deng, L. Tian, W. Guan and X. Bi, Directed Copper-Catalyzed Intermolecular Heck-Type Reaction of Unactivated Olefins and Alkyl Halides, J. Am. Chem. Soc., 2018, 140, 16929–16935.
29. X. Mo, H. Huang and G. Zhang, Tetrasubstituted Carbon Stereocenters via Copper-Catalyzed Asymmetric Sonogashira Coupling Reactions with Cyclic gem-Dihaloketones and Tertiary α-Carbonyl Bromides, ACS Catal., 2022, 12, 9944–9952.
30. V. Lee, Application of copper(i) salt and fluoride promoted Stille coupling reactions in the synthesis of bioactive molecules, Org. Biomol. Chem., 2019, 17, 9095–9123.
31. A. Adenot, L. Anthore-Dalion, E. Nicolas, J.-C. Berthet, P. Thuéry and T. Cantat, A Copper(I)-Catalyzed Sulfonylative Hiyama Cross-Coupling, Chem. – Eur. J., 2021, 27, 18047–18053.
32. S. Roy, M. M. Dutta, M. J. Sarma and P. Phukan, Accelerating Effect of DMAP on CuI Catalyzed Buchwald-Hartwig C-N Coupling: Mechanistic Insight to the Reaction Pathway, ChemistrySelect, 2019, 4, 13094–13098.
33. Z.-Q. Zhang, C.-T. Yang, L.-J. Liang, B. Xiao, X. Lu, J.-H. Liu, Y.-Y. Sun, T. B. Marder and Y. Fu, Copper-Catalyzed/Promoted Cross-coupling of gem-Diborylalkanes with Nonactivated Primary Alkyl Halides: An Alternative Route to Alkylboronic Esters, Org. Lett., 2014, 16, 6342–6345.
34. Y.-Y. Sun, J. Yi, X. Lu, Z.-Q. Zhang, B. Xiao and Y. Fu, Cu-Catalyzed Suzuki–Miyaura reactions of primary and secondary benzyl halides with arylboronates, Chem. Commun., 2014, 50, 11060–11062.
35. S. K. Gurung, S. Thapa, B. Shrestha and R. Giri, Copper-catalysed cross-couplings of arylboronate esters with aryl and heteroaryl iodides and bromides, Org. Chem. Front., 2015, 2, 649–653.
36. P. Basnet, S. Thapa, D. A. Dickie and R. Giri, The copper-catalysed Suzuki–Miyaura coupling of alkylboron reagents: disproportionation of anionic (alkyl)(alkoxy)borates to anionic dialkylborates prior to transmetalation, Chem. Commun., 2016, 52, 11072–11075.
37. T. Hergert, B. Varga, A. Thurner, F. Faigl and B. Mátravölgyi, Copper-facilitated Suzuki-Miyaura coupling for the preparation of 1,3-dioxolane-protected 5-arylthiophene-2-carboxaldehydes, Tetrahedron, 2018, 74, 2002–2008.
38. S.-P. Jiang, X.-Y. Dong, Q.-S. Gu, L. Ye, Z.-L. Li and X.-Y. Liu, Copper-Catalyzed Enantioconvergent Radical Suzuki–Miyaura C(sp3)–C(sp2) Cross-Coupling, J. Am. Chem. Soc., 2020, 142, 19652–19659.
39. Z. Zhang, B. Górski and D. Leonori, Merging Halogen-Atom Transfer (XAT) and Copper Catalysis for the Modular Suzuki–Miyaura-Type Cross-Coupling of Alkyl Iodides and Organoborons, J. Am. Chem. Soc., 2022, 144, 1986–1992.
40. Y. P. Budiman, A. Friedrich, U. Radius and T. B. Marder, Copper-Catalysed Suzuki-Miyaura Cross-Coupling of Highly Fluorinated Aryl Boronate Esters with Aryl Iodides and Bromides and Fluoroarene−Arene π-Stacking Interactions in the Products, ChemCatChem, 2019, 11, 5387–5396.
41. J. Wang, M. Sánchez-Roselló, J. L. Aceña, C. del Pozo, A. E. Sorochinsky, S. Fustero, V. A. Soloshonok and H. Liu, Fluorine in Pharmaceutical Industry: Fluorine-Containing Drugs Introduced to the Market in the Last Decade (2001–2011), Chem. Rev., 2014, 114, 2432–2506.
42. C. Zhang, K. Yan, C. Fu, H. Peng, C. J. Hawker and A. K. Whittaker, Biological Utility of Fluorinated Compounds: from Materials Design to Molecular Imaging, Therapeutics and Environmental Remediation, Chem. Rev., 2022, 122, 167–208.
43. Y. Sakamoto, T. Suzuki, A. Miura, H. Fujikawa, S. Tokito and Y. Taga, Synthesis, Characterization, and Electron-Transport Property of Perfluorinated Phenylene Dendrimers, J. Am. Chem. Soc., 2000, 122, 1832–1833.
44. M. Moral, A. Navarro, A. Garzón-Ruiz and E. M. García-Frutos, Tuning the Crystal Packing and Semiconductor Electronic Properties of 7,7′-Diazaisoindigo by Side-Chain Length and Halogenation, J. Phys. Chem. C, 2019, 123, 153–164.
45. H. Yi, M. Albrecht, A. Valkonen and K. Rissanen, Perfluoro-1,1′-biphenyl and perfluoronaphthalene and their derivatives as π-acceptors for anions, New J. Chem., 2015, 39, 746–749.
46. I. A. Rather, S. A. Wagay and R. Ali, Emergence of anion-π interactions: The land of opportunity in supramolecular chemistry and beyond, Coord. Chem. Rev., 2020, 415, 213327.
47. J. Jover, Computational insights into nucleophilic copper-catalyzed trifluoromethylation of aryl halides, ACS Catal., 2014, 4, 4389–4397.
48. J. Jover, F. M. Miloserdov, J. Benet-Buchholz, V. V. Grushin and F. Maseras, On the feasibility of nickel-catalyzed trifluoromethylation of aryl halides, Organometallics, 2014, 33, 6531–6543.
49. J. Jover, Quantitative DFT modeling of product concentration in organometallic reactions: Cu-mediated pentafluoroethylation of benzoic acid chlorides as a case study, Phys. Chem. Chem. Phys., 2017, 19, 29344–29353.
50. J. Jover, Zn(II) Byproduct Enhances the Cu-Catalyzed Cross-Coupling of Bromozinc Difluorophosphonate with Iodobenzoates: A DFT Study, Organometallics, 2018, 37, 327–336.
51. J. Jover, Nickel-catalyzed aryl trifluoromethyl sulfide synthesis: A DFT study, Catal. Sci. Technol., 2019, 9, 5962–5970.
52. J. Echeverría and J. Jover, Eur. J. Org. Chem., 2022, e202101243.
53. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016.
54. S. H. Vosko, L. Wilk and M. Nusair, Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis, Can. J. Phys., 1980, 58, 1200–1211.
55. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
56. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
57. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98, 11623–11627.
58. R. Ditchfield, W. J. Hehre and J. A. Pople, Self-Consistent Molecular Orbital Methods. 9. Extended Gaussian-type basis for molecular-orbital studies of organic molecules, J. Chem. Phys., 1971, 54, 724–728.
59. W. J. Hehre, R. Ditchfield and J. A. Pople, Self-Consistent Molecular Orbital Methods. 12. Further extensions of Gaussian-type basis sets for use in molecular-orbital studies of organic-molecules, J. Chem. Phys., 1972, 56, 2257–2261.
60. P. C. Hariharan and J. A. Pople, The influence of polarization functions on molecular orbital hydrogenation energies, Theor. Chim. Acta, 1973, 28, 213–222.
61. T. H. Dunning and P. J. Hay, in Methods of Electronic Structure Theory, ed. H. F. Schaefer, Springer US, Boston, MA, 1977, pp. 1–27.
62. M. Dolg, U. Wedig, H. Stoll and H. Preuss, Energy-adjusted ab initio pseudopotentials for the first row transition elements, J. Chem. Phys., 1987, 86, 866–872.
63. A. Bergner, M. Dolg, W. Küchle, H. Stoll and H. Preuß, Ab initio energy-adjusted pseudopotentials for elements of groups 13–17, Mol. Phys., 1993, 80, 1431–1441.
64. J. M. L. Martin and A. Sundermann, Correlation consistent valence basis sets for use with the Stuttgart–Dresden–Bonn relativistic effective core potentials: The atoms Ga–Kr and In–Xe, J. Chem. Phys., 2001, 114, 3408–3420.
65. J. Tomasi, B. Mennucci and R. Cammi, Quantum Mechanical Continuum Solvation Models, Chem. Rev., 2005, 105, 2999–3094.
66. G. Scalmani and M. J. Frisch, Continuous surface charge polarizable continuum models of solvation. I. General formalism, J. Chem. Phys., 2010, 132, 114110.
67. A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113, 6378–6396.
68. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465.
69. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+G basis set for first-row elements, Li-F, J. Comput. Chem., 1983, 4, 294–301.
70. M. J. Frisch, J. A. Pople and J. S. Binkley, Self-Consistent Molecular-Orbital Methods. 25. Supplementary Functions for Gaussian-Basis Sets, J. Chem. Phys., 1984, 80, 3265–3269.
71. K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, Systematically convergent basis sets with relativistic pseudopotentials. II. Small-core pseudopotentials and correlation consistent basis sets for the post-d group 16–18 elements, J. Chem. Phys., 2003, 119, 11113–11123.
72. K. A. Peterson and C. Puzzarini, Systematically convergent basis sets for transition metals. II. Pseudopotential-based correlation consistent basis sets for the group 11 (Cu, Ag, Au) and 12 (Zn, Cd, Hg) elements, Theor. Chem. Acc., 2005, 114, 283–296.
73. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, P. Karafiloglou, C. R. Landis and F. Weinhold, NBO 7.0., Theoretical Chemistry Institute, University of Wisconsin, Madison, 2018.
74. O. Lozano-Lavilla, P. Gómez-Orellana, A. Lledós and J. A. Casares, Transmetalation Reactions Triggered by Electron Transfer between Organocopper Complexes, Inorg. Chem., 2021, 60, 11633–11639.
75. M. Ohashi, N. Ishida, K. Ando, Y. Hashimoto, A. Shigaki, K. Kikushima and S. Ogoshi, CuI-Catalyzed pentafluoroethylation of Aryl Iodides in the Presence of Tetrafluoroethylene and Cesium Fluoride: Determining the Route to the Key pentafluoroethyl CuI Intermediate, Chem. – Eur. J., 2018, 24, 9794–9798.
76. G. Marcos-Ayuso, A. Lledós and J. A. Casares, Copper(i) activation of C–X bonds: bimolecular vs. unimolecular reaction mechanism, Chem. Commun., 2022, 58, 2718–2721.
77. L.-H. Zou, A. J. Johansson, E. Zuidema and C. Bolm, Mechanistic Insights into Copper-Catalyzed Sonogashira–Hagihara-Type Cross-Coupling Reactions: Sub-Mol% Catalyst Loadings and Ligand Effects, Chem. – Eur. J., 2013, 19, 8144–8152.
78. I. M. DiMucci, J. T. Lukens, S. Chatterjee, K. M. Carsch, C. J. Titus, S. J. Lee, D. Nordlund, T. A. Betley, S. N. MacMillan and K. M. Lancaster, The Myth of d8 Copper(III), J. Am. Chem. Soc., 2019, 141, 18508–18520.
79. H. P. Hratchian and H. B. Schlegel, Accurate reaction paths using a Hessian based predictor–corrector integrator, J. Chem. Phys., 2004, 120, 9918–9924.
80. H. P. Hratchian and H. B. Schlegel, Using Hessian Updating To Increase the Efficiency of a Hessian Based Predictor-Corrector Reaction Path Following Method, J. Chem. Theory Comput., 2005, 1, 61–69.
81. R. G. Parr, L. V. Szentpály and S. Liu, Electrophilicity Index, J. Am. Chem. Soc., 1999, 121, 1922–1924.
82. J. L. Gázquez, A. Cedillo and A. Vela, Electrodonating and Electroaccepting Powers, J. Phys. Chem. A, 2007, 111, 1966–1970.
83. C. Hansch and A. Leo, Substituent Constants for Correlation Analysis in Chemistry and Biology, John Wiley & Sons, New York, 1979.
84. B. G. Johnson, P. M. W. Gill, J. A. Pople and D. J. Fox, Computing molecular electrostatic potentials with the PRISM algorithm, Chem. Phys. Lett., 1993, 206, 239–246.
85. R. S. Mulliken, Electronic Population Analysis on LCAO–MO Molecular Wave Functions. I, J. Chem. Phys., 1955, 23, 1833–1840.
86. A. V. Marenich, S. V. Jerome, C. J. Cramer and D. G. Truhlar, Charge Model 5: An Extension of Hirshfeld Population Analysis for the Accurate Description of Molecular Interactions in Gaseous and Condensed Phases, J. Chem. Theory Comput., 2012, 8, 527–541.
87. J.-Y. Guo, Y. Minko, C. B. Santiago and M. S. Sigman, Developing Comprehensive Computational Parameter Sets To Describe the Performance of Pyridine-Oxazoline and Related Ligands, ACS Catal., 2017, 7, 4144–4151.
88. J. P. Reid, R. S. J. Proctor, M. S. Sigman and R. J. Phipps, Predictive Multivariate Linear Regression Analysis Guides Successful Catalytic Enantioselective Minisci Reactions of Diazines, J. Am. Chem. Soc., 2019, 141, 19178–19185.
89. B. C. Haas, A. E. Goetz, A. Bahamonde, J. C. McWilliams and M. S. Sigman, Predicting relative efficiency of amide bond formation using multivariate linear regression, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2118451119.

---

Footnote

† Electronic supplementary information (ESI) available: The computed barriers, energy terms to compute the Gibbs energy profiles and the MLR modeling can be found in the ESI file. All the computed structures (G16 input and output files) have been uploaded to the ioChem-BD database, and can be retrieved in the following link: https://doi.org/10.19061/iochem-bd-1-256. See DOI: https://doi.org/10.1039/d2cy02039d

---