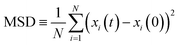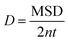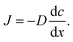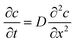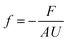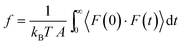Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mechanisms and models for water transport in reverse osmosis membranes: history, critical assessment, and recent developments†
Mohammad
Heiranian
 ab,
Hanqing
Fan
ab,
Hanqing
Fan
 a,
Li
Wang
a,
Li
Wang
 ac,
Xinglin
Lu
ac,
Xinglin
Lu
 d and
Menachem
Elimelech
d and
Menachem
Elimelech
 *a
*a
aDepartment of Chemical and Environmental Engineering, Yale University, New Haven, Connecticut 06520-8286, USA. E-mail: menachem.elimelech@yale.edu
bDepartment of Mechanical and Aerospace Engineering, North Carolina State University, Raleigh, North Carolina 27695-7910, USA
cCollege of Environmental Science and Engineering, Tongji University, Shanghai, China
dCAS Key Laboratory of Urban Pollutant Conversion, Department of Environmental Science and Engineering, National Synchrotron Radiation Laboratory, University of Science and Technology of China, Hefei 230026, China
First published on 27th October 2023
Abstract
Water scarcity is one of the greatest societal challenges facing humanity. Reverse osmosis (RO) desalination, a widely used membrane-based technology, has proven to be effective to augment water supply in water-stressed regions of our planet. However, progress in the design and development of RO membranes has been limited. To significantly enhance the performance of RO membranes, it is essential to acquire a deep understanding of the membrane separation and transport mechanisms. In this tutorial review, we cover the pivotal historical developments in RO technology, examine the chemical and physical properties of RO membrane materials, and critically review the models and mechanisms proposed for water transport in RO membranes. Based on recent experimental and computational findings, we conduct a thorough analysis of the key transport models—the solution–diffusion and pore-flow models—to assess their validity for accurately describing water transport in RO membranes. Our analysis involves examining the experimental evidence in favor of the solution–diffusion mechanism. Specifically, we explain whether the water content gradient within the membrane, cited as evidence for the key assumption in the solution–diffusion model, can drive a diffusive transport through RO membranes. Additionally, we review the recent molecular dynamics simulations which support the pore-flow mechanism for describing water transport in RO membranes. We conclude by providing future research directions aimed at addressing key knowledge gaps in water transport phenomena in RO membranes, with the goal of advancing the development of next-generation RO membranes.
Key learning points(1) Historical timeline of the development of desalination membranes for reverse osmosis.(2) Chemical and physical structure of reverse osmosis membranes. (3) All the models, theories, and mechanisms that have been proposed to describe water transport in reverse osmosis membranes. (4) Revisiting the solution–diffusion model and analyzing its associated experimental results. (5) How recent experimental and computational studies support a pore-flow mechanism for water transport in reverse osmosis membranes. |
1. Introduction
Water scarcity—when the demand for water surpasses the available supply—is one of the pressing societal challenges of our time.1,2 Freshwater, the most precious substance in our planet, is vital for human and ecosystem health as well as for economic growth and national security.1 Rapid global population growth, urbanization, and climate change exacerbate water scarcity in many parts of the world.3–5 At the core of addressing the water scarcity challenge, seawater desalination and water purification technologies can play a significant role in providing an adequate water supply.5 Reverse osmosis (RO) desalination, a membrane-based separation technology, is the most commonly used technology to secure additional freshwater supply and meet the ever-increasing demand in water-stressed regions all over the world.6–8 Today, RO-based desalination plants alone account for about 70% of the global desalination capacity.9The first municipal RO plant, built in 1965, produced 5000 gallons of freshwater per day to the residents of Coalinga, California.10 This early RO plant utilized a cellulose acetate membrane, an asymmetric polymeric membrane that was invented by S. Loeb and S. Sourirajan in 1960.11 However, RO technology owes its success in part to the development of highly permeable thin-film composite (TFC) membranes by J. Cadotte in the early 1970s.9,12 These TFC membranes are made of a thin polyamide layer on top of a porous support layer.5,12 Separation of water molecules from other species (e.g., salt ions) occurs within the thin polyamide layer.13 Because of their superior desalination performance over cellulose acetate membranes, TFC membranes have become the gold standard for RO applications.12
Despite the dominance of TFC membranes in desalination technology, their performance is hindered by some inherent properties of the thin active layer,9 most notably the lack of control of pore size uniformity which results in the permeability-selectivity tradeoff,5,14 propensity for fouling,15 and degradation in the presence of oxidants.16 Over the past few decades, extensive research has been carried out to improve the performance of these membranes. According to the records of Web of Science, more than 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 research articles (including proceeding papers) have been published in the area of reverse osmosis since 1970. Over 75% of these articles have been published since 2010, showing how RO-related research efforts have been intensified in recent years. Despite these efforts, advances in the development of membrane materials have remained limited, relying primarily on trial-and-error approaches, with little regard for the mechanism of water and salt transport.6,17,18 Substantially improving RO technology through redesigning TFC membranes or developing next-generation membranes requires a fundamental understanding of water and salt transport mechanisms.
000 research articles (including proceeding papers) have been published in the area of reverse osmosis since 1970. Over 75% of these articles have been published since 2010, showing how RO-related research efforts have been intensified in recent years. Despite these efforts, advances in the development of membrane materials have remained limited, relying primarily on trial-and-error approaches, with little regard for the mechanism of water and salt transport.6,17,18 Substantially improving RO technology through redesigning TFC membranes or developing next-generation membranes requires a fundamental understanding of water and salt transport mechanisms.
Two types of mechanisms were proposed to describe water transport in RO membranes. The first is the pore-flow (PF) model where water transport inside the membrane is driven by a pressure gradient. The second is the solution–diffusion (SD) model where water transport is governed by diffusion down a concentration gradient. Since the birth of RO technology, a debate has erupted over which model represents the true mechanism of water transport.18 By the late 1970s, the SD model had become the widely accepted mechanism for water transport in RO membranes.18 However, recent findings appear to challenge the SD model's key assumptions in describing water transport through RO membranes. Therefore, there is a critical need to revisit the models, theories, and mechanisms for describing water transport in RO membranes.
In this tutorial review article, we first provide a chronological timeline of the key historical developments relevant to RO technology, from the discovery of osmosis in the 18th century to the development of the recent models for transport in RO membranes. We then describe the chemical and physical structure of RO membrane materials and relevant analytical characterization techniques. Next, we review the key models and mechanisms that have been developed to describe water transport in RO membranes. In light of the recent experimental and computational findings, we provide an in-depth analysis of these proposed transport models, determining which model is appropriate for describing water transport in RO membranes. We conclude our analysis by proposing future research directions, thereby guiding the future design and development of next-generation membranes.
2. Historical background and model classification
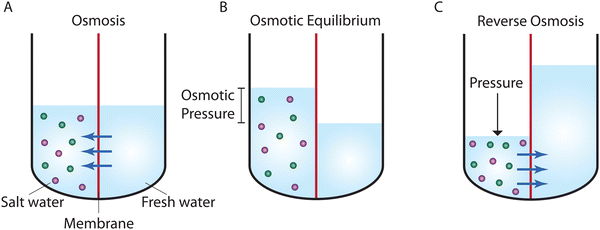
Osmosis, which is described in Fig. 1A, was first discovered by the 18th-century French physicist Jean-Antoine Nollet.19 More than a century later, it was Wilhelm Pfeffer20 who devised a method to conduct the first experiment measuring osmotic pressure across a membrane. These early measurements of osmosis were then used by van’t Hoff21 as the foundation for developing the theory of solutions in 1886. In this theory, solutes are assumed to behave like gas particles where the osmotic pressure is proportional to the molarity of the solution. van’t Hoff21 proposed a mechanism for osmosis where the osmotic pressure was assumed to be produced by one-sided bombardment of the membrane by solute molecules. He later abandoned the bombardment mechanism, stating that the true mechanism of osmosis was irrelevant as the osmotic pressure does not depend on the nature of the membrane.22 According to Ferry,23 who wrote a comprehensive review on ultrafilter membranes in 1934, the early proposed transport mechanisms were mostly based on mechanical sieving where small components of the solution are able to diffuse or flow through pores of the membrane. However, treating semipermeable membranes purely as mechanical sieves is a crude simplification considering that different types of interactions (e.g., Coulombic interactions) exist between the solution and membrane.At osmotic equilibrium (Fig. 1B), a hydrostatic pressure is established to stop the passage of the solvent by osmosis. This pressure is known as the osmotic pressure. When a pressure higher than the osmotic pressure is applied to the high concentration side, the solvent transport is reversed in a process known as reverse osmosis (Fig. 1C). The idea of utilizing reverse osmosis as a method to desalinate seawater was first proposed by C. E. Reid in 1953.24 Prior to this, however, G. L. Hassler proposed the same idea in an unpublished document in 1950.25 C. E. Reid's work was supported by the Office of Saline Water of the United States Department of the Interior.24 As a result of this funded program, C. E. Reid and E. K. Breton were able to discover cellulose acetate as a membrane material that possesses the semipermeable properties required for producing fresh water from saline water.26 This was done by employing a trial-and-error approach where the semipermeability of 19 different membranes was examined. These symmetric membranes, however, produced very low water fluxes, rendering them unsuitable for practical desalination applications.
A parallel research program at the University of California, Los Angeles, was initiated by S. T. Yuster, with the goal to produce a practical reverse osmosis membrane.27 In 1960, S. Loeb and S. Sourirajan11,28 from Yuster's laboratory developed the first technique for preparing asymmetric cellulose acetate membranes with sufficiently high water permeabilities to attract industrial interest. Following the breakthrough discovery of the asymmetric cellulose acetate membranes, the Office of Saline Water of the US Department of the Interior intensified research for addressing the knowledge gaps in our phenomenological understanding of transport and selectivity in such membranes. In addition, these developments led to the birth of membrane-related journals such as The Journal of Applied Polymer Science in 1959, Desalination in 1965, and later, The Journal of Membrane Science in 1976.25
Two general classes of models have been proposed to describe transport in RO membranes. The first class is based on irreversible thermodynamics,29 which treats the membrane as a black box where no information about the molecular mechanism of transport and microstructure of the membrane is required. The second class of models assumes a specific transport mechanism and subsequently derives expressions for water and solute fluxes based on the proposed mechanism. Within the second class, two transport mechanisms based on viscous pore flow and molecular diffusion have been assumed to formulate their associated models (i.e., the pore-flow model and solution–diffusion model) for describing transport in RO membranes.
The pore-flow model assumes that water flow is driven by a pressure gradient within the membrane. Lonsdale and coworkers,30 in their progress report to the Office of Saline Water in 1964, argued against the pore-flow model. They argued that in porous membranes, like ultrafiltration, the salt rejection decreases with increasing salt concentration due to charge screening, or as we understand nowadays due to reduced Donnan exclusion. Since cellulose acetate membranes have a high degree of ion rejection even at high salt concentrations, they argued that the pore sizes would have to be very small (i.e., on the order of the Debye length which is less than 0.5 nm for seawater), thereby not consistent with membranes having a pore structure.30 Following this line of argument, Lonsdale and coworkers31 proposed the solution–diffusion model which assumes molecular diffusion down a water concentration gradient within a non-porous membrane. Lonsdale and coworkers31 did not explain how a water concentration gradient is established within the membrane and what the role of the applied pressure is. Later in 1970, Paul and Ebra-Lima32 mathematically incorporated the concept of pressure-induced concentration gradient into the solution–diffusion framework by assuming that the pressure within the membrane remains uniform. In the following sections, we thoroughly review these transport models.
With apparent experimental evidence in favor of the SD model provided by Rosenbaum and Cotton33 and Paul and Ebra-Lima,32,34 the SD model for water transport became widely accepted by the scientific community in the late 1970s.35 These experiments, which are critically challenged in Section 8.1, claimed that a water concentration gradient exists within a membrane and that the water flux changes non-linearly at high applied pressures, consistent with the SD description. In 1995, the SD model was revisited by Wijmans and Baker,35 where an equation was derived for the salt flux in addition to the solvent flux equation given by Paul and Ebra-Lima.32
Despite the wide acceptance of the SD model, recent experimental and computational studies have challenged the core assumptions of the model.36 For example, advances in electron microscopy led to discovery of interconnected sub-nanometer pores in fully-aromatic polyamide RO membranes.37–41 Positron annihilation lifetime spectroscopy (PALS) revealed the average size of these pores in the polyamide RO membranes to be around 4–5 Å and 7–9 Å.42,43 The presence of such pores is not consistent with the assumption of dense, non-porous SD membranes. Additionally, recent molecular dynamics (MD) simulations suggest that water molecules move through inter-connected “pockets” inside the polyamide membrane without being dispersed.13,36,44,45 In marked contrast to the SD model, these simulations36 further show that water flux follows a linear relationship with pressure and water is driven by a pressure gradient within the membrane. These simulations are reviewed in detail in Section 8.2.
In the absence of an accurate model to describe transport in RO membranes, Biesheuvel, Elimelech, and coworkers46–50 developed a pore-flow transport model based on force balance on the solution species as they pass through RO membranes. This model, known as the solution–friction (SF) model, describes the coupled transport of water and ions. This approach is advantageous over Darcy's law, which is widely used for the pore-flow mechanism and only describes flow of water in RO membranes. More details about Darcy's law and the SF model are discussed in Sections 6 and 7.
A historical timeline of the developments discussed in this section is illustrated in Fig. 2.
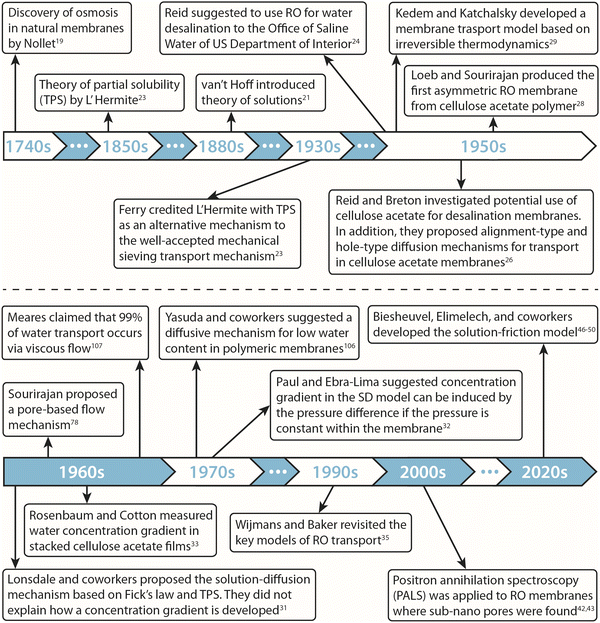 | ||
| Fig. 2 Historical timeline of the development of transport models and membrane materials for reverse osmosis processes. | ||
3. Chemical and physical structure of reverse osmosis membranes
3.1 Chemical structure
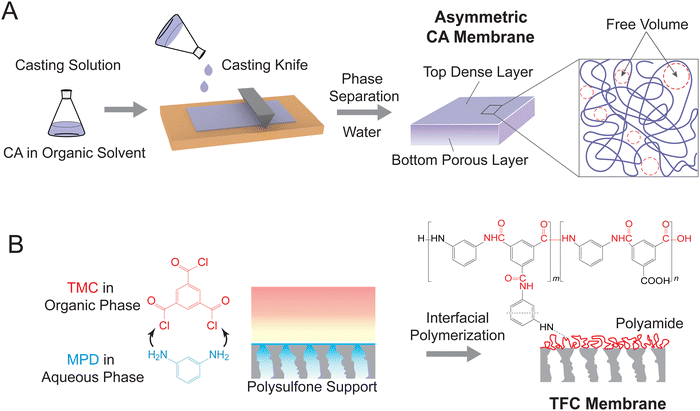
State-of-the-art reverse osmosis (RO) membranes can be categorized into two main types: asymmetric cellulose acetate (CA) membranes and thin-film composite (TFC) membranes.51 CA membranes are fabricated through a process known as non-solvent induced phase separation (NIPS), which involves the controlled precipitation of a dissolved polymer to create a porous membrane structure (Fig. 3A). In this process, a casting solution containing CA polymer and an organic solvent is spread as a thin film on a smooth substrate, followed by immersion in a non-solvent (typically water) to induce phase separation.52 The resulting membranes exhibit a typical asymmetric structure, with a dense layer on top of a porous bottom layer. Notably, the entanglement of CA polymer chains results in free volume or pore network within the dense layer. This free volume governs the water permeance and water-salt selectivity of the CA membranes.TFC membranes are fabricated through interfacial polymerization (Fig. 3B), which allows for the facile synthesis of an ultrathin selective layer.18 During this process, a porous support membrane is first immersed in an aqueous solution of diamine, most commonly m-phenylenediamine (MPD). The impregnated support layer is then brought into contact with an organic solution of acyl chloride—trimesoyl chloride (TMC). The immiscible water and organic solvent create an interface where a polycondensation reaction between MPD and TMC takes place, forming a thin layer of polyamide. As shown in Fig. 3B, the polyamide layer has a heterogeneous chemical structure consisting of a fully crosslinked portion with three amide linkages (i.e., “m” segment with a chemical structure of C18H12N3O3) and a linear portion with a free pendant carboxyl group (i.e., “n” segment with a chemical structure of C15H10N2O4). The crosslinked structure results in different pore structures, namely intrachain network pores and interchain aggregated pores. The networks constitute small pores generated within each polymer aggregate, while the aggregated pores are large chain-to-chain spaces between the aggregates containing crosslinked network pores.43,53
3.2 Physical structure and pore characteristics
Owing to significant challenges in analyzing the internal structure of RO membranes, previous studies assumed a non-porous structure of RO membranes.18,42 Consequently, permeation of solutes and solvent through RO membranes was traditionally described by the solution–diffusion model, which assumes the absence of pores in RO membranes.18,52 However, recent advances in characterization techniques have provided valuable insights into the internal structure of RO membranes,9,42,53 revealing the existence of a pore network in the membrane active later. These findings are vital for understanding the water and solute transport mechanisms, as well as for guiding the design of high-performance membranes.Positron annihilation lifetime spectroscopy (PALS) is a powerful tool for probing the free volume structure of polyamide membranes (Fig. 4A).42,54,55 During the measurement, low-energy positrons are injected into the polyamide layer, where each positron combines with an electron to form an electron-positronium (o-Ps) ion (left panel). These o-Ps ions accumulate in electron-deficient regions, such as free volume and pores, and undergo a slow self-annihilation process with a long lifetime. In electron-rich regions occupied by the polyamide matrix, the o-Ps ions interact with surrounding molecularly bound electrons, leading to a rapid annihilation process with a short lifetime. By correlating the lifetime of the injected positrons with the void size, PALS can provide valuable information on pore structure, such as size, distribution, and film thickness (middle panel). Using this technique, studies revealed a bimodal distribution of free volume radii (right panel), corresponding to the smaller intrachain network pores (radius of ∼2.0 Å) and the larger interchain aggregated pores (radius of ∼4.0 Å).43,53
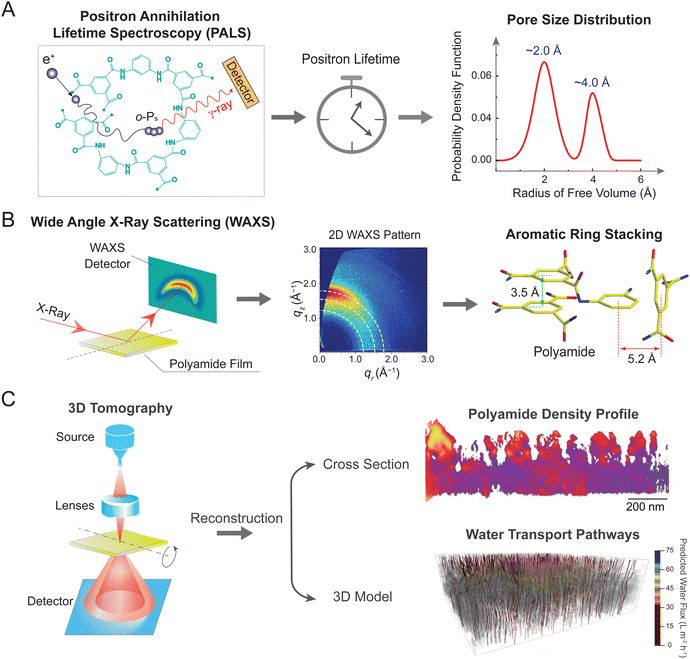 | ||
| Fig. 4 Emerging techniques for determining pore or free volume structure of RO membranes. (A) Positron annihilation lifetime spectroscopy (PALS). Injected low-energy positrons combine with an electron to form an electron-positronium (o-Ps) ion (left panel). These o-Ps ions undergo an annihilation process with the material matrix. By correlating the lifetime of the injected positrons with the void size (middle panel), PALS can reveal pore size distribution of the selective layer. A representative bimodal pore size distribution for polyamide TFC membranes (right panel). (B) Wide-angle X-ray scattering (WAXS). A membrane film is exposed to incident X-rays and scattered signals are detected by a 2D detector (left panel). Analysis of the 2D WAXS pattern (middle panel) reveals different stacking arrangements of aromatic rings in the polyamide network (right panel), corresponding to “π–π” parallel structure (with a distance of 3.5 Å) and “T-shaped” orthogonal structure (with a distance of 5.2 Å). Figure in the middle is adapted with permission from ref. 56 American Chemical Society. (C) Three-dimensional (3D) tomography. Schematic illustration of tomography analysis using high-angle annular dark-field (HAADF) scanning transmission electron microscopy (STEM) (left panel). A sample film is tilted at different angles to collect a range of high-resolution 2D images. Reconstruction of these 2D images results in a 3D structural model that enables analysis of polyamide density profile (upper right panel) and water transport pathways (lower right panel). The color bar represents predicted water flux in water transport pathways, ranging from 0 (dark red) to 75 (dark blue) L m−2 h−1. Figures are adapted with permission from ref. 41, the American Association for the Advancement of Science. | ||
Following the insights on pore size distribution, wide-angle X-ray scattering (WAXS) has been employed in recent years to investigate the molecular-level pore structure (Fig. 4B).56 Measurements were conducted by exposing a polyamide film to incident X-rays, with scattered signals subsequently collected by a detector (left panel).57 Analysis of two-dimensional (2D) WAXS patterns provides information on both molecular size and preferential orientation of polyamide network. Particularly, an arc-like meridional scattering feature in the WAXS pattern (middle panel), where intense scattering is preferentially aligned along the vertical qz direction, implies the in-plane orientation of aromatic stacking in the polyamide film.56 Plotting the scattered intensity versus scattering vector, q, suggests the presence of two peaks centered at 1.79 and 1.22 Å−1. According to Bragg's law (d = 2π/q), these two peaks correspond to molecular spacing, d, of 3.5 and 5.2 Å, respectively—generally consistent with the size of intrachain network pores observed by PALS. The 3.5 Å spacing is likely ascribed to “π–π” stacking of neighboring aromatic rings (green arrows in the right panel), while the 5.2 Å spacing is owing to the perpendicular packing of aromatic cores in a “T-shaped” configuration (red arrows in the right panel).56 These different stacking structures likely govern the mass transport characteristics of TFC membranes. For instance, previous studies have observed more favorable water self-diffusion in the “T-shaped” stacking than that in the “π–π” stacking.56,57
Recent advances in 3D tomography have enabled high-resolution imaging of pore structure (Fig. 4C).41,58 This technique relies on the use of scanning transmission electron microscopy (STEM), which utilizes a focused probe to scan across a sample (left panel). Dynamic focus of STEM effectively reduces defocus variation when imaging thick samples at high-tilt angles. Moreover, operating in high-angle annular dark-field (HAADF) mode enables STEM to decouple structural parameters of polyamide layers (e.g., density and thickness), thereby allowing for the independent analysis of nanoscale 3D distributions of each parameter. For example, a recent study mapped the spatial distribution of polyamide density, which is displayed as a heat map in the cross-section profile (right upper panel).41 The polyamide network exhibits nanoscale inhomogeneity, where red corresponds to areas with higher density and lower fractional free volume. Acquisition of tomographic tilt series at different angles enables 3D reconstruction of density profiles. The resulting 3D model, together with the modeling of water transport, leads to a visualized flow map of water transport pathways (right lower panel). In particular, gray areas represent regions of ultralow water diffusivity in membrane materials (Dw < 5 × 10−10 m2 s−1), corresponding to regions of high polyamide density and low fractional free volume. Notably, water transport pathways with the lowest water flux are predominantly located near the top surface of the polyamide layer, indicating regions of greatest resistance for water transport.
4. Irreversible thermodynamics-based models
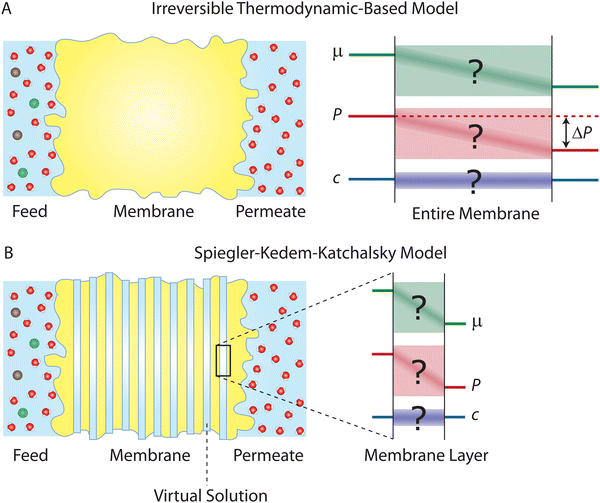
One major approach to describe the physical behavior of membrane permeation is based on non-equilibrium or irreversible thermodynamics.29,59–61 The significant progress in non-equilibrium thermodynamics in 20th-century physics paved the way for the development of first-principles-based thermodynamic theories for membrane transport. A central assumption in these theories is that irreversible transport processes in membranes can be divided into small subsystems at “local equilibrium”, i.e., not deviating too far from equilibrium. This assumption allows to express the fluxes across the membranes as linear functions of thermodynamic driving forces (Fig. 5A). Here, we review the seminal works by Kedem, Katchalsky, and Spiegler.29,614.1 The Kedem–Katchalsky model
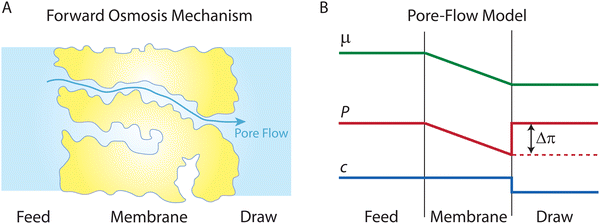
In 1958, Kedem and Katchalsky29 systematically formulated a theoretical framework for membrane permeation using irreversible thermodynamics. In irreversible processes, the rate of entropy density change, or the dissipation function, Φ, can be expressed as the summation of the product of fluxes, J, and thermodynamic forces, X; that is,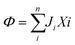 , where i is a component in the solution.
, where i is a component in the solution.
In an isothermal membrane process transferring water (w) and solute (s), the water and solute fluxes and the driving forces of the chemical potential differences, Δμ, form the dissipation function as follows:
| Φ = JwΔμw + JsΔμs | (4.1) |
The chemical potential of any component, i, can be defined as
μi = μ0i + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (γici) + (γici) + ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) i(P − P0) i(P − P0) | (4.2) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) is the partial molar volume, P is the pressure, and P0 is the reference pressure of the standard state condition. The chemical potential difference between the feed and permeate solutions, μ, is given by
is the partial molar volume, P is the pressure, and P0 is the reference pressure of the standard state condition. The chemical potential difference between the feed and permeate solutions, μ, is given byΔμi = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δln Δln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (γici) + (γici) + ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) iΔP iΔP | (4.3) |
Assuming that we have dilute solutions (where activity coefficients can be disregarded) and small differences in concentration across the membrane, the chemical potential differences of water and solute can be written as a function of solute concentration difference, cs, and pressure difference, P, between feed and permeate:29
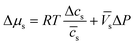 | (4.4a) |
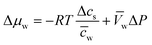 | (4.4b) |
![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) s and
s and ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) w are the mean solute and water concentrations in the feed and permeate, respectively. Substituting eqn (4.4a) and (4.4b) into eqn (4.1) yields an expression for Φ as a function of pressure and solute concentration differences:
w are the mean solute and water concentrations in the feed and permeate, respectively. Substituting eqn (4.4a) and (4.4b) into eqn (4.1) yields an expression for Φ as a function of pressure and solute concentration differences: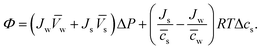 | (4.5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δcs can be defined as the total volume flux, Jv = Jw
Δcs can be defined as the total volume flux, Jv = Jw![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) w + Js
w + Js![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) s, and the relative velocity of solute with respect to solvent,
s, and the relative velocity of solute with respect to solvent, 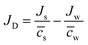 , respectively.
, respectively.
The general theory of linear irreversible thermodynamics describes the relationships between the newly-defined fluxes and forces as29,62
Jv = LpΔP + LpD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RT RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δcs Δcs | (4.6a) |
| JD = LDpΔP + LDRTΔcs | (4.6b) |
Considering the Onsager reciprocal relations63,64 (i.e., LpD = LDp) and rearranging eqn (4.6), the volume flux, Jv, which is approximately the same as the water flux (i.e., Jv = Jw), and salt flux, Js, can be expressed as
| Jv = Lp(ΔP − σΔπ) | (4.7a) |
Js = ωΔπ + (1 − σ)Jv![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) s s | (4.7b) |
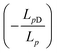 , Δπ is the osmotic pressure difference, ω is the solute mobility
, Δπ is the osmotic pressure difference, ω is the solute mobility 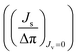 , and
, and ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) s is mean solute concentration of the feed and permeate. Different approximations may yield
s is mean solute concentration of the feed and permeate. Different approximations may yield ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) s as either an arithmetic29 or logarithmic mean
s as either an arithmetic29 or logarithmic mean 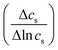 .59,65
.59,65
Eqn (4.7a) and (4.7b) are the core transport equations of the volume (water) and solute fluxes in the Kedem–Katchalsky model. We note that σ is equal to 1 when the membrane is ideally selective to solvent. Since RO membranes have a high salt rejection and the reflection coefficient can be set to 1 (σ = 1), eqn (4.7a), which is simplified as Jv = LP(ΔP−Δπ) for σ = 1, has been frequently used for describing water transport in RO membranes.
4.2 Improvement of the Kedem–Katchalsky model
The Kedem–Katchalsky equations, i.e., eqn (4.7), were derived by assuming that we have small thermodynamic forces, i.e., small pressure and concentration differences. For large pressure or concentration differences, the Kedem–Katchalsky model may predict inaccurate fluxes. Spiegler and Kedem61 improved the model by treating the membrane as a series of infinitesimal slices (Fig. 5B). Virtual solutions, which are imaginary aqueous solutions in equilibrium with the adjacent membrane layers, are inserted between the slices. The local transport equations are then expressed as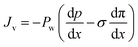 | (4.8a) |
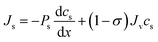 | (4.8b) |
The Spiegler–Kedem model,61 as an extension of the Kedem–Katchalsky model,29 yields less sensitive kinetic parameters to concentration differences.59,66 The considerations of large driving forces and the dependency of the kinetic coefficients on external conditions, such as pressure and concentration, are essential in improving the irreversible thermodynamic models.65 These questions may always be revisited for certain membranes and operating conditions. In addition to their efforts to enhance the accuracy of the model, Spiegler and Kedem expressed the reflection coefficient as a function of frictions within the membrane. However, the frictional relationship has relatively limited impacts compared to eqn (4.8a) and (4.8b), and fewer researchers adopted the relationship in membrane research.59,67
4.3 Significance of the irreversible thermodynamic models
The significance of the irreversible thermodynamics-based models developed by Kedem, Katchalsky, and Spiegler cannot be overstated. These models have had a profound impact on the field of membrane science and continue to shape our understanding of transport phenomena across membranes. Although they may be less discussed in contemporary membrane research, their contributions remain invaluable. The formalism reveals the essential relationships between fluxes and driving forces, standing with the rigor of thermodynamic principles. These a priori descriptions, such as eqn (4.7), of membrane water and salt permeation are the basis for understanding membrane transport.Notably, these thermodynamic principles are valid for any transport mechanisms or membrane microstructures. Therefore, when examining the transport mechanisms in RO membranes, the proposed models should not violate these basic thermodynamic laws. By adhering to these principles, researchers ensure that their analyses and interpretations uphold the fundamental laws that govern the behavior of transport phenomena.
In addition to mechanistic discussions, these models provide invaluable insights in designing or evaluating membrane processes within the framework of thermodynamics. Based on the established equations, the thermodynamic minimum energy required for separation is correlated with the osmotic pressure, while the excess energy from the applied pressure is dissipated through the membrane transport.68,69 In the development of new RO-based desalination processes, like low-salt-rejection RO (LSRRO),70 the reflection coefficient is crucial for characterizing the transport of “leaky” membranes.71 Overall, the irreversible thermodynamic models remain invaluable for investigating membrane transport and devising practical applications.
5. Diffusion-based models
In this section, we discuss the diffusion-based models that have been proposed to describe water transport in RO membranes. Our discussion begins with the very early diffusion-based models, ultimately leading to the solution–diffusion model. Generally, molecular diffusion is the thermal motion of molecules which results in a directional transport of molecules when a concentration gradient is present as described in Box 1.
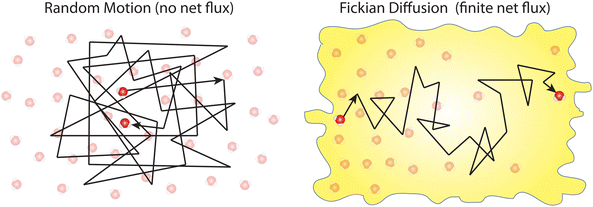
Box 1. Molecular diffusionMolecules in a fluid randomly move in different directions as a result of continuous collisions with neighboring molecules (left figure). This random motion is known as Brownian motion which is named after the Scottish botanist Brown.72 Brown was the first to observe the random motion of pollen grains under a microscope. In this case, there is no preferential direction of motion, which results in no net flux over time. However, these random motions cause molecules in a fluid to spread out. The degree to which molecules spread out and diffuse is described by the mean squared displacement (MSD) of molecules as follows:73
When there is a gradient in concentration of molecules (right figure) dispersed in a medium, molecules diffuse from a region of high concentration to a region of low concentration. Fick,74 who first observed a linear relationship between concentration gradient and mixing of salt and water, proposed the governing equations for diffusion based on an analogy with Fourier's law for heat conduction. In the first governing equation, known as Fick's first law, the flux of the dispersed molecules in a one-dimensional system is given by73
We emphasize that no net flux is produced as a result of random motion of molecules in a fluid (left figure). However, when there exists a concentration gradient of fluid molecules in a medium, a net flux is brought about by diffusion of molecules down the gradient (right figure). |
5.1 Early diffusion-based model for water transport in cellulose acetate
After reporting cellulose acetate as a potential membrane material for desalination, Reid and Breton26 proposed the first diffusion-based model for describing water transport in RO membranes. In their model, two specific diffusion mechanisms were suggested to describe water transport. In small pores where water molecules interact strongly with the membrane binding sites (e.g., hydrogen bonding to carbonyl oxygen atoms of cellulose acetate), water molecules were postulated to diffuse by jumping from one binding site to another through a network of aligned hydrogen bonds (i.e., alignment-type diffusion). On the other hand, water molecules in larger pores, which are not bound to the membrane walls, were proposed to transport by hole-type diffusion. Since cellulose acetate membranes have a high degree of crystallinity, the pore sizes were assumed to be small enough for transport to be mostly governed by alignment-type diffusion. Notably, no experimental or theoretical proofs for this water transport mechanism were given.Other diffusion-based models were proposed for water transport. For example, Clark75 proposed a modified diffusion coefficient which relates water flux directly to chemical potential gradient:
 | (5.1) |
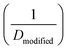 . This model treats chemical potential gradient as a single unifying driving force that drives a specific diffusive transport.
. This model treats chemical potential gradient as a single unifying driving force that drives a specific diffusive transport.
5.2 The solution–diffusion model
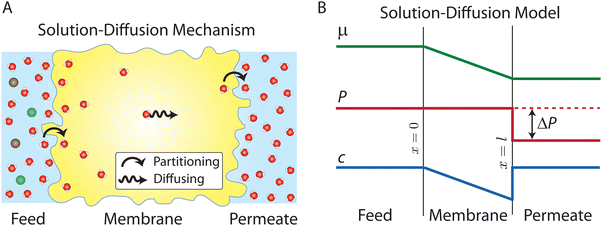
Contrary to the early diffusion mechanisms discussed in Section 5.1, Lonsdale et al.31 proposed that water transport is governed by simple molecular diffusion down a concentration gradient across the membrane where no specific modification to diffusion is needed. In this model, which came to be known as the solution–diffusion model, water molecules are assumed to dissolve into the membrane, based on the theory of partial solubility proposed by LHermite,23 diffuse through the membrane, and then partition out of the membrane (Fig. 6A).23 Lonsdale et al.31 mathematically formulated the water transport through RO membranes by applying Fick's law of diffusion. Notably, Lonsdale's SD description of transport did not explain how a pressure difference across the membrane induces a concentration gradient within the membrane. Later, Paul and Ebra-Lima32 incorporated this pressure-induced concentration gradient into the SD framework by assuming a constant pressure profile within the membrane. In the following paragraphs, we will present the key steps in the derivation of the SD equation for water transport in RO membranes.The gradient in chemical potential is the thermodynamic driving force that results in the transport of any permeants across a membrane.35 Accordingly, as discussed in Section 4, the flux of any component, i, can be expressed as
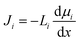 | (5.2) |
In the SD model, the pressure within the membrane is assumed to be constant and equal to the pressure in the feed reservoir (Fig. 6B). This assumption, which has never been proved to be true, implies that the pressure is transmitted through the membrane the same way it is transmitted through the feed water. In the absence of a pressure gradient within the membrane, the chemical potential gradient must be expressed only as a concentration gradient. Therefore, using eqn (4.3) and (5.2), the flux can be rewritten as
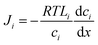 | (5.3) |
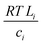 with the diffusion coefficient Di in eqn (5.3), we arrive at Fick's first law of diffusion for a single phase:
with the diffusion coefficient Di in eqn (5.3), we arrive at Fick's first law of diffusion for a single phase: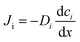 | (5.4a) |
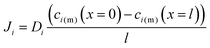 | (5.4b) |
Lonsdale et al.31 used eqn (5.3) as the starting point to mathematically derive the flux equation for water transport in the SD model. However, Paul and Ebra-Lima32 employed Fick's law of diffusion for a binary system (i.e., fluid and membrane material which are uniformly mixed) in their derivation of an expression for the fluid volumetric flux, Qi, which is given by
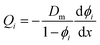 | (5.5) |
A reasonable assumption is that chemical equilibrium is maintained at the feed and permeate interfaces. To enforce the chemical equilibrium at the feed interface, we equate the chemical potential on either side of the interface, μi(x = 0) = μi(m)(x = 0). Using eqn (4.2) and assuming that ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) i =
i = ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) i(m), the equilibrium condition can be stated as
i(m), the equilibrium condition can be stated as
μ0i + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[γi(x = 0)ci(x = 0)] + ln[γi(x = 0)ci(x = 0)] + ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) i[P(x = 0) − P0] = μ0i + RT i[P(x = 0) − P0] = μ0i + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[γi(m)(x = 0)ci(m)(x = 0)] + ln[γi(m)(x = 0)ci(m)(x = 0)] + ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) i(m)[P(m)(x = 0) − P0] i(m)[P(m)(x = 0) − P0] | (5.6) |
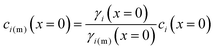 | (5.7) |
| ci(m)(x = 0) = Kici(x = 0) | (5.8) |
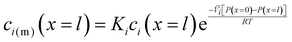 | (5.9) |
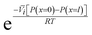 , appears in eqn (5.9) when compared to eqn (5.8) because the pressure in the membrane (i.e., P(m)(x = l)) abruptly drops to the permeate pressure (i.e., P(x = l)) at the permeate interface (see Fig. 6B).
, appears in eqn (5.9) when compared to eqn (5.8) because the pressure in the membrane (i.e., P(m)(x = l)) abruptly drops to the permeate pressure (i.e., P(x = l)) at the permeate interface (see Fig. 6B).
Inserting the expressions for the interface concentrations, eqn (5.8) and (5.9), into the Fick's law expression in eqn (5.4), the flux can be rewritten as
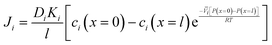 | (5.10) |
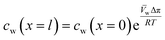 | (5.11) |
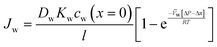 | (5.12) |
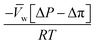 , is a very small value in practice. Therefore,
, is a very small value in practice. Therefore, 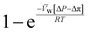 can be approximated by
can be approximated by 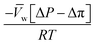 , which results in the final expression for the water flux:
, which results in the final expression for the water flux: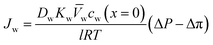 | (5.13a) |
| Jw = A(ΔP − Δπ) | (5.13b) |
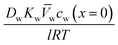 .
.
For the salt flux, the exponent 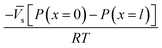 in eqn (5.10) is small because the molar volume of salt is large. Therefore, the salt flux can be obtained from the following simple expression:
in eqn (5.10) is small because the molar volume of salt is large. Therefore, the salt flux can be obtained from the following simple expression:
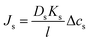 | (5.14a) |
| Js = BΔcs | (5.14b) |
 . Notably, salt flux is independent of the applied pressure according to the SD model.
. Notably, salt flux is independent of the applied pressure according to the SD model.
Eqn (5.13) and (5.14), obtained within the framework of the SD model, have been extensively used to describe water and salt transport in RO since the 1980s.35 However, some of the predicted behaviors by the SD model have been questioned. For example, eqn (5.9) predicts that the water concentration at the permeate interface inside the membrane exponentially decreases with increasing applied pressure difference. In other words, as the pressure difference increases, the water flux in eqn (5.12) reaches a limiting value (i.e., as ΔP → ∞, 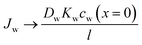 ), resulting in a non-linear flux-pressure relationship. We further discuss this behavior in Section 8.
), resulting in a non-linear flux-pressure relationship. We further discuss this behavior in Section 8.
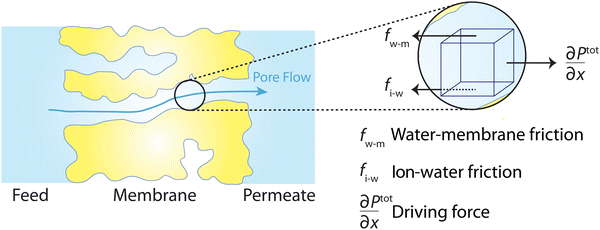
6. Viscous flow models
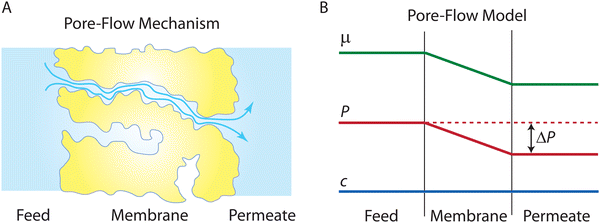
Following the demonstration of cellulose acetate as a semipermeable membrane material by Reid and Breton,26 Loeb and Sourirajan28 breakthrough discovery showed that making cellulose acetate membranes asymmetric can significantly enhance water flux. Soon after these discoveries, Sourirajan78 proposed an RO transport model that assumes a viscous-type flow mechanism (Box 2) for water transport in cellulose acetate membranes. This model was called the preferential sorption-capillary flow model. Inspired by Yuster,27 Sourirajan78 claimed that water is deionized at the feed interface because of the chemical nature of the membrane (preferential sorption) and then flows continuously through pores of the membrane (capillary flow).Other viscous-type flow models were also suggested. For example, Merten79 developed the finely-porous model which includes aspects of viscous-type flow and frictional models. However, the most widely-used viscous flow model is known as the pore-flow (PF) model (Fig. 7).35 In the PF model, a continuum water flow through the membrane pores is driven by a pressure gradient. As shown in Fig. 7B, water is assumed to be incompressible with a fixed concentration throughout the membrane. In this section, we will derive the PF expression describing flow through semipermeable membranes by revisiting eqn (5.2).
Since the chemical potential gradient is only expressed as the pressure gradient (Fig. 7B), combing eqn (4.3) and (5.2) yields the following expression for the water flux:
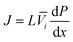 | (6.1) |
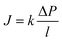 | (6.2) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) i. Eqn (6.1) or (6.2) can also be obtained by solving the Navier–Stokes equation for flow through a porous medium (i.e., known as Darcy flow80). Values of k depend on the solvent viscosity and structure of the membrane pores.81 Although the PF mechanism was predominantly rejected over the SD mechanism by the late 1970s,35 it has emerged as a reliable method of describing transport in RO membranes in recent studies.36,46,82
i. Eqn (6.1) or (6.2) can also be obtained by solving the Navier–Stokes equation for flow through a porous medium (i.e., known as Darcy flow80). Values of k depend on the solvent viscosity and structure of the membrane pores.81 Although the PF mechanism was predominantly rejected over the SD mechanism by the late 1970s,35 it has emerged as a reliable method of describing transport in RO membranes in recent studies.36,46,82
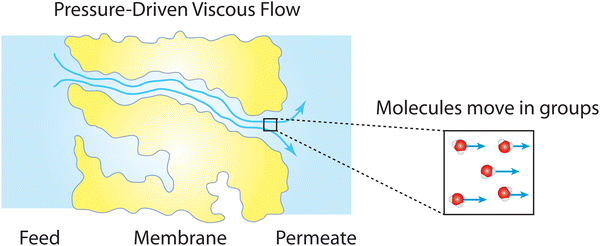
Box 2. Viscous flow through nanoporesViscous flow of a fluid involves transport of fluid molecules in groups (see figure below) which differs from diffusive transport where dispersed molecules travel individually down a concentration gradient as discussed in Box 1.83 The effect of fluid viscosity in a viscous flow is balanced by other forces due to fluid inertia, pressure gradient, and other body forces like gravity. This type of fluid motion is described by the classical continuum equations of motion such as the Navier–Stokes equation.84 The validity of these equations relies on the continuum hypothesis where the distance between the molecules of the fluid is assumed to be much smaller than the volume of the fluid for which the transport behavior is described.84 This hypothesis requires a macroscopically large scale where the fluid is perfectly uniform in structure and its properties are distributed uniformly over the fluid volume.Remarkably, in both experiments and molecular dynamics simulations,85–93 the Navier–Stokes equation has been shown to remain valid down to the nanometer scale when hydrodynamical properties such as viscosity and interfacial friction coefficients are adjusted. Considering the classical continuum hypothesis, the robustness of the Navier–Stokes equation down to the molecular scale is surprisingly unexpected. One possible explanation is that the complexity of fluid properties at the molecular scale can still be averaged out and distributed uniformly over the nanometer-scale fluid volume.85 Essentially, for viscous flow at the nanoscale, properties of fluids with their fine molecular structures and features can be well represented by a few macroscopic quantities (e.g., viscosity and friction coefficient) used in continuum-based equations. |
7. Solution–friction model
Recently, a mechanistic transport model, referred to as the solution–friction (SF) model,36,46–48 was developed based on force balances on the species transporting across an RO membrane. The SF model generally obeys a pore-flow or viscous flow mechanism.36 However, unlike Darcy's law, eqn (6.1), which only describes the pressure-driven water transport across a homogeneous porous medium, the SF model describes the coupled transport of both solvent and solutes. The SF model derives the equations for water and salt fluxes based on their respective force balances. These fluxes are interdependent due to the interactions between salt ions and water molecules. Before presenting the principles and governing equations of the SF model, we present the general concept of friction in Box 3.
Box 3. FrictionWhen there is a difference between the velocities of fluid molecules or/and pore molecules, a friction force is developed to reduce the difference between the velocities.84 For example, as fluid molecules transport through a stationary porous membrane, a friction between the fluid particles and pore walls is developed. Difference in velocities between fluid particles (e.g., water and ions) also result in internal friction. These frictional forces vary in size depending on the intermolecular interactions as well as the structure and chemistry of the fluid-pore interface. For example, friction between carbon nanotubes and water is shown to be very low because of the hydrophobic nature of the tube–water interactions and smooth surface of the tubes.86,94 To characterize these interfacial friction forces between fluids and pore walls, a friction coefficient f can be defined as85
Friction coefficients appear in transport theories that are developed based on force balances. These coefficients cannot be directly determined through experiments. Molecular dynamics simulations offer a reliable approach to calculate friction coefficients and can provide insights into how these coefficients depend on membrane properties such as pore size, chemistry, and structure.86,88 Here, the Green–Kubo formulas can be used to link the macroscopic friction coefficients to the fluctuations of microscopic forces in equilibrium molecular dynamics simulations:95
|
7.1 Ion transport through the membrane
The gradient of chemical potential within the membrane is the driving force for ion flux. Neglecting the frictions between the ions, and accounting for the ion–water and ion–membrane frictions, the force balance for ion i requires that the driving force (i.e., the chemical potential gradient) be equal to the sum of frictions:47,48−∇μi = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fi–w(vi − vw) + RT fi–w(vi − vw) + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fi–mvi fi–mvi | (7.1) |
The ion chemical potential can be expressed by
μi = μ0i + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ci + RT ci + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ziφ ziφ | (7.2) |
Substituting eqn (7.2) into eqn (7.1) yields an expression for the ion velocity:
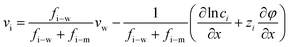 | (7.3) |
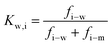 and considering only the coordinate perpendicular to the membrane surface, eqn (7.3) becomes
and considering only the coordinate perpendicular to the membrane surface, eqn (7.3) becomes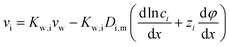 | (7.4) |
7.2 Water transport through the membrane
The driving force of water transport is the gradient in the total pressure (i.e., −∇Ptot),96 balanced by the water–membrane and ion–water frictions as shown in Fig. 8. This balance can be expressed as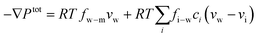 | (7.5) |
| Ptot = P − π | (7.6) |
Substituting the expression of ion velocity, eqn (7.4), into eqn (7.5), we arrive at the following expression for the force balance on water:
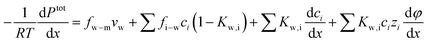 | (7.7) |
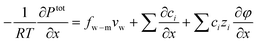 | (7.8) |
A close inspection of eqn (7.4) and (7.7) reveals that the salt transport and water transport are coupled. The equations must be solved simultaneously to obtain the water and salt fluxes for a given applied pressure. Alternatively, one can obtain the salt flux and the required applied pressure for a given water flux.
7.3 Simplified solution to water flux
When a membrane has a low volumetric charge density (i.e., within the membrane), like in typical RO membranes,98–100 the electrical potential gradient can be neglected as it is relatively small compared to the concentration gradient. Therefore, eqn (7.8) can be further simplified as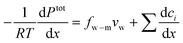 | (7.9) |
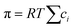 , into eqn (7.9) yields
, into eqn (7.9) yields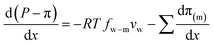 | (7.10) |
A salt partitioning coefficient Φ can be defined to relate π(m) to the osmotic pressure in the virtual solution that is in equilibrium with the membrane π, by π(m) = Φπ. Then we arrive at
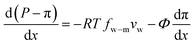 | (7.11) |
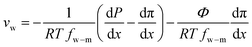 | (7.12) |
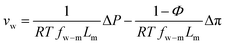 | (7.13) |
Defining 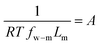 and 1 − Φ = σ, we obtain the water permeability velocity as
and 1 − Φ = σ, we obtain the water permeability velocity as
| vw = A(ΔP − σΔπ) | (7.14) |
We note that eqn (7.14) is identical in form to the Spiegler–Kedem–Katchalsky equation, eqn (4.7a). This ensures that the SF model does not violate the basic thermodynamic principles. The SF model has been able to successfully describe the transport of water and salt in RO membranes, showing good agreement with experiments.36,46,50,98,101
8. Solution–diffusion model versus pore-flow model
In this section, we focus our discussions on the two main mechanisms or models proposed for water transport in RO membranes: the SD and PF models. We conduct a thorough analysis of the recent experimental and computational results to show why the widely-accepted SD model is not appropriate for describing water transport in RO membranes. This analysis also includes revisiting the key experiments that were used as evidence in favor of the SD mechanism.8.1 Evidence in support of the solution–diffusion model is flawed
The solution–diffusion mechanism was historically supported by two key experimental observations: (i) the existence of a pressure-induced water concentration gradient and (ii) upper limit for solvent flux at high applied pressures. To provide evidence for the water concentration gradient within RO membranes, Rosenbaum and Cotton33 designed and performed water permeation experiments using five stacked cellulose acetate films—with a total thickness of ∼0.05 cm— across which pressure differences of 68 and 136 atm were applied. The results showed that the water concentration within the membrane varies with position and its gradient is proportional to the applied pressure (Fig. 9). However, as shown in Fig. 9, there are extreme outliers leading to very large error bars. Therefore, the magnitude of the water concentration gradient that Rosenbaum and Cotton33 drew from their experimental observations may be questionable. Additionally, the data for the 68 and 136 atm pressures in the original study were misplotted. The plotted 136-atm data points match the tabulated data for 68 atm pressure and vice versa. If the tabulated data are taken to be true, their observations disprove their argument, because increasing pressures induce smaller concentration gradients. We will revisit these experiments later in this subsection to explain the mechanisms for the observed behavior.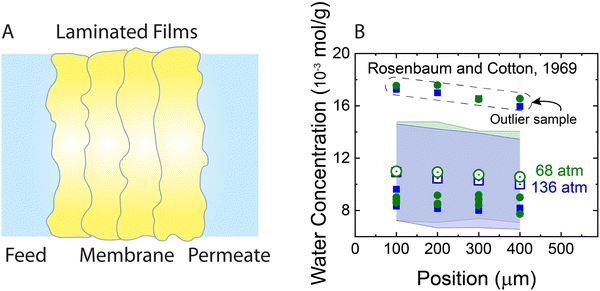 | ||
| Fig. 9 (A) Schematic representation of the stacked films used for measuring water concentration gradients (Rosenbaum and Cotton, 1969).33 The total thickness of the produced membrane is ∼0.05 cm. Five cellulose acetate films were stacked inside a pressurized cell to measure water content along the membrane. First a water permeation experiment was performed through the stacked films. At the end of the permeation experiment after the pressure was relaxed, the water content of each film was measured for only four of the films. (B) Water concentration in stacked cellulose acetate films as a function of position along the axis of transport inside the membrane. Open green circles and blue squares represent average concentrations for two different applied pressures of 68 and 136 bar, respectively. Solid circles and squares indicate the data for each one of the four membrane samples used for calculating the average concentrations. As shown, a group of outlier data points (inside the dashed box) lead to very large error bars (transparent green and blue bands). Note that the error bars were not explicitly presented in the original publication. | ||
As described in Section 5, water flux in the SD model approaches a limiting value as the pressure difference increases (i.e., 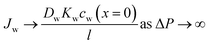 ). Because of the small partial molar volume of water, pressures beyond the common operational range are required to detect any SD-predicted deviation from linearity in the flux-pressure relationship (see eqn (5.12)). Instead of water as solvents, Paul and Ebra-Lima32,34 used organic solvents and a highly swollen rubber film to examine the existence of any limiting fluxes. Fig. 10A presents two representative flux-pressure curves for the solvents considered in their study: iso-octane and methyl ethyl ketone. The flux-pressure curves deviate from linearity as the pressure increases. However, compaction is expected to have a significant impact on the highly elastic and swollen rubber film (volume of sorbed solvent in the membrane is > 60%). Fig. 10B shows that compaction induces similar flux suppression of water transport in highly swollen hydrogels.102 Notably, the SD model predicts that we need pressures >136 bar to cause only ≈5% deviation from linearity for water.103 However, this deviation in Fig. 10 occurs for pressures <10 bar. Compaction is the only reasonable explanation since no other nonideality effects can explain this order of magnitude difference. In addition to the limiting fluxes, we calculated high solvent permeability (>10 μm L m−2 h−1 bar−1) for the rubber film in Fig. 10A, which is typical of ultrafiltration membranes. Therefore, it is questionable to apply these findings for highly porous and swollen rubber films directly to water transport in RO membranes or to consider a diffusion as a possible solvent transport mechanism.
). Because of the small partial molar volume of water, pressures beyond the common operational range are required to detect any SD-predicted deviation from linearity in the flux-pressure relationship (see eqn (5.12)). Instead of water as solvents, Paul and Ebra-Lima32,34 used organic solvents and a highly swollen rubber film to examine the existence of any limiting fluxes. Fig. 10A presents two representative flux-pressure curves for the solvents considered in their study: iso-octane and methyl ethyl ketone. The flux-pressure curves deviate from linearity as the pressure increases. However, compaction is expected to have a significant impact on the highly elastic and swollen rubber film (volume of sorbed solvent in the membrane is > 60%). Fig. 10B shows that compaction induces similar flux suppression of water transport in highly swollen hydrogels.102 Notably, the SD model predicts that we need pressures >136 bar to cause only ≈5% deviation from linearity for water.103 However, this deviation in Fig. 10 occurs for pressures <10 bar. Compaction is the only reasonable explanation since no other nonideality effects can explain this order of magnitude difference. In addition to the limiting fluxes, we calculated high solvent permeability (>10 μm L m−2 h−1 bar−1) for the rubber film in Fig. 10A, which is typical of ultrafiltration membranes. Therefore, it is questionable to apply these findings for highly porous and swollen rubber films directly to water transport in RO membranes or to consider a diffusion as a possible solvent transport mechanism.
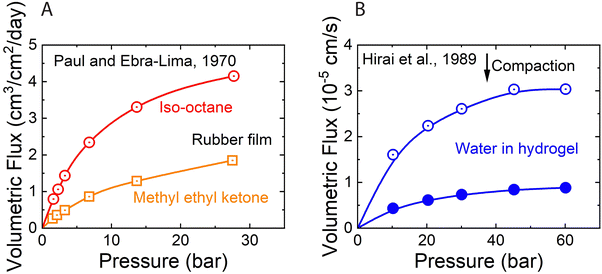 | ||
| Fig. 10 (A) Volumetric flux of organic solvents in highly swollen rubber films as a function of applied pressure. Red and yellow curves correspond to the data for iso-octane and methyl ethyl ketone, respectively. Data extracted from Paul and Ebra-Lima.32 (B) Volumetric flux of water in highly swollen hydrogels as a function of applied pressure. Open and solid circles represent the data for two hydrogels with different water swelling ratios. Data extracted from Hirai et al.102 | ||
Compaction can provide sound explanations for both the observed water content gradient (Fig. 9B) and the nonlinear solvent flux-pressure relationship (Fig. 10A). Based on mechanical equilibrium, the compacting pressure of the membrane, Pc, at any point within the membrane is equal to the feed pressure, Pf, minus the local fluid pressure, P, (i.e., Pc = Pf − P).104 Based on the pressure profile in Fig. 7B, the compacting pressure is expected to rise from zero at the feed side and reach a maximum value at the permeate side. Consequently, the volume fraction of the pores decreases across our elastic membrane along with the rising compacting pressure. The balance between the compacting pressure and other pressure components within the polymer–solvent system can be used to quantitatively predict the porosity profile.105 This dependence of porosity on compacting pressure explains the observations of Rosenbaum and Cotton33 of water content gradient in Fig. 9.
A recent study82 employing the poroelastic theory and treating the solvent within the membrane as a Newtonian fluid, derived a model for the fraction of solvent volume fraction, ϕs, across the membrane as a function of pressure:
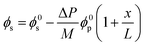 | (8.1) |
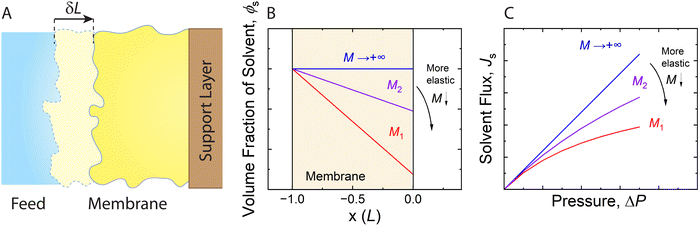 | ||
| Fig. 11 (A) Schematic representation of an elastic membrane compacted under an applied pressure. The change in the thickness of the membrane due to compaction is denoted by δL. (B) Water content gradient within the membrane and (C) solvent flux-pressure relationship as predicted by the poroelastic model.82 The volume fraction of solvent (ϕs) is calculated by eqn (8.1). The solvent flux (Js) as a function of the pressure difference across the membrane (ΔP) is estimated by eqn (8.2). The elastic modulus (M) is assumed to be constant within the membrane for conceptually illustrating the relationships. The membrane with a smaller elastic modulus (red, M1) has a more compressible matrix, showing a larger compaction gradient and greater deviation from linearity in the flux-pressure relationship, compared to a more rigid membrane (purple, M2). A fully inelastic membrane (blue, M → +∞) exhibits constant solvent content across the membrane and a linear flux-pressure relationship, which is identical to Darcy's law. | ||
Meanwhile, the compressed membrane has smaller pores and less accessible space for solvent transport. This confinement induced by compaction can decrease the solvent permeance,106 leading to the non-linear flux-pressure relationship in Fig. 10. The poroelastic model relates the solvent flux Js to the pressure though the following equation:82
 | (8.2) |
It should be noted that when water content varies across the membrane under compaction, it cannot lead to molecular diffusion down the water content gradient. Fig. 12A shows a hypothetical membrane with conical pores (i.e., larger pores near the feed side) when there is no pressure difference. Without any external driving force, it is self-evident that water never flows from the left to the right due to the water content gradient within the membrane. Otherwise, it implies that water would flow without any energy input, like a perpetual motion machine, violating the laws of physics. A more realistic polymeric membrane is illustrated in Fig. 12B where the pores near the feed side are hydrated to a higher degree. With the same line of reasoning, no water flow is expected in the membrane of Fig. 12B. Therefore, the membrane-scale water content measurements in Fig. 9B cannot be used as evidence for the solution–diffusion mechanism.
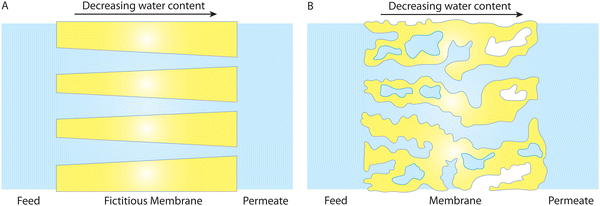 | ||
| Fig. 12 A water content gradient in hydrated membrane pores in the absence of a pressure difference. The membrane in (A) has fictitious cone-shape pores where the pores near the feed side are larger. In a more realistic system, the membrane in (B) has more wet (or hydrated) pores near the feed side of the membrane. In both (A) and (B), existence of a water content gradient at the membrane scale cannot cause a diffusive transport of water across the membranes as otherwise we will have a perpetual motion machine of the first kind that can do work indefinitely without an energy input. This implies that the results in Fig. 9B can not necessarily be used as hard evidence for the SD model. | ||
Directional diffusion transport occurs when there is a concentration gradient at the molecular scale, not at the membrane scale. As indicated in Box 1, dispersed molecules, such as solvent molecules uniformly mixed in another medium, can diffuse from regions of high concentration to regions of low concentration. A gradient in volume fraction of water at the membrane scale does not necessarily imply a gradient in concentration at the molecular scale. Variations in the number of hydrated pores along the membrane can also result in the membrane-scale measurements of water volume fraction gradient.
8.2 Evidence in support of the pore-flow model
In a recent study,36 nonequilibrium molecular dynamics (NEMD) simulations of water transport across a polyamide membrane were performed to better understand the molecular-level mechanism of transport in RO membranes. As shown in Fig. 13A, the simulation consists of a 10 nm-thick polyamide membrane, water molecules in the feed and permeate reservoirs, and two rigid graphene sheets acting as pistons. Different pressure differences between the two pistons were applied to drive water molecules through the membrane. As discussed in Sections 5 and 8.1, water flux would reach a limiting value for very large applied pressures if the water transport was governed by the SD mechanism. However, the NEMD simulations36 (Fig. 13B) show that water flux follows a linear relationship with pressure. This linear relationship contradicts the prediction of a limiting flux by the SD model and can be best described by a viscous-type pore-flow transport model.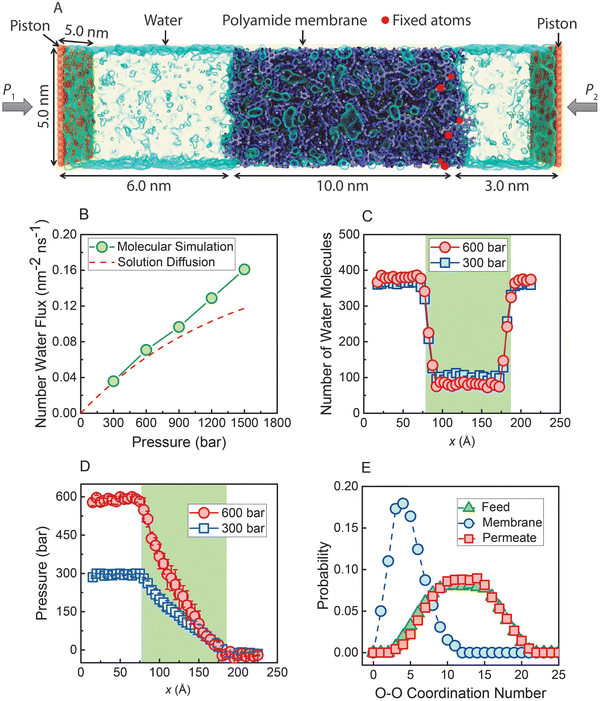 | ||
| Fig. 13 (A) Molecular simulations box. A polyamide membrane (purple) with a thickness of 10 nm is placed between two graphene sheet pistons (orange). Water molecules are visualized as a light blue transparent surface. Hydraulic pressure (P1) is applied to the left graphene sheet during the simulation, and a standard atmospheric pressure (P2) is applied on the right graphene sheet. (B) Water flux through the polyamide membrane as a function of applied pressure. The dash red line is calculated based on the SD model. Number of water molecules (C) and pressure (D) along x-direction through the polyamide membrane under two pressure differences (300 and 600 bar). (E) Probability distribution of water molecules in the feed reservoir, inside the polyamide membrane, and in the permeate reservoir obtained when a steady state condition is reached under 300 bar. Data taken from reference Wang et al. (ref. 36). | ||
In the SD model, the pressure inside the membrane is assumed to be constant and equal to the pressure in the feed reservoir (Fig. 6B). This assumption leads to the chemical potential gradient to be only expressed as the gradient in a water concentration gradient inside the membrane. However, the NEMD simulations36 show no indication of a water concentration gradient as shown in Fig. 13C. Additionally, NEMD-computed pressure in Fig. 13D changes linearly across the membrane, implying a pressure-driven transport within the membrane. These results in Fig. 13C and D provide compelling evidence that the water flux has no diffusive component and is only driven by a hydrostatic pressure.
The SD model relies on Fick's continuum law of diffusion for a binary system as described in Section 5. In such a continuum description, both components (i.e., membrane and water molecules) must be perfectly mixed for any given material element. In other words, water molecules in the SD model are expected to diffuse individually down a concentration gradient. However, the water–water coordination numbers obtained from the NEMD simulations36 paint a different picture of water phase and structure inside the membrane. As shown in Fig. 13E, a water molecule in the membrane is surrounded by ∼5 other water molecules in the simulations. This indicates that water molecules exist in clusters and travel across the membrane without being dispersed.
Overall, the NEMD simulations36,44,45 support the idea that transport is governed by a pore-flow mechanism. Of course, no fixed pores are expected to exist in a polymeric RO membrane. Rather, the network of water clusters or hydrated regions within the polymer matrix are constantly changing and fluctuating because of the applied pressure and thermal motion of the polymer matrix. In the NEMD simulations,36 a number of these water clusters can transiently be connected together, providing a passage or pore for water molecules to travel through the membrane. These transient passages and pores are constantly being formed and broken up as shown in recent NEMD simulations.36 The presence and dynamics of these pores are dependent upon the geometry of the polymer network, the relative size of the solvent molecules, applied pressure, and temperature. We note that for water transport to occur through such a dynamical network of pores, the generated pores and passages must remain long enough for the time scales of water flow through the membrane as illustrated in Fig. 14. Network of interconnected pores in RO membranes have also been observed in recent experimental studies.38,41
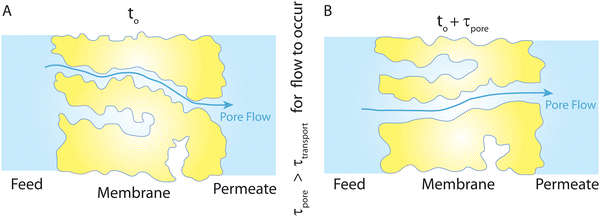 | ||
| Fig. 14 (A) Schematic representation of the PF-type water transport at time to. (B) Because of the thermal motion of the polymer chains, the existing pores at to can disappear and new pores can form at to + τpore (τpore is the time scale of pore formation/breakage). This viscous-type flow mechanism with transient pores is inspired by the molecular simulations,36 where trajectories of some tagged water molecules were monitored throughout their complete transport from the feed side to the permeate side. The presence of a feed-to-permeate passage through a network of pores that is long enough (τpore) for the time scales of water flow (τtransport) through the membrane ensures that transport is governed by a pore-flow mechanism in polyamide membranes through transiently available pores. | ||
The size of these pores in RO membranes is less than ∼1 nm.42,43 Therefore, continuum-based flow theories (e.g., Darcy law) may break down in describing water transport in RO membranes. However, water transport in these nanopores is still governed by viscous flow and driven by pressure gradient. For subnanometer nanopores in membranes with well-defined structures (e.g., carbon nanotubes and single-layer graphene nanopores), it has been shown that viscous flow governs water transport and continuum-based theories can still hold when hydrodynamical properties of water (i.e., viscosity and slip lengths) are adjusted for the effect of nanoconfinement.85–90
8.3 Is RO transport governed by both solution–diffusion and pore-flow mechanisms?
In the early years of RO desalination, enabled by the discovery of cellulose acetate membranes, a number of research studies suggested that both diffusive and viscous flows contribute to the total transport (i.e., Jtotal = Jviscous-flow + Jdiffusive-flow) in polymeric membranes.83,106,107 For example, Meares107 claimed that 99% of water transport occurs via viscous flow and only 1% by a diffusive mechanism in cellulose acetate membranes. In another study by Yasuda and coworkers,106 it was proposed that water transport is dominated by a diffusive mechanism for very low volume fractions of water in polymeric membranes, while for higher volume fractions of water, viscous flow governs the water transport.106 In these studies, the transport rate in experiments under applied pressure was compared to the pure diffusive transport rate, in which the diffusion coefficient of water (e.g., radiolabeled water molecules106) was determined from a concentration gradient driven experiment (i.e., in the absence of applied pressure). The water transport was assumed to be of diffusive nature when the pressure-driven transport rate was comparable to what would be expected from a pure diffusion-based transport mechanism. For larger transport rates than would be expected from a diffusion-based mechanism, a viscous mechanism was believed to govern the transport. However, having transport rates similar to the rates expected from diffusion does not imply the existence of a diffusive transport mechanism for experiments under pressure. Rather, it can be interpreted as a slow viscous-type flow whose rate happens to be on the same order of magnitude as for diffusion motion.A recent development of a model based on the poroelastic theory attempts to unify the pore-flow and solution–diffusion models.82 This so-called fluid-solid model presents a two-phase framework, treating the solvent phase as a Newtonian fluid and the membrane phase as a homogeneous elastic polymer. This continuum treatment requires the two phases to be perfectly mixed, which is not realistic for desalination membranes that are known to be highly heterogeneous.9,36 By simultaneously incorporating Fick's second law of diffusion for the binary system and the Navier–Stokes equation for solvent flow, the model achieves identical permeability values for both pore-flow and solution–diffusion mechanisms. Consequently, solving the coupled governing equations for these mechanisms ensures that the model predicts identical transport behavior.
However, this mathematical treatment raises concerns as it describes transport through pressure-driven flow at the pore level and concentration-driven transport at the membrane level (Fig. 15). In theory, the two driving forces could contribute additively to the total flux (i.e., Jtotal = JPF + JSD). However, the fluid-solid model imposes a condition where the two driving forces contribute to the same flux (i.e., Jtotal = JPF = JSD), which is deemed unphysical. Consequently, this conflicting transport description fails to provide a clear understanding of the true mechanism underlying water transport in RO membranes. Essentially, the model solves for transport in two separate realms—one where transport is governed by chemical diffusion and another where transport is driven by pressure as illustrated in Fig. 15.
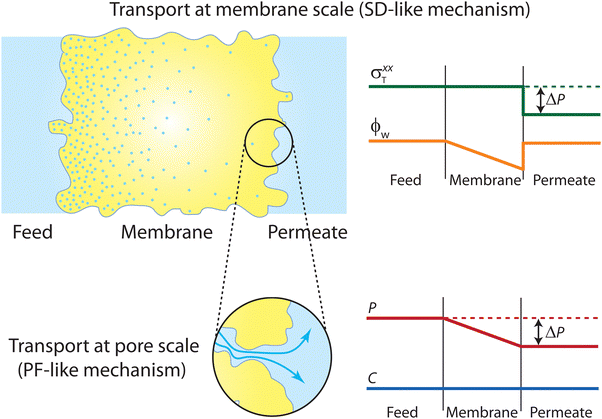 | ||
| Fig. 15 Schematic representation of the transport mechanism predicted by the unified SD–PF model developed by Hegde et al.82 At the membrane scale, transport is governed by an SD-type mechanism, where the total stress and water volume fraction profiles in the binary system follow that of the SD model. At the pore scale, transport is governed by a PF-type mechanism, with the pressure and concentration profiles of water obeying the PF model. These two entirely different mechanisms were coupled in the mathematical derivation of the unified SD–PF model, resulting in identical fluxes for both the SD and PF models. | ||
8.4 Osmosis is governed by pressure gradient, not a solution–diffusion mechanism
To better understand the true mechanism of water transport in RO membranes, it is important to revisit the physics of osmosis. Osmosis, by its very nature, is governed by a hydrostatic pressure gradient rather than a water concentration gradient. It is surprising that this fundamental concept needs reaffirmation even a century after its elucidation by two giants, van't Hoff and Debye.108 In 1923, Debye recognized that the imbalance of membrane-solute forces results in a pressure difference driving the osmotic water flow.108 Under no external applied hydraulic pressure (forward osmosis), the osmolality or concentration difference between the feed and permeate side solutions induces a hydrostatic pressure gradient within the semipermeable membrane (Fig. 16).109 The water molecules migrate down the pressure gradient during osmosis. This pressure profile for osmosis has been proposed or rediscovered by different researchers.110–115 Notably, the water transport driven by osmotic pressure is, in nature, not different from the transport driven by applied hydraulic pressure.Surprisingly, there is a widespread misconception that wrongly attributes the theoretical basis of osmosis to a water concentration gradient or the solution–diffusion mechanism. Accepting a concentration gradient-driven mechanism suggests that osmosis cannot occur in a rigid semipermeable pore, which is evidently incorrect.110 Moreover, the solution–diffusion model fails to explain water transport in forward osmosis. The solution–diffusion model claims that the hydrostatic pressure drop at the permeate side creates a water concentration gradient, but in forward osmosis, there is no applied hydrostatic pressure to create such a gradient of water concentration.
Additionally, the treatment of interfacial pressures in the solution–diffusion theory is self-contradictory. In osmotic processes, the driving force for water transport is the total pressure, Pt, which combines the hydrostatic pressure, P, and osmotic pressure, π (i.e., Pt = P−π). The profile of total pressure must be continuous from the feed solution, across the membrane, and to the permeate/draw solution. To yield a continuous total pressure, or equilibrium at the membrane–solution interfaces, the pressures at the membrane-bulk solution interfaces should follow46
| Pfaq − πfaq = Pfm − πfm | (8.3a) |
| Pdaq − πdaq = Pdm − πdm | (8.3b) |
A sound and consistent understanding of the physics behind osmosis is essential in both mechanistic studies and membrane development. From the perspective of a water molecule in motion within the membrane, there is no distinction between a pressure generated by external mechanical forces and a pressure originating from osmolality. Pressure denotes the volumetric density of intramolecular potential energy present within these water clusters throughout the membrane. The gradient shows how this pressure dissipates through the molecular friction between the solvent and membrane. The solution–friction model clearly portrays this concept.46
9. Conclusion and outlook
This tutorial review article has provided a comprehensive discussion of water transport in RO, starting with a historical timeline of the key developments in RO and progressing to the discussion of water transport mechanisms and models proposed for RO membranes. We also discussed the chemical and physical structure of RO membrane materials, supported by relevant analytical characterization techniques. Additionally, we have critically analyzed the key models and mechanisms for water transport in RO membranes. One notable finding is that the evidence supporting the widely-accepted solution–diffusion mechanism is flawed. Instead, our examination along with recent molecular dynamics simulations studies suggest that a pore-flow mechanism is more likely to occur in RO membranes. Through our analysis, we have highlighted the role of membrane compaction in creating a water content gradient, which does not involve molecular diffusion but rather signifies higher hydration on the feed side. Furthermore, it is important to note that the two water transport mechanisms, solution–diffusion and pore-flow, cannot be unified as recently suggested by Hegde et al.,82 as these mechanisms are quite different.Developing next-generation RO membranes requires a fundamental understanding of water and salt transport mechanisms. Such understanding necessitates the use of innovative in situ instrumentation that can reveal the molecular-level intricacies of water transport and pore dynamics during RO operation. While potent techniques like PALS, WAXS, and 3D tomography exist, they are used for static membrane samples. Future experiments should involve characterization of RO membranes under applied pressures to unveil the relationships among driving forces, pore structure, and transport of both solvent and solutes. These in situ characterization techniques require the coupling with novel testing devices compatible with pressurized water flows.
In recent molecular-level simulations,36,44,45 the presence of pores in polyamide membranes has been identified. However, our understanding of the pore structure and its influence on water transport remains somewhat limited. To gain deeper insights, future molecular simulations should focus on investigating the structure and dynamics of pores and how the transient network of these pores affect water transport in polyamide membranes. For these simulations, it is crucial to develop membrane models that accurately represent the true polyamide structure and chemistry. Currently, the polymerization simulations used to construct polyamide membrane models rely on distance-based bond reactions, which fail to describe bond formation and breakage at quantum level. Therefore, future research should focus on developing quantum-quality interatomic potentials that can effectively describe the realistic chemistry of polymerization. The advancement of machine learning techniques offers promising possibilities.13 By training interatomic potentials on quantum mechanical calculations, it has become possible to perform molecular simulations with the accuracy of quantum mechanical methods, while maintaining the computational efficiency of classical molecular dynamics. These machine learning-based reactive potentials have significantly enhanced the spatiotemporal capabilities of molecular dynamics simulations.13 This research direction holds great potential for advancing our molecular-level understanding of membrane behavior and water transport.
Swelling and deswelling mechanisms of RO membranes under varying feed salinities and pressures remain unclear and often overlooked. To gain a deeper understanding of these mechanisms, it is paramount to investigate the relationships between water molecules/clusters and the sub-nanometer pores of the membranes. Analyzing the energy barriers faced by water molecules at the pore entrance can shed light on these intricate relationships. Moreover, these energy barriers are believed to correlate closely with the frictional coefficients governing water transport within these pores.36 Advanced instrumental methods can be utilized to analyze the behavior of water molecules as they enter RO membranes under different external salinities and pressures. In parallel, computational simulations can be employed to investigate the friction between water molecules and the membrane matrix. The insights derived from such research efforts can substantially enhance our understanding of water transport, offering a roadmap for refining membrane production and optimizing operational methodologies.
Although compaction in elastic polymer systems is known to be a universal phenomenon, its occurrence in the selective layer is among the least explored aspects of RO membranes. There is a notable absence of an a priori model, particularly one centered on the forces between polymer and solvent molecules, to thoroughly explain polyamide compaction. Investigating stress and compaction in polyamide membranes is an essential step for better understanding RO water transport. Beyond analyzing the flux-pressure relationships, experimental characterization of the elasticity of solvent-swollen membranes deserves more research efforts. In addition, MD simulations can shed light on how compaction forces alter pore dimensions and subsequently affect transport. By synergizing modeling, simulations, and experimental investigations, we can develop a better understanding of compaction and its effect on water transport.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the financial support received from the Center for Enhanced Nanofluidic Transport (CENT), an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under Award No. DE-SC0019112.References
- M. Elimelech, J. Water Supply: Res. Technol. – AQUA, 2006, 55, 3–10 CrossRef
.
- M. A. Shannon, P. W. Bohn, M. Elimelech, J. G. Georgiadis, B. J. Marinas and A. M. Mayes, Nature, 2008, 452, 301–310 CrossRef CAS PubMed
.
- J. Schewe, J. Heinke, D. Gerten, I. Haddeland, N. W. Arnell, D. B. Clark, R. Dankers, S. Eisner, B. M. Fekete, F. J. Colon-Gonzalez, S. N. Gosling, H. Kim, X. Liu, Y. Masaki, F. T. Portmann, Y. Satoh, T. Stacke, Q. Tang, Y. Wada, D. Wisser, T. Albrecht, K. Frieler, F. Piontek, L. Warszawski and P. Kabat, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 3245–3250 CrossRef CAS PubMed
.
- C. He, Z. Liu, J. Wu, X. Pan, Z. Fang, J. Li and B. A. Bryan, Nat. Commun., 2021, 12, 4667 CrossRef CAS PubMed
.
- J. R. Werber, C. O. Osuji and M. Elimelech, Nat. Rev. Mater., 2016, 1, 16018 CrossRef CAS
.
- D. L. Gin and R. D. Noble, Science, 2011, 332, 674–676 CrossRef CAS PubMed
.
- S. K. Patel, C. L. Ritt, A. Deshmukh, Z. Wang, M. Qin, R. Epsztein and M. Elimelech, Energy Environ. Sci., 2020, 13, 1694–1710 RSC
.
- C. J. Porter, J. R. Werber, M. Zhong, C. J. Wilson and M. Elimelech, ACS Nano, 2020, 14, 10894–10916 CrossRef CAS PubMed
.
- X. Lu and M. Elimelech, Chem. Soc. Rev., 2021, 50, 6290–6307 RSC
.
- D. Stevens and S. Loeb, Desalination, 1967, 2, 56–74 CrossRef
.
- S. Loeb and S. Sourirajan, High flow porous membranes for separating water from saline solutions, https://patents.google.com/patent/US3133132A/en, (accessed July 20, 2023).
- M. Elimelech and W. A. Phillip, Science, 2011, 333, 712–717 CrossRef CAS PubMed
.
- M. Heiranian, R. M. DuChanois, C. L. Ritt, C. Violet and M. Elimelech, Environ. Sci. Technol., 2022, 56, 3313–3323 CrossRef CAS PubMed
.
- H. B. Park, J. Kamcev, L. M. Robeson, M. Elimelech and B. D. Freeman, Science, 2017, 356, eaab0530 CrossRef PubMed
.
- R. Zhang, Y. Liu, M. He, Y. Su, X. Zhao, M. Elimelech and Z. Jiang, Chem. Soc. Rev., 2016, 45, 5888–5924 RSC
.
- M. Ben-Sasson, X. Lu, E. Bar-Zeev, K. R. Zodrow, S. Nejati, G. Qi, E. P. Giannelis and M. Elimelech, Water Res., 2014, 62, 260–270 CrossRef CAS PubMed
.
- Y. Song, F. Xu, M. Wei and Y. Wang, J. Phys. Chem. B, 2017, 121, 1715–1722 CrossRef CAS PubMed
.
-
R. W. Baker, Membrane technology and applications, John Wiley & Sons, USA, 3rd edn, 2012 Search PubMed
.
-
J. A. Nollet, Leçons de physique expérimentale, Durand, Paris, 1748 Search PubMed
.
-
W. Pfeffer, Osmotische Untersuchungen: Studien zur Zellmechanik, W. Engelmann, Leipzig, 1877 Search PubMed
.
- J. H. van't Hoff, Kongl. Vetensk. Akad. Handl., 1886, 21, 58 Search PubMed
.
-
W. Ostwald, Lehrbuch der allgemeinen chemie, W. Engelmann, Leipzig, 1885 Search PubMed
.
- J. D. Ferry, Chem. Rev., 1936, 18, 373–455 CrossRef CAS
.
-
E. J. Breton and C. E. Reid, Progress Report No. 16, Office of Saline Water Research and Development, USA, 1957 Search PubMed
.
- J. Glater, Desalination, 1998, 117, 297–309 CrossRef CAS
.
- C. E. Reid and E. J. Breton, J. Appl. Polym. Sci., 1959, 1, 133–143 CrossRef CAS
.
- S. Loeb, ACS Symp. Ser. Am. Chem. Soc., 1981, 153, 1–9 CAS
.
- S. Loeb and S. Sourirajan, Adv. Chem., 1963, 38, 117–132 CAS
.
- O. Kedem and A. Katchalsky, Biochim. Biophys. Acta, 1958, 27, 229–246 CrossRef CAS PubMed
.
-
H. K. Lonsdale, U. Merten, R. L. Rilley, K. D. Vos and J. C. Westmoreland, Progress Report No. 111, Office of Saline Water Research and Development, USA, 1964 Search PubMed
.
- H. K. Lonsdale, U. Merten and R. L. Riley, J. Appl. Polym. Sci., 1965, 9, 1341–1362 CrossRef CAS
.
- D. R. Paul and O. M. Ebra-Lima, J. Appl. Polym. Sci., 1970, 14, 2201–2224 CrossRef CAS
.
- S. Rosenbaum and O. Cotton, J. Polym. Sci., Part A-1: Polym. Chem., 1969, 7, 101–109 CrossRef CAS
.
- D. R. Paul and O. M. Ebra-Lima, J. Appl. Polym. Sci., 1971, 15, 2199–2210 CrossRef CAS
.
- J. G. Wijmans and R. W. Baker, J. Membr. Sci., 1995, 107, 1–21 CrossRef CAS
.
- L. Wang, J. He, M. Heiranian, H. Fan, L. Song, Y. Li and M. Elimelech, Sci. Adv., 2023, 9, eadf8488 CrossRef CAS PubMed
.
- H. Yan, X. Miao, J. Xu, G. Pan, Y. Zhang, Y. Shi, M. Guo and Y. Liu, J. Membr. Sci., 2015, 475, 504–510 CrossRef CAS
.
- M. M. Klosowski, C. M. McGilvery, Y. Li, P. Abellan, Q. Ramasse, J. T. Cabral, A. G. Livingston and A. E. Porter, J. Membr. Sci., 2016, 520, 465–476 CrossRef CAS
.
- L. Lin, R. Lopez, G. Z. Ramon and O. Coronell, J. Membr. Sci., 2016, 497, 365–376 CrossRef CAS
.
- H. An, J. W. Smith, B. Ji, S. Cotty, S. Zhou, L. Yao, F. C. Kalutantirige, W. Chen, Z. Ou, X. Su, J. Feng and Q. Chen, Sci. Adv., 2022, 8, eabk1888 CrossRef CAS PubMed
.
- T. E. Culp, B. Khara, K. P. Brickey, M. Geitner, T. J. Zimudzi, J. D. Wilbur, S. D. Jons, A. Roy, M. Paul, B. Ganapathysubramanian, A. L. Zydney, M. Kumar and E. D. Gomez, Science, 2021, 371, 72–75 CrossRef CAS PubMed
.
- T. Fujioka, N. Oshima, R. Suzuki, W. E. Price and L. D. Nghiem, J. Membr. Sci., 2015, 486, 106–118 CrossRef CAS
.
- S. H. Kim, S. Y. Kwak and T. Suzuki, Environ. Sci. Technol., 2005, 39, 1764–1770 CrossRef CAS PubMed
.
- Z. E. Hughes and J. D. Gale, J. Mater. Chem., 2010, 20, 7788–7799 RSC
.
- T. Wei, L. Zhang, H. Zhao, H. Ma, M. S. J. Sajib, H. Jiang and S. Murad, J. Phys. Chem. B, 2016, 120, 10311–10318 CrossRef CAS PubMed
.
- L. Wang, T. Cao, J. E. Dykstra, S. Porada, P. M. Biesheuvel and M. Elimelech, Environ. Sci. Technol., 2021, 55, 16665–16675 CrossRef CAS PubMed
.
- P. M. Biesheuvel, S. Porada, M. Elimelech and J. E. Dykstra, J. Membr. Sci., 2022, 647, 120221 CrossRef CAS
.
- Y. S. Oren and P. M. Biesheuvel, Phys. Rev. Appl., 2018, 9, 024034 CrossRef CAS
.
- W. R. Bowen and J. S. Welfoot, Chem. Eng. Sci., 2002, 57, 1121–1137 CrossRef CAS
.
- P. M. Biesheuvel, S. B. Rutten, I. I. Ryzhkov, S. Porada and M. Elimelech, Desalination, 2023, 557, 116580 CrossRef CAS
.
- R. J. Petersen, J. Membr. Sci., 1993, 83, 81–150 CrossRef CAS
.
-
M. Mulder, Basic Principles of Membrane Technology, Kluwer Academic Pulisher, The Netherlands, 2nd edn, 1996 Search PubMed
.
- A. F. Ismail and T. Matsuura, Desalination, 2018, 434, 2–11 CrossRef CAS
.
- Z. Chen, K. Ito, H. Yanagishita, N. Oshima, R. Suzuki and Y. Kobayashi, J. Phys. Chem. C, 2011, 115, 18055–18060 CrossRef CAS
.
- P. S. Singh, A. P. Rao, P. Ray, A. Bhattacharya, K. Singh, N. K. Saha and A. V. R. Reddy, Desalination, 2011, 282, 78–86 CrossRef CAS
.
- Q. Fu, N. Verma, H. Ma, F. J. Medellin-Rodriguez, R. Li, M. Fukuto, C. M. Stafford, B. S. Hsiao and B. M. Ocko, ACS Macro Lett., 2019, 8, 352–356 CrossRef CAS PubMed
.
- Q. Fu, N. Verma, B. S. Hsiao, F. Medellin-Rodriguez, P. A. Beaucage, C. M. Stafford and B. M. Ocko, Synchrotron Radiat. News, 2020, 33, 40–45 CrossRef PubMed
.
- T. E. Culp, Y. Shen, M. Geitner, M. Paul, A. Roy, M. J. Behr, S. Rosenberg, J. Gu, M. Kumar and E. D. Gomez, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 8694–8699 CrossRef CAS PubMed
.
- M. Soltanieh and W. N. Gill, Chem. Eng. Commun., 1981, 12, 279–363 CrossRef CAS
.
- D. Van Gauwbergen and J. Baeyens, Sep. Purif. Technol., 1998, 13, 117–128 CrossRef CAS
.
- K. S. Spiegler and O. Kedem, Curr. Contents/Eng. Technol. Appl. Sci., 1983, 5, 16 Search PubMed
.
-
G. Lebon, D. Jou and J. Casas-Vázquez, Understanding Non-equilibrium Thermodynamics: Foundations, Applications, Frontiers, Springer Science & Business Media, Berlin, 2008 Search PubMed
.
- L. Onsager, Phys. Rev., 1931, 37, 405–426 CrossRef CAS
.
- L. Onsager, Phys. Rev., 1931, 38, 2265–2279 CrossRef CAS
.
- L. Song, Chem. Eng. Commun., 2000, 180, 145–167 CrossRef CAS
.
- J. Jagur-Grodzinski and O. Kedem, Desalination, 1966, 1, 327–341 CrossRef CAS
.
- T. G. Kaufmann and E. F. Leonard, AIChE J., 1968, 14, 110–117 CrossRef CAS
.
- L. Wang, C. Violet, R. M. DuChanois and M. Elimelech, J. Chem. Educ., 2020, 97, 4361–4369 CrossRef CAS
.
- C. Liu, K. Rainwater and L. Song, Desalination, 2011, 276, 352–358 CrossRef CAS
.
- Z. Wang, A. Deshmukh, Y. Du and M. Elimelech, Water Res., 2020, 170, 115317 CrossRef CAS PubMed
.
- Y. Du, L. Wang, A. Belgada, S. A. Younssi, J. Gilron and M. Elimelech, J. Membr. Sci., 2023, 678, 121642 CrossRef CAS
.
- X. Bian, C. Kim and G. E. Karniadakis, Soft Matter, 2016, 12, 6331–6346 RSC
.
-
E. L. Cussler, Diffusion: mass transfer in fluid systems, Cambridge University Press, UK, 3rd edn, 2009 Search PubMed
.
- A. Fick, J. Membr. Sci., 1995, 100, 33–38 CrossRef CAS
.
- W. E. Clark, Science, 1962, 138, 148–149 CrossRef CAS PubMed
.
-
J. Welty, G. L. Rorrer and D. G. Foster, Fundamentals of Momentum, Heat, and Mass Transfer, John Wiley & Sons, 7th edn, 2020 Search PubMed
.
- A. Peterlin and H. Yasuda, J. Polym. Sci., Polym. Phys. Ed., 1974, 12, 1215–1220 CrossRef CAS
.
- S. Sourirajan, Ind. Eng. Chem., 1963, 2, 51–55 CAS
.
-
U. Merten, Desalination by Reverse Osmosis, MIT Press, USA, 1966 Search PubMed
.
- J. M. Sharp Jr. and C. T. Simmons, Ground Water, 2005, 43, 457–460 CrossRef PubMed
.
- A. Zick and G. Homsy, J. Fluid Mech., 1982, 115, 13–26 CrossRef CAS
.
- V. H. Hegde, M. F. Doherty and T. M. Squires, Science, 2022, 377, 186–191 CrossRef CAS PubMed
.
- L. B. Ticknor, J. Phys. Chem., 1958, 62, 1483–1485 CrossRef CAS
.
-
G. K. Batchelor, An introduction to fluid dynamics, Cambridge University Press, UK, 1st edn, 1967 Search PubMed
.
- L. Bocquet and E. Charlaix, Chem. Soc. Rev., 2010, 39, 1073–1095 RSC
.
- K. Falk, F. Sedlmeier, L. Joly, R. R. Netz and L. Bocquet, Nano Lett., 2010, 10, 4067–4073 CrossRef CAS PubMed
.
- E. Secchi, S. Marbach, A. Nigues, D. Stein, A. Siria and L. Bocquet, Nature, 2016, 537, 210–213 CrossRef CAS PubMed
.
- M. Heiranian and N. R. Aluru, ACS Nano, 2020, 14, 272–281 CrossRef CAS PubMed
.
- M. Heiranian and N. R. Aluru, Phys. Rev. E, 2022, 105, 055105 CrossRef CAS PubMed
.
- M. Heiranian, A. Taqieddin and N. R. Aluru, Phys. Rev. Res., 2020, 2, 043153 CrossRef CAS
.
- U. Raviv and J. Klein, Science, 2002, 297, 1540–1543 CrossRef CAS PubMed
.
- T. Li, J. Gao, R. Szoszkiewicz, U. Landman and E. Riedo, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 115415 CrossRef
.
- D. Shi, H. Li, X. Yu, Z. Zhang, Y. D. Yuan, W. Fan, H. Yuan, Y. Ying, H. Yang, C. Shang, J. Imbrogno and D. Zhao, J. Am. Chem. Soc., 2023, 145, 15848–15858 CrossRef CAS PubMed
.
- S. Joseph and N. R. Aluru, Nano Lett., 2008, 8, 452–458 CrossRef CAS PubMed
.
- L. Bocquet and J. Barrat, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 3079–3092 CrossRef CAS PubMed
.
- J. R. Pappenheimer, Physiol. Rev., 1953, 33, 387–423 CrossRef CAS PubMed
.
- P. M. Biesheuvel, J. Colloid Interface Sci., 2011, 355, 389–395 CrossRef CAS PubMed
.
- L. Wang, T. Cao, K. E. Pataroque, M. Kaneda, P. M. Biesheuvel and M. Elimelech, Environ. Sci. Technol., 2023, 57, 3930–3939 CrossRef CAS PubMed
.
- O. Coronell, B. J. Marinas, X. Zhang and D. G. Cahill, Environ. Sci. Technol., 2008, 42, 5260–5266 CrossRef CAS PubMed
.
- B. Blankert, F. D. Martinez, J. S. Vrouwenvelder and C. Picioreanu, J. Membr. Sci., 2023, 679, 121675 CrossRef CAS
.
- P. M. Biesheuvel, J. E. Dykstra, S. Porada and M. Elimelech, J. Membr. Sci. Lett., 2022, 2, 100010 CrossRef
.
- T. Hirai, Y. Asada, T. Suzuki, S. Hayashi and M. Nambu, J. Appl. Polym. Sci., 1989, 38, 491–502 CrossRef CAS
.
- D. R. Paul, J. Membr. Sci., 2004, 241, 371–386 CrossRef CAS
.
- A. Peterlin and J. L. Williams, J. Appl. Polym. Sci., 1971, 15, 1493–1505 CrossRef CAS
.
- P. M. Biesheuvel, H. Fan and M. Elimelech, arXiv, 2023, preprint, arXiv:2307.16146v3, DOI:10.48550/arXiv.2307.16146.
- H. Yasuda, C. E. Lamaze and A. Peterlin, J. Polym. Sci., Part A-2, 1971, 9, 1117–1131 CrossRef CAS
.
- P. Meares, Eur. Polym. J., 1966, 2, 241–254 CrossRef CAS
.
- P. Debye, Recl. Trav. Chim. Pays-Bas, 1923, 42, 597–604 CrossRef CAS
.
- L. Song, M. Heiranian and M. Elimelech, Desalination, 2021, 520, 115360 CrossRef CAS
.
- A. Mauro, Science, 1965, 149, 867–869 CrossRef CAS PubMed
.
- A. Mauro, Science, 1957, 126, 252–253 CrossRef CAS PubMed
.
- L. Vegard, Proc. Cambridge Philos. Soc., 1910, 15, 13–23 Search PubMed
.
- J. Dainty, Symp. Soc. Exp. Biol., 1965, 19, 75–85 CAS
.
- G. S. Manning, J. Chem. Phys., 1968, 49, 2668–2675 CrossRef CAS
.
- G. S. Manning and A. R. Kay, J. Gen. Physiol., 2023, 155, e202313332 CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cs00395g |
| This journal is © The Royal Society of Chemistry 2023 |