 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Correction: Increasing ion yield circular dichroism in femtosecond photoionisation using optimal control theory
Manel
Mondelo-Martell
a,
Leon A.
Kerber
a,
Daniel
Basilewitsch†
a,
Hendrike
Braun
b,
Christiane P.
Koch
a and
Daniel M.
Reich
*a
aDahlem Center of Complex Quantum Systems & Department of Physics, Freie Universität Berlin, Berlin, Germany. E-mail: christiane.koch@fu-berlin.de; danreich@zedat.fu-berlin.de
bInstitute of Physics, Universität Kassel, Kassel, Germany. E-mail: braun@physik.uni-kassel.de
First published on 24th August 2023
Abstract
Correction for ‘Increasing ion yield circular dichroism in femtosecond photoionisation using optimal control theory’ by Manel Mondelo-Martell et al., Phys. Chem. Chem. Phys., 2022, 24, 9286–9297, https://doi.org/10.1039/D1CP05239J.
The authors have detected two issues in the numerical simulations reported in the originally published version of the article. First, the values of the electric and magnetic transition moments, obtained from quantum chemistry calculations were not sufficiently converged. Second, there was a mistake in the implementation of the rotational averaging in the model. After fixing these errors and choosing an improved optimisation functional, new simulations yield quantitatively different results. However, the physical mechanisms of the optimised pulses identified in the original paper remain valid. Here, the authors summarise the origin of the errors in the original publication and present newly converged energies, permanent and transition moments, as well as corrected figures and conclusions. Specifically, Tables 1 and 2 in the original article have been replaced with the corresponding tables in this correction, and Fig. 2–5 in the original article by Fig. 1–4 in this correction respectively. The authors also introduce and explain the new functional that has been used to optimise the pulse.
1 New ab initio data
Additional electronic structure calculations on fenchone have revealed that the basis set used in the original article (6-31G) was insufficient to correctly represent the system. The authors have therefore performed additional calculations with correlation consistent basis sets, following previous work.1 The results that have been obtained using a cc-pVTZ basis set are summarised in Table 1. Compared to the parameterisation in the original article, the two main differences are the overall excitation energy (from 4.04 eV to 4.44 eV) and the qualitative changes in the y and z components of the electric dipole transition moment. Since the circular dichroism is, to first order, given by the overlap between magnetic and electric dipole transition moments, these changes cause qualitative differences to the behaviour of the system upon irradiation.2 Description of the coding mistake in the original article and the solution
The error in the numerical code originated in the implementation of the negative sign accompanying the x component of the magnetic transition moment in the Hamiltonian (eqn (7) in the original article). There, the sign was included as a part of the x component during the rotation operations that generate the ensemble for the rotational averaging, but it should have only been present in the final expression of the Hamiltonian. After fixing this, as seen in Fig. 1, the g factor in the simulations with a circularly polarised guess pulse is ≈0.7, significantly higher than the previous value of 0.06, which coincidentally was in close agreement with experimental data.2The authors attribute the discrepancy between the currently calculated and experimental g value to neglecting the vibrational substructure of the electronic bands. In a real system, different geometries beyond the minimum of the electronic ground state potential energy surface contribute to the absorption even for the vibrational ground state. The corresponding nuclear displacements can be seen as perturbations to the equilibrium system, mixing its eigenstates, which leads to an intensity borrowing mechanism.3,4 Particularly for the n → π* transition in carbonyl groups, these vibrational structure effects are known to be important.4–6 This transition is very weak and thus the impact of mixing with electric dipole allowed transitions is comparatively large. As a result, the neglection of vibrational structure is a limitation of the model that the authors aim to address in a future study.
The functional used in the original manuscript, eqn (11), was designed to maximise the absolute difference in population,
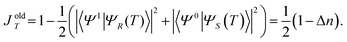 | (1) |
 has been included, which allows movement of the optimisation towards very low overall absorptions to be avoided. These ideas lead to defining the following new optimisation functional,
has been included, which allows movement of the optimisation towards very low overall absorptions to be avoided. These ideas lead to defining the following new optimisation functional,| JnewT = 2 − |Δn|ag. | (2) |
With this new functional, the relation between the fidelity and the difference in excited-state population between R and S enantiomers (eqn (17) in the original article) is less direct. Therefore, for the purpose of Fig. 3 and 4, the population difference, Δn, has been directly plotted. This facilitates distinguishing whether a given pulse favours absorption in the R enantiomer (to which positive values of Δn are assigned) or the S enantiomer (negative values of Δn).
3 New optimisation results
Fig. 1 (taking the role of Fig. 2 from the original article) shows the excited-state population as a function of time for the R and S enantiomers, as well as the g factor, under irradiation with a circularly polarised pulse (dashed lines), respectively the optimised pulse (solid lines). With the new ab initio data and corrected code, an improvement of about 20% in the g factor (from g = 0.69 to g = 0.86) has been obtained using the new functional in eqn (2), although this comes at the cost of a reduced absolute absorption. The parameters of the optimised pulse are given in Table 2. The increase obtained is appreciably lower compared to the results from the original publication (from g = 0.06 to g ≈ 1). Nonetheless, the model still predicts that it is possible to increase the anisotropy factor of fenchone using optimal control.| Optimised pulse | Guess pulse | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E (0) (GV m−1) | E (1) (GV m−1) | E (2) (GV m−1) | ω (1) (eV) | ω (2) (eV) | φ | E (0) (GV m−1) | E (1) (GV m−1) | E (2) (GV m−1) | ω (1) (eV) | ω (2) (eV) | φ | |
| E x | 25.71 | 24.91 | 25.71 | 4.22 | 2.11 | 1.53 | 0.0 | 25.71 | 0.0 | 4.44 | — | 1.57 |
| E y | 0.0 | 25.39 | 5.92 | 4.22 | 2.11 | 0.0 | 25.71 | 0.0 | 4.44 | — | ||
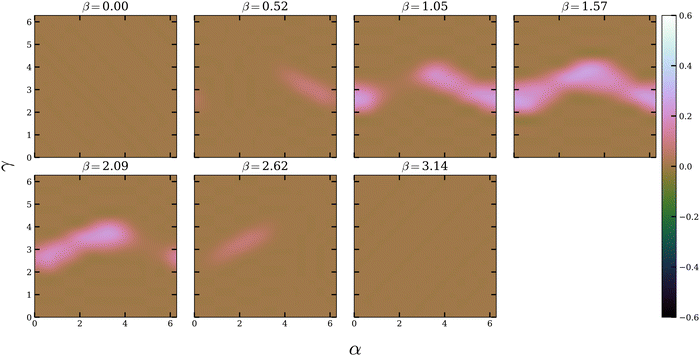
The population difference between the excited states of the R and S enantiomers irradiated with pulses optimised for each particular orientation is shown in Fig. 3. The predominance of light-coloured areas in this figure shows that for most orientations it is possible to find an optimal pulse that significantly increases the difference in excited-state population. This behaviour was similarly seen in Fig. 4 of the original article.
Fig. 4 shows the excited-state population difference between enantiomers when all orientations are irradiated with the optimised pulse shown in Fig. 1. Although the shape of the light-coloured areas indicating high chiral distinguishability is different from the previous results, cf. Fig. 5 of the original article, the crucial feature is preserved – the light-coloured areas are found predominantly in the panels close to β = π/2. This shows that the optimisation algorithm still focuses on increasing the population difference for those orientations that have a greater weight in the ensemble, as discussed in the original article.
The new simulations also confirm the importance of the DC contribution for the optimisation pulse. Analogously to the original article, this has been conformed by performing different pulse optimisations on the orientationally averaged system when considering different constraints to the pulse during the optimisation, namely: (i) forcing a null DC contribution to the field and (ii) forcing a null ω(2) contribution to the field. The resulting excited-state population dynamics are shown in the middle (case (i)) and bottom panels (case (ii)) of Fig. 2, which corresponds to Fig. 3 in the original manuscript. In both old and new simulations, it is clear that the algorithm is not able to find a suitable pulse without a DC contribution, and that the electric quadrupole (coupling to the field predominantly with frequency ω(2)) only has a minor effect on the overall optimisation.
 | ||
| Fig. 3 Value of the difference in excited-state population between R and S enantiomers, Δn, optimised for individual orientations of fenchone as a function of the Euler angles α, β and γ. | ||
 | ||
| Fig. 4 Value of the difference in excited-state population between R and S enantiomers, Δn, after irradiation with the ensemble optimised pulse (Table 2 and Fig. 1) as a function of the Euler angles α, β and γ. | ||
The Royal Society of Chemistry apologises for these errors and any consequent inconvenience to authors and readers.
References
- R. E. Goetz, T. A. Isaev, B. Nikoobakht, R. Berger and C. P. Koch, J. Chem. Phys., 2017, 146, 024306 CrossRef CAS PubMed.
- F. Pulm, J. Schramm, J. Hormes, S. Grimme and S. D. Peyerimhoff, Chem. Phys., 1997, 224, 143–155 CrossRef CAS.
- G. Herzberg and E. Teller, Z. Phys. Chem., 1933, 21B, 410–446 CrossRef.
- P. W. Atkins and R. S. Friedman, Molecular Quantum Mechanics, Oxford University Press, Oxford, 3rd edn, 1997 Search PubMed.
- W. Moffitt and A. Moscowitz, J. Chem. Phys., 1959, 30, 648–660 CrossRef CAS.
- Circular Dichroism: principles and applications, ed. K. Nakanishi, N. Berova and R. W. Woody, VCH, New York, 1994 Search PubMed.
Footnote |
| † Present address: Institut für Theoretische Physik, Universität Innsbruck, Germany. E-mail: daniel.basilewitsch@uibk.ac.at |
| This journal is © the Owner Societies 2023 |












