¹³C pNMR shifts of MOFs based on Cu(II)-paddlewheel dimers – DFT predictions for spin–1/2 defects

Abstract

We present DFT predictions (CAM-B3LYP/II level) for the paramagnetic Nuclear Magnetic Resonance (pNMR) spectra of small molecular models based on the Cu(II)-paddlewheel dimer motif that is present in metal–organic frameworks (MOFs, notably the HKUST and STAM families). We explore potential point defects with spin–1/2 discovered through electron paramagnetic resonance (EPR) experiments. We consider defects through substitution of one Cu(II) centre in the dimer with protons, or through one-electron reduction, affording a mixed-valence dimer. While most of the defects have predicted pNMR shifts at room temperature in the range of those for the non-defective MOFs, their detection and assignment should be possible based on their distinct temperature dependence.

---

Introduction

Metal organic frameworks (MOFs) are crystalline materials, also known as coordination polymers. They have two components: organic ligands (such as phosphonates, carboxylates, sulfonates or imidazolates) and a metal centre (such as Cu²⁺, Zn²⁺, Al³⁺ or Cr³⁺), and variation in both of these can result in different structural forms or changes in the physical or chemical properties.¹ MOFs are widely studied and often a centre of attention for the scientific community due to their versatility and tunability. In fact, MOFs find application in several sectors such as medicine, catalysis and gas storage.^2–7 For this work, the interest lies in MOFs that are based on copper paddlewheel dimer building blocks. This motif is composed of two copper atoms in the +2 oxidation state, and the specific MOFs considered here contain 1,3,5-benzene tricarboxylic acid (BTC) and derivatives thereof as the organic linker(s). In these cases, four O atoms, from four different acetate groups of BTC, coordinate the copper atoms in the equatorial plane, affording the characteristic “paddlewheel” structure and leaving one axial coordination site free for each metal centre (see Fig. 1). These sites are the key to the chemistry of the material as they act as anchor points for small ligands, such as gasses which are stored in the MOF pores.

Fig. 1 Schematic showing a paddlewheel dimer with axial ligand site, L.

HKUST-1 was one the first MOFs discovered, being synthesized for the first time in 1999.⁸ The material is characterised by having pores with three different sizes (ranging from 5 to 13.5 Å) to which several polar and non-polar molecules (including Ar, N₂, O₂, CH₄, H₂O, MeOH and EtOH) have access.⁹ Porous materials such as HKUST-1 and other related MOFs are interesting for gas storage applications and therefore understanding the intimate connection between function and structure is crucial in order to fine tune their properties. Moreover, when considering the impact of small chemical changes at the molecular level it is clear that an analytical technique that is able to report on such changes is necessary. To this end, experimental solid-state NMR spectroscopy paired with theoretical prediction can aid in unravelling the structure of such paramagnetic MOFs and aid in the optimisation of their properties. Ke et al.^10,11 have established a DFT-based methodology to compute the paramagnetic NMR (pNMR) chemical shifts of Cu-based MOFs using suitable model complexes. The paddlewheel type of system is special due to the coupling of the spins within each dimer. Experimentally observed ¹³C pNMR shifts could be reproduced by assuming a Boltzmann equilibrium between a diamagnetic ground state and thermally populated, excited paramagnetic states of molecular models with one or more dimers present, and also giving rise to the unusual temperature dependence of the pNMR shifts seen experimentally. Usually, the pNMR shift has an inverse linear relationship with temperature (because of the macroscopic magnetic susceptibility of paramagnetic materials). However, for HKUST-1 and select members of the related STAM family^12,13 (based on different BTC derivatives) the relationship is non-linear.^11,14 Ref. 10 proved that such behaviour arises from the thermal population of the accessible excited paramagnetic spin states in addition to a diamagnetic ground state. The smallest models used in ref. 10 were based on a single paddlewheel dimer (as shown in Fig. 1) with antiparallel and parallel electron spins within the dimer pair (corresponding to a total electron spin of 0 or 1, respectively). However, analysis of magnetic measurements (from Electron Paramagnetic Resonance, EPR, spectroscopy) has provided evidence for the presence of a sizeable amount of spin−1/2 centres, accounting for up to 10% of spin centres.¹⁵ Although the presence of such defects is appreciated in Cu-paddlewheel MOFs,¹⁶ the precise nature of these is still unclear and so far they do not appear to have been identified in solid-state NMR spectra, which could either be due to their low abundance (i.e., low signal intensity), excessive line widths, or occurrence of the signals in a spectral area that has not so far been considered (i.e., outside the spectral range usually acquired even for pNMR spectra). This raises the question, what is the nature of the spin–1/2 defects and in what region of the ¹³C (and ¹H) NMR spectra would these be expected to appear?

Assuming the overall MOF structure remains intact around the defect sites (as there are no indications to the contrary from X-ray diffraction¹¹), a single Cu(II) site surrounded by four carboxylate moieties would carry two negative charges. In reality, some charge balancing would be expected to occur. In this work, we have considered two possible situations; one where electroneutrality is maintained by substitution of one Cu centre in a dimer with two bridging H atoms, and one where the paddlewheel is negatively charged, with both Cu atoms remaining in place but with one Cu adopting a +1 oxidation state, resulting in a mixed valence defect.

Results and discussion

Proton-containing defect

Structures. Assuming that the defects are incorporated into the overall structure of the MOF (HKUST-1 and STAM-based MOFs for the hydrated models; HKUST-1 for the activated model), they will need to be accommodated by the carboxylate groups of the linker. If only one Cu(II) is present to bind to four carboxylates, two negative charges would need to be balanced. Here we assume this charge balance to be through protons (i.e., some of the neutral aromatic acid precursors would not be deprotonated during MOF formation). Replacing one Cu in a dimer with two protons affords the structural models shown in Fig. 2.

Fig. 2 Molecular models of the Cu(H)₂ (1a, top) and hydrated Cu(H)₂ defects (bottom), optimised at xTB (left) and PBE0-D3 level (middle); right: labelling scheme (C3 is the ortho carbon nearest to the Cu centre).

This model corresponds to model M1 in ref. 10, with four Ph groups around a single paddlewheel dimer, and gives a simple model for the MOF. Most results in the previous work for models containing a single dimer were based on a structure with one Ph and three Me groups (model M4 in ref. 10) to reduce computational cost. However, owing to the reduced symmetry of models containing protonated defects we decided to retain the four phenyl groups in this study.

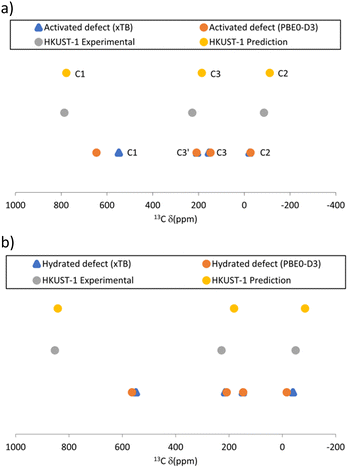
To effectively investigate the protonated defect, we consider two states of each structural model, “activated” (i.e., no axial guest bound to Cu), and “hydrated” (i.e., one axial water bound to Cu). The latter would correspond to the STAM and HKUST-1 MOFs as obtained from hydrothermal synthesis, the former to the dehydrated (or “activated”) form of HKUST-1. Using the same methodology as in ref. 10, we have computed the ¹³C and ¹H chemical shifts for these models in their doublet (spin–1/2) states. Because the actual linkers in the MOFs have carboxylate substituents in the meta position we only report data for C1, C2, C3 and C3′ (cf. labelling scheme in Fig. 2 – note that for paddlewheel motifs with two Cu atoms C3 and C3′ sites become equivalent).

pNMR properties. For these spin–1/2 models, no Boltzmann averaging (and no scaling of energy levels due to potential problems of DFT in describing energy differences between different spin states) is necessary. To probe for the sensitivity of the computed pNMR shifts to the underlying structure we have used structures optimised both at PBE0-D3 and xTB levels (see Fig. 2 for the structures and Fig. 3 and Table S2 (ESI†) for the pNMR data). The predicted pNMR shifts for our models of the defective HKUST-1 or STAM-based materials are relatively close (when considering the typical ranges of pNMR shifts) to their non-defective counterparts (shown in yellow) for both activated and hydrated models. Only the shift of C1 shows a significant difference of around 200 ppm. For instance, for the hydrated model at room temperature, the C1 resonance is predicted to be shifted from δ of ∼800 ppm to ∼600 pm upon defect formation (similar to the activated model, albeit with some dependence on the geometry optimisation method used in the calculations, i.e., compare the data points for the xTB and PBE0-D3 structures in Fig. 3a).

Fig. 3 Schematic plots of predicted pNMR ¹³C peak positions of the Cu(H)₂ defect models (blue points for xTB and orange for PBE0-D3 optimised structures) and of the experimental HKUST-1 (grey) and computed non-defective MOF models for (a) activated defect and (b) hydrated defect.

Because all shifts are expected in a similar range in the NMR spectrum, this could make the unambiguous experimental identification of signals resulting from this defect challenging, particularly given the expected lower intensities. However, the temperature behaviour of the signals should be different, as the defective material is expected to have a linear relationship with inverse temperature,^17–19 whereas it is known to be non-linear for the pristine material, as discussed above.¹⁰ Therefore, in principle, it should be possible to distinguish between signals from defective and pristine materials using variable temperature pNMR experiments. Considering such an experiment over the 250–350 K range, the expected pNMR shift of the defect would evolve as shown in Table S2 (ESI†). The C1 signal is predicted to be the most sensitive to temperature changes as shown in Fig. 4a and b (although perhaps the hardest signal to see experimentally owing, at least in the pristine material, to the much larger linewidths and extreme shift, typically requiring a change in the carrier frequency to ensure efficient excitation). Moreover, for the non-defective material a decrease in chemical shift for C1 and an increase for C2 is predicted with increasing T, which is the opposite of the behaviour predicted for the defect, making identification of spectral signals easier. Lastly, valuable information can be gathered from the chemical shift of the protons involved in the metal substitution (with predicted chemical shifts between ca. 10–13 ppm at room temperature, see Table S3, ESI†) if they are indeed present to balance the charge as assumed here.

Fig. 4 Predicted temperature dependence of pNMR shifts for ¹³C and ¹H signals in the Cu(H)₂ defect models for (a) activated and (b) hydrated models.

Thermodynamics of defect formation. Efforts to predict the thermodynamic accessibility of protonated defects from the energies of the optimised molecular models were inconclusive. While some driving forces for formation of activated or hydrated 1a from the non-defective dimer were favourable based on computed potential energies, uncertainties from entropic contributions and effects from formation of the bulk MOF structure precluded qualitative predictions regarding the accessibility of such defects, let alone their quantification (see section on “Thermodynamics of proton defects” in the ESI†).

Alternative and constrained models. It should be noted that the coordination environment proposed so far for the protonated defect is not the only possible one. In 1a, the two protons are located on the same face of the cube spanned by the 8 O atoms (opposite the face containing the CuO₄ plane, see Fig. 2). We also explored the possibility that they could be located on opposite faces. A corresponding minimum could be located (1b, Fig. S1, ESI†). Upon optimisation, the copper atom resides at the centre of the distorted cube spanned by the 8 O atoms. Based on the computed distortion energies (see below), this model appears to be significantly less favourable than 1a. Data analysis and discussion on 1b are reported in the ESI.†

It should be noted that all defect models considered so far, being activated or hydrated, have been fully optimised, resulting in large distortions from the ideal paddlewheel building block with Ph groups protruding radially from a four-fold axis. In most cases minima with a “folded” structure are obtained due to π-stacking interactions between adjacent Ph groups (see Fig. 5 left). It is unlikely that such distortions can be sustained in the extended MOF structure where most paddlewheel dimers will have the conventional structure. We have attempted to model defects more compatible with the extended MOF by imposing constraints during the geometry optimisation that prevent intramolecular π-stacking interactions from occurring. These models restrict the phenyl rings to be fixed to their positions in the non-defect dimers (xTB and PBE0-D3 geometry optimised positions, respectively), and ensure that the geometry remains compatible with the extended network. Such models could be a valid alternative to the global folded minimum structure. Some differences were found in terms of the predicted pNMR shifts between the constrained and unconstrained models, as shown in Fig. 6 and Table S7 (ESI†). When the models are optimised using xTB the biggest changes were for C1 and C2, whereas the C3 shift and the proton shifts are mostly conserved. However, models optimised at the PBE0-D3 level retain the pNMR parameters predicted previously to a higher degree once constraints are applied. There remains a significant shift of C1 between constrained and unconstrained models; however, C2, C3 and H differ by less than 60 and 4 ppm, respectively. Given the ppm range investigated, and the typical magnitude of paramagnetic NMR shifts, we deem a change over 200 ppm for the C sites significant. If the overall shift change is considered (defined as the average shift difference for each C atom with respect to the unconstrained model), all of the models, irrespective of the optimisation method used, show changes below 200 ppm (see Fig. 6a and b and Table S7, ESI†).

Fig. 5 Left: Fully optimised (unconstrained) model for the activated proton defect (1a); right: partially optimised after imposing constraints to ensure compatibility with the MOF structure. Both models were optimised at the PBE0-D3 level.

Fig. 6 Schematic plot of predicted ¹³C pNMR peak positions of the constrained and unconstrained Cu(H)₂ defect models optimised at the xTB and PBE0-D3 level for (a) activated and (b) hydrated models.

Structurally, the constrained models afford a more symmetric coordination site (see Fig. 5 right), emphasized by the O⋯H–O distance. The model becomes more symmetric with the constraints, as apparent in the Δd(OH), defined as the difference between the O⋯H and H–O distances, which decreases from Δd ≈ 0.6 Å in the fully optimised minima to Δd ≈ 0.5 Å in the constrained structures.

Notable distortion energies (i.e., energy differences between constrained and fully optimised models) are computed at the CAM-B3LYP-D3 level, especially for the PBE0-D3 optimised structures where the deformation energies exceed 10 kcal mol⁻¹ (see Table S8, ESI†). It is unclear at this point to what extent deformation energies of individual molecules would translate into resistance toward defect incorporation into the extended MOF frameworks, and we would not refute the existence of defects modelled by 1a based on these energetic arguments. Further study of this aspect could be rewarding.

Mixed valence defect

Structures. Defects bearing a spin of 1/2 are not only possible through chemical substitution but can arise from a change in oxidation state of one of the copper centres. For instance, a one-electron reduction of one metal centre would lead to an anionic Cu(II)–Cu(I) mixed-valence dimer. Support for the existence of such single (molecular) dimers in solution has been reported following photochemical activation.²⁰ It is not clear if such processes could also happen during MOF synthesis (although a mixed-valence MOF has been reported containing Cu(II) paddlewheel dimers and discrete Cu(I) sites in correspondingly designed linkers).²¹ Also, it is unlikely that the number of counterions required to be incorporated into the material to charge balance up to 10% of such defects would go unnoticed. These Cu(II)–Cu(I) mixed-valence paddlewheel defects are thus probably not a serious contender for the majority of MOF defects in general, but are of interest in their own right. As with 1b, xTB and DFT optimised structures predicted for the mixed valence defects are very different (see Fig. 7). This discrepancy is observed in both activated and hydrated models. Specifically, the structures predicted by DFT exhibit a significant asymmetry in the coordination environment of the metal centres, whereas those optimised by xTB maintain approximate C_4h symmetry. This difference is reflected in the disparity in the computed spin density between the two methods. DFT predicts a completely localised spin centre, whereas xTB indicates that the spin is equally distributed between the two metal centres (Fig. 7). It should be noted that the structures predicted by DFT are not compatible with the extended network of the MOFs and would induce strong structural distortions.

Fig. 7 Molecular models with corresponding spin density of the activated Cu(I)Cu(II) (top) and hydrated Cu(I)Cu(II) defects (bottom), optimised at xTB (left) and PBE0-D3 level (right).

For the localised static structures (favoured by PBE0-D3) we expect a dynamic delocalisation through rapid interconversion between two isomers on the NMR time scale with the spin localised at either metal centre (and have averaged the computed pNMR shifts in the static minima accordingly – this would correspond to a type II complex in the Robin–Day classification, though we do not imply such an assignment, which will need further analysis, see ref. 22). At the DFT level, a delocalised structure can be enforced by imposing symmetry. For the activated model a structure with D_2d symmetry (a higher-order saddle point) is 10 kcal mol⁻¹ above the asymmetric minimum at the CAM-B3LYP-D3//PBE0-D3 level, fully in line with the expected fluxionality.

pNMR properties. In terms of the pNMR properties, the most significant impact of spin (de)localisation is observed on C1 and C2 (see Fig. 8). In the activated model, the defect with spin delocalisation is predicted to have a C1 shift that is substantially more shielded compared to its spin-localised counterpart, while C2 and C3 are more deshielded. Overall, all the signals from the defect are predicted to be well separated from the pristine material at room temperature. When considering the hydrated model, the spin-localised structure shows a chemical shift for C1 and C3 that is remarkably close to the computed and experimental values of the pristine (non-defective) model and material, whereas C2 shows a 100 ppm difference. It must be noted, that for the pristine system a scaling procedure had to be used in order to correctly reproduce the experimental results¹⁰ (through fitting of a uniform scaling factor of energy gaps between the spin states). The two different electronic structures, i.e., where spin density is localised or delocalised, show very significant differences in their predicted pNMR shifts. The localised structure, favoured by DFT, may be difficult to identify unambiguously as its predicted shifts are very close to those of the pristine model (although the signals might still be distinguishable with variable temperature experiments, see temperature dependence in Fig. 9). The delocalised structure, in contrast, shows predicted shifts far outside the range observed for the non-defective models. Therefore, pNMR spectroscopy could not only be a means to detect the possible occurrence of such mixed-valence defects, but could directly reveal insights into their nature in terms of electronic structure.

Fig. 8 Schematic plot of predicted ¹³C pNMR peak positions of the Cu(I)Cu(II) defect models (blue and orange points for structure optimised with xTB and PBE0-D3) and of the experimental HKUST-1 (grey points) and non-defective (yellow) HKUST-1 models; for (a) activated and (b) hydrated models.

Fig. 9 Predicted temperature dependence of ¹³C pNMR shifts, δ, in the mixed valence defects for (a) activated and (b) hydrated models.

Note that the previously mentioned D_2d symmetric saddle point shows similar spin and magnetic properties as the xTB optimised structure. Such a D_2d symmetric structure captures the transition between the two spin-localised isomers and shows a full spin delocalisation and a strongly deshielded C1 and shielded C2 (see Table 1 and Table S7 for the temperature dependence, ESI†).

Table 1 Predicted pNMR chemical shifts, δ (CAM-B3LYP level), for the mixed-valence defect transition state (TS)^a and minima optimised at the PBE0-D3 and xTB level

Site	TS (DFT)	Min (DFT)	Min (xTB)
a Higher-order saddle point, to be precise.
C1	1521	933	1605
C2	−265	−78	−235
C3	47	180	46

---

Based on the computed pNMR data, the presence of the spin-delocalised defect should be easier to identify than the proton defect discussed above, as the separation of its signals from those of the pristine material are stark for C1 and C3, while for the spin-localised defect only C2 can be used to distinguish between a defective and non-defective material. Nevertheless, employing a variable-temperature approach would still provide the best analytical method to distinguish between defective and non-defective signals, as the temperature dependence is different¹⁰ (see the strictly linear dependence on 1/T for the defects in Fig. 9a and b and Table S10 (ESI†), as opposed to the nonlinear dependencies in the pristine material, reported in ref. 10).

Constrained models. As mentioned previously for the protonated defect, strong structural variations will likely not be compatible with the extended framework of the MOF. Therefore, constraints were once again imposed in the optimisation with the positions of the phenyl rings fixed and the impact on the pNMR properties and spin density explored. The latter is of particular interest, and it will provide insight into whether various optimization methods still predict a localised or delocalised spin distribution.

In terms of their pNMR properties, both activated and hydrated constrained models do not afford significant changes when compared to their unconstrained counterpart (see Fig. 10). The xTB optimised models predict greater deshielding of C1, whereas the PBE0 optimised models display the opposite behaviour, i.e., larger shielding, while C2 and C3 are more shielded in the constrained model, irrespective of the optimisation method used. It must be pointed out that given the magnitude of the explored chemical shift range, such changes are perhaps not significant as they are below 200 ppm.

Fig. 10 Schematic plot of predicted ¹³C pNMR peak positions for the constrained and unconstrained mixed valence defect models optimised at the xTB and PBE0-D3 level for (a) activated and (b) hydrated models.

The spin density follows a similar trend as the pNMR shifts just discussed, since no significant changes are found between the constrained and unconstrained models. The models optimised with PBE0 retain a spin localised nature, while xTB optimisation produces full spin delocalisation between metal centres (see Fig. 11).

Fig. 11 Molecular models with corresponding spin density of the activated Cu(I)Cu(II) (top) and hydrated Cu(I)Cu(II) (bottom) defect models constrained during optimisation, optimised at xTB (left) and PBE0-D3 levels (right).

Energetics of constrained models. A stark difference between the protonated and mixed valence constrained models is found in their relative energies with respect to the fully optimised minima. The proton models were strongly disfavoured having distortion energies well over 10 kcal mol⁻¹ (see Table S8, ESI†), whereas for the mixed valence system the relative energies are noticeably smaller (except for one case, see Table 2).

Table 2 Relative energies between constrained and unconstrained models for the mixed-valence defect

Model (fully optimised/constrained)^a	Optimisation method	ΔE^b (kcal mol^−1)
a Fully optimised (i.e., unconstrained) or constrained (see text). b Energies are calculated relative to the unconstrained model.
Activated (fopt)	xTB	0.00
activated (cons)	xTB	4.03
Hydrated (fopt)	xTB	0.00
hydrated (cons)	xTB	6.95
Activated (fopt)	PBE0-D3	0.00
activated (cons)	PBE0-D3	4.80
Hydrated (fopt)	PBE0-D3	0.00
hydrated (cons)	PBE0-D3	11.74

---

Given their magnetic properties and their framework-compatible geometry, these models could be a valid alternative to the fully optimised ones.

In view of the abovementioned uncertainty as to the practical viability of such mixed-valence dimers as possible candidates for the defects seen in MOFs, no attempt was made to estimate driving forces for their formation (which would come down to the prediction of redox potentials, which has its own methodological challenges). From the distortion energies in Table 2 it appears that if one-electron reduction of individual dimers were possible during MOF formation, their incorporation into the resulting porous framework would not be prohibitive.

Conclusions

Defects based on the copper paddlewheel motif have been explored for small model complexes in order to gain insight into previous EPR findings for HKUST-1 and the STAM family of MOFs,¹¹ both in their hydrated and activated forms, and the viability of their observation using pNMR spectroscopy. The neutral protonated defect, Cu(H)₂, affords a predicted pNMR spectrum in the same spectral region as that for the non-defective material. Nevertheless, we suggest that variable temperature NMR measurements would be an effective strategy to distinguish between defective and non-defective signals, owing to the linearly inverse relationship with temperature of the defect signals. Regarding the negatively charged, mixed valence defect, the results have a strong method dependence. Irrespective of applying structural constraints to accommodate the defect in the extended MOF, or of using hydrated or activated models, for PBE0-D3 optimised structures the predicted pNMR spectra are close to that of the non-defective material, whereas xTB-optimised structures show strong differences for C1 and C2, i.e., the more deshielded and shielded carbon atoms in the system. Once more, the temperature dependence is indicated to be the key to assign signals belonging to the defect.

In summary, we have used an established protocol to predict the pNMR spectral characteristics of potential spin–1/2 defects in MOFs based on Cu paddlewheel dimers. We expect this information to be useful for a more complete spectroscopic characterisation of such defects, eventually leading to an improved understanding of the structure (geometric and electronic) of these important materials.

Methods

Geometry optimisation was performed by using the semi-empirical method GFN2-xTB^23–28 (here referred to as xTB for short) and DFT with the functional PBE0²⁴ with D3 dispersion corrections²⁵ as implemented in Gaussian09.²⁹ The 6-31G* basis set was used for all atoms except for Cu, for which an augmented Wachters basis set^30,31 was used (62111111/3311111/3111). For the constrained optimisations, all 24 atoms of the phenyl rings were frozen in their positions in the non-defective paddlewheel dimers optimised at the respective level of theory, and all other atoms were relaxed. Amongst the existing methodologies for computing pNMR shifts,^19,32–34 we adopted that from Hrobárik and Kaupp,³² where the isotropic shielding, σ_iso, is computed according to eqn (1):in a temperature range of 100 K, from 250 K to 350 K in steps of 20 K. The magnetic parameters were computed at the CAM-B3LYP³⁷ level of theory employing 9s7p4d (621111111/3311111/3111) basis sets on Cu (derived from Ahlrichs-type bases)³⁸ and IGLO-basis II³⁹ on the ligands. Orbital shieldings were calculated using Gaussian09, and the ORCA software for the computation of the g and A tensors.⁴⁰ Chemical shifts are referenced to TMS, where orbital shieldings are computed at the same level (total shieldings σ = 32.2 and 187 ppm for ¹H and ¹³C, respectively). Shieldings were averaged over the corresponding sites across all four Ph rings in the models (for the mixed-valence defect, C3 and C3′ were also averaged and only reported as C3). This methodology has been used and validated in our previous studies on Cu complexes.^10,11,17 Hybrid functionals such as PBE0-D3 and the semiempirical xTB method have been shown previously to perform very well for geometries of transition metal complexes.^35,36 For pNMR properties of such complexes, hybrid functionals with large fractions of HF exchange have been shown to be superior to GGAs or standard hybrids,^17,24 and the good performance of the range-separated hybrid functional CAM-B3LYP for Cu paddle wheel dimers has been established in ref. 10.

For the formation energies of the defect, single point calculations were performed at the CAM-B3LYP-D3/IGLO-II level detailed above (augmented with Grimme dispersion corrections) using Gaussian09. For the Cu₂(O₂CPh)₄ dimer, the triplet state was used for these energy evaluations. Lastly, to account for the polar environment the single-point energies were also calculated with a simple polarisable continuum model (PCM)⁴¹ employing the parameters of water (ε = 80). All Gaussian calculations employed the default convergence criteria (maximum change in density matrix elements 10⁻⁸ a.u., maximum change in energy 10⁻⁶ a.u. for SCF, maximum and RMS gradient 4.5 × 10⁻⁴ a.u. and 3 × 10⁻⁴ a.u., respectively, for geometry optimisations), whereas very tight convergence criteria were used for the xTB geometry optimisation (maximum energy change 10⁻⁷ a.u. for SCF, and maximum gradient 2 × 10⁻⁴ a.u. for optimisations) and the ORCA properties calculations (maximum energy change 10⁻⁸ a.u.).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

M. B. thanks the EaStCHEM School of Chemistry for support. We thank Dr Hassane El Mkami for helpful discussions. Computations were performed on a local HPC cluster maintained by Dr H. Früchtl. The research data supporting this publication can be accessed at https://doi.org/10.17630/f9ce99be-957f-43d4-b289-d6654b2a9323.

References

1. H. C. Zhou, J. R. Long and O. M. Yaghi, Chem. Rev., 2012, 112, 673–674.
2. J. Han, B. Xiao, P. K. Le and C. Mangwandi, Materials, 2023, 16, 1554.
3. S. Gautam, J. Singhal, H. K. Lee and K. H. Chae, Mater. Today Chem., 2022, 23, 2468–5194.
4. D. Sharma, S. Rasaily, S. Pradhan, K. Baruah, S. Tamang and A. Pariyar, Inorg. Chem., 2021, 60, 7794–7802.
5. X. Ma, L. Wang, H. Wang, J. Deng, Y. Song, Q. Li, X. Li and A. M. Dietrich, J. Hazard. Mater., 2022, 424, 0304–3894.
6. A. Rosado, A. Borrás, J. Fraile, J. A. R. Navarro, F. Suarez-Garcia, K. C. Stylianou, A. M. López-Periago, J. G. Planas, C. Domeingo and A. Yazdi, ACS Appl. Nano Mater., 2021, 4, 12712–12725.
7. Y. Cui, B. Li, H. He, W. Zhou, B. Chen and G. Qian, Acc. Chem. Res., 2016, 49, 483–493.
8. S. S. Chui, S. M. Lo, J. P. Charmant, A. G. Orpen and I. D. Williams, Science, 1999, 283, 1148–1150.
9. J. J. Gutiérrez, J. M. Vicent-Luna, D. Dubbeldam and S. Calero, J. Phys. Chem. C, 2013, 117, 11357–11366.
10. Z. Ke, D. M. Dawson, S. E. Ashbrook and M. Bühl, Chem. Sci., 2022, 13, 2674–2685.
11. D. M. Dawson, C. E. F. Sansome, L. N. McHugh, M. J. McPherson, L. J. McCormick McPherson, R. E. Morris and S. E. Ashbrook, Solid State Nucl. Magn. Reson., 2019, 101, 44–50.
12. M. I. H. Mohideen, B. Xiao, P. S. Wheatley, A. C. McKinlay, Y. Li, A. M. Z. Slawin, D. W. Aldous, N. F. Cessford, T. Düren, X. Zhao, R. Gill, J. M. Griffin, S. E. Ashbrook and R. E. Morris, Nat. Chem., 2011, 3, 304–310.
13. L. N. McHugh, M. J. McPherson, L. J. McCormick, S. A. Morris, P. S. Wheatley, S. J. Teat, D. McKay, D. M. Dawson, C. E. F. Sansome, S. E. Ashbrook, C. A. Stone, M. W. Smith and R. E. Morris, Nat. Chem., 2018, 10, 1096–1102.
14. D. M. Dawson, L. E. Jamieson, M. I. H. Mohideen, A. C. McKinlay, I. A. Smellie, R. Cadou, N. S. Keddie, R. E. Morris and S. E. Ashbrook, Phys. Chem. Chem. Phys., 2012, 15, 919–929.
15. H. E. Mkami, M. I. Mohideen, C. Pal, A. McKinlay, O. Scheimann and R. E. Morris, Chem. Phys. Lett., 2012, 544, 17–21.
16. M. D. Allendorf, V. Stavila, M. Witman, C. K. Brozek and C. H. Hendon, J. Am. Chem. Soc., 2021, 143, 6705–6723.
17. M. Bühl, S. E. Ashbrook, D. M. Dawson, R. A. Doyle, P. Hrobárik, M. Kaupp and I. A. Smellie, Chem. – Eur. J., 2016, 22, 15328–15339.
18. A. J. Pell, G. Pintacuda and C. P. Grey, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 111, 1–271.
19. S. Moon and S. Patchkovskii, in Calculation of NMR and EPR Parameters: Theory and Applications, ed. M. Kaupp, M. Bühl and V. G. Malkin, Wiley, Weinheim (Germany), 2004, pp. 325–340.
20. I. G. Crivelli and C. G. Andrade, Inorg. Chim. Acta, 1993, 203, 115–120.
21. M. Šimėnas, M. Kobalz, M. Mendt, P. Eckold, H. Krautscheid, J. Banys and A. Pöppl, J. Phys. Chem. C, 2015, 119, 4898–4907.
22. M. Parthey and M. Kaupp, Chem. Soc. Rev., 2014, 43, 5067–5088.
23. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
24. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985.
25. A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101.
26. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
27. E. R. Johnson and A. D. Becke, J. Chem. Phys., 2006, 124, 174104.
28. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671.
29. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Revision D.01, Gaussian Inc., 2013.
30. A. J. Wachters, J. Chem. Phys., 1970, 52, 1033–1036.
31. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.
32. P. Hrobárik, R. Reviakine, A. V. Arbuznikov, O. L. Malkina, V. G. Malkin, F. H. Köhler and M. Kaupp, J. Chem. Phys., 2007, 126, 024107.
33. T. O. Pennanen and J. Vaara, Phys. Rev. Lett., 2008, 100, 133002.
34. B. Martin and J. Autschbach, Phys. Chem. Chem. Phys., 2016, 18, 21051–21068.
35. M. Bühl, C. Reimann, D. A. Pantazis, T. Bredow and F. Neese, J. Chem. Theory Comput., 2008, 4, 1449–1459.
36. M. Bursch, H. Neugebauer and S. Grimme, Angew. Chem., Int. Ed., 2019, 58, 11078–11087.
37. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
38. M. Munzarova and M. Kaupp, J. Phys. Chem. A, 1999, 103, 9966–9983.
39. U. F. W. Kutzelnigg and M. Schindler, NMR Basic Principles and Progress, Springer, Berlin, 1990, vol. 23, pp. 165–262.
40. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
41. S. Miertu, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04618d

---