 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Orientational dynamics in supercooled glycerol computed from MD simulations: self and cross contributions†
Marceau
Hénot
 *a,
Pierre-Michel
Déjardin
*a,
Pierre-Michel
Déjardin
 b and
François
Ladieu
a
b and
François
Ladieu
a
aSPEC, CEA, CNRS, Université Paris-Saclay, CEA Saclay Bat 772, 91191 Gif-sur-Yvette Cedex, France. E-mail: marceau.henot@cea.fr
bLaboratoire de Modélisation Pluridisciplinaire et Simulations, Université de Perpignan Via Domitia, 52 avenue Paul Alduy, F-66860 Perpignan, France
First published on 11th October 2023
Abstract
The orientational dynamics of supercooled glycerol is probed using molecular dynamics simulations for temperatures ranging from 323 K to 253 K, through correlation functions of first and second ranks of Legendre polynomials, pertaining respectively to dielectric spectroscopy (DS) and depolarized dynamic light scattering (DDLS). The self, cross, and total correlation functions are compared with relevant experimental data. The computations reveal the low sensitivity of DDLS to cross-correlations, in agreement with what is found in experimental work, and strengthen the idea of directly comparing DS and DDLS data to evaluate the effect of cross-correlations in polar liquids. The analysis of the net static cross-correlations and their spatial decomposition shows that, although cross-correlations extend over nanometric distances, their net magnitude originates, in the case of glycerol, from the first shell of neighbouring molecules. Accessing the angular dependence of the static correlation allows us to get a microscopic understanding of why the rank-1 correlation function is more sensitive to cross-correlation than its rank-2 counterpart.
1 Introduction
Dielectric spectroscopy (DS) is a powerful tool for studying polar supercooled liquid dynamics.1–3 The outcome of the measurement, the complex dielectric permittivity ε(ω), contains a wealthiness of information regarding the collective orientational motion of the permanent dipoles of the constitutive molecules, and more precisely on the relaxation processes at work in the liquid under scrutiny.4,5 The broad range of available frequencies (10−5–1013 Hz) for a wide range of temperatures, allows to follow the slow down of the structural α relaxation upon cooling close to the glass transition temperature as well as the emergence of secondary relaxation processes such as JG processes, believed to be an intrinsic characteristic of glassy dynamics,6 or the excess wing, recently associated with dynamical facilitation.7 DS can also be used to characterize the cooperative nature of the α relaxation,8 to determine density scaling of the relaxation time,9,10 or to study physical aging of out-of-equilibrium liquids.11,12The complex dielectric permittivity obtained from DS measurements can be linked to the time-dependent equilibrium field free total dipole moment correlation function C1(t) through a Fourier–Laplace transform13–15
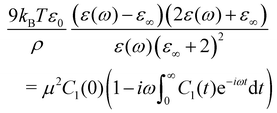 | (1) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is:
is: | (2) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is the Legendre polynomial of rank
is the Legendre polynomial of rank ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and ϑi,j(t0,t0 + t) corresponds to the angle between molecule i at time t0 and j at t0 + t. In DS, this angle is measured between dipole moments and the technique is sensitive to the order
and ϑi,j(t0,t0 + t) corresponds to the angle between molecule i at time t0 and j at t0 + t. In DS, this angle is measured between dipole moments and the technique is sensitive to the order ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 leading to:
= 1 leading to: | (3) |
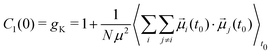 | (4) |
Recently, results from DS were compared to other techniques less sensitive to cross-correlations. The fluorescence response of a local probe diluted in a mono-alcohol was shown to be insensitive to the Debye relaxation of the liquid, allowing it to disentangle it from the other relaxation processes.18 Another technique that has been proven useful in that regard is depolarized dynamic light scattering (DDLS) which probes molecular orientations through the anisotropy of the polarizability. The relevant correlation function is given by eqn (2) with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2. It follows that the technique does not distinguish between parallel and antiparallel alignments. There is strong experimental evidence that DDLS is insensitive to cross-correlations. For example, Gabriel et al.19 showed that in mono-alcohols DDLS displays an α peak but no Debye peak. In addition, in a non-associating liquid, Pabst et al.20 showed that progressively diluting the system in a non-polar solvent leads the DS spectra to look more and more alike the DDLS spectra. All of this illustrates the importance of cross-correlation effects in DS which can significantly broaden the α peak. Moreover, while the shape of the α peak in DS spectra is system dependent, it was shown in DDLS to follow a generic line shape of slope − 1/2 on the high-frequency flank.21 There is still debate, however, on whether this generic response reflects the true structural relaxation better than the dielectric one.22
= 2. It follows that the technique does not distinguish between parallel and antiparallel alignments. There is strong experimental evidence that DDLS is insensitive to cross-correlations. For example, Gabriel et al.19 showed that in mono-alcohols DDLS displays an α peak but no Debye peak. In addition, in a non-associating liquid, Pabst et al.20 showed that progressively diluting the system in a non-polar solvent leads the DS spectra to look more and more alike the DDLS spectra. All of this illustrates the importance of cross-correlation effects in DS which can significantly broaden the α peak. Moreover, while the shape of the α peak in DS spectra is system dependent, it was shown in DDLS to follow a generic line shape of slope − 1/2 on the high-frequency flank.21 There is still debate, however, on whether this generic response reflects the true structural relaxation better than the dielectric one.22
When dealing with physical processes taking place at the nanometric scale, molecular dynamics (MD) simulation is an attractive method that can give access to microscopic observables that are otherwise hard, or impossible, to obtain experimentally. This method is however limited to high temperatures or simplified systems, due to its computational cost. To study the generic behavior of liquid glass-formers, model systems can be thought of being made of polydisperse beads interacting through a Lennard-Jones potential. This helped give information on the spatio-temporal nature of relaxations.7,23 Another approach, more suitable for direct comparison with experiments, is to rely on a more precise modelization of specific molecules, taking into account their dipolar nature and electrostatic interactions. This gives access to their dielectric response.24–28 Recently, MD simulations on a model dipolar system showed that, while the orientational ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 correlation function of weakly polar systems is dominated by the self response, strongly polar liquids are much affected by cross-correlations.29
= 1 correlation function of weakly polar systems is dominated by the self response, strongly polar liquids are much affected by cross-correlations.29
The wide variety of organic liquids available has led to the choice of some systems, considered as models or representatives. Glycerol, by its apparent simplicity and its low tendency to crystallize, has long been the subject of extensive studies, by various techniques including dielectric spectroscopy,2,11,30–32 neutron spectroscopy,33 nuclear magnetic resonance (NMR),34 DDLS35,36 and MD simulations.37–44 Its dynamics is, however, not particularly simple. As a tri-alcool, it is subject to H-bonds but does not display a Debye peak that would result from linear supramolecular chains. Shear mechanical spectroscopy has shown the existence of a low-frequency mode that is believed to result from the hydrogen-bonded network formed between molecules.45
In this article, we report a MD study of the orientational dynamics of glycerol, on a large temperature range (from 253 to 323 K) reaching the moderately supercooled regime, simulated from a model already widely used in the literature37–40,44 over durations of up to 7 s. We first compute the self response of the dipolar moment for ranks ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 and 2 from which we deduce the loss function
= 1 and 2 from which we deduce the loss function  for frequencies down to 200 kHz. We then analyze the cross-correlation and we exploit the possibility offered by MD to decompose this part of the response as a function of the relative distance and orientation of the dipoles. We compute the total loss function for both ranks as well as the part resulting from cross-correlations alone which allowed us to verify that cross-correlations play a major role in the
for frequencies down to 200 kHz. We then analyze the cross-correlation and we exploit the possibility offered by MD to decompose this part of the response as a function of the relative distance and orientation of the dipoles. We compute the total loss function for both ranks as well as the part resulting from cross-correlations alone which allowed us to verify that cross-correlations play a major role in the ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 response while being almost negligible for
= 1 response while being almost negligible for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2. We compare these data to experimental DS and DDLS spectra and obtain similar temperature dependence for the relaxation time and slope of the high-frequency flank of the α peak. We discuss how the differences in the spectra associated with different ranks can be related to the underlying molecular relaxation mechanisms. Moreover, we show that, for glycerol, the net cross-correlation originates only from the first shell of neighouring molecules. This is the case for both
= 2. We compare these data to experimental DS and DDLS spectra and obtain similar temperature dependence for the relaxation time and slope of the high-frequency flank of the α peak. We discuss how the differences in the spectra associated with different ranks can be related to the underlying molecular relaxation mechanisms. Moreover, we show that, for glycerol, the net cross-correlation originates only from the first shell of neighouring molecules. This is the case for both ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 and 2 although their different sensitivity to orientational correlations leads, at the end, to significant differences in the importance of contributions coming from cross-correlations.
= 1 and 2 although their different sensitivity to orientational correlations leads, at the end, to significant differences in the importance of contributions coming from cross-correlations.
2 Methods
The molecular dynamics (MD) simulations were performed using OpenMM46 on an Nvidia RTX A5000 GPU. Glycerol has been modeled using the re-parameterized AMBER force field previously employed in the literature37–42,44 and whose parameters are given in the ESI† atoms belonging to the same molecule interact through harmonic potentials for bond length and angle and a periodic potential for bond torsion. Non-bounded atoms interact through a Lenard Jones potential with a 1 nm cutoff and a coulomb interaction computed using a Particle Mesh Ewald (PME) algorithm (1 nm cutoff and 0.0005 error tolerance). The simulation does not account for electronic polarizability. Each atom carries a constant partial charge originally derived by Chelli et al.37 from quantum mechanical calculations. Later, Blieck et al.39 noticed that this parameterization led, in the temperature range 333–413 K, to a dynamics 10 times faster than measured experimentally by neutron spectroscopy. They slowed down the dynamics by the right amount by reducing by 5% the hydroxyl group atomic charges. They also checked that the simulation reproduced fairly well the static structure factor measured by neutron scattering.47 This corresponds to a mean dipole moment of 〈μ〉 = 3.2 D which is higher than the μexp = 2.68 D value measured in a nonpolar solvent.48 This can be seen as a way to compensate for the absence of electronic polarizability which leads, in the real system, through the reaction field, to an effective dipole moment greater than μexp.4 The same parameters were later used by Egorov et al.40 (who corrected slightly the charges to ensure the molecule neutrality, and made all bound flexible) to study glycerol-water mixtures and more recently by Becher et al.44 to reproduce NMR spectra in the 300–540 K range. The parameters used in this work were almost identical with only small modifications intended to reduce the computational cost: the length of bonds involving hydrogen were fixed (as in ref. 37 and 39) and hydrogen atom mass was increased by 40% allowing to use an integration time of 4 fs. The simulations were carried out on a system of N = 2160 molecules (30 240 atoms) in a cubic cell of side length a ≈ 65 Å with periodic boundary conditions (PBCs), in the NPT ensemble at eight different temperatures T (from 323 to 253 K) and at pressure P = 1 bar using a Monte Carlo barostat and a Nosé–Hoover thermostat. In order to study the effect of the system size, a simulation at T = 323 K was performed on a system consisting only of N = 540 molecules (a ≈ 41 Å). Random initial states were generated using Packmol,49 equilibrated at 323 K and progressively cooled down to 253 K by 10 K steps by waiting at each step an equilibration time corresponding to 98 to 200τα, reaching 7 s (see details in the ESI†). At each temperature, simulation runs lasted from more than 180τα for T ≥ 263 K and 67τα at 253 K (corresponding to 4 s). For all simulation runs, the dipole of each molecule![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) i(t) (i∈[1,N]) and its position
i(t) (i∈[1,N]) and its position ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(t) were determined by computing the barycenter of the positive (q+ at
i(t) were determined by computing the barycenter of the positive (q+ at ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) +) and negative charges (q− = −q+ at
+) and negative charges (q− = −q+ at ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) −) with
−) with ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) = q+(
= q+(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) + −
+ − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) −) and
−) and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) = (
= (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) + +
+ + ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) −)/2.
−)/2.
3 Results and discussion
3.1 Self correlation
The self dipole correlation function is defined by:Cself![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (t) = 〈P (t) = 〈P![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) [cos [cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑi,i(t0,t0 + t)]〉i,t0 ϑi,i(t0,t0 + t)]〉i,t0 | (5) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 and 2 (see ESI† for a log vertical axis). Three regimes can be observed: at short time (t < 100 fs) a small decorrelation occurs and a boson peak is visible at t ≈ 70 fs. At long time, there is a complete, non-exponential decorrelation (Cself
= 1 and 2 (see ESI† for a log vertical axis). Three regimes can be observed: at short time (t < 100 fs) a small decorrelation occurs and a boson peak is visible at t ≈ 70 fs. At long time, there is a complete, non-exponential decorrelation (Cself![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (t) reaches 0) corresponding to the α relaxation. At intermediate times the correlation is high but slowly decreasing. This regime is almost nonexistent at 323 K but extends over two decades at T = 253 K. While the global shape is the same for
(t) reaches 0) corresponding to the α relaxation. At intermediate times the correlation is high but slowly decreasing. This regime is almost nonexistent at 323 K but extends over two decades at T = 253 K. While the global shape is the same for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 and 2, the short time decorrelation appears more intense for
= 1 and 2, the short time decorrelation appears more intense for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2. This is simply due to the quicker decreases of P2(cos
= 2. This is simply due to the quicker decreases of P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ) compared to P1(cos
ϑ) compared to P1(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ) for ϑ ≪ 1.
ϑ) for ϑ ≪ 1.
The mean self relaxation time is obtained from  and is shown as a function of 1/T in blue in Fig. 6a. The relaxation times are shorter for
and is shown as a function of 1/T in blue in Fig. 6a. The relaxation times are shorter for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 (empty markers) than for
= 2 (empty markers) than for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 (solid markers) and they both display a super-activated behaviour.
= 1 (solid markers) and they both display a super-activated behaviour.
The self loss function was obtained, following eqn (1), by applying the fluctuation-dissipation theorem:50 where TF is the Fourier transform, computed using the fftlog algorithm adapted to log spaced data.51 The fact that the correlation function was averaged on long times (≈100τα) leads to a fairly low amount of noise on the spectra, shown in Fig. 1b. They were all rescaled by superimposing their microscopic peaks at 1013 Hz. The frequency at which the maximum of the α peak is reached was found to correspond (within the uncertainty) to 1/(2πτself
where TF is the Fourier transform, computed using the fftlog algorithm adapted to log spaced data.51 The fact that the correlation function was averaged on long times (≈100τα) leads to a fairly low amount of noise on the spectra, shown in Fig. 1b. They were all rescaled by superimposing their microscopic peaks at 1013 Hz. The frequency at which the maximum of the α peak is reached was found to correspond (within the uncertainty) to 1/(2πτself![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ). On the low-frequency side, the spectra follow a power law with slope 1, as expected. On the high-frequency flank of each spectrum, there is a power law regime on one to two decades in frequency with a slope −βself
). On the low-frequency side, the spectra follow a power law with slope 1, as expected. On the high-frequency flank of each spectrum, there is a power law regime on one to two decades in frequency with a slope −βself![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , interrupted by the fast process.3 The corresponding values of βself
, interrupted by the fast process.3 The corresponding values of βself![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) are shown in blue in Fig. 6b. For
are shown in blue in Fig. 6b. For ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 (solid markers), slope increases with temperature (ranging from 0.36 at 253 K to 0.46 at 323 K) while for
= 1 (solid markers), slope increases with temperature (ranging from 0.36 at 253 K to 0.46 at 323 K) while for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 (empty markers), it is temperature independent and systematically smaller (≈0.27). These low β values are associated with the non-exponential nature of the relaxation process.
= 2 (empty markers), it is temperature independent and systematically smaller (≈0.27). These low β values are associated with the non-exponential nature of the relaxation process.
3.2 Static cross-correlation
As stated in the introduction, experimental methods such as DS and DDLS are sensitive, not only to the self correlation function, but rather to a total correlation made of the self part and of a cross-correlation part. We thus need to get access to the correlation function associated to cross-correlation: | (6) |
We decompose the cross-correlation function Ccross![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (t) into contributions per unit distance denoted c
(t) into contributions per unit distance denoted c![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (r,t) depending on the distance r = ‖
(r,t) depending on the distance r = ‖![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j −
j − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i‖ between the reference molecule i and all molecules within [r,r + dr]. This quantity, computed for slices of 0.5 Å and averaged over i and t0, is plotted in Fig. 2a for the static case (t = 0) for
i‖ between the reference molecule i and all molecules within [r,r + dr]. This quantity, computed for slices of 0.5 Å and averaged over i and t0, is plotted in Fig. 2a for the static case (t = 0) for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 and 2. The dipole density n(r) is plotted in black in Fig. 2b alongside with the parabola in red that would be obtained for a homogeneous system of the same average density. The difference between these two curves shows a series of maxima that corresponds to the first, second and third neighbour peaks. For
= 1 and 2. The dipole density n(r) is plotted in black in Fig. 2b alongside with the parabola in red that would be obtained for a homogeneous system of the same average density. The difference between these two curves shows a series of maxima that corresponds to the first, second and third neighbour peaks. For ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, it appears that the cross-correlation contribution c1(r) (in blue) is maximum for the first neighbours and reaches zero before the second layers of neighbours. Fig. 2c represents, as a function of r, the total contribution
= 1, it appears that the cross-correlation contribution c1(r) (in blue) is maximum for the first neighbours and reaches zero before the second layers of neighbours. Fig. 2c represents, as a function of r, the total contribution  integrated within a sphere of radius r. We see that the cross-correlation reaches a plateau at r ≈ 7 Å while the cross-correlation coming from PCBs starts to be perceptible for r > 20 Å (see ESI†). It is also interesting to study the mean level of static cross-correlation Γ(r) = c(r)/n(r), plotted in Fig. 2d that shows that the cross-correlation per dipole is positive, is a strictly decreasing function of the distance and is only of the order of 5–15% in average for the nearest neighbours. From these data, we can deduce the Kirkwood factor
integrated within a sphere of radius r. We see that the cross-correlation reaches a plateau at r ≈ 7 Å while the cross-correlation coming from PCBs starts to be perceptible for r > 20 Å (see ESI†). It is also interesting to study the mean level of static cross-correlation Γ(r) = c(r)/n(r), plotted in Fig. 2d that shows that the cross-correlation per dipole is positive, is a strictly decreasing function of the distance and is only of the order of 5–15% in average for the nearest neighbours. From these data, we can deduce the Kirkwood factor  at 273 K, with rlim = 7.5 Å. This is smaller than the 2.6 ± 0.2 value reported in the literature and deduced from static permittivity measurements36 but it is compatible with previous numerical results on glycerol for T > 250 K.43 It is also interesting to note that our value of μ2gK (which is the quantity accessible from the experiments, see eqn (1)) matches exactly the experimental value and displays the same temperature dependence (cf. Fig. S4 in ESI†). In other words, the simulation gives the expected value of ε(0) in the whole temperature range. However, as the dipolar moment of glycerol has been measured with a reasonable accuracy in a non-polar solvent,48 it is likely that the MD simulation underestimate the value of gK. For
at 273 K, with rlim = 7.5 Å. This is smaller than the 2.6 ± 0.2 value reported in the literature and deduced from static permittivity measurements36 but it is compatible with previous numerical results on glycerol for T > 250 K.43 It is also interesting to note that our value of μ2gK (which is the quantity accessible from the experiments, see eqn (1)) matches exactly the experimental value and displays the same temperature dependence (cf. Fig. S4 in ESI†). In other words, the simulation gives the expected value of ε(0) in the whole temperature range. However, as the dipolar moment of glycerol has been measured with a reasonable accuracy in a non-polar solvent,48 it is likely that the MD simulation underestimate the value of gK. For ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2, the cross-correlation (in orange) appears to be also due to the first layer of neighbours but is much less intense than for
= 2, the cross-correlation (in orange) appears to be also due to the first layer of neighbours but is much less intense than for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 and its integrated value saturates for a slightly higher radius. With rlim = 9.5 Å, the quantity analogous to the Kirkwood factor for
= 1 and its integrated value saturates for a slightly higher radius. With rlim = 9.5 Å, the quantity analogous to the Kirkwood factor for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 would be only 1.11 ± 0.01.
= 2 would be only 1.11 ± 0.01.
The dipolar interaction is anisotropic in nature and it makes sense, rather than averaging the cross-correlation over all dipoles situated at a given distance, to distinguish the contribution as a function of the relative orientation. Spherical coordinates (r,θ,ϕ) can be defined with respect to the reference dipole i where θ is the angle between ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) i and
i and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) =
= ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j −
j − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i. By symmetry, the contribution should not depend on the azimuthal angle ϕ. The cross-correlation contribution c
i. By symmetry, the contribution should not depend on the azimuthal angle ϕ. The cross-correlation contribution c![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (r,θ) per unit distance and solid angle is shown in the static case in Fig. 3a (
(r,θ) per unit distance and solid angle is shown in the static case in Fig. 3a (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1) and b (
= 1) and b (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2) as a function of r and θ. For
= 2) as a function of r and θ. For ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, similarly to a recent observation in water,28 the spatial distribution of cross-correlation appears strikingly different than the θ averaged curves shown previously. The correlation is positive in an angular sector situated above and below the dipole of reference |cos
= 1, similarly to a recent observation in water,28 the spatial distribution of cross-correlation appears strikingly different than the θ averaged curves shown previously. The correlation is positive in an angular sector situated above and below the dipole of reference |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ| < cos
θ| < cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θlim and mostly negative on its sides. It is null on lines of constant |cos
θlim and mostly negative on its sides. It is null on lines of constant |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ| = cos
θ| = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θlim shown in grey with θlim = 52°. The cross-correlation contributions summed over these two angular sectors are shown in Fig. 3c (top). These positive and negative contributions extend way over what is visible when considering their sum and, while decreasing, are far from negligible at r = 16 Å. However, these contributions cancel each other for r > 7.5 Å. This angular dependence of the cross-correlation is what is expected when considering the energy interaction between two electrostatic dipoles as a function of their relative orientation53 and drawings of the most favorable dipoles orientations are shown in Fig. 3a. The net contribution of cross-correlation comes from the first shell of neighbouring molecules. Close molecules situated above and below are strongly positively correlated (even more above than below) with an alignment rate reaching 50%. This correlation is favored by the dipole–dipole interaction although the top-bottom asymmetry illustrates that at such a close distance, it is not the only interaction playing a role. On the sides, molecules belonging to the first shell but further than 5.2 Å (corresponding to the first neighbor peak) are on average anti-aligned (again as favored by the dipole–dipole interaction), although not enough to compensate for the positive correlation. Finally, side molecules closer than 5.2 Å are positively aligned. This means that there exists other effects (that may be related to constraints on molecule conformation or to the presence of H-bonds) able to compensate for the a priori unfavorable situation of having barycenters of the same sign charges facing each other on average.
θlim shown in grey with θlim = 52°. The cross-correlation contributions summed over these two angular sectors are shown in Fig. 3c (top). These positive and negative contributions extend way over what is visible when considering their sum and, while decreasing, are far from negligible at r = 16 Å. However, these contributions cancel each other for r > 7.5 Å. This angular dependence of the cross-correlation is what is expected when considering the energy interaction between two electrostatic dipoles as a function of their relative orientation53 and drawings of the most favorable dipoles orientations are shown in Fig. 3a. The net contribution of cross-correlation comes from the first shell of neighbouring molecules. Close molecules situated above and below are strongly positively correlated (even more above than below) with an alignment rate reaching 50%. This correlation is favored by the dipole–dipole interaction although the top-bottom asymmetry illustrates that at such a close distance, it is not the only interaction playing a role. On the sides, molecules belonging to the first shell but further than 5.2 Å (corresponding to the first neighbor peak) are on average anti-aligned (again as favored by the dipole–dipole interaction), although not enough to compensate for the positive correlation. Finally, side molecules closer than 5.2 Å are positively aligned. This means that there exists other effects (that may be related to constraints on molecule conformation or to the presence of H-bonds) able to compensate for the a priori unfavorable situation of having barycenters of the same sign charges facing each other on average.
 | ||
Fig. 3 Relative orientation and distance dependence of the static dipole cross-correlation functions at T = 273 K. (a) Contribution c per unit distance and solid angle to the cross-correlation (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1) of all the molecules situated at r and at angle θ. Red zones are positively correlated while blue zones are anti-correlated as illustrated by the grey dipole drawings. (b) Same plot than a. for = 1) of all the molecules situated at r and at angle θ. Red zones are positively correlated while blue zones are anti-correlated as illustrated by the grey dipole drawings. (b) Same plot than a. for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2. (c) Same quantity as in Fig. 2a, for = 2. (c) Same quantity as in Fig. 2a, for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 (top) and = 1 (top) and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 (bottom), but with distinguished contribution from the red sector (|cos = 2 (bottom), but with distinguished contribution from the red sector (|cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ| > 0.62, see grey lines on a,b) and from the complement blue sector. Drawings close to the vertical axes illustrate the physical meaning of the correlation sign for θ| > 0.62, see grey lines on a,b) and from the complement blue sector. Drawings close to the vertical axes illustrate the physical meaning of the correlation sign for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 (right) and = 1 (right) and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 (left). = 2 (left). | ||
For ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 also, a complex spatial dependence of the cross-correlation is visible in Fig. 3b. As this quantity is not sensitive to the correlation sign, it shows a very different behavior than
= 2 also, a complex spatial dependence of the cross-correlation is visible in Fig. 3b. As this quantity is not sensitive to the correlation sign, it shows a very different behavior than ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1. Some oscillations, that correlate well with the density inhomogeneity, are visible. Those also appear for
= 1. Some oscillations, that correlate well with the density inhomogeneity, are visible. Those also appear for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 but dominate here. After the first layer of neighbours, the contribution from the two angular sectors are in anti-phase and cancel each other on average. Similarly to the
= 1 but dominate here. After the first layer of neighbours, the contribution from the two angular sectors are in anti-phase and cancel each other on average. Similarly to the ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 case, the net contribution comes from the first neighbour shell but it is interesting to observe, that its different sensitivity to orientational correlations makes this quantity significantly less sensitive to cross-correlations in the case of glycerol.
= 1 case, the net contribution comes from the first neighbour shell but it is interesting to observe, that its different sensitivity to orientational correlations makes this quantity significantly less sensitive to cross-correlations in the case of glycerol.
3.3 Global dipole dynamics
For the reason mentioned above and related to the effect of PBCs, the cross-correlation function Ccross![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (t) is computed in the following from eqn (6) by considering only the molecules located within a sphere of radius rlim rather than in all the simulation box. The resulting normalized cross-correlation function is shown in green in Fig. 4a (
(t) is computed in the following from eqn (6) by considering only the molecules located within a sphere of radius rlim rather than in all the simulation box. The resulting normalized cross-correlation function is shown in green in Fig. 4a (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1) and Fig. 4b (
= 1) and Fig. 4b (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2) at T = 273 K. The self part is shown in blue and the total correlation function Ctot
= 2) at T = 273 K. The self part is shown in blue and the total correlation function Ctot![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (t) = Cself
(t) = Cself![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (t) + Ccross
(t) + Ccross![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (t) is shown in red. The cross part does not display a short time decorrelation but for
(t) is shown in red. The cross part does not display a short time decorrelation but for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, a small amplitude peak is visible at short time (t < 1 ps) (see inset of Fig. 4a). The mean cross τcross
= 1, a small amplitude peak is visible at short time (t < 1 ps) (see inset of Fig. 4a). The mean cross τcross![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and total τtot
and total τtot![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) relaxation time, computed by integrating the corresponding normalized correlation functions, are shown for all temperatures in green and red in Fig. 6a. They follow τself
relaxation time, computed by integrating the corresponding normalized correlation functions, are shown for all temperatures in green and red in Fig. 6a. They follow τself![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) < τtot
< τtot![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) < τcross
< τcross![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) but with only a 15% increase on average between the self and total mean relaxation times for
but with only a 15% increase on average between the self and total mean relaxation times for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 and a 25% increase for
= 1 and a 25% increase for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2. This means that the Kivelson and Madden relationship54 (τtot = gKτself) does not seem to be verified in glycerol contrary to other systems such as water.55
= 2. This means that the Kivelson and Madden relationship54 (τtot = gKτself) does not seem to be verified in glycerol contrary to other systems such as water.55
In the same way as for the self part, a loss function χ′′(f) can be computed from the cross part and for the total correlation. The results are plotted for 273 K in Fig. 4c (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1) and d (
= 1) and d (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2). It is well visible that the amplitude of the cross-correlation is of the same order as the self part for
= 2). It is well visible that the amplitude of the cross-correlation is of the same order as the self part for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 while it is much smaller for
= 1 while it is much smaller for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2. On each spectrum, the high frequency flank of the α peak has a power law slope −β such that βself
= 2. On each spectrum, the high frequency flank of the α peak has a power law slope −β such that βself![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) < βcross
< βcross![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) < 1. The slope of the total loss function βtot
< 1. The slope of the total loss function βtot![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) results from both previous slopes as well as the strength of the cross-correlation and takes an intermediate value. The total spectra for all temperatures are shown in Fig. 5a and the values of the slopes β are shown in Fig. 6b as a function of T: β1tot is increasing with T while βtot2 appears constant close to 0.3. This is already visible on the spectra of Fig. 5a but it is even clearer in Fig. 5b where the spectra are shown as a function of a dimensionless frequency ωτself1. The collapse of the high-frequency side is much better for the total spectra with
results from both previous slopes as well as the strength of the cross-correlation and takes an intermediate value. The total spectra for all temperatures are shown in Fig. 5a and the values of the slopes β are shown in Fig. 6b as a function of T: β1tot is increasing with T while βtot2 appears constant close to 0.3. This is already visible on the spectra of Fig. 5a but it is even clearer in Fig. 5b where the spectra are shown as a function of a dimensionless frequency ωτself1. The collapse of the high-frequency side is much better for the total spectra with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 (although the α peak slightly broadens upon cooling) than for
= 2 (although the α peak slightly broadens upon cooling) than for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 (self or total).
= 1 (self or total).
 | ||
Fig. 5 Orientational loss function for all temperatures (same color scale than in Fig. 1) studied as a function of f (a) and ωτself1 (b). The total loss function is shown for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 (top, left scale in a) and = 1 (top, left scale in a) and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 (bottom, right scale in b). The self part for = 2 (bottom, right scale in b). The self part for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 is shown in (a) only for the extreme temperatures and for all temperatures in (b) (middle). (c) For several temperatures, = 1 is shown in (a) only for the extreme temperatures and for all temperatures in (b) (middle). (c) For several temperatures, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 total spectra (orange) plotted with a scale factor (chosen to correspond to the one determined experimentally by Gabriel et al.36) alongside with the = 2 total spectra (orange) plotted with a scale factor (chosen to correspond to the one determined experimentally by Gabriel et al.36) alongside with the ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 self (blue) and total (red) spectra. The vertical dashed lines shows where the crossing between DS and DDLS data occurs on experimental data. = 1 self (blue) and total (red) spectra. The vertical dashed lines shows where the crossing between DS and DDLS data occurs on experimental data. | ||
 | ||
Fig. 6 (a) Mean relaxation time obtained by integrating the self (blue squares), cross (green triangles) and total (red circles) dipole correlation function for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 (solid markers) and = 1 (solid markers) and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 (empty markers). Markers are linked to improve readability. Relaxation time measured experimentally by DDLS (empty circles) from ref. 35 and 36 and DS (solids circles) from ref. 2, 31 and 36 are shown in grey. (b) and (d) Power law exponent β of the high-frequency wing of the loss function for = 2 (empty markers). Markers are linked to improve readability. Relaxation time measured experimentally by DDLS (empty circles) from ref. 35 and 36 and DS (solids circles) from ref. 2, 31 and 36 are shown in grey. (b) and (d) Power law exponent β of the high-frequency wing of the loss function for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 (b) and = 1 (b) and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 (d). The color code is the same as for (a). (c) Temperature dependence of the ratio of self mean relaxation time for = 2 (d). The color code is the same as for (a). (c) Temperature dependence of the ratio of self mean relaxation time for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 and = 1 and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2. In b. and d. experimental data, from ref. 31 and 36 for DS and ref. 35 and 36 for DDLS are shown in grey. = 2. In b. and d. experimental data, from ref. 31 and 36 for DS and ref. 35 and 36 for DDLS are shown in grey. | ||
3.4 Comparison with DS and DDLS experiments
The spectra of Fig. 5a can be compared to experimental glycerol dielectric spectra. The general allure corresponds well to the measurements of Lunkenheimer & Loidl2 with a clear α peak showing no excess wing in this range of temperature and a small Boson peak around 1012 Hz. The temperature dependence of the α relaxation time is compared in Fig. 6a, with DS data as grey solid circles and corresponding MD data τtot1 in red. They show the same trend and could be fitted with a WFL law with close parameters (up to a vertical prefactor). However, the MD α relaxation time is systematically shorter than its experimental DS counterpart by a factor 2 to 3. It is important to note the absolute value of the relaxation time is affected in the simulation by the choice of μ which was optimized by Blieck et al.39 on neutron scattering data for temperatures larger than 333 K (it was already visible that at the smallest temperature simulated by the authors, 313 K, the relaxation time was underestimated). It seems that this is also the case for other studies using the same parameters.44 The temperature evolution of the slope βtot1 is also comparable in MD and in experiments (for which it comes from a Cole-Davidson fit to the spectra), as shown by grey solid circles in Fig. 6b but the slopes are systematically underestimated by the simulation.
of Fig. 5a can be compared to experimental glycerol dielectric spectra. The general allure corresponds well to the measurements of Lunkenheimer & Loidl2 with a clear α peak showing no excess wing in this range of temperature and a small Boson peak around 1012 Hz. The temperature dependence of the α relaxation time is compared in Fig. 6a, with DS data as grey solid circles and corresponding MD data τtot1 in red. They show the same trend and could be fitted with a WFL law with close parameters (up to a vertical prefactor). However, the MD α relaxation time is systematically shorter than its experimental DS counterpart by a factor 2 to 3. It is important to note the absolute value of the relaxation time is affected in the simulation by the choice of μ which was optimized by Blieck et al.39 on neutron scattering data for temperatures larger than 333 K (it was already visible that at the smallest temperature simulated by the authors, 313 K, the relaxation time was underestimated). It seems that this is also the case for other studies using the same parameters.44 The temperature evolution of the slope βtot1 is also comparable in MD and in experiments (for which it comes from a Cole-Davidson fit to the spectra), as shown by grey solid circles in Fig. 6b but the slopes are systematically underestimated by the simulation.
Contrary to DS, which probes the reorientational dynamics of the molecules by following the permanent dipolar moment, DDLS does it by following the anisotropy of the polarisability tensor. Glycerol molecules are believed to rotate as a rigid entity44 and we can reasonably assume that both techniques probe the same dynamics (although giving access to different ranks ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ). It is also worth noting that results from DDLS experiments can also be affected by a scattering mechanism called dipole-induced-dipole related to the fluctuation of the internal field. Cummins et al.56 have argued that this effect may be neglected in the experimental spectra of supercooled liquids. Here we follow these authors. The spectra
). It is also worth noting that results from DDLS experiments can also be affected by a scattering mechanism called dipole-induced-dipole related to the fluctuation of the internal field. Cummins et al.56 have argued that this effect may be neglected in the experimental spectra of supercooled liquids. Here we follow these authors. The spectra  , from the simulation, should therefore be comparable with the Fourier transform of the DDLS correlation function reported by Gabriel et al.36 The authors concentrated mainly on frequencies under a few MHz and thus on temperatures smaller than 260 K (although they also performed a measurement at 323 K). Here also, the MD spectra show a good qualitative agreement with experiments. The DDLS mean relaxation time is shorter than in DS by an amount that appears similar in the experiments and in MD. The inequality βtot2 < βtot1 is also verified for both. In the DDLS experiments (see grey empty circles in Fig. 6d), given the uncertainty, the slope βtot2 does not appear to depend much on the temperature and it is also the case in the simulation (empty red circles). However, here again, the slopes are underestimated in the simulation.
, from the simulation, should therefore be comparable with the Fourier transform of the DDLS correlation function reported by Gabriel et al.36 The authors concentrated mainly on frequencies under a few MHz and thus on temperatures smaller than 260 K (although they also performed a measurement at 323 K). Here also, the MD spectra show a good qualitative agreement with experiments. The DDLS mean relaxation time is shorter than in DS by an amount that appears similar in the experiments and in MD. The inequality βtot2 < βtot1 is also verified for both. In the DDLS experiments (see grey empty circles in Fig. 6d), given the uncertainty, the slope βtot2 does not appear to depend much on the temperature and it is also the case in the simulation (empty red circles). However, here again, the slopes are underestimated in the simulation.
The differences between the simulation and the real system must be weighed against the relative simplicity of the modeling. Indeed, force field parameters, that control intra and inter-molecular interactions were not adjusted specifically on glycerol but were designed to be applicable to the widest range possible of organic compounds. The only parameter that was adjusted specifically to glycerol was μ. Moreover, the partial charges in the molecule are considered as fixed point charges at the center of each atom, the electronic polarizability is not taken into account and H-bonds are mimicked only by electrostatic interactions of these fixed charges which can limit their strength.57 Nonetheless, it is already impressive that a classical model can reproduce well some aspects of the real system. With these limitations in mind, MD simulations can be used, as demonstrated recently by Becher et al.,44 to obtain information on microscopic observables or on the relative effect of external parameters such as the temperature.
For ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2, and in contrast to the
= 2, and in contrast to the ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 case, the effect of cross-correlation is very weak and the total loss function can reasonably be assimilated to the self loss function alone (see Fig. 4d). This is in complete agreement with the observations of Gabriel et al.36 and previous work by the same team19,20 on the ability for DDLS to give access to the self orientational dynamics. This is also in agreement with the recent MD observations on a model system of Koperwas et al.29 who compared the self and total correlation functions for
= 1 case, the effect of cross-correlation is very weak and the total loss function can reasonably be assimilated to the self loss function alone (see Fig. 4d). This is in complete agreement with the observations of Gabriel et al.36 and previous work by the same team19,20 on the ability for DDLS to give access to the self orientational dynamics. This is also in agreement with the recent MD observations on a model system of Koperwas et al.29 who compared the self and total correlation functions for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 at long times (t ≥ τα).
= 2 at long times (t ≥ τα).
The ratio of the self relaxation times τself1/τself2, shown in Fig. 6c, ranges from 1.4 to 2.0 and is increasing with temperature. This quantity is affected by the details of the molecular relaxation mechanism with two limiting cases leading to values of 3 for isotropic rotational diffusion and 1 for discrete jumps of random amplitude.5 However, a given value of this ratio cannot be associated with a typical orientational jump amplitude. For example, in a mean field model, tuning the interaction parameter allows to change continuously this ratio.58 In the present case, it is more likely that its value reflects a dynamics governed by rare relaxation events, that are less averaged for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 than for
= 2 than for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1.59 In this case, its decrease upon cooling could be associated with rarer and rarer events. The slope β < 1 can also be linked with a dynamic governed by relatively rare events, spread on long time scales, that does not average enough to produce an exponential relaxation (β = 1).59 In this context, as C2 cancels out for smaller angles than C1, it is less averaged over relaxation events leading to β2 < β1, consistently with our observations.
= 1.59 In this case, its decrease upon cooling could be associated with rarer and rarer events. The slope β < 1 can also be linked with a dynamic governed by relatively rare events, spread on long time scales, that does not average enough to produce an exponential relaxation (β = 1).59 In this context, as C2 cancels out for smaller angles than C1, it is less averaged over relaxation events leading to β2 < β1, consistently with our observations.
In the DDLS works mentioned above,19,20,36 the authors suggested to use these measurements as a proxy to approach the DS self response, which is not accessible experimentally. This means admitting that the response is reasonably independent of the rank ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) but this also requires a way to normalize the DDLS data so that they can be quantitatively compared to DS spectra. With a well-chosen, temperature independent, scaling factor, it is possible a get a perfect overlap of the DS and DDLS spectra on the excess wing flank at low temperature (T < 200 K). From this, it was shown that the DS signal could be well fitted by the sum of the DDLS signal and a cross-correlation term (described by a stretched exponential of fixed stretching parameter), with the relative weight of these two terms perfectly matching the Kirkwood correlation factor at all temperatures.36 This demonstrates the usefulness and relevance of the direct comparison between DDLS and DS spectra.
but this also requires a way to normalize the DDLS data so that they can be quantitatively compared to DS spectra. With a well-chosen, temperature independent, scaling factor, it is possible a get a perfect overlap of the DS and DDLS spectra on the excess wing flank at low temperature (T < 200 K). From this, it was shown that the DS signal could be well fitted by the sum of the DDLS signal and a cross-correlation term (described by a stretched exponential of fixed stretching parameter), with the relative weight of these two terms perfectly matching the Kirkwood correlation factor at all temperatures.36 This demonstrates the usefulness and relevance of the direct comparison between DDLS and DS spectra.
In our numerical work, we were not able to reach the range of low temperatures in which the excess wing appears. This prevented us from using the method described above to determine from scratch a scaling factor between the ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 and
= 1 and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 spectra. We instead had to rely on the experimental determination by Gabriel et al.36 Indeed, while the DS and DDLS spectra collapse on the excess wing for T < 200 K, they cross at a finite frequency fcross for higher temperatures. We determined a (T independent) scaling factor by making sure that the
= 2 spectra. We instead had to rely on the experimental determination by Gabriel et al.36 Indeed, while the DS and DDLS spectra collapse on the excess wing for T < 200 K, they cross at a finite frequency fcross for higher temperatures. We determined a (T independent) scaling factor by making sure that the ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 and
= 1 and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 total spectra cross at the same fcross/fα than the experiments for T = 323 K and T = 263 K (see vertical dashed lines in Fig. 5c). The result is shown in Fig. 5c and it appears that, for all temperatures, the α peak of the total
= 2 total spectra cross at the same fcross/fα than the experiments for T = 323 K and T = 263 K (see vertical dashed lines in Fig. 5c). The result is shown in Fig. 5c and it appears that, for all temperatures, the α peak of the total ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 and the self
= 2 and the self ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 spectra match fairly well. The difference of slopes β is small enough so that the discrepancy remains low (<30%) under the frequency at which the fast process starts to be perceptible. This allows us to understand the success of the experimental approach consisting of a direct comparison between DS and DDLS data.19,20,36
= 1 spectra match fairly well. The difference of slopes β is small enough so that the discrepancy remains low (<30%) under the frequency at which the fast process starts to be perceptible. This allows us to understand the success of the experimental approach consisting of a direct comparison between DS and DDLS data.19,20,36
4 Conclusion and perspectives
In this work, we studied using MD simulations, the orientational dynamics of glycerol from which we extracted the self correlation function and the associated loss function for different ranks![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) of the Legendre polynomial. For
of the Legendre polynomial. For ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 and 2, we studied the spatial dependence of the cross-correlation and showed that they play a significant role in the
= 1 and 2, we studied the spatial dependence of the cross-correlation and showed that they play a significant role in the ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 response while being almost negligible for
= 1 response while being almost negligible for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2. In accordance with recent experimental observations based on a comparison between DDLS and DS spectra, we showed that, although these techniques give access to different ranks
= 2. In accordance with recent experimental observations based on a comparison between DDLS and DS spectra, we showed that, although these techniques give access to different ranks ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) of the correlation function (and consequently do not lead to the exact same spectra, in particular regarding the slope β), the scaling factor that corresponds to a merging of the excess wing of DS and DDLS spectra at low temperatures leads to a fairly good merging of the self part of the
of the correlation function (and consequently do not lead to the exact same spectra, in particular regarding the slope β), the scaling factor that corresponds to a merging of the excess wing of DS and DDLS spectra at low temperatures leads to a fairly good merging of the self part of the ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 and the total
= 1 and the total ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 spectra. This strengthens the idea that useful information can arise from a direct comparison between DDLS and DS measurements.
= 2 spectra. This strengthens the idea that useful information can arise from a direct comparison between DDLS and DS measurements.
Moreover, we took advantage of the possibility given by MD simulations to access molecular observables to discuss the microscopic origin of the cross-correlation observed in DS. We found out that the net cross-correlation originates from the first shell of neighbouring molecules that tend to positively align independently of their orientation. Investigating in more detail the molecular origin of the cross-correlations, and their link with molecular conformation and H-bonds will be the subject of future work.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank J. P. Gabriel for sharing the data published in ref. 36 and C. Alba-Simionesco for discussions. M.H is grateful to LABEX PALM, IRAMIS Institute and Paris-Saclay University for financial support. This work was supported by ANR PIA funding: ANR-20-IDEES-0002.Notes and references
- F. Kremer and A. Schönhals, Broadband dielectric spectroscopy, Springer Science & Business Media, 2002 Search PubMed.
- P. Lunkenheimer and A. Loidl, Chem. Phys., 2002, 15, 205–219 CrossRef.
- P. Lunkenheimer and A. Loidl, Glassy dynamics: From millihertz to terahertz, in The Scaling of Relaxation Processes, ed. F. Kremer and A. Loidl, Springer International Publishing, Cham, 2018, pp. 23–59 Search PubMed.
- C. Böttcher, Theory of electric polarization: Dielectrics in static fields, Elsevier, 1973, vol. 1 Search PubMed.
- C. Böttcher and P. Bordewijk, Dielectrics in time-dependent fields. theory of electric polarization, 2nd edn, 1978, vol. 2 Search PubMed.
- K. Ngai and M. Paluch, J. Chem. Phys., 2004, 120, 857 CrossRef CAS PubMed.
- B. Guiselin, C. Scalliet and L. Berthier, Nat. Phys., 2022, 18, 468 Search PubMed.
- L. Berthier, G. Biroli, J.-P. Bouchaud, L. Cipelletti, D. E. Masri, D. L’Hôte, F. Ladieu and M. Pierno, Science, 2005, 310, 1797 CrossRef CAS PubMed.
- C. Alba-Simionesco, D. Kivelson and G. Tarjus, J. Chem. Phys., 2002, 116, 5033 CrossRef CAS.
- C. Roland, S. Hensel-Bielowka, M. Paluch and R. Casalini, Rep. Prog. Phys., 2005, 68, 1405 CrossRef CAS.
- R. L. Leheny and S. R. Nagel, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57(9), 5154 CrossRef CAS.
- T. Hecksher, N. B. Olsen, K. Niss and J. C. Dyre, J. Chem. Phys., 2010, 133, 174514 CrossRef PubMed.
- D. D. Klug, D. E. Kranbuehl and W. E. Vaughan, J. Chem. Phys., 1969, 50, 3904 CrossRef CAS.
- J.-L. Rivail, J. Chem. Phys., 1969, 66, 981 Search PubMed.
- B. K. P. Scaife, Principles of Dielectrics, Clarenton Press, Oxford, 1998 Search PubMed.
- R. Böhmer, C. Gainaru and R. Richert, Phys. Rep., 2014, 545, 125 CrossRef.
- P.-M. Déjardin, S. V. Titov and Y. Cornaton, Phys. Rev. B, 2019, 99, 024304 CrossRef.
- P. Weigl, D. Koestel, F. Pabst, J. P. Gabriel, T. Walther and T. Blochowicz, Phys. Chem. Chem. Phys., 2019, 21, 24778 RSC.
- J. Gabriel, F. Pabst and T. Blochowicz, J. Phys. Chem. B, 2017, 121, 8847 CrossRef CAS PubMed.
- F. Pabst, A. Helbling, J. Gabriel, P. Weigl and T. Blochowicz, Phys. Rev. E, 2020, 102, 010606 CrossRef CAS PubMed.
- F. Pabst, J. P. Gabriel, T. Böhmer, P. Weigl, A. Helbling, T. Richter, P. Zourchang, T. Walther and T. Blochowicz, J. Phys. Chem. Lett., 2021, 12, 3685 CrossRef CAS PubMed.
- K. Moch, P. Münzner, R. Böhmer and C. Gainaru, Phys. Rev. Lett., 2022, 128, 228001 CrossRef CAS PubMed.
- R. S. L. Stein and H. C. Andersen, Phys. Rev. Lett., 2008, 101, 267802 CrossRef PubMed.
- D. M. Edwards, P. A. Madden and I. R. McDonald, Mol. Phys., 1984, 51, 1141 CrossRef CAS.
- L. Saiz, E. Guàrdia and J.-A. Padró, J. Chem. Phys., 2000, 113, 2814 CrossRef CAS.
- C. Zhang and M. Sprik, Phys. Rev. B, 2016, 93, 144201 CrossRef.
- B. Atawa, N. T. Correia, N. Couvrat, F. Affouard, G. Coquerel, E. Dargent and A. Saiter, Phys. Chem. Chem. Phys., 2019, 21, 702 RSC.
- J.-F. Olivieri, J. T. Hynes and D. Laage, J. Phys. Chem. Lett., 2021, 12, 4319 CrossRef CAS PubMed.
- K. Koperwas and M. Paluch, Phys. Rev. Lett., 2022, 129, 025501 CrossRef CAS PubMed.
- D. W. Davidson and R. H. Cole, J. Chem. Phys., 1951, 19, 1484 CrossRef CAS.
- U. Schneider, P. Lunkenheimer, R. Brand and A. Loidl, J. Non-Cryst. Solids, 1998, 235, 173 CrossRef.
- A. Kudlik, S. Benkhof, T. Blochowicz, C. Tschirwitz and E. Rössler, J. Mol. Struct., 1999, 479, 201 CrossRef CAS.
- J. Wuttke, W. Petry and S. Pouget, J. Chem. Phys., 1996, 105, 5177 CrossRef CAS.
- R. Meier, D. Kruk, J. Gmeiner and E. Rössler, J. Chem. Phys., 2012, 136, 034508 CrossRef CAS PubMed.
- A. Brodin and E. A. Rössler, Eur. Phys. J. B, 2005, 44, 3 CrossRef CAS.
- J. P. Gabriel, P. Zourchang, F. Pabst, A. Helbling, P. Weigl, T. Böhmer and T. Blochowicz, Phys. Chem. Chem. Phys., 2020, 22, 11644 RSC.
- R. Chelli, P. Procacci, G. Cardini, R. G. Della Valle and S. Califano, Phys. Chem. Chem. Phys., 1999, 1, 871 RSC.
- R. Chelli, Phys. Chem. Chem. Phys., 1999, 1, 879 RSC.
- J. Blieck, F. Affouard, P. Bordat, A. Lerbret and M. Descamps, Chem. Phys., 2005, 5, 253 CrossRef.
- A. V. Egorov, A. P. Lyubartsev and A. Laaksonen, J. Phys. Chem. B, 2011, 115, 14572 CrossRef CAS PubMed.
- R. Busselez, R. Lefort, A. Ghoufi, B. Beuneu, B. Frick, F. Affouard and D. Morineau, J. Phys.: Condens. Matter, 2011, 23, 505102 CrossRef CAS PubMed.
- R. Busselez, T. Pezeril and V. E. Gusev, J. Chem. Phys., 2014, 140, 234505 CrossRef PubMed.
- S. Seyedi, D. R. Martin and D. V. Matyushov, Phys. Rev. E, 2016, 94, 012616 CrossRef PubMed.
- M. Becher, T. Wohlfromm, E. Rössler and M. Vogel, J. Chem. Phys., 2021, 154, 124503 CrossRef CAS PubMed.
- M. H. Jensen, C. Gainaru, C. Alba-Simionesco, T. Hecksher and K. Niss, Phys. Chem. Chem. Phys., 2018, 20, 1716 RSC.
- P. Eastman, J. Swails, J. D. Chodera, R. T. McGibbon, Y. Zhao, K. A. Beauchamp, L.-P. Wang, A. C. Simmonett, M. P. Harrigan, C. D. Stern, R. P. Wiewiora, B. R. Brooks and V. S. Pande, PLoS Comput. Biol., 2017, 13, 1 CrossRef PubMed.
- D. Champeney, R. Joarder and J. Dore, Mol. Phys., 1986, 58, 337 CrossRef CAS.
- H. Rizk and I. Elanwar, Can. J. Chem., 1968, 46, 507 CrossRef CAS.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157 CrossRef PubMed.
- R. Livi and P. Politi, Nonequilibrium Statistical Physics: A Modern Perspective, Cambridge University Press, 2017 Search PubMed.
- A. J. S. Hamilton, Mon. Not. R. Astron. Soc., 2000, 312, 257 CrossRef.
- J. Caillol, J. Chem. Phys., 1992, 96, 7039 CrossRef CAS.
- G. C. Maitland, M. Rigby, E. B. Smith, W. A. Wakeham, Intermolecular Forces: Their Origin and Determination, International series of monographs on chemistry, Clarendon Press, 1981 Search PubMed.
- D. Kivelson and P. Madden, Mol. Phys., 1975, 30, 1749 CrossRef CAS.
- T. Samanta and D. V. Matyushov, J. Mol. Liq., 2022, 364, 119935 CrossRef CAS.
- H. Cummins, G. Li, W. Du, R. M. Pick and C. Dreyfus, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 896 CrossRef CAS PubMed.
- H. Xu, H. A. Stern and B. Berne, J. Phys. Chem. B, 2002, 106, 2054 CrossRef CAS.
- W. Coffey, D. Crothers, Y. P. Kalmykov and P.-M. Déjardin, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2005, 71, 062102 CrossRef CAS PubMed.
- G. Diezemann, H. Sillescu, G. Hinze and R. Böhmer, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 4398 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04578a |
| This journal is © the Owner Societies 2023 |



