Dynamics of organophosphate guest encapsulation in heteroleptic coordination cages

Abstract

Heteroleptic coordination cages allow the design of different host structures that can bind guest molecules within their cavities. In a previous work, the energetics of organophosphate encapsulation in palladium(II)-based heteroleptic coordination cages that differ in terms of their ability to form hydrogen bonds have been investigated [Platzek et al., Endohedrally Functionalized Heteroleptic Coordination Cages for Phosphate Ester Binding, Angew. Chem., Int. Ed. 2022, 61, e2022093]. The present work focuses on the dynamics of this system. Dynamic information is obtained through the application of a Markov state model (MSM) to unbiased multi-microsecond atomistic molecular dynamics simulations of guest binding and release. The MSM reveals that both the bound state and the binding/unbinding pathways are highly dynamic, with different types of interactions mediating the binding of the diphenylphosphate guest. Thus, the simulations highlight the dynamic nature of the nanoconfinement in the host–guest systems, with possible implications for the use of such coordination cages as catalysts.

---

1. Introduction

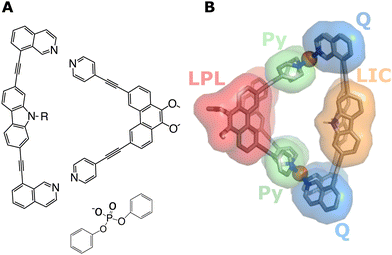
In supramolecular chemistry, advances of both experimental and computational approaches extend the possibilities to design specific hosts with a variety of structural features to target the encapsulation of guest molecules.^1–7 Commonly, the host molecules consist of one type of ligand, which form supramolecular complexes with predetermined structures (so-called homoleptic cages). This concept can be extended by using several different ligand species that stoichiometrically self-assemble into specific coordination cages (so-called heteroleptic systems), hence allowing for a larger degree of flexibility in cavity design. Despite these advances, not much is known so far about the molecular-level effects that the different cage-forming ligands and their functional groups have on the strength and specificity of the interactions with guest molecules that are encapsulated inside the cavity of such heteroleptic cages.

In a recent combined experimental/theoretical study,⁸ we investigated a palladium(II)-based heteroleptic coordination cage of the type [Pd₂L₂L₂′]⁴⁺, which binds to different organophosphate guests. Fig. 1 shows the Lewis structures of the two different cage-forming ligands and a structural model of the cage. Our previous work focused on the chemical synthesis and on the binding thermodynamics of the guests.⁸ The effect of different functional groups of the ligands on the binding of the guests was investigated through targeted chemical modifications, and binding energetics were characterised with NMR as well as with molecular dynamics (MD) simulations. The two amino groups of the cage were either secondary amines (that is, R = H in Fig. 1, referred to in the following as NH-cage) or tertiary amines in which the ability of the ligands to form hydrogen bonds (H-bonds) with the encapsulated guest was abolished by introducing methyl groups (R = CH₃, referred to in the following as Me-cage).

Fig. 1 Panel (A) shows the Lewis structures of the two ligands, L′ and L, forming the [Pd₂L₂L′₂]⁴⁺ cage and of the diphenylphosphate (DPP) guest. Panel (B) shows a 3D structural model of the cage. The coloured transparent surfaces indicate different structural components.

In the methylated Me-cage, guest binding was still observed, but binding was significantly weaker (association constant K_a = 2062 M⁻¹ for the NH-cage vs. 77 M⁻¹ for the Me-cage). This observation revealed that the organophosphate does not exclusively bind only due to the interaction with the H-bond donating NH groups at the centre of the cavity, but other parts of the heteroleptic cage also play a role, supporting the flexible design idea (see above). All-atom MD simulations could not only support the experimentally observed difference of the binding free energies between the NH-cage and the Me-cage, but they also revealed the individual contributions of the different parts of the ligands (coloured surfaces in Fig. 1b) that govern the encapsulation of the guest.⁸

The work of Platzek and coworkers⁸ provided valuable insights into the thermodynamics of guest binding to the heteroleptic cages and into the specific roles of the individual cage ligands, but the dynamics of the process remain unexplored at the molecular level. The present work aims at closing this gap. Specifically, we address the following questions. First, which pathways are followed by the organophosphate guest molecule to enter into and exit from the cage cavity? Second, is the bound state, in which the guest is confined inside the cage, static or dynamic? And third, how are these dynamic aspects modulated by the nature of the cage-forming ligands, that is, by the functional groups with or without an H-bonding capability at the cage centre.

In principle, in the cavity of the NH-cage two H-bonds can be formed between host and organophosphate guest (each of the two NH-containing “LIC” ligands (Fig. 1b) can form one H-bond). The simultaneous formation of the two H-bonds would imply a static, constrained guest binding mode, at least if the lifetime of the H-bonds is long. Conversely, if the lifetime is short and/or not both H-bonds are present at the same time (but continuously forming and breaking), guest binding would be more dynamic. These considerations do not only apply to the H-bonds, but also to the nonpolar contacts that the guest can form with the other chemical moieties of the ligands (which, for the Me-cage, are the only possible interactions).

Here, extended multi-microsecond all-atom MD simulations of different DPP-binding heteroleptic cages in explicit DMSO solvent were carried out (see Methods). In addition to the two previously synthesised cages, the NH-cage and the Me-cage (see above), we generated a computational model of a mixed cage with one NH-containing ligand and one N-CH₃ containing ligand, that is, a cage of the type [Pd₂L₂L′L′′]⁴⁺, where L′ and L′′ denote the two LIC ligands with different amino groups (referred to in the following as hybrid or H-cage).

The information about the molecular dynamics of the cage–guest interaction is contained in unbiased MD simulations, that is, simulations without artificial bias forces that would enforce the binding/unbinding process along certain predefined pathways. A key precondition for the validity of such an unbiased MD approach is that the time scale of the simulations is sufficiently long to observe a statistically meaningful number of spontaneous binding and unbinding events, which in the current case required an aggregated simulation time of 50 μs for each of the three cages. To extract the desired information about the different relevant states and the dynamic transitions between them, a Markov state model (MSM) is applied. A Markov state model is a master equation framework in which the entire dynamics of the system are included,^9,10 hence providing a full dynamic picture of the host–guest system (in terms of a given set of states). MSMs have been widely applied to proteins,^11–14 but much less to cage–guest systems. Ge and Voelz applied MSMs to a toy system comprised of a model guest, represented by a single Lennard-Jones particle, which binds to an idealised icosahedral host consisting of 11 Lennard-Jones particles.¹⁵ However, to our knowledge, MSMs have not yet been applied to real chemical cage–guest systems.

The rest of the manuscript is organised as follows. In the Methods section, after describing the details of the MD simulations, we explain how the MSM was constructed and applied, and provide the details of the quantum chemical calculations that were carried out to further characterise the cage–guest complexes. In the Results section, we start by discussing the free energies of binding of the DPP guest to the three different heteroleptic cages. The main part is then devoted to the dynamics of binding, as revealed by the MSM. After describing each of the three systems individually, they are compared and discussed in terms of similarities and differences. The manuscript closes with a summary of the main findings and a brief discussion of possible implications of the present work for the use of the heteroleptic coordination cages as catalysts.

2. Methods

2.1 MD simulations

Initial parameter files for the general AMBER force field (GAFF)¹⁶ and topology files for the cages as well as for the diphenylphosphate (DPP) were generated with the CHIMERA software.¹⁷ Parameters for the bonds and angles involving Pd atoms were taken from our previous work,¹⁸ and Lennard-Jones (6,12) parameters for the palladium were taken from Yoneya et al.¹⁹ Atomic partial charges for host and guest were calculated with the electrostatic potential (ESP) fitting method using the DFT functional B3LYP with the 6-31G* all-electron basis set for all atoms except Pd, for which the Stuttgart–Dresden (SDD) pseudopotentials²⁰ were used. For the H-cage, the force field topologies and atomic partial charges of the Me-cage and the NH-cage were used for the two different LIC ligands (the remaining parts of the cages are identical in all systems). All force field topology files are provided in ESI.†

After force field parametrisation, the cage and one unbound DPP molecule were placed in a periodic simulation box with a volume of ca. 67 nm³ and solvated in DMSO, for which parameters were taken from the work of Caleman and coworkers.²¹ Three tetrafluoroborate anions were added in the solvent to keep the overall charge of the simulation box zero (DPP has −1 charge). All simulations were carried out with the MD engine GROMACS.²² The systems were energy minimized using steepest descent and then equilibrated at 298 K in a 500 ps NVT simulation, followed by 500 ps NpT simulation. The LINCS algorithm²³ was used to constrain bond lengths involving H-atoms, allowing to integrate the equations of motion with 2 fs time steps using the leapfrog integrator. Temperature was kept constant at 298 K with the velocity-rescaling thermostat of Bussi and coworkers²⁴ with a coupling time constant of 0.1 ps. To maintain constant 1 bar pressure, an isotropic Berendsen barostat was used with a coupling time constant of 2 ps. Short-range Lennard-Jones (6,12) and Coulomb interactions were treated with a buffered Verlet neighbor list²⁵ with a cut-off of 1.0 nm. Long-range Coulomb interactions were treated with the particle mesh Ewald algorithm^26,27 with 0.12 nm grid spacing. Analytical corrections to energy and pressure were applied to compensate for the truncation of the Lennard-Jones interactions. An MD-parameter file is provided in ESI.†

Finally, for each of the three systems investigated, ten 5 μs simulations were carried out in the NpT ensemble, thus yielding a total simulation time of 150 μs. Coordinates were saved to disk every 20 ps for analysis. For each simulated system, the initial and final coordinate files of one of the ten repeat simulations are provided in ESI.†

2.2 Markov state model (MSM)

MSMs require the simulation data to be discretised such that every snapshot is assigned to a (predefined) state. On the basis of our prior knowledge,⁸ the relevant states that the heteroleptic cage–guest systems visit during the simulation were defined in a way that is suitable to investigate the bound state and the entry/exit pathways of the guest (see below). As a main goal was to further characterize the bound state of the system, it was split into substates that characterise the different binding modes. Altogether, this resulted in the following six different states for the MSM.

For the NH-cage, the first state (termed “H-bond 1”) is characterised by the presence of one H-bond between the DPP guest and one of the two LIC ligands of the cage. The “H-bond 1” state is present if the P-atom of the DPP guest is within <0.5 nm to the N-atom of the amino group of LIC1 and >0.5 nm from the N-atom of the other ligand, LIC2. Deliberately, the P-atom was chosen as a reference for the analysis (instead of the DPP O-atoms, which are the actual H-bond acceptors), because the definition of a contact should not discriminate between the different oxygen atoms of the phosphate group; for similar reasons no angle criterion was used. The second, symmetry-equivalent “H-bond 2” state was defined equivalently for an H-bond between DPP and LIC2. The third H-bonded state contains two cage–guest H-bonds simultaneously. Consistent with the above definition of the first two states, this “H-bonds 1 & 2” state was defined by <0.5 nm distances between the DPP P-atom and the N-atoms of the two LIC ligands for both ligands simultaneously. Fourth, a bound state without any H-bond was defined to be adopted (coined “no H-bond”) if both P–N distances are >0.5 nm and the distance between the P-atom and the centre of the cage cavity, defined as the centre-of-mass of the two Pd-atoms, is <1.0 nm.

In addition to these four bound states, to investigate not only the dynamic nature of the bound state but also the pathways of guest encapsulation, two additional states were defined. One of these additional states was defined such that the distance between the P-atom of DPP to either one of the two Pd atoms was <1.0 nm, while the distance to the other Pd-atom was >1.5 nm. This state, referred to as “Pd-bound” or “on-top” state, corresponds to the guest associating on the outside of the cage close to one of the two Pd atoms (in contrast to the “H-bond 1/2” states, we did not discriminate between the two symmetry-equivalent Pd-bound states). Finally, in the fully “unbound” state, there are no contacts between the host and the guest, that is, none of the above conditions are fulfilled but the distance between the cage centre and the DPP P-atom was >1.0 nm. With these criteria, every simulation frame was assigned to one particular state (no double labelling occurred, no unlabeled snapshots remained).

For the Me-cage, the six states were defined such that they correspond as closely as possible to the ones of the NH-cage described above. Also here, four different bound states were defined. However, hardly any close interactions between the N-CH₃ groups and the O-atoms of the DPP guest were detected during the simulations. Instead, nonpolar contacts between the DPP phenyl rings and the methyl groups of the LIC ligands occured. Therefore, a “methyl contact 1” state was defined in which one of the two base C-atoms of the DPP phenyl rings, that is, the C-atoms that are bonded to the ester oxygens, was within < 0.8 nm of the N-methyl C-atom of LIC1, while the corresponding distance to the LIC2 methyl was >0.8 nm. The symmetry-equivalent “methyl contact 2” state state was defined in the same way for the contact to LIC2. The “methyl contacts 1 & 2” state with two concurrent contacts is present if either one of the two phenyl C-atoms was within <0.8 nm to the methyl group in LIC1, and the other phenyl C-atom within <0.8 nm from the LIC2 methyl. If all phenyl-Cs are further away than 0.8 nm to either one of the two methyl-Cs but the distance of the P atom of the guest and the center-of-mass of the two Pd atoms was smaller than 1.2 nm, the guest was considered to be bound but not in contact with a methyl group. The two unbound states were defined equivalently to the NH-cage (described above).

For the H-cage one bound state was defined in which the guest was H-bonded to the NH-containing ligand (“H-bond”), while the second state was defined as the guest associating through nonpolar contacts with the methyl group of the ligand (“methyl contact”). The same distance criteria for the H-bond and the nonpolar contact to the methyl were used, as described above for the NH- and the Me-cage, respectively. The third bound state, “contacts 1 & 2”, was defined by the guest being H-bonded while also being in contact with the N-methyl group of the other ligand; the remaining states were defined analogous to the NH- and Me-cages.

Discretisation of the trajectory into the states was performed with a python script. For the MSMs, the count matrix, the transition matrix, and the rate matrix were computed with the python library deeptime.²⁸

2.3 DFT calculations

To further investigate the identified states from the structural and energetic perspective, snapshots from the force field MD simulations were subjected to quantum chemical calculations at the density functional theory (DFT) level, which have been performed with Orca (version 5.0.3).²⁹ The dispersion-corrected ωB97X-D3 functional^30,31 was used with the Def2-SVP³² basis set and Def2-ECPs for the Pd atoms.^33,34 All calculations were performed with a polarisable continuum implicit DMSO solvent model.³⁵ Hessian matrices were calculated for optimised geometries to verify that the structures are minima on the potential energy surface.

In addition, a single-point energy was calculated for the structure of the NH-cage optimised in presence of a guest (bound via one or two H-bonds) after removing the guest molecule (and changing the overall charge to +4). By taking the difference between that energy and the energy of the cage optimised without a bound guest, the strain energy that the cage has to invest upon binding the guest was obtained. As starting structures for the geometry optimisations of the empty cage, the single H-bonded guest, and the doubly H-bonded guest, 5, 5, and 8 snapshots were extracted from the MD trajectories, respectively, and the corresponding energies were Boltzmann-averaged.

Another interesting point in the encapsulation of guests inside cages is their potential to enhance chemical reactivity, that is, to act as catalysts.^36,37 In the present case, if the phosphate group of the guest was polarised through interactions with the cage, the guest molecule might be activated for chemical reactions, such as nucleophilic substitutions. To investigate whether the DPP guest is polarised by the NH-cage, Hirshfeld charges³⁸ of unbound DPP in DMSO were compared to DPP bound inside the cage cavity via one H-bond and also via two H-bonds.

3. Results and discussion

3.1 Energetics of guest encapsulation

First, the energetics of guest encapsulation are discussed, before we will address the dynamics of the system in the subsequent sections. The free energies of binding of the DPP guest to the three different heteroleptic cages investigated in this work are summarised in Table 1. As described previously,⁸ these binding free energies were obtained from the MD trajectories by counting the fraction of the total simulation time spent in the bound and unbound states,³⁹ which directly reflect the probabilities of the states and thus the free energy difference between them according towhere R is the gas constant, T is the temperature, V is the volume of the simulation box, and V_ref = 1.66 nm³ is the reference volume that corresponds to a standard-state concentration of 1 mol L⁻¹. The large number of binding/unbinding events during the 50 μs of accumulated simulation time for each cage/guest system allow one to extract binding free energies with reasonable statistical precision (see Table 1).

Table 1 Free energies of DPP binding to the heteroleptic cages from MD simulations. The statistical uncertainties are the standard deviations from the 10 individual MD simulation trajectories, each of which is 5 μs long (see Methods). The binding free energies of DPP to the NH-cage and to the Me-cage were reported previously⁸

	ΔGbind (kJ mol^−1)
NH-cage	−13.3 ± 1.4
Me-cage	−6.6 ± 0.2
H-cage	−9.7 ± 2.5

---

The absolute values of the binding free energies are smaller in the MD simulations than in the experiments, but importantly, the difference in binding free energies between the NH- and Me-cages, ΔΔG_bind, of 6.7 kJ mol⁻¹ agrees well with the experimentally determined ΔΔG_bind of RT ln(2062/77) = 8.2 kJ mol⁻¹. The reduced binding affinity of the Me-cage can be attributed to the lack of an H-bonding donor in the cage-forming ligands. Indeed, an analysis of the contacts between cage and guest (Table 2) shows that, when the guest is bound inside the cage cavity, the NH-group of the cage is in contact with the oxygen atoms of the organophosphate guest for 98% of the time. The N-methyl group of the Me-cage forms less and also energetically weaker contacts,⁸ which are only partially compensated for by an increase of favourable interactions between the guest and the other parts of the Me-cage (Table 2).

Table 2 Cage–guest contacts (given in percent) during MD simulations of the DPP guest bound to the NH-, Me-, and H-cages. The percentages indicate the likelihood that the bound guest forms the respective contacts with the different chemical moieties of the cages, as indicated in Fig. 1. LIC refers to the orange moiety (Fig. 1), with the exclusion of the NH/N-methyl groups that are analysed separately, LPL to the red part, Py to the green part, and Q to the blue part

Moiety	NH-cage	Me-cage	H-cage
NH	98	—	98
N-Methyl	—	63	1
LIC	53	57	46
LPL	70	80	84
Py	58	68	58
Q	11	1	6

---

Interestingly, closer analysis of the H-bonded bound states in the MD simulations revealed that, although the NH-cage can in principle form two H-bonds with organophosphate guests via the two NH-groups (Fig. 2), most of the time only a single H-bond between the cage and the DPP is formed, with frequent dynamical transitions (“switches”) between the two equivalent poses via a doubly H-bonded intermediate (see below). This prompted us to also simulate a hybrid cage (H-cage) in which one LIC ligand has an NH-group and the other LIC ligand bears a methylated N-CH₃ group. Naively, one could expect that this H-cage should have a similar binding affinity towards DPP as the NH-cage has, because a single H-bond is also possible in the H-cage. However, this assumption neglects the entropy penalty resulting from the loss of one of the two equivalent binding sites. This reduction of the number of symmetry-equivalent microstates is associated with a free energy penalty of −TΔS = RT ln2 = 1.7 kJ mol⁻¹ at 298 K.

Fig. 2 Snapshot from MD simulation, in which two H-bonds (red dashed lines) are formed between the NH-cage and the DPP guest.

The binding free energy obtained from the MD simulations of the H-cage of −9.7 kJ mol⁻¹ (Table 1) shows that neither of the above simple assumptions provides a complete picture. Instead, although an H-bond is present 98% of the time also for the H-cage, ΔG_bind is almost exactly in the middle of the two other cages. This supports the notion that in addition to the H-bonds, also the other parts of the cage contribute to organophosphate binding by forming nonpolar contacts with the guest, thus partially compensating for the loss of other interactions. This observation suggests some degree of flexibility of the cage–guest complex, an expectation that is confirmed by the analyses of the system's dynamics, which are described below.

The finding that the doubly H-bonded guest in the NH-cage is only infrequently visited in the MD simulations (population of 3%) might appear counterintuitive at first sight, because an H-bond is typically associated with a favourable interaction energy. To further investigate this, 8 snapshots in which two H-bonds were found were extracted from the MD simulations and subjected to geometry optimisations at the ωB97X-D3 DFT level (see Methods). All optimised structures are minima on the potential energy surface (no imaginary frequencies). Two different doubly H-bonded configurations were found in the MD simulations, one in which one H-bond is formed between the (formally) anionic oxygen atom of the phosphate and the NH-group of the ligand, while the other NH-containing ligand forms an H-bond with the “bridging” ester oxygen atom of DPP (Fig. 2). In the second set of conformations, both H-bonds were formed with the two anionic oxygen atoms of the phosphate. The geometry optimisations at the DFT level confirm this structural feature.

One possible explanation for the observation that the bound state with a doubly H-bonded guest has a low population in the MD simulations could be strain. Upon guest encapsulation the cage needs to adapt to accommodate the guest in its cavity. To investigate the energetic cost for this structural reorganisation, single-point energies for the empty cage were calculated at the ωB97X-D3 level, once for the geometry-optimised empty cage and once for the cage optimised in the presence of the bound DPP guest. The difference of these energies is the strain, that is, the energetic cost of cage reorganisation due to guest binding. We obtained a strain energy of 27 kJ mol⁻¹ for the cage with a doubly H-bonded DPP guest, as compared to only 2 kJ mol⁻¹ for the singly H-bonded state. Although this strain energy calculation can only provide an approximate picture, due to the use of an implicit solvation model and the limited conformational sampling in the DFT calculations, the data suggest that forming two H-bonds with the guest imposes strain on the system. Next, instead of trying to exhaustively sample conformations in the DFT calculations, which will inevitably be limited, we turn to the MSM approach, which can provides a more complete picture of the dynamics of the systems.

3.2 Dynamics of guest encapsulation and release

Markov state model (MSM) analyses of the MD simulation data for the NH-, Me- and the H-cage with the DPP guest can provide detailed insights into the nature of the different bound states and the dynamic transitions between them, as well as on the entry and exit pathways of the guest into and out of the cage cavity. The results of the MSMs are visualised in Fig. 3–5 for the NH-cage, Me-cage, and H-cage, respectively. In the following, the results for the three cages are shown separately, but commonalities and differences between the three systems are also discussed in a comparative way.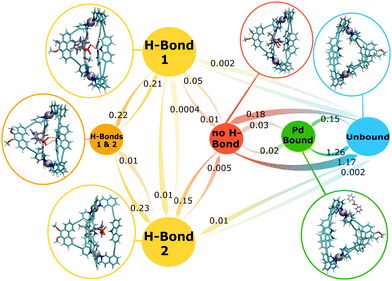

Fig. 3 MSM for the NH-cage/guest system. The numbers next to the arrows are the transition rates (in ns⁻¹) between the states. The circle sizes roughly correspond to the state populations.

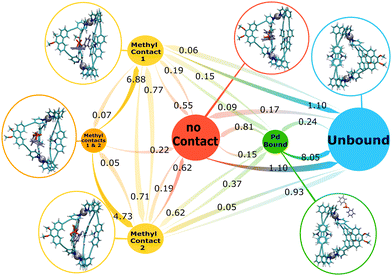Fig. 4 MSM for the Me-cage/guest system. The numbers next to the arrows are the transition rates (in ns⁻¹) between the states. The circle sizes roughly correspond to the state populations.

Fig. 5 MSM for the H-cage/guest system. The numbers next to the arrows are the transition rates (in ns⁻¹) between the states. The circle sizes roughly correspond to the state populations.

3.2.1 Dynamics of the H-bonding NH-cage. The MSM for the NH-cage is visualised in Fig. 3 and shows that the system is quite dynamic, both concerning the process of guest encapsulation/release and also the transitions between the different bound states. We shall start with the latter, before discussing the encapsulation.

All four of the possible states representing the guest being encapsulated inside of the cage cavity are observed, “H-bond 1”, “H-bond 2”, “H-bonds 1 & 2”, and “no H-bond” (Fig. 3). However, the occupancies of these states differ significantly. Taken together, the two equivalent states with one H-bond between cage and guest, “H-bond 1” and “H-bond 2”, account for 74% of the total simulation time, showing that the state with one H-bond is the preferred state of the system. The bound state with two cage–guest H-bonds is also populated in the simulation, but has a population of only 3%. The low prevalence of this “H-bonds 1 & 2” state suggests that this state is rather unstable and might act as a transient intermediate for the switching of the H-bond between the two ligands. A similar low probability of 3% is found for the loosely bound “no H-bond” state, in which the guest is encapsulated within the cavity but does not form any H-bond. Overall, the system is in one of these four bound states during 80% of the total simulation time, while the “Pd-bound” and fully “unbound” states have probabilities of 2% and 18%, respectively.

The arrows in Fig. 3 show the observed transitions between the different states, with the numbers next to the arrows giving the rates for each transition in ns⁻¹. Focusing on the transitions between the different bound states, the MSM reveals that the switch of the guest between the two H-bonded ligands occurs predominantly via the state with two H-bonds. From this “H-bonds 1 & 2” state, the system only transitions into a state with one H-bond, but no guest unbinding can be observed from this state. The alternative pathway for H-bond switching is to proceed through the loosely bound “no H-bond” state. This pathway is indeed found in the simulation, but with a much slower rate than through the doubly H-bonded intermediate. Direct transitions between the two states with one H-bond are very rare (that is, slow rates).

In addition to the characterisation of the bound state, the MSM also reveals the (un-)binding pathways of the guest. Fig. 3 shows that unbinding from any of the three H-bonded states is extremely slow (if possible at all). Instead, guest unbinding always involves the loosely bound state as a stepping stone, from which the fully unbound state can be reached either directly or – much slower – via the “Pd-bound” intermediate. In any case, the H-bond has to break before the guest can leave the host cavity.

Guest uptake also proceeds via the loosely bound state in the majority of cases, but this is not the only possible pathway. The bound states can be accessed from the unbound state in two ways. Either the guest directly enters the cavity from the solution, or the guest first associates with a Pd centre from the outside (“Pd-bound”) of the cage and then swings into the cavity. This transition from the “Pd-bound” to the “no H-bond” state occurs with a rate of 0.03 ns⁻¹, while the direct entrance into the loosely bound state has a faster rate of 0.18 ns⁻¹. In principle, another alternative uptake pathway exists in which the guest is directly captured from the solution via the formation of an H-bond, but the rate is slow (0.01/0.002 ns⁻¹). The reverse transition from the loosely bound “no H-bond” state to the “Pd-bound” state also has a slow rate (0.02 ns⁻¹), thus not every such transition eventually leads to the guest being bound. In general, the transitions out of the “no H-bond” state reveal that the unbinding of the guest occurs with a higher rate (1.17 ns⁻¹) than any other transition from this state, underlining the “stepping stone” character of this loosely bound state, both in the binding and the unbinding direction.

The differences between the rates of the symmetry-equivalent transitions in Fig. 3 suggest that even the 50 μs of simulation time do not fully suffice, as these rates should obviously be identical in the infinite sampling limit. Longer simulations would thus be desirable, of course especially to improve the statistics for the slow transitions from the lowly populated states. However, the differences are reasonably small and, most importantly, they do not change the overall picture of the dynamics of this cage–guest system, as provided by the MSM shown in Fig. 3.

In sum, the MSM of the NH-cage reveals a dynamic bound state and different pathways for guest uptake and release. In the next section, it is investigated how the substitution of the NH-groups by N-CH₃ groups affects the states and the dynamic equilibria between them.

3.2.2 Increased dynamics of the methylated Me-cage. Fig. 4 reveals that the encapsulation of the DPP guest in the Me-cage is even more dynamic than the NH-cage/guest system. Almost all theoretically possible state-to-state transitions are observed in the simulation, and the transition rates (indicated next to the arrows in Fig. 4) are generally faster than for the NH-cage.

Unlike for the NH-cage, for the Me-cage/guest system the majority of simulation time samples the fully “unbound” state (78% population; the Pd-bound state is less prevalent with 2% population). The DPP guest is bound only 20% of the simulation time, as is reflected also in the lower binding affinity (see above). Among the four bound states, the most prevalent one is the loosely bound “no contact” state (12% population), in which the DPP guest is not in direct contact with the N-methyl groups of the ligands. Each of the two states with one methyl contact has 4% population, while the state in which the guest is in contact with both N-methyl groups simultaneously is occupied less than 1%.

The MSM in Fig. 4 reveals a very dynamic bound state and again three different entry pathways for guest encapsulation. In the bound state, the transition between the two equivalent methyl contact states, “methyl contact 1” and “methyl contact 2”, can occur directly with a rate of 0.7 ns⁻¹, or also via the “methyl contacts 1 & 2” state with simultaneous guest contact to both methyl groups, but with a much slower rate (0.07/0.05 ns⁻¹). The latter state is rather unstable, as is reflected in the fast rates of leaving this state and transitioning into a state with contact to only one of the N-methyl groups.

Guest unbinding can occur from any of the bound states, with the exception of the state with two methyl contacts. The major unbinding pathways are the transition from the loosely bound “no contact” state to the fully unbound state (1.10 ns⁻¹), and the transition from one of the two single methyl contact states to the fully unbound state (1.10/0.93 ns⁻¹; the difference between the rates for these two symmetry-equivalent transitions again reflects the statistical uncertainty, as discussed above for the NH-cage). Unbinding via the Pd-bound state is observed as well, but with a relatively slow rate (0.15 ns⁻¹).

As for the guest release, also for the guest uptake pathways all possible scenarios are found in the simulations. Direct binding from the fully unbound state to the loosely bound “no contact” state has a relatively slow rate (0.17 ns⁻¹), while the binding to the loosely bound state from the Pd-bound state has a faster rate of 0.81 ns⁻¹. Encapsulation of the guest by directly binding to one of the two N-methyl groups is also possible, but much slower than the other two more prevalent uptake pathways.

To summarise, the Me-cage/guest system displays more pronounced dynamics than the NH-cage. The nature of the different states is similar, but the transitions between them are much faster, and also the binding/unbinding equilibrium is more dynamic and shifted to the unbound state. In the following, we turn to DPP binding to the hybrid H-cage with one NH- and one N-methyl LIC ligand, a cage that has not yet been experimentally realised. The aim is to investigate whether the above described dynamic effects are additive, and to probe whether the second H-bonding capability is dispensable or not.

In addition to the insights into the nature of the bound state, information on the binding pathways was revealed as well. Binding through association of the guest first with one Pd-center and subsequent downwards movement of the guest into the loosely bound state inside the cavity, has the highest rate in the Me-cage. Direct binding from the solution into the loosely bound state has a slower rate than binding through the loosely bound state. Direct association with one methyl, or the formation of one H-bond, respectively, is the third possibility. This pathway is associated with the slowest rate of the possible entry pathways.

3.2.3 Intermediate dynamics of the H-cage. The hybrid H-cage bears an H-bonding NH-group in one of the LIC ligands and and a methylated N-CH₃ amino group in the other LIC ligand. The MSM in Fig. 5 shows that the prevalence of the bound states is higher than in the Me-cage but lower than in the NH-cage. For the H-cage/guest system, the DPP guest samples one of the bound states 44% of the simulation time, whereas the population of the unbound states, the “Pd-bound” and the fully “unbound” state, is 56%. Loosing one H-bond therefore does reduce the affinity for guest binding (see also Table 1), although the presence of one H-bonding ligand increases the population of the bound state compared to the Me-cage.

Overall, the bound state is on the one hand more static than for the Me-cage/guest system, but on the other hand more dynamic than for the NH-cage/guest system. The overall prevalence of the cage–DPP H-bond is lower than in the NH-cage. Here, 26% of the simulation time an H-bond is present with the NH-group, and a contact with the N-methyl group is established 11% of the time.

When considering the guest binding pathways, no uptake of the guest into the cage cavity by direct capture from the solution through H-bonding is observed. Instead, DPP encapsulation always implies the previous formation of a DPP–methyl contact. In total, the same three guest binding pathways are found as for the other two cages described above. The guest can enter into the cage cavity through either by entering directly into the “no contact” state, that is, loose encapsulation without the formation of any specific contacts, with a rate of 0.15 ns⁻¹. Alternatively, binding can occur through association with a Pd-atom and subsequent entry into the cage cavity via the formation of a contact to the N-methyl group, or through direct contact of the guest with the methyl group. The latter two pathways have rather slow rates (0.07 ns⁻¹ and 0.06 ns⁻¹, respectively).

Comparing the binding behaviour between the NH-, Me- and H-cages, the most dynamic picture is seen for the Me-cage. The transition rates in the H-cage are generally faster than in the NH-cage but slower than in the Me-cage. Transitions between the four different bound states have slower rates than in the Me-cage, suggesting a more static bound state. The asymmetry of the H-cage structure is also reflected in the rates. H-bond breakage transitions have slower rates than the reverse transitions in which an H-bond is formed. Compared to the NH-cage, in the H-cage/guest system the transition rates within the bound states are higher. Direct transitions from the H-bonded state to any of the unbound states are not observed, meaning that H-bond breakage exclusively occurs via an intermediate state with a contact between the DPP guest and the N-methyl group of the LIC ligand.

Taken together, the MSM reveals that for the H-cage/guest system, the bound state is less static than for the NH-cage, even though an H-bond donating ligand is present in the cage. H-bond breakage transitions are slower than the reverse transitions in which the H-bond is formed. Guest uptake from the solution does not occur via the direct formation of the H-bond, but via intermediate states in which the DPP guest forms a contact with the N-CH₃ group of the other ligand, which thus plays a key role for the recruitment of the guest.

3.3 Guest polarisation through H-bonding

Another interesting aspect linked to H-bond formation between the heteroleptic cages and the organophosphate guest is the possible activation of the guest for chemical reactions. The H-bond with the cage could polarise the phosphate group of the guest. Withdrawing electron density from the phosphorus atom could activate the phosphate for nucleophilic attack, which could foster nucleophilic substitution reactions such as ester hydrolysis or transesterification. The atomic partial charges of the guest inside and outside of the cage cavity can provide a hint at guest polarisation, as a first step towards investigating a possible catalytic function of the cage.

To study the polarisation of the DPP guest within the cage cavity by the H-bonds between host and guest, Hirshfeld atomic charges of the guest in solution and bound inside the NH-cage cavity were computed. For free (unbound) DPP in solution, the DPP phosphate atom has a partial charge of +0.44. Four conformations of the guest were considered in solution, differing in the relative orientation of the phenyl rings. In three of the conformations a charge of +0.44 was found and in the fourth conformation the charge of the P-atom was +0.43, showing that the conformational variation of the partial charge is minimal.

Concerning DPP encapsulated in the cage cavity, the strongest polarisation of the phosphate group is expected for the doubly H-bonded state. Indeed, the partial charge of the phosphate P-atom is +0.48 and thus more positive than for the unbound guest in solution. However, the conformation with two H-bonds has a small population (only 3%) and might thus be of low relevance. More interesting in this regard are the conformations with a single H-bond, since these states are highly populated (about 74%). Interestingly, the partial charge of the P-atom is also +0.48 for the singly H-bonded DPP guest, showing that the presence of one H-bond suffices to polarise the phosphate group to a similar extent. As such cage-induced polarisation may activate the phosphate and foster nucleophilic attack, it could open the way for future studies of cage-catalysed nucleophilic substitution reactions. However, successful implementation would imply that also other crucial factors can be controlled, such as product inhibition.

4. Summary and conclusions

In the present work, the dynamics underlying the encapsulation of a diphenylphosphate (DPP) guest molecule in different palladium(II)-based heteroleptic coordination cages was investigated by applying a Markov state model (MSM) framework to all-atom MD simulations on multi-μs time scales. The MSM approach revealed a dynamic nature of the guest-bound state and characterised different pathways for guest binding and release.

It is shown that, even though the guest is confined within the cage cavity, the systems still display rich dynamics. The DPP guest switches between the different states, characterised by different cage–guest interactions within the cavity, with varying rates depending on the strength of the interactions. In the cage with the H-bond donating NH-groups, the transitions are less frequent than in the methylated Me-cage, in which the guest can only form weaker nonpolar contacts. In the hybrid H-cage, dynamics are reduced in comparison to the Me-cage but increased compared to the NH-cage.

Furthermore, the study revealed that even though two H-bond donating ligands are present in the NH-cage, only one H-bond is formed and the guest dynamically switches between the two equivalent H-bonded configurations. A state with two simultaneous H-bonds is possible, but has a low probability; this state acts as a transient intermediate between the two singly H-bonded states.

From a broader perspective, the present work shows that guest confinement in the cages does not involve the lack of motion of the guest within the binding site. Instead, a dynamic confinement is found, meaning a dynamic situation with frequent transitions between different interaction sites within the confining environment formed by the coordination cage, which itself also contributes to the dynamics with its structural flexibility. As was demonstrated for the three different heteroleptic cages investigated in this work, the degree or “amount” of dynamics can be fine-tuned via the chemical nature of the cage-forming ligands. This could provide a means for rational design of cage–guest systems through a thus far often overlooked mechanism, which in addition to the energetics also takes the dynamics into account. For example, the dynamic nature of the bound state might be linked to a reduced entropy penalty upon guest encapsulation, which could be exploited to steer binding affinity.

Stronger interactions between the cage and the guest do lead to reduced dynamics, but the connections between these two different aspects are rather intricate, even for the – seemingly – simple systems studied here. For example, even the presence of two H-bond donating ligands does not imply a static bound state with the guest being constantly attached to both ligands, but instead offers the possibility to dynamically switch between the equivalent binding sides. On the other hand, the Me-cage only confines the guest through different types of weak nonpolar contacts and thus has an even more dynamic bound state. When only one single H-bond donating ligand is present, as in the hybrid H-cage, the dynamics are reduced but transition rates are still higher than in the NH-cage with two H-bond donating ligands.

In addition to the characterisation of the bound states, the MSM also allowed the detailed characterisation of binding/unbinding pathways. It was revealed that the organophosphate guest can enter the cage cavity either by entering directly from solution, that is, without forming a specific interaction within the cage, or alternatively through establishing a contact with an NH- or N-methyl group prior to full encapsulation. Another pathway was revealed in which the guest first associates with one of the Pd-centres from the outside of the cage, and then enters the cavity from that Pd-bound state.

Finally, it was shown that the H-bond formed between the cage and the encapsulated DPP guest polarises the phosphate group, thus possibly activating it for nucleophilic attack. This finding suggests that the investigated heteroleptic cages could be a viable target for catalytic studies, an endeavor to which computational methods can make valuable contributions, as recent developments show.^7,40–43 In this respect, exploring and also exploiting the dynamic nature of cage–guest complexes can extend our understanding and possibly open up new routes for their targeted improvement.

Author contributions

S. J. carried out all computations, analysed and interpreted the data (together with L. V. S.), created the figures, and wrote the initial draft of the manuscript. L. V. S. conceptualised and supervised the project, and he finalised the writing of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Guido Clever (TU Dortmund) for useful discussions. This work was supported by the Research Training group Confinement-controlled Chemistry, funded by the Deutsche Forschungsgemeinschaft (DFG) under Grant GRK2376/331085229.

Notes and references

1. R. Chakrabarty, P. S. Mukherjee and P. J. Stang, Chem. Rev., 2011, 111, 6810–6918.
2. M. M. J. Smulders, I. A. Riddell, C. Browne and J. R. Nitschke, Chem. Soc. Rev., 2013, 42, 1728–1754.
3. K. Harris, D. Fujita and M. Fujita, Chem. Commun., 2013, 49, 6703–6712.
4. T. R. Cook and P. J. Stang, Chem. Rev., 2015, 115, 7001–7045.
5. S. Saha, I. Regeni and G. H. Clever, Coord. Chem. Rev., 2018, 374, 1–14.
6. A. Tarzia and K. E. Jelfs, Chem. Commun., 2022, 58, 3717–3730.
7. T. K. Piskorz, V. Martí-Centelles, T. A. Young, P. J. Lusby and F. Duarte, ACS Catal., 2022, 12, 5806–5826.
8. A. Platzek, S. Juber, C. Yurtseven, S. Hasegawa, L. Schneider, C. Drechsler, K. E. Ebbert, R. Rudolf, Q.-Q. Yan, J. J. Holstein, L. V. Schäfer and G. H. Clever, Angew. Chem., Int. Ed., 2022, 61, e202209305.
9. J.-H. Prinz, H. Wu, M. Sarich, B. Keller, M. Senne, M. Held, J. D. Chodera, C. Schütte and F. Noé, J. Chem. Phys., 2011, 134, 174105.
10. B. E. Husic and V. S. Pande, J. Am. Chem. Soc., 2018, 140, 2386–2396.
11. V. S. Pande, K. Beauchamp and G. R. Bowman, Methods, 2010, 52, 99–105.
12. J. D. Chodera and F. Noé, Curr. Opin. Struct. Biol., 2014, 25, 135–144.
13. X. Wang, I. C. Unarta, P. P.-H. Cheung and X. Huang, Curr. Opin. Struct. Biol., 2021, 67, 69–77.
14. K. A. Konovalov, I. C. Unarta, S. Cao, E. C. Goonetilleke and X. Huang, JACS Au, 2021, 1, 1330–1341.
15. Y. Ge and V. A. Voelz, J. Chem. Phys., 2022, 156, 134115.
16. D. A. Case, J. M. Wang, R. M. Wolf, J. W. Caldwell and P. A. Kollman, J. Comput. Chem., 2004, 25, 1157–1174.
17. E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612.
18. S. Juber, S. Wingbermühle, P. Nuernberger, G. H. Clever and L. V. Schäfer, Phys. Chem. Chem. Phys., 2021, 23, 7321–7332.
19. M. Yoneya, S. Tsuzuki, T. Yamaguchi, S. Sato and M. Fujita, ACS Nano, 2014, 114, 1290–1296.
20. A. Bergner, M. Dolg, W. Küchle, H. Stoll and H. Preuß, Mol. Phys., 1993, 80, 1431–1441.
21. C. Caleman, P. J. van Maaren, M. Hong, J. S. Hub, L. T. Costa and D. van der Spoel, J. Chem. Theory Comput., 2012, 8, 61–74.
22. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25.
23. B. Hess, J. Chem. Theory Comput., 2008, 4, 116–122.
24. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
25. S. Páll and B. Hess, Comput. Phys. Commun., 2013, 184, 2641–2650.
26. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
27. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
28. M. Hoffmann, M. Scherer, T. Hempel, A. Mardt, B. de Silva, B. E. Husic, S. Klus, H. Wu, N. Kutz, S. L. Brunton and F. Noé, Mach. Learn.: Sci. Technol., 2022, 3, 015009.
29. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
30. J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106.
31. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104-1–154104-19.
32. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
33. M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1989, 90, 1730–1734.
34. X. Cao and M. Dolg, J. Chem. Phys., 2001, 115, 7348–7355.
35. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001.
36. C. J. Brown, F. D. Toste, R. G. Bergman and K. N. Raymond, Chem. Rev., 2015, 115, 3012–3035.
37. A. B. Grommet, M. Feller and R. Klajn, Nat. Nanotechnol., 2020, 15, 256–271.
38. F. L. Hirshfeld, Theor. Chem. Acc., 1977, 44, 129–138.
39. D. H. de Jong, L. V. Schäfer, A. H. de Vries, S. J. Marrink, H. J. C. Berendsen and H. Grubmüller, J. Comput. Chem., 2011, 32, 1290–1296.
40. V. V. Welborn, W.-L. Li and T. Head-Gordon, Nat. Commun., 2020, 11, 415.
41. G. Norjmaa, J.-D. Maréchal and G. Ujaque, Chem. – Eur. J., 2020, 26, 6988–6992.
42. G. Sciortino, G. Norjmaa, J. D. Maréchal and G. Ujaque, Catalysis by Metal-Organic Cages: A Computational Perspective, John Wiley & Sons, Ltd, 2022, ch. 19, pp. 271–285.
43. M. Delle Piane, L. Pesce, M. Cioni and G. M. Pavan, Chem. Sci., 2022, 13, 11232–11245.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04342h

---