Refining the thermochemical properties of CF, SiF, and their cations by combining photoelectron spectroscopy, quantum chemical calculations, and the Active Thermochemical Tables approach

Abstract

Fluorinated species have a pivotal role in semiconductor material chemistry and some of them have been detected beyond the Earth's atmosphere. Achieving good energy accuracy on fluorinated species using quantum chemical calculations has long been a challenge. In addition, obtaining direct experimental thermochemical quantities has also proved difficult. Here, we report the threshold photoelectron and photoion yield spectra of SiF and CF radicals generated with a fluorine reactor. The spectra were analysed with the support of ab initio calculations, resulting in new experimental values for the adiabatic ionisation energies of both CF (9.128 ± 0.006 eV) and SiF (7.379 ± 0.009 eV). Using these values, the underlying thermochemical network of Active Thermochemical Tables was updated, providing further refined enthalpies of formation and dissociation energies of CF, SiF, and their cationic counterparts.

---

Introduction

The first group 14 monofluoride radicals, namely fluoromethylidyne (CF) and fluorosilylidyne (SiF), along with their cations fluoromethyliumylidene (CF⁺) and fluorosilyliumylidene (SiF⁺), are commonly found in plasmas employed for the purpose of silicon-containing semiconductor material surface etching.^1–3 In addition to being one of the most abundant ions present in semiconductor processing,³ CF⁺ has been detected in diverse regions of outer space.^4–7 It has thus been identified as a key intermediate in the chemistry of fluorine-bearing molecules in diffuse and dense interstellar gas clouds.^8,9 Although we are still awaiting the astronomical detection of SiF and SiF⁺, their presence in outer space as well as their role in the chemistry of silicon in the gas phase and on grains is strongly suspected. Indeed, reactions involving SiF⁺ are already incorporated in astrochemical models.⁸

Thermodynamic properties such as enthalpies of formation, dissociation energies, and adiabatic ionisation energies are of utmost importance for refining chemical models of fluorinated chemistry in plasmas and in space. Furthermore, accurate thermodynamic properties are very well suited to benchmarking the accuracy of existing and upcoming state-of-the-art quantum chemical calculations, particularly with respect to pushing the limits of the long-standing challenge of obtaining accurate thermochemical data for fluorinated compounds.^10–14

Dyke and coworkers have published two papers presenting the He I photoelectron spectra of CF^15,16 from which they determined the adiabatic ionisation energies of the X^{+ 1}Σ⁺ ← X ²Π and a^{+ 3}Π ← X ²Π ionising transitions of CF to be 9.11 ± 0.02 eV and 13.94 ± 0.02 eV, respectively. From photoelectron spectra, the ω_e⁺ value of CF⁺ was derived initially to be 1840 ± 30 cm⁻¹,¹⁵ and later revised to 1810 ± 30 cm⁻¹.¹⁶

The CF⁺ cation has also been investigated using direct infrared (IR) diode laser spectroscopy.^17,18 Preliminary work from Hirota and coworkers¹⁷ yielded precise structural information on CF⁺ from its vibronic ground state (r_e⁺ = 1.154272(35) Å). Subsequently, Saykally and coworkers¹⁸ have extended the IR study of CF⁺ to the seven lowest vibrational levels of the electronic ground state, providing precise vibrational constants such as ω_e⁺ = 1792.6654(18) cm⁻¹ and ω_ex_e⁺ = 13.229668(54) cm⁻¹, as well as r_e⁺ = 1.1542551(25) Å, the latter being in good agreement with the results of Hirota et al. However, of the two photoelectron spectroscopic studies, only the most recent one¹⁶ reported a vibrational frequency (1810 ± 30 cm⁻¹) congruent with the accurate constants of Saykally and coworkers.¹⁸ The spectroscopic molecular constants were also well predicted using multireference configuration interaction (MRCI) calculations for the lowest singlet and triplet electronic states of CF⁺.¹⁹ Subsequently, the landscape of the CF⁺ electronic states has been further explored along with several Rydberg states.^20,21

The dissociation energy of the CF⁺ ground state has been estimated¹⁶ as D₀(CF⁺) = 7.82 ± 0.12 eV, based on combining the ionisation energies of CF and carbon atom with the dissociation energy of CF of 5.67 ± 0.10 eV from electron-ionisation mass spectrometric studies.²² This is just within the combined error bars compared to the value obtained in the work of Saykally,¹⁸D₀(CF⁺) = 7.698 ± 0.004 eV, extracted from the fit based on a crude Morse potential model. Theodorakopoulos and coworkers²⁰ calculated the dissociation energy of CF⁺ using MRCI and obtained a significantly underestimated value (D₀(CF⁺) = 6.73 eV) compared to those extracted from experimental studies. Later, Letelier and coworkers²³ made the first step toward reconciliation of the experimental results with theory by using MRCI+Q/aug-cc-pV5Z calculations. They obtained a D₀ value of 7.54 eV.

There is a remarkable paucity of photoelectron spectroscopic data available for SiF. No direct measurement of the adiabatic ionisation energy of SiF has been obtained, and the indirectly derived values span a rather large energy range. Using ion chemistry, one can estimate 7.54 ± 0.16 eV²⁴ and 7.08 ± 0.10 eV,²⁵ whereas extrapolation from Rydberg spectroscopy leads to 7.26 eV,²⁶ 7.31 eV,²⁷ and 7.31 ± 0.02 eV.²⁸ The two calculations of the adiabatic ionisation energy available in the literature report 7.36 eV at the coupled cluster single, double, and perturbative triple level and complete basis set extrapolation (CCSD(T)/CBS)²⁹ and 7.41 eV at the G3(CC)/B2df+ level,³⁰ although neither of the two is sufficiently accurate to confidently provide a value within chemical accuracy (with uncertainty less than ±1 kcal mol⁻¹ or ±0.04 eV). However, the SiF⁺ structural information and vibrational properties in the electronic ground state have been precisely determined using microwave (r_e⁺ = 1.5264950(2) Å; ω_e⁺ = 1050.7(2) cm⁻¹)³¹ and IR spectroscopy (r_e⁺ = 1.5265(8) Å; ω_e⁺ = 1050.3757(13) cm⁻¹; ω_ex_e⁺ = 4.9462(4) cm⁻¹).³² Several values for the SiF⁺ dissociation energy have been extracted from experimental studies, D₀(SiF⁺) = 6.3 eV,³³ 6.46 ± 0.14 eV,³⁴ and 6.32 ± 0.11 eV,²⁴ all of which are lower than the most accurate theoretical values obtained either using CCSD(T) with CBS extrapolation,³⁵D₀ = 6.92 ± 0.04 eV, the configuration-interaction method,³⁶D₀ = 6.60 eV, or MP4SDTQ,¹⁹D₀ = 6.85 eV. It is worth noting that, while high-level calculations appear to underestimate the experimentally derived dissociation energy of CF⁺, they seem to overestimate that of SiF⁺.

This paper presents the threshold photoelectron and photoion yield spectra of SiF and CF radicals in the vicinity of their first ionisation threshold. The spectra are analysed with the support of ab initio calculations that aid the extraction of relevant spectroscopic parameters. The new experimental values were added to the thermochemical network underlying the Active Thermochemical Tables (ATcT) approach,^37–39 thus producing further improved thermochemical parameters of SiF, CF and the corresponding cations.

Methodologies

Experimental details

The experiments were performed at the SOLEIL synchrotron facility, on the DESIRS beamline.⁴⁰ The experimental setup combining the DELICIOUS3 spectrometer^41,42 and the flow-tube reactor has been described elsewhere.^43,44

The experimental spectra recorded for CF and SiF have been obtained using the conditions described in ref. 45 and 46, respectively, in which CF and SiF were side products of the reaction of F with CH₄ (or C₂H₄) or SiH₄, respectively. The output of the flow-tube reactor was sampled through two consecutive skimmers before reaching the interaction region at the centre of DELICIOUS3. From CF⁺ and SiF⁺ photoion images, mean velocities were measured along the molecular beam at 915 and 1010 m s⁻¹, corresponding to translational temperatures in the 200–220 K range.

In the present paper, only details concerning the resolutions of the presented spectra are summarised. The spectral resolutions of the ion yields are 0.72 Å (5.8 meV at 10 eV) for CF and 2.16 Å (17.4 meV at 10 eV) for SiF, which correspond to the photon spectral resolution. The final spectral resolutions δE of the slow photoelectron spectra (SPES) are estimated to be 14 meV at 9.5 eV and 24 meV at 7.5 eV for the CF and SiF spectra, respectively. The energy scale has been calibrated using the He third order and Si atomic transitions, with an energy scale uncertainty of ±3 meV for CF and ±6 meV for SiF, respectively. Note that the extraction field (F) used to extract the ions and the electrons (88.7 V cm⁻¹) leads to a field-induced downshift of the ionisation energies of approximately 7 meV, following the well-established formula 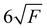(in cm⁻¹ with F in V cm⁻¹).⁴⁷

Although the universality of the Stark shift in polyatomic systems has been previously questioned,^48,49 we have checked in our experiment using absorption lines from the gas filter (not subject to the Stark shift) and known adiabatic ionisation energies of molecules that the above-mentioned Stark shift applied within the error bars.

Calculation details

Supporting ab initio calculations on the electronic states of CF, CF⁺, SiF, and SiF⁺ were carried out using the internally contracted multireference configuration interaction method with Davidson correction (icMRCI+Q) with complete active space self-consistent field (CASSCF) wave-functions. The CASSCF and MRCI calculations were performed at full valence, i.e., 11 electrons for CF and SiF (10 for CF⁺ and SiF⁺). These electrons were distributed in 8 orbitals keeping the 1s orbital of carbon and fluorine atoms and the 1s, 2s, and 2p orbitals of silicon atom doubly occupied. All calculations were performed using the MOLPRO 2016 package.⁵⁰ Single point calculations were performed at the aug-cc-pV nZ (n = T, Q, 5, and 6) basis set⁵¹ for the equilibrium geometries and anharmonic frequencies (using the DIATOMIC routine in MOLPRO where the potential curves were fitted with a polynomial of 8th order) allowing the spectroscopic constants to be calculated (ω_e, ω_ex_e, and ω_ey_e) for the CF(X ²Π), CF⁺ (X^{+ 1}Σ⁺), SiF(X ²Π) and SiF⁺ (X^{+ 1}Σ⁺) states. CBS extrapolations were carried out using the aug-cc-pV nZ (n = T, Q, 5, and 6) basis set series. The CASSCF and dynamical correlation (E_MRCI+Q − E_CASSCF) energies were extrapolated using the E_CASSCF(CBS) + A × exp(−Bn) and E_Corr(CBS) + C × n⁻³ functions, respectively. The calculated energies reported in this paper correspond to E_CASSCF(CBS) + E_corr(CBS). The anharmonic constants (ω_ex_e and ω_ey_e) could not be confidently extrapolated to CBS because of their weak dependence on the basis used; instead, the values obtained with the largest basis set (aug-cc-pV6Z) were used. Our calculated values are reported in Tables 1 and 2 and discussed in the following section.

Table 1 Calculated and experimental equilibrium spectroscopic properties of the ground electronic states of CF, CF⁺, SiF, and SiF⁺. See the text for details

	r e/Å	ω e/cm^−1	ω e x e/cm^−1	ω e y e/cm^−1	Ref.
CF	1.2731	1303.06	10.76	0.08	Calc.
CF^+	1.1558	1773.21	13.16	0.05	Calc.
		1786.5	11.89		Exp.
	1.154	1810			16
	1.1542551	1792.6654	13.229668		18
SiF	1.6143	833.16	4.45	0.02	Calc.
SiF^+	1.5394	1024.44	4.69	0.01	Calc.
		1056.8	5.17		Exp.
	1.5264950	1050.7			31
	1.52652	1050.3757	4.9462		32

---

Table 2 Calculated and experimental adiabatic ionisation energies of the X^{+ 1}Σ⁺ ← X ²Π photoionising transition of CF and SiF. See the text for details

	IEad/eV	IEad,corrZPE/eV	IEad,exp./eV	Ref.
CF	9.029	9.059	9.128	This work
			9.11	15, 16
SiF	7.325	7.337	7.379	This work
			7.54	24
			7.08	25
			7.31	26
			7.31	28

---

Results

The first ionising transitions of CF and SiF arise from one-electron removal from the 2π orbital, which is the first anti-bonding (π*) orbital. This leads to a X^{+ 1}Σ⁺ ← X ²Π_r photoionising transition. Looking at the molecular orbital diagrams, one can assume that the ionisation process removes mainly one of the unpaired p-electrons on C (³P) and Si (³P) atoms for CF and SiF, respectively. In the analogous cases of SiH and CH, the p orbitals are rather weakly perturbed, as witnessed by the modest difference in the ionisation energies (IEs) of Si (8.15166 ± 0.00003 eV)⁵² and SiH (7.934 ± 0.005 eV),⁴⁶ or those of C (11.260288 ± 0.000002 eV)⁵³ and CH (10.640 ± 0.004 eV).⁵⁴ In CF and SiF radicals, the interactions between the p-orbitals of C/Si atoms and the doubly occupied p-orbital of the fluorine atom are greater, which leads to a more pronounced decrease of IEs for CF (9.128 ± 0.006 eV) and SiF (7.381 ± 0.009 eV).

Photoelectron and photoion yield spectra of CF

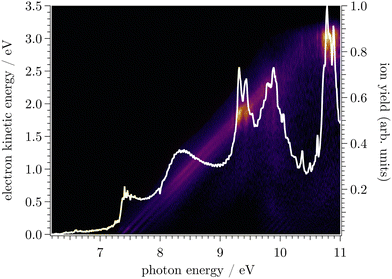
In Fig. 1, the mass-selected ion yield of CF is depicted on top of the photoelectron signal (PES) matrix, i.e. the coincidence signal of the electrons (resolved by kinetic energy) as a function of photon energy. The vertical lines (resonant with photon energy) observed above 11 eV correspond to autoionisation of neutral CF Rydberg states converging to several vibronic states of CF⁺.

Fig. 1 Mass-selected photoelectron signal of CF as a function of the photon energy (horizontal axis) and electron kinetic energy (vertical axis) for m/z 31. The corresponding total ion yield obtained by integrating over all electron energies is represented by the white curve.

In Fig. 2, the corresponding CF threshold photoelectron spectrum is displayed in black and compared with our harmonic Franck–Condon (FC) simulation in red. The experimental spectrum exhibits a progression up to v⁺ = 6, as well as one hot band around 9 eV arising from the v⁺ = 0 ← v = 1 transition. While the agreement is satisfactory at low energy, the calculated spectrum starts to progressively deviate from the experimental spectrum above 9.75 eV due to the absence of the anharmonic component in the simulation. Based on the vibrational FC simulation, the origin band is unambiguously assigned. From the prominent vibrational progression, one can extract the harmonic frequency ω_e⁺ and the corresponding anharmonic constant ω_ex_e⁺. Fig. 3 shows a plot of the observed peak apexes as a function of (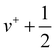). The obtained data set was fitted using a second-order polynomial expression. Note that, owing to the aforementioned autoionisation processes, the transition to v⁺ = 11 was observed, from which the quality of the fit and thus of evaluation of the anharmonicity was greatly improved. Indeed, autoionisation resonances allow sampling of the molecular potential beyond the Franck–Condon region that is not accessible by one-photon direct ionisation.⁵⁵ The fitted spectroscopic constants are ω_e⁺ = 1786.5 ± 5.5 cm⁻¹ and ω_ex_e⁺ = 11.89 ± 0.44 cm⁻¹, in reasonable agreement with the very accurate constants obtained by Saykally,¹⁸ as well as with the frequency of 1810 ± 30 cm⁻¹ reported by Dyke et al.¹⁶ (see Table 1).

Fig. 2 Experimental threshold photoelectron spectrum of CF in the vicinity of the X^{+ 1}Σ⁺ ← X ²Π photoionising transition (in black) compared with our harmonic Franck–Condon calculation convolved with a Gaussian line shape (FWHM = 26 meV) at a vibrational temperature of 600 K (in red). The red assignment corresponds to our harmonic calculation whereas the black comb follows the anharmonicity which allows an unambiguous attribution of the ionising transition towards v⁺ = 11 (observed through autoionisation). See the text for details.

Fig. 3 Energies of the lowest vibrational levels of the electronic ground state of CF⁺ with respect to its v⁺ = 0 level as a function of (). The red crosses represent our harmonic calculations and the black circles our measurements. The blue line corresponds to a second-order polynomial fit of our experimental values. See the text for details.

The apex position of the origin band in Fig. 2 can be determined as 9.121 eV, which, after a correction for the Stark shift, becomes 9.128 ± 0.004 eV. It is important to note here that the adiabatic ionisation energy, which is a thermodynamically-relevant quantity, by definition corresponds to the energy difference between the lowest actually existing rovibronic level of the neutral and that of the ion.⁵⁶ (Mutatis mutandis, the same is true for all thermodynamically-relevant quantities, such as dissociation energies and other reaction energies at 0 K.⁵⁶) Thus, in CF the adiabatic ionisation energy corresponds to the X^{+ 1}Σ⁺(v⁺ = 0,  J⁺ = 0) ← X ²Π_1/2(v = 0, J = 1/2) transition.

In regular photoelectron spectroscopy, when individual rotational transitions are not resolved, the standard practice is to report the apex of the vibrational peak that was identified as the v⁺ = 0 ← v = 0 transition as the adiabatic ionisation energy. This tacitly implies the assumption that the underlying rotational envelope is not shaded either to the red or to the blue, i.e. that the Q branch is rather compact and that the lateral branches (P and R, as well as higher branches, such as O and S, if they happen to be allowed) are symmetric, which may or may not be correct.

However, the nature of the ground state of neutral CF introduces an additional complication. Namely, X ²Π_r undergoes spin–orbit coupling (as quantified by the corresponding coupling constant^57,58A₀ = 77.11 ± 0.01 cm⁻¹), with ²Π_1/2 as the lower and ²Π_3/2 as the higher component. Consequently, the v⁺ = 0 ← v = 0 spectral peak in Fig. 2 almost certainly contains an unresolved hot band originating from the upper ²Π_3/2 component of the neutral. Prima facie, one would expect that the presence of such an unresolved hot band will cause a shift of the apparent apex to the red, the amount of which depends, inter alia, on the thermal population of the additional component.

To that end, an approximate simulation of the rotational envelope has been performed to estimate the potential shift of the peak apex relative to the adiabatic ionisation energy. While the energy terms of ¹Σ⁺ rotational levels are straightforward, the rotational levels of the ²Π state were calculated using the Hamiltonian that correctly describes the coupling of the spin with the orbital and the rotational angular momenta, as appropriate for partial spin uncoupling pertinent to a transition from Hund's case (a) to case (b),^59,60 following the elegantly re-derived formulation by Hougen.⁶¹ The spectroscopic constants of CF and CF⁺ were taken from ref. 58 and 17 respectively. With these, the Hamiltonian for the X ²Π_r state of CF produces the term values of F₁ = −37.15 cm⁻¹ for ²Π_1/2, J = 1/2 and F₂ = 41.46 cm⁻¹ for ²Π_3/2, J = 3/2. Notably, the lowest rotational levels of each of the two spin–orbit components of ²Π_r of CF appear to be almost symmetrically split by roughly ±A₀/2 below and above the reference level (vibrationless/rotationless energy level before any spin–orbit consideration). This is in rather stark contrast to the recently discussed situation of spin–orbit-rotation coupling in the otherwise analogous case of X ²Π_r of CH,⁶² where both F₁ = 0.15 cm⁻¹ and F₂ = 17.97 cm⁻¹ are positive quantities, or, for that matter, to the quite asymmetric splitting in the well-known case of X ²Π_i of OH,^63–65 neither of which conforms to a symmetric ±A₀/2 splitting of the spin–orbit components that is frequently presumed in theoretical calculations.

For the spectral simulation of the rotational envelope, the rotational temperature of 200 K was used as it corresponds to the translational temperature of the beam at the output of the flowtube reactor (see the “Experimental details” subsection). The simulated envelope strongly suggests that the adiabatic ionisation energy (X^{+ 1}Σ⁺(v⁺ = 0,  J⁺ = 0) ← X ²Π_1/2(v = 0, J = 1/2)) is, in fact, quite close to the actual maximum of the observed band, primarily because of two opposing tendencies: the unresolved hot band originating from X ²Π_3/2 indeed tends to shift the apex of the experimental peak slightly toward the red, but this is nearly entirely counteracted by the shading toward the blue of the rotational envelope belonging to transitions that originate from X ²Π_1/2.

After the field-induced Stark-shift correction of 7 meV and an estimation of the uncertainty from our rotational contour simulation, the resulting adiabatic ionisation energy is IE_ad(CF) = 9.128 ± 0.006 eV. This can be compared to the value of 9.120 ± 0.005 eV obtained from the publicly available version of ATcT (ver. 1.124).³⁹ A variance decomposition analysis of the provenance⁶⁶ indicates that the two top contributors to the ATcT value are the experimental ionisation energy of 9.11 ± 0.01 eV determined by Dyke et al.¹⁵ and the difference between the adiabatic ionisation energies of CF₃ and CF of 0.055 ± 0.03 eV determined by Asher and Ruscic.⁶⁷ It is also of note that our calculated adiabatic ionisation energy, 9.059 eV (see Table 2), slightly underestimates the experimental value (by 0.07 eV), but is otherwise in quite reasonable agreement with the experiment, particularly if one considers that the species in question is fluorinated.

Photoelectron and photoion yield spectra of SiF

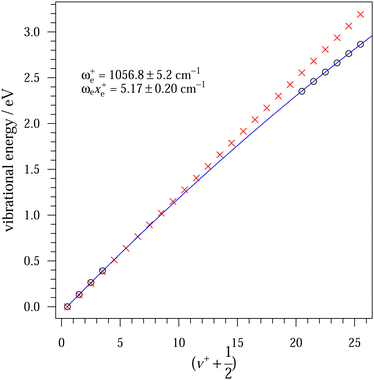
Similarly as for CF, Fig. 4 represents the mass-selected ion yield of SiF superimposed on the PES matrix, where autoionisation features are observed. Fig. 5 displays the threshold photoelectron spectrum (black trace) and its harmonic FC simulation (red trace). The spectrum consists of one hot band, a progression in SiF vibration from the origin band to v⁺ = 3, followed at higher energy by a long high v⁺ series from 20 to 25 caused by resonant autoionisation processes. From our ab initio calculations, we checked that no other electronic states of SiF⁺ were located in this energy region. Indeed, the first triplet (³Π) and singlet (¹Σ⁺) states are located around 11.83 eV and 13.71 eV above the neutral ground state, respectively. The harmonic FC calculation reproduces satisfactorily the experimental spectrum. The observed energies in the vibrational progression are plotted as a function of (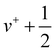) in Fig. 6. The blue line results from a second-order polynomial fit, leading to ω_e⁺ = 1056.8 ± 5.2 cm⁻¹ and ω_ex_e⁺ = 5.17 ± 0.20 cm⁻¹ in good agreement with the literature values, see Table 1. As in the case of CF, the inclusion of high v⁺ states accessible via autoionisation processes significantly improves the obtained fit.

Fig. 4 Mass-selected photoelectron signal of SiF as a function of the photon energy (horizontal axis) and electron kinetic energy (vertical axis) for m/z 47. The corresponding total ion yield obtained by integrating over all electron energies is represented by the white curve.

Fig. 5 Experimental threshold photoelectron spectrum of SiF in the vicinity of the X^{+ 1}Σ⁺ ← X ²Π photoionising transition (in black) compared with our harmonic Franck–Condon calculation convolved with a Gaussian line shape (FWHM = 40 meV) at a vibrational temperature of 600 K (in red). The above red assignment corresponds to our harmonic calculation whereas the black comb follows the anharmonicity which allows an unambiguous attribution of the ionising transitions towards v⁺ = 20–25 (observed through autoionisation). See the text for details.

Fig. 6 Energies of the lowest vibrational levels of the electronic ground state of SiF⁺ with respect to its v⁺ = 0 level as a function of (). The red crosses represent our harmonic calculations and the black circles our measurements. The blue line corresponds to a second-order polynomial fit of our experimental values.

From our measurement displayed in Fig. 5, we can extract the band maximum of the origin band of the SiF photolectron spectrum to be 7.372 ± 0.007 eV. Similarly to the case of CF, the rotational envelope was estimated using the spectroscopic constants for SiF and SiF⁺ from ref. 68 and 31 respectively. Once again, it was found that the adiabatic ionisation energy (X^{+ 1}Σ⁺(v⁺ = 0, J⁺ = 0) ← X ²Π_1/2(v = 0, J = 1/2)) is very close to the band maximum, for essentially the same reasons as in the case of CF. The adiabatic ionisation energy is obtained after correcting for field-induced Stark shift (+7 meV) and estimating the uncertainty in the position of the apex of the vibrational peak from our rotational contour simulation. The corresponding final value of the adiabatic ionisation energy IE_ad(SiF) = 7.379 ± 0.009 eV. Again, our calculated adiabatic ionisation energy, 7.337 eV (see Table 2), slightly underestimates the experimental value (by 0.04 eV), but is otherwise in reasonable agreement.

Thermochemical considerations

The usual approach to developing new or improved thermodynamic quantities in studies like the present one is to use traditional sequential thermochemistry (A begets B, B begets C, etc.). For instance, since the adiabatic ionisation energy defines the thermodynamic difference between the 0 K enthalpies of formation of the cation and the neutral, the presently determined IE_ad(CF) = 9.128 ± 0.006 eV can be combined with the 0 K enthalpy of formation of CF, such as that currently available from ATcT,³⁹ Δ_fH₀°(CF) = 58.107 ± 0.029 kcal mol⁻¹, to derive Δ_fH₀°(CF⁺) = Δ_fH₀°(CF) + IE_ad(CF) = 268.60 ± 0.14 kcal mol⁻¹ (which can be in turn compared to the 0 K value for the ion of 268.42 ± 0.11 kcal mol⁻¹ available directly from ATcT³⁹; notably, the corresponding IE_ad(CF), as reported by ATcT, is 9.116 ± 0.005 eV, the difference from the current experiment being just about contained – within a round-off error – by the combined uncertainties). After setting the 0 K enthalpies of formation, the corresponding 298.15 K values can be derived as Δ_fH₂₉₈°(CF) = 58.968 ± 0.029 kcal mol⁻¹ and Δ_fH₂₉₈°(CF⁺) = 269.37 ± 0.14 kcal mol⁻¹ (the latter within the stationary electron convention⁵⁶) with the aid of the 298.15 K enthalpy increments of CF (2.167 kcal mol⁻¹),⁶⁹ CF⁺ (2.074 kcal mol⁻¹),³⁹ graphite (0.251 kcal mol⁻¹),⁷⁰ and F₂ (2.109 kcal mol⁻¹).⁷⁰

Going further with the sequential thermochemistry approach, one can take the 0 K dissociation energy of CF, D₀(CF) = 5.654 ± 0.002 eV from ATcT³⁹ and combine it with the currently determined IE_ad(CF) and the accurately known IE(C)⁵³ to obtain D₀(CF⁺) = D₀(CF) + IE(C) − IE_ad(CF) = 7.786 ± 0.007 eV (which can again be compared to the publicly available ATcT value of 7.794 ± 0.005 eV).³⁹ The corresponding 298.15 K bond dissociation enthalpies are BDE₂₉₈(CF) = 5.695 ± 0.002 eV and BDE₂₉₈(CF⁺) = 7.833 ± 0.007 eV (after utilising the aforementioned enthalpy increments for CF and CF⁺ together with those of the C atom, C⁺ ion, and F atom, of 1.562, 1.589, and 1.558 kcal mol⁻¹, respectively).⁶⁹

However, the derivations delineated above are entirely dependent not only on the accuracy of the newly determined IE_ad(CF), but also on the tacit assumption that auxiliary thermochemical quantities, in this case Δ_fH₀°(CF) and D₀(CF), have been a priori firmly established, and that thus the new IE_ad(CF) leads simply to a revision of Δ_fH₀°(CF⁺) and D₀(CF⁺). In this particular case the putative robustness of the available values for Δ_fH₀°(CF) and D₀(CF) does not appear unreasonable, given that the provenances of the ATcT values include, inter alia, state-of-the-art electronic structure computations capable of sub-kJ mol⁻¹ accuracies, such as several flavors of W4,^71–74 HEAT,^65,75 and FPD,⁷⁶ all of which appear mutually entirely consistent.

Nonetheless, in a general case the assumptive premise of robustness of the auxiliary thermochemistry may or may not be warranted. In fact, the new measurement may very well also imply the need for revisions or adjustments of the auxiliary thermochemistry. One of the additional potential problems of sequential thermochemistry is that while it tends to produce an improvement in the derived thermodynamic quantity of the targeted chemical species, it also frequently introduces new inconsistencies with previously established thermochemistry of other related species. Namely, their thermochemistry may have been obtained via sequential derivations that were pegged to the old value of the just revised species and should therefore be also revised: an essentially impossible task, since in tabulations obtained by sequential thermochemistry the intricate progenitor-progeny relationships are concealed. In addition, by virtue of pairing down competitive determinations by selecting what subjectively appears to be the “best” determination, traditional sequential thermochemistry chronically under-utilises the available thermochemically-relevant knowledge.

In fact, while in the case of CF and CF⁺ the situation is relatively benign, there being available thermochemical values for CF that arguably appear reliable, things are veritably more complicated in the case of SiF and SiF⁺. Namely, the values for the enthalpy of formation of SiF available from the literature^{24,25,29,69,71,77–88} encompass a spectacularly wide range, differing on the extremes by more than 16 kcal mol⁻¹, as demonstrated in Table 3. In principle, one might venture assuming that the values reported from the three most accurate electronic structure approaches^71,81,82 are likely the most reliable. However, all three enthalpies of formation of SiF were derived from computations of the dissociation energy D₀(SiF) and thus directly depend on the selected enthalpy of formation of Si atom. Notably, the recent introduction of key Si-containing chemical species in ATcT³⁹ has produced a significantly revised (and improved) value Δ_fH₀°(Si) = 107.63 ± 0.14 kcal mol⁻¹, which can be compared with the generally accepted, but 1 kcal mol⁻¹ lower (and substantially less accurate) value of 106.5 ± 1.9 kcal mol⁻¹ derived by Gurvich et al.,⁶⁹ recommended by CODATA,⁷⁰ and used in JANAF⁸⁸ and other tabulations. The older (and higher) value of 107.6 ± 0.1 kcal mol⁻¹ found in the NBS Tables⁸⁶ is, in retrospect, in excellent agreement with the new ATcT value, as is the revised value of 107.2 ± 0.2 kcal mol⁻¹ recently proposed by Karton and Martin.⁷¹

Table 3 Compilation of prior literature values for the SiF enthalpies of formation at 0 K and 298 K, Δ_fH₀°(SiF) and Δ_fH₂₉₈°(SiF), in kcal mol⁻¹

ΔfH0°(SiF)	ΔfH298°(SiF)	Ref.
	−14.2 ± 2.0	78 (theory)
−12.70 ± 3.0	−12.42 ± 3.0	79 (theory)
	−5 ± 3	24 (exp)
−11.7 ± 2.1	−11.2 ± 2.1	25 (exp)
	−13.4	80 (theory)
	−14.0 ± 2.0	29, 77 (theory)
−14.8 ± 0.4		81 (theory)
−14.9 ± 0.3		71 (theory)
	−13.90 ± 0.35	82 (theory)
−14.79	−14.36	83 (theory)
−15.25 ± 2.00	−14.95 ± 2.00	84 (theory)
−14.4		85 (theory)
1.0 ± 1.0	1.7 ± 1.0	86 (eval)
	−5 ± 6	87 (eval)
−5.2 ± 3.0	−4.8 ± 3.0	88 (eval)
−6.5 ± 2.6	−6.0 ± 2.6	69(eval)

---

As opposed to the sequential thermochemistry approach, Active Thermochemical Tables rely on a different paradigm, rooted in constructing, statistically analysing, and solving a thermochemical network (TN) that contains all available determinations relevant to the thermochemistry of the included species, irrespective of whether they originate from experiment or high-level electronic structure theory.^37,38,89

The current public version of ATcT (ATcT TN ver. 1.124),³⁹ which contains nearly 2800 chemical species, has been developed within the context of several studies, such as the report on thermophysical and thermochemical properties of CH₂ and CH₃ using nonrigid rotor anharmonic oscillator (NRRAO) partition functions,⁹⁰ the development and benchmarking of a state-of-the-art computational approach that aims to reproduce total atomisation energies of small molecules within 10–15 cm⁻¹,⁹¹ as well as the study of the reversible reaction C₂H₃ + H₂ ⇄ C₂H₄ + H ⇄ C₂H₅.⁹²

Since then, the underlying ATcT TN has been successively expanded to fulfil the needs of subsequent studies, such as those involving enthalpies of formation of key bromo- and iodo-methanes, ethenes and ethynes,⁹³ the ring-opening dynamics of cyclopropyl and cyclopropylium (ATcT TN versions 1.128 and 1.130),⁹⁴ the bond dissociation energy and the adiabatic ionisation energy of CH (ATcT TN ver. 1.140),⁶² the role of methanediol in the atmosphere (ATcT ver. 1.148),⁹⁵ as well as a number of ongoing studies, eventually leading to the current developmental version ATcT TN 1.156. The latter contains more than 3150 species interconnected by over 30 000 thermochemically relevant determinations, but does not (yet) include the present experimental adiabatic ionisation energies.

Although ATcT TN ver. 1.156 includes more than 350 new species and several thousand new determinations (a few of which do include CF or CF⁺ as reactant or product), the thermochemistry of CF and CF⁺ has remained nearly the same: Δ_fH₀°(CF) = 58.124 ± 0.026 kcal mol⁻¹ and Δ_fH₀°(CF⁺) = 268.41 ± 0.11 kcal mol⁻¹, the differences in comparison with the already discussed ATcT TN ver. 1.124³⁹ (less than 0.02 kcal mol⁻¹) comfortably contained within the associated (and slightly tighter) uncertainties. The resulting IE_ad(CF) = 9.119 ± 0.005 eV is in agreement (within the combined uncertainties) with the current direct experimental value of IE_ad(CF) = 9.128 ± 0.006 eV.

However, of particular relevance to the current study is that this version includes the SiF_n, n = 1–4 group of species and their ions. Thus, ATcT TN ver. 1.156 produces Δ_fH₀°(SiF) = −14.40 ± 0.15 kcal mol⁻¹ and Δ_fH₂₉₈°(SiF) = −13.97 ± 0.15 kcal mol⁻¹ (where the 0 to 298.15 conversion exploits the 298.15 K enthalpy increments of SiF, 2.261 kcal mol⁻¹ – slightly updated from Gurvich et al.⁶⁹ using the NASA PAC program⁹⁶ and spectroscopic constants from Huber and Herzberg,⁵⁷ crystal silicon, 0.769 kcal mol⁻¹,⁷⁰ and 1/2 of the already mentioned enthalpy increment for F₂, 2.109 kcal mol⁻¹).⁷⁰ The matching 0 K dissociation energy of SiF is D₀(SiF) = 6.093 ± 0.005 eV, and the corresponding BDE₂₉₈(SiF) = 6.140 ± 0.005 eV. We note here that the ATcT value for D₀(SiF) is significantly influenced by highly accurate state-of-the-art W4⁷¹ and FPD⁸¹ calculations of the same quantity extant in the ATcT TN, and that the corresponding Δ_fH₀°(SiF) makes use of the newly revised enthalpy of formation for gas-phase silicon atom, as already mentioned earlier, and which in this version of ATcT results amounts to Δ_fH₀°(Si) = 107.63 ± 0.14 kcal mol⁻¹.

For the cation, ATcT TN ver. 1.156 produces Δ_fH₀°(SiF⁺) = 154.91 ± 0.39 kcal mol⁻¹ and Δ_fH₂₉₈°(SiF⁺) = 155.18 ± 0.39 kcal mol⁻¹ (where the conversion peruses the 298.15 K enthalpy increment of SiF⁺ of 2.094 kcal mol⁻¹, as obtained from available spectroscopic constants^31,32,57 by using the NASA PAC program⁹⁶). A variance decomposition analysis indicates that the primary contributors to Δ_fH°(SiF⁺) are the literature values for IE_ad(SiF) included in the ATcT TN, combined with Δ_fH°(SiF), and only to a minor degree the theoretical D₀(SiF⁺), such as 159.58 (±1.5, estimated) kcal mol⁻¹.⁷⁷

Noting again that ATcT TN ver. 1.156 does not (yet) include the current experimental ionisation energies of CF and SiF, it is interesting to inspect the difference in ATcT 0 K enthalpies of formation of SiF⁺ and SiF, which implies an adiabatic ionisation energy of SiF of 7.342 ± 0.016 eV. Curiously, while standard in-house mid-level composite methods extant in the TN suggest adiabatic ionisation energies ranging between 7.31 ± 0.10 eV (CBS-QB3) and 7.41 ± 0.08 eV (G4), with 7.36 ± 0.04 eV (W1) perhaps as a midpoint, the resulting ionisation energy is pushed toward the lower end of this range by the ostensibly accurate experimental value of 7.310 ± 0.011 eV^27,28 extracted from VUV absorption spectra, in spite of the fact that, based on a critical evaluation of those studies, the uncertainty initially assigned (a.k.a. ‘prior’) in the TN to this determination was double the uncertainty declared by the authors, and that the subsequent ATcT statistical analysis, which evaluates the internal consistency of the determinations in the TN, has further increased its uncertainty to ±0.032 eV.

Clearly, the above IE_ad of 7.342 ± 0.016 eV is appreciably less accurate than the current experimental IE_ad(SiF) = 7.379 ± 0.009 eV, and it also appears inconsistent, given that the difference (0.037 eV) is significantly larger than the combined uncertainties. The normal course of action within the ATcT approach is to add the new results to the TN, and let the ATcT statistical analysis arbitrate between potentially inconsistent determinations.

The addition of the two experimental ionisation energies creates a new version, ATcT TN 1.158. The resulting thermochemical values of relevance to the present study are given in Table 4.

Table 4 Recommended thermochemical values for CF, SiF, and their cations from ATcT TN ver. 1.158

Quantity	0 K	298.15 K	Uncert.	Units
a Current experimental adiabatic ionisation energy. b BDE0(AB) is synonymous with D0(AB). c Recently revised value from ATcT, significantly improved over the CODATA^70 value of ΔfH0°(Si) = 106.5 ± 1.9 kcal mol^−1 and ΔfH298°(Si) = 107.6 ± 1.9 kcal mol^−1; see the text.
ΔfHT°(CF)	58.123	58.984	±0.026	kcal mol^−1
ΔfHT°(CF^+)	268.522	269.290	±0.089	kcal mol^−1
IEad(CF)	9.124		±0.004	eV
	(9.128)^a		(±0.006)^a	eV
BDET(CF)^b	5.653	5.695	±0.001	eV
BDET(CF^+)^b	7.790	7.836	±0.004	eV
ΔfHT°(SiF)	−14.42	−13.98	±0.15	kcal mol^−1
ΔfHT°(SiF^+)	155.62	155.89	±0.24	kcal mol^−1
IEad(SiF)	7.373		±0.008	eV
	(7.379)^a		(±0.009)^a	eV
BDET(SiF)^b	6.093	6.141	±0.005	eV
BDET(SiF^+)^b	6.872	6.924	±0.009	eV
ΔfH0°(C)	170.029	171.340	±0.010	kcal mol^−1
ΔfH0°(C^+)	429.697	431.035	±0.010	kcal mol^−1
ΔfH0°(F)	18.464	18.967	±0.004	kcal mol^−1
ΔfH0°(Si)^c	107.63	108.67	±0.14	kcal mol^−1
ΔfH0°(Si^+)	295.62	296.60	±0.14	kcal mol^−1

---

While the introduction of IE_ad(CF) has not particularly affected the thermochemistry of neutral CF, with Δ_fH°(CF) and D₀(CF) remaining essentially identical, it does affect and improve the thermochemistry of CF⁺, adjusting Δ_fH₀°(CF⁺) upward (by 0.113 kcal mol⁻¹) and becoming slightly more accurate (±0.089 kcal mol⁻¹, cf. to earlier ±0.11 kcal mol⁻¹). Importantly, the updated ATcT thermochemistry of the ion corresponds to D₀(CF⁺) = 7.790 ± 0.004 eV and to IE_ad(CF) = 9.124 ± 0.004 eV, the latter being in excellent agreement with the very slightly higher experimental value of 9.128 ± 0.006 eV.

As one might have expected, the introduction of the experimental IE_ad(SiF) into the ATcT TN has a more pronounced effect on the relevant species than the introduction of IE_ad(CF). Also not surprisingly, the thermochemistry of neutral SiF is affected less than that of the ion, given that the former is constrained by D₀(SiF) obtained from high-level electronic structure computations.^71,81 Thus, D₀(SiF) = 6.093 ± 0.005 eV, corresponding to Δ_fH₀°(SiF) = −14.42 ± 0.15 kcal mol⁻¹, which is only marginally different than the value of −14.40 ± 0.15 kcal mol⁻¹ from the preceding version of ATcT TN. However, the new and improved value for Δ_fH₀°(SiF⁺) is now 155.62 ± 0.24 kcal mol⁻¹, rather significantly different than the value of 154.91 ± 0.39 kcal mol⁻¹ from the previous version. The new thermochemistry of SiF⁺ corresponds to D₀(SiF⁺) = 6.872 ± 0.009 eV and to IE_ad(SiF) = 7.373 ± 0.008 eV, in superb agreement with the experimental value of 7.379 ± 0.009 eV. For reference purposes, Table 4 also includes the current ATcT values for the constituent atoms. Enthalpies of formation of atoms were considered as ‘key’ quantities already by CODATA,⁷⁰ but since then they have gained additional importance, because they are needed to convert theoretically computed total atomisation energies to practical enthalpies of formation. While the genesis of the ATcT revision of the enthalpy of formation of C atom was discussed elsewhere,⁹⁷ the new and improved ATcT enthalpy of formation of Si atom is formally given here for the first time.

Conclusion

In this study we presented photoelectron spectroscopic measurements of the first two group 14 monofluorides, CF and SiF, together with supporting quantum chemical calculations, further amplified by utilising the new experimental ionisation energies in conjunction with the Active Thermochemical Tables approach. The latter combination results in significant refinements of the related thermochemical properties, particularly those of SiF⁺, as well as those of CF⁺. The recommended new enthalpies of formation and dissociation energies of the neutral CF and SiF and their cationic counterparts, together with the resulting adiabatic ionisation energies, are summarised in Table 4.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was performed on the DESIRS Beamline at SOLEIL synchrotron under project numbers 20200996 and 20140832. The authors are grateful to the whole staff of SOLEIL for running the facility. The work at Argonne National Laboratory (B.R.) was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Chemical Sciences, Geosciences and Biosciences Division, under Contract No. DE-AC02-06CH11357, through the Gas-Phase Chemical Physics Program. Ning L. Chen acknowledges the support from the Paris Ile-de-France Region (DIM ACAV+) for her PhD grant. This work has also received financial support from the French “Agence Nationale de la Recherche” (ANR) under Grant No. ANR- 12-BS08-0020-02 (Project SYNCHROKIN). This work was supported by the Programme National “Physique et Chimie du Milieu Interstellaire” (PCMI) of CNRS/INSU with INC/INP cofunded by CEA and CNES. The Active Thermochemical Tables are a U.S. Department of Energy Office of Science Public Reusable Research (DOE SC PuRe) Data Resource.⁹⁸

References

1. P. Ho, J. E. Johannes, R. J. Buss and E. Meeks, J. Vac. Sci. Technol., A, 2001, 19, 2344–2367.
2. K. Williams and E. Fisher, J. Vac. Sci. Technol., A, 2003, 21, 1024–1032.
3. J. M. Stillahn, K. J. Trevino and E. R. Fisher, Annu. Rev. Anal. Chem., 2008, 1, 261–291.
4. D. A. Neufeld, P. Schilke, K. M. Menten, M. G. Wolfire, J. H. Black, F. Schuller, H. S. Müller, S. Thorwirth, R. Güsten and S. Philipp, Astron. Astrophys., 2006, 454, L37–L40.
5. H. Liszt, J. Pety, M. Gerin and R. Lucas, Astron. Astrophys., 2014, 564, A64.
6. H. Liszt, V. Guzmán, J. Pety, M. Gerin, D. Neufeld and P. Gratier, Astron. Astrophys., 2015, 579, A12.
7. S. Muller, K. Kawaguchi, J. Black and T. Amano, Astron. Astrophys., 2016, 589, L5.
8. D. A. Neufeld, M. G. Wolfire and P. Schilke, Astrophys. J., 2005, 628, 260.
9. K. Acharyya and E. Herbst, Astrophys. J., 2017, 850, 105.
10. L. A. Curtiss, K. Raghavachari, P. C. Redfern and J. A. Pople, J. Chem. Phys., 1997, 106, 1063–1079.
11. B. Ruscic, J. V. Michael, P. C. Redfern, L. A. Curtiss and K. Raghavachari, J. Phys. Chem. A, 1998, 102, 10889–10899.
12. Á. Ganyecz, M. Kállay and J. Csontos, J. Phys. Chem. A, 2018, 122, 5993–6006.
13. E. Paulechka and A. Kazakov, J. Chem. Eng. Data, 2019, 64, 4863–4874.
14. Y. Si, Y. Liu, W. Lai, Y. Ma, J. Shi, B. Wang, M. Liu and T. Yu, Adv. Theory Simul., 2022, 2200093.
15. J. Dyke, A. Lewis and A. Morris, J. Chem. Phys., 1984, 80, 1382–1386.
16. J. Dyke, N. Hooper and A. Morris, J. Electron Spectrosc. Relat. Phenom., 2001, 119, 49–56.
17. K. Kawaguchi and E. Hirota, J. Chem. Phys., 1985, 83, 1437–1439.
18. M. Gruebele, M. Polak and R. J. Saykally, Chem. Phys. Lett., 1986, 125, 165–169.
19. K. A. Peterson, R. C. Woods, P. Rosmus and H.-J. Werner, J. Chem. Phys., 1990, 93, 1889–1894.
20. I. D. Petsalakis and G. Theodorakopoulos, Chem. Phys., 2000, 254, 181–186.
21. I. D. Petsalakis and G. Theodorakopoulos, Chem. Phys. Lett., 2011, 508, 17–21.
22. D. Hildenbrand, Chem. Phys. Lett., 1975, 32, 523–526.
23. N. Inostroza, J. Letelier, M. L. Senent and P. Fuentealba, Spectrochim. Acta, Part A, 2008, 71, 798–802.
24. M. Weber and P. Armentrout, J. Chem. Phys., 1988, 88, 6898–6910.
25. E. R. Fisher, B. L. Kickel and P. Armentrout, J. Phys. Chem., 1993, 97, 10204–10210.
26. J. Johns and R. Barrow, Proc. Phys. Soc., 1958, 71, 476.
27. F. Remy, E. Mahieu, D. Macau-Hercot, I. Dubois, H. Bredohl, J. Breton, F. Launay and M. Benharrous, J. Mol. Spectrosc., 1992, 152, 131–136.
28. H. Bredohl, J. Breton, I. Dubois, J. Esteva, D. Macau-Hercot and F. Remy, J. Mol. Spectrosc., 1999, 195, 281–283.
29. A. Ricca and C. W. Bauschlicher, J. Phys. Chem. A, 1998, 102, 876–880.
30. L. Wang and Y.-L. He, Int. J. Mass Spectrom., 2008, 276, 56–76.
31. R. H. Petrmichl, K. A. Peterson and R. C. Woods, J. Chem. Phys., 1988, 89, 5454–5459.
32. Y. Akiyama, K. Tanaka and T. Tanaka, Chem. Phys. Lett., 1989, 155, 15–20.
33. P. Wilkinson, Astrophys. J., 1963, 138, 778.
34. R. Reddy, T. Rao and R. Viswanath, Astrophys. Space Sci., 1992, 189, 29–38.
35. A. Ricca and C. W. Bauschlicher Jr, Chem. Phys. Lett., 1998, 287, 239–242.
36. S. Karna and F. Grein, J. Mol. Spectrosc., 1987, 122, 28–40.
37. B. Ruscic, R. E. Pinzon, M. L. Morton, G. von Laszewski, S. J. Bittner, S. G. Nijsure, K. A. Amin, M. Minkoff and A. F. Wagner, J. Phys. Chem. A, 2004, 108, 9979–9997.
38. B. Ruscic, R. E. Pinzon, G. von Laszewski, D. Kodeboyina, A. Burcat, D. Leahy, D. Montoya and A. F. Wagner, J. Phys. Conf. Ser., 2005, 16, 561–570.
39. B. Ruscic and D. H. Bross, Active Thermochemical Tables (ATcT) values based on ver. 1.124 of the Thermochemical Network, Argonne National Laboratory, Lemont, Ill. 2022, https://atct.anl.gov/, accessed August 2023.
40. L. Nahon, N. D. Oliveira, G. A. Garcia, J. F. Gil, B. Pilette, O. Marcouillé, B. Lagarde and F. Polack, J. Synchrotron Radiat., 2012, 19, 508–520.
41. G. A. Garcia, B. K. de Miranda, M. Tia, S. Daly and L. Nahon, Rev. Sci. Instrum., 2013, 84, 053112.
42. X. Tang, G. A. Garcia, J.-F. Gil and L. Nahon, Rev. Sci. Instrum., 2015, 86, 123108.
43. G. A. Garcia, X. Tang, J.-F. Gil, L. Nahon, M. Ward, S. Batut, C. Fittschen, C. A. Taatjes, D. L. Osborn and J.-C. Loison, J. Chem. Phys., 2015, 142, 164201.
44. G. A. Garcia, B. Gans, X. Tang, M. Ward, S. Batut, L. Nahon, C. Fittschen and J. C. Loison, J. Electron Spectrosc. Relat. Phenom., 2015, 203, 25–30.
45. G. A. Garcia, J.-C. Loison, F. Holzmeier, B. Gans, C. Alcaraz, L. Nahon, X. Wu, X. Zhou, A. Bodi and P. Hemberger, Mol. Phys., 2020, 119, e1825851.
46. N. L. Chen, B. Gans, S. Hartweg, G. A. Garcia, S. Boyé-Péronne and J.-C. Loison, J. Chem. Phys., 2022, 157, 014303.
47. W. A. Chupka, J. Chem. Phys., 1993, 98, 4520–4530.
48. P. Hemberger, Z. Pan, X. Wu, Z. Zhang, K. Kanayama and A. Bodi, J. Phys. Chem. C, 2023, 127, 16751–16763.
49. J. Harvey, P. Hemberger, A. Bodi and R. P. Tuckett, J. Chem. Phys., 2013, 138, 124301.
50. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO, version 2016, a package of ab initio programs, 2016, see https://www.molpro.net.
51. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
52. C. Brown, S. Tilford, R. Tousey and M. Ginter, J. Opt. Soc. Am., 1974, 64, 1665–1682.
53. K. Haris and A. Kramida, Astrophys. J., Suppl. Ser., 2017, 233, 16.
54. B. Gans, F. Holzmeier, J. Krüger, C. Falvo, A. Röder, A. Lopes, G. Garcia, C. Fittschen, J.-C. Loison and C. Alcaraz, J. Chem. Phys., 2016, 144, 204307.
55. M. Briant, L. Poisson, M. Hochlaf, P. de Pujo, M.-A. Gaveau and B. Soep, Phys. Rev. Lett., 2012, 109, 193401.
56. B. Ruscic and D. H. Bross, Comput.-Aided Chem. Eng., 2019, 45, 3–114.
57. K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure. IV. Constants of Diatomic Molecules, Reinhold, New York, 1979.
58. T. Porter, D. Mann and N. Acquista, J. Mol. Spectrosc., 1965, 16, 228–263.
59. E. Hill and J. H. Van Vleck, Phys. Rev., 1928, 32, 250–272.
60. G. Herzberg, Molecular Spectra and Molecular Structure. I. Spectra of Diatomic Molecules, D. Van Nostrand, N. J. Princeton, 2nd edn, 1950.
61. J. T. Hougen, The calculation of rotational energy levels and rotational line intensities in diatomic molecules, US National Bureau of Standards, 1970, vol. NIST MN-115.
62. J. H. Thorpe, D. Feller, D. H. Bross, B. Ruscic and J. F. Stanton, Phys. Chem. Chem. Phys., 2023, 25, 21162–21172.
63. B. Ruscic, A. F. Wagner, L. B. Harding, R. L. Asher, D. Feller, D. A. Dixon, K. A. Peterson, Y. Song, X. Qian, C.-Y. Ng, J. Liu, W. Chen and D. W. Schwenke, J. Phys. Chem. A, 2002, 106, 2727–2747.
64. B. Ruscic, D. Feller, D. A. Dixon, K. A. Peterson, L. B. Harding, R. L. Asher and A. F. Wagner, J. Phys. Chem. A, 2001, 105, 1–4.
65. M. E. Harding, J. Vázquez, B. Ruscic, A. K. Wilson, J. Gauss and J. F. Stanton, J. Chem. Phys., 2008, 128, 114111.
66. B. Ruscic, D. Feller and K. A. Petrson, Theor. Chem. Acc., 2014, 133, 1415.
67. R. L. Asher and B. Ruscic, J. Chem. Phys., 1997, 106, 210–221.
68. Y. Houbrechts, I. Dubois and H. Bredohl, J. Phys. B: At., Mol. Opt. Phys., 1980, 13, 3369.
69. L. V. Gurvich, I. V. Veyts and C. B. Alcock, Thermodynamic Properties of Individual Substances, Hemisphere, New York, 4th edn, 1990, vol. 2.
70. J. D. Cox, D. D. Wagman and V. A. Medvedev, CODATA Key Values for Thermodynamics, Hemisphere, New York, 1989.
71. A. Karton and J. M. L. Martin, J. Phys. Chem. A, 2007, 111, 5936–5944.
72. A. Karton, A. Tarnopolsky, J.-F. Lamere, G. C. Schatz and J. M. L. Martin, J. Phys. Chem. A, 2008, 112, 12868–12886.
73. A. Karton, S. Daon and J. M. L. Martin, Chem. Phys. Lett., 2011, 510, 165–178.
74. A. Karton, E. Rabinovich, J. M. L. Martin and B. Ruscic, J. Chem. Phys., 2006, 125, 144108.
75. A. Tajti, P. G. Szalay, A. G. Császár, M. Kállay, J. Gauss, E. F. Valeev, B. A. Flowers, J. Vázquez and J. F. Stanton, J. Chem. Phys., 2004, 121, 11599–11613.
76. D. Feller, K. A. Peterson and D. A. Dixon, J. Chem. Phys., 2008, 129, 204105.
77. A. Ricca and C. W. Bauschlicher, J. Phys. Chem. A, 1998, 102, 876–880.
78. E. W. Ignacio and H. B. Schlegel, J. Chem. Phys., 1990, 92, 5404–5416.
79. P. Ho and C. F. Melius, J. Phys. Chem., 1990, 94, 5120–5127.
80. H. H. Michels and R. H. Hobbs, Chem. Phys. Lett., 1993, 207, 389–396.
81. D. Feller and D. A. Dixon, J. Phys. Chem. A, 1999, 103, 6413–6419.
82. B. P. Prascher, R. M. Lucente-Schultz and A. K. Wilson, Chem. Phys., 2009, 359, 1–13.
83. P. Sukkaew, L. Ojamäe, O. Kordina, E. Janzén and Ö. Danielsson, ECS J. Solid State Sci. Technol., 2015, 5, P27.
84. A. Burcat and E. Goos, Int. J. Chem. Kinet., 2018, 50, 633–650.
85. J. Guo, S. Tang, L. Chen, D. Wei and A. Tang, Int. J. Quantum Chem., 2023, 123, e27063.
86. D. D. Wagman, W. H. Evans, V. B. Parker, R. H. Schumm, I. Halow, S. M. Bailey, K. L. Churney and R. L. Nuttall, J. Phys. Chem. Ref. Data, 1982, 11, 2.
87. R. Walsh, J. Chem. Soc., Faraday Trans. 1, 1983, 79, 2233–2248.
88. M. W. Chase Jr, J. Phys. Chem. Ref. Data, 1985, 14(Suppl. 1).
89. B. Ruscic, R. E. Pinzon, M. L. Morton, N. K. Srinivasan, M.-C. Su, J. W. Sutherland and J. V. Michael, J. Phys. Chem. A, 2006, 110, 6592–6601.
90. B. Ruscic and D. H. Bross, Mol. Phys., 2021, 119, e1969046.
91. J. H. Thorpe, J. L. Kilburn, D. Feller, P. B. Changala, D. H. Bross, B. Ruscic and J. F. Stanton, J. Chem. Phys., 2021, 155, 184109.
92. T. L. Nguyen, D. H. Bross, B. Ruscic, G. B. Ellison and J. F. Stanton, Faraday Discuss., 2022, 238, 405–430.
93. D. H. Bross, G. B. Bacskay, K. A. Peterson and B. Ruscic, J. Phys. Chem., 2023, 127, 704–723.
94. N. Genossar, P. B. Changala, B. Gans, J.-C. Loison, S. Hartweg, M.-A. Martin-Drumel, G. A. Garcia, J. F. Stanton, B. Ruscic and J. H. Baraban, J. Am. Chem. Soc., 2022, 144, 18518–18525.
95. T. L. Nguyen, J. Peeters, J.-F. Müller, A. Perera, D. H. Bross, B. Ruscic and J. F. Stanton, Proc. Natl. Acad. Sci. U. S. A., 2023 DOI:10.1073/pnas.2304650120.
96. B. J. McBride and S. Gordon, Properties and Coefficients: Computer Program for Calculating and Fitting Thermodynamic Functions, National Aeronautics and Space Administration, 1999.
97. P. B. Changala, T. L. Nguyen, J. H. Baraban, J. F. Stanton, D. H. Bross and B. Ruscic, J. Phys. Chem. A, 2017, 121, 8799–8806.
98. PuRe Data Resources at a Glance, https://science.osti.gov/Initiatives/PuRe-Data/Resources-at-a-Glance, accessed August 2023.

---