Binding of carboxylate and water to monovalent cations

Abstract

The interactions of carboxylate anions with water and cations are important for a wide variety of systems, both biological and synthetic. To gain insight on properties of the local complexes, we apply density functional theory, to treat the complex electrostatic interactions, and investigate mixtures with varied numbers of carboxylate anions (acetate) and waters binding to monovalent cations, Li⁺, Na⁺ and K⁺. The optimal structure with overall lowest free energy contains two acetates and two waters such that the cation is four-fold coordinated, similar to structures found earlier for pure water or pure carboxylate ligands. More generally, the complexes with two acetates have the lowest free energy. In transitioning from the overall optimal state, exchanging an acetate for water has a lower free energy barrier than exchanging water for an acetate. In most cases, the carboxylates are monodentate and in the first solvation shell. As water is added to the system, hydrogen bonding between waters and carboxylate O atoms further stabilizes monodentate structures. These structures, which have strong electrostatic interactions that involve hydrogen bonds of varying strength, are significantly polarized, with ChelpG partial charges that vary substantially as the bonding geometry varies. Overall, these results emphasize the increasing importance of water as a component of binding sites as the number of ligands increases, thus affecting the preferential solvation of specific metal ions and clarifying Hofmeister effects. Finally, structural analysis correlated with free energy analysis supports the idea that binding to more than the preferred number of carboxylates under architectural constraints are a key to ion transport.

---

1 Introduction

The binding of ions to ligands is a fundamental phenomenon in chemistry that controls the behavior of many important systems. In particular, the preferential solvation of specific metal ions by a ligand determines the nature of ion solvation.^1–3 Not only is static structure determined by ion solvation, but so are the dynamics of ion transport.^4–6 Such ion dynamics are important in a wide range of applications, including energy storage,^7,8 water filtration,^9,10 and ion channel proteins.^6,11–13 Density functional theory (DFT), which can characterize the binding between ligands and ions accurately, has been used to make substantial progress in understanding the fundamental properties of such ionic systems.^14–17 Most DFT calculations have treated binding of a single ligand, but most systems possess a concentration of ligands. Furthermore, many binding sites include a mixed ligand composition. A mixed ligand binding site may include water, but fundamental understanding of the role of water in a binding site is lacking. Here, we present a new DFT study of the binding of multiple carboxylate groups to a series of monovalent ions in the presence of water in the binding site.

In this study, we focus on ligand mixtures of acetate, with the carboxylate functional group (–COO⁻), and water. This combination is ubiquitous in biological¹⁸ and synthetic molecules.^19–21 In biological ion channels¹¹ and synthetic ionomers,²⁰ carboxylates may form binding sites that solvate simple metal ions and lower free energy barriers to ion conduction. Acetate is also commonly used in nanoparticle synthesis because of its ability to bind positively charged metal atoms.^22–25 Recent work has highlighted the importance of acetate in perovskite solar cell fabrication.²⁵ Some of these acetate precursors are hydrates, and thus the structure and interactions among the cation, acetate and water are important. The broad occurrence of carboxylate binding to cations in water means that understanding the binding of these systems at a fundamental quantum level will be broadly impactful.

The acidic amino acids, aspartate (Asp, D) and glutamate (Glu, E), contain carboxylates that, inside the pores of ion channels, interact with cations and play important roles in the selectivity of which ion permeates the channel. For example, the selectivity filter of the bacterial voltage-gated sodium channel is composed in part by four Glu residues that bind to Na⁺. The interactions with the carboxylates in the channel draw Na⁺ into the selectivity filter and promote permeation, but deny K⁺ permeation.^26–28 The measured electron density for the ion channel NavAb indicates four well-bound water molecules near the ion, implying that the selectivity filter selects and conducts Na ions in a mostly hydrated form, in contrast to the potassium (K⁺) channel (e.g., KcsA).²⁶

Another group of ion channels that contain Glu residues in the channel are the pentameric ligand-gated ion channels (pLGICs), which are archetypal mediators of electrochemical signal transduction.^29,30 The pLGICs have a wide range of behaviors. For the cation-selective pLGIC, pore-lining glutamates are often invoked to explain selectivity for cations.^31,32 Recent work has provided evidence that charge selectivity is dependent on the conformation of the charged side chain, specifically of the glutamate ring in pLGIC.^32,33 This requirement is consistent with the idea that local ligand positioning about an ion yields a varying free energy landscape, with the free energy differences for different ions resulting in selectivity.^{14,15,17,34–36} As such, these free energy landscapes define the necessary conditions for selectivity.

To address shortcomings of present lithium batteries, researchers have been trying to develop single ion conductors composed of polymers with ion-containing groups.^8,37–39 Polymers with precisely spaced carboxylate groups have been synthesized and studied,^40–42 and intriguing layered structures have been observed.^42,43 Strong interactions between the cation (typically Li) and the carboxylate-containing side-groups lead to aggregate formation. Much of this research has focused on polymer systems that are ‘dry’; that is, without any water content, but water is a common component of the ionomer systems and relevant for a broader range of applications, especially fuel cell systems.^42,44 The effect of water in these systems would be interesting to characterize, especially the effect on the aggregate morphology.

To treat the strong electrostatic interactions involving cations and carboxylates accurately, density functional theory (DFT) methods have been employed. By using DFT, electronic effects, such as polarization and charge transfer from the carboxylates to the metal cation, are treated accurately, unlike in almost all molecular dynamics force-fields.⁴⁵ DFT can determine, with high accuracy, whether the carboxylate binding involves either one (mono-) or two oxygens (bi-dentate), which is especially important for the coordination of the cation and the overall optimal geometry. Some previous DFT calculations have studied acetates with multiple water molecules.^46–48 DFT studies of the glutamate selectivity filter explain why selectivity filters with the same EEEE motif are Na⁺-selective in bacterial Na_v channels, but Ca²⁺-selective in high voltage-activated Ca_v channels.⁴⁹

In previous work,^50,51 we addressed the binding of carboxylate ligands to a single metal ion, and also to multiple metal ions. In the first study, we resolved two competing hypotheses for the (inverse) Hofmeister series.^3,52–54 In the ‘ligand field strength’ hypothesis, higher anionic field strength of a binding site should favor smaller over larger cations,⁵² but in the ‘equal affinities’ hypothesis,⁵³ entities with matching hydration free energies tend to associate. Our results supported the ligand field strength hypothesis and follow the reverse Hofmeister series for ion solvation⁵⁵ and ion transfer from aqueous solution to binding sites with the preferred number of ligands. In addition, a key insight arose from the finding that ion-binding sequences can be manipulated and even reversed just by constraining the number of carboxylate ligands in the binding sites. That finding provided additional support for an earlier idea that architectural constraints determine selectivity in ion permeation.^{6,14,34,56–58} In our second work, we studied two cations interacting with acetates.⁵¹ We found that, for Li⁺, Na⁺ and K⁺, the preferred optimal structure with two cations is favored over a mixture of single cation complexes, providing a basis for understanding ionic cluster formation that is relevant for engineering proteins and other materials for rapid, selective ion transport.

Here, we address the binding of carboxylate and water molecules to monovalent cations, Li, Na, and K, using DFT. We determine the lowest binding free energy and structure in the gas phase for a variable number of acetate n_A and water n_W molecules. These calculations address the competitive binding between water and a carboxylate ligand, acetate, without the constraints due to the ligand bound in the protein's amino acid sequence or polymer's configurations. Polarization is significant, particularly due to the strong electrostatic interactions involving carboxylates, and is examined through calculation of the ChelpG partial charges. Differences among the three cations occur primarily due to the different carboxylate oxygen:cation bond distance and the geometric constraint that distance imposes on the molecular arrangement within the complex. With waters present in the complexes, the role of hydrogen bonding in the structure of the complexes is shown to be important and varies among the cations in response to the carboxylate oxygen:cation binding geometry.

2 Methods

The local clustering of acetate and water ligands about an ion corresponds to the following reaction,

X⁺ + n_ACH₃COO⁻ + n_WH₂O ⇄ X⁺(CH₃COO⁻)_nA(H₂O)_nW, (1)

where X⁺ indicates a cation with a single charge binding with n_A charged acetate ligands (CH₃COO⁻) and n_W water molecules to form a complex. We assume the clustering equilibria take place in an idealized environment that does not influence the reaction through long-ranged dispersive and electrostatic interactions or structural constraints on the clusters. Our treatment is thus equivalent to an uncoupled quasi-chemical analysis carried out in a low dielectric environment (ε = 1).^14,59–62 Note that, while the reaction components are treated in the gas phase, the local environment around the ion complex is treated explicitly to capture the dielectric function where electrostatic interactions are expected to be most complex. As a first approximation, this treatment is appropriate for an ionomer system because polymers can have significant flexibility and they occupy a low dielectric environment. Ion channels and ionophore binding sites may also be surrounded by an environment equivalent to a low dielectric medium.^6,57

We calculated the free energy change (ΔG) for the reactions in eqn (1) using the Gaussian 16 quantum chemistry package.⁶³ The geometry optimizations were carried out in the gas phase using the density functional theory approach with the hybrid ωB97X-D approximation to the exchange–correlation energy.⁶⁴ This choice is based on previous work on DFT of ionic systems^65,66 and treats the van der Waals interactions, which are important for the large clusters treated here. For the basis sets, we used Dunning's correlation-consistent polarized double-zeta basis sets augmented with diffuse functions (aug-cc-pvDz).^67,68 The double zeta is a good compromise between accuracy and calculation speed.⁶⁶ The correlation-consistent basis sets were developed to describe core-core and core-valence electron correlation effects in molecules, and previously have been shown to be accurate for a single carboxylate.⁴⁷

To obtain free energies, we performed a normal mode frequency analysis⁶⁹ using the same level of theory as for optimization. Stable structures, for which the forces are zero and frequencies positive, confirmed true minima on the potential energy surfaces. The thermodynamic analysis yielded zero point energies and thermal corrections to the electronic energy due to translational, electronic, and vibrational motions calculated at a temperature of 298 K and pressure of 1 atm.

To calculate the free energy change for the reactions in eqn (1), we calculated the difference in free energy between the product (p) and the sum of the reactants (r) in stoichiometric proportions (n_r):

ΔG = G_p − Σn_rG_r. (2)

The enthalpic component of the reaction free energy (ΔH) is computed with an analogous equation.

To benchmark these studies, we performed additional calculations. First, we evaluated basis set superposition error (BSSE) on selected cases, including the most optimal structures for each cation. Second, we tested the use of the hybrid ωB97X-D approximation to the exchange–correlation energy by comparing with a different hybrid functional (B3LYP), Moeller–Plesset perturbation theory (MP2), and a coupled-cluster method that includes single and double electronic excitations and an estimate of contributions from connected triple excitations (CCSD(T)). The latter two approaches are post-Hartree Fock ab initio methods. Finally, we varied the basis set to aug-cc-pvTz and 6-311+G(2df,2pd) for a complex of acetate and K⁺ to test the sensitivity of the results to different combinations of functional and basis set. The results are presented in the ESI,† and summarized below.

3 Results

3.1 Free energies

We first consider the free energies of binding, based on eqn (2), as a function of varying n_A and n_W. Fig. 1 shows a plot of ΔG for each cation as a function of the total number of ligands, n = n_A + n_W. We will use the notation (n_A,n_W) to designate the number of acetates and waters in a complex; for example, (2,3) has 2 acetates and 3 waters.

Fig. 1 The free energy difference, ΔG, for varying numbers of acetates n_A and waters n_W binding to Li⁺, Na⁺ and K⁺ (top to bottom). The numbers by the points are n_A (left side) and n_W (right side). The data for fixed n_W are fit by a quadratic, shown as a solid line with color varying to distinguish the cases. The data for fixed n_A are connected by dashed lines. Numerical values are given in the ESI† (Table S1).

One simplifying organization of the plot (Fig. 1) is the solid lines that connect the ΔG values for fixed n_W. These lines are quadratic fits, which are remarkably good.‡ The fit lines shift to the right as n_W increases, with the minimum point at n_A = 2 for all n_W and all cations. The lowest values are for Li⁺ near −200 kcal mol⁻¹ (see Table 1) because Li⁺ has the shortest separation distance with O, and thus the lowest electrostatic energy.

Table 1 Free energy differences for n_A = 2 and varying waters, which are the lowest free energy complexes. ΔΔG in kcal mol⁻¹

n W	ΔG (Li^+)	ΔG (Na^+)	ΔG (K^+)
1	−202.3	−175.6	−157.5
2	−206.2	−178.8	−160.6
3	−209.2	−182.2	−163.4
4	−211.6	−185.6	−165.9
5	−210.8	−186.7	−166.1

---

The overall lowest ΔG is for (n_A,n_W) = (2,4) for Li⁺. For Na⁺ and K⁺, the lowest values are at (2,5) (Table 1). Note that the minimum point does not occur at zero net charge, but at −1 with an excess acetate.

The quadratic dependence as a function of n_A at constant n_W implies that ΔG increases substantially when n_W is changed by ±1, starting from the minimum at n_A = 2. This behavior is consistent with the strong electrostatic interactions among the acetates and the cation. Starting from the minimum free energy state, and increasing the total charge by adding an acetate, ΔG sharply rises due to repulsion among the acetates. For example, an increase of 30–50 kcal mol⁻¹ occurs as n_A increases from 2 to 3. However, the complex is stable (ΔG < 0) for all cations up to n_A = 4 (net charge −3). Beyond n_A = 4, the complex becomes unstable. For that reason, we did not study complexes in this range.

While the effect on ΔG of varying n_W for fixed n_A is relatively small compared to the acetate effect, the role of the number of binding waters is important in many systems and nonnegligible. As already noted, the complexes with the lowest ΔG include water. Water can bind to the cation, screen the carboxylate electrostatic interactions, and form hydrogen bonds. In Table 1, the ΔΔG between successive numbers of waters is a few kcal mol⁻¹. At other n_A, ΔΔG is larger, especially for adding the first water, but generally below −10 kcal mol⁻¹. At sufficiently large n_W, the decrease in ΔG saturates. As will be discussed below, the saturation occurs past the point where additional waters go into the second shell.

The energetics of transitioning from a minimum energy state is related to the free energy differences of the exchange between water and acetate ligands. The energetic strength of different exchanges can be seen specifically in the example of n = 5, where (2,3) is the minimum free energy complex. Moving in the vertical direction in Fig. 1, the neighboring state to (2,3) with the next-lowest ΔG is (1,4), which exchanges an acetate for a water. Above, with a higher ΔG, is the (3,2) state, which exchanges a water for an acetate. This preference for adding a water over an acetate is consistent, independent of the cation.

The ΔΔG between the (1,4) and (3,2) states are −18.3, −16.0, and −15.6 kcal mol⁻¹ for Li⁺, Na⁺, and K⁺, respectively. These values show that the free energy difference is not small for replacing an acetate with a water in going from (2,3) to (1,4) versus replacing a water with an acetate in going from (2,3) to (3,2). One reason that replacing a water with an acetate is relatively expensive is that the complex now has a net charge of −2. In contrast, the (1,4) complex is neutral.

This ordering repeats for all the cases studied for n ≥ 3, as the states (1,m) have lower ΔG than the states (3,m − 2). As n increases, the ΔΔG between the two states decreases because the complex becomes progressively more composed of water. This free energy difference is relevant for the exchange between water and acetate. The free energy results show that two acetates or two carboxylate binding groups are most favored. From this most favored complex, adding waters is favored over adding acetates. Exchanging acetates and waters from the low free energy states is expensive relative to k_BT, which implies that the acetate content of clusters formed in condensed systems will be stable.

Results of the benchmarking studies for the free energies of ion binding appear in the ESI† (Tables S2–S7) and support the chosen level of theory. In brief, we find small basis set superposition errors relative to the size of the free energy changes, and thus BSSE does not affect the observed dependencies or derived conclusions. Comparisons of enthalpy changes between DFT (ωB97X-D) and post-Hartree Fock ab initio methods (MP2, CCSD(T)) show good agreement for Li⁺ and Na⁺, while differences are larger for K⁺. At the same time, different combinations of DFT (ωB97X-D, B3LYP) and basis set (aug-cc-pvDz, aug-cc-pvTz, 6-311+G(2df,2pd)) for the K⁺ and single acetate complex provide enthalpy values in good agreement. An earlier study of adiabatic detachment energy for K⁺ in complex with sulfate by Wang and colleagues shows that DFT methods compare well with experimental data while post-Hartree Fock analyses are off by 5–7 kcal mol⁻¹.⁷⁰ In absence of direct experimental data on K⁺ and acetate for benchmarking purposes here, the results by Wang et al. support the use of DFT and suggest that post-Hartree Fock methods do not describe K⁺ sufficiently well for highly accurate calculations.

3.2 Ion transfer and Hofmeister series

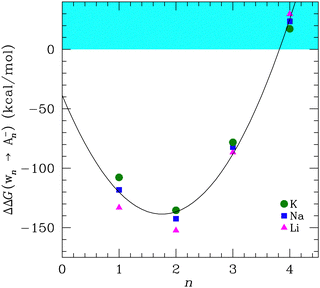
Previously, we addressed the ion partitioning from bulk water into the binding sites of ion channels by calculating the ion transfer free energies between water and acetate clusters, ΔΔG_W→An⁻.⁵⁰ The transfer free energy is the difference in free energies for ion solvation in an n-fold acetate cluster (denoted as A_n⁻) and ion hydration in a water solution (W). In our previous calculation, we used the experimental value for bulk ΔG_W.

Here, we calculate ΔG_Wn for water clusters of size n about each cation with the same basis and density functional. The transfer free energy can be calculated as a function of the cluster size, n,

ΔΔG_Wn→An⁻ = ΔG_An⁻ − ΔG_Wn. (3)

In Fig. 2 we plot ΔΔG_Wn→An⁻vs. n for each of the cations. The results are similar to our previous finding. The monovalent cations favor complexing with the carboxylate group in the acetate for n = 1–3, but favor hydration at n = 4. In the preferred binding site composition at n = 2, the ions are ordered by size: Li⁺ < Na⁺ < K⁺, which corresponds to the ligand field strength theory for lowest free energy compositions. However, away from the preferred composition at n = 4, the ordering reverses, yielding an inverse size order: K⁺ < Na⁺ < Li⁺.

Fig. 2 The change in free energy (ΔΔG) for ion transfer from water to acetate complexes (W_n → A_n⁻) in a low dielectric environment (ε = 1) as a function of the number (n) of ligands. The cyan region indicates transfer free energies that favor ion solvation in water (ΔΔG > 0), while the white region indicates favored ion solvation in n-coordinate acetate complexes (ΔΔG < 0).

3.3 Structure

To understand better the energetics, we now examine the structures of the optimized systems. Fig. 3 shows the optimized structures with the lowest ΔG that occur at n_A = 2 for n_W = 1–4. For most n_W the structures are similar across the different cations. The connectivity is mostly the same for the ionic bonds between carboxylate oxygen atoms and the cations, and for hydrogen bonds involving the water molecules. Naturally, the bond distances vary with cation, and other lengths or angles vary, too. The coordination of the cation is almost always 4-fold. This coordination matches the hydration coordination, and thus suggests possibilities of hydration mimicry, where the local carboxylate arrangement mimics the local ion hydration environment.¹⁷ One exception is the 3-fold coordinated (2,1) Li⁺ structure, which has both acetates monodentate and the water hydrogen bonding to each of the carboxylate oxygen atoms that are not bonded to Li⁺. In contrast, the Na⁺ and K⁺ 4-fold coordinated structures have one monodentate and one bidentate carboxylate, because the bond distance between the cation and the carboxylate oxygen is sufficiently large that the water molecule can only hydrogen bond to one of the free carboxylate oxygen atoms. Li⁺ is a special case because the Li:O bond distance is sufficiently short to allow the hydrogen bonding of a single water to each of the free carboxylate oxygen atoms. The other distinct case is for K⁺ at (2,4), where both of the acetates are bidentate, and for Na⁺ one of the acetates is bidentate. For all other cases with n_W ≥ 2, both acetates are monodentate.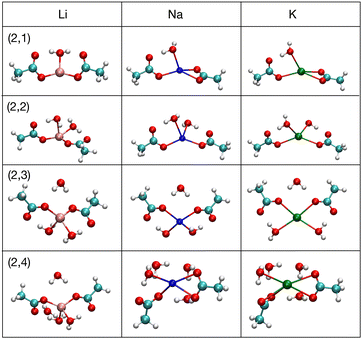

Fig. 3 Images⁷¹ of lowest free energy structures at (n_A,n_W) for n_W = 1–4 for Li⁺, Na⁺ and K⁺ at n_A = 2.

Another important aspect of Fig. 3 is the positioning of the waters with respect to first and second solvation shells. For n_W ≤ 2, the waters are in the first shell binding directly to the cation, while also possessing at least one hydrogen bond to a carboxylate O atom. At (2,3), one of the waters is in the second solvation shell of the ion and hydrogen bonds to the carboxylate O atoms that bind to the cation. Thus, the (2,2) complex has the lowest free energy, with ligands only in the first shell. In general for n_A > 0, as waters are added beyond n_W = 2, they go to the second shell and the ΔΔG decreases, becoming progressively small (about 1 kcal mol⁻¹). For all (n_A, n_W), the hydrogen bonding in the optimal structures is typically maximized and this pattern determines the positioning of the water molecules, especially beyond the first shell.

As noted above, the free energy increases strongly as n_A increases for fixed n_W. The structures as n_A increases possess these basic features: (1) all the acetates are in the first shell and monodentate binding to the cation, (2) most of the water hydrogens are hydrogen bonded to an oxygen, (3) the cations are 4-fold coordinated. The (2,2) complex (Fig. 3), which has the lowest free energy and without waters in the second shell, has already been discussed above and follows these features. Fig. 4 shows the (3,2) optimal structure for Na⁺ and (4,2) optimal structure for K⁺ which exhibit these characteristics. For both of these cases, the bonding connectivity is the same for all cations and the cations are 4-fold coordinated, with all the carboxylates being monodentate. In the (3,2) structure, a fourth O:cation bond is made by a water molecule. The two water molecules in this structure each form two hydrogen bonds to carboxylate O atoms. The (4,2) structure has a high level of symmetry. Each acetate shows a monodentate binding to the cation. The acetate C:C bond points alternately up and down, as one goes around the cation, to achieve a near tetrahedral structure. All the O atoms bonding to the cation in the (4,2) structure are carboxylate O atoms; all the waters are in the second shell. The two waters are on top and bottom, respectively, forming hydrogen bonds to the two binding O atoms of the acetates. This coordination has been seen previously and described as a 4+2 coordinated structure, indicating the 4-fold first shell oxygens and 2 additional second shell oxygens.^65,72–77

Fig. 4 Images of complexes with n_W = 2 (a) at n_A = 3 for Na⁺ and (b) at n_A = 4 for K⁺.

The net charge of the complex for (3,2) and (4,2) is −2 and −3, respectively. This net charge produces a strong, destabilizing repulsion, but the total ΔG remains negative for these n_A. The bond lengths increase by about 0.1 Å in going from (3,2) to (4,2). As noted above while discussing the ΔG plots, ΔΔG is increasing approximately quadratically in n_A. We find that by n_A = 5, the extrapolated ΔΔG is positive, indicating an unstable structure. This lack of stable arrangements is one of the reasons we did not attempt to treat n_A = 5.

In most cases that we studied, the carboxylates are monodentate, particularly for n_A > 2, because this arrangement allows all the acetates to be in the first shell. Once waters are also included, hydrogen bonding between waters and the carboxylate O atoms further stabilizes the monodentate structure. Overall, this structure is highly interconnected and maximizes the number of strong ionic and hydrogen bonds (see structures illustrated in Fig. S1–S9 in ESI†).

There are a few exceptions to the monodentate patterns, where bidentate binding is optimal. The optimal structure for the (2,5) mixtures has one bidentate carboxylate for all the cations. We note that, for Li⁺, there are two structures at (2,5) that have almost the same free energy (ΔG = 0.3 kcal mol⁻¹); one has a bidentate and a monodentate carboxylate and the other has both carboxylates monodentate. Structurally, the difference between these two cases is the location of one of the second shell waters (Fig. S3, ESI†). Not surprisingly, as long as the second shell water can H-bond to two first shell O atoms in both cases, the energy difference is small. At (2,4) the optimal K⁺ complex has both carboxylates bidentate, and the optimal Na⁺ complex has a single bidentate binding, but Li⁺ has only monodentate binding.

We note that we considered a variety of starting configurations, including bipyramidal structures found in studies of N-methylacetamide, which has carbonyls binding to the cations.⁴⁹ Attempts starting with a bipyramidal structure with Na⁺ for (3,3) are not stable and converge to the structure already determined (see Fig. S6, ESI†). While the bipyramidal structure can be setup to have the waters hydrogen bonding to the carboxylates in the optimal structure, the water positions move substantially to much better positions for hydrogen bonding. Probably the most important structural change is that one water moves to bind directly to the Na⁺, which breaks the bipyramidal symmetry of (n_A,n_W).

3.4 Charge and polarization

As noted in the Introduction, charge polarization is an important effect in these systems. To quantify this electrostatic effect, we calculated the ChelpG charges.⁷⁸ Averaging over all the complexes, the ChelpG charge magnitude for the oxygen atoms and the cations is 0.826 e (see Table 2). Thus, there is clearly a polarization that reduces the charge from the full electron charge. Furthermore, the variation about this average charge is about 0.5 e, which is rather large, indicating the individual charges depend on the values of n_A and n_W, and positioning of the atoms. (The full data sets are shown in Fig. S10–S12 and the files in the ESI.†) Such large variation indicates the importance of treating polarization explicitly in systems involving mixtures of carboxylates and water, and suggests more generally that systems with strong electrostatics need treatment of polarization.

Table 2 Average of ChelpG charges for cations and for carboxylate and water oxygen atoms in units of an electron charge

X	〈qOC〉	〈qOH〉	〈qX〉
Li	−0.815	−0.824	0.823
Na	−0.822	−0.835	0.869
K	−0.812	−0.803	0.835

---

In Fig. 5 for the optimal structures with n_A = 2, we plot the magnitude of the ChelpG charges |q| for the first shell O atoms, distinguishing between the carboxylate oxygens (OC) and the water oxygens (OH). Since n_A = 2, there are 4 carboxylate oxygen atoms in all these systems. For systems without water, there is only one value for the charge since the binding is bidentate, making both OC atoms equivalent electrostatically. Consequently, the variation in the OC charge is much smaller in this subset than in the full data set (see ESI†). At (2,2) the carboxylates are monodentate and one OC binds to water, yielding the two distinct values of q (see Fig. 3). Both of the two waters bind to a cation and to a nonbinding OC atom. The two charges occur because only one water has an O atom that H-bonds to the other water. At (2,4) there are two charge values for Li⁺, but only one for Na⁺ and K⁺, because the latter two have bidentate bindings and only one OH binding to the cation. We plotted data for both (2,5) Li⁺ complexes, which have effectively identical ΔG and both of these structures would occur in a thermal system. Plotting both cases shows a larger variation of charge for Li⁺ than the other cations, and it directly shows that the charges depend significantly on the structure. Two somewhat similar, but different, Li⁺ structures yield different charges due to the structural differences. In general, differences in the binding geometry lead to differences in the ChelpG charges.

Fig. 5 ChelpG charges for n_A = 2 for carbonyl oxygen (OC) and water oxygen (OH) as a function of n_W for Li, Na and K. Only data for first shell oxygen atoms are shown. The Li (2,5) complex has two data sets since the free energy is almost identical for the two.

The average of the ChelpG charge magnitude being about 0.8 is interesting given that some molecular dynamics simulations of ionomer systems have found that scaling the charges to 0.8, yields better results than using full +e charge for cations.^79,80 This value is also close to a simplified treatment of polarization in molecular dynamics simulations, the molecular dynamics in electronic continuum method.^81,82 Our DFT results suggest using such scaled charges is an improvement on average over the unscaled charges. For systems without water, such scaling is more likely to be successful, as they may have only a few ionic local environments. An example is the scaling of carbonate solvent charge by 0.8 to produce accurate lithium ion solvation and diffusion properties with molecular dynamics simulations.⁸³ However, especially in the presence of water, there is substantial variation in the ChelpG charges and the value of the scaled charge is only approximately equal to the average ChelpG charge. This variation is probably related to the limited success of using scaled charges in these ionomer systems. For example, while full charges can yield dynamics that is too slow, scaled charges can yield dynamics that is too fast.⁸⁴ In addition, the distances between cation and anion can be shifted.⁸⁵ Simulation of sulfonated ionomers also yielded mixed results for using scaled charges.^79,86

3.5 Effect of cation:oxygen bond lengths and hydrogen bonding in water complexes

While the focus of this article is on mixtures, pure water systems with n_W ≥ 5 are important points on the free energy plots in Fig. 1. Systems with 5 or more waters (and no acetates) possess some interesting structures, especially with respect to comparison among the three cations studied. The structures for 1 to 4 waters about a cation are the same coordination and basic structure among all the cations, with the main geometric difference being just the different O:X⁺ distances. For these systems, there is nothing substantial to add to the many DFT studies of ion hydration.^{35,65,72–74,76,77,87–93} The coordination numbers for Na⁺ and K⁺ at large n_W have been discussed previously.^6,17,57,94 Here we focus on comparisons of the geometry and the role of hydrogen bonding. We note that these gas phase structures are rarely observed in aqueous solution at room temperature due to large thermal fluctuations and surrounding solvent, and are presented for a full characterization of the structures in Fig. 1.¹⁷

In the systems with 5 or more waters, the role of hydrogen bonding is often different among the different cations. This difference is mainly due to the effect of the differing cation:oxygen bond lengths putting constraints on the potential hydrogen bond geometry. On the one hand, the shorter and stronger bonds for Li⁺ limit the geometry for hydrogen bonding among the ligating waters the most and results in structures that differ from Na⁺ and K⁺. On the other hand, K⁺, with the largest bonding length, can incorporate all the waters at least up to 8 in the first shell. In general, the hydrogen bonding among the waters is present and stronger than the thermal energy, but the angular orientation is on the weak side of the energy distribution. To keep the H atoms away from the cation requires the orientation of the hydrogen bonds to have large angles formed by the HO bond in one water and the O atoms of another (HO–O angle). In addition, because of the many possible arrangements of waters and their hydrogen bonding, there are multiple configurations, which can have only small free energy differences (∼1 kcal mol⁻¹) due to the weak hydrogen bonding,

At 5 waters, the role of H-bonding among the waters leads to a different distribution for Li⁺ (Fig. 6). In the Li⁺ structure, four of the waters are coplanar, with the fifth water having a bond perpendicular to this plane. There is no H-bonding among the coplanar waters, even though some of the O atoms are close enough for H-bonding. The O atoms of the 4 waters form a rectangle with side lengths 2.76 Å and 3.08 Å. The shorter length is appropriate for H-bonding, but the HO–O angle is 60 degrees, which is too large for an H-bond. The small HO–O angle necessary for a H-bond would bring the positively charged H atom close to the Li⁺ atom, which is unfavorable and consequently does not occur in the optimal structure.

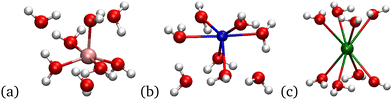
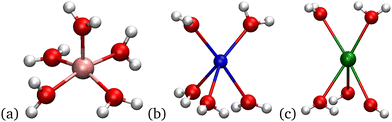Fig. 6 From (a)–(c), are images of the Li⁺, Na⁺, and K⁺ systems with 5 waters. Only bonds between O and each cation are shown.

In contrast, the Na⁺ and K⁺ at n_W = 5 have all the waters in the first shell in a two-layer structure consisting of three waters in one layer below the cation and two waters in a layer above, as shown in Fig. 6. In the three water layer, the O:O separations are suitable for H-bonding, even though the HO–O angles are large. For Na⁺, one of the O:O separations among the 3 waters in the bottom layer is 2.76 Å and the other two are 2.80 Å. The HO–O angles are 40 to 44°. For K⁺, the O:O separations among the 3 waters in the bottom layer are 2.77 Å, and the HO–O angles are 34–35°. The smaller angle is possible because the larger O:K⁺ distance allows the H atom to rotate more before the repulsion of the K⁺ precludes further rotation. Calculations of the H-bond energy as a function of the HO–O angle have been done using MP2 with aug-cc-pVTZ basis functions.⁹⁵ While the optimal angle is near 0°, 40° is within the attractive well with a depth of 1–2 kcal mol⁻¹. Thus, H-bonding along with van der Waals attraction is resulting in close clustering of the waters in the Na⁺ and K⁺ cases. In Li⁺, the short O:Li⁺ binding distance prevents H-bonding from occurring.

In the 6 water structures (Fig. 7), the two-layer geometry is again present for Na⁺ and K⁺, now with both layers having 3 waters that H-bond amongst themselves. The O:O separations in the layers are 2.76 Å and 2.77 Å for K⁺ and Na⁺, respectively. The HO–O angles are similar to that found for 5 waters. In K⁺ the HO–O angle is 33–34°, and the angles for Na⁺ are larger, at 41°. At these angles, there is H-bonding, albeit weak, but this interaction along with the van der Waals interactions makes this structure preferred over, for example, an octahedral structure.

Fig. 7 Images of the 6 water systems showing that (a) Li⁺ has a distinct distorted octahedral structure, while (b) Na⁺ and (c) K⁺ also have 6-fold coordination, but with two layers containing 3 waters each that H bond together.

The Li⁺ structure shown in Fig. 7 is slightly distorted from an octahedral structure, with 6 O:O separations that are 2.72 Å and the HO–O angles in the range 41–44°. The image shows a viewing orientation with a hexagonal projection of the O atoms. While the HO–O angles are large, there is a weak H-bonding between each of these O pairs that stabilizes the distorted octahedral structure over the ideal octahedral structure. Another optimized structure (see Fig. S2, ESI†) was found that has 4 waters in the first shell and two in the second shell. The second shell waters are positioned for 3 hydrogen bonds with first shell waters to be possible. The OH–H angles are smaller than the 6+0 structure, varying between 20 and 34. The enthalpy of the 4 + 2 structure is lower by 1.3 kcal mol⁻¹, but the 6+0 free energy is lower by 0.85 kcal mol⁻¹. These two structures show that, with this many waters, there are multiple configurations that are close in energy and would coexist thermally.

At 7 waters (Fig. 8), none of the three structures are similar. Li⁺ is four-fold coordinated in the first shell, with 3 waters in the second shell. Having 3 waters in the second shell enables several hydrogen bonds between these waters and first shell waters. The 6+1 structure is unstable and converges to the 4+3 structure, showing that the 4-fold first shell with hydrogen bonding among the second shell waters lowers the free energy relative to the 6+1 structure, which is stable for Na⁺.

Fig. 8 Images of the 7 water systems. (a) Li⁺ has a 4+3 structure. (b) Na⁺ has a 6+1 structure and (c) Only K⁺ has all waters in the first shell.

The optimal Na⁺ structure, a 6+1 structure, can be viewed as two nonparallel layers with 4 waters in one layer and 3 in the other layer. There is one hydrogen bond between the layers that leads to the nonparallel geometry. The O:Na⁺ bond lengths vary from 2.30 Å to 2.61 Å, which is rather large, but compensated by the hydrogen bonding among the waters. In the 4 water layer, r_OO ranges between 2.69 and 2.73 Å. The HO–O angles are 18, 19, 25 and 30°. Thus, stronger hydrogen bonding going around the sides of the quadrilateral result for this layer than in the 6 water structure.

The K⁺ structure is distinct by having all 7 waters in the first shell in a parallel two layer structure with 4 waters in one layer and 3 in the other. The r_OO is 2.70 Å in the layer with 4 waters and 2.75 Å in the 3 water layer. The HO–O angles in the 4 water layer are 21°, which is much smaller than in the 6 water structure. In the 3 water layer, the angles are larger, at 33°. Again, the longer O:K⁺ separation allows for more and stronger H-bonding among the waters in the K⁺ than in either Na⁺ or Li⁺. It is not surprising that when altering the K⁺ structure for Na⁺ with shorter O:Na⁺ bond length, the 3 water layer is not found to be optimal. The more compact Na⁺ structure would require larger HO–O angles and thus very weak hydrogen bonds. Therefore, a different structure arises in the optimization.

At 8 waters, the structures are distinct for each cation, as shown in Fig. 9. The Li⁺ optimal structure is a 5+3 structure. Compared to the 7 water 4+3 structure, adding a water increases the number of first shell waters. In the Na⁺ structure, there are 6 waters bound to the Na⁺ atom even though the O:Na⁺ separation varies by 0.36 Å. The first shell O with the largest separation of 2.69 Å is at the top back in Fig. 9, and the O with the shortest separation of 2.33 Å is at the top front. Two waters (left and right front in figure) are in the second shell and each hydrogen bonds to two waters directly bonded to Na⁺. The K⁺ optimal structure has all the waters in the first shell composed of two layers of 4 waters each, which are bonded to the K⁺, with separation of 2.93 Å. Within each layer, the waters are hydrogen bonded, with r_OO = 2.70 Å, and the HO–O angle is 21° going around the 4 waters. We note that an optimization was performed on the Na⁺ system starting from the K⁺ structure, but with the corresponding O:Na⁺ separation. This structure was not optimal and instead converged to the 6+2 structure. This result again shows that the shorter O:Na⁺ bond length requires water positions that keep the H atoms further away than in the K⁺ structures.

Fig. 9 Images of the 8 water systems. (a) Li⁺ is a 5+3 structure. (b) Na⁺ is a 6+2 structure. (c) K⁺ is an 8+0 structure.

4 Discussion

The most optimal binding of just carboxylates to a cation is strong for each of the cations (−154 to −198 kcal mol⁻¹). The lowest free energy complexes that include water also have strong binding, with free energies between −157 to −210 kcal mol⁻¹. Such strong binding implies that these optimal structures will be stable in condensed states. With respect to changing the state from one complex to another, there is a preference for exchanging an acetate for a water over the opposite exchange of water for an acetate. The barrier for this exchange is large relative to k_BT, which implies that thermal exchange will not occur readily. In particular, the barrier of going from the most optimal (2,2) complex to the (1,3) complex is about 28 kcal mol⁻¹ for each of the cations. This high barrier implies that the local, first shell structure will be rather stable and exchanges with other local structures will be slow. Consequently, if these optimal structures can form, ion transport will be slow in the presence of water as well. In order to have fast transport, constraints on the structure must exist that prevent the optimal structures from forming.⁵⁰

We have not addressed in this article the binding of multiple cations, which could alter the free energy space of complexes. Previously, in our study of two cations binding to acetates, we found that the two-cation complexes are more energetically favored over two single-cation complexes.⁵¹ It would not be surprising to find the same result for complexes including water, which would alter the free energy landscape. The barrier to transport from optimal structures would still be large for multi-cation complexes.

Condensed systems of interest, such as ionomers,³⁷ have constraints on the available conformation from the polymer structure. The same is true for ion channels, which have constraints from the protein matrix on the available conformations.⁵⁸ These constraints inhibit some optimal structures and shift the attainable lowest-energy structure to a different part of the free energy diagram, which would not be as strongly bound.⁵⁷ There remains much to be done to connect the quantum level binding to the transport dynamics in ionomers, for example, but the present results do have important implications. As stated above, to obtain fast transport, the system needs constraints to intrinsically prevent formation of the strongly bound states. Alternatively, other ligands could be used.^37,79

As found in binding just to acetate ligands, the binding strength has the order Li⁺ > Na⁺ > K⁺, which corresponds to the cation size and the bond lengths. The shorter bond lengths of Li⁺ yield some structures distinct from the other cations by enabling shorter distances that are viable for water to hydrogen bond, particularly to carboxylate O atoms. In solution, the experimental data on binding strength order is not clear and may depend on other factors. One measurement by X-ray adsorption spectroscopy on the carbon K-edge in 2 M acetate solutions found the same order and a notably strong Li⁺ binding.⁹⁶ Another X-ray adsorption measurement on oxygen K-edge in 1 M solutions switches the order of Li⁺ and Na⁺.⁹⁷ One potential explanation for the contradictory results is the dependence on protonation states.^98,99 Our work does not treat varying protonation as this would increase the number of possible structures beyond what is manageable.

Previous DFT calculations were performed for a single sodium and acetate binding to a range of water molecules.⁴⁸ That work used the long-range corrected hybrid functional LC-ωPBE and the Pople 6-311++G(d,p) basis set. They found multiple structures near in energy to the optimal structure, which we also find. Our optimal structures agree with one exception. For Na⁺ (1,2), our calculations give a different structure, which has a lower free energy, but higher enthalpy. The differences are less than 1 kcal mol⁻¹ and thus the results are within the uncertainty of the calculations. We also note that the K⁺ (1,2) structure is different from the corresponding Na⁺ structure of Zhang et al., which is due to the stronger H-bonds possible for the K⁺ structure (see Fig. S7, ESI†). Our results are also in agreement with DFT calculations of Tafilpolsky and Schmid for sodium acetate with multiple waters using B3LYP and aug-cc-pVDZ basis set.⁴⁷

For the calculation of the ΔG vs. n plot, we performed calculations for water only binding to the cation up to n_W = 8. As noted earlier, there is nothing new for n_W ≤ 5. For n_W = 6 to 8, we started calculations with all the waters in the first shell and the waters remained in the first shell for the converged structures. We did only limited investigation of other structural options. Our focus here is on hydrogen bonding structure among the waters, which we find to be significant in determining the overall structure. Hydrogen bonding among the waters occurs, but tends to be weak because the angles are rather large. In a liquid state, reasonable expectations include variation in the positioning of some waters that varies the H-bond strength and variation in the number of first shell waters.^72–74

Recent experiments and ab initio MD simulations of Na⁺ hydration have found some significant differences.¹⁰⁰ The O–Na⁺ bond distance is 2.38 Å from experiment, but calculations yield distances of 0.1 Å larger, which is similar to our gas phase calculations. This experimental coordination number is 5.5, while the calculated value was about 6.0 when dispersion was included. These results led to more advanced DFT calculations using the SCAN functional for Na⁺ and K⁺ hydration.⁹¹ The SCAN functional accurately reproduces the structural properties of water around Na⁺ and K⁺.

Our calculations find the free energy for Na⁺ binding to waters only in gas phase is rather flat near n_W = 6, which suggests a coordination number above 5. However, we have not considered starting geometries with 2nd shell waters and cannot make a judgement on the coordination number. We can only say there are low energy states with high coordination number.

Our DFT calculations of the combined carboxylate and water binding to the monovalent cations provides the basis for further analysis of ion channels, such as the pentameric ligand-gated and sodium voltage-gated ion channels, which have carboxylate-containing glutamates lining the pore and being a key element of the channel's selectivity. Our calculations provide the preferred binding structures without constraints and the associated binding energies. In the ion channel, the carboxylates have constrained positioning due to being part of the folded protein structure.⁵⁰ Further studies are required to address those constraints directly and calculate the corresponding free energies. However, the present calculations do provide new information and additional insight into the structure and energetics involved in ion channels such as the pLGICs and Na_v.

Cymes and Grosman studied the link between amino acid sequence and charge selectivity in the pLGICs.³² They specifically concluded that the glutamate ring dominates the permeation free-energy landscape of the wild-type cation-selective pLGIC. Not only did they provide evidence for the critical role of charged side-chains, but also proposed that a proper conformation of the side-chain is required for charge selectivity.

In the crystal structure of pLGIC (PDB ID 4HFI) by Sauguet et al., Na⁺ sits between two layers of 5 O atoms.²⁹ One layer is composed of water molecules; the other layer is composed of the threonine hydroxyl O atoms. In the X-ray structure, the Glu ring is next along the channel pore to the Thr ring. The Thr pentagon diagonal length between hydroxyl O atoms is 8.1 Å, which is narrower than the Glu pentagon diagonal at about 12 Å. There is space for the Glu side chains to change conformation such that the carboxylates are closer to the pore center, and a variety of binding options are available to Na⁺ or K⁺. In fact, the Glu side chains have to change conformations to bind to a cation in the channel. These shifted positions would enable direct binding by Na⁺ to one or more carboxylates. Since the Glu are in a ring about the pore center, the binding geometry will be somewhat planar, in contrast to the unconstrained optimal geometry of our calculations. Additional binding by water molecules, as in the two-layer structure of the X-ray structure, is geometrically possible and favored by the DFT free energy.

The crystal structure of the sodium voltage gated ion channel in the open state also shows the pore size at the selectivity filter is sufficiently large to allow the Glu side chains to move among multiple conformations.^26,101,102 Microsecond atomistic simulations of the voltage-gated sodium ion channel have found the flexibility of the Glu are important features of the selectivity filter and multiple Na⁺ are present in the channel simultaneously.¹⁰³ Protonation of the Glu residues plays a role as well. The simulations find that conduction occurs with either zero or one protonation of the Glu residues in the selectivity filter.

Our DFT calculations imply that the lowest free energy structures are not relevant for the ion channel dynamics, and, given the pore structure, binding to more than the preferred number of carboxylates under constraints are a key to the dynamics. From Fig. 1, the value of ΔG varies strongly on the one hand for sequence (n_A,0), with a minimum at two acetates or carboxylates, and on the other hand, is smallest for 4 carboxylates for all the cations. Either Na⁺ or K⁺ bound to two carboxylates in the optimal structure would be strongly bound and yield poor permeation. In contrast, if the cation is bound to all 4 carboxylates in the Na_v channel, then the binding is not so strong. For the optimized structures we have for Na⁺, ΔG = −20.2 kcal mol⁻¹ and for K⁺, ΔG = − 11.6 kcal mol⁻¹. Moreover, the optimized structure has tetrahedral geometry, which is not possible for the ring of glutamates. The constrained structures would have an even lower binding energy, which would be more conducive to permeation. Calculations of such a constrained structure are to be done and might distinguish between Na⁺ and K⁺ binding and permeation. We also note that the MD simulations found multiple Na⁺ in the channel and we have found that calculations with two cations yield stronger binding for two-ion complexes than for two separate single-cation complexes.⁵¹ Our results suggest that a more complicated ionic complex is involved in the selectivity filter, which depends on the multiple cations and multiple conformations.

5 Conclusion

Using DFT, we investigated the binding of mixtures of a carboxylate ligand, acetate, and water molecules to monovalent cations Li⁺, Na⁺ and K⁺. In many synthetic and biological systems, carboxylate binding to cations is a key component and water plays an additional important role. By performing DFT calculations, we obtained an accurate calculation of the strong electrostatic interactions that determine the overall energetics, the geometry of the complex and the charge distribution. We found both common features among the different cations and a few distinct features in particular cases.

The binding strength takes the following order: Li⁺ > Na⁺ > K⁺, which is the same as that for binding to only acetate ligands.⁵⁰ We found that all the acetates are in the first shell and organize in mostly monodentate binding to the cation. The lowest free energy complexes have two acetates and the lowest free energy complex with all molecules in the first shell is two acetates with two waters, forming a 4-fold coordinated structure. In general, the positions of the water molecules in the optimal structures maximizes the number of hydrogen bonds. The monodentate binding enables more hydrogen bonds. The cations are typically 4-fold coordinated, when there are acetates in the mixture. Evaluation of the ChelpG charges shows that the charge on the cations and the O atoms varies significantly among the different complexes. That is, the charge depends on the number of acetates and waters and the positioning of the molecules. The large binding strengths imply that constraints that prevent the optimal binding structures from forming are key for many systems that transport ions, including ion channels and single ion conductors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was performed, in part, at the Center for Integrated Nanotechnologies, an Office of Science User Facility operated for the U.S. Department of Energy (DOE) Office of Science. Sandia National Laboratories is a multimission laboratory managed and operated by National Technology & Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International, Inc., for the U.S. DOE's National Nuclear Security Administration under contract DE-NA-0003525. We gratefully thank Sandia's Laboratory-Directed Research and Development program for funding. The views expressed in the article do not necessarily represent the views of the U.S. DOE or the United States Government.

Notes and references

1. O. S. Andersen, J. Gen. Phys., 2011, 137, 393–395.
2. P. Lo Nostro and B. W. Ninham, Chem. Rev., 2012, 112, 2286–2322.
3. P. Jungwirth and P. S. Cremer, Nat. Chem., 2014, 6, 261–263.
4. Z. Li, O. Borodin, G. D. Smith and D. Bedrov, J. Phys. Chem. B, 2015, 119, 3085–3096.
5. D. J. Siegel, L. Nazar, Y.-M. Chiang, C. Fang and N. P. Balsara, Trends Chem., 2021, 3, 807–818.
6. S. Varma and S. B. Rempe, Biophys. J., 2007, 93, 1093–1099.
7. S. Mogurampelly, O. Borodin and V. Ganesan, Ann. Rev. Chem. Biomol. Eng., 2016, 7, 349–371.
8. V. Bocharova and A. P. Sokolov, Macromol., 2020, 53, 4141–4157.
9. R. T. Cygan, C. J. Brinker, M. D. Nyman, K. Leung and S. B. Rempe, MRS Bull., 2008, 33, 42–47.
10. M. Elimelech and W. A. Phillip, Science, 2011, 333, 712–717.
11. B. Hille, Ionic Channels of Excitable Membranes, Sinauer Associates: Sunderland, MA, 3rd edn, 2001.
12. E. Gouaux and R. MacKinnon, Science, 2005, 310, 1461.
13. B. Roux, Essays Biochem., 2017, 61, 201–209.
14. D. M. Rogers, D. Jiao, L. Pratt and S. Rempe, Ann. Rep. Comput. Chem., 2012, 8, 71.
15. T. Dudev and C. Lim, Chem. Rev., 2014, 114, 538–556.
16. T. T. Duignan, M. D. Baer and C. J. Mundy, Curr. Opin. Colloid Interface Sci., 2016, 23, 58–65.
17. M. I. Chaudhari, J. M. Vanegas, L. Pratt, A. Muralidharan and S. B. Rempe, Ann. Rev. Phys. Chem., 2020, 71, 461–484.
18. J. P. Glusker, Adv. Prot. Chem., 1991, 42, 1–76.
19. S. R. Sandler and W. Karo, Polymer Synthesis, Elsevier Inc., 2nd edn, 1996.
20. T. Baughman, C. Chan, K. Winey and K. Wagener, Macromolecules, 2007, 40, 6564–6571.
21. J. M. D. Lane, M. Chandross, M. J. Stevens and G. S. Grest, Langmuir, 2008, 24, 5209–5212.
22. E. A. Meulenkamp, J. Phys. Chem. B, 1998, 102, 5566–5572.
23. N. Dharmaraj, P. Prabu, S. Nagarajan, C. Kim, J. Park and H. Kim, Mater. Sci. Eng., B, 2006, 128, 111–114.
24. A. M. Pourrahimi, D. Liu, L. K. H. Pallon, R. L. Andersson, A. M. Abad, J.-M. Lagarón, M. S. Hedenqvist, V. Ström, U. W. Gedde and R. T. Olsson, RSC Adv., 2014, 4, 35568–35577.
25. B. J. Kim and G. Boschloo, Nanoscale, 2021, 13, 11478–11487.
26. J. Payandeh, T. Scheuer, N. Zheng and W. A. Catterall, Nature, 2011, 475, 353–358.
27. T. Dudev and C. Lim, Phys. Chem. Chem. Phys., 2012, 12451–12456.
28. E. Flood, C. Boiteux and T. W. Allen, PLoS Comput. Biol., 2018, 14, 1–32.
29. L. Sauguet, F. Poitevin, S. Murail, C. Van Renterghem, G. Moraga-Cid, L. Malherbe, A. W. Thompson, P. Koehl, P.-J. Corringer, M. Baaden and M. Delarue, EMBO J., 2013, 32, 728–741.
30. H. Hu, R. J. Howard, U. Bastolla, E. Lindahl and M. Delarue, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 13437–13446.
31. R. J. Howard, J. Mol. Biol., 2021, 433, 167128.
32. G. D. Cymes and C. Grosman, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E7106–E7115.
33. T. J. Harpole and C. Grosman, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E3196–E3205.
34. D. M. Rogers and S. B. Rempe, J. Phys. Chem. B, 2011, 115, 9116–9129.
35. M. I. Chaudhari and S. B. Rempe, J. Chem. Phys., 2018, 148, 222831.
36. Z. Jing, J. A. Rackers, L. R. Pratt, C. Liu, S. B. Rempe and P. Ren, Chem. Sci., 2021, 12, 8920–8930.
37. H. Zhang, C. Li, M. Piszcz, E. Coya, T. Rojo, L. M. Rodriguez-Martinez, M. Armand and Z. Zhou, Chem. Soc. Rev., 2017, 46, 797–815.
38. E. Strauss, S. Menkin and D. Golodnitsky, J. Solid State Electrochem., 2017, 21, 1879–1905.
39. J. Park, A. Staiger, S. Mecking and K. I. Winey, Macromolecules, 2021, 54, 4269–4279.
40. M. Seitz, C. Chan, K. Opper, T. Baughman, K. Wagener and K. Winey, J. Am. Chem. Soc., 2010, 132, 8165–8174.
41. D. S. Bolintineanu, M. J. Stevens and A. Frischknecht, Macromol., 2013, 46, 5381.
42. E. B. Trigg, M. J. Stevens and K. I. Winey, J. Am. Chem. Soc., 2017, 139, 3747–3755.
43. L. Yan, M. Häußler, J. Bauer, S. Mecking and K. I. Winey, Macromol., 2019, 52, 4949–4956.
44. E. Trigg, T. W. Gaines, M. Maréchal, D. E. Moeda, P. Rannou, K. B. Wagener, M. J. Stevens and K. I. Winey, Nat. Mater., 2018, 17, 725–731.
45. A. Y. Mehandzhiyski, E. Riccardi, T. S. van Erp, H. Koch, P.-O. Åstrand, T. T. Trinh and B. A. Grimes, J. Phys. Chem. A, 2015, 119, 10195–10203.
46. X.-B. Wang, B. Jagoda-Cwiklik, C. Chi, X.-P. Xing, M. Zhou, P. Jungwirth and L.-S. Wang, Chem. Phys. Lett., 2009, 477, 41–44.
47. M. Tafipolsky and R. Schmid, J. Chem. Theory Comput., 2009, 5, 2822–2834.
48. W.-J. Zhang, G.-L. Hou, P. Wang, H.-G. Xu, G. Feng, X.-L. Xu and W.-J. Zheng, J. Chem. Phys., 2015, 143, 054302.
49. T. Dudev and C. Lim, J. Phys. Chem. B, 2012, 116, 10703–10714.
50. M. J. Stevens and S. L. B. Rempe, J. Phys. Chem. B, 2016, 120, 12519–12530.
51. M. J. Stevens and S. L. B. Rempe, Phys. Chem. Chem. Phys., 2022, 24, 22198–22205.
52. G. Eisenman and R. Horn, J. Membr. Biol., 1983, 76, 197–225.
53. K. Collins, Biophys. J., 1997, 72, 65–76.
54. J. Kherb, S. C. Flores and P. S. Cremer, J. Phys. Chem. B, 2012, 116, 7389–7397.
55. B. Hess and N. F. A. van der Vegt, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 13296–13300.
56. S. Varma, D. Sabo and S. B. Rempe, J. Mol. Biol., 2008, 376, 13–22.
57. S. Varma and S. B. Rempe, J. Am. Chem. Soc., 2008, 130, 15405–15419.
58. S. Varma, D. M. Rogers, L. R. Pratt and S. B. Rempe, J. Gen. Phys., 2011, 137, 479–488.
59. L. R. Pratt and S. B. Rempe, in Quasi-Chemical Theory and Solvent Models for Simulations, ed. G. Hummer and L. R. Pratt, AIP Conf. Proc., 1999, vol. 492, pp. 172–201.
60. T. L. Beck, M. E. Paulaitis and L. R. Pratt, The Potential Distribution Theorem and Models of Molecular Solutions, Cambridge University Press, 2006.
61. D. Asthagiri, P. D. Dixit, S. Merchant, M. E. Paulaitis, L. R. Pratt, S. B. Rempe and S. Varma, Chem. Phys. Lett., 2010, 485, 1–7.
62. M. I. Chaudhari, L. R. Pratt and S. B. Rempe, Mol. Sim., 2018, 44, 110–116.
63. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian-16 Revision C.01, Gaussian Inc., Wallingford CT, 2016.
64. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
65. M. Soniat, D. M. Rogers and S. B. Rempe, J. Chem. Theory Comput., 2015, 2958–2967.
66. Z. L. Seeger and E. I. Izgorodina, J. Chem. Theory Comput., 2020, 16, 6735–6753.
67. K. A. Peterson and T. H. Dunning, J. Chem. Phys., 2002, 117, 10548.
68. J. G. Hill and K. A. Peterson, J. Chem. Phys., 2017, 147, 244106.
69. S. B. Rempe and H. Jónsson, Chem. Educ., 1998, 3, 1–17.
70. X.-B. Wang, C.-F. Ding, J. B. Nicholas, D. A. Dixon and L.-S. Wang, J. Phys. Chem. A, 1999, 103, 3423–3429.
71. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
72. S. Rempe, L. Pratt, G. Hummer, J. Kress, R. L. Martin and A. Redondo, J. Am. Chem. Soc., 2000, 122, 966–967.
73. S. B. Rempe and L. R. Pratt, Fl. Phase Eq., 2001, 183, 121–132.
74. S. B. Rempe, D. Asthagiri and L. R. Pratt, Phys. Chem. Chem. Phys., 2004, 6, 1966.
75. T. M. Alam, D. Hart and S. L. B. Rempe, Phys. Chem. Chem. Phys., 2011, 13, 13629–13637.
76. D. Sabo, D. Jiao, S. Varma, L. R. Pratt and S. B. Rempe, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2013, 109, 266–278.
77. M. I. Chaudhari, M. Soniat and S. B. Rempe, J. Phys. Chem. B, 2015, 119, 8746–8753.
78. L. E. Chirlian and M. M. Francl, J. Comput. Chem., 1987, 8, 894–905.
79. B. Paren, B. Thurston, A. Kanthawar, W. Neary, A. Kendrick, M. Marechal, J. Kennemur, M. J. Stevens, A. Frischknecht and K. Winey, Chem. Mater., 2021, 33, 6041–6051.
80. J. R. Keith and V. Ganesan, J. Chem. Phys., 2019, 151, 124902.
81. I. V. Leontyev, M. V. Vener, I. V. Rostov, M. V. Basilevsky and M. D. Newton, J. Chem. Phys., 2003, 119, 8024–8037.
82. I. Leontyev and A. Stuchebrukhov, Phys. Chem. Chem. Phys., 2011, 13, 2613–2626.
83. M. Chaudhari, J. R. Nair, L. R. Pratt, F. A. Soto, P. B. Balbuena and S. B. Rempe, J. Chem. Theory Comput., 2016, 12, 5709–5718.
84. F. Müller-Plathe and W. F. van Gunsteren, J. Chem. Phys., 1995, 103, 4745–4756.
85. K.-J. Lin and J. Maranas, Macromol., 2012, 45, 6230–6240.
86. B. Paren, B. Thurston, W. Neary, A. Kendrick, J. Kennemur, M. J. Stevens, A. Frischknecht and K. Winey, Macromol., 2020, 53, 8960.
87. D. Asthagiri, L. R. Pratt, M. E. Paulaitis and S. B. Rempe, J. Am. Chem. Soc., 2004, 126, 1285–1289.
88. D. Jiao, K. Leung, S. B. Rempe and T. M. Nenoff, J. Chem. Theory Comput., 2011, 7, 485–495.
89. T. Whitfield, S. Varma, E. Harder, G. Lamoureux, S. B. S. B. Rempe and B. Roux, J. Chem. Theory Comput., 2007, 3, 2068–2082.
90. P. E. Mason, S. Ansell, G. Neilson and S. B. Rempe, J. Phys. Chem. B, 2015, 119, 2003–2009.
91. T. T. Duignan, G. K. Schenter, J. L. Fulton, T. Huthwelker, M. Balasubramanian, M. Galib, M. D. Baer, J. Wilhelm, J. Hutter, M. Del Ben, X. S. Zhao and C. J. Mundy, Phys. Chem. Chem. Phys., 2020, 22, 10641–10652.
92. A. Bankura, V. Carnevale and M. L. Klein, J. Chem. Phys., 2013, 138, 014501.
93. D. Gomez, L. R. Pratt, D. N. Asthagiri and S. B. Rempe, Acc. Chem. Res., 2022, 55, 2201–2212.
94. S. Varma and S. B. Rempe, Biophys. Chem., 2006, 124, 192–199.
95. J. Scott and J. Vanderkooi, Water, 2010, 2, 14–28.
96. J. S. Uejio, C. P. Schwartz, A. M. Duffin, W. S. Drisdell, R. C. Cohen and R. J. Saykally, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 6809–6812.
97. E. F. Aziz, N. Ottosson, S. Eisebitt, W. Eberhardt, B. Jagoda-Cwiklik, R. Vácha, P. Jungwirth and B. Winter, J. Phys. Chem. B, 2008, 112, 12567–12570.
98. N. Schwierz, D. Horinek and R. R. Netz, Langmuir, 2013, 29, 2602–2614.
99. A. Sthoer, J. Hladlková, M. Lund and E. Tyrode, Phys. Chem. Chem. Phys., 2019, 21, 11329–11344.
100. M. Galib, M. D. Baer, L. B. Skinner, C. J. Mundy, T. Huthwelker, G. K. Schenter, C. J. Benmore, N. Govind and J. L. Fulton, J. Chem. Phys., 2017, 146, 084504.
101. E. C. McCusker, C. Bagnéris, C. E. Naylor, A. R. Cole, N. D'Avanzo, C. G. Nichols and B. A. Wallace, Nat. Commun., 2012, 3, 1102.
102. M. J. Lenaeus, T. M. G. El-Din, C. Ing, K. Ramanadane, R. Pomès, N. Zheng and W. A. Catterall, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E3051–E3060.
103. C. Boiteux, I. Vorobyov and T. W. Allen, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 3454–3459.

---

Footnotes

† Electronic supplementary information (ESI) available: Images of additional geometries of optimal structures and figures of ChelpG charges are given. See DOI: https://doi.org/10.1039/d3cp04200f

‡ The purpose here is to simplify the plot and we will not here address the functional nature of the dependence.

---