Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Sulfur-deficient edges as active sites for hydrogen evolution on MoS2†
Sander Ø.
Hanslin
 ab,
Hannes
Jónsson
ab,
Hannes
Jónsson
 b and
Jaakko
Akola
b and
Jaakko
Akola
 *ac
*ac
aDepartment of Physics, Norwegian University of Science and Technology, No-7491, Trondheim, Norway. E-mail: jaakko.akola@ntnu.no
bScience Institute and Faculty of Physical Sciences, University of Iceland, IS-107 Reykjavík, Iceland
cComputational Physics Laboratory, Tampere University, FI-33101 Tampere, Finland
First published on 20th November 2023
Abstract
A grand-canonical approach is employed to calculate the voltage-dependent activation energy and estimate the kinetics of the hydrogen evolution reaction (HER) on intrinsic sites of MoS2, including edges of varying S-coverage as well as S-vacancies on the basal plane. Certain edge configurations are found to be vastly more active than others, namely S-deficient edges on the Mo-termination where, in the fully S-depleted case, HER can proceed with activation energy below 0.5 eV at an electrode potential of 0 V vs. SHE. There is a clear distinction between the performance of Mo-rich and S-rich adsorption sites, as HER at the latter sites is characterized by large (generally above 1.5 eV) Heyrovsky and Tafel energy barriers despite near-thermoneutral hydrogen adsorption energy. Thus, exposing Mo-atoms on the edges to which hydrogen can directly bind is crucial for efficient hydrogen evolution. While S-vacancies on the basal plane do expose Mo-rich sites, the energy barriers are still significant due to high coordination of the Mo atoms. Kinetic modelling based on the voltage-dependent reaction energetics gives a theoretical overpotential of 0.25 V and 1.09 V for the Mo-edge with no S atoms and the weakly sulfur-deficient (2% S-vacancies) basal plane, respectively, with Volmer–Heyrovsky being the dominant pathway. These values coincide well with reported experimentally measured values of the overpotential for the edges and basal plane. For the partly Mo-exposed edges, the calculated overpotential is 0.6–0.7 V while edges with only S-sites give overpotential exceeding that of the basal plane. These results show that the overpotential systematically decreases with increased sulfur-deficiency and reduced Mo-coordination. The fundamental difference between Mo- and S-rich sites suggests that catalyst design of transition metal dichalcogenides should be focused on facilitating and modifying the metal sites, rather than activating the chalcogen sites.
1 Introduction
Transition metal dichalcogenides such as MoS2 are emerging as interesting candidates for the purpose of replacing precious metals in electrocatalysts with more earth-abundant elements.1–4 MoS2 has been found to catalyze the hydrogen evolution reaction (HER) and the edges are understood to be more active than the basal plane.5–11 However, certain defect sites on the basal plane are also potentially of relevance, namely S-vacancies and doping-activated sites. In terms of the free energy of hydrogen adsorption, these sites fulfill the criterion that the adatom binding should be neither too strong nor too weak.12–16 However, such a thermodynamic criterion is only a necessary but not a sufficient one for efficient catalysis as there still can be significant activation energy for the reaction, i.e. high energy transition states need to be overcome. Theoretical work has shown that the molybdenum hydride configuration on MoS2 enables more rapid Heyrovsky combination than via sulfur–bound hydrogen,17 and that the Heyrovsky barrier for transition metal dichalcogenides is systematically increased with respect to that for pure metals when hydrogen is bound to chalcogen atoms.18 The increased barrier is attributed to the fact that the hydrogen adatoms are more positively charged than those bound to a metal surface, introducing repulsion with the solvated proton and thus hindering the combination involved in forming H2. Coinciding results were found on the doped MoS2 basal plane, where the Heyrovsky barriers are large despite the fact that doping enabled near-thermoneutral H atom adsorption.19 Therefore, sites predicted to be active by satisfying the simple adsorption free energy criterion may still not be responsible for the experimentally measured activity. Exposed Mo-rich sites may, in particular, be required to achieve significant catalytic activity. Experimentally, it has indeed been shown that sulfur-deficiency is associated with increased electrochemical current densities.12,13,20,21The objective of the present work is to estimate the activity of the various intrinsic sites in MoS2 and identify the possible HER reaction mechanisms. Our focus is on establishing how the activity depends on the S-coverage on the edges as well as the presence of S-vacancies on the basal plane. This is done by calculating the activation energy for the elementary steps involved in the hydrogen evolution reaction. The electrochemical nature of the reactions is accounted for by calculating the activation energy for the elementary steps at a specific electrode potential through a grand-canonial treatment, as well as by taking the presence of the electrolyte solution into account with a continuum description. This enables assessment and comparison of voltage-dependent energy barriers and kinetics.
2 Methods
Results were obtained using spin-polarized density-functional theory (DFT) calculations, employing the revised Perdew–Burke–Ernzerhof (RPBE)22 exchange–correlation functional plus van der Waals interactions estimated with D323 parameters and using the damping function form of Chai and Head-Gordon.24 Valence electrons are described with a plane wave basis set up to a kinetic energy of 400 eV. The effect of inner electrons is described by the projector augmented wave method as implemented in the Vienna ab initio simulation package (VASP).25The activation energy for elementary steps was calculated within harmonic transition state theory by finding saddle points on the potential energy surface, initially with the climbing-image nudged elastic band method26 and subsequently using minimum mode following27 for a given applied voltage in the grand canonical formulation. The maximum force criteria for geometry optimization were 0.02 eV Å−1 and 0.05 eV Å−1 for minima and saddle points, respectively. The reaction structures computed from neutral supercells are available on Zenodo.28
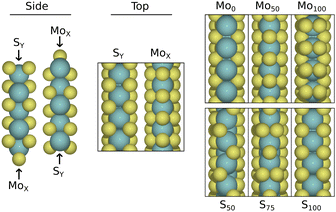
The edges were investigated using a slab model where alternating vertically aligned layers of 2H-MoS2 are periodically stacked. Each layer is terminated along the zig-zag direction, and will have Mo and S-terminations on opposite sides. These may further be filled with a certain S-coverage, as indicated in Fig. 1. We use configurations with S-coverages of 0%, 50%, 100% for the Mo-terminations, and 50%, 75%, 100% for the S-terminations. Below, these are referred to as Mox/Sx where x is the S-coverage as a percentage of that in the pristine stoichiometry. The periodically repeated supercell contains two 4 × 3 or 4 × 5 layers. This corresponds to 72 or 120 atoms in the stoichiometric case, and before considering the presence of hydrogen and water. For adsorption calculations and reaction modelling, the smaller model is used. Convergence testing with respect to the Heyrovsky barrier on the Mo0 edge showed variance of only 0.04 eV between slab systems with 3 and 7 layers (larger barrier in the latter). Similar change was seen in the reaction energy. Such deviation is deemed acceptable for the purpose of finding interesting configurations which display reasonably small energy barriers. This model represents the edge plane that may be exposed in MoS2 particles or films. Depending on the synthesis, however, MoS2 may take other forms in experiments. For example islands with one or a few layers would constitute a different regime, as the ratio of S/Mo-terminated edges is skewed, and the top layer is not subject to interaction from both sides.
The basal plane is modelled with a single 5 × 5 (75 atoms) MoS2 monolayer for investigating selected single and double S-vacancy configurations. These correspond to 2% and 4% sulfur-deficiency, respectively. In all cases a vacuum region of at least 9 Å is used to decouple periodic images in the vertical direction.
A grand canonical approach is used to obtain the voltage dependence of reaction and activation energy of each elementary step by varying the number of electrons in the supercell. The grand canonical energy is then computed in terms of the electrode potential U as  , where
, where 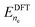 refers to the DFT energy obtained with ne electrons, and δne is the number of excess electrons with respect to the neutral case. U is given by the work function and referred to the standard hydrogen electrode ϕSHE = 4.43 V. For further details, we refer to previous works.19,29 The electrolyte is represented explicitly by an Eigen cation water cluster (H9O4+), and implicitly (outside the cluster) by a polarizable continuum model as implemented in VASPSol.30,31 It has been observed that the cutoff charge density nc must be reduced significantly from its default value of 0.0025 e Å−3 to ensure vanishing concentration of implicit counter-ions between MoS2 layers.32 Our benchmark simulations of the Mo0 edge and Pt(111) show that changing nc alters the description of the water–solid interface significantly (see Fig. S2, ESI†), and therefore, we proceed with the default value in this work. An asymmetric slab system is used and its point-symmetrization did not lead to significant changes in the grand-canonical energy, see Fig. S3 (ESI†). Lateral interaction between periodic images of the Eigen cation is negligible for the chosen supercell size, as seen in Fig. S4 (ESI†).
refers to the DFT energy obtained with ne electrons, and δne is the number of excess electrons with respect to the neutral case. U is given by the work function and referred to the standard hydrogen electrode ϕSHE = 4.43 V. For further details, we refer to previous works.19,29 The electrolyte is represented explicitly by an Eigen cation water cluster (H9O4+), and implicitly (outside the cluster) by a polarizable continuum model as implemented in VASPSol.30,31 It has been observed that the cutoff charge density nc must be reduced significantly from its default value of 0.0025 e Å−3 to ensure vanishing concentration of implicit counter-ions between MoS2 layers.32 Our benchmark simulations of the Mo0 edge and Pt(111) show that changing nc alters the description of the water–solid interface significantly (see Fig. S2, ESI†), and therefore, we proceed with the default value in this work. An asymmetric slab system is used and its point-symmetrization did not lead to significant changes in the grand-canonical energy, see Fig. S3 (ESI†). Lateral interaction between periodic images of the Eigen cation is negligible for the chosen supercell size, as seen in Fig. S4 (ESI†).
Based on the voltage-dependent reaction and activation energies, a kinetic model was used to estimate the reaction rates. The rate of a given elementary step was defined as
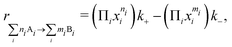 | (1) |
 | (2) |
 represents the forward (reverse) barrier. Dependence on the applied voltage is directly included in these grand-canonical energy barriers, so no assumption needs to be made about symmetry factors.
represents the forward (reverse) barrier. Dependence on the applied voltage is directly included in these grand-canonical energy barriers, so no assumption needs to be made about symmetry factors.
The elementary steps considered are the Volmer (H+ + e− → H*), Heyrovsky (H+ + e− + H* → H2) and Tafel (2H* → H2) steps, where the first supplies H* to the surface and the latter two compete towards H2 combination. Assuming concentrations of unity for dissolved species, the rates are rv = (1 − θ)kv+ − θkv−, rh = θkh+ − (1 − θ)kh−, rt = θ2kt+ − (1 − θ)2kt−, where θ now represents the hydrogen surface coverage. Further, the reverse Heyrovsky and Tafel steps are neglected, corresponding to the limit cH2 → 0. Considering the steady-state condition, the balance equation rv+ = rv− + rh+ + 2rt+ can be solved for θ. Finally, the current density due to the electrochemical steps is obtained as
| j = −e/A(rv+ − rv− + rh+), | (3) |
3 Edges and adsorption
The relative stability of edges with differing S-coverage will depend on the electrochemical conditions, and specifically on the effective chemical potential of S as well as stabilizing effects of the solvent species.33 As we consider acidic conditions, we perform first a brief study of the relative stabilities in a low pH environment. In this model, the free energy of a given configuration with a(b) S and x(y) H-atoms on the Mo (S)-terminus is defined as | (4) |
| ΔGai = Eijab − Ei−1,jab − μH+ + e− + ΔEzpe − TΔS | (5) |
| μS = μH2S − 2μH+ + e−. | (6) |
 | (7) |
 , where
, where 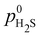 is the partial pressure under reference (standard) conditions.
is the partial pressure under reference (standard) conditions.
Using these equations we can construct a Pourbaix-like diagram for the edge configurations, though the DFT energies are not grand-canonical in this case. For the diagram, we consider acidic conditions (no OH− species) and neglect oxide formation as well as adsorption of H2O, i.e. we consider just the relative stability of various sulfur/hydrogen coverage configurations. Assuming a low partial pressure of H2S and using  , the resulting diagram is shown in Fig. 2.
, the resulting diagram is shown in Fig. 2.
As shown below, the sulfur-deficient edges and particularly Mo0 seem to be highly active for HER. The presence of this edge in the system is therefore of interest. For pH = 0, Fig. 2 indicates that this edge is only dominant at electrode potential below −0.5 V, which is a significant applied potential in the context of efficient hydrogen evolution. Assuming that the configurations follow a Boltzmann distribution, the fractional presence of Mo0 is not large at small applied potentials (roughly 5% at U = 0 V and 10% at U = −0.2 V). Though small, such fractions could yield significant evolution if the kinetics are superior. This diagram is meant to give a brief indication of the stability of different edges under relevant conditions, but experiment may differ in some ways. Importantly, as noted in ref. 33, the release of H2S from the surface is irreversible in the absence of a S-containing electrolyte. The desulfurisation is then kinetically determined by the required activation of the H2S-release, which if small enough would lead to a larger experimental presence of S-deficient configurations. Further, in alkaline conditions the edges are at risk of deactivation due to highly favorable OH-adsorption in absence of S.33 Such mechanisms may be relevant to a lesser degree for H2O-species under acidic conditions. We find that H-adsorbates are preferred over H2O on Mo0 below −0.2 V, see Fig. S1 (ESI†).
4 Reaction path
We consider the Volmer, Heyrovsky and Tafel steps to determine which reaction mechanism is likely to be dominant on the different edges. The Volmer step is always relevant, while the Heyrovsky and Tafel mechanisms compete in the H2 formation step.4.1 Potential of zero charge
The scaling relations obtained from neutral supercells are shown in Fig. 3, where we distinguish between occupation of the deep Mo-bound sites and the S-bound sites for the S50 edge, denoted as S50(Mo) and S50(S) from here on. Most systems follow a linear correlation between ΔE and E in agreement with the Brønsted–Evans–Polanyi principle, though with some exceptions. Considering first the Volmer step, most systems have moderate barriers, which are only somewhat higher than the reaction energy. Hence, the overall trend is truncated as the barriers reach 0 eV in exothermic cases. In the Heyrovsky case, however, the barriers are significantly larger than the corresponding reaction energies, but the overall trend is clearly linear. The notable exceptions to this are the Mo0 and S50(Mo) edges, where the Heyrovsky barriers are anomalously low. In these systems H binds directly to Mo, while hydrogen adsorption occurs onto sulfur atoms in the remaining systems. For the Tafel step, the overall picture is fairly similar, with S-bound hydrogen having relatively large barriers, while again Mo0 and S50(Mo) display lower barriers, much closer to the limits set by the reaction energy. Considering also the Volmer barriers, these neutral-cell results indicate that Mo0 is the strongest candidate for active edges. In the following, this will be tested further by fixing the electrode potential.Regarding the S50 system, we note that the Volmer barrier for adsorption onto the deep Mo-sites is higher than for the top S-sites, despite being more favorable thermodynamically. This is due to increased repulsion between the water cluster and the surface as the cluster deposits the proton onto the deep site. Deposition onto the top site followed by diffusion is an alternative pathway, as the diffusion from S to Mo is accompanied by a slightly smaller barrier. Hence, the relative population of these sites will be kinetically determined, especially considering the fact that the Mo-sites have low Heyrovsky and Tafel barriers. This is further explored in the following subsections. After the first monolayer, the Mo-sites on S50 are all occupied, so that the adsorption leading to coverage θH = 1.25 ML is onto a top S-site. As expected, the Volmer energetics of this process are seen to match those of the direct S-site population. The same trend is seen in the Heyrovsky energetics.
On Mo0, the direct binding to Mo allows for a more favorable Tafel path including a Kubas complex intermediate, as shown in Fig. 4. Thus, direct Mo-binding seems to be essential for the possibility of a Tafel process. In cases where hydrogen is bound to the terminating sulfur atoms, no such intermediate is available, and generally the barriers are significantly higher. Tests show that dihydrogen complexes are energetically highly unfavorable on sulfur atoms.
4.2 Constant potential (grand canonical)
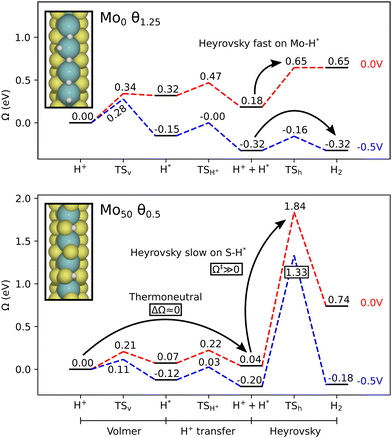
Considering next the results for constant electrode potential, Fig. 5 shows the grand-canonical activation energy for each step in the evolution process, evaluated at U = 0 V vs. SHE. We note that many of these systems are limited by large Heyrovsky and Tafel barriers. Mo0 still stands out as the most promising edge in terms of reaction kinetics, with both the Volmer–Heyrovsky and Volmer–Tafel mechanisms as possible pathways. The Tafel barrier is lower at θ1.25, but two subsequent Volmer steps are required for the Volmer–Tafel cycle. The large Volmer barrier of the prior θ1.0 case could limit the viability of this process. However, in conditions where Mo0 is stable, the H-coverage may even exceed those considered herein, i.e. there can be a surplus of available H on the tilted top sites. In such cases, Volmer–Tafel can proceed readily. Nonetheless, the Volmer–Heyrovsky process is also shown to have barriers below 0.5 eV. We should note that the high Volmer barrier on θ1.0 is related to an increase in symmetry as the full monolayer is reached. Below that point we see dimerization of the terminal Mo atoms, depending on the coverage.The S50 edge shows some interesting Tafel barriers between H atoms bound to Mo on the sides of the edge. However, these sites are rather deep and the Volmer barrier is high accordingly, as the water cluster is hindered from depositing the proton. In the θ1.25 case, the proton is deposited onto an S-atom in the Volmer step, while the Tafel step still occurs between two Mo-bound H. Hence, Volmer–Tafel may not proceed without the larger Volmer barriers of the preceding steps (θ0.75–1.0), or via diffusion from the S-site to the Mo-site. For the remaining systems, the Mo100 (θ1.25), S75 (θ1.0) and S100 (θ1.0–1.25) systems show rate-limiting barriers around 1 eV, while the rest are above 1.5 eV.
As the neutral-cell calculations indicated, it appears that the Mo-bound H are essential for achieving good kinetics of the hydrogen evolution, as the edges with S-bound H end up with imbalance between the Volmer and the subsequent Tafel or Heyrovsky barriers, where a near thermoneutral Volmer process is associated with large activation costs for the latter processes. In Fig. 6, the differing behavior of Mo-bound and S-bound H is illustrated by the Mo0 and Mo50 systems, respectively. The latter is considered to be an active edge by the thermochemical approach, due to values of ΔGH near 0. However, the following Heyrovsky step requires a very large activation energy, meaning that the mechanism is not viable. The Tafel barrier is similarly large. Overall, these results suggest that there is a distinct shift in behavior enabled by the direct binding to Mo, which is necessary for providing viable kinetics of hydrogen evolution. In other words, the thermoneutral binding of H to S is not as optimal as that for Mo.
4.3 Diffusion to Mo-sites
It was found in ref. 17 and 18 that diffusion of the S-bound hydrogen atom on Mo50 to a Mo-site followed by the Heyrovsky step significantly reduced the barrier with respect to the direct mechanism. We find a similar reduction, but the obtained barrier is still large (1.45 eV at 0 V and θH = 0.50 ML). The large barrier is mostly due to the diffusion onto the Mo-site, which is circa 1 eV uphill in energy at 0 V.In general, diffusion from S- to Mo-sites may provide a way to avoid the large Heyrovsky barriers of the positively charged S–H* species. On S50 this is especially relevant, because of the small Volmer barriers for adsorption onto S, while the Mo–Mo bridge sites are lower in energy and also enable a lower barrier Heyrovsky process. The viability of this process depends on the diffusion energetics, which for S50 is characterized by a barrier of 0.3 eV at 0 V, weakly scaling to 0.4 eV at −1 V. For the sake of further investigating this type of process, we introduce also a new system Mo50–VS where the Mo50 edge now contains an additional sulfur vacancy (equivalent to Mo37.5). This exposes isolated Mo–Mo bridge sites like those on the Mo0 edge. Diffusion onto this site from the neighboring S-site is favorable and the barrier is nearly identical to the S50 case. In both these cases, the diffusion-mediated process then seems to be viable, as the large Heyrovsky barrier is significantly reduced at the cost of a small additional diffusion barrier. The kinetics of these systems are evaluated and compared in the section on kinetics.
5 Basal plane S-vacancies
MoS2 is often synthesized with sulfur-deficient stoichiometries, which means that, in addition to the edges, a significant amount of the basal plane sulfur sites may be vacant. The single S-vacancy creates a site for H-adsorption with ΔG = 0.08 eV. Similarly, the double S2-vacancy (on opposing sides of the MoS2-layer), creates a site with ΔG = −0.01 eV. These values indicate good potential for HER, but neglect the possible reaction mechanisms. Importantly, the adsorption sites on surrounding S-atoms are not significantly affected by the neighboring vacancy. In both cases, these sites have values of ΔG exceeding 1.4 eV. This unfavorable binding of H means that the Volmer–Heyrovsky pathway is the only possibility for hydrogen evolution through these sites. However, as the basal plane likely contains several S-vacancies, the interaction between them must also be considered. Assuming that the energy barrier for migrating from one side of the MoS2-layer to the other is significantly larger than diffusion of the vacancy site within the same side of the layer, we consider briefly the energetics of same-side vacancy configurations. We find that adjacent vacancies are more favorable than dispersed ones, which is also in accordance with previous work.12 Higher-order clustered vacancy-configurations are interesting for possible Tafel mechanism on low-coordinated Mo, and would be present at high level of S-deficiency. For now, however, we consider single and zig-zag/linearly distributed vacancies. The latter case is modelled by a simple 2S-vacancy, see Fig. 7a. This enables a Tafel process between H adsorbed in the neighboring vacancy sites, and should capture the effect of these vacancy distributions to a first approximation. In such cases, the free energy of adsorption onto the vacancy site is within the thermoneutral regime, with values between −0.1 and 0.1 eV as shown in Fig. 7a.With the same methodology as for the edges, we obtain the reaction barriers at U = 0 V vs. SHE, which are presented in Fig. 7b. The Volmer and Heyrovsky steps were only calculated for the single vacancy (VS), and, naturally, the Tafel step was only calculated for the double vacancy V2S. First, we note that the Volmer–Heyrovsky path via VS appears not to be viable due to a large Heyrovsky barrier of 1.3 eV. Since adsorption onto the V2S sites is more favorable than onto VS, the Volmer barrier is expected to slightly decrease for the V2S case. This is not critical, as the limiting step is in any case the combination step, with a Tafel barrier of around 0.9 eV. This is a significant improvement in activation with respect to the pristine basal plane, where the initial adsorption costs 1.8 eV. Although the Tafel barrier is larger than for the Mo0 edge, we find a similar pathway via the vacancy sites with an H2 complex intermediate, see Fig. 7c. The increased Tafel barrier can be attributed to the higher coordination of the Mo-atoms.
6 Kinetics
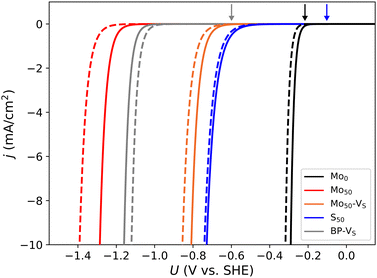
The calculated values of the activation energy at 0 V applied potential indicate that the Volmer–Tafel process is favored on the basal plane, as well as certain edges such as Mo0 and S50. However, since the Heyrovsky barrier scales with the potential, there is a point where it becomes the favored mechanism. The consequence of this is investigated using the kinetic model described in Section 2. Fig. 8 shows theoretical polarization curves for selected edges and the basal plane, where dashed lines are normalized to the voltage-dependent fractional presence of the relevant edge. We find that, for most systems, the point where the Heyrovsky rate surpasses the Tafel rate occurs well before the onset potential, see the arrows in Fig. 8. Thus, the absolute contribution from the Volmer–Tafel mechanism is insignificant. On Mo0 the Tafel and Heyrovsky rates are of comparable magnitude at the onset potential, but the Tafel contribution is rapidly outscaled. Although the absolute magnitude of the current density may be subject to inaccuracies with this simple kinetic model, these results give an indication of the relative overpotential required for the different systems.As expected from the 0 V barriers, the Mo0 edge requires the smallest overpotential by a large margin. As indicated by the dashed line, the low fractional presence of Mo0 only slightly affects the onset potential. Despite the lowered Heyrovsky barrier on Mo50 due to diffusion onto the Mo site, the kinetics are even worse than on the basal plane, i.e. the Heyrovsky barrier is still too large and this mechanism is unlikely on Mo50. However, the similar diffusion-mediated mechanisms on S50 and Mo50–VS show promising kinetics.
The remaining systems (generally sulfur-rich) are not shown but have onset potential similar to or exceeding that of Mo50. Overall, this indicates that accessible Mo-sites are necessary for significant hydrogen evolution at a moderate overpotential, and the completely sulfur-depleted Mo-edge represents the limiting case of activity within this scope. We also make a comparison with experimental results with some reservations regarding the absolute magnitudes. In ref. 11 the overpotentials (defined as where j = 0.6 mA cm−2) of basal- and edge-oriented crystals were determined to be in the range of 0.9–1.1 V and 0.3–0.4 V, respectively. Using the same criterion, we obtain values of 1.09, 0.72, 0.61 and 0.25 V for the overpotential at the basal plane, Mo50–VS, S50 and Mo0, respectively.
The current density obtained from this kinetic model can be considered as an upper bound for the given barrier values, as reorientation of the electrolyte interface and electron transport within the material is neglected. These effects are likely comparable between the systems we are considering, except for the difference between intra- and interlayer conductivity. The dashed line in Fig. 8 indicates that the relatively low fraction of Mo0 does not hinder the performance. However, if the desulfurization is controlled by slow kinetics or otherwise differs from our calculations, this can manifest as a lower current density also. Since such a large overpotential is required for evolution through the basal plane, configurations with multiple H-adsorption in the vacancy site could be relevant at these negative potentials. This has been addressed in previous works using the grand-canonical formulation, where a 2H-configuration is favored below −0.7 V.34 However, with a similar H9O4+ cation model as used in the present work, this is not found to affect the Heyrovsky energy barrier significantly,35 being in fact slightly higher for the second H. Hence the kinetics of the evolution should be comparable even with multiple H in the vacancy site.
7 Conclusions
The voltage-dependent reaction and activation energies for the elementary HER steps on MoS2 edges and defects are obtained through implicit solvent grand-canonical DFT calculations. There is a clear distinction in behavior between S-bound and Mo-bound hydrogen atoms, where the former displays disproportionately large Heyrovsky and Tafel barriers, meaning that a thermoneutral adsorption (ΔG ∼ 0 eV) is not a sufficient descriptor. The Mo50 edge, which is often suggested as the active edge, is found to exhibit a too large Heyrovsky barrier, even after diffusion of the hydrogen atom to a (high energy) Mo site. By introducing further sulfur-deficiency, more adsorption sites on Mo atoms are exposed. Evolution through these sites is similar to that on metals, with significantly reduced barriers for the H2 combination process.Kinetic modelling shows that the Volmer–Heyrovsky path is the predominant reaction mechanism, while the Volmer–Tafel contribution is negligible for most systems aside from the Mo0 edge. The Tafel process is outscaled by Heyrovsky on the basal plane also due to the large overpotential required. The theoretical estimates of the overpotential were found to be 1.09 V and 0.25 V for the weakly sulfur-deficient basal plane and the sulfur-depleted Mo0 edge, respectively. These values are in good agreement with the experiment, and their large discrepancy indicates that the experimental activity should be determined by the Mo-exposed edges completely.
Finally, we remark that due to the fundamental difference in performance between S-bound and Mo-bound hydrogen, future catalyst design should focus towards facilitating and modifying the Mo-sites, rather than trying to activate the S-sites. This conclusion can be extended to transition metal dichalcogenides in general, and similar trends can be relevant when considering other transition metal compounds containing p-block elements.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The calculations were performed on resources provided by Sigma2 – the National Infrastructure for High Performance Computing and Data Storage in Norway, project No. NN9497K. J. A. acknowledges financial support from the Academy of Finland, project No. 322832 “NANOIONICS”. H. J. acknowledges financial support from the Icelandic Research Fund, project No. 207283-053.References
- H. Jin, C. Guo, X. Liu, J. Liu, A. Vasileff, Y. Jiao, Y. Zheng and S.-Z. Qiao, Chem. Rev., 2018, 118, 6337–6408 CrossRef CAS.
- J. Yang and H. S. Shin, J. Mater. Chem. A, 2014, 2, 5979–5985 RSC.
- M. S. Faber and S. Jin, Energy Environ. Sci., 2014, 7, 3519–3542 RSC.
- D. Merki and X. Hu, Energy Environ. Sci., 2011, 4, 3878–3888 RSC.
- B. Hinnemann, P. G. Moses, J. Bonde, K. P. Jørgensen, J. H. Nielsen, S. Horch, I. Chorkendorff and J. K. Nørskov, J. Am. Chem. Soc., 2005, 127, 5308–5309 CrossRef CAS.
- T. F. Jaramillo, K. P. Jørgensen, J. Bonde, J. H. Nielsen, S. Horch and I. Chorkendorff, Science, 2007, 317, 100–102 CrossRef CAS.
- J. Bonde, P. G. Moses, T. F. Jaramillo, J. K. Nørskov and I. Chorkendorff, Faraday Discuss., 2009, 140, 219–231 RSC.
- J. Kibsgaard, Z. Chen, B. N. Reinecke and T. F. Jaramillo, Nat. Mater., 2012, 11, 963–969 CrossRef CAS.
- J. D. Benck, Z. Chen, L. Y. Kuritzky, A. J. Forman and T. F. Jaramillo, ACS Catal., 2012, 2, 1916–1923 CrossRef CAS.
- J. Xie, H. Zhang, S. Li, R. Wang, X. Sun, M. Zhou, J. Zhou, X. W. D. Lou and Y. Xie, Adv. Mater., 2013, 25, 5807–5813 CrossRef CAS.
- S. M. Tan, A. Ambrosi, Z. Sofer, Š. Huber, D. Sedmidubský and M. Pumera, Chem. – Eur. J., 2015, 21, 7170–7178 CrossRef CAS.
- C. Tsai, H. Li, S. Park, J. Park, H. S. Han, J. K. Nørskov, X. Zheng and F. Abild-Pedersen, Nat. Commun., 2017, 8, 15113 CrossRef.
- H. Li, C. Tsai, A. L. Koh, L. Cai, A. W. Contryman, A. H. Fragapane, J. Zhao, H. S. Han, H. C. Manoharan, F. Abild-Pedersen, J. K. Nørskov and X. Zheng, Nat. Mater., 2016, 15, 48–53 CrossRef CAS.
- M. Hakala, R. Kronberg and K. Laasonen, Sci. Rep., 2017, 7, 15243 CrossRef.
- H. Li, S. Wang, H. Sawada, G. G. D. Han, T. Samuels, C. S. Allen, A. I. Kirkland, J. C. Grossman and J. H. Warner, ACS Nano, 2017, 11, 3392–3403 CrossRef CAS.
- J. Deng, H. Li, J. Xiao, Y. Tu, D. Deng, H. Yang, H. Tian, J. Li, P. Ren and X. Bao, Energy Environ. Sci., 2015, 8, 1594–1601 RSC.
- Y. Huang, R. J. Nielsen, W. A. I. Goddard and M. P. Soriaga, J. Am. Chem. Soc., 2015, 137, 6692–6698 CrossRef CAS.
- Z. Wang, M. T. Tang, A. Cao, K. Chan and J. K. Nørskov, J. Phys. Chem. C, 2022, 126, 5151–5158 CrossRef CAS.
- S. Ø. Hanslin, H. Jónsson and J. Akola, Phys. Chem. Chem. Phys., 2023, 25, 15162–15172 RSC.
- S. Saleem, M. Salman, S. Ali, Y. Ling and M. Khan, Int. J. Hydrogen Energy, 2022, 47, 7713–7723 CrossRef CAS.
- L. Lin, N. Miao, Y. Wen, S. Zhang, P. Ghosez, Z. Sun and D. A. Allwood, ACS Nano, 2016, 10, 8929–8937 CrossRef CAS.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 1999, 111, 7010–7022 CrossRef CAS.
- S. Ø. Hanslin, H. Jónsson and J. Akola, Supporting data set for: Sulfur-deficient edges as active sites for hydrogen evolution on MoS2, 2023 DOI:10.5281/zenodo.10074994.
- M. Van den Bossche, E. Skúlason, C. Rose-Petruck and H. Jónsson, J. Phys. Chem. C, 2019, 123, 4116–4124 CrossRef CAS.
- K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140, 084106 CrossRef.
- K. Mathew, V. S. C. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, J. Chem. Phys., 2019, 151, 234101 CrossRef.
- N. Abidi, A. Bonduelle-Skrzypczak and S. N. Steinmann, ACS Appl. Mater. Interfaces, 2020, 12, 31401–31410 CrossRef CAS.
- N. Abidi, A. Bonduelle-Skrzypczak and S. N. Steinmann, J. Phys. Chem. C, 2021, 125, 17058–17067 CrossRef CAS.
- Y. Huang, R. J. Nielsen and W. A. I. Goddard, J. Am. Chem. Soc., 2018, 140, 16773–16782 CrossRef CAS.
- N. Abidi, A. Bonduelle-Skrzypczak and S. N. Steinmann, Int. J. Hydrogen Energy, 2023, 48, 8478–8488 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04198k |
| This journal is © the Owner Societies 2023 |