Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The structure of liquid thiophene from total neutron scattering†
Thomas F
Headen
 *a,
Camilla
Di Mino
bc,
Tristan GA
Youngs
a and
Adam J
Clancy
*a,
Camilla
Di Mino
bc,
Tristan GA
Youngs
a and
Adam J
Clancy
 *d
*d
aISIS Neutron and Muon Source, STFC Rutherford Appleton Laboratory, Didcot, OX11 0QX, UK. E-mail: tom.headen@stfc.ac.uk
bDepartment of Materials, University of Oxford, 21 Banbury Rd, Oxford, OX2 6NN, UK
cDepartment of Physics & Astronomy, University College London, Gower St, London WC1E 6BT, UK
dDepartment of Chemistry, University College London, 20 Gordon St, London, WC1H 0AJ, UK. E-mail: a.clancy@ucl.ac.uk
First published on 8th September 2023
Abstract
The structure of pure liquid thiophene is revealed by using a combination of total neutron scattering experiments with isotopic substitution and molecular simulations via the next generation empirical potential refinement software, Dissolve. In the liquid, thiophene presents three principle local structural motifs within the first solvation shell, in plane and out of the plane of the thiophene ring. Firstly, above/below the ring plane thiophenes present a single H towards the π cloud, due to a combination of electrostatic and dispersion interactions. Secondly, around the ring plane, perpendicular thiophene molecules find 5 preferred sites driven by bifurcated C–H⋯S interactions, showing that hydrogen–sulfur bonding prevails over the charge asymmetry created by the heteroatom. Finally, parallel thiophenes sit above and below the ring, excluded from directly above the ring center and above the sulfur.
Introduction
Thiophene is a room temperature liquid consisting of a 5-membered sulfur-containing heterocycle (C4H4S, Fig. 1) with aromaticity derived from two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds and a sulfur lone pair, leaving the second lone pair projecting outward, planar to the ring. Molecular thiophene itself has found use as a solvent2 and for fundamental studies due to its unique excited-state properties,3,4 and its presence on Mars is one of the flagship discoveries of the Curiosity rover program,5 linked to possible extra-terrestrial life. Most commonly however, thiophene is used as a precursor for other organic species, with the thiophene molecular motif ubiquitous in a remarkably wide range of applications including pharmaceuticals,6 covalent organic frameworks,7 liquid crystals,8 water-splitting photocatalysts,9 asphaltenes,10 and bioimaging fluorophores.11 The most famous contemporary application of thiophene is plastic electronics12 such as OLEDs,13 transistors,14 and solar cells15 based on polymerised thiophenes, due to their tuneable bandgap and high electron mobility in the oxidised state, the discovery of which contributed to the Chemistry Nobel Prize in 2000. Notably, unmodified polythiophenes are insoluble in virtually all solvents (with the exception of arsenic fluorides16) so are usually modified through alkylation (e.g. poly-3-hexylthiophene) and/or copolymerisation (e.g. PEDOT:PSS) with the additional species providing solubility through favourable solvent-alkyl/copolymer interactions, enabling liquid-phase assembly of devices. The poor solubility of unmodified polythiophenes is at odds with the chemical compatibility of the parent molecular thiophene which is miscible with organic solvents of every variety including alkanes, organohalides, aromatics, alcohols, amides, ethers, and ionic liquids; thiophene even has non-negligible solubility in water (∼3 g dm−3).
C bonds and a sulfur lone pair, leaving the second lone pair projecting outward, planar to the ring. Molecular thiophene itself has found use as a solvent2 and for fundamental studies due to its unique excited-state properties,3,4 and its presence on Mars is one of the flagship discoveries of the Curiosity rover program,5 linked to possible extra-terrestrial life. Most commonly however, thiophene is used as a precursor for other organic species, with the thiophene molecular motif ubiquitous in a remarkably wide range of applications including pharmaceuticals,6 covalent organic frameworks,7 liquid crystals,8 water-splitting photocatalysts,9 asphaltenes,10 and bioimaging fluorophores.11 The most famous contemporary application of thiophene is plastic electronics12 such as OLEDs,13 transistors,14 and solar cells15 based on polymerised thiophenes, due to their tuneable bandgap and high electron mobility in the oxidised state, the discovery of which contributed to the Chemistry Nobel Prize in 2000. Notably, unmodified polythiophenes are insoluble in virtually all solvents (with the exception of arsenic fluorides16) so are usually modified through alkylation (e.g. poly-3-hexylthiophene) and/or copolymerisation (e.g. PEDOT:PSS) with the additional species providing solubility through favourable solvent-alkyl/copolymer interactions, enabling liquid-phase assembly of devices. The poor solubility of unmodified polythiophenes is at odds with the chemical compatibility of the parent molecular thiophene which is miscible with organic solvents of every variety including alkanes, organohalides, aromatics, alcohols, amides, ethers, and ionic liquids; thiophene even has non-negligible solubility in water (∼3 g dm−3).
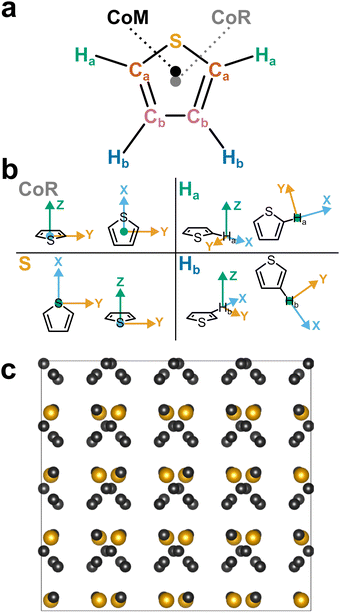 | ||
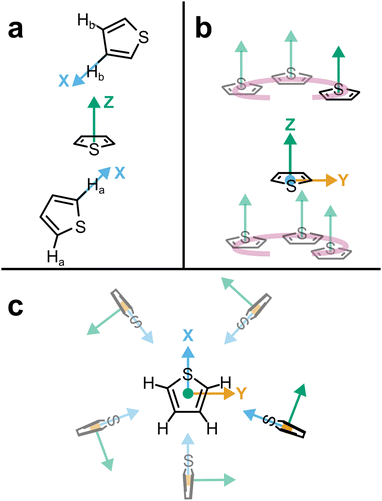
| Fig. 1 (a) Schematic structure of thiophene with atom assignments and CoR/CoM positions. Accurate coordinates provided in the (Table S1, ESI†). (b) Assigned axes at CoR, Ha, S, and Hb analysis sites. (c) 1 × 2 × 2 supercell of solid thiophene-I (sulfur and carbon only) down the a-axis, as described by Abrahams & Lipscomb.1 | ||
Pure thiophene freezes at −38 °C to thiophene-I, with further cooling to −98 °C and below leading to four further crystalline (II–V) phases observed by calorimetry. The crystal structure of thiophene-I was established by Abrahams & Lipscomb1 in 1952 using X-ray scattering, showing orthorhombic crystals (a = 9.76 Å, b = 7.20 Å, c = 6.67 Å) with rings ordered in head-to-tail confirmation down the (100) plane with the ring planes alternatingly tilted 47.8° from the b plane in an alternating manner (i.e. near right angles to each other down the a axis, Fig. 1c). Notably, while the ring-plane position is well defined, the ring orientations are highly disordered, implying an ability to spin about the ring axis.
Understanding the interactions of thiophene in the liquid state is critical to rationalise and improve liquid-phase processing of thiophene and its derivatives. The simplest case, the self-solvation behaviour of thiophene, is vital to that understanding. These thiophene–thiophene interactions are reasonably strong, as illustrated by thiophene's boiling point (84 °C) and must be broken to form interactions with other molecules. Like other small aromatics, thiophene can be expected to have a rich array of competing and potentially cooperative intermolecular interactions. Its delocalised aromatic structure may give rise to π–π interactions, which in themselves arise from a subtle balance of competing non-directional intermolecular forces: dispersion attraction, exchange repulsion and multipolar electrostatics, with recent analyses also showing charge penetration to be particularly important.17 In addition, thiophene is sufficiently polar18 (μ = 0.533 D) for dipole–dipole interactions, while its high anisotropic polarizability19 arising from the diffuse 3p sulfur orbitals facilitates strong dispersion interactions. Furthermore, thiophene's sulfur bears a non-delocalised lone pair which may give rise to weak C–H⋯S hydrogen bonds.20
In previous work we have used the experimental technique of Neutron Diffraction with Isotopic Substitution (NDIS) as a window through which to view these interactions between simple aromatic molecules in the liquid state. Benzene shows a preference for neighbouring molecules to be perpendicular in a “Y-shaped” geometry,21,22 with the slightly larger aromatic naphthalene conversely showing a strong propensity for offset parallel stacked structures.23 Pyridine shows a surprisingly similar local structure to benzene, given the addition of a molecular dipole. It shows a preference for perpendicular nearest neighbours, again in a Y-stacked geometry, with the nitrogen atoms on opposite side on adjacent rings.23
To date, little work has been taken to understand the relative balance of aromatic–aromatic interactions in neat liquid thiophene. Computational studies of thiophene dimers have predicted that the lowest energy structures are of perpendicular molecules.24,25 Tsuzuki et al. estimated CCSD(T) interaction energies between dimers, these indicated that dispersion interactions dominate, attributed to the sulfur polarizability, predicting preferential perpendicular arrangement.25 The modelled bonding involves the sulfur-adjacent hydrogen (Ha) directed towards the π-cloud leaving a centre-of-ring (CoR) separation of 3.326 Å. Experimentally, thiophene's liquid structure has, to date, only been experimentally measured with energy dispersive X-ray diffraction26 showing an ordered liquid structure with a principal peak at 1.38 Å−1. However, accurate assignment and additional spatial details are hampered by thiophene's atomic makeup: per molecule there is only one sulphur which scatters X-rays strongly, while carbon is a weaker scatterer, and the perimeter hydrogens are virtually invisible to X-rays. In contrast, neutron scattering provides a more powerful route to derive the atomistic structure of hydrogen-containing species, owing to hydrogen's significant coherent neutron scattering cross-section. Further, by providing a range of isotopic compositions via deuteration, multiple distinct scattering patterns may be taken for the same chemical structure, allowing a greater degree of constraint when modelling the system.
Here, total neutron scattering combined with isotopic substitution is used to provide a comprehensive atomic understanding of the structure of liquid thiophene. On a fundamental level this can be compared to nearest neighbour structures in benzene and pyridine – allowing us to understand how the increase dispersion afforded by the larger sulfur atom effects structure. It is also important at a more applied level, increase our understanding of local forces in these archetypal molecules for organic electronics, and provide a robust structural benchmark with which to compare to simulation force-fields.27
Experimental methods
Scattering data28 were collected using the Small Angle Neutron Diffractometer for Amorphous and Liquid Samples (SANDALS) at the ISIS spallation neutron source at the STFC Rutherford Appleton Laboratory, U.K. Having a large number of high-efficiency, forward-scattering detectors, and an under-moderated source with a higher proportion of high energy (epithermal) neutrons, SANDALS is optimized to reduce inelastic scattering effects for light elements, such as hydrogen, allowing the use of hydrogen/deuterium isotopic substitution techniques. Neutron scattering data on three isotopically distinct samples of neat liquid thiophene were collected: (i) fully deuterated (CND isotopes, 98.9 at% D), (ii) hydrogenated thiophene (Sigma Aldrich, 99%+ purity) and (iii) an equimolar mixture of the two. The liquids were used as received and inserted into a flat-plate null scattering TiZr cell, with 1 mm path length and wall thicknesses. This container geometry minimizes multiple neutron scattering and attenuation effects. The temperature was maintained at 25 °C by using a sample changer coupled with a circulating water bath. Typical counting times were ∼6 hours for each sample. For data correction and calibration, scattering data were also collected from the empty instrument, the empty sample container, and a null scattering Vanadium–Niobium alloy standard slab of thickness 3 mm. Background subtraction, and multiple scattering, absorption, and normalization correction procedures were performed using GUDRUN,29 to give the interference differential scattering cross-section for each isotopically distinct sample. Particular attention needs to be paid to correction of inelasticity effects, especially for the samples containing hydrogen. The self-scattering background and inelasticity effects were removed from the total differential scattering cross section using an iterative method developed by Soper.30,31Relevant theory and data analysis
After appropriate corrections of the raw scattering data (see Methods) we obtain the total structure factor, F(Q). In order to obtain the most complete set of structural data we take advantage of the fact that neutrons scatter from atomic nuclei, and therefore the scattering length varies between isotopes. Specifically, substitution of hydrogen (bH = −3.74 fm) for deuterium (bD = 6.67 fm), is relatively easy for many organic molecules, therefore by performing the experiment on three isotopically exchanged samples it is possible for us to determine more reliable structural quantities, as the complimentary data sets place stronger constraints on the simulation-based refinement methods used (see below).In general we measure several total structure factors, Fi(Q), each of which has the same chemical composition but a different isotopic composition. This is a weighted sum of the different partial structure factors arising from different pairs of atoms α, β.
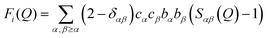 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) λ−1 (i.e. the magnitude of the momentum change vector of the scattered neutrons), and Sαβ(Q) is the Faber–Ziman partial structure factor involving atoms α and β only. This partial structure factor contains information about correlations between the two atomic species α and β in Q-space, and is defined as:
θ) λ−1 (i.e. the magnitude of the momentum change vector of the scattered neutrons), and Sαβ(Q) is the Faber–Ziman partial structure factor involving atoms α and β only. This partial structure factor contains information about correlations between the two atomic species α and β in Q-space, and is defined as: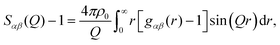 | (2) |
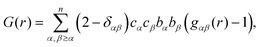 | (3) |
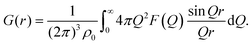 | (4) |
In order to gain a full 3-dimensional understanding of thiophene liquid structure, we employed the empirical potential structure refinement (EPSR) method.32,33 In summary this starts with a Monte Carlo molecular simulation of the liquid, at known experimental density (1.051 g mL−1), and using classical potentials for the inter- and intra-molecular interactions, available from the literature and/or parameter generators such as LigParGen.34 Once the systems has equilibrated, the total structure factors for each isotopically substituted sample are calculated (using eqn (1) and (2)) from radial distribution functions computed from the simulation over several iterations. An additional “empirical potential” is then calculated based on the mismatch between experimental and simulated data and added on to the reference potential. This process occurs iteratively to obtain a best possible match between the simulation and experiment. The positions of the atoms over several iterations can then be used to calculate the local structural properties within the liquid. The method has been successfully applied to a number of different amorphous systems, including aromatic liquids.21–23
Herein we used the Dissolve (v.1.3.2) software package.35–37 This software implements the core methodology of empirical potential structure refinement as found in the EPSR software as part of a flexible framework of classical molecular simulation and scattering data refinement and analysis tools.
For this study initial reference forcefield potentials were taken from the LigParGen service of Yale University34 using a thiophene molecule coordinates initially relaxed via MM2 forcefield, and imported directly into Dissolve. A cubic simulation box of 51.0369 Å3 was populated with 1000 thiophene molecules and this initial configuration was relaxed with a standard molecular Monte Carlo simulation. Once the energy had stabilised, a 50-step molecular dynamics (MD) simulation was introduced every fifth Monte Carlo cycle in order to relax the intramolecular structure and explore the relevant degrees of freedom and was repeated until the system energy stabilised once more. This approach is distinct from the MC-only modelling employed by the EPSR code, with the MD steps describing the intra-molecular flexibility. Subsequently, EPSR module of Dissolve was introduced to the loop to modify the intermolecular potentials to better match the simulated-box scattering data to the three experimental neutron scattering datasets. Once good agreement was reached, the MC/MD(1-in-5)/EPSR loop was allowed to continue while accumulating relative atomic positions.
Discussion
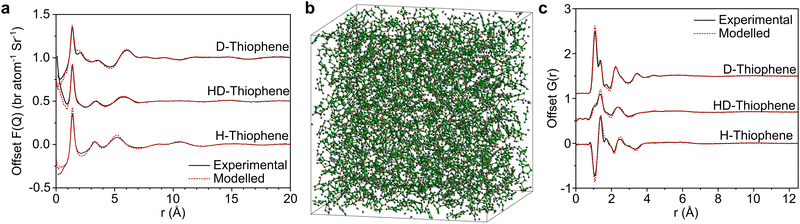
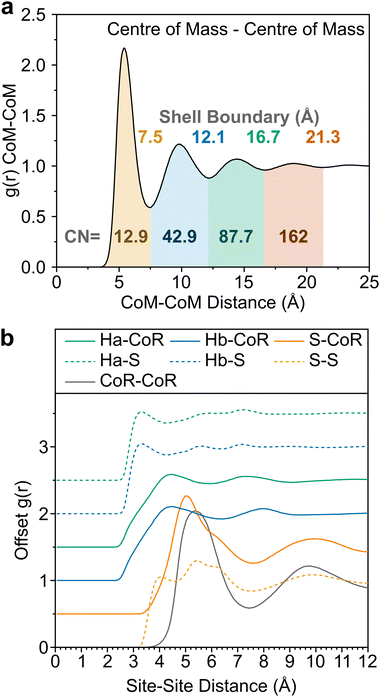
In Fig. 2 we show the measured F(Q) and its Fourier transform to G(r), and the Dissolve fit for both for each of the three datasets. There is a good agreement to the data for all samples, with some minor discrepancy at low Q for the hydrogenous samples, due to the well documented difficulty in unambiguously employing inelasticity corrections for these samples.The experimentally-driven simulation can now be analysed in detail to derive the liquid structure of thiophene over all dimensions and molecular orientations. The CoM–CoM radial distribution function (RDF) g(r) shows a relatively sharp first peak, indicating local ordering (Fig. 3). There then follows three clear solvation shells with minima at 7.5, 12.1, and 16.7 Å, with a distinctly less ordered 4th shell out to ∼21.3 Å (Fig. 2a). The coordination number within the first shell is 12.9, comparable to previously measured small aromatic liquids.22,23 While the radial distribution functions between CoM sites, and related Centre of Ring (CoR) sites, show a singular broad peak within the first solvation shell, a more complex picture emerges from the atomic site radial distribution functions due to local preferences to relative molecular orientation (Fig. 3b). The closest atoms to the CoR are Ha and Hb which show very similar short-range ordering, consisting of two overlapping peaks, while the CoR–S RDF shows several distinct behaviours within the first shell.
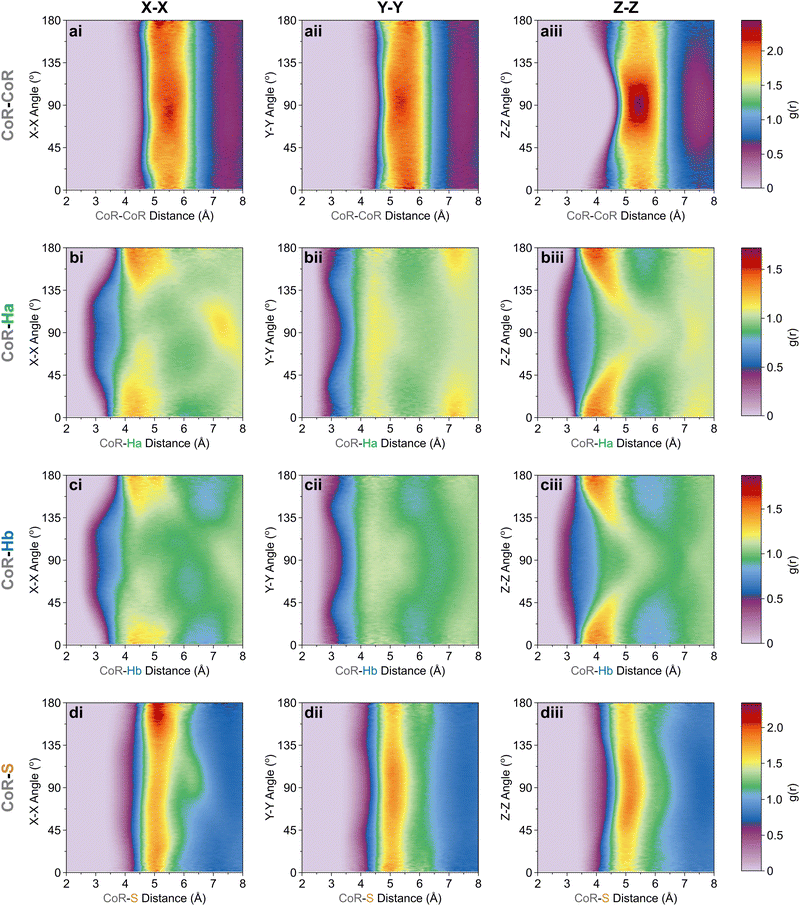
To better understand the local ordering, the RDF contributions are separated by the angle between assigned vectors (Fig. 1b) to give angular radial distribution function (ARDFs, Fig. 4). The CoR–CoR ARDF with the clearest differences as a function of angle is the z-axes, representing the angle between the aromatic planes. There is a broad dominant peak centred at 5.4 Å attributed to perpendicular ordering, i.e., with z-axes at 90° to each other. This is similar to the local structure in other small aromatics such as benzene and pyridine.22,23 In order to understand the local solvation environment in three dimensions we employ the use of Spatial Density Functions (SDFs). These allow visualisation of the most likely relative positions of a site around the average thiophene molecule. The CoR–CoR SDF across the entire first solvation shell (Fig. 5a and Fig. S1, ESI†) shows preferred spatial structure directly above/below the ring plane and in two lobes intersecting the S–Ha region, similar to the lantern-lobes in-between ring substituents as seen for other planar aromatics.22,23 At higher percentages of most likely positions, the lobes between Ha–Hb and Hb–Hb become apparent (Fig. S1, ESI†). Subdivision to display the location of only the closest species (<4.7 Å, from Fig. 4aiii) highlights clear preference for orientations directly above and below the ring plane, indicating interactions with the π system (Fig. 5b). At further distances (5.1–7.5 Å, Fig. 5c) the preference is for the equatorial lobes, forming five circumferential lobes which bifurcate the perimeter H/S sites.
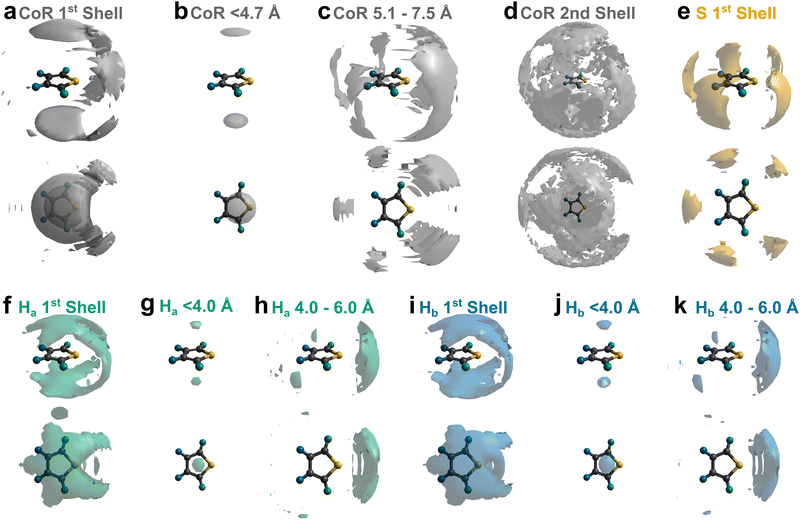 | ||
| Fig. 5 (a)–(d) SDFs highlighting most likely 10% position of the CoR of adjacent thiophene molecules in (a) the first solvation shell, ≤7.5 Å, (b) <4.7 Å, (c) 5.1–7.5 Å, and (d) second solvation shell (7.5–12.1 Å). (e)–(k) SDFs highlighting most likely 5% of positions of atomic sites [(e), S; (f)–(h), Ha; (i)–(k), Hb] of adjacent thiophene molecules at various distances: (e), (f), and (i) the first solvation shell; ≤7.5 Å, (g) and (j) <4.0 Å; (h) and (k) 4.0–6.0 Å. Additional 1st shell CoR SDFs provided at various percentage most likely positions provided in ESI,† Fig. S1. | ||
The orientation and bonding motifs at each of these thiophene positions can be further explained from the atomic site structures. From Fig. 3b it is clear that the closest atoms to the CoR are the hydrogens, with both Ha and Hb showing similar behaviours with weak peaks concurrently emerging from ∼2.5 Å, in advance of stronger peaks with maxima at 4.5 Å. The CoR–Ha/Hb ARDFs of the first feature (<4 Å) show it is centred around ∼55° (plus a symmetric ∼125° feature) between the x-axes of H and CoR sites, i.e. the angle between the C–H bond and the CoR–S direction (Fig. 4b and c). The SDFs of the most likely Ha/Hb positions <4 Å from a CoR confirm that these interactions relate to the hydrogens being directly above/below the thiophene ring center (Fig. 5g and j); these interactions show closer interactions with the CoR than the sulfur (ESI,† Fig. S2). This suggests that they are C–H⋯π interactions, although we note that the large distances involved (peaking at 3.2 Å) imply that these should not be considered as weak hydrogen bonding. The directionality of the C–H bond can be characterised by the angle between the Ha/bx-axis and the CoR z-axis, where C–H normal to the ring plane would give ∠ZX 0°, and a Y configuration of a centred perpendicular thiophene with two C–H bonds pointing down (as seen in benzene22) would give ∠ZX ∼33°. Here, the Z(CoR)–X(Ha/b) ARDFs (Fig. 6a and b) have a peak maximum at ∼42°. This value implies a similar Y-like configuration but with a small preference for a more tilted ring, with molecule centres displaced to align a single H above the CoR. The motif is similar to the previously modelled preferential C–Ha⋯π interactions of thiophene dimers,25 but here is agnostic to the H type, showing C–H⋯π bonding for both Ha and Hb.
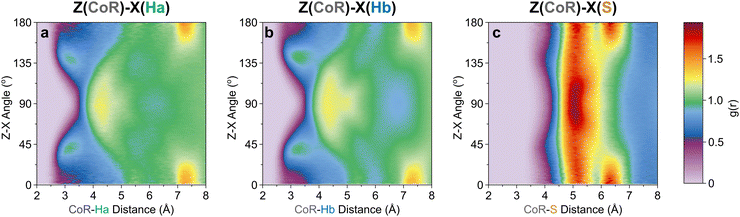 | ||
| Fig. 6 Z[CoR]–X[site] ARDF contour plots of (a) Ha, (b) Hb, and (c) S sites. Z-Scale colours relate to g(r) intensities set between 0 and 1.94, the maximum intensity of any plot (found in CoR–S). | ||
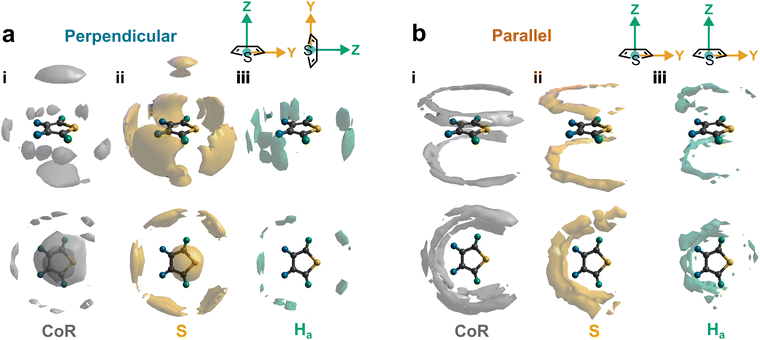
Further out, the arrangements of thiophenes about the ring plane in 5 positions can be seen to derive from S⋯H interactions. The SDFs of sulfur in the first solvation shell (Fig. 5e) clearly shows three positions bifurcating two C–H sites, with two further positions between the C–Ha and S site, closer to the hydrogen. Concurrently, SDFs of Ha and Hb beyond 4 Å show a clear preference for positioning adjacent to sulfur (Fig. 5h and k). These interactions are weakly directional, as seen in the X(S)–X(Ha/b) ARDFs which at S–H distances of ∼3.2 Å show antiparallel vectors, but with a broad peak between 100–180° (Fig. 7). The relative orientation of the aromatic plane of the thiophenes at these five sites is most likely perpendicular, as best illustrated through SDFs of only perpendicular molecules where the lobes are well defined, while they are absent for parallel thiophenes (Fig. 8). The perpendicular orientation is likely due to steric constrains of fitting adjacent equatorial thiophenes around a central molecule – having all species coplanar with the central thiophene would push Ha atoms of adjacent thiophenes together. This templated packing in the first solvation shell is reflected in the second, where the in-plane lobes can be seen to propagate in the second solvation shell (7.5–12.1 Å, Fig. 5d)
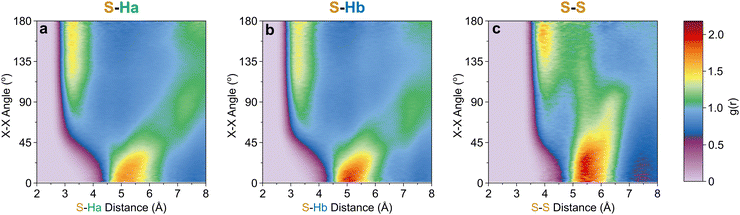 | ||
| Fig. 7 X[S]–X[site] ARDF contour plots of (a) Ha, (b) Hb, and (c) S sites. Z-Scale colours relate to g(r) intensities set between 0 and 2.19, the maximum intensity of any plot (found in S–Hb). | ||
The SDF of only parallel thiophenes (Fig. 8b) highlight a third distinct behaviour, forming crescent halos above and below the ring plane, with a gap above/below the sulfur. The presence of these thiophenes can also be inferred from shoulders appearing in the Z(CoR)–Z(CoR) ARDF with parallel preference, i.e., around ∠ZZ 0° and 180° (Fig. 4aiii). The gap of the crescent above S is likely due to more likely presence of perpendicular thiophene with two Ha/b atoms located in these positions, close to the central thiophene's sulfur. These parallel thiophene in the crescent halos constitute those with the closest CoR–CoR distances, as seen in the ARDFs (Fig. 4aiii). Within the crescent, there is a preference for the x-axes of S atoms appearing broadly antiparallel (Fig. 7c), as also supported by the S crescent not extending as far forward as the CoR.
Taken together these neutron scattering data present a robust experimental benchmark for which to test simulation force-fields – as previously shown for benzene,38 naphthalene, and pyridine.23 Here we do not attempt a full survey of simulation force-fields (where it is established that developing accurate potential parameters for sulfur is a challenge,39 due to the softer, highly polarisable lone pairs) however we do note that a recently published force-field, derived specifically for thiophene from DFT data,27 does agree well with our experimentally derived CoR–CoR and S–S g(r)'s (see ESI,† Fig S3), the small differences being slightly greater ordering and a more pronounced short range S–S peak for the experimentally derived data.
Conclusions
In conclusion, neutron total scattering, combined with isotopic substitution analysed by a combined Monte Carlo and molecular dynamics simulation refined against that data, have been used to elucidate the rich structures of liquid thiophene over all directions and relative orientations. We identify three principle local structural motifs within the first solvation shell (Fig. 9). Firstly, perpendicular thiophenes arrange above/below the ring plane oriented with a single H directed to the π cloud, due to dispersion interactions, this is similar to the energy minimum for a molecular dimer.24,25 Secondly, perpendicular molecules have 5 preferred sites around the thiophene plane, with attractive forces driven by bifurcating C–H⋯S interactions with no preference between H-type. Finally, parallel thiophenes sit above and below the ring, but are relatively excluded from directly above the ring center and above the sulfur; they do not appear to form short range π-stacked structures. Taken together, the alternating ring plane orientations are reminiscent of the solid structure of thiophene-I.Author contributions
T. F. H. conceptualization, data curation, formal analysis, investigation, writing (review & editing), project administration. C. D. M. formal analysis, investigation, writing (review & editing). T. G. A. Y. formal analysis, software, methodology, writing (review & editing). A. J. C. Formal analysis, investigation, writing (original draft), visualisation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. J. C. would like to thank The Royal Society (URF\R1\221476, RF\ERE\221017) for funding through the University Research Fellowship scheme. T. F. H. would like to acknowledge EPSRC and NSF for funding of the project “Molecular Engineering of Inhibitors to Self-Assembly: Fundamental structure informing in silico design” (EP/R013195/1), thank Prof. Erich Müller and Prof. Michael Hoepfner for helpful discussions in formulating the experiment and thank Dr. Guadalupe Jimenez–Serratos for assistance with the neutron experiment. We kindly acknowledge STFC for the award of beamtime at ISIS Neutron and Muon Source (beamtime allocation number RB1820594). The authors would like to thank Prof Giacomo Prampolini of CNR-ICCOM for graciously providing the data from de Silveira et al.27 for comparison to our work.References
- S. Abrahams and W. Lipscomb, Acta Crystallogr., 1952, 5, 93–99 CrossRef CAS.
- Y. Xu, L. Sun, J. Wu, W. Ye, Y. Chen, S. Zhang, C. Miao and H. Huang, Dyes Pigm., 2019, 168, 36–41 CrossRef CAS.
- T. Schnappinger, P. Kölle, M. Marazzi, A. Monari, L. González and R. de Vivie-Riedle, Phys. Chem. Chem. Phys., 2017, 19, 25662–25670 RSC.
- A. Loupas, K. Regeta, M. Allan and J. D. Gorfinkiel, J. Phys. Chem. A, 2018, 122, 1146–1155 CrossRef CAS PubMed.
- J. L. Eigenbrode, R. E. Summons, A. Steele, C. Freissinet, M. Millan, R. Navarro-González, B. Sutter, A. C. McAdam, H. B. Franz and D. P. Glavin, Science, 2018, 360, 1096–1101 CrossRef CAS PubMed.
- R. Shah and P. K. Verma, Chem. Cent. J., 2018, 12, 1–22 CrossRef PubMed.
- D. Li, C. Li, L. Zhang, H. Li, L. Zhu, D. Yang, Q. Fang, S. Qiu and X. Yao, J. Am. Chem. Soc., 2020, 142, 8104–8108 CrossRef CAS PubMed.
- R. Cai and E. T. Samulski, Liq. Cryst., 1991, 9, 617–634 CrossRef CAS.
- J.-Z. Cheng, Z.-R. Tan, Y.-Q. Xing, Z.-Q. Shen, Y.-J. Zhang, L.-L. Liu, K. Yang, L. Chen and S.-Y. Liu, J. Mater. Chem. A, 2021, 9, 5787–5795 RSC.
- D.-M. Kaimaki, B. Haire, H. Ryan, G. Jiménez-Serratos, R. M. Alloway, M. Little, J. Morrison, I. Salama, M. Tillotson and B. E. Smith, Energy Fuels, 2019, 33, 7216–7224 CrossRef CAS.
- Q. Yang, Z. Hu, S. Zhu, R. Ma, H. Ma, Z. Ma, H. Wan, T. Zhu, Z. Jiang and W. Liu, J. Am. Chem. Soc., 2018, 140, 1715–1724 CrossRef CAS PubMed.
- X. Guo, M. Baumgarten and K. Müllen, Prog. Polym. Sci., 2013, 38, 1832–1908 CrossRef CAS.
- S. C. Rasmussen, S. J. Evenson and C. B. McCausland, Chem. Commun., 2015, 51, 4528–4543 RSC.
- H. E. Katz, Z. Bao and S. L. Gilat, Acc. Chem. Res., 2001, 34, 359–369 CrossRef CAS PubMed.
- A. Saeed and M. Faisal, Synth. Met., 2018, 241, 54–68 CrossRef.
- J. E. Frommer, Acc. Chem. Res., 1986, 19, 2–9 CrossRef CAS.
- K. Carter-Fenk and J. M. Herbert, Phys. Chem. Chem. Phys., 2020, 22, 24870–24886 RSC.
- A. L. McClellan, Tables of experimental dipole moments, WH Freeman, 1963 Search PubMed.
- K. Jug, S. Chiodo, P. Calaminici, A. Avramopoulos and M. G. Papadopoulos, J. Phys. Chem. A, 2003, 107, 4172–4183 CrossRef CAS.
- H. A. Fargher, T. J. Sherbow, M. M. Haley, D. W. Johnson and M. Pluth, Chem. Soc. Rev., 2022, 51, 1454–1469 RSC.
- T. F. Headen, Mol. Phys., 2019, 117, 3329–3336 CrossRef CAS.
- T. F. Headen, C. A. Howard, N. T. Skipper, M. A. Wilkinson, D. T. Bowron and A. K. Soper, J. Am. Chem. Soc., 2010, 132, 5735–5742 CrossRef CAS PubMed.
- T. Headen, P. Cullen, R. Patel, A. Taylor and N. Skipper, Phys. Chem. Chem. Phys., 2018, 20, 2704–2715 RSC.
- M. Jacobs, L. Greff Da Silveira, G. Prampolini, P. R. Livotto and I. Cacelli, J. Chem. Theory Comput., 2018, 14, 543–556 CrossRef CAS PubMed.
- S. Tsuzuki, K. Honda and R. Azumi, J. Am. Chem. Soc., 2002, 124, 12200–12209 CrossRef CAS PubMed.
- L. Gontrani, F. Ramondo and R. Caminiti, Chem. Phys. Lett., 2006, 422, 256–261 CrossRef CAS.
- L. Greff da Silveira, M. Jacobs, G. Prampolini, P. R. Livotto and I. Cacelli, J. Chem. Theory Comput., 2018, 14, 4884–4900 CrossRef CAS PubMed.
- T. Headen, E. Muller, M. Hoepfner, G. J. Serratos and K. M. R. Rahman, STFC ISIS Neutron and Muon Source, 2018 DOI:10.5286/ISIS.E.RB1820594, https://data.isis.stfc.ac.uk/doi/STUDY/103197017/.
- A. K. Soper, GudrunN and GudrunX: programs for correcting raw neutron and X-ray diffraction data to differential scattering cross section, Science & Technology Facilities Council Swindon, UK, 2011 Search PubMed.
- A. K. Soper, Int. Scholarly Res. Not., 2013, 279463 Search PubMed.
- A. K. Soper, Mol. Phys., 2009, 107, 1667–1684 CrossRef CAS.
- A. K. Soper, Mol. Simul., 2012, 38, 1171–1185 CrossRef CAS.
- A. Soper, Chem. Phys., 1996, 202, 295–306 CrossRef CAS.
- L. S. Dodda, I. Cabeza de Vaca, J. Tirado-Rives and W. L. Jorgensen, Nucleic Acids Res., 2017, 45, W331–W336 CrossRef CAS PubMed.
- T. Youngs, Mol. Phys., 2019, 117, 3464–3477 CrossRef CAS.
- T. G. Youngs, GitHub Repository, 2023, https://github.com/disorderedmaterials/dissolve/releases/tag/1.3.2 Search PubMed.
- A. Soper, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 104204 CrossRef.
- C.-F. Fu and S. X. Tian, J. Chem. Theory Comput., 2011, 7, 2240–2252 CrossRef CAS PubMed.
- G. Jiménez-Serratos, T. S. Totton, G. Jackson and E. A. Müller, J. Phys. Chem. B, 2019, 123, 2380–2396 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp03932c |
| This journal is © the Owner Societies 2023 |