Open Access Article
Open Access ArticleUnraveling the electronic origin of a special feature in the triplet-minus-singlet spectra of carotenoids in natural photosystems†
Agostino
Migliore
 *a,
Stefano
Corni
*a,
Stefano
Corni
 ab,
Alessandro
Agostini
ab,
Alessandro
Agostini
 a and
Donatella
Carbonera
a and
Donatella
Carbonera
 *a
*a
aDepartment of Chemical Sciences, University of Padova, Via Marzolo 1, 35131 Padova, Italy. E-mail: agostino.migliore@unipd.it; donatella.carbonera@unipd.it
bCNR Institute of Nanoscience, 41125 Modena, Italy
First published on 20th October 2023
Abstract
The influence of carotenoid triplet states on the Qy electronic transitions of chlorophylls has been observed in experiments on light-harvesting complexes over the past three decades, but the interpretation of the resulting spectral feature in the triplet minus singlet (T–S) absorption spectra of photosystems is still debated, as the physical–chemical explanation of this feature has been elusive. Here, we resolve this debate, by explaining the T–S spectra of pigment complexes over the Qy-band spectral region through a comparative study of chlorophyll–carotenoid model dyads and larger pigment complexes from the main light harvesting complex of higher plants (LHCII). This goal is achieved by combining state-of-the-art time-dependent density functional theory with analysis of the relationship between electronic properties and nuclear structure, and by comparison to the experiment. We find that the special signature in the T–S spectra of both model and natural photosystems is determined by singlet-like triplet excitations that can be described as effective singlet excitations on chlorophylls influenced by a stable electronic triplet on the carotenoid. The comparison with earlier experiments on different light-harvesting complexes confirms our theoretical interpretation of the T–S spectra in the Qy spectral region. Our results indicate an important role for the chlorophyll–carotenoid electronic coupling, which is also responsible for the fast triplet–triplet energy transfer, suggesting a fast trapping of the triplet into the relaxed carotenoid structure. The gained understanding of the interplay between the electronic and nuclear structures is potentially informative for future studies of the mechanism of photoprotection by carotenoids.
1. Introduction
Among the accessory pigments participating in the natural light harvesting processes, carotenoid (Car) is of paramount importance.1 The function of carotenoids in photosynthesis is twofold, stemming from their remarkable photophysical and photochemical properties. They not only complement the absorption of chlorophyll (Chl) in the green and blue spectral regions, but also play the indispensable role of preventing the formation of singlet oxygen and subsequent harmful oxidation reactions, thus protecting photosystems from photo-oxidative damage.2–4 In fact, it is well known that, under light-stress conditions, the formation of Chl triplet states (3Chl) and singlet oxygen (1O2) in the photosynthetic apparatus can be particularly significant. Therefore, the constitutive mechanism of triplet–triplet energy transfer (TTET), carried out by carotenoids to quench 3Chl (Car + 3Chl → 3Car + Chl), represents a fast and efficient response to excess illumination before other slower photoprotective mechanisms become fully functional. Once populated, 3Car, lying at a lower energy than 1O2, relaxes harmlessly to the ground state on a microsecond time scale.5,6 TTET has been shown to occur in light harvesting complexes from photosynthetic bacteria and algae, as well as in the antennas of the light harvesting complex (LHC) superfamily.7–10TTET from 3Chl to 1Car requires a Dexter-type exchange mechanism. Its occurrence is therefore limited to rather short distances between the two molecules.11–13
Time-resolved EPR (TR-EPR) and pulse EPR have been extensively employed in the past to gain insight into the TTET mechanism in several light harvesting complexes, revealing some structural requirements for efficient Chl triplet quenching, and especially a short center-to-center distance between the excitation donor and acceptor.9,14 Interestingly, microwave induced triplet minus singlet (T–S) absorption spectra of carotenoids in several light harvesting complexes, obtained via absorption detected magnetic resonance, have shown the presence of bands in the Qy region (i.e., the S0 → S1 electronic transition) of chlorophyll. Such bands have been attributed to a change in the interaction between chlorophyll and carotenoid as the latter accedes its triplet state. These interaction bands were first observed in the T–S spectra of the light harvesting complex II (LHCII) from higher plants, and later they have been also observed in the T–S spectra of a variety of light-harvesting complexes, such as LH2 from purple photosynthetic bacteria, PCP and LHC from dinoflagellates, FCP from diatoms, and VCP from eustigmatophytes,7,10,15–17 thus leading to their consideration as a general signature of Chl–Car interaction in photosynthetic systems (see Fig. 1).
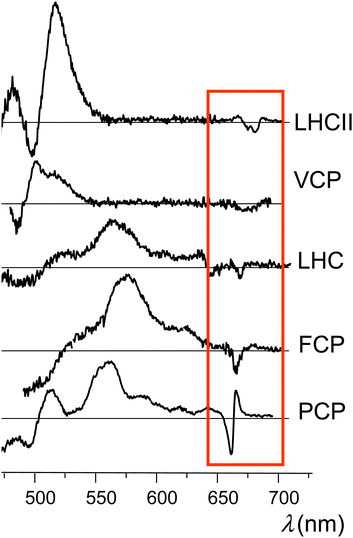 | ||
| Fig. 1 Experimental T–S spectra obtained from different light-harvesting complexes (we refer to the indicated experimental studies for details). These traces (from the top to down) were produced making use of data published in ref. 10 and 30 (Copyright 2014, Elsevier), ref. 14 (Copyright 2010, Elsevier), ref. 31 (Copyright 2012, Elsevier), and ref. 32 (Copyright 2008, Elsevier). The red box encloses the special features in the Qy spectral region. | ||
Later, the same bands have also been identified in the time-resolved optical spectra not only of light harvesting complexes18–22 but also of carotenoporphyrin molecular dyads.23 The intensity and shape of the bands are characteristic of the molecular systems, but, in all cases, the major feature is a main bleaching surrounded by positive bands in either the red or the blue side, or both.
Fourier-transform infrared spectroscopy T–S spectra performed on light harvesting complexes have shown the presence of bands assigned to a 3Chl a contribution long after the initial excitation, which in principle might explain the presence of the bands in the Qy region mentioned above. The hypothesis advanced to explain those data is that the triplet electron density could be shared between the carotenoid and chlorophyll molecules,24 and it has been inferred that the resonance Raman spectra reported in ref. 25 provide further indication of triplet sharing. However, such a delocalization of the electronic triplet is considered unlikely, due to the large energy gap between the triplet states of carotenoid found in natural photosystems and those of chlorophyll molecules.23,26 Indeed, electron nuclear double resonance experiments on carotenoid triplet states populated in LHCII and PCP have demonstrated that the triplet state resides only in the carotenoid moiety.27–29
Despite numerous observations that the presence of the triplet state on the carotenoid has a strong perturbation on the Qy electronic transition of Chl a, a convincing explanation of the origin of such a perturbation has not yet been produced. The common occurrence of positive bands (Fig. 1) makes the T–S feature even more intriguing, because it would apparently require that, in the illuminated sample, the pigment complexes in the triplet state can undergo (triplet) transitions with frequencies in the Qy spectral region (which would be missing when these pigment complexes are in their singlet ground electronic state), although the triplet spin density of chlorophyll–carotenoid systems or their mimics is known to be localized on the carotenoid23,27 and triplet electronic excitations of the carotenoid do not occur in this spectral range. In summary, although many details of the excited state properties of carotenoids are known, there are still many controversies and unraveled aspects concerning the molecular mechanisms through which carotenoids perform their photoprotective function.
In this work, we perform extended time-dependent density functional theory (TDDFT) calculations with the aim of explaining the physicochemical basis of the relationship between triplet and singlet transitions in the Car–Chl complexes of natural photosystems over a spectral range of particular spectroscopic interest. We especially focus on LHCII and the emerging physicochemical picture allows us to consistently explain the specific feature appearing in the T–S spectra of carotenoids in natural photosystems. By examining the interplay of electronic and structural features in the response of the systems to irradiation, we show that the structure-dependent electronic interaction between the carotenoid and the chlorophylls plays a fundamental role in determining the appearance of the T–S spectroscopic signature in the Qy spectral region. We examine the shape of the T–S signal in realistic molecular models from LHCII, for which we obtain a T–S feature similar to that observed experimentally, and also in a model dyad23 which mimics the simplest carotenoid–chlorophyll system still able to perform TTET. In more general terms, our analysis helps us understand the mutual electronic interaction between the carotenoid and chlorophyll pigments in both pigment complexes from natural photosystems and model dyads. Therefore, the gained information may also aid the implementation of bioinspired pigment complexes characterized by a suitable photo-resistance.
2. Methods
2.1 Molecular structures
We first investigated the ortho-carotenoporphyrin dyad from ref. 23, with coordinates optimized23 in both its singlet and triplet electronic states (Fig. 2a). We also used this model system to test the robustness of our theoretical conclusions with respect to the computational setup employed and possible effects of the molecular environment on the electronic excitations. All other molecular structures used were instead derived from an X-ray structure of LHCII.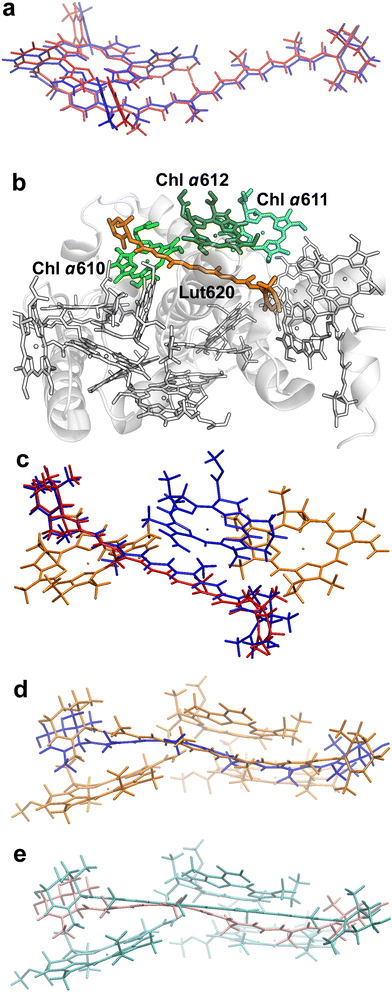 | ||
| Fig. 2 Molecular structures investigated. (a) Minimum-energy atomic structures of the ortho-carotenoporphyrin dyad in the singlet (blue) and triplet (red) spin states (coordinates from ref. 23). (b) Crystal structure of LHCII's monomer A from PDB file 1RWT.33 The pigments are drawn in the Licorice style (the phytyl chains of chlorophylls are not shown). The Car and Chl moieties used in our TDDFT study are colored in orange and different shades of green, respectively, while the other pigments and the protein are in white. (c) Comparison of M and M′ structures. Chlorophylls a610, a611 (colored in orange), and a612 (blue) have the same coordinates in the two model systems. The geometries of Lut620 in M (i.e., the singlet structure) and M′ (triplet) are represented in red and blue, respectively. (d) Comparison of structure M (orange) with M′′ (blue). (e) Comparison of the triplet structures M′ (cyan) and M′′′′ (pink). | ||
The crystal structure of LHCII was taken from the PDB file with ID 1RWT.33 Its monomer A was used for our investigation. Each monomer in the light-harvesting complex contains four carotenoids, eight Chls a and six Chls b, which are involved in the light harvesting mechanism. Moreover, the carotenoids sitting in site L1 are also involved in the protection from photooxidative stress.23 The L1 site comprises a lutein (Lut620) in the vicinity of three chlorophylls (Chls a610, a611, and a612) (Fig. 2). These molecular moieties were pruned from chain A, and the resulting model system was saturated with H atoms using the VMD program.34 The positions of all H atoms were then refined by means of a density functional theory (DFT) geometry optimization of the system in its ground singlet (S0) electronic state, with the heavy atoms fixed. The optimization was carried out using the NWChem software package,35,36 with the DRIVER optimizer, the 6-31g* basis set, and the M06-2X exchange–correlation functional.37 This density functional has been shown to yield reliable conformations of the carotenoporphyrin dyads23 thanks to its implicit inclusion of the dispersion energy.38
The model system {Lut620, Chl a610–612} thus obtained is herein denoted M. To investigate the excitonic coupling effects resulting from the close proximity of the chlorophylls, we also studied the model systems Mk ≡ {Lut620, Chl ak}, with k = 610, 611, and 612. Since we are interested in triplet-minus-singlet (T–S) spectra, and the triplet spin density is expected to be localized on the carotenoid moiety,23,27 we also optimized the geometry of Lut620 in the lowest triplet (T0) electronic state. As a first approximation, we optimized the geometry of the isolated Lut620 molecular moiety, which was then reinserted into the complete model. The H atoms of a Lut620 methyl group turned out to be quite close to Chl a612; therefore, their positions were further optimized in the presence of the chlorophyll moiety. The geometry relaxation was performed in a solvent modeled as a continuum with a dielectric constant εTHF= 7.4257 representative of tetrahydrofuran (THF) (this choice made for the geometry optimization of the carotenoid moiety helps the comparison with the computations in the model dyad), by using the default self-consistent reaction field method implemented in the Gaussian 16 software39 (that is, the polarizable continuum model using the integral equation formalism,40 requested by the SCRF keyword), with the ωB97X-D functional41 and the 6-31g* basis set (this computational setup was recently used to describe carotenoporphyrin dyads that mimic carotenoid–chlorophyll pairs in ref. 23). The resulting structure, M′, is compared with M in Fig. 2c.
As the above approach neglects the correlations of both nuclear and electronic degrees of freedom of Lut620 with those of Chls a610 and a611, we also took a more accurate approach which consisted in optimizing the geometry of Lut620 under the constraint of a triplet electronic state for the entire M system, with fixed chlorophylls. Moreover, also to assess the robustness of our theoretical conclusions with respect to both the approximations inherent in the model system and the computational setup of choice, geometry optimization was performed in a continuum medium with εp = 4, which mimics the interior of a protein (and thus, in particular, the internal protein environment of LHCII).42,43 This procedure yielded structure M′′, which is compared with M and M′ in Fig. 2d and e, respectively.
2.2 Electronic excitation calculations
The computations of electronic state excitations were all performed using the Gaussian 16 software package. We used the TDDFT method, with the ωB97X-D density functional41 and the 6-31g* basis set where not otherwise specified. Computational tests were performed using the CAM-B3LYP44 and M06-2X density functionals, as well as different basis sets (see the ESI†).We studied the electronic excitations for the different model systems in a vacuum and in continuous polarizable media that mimic protein interiors, THF, and protein surfaces (εs = 2045). The absorption properties of the molecular systems are described in terms of the electronic dipole oscillator strength (f)46–48 distributions of the singlet and triplet excitations. A Gaussian broadening of these distributions is used to better visualize the T–S spectra. The spin contamination49 is used to assess the reliability of the triplet excited states obtained using spin-unrestricted TDDFT. These states are considered for the analysis if the computed expectation value of S2 (where S is the total spin operator) differs from the exact one by about 10% or less.
The redistribution of electron density on the molecular systems as a result of electronic transitions is derived from the Mulliken population analysis50 of the DFT molecular orbitals (MOs) involved in the transitions within the TDDFT description. DFT MOs are consistently used within the framework of TDDFT. In more general terms, despite the fundamental conception of DFT, the utilization of DFT MOs is supported by a vast literature.48,51–53 Furthermore, we use natural transition orbitals (NTOs)54 to provide a compact qualitative description of the excitations. We find that most electronic transitions cannot simply be described as occurring from the highest occupied NTO to the lowest empty NTO. However, few NTOs are required in general for an adequate description of the electronic transitions.
The use of the Mulliken scheme is the default in the Gaussian program and has been supported by quantum mechanical analysis,55 as well as by a wide use (also in post-Hartree Fock approaches56,57) of chemical–physical contexts that range from the spectroscopic properties of molecules to the dynamics of chemical bonding,56,58–63 although they have been shown not to be an optimal choice in some cases (e.g., see ref. 64, where the iterative Hirshfeld method shows a better performance). Furthermore, our analysis implicitly explores the robustness of the theoretical conclusions (which consistently interpret the experiments) with respect to variations of the Mulliken population, as the latter is sensitive to the different molecular models and approximations to the exchange–correlation energy here employed.
3. Results and discussion
3.1 Electronic excitation in a model carotenoid-porphyrin dyad
To investigate if the special spectral feature in the Qy region of the T–S spectrum is intrinsically present in simple synthetic model systems or requires pigment–protein interactions, we first study an ortho-carotenoporphyrin dyad reported to be capable of rapid chlorophyll-to-carotenoid triplet–triplet energy transfer.23 Consistently with electron paramagnetic resonance27 and DFT23 analyses, we find that, in the dyad with optimal coordinates for the triplet electronic state, the electron spin density is localized on the carotenoid. In fact, calculating the total densities of excess spin-up (n↑) and spin-down (n↓) electrons around the atoms of the two molecular moieties, we obtain n↑–n↓ = 1.998 on the carotenoid and thus n↑–n↓= 0.002 on the tetra(4-methylphenyl)porphyrin (see also the ESI,† Fig. S1).The root-mean-square deviation between the optimized structures of the dyad in the lowest singlet and triplet states is 1.08 Å, which is within the range one may expect from the dynamics of a molecular system of this size. However, for the S0 state of the dyad with the optimal atomic coordinates of the lowest triplet state (T1), in a protein-interior (or THF) environment, we obtain a DFT total energy that is 1.23 (or 1.25) eV higher than that of the optimal geometry of the S0 state. This energy difference indicates that the thermal fluctuations of the molecular dyad in its state S0 cannot cause it to take conformations optimal for state T1, in which electronic excitation by irradiation and following intersystem crossing to a triplet state would lead directly to the localization of the electron spin density on the carotenoid component. However, even at low temperatures, if the system reaches the T1 excited state upon irradiation while it is still in a typical S0- or S1-state atomic conformation, the molecular structure will relax to an optimal one for a triplet electronic state, with localization of the triplet on the carotenoid, as this relaxation is an exergonic process, unless a barrier in the free energy landscape of the molecular complex hinders the relaxation process at very low temperatures. De facto, there is experimental evidence for the localization of the triplet states on carotenoids in light-harvesting complexes even at cryogenic temperatures.27–29
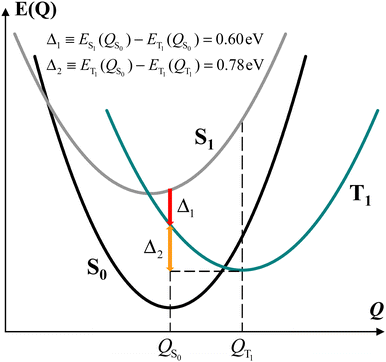
For the model dyad considered, our DFT analysis suggests the energy landscape patterns sketched in Fig. 3. For simplicity, we used the parabolic approximation to represent the energies of S0, S1, and T1 as functions of the nuclear coordinates Q. In this approximation and defining Q as a single, collective nuclear coordinate, the relative positions of the energy curves are consistent with the computational data. Although we did not determine the actual energy landscape and therefore the real relative positions of the state energy minima along Q, this energy scheme reflects the energy differences among the three electronic states at the QS0 and QT1 coordinates as computed for the dyad in the protein-interior environment. Fig. 3 shows that the energy of state T1 is lower than that of state S1 also at the molecular conformation QS0 of minimum energy for state S0, and, in addition, the relaxation of the dyad in its triplet state from the S0 to the T1 minimum-energy structure (QT1) releases an energy of 0.78 or 0.75 eV in a protein interior or a THF-like environment, respectively.
It is worth noting that, since the TTET is ultrafast, ref. 23 suggests that the donor triplet state of the porphyrin moiety (which replaces chlorophyll in the experimentally produced carotenoporphyrin mimics of chlorophyll–carotenoid dyads) corresponds to still unrelaxed QS1 coordinates. Furthermore, in calculating the chlorophyll–carotenoid electronic coupling, QS1 is assumed to be close to QS0 and is thus replaced by the latter.23Fig. 3 supports this assumption, as the potential energy curve of state T1 crosses that of state S1 near its minimum, and the intersection point is expected to be the starting point for the TTET.
We can gain insight into the photoexcitation processes in the dyad by considering the singlet and triplet excitations at the coordinates of minimum energy for both the singlet state (QS0) and the triplet state (QT1) of the dyad. In particular, this means to also consider the S0(QT1) → Sn(QT1) transitions. Incidentally, we note that, although the state S0(QT1) cannot be reached by thermal fluctuation of the dyad, since its energy is ∼1.2 eV higher than that of the minimum of the S0 parabola at S0(QS0) (as is discussed above), the dyad can also be considered, to some extent, as a model for pigment pairs in fast TTET configuration within natural photosystems, where the interactions with other pigments nearby and the protein environment can change the (free) energy landscape of the system and could allow for a non-negligible population of the analog of the S0(QT1) state in the real system.
Fig. 4a and Table 1 describe and compare S0(QS0) → Sn(QS0) and S0(QT1) → Sn(QT1) transitions derived for the dyad. The intensities of the excitations are described by their dipole oscillator strengths. In the conformation QT1, we obtain an S0–S1 transition, at a wavelength of 978 nm (the properties of this transition are reported in ESI,† Table S1), which is absent in QS0 and is primarily characterized as an electronic transition between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) occurring inside the carotenoid moiety (the highest densities of HOMO and LUMO are found respectively on atoms C8′ and C4 of the carotenoid moiety, with atomic indices as in ref. 23; see the ESI†). Although this transition shares properties with the bright S0 → S2 transitions in a number of carotenoids, the following points should be noted: (i) the singlet electronic excitations are sensitive to the flexible structure of carotenoids.65,66 (ii) S0(QT1) → Sn(QT1) transitions refer to the ortho-carotenoporphyrin dyad (where the carotenoid structure is influenced by the strong coupling with the porphyrin23) at the equilibrium coordinates of the triplet electronic state, QT1. Therefore, we expect substantial differences from the singlet electronic transitions of an isolated carotenoid in or near its ground singlet state coordinates.65 (iii) Different basis sets and exchange–correlation functionals (ωB97X-D, M06-2X, and M1167) describe the lowest-lying singlet electronic transitions S0(QT1) → S1(QT1) in a similar way (see the ESI,† Section S3). This excitation corresponds to the bright transition S0 → S2 in isolated carotenoids with the S0 geometry, but at the QT1 coordinates of the carotenoporphyrin dyad it is much lower in energy than both S0→S1 and S0 → S2 electronic excitations in isolated carotenoids. Moreover, it is worth noting that, at the QS0 coordinates of the dyad, the S0→S1 transition typical of the isolated carotenoid contaminates the lowest-lying singlet transitions of the dyad mainly localized on porphyrin, while the bright transition is higher in energy (ESI,† Table S1) as expected, and can be mostly identified with the S0 → S3 transition of the dyad. The S0(QT1) → S2(QT1) transition is instead substantially localized on the porphyrin portion of the dyad, in agreement with the Qy excitation in Chl a,68 (see the ESI,† Fig. S3), while an examination of the higher singlet states shows more significant mixing of the porphyrin and carotenoid electronic structures.
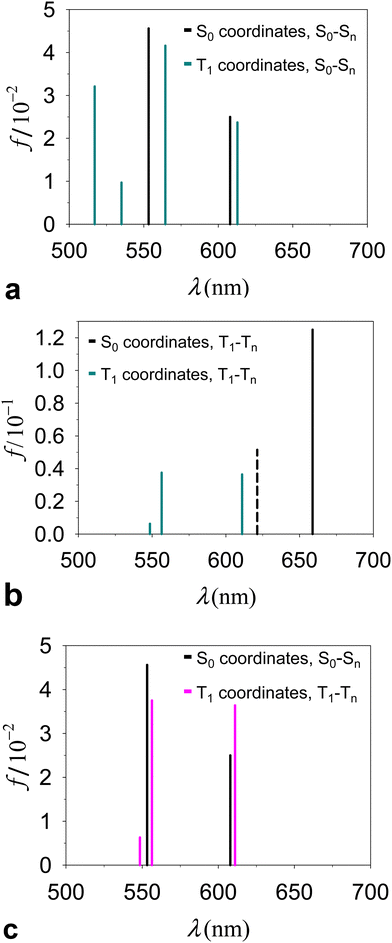 | ||
| Fig. 4 Electronic excitations in the ortho-carotenoporphyrin dyad proposed in ref. 23, studied by TDDFT at the ωB97X-D/6-31g* computational level of accuracy. The dyad was surrounded by THF, consistent with the environment used in ref. 23 to perform the experiments and optimize the geometry of the dyad. (a) Excitation wavelength (λ) and oscillator strength (f) of the singlet transitions from state S0 to Sn in the global energy minimum dyad structures with S0 and T1 spin states (the absorption spectra are shown over a wider λ range in the ESI,† Fig. S2a). (b) Analog of Fig. 4a for triplet transitions in the two conformations of the dyad. The dashed vertical line represents the rejected excitation with λ = 621.25 nm. (c) Singlet and triplet excitations in the QS0 and QT1 structures, respectively. | ||
| Functional | Conformation | Electron transition | λ (nm) | f | 〈S2〉b |
|---|---|---|---|---|---|
| a Excitations with similar electron density redistribution are distinguished by whether or not italics are used. The complete set of calculated electronic transitions is reported in the ESI, Table S1. The numbering of the triplet transitions takes into account only the excitations obtained with acceptable spin contamination. Similar triplet excitations are obtained in protein environment (ESI, Table S2). b These values are to be compared with the expected value of 2. | |||||
| ωB97X-D | Q S0 | S 0 → S 1 | 607.94 | 0.025 | |
| S0 → S2 | 553.25 | 0.046 | |||
| Q T1 | S 0 → S 2 | 612.90 | 0.024 | ||
| S0 → S3 | 564.48 | 0.042 | |||
| T 1 → T 2 | 611.02 | 0.036 | 2.27 | ||
| T1 → T3 | 556.44 | 0.038 | 2.24 | ||
| CAM-B3LYP | Q T1 | T 1 → T 2 | 595.83 | 0.041 | 2.26 |
| T1 → T3 | 543.94 | 0.029 | 2.29 | ||
While the absorption spectrum depends, as expected, on the nuclear coordinates, by inspection of the electronic excitations we find a physical correspondence between singlet transitions in the QS0 or QT1 structures that involve electron densities mainly localized on the tetrapyrrole. In particular, we focus on the singlet excitation from S0 to S1 in the QS0 structure (which occurs at a wavelength of 607.94 nm) and the excitation with the closest wavelength in the QT1 structure, that is, the S0–S2 transition, which occurs at 612.90 nm. These wavelengths lie within the range [600, 700] nm of our interest in the T–S spectrum (more specifically, we are interested in the peculiar signal appearing in the spectral region of the Qy band of chlorophyll a), also considering that the wavelength of the Qy electronic transition of chlorophyll a is expected to have a wavelength of about 623 nm from quantum chemistry vertical excitation calculations.68,69 The two electronic transitions are characterized by similar dipole oscillator strengths (namely, 0.0250 and 0.0237, respectively) and involve initial and final wave functions with similar spatial densities on the two structures. The electron densities involved in the transition are mainly localized on the porphyrin, with small tails on the carotenoid component (see the ESI,† Section S3). Such tails are a consequence of the proximity of the carotenoid to the porphyrin (and hence of their strong electronic coupling) and, obviously, they also depend on the covalent bonding of the two molecular moieties in the model dyad. The tail of the S0 electronic state is slightly larger in structure QT1 than in structure QS0, which can be interpreted as being due to the slightly less stable localization of the ground singlet state on the porphyrin in the non-optimal QT1 structure. On the other hand, one expects less influence of the nuclear geometry on the excited singlet state. Therefore, the excitation energy is lowered in structure QT1, compared to QS0 (the wavelength associated with the electronic transition increases from 607.94 nm to 612.90 nm). Apart from these small and yet appreciable differences, the similarity of excitations S0(QS0) − S1(QS0) and S0(QT1) − S2(QT1) is an expression of the adiabatic approximation inherent in the Born–Oppenheimer approximation,70 applied to electronic states mostly localized on the tetrapyrrole that are rather insensitive to relatively small changes in the coordinates of the same porphyrin and to even larger changes in the coordinates of the outer nuclear environment represented by the carotenoid moiety.
Contrary to the above, triplet excitations show stronger variations in response to structural changes leading from QS0 to QT1 (see Fig. 4b). However, the comparison of the electronic excitations of our primary interest is hindered by the spin contamination issue. In fact, while the triplet excitation in the QT1 structure (λ = 611.02 nm) was obtained with an acceptable spin contamination, the closest triplet electronic excitation in the QS0 structure (λ = 621.25 nm) was obtained with unacceptable spin contamination (〈S2〉 = 2.9; see the ESI,† Table S3, and see the ESI,† Table S4 for the dyad in different media). Importantly, we find that in the QS0 conformation the spin density is localized on the tetrapyrrole moiety, where n↑−n↓ = 1.992. This fact indicates that the carotenoid must rearrange its nuclear structure, compared to that in the (singlet) ground state, in order to host the triplet electronic state.
In Fig. 4c (see values in Table 1 and the ESI,† Table S1) we compare directly the singlet and triplet excitations occurring in the respective singlet (QS0) and triplet (QT1) equilibrium structures. The presence of the triplet causes frequency shifts and changes in the oscillator strengths of the relevant transitions which, although relatively small, are responsible for the observed special feature in the T–S spectrum. We also tested the properties of the triplet electronic excitations in the QT1 structure with respect to the computational approach, by using different basis sets and the CAM-B3LYP44 exchange–correlation functional. The basis set effects are unimportant (e.g., see the ESI,† Table S5). CAM-B3LYP, compared to ωB97X-D, produces triplet electronic excitations with shorter wavelengths in the relevant spectral region (Table 1 and ESI,† Table S6). This difference may result both from the fact that the geometry of the system was optimized using ωB97X-D and from the different approximations to the exchange and correlation energies in the two functionals. However, the physical properties of such excitations are very similar. In particular, we find that, in both cases, the lowest (reliable) triplet transition essentially corresponds to a redistribution of electron charge on the porphyrin moiety, while the electron spin density remains localized on the carotenoid moiety.
The S0(QS0) → S1(QS0), S0(QT1) → S2(QT1), and T1(QT1) → T2(QT1) transitions reported in Fig. 4a–c are contrasted in the unified and magnified view of Fig. 5a. In spite of their differences in spin multiplicity and/or underlying nuclear framework, these transitions are characterized by comparable wavelengths and oscillator strengths and share the localization of the electron density changes on the porphyrin moiety (Fig. 6). In particular, the singlet transitions in the two molecular conformations occur between quite similar electronic states, with oscillator strengths differing by only 5% (Fig. 6 shows the two most representative NTOs for each transition, while more NTOs are reported in the ESI,† Fig. S3), thus highlighting the robustness of this type of singlet excitation with respect to changes in the atomic frame. The comparison of the S0(QT1) → S2(QT1) and T1(QT1) → T2(QT1) excitations in Fig. 5a and 6 shows that the triplet state excitation is, essentially, a singlet transition localized on the porphyrin with no significant change of the triplet electron spin density residing in the carotenoid moiety (this fact is analyzed in the next section and is supported by the data in the ESI,† Table S7, which show that upon the transition the electron spin density changes by at most a very few percent, around a few atoms). That is, (i) the differences in the spin-up and spin-down electron densities occur within the carotenoid portion of the system and very similarly in the T1 and T2 states; (ii) upon transition from T1 and T2, the electron density changes in a molecular region (within porphyrin) in which the spin-up and spin-down electron densities essentially coincide and hence a singlet-like electron density is observed. Therefore, T1 and T2 essentially differ by a change in singlet-like electron density on the porphyrin moiety. Compared to the singlet excitation in the same QT1 conformation, the triplet excitation is characterized by a higher, but comparable oscillator strength and by quite similar (and substantially of the same kind) NTOs for both spin-up (α) and spin-down (β) electrons. The similarity of electron density redistribution in these two transitions, combined with the insensitivity of the singlet transition to the nuclear frame, explains the occurrence of the triplet transition T1(QT1) → T2(QT1) and the singlet transition S0(QS0) → S1(QS0) in the same spectral range. Yet, the differences in the λ and f values between these electronic excitations produces a spectral signal in the T–S spectrum of the molecular dyad over a wavelength range assimilable68 to that of the Qy band of chlorophyll a. This spectral feature is shown in Fig. 5b, where it is described in terms of triplet–singlet oscillator strength difference.
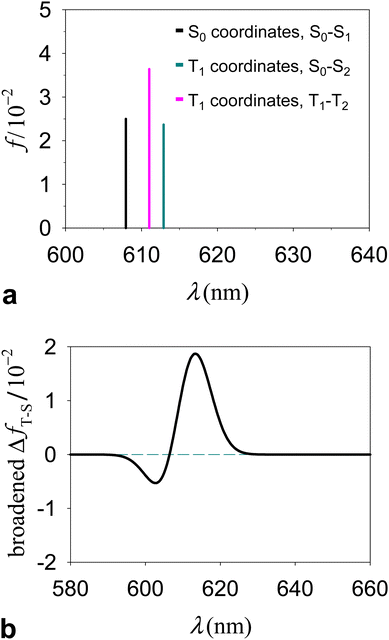 | ||
| Fig. 5 (a) Comparison between the wavelengths and oscillator strengths of the electronic excitations S0(QS0) → S1(QS0), S0(QT1) → S2(QT1), and T1(QT1) → T2(QT1). (b) T–S spectrum expressed in terms of the difference in oscillator strength distribution, ΔfT−S(λ), between the triplet electronic transitions in structure QT1 and the singlet transitions in structure QS0. To better visualize ΔfT−S(λ), we show its Gaussian broadening with a width parameter of 5 nm (the value of the width parameter influences the peak shape but not its position; see the ESI,† Fig. S4 for example). This broadening has clearly no connection with the vibrational broadening in the experimental spectra. | ||
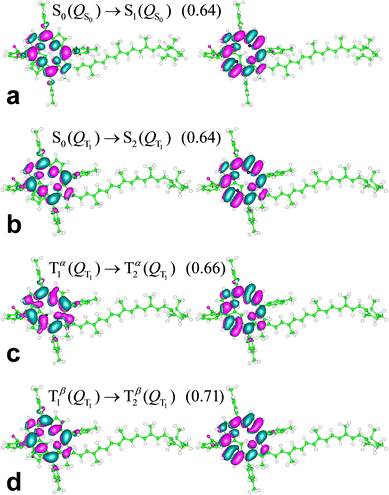 | ||
| Fig. 6 NTOs most representative of the indicated electronic excitations (their weights are provided in parentheses) of the ortho-carotenoporphyrin molecular dyad in THF-like solvent, represented using an isovalue of 0.02. Lobes of different signs are drawn in different colors. This distinction is used for better visualization but is clearly irrelevant for describing the degree of MO similarity. The MOs were rendered using the gOpenMol 3.00 molecular visualization program.71,72 | ||
3.2 Effects of the structure and electronic interaction on the electronic excitations
The theoretical analysis in this section provides a compact formulation and a physical characterization of the relationships between the relevant electronic excitations considered in Fig. 4–6, also helping us understand the physical origin of the T–S spectrum in Fig. 5b.By limiting the description of the system state to linear combinations of Slater determinants of the most relevant MOs and neglecting their tails at the covalent link between the porphyrin and carotenoid moieties (in accordance with the results shown in Fig. 6 and the ESI,† Fig. S3), the S0(QS0) → S1(QS0) transition can be approximately described in terms of tensor product states of the system components as
| |S0(P;QS0) 〉|S0(C;QS0)〉 → |S1(P;QS0)〉|S0(C;QS0)〉 | (1a) |
| |S0(P;QS0)〉 → |S1(P;QS0)〉 | (1b) |
| |S0(P; QT1)〉|S0(C; QT1)〉 → |S2(P; QT1)〉|S0(C; QT1)〉 | (2a) |
| |S0(P; QT1)〉 → |S2(P; QT1)〉 | (2b) |
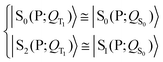 | (3) |
| |S′(P; QT1)〉|T1(C; QT1)〉 → |S′′(P; QT1)〉|T1(C; QT1)〉 | (4a) |
| |S′(P; QT1)〉 → |S′′(P; QT1)〉 | (4b) |
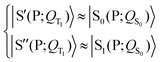 | (5) |
Eqn (3) and (5) summarize the effects of the triplet localized in the carotenoid on the singlet excitation in the porphyrin (which corresponds to the Qy transition in chlorophyll a) within the dyad model. As for the electron densities involved in the singlet electronic transition, eqn (3) and (5) mean that the effect of the interaction (which can be seen primarily as a polarization interaction in the approximate picture in terms of tensor-product states) between the electron density on the porphyrin and the electron spin density on the carotenoid is clearly greater than the effect of the change in the nuclear framework, in agreement with what has been suggested by recent studies (see ref. 30 and references therein).
Next, we use the above approximations to gain insight into the positioning of the spectral lines in Fig. 5a and therefore understand the T–S spectrum of Fig. 5b. Eqn (1b) and (2b) would entail equal excitation energies for the homologous singlet transitions in the two structures of the dyad if the electronic structures were fully independent of the QS0–QT1 structural change. In reality, the electronic wave functions at stake depend to some extent on the nuclear coordinates, and a more appreciable dependence is expected for the lower singlet states of the two transitions. Then, since QS0 is the conformation of minimum energy for the singlet ground state, the energy gap is expected to be larger (and hence the wavelength shorter) for the S0(QS0) → S1(QS0) transition than for S0(QT1) → S2(QT1). A similar consideration applies to the comparison of eqn (1b) and (4b). Furthermore, as the optimization of the overall dyad structure in the triplet electronic state primarily reduces the energy of state T1, from the comparison of the electronic states in eqn (2b) and (4b) it is expected that the excitation energy in the T1(QT1) → T2(QT1) transition is larger than that in S0(QT1) → S2(QT1). These simple considerations provide a rationale for the relative positions of the excitation frequencies in Fig. 5a. In particular, the occurrence of T1(QT1) → T2(QT1) at a longer wavelength than S0(QS0) → S1(QS0) explains the T–S signal of Fig. 5b, considering that only the transitions T1(QT1) → T2(QT1) and S0(QS0) → S1(QS0) are visible in the range of wavelength represented. Ultimately, we predict that the model dyad produced in ref. 23 shows a T–S spectrum like that in Fig. 5b, which is a signature of electronic interaction between the porphyrin and carotenoid moieties and takes place over a spectral range assimilable to that of the Qy band of chlorophyll a in a real pigment pair. This theoretically predicted T–S feature differs from that observed experimentally for the LHCII system,30 while it qualitatively resembles that measured in the peridinin-chlorophyll a-protein (PCP).32 Finally, we incidentally note that based on the results in Fig. 4a and b we expect a T–S feature of similar shape if both singlet and triplet transitions can occur in the QS0 conformation or a similar one, although the comparison is hampered by spin contamination. This comparison is instead feasible for the molecular systems drawn from the crystal structure of LHCII (see the next section).
3.3 Electronic excitations in LHCII carotenoid–chlorophyll systems
The results in the previous section predict the influence of the carotenoid triplet state on the Qy electronic transitions for a simplified model of chlorophyll–carotenoid pair consisting of covalently bonded porphyrin and carotenoid. We now study LHCII, the first system for which this triplet effect was experimentally observed. The molecular complex here investigated via TDDFT was derived from a monomer (A) of the LHCII crystal structure in the PDB file 1RWT33 (Fig. 2) and comprises one carotenoid (Lut620) and three chlorophylls (Chls a610-612). This pigment complex has been recognized as the site of the photoprotective function in LHCII,73 and it is characterized by the proximity of the three chlorophylls to each other, which has exciton effects on the relevant electronic excitations,74–78 and the vicinity of the carotenoid to the chlorophylls, and especially to Chls a610 and a612, which is responsible for a strong chlorophyll–carotenoid electronic coupling and can therefore enable a fast TTET. Performing the TDDFT investigation on the full pigment complex (317 atoms in total), we retain the effects of both structural features on the electronic wave functions. In particular, we take into account exciton effects, thus avoiding the possible artificial localization of electron density involved in excitations on individual chlorophyll–carotenoid pairs.The singlet and triplet excitations that occur in M = {Lut620, Chl a610–612} (which is part of a molecular system in its ground singlet state S0), with wavelengths in the Qy region of chlorophyll a and large, or appreciable, f values, are reported in Table 2 (the entire set of excited states obtained by TDDFT computation and the expectation values of S2 for the triplet states are given in the ESI,† Table S8). In this system, the wavelengths of the relevant transitions are longer than those found for the dyad model, that is, in between the wavelength expected theoretically for the Qy transition in chlorophyll a68,69 and the experimental spectral region of the Qy band, over which the T–S signal is observed.10,14,30–32 Furthermore, and importantly, the oscillator strengths of these electronic transitions are one order of magnitude larger than those associated with the relevant transitions in the model dyad (note that the crystal structure is expected to belong to the minimum of the singlet ground state in the free energy landscape of LHCII, and therefore these electronic excitations should be compared to the singlet and triplet excitations in the QS0 structure of the ortho-carotenoporphyrin dyad). All these characteristics of the excitations are similarly obtained simulating the system in the polarizable continuum models of protein interior, THF solvent, solvated-protein surface, and vacuum (see the ESI†).
| Environment | Singlet transition | λ S (nm) | f S | Triplet transition a | λ T (nm) | f T |
|---|---|---|---|---|---|---|
| a The triplet state numbering results from the fact that the TDDFT calculations also yielded triplet excitations with small oscillator strengths and longer wavelengths (see ESI Table S8). | ||||||
| Protein interior | S0 → S1 | 652.11 | 0.74 | |||
| S0 → S2 | 643.19 | 0.18 | T1 → T6 | 644.23 | 0.49 | |
| S0 → S3 | 632.62 | 0.09 | T1 → T7 | 639.19 | 0.27 | |
| THF | S0 → S1 | 656.24 | 0.76 | |||
| S0 → S2 | 645.65 | 0.21 | T1 → T6 | 646.69 | 0.53 | |
| S0 → S3 | 637.65 | 0.09 | T1 → T7 | 642.95 | 0.23 | |
NTOs representative of the singlet and triplet electronic excitations in internal protein environment are shown in Fig. 7. This is the most appropriate environment for the LHCII subsystems considered here, but similar NTOs are obtained in the other model environments, and especially in THF (ESI,† Fig. S5–S7), as its characteristic dielectric constant is quite similar to expected values within proteins.
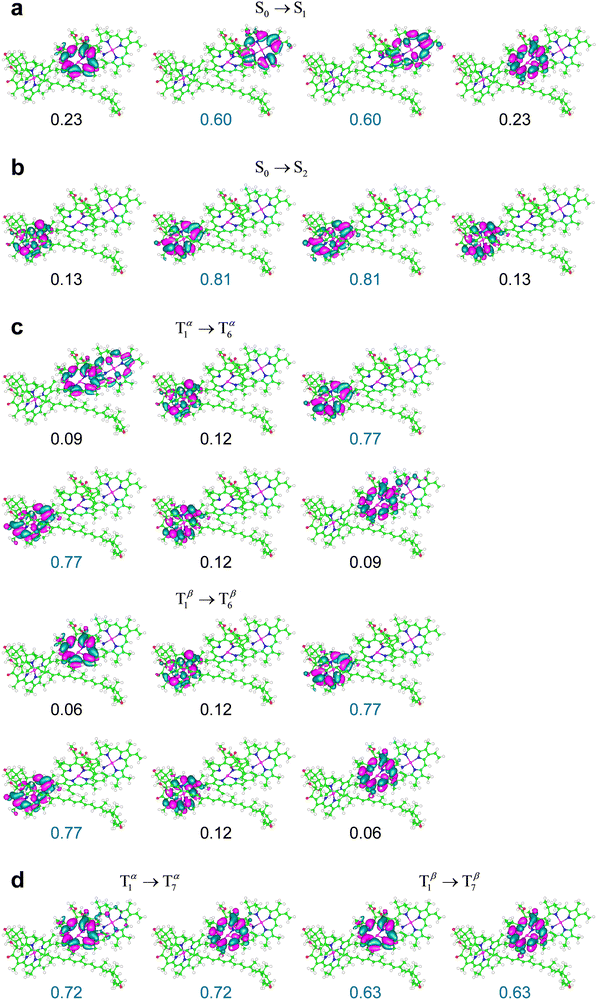 | ||
| Fig. 7 NTOs most representative of the indicated electronic transitions in the M subsystem of the LHCII crystal structure from the PDB file 1RWT,33 surrounded by an inner protein-like medium. The weaker S0 → S3 transition is not shown. The weights for the highest occupied and lowest unoccupied NTOs are in blue. The isovalue 0.02 is shown. Chl a610 is on the left (cf.Fig. 2b). | ||
Fig. 7 shows that the initial and final states of various electronic transitions are mainly localized on one of the three chlorophyll and also spread over one or both other chlorophylls. For example, the S0 → S1 transition primarily involves electron density changes on Chl a611, but also well-appreciable changes on Chl a612 (see Fig. 7a). This feature is a consequence of the excitonic coupling between chlorophylls. The S0 → S2 excitation is instead essentially localized on Chl a610 (Fig. 7b). The S0 → S1 excitation is stronger than S0 → S2, but both electronic transitions are characterized by relatively large oscillator strengths (see f values in Table 2). T1 → T6 mostly takes place on the Chl a610 (Fig. 7c). The T1 → T7 excitation mainly involves Chl a612 instead (Fig. 7d). It is worth noting that the triplet transitions (as well as S0 → S2) primarily involve the two chlorophylls that are spatially closer and therefore more strongly coupled to the carotenoid, compared to Chl a611, therefore confirming the significance of the chlorophyll–carotenoid coupling for the electronic excitations at stake. The exciton coupling effects are also clear in the triplet transitions and can be influenced by the environment. For example, while the T1 → T6 transition mainly involves Chl a610 in both protein interior and THF-like environments, the localizations of the NTOs describing the second and third largest contributions to the excitation (which are similar to each other in size) are inverted in the two media (cf. ESI,† Fig. S5, as well as the ESI,† Fig. S6 and S7 for the molecular system in a polarizable continuous medium that mimics protein surfaces and in a vacuum, respectively).
Both T1 → T6 and T1 → T7 excitations do not involve any significant change in the electron spin density. Thus, these triplet transitions can be approximately described as singlet transitions within the subsystem of chlorophylls in the presence of a triplet distribution that essentially remains as in the T1 state (for example, see the high similarity between the electron density redistributions in the S0 → S2 and T1 → T6 transitions in Fig. 7b and c). Thereby, over the spectral region of interest, the comparison between the triplet and singlet excitations describes the effects of a stable triplet on the properties of the singlet excitations nearby.
The similarity of the electron density redistribution in the singlet and triplet transitions analyzed explains the occurrence of the latter in the Qy spectral region. However, since the M system is derived from the crystal structure of LHCII, which is expected to be in the singlet ground state, we accordingly find that the triplet density is localized on the chlorophylls portion of the system. The same holds for the subsystems Mk ≡ {Lut620, Chl ak} (k = 610, 611, 612) (the excitations in M612 are reported in the ESI,† Tables S9–S11), consistent with the triplet localization on the tetrapyrrole moiety found for the ortho-carotenoporphyrin model dyad in the QS0 conformation. The experiments show instead that the triplet resides in the carotenoid moiety,23,27,28 and the TDDFT study of the ortho-carotenoporphyrin mimic (albeit with some limitations) of chlorophyll–carotenoid pairs showed that both the triplet ground state T123 and the triplet excited states with frequencies in the Qy range are localized on the carotenoid after geometry optimization of the full system in the triplet state. This means that, beginning with the excited system in singlet coordinates, the triplet spin density localizes on the carotenoid moiety only after adequate structural changes. Therefore, in chlorophyll–carotenoid complexes, the population of state T1 is expected to be accompanied by the relaxation of the carotenoid moiety to a geometry optimal to accommodate the pertinent spin density. Furthermore, this relaxation is an exergonic process, which can thus occur even at cryogenic temperatures.
Based on the above considerations, although the electronic excitations described by Table 2 and Fig. 7 can in principle give rise to a signal in the Qy region (and, therefore, could be of interest for understanding the behavior of biomimetic chlorophyll complexes), we performed the analysis of the singlet and triplet electronic excitations in the M′ and M′′ structures resulting from triplet-constrained optimization of Lut620 isolated and in the presence of the chlorophylls, respectively (see Methods). In the M′ and M′′ structures, the positioning of the carotenoid relative to the chlorophylls is, overall, somewhat similar to that in the LHCII crystal structure, but part of Lut620 is closer to the chlorophylls and the internal coordinates of Lut620 are optimal to accommodate a triplet spin density.
Table 3 summarizes the properties of the singlet and triplet electronic excitations of the M′ and M′′ systems in a protein environment with wavelengths that are, computationally, in the spectral region of the Qy band of chlorophyll a (the complete sets of excited states obtained using the density functionals indicated are reported in the ESI,† Tables S12–S14; the excitations in the M612 ≡ {Lut620, Chl a612} pigment pair are also reported in the ESI,† Table S15). Note that in M′ (M′′), compared to M, the Lut620 moiety is closer to Chl a612 (a610), thus favoring higher spin contaminations of the triplet states on average. The electronic transitions obtained with the M06-2X functional are shifted to higher frequencies with respect to those obtained using the ωB97X-D functional. This fact indicates the importance of the short and medium range exchange–correlation energy in these excitations, as the ωB97X-D functional is characterized by a relatively small value of the range-separation parameter (ω = 0.2) and the short-range Hartree–Fock component (22.2%) of the exchange term in ωB97X-D is much smaller than that in the global hybrid M06-2X functional (that is, 54% at all distances). We only report the two singlet and triplet transitions computed using M06-2X with relatively large oscillator strengths (the other excitations in the relevant wavelength range, which have f values of at most a few cents, are reported in the ESI,† Table S14).
| System | Method | Singlet transition | λ S (nm) | f S | Triplet transition a | λ T (nm) | f T |
|---|---|---|---|---|---|---|---|
| a For this triplet excitation in system M′, the triplet excited state was obtained with an S2 expectation value of 2.31, which is above the acceptation threshold. | |||||||
| M′ | ωB97X-D | S0 → S3 | 651.30 | 0.66 | T1 → T2a | 656.60 | 0.43 |
| S0 → S4 | 642.50 | 0.21 | T1 → T3 | 644.06 | 0.47 | ||
| T1 → T4 | 641.35 | 0.03 | |||||
| S0 → S5 | 632.77 | 0.07 | |||||
| M06-2X | S0 → S4 | 624.33 | 0.68 | T1 → T4 | 623.06 | 0.65 | |
| S0 → S5 | 611.97 | 0.36 | T1 → T5 | 611.84 | 0.37 | ||
| M′′ | ωB97X-D | S0 → S3 | 650.03 | 0.64 | |||
| S0 → S4 | 646.26 | 0.10 | T1 → T2 | 643.71 | 0.20 | ||
| S0 → S5 | 628.11 | 0.09 | T1 → T3 | 633.96 | 0.07 | ||
| M06-2X | S0 → S4 | 623.37 | 0.79 | T1 → T3 | 622.95 | 0.75 | |
| S0 → S6 | 613.40 | 0.27 | T1 → T4 | 613.44 | 0.25 | ||
The spin density is substantially localized on Lut620 in both model molecular systems. In fact, the electron spin densities on the Lut620 atoms add up to n↑–n↓ = 1.982 for the M′ system in both protein and THF environments, and to 1.994 (1.993) for the M′′ system in a protein interior (THF) environment. Similar conclusions are obtained for the subsystems from LHCII with one chlorophyll. For example, in the triplet state of M612 ≡ {Lut620, Chl a612} the electron spin density on Lut620 is n↑–n↓ = 0.002 or n↑–n↓ = 1.993 depending on whether this pigment pair is in crystallographic coordinates (as it is derived from M) or in the M′′ geometry, respectively. All such results consistently indicate the triplet localization on the carotenoid after appropriate rearrangement of its nuclear coordinates, irrespective of the fact that the partner chlorophyll system consists of one or more chlorophylls.
Some relevant excitations in M′ obtained using ωB97X-D are described by the NTOs in Fig. 8. The S0 → S3 and S0 → S4 transitions in M′ are primarily localized on Chl a611 and Chl a610, and are very similar to the S0 → S1 and S0 → S2 transitions in system M, respectively (compare Fig. 7a and b with Fig. 8a and b). The weaker S0 → S5 transition mainly involves Chl a612 (ESI,† Fig. S8). The energy ordering of the electronic excitations occurring on the three chlorophylls agrees with the expectations based on the singlet excitation energies of the individual chlorophylls from LHCII (see Table S16 in the ESI† and cf. ref. 76). Moreover, the three singlet transitions obtained in the full model system are clearly identified with transitions S0 → S1(Qy), each mainly localized on one of the chlorophylls, with some spreading on the other two chlorophylls due to excitonic coupling (see the ESI,† Table S17 and its discussion in the ESI†). These considerations hold for M, M′, and M′′, that is, regardless of Lut620 relaxation to its optimal triplet geometry.
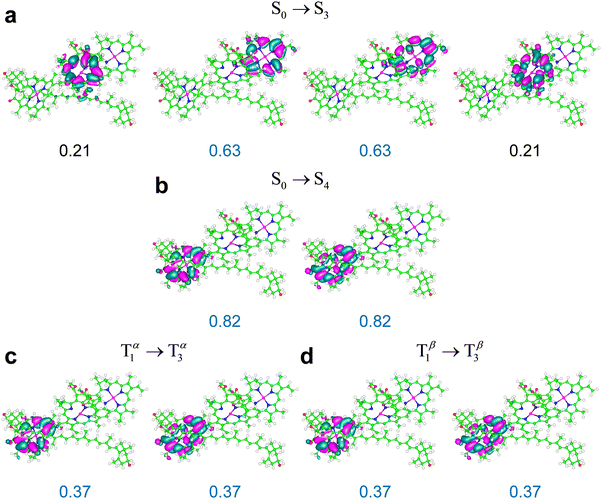 | ||
| Fig. 8 NTOs most representative of the indicated electronic transitions in the M′ system, which is shown in Fig. 2c (NTOs for the weaker S0 → S5 and T1 → T4 transitions in Table 3 are reported in the ESI,† Fig. S8), obtained using the ωB97X-D exchange–correlation functional. The weights of the highest occupied and lowest unoccupied NTOs are in blue. An isovalue of 0.02 is used. | ||
The most representative NTOs for the description of the T1 → T3 and T1 → T4 excitations are very similar to each other (e.g., see the NTOs for the stronger T1 → T3 excitation in Fig. 8) and closely resemble the NTOs for the T1 → T6 transition in system M (compare the highest occupied and lowest unoccupied NTOs in Fig. 7c and 8c, d). The electron spin density rearrangements in these triplet transitions are minor. Therefore, a picture similar to the one emerging for the ortho-carotenoporphyrin dyad (eqn (4) and (5)) applies to transitions such as, e.g., S0 → S4 and T1 → T3, which, like S0 → S2 and T1 → T6 in the M system, are characterized by very similar electron density redistributions (compare Fig. 8b–d). The comparison between the S0 → S3 and T1 → T2 excitations is instead affected by the rather significant spin contamination in the determination of the latter (this issue is exacerbated in the M′′ structure, for which the triplet excitation with similar frequency and oscillator strength was obtained with an expectation value of S2 close to 3; see ESI† Table S12). Clearly, this spin contamination also affects the electron spin density, and therefore the changes in electron density distribution for the computed T1 → T2 excitation. Nevertheless, the wavelength and value of f for this transition show its correspondence to the S0 → S3 transition and its physical meaning, as arising from a due79 comparison with the experimental evidence, cannot be neglected.
It can be expected that this spin contamination problem is favored by the proximity of chlorophylls to the carotenoid, which is accentuated in the M′ and M′′ systems compared to M (in particular, Chl a612 is closer to the carotenoid in M′ than in M, as is shown by Fig. 2c, while Chls a610 and a611 are closer to Lut620 in M′′ than in M, as shown by Fig. 2d), and, in principle, a different description of the electron exchange and correlation may more appropriately describe the T1 → T2 excitation and the corresponding triplet excitation in M′ and M′′. In fact, we obtained these excitations with spin contaminations well within the common acceptance range using the M06-2X density functional (see Table 3 and the ESI,† Table S14). Moreover, we again find that the triplet excitations in the relevant frequency range entail minor changes in the spin density on the carotenoid and singlet-like electron density variations on the chlorophylls. For example, Fig. 9 shows the singlet and triplet transitions in M′′ in terms of the NTOs obtained using the M06-2X functional. The electron density changes describing the triplet transition T1 → T3 are delocalized on Chl a611 and Chl a612, with a larger component on the former, as is shown by the NTOs in Fig. 9c. Such a delocalization is slightly more accentuated in the S0 → S4 transition, and thus its most representative NTOs are spread over the two chlorophylls (Fig. 9a). However, the electron density redistributions in the S0 → S4 and T1 → T3 excitations are very similar to each other. In fact, the two highest occupied NTOs describing the S0 → S4 excitation in Fig. 9a resemble each other and can be approximately constructed as linear combinations of the two occupied NTOs describing the T1 → T3 excitation in Fig. 9c; and the same consideration holds for the empty NTOs. The S0 → S6 and T1 → T4 excitations are, instead, very similarly localized on Chl a 610.
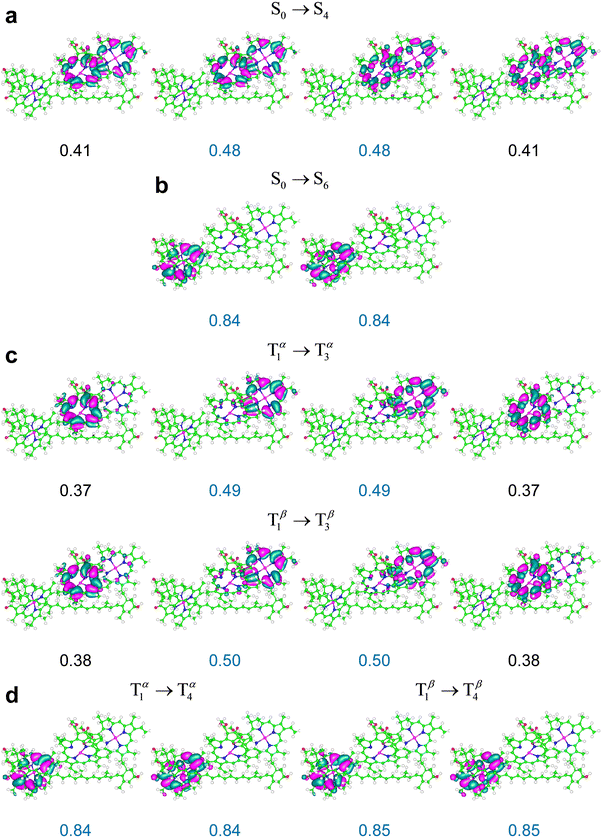 | ||
| Fig. 9 NTOs most representative of the indicated electronic transitions in system M′′ (Fig. 2d), obtained using the M06-2X exchange–correlation functional An isovalue of 0.02 is represented. | ||
Although the extent of the electronic excitation delocalization on the chlorophylls can also depend on the amount of Hartree–Fock exchange in the exchange–correlation functional used, the singlet-like character of the triplet transitions robustly emerges from the TDDFT computations as a characteristic of the photosystem response to irradiation. This property explains the occurrence of triplet excitations in the Qy frequency region (as these excitations entail electron density rearrangements similar to those produced by Qy transitions) and the resulting T–S absorption spectra with a bleaching flanked by two positive bands shown in Fig. 10.
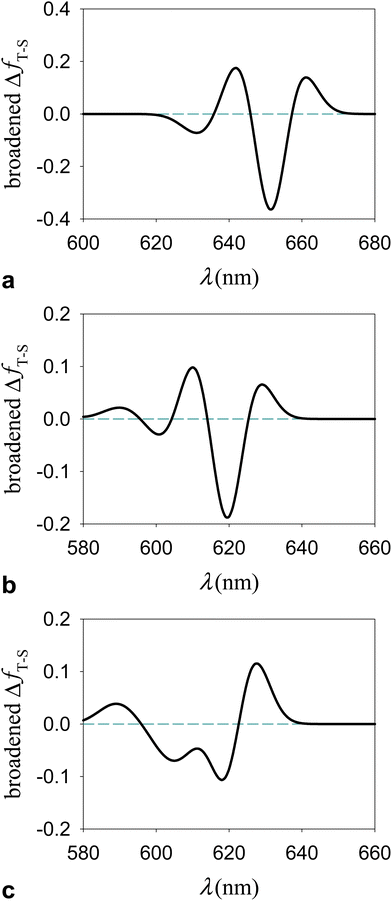 | ||
| Fig. 10 T–S spectrum in terms of electronic dipole oscillator strengths, ΔfT−S(λ), for the subsystem {Lut620, Chl a610 − 612} of LHCII in a model protein environment. ΔfT−S(λ) is represented using a Gaussian broadening with a width parameter of 5 nm. The T–S absorption spectrum for the M′ system was computed using the (a) ωB97X-D/6-31g* and (b) M06-2X/6-31g* computational setups. (c) The T–S spectrum of M′′ was obtained using the M06-2X functional. The λ and f values producing the T–S signals are reported in ESI† Tables S12–S14 (ESI†). | ||
The singlet and triplet electronic excitations leading to the T–S spectra in Fig. 10 were obtained at the respective optimal nuclear coordinates of the carotenoid. They thus represent the most realistic situation in which (i) the carotenoids in the sample are initially in their singlet states, with accordingly optimal nuclear structures, and the chlorophyll–carotenoid complexes are liable to singlet excitations; (ii) under suitable – approximately stationary over a certain time range – illumination, the sample has a triplet-state population, or change in population depending on the experimental technique used,80 with such triplets, or extra triplets, localized on some carotenoids of the sample, which have readily relaxed to their optimal triplet geometries. It is worth stressing that the difference spectra shown in Fig. 10 are described in terms of dipole oscillator strengths (which measure the integrated line-shapes, as they are obtained by integrating the extinction coefficient over frequency81,82) and therefore do not account for the vibrational broadening of spectral lines observed in the experiments. Nevertheless, these T–S absorption spectra can be compared to those experimentally observed in natural photosystems10,14,30,31,83 (see the next section).
Fig. 10a and b highlight the substantial robustness of the T–S absorption spectra with respect to the computational setup employed. The comparison between Fig. 10b and c (both computed using the M06-2X functional) highlights the dependence of the signal shape on the relative positions of the chlorophylls and the carotenoid, which are appreciably different in M′ and M′′ (Fig. 2e) and clearly influence their interaction, whence the electronic properties of the Qy excitations on the chlorophylls. In all cases, the bleaching is more pronounced than the absorption enhancement over the Qy region, and inspection of the computational data (see ESI† Tables S12–S14) suggests that the missing oscillator strength is at least partly redistributed over the Qx spectral region.
3.4 Comparison with experiments and their interpretation
Fig. 1 reports T–S spectra obtained experimentally by optically detected magnetic resonance at 1.8 K from different light-harvesting systems. Fig. 11 reports the T–S spectrum of LHCII detected at 77 K by time resolved absorption. Our computed T–S spectrum for the ortho-carotenoporphyrin model dyad (Fig. 5b) qualitatively resembles the experimental one for PCP (see the last panel in Fig. 1), but we found no obvious structural basis for this similarity, which deserves future investigation.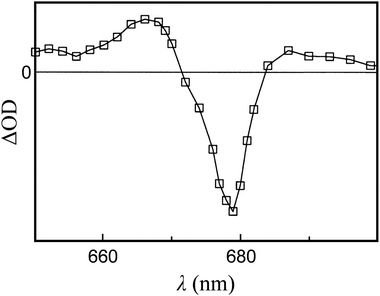 | ||
| Fig. 11 T–S spectrum, over the Qy spectral region, of LHCII monomers at a temperature of 77 K. The decay associated spectrum is shown. The curve describes the 12 μs signal due to 3Car (the open squares represent the experimental data points). Adapted from ref. 83. Copyright 1997, American Chemical Society. | ||
Inspection of the experimental spectra in Fig. 1 and 11 shows that the shape of the special feature in the T–S spectrum is strongly system-dependent. The T–S feature is sensitive to the relative positions and oscillator strengths of the singlet and triplet excitations, which depend on the interaction between the electron spin density on the carotenoid and the electron density on the chlorophylls. In turn, this interaction depends on the specific mutual geometry of chlorophylls and carotenoid, as is exemplified by Fig. 10b and c. Our theoretical T–S absorption spectra in Fig. 10b and c show a noticeable agreement with the T–S spectra obtained experimentally for LHCII in ref. 83 and 30, respectively. This agreement underlines the interpretative value of our theoretical-computational analysis, as the atomistic models employed were derived from the LHCII system.
4. Conclusions
Via TDDFT study of chlorophyll–carotenoid complexes, we explain the interplay between nuclear framework and electronic interactions among pigments which is at the origin of the special signature in the T–S spectra of natural photosystems such as LHCII. We consistently predict the T–S feature for model carotenoporphyrin dyads, which allows us to emphasize that this feature is not due to influence of the protein environment, except for its keeping the molecules in close relative positions.We find that, in LHCII, the triplet on the carotenoid perturbs several Qy transitions, which primarily occur on one of the chlorophylls but also involve the other two due to their exciton coupling. The perturbation caused by the interaction of the triplet electron density on the carotenoid with the electron density on the chlorophyll subsystem is greater than that due to structural changes of the carotenoid upon triplet localization (this was described by means of eqn (3) and (5) in the case of the model dyad). Our analysis shows that the triplet excitations involved in the T–S signal cause no significant change in the triplet electron density on the carotenoid moiety, since they essentially consist in electron density changes on the chlorophylls similar to those produced by the Qy singlet transitions of the system in its overall singlet spin state. This similarity enables the description of the relevant triplet excitations as singlet excitations occurring in the chlorophyll subsystem with a triplet maintained approximately unaltered on the carotenoid subsystem (as is described by eqn (1)–(5) for the ortho-carotenoporphyrin model dyad and the natural extension of these equations to the pigment complex containing several chlorophylls in LHCII), thus explaining the similar wavelengths of the relevant singlet and triplet transitions in the Qy region. However, the singlet-like triplet transitions are expectedly perturbed by the nearby triplet, so as to differ in wavelength and electronic oscillator strength (namely, absorption intensity) from the singlet transitions observed for the system in overall singlet state to an extent that determines the T–S signal in both the model dyad (Fig. 4–6) and the pigment complex from LHCII (Fig. 7–10).
The understanding of the electronic properties underlying the T–S spectra also enhances our understanding of the molecular mechanisms of the carotenoid photoprotection function and guide future implementations of biomimetic pigment structures in photosynthesis research. The electronic coupling between the chlorophyll and carotenoid subsystems which is responsible for the T–S spectral feature is also a determinant of the fast TTET. In photosynthetic light-harvesting systems, the relative geometry of the chlorophyll and carotenoid moieties seems to be optimized to reach picosecond time scales for TTET.84,85 Given the large TTET rate, the chlorophyll triplet state from which the excitation transfer takes place may correspond to S1 coordinates rather than to relaxed T1 coordinates (this approximation was used to calculate the electronic coupling between porphyrin and carotenoid in the model dyad,23 and it is meaningful if the vibrational energy relaxation involves slow modes, thus requiring up to tens of picoseconds as in other systems86). If we assume a parabolic behavior for the energies of the electronic states of the pigment complex as a function of the nuclear coordinates, such as in Fig. 3, the energy of state T1 crosses that of state S1 near its minimum, and (based on the high speed of TTET), moving down the T1 curve, the localization of the triplet on the carotenoid could occur appreciably before the full relaxation to the nuclear coordinates of triplet minimum energy. These considerations, while deserving future investigation (and facing the experimental difficulty of correlating triplet state kinetics to band intensity), theoretically relate the T–S feature in the Qy spectral region to the photoprotective mechanism efficiency.
Data availability statement
Details of the properties of the electronic excitations, tests of computational accuracy, complete sets of excited states, additional NTOs, transition electron density, T–S spectrum with different broadening width parameter, properties of the singlet transitions, coordinates of the M, M′ and M′′ systems are provided in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. M. and S. C. acknowledge funding from the European Union's Horizon 2020 research and innovation programme – Grant Agreement no. 964363 “ProID” – H2020-FETOPEN-2018-2020. A. A. and D. C. gratefully acknowledge financial support from the University of Padova (P-DiSC-2019).References
- H. A. Frank and R. J. Cogdell, Carotenoids in photosynthesis, Photochem. Photobiol., 1996, 63, 257–264 CrossRef CAS PubMed.
- D. Siefermann-Harms, The Light-Harvesting and Protective Functions of Carotenoids in Photosynthetic Membranes, Physiol. Plant., 1987, 69, 561–568 CrossRef CAS.
- D. Siefermann-Harms and A. Angerhofer, in Photosynthesis: From Light to Biosphere, ed. P. Mathis, Kluwer Akademic Publishers, Dordrecht, The Netherlands, 1995, vol. 4, pp. 71–74 Search PubMed.
- D. Siefermann-Harms and A. Angerhofer, Evidence for an O2-barrier in the light-harvesting chlorophyll-a/b-protein complex LHC II, Photosynth. Res., 1998, 55, 83–94 CrossRef CAS.
- T. Javorfi, G. Garab and K. R. Naqvi, Reinvestigation of the triplet-minus-singlet spectrum of chloroplasts, Spectroc. Acta Pt. A-Molec. Biomolec. Spectr., 2000, 56, 211–214 CrossRef PubMed.
- M. Mozzo, L. Dall’Osto, R. Hienerwadel, R. Bassi and R. Croce, Photoprotection in the antenna complexes of photosystem II-Role of individual xanthophylls in chlorophyll triplet quenching, J. Biol. Chem., 2008, 283, 6184–6192 CrossRef CAS PubMed.
- A. Angerhofer, F. Bornhauser, A. Gall and R. J. Cogdell, Optical and Optically Detected Magnetic Resonance Investigation on Purple Photosynthetic Bacterial Antenna Complexes, Chem. Phys., 1995, 194, 259–274 CrossRef CAS.
- R. Bittl, E. Schlodder, I. Geisenheimer, W. Lubitz and R. J. Cogdell, Transient EPR and absorption studies of carotenoid triplet formation in purple bacterial antenna complexes, J. Phys. Chem. B, 2001, 105, 5525–5535 CrossRef CAS.
- M. Di Valentin, F. Biasibetti, S. Ceola and D. Carbonera, Identification of the Sites of Chlorophyll Triplet Quenching in Relation to the Structure of LHC-II from Higher Plants. Evidence from EPR Spectroscopy, J. Phys. Chem. B, 2009, 113, 13071–13078 CrossRef CAS PubMed.
- D. Carbonera, A. Agostini, M. Di Valentin, C. Gerotto, S. Basso, G. M. Giacometti and T. Morosinotto, Photoprotective sites in the violaxanthin-chlorophyll alpha binding Protein (VCP) from Nannochloropsis gaditana, Biochim. Biophys. Acta-Bioenerg, 2014, 1837, 1235–1246 CrossRef CAS PubMed.
- G. Renger, in The Photosystems, ed. J. Barber, Elsevier, Amsterdam, 1992, pp. 45–99 Search PubMed.
- R. van Grondelle, J. P. Dekker, T. Gillbro and V. Sundstrom, Energy-Transfer and Trapping in Photosynthesis, Biochim. Biophys. Acta-Bioenerg., 1994, 1187, 1–65 CrossRef.
- D. Carbonera, M. Di Valentin, G. Agostini, G. Giacometti, P. A. Liddell, D. Gust, A. L. Moore and T. A. Moore, Energy transfer and spin polarization of the carotenoid triplet state in synthetic carotenoporphyrin dyads and in natural antenna complexes, Appl. Magn. Reson., 1997, 13, 487–504 CrossRef CAS.
- M. Di Valentin, E. Salvadori, G. Agostini, F. Biasibetti, S. Ceola, R. Hiller, G. M. Giacometti and D. Carbonera, Triplet–triplet energy transfer in the major intrinsic light-harvesting complex of Amphidinium carterae as revealed by ODMR and EPR spectroscopies, Biochim. Biophys. Acta-Bioenerg., 2010, 1797, 1759–1767 CrossRef CAS PubMed.
- R. Van der Vos, D. Carbonera and A. J. Hoff, Microwave and optical spectroscopy of carotenoid triplets in light-harvesting complex LHC II of spinach by absorbance-detected magnetic resonance, Appl. Magn. Reson., 1991, 2, 179–202 CrossRef CAS.
- A. Agostini, C. Buchel, M. Di Valentin and D. Carbonera, A distinctive pathway for triplet-triplet energy transfer photoprotection in fucoxanthin chlorophyll-binding proteins from Cyclotella meneghiniana, Biochim. Biophys. Acta-Bioenerg., 2021, 1862, 148310 CrossRef CAS PubMed.
- M. Di Valentin, S. Ceola, E. Salvadori, G. Agostini, G. M. Giacometti and D. Carbonera, Spectroscopic properties of the peridinins involved in chlorophyll triplet quenching in high-salt peridinin-chlorophyll a-protein from Amphidinium carterae as revealed by optically detected magnetic resonance, pulse EPR and pulse ENDOR spectroscopies, Biochim. Biophys. Acta-Bioenerg., 2008, 1777, 1355–1363 CrossRef CAS PubMed.
- S. S. Lampoura, V. Barzda, G. M. Owen, A. J. Hoff and H. van Amerongen, Aggregation of LHCII leads to a redistribution of the triplets over the central xanthophylls in LHCII, Biochemistry, 2002, 41, 9139–9144 CrossRef CAS PubMed.
- E. J. G. Peterman, F. M. Dukker, R. van Grondelle and H. van Amerongen, Chlorophyll a and carotenoid triplet states in light-harvesting complex II of higher plants, Biophys. J., 1995, 69, 2670–2678 CrossRef CAS PubMed.
- P. Khoroshyy, D. Bína, Z. Gardian, R. Litvín, J. Alster and J. Pšenčík, Quenching of chlorophyll triplet states by carotenoids in algal light-harvesting complexes related to fucoxanthin-chlorophyll protein, Photosynth. Res., 2018, 135, 213–225 CrossRef CAS PubMed.
- Z. Kvíčalová, J. Alster, E. Hofmann, P. Khoroshyy, R. Litvín, D. Bína, T. Polívka and J. Pšenčík, Triplet-triplet energy transfer from chlorophylls to carotenoids in two antenna complexes from dinoflagellate Amphidinium carterae, Biochim. Biophys. Acta-Bioenerg., 2016, 1857, 341–349 CrossRef PubMed.
- A. Agostini, D. Bína, D. Carbonera and R. Litvín, Conservation of triplet-triplet energy transfer photoprotective pathways in fucoxanthin chlorophyll-binding proteins across algal lineages, Biochim. Biophys. Acta-Bioenerg., 2023, 1864, 148935 CrossRef CAS PubMed.
- J. Ho, E. Kish, D. D. Méndez-Hernández, K. WongCarter, S. Pillai, G. Kodis, J. Niklas, O. G. Poluektov, D. Gust, T. A. Moore, A. L. Moore, V. S. Batista and B. Robert, Triplet–triplet energy transfer in artificial and natural photosynthetic antennas, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E5513–E5521 CAS.
- M. T. A. Alexandre, D. C. Lührs, I. H. M. van Stokkum, R. Hiller, M.-L. Groot, J. T. M. Kennis and R. van Grondelle, Triplet state dynamics in peridinin-chlorophyll-a-protein: A new pathway of photoprotection in LHCs?, Biophys. J., 2007, 93, 2118–2128 CrossRef CAS PubMed.
- A. Gall, R. Berera, M. T. Alexandre, A. A. Pascal, L. Bordes, M. M. Mendes-Pinto, S. Andrianambinintsoa, K. V. Stoitchkova, A. Marin, L. Valkunas, P. Horton, J. T. Kennis, R. van Grondelle, A. Ruban and B. Robert, Molecular adaptation of photoprotection: triplet states in light-harvesting proteins, Biophys. J., 2011, 101, 934–942 CrossRef CAS PubMed.
- F. S. Rondonuwu, T. Taguchi, R. Fujii, K. Yokoyama, Y. Koyama and Y. Watanabe, The energies and kinetics of triplet carotenoids in the LH2 antenna complexes as determined by phosphorescence spectroscopy, Chem. Phys. Lett., 2004, 384, 364–371 CrossRef CAS.
- E. Salvadori, M. Di Valentin, C. W. Kay, A. Pedone, V. Barone and D. Carbonera, The electronic structure of the lutein triplet state in plant light-harvesting complex II, Phys. Chem. Chem. Phys., 2012, 14, 12238–12251 RSC.
- M. Di Valentin, S. Ceola, G. Agostini, G. M. Giacometti, A. Angerhofer, O. Crescenzi, V. Barone and D. Carbonera, Pulse ENDOR and density functional theory on the peridinin triplet state involved in the photo-protective mechanism in the peridinin-chlorophyll a-protein from Amphidinium carterae, Biochim. Biophys. Acta-Bioenerg., 2008, 1777, 295–307 CrossRef CAS PubMed.
- J. Niklas, T. Schulte, S. Prakash, M. van Gastel, E. Hofmann and W. Lubitz, Spin-density distribution of the carotenoid triplet state in the peridinin-chlorophyll-protein antenna. A Q-band pulse electron-nuclear double resonance and density functional theory study, J. Am. Chem. Soc., 2007, 129, 15442–15443 CrossRef CAS PubMed.
- D. Carbonera, A. Agostini, M. Bortolus, L. Dall’Osto and R. Bassi, Violaxanthin and zeaxanthin may replace lutein at the L1 Site of LHCII, conserving the interactions with surrounding chlorophylls and the capability of triplet–triplet energy transfer, Int. J. Mol. Sci., 2022, 23, 4812 CrossRef CAS PubMed.
- M. Di Valentin, C. Büchel, G. M. Giacometti and D. Carbonera, Chlorophyll triplet quenching by fucoxanthin in the fucoxanthin-chlorophyll protein from the diatom Cyclotella meneghiniana, Biochem. Biophys. Res. Commun., 2012, 427, 637–641 CrossRef CAS PubMed.
- M. Di Valentin, G. Agostini, E. Salvadori, S. Ceola, G. M. Giacometti, R. G. Hiller and D. Carbonera, Triplet-triplet energy transfer in Peridinin-Chlorophyll a-protein reconstituted with Chl a and Chl d as revealed by optically detected magnetic resonance and pulse EPR: Comparison with the native PCP complex from Amphidinium carterae, Biochim. Biophys. Acta-Bioenerg., 2009, 1787, 168–175 CrossRef CAS PubMed.
- Z. F. Liu, H. C. Yan, K. B. Wang, T. Y. Kuang, J. P. Zhang, L. L. Gui, X. M. An and W. R. Chang, Crystal structure of spinach major light-harvesting complex at 2.72 Å resolution, Nature, 2004, 428, 287–292 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graph., 1996, 14, 33–38 CrossRef CAS PubMed.
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, NWChem: a comprehensive and scalable open-source solution for large scale molecular simulations, Comput. Phys. Commun., 2010, 181, 1477 CrossRef CAS.
- E. Aprà, E. J. Bylaska, W. A. de Jong, N. Govind, K. Kowalski, T. P. Straatsma, M. Valiev, H. J. J. van Dam, Y. Alexeev, J. Anchell, V. Anisimov, F. W. Aquino, R. Atta-Fynn, J. Autschbach, N. P. Bauman, J. C. Becca, D. E. Bernholdt, K. Bhaskaran-Nair, S. Bogatko, P. Borowski, J. Boschen, J. Brabec, A. Bruner, E. Cauët, Y. Chen, G. N. Chuev, C. J. Cramer, J. Daily, M. J. O. Deegan, T. H. Dunning Jr., M. Dupuis, K. G. Dyall, G. I. Fann, S. A. Fischer, A. Fonari, H. Früchtl, L. Gagliardi, J. Garza, N. Gawande, S. Ghosh, K. Glaesemann, A. W. Götz, J. Hammond, V. Helms, E. D. Hermes, K. Hirao, S. Hirata, M. Jacquelin, L. Jensen, B. G. Johnson, H. Jónsson, R. A. Kendall, M. Klemm, R. Kobayashi, V. Konkov, S. Krishnamoorthy, M. Krishnan, Z. Lin, R. D. Lins, R. J. Littlefield, A. J. Logsdail, K. Lopata, W. Ma, A. V. Marenich, J. Martin del Campo, D. Mejia-Rodriguez, J. E. M. Moore, J. M. Mullin, T. Nakajima, D. R. Nascimento, J. A. Nichols, P. J. Nichols, J. Nieplocha, A. Otero-de-la-Roza, B. Palmer, A. Panyala, T. Pirojsirikul, B. Peng, R. Peverati, J. Pittner, L. Pollack, R. M. Richard, P. Sadayappan, G. C. Schatz, W. A. Shelton, D. W. Silverstein, D. M. A. Smith, T. A. Soares, D. Song, M. Swart, H. L. Taylor, G. S. Thomas, V. Tipparaju, D. G. Truhlar, K. Tsemekhman, T. Van Voorhis, Á. Vázquez-Mayagoitia, P. Verma, O. Villa, A. Vishnu, K. D. Vogiatzis, D. Wang, J. H. Weare, M. J. Williamson, T. L. Windus, K. Woliński, A. T. Wong, Q. Wu, C. Yang, Q. Yu, M. Zacharias, Z. Zhang, Y. Zhao and R. J. Harrison, NWChem: Past, Present, and Future, J. Chem. Phys., 2020, 152, 184102 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- N. Ramos-Berdullas, I. Pérez-Juste, C. Van Alsenoy and M. Mandado, Theoretical study of the adsorption of aromatic units on carbon allotropes including explicit (empirical) DFT dispersion corrections and implicitly dispersion-corrected functionals: the pyridine case, Phys. Chem. Chem. Phys., 2015, 17, 575–587 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. E. Peralta, Jr., F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Quantum mechanical continuum solvation models, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- J. D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- L. I. Krishtalik, A. M. Kuznetsov and E. L. Mertz, Electrostatics of proteins: description in terms of two dielectric constants simultaneously, Proteins, 1997, 28, 174–182 CrossRef CAS.
- R. Pethig, Dielectric and electronic behavior of biological materials, John Wiley & Sons, New York, 1979 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- L. Li, C. Li, Z. Zhang and E. Alexov, On the Dielectric “Constant” of Proteins: Smooth Dielectric Function for Macromolecular Modeling and Its Implementation in DelPhi, J. Chem. Theory Comput., 2013, 9, 2126–2136 CrossRef CAS PubMed.
- B. H. Bransden and C. J. Joachain, Physics of atoms and molecules, John Wiley & Sons, New York, 1988 Search PubMed.
- M. C. Gupta, Atomic and Molecular Spectroscopy, New Age International (P), New Delhi, 2007 Search PubMed.
- L. J. Zheng, N. F. Polizzi, A. R. Dave, A. Migliore and D. N. Beratan, Where Is the Electronic Oscillator Strength? Mapping Oscillator Strength across Molecular Absorption Spectra, J. Phys. Chem. A, 2016, 120, 1933–1943 CrossRef CAS PubMed.
- W. Koch and M. C. Holthausen, Chemist's Guide to Density Functional Theory, Wiley, New York, 2000 Search PubMed.
- F. Jensen, Introduction to Computational Chemistry, John Wiley & Sons, Chichester, 2nd edn, 2007 Search PubMed.
- R. Stowasser and R. Hoffmann, What do the Kohn-Sham orbitals and eigenvalues mean?, J. Am. Chem. Soc., 1999, 121, 3414–3420 CrossRef CAS.
- P. Bouř, Comparison of Hartree-Fock and Kohn-Sham determinants as wave functions, J. Comput. Chem., 2000, 21, 8–16 CrossRef.
- N. Gillet, L. Berstis, X. J. Wu, F. Gajdos, A. Heck, A. de la Lande, J. Blumberger and M. Elstner, Electronic coupling calculations for bridge-mediated charge transfer using constrained density functional theory (CDFT) and effective Hamiltonian approaches at the density functional theory (DFT) and fragment-orbital density functional tight binding (FODFTB) level, J. Chem. Theory Comput., 2016, 12, 4793–4805 CrossRef CAS PubMed.
- R. L. Martin, Natural transition orbitals, J. Chem. Phys., 2003, 118, 4775–4777 CrossRef CAS.
- R. Carbo-Dorca and P. Bultinck, Quantum mechanical basis for Mulliken population analysis, J. Math. Chem., 2004, 36, 231–239 CrossRef CAS.
- L. Blancafort and A. A. Voityuk, MS-CASPT2 calculation of excess electron transfer in stacked DNA nucleobases, J. Phys. Chem. A, 2007, 111, 4714–4719 CrossRef CAS PubMed.
- P. Tecmer, A. S. P. Gomes, U. Ekström and L. Visscher, Electronic spectroscopy of UO22+, NUO+ and NUN: an evaluation of time-dependent density functional theory for actinides, Phys. Chem. Chem. Phys., 2011, 13, 6249–6259 RSC.
- T. Kamachi, N. Kihara, Y. Shiota and K. Yoshizawa, Computational exploration of the catalytic mechanism of dopamine β-monooxygenase: Modeling of its mononuclear copper active sites, Inorg. Chem., 2005, 44, 4226–4236 CrossRef CAS PubMed.
- D. S. E. Sayed and E. M. Abdelrehim, Spectroscopic details on the molecular structure of pyrimidine-2-thiones heterocyclic compounds: computational and antiviral activity against the main protease enzyme of SARS-CoV-2, BMC Chem., 2022, 16, 82 CrossRef CAS PubMed.
- A. A. Voityuk and N. Rosch, Fragment charge difference method for estimating donor-acceptor electronic coupling: Application to DNA π-stacks, J. Chem. Phys., 2002, 117, 5607–5616 CrossRef CAS.
- S. Yokomori, S. Dekura, T. Fujino, M. Kawamura, T. Ozaki and H. Mori, Vapochromism induced by intermolecular electron transfer coupled with hydrogen-bond formation in zinc dithiolene complex, J. Mater. Chem. C, 2020, 8, 14939–14947 RSC.
- N. V. Ilawe, M. B. Oviedo and B. M. Wong, Effect of quantum tunneling on the efficiency of excitation energy transfer in plasmonic nanoparticle chain waveguides, J. Mater. Chem. C, 2018, 6, 5857–5864 RSC.
- A. Al-Haddad, S. Oberli, J. Gonzalez-Vazquez, M. Bucher, G. Doumy, P. Ho, J. Krzywinski, T. J. Lane, A. Lutman, A. Marinelli, T. J. Maxwell, S. Moeller, S. T. Pratt, D. Ray, R. Shepard, S. H. Southworth, A. Vazquez-Mayagoitia, P. Walter, L. Young, A. Picon and C. Bostedt, Observation of site-selective chemical bond changes via ultrafast chemical shifts, Nat. Commun., 2022, 13, 7170 CrossRef CAS PubMed.
- R. J. MacDonell, S. Patchkovskii and M. S. Schuurman, A Comparison of Partial Atomic Charges for Electronically Excited States, J. Chem. Theory Comput., 2022, 18, 1061–1071 CrossRef CAS PubMed.
- E. Coccia, D. Varsano and L. Guidoni, Ab Initio Geometry and Bright Excitation of Carotenoids: Quantum Monte Carlo and Many Body Green's Function Theory Calculations on Peridinin, J. Chem. Theory Comput., 2014, 10, 501–506 CrossRef CAS PubMed.
- R. Spezia, S. Knecht and B. Mennucci, Excited state characterization of carbonyl containing carotenoids: a comparison between single and multireference descriptions, Phys. Chem. Chem. Phys., 2017, 19, 17156–17166 RSC.
- R. Peverati and D. G. Truhlar, Improving the accuracy of hybrid meta-GGA density functionals by range separation, J. Phys. Chem. Lett., 2011, 2, 2810–2817 CrossRef CAS.
- A. Sirohiwal, R. Berraud-Pache, F. Neese, R. Izsak and D. A. Pantazis, Accurate Computation of the Absorption Spectrum of Chlorophyll a with Pair Natural Orbital Coupled Cluster Methods, J. Phys. Chem. B, 2020, 124, 8761–8771 CrossRef CAS PubMed.
- E. Gruber, C. Kjaer, S. B. Nielsen and L. H. Andersen, Intrinsic Photophysics of Light-harvesting Charge-tagged Chlorophyll a and b Pigments, Chem. – Eur. J., 2019, 25, 9153–9158 CrossRef CAS PubMed.
- M. Weissbluth, Atoms and Molecules, Academic Press, New York, 1978 Search PubMed.
- L. Laaksonen, A Graphics Program for the Analysis and Display of Molecular-Dynamics Trajectories, J. Mol. Graph., 1992, 10, 33–34 CrossRef CAS PubMed.
- D. L. Bergman, L. Laaksonen and A. Laaksonen, Visualization of solvation structures in liquid mixtures, J. Mol. Graph., 1997, 15, 301–306 CrossRef CAS PubMed.
- A. Agostini, L. Nicol, N. Da Roit, M. Bortolus, R. Croce and D. Carbonera, Altering the exciton landscape by removal of specific chlorophylls in monomeric LHCII provides information on the sites of triplet formation and quenching by means of ODMR and EPR spectroscopies, Biochim. Biophys. Acta-Bioenerg., 2021, 1862, 148481 CrossRef CAS PubMed.
- F. Müh, A. El-Amine Madjet and T. Renger, Structure-based identification of energy sinks in plant light-harvesting complex II, J. Phys. Chem. B, 2010, 114, 13517–13535 CrossRef PubMed.
- V. I. Novoderezhkin and R. van Grondelle, Modeling of excitation dynamics in photosynthetic light-harvesting complexes: exact versus perturbative approaches, J. Phys. B: At., Mol. Opt. Phys., 2017, 50, 124003 CrossRef.
- V. Sláma, L. Cupellini and B. Mennucci, Exciton properties and optical spectra of light harvesting complex II from a fully atomistic description, Phys. Chem. Chem. Phys., 2020, 22, 16783–16795 RSC.
- C. König and J. Neugebauer, First-principles calculation of electronic spectra of light-harvesting complex II, Phys. Chem. Chem. Phys., 2011, 13, 10475–10490 RSC.
- P. López-Tarifa, N. Liguori, N. van den Heuvel, R. Croce and L. Visscher, Coulomb couplings in solubilised light harvesting complex II (LHCII): challenging the ideal dipole approximation from TDDFT calculations, Phys. Chem. Chem. Phys., 2017, 19, 18311–18320 RSC.
- D. Young, Computational Chemistry: A Practical Guide for Applying Techniques to Real World Problems, John Wiley & Sons, Inc., New York, 2001 Search PubMed.
- D. Carbonera, Optically Detected Magnetic Resonance (ODMR) of photoexcited triplet states, Photosynth. Res., 2009, 102, 403–414 CrossRef CAS PubMed.
- A. Nitzan, Chemical dynamics in condensed phases, Oxford University Press, Oxford, 2007 Search PubMed.
- L. Zheng, N. F. Polizzi, A. R. Dave, A. Migliore and D. N. Beratan, Where Is the Electronic Oscillator Strength? Mapping Oscillator Strength across Molecular Absorption Spectra, J. Phys. Chem. A, 2016, 120, 1933–1943 CrossRef CAS PubMed.
- E. J. G. Peterman, C. C. Gradinaru, F. Calkoen, J. C. Borst, R. van Grondelle and H. van Amerongen, Xanthophylls in light-harvesting complex II of higher plants: Light harvesting and triplet quenching, Biochemistry, 1997, 36, 12208–12215 CrossRef CAS PubMed.
- R. Schödel, K. D. Irrgang, J. Voigt and G. Renger, Rate of carotenoid triplet formation in solubilized light-harvesting complex II (LHCII) from spinach, Biophys. J., 1998, 75, 3143–3153 CrossRef PubMed.
- D. M. Niedzwiedzki, J. Jiang, C. S. Lo and R. E. Blankenship, Spectroscopic properties of the Chlorophyll a–Chlorophyll c2–Peridinin-Protein-Complex (acpPC) from the coral symbiotic dinoflagellate Symbiodinium, Photosynth. Res., 2014, 120, 125–139 CrossRef CAS PubMed.
- H. Fujisaki and J. E. Straub, Vibrational energy relaxation in proteins, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6726–6731 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp03836j |
| This journal is © the Owner Societies 2023 |