 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Anion dynamics and motional decoupling in a glycerol–choline chloride deep eutectic solvent studied by one- and two-dimensional 35Cl NMR†
Yannik
Hinz
 ,
Joachim
Beerwerth
,
Joachim
Beerwerth
 and
Roland
Böhmer
and
Roland
Böhmer

Fakultät Physik, Technische Universität Dortmund, 44221 Dortmund, Germany
First published on 11th October 2023
Abstract
Chlorine-35 is among the few nuclides that provide an experimental handle on the anion dynamics in choline based deep eutectic solvents. By combining several nuclear magnetic resonance (NMR) techniques, the present work examines the Cl− motions within glyceline, a glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) choline chloride 2
choline chloride 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solution, in a large temperature range down to the glass transition temperature Tg. The applied methods include spin relaxometry, second-order line shape analysis, as well as two-dimensional central-transition exchange and stimulated-echo spectroscopy. The finding of unstructured central-transition NMR spectra characterized by a relatively small average quadrupolar coupling attests to a highly disordered, essentially nondirectional anionic coordination in glyceline. For temperatures larger than about 1.3Tg the chlorine motions are well coupled to those of the glycerol and the choline moieties. At lower temperatures the local translational anion dynamics become Arrhenian and increasingly faster than the motion of glyceline's matrix molecules. Upon further cooling, the overall ionic conductivity continues to display a super-Arrhenius behavior, implying that the choline cations rather than the Cl anions dominate the long-range charge transport also near Tg.
1 solution, in a large temperature range down to the glass transition temperature Tg. The applied methods include spin relaxometry, second-order line shape analysis, as well as two-dimensional central-transition exchange and stimulated-echo spectroscopy. The finding of unstructured central-transition NMR spectra characterized by a relatively small average quadrupolar coupling attests to a highly disordered, essentially nondirectional anionic coordination in glyceline. For temperatures larger than about 1.3Tg the chlorine motions are well coupled to those of the glycerol and the choline moieties. At lower temperatures the local translational anion dynamics become Arrhenian and increasingly faster than the motion of glyceline's matrix molecules. Upon further cooling, the overall ionic conductivity continues to display a super-Arrhenius behavior, implying that the choline cations rather than the Cl anions dominate the long-range charge transport also near Tg.
1. Introduction
Deep eutectic solvents (DESs) represent an important class of materials1 because of the many applications for which they are discussed2–4 as well as for the scientific challenges they provide. Typical DESs are produced by mixing a hydrogen bond acceptor (HBA) with a hydrogen bond donor (HBD). Knowledge regarding the properties of the components within a given DES and the mutual interplay of all of the components forming liquids such as glyceline (a mixture of glycerol and choline chloride) is essential to achieve further progress in the field. Yet, most studies focus either on the response of the DES as a whole or on the dynamics of the HBD and/or the choline ion, while the mobility of the anion was barely addressed, so far. In fact, heretofore in DESs the Cl− dynamics were probably investigated explicitly only using computer simulations.5,6 Chlorine as a probe in nuclear magnetic resonance (NMR) experiments should definitively be useful in this context as well. However, its full potential to monitor dynamic processes in DESs remains to be explored.As a prerequisite for an understanding of the anionic motion in DESs, knowledge regarding the local structures in which the Cl− ions reside is vital. To unravel these structures, neutron diffraction, most profitably in combination with numerical simulations, has been exploited and optimized structural motifs centered about the Cl− ions have been presented: examples include 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixtures of the HBA choline chloride with glycerol (forming glyceline),7–9 with ethylene glycol (forming ethaline),7,10 and urea (forming reline).10,11
2 mixtures of the HBA choline chloride with glycerol (forming glyceline),7–9 with ethylene glycol (forming ethaline),7,10 and urea (forming reline).10,11
For glyceline, which is in the focus of the present study, it was reported that the Cl− ions are predominantly solvated by the glycerol molecules, more precisely by the protons (HG) of their hydroxyl groups, and to a much lesser extent by the OHC group of the choline cations:12 In the first correlation shell, the coordination number of the Cl⋯HG hydrogen bonds was found to be about 2.4 and that of the Cl⋯HC bond roughly ten times smaller. With respect to the choline moiety, in glyceline the Cl− ion is obviously located in a region between the –OHC and the –N(CH3)3 groups, a finding that is consistent with results from density-functional modeling13 and molecular dynamics simulation.14
Based not the least on neutron spin-echo experiments on glyceline which, like most of the simulations, also focus on the rather fluid and only moderately viscous regime of the DESs, it was suggested that glycerol's hydrogen-bonding network is barely disrupted by the addition of the choline moieties which rather reside in voids of the HBD network.7,15 The function of the glycerol-solvated anions was described as mediating a bridge between choline-rich and glycerol-rich clusters.12 Furthermore, it was suggested that the “Cl anions have a greatest correlation through ion–ion attraction with the charged choline cation N-centre rather than through hydrogen bonding to the hydroxyl moiety”.12 This kind of chlorine coordination appears special among choline based DESs: for instance in mixtures of choline chloride and urea, the HBD⋯Cl interactions are much more prominent.16–18
Apart from scattering techniques, also vibrational11 and NMR spectroscopies allow for a selective access to the dynamics of the HBD and HBA components in DESs. To study the mobilities of these components 1H,19–232H,2413C25 and other nuclides26 were exploited as probes. Even the 35Cl nuclide (which is three times more abundant than 37Cl) was already used, however, barely to unravel dynamical properties of DESs,27 but mostly to monitor hydration-induced chemical shifts.28–31 The rare exploitation of the 35Cl resonance is probably due to the fact that for halide ions spin relaxation times can become fairly short (down to the μs regime).32,33 Nevertheless, the 35Cl probe was utilized34 to explore static material properties for ordered crystals,35–37 glassy crystals,38 and glasses,39 and for liquids as well.40–42
For glyceline, strongly quadrupolarly perturbed spin I = 3/2 nuclei such as 35Cl should be well suited to study the dynamics of the anion itself or that in its local environment. Since glyceline is glass forming, with a calorimetric glass transition at Tg = 175 K,43 for its detailed study a combination of techniques is required that cover a wide range of ionic correlation times. Therefore, apart from applying spin-relaxometry and wideline spectroscopy,44–46 that are particularly sensitive to faster motions in the nano- to microsecond range, one goal of the present study is to adapt two-dimensional central-transition slow-motion techniques for use also with the 35Cl probe. Here, we have in mind the stimulated-echo methods that were developed for (other) quadrupolar nuclei in order to examine the dynamics in the milliseconds regime.47–49
The present results regarding the dynamics of the Cl− ions will be compared with the time constants reported24,25 for the choline cations as well as for glycerol in glyceline and of course also with its overall response that has been studied over a wide dynamic range by means of dielectric spectroscopy15,43,50 and shear rheology.51
2. Experimental details
All 35Cl NMR experiments were carried using a Bruker Avance III spectrometer working at 39.2 MHz with an estimated dead time of about 15 μs. The 35Cl frequencies are referenced with respect to a 0.1 M solution of NaCl in D2O. The π/2 pulse length for the central-transition excitation was 6.3 to 7.0 μs. Proton decoupling usually showed no discernible effect on the spectra and therefore was not applied, unless noted otherwise. We study 33 mol% methyl deuterated choline chloride (ChCl-d9) in protonated glycerol, here simply called glyceline (or glyceline-d9 in previous work).24For T > 300 K, the spectra were directly obtained from the free-induction decay, otherwise a π/2 − π sequence was used. For the processing of the 35Cl spectra we applied a Gaussian apodization with a spectral width of 0.1 kHz for T > 302 K, of 1 kHz for 202 and 196 K, and otherwise of 0.5 kHz. Details regarding the two-dimensional 35Cl NMR carried out in the frequency and in the time domains will be given in Section 3.C, below.
Additionally, deuteron stimulated-echo experiments were performed using a home-built spectrometer operated at 45.6 MHz on glyceline-d4 (featuring alkyl deuterated choline chloride, ChCl-d4) and glyceline-d5 (featuring glycerol-d5) for which 2H spin relaxation times were reported in ref. 24.
3. Results and analyses
A. Temperature dependent 35Cl spectra
In Fig. 1 we present 35Cl spectra recorded for glyceline. Near 330 K where, e.g., from dielectric measurements,43 the glyceline dynamics is expected to be much faster than the present 35Cl Larmor frequency, the narrow absorption line is centered at 0.87 kHz (22 ppm). The motionally fully narrowed line, which comprises the magnetization of the central +1/2 ↔ −1/2 transition and of the satellite ±1/2 ↔ ±3/2 transitions, broadens significantly as the sample is cooled closer to room temperature. Then, below about 280 K, the appearance of very short spin relaxation times (see Section 3.B) hampers the data acquisition. | ||
| Fig. 1 35Cl spectra of glyceline as measured for a range of temperatures are shown as solid lines. The vertical lines and the arrows mark a line shift of about 10.6 ± 0.3 kHz. The dashed line represents the Czjzek model, see eqn (1), and is calculated using σCz = 0.85 MHz and a 2 kHz Gaussian apodization. | ||
Only near 240 K it became possible again to record spectra. The arrows in Fig. 1 indicate that these have undergone a pronounced shift with respect to their high-temperature position. Below ≈240 K the spectra, now reflecting only the central +1/2 ↔ −1/2 transition of the 35Cl nucleus, eventually broaden significantly and develop an asymmetric shape. At the lowest temperature reached in the present work the spectrum exhibits a central second moment M2 of about (2π × 12.5 kHz)2.
Broad, essentially featureless asymmetric lines of the type seen in Fig. 1 are characteristic for quadrupolar nuclei in strongly disordered environments.52 In this situation, the components |VZZ| ≥ |VYY| ≥ |VXX| of the electrical field gradient (EFG) tensor at the nuclear site are typically subject to considerable disorder. Thus, a large variation of the quadrupolar coupling constant CQ = eQVZZ/h and of the asymmetry parameter η = (VXX − VYY)/VZZ arises.53–56 For I = 3/2 nuclei such as chlorine-35, CQ is related to the quadrupolar frequency via νQ = CQ/2. In the limit of so called Gaussian disorder where all tensor elements are characterized by the same variance, the Czjzek model can be derived which involves a bivariate frequency distribution57–61
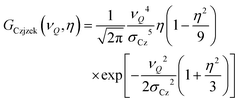 | (1) |
| 〈CQη2〉 = 〈CQ2(1 + η2/3)〉 = 20σCz2 | (2) |
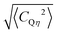 for which eqn (2) yields 3.8 MHz.
for which eqn (2) yields 3.8 MHz.
From the spectra measured on both sides of the 240 to 280 K interval, in which spectra could not be recorded, one recognizes that that their center of gravity has shifted considerably. This so-called dynamic frequency shift or quadrupolar induced shift, which can be related to the imaginary part of the spectral density function,62 is well-known for halfinteger quadrupolar nuclei.63–69 Towards low temperatures the NMR line seemingly returns back to its high-temperature position (in fact only the peak absorption does). This observation is similar to that reported for other strongly quadrupolarly perturbed nuclei in disordered materials.48 There, this phenomenon was rationalized by noting that for the asymmetric Czjzek line shape the peak frequency does not agree with its center of gravity. Further analyses of the second-order central-transition 35Cl line shapes, in particular of their widths are provided in the following.
B. Spin relaxation
To be sensitive to the fluctuations of the anionic resonance frequencies, we measured the decay of the 35Cl longitudinal magnetization Mz using inversion recovery. The transversal dephasing Mxy was recorded by employing a π/2 − t − π sequence as a function of the pulse separation t. The resulting magnetization curves were fitted by stretched exponential functions or, for very short transversal dephasing, by an exponential function to obtain spin–lattice relaxation times T1 and spin–spin relaxation times T2.The temperature dependence of glyceline's 35Cl spin-relaxation times is presented in Fig. 2. At temperatures larger than corresponding to the (unobserved) minima of the spin relaxation times we find T1 ≈ T2, demonstrating that the motional correlation times are shorter than the inverse Larmor frequency, i.e., short on the nanosecond scale. With the spin relaxation times turning comparable to or even shorter than the spectrometer dead time, measurements could not be carried out in the regime near the expected T1 and T2 (global) minima. Below this gap, T1 increases in a monotonic fashion, while T2 displays a maximum near 225 K and a minimum near 210 K before it tends to saturate towards a low-temperature value near about 470 μs. This value can be compared to the inverse of the largest heteronuclear dipolar coupling of 35Cl. Taking the shortest Cl–H distance, rCl–H ≈ 2.1 Å, reported for glyceline,12 from  one has vD ≈ 1.3 kHz as a measure of the dipolar frequency scale.
one has vD ≈ 1.3 kHz as a measure of the dipolar frequency scale.
 | ||
Fig. 2 Chlorine-35 spin–lattice relaxation times T1 (red triangles) and spin–spin relaxation times T2 (green dots) of glyceline measured at 39.2 MHz. The red solid line for T1 is calculated using eqn (3) and the green dashed line for T2 is calculated using eqn (8). The green plusses (+) refer to the effective transversal dephasing time 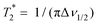 as obtained from the 35Cl spectral width Δν1/2. For comparison as blue dash-dotted line we added the fit to the deuteron T1 times, measured at a 45.6 MHz, that relate to alkyl chain deuterated glyceline-d4.24 This fit is based on eqn (7) in conjunction with the timescale parameters given in ref. 24 for T > 220 K, i.e., τ∞ = 2 × 10−13 s, D = 7.75, and T0 = 153 K. To achieve an approximate overlap of the spin relaxation times at high temperatures, the values relating to the 2H fit curve were divided by a factor of 280. This number reflects primarily the different 2H and 35Cl quadrupolar couplings. as obtained from the 35Cl spectral width Δν1/2. For comparison as blue dash-dotted line we added the fit to the deuteron T1 times, measured at a 45.6 MHz, that relate to alkyl chain deuterated glyceline-d4.24 This fit is based on eqn (7) in conjunction with the timescale parameters given in ref. 24 for T > 220 K, i.e., τ∞ = 2 × 10−13 s, D = 7.75, and T0 = 153 K. To achieve an approximate overlap of the spin relaxation times at high temperatures, the values relating to the 2H fit curve were divided by a factor of 280. This number reflects primarily the different 2H and 35Cl quadrupolar couplings. | ||
Fig. 2 also includes the temperature dependent full line widths at half maximum, Δν1/2(T), in the form of the effective transversal dephasing times  . Interestingly, below about 200 K,
. Interestingly, below about 200 K,  continues to be somewhat T dependent. Thus, although barely visible from Fig. 1, the line width broadens slightly upon cooling in this range, obviously reflecting the freeze-out of librational motions on the μs scale. Eventually, at sufficiently low temperatures
continues to be somewhat T dependent. Thus, although barely visible from Fig. 1, the line width broadens slightly upon cooling in this range, obviously reflecting the freeze-out of librational motions on the μs scale. Eventually, at sufficiently low temperatures  is governed by a broad, essentially static distribution of (quadrupolar) precession frequencies. Using the π/2 − t − π sequence a refocusing is achieved for the T2 measurements and thus one has
is governed by a broad, essentially static distribution of (quadrupolar) precession frequencies. Using the π/2 − t − π sequence a refocusing is achieved for the T2 measurements and thus one has  in the low-temperature regime.
in the low-temperature regime.
As soon as motional processes come into play, the fluctuations of the large quadrupolar interactions govern the spin relaxation at the chlorine site. Hence, in good approximation the spin–lattice relaxation time can be described by70
 | (3) |
| 1/T2 = KQ2[J(ωL) + J(2ωL)]. | (4) |
 relates to the fluctuating part of the quadrupolar product. Furthermore, J(ω) denotes the spectral density which is a measure for the fluctuation probability of the quadrupolar frequency at the chlorine site on the scale of the Larmor frequency. In the presence of a unique correlation time τc, the spectral density71
relates to the fluctuating part of the quadrupolar product. Furthermore, J(ω) denotes the spectral density which is a measure for the fluctuation probability of the quadrupolar frequency at the chlorine site on the scale of the Larmor frequency. In the presence of a unique correlation time τc, the spectral density71| J(ω) = τc/[1 + (ωτc)2], | (5) |
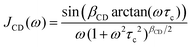 | (6) |
In glassforming materials the temperature dependent correlation times τc often obey the Vogel–Fulcher law
τc = τ∞![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[DT0/(T − T0)] exp[DT0/(T − T0)] | (7) |
Note that in Fig. 2 the lines for the description of the 35Cl spin relaxation times are calculated using KQ = 6.5 × 106 s−1 (corresponding to  ) and an exponent βCD = 0.38 (close to the exponent reported on the basis of the 2H spin relaxation times24). Furthermore, also the timescale parameters, for convenience reproduced in the caption of Fig. 2, are those used in ref. 24. One notes that the (fluctuating part of the) root mean square quadrupolar product given here differs somewhat from
) and an exponent βCD = 0.38 (close to the exponent reported on the basis of the 2H spin relaxation times24). Furthermore, also the timescale parameters, for convenience reproduced in the caption of Fig. 2, are those used in ref. 24. One notes that the (fluctuating part of the) root mean square quadrupolar product given here differs somewhat from  extracted on the basis of the spectra shown in Fig. 1. Part of this discrepancy certainly stems from the fact, that the spectral shape implied by eqn (1) does not fully match the measured one.
extracted on the basis of the spectra shown in Fig. 1. Part of this discrepancy certainly stems from the fact, that the spectral shape implied by eqn (1) does not fully match the measured one.
To obtain the dashed (T2) line shown in Fig. 2, another effect was taken into account: When the correlation times τc are shorter than 1/ωL (≈ 1 ns) fluctuations of the second-order quadrupolar interaction can become relevant. Thus, down to timescales of 1/(2πM21/2) ≈ 6.4 μs rather than eqn (4), the central-transition spin–spin relaxation time has to be written as74–76
 | (8) |
 . Similar to ref. 77, for βCD = 0.38 the value numerically obtained (see Fig. S2 of the ESI†) from eqn (8) is τc ≈ 2.5 μs. For I = 3/2 nuclei it has been pointed out that at somewhat lower temperatures a local T2 minimum appears near the onset of motional narrowing. At this point the corresponding motional correlation time can be estimated from45
. Similar to ref. 77, for βCD = 0.38 the value numerically obtained (see Fig. S2 of the ESI†) from eqn (8) is τc ≈ 2.5 μs. For I = 3/2 nuclei it has been pointed out that at somewhat lower temperatures a local T2 minimum appears near the onset of motional narrowing. At this point the corresponding motional correlation time can be estimated from45| τc ≈ 1/(2.56M21/2). | (9) |
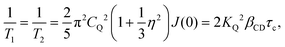 | (10) |
C. Stimulated 35Cl echoes and 2D exchange spectra
Ultraslow anionic motions referring to correlation times in the milliseconds regime are accessible using two-dimensional spectroscopy. Corresponding measurements can be carried out in the time domain using stimulated echoes or in the frequency domain using exchange spectroscopy. Since presently we exploit quadrupolar central-transition frequencies, in both cases it is essential to utilize appropriately phase cycled three- (or more) pulse sequences, to generate central-transition signals of the form78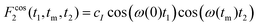 | (11a) |
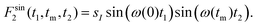 | (11b) |
To acquire two-dimensional 35Cl central-transition NMR spectra for glyceline we employed a five-pulse sequence,84 thereby generating the signals summarized in eqn (11). The echo delays between the first and the second and the fourth and the fifth pulse were fixed to 10 and 35 μs, respectively. For the spectra shown in Fig. 3 we collected (a) 160 × 512 data points and co-added 240 scans (25 W continuous-wave proton decoupling, Rabi frequency 10.5 kHz), (b) 128 × 8192 points (16384 scans, no decoupling), and (c) 208 × 8192 points (32768 scans, no decoupling). The t1 increment was 1 μs and the t2 increment was 4 μs. After symmetrization and zero filling to 2048 × 8192 points a Gaussian apodization of 2 kHz was applied. Due to the short 35Cl T1 times relative to the correlation times τc and the constraints imposed also by T2 we were unable to record an initial-state (=diagonal) and a final-state (tm ≫ τc) two-dimensional spectrum at the same temperature.
 | ||
| Fig. 3 Two-dimensional 35Cl central-transition exchange spectra recorded for (a) a mixing time tm = 10 ms at 151 K, (b) tm = 10 μs at 186 K, and (c) tm = 5 ms at 186 K. | ||
Therefore, as Fig. 3(a) we show a diagonal low-temperature spectrum which documents the absence of any translational ionic hops. The spectrum recorded at the higher temperature, see Fig. 3(b), reveals the presence of some exchange processes, although it is collected for a very short mixing time tm = 10 μs. From the two-dimensional spectrum measured at 186 K for a much longer mixing times of 5 ms, one recognizes that the spectral intensity has spread out much more into the exchange plane, cf.Fig. 3(c). These somewhat time consuming experiments are helpful in order to demonstrate that at the higher temperature the Cl− ions are mobile on the millisecond time scale. However, these spectra are less suited to retrieve quantitative information.
Alternatively, rather than recording two-dimensional spectra in the frequency domain, in the time domain one can monitor the decay of the F2 signals as a function of tm for fixed tp = t1 = t2. This way, eqn (11) yields correlation functions that characterize the motionally induced changes of the local 35Cl precession frequencies ω(t) directly.
For glyceline corresponding stimulated 35Cl echo measurements, with the evolution time set to 25 μs, are presented in Fig. 4. For lower temperatures more slowly decaying anionic correlation functions are observed. To extract the correlation times τc and other parameters, the measured signals S2(tm) are written as F2(tm)Mz(tm). For the analysis, the parameters entering the longitudinal magnetization Mz(tm) are taken from independent T1 measurements, cf. the arrows in Fig. 4. This accounts for the fact that also spin–lattice relaxation takes place during tm. The F2(tm) part which reflects the motion-induced correlation decay, in practical terms, is written here as a normalized Kohlrausch function
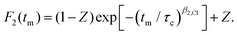 | (12) |
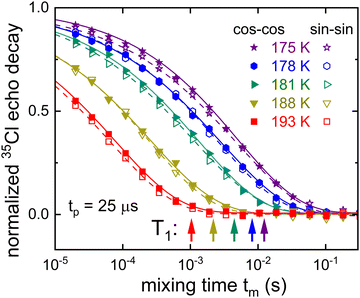 | ||
| Fig. 4 Temperature dependent 35Cl stimulated-echo amplitudes measured for glyceline. Based on eqn (12), the solid and dashed lines are fits to the normalized cos-cos and sin-sin amplitudes, respectively. The arrows indicate the 1/e decay times of the normalized longitudinal magnetization recoveries Mz(tm). | ||
For comparison of the 35Cl based time scales with those on which the HBA and HBD components move, we performed deuteron stimulated-echo experiments for glyceline-d4 and for glyceline-d5. Such experiments yield signals of the form given by eqn (11), however, with s1 = 3/4 and c1 = 1.85 Since the main focus of the present work is on the 35Cl resonance, we provide the 2H stimulated-echo decay data (recorded for tp = 20 μs) as Fig. S4 of the ESI.† The results from the analysis of these data, again carried out in terms of eqn (12), are compiled together with the 35Cl based time scales in Section 4, below.
4. Discussion
The Arrhenius plot shown as Fig. 5 compiles the anionic correlation times that we detected using 35Cl spin relaxometry and stimulated-echo spectroscopy and compares these time scales with results from dielectric relaxation spectroscopy,43 shear rheology,51 and 2H NMR.24 For temperatures larger than about 280 K it is seen that by and large all time scales follow the same overall Vogel–Fulcher type of behavior. However, starting from the high-T regime, the Cl− motion appears to be slightly faster as compared to that of the HBD molecules (as measured for glycerol in glyceline-d5) and of the HBA cations (as measured for choline in glyceline-d4).24 | ||
Fig. 5 Time constants for glyceline from measurements of the dielectric constant ε43 and the shear compliance J51 as well as from 2H-T124 experiments are compared with the data from the present work: These include the 35Cl based correlation times from eqn (10) and (12), from the measured T2 minimum, see eqn (9), and maximum, see below eqn (8), as well as those obtained after rescaling (see text) from stimulated deuteron echo spectroscopy, see Fig. S4 of the ESI.† The dash-dotted line represents eqn (7) using the parameters listed in the caption of Fig. 2. As a guide to the eye, the dashed line connects data obtained from the 35Cl spin relaxation times. The solid line reflects an Arrhenius law, eqn (13), with τ∞,Cl = 3 × 10−18 s and ECl = 5150 K. The yellow dotted line marks an effective low-temperature energy barrier Eeff,Ch = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 K that is introduced here for later analyses. 900 K that is introduced here for later analyses. | ||
At first glance, the temperature dependence of the 35Cl spin-relaxation times, see Fig. 2, is reminiscent of that previously measured using 2H NMR.24 Despite the similar temperature dependence of 2H and 35Cl based correlation times for T > 280 K, it has to be emphasized that the two nuclei are sensitive to rather different dynamical processes. The deuteron frequencies probe the reorientational motion of the C–D bonds in the glycerol molecules or in the choline cations.
Conversely, judged from their relatively small 35Cl quadrupolar coupling constant (on the 67.6 MHz scale set by the covalently bonded HCl molecules),86,87 in glyceline the Cl− anions with their almost 100% ionicity cannot directly be sensitive to reorientational motions. Rather they can sense the motions of the (partially) charged moieties in their immediate environments. Here, for the mobile anions two limiting scenarios can be envisioned: (1) Assuming that the Cl− ions hop (translationally and “actively”) from site to site, each time into a completely different charge environment, their field gradient tensor and thus their local precession frequencies are expected88 to display significant, i.e., relatively large jumps. The other scenario assumes that (2) at a spatially fixed Cl− ion site the motion of the (partial) charges δq in its vicinity changes the EFG experienced by that nuclear probe. The magnitude of the EFG is ∝|δq|/r3, so that for scenario (2) the motions of glycerol's hydroxyl groups (with the HG protons carrying a partial charge |δq| = 0.39e at a distance of rCl–H ≈ 2.1 Å),12 govern the (“passive”) fluctuations of the quadrupolar frequency at the Cl− site. It is highly improbable that all of the 2 to 3 Cl⋯HG hydrogen bonds which coordinate each Cl− ion move simultaneously. Therefore, within scenario (2) the frequency jumps experienced by the mobile Cl− ions should be smaller than for scenario (1).
The approximate coupling of the anionic and the other time scales that we observe in the fluid and the moderately viscous regimes of glyceline favor a mixture of scenarios (1) and (2). Thus, like for many other weakly supercooled liquids,89–92 the rotational and translational motions appear to be intimately coupled at high temperatures. Also, force field based calculations carried out near room temperature for glyceline (and ethaline),5,6 show that for all three components (HBA, HBD, and chlorine) the self-diffusion coefficients agree within a factor of about 2 (with the cation diffusing slightly faster than the anion which in turn displays a diffusion coefficient similar to that of the HBD).
However, below about 230 K which corresponds to about 1.3Tg (also like for other glass formers),89,90 from Fig. 5 the situation is seen to change qualitatively. While the motion of the glycerol and the choline components continue their Vogel–Fulcher type of slowdown, the temperature dependence of the Cl− ion dynamics turns over to a less steep behavior. Here, the time constants follows an Arrhenius law
τc = τ∞,Cl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(ECl/T). exp(ECl/T). | (13) |
Thus clearly, in the low-temperature range scenario (1) is applicable: Here, at the Cl− sites, the local precession frequencies are “actively” modulated in large steps by translational hops of the mobile anions. In this scenario and in harmony with findings regarding the ionic hops in a molten salt,48 the stimulated-echo functions should barely depend on the evolution time.93 This situation is to be distinguished from that known for the reorientational molecular motion near the glass transition temperature of low-molecular weight glass formers:94 Here, the deuteron F2 functions typically display a strong tp dependence so that the rotational correlation functions (i.e., the tp → 0 limit of Legendre polynomial rank l = 2 functions) can be a factor of 5 to 10 faster than for tp = 20 μs. For comparison of the dielectric (rank l = 1) with the time scales detected by NMR, and depending on the motional model, an additional factor of 1 to 3 can be required to achieve overlap of the deuteron echo time scales with the dielectric ones.95 In harmony with these expectations, from Fig. 5 one recognizes that an overall factor of 8, applied to the deuteron stimulated-echo times, aligns all of the matrix correlation times.
At first, the finding of a decoupled 35Cl motion may appear unexpected because the temperature dependence of the overall electrical conductivity (to which obviously also the choline ions contribute) parallels the correlation times determined for the matrix moieties.51 However, one has to realize that the 35Cl stimulated-echo functions probe the elementary step of the translational dynamics. And with scenario (1) being prevalent, a single step is sufficient to lead to a complete decay of the 35Cl F2 function. Hence, it appears likely that the translational motion of the mobile Cl ions is of a spatially localized nature (e.g., taking place within a clustered structure) or is highly obstructed.
In addition, as signified by the final-state amplitude Z, the fraction of immobile anions increases upon cooling. From the temperature T1/2 ≈ 175 K at which Z is about 0.5, see Fig. S3 (ESI†), the (mean) energy barrier against Cl− hopping can be assessed. Following the analysis applied for other ion conducting materials,96–98Emean can be inferred from the Arrhenius law written as Emean = T1/2ln(τ*/τ∞,Cl). Using τ* = 25 μs and τ∞,Cl, see the caption of Fig. 5 we find Emean = 5200 ± 450 K. This barrier is close to ECl = 5150 K as determined directly from the correlation times shown in Fig. 5. Yet, another independent estimate for the energy barrier is possible: Within the framework of the coupling model, based on the (energy barrier Ep of the) so called primitive or elementary relaxation, the (energy barrier Ec of the) coupled process is obtained.99 This approach predicts that Ep/Ec = β2. Identifying Ep with ECl and Ec with Eeff,Ch, the ratio of the corresponding energy barriers (for their values and how they are determined, see the caption of Fig. 5) yields β2 = 0.35 ± 0.04. This exponent compares favorably with the stretching parameter describing the stimulated-echo decays measured for the cations (β2,Ch = 0.34, see Fig. S4, ESI†) and for the anions (β2,Cl = 0.39, see Section 3.C). Thus, consistent values for the activation energy describing the anionic hopping in the low-temperature regime are arrived at by pursuing several independent routes.
The decoupling of the anionic dynamics from that of the glyceline matrix may appear somewhat surprising. However, one has to realize that similar dynamic decoupling phenomena are in fact well known for a wide range of highly concentrated ion conducting materials.100–103 To conclude this section, we wish to emphasize that the two-dimensional and two-time 35Cl NMR methodology applied and refined in the present work should be useful for future studies of motional processes. This includes not only further DESs, but systems such as ZnCl2 or other chlorides either in molten salts, in ionic liquids, and in aqueous solutions as well.104–106
5. Conclusions
With the goal to unravel the anion dynamics in glyceline, the present work exploits 35Cl NMR, an approach which has barely been applied to DESs and other liquids in their highly viscous states. First, we examined the thermal evolution of the absorption spectra. Their widths, like those of the spin–spin relaxation times display the non-monotonous temperature dependence expected for nuclei that are predominantly subjected to second-order quadrupolar interactions. Furthermore, the line shape analysis revealed the nondirectional bonding character at the site of the anions. By combining the results from the spin relaxation times with those from two-dimensional exchange spectra and stimulated-echo decays, the chlorine mobility could be explored over wide dynamic and temperature ranges. We found that above about 230 K, the dynamics of the chlorine ions basically trace those of glyceline's matrix components, i.e., of glycerol and choline. Then, below about 1.3Tg, a motional decoupling is observed. Here, the local 35Cl precession frequencies are modulated by translational jumps of the mobile chlorine ions, which become increasingly slower than those of the matrix species. Nevertheless, the comparison of the vastly different anionic and cationic mobilities, in the low-temperature range following an Arrhenius and a super-Arrhenius behavior, respectively, demonstrates that the choline molecular ions continue to dominate the overall electrical conductivity. The finding that the much larger cationic rather than the smaller anionic species governs the charge transport, can be rationalized in a scenario in which the chlorine ions perform a localized or otherwise highly obstructed type of motion. Taken together, with the previous and current results from deuteron NMR and based on the component-selective detection that we have exploited, the present work provides important insights regarding the motional interplay of all of the three species forming the deep eutectic glyceline solvent.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was financially supported by the Deutsche Forschungsgemeinschaft under project no. 444797029.References
- Y. Marcus, Deep Eutectic Solvents, Springer, Switzerland, 2019 DOI:10.1007/978-3-030-00608-2.
- E. L. Smith, A. P. Abbott and K. S. Ryder, Deep Eutectic Solvents (DESs) and Their Applications, Chem. Rev., 2014, 114, 11060 CrossRef CAS PubMed.
- B. B. Hansen, S. Spittle, B. Chen, D. Poe, Y. Zhang, J. M. Klein, A. Horton, L. Adhikari, T. Zelovich, B. W. Doherty, B. Gurkan, E. J. Maginn, A. Ragauskas, M. Dadmun, T. A. Zawodzinski, G. A. Baker, M. E. Tuckerman, R. F. Savinell and J. R. Sangoro, Deep Eutectic Solvents: A Review of Fundamentals and Applications, Chem. Rev., 2021, 121, 1232 CrossRef CAS PubMed.
- C. J. Clarke, W. C. Tu, O. Levers, A. Bröhl and J. P. Hallett, Green and Sustainable Solvents in Chemical Processes, Chem. Rev., 2018, 118, 747 CrossRef CAS PubMed.
- S. L. Perkins, P. Painter and C. M. Colina, Experimental and computational studies of choline chloride-based deep eutectic solvents, J. Chem. Eng. Data, 2014, 59, 3652 CrossRef CAS.
- E. S. C. Ferreira, I. V. Voroshylova, C. M. Pereira and M. N. D. S. Cordero, Improved force field model for deep eutectic solvent ethaline: reliable physicochemical properties, J. Phys. Chem. B, 2014, 120, 10124 CrossRef PubMed.
- D. V. Wagle, G. A. Baker and E. Mamontov, Differential Microscopic Mobility of Components within a Deep Eutectic Solvent, J. Phys. Chem. Lett., 2015, 6, 2924 CrossRef CAS PubMed.
- Z. Naseem, R. A. Shehzad, A. Ihsan, J. Iqbal, M. Zahid, A. Pervaiz and G. Sarwari, Theoretical investigation of supramolecular hydrogen-bonded choline chloride-based deep eutectic solvents using density functional theory, Chem. Phys. Lett., 2021, 769, 138427 CrossRef CAS.
- S. Spittle, D. Poe, B. Doherty, C. Kolodziej, L. Heroux, M. A. Haque, H. Squire, T. Cosby, Y. Zhang, C. Fraenza, S. Bhattacharyya, M. Tyagi, J. Peng, R. A. Elgammal, T. Zawodzinski, M. Tuckerman, S. Greenbaum, B. Gurkan, C. Burda, M. Dadmun, E. J. Maginn and J. Sangoro, Evolution of microscopic heterogeneity and dynamics in choline chloride-based deep eutectic solvents, Nat. Commun., 2022, 13, 219 CrossRef CAS PubMed.
- D. V. Wagle, C. A. Deakyne and G. A. Baker, Quantum Chemical Insight into the Interactions and Thermodynamics Present in Choline Chloride Based Deep Eutectic Solvents, J. Phys. Chem. B, 2016, 120, 6739 CrossRef CAS PubMed.
- C. F. Araujo, J. A. P. Coutinho, M. M. Nolasco, S. F. Parker, P. J. A. Ribeiro-Claro, S. Rudić, B. I. G. Soares and P. D. Vaz, Inelastic neutron scattering study of reline: shedding light on the hydrogen bonding network of deep eutectic solvents, Phys. Chem. Chem. Phys., 2017, 19, 17998 RSC.
- A. H. Turner and J. D. Holbrey, Investigation of glycerol hydrogen-bonding networks in choline chloride/glycerol eutectic-forming liquids using neutron diffraction, Phys. Chem. Chem. Phys., 2019, 21, 21782 RSC.
- R. Stefanovic, M. Ludwig, G. B. Webber, R. Atkin and A. J. Page, Nanostructure, hydrogen bonding and rheology in choline chloride deep eutectic solvents as a function of the hydrogen bond donor, Phys. Chem. Chem. Phys., 2017, 19, 3297 RSC.
- B. Doherty and O. Acevedo, OPLS Force Field for Choline Chloride-Based Deep Eutectic Solvents, J. Phys. Chem. B, 2018, 122, 9982 CrossRef CAS PubMed.
- A. Faraone, D. V. Wagle, G. A. Baker, E. Novak, M. Ohl, D. Reuter, P. Lunkenheimer, A. Loidl and E. Mamontov, Glycerol hydrogen-bonding network dominates structure and collective dynamics in a deep eutectic solvent, J. Phys. Chem. B, 2018, 122, 1261 CrossRef CAS PubMed.
- O. S. Hammond, D. T. Bowron and K. J. Edler, Liquid structure of the choline chloride-urea deep eutectic solvent (reline) from neutron diffraction and atomistic modelling, Green Chem., 2016, 18, 2736 RSC.
- S. Kaur, S. Sharma and H. K. Kashyap, Bulk and interfacial structures of reline deep eutectic solvent: A molecular dynamics study, J. Chem. Phys., 2017, 147, 194507 CrossRef PubMed.
- M. Gilmore, L. M. Moura, A. H. Turner, M. Swadźba-Kwaśny, S. K. Callear, J. A. McCune, O. A. Scherman and J. D. Holbrey, A comparison of choline:urea and choline:oxalic acid deep eutectic solvents at 338 K, J. Chem. Phys., 2018, 148, 193823 CrossRef PubMed.
- C. D’Agostino, R. C. Harris, A. P. Abbott, L. F. Gladden and M. D. Mantle, Molecular motion and ion diffusion in choline chloride based deep eutectic solvents studied by 1H pulsed field gradient NMR spectroscopy, Phys. Chem. Chem. Phys., 2011, 13, 21383 RSC.
- C. D’Agostino, L. F. Gladden, M. D. Mantle, A. P. Abbott, E. I. Ahmed, A. Y. M. Al-Murshedi and R. C. Harris, Molecular and ionic diffusion in aqueous – deep eutectic solvent mixtures: probing inter-molecular interactions using PFG NMR, Phys. Chem. Chem. Phys., 2015, 17, 15297 RSC.
- R. Häkkinen, O. Alshammari, V. Timmermann, C. D’Agostino and A. Abbott, Nanoscale Clustering of Alcoholic Solutes in Deep Eutectic Solvents Studied by Nuclear Magnetic Resonance and Dynamic Light Scattering, ACS Sustainable Chem. Eng., 2019, 7, 15086 CrossRef.
- G. de Araujo Lima e Souza, M. E. Di Pietro, F. Castiglione, V. Vanoli and A. Mele, Insights into the Effect of Lithium Doping on the Deep Eutectic Solvent Choline Chloride:Urea, Materials, 2022, 15, 7459 CrossRef CAS PubMed.
- K. Dziubinska-Kühn, M. Pupier, J. Matysik, J. Viger-Gravel, B. Karg and M. Kowalska, Time-Dependent Hydrogen Bond Network Formation in Glycerol-Based Deep Eutectic Solvents, Chem. Phys. Chem., 2022, 23, e202100806 CrossRef.
- Y. Hinz and R. Böhmer, Deuteron nuclear magnetic resonance of glyceline deep eutectic solvents: Selective detection of choline and glycerol dynamics, J. Chem. Phys., 2022, 156, 194506 CrossRef CAS PubMed.
- C. C. Fraenza, R. A. Elgammal, M. N. Garaga, S. Bhattacharyya, T. A. Zawodzinski and S. G. Greenbaum, Dynamics of Glyceline and Interactions of Constituents: A Multitechnique NMR Study, J. Phys. Chem. B, 2022, 126, 890 CrossRef CAS PubMed.
- A. P. Abbott, C. D'Agostino, S. J. Davis, L. F. Gladden and M. D. Mantle, Do group 1 metal salts form deep eutectic solvents?, Phys. Chem. Chem. Phys., 2016, 18, 25528 RSC.
- F. Gabriele, M. Chiarini, R. Germani and N. Spreti, Understanding the role of temperature in structural changes of choline chloride/glycols deep eutectic solvents, J. Mol. Liq., 2023, 385, 122332 CrossRef CAS.
- F. Gabriele, M. Chiarini, R. Germani, M. Tiecco and N. Spreti, Effect of water addition on choline chloride/glycol deep eutectic solvents: Characterization of their structural and physicochemical properties, J. Mol. Liq., 2019, 291, 111301 CrossRef CAS.
- M. E. Di Pietro, O. Hammond, A. van den Bruinhorst, A. Mannu, A. Padua, A. Mele and M. Costa Gomes, Connecting chloride solvation with hydration in deep eutectic systems, Phys. Chem. Chem. Phys., 2021, 23, 107 RSC.
- A. S. D. Ferreira, R. Craveiro, A. R. Duarte, S. Barreiros, E. J. Cabrita and A. Paiva, Effect of water on the structure and dynamics of choline chloride/glycerol eutectic systems, J. Mol. Liq., 2021, 342, 117463 CrossRef CAS.
- H. Wang, S. Liu, Y. Zhao, J. Wang and Z. Yu, Insights into the Hydrogen Bond Interactions in Deep Eutectic Solvents Composed of Choline Chloride and Polyols, ACS Sustainable Chem. Eng., 2019, 7, 7760 CrossRef CAS.
- V. Klimavicius, Z. Gdaniec and V. Balevicius, Very short NMR relaxation times of anions in ionic liquids: New pulse sequence to eliminate the acoustic ringing, Spectrochim. Acta A, 2014, 132, 879 CrossRef CAS PubMed.
- T. Endo, M. Imanari, Y. Hidaka, H. Seki, K. Nishikawa and S. Sen, Structure and dynamics of room temperature ionic liquids with bromide anion: results from 81Br NMR spectroscopy, Magn. Reson. Chem., 2015, 53, 369 CrossRef CAS PubMed.
- M. E. Smith, Recent progress in solid-state nuclear magnetic resonance of half-integer spin low-γ quadrupolar nuclei applied to inorganic materials, Magn. Reson. Chem., 2021, 59, 864 CrossRef CAS PubMed.
- P. M. J. Szell and D. L. Bryce, Recent advances in chlorine, bromine, and iodine solid-state NMR spectroscopy, Annu. Rep. NMR Spectrosc., 2020, 100, 97 CrossRef CAS; R. P. Chapman, C. M. Widdifield and D. L. Bryce, Solid-state NMR of quadrupolar halogen nuclei, Prog. Nucl. Magn. Reson. Spectrosc., 2009, 55, 215 CrossRef.
- S. T. Holmes, J. M. Hook and R. W. Schurko, Nutraceuticals in Bulk and Dosage Forms: Analysis by 35Cl and 14N Solid-State NMR and DFT Calculations, Mol. Pharmaceutics, 2022, 19, 440 CrossRef CAS PubMed.
- P. M. J. Szell, Z. Rehman, B. P. Tatman, L. P. Hughes, H. Blade and S. P. Brown, Exploring the Potential of Multinuclear Solid-state 1H, 13C, and 35Cl Magnetic Resonance To Characterize Static and Dynamic Disorder in Pharmaceutical Hydrochlorides, ChemPhysChem, 2022, 24, e202200558 CrossRef PubMed.
- H. Fujimori and T. Asaji, 35CI NQR in Glassy Crystal of 2-chlorothiophene, Z. Naturforsch. A, 2000, 55, 183 CrossRef CAS.
- A. Baasner, I. Hung, T. F. Kemp, R. Dupree, B. C. Schmidt and S. L. Webb, Constraints on the incorporation mechanism of chlorine in peralkaline and peraluminous Na2O-CaO-Al2O3-SiO2 glasses, Am. Mineral., 2014, 99, 1713 CrossRef.
- M. A. Fedotov, O. L. Malkina and V. G. Malkin, 35/37Cl NMR chemical shifts and nuclear quadrupole couplings for some small chlorine compounds: experimental and theoretical study, Chem. Phys. Lett., 1996, 258, 330 CrossRef CAS.
- R. C. Remsing, J. L. Wildin, A. L. Rapp and G. Moyna, Hydrogen Bonds in Ionic Liquids Revisited:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35/37Cl NMR Studies of Deuterium Isotope Effects in 1-n-Butyl-3-Methylimidazolium Chloride, J. Phys. Chem. B, 2007, 111, 11619 CrossRef CAS PubMed.
35/37Cl NMR Studies of Deuterium Isotope Effects in 1-n-Butyl-3-Methylimidazolium Chloride, J. Phys. Chem. B, 2007, 111, 11619 CrossRef CAS PubMed. - P. G. Gordon, D. H. Brouwer and J. A. Ripmeester, Probing the Local Structure of Pure Ionic Liquid Salts with Solid- and Liquid-State NMR, Chem. Phys. Chem., 2010, 11, 260 CrossRef CAS PubMed.
- D. Reuter, C. Binder, P. Lunkenheimer and A. Loidl, Ionic conductivity of deep eutectic solvents: the role of orientational dynamics and glassy freezing, Phys. Chem. Chem. Phys., 2019, 21, 6801 RSC.
- L. Werbelow, Adiabatic Nuclear Magnetic Resonance Linewidth Contributions for Central Transitions of I > 1/2 Nuclei, J. Chem. Phys., 1996, 104, 3457 CrossRef CAS.
- S. H. Chung, K. R. Jeffrey and J. R. Stevens, Dynamics of sodium ions in NaClO4 complexed in poly(propylene-oxide): A 23Na nuclear magnetic resonance study, J. Chem. Phys., 1998, 108, 3360 CrossRef CAS.
- M. Witschas and H. Eckert, 31P and 23Na Solid-State NMR Studies of Cation Dynamics in HT-Sodium Orthophosphate and the Solid Solutions (Na2SO4)x–(Na3PO4)1–x, J. Phys. Chem. A, 1999, 103, 10764 CrossRef CAS.
- M. Adjei-Acheamfour and R. Böhmer, Second-order quadrupole interaction based detection of ultra-slow motions: Tensor operator framework for central-transition spectroscopy and the dynamics in hexagonal ice as an experimental example, J. Magn. Reson., 2014, 249, 141 CrossRef CAS PubMed.
- J. Beerwerth, S. P. Bierwirth, J. Adam, C. Gainaru and R. Böhmer, Local and global dynamics of the viscous ion conductors 2Ca(NO3)2-3KNO3 and 2Ca(NO3)2-3RbNO3 probed by 87Rb nuclear magnetic resonance and shear rheology, J. Chem. Phys., 2019, 150, 194503 CrossRef PubMed.
- L. Hoffmann, J. Beerwerth, D. Greim, J. Senker, C. Sternemann, W. Hiller and R. Böhmer, Reorientational dynamics of trimethoxyboroxine: A molecular glass former studied by dielectric spectroscopy and 11B nuclear magnetic resonance, J. Chem. Phys., 2020, 152, 034503 CrossRef CAS PubMed.
- V. Agieienko and R. Buchner, Dielectric relaxation of deep eutectic solvent + water mixtures: structural implications and application to microwave heating, Phys. Chem. Chem. Phys., 2020, 22, 20466 RSC.
- D. Reuter, P. Münzner, C. Gainaru, P. Lunkenheimer, A. Loidl and R. Böhmer, Translational and reorientational dynamics in deep eutectic solvents, J. Chem. Phys., 2021, 154, 154501 CrossRef CAS PubMed.
- A. E. Wolfenson, A. H. Brunetti, D. J. Pusiol and W. M. Pontuschka, Nuclear quadrupole resonance of Cl nuclei in glassy solution of chlorobenzene in pyridine, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 6257 CrossRef CAS PubMed.
- H.-A. Stöckmann, Electric field gradients resulting from randomly distributed unscreened point charges, J. Magn. Reson., 1981, 44, 145 Search PubMed.
- M. Maurer, Electric field gradients of randomly disordered compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 8996 CrossRef CAS PubMed.
- K. Seleznyova, N. A. Sergeev, M. Olszewski, P. Stepien, S. V. Yagupov, M. B. Strugatsky and J. Kliava, Fitting MAS NMR spectra in crystals with local disorder: Czjzek's vs. Maurer's model for 11B and 71Ga in polycrystalline gallium borate, Solid State Nucl. Magn. Reson., 2017, 85–86, 12 CrossRef CAS PubMed.
- M. Olszewski, Structural Disorder and NMR of Quadrupolar Nuclei, Appl. Magn. Reson., 2019, 50, 835 CrossRef.
- G. Czjzek, J. Fink, F. Götz, H. Schmidt, J. M. D. Coey, J.-P. Rebouillat and A. Liénard, Atomic Coordination and the Distribution of Electric-Field Gradients in Amorphous Solids, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 2513 CrossRef CAS.
- G. Le Caër and R. A. Brand, General Models for the Distributions of Electric Field Gradients in Disordered Solids, J. Phys.: Condens. Matter, 1998, 10, 10715 CrossRef.
- J.-B. d’Espinose de Lacaillerie, C. Fretigny and D. Massiot, MAS NMR Spectra of Quadrupolar Nuclei in Disordered Solids: The Czjzek Model, J. Magn. Reson., 2008, 192, 244 CrossRef PubMed.
- B. Bureau, G. Silly, J. Y. Buzaré, B. Boulard and C. Legein, Nuclear magnetic resonance quadrupolar parameters and short range order in disordered ionic fluorides, J. Phys.: Condens. Matter, 2000, 12, 5775 CrossRef CAS.
- G. Czjzek, Distribution of nuclear quadrupole splittings of 57Fe in amorphous ferric fluorides: Structural implications, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 25, 4908 CrossRef CAS.
- A. Abragam, Principles of Nuclear Magnetism, Oxford University Press, London, 1961, p. 279 Search PubMed.
- P. S. Hubbard, Nonexponential Nuclear Magnetic Relaxation by Quadrupole Interactions, J. Chem. Phys., 1970, 53, 985 CrossRef CAS.
- A. Baram, Z. Luz and S. Alexander, Resonance Line Shapes for Semi-Integer Spins in Liquids, J. Chem. Phys., 1973, 58, 4558 CrossRef CAS.
- L. Werbelow, NMR dynamic frequency shifts and the quadrupolar interaction, J. Chem. Phys., 1979, 70, 5381 CrossRef CAS.
- K. D. Becker, Nuclear Magnetic Relaxation Induced by the Dynamics of Lattice Defects in Solids (I = 3/2, I = 2, and I = 5/2), Z. Naturforsch. A, 1982, 37, 697 Search PubMed.
- D. Brinkmann, M. Mali, J. Roos, R. Messer and H. Birli, Diffusion processes in the superionic conductor Li3N: An NMR study, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26, 4810 CrossRef CAS.
- D. Freude, J. Haase, J. Klinowski, T. A. Carpenter and G. Ronikier, NMR Line Shifts Caused by the Second-Order Quadrupolar Interaction, Chem. Phys. Lett., 1985, 119, 365 CrossRef CAS.
- L. Werbelow and R. E. London, Dynamic frequency shift, Concepts Magn. Reson., 1996, 8, 325 CrossRef CAS.
- H. W. Spiess, Rotation of molecules and nuclear spin relaxation, Dynamic NMR Spectroscopy, Springer, Berlin, 1978 Search PubMed.
- N. Bloembergen, E. M. Purcell and R. V. Pound, Relaxation Effects in Nuclear Magnetic Resonance Absorption, Phys. Rev., 1948, 73, 679 CrossRef CAS.
- P. A. Beckmann, Spectral densities and nuclear spin relaxation in solids, Phys. Rep., 1988, 171, 85 CrossRef.
- C. A. Angell, Relaxation in liquids, polymers and plastic crystals—strong/fragile patterns and problems, J. Non-Cryst. Solids, 1991, 131–133, 13 CrossRef CAS.
- A. Baram, Z. Luz and S. Alexander, Resonance Line Shapes for Semi-Integer Spins in Liquids, J. Chem. Phys., 1973, 58, 4558 CrossRef CAS.
- J. Shen, V. Terskikh and G. Wu, Observation of the Second-Order Quadrupolar Interaction as a Dominating NMR Relaxation Mechanism in Liquids: The Ultraslow Regime of Motion, J. Phys. Chem. Lett., 2016, 7, 3412 CrossRef CAS PubMed.
- G. Wu, 17O NMR studies of organic and biological molecules in aqueous solution and in the solid state, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 114–115, 135 CrossRef CAS PubMed.
- L. Hoffmann, J. Beerwerth, K. Moch and R. Böhmer, Phenol, the simplest aromatic monohydroxy alcohol, displays a faint Debye-like process when mixed with a nonassociating liquid, Phys. Chem. Chem. Phys., 2023, 25, 24042 RSC.
- R. Böhmer, M. Storek and M. Vogel, NMR studies of ionic dynamics, in Modern Methods in Solid-State NMR: A Practitioners’ Guide, ed. P. Hodgkinson, Royal Society of Chemistry, 2018, ch. 7, pp. 193–230 Search PubMed.
- M. Adjei-Acheamfour, M. Storek, J. Beerwerth and R. Böhmer, Two-dimensional second-order quadrupolar exchange powder spectra for nuclei with half-integer spins. Calculations and an experimental example using oxygen NMR, Solid State Nucl. Magn. Reson., 2015, 71, 96 CrossRef CAS PubMed.
- R. Böhmer, M. Storek and M. Vogel, Magnetic Resonance Studies of Heterogeneous Rotational and Translational Dynamics in Glasses and other Disordered Materials, in Modern Magnetic Resonance, second edition, ed. G. A. Webb, Springer, Cham, 2017, pp. 1–20 Search PubMed.
- M. Mackowiak, N. Sinyavsky and B. Blümich, Two-dimensional exchange 35Cl NQR spectroscopy of hexachloroethane, J. Mol. Struct., 2005, 743, 53 CrossRef CAS.
- E. Rommel, P. Nickel, F. Rohmer, R. Kimmich, C. Gonzales and D. Pusiol, Two-dimensional Exchange Spectroscopy Using Pure NQR, Z. Naturforsch. A, 1992, 47, 382 CrossRef CAS.
- M. Mackowiak, p-Chlorobenzotrichloride revisited: novel analytical treatments of 2D exchange NQR in molecular crystals, Magn. Reson. Chem., 2011, 49, 38 CrossRef CAS PubMed.
- J. Beerwerth, M. Storek, D. Greim, J. Lueg, R. Siegel, B. Cetinkaya, W. Hiller, H. Zimmermann, J. Senker and R. Böhmer, Two-site jumps in dimethyl sulfone studied by one- and two-dimensional 17O-NMR spectroscopy, J. Magn. Reson. B, 2018, 288, 84 CrossRef CAS PubMed.
- K. Schmidt-Rohr and H. W. Spiess, Multidimensional Solid-State NMR and Polymers, Academic Press, London, 1994 Search PubMed.
- P. Ingman and G. W. Driver, A quantitative ionicity scale for liquid chloride salts, Phys. Chem. Chem. Phys., 2012, 14, 13053 RSC.
- J. G. Powles and M. Rhodes, Deuteron and 35Cl spin lattice relaxation in DCl and HCl, Phys. Lett. A, 1967, 24, 523 CrossRef CAS.
- M. Storek, K. R. Jeffrey and R. Böhmer, Local-field approximation of homonuclear dipolar interactions in 7Li-NMR: Density-matrix calculations and random-walk simulations tested by echo experiments on borate glasses, Solid State Nucl. Magn. Reson., 2014, 59–60, 8 CrossRef CAS PubMed.
- F. Fujara, B. Geil, H. Sillescu and G. Fleischer, Translational and rotational diffusion in supercooled orthoterphenyl close to the glass transition, Z. Phys. B, 1992, 88, 195 CrossRef CAS.
- I. Chang and H. Sillescu, Heterogeneity at the glass Transition: Translational and rotational self-diffusion, J. Phys. Chem. B, 1997, 101, 8794 CrossRef CAS.
- S. F. Swallen, K. Traynor, R. J. McMahon, M. D. Ediger and T. E. Mates, Selfdiffusion of supercooled tris-naphthylbenzene, J. Phys. Chem. B, 2009, 113, 4600 CrossRef CAS PubMed.
- J. R. Rajian, W. Huang, R. Richert and E. L. Quitevis, Enhanced translational diffusion of rubrene in sucrose benzoate, J. Chem. Phys., 2006, 124, 014510 CrossRef PubMed.
- B. Geil, G. Diezemann and R. Böhmer, Calculations of stimulated echoes and two-dimensional nuclear magnetic resonance spectra for solids with simple line shapes, J. Chem. Phys., 2008, 128, 114506 CrossRef PubMed.
- R. Böhmer, G. Diezemann, G. Hinze and E. Rössler, Dynamics of supercooled liquids and glassy solids, Prog. Nucl. Magn. Reson. Spectrosc., 2001, 39, 191 CrossRef.
- G. Diezemann, R. Böhmer, G. Hinze and H. Sillescu, Reorientational dynamics in simple supercooled liquids, J. Non-Cryst. Solids, 1998, 235–237, 121 CrossRef CAS.
- S. Berndt, K. R. Jeffrey, R. Küchler and R. Böhmer, Silver ion dynamics in silver borate glasses: spectra and multiple-time correlation functions from 109Ag NMR, Solid State Nucl. Magn. Reson., 2005, 27, 122 CrossRef CAS PubMed.
- M. Vogel and T. Torbrügge, Ion and polymer dynamics in polymer electrolytes PPO-LiClO4, I. Insights from NMR line-shape analysis, J. Chem. Phys., 2006, 125, 054905 CrossRef CAS PubMed.
- S. Faske, H. Eckert and M. Vogel, 6Li and 7Li NMR line-shape and stimulated-echo studies of lithium ionic hopping in LiPO3 glass, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 104301 CrossRef.
- K. L. Ngai, Relaxation and Diffusion in Complex Systems, Springer, Berlin, 2011 Search PubMed.
- F. Mizuno, J. P. Belieres, N. Kuwata, A. Pradel, M. Ribes and C. A. Angell, Highly decoupled ionic and protonic solid electrolyte systems, in relation to other relaxing systems and their energy landscapes, J. Non-Cryst. Solids, 2006, 352, 5147 CrossRef CAS.
- Z. Wojnarowska, J. Knapik, J. Jacquemin, S. Berdzinski, V. Strehmel, J. R. Sangoro and M. Paluch, Effect of pressure on decoupling of ionic conductivity from segmental dynamics in polymerized ionic liquids, Macromolecules, 2015, 48, 8660 CrossRef CAS.
- J. Habasaki, C. León and K. L. Ngai, Dynamics of Glassy, Crystalline and Liquid Ionic Conductors: Experiments, Theories, Simulations, Springer, Switzerland, 2017 Search PubMed.
- F. Wieland, A. P. Sokolov, R. Böhmer and C. Gainaru, Transient nonlinear response of dynamically decoupled ionic conductors, Phys. Rev. Lett., 2018, 121, 064503 CrossRef CAS PubMed.
- J. D. Mackenzie and W. K. Murphy, Structure of Glass-Forming Halides. II. Liquid Zinc Chloride, J. Chem. Phys., 1960, 33, 366 CrossRef CAS.
- S. B. Pillai, R. J. Wilcox, B. G. Hillis, B. P. Losey and J. D. Martin, Understanding the Water-in-Salt to Salt-in-Water Characteristics across the Zinc Chloride: Water Phase Diagram, J. Phys. Chem. B, 2022, 126, 2265 CrossRef CAS PubMed.
- Q. Zhang, Y. Ma, Y. Lu, L. Li, F. Wan, K. Zhang and J. Chen, Modulating electrolyte structure for ultralow temperature aqueous zinc batteries, Nat. Commun., 2020, 11, 4463 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp03668e |
| This journal is © the Owner Societies 2023 |
