Revisiting the bonding evolution theory: a fresh perspective on the ammonia pyramidal inversion and bond dissociations in ethane and borazane

Abstract

This work offers a comprehensive and fresh perspective on the bonding evolution theory (BET) framework, originally proposed by Silvi and collaborators [X. Krokidis, S. Noury and B. Silvi, Characterization of elementary chemical processes by catastrophe theory, J. Phys. Chem. A, 1997, 101, 7277–7282]. By underscoring Thom's foundational work, we identify the parametric function characterizing bonding events along a reaction pathway through a three-step sequence to establish such association rigorously, namely: (a) computing the determinant of the Hessian matrix at all potentially degenerate critical points, (b) computing the relative distance between these points, and (c) assigning the unfolding based on these computations and considering the maximum number of critical points for each unfolding. In-depth examination of the ammonia inversion and the dissociation of ethane and ammonia borane molecules yields a striking discovery: no elliptic umbilic flag is detected along the reactive coordinate for any of the systems, contradicting previous reports. Our findings indicate that the core mechanisms of these chemical reactions can be understood using only two folds, the simplest polynomial of Thom's theory, leading to considerable simplification. In contrast to previous reports, no signatures of the elliptic umbilic unfolding were detected in any of the systems examined. This finding dramatically simplifies the topological rationalization of electron rearrangements within the BET framework, opening new approaches for investigating complex reactions.

---

Introduction

The concept of a chemical bond has long been intensely debated. On the one hand, it encapsulates our understanding of matter's existence and stability. On the other hand, it lacks a quantitative measure to establish whether two atoms are chemically bonded, making it a non-physical observable.^1–4 This dichotomy has led to various methodologies to decipher this elusive construct. In 1916 Lewis⁵ proposed that a chemical bond could be interpreted as an electron pair shared by two atoms, an idea that has since profoundly ingrained itself in the minds of chemists.^6–8 Fifteen years later, Pauling⁹ translated Lewis sharing idea into the emerging quantum mechanics language, building on Heitler and London's work.¹⁰ Bader and Henneker¹¹ used the electric field to explore a completely different interaction – the ionic bond. Gadre and co-workers¹² combined this field with topological concepts to describe various bonding situations in neutral and electrically charged molecular systems. Researchers have sought conclusive evidence for decades to resolve the dichotomy between the relevance of kinetic and potential energies in chemical bonding.^13–20

Bader's seminal work on the topological analysis of the electron density²¹ introduced a new way to gain insights into the characterization of the chemical structure and bonding concepts. This method has also been applied to other local functions, including the electron localization function (ELF),²² the nuclear potential,²³ the virial field,²⁴ the magnetically induced molecular current distribution,²⁵ and the spin density.²⁶ Such type of analysis has been proposed to be classified as quantum chemical topology (QCT).²⁷ QCT leverages the topographical analysis of the gradient vector field generated by scalar functions to extract valuable chemical information without explicitly mentioning the reference state. These approaches enable a definition of topological domains using partitioning schemes, which are parameter-free.²⁸ Krokidis, Noury, and Silvi²⁹ explored for the first time the application of Thom's catastrophe theory (CT)³⁰ to the analysis of topographical changes of ELF²² along a given coordinate, i.e., defining the so-called bonding evolution theory (BET) methodology. BET has been applied in an ever-increasing fashion over the last three decades to gain a deeper understanding of different covalent bonding situations,²⁹ C–H bonds activation,³¹ proton transfer reactions,³² cycloadditions,^2,33–37 phase transition of the 14 group elements,³⁸ hemiaminals formation,^39,40 computing local and global properties of solids,⁴¹ and deducing linear models for predicting activation enthalpies of organic and organometallic systems.⁴²

The BET critical idea is modeling any reaction system as a gradient dynamical system (GDS) using the ELF as its potential. The gradient nullity condition applied to ELF yields four types of equilibria since this smooth function is defined on : attractors (ELF maxima, hereafter labeled as a), saddle points of index one and two (hereafter designated as s₁ and s₂, respectively), and repellors (ELF minima, hereafter denoted as m). Following the changes of these solutions along a reaction path (e.g., the IRC⁴³), a rationalization of electronic events in terms of the so-called universal unfoldings³⁰ is carried out. These unfoldings are parametric polynomials of degree equal to or greater than 3, which accurately approximate the ELF shape in the locality of a topographical bifurcation if some requirements are met.^44–46 Each function describes one of the seven types of degeneracy exhibited by ELF critical points (CPs). A CP is said to be degenerate if evaluating the determinant of the Hessian matrix yields 0; otherwise, it is called hyperbolic.^44,46,47 The collection of the hyperbolic (Morse-type) CPs and the gradient lines connecting them is called a topographic map or phase-space portrait.^48–53 Abrupt changes in such a space comprising both the type and number of CPs are frequently referred to as topological bifurcations.^48–53 Poincaré–Hopf theorem⁵⁴ imposes a strong constrain for all these changes since n₀ − n₁ + n₂ − n₃ = 1, where n₀, n₁, n₂, and n₃ stand for the number of attractors, saddles of index one, saddles of index two, and repellors, respectively. Note that the subscript coincides with the index of the CP. This alternating sum yields zero in the context of periodic systems, such as crystalline structures. Herein we will follow the convention that the index represents the number of positive eigenvalues of the Hessian matrix at the point.⁵⁵ Therefore, a CP with any positive eigenvalue is classified as a maximum of the function. In contrast, the critical point is indicative of a minimum on the potential landscape in cases where all its three eigenvalues are positive. The other two possible scenarios (on ) involving combinations of one and two positive eigenvalues lead to saddle points of indices one and two, respectively. On the other hand, there is a (big) set of points where the ELF gradient does not vanish, and more importantly, a departing trajectory of such points from the neighborhood of a Morse-type CP will never return. These intriguing points are the so-called wandering points.⁴⁵ It is essential to emphasize that the BET has been applied to the study of a wide variety of chemical reactions ranging from the gas phase to the solid state;⁵⁶ however, despite its popularity, the identifying-assigning process of the correct unfolding to describe the formation/scissions of chemical bonds is not well understood.

Our group has described the electron reorganizations along a reactive coordinate in the ground^57,58 and electronically excited states^59–63 following the determinant of Hessian at all potentially degenerate CPs and their relative distance.⁵⁶ This procedure guarantees a rigorous application of BET proposal by recovering the fundamentals underpinning Thom's works and leading to surprising findings.^64,65 Furthermore, by combining this robust version of BET and other topological concepts, we have recently proposed a model for predicting the activation energy of organic and organometallic reacting systems at 0 K.⁴²

In the seminal work of Silvi et al.²⁹ the inversion of ammonia, the dissociation of ethane into two CH₃ radicals, and the N-B bond scission of BH₃NH₃ molecules were used as prototypical examples to show the BET capabilities. The electronic preparation stages of ethane C–C bond scission were described through an elliptic umbilic and three simultaneous folds. The bond between the two carbons finally cracks following a cusp function. On the other hand, they rationalized the umbrella inversion via two elliptic umbilic polynomials. The topographical description of the dative bond breakage comprises one elliptic umbilic and four fold bifurcations. Despite the cryptic character of the assigning, this methodology is now a standard tool for studying different bonding situations and gaining deeper insights into chemical reactivity in a wide range of research fields. The amount of accumulated data available due to the widespread usage of BET covering several research fields has led some authors to point out that only these unfoldings (fold, cusp, and elliptic umbilic) have a precise chemical meaning.^{2,3,33,66–71} However, the elliptic umbilic contains three parameters,³⁰ which must be associated with real objects controlling the reaction. Typically, the distance between two reacting centers is employed as a parameter,^56,57 leaving the physical interpretation of the other coefficients unclear.

This paper aims to re-examine the three reactions discussed by Silvi and co-workers,²⁹ focusing on the assigning process of bifurcations via monitoring the Hessian determinant at potentially degenerate CPs and the relative distances between them, as recently proposed by Ayarde–Henríquez and collaborators.⁵⁶ The second goal is to show the need for consistency with the theoretical basis of CT since ignoring them would question the rigor of past and current applications of BET, casting strong doubts on how reactive processes have been rationalized via unfoldings over the last 30 years.

Results and discussion

Understanding the pyramidal inversion of ammonia

The process of an atom shifting from its original trivalent or tricoordinate (ground state) configuration through a planar formation and then returning to its initial geometric structure is what we call a pyramidal inversion. This fluxional process is an ideal example of dynamic stereoisomerism, a process where the arrangement of atoms changes without the formation or breakage of bonds.^72,73 To understand this process better, we often refer to Linus Pauling's hybridization concept. The original molecule configuration (C_3v) shifts to a planar configuration (D_3h) during the transition state (TS). This process can be described by a sequence of hybridization transitions: sp³ → sp² → sp³ (see Scheme 1).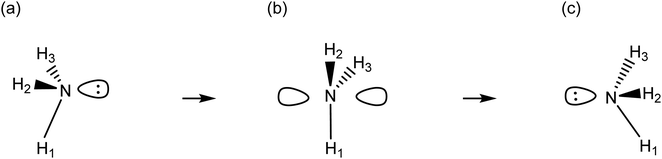

Scheme 1 Lewis-like structures depicting the prototypical pyramidal inversion of ammonia. The system commutes between C_3v configurations, (a) and (c) by passing through a D_3h transition state (b).

It is well known that the activation barrier (E_a) for the 15 group elements highly depends on the inversion center. The umbrella inversion of ammonia is almost barrierless, demanding only 5.8–5.9 kcal mol⁻¹ at room temperature (T = 298 K).^74,75 Similar spectroscopic approaches estimate significantly higher E_a for phosphine (PH₃) and arsine (AsH₃): 17.1 and 32.1 kcal mol⁻¹, respectively.⁷⁶ Indeed, a higher value of 31.6 kcal mol⁻¹ has also been reported for PH₃.⁷⁷ Predicted activation enthalpies (ΔH^‡), calculated in the gas phase using range-separated corrected global-hybrid DFT functionals^78,79 match closely with the experimental values. Any discrepancies range from 0.17 to 0.78 kcal mol⁻¹ for ammonia, 7.36 to 10.93 kcal mol⁻¹ for phosphine, and 3.71 to 7.82 kcal mol⁻¹ for arsine. These consistent results across various systems suggest that the methodologies used are appropriate for examining the ELF topography along the IRC, yielding consistent results across various systems. Furthermore, these results indicate the analysis performed is independent on the computational method, aligning with recent observations.⁵⁶ Please refer to the ESI† for additional details.

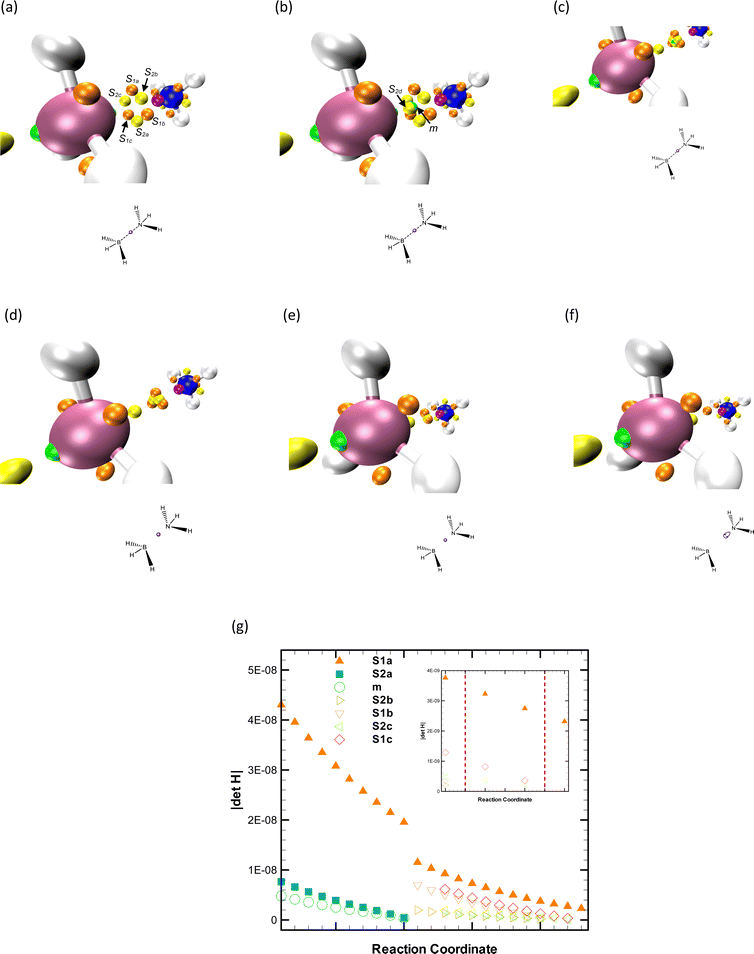
Using the foundational BET framework, Silvi and collaborators²⁹ attempted to describe the inversion of ammonia through two elliptic umbilic functions. However, this model does not hold up when we examine the Hessian determinant at potentially involved critical points (CPs) and their relative distance.⁵⁶Fig. 1 illustrates the changes in the topographic map before and after the inversion. Nonetheless, it should be stressed that identifying the colliding CPs cannot be performed by a visual inspection but rather by using the mathematical principles supporting CT, which are crucial in selecting the right unfolding featuring the chemical process. Indeed, considering the Poincaré–Hopf theorem, one can assert that only two CPs coalesce, having such points different indices. Yet, no unfolding can accurately capture this topographic event, as the involved CPs are saddle points.^44,45

Fig. 1 The image depicts fragments of the ELF topographic map of the ammonia molecule before (panel a) and after merging two saddle points with differing indices (panel b). Following this merger, there is an appearance of a₂ and s_1d near the remaining saddles, which showcases a fold catastrophe (panel c). In the visualization, the different map features are distinguished by color: attractors are shown in purple, saddles of index one in orange, saddles of index two in yellow, and repellors in green. For ease of interpretation, gradient lines are not displayed. In addition, Lewis-like structures are provided to help understand the molecular configurations associated with these changes.

Fig. 2, panel a, is essential to effectively apply Thom's functions⁵⁶ since it displays the absolute value of the Hessian determinant, |ΔH|. This is shown for the index-one saddles (s_1a, s_1b, and s_1c) and the index-two saddle (s_2a). It is worth mentioning that this step is not strictly necessary as the collision between saddles leads to topographical bifurcations rather than catastrophic ones. As the phase portrait is about to change, we can observe that the |ΔH| at s_1c decreases slightly faster than that of the other saddles of index one (s_1a and s_1b). This is reflective of the impending change. A similar pattern can be seen in the relative distance s_1c–s_2a, indicating that s_1c and s_2a are approaching each other at the highest rate. It is also important to note that as the bifurcation is imminent, the separation symmetry between the s_2a and the three index-one saddles is lost. This transformation is depicted in Fig. 2, panel b.

Fig. 2 The diagram showcases two primary aspects of the ammonia umbrella inversion process: panel a represents the alteration in the modulus of the Hessian matrix at the points s_2a, s_1a, s_1b, and s_1c when we traverse the IRC. The inset graph shows the asymptotic behavior of |ΔH| near the bifurcation, and the dashed red line indicates the transformation occurring in the phase space. Panel b demonstrates the variations in the relative distances between the point pairs s_2a–s_1a, s_2a–s_1b, and s_2a–s_1c as we move along the IRC. This change in distances provides valuable insight into the evolving structure and interaction dynamics during the ethane molecule's dissociation.

After the disappearance of saddles of s_2a and s_1c, the remaining saddles, s_1a and s_1b, gradually increase their relative distance, leading to a corresponding increase in their |ΔH| value. This shift sets the stage for the appearance of a new attractor a₂ and another saddle s_1d near the original saddles, as depicted in Fig. 1, panel c. The emergence of this new attractor can be classified as a fold-type catastrophe, indicating that neither s_1a nor s_1b are degenerate. Within the original BET framework, considering the principles of Thom's work, this observation suggests that there are no signs of an elliptic umbilic yet. As the reaction progresses, on the opposite side of the plane that contains the nitrogen atom and orthogonal to the C₃ axis, the coalescence of a₁ and s_1g forms a wandering point;⁷ as seen in Fig. 3, panels a and b. The subsequent loss of this lone pair is best described through a fold catastrophe, as illustrated in Fig. 3, panels d and e. Lastly, the emergence of saddles s_1h and s_2b near the remaining pair (s_1e, s_1f) marks the final topographic alteration along the IRC. This is shown in Fig. 3, panel c.

Fig. 3 The image features segments of the ELF topographic map of the ammonia molecule before (panel a) and after the coalescence of a₁ and s_1g (panel b). Post this merging, the saddles s_1h and s_2b emerge through a topographical bifurcation, an event that cannot be described in terms of any unfolding (panel c). Panel d visualizes the variation in the modulus of the Hessian matrix at points a₁, s_1e, s_1f, and s_1g as we move along the IRC. The inner plot depicts the asymptotic behavior of |ΔH| near the bifurcation, and the dashed red line represents the transformation in the phase space. Panel e shows the change in the relative distances a₁–s_1e, a₁–s_1f, and a₁–s_1g as we progress along the IRC. For ease of understanding, various features of the map are color-coded: attractors in purple, saddles of index one in orange, saddles of index two in yellow, and repellors in green. The map does not display gradient lines for simplicity. Additionally, Lewis-like structures are also provided to give a clearer idea of the associated molecular configurations.

This analysis reveals that the inversion of the ammonia molecule only triggers flags for the most basic parametric function of Thom's catastrophe theory, contradicting a previous report.²⁹ This significantly simplifies the topological rationalization of this reaction by eliminating the umbilic complexities because this unfolding is not a cuspoid, which means that it has more than one state variable, and more importantly, three (control) parameters are needed to remove its degenerations entirely. The parameter of the fold function typically has a straightforward physical interpretation. One suitable alternative for the chemical process at hand is the angular displacement (μ) conveniently defined by the C₃ axis and the N–H bonds.²⁹ See ref. 29 for further details on the critical values of this parameter. In this scenario, smooth changes in μ lead to the creation/annihilation of (attractor, saddle) pairs when a critical value μ_* is reached, ‘‘jumping’’ the reacting system between regions (structural stability domains) with any and two CPs, as displayed in Fig. 4. In essence, within this succinct topographical description of the ammonia pyramidal inversion, μ controls the changes in sp hybridization. However, it is crucial to underscore that giving a specific interpretation to each parameter in the context of the umbilic catastrophe remains a challenging task.

Fig. 4 The image depicts a fragment of the ELF topographic map, showcasing a typical fold flag. This ‘‘jump’’ between regions with none and two CPs happens when a critical value of μ_* is achieved. Attractors are depicted in purple and the saddle points of index one are represented in orange. This image is reproduced from the work of Ayarde-Henríquez et al.⁵⁶

Dissociation of ethane (breaking of the C–C bond)

The dissociation of ethane involves the breaking of the C–C bond. Under this process, the high molecular symmetry of ethane leads to the production of two identical fragments. Each of these moieties retains an unpaired electron, representing Lewis’ concept of shared electron pairs. In some instances, this dissociation may also result in two charged fragments.⁸⁰ Remarkably, the dissociation of ethane is not a simple process. It demands a significant amount of energy. Experimental data estimates this to be around 89.9 kcal mol⁻¹ at 298 K in the gas phase.⁸⁰ In our studies using the complete active-space self-consistent field (CASSCF) and its second-order perturbation theory (CASSPT2) methods, we found a range of required energies deviating from 1.56 to 8.15 kcal mol⁻¹. For detailed information, refer to the ESI.†

The first changes in the locality of each carbon take place as the relative separation between s_1a and the three saddles of index two (s_2a, s_2b, and s_2c) decreases. Since the Poincaré–Hopf formula⁵⁴ dictates both the number and type of CPs variations, only one of the three saddles of index two is involved in the bifurcation, as presented in Fig. 5, panels a and b. We again relied on the |ΔH| at CPs and their relative distance to determine that such a saddle is s_2a, meaning that this point and s_1a coalesce, and thus, the latter CP does not change its index but rather disappears through a bifurcation that cannot be rationalized using any unfolding;^44,45 see Fig. 5, panels c and d.

Fig. 5 The image represents fragments of the ELF topographic map of the ethane molecule before (panel a) and after the merging of s_1a and s_2a (panel b). (Panel c) shows the change in the modulus of the Hessian matrix at s_1a, s_2a, s_2b, and s_2c along the reaction pathway. The inner plot indicates the asymptotic behavior of |ΔH| near the bifurcation, and the dashed red line marks the change in the phase space. (Panel d) displays the variation of the relative distances s_1a–s_2a, s_1a–s_2b, and s_1a–s_2c along the CC reactive coordinate. The various features of the map are color-coded: attractors are represented in purple, saddles of index one in orange, saddles of index two in yellow, and repellors in green. To simplify the visual, gradient lines are not shown. The dashed lines in the Lewis-like structures represent the bonds that are breaking.

As the CC bond further stretches, an index-two saddle (s_2d) and one repellor (m₄) arise in the vicinity of the remaining points, s_2b and s_2c. Therefore, a fold catastrophe describes this topographic event since one of the new CPs is not a saddle, ‘‘jumping’’ the reaction system between topographic regions with a difference in the CPs number equal to two. We agree with Silvi and coworkers²⁹ that the simplest unfolding correctly describes the following three (simultaneous) changes since repellors m₁, m₂, and m₃ and saddles s_2b, s_2c, and s_2d collide and annihilate, respectively, as depicted in Fig. 6.

Fig. 6 This graphic displays segments of the ELF topographic map of the ethane molecule before (panel a) and after the occurrence of three simultaneous folds, characterized by the annihilation of the pairs (s_2b, m₁), (s_2c, m₂), and (s_2d, m₃) (panel b). Different features on the map are color-coded for clarity: attractors are shown in purple, saddles of index one in orange, saddles of index two in yellow, and repellors in green. For simplicity, gradient lines are not depicted. The image also includes Lewis-like structures with dashed lines representing the bonds that are breaking, providing a clearer understanding of the molecular transformations taking place.

One of the most pivotal and intriguing events during this process is the division of the attractor a₁ into a₂, a₃, and s_1b. This event signals the beginning of the CC bond cleavage. For in-depth insights into the critical distances between carbons, we refer the reader to ref. 29. As demonstrated in Fig. 7, the topographic analysis of the ELF gradient offers a precise and intuitive depiction that aligns well with a chemist's expectations.

Fig. 7 The topographic map of the ethane molecule depicts the phase transition before (a) and after (b) the a₁ attractor splits into a₂, a₃, and s_1b, illustrating a cusp catastrophe. The change in the modulus of the Hessian matrix at a₁, a₂, a₃, and s_1b along the reaction coordinate is marked, with the dashed red line signifying the transformation in the phase space (c). The relative distances s_1b–a₂ and s_1b–a₃ as a function of the pathway are also indicated (d). Color-coded points indicate the attractors (in purple), saddles of index one (in orange), saddles of index two (in yellow), and repellors (in green). For simplicity, gradient lines are not displayed. The dashed lines in Lewis-like structures represent the breaking bonds.

The absolute value of the Hessian determinant at a₁ diminishes as the distance between the carbon atoms grows. This culminates in the degeneration of this CP and its subsequent division into two new attractors (a₂ and a₃) and a saddle of index one (s_1b). The maintained symmetry in both the |ΔH| at a₂ and a₃ and the relative distance between these attractors and s_1b along the CC reactive coordinate is of critical importance. These elements corroborate the occurrence of a cusp catastrophe, in line with the classification provided by Silvi and collaborators,²⁹ see Fig. 7, panels c and d. Although CT offers a straightforward methodology for identifying the correct unfolding to characterize meaningful electron fluxes along reactive coordinates, interpreting the parameter(s) of such a polynomial remains an open area of research, as this exceeds the scope of Thom's theory. By following the logic applied to the inversion of the ammonia molecule, the linear monomial coefficient of the cusp could be linked with the distance between the carbon atoms. Moreover, given that cusp flags have been observed in highly symmetrical reactive systems involving homolytic bond cleavage,^29,60 it seems plausible to associate the other parameter (bias⁸¹) with the radical character of the components. The distance between the reacting centers and the biradical nature of the system are not independent variables; therefore, this relationship must be conceptually associated with the one characterizing the cusp parameters, i.e., a semi-cubic parabola. The function describing the unfolding coefficients thus requires us to associate them with physical quantities that are inherently correlated, further enhancing the comprehensiveness of BET applications. From a qualitative perspective, a complete correspondence between the cusp and the ELF geometric shape near the bifurcation requires the use of the dual of this unfolding (i.e., its negative version), as initially reported;²⁹ see Fig. 8.

Fig. 8 The symmetrical changes in the ELF shape disclose the cusp nature of the system's transition from none to a biradical character, resulting from the continuous separation of carbon atoms. The correlation between this biradical nature and the distance between reactive centers makes it apt to interpret the parameters of the cusp. This provides a deeper understanding of the system's behavior during this transition and can potentially aid in predicting and manipulating similar reactions in the future.

Dissociation of ammonia borane (breaking of the B–N dative bond)

The so-called dative bond, less frequently referred to as a covalent bond,⁸² a coordinate link,⁸³ and a semipolar double bond,⁸⁴ is an interesting bonding situation in which the lone pair of an atom (e.g., nitrogen) is transferred to the unoccupied orbital of other (e.g., boron). Usually, systems characterized by such a bond are called electron donor–acceptor complexes,⁸⁵ Lewis acid–base adducts,⁸⁶ or coordination compounds.⁸⁷ Ammonia borane is the textbook example used to illustrate this bonding situation due to its simplicity,^80,88,89 and due to this, it has been investigated through both theoretical^29,90,91 and experimental^92,93 approaches. Regardless that H₃CCH₃ and H₃BNH₃ are isoelectronic molecules exhibiting similar structural forms, they differ significantly in their physical and chemical properties, as well as in their dissociation processes. The dissociation of the BN bond in ammonia borane is heterolytic, which means it breaks in such a way that the shared electron pair is entirely taken by one of the atoms. Conversely, the CC bond in ethane breaks homolytically, where each carbon atom takes one electron from the shared pair.^80,88 Specifically, the experimental dissociation energy of ammonia borane in the gas phase is about 31.1–37.5 kcal mol⁻¹ at 298 K,^80,94 which is approximately a third lower than the energy required for ethane. In our calculations, using global hybrid functionals, the absolute error ranges from 2.33 to 3.71 kcal mol⁻¹. In addition, we investigated changes in the molecular graph of phosphine borane along the dissociation pathway. Unfortunately, no experimental dissociation energy values for this molecule were found in the existing literature. As expected, the ELF topological analysis of both systems provides consistent results across different levels of theory. For further details, please refer to the ESI.†

The topological explanation for the dissociation of the dative bond between boron and nitrogen in ammonia borane is indeed compelling. Just as with the case of ethane that we discussed earlier, the breaking of the bond can be rationalized and visualized uniquely using topological methods. These methods provide valuable insights into the bond dissociation processes, adding depth to our understanding of the structural changes occurring during these reactions. In the case of the ammonia borane complex, while boron and nitrogen separate, the repellor m and the saddle point s_2d appear within the loop formed by the collection of saddles s_1i and s_2i, i = a, b, and c. Thus, this topographic change corresponds to a fold catastrophe as first identified by Silvi and co-workers;²⁹ see Fig. 9, panels a and b. The phase space between the reacting centers flattens due to the annihilation of the (m, s_2a) pair through a fold upon further stretching of the B–N bond (Fig. 9 panels c and d). Detailed information concerning the B–N critical values can be found in ref. 29. Finally, two pairs of saddles coalesce not simultaneously; see Fig. 9, panels d–f. Regardless that any topographical change resulting from merging/arising saddles cannot be describe via any unfolding,^44,45 the |ΔH| at all these CPs is provided for illustrating the assigning procedure; see Fig. 9 panel g. Relying on Thom's catastrophe theory, no umbilic fingerprint is detected, as no critical point changes its index. This indicates that a function with one parameter and one state variable is the correct polynomial for characterizing this reaction from a topological standpoint. This is contrary to the report by Silvi and collaborators.²⁹ Additionally, the number of eigenvalues of |ΔH| tending to zero is a critical variable often overlooked when classifying relevant chemical processes along a reaction pathway via unfoldings. From a pure topological perspective, distinguishing between unfoldings with one and two state variables can only be done considering the number of null eigenvalues.⁵⁶ Hence, we propose that the BH₃NH₃ dissociation has to be characterized via a cuspoid (i.e., a one-state-variable function) and not in terms of an umbilic (i.e., a two-state-variable function), as only one eigenvalue of the CPs involved in the fold catastrophe tends to zero value. For this reaction, it is appropriate to consider the fold parameter controlling the changes in the ELF topography as the negative of the B–N enlargement since catastrophic bifurcations result from changes in this bond length.

Fig. 9 ELF topography of ammonia borane before (a) and after s_2d and m arise through a fold (b). The repellor m and the saddle s_2a coalesce through a fold (c) and (d). Sequence of bifurcations that cannot be assigned to any unfolding since only saddles are involved (d)–(f). Change in the modulus of the Hessian matrix at m, s_1i, and s_2i (i = a, b, and c) altogether with the asymptotic behavior of |ΔH| near the bifurcation (inner plot), dashed red lines indicate changes in the phase space along the BN reactive coordinate (g). Attractors are represented in purple, saddles of index one in orange, saddles of index two in yellow, and repellors in green. Gradient lines are not shown for simplicity. The gradient lines are left out for simplicity, and the dashed lines in the Lewis-like structures indicate the breaking bonds during the reaction.

Concluding remarks

This work focuses on the conceptual foundations of identifying-assigning elementary catastrophes within the so-called bonding evolution theory (BET) framework.²⁹ In contrast to the earlier discussion concerning the bonding nature along the ammonia inversion and the dissociation of ethane and ammonia borane molecules, no signatures of the elliptic umbilic unfolding have been detected. Such a finding rest upon rigorous examination of the determinant of the Hessian at critical points and the relative distance between them in each of the reacting systems, a result which is also tested to be independent of the level of theory and substituents. Such a methodological framework leads to rigorously elucidating the nature of each catastrophe by being coherent with the formalities underpinning BET, suggesting that the identified Thom's functions are signatures of the investigated electron rearrangements. From a topological point of view, only two folds are required to rationalize the whole reaction mechanism of the ammonia inversion and ammonia borane dissociation. The CC cleavage in the ethane molecule is correctly characterized using the dual cusp polynomial, in agreement with Silvi and collaborators.²⁹ These results constitute a substantial simplification because the fold is the one-parameter and one-state-variable function, i.e., the simplest polynomial of Thom's theory; in contrast, the elliptic umbilic contains three control parameters and two state variables. Furthermore, it was shown that the physical interpretation of the fold and cusp parameters is somewhat clear, and even though it is still an arbitrary process, we justified the proposed meaning of the latter unfolding coefficients based on their functional relationship, providing a higher degree of completeness to BET applications. Nonetheless, the rationalization of electron reorganizations along a reaction coordinate through higher-order parametric functions continues to be limited by the chemical/physical meaning of such coefficients and their correlations, remaining an open topic for further investigations.

Considering these findings, we here summarize a simple procedure for examining chemical bonding-related processes within the BET methodological framework, which aims to be consequent with the conceptual fundaments of Thom's works, thus unambiguously establishing the link between unfoldings and electron reorganizations, i.e., step (a): the determinant of the Hessian matrix must be computed at all potentially degenerate critical points, i.e., all approaching points along a reactive coordinate, unless they are all saddle points; step (b): the relative distance between potentially degenerate critical points must be computed (unless they are all saddle points) to have additional information, which is particularly useful when the potential energy surface is relatively flat; and step (c): the unfolding assignment must rely on results of steps (a), (b), and considering the maximum number of critical points of each unfolding. The first step is critical since it allows distinguishing between potentially and degenerate points as well as determining the number of eigenvalues tending to zero value, i.e., providing key knowledge concerning how many state variables should have the correct unfolding. It is customary to use the Poincaré–Hopf theorem to further validate the results of steps (a) and (b). It should be underscored that special care must be considered when applying this methodical yet easy-to-follow receipt to investigate more intricate potential energy surfaces (e.g., almost barrierless rate processes). Reactions involving transition metals constitute typical examples of this critical bonding situation. In these cases, degenerate critical points (CPs) tend to exhibit a relatively low exposure factor (i.e., a metric that quantifies the CP appearance frequency in IRC frames⁴²) due to the flatness of the phase space portrait. To increase this metric, the reaction pathway must be computed using the smallest achievable step size, resulting in more Hessian data points. The ramifications of these findings are considerable. They challenge our present understanding of key chemical processes in terms of unfoldings and cast doubts on both historical and current applications of BET. As such, it is suggested that systems previously examined over the last three decades within the original BET framework should be re-evaluated considering these new insights.

Theory and computational details

Within the BET framework,²⁹ a reaction becomes modeled as a gradient dynamical system, with the electron localization function (ELF)²² serving as the time-independent “potential function”.⁴⁵ ELF acts as a quantum probe for visualizing the Pauli exclusion principle. It is well known that ELF maxima correlate with predictions from the valence-shell electron pair repulsion theory (VSEPR),⁹⁵ providing thus a solid connection to Lewis bonding ideas in terms of valence, bonds, core, and lone pairs concepts.^96,97 The topographical analysis of ELF is independent of the theoretical level of theory,^56,98,99 and indeed, such a function has also been approximately obtained from electron densities derived from X-ray diffraction data.^100,101 The BET approach enables us to identify distinct, neighboring structural stability domains (SSDs), each featuring a unique set of nondegenerate critical points. Every SSD can, in principle, be associated with a given bonding state of the evolving system. The abrupt change from one state to another can be traced back to a bifurcation catastrophe in the form of the potential originated by a small change in parameters on which the function depends. Considering Thom's conceptual foundation for these polynomials (unfoldings),³⁰ it is necessary to highlight that merely counting changes in the number and type of Morse critical points separating adjacent SSDs is insufficient for determining the associated parametric unfolding.

Let us briefly outline the basis of CT,³⁰ as comprehensive resources are readily available.^30,44,45,47 The gradient nullity condition applied to an -potential, ∇_rη(r,μ) = 0, where η stands for the ELF, r represents the Cartesian coordinates, r = r(x, y, z), and ∇_r = (∂/∂x)i + (∂/∂y)j + (∂/∂z)k yields four types of equilibria: attractors, saddles of index one and two, and repellors. The collection of these singular solutions is often referred to as the topographic map, molecular map, or phase-space portrait of the function or, more precisely, of its gradient.^21,102,103 The phase space between equilibria, or critical points (CPs) of the function, flattens when the relative distance between two or more equilibria decreases. This change in the space curvature can be directly computed via the determinant of the Hessian matrix, |ΔH|. This matrix, H, is a somewhat arbitrary construct for tabulating the second-order derivatives of a function, i.e., H_ij = ∂²η(r, μ)/∂r_i∂r_j. It is significant to note that i, j = x, y, and z. A CP is termed degenerate if the |ΔH| evaluated at this point yields a zero value.^44,46,47 CT is a robust mathematical program that succeeded in describing all distinct changes in the geometric shape of (generic) parametric families triggered by the creation/annihilation of CPs through seven unfoldings constrained to have four parameters at most. One-state-variable unfoldings are called cuspoids, and their common characteristic is to have only one null eigenvalue. In contrast, parametric functions containing two state variables are referred to as umbilics, which describe changes in the geometric shape of a function resulting from two null eigenvalues. Eigenvalues result from a systematic sequence of algebraic operations applied to a square matrix, such as H, through a process called diagonalization. From a geometric standpoint, this procedure entails matrix rotations aimed at simplifying its form by eliminating mixed spatial-derivative terms. Table 1 lists the adapted^44,47 Thom's unfoldings for suitable usage in bonding situations. The negative sign corresponds to the so-called dual function, whereas including a Morse-type function (y²) in all cuspoids allows their application in 3D phenomena.^44,47

Table 1 Features of modified unfoldings for describing bond forming/breaking processes along a reactive pathway

Name	Adapted unfolding	No. of null eigenvalues	Maximum no. of critical points
Fold	±(x^3 + μx + y^2)	1	2
Cusp	±(x^4 + νx^2 + μx + y^2)	1	3
Swallow tail	±(x^5 + δx^3 + νx^2 + μx + y^2)	1	4
Butterfly	±(x^6 + εx^4 + δx^3 + νx^2 + μx + y^2)	1	5
Hyperbolic umbilic	±(x^3 + y^3 + νxy + μx + ϑy)	2	4
Elliptic umbilic	±[x^3 − xy^2 + ν(x^2 + y^2) + μx + ϑy]	2	2
Parabolic umbilic	±(y^4 + x^2y + νx^2 + γy^2 + μx + ϑy)	2	3

---

Possible combinations of critical points featuring a catastrophe can be straightforwardly found by combining the Poincaré–Hopf theorem and the maximum number of the unfolding CPs.⁶⁴ Typical examples of fold in the ELF topography are the following: (attractor, saddle of index one) ↔ wp and (repellor, saddle of index 2) ↔ wp, where wp stands for a wandering point. For the cusp, one can have: (attractor, attractor, saddle of index one) ↔ attractor and (repellor, repellor, saddle of index 2) ↔ repellor. Recall that a wp is not a CP, and therefore it describes unbounded trajectories. For further clarification on how to use the information provided in Table 1, let us reconsider the ammonia borane dissociation. We already showed that the fold characterizes the electron rearrangements of this reaction by following the |ΔH| at potentially degenerate CPs and their relative distance. This information is further verified using Poincaré–Hopf's relationship, yielding that one repellor and one saddle coalesced. Thus, this abrupt change should be described via a fold or an elliptic umbilic since these are the only functions with two CPs. However, the correct function is the fold since only one eigenvalue tends to zero value. Considering that the control parameter μ was conveniently defined as μ = d − d_* (where d and d_* correspond to the initial and bifurcation distances between reacting centers, respectively), the coalesce visualization and description is straightforward. Differentiating the fold with respect to the state variable x yields a quadratic expression with two real solutions, if and only if, μ < 0. Indeed, this parameter is negative because the B–N bond is stretching.

All geometry optimizations were performed using the M06-2X⁷⁹ and ωB97X-D⁷⁸ global hybrid functionals, each combined with the 6-31G(d), 6-31G(d,p), 6-31+G(df), 6-31+G(df,p) split-valence basis sets and using the Gaussian 16 package of programs.¹⁰⁴ The pyramidal inversion of ammonia, phosphine, and arsine was conducted following the IRC path with a step size equal to 0.001 amu^1/2Bohr. In contrast, a relaxed scan with a step of 0.010 Bohr was employed for studying the dissociation of ethane, ammonia borane, and phosphine borane molecules. For the former system, the multiconfigurational character due to the spin multiplicity was assessed through the complete active-space self-consistent field (CASSCF)¹⁰⁵ employing the same number, six and eight, of electrons and virtual orbitals using ORCA 5.0.¹⁰⁶ The energy was further corrected via a CAS second-order perturbation theory (CASPT2).^107,108 The topological analysis of the ELF and the characterization of its phase space were carried out using the Multiwfn program.¹⁰⁹ The images of the topographic map were generated using the VMD software.¹¹⁰ The fulfillment of the Poincaré–Hopf theorem was verified for all topographic maps along the pathway. The classification of bifurcations was carried out by strictly examining the absolute value of the Hessian determinant evaluated at all potentially degenerate critical points and their relative distance near the degeneration region.

Author contributions

L. A.-H., C. G., E. C.: project supervision, conceptualization, data analysis, and manuscript writing; L. A.-H., C. G., M. D.-N.: calculations, reaction paths, and characterization; M. D.-N.: data analysis and calculations. All authors reviewed and commented on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge UNAB and ANID/CONICYT PhD scholarships awarded to C. G. and L. A.-H., respectively. We also are indebted to the Fondo Nacional de Ciencia y Tecnología (FONDECYT-ANID, Chile) for the continuous financial and academic support provided through project no. 1181582, 1221383, and 1231018 granted to Prof. E. C.

References

1. B. Silvi and I. Fourre, Invited Review The Topological Analysis of the Electron Localization Function. A Key for a Position Space Representation of Chemical Bonds, Monatsh. Chem., 2005, 879, 855–879.
2. V. Polo, J. Andres, S. Berski, L. R. Domingo and B. Silvi, Understanding reaction mechanisms in organic chemistry from catastrophe theory applied to the electron localization function topology, J. Phys. Chem. A, 2008, 112, 7128–7136.
3. J. Andrés, P. González-Navarrete and V. S. Safont, Unraveling reaction mechanisms by means of Quantum Chemical Topology Analysis, Int. J. Quantum Chem., 2014, 114, 1239–1252.
4. A. I. Adjieufack, B. M. Mbah, M. J. Ketcha, N. I. Mbouombouo, J. Andrés, M. Oliva and V. S. Safont, How effectively bonding evolution theory retrieves and visualizes curly arrows: The cycloaddition reaction of cyclic nitrones, Int. J. Quantum Chem., 2019, 119, 1–14.
5. N. Lewis, The atom and the molecule, J. Am. Chem. Soc., 1916, 38, 762–785.
6. R. J. Gillespie and E. A. Robinson, Lewis and the chemical bond, J. Comput. Chem., 2007, 28, 87–97.
7. S. Shaik, Essay The Lewis Legacy: The Chemical Bond—A Territory and Heartland of Chemistry, J. Comput. Chem., 2007, 28, 51–61.
8. B. Silvi, About Lewis's heritage: chemical interpretations and quantum chemistry, Theor. Chem. Acc., 2017, 136, 1–6.
9. L. Pauling, The Nature of the chemical bond. The one-electron bond and the three-electron bond, J. Am. Chem. Soc., 1931, 53, 3225–3237.
10. W. Heitler and F. London, Wechselwirkung neutraler atome und homoopolare bindung nach der Quantenmechanik, Z. Phys., 1927, 44, 455–472.
11. R. F. W. Bader and W. H. Henneker, The ionic bond, J. Am. Chem. Soc., 1965, 87, 3063–3068.
12. S. R. Gadre, S. A. Kulkarni and I. H. Shrivastava, Molecular electrostatic potentials: A topographical study, J. Chem. Phys., 1992, 96, 5253–5260.
13. K. Ruedenberg, The physical nature of the chemical bond, Rev. Mod. Phys., 1962, 34, 326–376.
14. C. W. Wilson and W. A. Goddard, The role of kinetic energy in chemical binding. The nonclassical or exchange kinetic energy, Theoret Chim Acta (Berl.), 1972, 26, 195–210.
15. W. Kutzelnigg, The physical mechanism of the chemical bond, Angew. Chem., Int. Ed. Engl., 1971, 12, 546–562.
16. A. Kovács, C. Esterhuysen and G. Frenking, The nature of the chemical bond revisited: An energy-partitioning analysis of nonpolar bonds, Chem. – Eur. J., 2005, 11, 1813–1825.
17. R. F. W. Bader, J. Hernández-Trujillo and F. Cortés-Guzmán, Chemical bonding: From Lewis to atoms in molecules, J. Comput. Chem., 2007, 28, 4–14.
18. K. Ruedenberg and M. W. Schmidt, Physical understanding through variational reasoning: Electron sharing and covalent bonding, J. Phys. Chem. A, 2009, 113, 1954–1968.
19. G. B. Bacskay and S. Nordholm, Covalent bonding: The fundamental role of the kinetic energy, J. Phys. Chem. A, 2013, 117, 7946–7958.
20. G. B. Bacskay, S. Nordholm and K. Ruedenberg, The virial theorem and covalent bonding, J. Phys. Chem. A, 2018, 122, 7880–7893.
21. R. F. W. Bader, Atoms in molecules. A Quantum theory, Clarendon Press, Oxford, 1st edn, 1994.
22. A. D. Becke and K. E. Edgecombe, A simple measure of electron localization in atomic and molecular systems, J. Chem. Phys., 1990, 92, 5397–5403.
23. P. L. A. Popelier and É. A. G. Brémond, Geometrically faithful homeomorphisms between the electron density and the bare nuclear potential, Int. J. Quantum Chem., 2009, 109, 2542–2553.
24. T. A. Keith, R. F. W. Bader and Y. Aray, Structural homeomorphism between the electron density and the virial field, Int. J. Quantum Chem., 1996, 57, 183–198.
25. T. A. Keith and R. F. W. Bader, Topological analysis of magnetically induced molecular current distributions, J. Chem. Phys., 1993, 99, 3669–3682.
26. G. Bruno, G. Macetti, L. Presti and C. Gatti, Spin density topology, Molecules, 2020, 25, 3537–3563.
27. P. L. A. Popelier and F. M. Aicken, Atomic properties of amino acids: Computed atom types as a guide for future force-field design, Chem. Phys. Chem., 2003, 4, 824–829.
28. P. L. A. Popelier, in The Chemical Bond - 100 years old and getting stronger, ed. M. Mingo, Springer International Publishing Switzerland, 2016, pp. 71–118.
29. X. Krokidis, S. Noury and B. Silvi, Characterization of elementary chemical processes by catastrophe theory, J. Phys. Chem. A, 1997, 101, 7277–7282.
30. R. Thom, Structural Stability and Morphogenesis, Taylor & Francis Group LLC, 1st edn, 1972.
31. A. S. Nizovtsev, Activation of C–H bond in methane by Pd atom from the bonding evolution theory perspective, J. Comput. Chem., 2013, 34, 1917–1924.
32. I. Viciano, P. González-Navarrete, J. Andrés and S. Martí, Joint Use of bonding evolution theory and QM/MM hybrid method for understanding the hydrogen abstraction mechanism via cytochrome P450 aromatase, J. Chem. Theory Comput., 2015, 11, 1470–1480.
33. P. González-Navarrete, L. R. Domingo, J. Andres, S. Berski and B. Silvi, Electronic fluxes during Diels-Alder reactions involving 1,2-benzoquinones: Mechanistic insights from the analysis of electron localization function and catastrophe theory, J. Comput. Chem., 2012, 33, 2400–2411.
34. A. I. Adjieufack, V. Liégeois, I. N. Mboumbouo, M. J. Ketcha and B. Champagne, Intramolecular [3+2] Cycloaddition Reactions of Unsaturated Nitrile Oxides. A Study from the Perspective of Bond Evolution Theory (BET), J. Phys. Chem. A, 2018, 122, 7472–7481.
35. M. Ríos-Gutiérrez, P. Pérez and L. R. Domingo, A bonding evolution theory study of the mechanism of [3+2] cycloaddition reactions of nitrones with electron-deficient ethylenes, RSC Adv., 2015, 5, 58464–58477.
36. P. Merino, T. Tejero, I. Delso and R. Matute, New mechanistic interpretations for nitrone reactivity, Org. Biomol. Chem., 2017, 15, 3364–3375.
37. A. I. Adjieufack, I. M. Ndassa, I. Patouossa, J. K. Mbadcam, V. S. Safont, M. Oliva and J. Andrés, On the outside looking in: rethinking the molecular mechanism of 1,3- dipolar cycloadditions from the perspective of bonding evolution theory. The reaction between cyclic nitrones and ethyl acrylate, Phys. Chem. Chem. Phys., 2017, 19, 18288–18302.
38. O. Matthies, Y. Grin and M. Kohout, Absent Diamond-to-β-Sn Phase Transition for Carbon: Quantum Chemical Topology Approach, Chemistry Select, 2017, 2, 7659–7669.
39. S. Berski and L. Z. Ciunik, The mechanism of the formation of the hemiaminal and Schiff base from the benzaldehyde and triazole studied by means of the topological analysis of electron localisation function and catastrophe theory, Mol. Phys., 2015, 113, 765–781.
40. A. Ćmikiewicz, A. J. Gordon and S. Berski, Characterisation of the reaction mechanism between ammonia and formaldehyde from the topological analysis of ELF and catastrophe theory perspective, Struct. Chem., 2018, 29, 243–255.
41. J. Contreras-García, A. Martín Pendás, J. M. Recio and B. Silvi, Computation of local and global properties of the electron localization function topology in crystals, J. Chem. Theory Comput., 2009, 5, 164–173.
42. L. Ayarde-Henríquez, C. Guerra, M. Duque-Noreña and E. Chamorro, A simple topology-based model for predicting the activation barriers of reactive processes at 0 K, Phys. Chem. Chem. Phys., 2023, 25, 14274–14284.
43. K. Fukui, A formulation of the reaction coordinate, J. Phys. Chem., 1970, 74, 4161.
44. R. Gilmore, Catastrophe Theory for Scientists and Engineers, Dover Publications, Pennsylvania, 1st edn, 1993.
45. V. I. Arnol’d, V. Afrajmovich, Y. Il’yashenko and L. Shil’nikovn, Dynamical Systems V, Springer-Verlag Berlin Heidelberg, 1st edn, 1994, vol. 5.
46. D. Castrigiano and S. Hayes, Catastrophe Theory, CRC Press, 2nd edn, 2018, vol. 6.
47. T. Poston and I. Stewart, Catastrophe Theory and its Applications, Pitman Publishing Limited, London, 1st edn, 1979.
48. D. Michel, Bifurcations and Catastrophes, Springer-Verlag Berlin Heidelberg, 1st edn, 2000.
49. J. Guckenheimer and P. Holmes, Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, 1983.
50. D. Luo, X. Wang, D. Zhu and M. Han, Bifurcation Theory and Methods of Dynamical Systems, World Scientific Publishing Co. Pte. Ltd., 1997, vol. 15.
51. H. W. Lorenz, Nonlinear Dynamical Economics and Chaotic Motion, Springer-Verlag Berlin Heidelberg, 2nd edn, 1993, vol. 6.
52. T. Bedford and J. Swift, London Mathematical Society Lecture Note Series, Cambridge University Press, London, 2nd edn, 2008.
53. A. Katok and B. Hasselblatt, Introduction to the Modern Theory of Dynamical Systems, Cambridge University Press, 1996.
54. S. Albeverio, J. B. Alblas, S. A. Amitsur, I. J. Bakelman, G. Bakker, J. W. de Bakker, C. Bardos, H. Bart, H. Bass, A. Bensoussan, M. Bercovier, L. Berkovitz, M. Berger, E. A. Bergshoeff, E. Bertin, F. Beukers, A. Beutelspacher, H. P. Boas, J. Bochnak, H. J. M. Bos, B. L. J. Braaksma, T. P. Branson, D. S. Bridges, A. E. Brouwer, M. G. de Bruin, R. G. Bums, H. Capel, P. Cartier, C. Cercignani, J. M. C. Clark, Ph. Clement, A. M. Cohen, J. W. Cohen, P. Conrad, H. S. M. Coxeter, R. F. Curtain, M. H. A. Davis, M. V. Dekster, C. Dellacherie, G. van Dijk, H. C. Doets, I. Dolgachev, A. Dress, J. J. Duistermaat, D. van Dulst, H. van Duyn, H. Dym, A. Dynin, M. L. Eaton, W. Eckhaus, P. van Emde Boas, H. Engl, G. Ewald, V. I. Fabrikant, A. Fasano, M. Fliess, R. M. Fossum, B. Fuchssteiner, G. B. M. van der Geer, R. D. Gill, V. V. Goldberg, J. de Graaf, J. Grasman, P. A. Griffith, A. W. Grootendorst, L. Gross, P. Gruber, K. P. Hart, G. Heckman, A. J. Hermans, W. H. Hesselink, C. C. Heyde, M. W. Hirsch, K. H. Hofmann, A. T. de Hoop, P. J. van der Houwen, N. M. Hugenholtz, J. R. Isbell, A. Isidori, E. M. de Jager, D. Johnson, P. T. Johnstone, D. Jungnickel, M. A. Kaashoek, V. Kac, W. L. J. van der Kallen, D. Kanevsky, Y. Kannai, H. Kaul, E. A. de Kerf, W. Klingenberg, T. Kloek, J. A. C. Kolk, G. Komen, T. H. Koomwinder, L. Krop, B. Kuperschmidt, H. A. Lauwerier, J. van Leeuwen, H. W. Lenstra Jr., J. K. Lenstra, H. Lenz, M. Levi, J. Lindenstrauss, J. H. van Lint, F. Linton, A. Liulevicius, M. Livshits, W. A. J. Luxemburg, R. M. M. Mattheij, L. G. T. Meertens, I. Moerdijk, J. P. Murre, H. Neunzert, G. Y. Nieuwland, G. J. Olsder, B. ørsted, F. van Oystaeyen, B. Pareigis, K. R. Parthasarathy, K. R. Parthasarathy, I. I. Piatetskii-Shapiro, H. G. J. Pijls, N. U. Prabhu, E. Primrose, A. Ramm, C. M. Ringel, J. B. T. M. Roerdink, K. W. Roggenkamp, G. Rozenberg, W. Rudin, S. N. M. Ruysenaars, A. Salam, A. Salomaa, P. Saunders, J. P. M. Schalkwijk, C. L. Scheffer, R. Schneider, J. A. Schouten, F. Schurer, J. J. Seidel, A. Shenitzer, V. Snaith, T. A. Springer, J. H. M. Steenbrink, J. D. Stegeman, F. W. Steutel, P. Stevenhagen, I. Stewart, R. Stong, L. Streit, K. Stromberg, L. G. Suttorp, D. Tabak, F. Takens, R. J. Takens, N. M. Temme, S. H. Tijs, B. Trakhtenbrot, N. S. Tmdinger, L. N. Vaserstein, M. L. J. van de Vel, F. D. Veldkamp, W. Vervaat, P. M. B. Vitanyi, N. J. Vlaar, H. A. van der Vorst, J. de Vries, F. Waldhausen, B. Wegner, J. J. O. O. Wiegerinck, J. C. Willems, J. M. Wills, B. de Wit, S. A. Wouthuysen, S. Yuzvinskii and L. Zalcman, Encyclopedia of Mathematics, Kluwer Academic Publishers, Dordrecht, 1991.
55. R. S. Palais, Morse theory on Hilbert manifolds, Topology, 1963, 2, 299–340.
56. L. Ayarde-Henríquez, C. Guerra, M. Duque-Noreña, E. Rincón, P. Pérez and E. Chamorro, Are There Only Fold Catastrophes in the Diels–Alder Reaction Between Ethylene and 1,3-Butadiene?, J. Phys. Chem. A, 2021, 125, 5152–5165.
57. L. Ayarde-Henríquez, C. Guerra, M. Duque-Noreña, E. Rincón, P. Pérez and E. Chamorro, On the Notation of Catastrophes in the Framework of Bonding Evolution Theory: Case of Normal and Inverse Electron Demand Diels-Alder Reactions, Chem. Phys. Chem., 2022, 23, e202200343.
58. L. Ayarde-Henríquez, C. Guerra, M. Duque-Noreña and E. Chamorro, Unraveling the role of the electron-pair density symmetry in reaction mechanism patterns: the Newman-Kwart rearrangement, New J. Chem., 2022, 46, 12002–12009.
59. C. Guerra, L. Ayarde-Henríquez, M. Duque-Noreña, C. Cárdenas, P. Pérez and E. Chamorro, On the nature of bonding in the photochemical addition of two ethylenes: C-C bond formation in the excited state?, Phys. Chem. Chem. Phys., 2021, 23, 20598–20606.
60. C. Guerra, L. Ayarde-Henríquez, M. Duque-Noreña and E. Chamorro, On Electron Pair Rearrangements in Photochemical Reactions: 1,3-Cyclohexadiene Ring Opening, J. Phys. Chem. A, 2021, 126, 395–405.
61. C. Guerra, L. Ayarde-Henríquez, M. Duque-Noreña and E. Chamorro, Photochemically induced 1,3-butadiene ring-closure from the topological analysis of the electron localization function viewpoint, Chem. Phys. Chem., 2022, 23, 202200217.
62. C. Guerra, L. Ayarde-Henríquez, E. Chamorro and A. Ensuncho, Uncovering Triradicaloid Structures in S1 Benzene Photochemistry, Chem. Photo Chem., 2023, 7, e202200263.
63. C. Guerra, L. Ayarde-Henríquez, Y. A. Rodríguez-Núñez, A. Ensuncho and E. Chamorro, Elucidating the N−N and C−N Bond-breaking Mechanism in the Photoinduced Formation of Nitrile Imine, Chem. Phys. Chem., 2023, 24, e202200867.
64. E. Chamorro, C. Guerra, L. Ayarde-Henríquez, M. Duque-Noreña, P. Pérez and E. Rincón, in Chemical Reactivity: Theories and Principles, ed. S. Kayas, L. von Szentpály, G. Serdaroglu and L. Guo, Elsevier, 2023, vol. 1, pp. 465–481.
65. C. Guerra, L. Ayarde-Henríquez, M. Duque-Noreña and E. Chamorro, Unraveling the Bonding Nature Along the Photochemically Activated Paterno-Büchi Reaction Mechanism, Chem. Phys. Chem., 2021, 22, 2342–2351.
66. S. Berski, J. Andrés, B. Silvi and L. R. Domingo, The joint use of catastrophe theory and electron localization function to characterize molecular mechanisms. A density functional study of the Diels-Alder reaction between ethylene and 1,3-butadiene, J. Phys. Chem. A, 2003, 107, 6014–6024.
67. M. A. Merli, F. A. Nestola, L. U. Sciascia and V. Giotto, Bader's analysis of the electron density in the Pbca enstatite – Pbcn protoenstatite phase transition, Eur. J. Mineral., 2011, 23, 197–205.
68. F. Parisi, L. Sciascia, F. Princivalle and M. Merli, Pressure stability field of Mg-perovskite under deep mantle conditions: A topological approach based on Bader's analysis coupled with catastrophe theory, Ceram. Int., 2019, 45, 2820–2827.
69. V. Polo, J. Andres, R. Castillo, S. Berski and B. Silvi, Understanding the molecular mechanism of the 1,3-dipolar cycloaddition between fulminic acid and acetylene in terms of the electron localization function and catastrophe theory, Chem. – Eur. J., 2004, 10, 5165–5172.
70. E. Chamorro and E. Rincón, Unraveling the sequence of the electronic flow along the water-assisted ring-opening reaction in mutagen MX, Theor. Chem. Acc., 2019, 138, 2–10.
71. E. Chamorro, M. Duque-Noreña, N. Gutierrez-Sánchez, E. Rincón and L. R. Domingo, A Close Look to the Oxaphosphetane Formation along the Wittig Reaction: A [2 + 2] Cycloaddition?, J. Org. Chem., 2020, 85, 6675–6686.
72. A. Rauk, L. C. Allen and K. Mislow, Pyramidal Inversion, Angew. Chem., Int. Ed. Engl., 1970, 9, 400–414.
73. K. D. Reichl, D. H. Ess and A. T. Radosevich, Catalyzing pyramidal inversion: Configurational lability of P-stereogenic phosphines via single electron oxidation, J. Am. Chem. Soc., 2013, 135, 9354–9357.
74. J. D. Swalen and J. A. Ibers, Potential function for the inversion of ammonia, J. Chem. Phys., 1962, 36, 1914–1918.
75. M. F. Manning, Energy levels of a symmetrical double minima problem with applications to the NH3 and ND3 molecules, J. Chem. Phys., 1935, 3, 136–138.
76. C. C. Costain and G. B. B. M. Sutherland, A method of determining the potential barriers restricting inversion in ammonia, phosphine and arsine from vibrational force constants, J. Phys. Chem., 1952, 56, 321–324.
77. R. E. Weston, Vibrational energy level splitting and optical isomerism in pyramidal molecules of the type XY31, J. Am. Chem. Soc., 1954, 76, 2645–2648.
78. J. D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
79. Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other function, Theor. Chem. Acc., 2008, 120, 215–241.
80. A. Haaland, Covalent versus dative bonds to main group metals, a useful distinction, Angew. Chem., Int. Ed. Engl., 1989, 28, 992–1007.
81. S. J. Guastello, A Butterfly Catastrophe Model of Motivation in Organizations: Academic Performance, J. Appl. Psychol., 1987, 72, 165–182.
82. R. Glaser and N. Knotts, Coordinate covalent C → B bonding in phenylborates and latent formation of phenyl anions from phenylboronic acid, J. Phys. Chem. A, 2006, 110, 1295–1304.
83. E. P. Linton, The dipole moments of amine oxides, J. Am. Chem. Soc., 1940, 62, 1945–1948.
84. J. Chatt, P. B. Hitchcock, A. Pidcock, C. P. Warrens and K. R. Dixon, The nature of the co-ordinate link. Part 11. Synthesis and phosphorus-31 nuclear magnetic resonance spectroscopy of platinum and palladium complexes containing side-bonded (E)-diphenyldiphosphene. X-Ray crystal and molecular structures of [Pd{(E)-PhP[double bond, length as m-dash]PPh}(Ph2PCH2CH2PPh2)] and [Pd{[(E)-PhP[double bond, length as m-dash]PPh][W(CO)5]2}(Ph2PCH2CH2PPh2)], J. Chem. Soc., Dalton Trans, 1984, 10, 2237–2244.
85. V. Gutmann, The Donor-Acceptor Approach to Molecular Interactions, Plenum Press, New york, 1st edn, 1978.
86. W. B. Jensen, The Lewis Acid-Base Concepts: An Overview, Wiley, New York, 1st edn, 1980.
87. G. B. Kauffman, Classics in Coordination Chemistry: The Selected Papers of Alfred Werner, Dover Publications, New York, 1968.
88. Y. Mo, L. Song, W. Wu and Q. Zhang, Charge Transfer in the Electron Donor-Acceptor Complex BH 3NH3, J. Am. Chem. Soc., 2004, 126, 3974–3982.
89. J. A. Plumley and J. D. Evanseck, Covalent and ionic nature of the dative bond and account of accurate ammonia borane binding enthalpies, J. Phys. Chem. A, 2007, 111, 13472–13483.
90. S. D. Peyerimhoff and R. J. Buenker, Further study of umbrella vs bridged geometries: SCF-MO and CI calculations for C2H6 + + and ammonia borane, J. Chem. Phys., 1968, 49, 410–419.
91. J. Dillen and P. Verhoeven, The end of a 30-year-old controversy? A computational study of the B–N stretching frequency of BH3-NH3 in the solid state, J. Phys. Chem. A, 2003, 107, 2570–2577.
92. L. R. Thorne, R. D. Suenram and F. J. Lovas, Microwave spectrum, torsional barrier, and structure of BH3NH3, J. Chem. Phys., 1982, 78, 167–171.
93. S. Trudel and D. F. R. Gilson, High-pressure Raman spectroscopic study of the ammonia-borane complex. Evidence for the dihydrogen bond, Inorg. Chem., 2003, 42, 2814–2816.
94. L. V. Gurvich, I. V. Veyts and C. B. Alcock, Thermodynamic Properties of Individual Substances, Hemisphere Publishing, New York, 4th edn, 1994, vol. 3.
95. R. J. Gillespie and R. S. Nyholm, A simple electrostatic theory: The arrangement of electron pairs in valency shells, Q. Rev., Chem. Soc., 1957, 11, 339–380.
96. B. Silvi, The synaptic order: A key concept to understand multicenter bonding, J. Mol. Struct., 2002, 614, 3–10.
97. A. Savin, B. Silvi and F. Colonna, Topological analysis of the electron localization function applied to delocalized bonds, Can. J. Chem., 1996, 74, 1088–1096.
98. J. K. Burdett and T. A. McCormick, Electron localization in molecules and solids: The meaning of ELF, J. Phys. Chem. A, 1998, 102, 6366–6372.
99. M. Kohout and A. Savin, Influence of core-valence separation of electron localization function, J. Comput. Chem., 1997, 18, 1431–1439.
100. V. Tsirelson and A. Stash, Determination of the electron localization function from electron density, Chem. Phys. Lett., 2002, 351, 142–148.
101. D. J. Grimwood, I. A. N. Bytheway and D. Jayatilaka, Wave Functions Derived from Experiment V. Investigation of Electron Densities, Electrostatic Potentials, and Electron Localization Functions for, J. Comput. Chem., 2003, 470–483.
102. C. Robinson, Dynamical Systems, CRC Press, 2nd edn, 1999.
103. R. Gilmore, Encyclopedia of Applied Physics, VCH Publisher, 1st edn, 1992, vol. 3.
104. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinhe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, E. J. J. Heyd, N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, J. R. Cammi, W. Ochterski, R. L. Martin, K. Morokuma, Ö. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, 2016.
105. B. O. Roos and P. R. Taylor, A complete active space method (CASCF) using a density matrix formulated super-CI approach, Chem. Phys., 1980, 48, 157–173.
106. F. Neese, Software update: The ORCA program system—Version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, 1–15.
107. K. Andersson, P. A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, Second-order perturbation theory with a CASSCF reference function, J. Phys. Chem., 1990, 94, 5483–5488.
108. K. Andersson, P. Å. Malmqvist and B. O. Roos, Second-order perturbation theory with a complete active space self-consistent field reference function, J. Chem. Phys., 1992, 96, 1218–1226.
109. T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592.
110. K. S. W. Humphrey and A. Dalke, VMD: visual molecular dynamics, J. Mol. Graph., 1996, 14, 33–38.

---

Footnote

† Electronic supplementary information (ESI) available: Optimized geometries of minima and first-order saddle points on the potential energy surface (PES) for ammonia, phosphine, and arsine using the M06-2X and ωB97X-D functionals each combined with 6-31G(d), 6-31G(d,p), 6-31+G(df), and 6-31+G(df,p). Optimized geometries of ammonia borane minima obtained via M06-2X and ωB97X-D global hybrid combined with 6-31G(d) and 6-31G(d,p) People basis sets. Optimized geometries of ethane minima at the CASSCF in combination with different numbers of electrons and virtual orbitals. Thermochemistry properties, including activation and dissociation enthalpies at different temperatures, are provided for all systems. Animated illustrations of ELF bifurcations for all systems are also available. See DOI: https://doi.org/10.1039/d3cp03572g

---