Dynamic geometry design of cyclic peptide architectures for RNA structure†
Shangbo
Ning‡
a,
Min
Sun‡
b,
Xu
Dong
 b,
Anbang
Li
a,
Chen
Zeng
c,
Maili
Liu
b,
Anbang
Li
a,
Chen
Zeng
c,
Maili
Liu
 b,
Zhou
Gong
*b and
Yunjie
Zhao
b,
Zhou
Gong
*b and
Yunjie
Zhao
 *a
*a
aInstitute of Biophysics and Department of Physics, Central China Normal University, Wuhan, 430079, China. E-mail: yjzhaowh@mail.ccnu.edu.cn
bState Key Laboratory of Magnetic Resonance and Atomic Molecular Physics, Innovation Academy for Precision Measurement Science and Technology Chinese Academy of Sciences, Wuhan, Hubei 430071, China. E-mail: gongzhou@wipm.ac.cn
cDepartment of Physics, The George Washington University, Washington, DC 20052, USA
First published on 15th September 2023
Abstract
Designing inhibitors for RNA is still challenging due to the bottleneck of maintaining the binding interaction of inhibitor-RNA accompanied by subtle RNA flexibility. Thus, the current approach usually needs to screen thousands of candidate inhibitors for binding. Here, we propose a dynamic geometry design approach to enrich the hits with only a tiny pool of designed geometrically compatible scaffold candidates. First, our method uses graph-based tree decomposition to explore the complementarity rigid binding cyclic peptide and design the amino acid side chain length and charge to fit the RNA pocket. Then, we perform an energy-based dynamical network algorithm to optimize the inhibitor-RNA hydrogen bonds. Dynamic geometry-guided design yields successful inhibitors with low micromolar binding affinity scaffolds and experimentally competes with the natural RNA chaperone. The results indicate that the dynamic geometry method yields higher efficiency and accuracy than traditional methods. The strategy could be further optimized to design the length and chirality by adopting nonstandard amino acids and facilitating RNA engineering for biological or medical applications.
Introduction
RNA is central to diverse biological functions, including protein synthesis, gene expression, and virus-like particle packaging.1–5 For instance, the ribosome is a large RNA–protein complex for protein synthesis.6 The RRE RNA regulates viral gene expression by interacting with the HIV-1 Rev protein.7 The TAR RNA regulates transcription elongation by binding the P-TEFb and Tat proteins.8 The SL3 RNA interacts with the NC protein to recognize and package the HIV-1 genome.9 All the above RNAs utilize the hairpin stem loop structure to bind the corresponding proteins for their functions. Thus, targeting RNA may be an alternative approach if the protein targets may lead to side effects.10Experiments can determine the RNA-inhibitor structures.11 X-Ray crystallography requires sample crystallization to determine the atomic structure.12 However, RNA is hard to crystallize due to its high structural flexibility.13 The sample of Cryo-EM is prepared by rapidly cooling the particles to cryogenic temperatures, preserving structural heterogeneity present in solutions.14–16 In general, the electron microscope can be used in large molecular systems. However, it is difficult to be applied in small systems.13 NMR can analyze the molecules in solution, access conformational dynamics within various timescales, and directly capture binding states under near-physiological conditions.17–19 ITC and other experiments can obtain thermodynamic or kinetic parameters without structural information. However, high-throughput screening is time-consuming and expensive. The bottleneck is to screen thousands of candidate inhibitors for binding. Large-scale screening and testing need the guidance of theoretical calculations. The major theoretical approaches are molecular docking and molecular dynamics (MD) simulation.20 Compared to proteins, RNAs are structurally more flexible with negative charges.21,22 The existing RNA ligands show limited binding interactions and surface areas.
Human immunodeficiency virus-1 (HIV-1) is a retrovirus that progressively attacks the immune system.23 The TAR, SL3, and RBE RNAs are crucial in viral genome replication and packaging of HIV-1. Stem loop 3 RNA (SL3) in ψ-RNA is a GGAG hairpin that is highly conserved among different strains of HIV-1 and plays a critical role in recognizing and packaging the viral genome.9,24,25 The Rev response element (RRE) mediates the transport of viral mRNA from the nucleus to the cytoplasm by binding with the Rev protein, and the Rev binding element (RBE) located on the stem loop IIB domain of the RRE is the binding surface with the Rev protein.26,27 Therefore, targeting the RNA hairpin stem loop can inhibit the corresponding functions. There has been a wide array of inhibitors designed to target RNA, including small molecules, heterocycles, aminoglycosides, antisense oligonucleotides, peptide nucleic acids, metallopeptide complexes, cyclic peptides, α-helical peptidomimetics, and various bifunctional conjugates, but to date, none has seen clinical success.28–30 This is partly due to the inherent challenges of targeting RNA that hinder the design of selective and effective ligands.31,32 Previously, Warui et al. found that four RNA ligands can break the interactions between SL3 RNA and NC protein with the lowest binding affinity of 68 μM.24 Davidson et al. proposed a cyclic peptide mimic of the Tat protein named L22 that can bind to TAR RNA with a binding affinity of ∼30 nM.23 Shortridge et al. optimized this cyclic peptide with non-standard amino acids to fit the specific stem loop conformation well to generate the JB181 that binds to the stem loop of TAR RNA.33 The cyclic peptide with higher stability is a promising inhibitor to increase the binding interactions with RNA targets. According to previous research, around 70% of the protein binds to the RNA stem loop structure.34 This structure is a potential target for regulating biological functions. Our study focuses on analyzing specific stem loop RNAs and redesigning cyclic peptides better to fit the flexibility of the RNA stem loop.
Here, we proposed a dynamic geometry computational strategy to provide a small pool of cyclic peptides for experimental validation. Compared with traditional methods, our workflow mainly includes the following three advances. (1) We use a graph-based tree decomposition algorithm to enrich the hits with only a tiny pool of designed geometrically compatible scaffold candidates. (2) We perform the energy-based dynamical network algorithm to optimize the inhibitor-RNA hydrogen bonds. (3) We use the NMR experiment to validate the binding affinity and sites. As a result, we successfully designed two rigid cyclic peptides binding to RNA hairpin and stem loop structures with low micromolar binding affinity. Unlike the traditional inhibitor screening methods using extensive inhibitor libraries, the method developed here allows us to shift the high-throughput screening to a target design rapidly.
Materials and methods
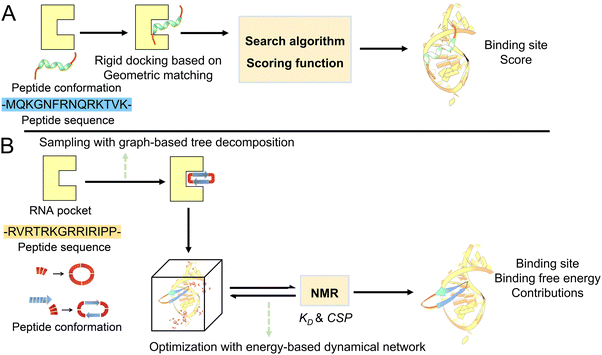
One of the most feasible strategies for peptide inhibitor design is starting from the existing interaction fragment and then predicting and optimizing the sequence by docking (Fig. 1A). Instead of inputting an existing interaction fragment, we generated completely cyclic peptides and fed these to complex predictions (Fig. 1B). As expected, the probability of the cyclic peptide binding tightly to the RNA target was low. We then sought to optimize the sequences from binding affinity contributions of per-residues. We performed a molecular dynamics simulation for each sequence to predict binding free energy using MM-GBSA. The trajectories started from different cyclic peptides and resulted in different binding modes. The predicted binding affinity becomes progressively sharper during the five rounds of screening. Next, the top 10 peptides with the highest binding affinity with the RNA target were selected to perform NMR experiments to verify the effect of the top 10 cyclic peptides. Finally, the cyclic peptides consistent with the experiments were re-performed in MD simulations to explore the binding mechanism.Geometrical information analysis
The RNA pockets were determined using the rolling probe method.35,36 The pocket is detected by calculating the translational degrees of freedom of the probe ball. The center of the probe is recorded if the probe contacts more than two atoms on the molecule. These discrete positions form the rolling boundary of the pocket. The volume and surface area values were calculated using the discrete volume method. The sphericity (Ψ) was used to measure the matching between the pocket and peptides using the following equation: | (1) |
Sampling with graph-based tree decomposition
The initial cyclic peptide is started from the L22 cyclic peptide (PDB ID: 2KDQ).23 As shown in Fig. 3D, the L22 peptide is a structurally constrained β-hairpin cyclic peptide that mimics the HIV-1 Tat protein that binds to TAR RNA. The SL3 RNA (Fig. 3E) is derived from the NMR structure (PDB ID: 1A1T) binding with the nucleocapsid (NC) protein.9 The RBE RNA (Fig. 3F) is derived from the HIV-1 RRE IIB stem loop complex with the RSG-1.2 peptide (PDB ID: 1G70) determined by solution NMR. The sequence of cyclic peptides is optimized according to the binding affinity contributions. Firstly, we identified the five residues in the cyclic peptide with the smallest binding affinity contributions based on molecular docking and MD simulations to perform side-chain optimization. To predict the optimized side chain, the coordinates of amino acids are inputted and used to calculate the self-energy and paired energy of the structure. Subsequently, an interaction graph is constructed to represent the side chain placement. Then, the interaction graph is solved via tree decomposition, and the optimal conformation of the mutation model is saved. Compared with the previous graph decomposition methods, the tree decomposition of the graph method is more accurate for a longer-range energy function and sampling about the rotameric dihedral angle.37 Finally, a total of 3995 cyclic peptides were generated by this program.Preliminary screening of peptides by docking
RNA-related complex structure prediction is still a challenging problem. Here, we used HDOCKlite for the initial screening from the sequence pool.38 HDOCKlite is a fast Fourier transform (FFT)-based docking program. The first step is to sample the peptide conformations by rotation and translation. An angle interval of 15° and a spacing of 1.2 Å are used for rotational and translational samplings. The top 10 translations with the best shape complementarities for each rotation are optimized. For each rotation, the top 10 translations with the best shape complementarities from the FFT search are optimized by the iterative knowledge-based scoring functions. The second step is identifying the binding mode by scoring function by considering neighboring and other receptor contributions (Fig. 2A). Finally, we selected the top 1 prediction for further simulation.Optimization with an energy-based dynamical network
The MD simulations were performed with AMBER 20 (CUDA-version) software using the AMBERFF14SB force field and TIP3P model.39–41 Firstly, the PDB4AMBER module of AMBER20 was employed to remove the initial solvent and ions. Then, the TLEAP module was used to solvate the complex in a cubic box with periodic boundary conditions. The Na+ and Cl− ions were added to neutralize the net charge of the system. Finally, the box size of L22-SL3 was about 68.87 × 68.87 × 68.87 Å3, while the system of L22-RBE was set as the same size. The Particle Mesh Ewald (PME) method was used to calculate the long-range electrostatic interactions.42 The energy minimization was performed with the steepest descent method until the maximum iteration steps reached 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. Then, the system was heated to 300 K in two steps with the Nose–Hoover thermostat method.43 Subsequently, the NPT ensemble experiences a 1 ns unrestrained equilibration with the Parrinello–Rahman barostat.44 The integrating step was 2 fs in all the simulations. The hydrogen bonds are constrained by the SHAKE algorithm.45 Finally, a 50 ns production simulation for every structure in the top 50 was performed with the same parameters of NPT equilibration. For the long MD simulation, the system of L22#15-SL3 was simulated for five 200 ns trajectories with the same parameter settings. The NC-SL3 and L22-SL3 were used as controls for the 200 ns simulation. Therefore, there are 2.5 μs MD simulations for top 50 structures and SL3, 1 μs for L22#15-SL3, 200 ns for NC-SL3 and L22-SL3, respectively. For the RBE RNA, a long MD simulation was performed for the L22 + 16-RBE with the same mode as L22#15-SL3.
000. Then, the system was heated to 300 K in two steps with the Nose–Hoover thermostat method.43 Subsequently, the NPT ensemble experiences a 1 ns unrestrained equilibration with the Parrinello–Rahman barostat.44 The integrating step was 2 fs in all the simulations. The hydrogen bonds are constrained by the SHAKE algorithm.45 Finally, a 50 ns production simulation for every structure in the top 50 was performed with the same parameters of NPT equilibration. For the long MD simulation, the system of L22#15-SL3 was simulated for five 200 ns trajectories with the same parameter settings. The NC-SL3 and L22-SL3 were used as controls for the 200 ns simulation. Therefore, there are 2.5 μs MD simulations for top 50 structures and SL3, 1 μs for L22#15-SL3, 200 ns for NC-SL3 and L22-SL3, respectively. For the RBE RNA, a long MD simulation was performed for the L22 + 16-RBE with the same mode as L22#15-SL3.
The binding free energy was calculated with MM-GBSA in AMBER20.46 The last 500 snapshots of the top 50 trajectories in the MD simulations were used in the binding free energy (ΔGBind) calculations (Fig. 2B) (eqn 2). The contributions of binding free energy (ΔG) are composed of the following terms:
| ΔGBind = ΔGgas + ΔGSolv − TΔS | (2) |
| ΔGgas = EVdw + EEle | (3) |
| ΔGSolv = EGB + ESurf | (4) |
The CPPTRAJ module in AMBER20 was employed to analyze the hydrogen bonds and dynamic changes. The radius of gyration (Rg) of the cyclic peptide was calculated by GROMACS.47 The code for contact map analysis was encoded using C language. All the three-dimensional structures and structural details were visualized by using CHIMERA-11.5.48 The principal component analysis (PCA) was performed by using the CPPTRAJ module in AMBER20.49 The dynamic cross-correlation matrix (DCC) was calculated by using GROMACS.50
Sample preparation
All peptides used in NMR experiments were purchased from GL Biochem Ltd (Shanghai) as high-performance liquid chromatography (HPLC) purified. The products were confirmed through electrospray ionization mass spectrometry (ESI-MS). The SL3 and RBE were prepared using in vivo transcription with T7 RNA polymerase, with uniformly 13C/15N labeled rNTPs (Cambridge Isotope Laboratories, CIL) using a standard protocol.51 The purification was performed with a Source Q column (GE Healthcare). The RNA samples were annealed to 95 °C for 5 min and then put on ice immediately. The purity was identified by electrophoresis on a 15% polyacrylamide gel and analyzed by NMR.The 55-residue NC protein was cloned in a pET22b vector. BL21 star cells were used for protein expression and grown in LB medium at 37 °C to an absorbance at 600 nm of 0.5 before induction with 1 mM IPTG (isopropyl-β-D-thiogalactopyranoside). The cells were harvested after 4 hours and lysed by sonication in lysis buffer (50 mM Tris–HCl, 10%(v/v) glycerol, 0.1 M NaCl, 0.1 mM ZnCl2, 5 mM dithiothreitol, 2 mM EDTA, pH8.0) with 172 μL of 10 mM PMSF (phenylmethylsulfonyl fluoride). Proteins were purified using a Source S column and Sephacryl S100 column (GE Healthcare). The purified NC proteins were further verified by electrospray mass spectrometry and SDS-PAGE.
NMR spectroscopy and analysis
All RNA and NC protein samples were buffer-exchanged (Amicon Ultra) into NMR buffer (NaH2PO4 25 mM, NaCl 100 mM, D2O 10%, and pH 6.8). NMR experiments were carried out on a Bruker 700 MHz or 600 MHz spectrometer equipped with a cryogenic probe.A series of 1H–13C HSQC spectra were recorded to monitor the chemical shift changes upon peptide titration at 280 K for SL3 or 298 K for RBE. The substrate peptides were dissolved in NMR buffer before being titrated into 200 μM SL3 or RBE solution, with the concentration gradient of 0 μM, 100 μM, 200 μM, 300 μM, and 400 μM. The binding experiment of NC to SL3 was performed with a combination of 100 μM SL3 and 100 μM NC samples. After that, the L22#15 peptide was added to the former sample with the final concentration of 100 μM.
The obtained HSQC spectra were processed using NMRPipe, and the chemical shift perturbation (CSP) was calculated with the equation (0.5 × (ΔδH)2 + 0.1 × (ΔδC)2)0.5, where ΔδH and ΔδC are the chemical shift changes in the proton and carbon dimensions, respectively. The CSPs were globally fitted to a two-state binding equation as below,
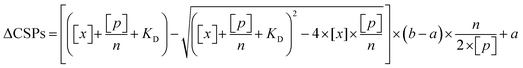 | (5) |
Results and discussion
The overview of RNA structures
Previous research indicates that the binding site between proteins and RNAs is mainly located in the hairpin and stem loop.34 The TAR RNA is a widely studied case that contains both the hairpin loop, stem loop, and bulge loop (Fig. 3A).23,33 Here, we focus on designing cyclic peptides targeting the RNA stem loop. Another example is the SL3 RNA, which is highly conserved among different strains of HIV-1 and adopts the hairpin and stem loop.52,53 SL3 is crucial in recognizing the HIV-1 genome by binding to nucleocapsid (NC) proteins.9 Furthermore, Julia et al. showed that the peptides binding to the SL3 stem loop region could inhibit its virus activity.54 The other example is RBE RNA, a highly structured 30-residue stem loop IIB domain. The RBE is crucial in transporting viral mRNA from the nucleus to the cytoplasm by binding to the Rev protein. The sequence similarity of the hairpin stem loop (20 bp) between TAR and SL3, TAR and RBE, and SL3 and RBE was 56%, 40.74%, and 60.87%, respectively. TAR RNA contains the bulge loop, and RBE includes an internal loop. Although the three RNAs have similar three-dimensional structures, there is a significant difference in sequence and secondary structure of the hairpin stem loop. Therefore, it is crucial to redesign inhibitors based on differences in RNA pocket geometry and sequence specificity. Finally, the SL3 RNA structure from the crystal (PDBID: 1A1T) and RBE RNA from the crystal (PDBID: 1G70) are used for the geometric information analysis, docking, and MD simulation.Peptide sequence and structure optimization
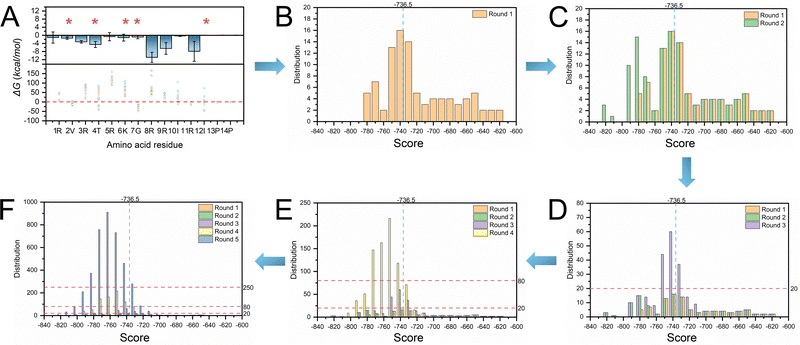
We first obtained the geometrical information of the RNA pocket using the rolling probe method. The sphericity (Ψ), surface area, and volume of the SL3 RNA pocket are 0.79, 295 Å2, and 337 Å3, respectively. The sphericity of the NC protein fragment (residue 1–14) is 0.70, suggesting that an ellipsoid-like structure may be the candidate inhibitor for SL3 RNA binding. L22 is a cyclic peptide mimic of the Tat protein that can bind to TAR RNA with a binding affinity of ∼30 nM, which adopts the anti-parallel β-sheet secondary structure. The geometrical shape of L22 is an ellipsoid-like structure with a sphericity of 0.77. Therefore, we utilized L22 as the starting structure for the inhibitor design.We performed mutations to optimize the L22 side chains to adjust the geometric matching conformations and increase interactions for binding. The first step is identifying the five residue positions by considering binding and per-residue free energy contributions. Then, we performed docking to evaluate the per-residue free energy contributions. Fig. 4A shows that V2, T4, K6, G7, and I12 residue positions contribute the least to RNA binding. Thus, we performed single mutation calculations of V2, T4, K6, G7, and I12 for structural optimization. In total, 5 × 19 samples were generated in the first step, and 45.26% showed higher binding affinity than L22 (−736.50 kcal mol−1). The second step is to optimize the residue positions of G7 and I12. We selected the top 5 samples in the first step and optimized them to generate 25 models. The docking score decreased to around −800 kcal mol−1 compared to the first step, with 56.67% showing higher binding affinity than L22. The third step is to optimize the residue positions of K6, G7, and I12 and generate 125 samples. A total of 155 samples (63.27%) showing higher binding affinity than L22 were generated in the three steps. We mutated V2, K6, G7, and I12 in the fourth step to generate 625 samples. Nine samples had scores lower than −800 kcal mol−1, with 85.52% showing higher binding affinity than L22. The fifth step generated 3125 models by mutating V2, T4, K6, G7, and I12. Again, 101 conformations showed lower free energy with less than −800 kcal mol−1, with 88.96% showing higher binding affinity than L22. The top 50 out of 3995 samples were selected for further MD simulations.
The values of Rg around the X, Y, and Z axes can describe the molecule's shape. For example, the initial Rg values of L22 are 5.9 Å, 6.1 Å, and 6.8 Å, respectively. After the side chain optimization, the average Rg values of the top 50 inhibitors shifted to 7.3 Å, 7.4 Å, and 4.7 Å, respectively. Fig. S1 (ESI†) shows that the geometric shapes of the top 50 inhibitors are more ellipsoid-like structures, which may match the RNA hairpin stem loop pocket better.
Binding modes of top 10 cyclic peptides
To accurately evaluate the binding affinity of peptides and RNA, we performed 50 ns MD simulations for the top 50 predictions and L22 to calculate the binding free energy and interactions for the last 20 ns trajectories. Fig. 5 and Fig. S2, S3 and Tables S1, S2 (ESI†) show the binding mode of the top 10 prediction peptides. The diagonal line in Fig. 5A represents the interactions between adjacent residues. The sites labeled by a red circle represent the antiparallel β-sheet or hairpin, and the region labeled blue represents the interaction surface between L22#15 and SL3 RNA. During the simulations, 70% of the top 10 predictions remain in the β-sheet structure. The disconnected lines in ranking 2, 5, and 6 predictions suggest that these predictions adopt the conformations without β-sheet (Fig. S2 and S3, ESI†). All conformations of the top 10 samples adopt the lysine at the 12th position. Lysine occurs 3 times on the 7th, indicating that the electrostatic interactions at these two sites are essential for binding RNA. Fig. 5B shows that the top 1 cyclic peptide of L22#15 binds to the SL3 RNA hairpin backbone via positively charged amino acids R1, R3, R5, K7, R8, and K12. Besides, the cyclic peptide L22#15 is inserted into the hairpin stem loop to form electrostatic and hydrogen interactions. The top 2–10 cyclic peptides follow a similar binding mode, binding to the SL3 RNA hairpin backbone via positively charged amino acids. The cyclic peptides are locally inserted into the RNA hairpin from different directions to form electrostatic and hydrogen interactions. The predictions of top 1 (L22#15) and top 4 (L22#13) show more interactions compared to L22 and SL3 after side chain interaction optimization (Fig. 5E). The binding free energy of L22#15 (−121.84 kcal mol−1) also increased by 143.29% compared to L22 (−50.08 kcal mol−1). The top 10 predictions were employed to perform NMR experiments for further validation. The KD values of L22#15 and L22#13 in experiments (Table 1) are consistent with the theoretical calculation. The increased interactions of the top 6–10 to SL3 decreased again after the last 25 ns MD simulations (Fig. 5F), which explains the lower binding affinity of the top 6–10 to SL3 in the experiments.| Peptide | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13a | 14 | K D (μM) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a The lowercase p at residue 13 indicates the presence of D-Proline. | |||||||||||||||
| L22 | R | V | R | T | R | K | G | R | R | I | R | I | p | P | NA |
| L22#15 | C | P | R | A | R | L | K | R | R | I | R | K | p | C | 5.22 ± 6.05 |
| L22#09 | C | P | R | A | R | L | V | R | R | I | R | K | p | C | 98.92 ± 98.00 |
| L22#01 | C | V | R | T | R | K | M | R | R | I | R | K | p | C | >1000 |
| L22#13 | C | N | R | A | R | L | K | R | R | I | R | K | p | C | 484.27 ± 345.67 |
| L22#29 | C | K | R | S | R | L | M | R | R | I | R | K | p | C | >1000 |
| L22#06 | C | P | R | A | R | L | M | R | R | I | R | K | p | C | 35.46 ± 47.48 |
| L22#16 | C | W | R | A | R | L | K | R | R | I | R | K | p | C | >1000 |
| L22#11 | C | N | R | A | R | L | V | R | R | I | R | K | p | C | >1000 |
| L22#22 | C | W | R | A | R | Q | M | R | R | I | R | K | p | C | >1000 |
| L22#43 | C | P | R | S | R | L | M | R | R | I | R | K | p | C | >1000 |
Binding affinity determination by NMR spectroscopy
We synthesized the top 10 peptides and prepared an isotope-labeled SL3 RNA sample to verify the binding of peptides to RNA. A series of 1H–13C HSQC spectrums were recorded for peptides to RNA titration experiments. The peaks of nucleotide bases in SL3 RNA were used for further analysis. The titration caused chemical shift perturbations (CSPs) for most of the peaks in SL3 RNA (Fig. 5C). As expected, L22#15 caused the largest CSPs of SL3 RNA. Meanwhile, the fitting of the binding equilibrium constants from NMR titration also indicated that L22#15 has the lowest dissociation constant (KD ≈ 5 μM), that is, the binding of L22#15 to SL3 RNA was the strongest (Fig. 5D and Table 1). CSPs offer valuable insights into the interactions between the peptide and RNA, including potential conformational changes and the formation of specific intermolecular contacts. The observed CSPs indicated changes in the local environment of nucleotides upon binding of the L22#15 peptide to the SL3 RNA. The nucleotides with significant CSPs suggested that these positions likely formed the interaction interface with L22#15. By further analysis and global fitting of these nucleotides, essential information, such as the binding affinity (KD value), can be obtained (Fig. 5C). Moreover, the NMR titration experiments were also performed by adding 9 other peptides. These peptides could cause different degrees of CSP to RNA, indicating the binding of these peptides to RNA (Fig. S4, ESI†). However, compared with the L22#15, the KD of these peptides was weakened, and some were too weak to fit accurately (Fig. S5, ESI†).Since the SL3 RNA was responsible for binding HIV-1 nucleocapsid protein, we further tested whether the L22#15 peptide could inhibit the binding of SL3 RNA and HIV-1 nucleocapsid protein. First, the 100 μM recombinant expressed HIV-1 nucleocapsid protein was added to the 100 μM SL3 RNA sample. The NMR experiment showed that the addition of the nucleocapsid protein also perturbed the chemical shifts of SL3 RNA, confirming that the nucleocapsid protein can bind to RNA (Fig. 6G). After that, the L22#15 peptide was added to the sample of the RNA–protein complex with the same concentration. The 1H–13C HSQC experiment shows that the peaks of SL3 RNA shifted to other directions close to the bound state of RNA-L22#15 but away from the peak of the bound state of RNA-NC, especially for the nucleotide U18 (Fig. 6H). The result indicates that in the presence of the nucleocapsid protein, the L22#15 can competitively participate in the binding of SL3 RNA, thereby inhibiting the binding of SL3 RNA to the nucleocapsid protein.
Binding mechanism for L22#15 peptide
We performed five 200 ns L22#15-SL3 and one 200 ns L22-SL3 and NC-SL3 simulations to explore the binding mechanism. The binding free energy and MD simulation analyses were performed with the last 50 ns trajectories (Fig. S6, ESI†). To evaluate the convergence of MM-GBSA calculations, we calculated the error ranges of binding free energy and the entropy contribution in five 200 ns MD simulations. The quasi-harmonic entropy was calculated by using the ptraj module in AMBER. In Tables S6–S8 (ESI†), the error of the binding free energy is 5.02 kcal mol−1, and the entropy error is only 1.42 kcal mol−1. The results indicate that the convergence of binding free energy is acceptable in the simulations. The NC protein fragment bound to SL3 by inserting an α-helix into the groove (Fig. 6D). The binding free energy (ΔGbinding) of NC-SL3 calculated in the last 50 ns MD simulation is −9.27 kcal mol−1. The root-mean-square deviation (RMSD) values of the L22#15-SL3 are lower than those of NC-SL3 during the MD simulations (Fig. S7A, ESI†). The optimized cyclic peptide L22#15 shows much stronger binding free energy with ΔGbinding = −36.86 kcal mol−1 and more contact with SL3 RNA than NC and L22 (Fig. 6A–C). The results showed that the dynamic geometry method can quickly adjust the backbone structure to adapt the RNA pocket. Then, the side chain optimization can further evaluate the interaction stability between the cyclic peptide and RNA pocket (Fig. 6D and E). Compared to L22 and NC, L22#15 shows two additional binding contributions at the R3 and R5 sites (Fig. S7C, ESI†). The root-mean-square fluctuations (RMSF) and per-residue free energy decomposition at residues A6-C8 of SL3 RNA agree with the competitive-binding assay (Fig. 6G and H and Fig. S7, ESI†). The differences in van der Waals energy values in the three SL3 RNA-related simulations are less than −5 kcal mol−1 (Fig. S8A, ESI†). The residue R11 in the cyclic peptide significantly improves −2.42 kcal mol−1 after side chain optimization. For electrostatic interaction analysis, Fig. S8B (ESI†) shows that mutation in I12 K significantly increased the energy contribution (−192.15 kcal mol−1). The polar and non-polar interactions provide limited energy contributions with less than −2 kcal mol−1 for the L22#15-SL3 binding (Fig. S8C and D, ESI†). It is noted that the number of hydrogen bonds significantly increased for L22#15-SL3 binding compared with NC-Sl3 and L22-SL3. The optimizations of electrostatic interactions and hydrogen bonds significantly improve the binding interactions of L22#15 and SL3 RNA.We performed the principal component analysis (PCA) (Fig. S6A and B), dynamic cross-correlation matrix (DCC) (Fig. S6D–F, ESI†), and contact maps (Fig. S6G–I, ESI†) to understand the behavior of the complexes. The PCA shows one minimum energy cluster for each MD simulation, indicating only one binding mode in the simulations (Fig. S6A–C, ESI†). The minimum of PC1 is around −10 in the SL3-NC protein simulation. However, the minimum values of PC1 are around −2 and −1 for SL3-L22 and SL3-L22#15 simulations. Thus, the structural difference between SL3-L22 and SL3-L22#15 is small, while the structural differences between SL3-NC and SL3-L22/L22#15 are significant. The DCC analysis shows consistent results with the PCA. For the dynamic cross-correlation, the cross-correlation between SL3 RNA and NC protein was mainly negative (orange), thereby leading to unstable binding. The negative correlation between SL3-L22 and SL3-L22#15 is significantly reduced, indicating that the binding between the two systems becomes more stable. The contact map analysis shows that the L22#15-SL3 interactions are much more than L22/NC-SL3 interactions, indicating that L22#15-SL3 shows higher binding affinity than the L22/NC-SL3 complex (Fig. S6G–I, ESI†). Together, all the results suggest that L22#15 has stronger binding interactions and is a competing inhibitor with the NC protein.
Design of cyclic peptides for the RBE RNA
We also applied the dynamic geometry strategy to design cyclic peptides for RBE RNA. We identified five residue sites (R1, V2, T4, R8, and I10) for mutation optimizations. A total of 3995 samples were generated (Fig. S9, ESI†). 921 (23.05%) conformations showed lower free energy less than −800 kcal mol−1, and 74.67% of the samples showed higher binding affinity than L22 binding to RBE (−741.69 kcal mol−1). Again, the top 50 peptides were employed to perform 50 ns MD simulations with RBE RNA. The binding free energy and contact map for each peptide-RBE structure were calculated using the last 20 ns trajectory. Finally, the top 10 cyclic peptides were selected by considering both docking score and binding free energy (Tables S3 and S4, ESI†).The binding mode of the top 10 cyclic peptides to RBE RNA significantly differs from the case of SL3 (Fig. S10 and S11, ESI†). For the RBE RNA study, the top 1 cyclic peptide of L22 + 16 inserts into the RNA major groove by interacting with the phosphoric acid group of R3, R5, K6, R9, and R11 (Fig. S11B, ESI†). The top 2–10 cyclic peptides also use positively charged amino acids to bind to the backbone to insert into the RNA major groove. The interaction surface between the cyclic peptides and RBE is mainly located in two regions, G2-C11 and G18-U25. Cyclic peptides designed for SL3 RNA bind to RNA by global interactions. These results demonstrate that we can design cyclic peptides for RNAs with high specificity. After the side chain optimizations, the predictions of top 1 (L22 + 16) and top 3 (L22 + 23) show more interactions with RBE RNA compared to L22-RBE (Fig. S11E, ESI†). The binding free energy of L22 + 16 (−105.38 kcal mol−1) also increases by 40.47%. The top 10 predictions were employed to perform further experimental validation. The NMR titration experiments were also performed for the top 10 cyclic peptides to RBE RNA. The top 6–10 contact values decreased after 20 ns MD simulation and showed lower binding affinity in NMR experiments (Fig. S11F, ESI† and Table 2).
| Peptide | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13a | 14 | K D (μM) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a The lowercase p at residue 13 indicates the presence of D-Proline. | |||||||||||||||
| L22 | R | V | R | T | R | K | G | R | R | I | R | I | p | P | NA |
| L22 + 16 | C | G | R | R | R | K | G | T | R | T | R | I | p | C | 11.17 ± 10.34 |
| L22 + 05 | C | V | R | T | R | K | G | R | R | T | R | I | p | C | 52.49 ± 23.30 |
| L22 + 23 | C | H | R | K | R | K | G | T | R | K | R | I | p | C | 730.71 ± 473.15 |
| L22 + 49 | C | G | R | R | R | K | G | C | R | T | R | I | p | C | 339.04 ± 266.25 |
| L22 + 40 | C | G | R | R | R | K | G | T | R | K | R | I | p | C | >1000 |
| L22 + 34 | C | W | R | Q | R | K | G | T | R | K | R | I | p | C | >1000 |
| L22 + 25 | C | G | R | R | R | K | G | A | R | T | R | I | p | C | >1000 |
| L22 + 41 | C | G | R | W | R | K | G | T | R | T | R | I | p | C | 687.62 ± 317.46 |
| L22 + 09 | C | V | R | T | R | K | G | R | R | F | R | I | p | C | >1000 |
| L22 + 42 | C | H | R | R | R | K | G | P | R | K | R | I | p | C | 452.71 ± 294.46 |
We also performed five 200 ns long MD simulations for the L22 + 16-RBE and one 200 ns for the L22-RBE and RSG-1.2-RBE. The analysis was performed with the last 50 ns trajectories. The binding free energy (ΔGbinding) of RSG-1.5 and L22 peptide binding to the RBE hairpin stem loop is −16.18 kcal mol−1 and −15.77 kcal mol−1, respectively. The RMSD values of the L22 + 16-RBE are lower than those of L22-RBE but slightly larger than those of RSG-1.2-RBE during the MD simulations (Fig. S12A, ESI†). The optimized cyclic peptide L22 + 16 shows stronger binding free energy with ΔG = −23.06 kcal mol−1. The interaction surface of L22 + 16 and RBE is more extended (Fig. S14 and S15, ESI†). The RSG-1.2 bound to the RBE RNA with high binding affinity at R10-R12 sites (Fig. S12C, ESI†). However, the contributions of binding free energy between L22 + 16 and RBE are derived from the residue R3-K6. The van der Waals energy values of RBE-L22 + 16 significantly improve after side-chain optimization. For example, the residue R3 significantly improves with −4.81 kcal mol−1 (Fig. S13A, ESI†). For electrostatic interaction analysis, Fig. S13B (ESI†) shows that mutation in T4R significantly increased the energy contribution (−324.61 kcal mol−1). The polar and non-polar interactions also provide limited energy contributions with less than −1 kcal mol−1 for the L22 + 16-RBE binding (Fig. S13C and D, ESI†). Therefore, the optimizations of electrostatic interactions and hydrogen bonds significantly improve the binding interactions of L22 + 16 and RBE RNA.
In the cases of RBE, PC1, and PC2, the three simulations show structural differences (Fig. S14, ESI†). The minimum of PC1 is around 0 in the RBE-RSG-1.5 simulation. However, the minimum values of PC1 are around 1 and 4 for RBE-L22 and RBE-L22 + 16 simulations. It suggests that the structural differences between the three simulations are large. The PCA of RBE-L22 + 16 shows two minimum energy clusters, indicating two binding modes in the RBE-L22 + 16 simulation. The DCCs are also consistent with the PCA. However, the cross-correlation between RBE RNA and L22 shows a more negative correlation. The binding of RBE-RG-1.5 and RBE-L22 + 16 is more stable (Fig. S14D and F, ESI†). The contact map analysis shows that the interactions between L22 + 16 and RBE are much more than L22/RSG-1.5 to RBE RNA, indicating that L22 + 16-RBE shows higher binding affinity than the latter two complexes (Fig. S14G–I, ESI†). Together, all the results suggest that L22 + 16 has stronger binding interactions with RBE RNA.
The experimental results also indicated that L22 + 16 has a strong binding affinity with RBE RNA (KD ≈ 11.17 ± 10.34 μM, Table 2 and Fig. S11D, ESI†). The other 9 predicted peptides showed lower binding affinity values (Fig. S16 and S17, ESI†). Two key factors are considered when assessing the strength of affinity through titration: the slope and the presence of a plateau in the titration curve. A steep slope typically indicates a higher affinity, reflecting a rapid change in the binding event. If the titration curve continuously increases without reaching a plateau, it suggests the presence of non-specific interactions between the substrate and the peptide. This absence of a plateau indicates weak binding affinity, characterized by a lack of stable, specific interactions between the molecules. Our study observed a significant initial slope during the titration process, indicating a rapid and strong interaction between L22 + 16 and the RBE RNA. As the L22 + 16 to RBE concentration ratio approached 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the titration curve exhibited a more gradual trend, suggesting a transition toward a saturated binding state. Remarkably, this trend was consistent across all nucleotides. In contrast, the titration curves of the other 9 peptides showed a less pronounced or nearly linear plateau, implying weaker or non-specific binding interactions. The determined KD values further supported our observation that L22 + 16 exhibited the highest affinity among the tested peptides toward the RBE RNA.
1, the titration curve exhibited a more gradual trend, suggesting a transition toward a saturated binding state. Remarkably, this trend was consistent across all nucleotides. In contrast, the titration curves of the other 9 peptides showed a less pronounced or nearly linear plateau, implying weaker or non-specific binding interactions. The determined KD values further supported our observation that L22 + 16 exhibited the highest affinity among the tested peptides toward the RBE RNA.
Discussion
Targeting the flexible RNA with inhibitors is one of the most challenging problems in biophysics. Here, we utilize the dynamic geometry strategy to illustrate a novel inhibitor design framework to overcome the flexibility and sampling problems. The cyclic peptide can adjust its structure to bind the flexible RNA pocket with more interactions. The dynamical network approach combined with docking considers both dynamic and static features. Besides, NMR experiments were further performed to confirm the binding affinity of designed cyclic peptides. After the side chain optimization, the cyclic peptide geometrical characteristic is more compatible with the RNA pocket (Fig. S1, ESI†).The cyclic peptides are more stable by forming α-helix or β-sheet structures to bind the RNA pocket. Besides, the side chain of cyclic peptides has a degree of flexibility and can be optimized to generate more interactions with RNA targets. Therefore, cyclic peptide inhibitors are more suitable for designing specific inhibitors with higher binding affinity and fewer side effects. Moreover, the cyclic peptides designed in this work all use natural amino acids that are easier to synthesize and cheap. The dynamic geometry design method can generate high-binding affinity cyclic peptides in a short time. Our previous work suggested that the dynamical network correlations via an energy-based method55 can observe subtle changes and are consistent with experimental results. Thus, we can perform an energy-based analysis to identify the interaction stability and optimize the hydrogen bonds of inhibitors-RNA. This framework can consider local and global pocket information and both dynamic and static structural changes. As shown in Fig. 7A–C, the number of hydrogen bonds (9 pairs) between the L22 peptide and SL3 is more than that of the SL3 to NC protein fragment (6 pairs). The number of hydrogen bonds with RNA further increased to 13 pairs in the optimized L22#15 peptide case. In addition, the interaction details found in our predictions are consistent with the NMR experiments. For instance, in the case of L22#15-SL3, the CSP of G12-G13 on SL3 is compatible with the RMSF and contribution of binding free energy in our theoretical calculation. Moreover, the top 1 (L22 + 16) cyclic peptide designed for the RBE RNA shows the strongest binding affinity in the NMR experiments. These results demonstrate the universality of our design strategies.
Previous research suggested that the geometrical information of the RNA pocket is crucial for binding. Zhou et al. employed the RPDescriptor model to calculate the pocket geometrical characteristics quantitatively. The RNA pocket can be divided into three categories: sphere-like (20.83%), disc-like (16.67%), and rod-like (62.50%) pockets (Fig. 7D).11 The RNA pocket targeted in this work is the most frequent rod pocket, and we further designed the rod-like cyclic peptides, which adopted an anti-parallel β-sheet. Moreover, the length and secondary structure can be changed to fit more pockets. For instance, the cyclic peptide can also be designed to be sphere-like by reducing the size of the cyclic peptide or adopting an α-helix.
The secondary structure of RNA is also crucial for the specific peptide design. The structure of RNAs mainly adopts the following five ordered secondary structures: hairpin loop, stem loop, bulge loop, internal loop, and multi-branched loop. Previous research has extensively focused on the stem loop of RNA and has demonstrated that the RNA stem loop holds a pivotal function in the reproduction of HIV-1.23,24,33 Yang et al. analyzed the RNA–protein interactions from a non-redundant RNA–protein structure database. Their study found that 71.68 ± 2.85% of proteins bound to the RNA hairpin stem loop.34 RNA–protein interactions are predominant in the stem loop region, which is why screening or designing inhibitors in this area could offer valuable insights into RNA inhibitor research. Our project delved deeply into the geometric and dynamic properties of the RNA stem loop. We aimed to craft a cyclic peptide inhibitor tailored to the unique characteristics of flexible stem loops in various RNA molecules. We are confident that our efforts will provide significant insights into RNA inhibitor design research. In this case, the RNAs contain all kinds of RNA secondary structures except multi-branched loops. To investigate the correlation and specificity between cyclic peptide structures and RNA secondary structures, we searched for an additional HIV-1-associated RNA structure adopting the multi-branched loop named PBS to discuss with the other three RNAs in this work. After changing the amido bond to a disulfide bond, we re-docked the two cyclic peptides, L22#15 and L22 + 16, which performed best with SL3 and RBE to other RNA targets. Fig. 8A shows the top 1 conformations of two cyclic peptides bound to TAR RNA in different regions. Because of the bulge loop, the different lengths of the side chain of the cyclic peptide lead the cyclic peptide to bind to RNA with different poses. The PBS RNA shows the same results: the two cyclic peptides bind to different locations in the multi-branched loop of RNA. In the cases of SL3 and RBE, the cyclic peptides bind to SL3 between the hairpin loop and stem loop, while the cyclic peptides bind to RBE in the internal loop. As shown in Table S5 (ESI†), L22#15 shows the highest binding affinity (−713.44 kcal mol−1) in SL3, and L22 + 16 shows the second-highest binding affinity (−710.19 kcal mol−1), only slightly below PBS (−731.30 kcal mol−1). These results indicate that two of our designed cyclic peptides show specificity with the specifically designed RNAs, while L22 showed weak specificity with TAR. Therefore, the binding modes of cyclic peptide and RNA are determined by the cyclic peptide's sequence, namely characteristics of the amino acid side chain and the secondary structural characteristics of the RNA pocket. In this work, we improved the binding affinity of cyclic peptides with the targets only by changing the length and charge properties of the amino acid side chain, and only 20 standard amino acids were used in this work. In future work, applying non-standard amino acids to design the length, chirality, charge, and hydrophobicity of amino acid side chains will further improve the binding affinity of cyclic peptides to targets (Table S9, ESI†).
Conclusions
In summary, we proposed a dynamic geometry strategy for RNA inhibitor design. We first use a decomposition algorithm to determine the optimal mutation conformations. Then, we utilize free energy and docking calculations to enrich the hits with only a tiny pool of geometrically compatible scaffold candidates. This method can explicitly and rapidly consider the geometrical information of the RNA pocket to design the cyclic peptide structure. Furthermore, the dynamic geometry method can optimize multiple interactions between cyclic peptides and RNA targets by side chain optimization. Together with the NMR experiment validations, the correlations between predicted binding free energy and experiment binding affinity support our inhibitor design strategy. We successfully designed two cyclic peptide inhibitors binding to RNA hairpin and stem loop structures. The designed L22#15 achieves low micromolar binding affinity, ∼5 μM, better than existing SL3 RNA inhibitors. The other case example of the RBE inhibitor L22 + 16 also achieves ∼11 μM. The strategy could still be referenced by further optimization and facilitating RNA engineering for biological or medical applications.Data availability
The supporting information is available Online. All simulation code is available at https://zhaoserver.com.cn/DGDesign/DGDesign.html.Author contributions
SN performed the analysis and wrote the paper; MS performed the experiments; ML, CZ, and XD helped with the discussion; ZG and YZ supervised the overall study and edited the manuscript.Abbreviations
| ncRNA | non-coding RNA |
| NC protein fragment | Nucleocapsid protein (residue 1–14) |
| SL3 | SL3 ψ-RNA |
| RRE | Rev responsive element |
| RBE | Rev binding element |
| MM-GBSA | Molecular mechanics-generalized Born surface area |
| CSP | Chemical shift perturbation |
Conflicts of interest
The authors declare that they have no conflict of interest.Acknowledgements
This work is supported by the National Natural Science Foundation of China 12175081 (YZ), 31971155 (ZG), Fundamental Research Funds for the Central Universities CCNU22QN004 (YZ), Youth Innovation Promotion Association of the Chinese Academy of Sciences 2020329 (ZG), and Excellent doctorial dissertation cultivation grant from Central China Normal University 2022YBZZ043 (SN).References
- P. A. Sharp, Cell, 2009, 136, 577–580 CrossRef CAS PubMed.
- T. R. Cech and Joan A. Steitz, Cell, 2014, 157, 77–94 CrossRef CAS PubMed.
- J. E. Butler and J. T. Kadonaga, Genes Dev., 2002, 16, 2583–2592 CrossRef CAS PubMed.
- A. M. Khalil and J. L. Rinn, Semin. Cell Dev. Biol., 2011, 22, 359–365 CrossRef CAS PubMed.
- Z. Li and P. D. Nagy, RNA Biol., 2011, 8, 305–315 CrossRef CAS PubMed.
- I. G. Wool, Annu. Rev. Biochem., 1979, 48, 719–754 CrossRef CAS PubMed.
- L.-W. Hung, E. L. Holbrook and S. R. Holbrook, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 5107–5112 CrossRef CAS PubMed.
- U. Schulze-Gahmen and J. H. Hurley, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 12973–12978 CrossRef CAS PubMed.
- R. N. De Guzman, Z. R. Wu, C. C. Stalling, L. Pappalardo, P. N. Borer and M. F. Summers, Science, 1998, 279, 384–388 CrossRef CAS PubMed.
- M. Matsui and D. R. Corey, Nat. Rev. Drug Discovery, 2017, 16, 167–179 CrossRef CAS PubMed.
- T. Zhou, H. Wang, C. Zeng and Y. Zhao, BMC Bioinf., 2021, 22, 428 CrossRef CAS PubMed.
- P. G. Vekilov, S. Chung and K. N. Olafson, MRS Bull., 2016, 41, 375–380 CrossRef CAS.
- S. L. Bonilla and J. S. Kieft, J. Mol. Biol., 2022, 434, 167802 CrossRef CAS PubMed.
- L. V. Bock and H. Grubmüller, Nat. Commun., 2022, 13, 1709 CrossRef CAS PubMed.
- T. Nakane, D. Kimanius, E. Lindahl and S. H. W. Scheres, eLife, 2018, 7, e36861 CrossRef PubMed.
- E. D. Zhong, T. Bepler, B. Berger and J. H. Davis, Nat. Methods, 2021, 18, 176–185 CrossRef CAS PubMed.
- L. Salmon, S. Yang and H. M. Al-Hashimi, Annu. Rev. Phys. Chem., 2014, 65, 293–316 CrossRef CAS PubMed.
- L. G. Scott and M. Hennig, in Bioinformatics: Data, Sequence Analysis and Evolution, ed. J. M. Keith, Humana Press, Totowa, NJ, 2008, pp. 29–61 DOI:10.1007/978-1-60327-159-2_2.
- J. R. Bothe, E. N. Nikolova, C. D. Eichhorn, J. Chugh, A. L. Hansen and H. M. Al-Hashimi, Nat. Methods, 2011, 8, 919–931 CrossRef CAS PubMed.
- P. Gotwals, S. Cameron, D. Cipolletta, V. Cremasco, A. Crystal, B. Hewes, B. Mueller, S. Quaratino, C. Sabatos-Peyton, L. Petruzzelli, J. A. Engelman and G. Dranoff, Nat. Rev. Cancer, 2017, 17, 286–301 CrossRef CAS PubMed.
- L. Guan and M. D. Disney, ACS Chem. Biol., 2012, 7, 73–86 CrossRef CAS PubMed.
- K. D. Warner, C. E. Hajdin and K. M. Weeks, Nat. Rev. Drug Discovery, 2018, 17, 547–558 CrossRef CAS PubMed.
- A. Davidson, T. C. Leeper, Z. Athanassiou, K. Patora-Komisarska, J. Karn, J. A. Robinson and G. Varani, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 11931–11936 CrossRef CAS PubMed.
- D. M. Warui and A. M. Baranger, J. Med. Chem., 2012, 55, 4132–4141 CrossRef CAS PubMed.
- D. M. Warui and A. M. Baranger, J. Med. Chem., 2009, 52, 5462–5473 CrossRef CAS PubMed.
- J. L. Battiste, H. Mao, N. S. Rao, R. Tan, D. R. Muhandiram, L. E. Kay, A. D. Frankel and J. R. Williamson, Science, 1996, 273, 1547–1551 CrossRef CAS PubMed.
- Y. Gosser, T. Hermann, A. Majumdar, W. Hu, R. Frederick, F. Jiang, W. Xu and D. J. Patel, Nat. Struct. Biol., 2001, 8, 146–150 CrossRef CAS PubMed.
- Y. Dai, J. E. Wynn, A. N. Peralta, C. Sherpa, B. Jayaraman, H. Li, A. Verma, A. D. Frankel, S. F. Le Grice and W. L. Santos, J. Med. Chem., 2018, 61, 9611–9620 CrossRef CAS PubMed.
- S. Hyun, K. H. Lee and J. Yu, Bioorg. Med. Chem. Lett., 2006, 16, 4757–4759 CrossRef CAS PubMed.
- Y. Jin and J. A. Cowan, J. Am. Chem. Soc., 2006, 128, 410–411 CrossRef CAS PubMed.
- J. Lu, B. M. Kadakkuzha, L. Zhao, M. Fan, X. Qi and T. Xia, Biochemistry, 2011, 50, 5042–5057 CrossRef CAS PubMed.
- B. S. Morgan, J. E. Forte, R. N. Culver, Y. Zhang and A. E. Hargrove, Angew. Chem., Int. Ed., 2017, 56, 13498–13502 CrossRef CAS PubMed.
- M. D. Shortridge, P. T. Wille, A. N. Jones, A. Davidson, J. Bogdanovic, E. Arts, J. Karn, J. A. Robinson and G. Varani, Nucleic Acids Res., 2019, 47, 1523–1531 CrossRef CAS PubMed.
- R. Yang, H. Liu, L. Yang, T. Zhou, X. Li and Y. Zhao, Int. J. Mol. Sci., 2022, 23, 6903 CrossRef CAS PubMed.
- N. R. Voss and M. Gerstein, Nucleic Acids Res., 2010, 38, W555–W562 CrossRef CAS PubMed.
- B. Lee and F. M. Richards, J. Mol. Biol., 1971, 55, 379–400 CrossRef CAS PubMed.
- G. G. Krivov, M. V. Shapovalov and R. L. Dunbrack Jr, Proteins: Struct., Funct., Bioinf., 2009, 77, 778–795 CrossRef CAS PubMed.
- Y. Yan, D. Zhang, P. Zhou, B. Li and S.-Y. Huang, Nucleic Acids Res., 2017, 45, W365–W373 CrossRef CAS PubMed.
- D. A. Case, T. E. Cheatham Iii, T. Darden, H. Gohlke, R. Luo, K. M. Merz Jr, A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, J. Comput. Chem., 2005, 26, 1668–1688 CrossRef CAS PubMed.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- B. R. Miller, T. D. McGee, J. M. Swails, N. Homeyer, H. Gohlke and A. E. Roitberg, J. Chem. Theory Comput., 2012, 8, 3314–3321 CrossRef CAS PubMed.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef CAS PubMed.
- R. Galindo-Murillo, D. R. Roe and T. E. Cheatham, Nat. Commun., 2014, 5, 5152 CrossRef CAS PubMed.
- H. Yu and P. A. Dalby, in Methods in Enzymology, ed. D. S. Tawfik, Academic Press, 2020, vol. 643, pp. 15–49 Search PubMed.
- E. A. Dethoff, A. L. Hansen, C. Musselman, E. D. Watt, I. Andricioaei and H. M. Al-Hashimi, Biophys. J., 2008, 95, 3906–3915 CrossRef CAS PubMed.
- T. Hayashi, Y. Ueno and T. Okamoto, FEBS Lett., 1993, 327, 213–218 CrossRef CAS PubMed.
- T. Hayashi, T. Shioda, Y. Iwakura and H. Shibuta, Virology, 1992, 188, 590–599 CrossRef CAS PubMed.
- J. Dietz, J. Koch, A. Kaur, C. Raja, S. Stein, M. Grez, A. Pustowka, S. Mensch, J. Ferner, L. Möller, N. Bannert, R. Tampé, G. Divita, Y. Mély, H. Schwalbe and U. Dietrich, ChemMedChem, 2008, 3, 749–755 CrossRef CAS PubMed.
- S. Ning, H. Wang, C. Zeng and Y. Zhao, Briefings Bioinf., 2022, 23, bbac290 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp03384h |
| ‡ SN and MS contributed equally to this work. |
| This journal is © the Owner Societies 2023 |