Enhancement of cell membrane permeability by using charged nanoparticles and a weak external electric field

Abstract

Because the cell membrane is the main barrier of intracellular delivery, it is important to facilitate and control the translocation of extracellular compounds across it. Our earlier molecular dynamics simulations suggested that charged nanoparticles under a weak external electric field can enhance the permeability of the cell membrane without disrupting it. However, this membrane permeabilization approach has not been tested experimentally. This study investigated the membrane crossing of a model compound (dextran with a M_w of 3000–5000) using charged nanoparticles and a weak external electric field. A model bilayer lipid membrane was prepared by using a droplet contact method. The permeability of the membrane was evaluated using the electrophysiological technique. Even when the applied electric field was below the critical strength for membrane breakdown, dextran was able to cross the membrane without causing membrane breakdown. These results indicate that adding nanomaterials under a weak electric field may enhance the translocation of delivery compounds across the cell membrane with less damage, suggesting a new strategy for intracellular delivery systems.

---

Introduction

Intracellular delivery is a key technology in biological research and biomedical/therapeutic applications. For instance, the delivery of DNA, RNA, and proteins is vital for gene editing and gene therapy.^1–4 Engineered nanoparticles (NPs) have been extensively studied for carrying extracellular compounds, drug delivery, intracellular imaging, etc.^5,6 A variety of NPs were designed and synthesized to achieve high delivery efficacy and multiple functionalities.^5,6 Despite a large body of research, however, the development of efficient intracellular delivery systems remains a major challenge.

The cell membrane is the main barrier of intracellular delivery. To facilitate and control the translocation of extracellular compounds, researchers frequently enhance the permeability of the cell membrane by subjecting cells to external force fields.^2,7 Electroporation is a common physical method⁸ that applies an external electric field (high-intensity electric pulse) to the cell. This electric field can cause transient membrane disruption and thus facilitate subsequent translocation of extracellular compounds across the membrane. Unfortunately, electroporation also exposes cells to excessive stress and thus increases their mortality.

Previously, we used molecular dynamics (MD) simulation to investigate the translocation of charged NPs across a phospholipid bilayer (a model for the cell membrane) under an external electric field.^9–11 Under the applied electric field, charged NPs can directly translocate across the bilayer without the membrane wrapping around them. There was no membrane disruption after the translocation of NPs. Remarkably, the NPs could cross the membrane under a weak electric field below the critical strength for membrane disruption. In other words, there is no need to disrupt the cell membrane prior to NP crossing, which is different from the conventional electroporation approach. It is also noteworthy that after the NPs passed through, the membrane showed self-resealing, suggesting less damage. Our studies further revealed that this membrane crossing can be driven by a locally enhanced electric potential across the membrane that is induced by superimposing the potential of charged NPs and the externally applied electric potential.¹⁰ These findings suggest that combining charged NPs with a weak electric field can enhance cell membrane permeability without causing membrane disruption. Nevertheless, no experimental studies have used this membrane permeabilization approach for the translocation of delivery compounds across the cell membrane.

Artificial phospholipid bilayer membranes are an ideal model system for the experimental exploration of physicochemical interactions between NPs and cell membrane.^12,13 Such bilayer membranes can be prepared as either three-dimensional liposomes and vesicles or two-dimensional supported and free-standing bilayers. Planar bilayer lipid membranes (BLMs) were used to experimentally investigate the cell membrane-crossing of ions and compounds under an electric field with the electrophysiological technique.^12,13 Numerous studies on membrane proteins such as ion channels were conducted on BLMs with the electrophysiology technique.¹⁴ Recently, BLMs with the electrophysiological technique were also used to investigate the interaction between nanomaterials and phospholipid bilayer membrane.^15–21 Several studies found that NPs could alter membrane permeability, sometimes leading to pore formation and membrane breakdown.^22–27 However, there has been no attempt to utilize NPs and an external electric field to facilitate the translocation of compounds across the BLM while minimizing membrane damage.

This study tested the aforementioned cell membrane permeabilization strategy suggested by MD simulations. The lipid membrane-crossing of a model delivery compound without membrane breakdown was experimentally investigated under the combined effects of charged NPs and a weak external electric field. The BLM was prepared by the droplet contact method.²⁸ The critical applied voltage for membrane breakdown was measured. Then, effects of NPs on electrical properties of the BLM (such as membrane capacitance) were evaluated using an electrophysiological technique to identify experimental conditions that influence membrane permeability. Finally, charged NPs and the model delivery compound were added together to the BLM system, and experiments were conducted to examine whether the NPs under the weak electric field could induce the model delivery compound to cross the BLM without membrane breakdown.

Materials and methods

Reagents and chemicals

The following reagents were used in this study: 1,2-diphytanoyl-sn-glycero-3-phosphocholine (DPhPC, Avanti Polar Lipids, 850356), n-decane (040-21602, FUJIFILM Wako Pure Chemical), and KCl (169-03542, FUJIFILM Wako Pure Chemical). Fluorescein isothiocyanate-labeled dextran (FITC–dextran, Sigma-Aldrich, FD4) was used as the model delivery compound, because its molecular weight (3000–5000) is similar to typical delivery compounds such as SiRNA.²⁹ Two types of NPs were used: amine-modified polystyrene nanoparticles (amine-PSL-NPs, Sigma-Aldrich, L0780) and carboxylate-modified polystyrene nanoparticles (carboxy-PSL-NPs, Micromod, 01-02-501). Their preliminary characterization results are shown in Table 1. The mean diameter and surface potential were measured using a surface potential and particle size analyzer (Zetasizer Nano ZS, Malvern). The amine-PSL-NPs were positively charged, while the carboxy-PSL-NPs were negatively charged. These NPs have sufficiently high surface potentials even when dispersed in 50 mM KCl solution (the electrolyte used for BLM in this study). Their measured mean diameters were the same as the nominal value of 50 nm, indicating good dispersibility of the NPs.

Table 1 Physical properties of charged NPs used in this study

Nanoparticle (NP)	Median diameter^a [nm]	Surface potential^a [mV]
a Measured in 50 mM KCl (aq.), which was used in the BLM experiments.
Amine-PSL	42.5	36.2
Carboxy-PSL	52.1	−27.0

---

Setup and procedure

Planar BLMs were prepared by the droplet contact method (DCM)^28,30,31 as shown in Fig. 1a. First, two aqueous droplets covered with lipid monolayers were prepared in a lipid/oil solution. When the two droplets contacted each other, a BLM was spontaneously formed at the contact interface. A double-well device (Fig. 1b and c) was employed to prepare a BLM by the DCM, and details of the device were described in the literature.^28,30,31 Briefly, the device consisted of two wells (4.0 mm in diameter and 5.0 mm in depth), a separator with a single through-hole (100 μm in diameter), and an Ag/AgCl electrode at the bottom of each well. The two droplets contacted each other at the through-hole to form the BLM there. The Ag/AgCl electrodes allow the application of a transmembrane external electric field and the measurement of transmembrane current.

Fig. 1 (a) Planar bilayer lipid membrane (BLM) prepared by the droplet contact method (DCM). (b) Top view and (c) side view of the double-well device used in this study.

Fig. 2a shows the experimental setup, which was composed of the double-well device, recording electrodes, patch-clamp amplifier, function generator, and personal computer for controlling and data recording. To monitor transmembrane current through the BLM, the double-well device was connected to the multi-channel patch-clamp amplifier (Flex, Tecella). The patch-clamp amplifier was also connected to the function generator (FG110, Yokogawa Electric) for applying transmembrane voltage to the BLM. Ag/AgCl electrodes at the bottom of well were attached to a solderless breadboard, which was connected to a recording electrode to the patch-clamp amplifier (Fig. 2b). In the study, multiple double-well devices were connected to the recording electrode, and the BLM experiments were performed in parallel. To minimize noise, the double-well devices and patch-clamp amplifier were placed in a Faraday cage.

Fig. 2 (a) Experimental setup. (b) Double-well devices connected to the solderless breadboard and recording electrode.

The experimental procedures were as follows. First, 1.2 μL of lipid/oil solution (10 mg mL⁻¹ of DPhPC/n-decane) was dropped into each well. Second, 20 μL of KCl solution (50 mM) without NPs or FITC–dextran was dropped into each well. Within a few minutes of adding KCl solution, the two droplets contacted each other at the single through-hole in the separator to form a BLM. To ensure proper BLM formation, the membrane resistance R_m and capacitance C_m were measured in situ using a discharge pulse method.³² A suitable BLM was considered to have R_m ≥ 1 GΩ and C_m ≥ 0.4 μF cm⁻². After the BLM passed the quality check, 2.0 μL of KCl solution (50 mM) containing NPs and FITC–dextran was then injected into one of the aqueous droplets by pipetting under predetermined conditions. Finally, an external voltage was applied to the BLM, and the transmembrane current was detected using a 0.25 kHz low-pass filter at a sampling frequency of 1.0 kHz.

Results and discussion

Critical applied voltage for membrane breakdown

Before investigating the proposed cell membrane permeabilization, it is necessary to ascertain the critical applied voltage for membrane breakdown (Δψ_appl,C). We measured Δψ_appl,C in a voltage-controlled experiment,³² by applying a linearly rising transmembrane voltage (slope: 20 mV s⁻¹) to the BLM and monitoring the transmembrane current. Fig. 3 shows the typical current response. The current noise observed in this study was approximately ±5 pA, thus, the current noise was not appreciable in Fig. 3. Under the linearly rising applied voltage (black solid line), the transmembrane current (red solid line) initially remained very low and then suddenly increased to reach the maximum measurable current of the amplifier (blue dashed line). The voltage at which the current increased rapidly was defined as Δψ_appl,C (black dashed line). We measured Δψ_appl,C in 26 independent experiments, and the 10% trimmed mean was calculated. As indicated on Fig. 3, the determined Δψ_appl,C was 372 ± 70 mV (mean ± S.D.). This value is very similar to those reported in previous studies,^33,34 confirming the validity of Δψ_appl,C measurement here.

Fig. 3 Typical current response of a BLM under linearly rising membrane voltage. Δψ_appl,C denotes the critical applied voltage for membrane breakdown. The mean value of Δψ_appl,C is indicated on the figure.

Effects of NPs on the electrical properties of BLM

To identify the experimental conditions that affect membrane permeability, the BLM properties were measured in the presence and absence of NPs. After forming the BLM, a specific amount of NPs with positive or negative surface charge was injected into the aqueous droplets. A pulsed voltage smaller than Δψ_appl,C (100 mV for 20 ms and 0 mV for 40 ms) was then continuously applied, and the membrane stability and membrane capacitance were measured at different exposure times.

Fig. 4 shows the probability of membrane breakdown (based on 5 experimental runs) at different concentrations of amine-PSL-NPs and exposure times. The membrane breakdown was defined as when the current reached the maximum measurable current during the experiment. The amine-PSL-NPs were added to the well connected to the positive voltage side (inset in Fig. 4). The NP concentration corresponds to the NP number concentration based on the final aqueous droplet in the well. Membrane breakdown was more likely at higher NP concentrations, particularly above 1.0 × 10⁶ particles per μL. The probably of membrane breakdown also became higher at longer exposure times, indicating that destabilization of BLM by NPs is a time-dependent phenomenon. However, the probability of membrane breakdown was the same at 10 and 30 min, suggesting that BLM destabilization did not progress significantly after 10 min.

Fig. 4 Fraction of membrane breakdown (n = 5) at different NP concentrations and exposure times. The amine-PSL-NPs were added to the well connected to positive voltage side (inset).

We also recorded the capacitance of the surviving BLMs and calculated its increase (ΔC_m = C_m(t) − C_m0, where C_m(t) is the membrane capacitance at exposure time t and C_m0 is the initial membrane capacitance before adding NPs). Fig. 5 shows ΔC_m as a function of exposure time at different concentrations of amine-PSL-NPs. There was no significant change in ΔC_m at NP concentrations below 1.0 × 10⁹ particles per μL, whereas at 1.0 × 10¹⁰ particles per μL ΔC_m exhibited a considerable increase. This increase in membrane capacitance may be attributed to the thinning of BLM and a higher charge on its surface, which can be caused by the closer association of concentrated charged NPs with the BLM.

Fig. 5 Temporal change in the increase in membrane capacitance (ΔC_m) at different concentrations of amine-PSL-NPs.

To further investigate the impact of NPs on the BLM, we varied the direction of the Coulomb force exerted on the NPs. Specifically, we measured the temporal change in ΔC_m in two scenarios depicted in Fig. 6a. Positively charged amine-PSL-NPs were added to either the well connected to the positive voltage side (top) or the other well connected to the ground (bottom). Similar experiments were performed with negatively charged carboxy-PSL-NPs (Fig. 6b). The schematics in Fig. 6 also depict the direction of the electric field across the BLM (E⃑). For amine-PSL-NPs, an increase in ΔC_m was observed when the NPs were added to the well connected to the positive voltage side but not that connected to the ground. The opposite trend was observed for carboxy-PSL-NPs, namely that ΔC_m increased when the NPs were added to the well connected to the ground rather than the positive voltage side. Thus, ΔC_m increased when the Coulomb force exerted on the NPs was oriented toward the BLM, whether the NPs carried positive or negative surface charge. These results indicate that the increase in ΔC_m was caused by the approach and accumulation of charged NPs on the membrane, which were mainly driven by electrophoresis.

Fig. 6 Temporal change in ΔC_m after adding NPs to the well connected to either the positive voltage side or the ground. (a) Amine-PSL-NPs with positive surface charge and (b) carboxy-PSL-NPs with negative surface charge.

Membrane crossing of FITC–dextran assisted by charged NPs and a weak electric field

Next, we examined whether the charged NPs facilitate the membrane crossing of delivery compounds (represented here by FITC–dextran) under a weak electric field without inducing membrane breakdown. First, a BLM was formed from aqueous droplets free of NPs and FITC–dextran. Subsequently, the amine-PSL-NPs and FITC–dextran were injected into the droplet connected to the positive voltage side, as depicted in Fig. 7a. The FITC–dextran concentration in the aqueous droplet was adjusted to 1.0 mg mL⁻¹. The NP concentration was set at 10⁶ particles per μL or higher based on the results in Fig. 4. A pulsed voltage (100 mV for 20 ms and 0 mV for 40 ms) was then applied for several tens of seconds to measure the initial membrane capacitance and resistance. Subsequently, a constant positive voltage smaller than Δψ_appl,C was applied for 3 min to facilitate the membrane crossing of FITC–dextran, and the transmembrane current was monitored at the same time. After removing the applied voltage, the membrane capacitance and resistance were measured again. Finally, the aqueous droplets in both wells were sampled by pipetting, and their absorbance at 494 nm was measured using a microvolume spectrophotometer (Nano Drop, Thermo Fisher Scientific) to quantify the FITC–dextran concentration in each droplet. Because the amin-PSL-NPs exhibit negligible absorbance at wavelengths above 400 nm, the measured absorbance at 494 nm should be solely due to FITC–dextran.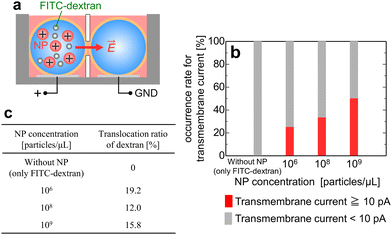

Fig. 7 (a) Schematic of experiments with charged NPs and FITC–dextran. Both amine-PSL-NPs and FITC–dextran were injected into the droplet connected to the positive voltage side. The applied voltage was 0.8 Δψ_appl,C, which was select based on our MD simulation results.^9–11 (b) Occurrence rate for transmembrane current signal higher or lower than 10 pA as a function of NP concentration (n = 4 experiments). (c) Translocation ratio of FITC–dextran across the BLM defined as A_PV/(A_PV + A_G) [%], where A_PV and A_G are the absorbances of FITC–dextran in the droplets connected to the positive voltage side and ground, respectively.

If FITC–dextran translocates across the BLM in the experimental system, the transmembrane current should be significantly higher than that without translocation. Thus, we first measured the transmembrane current. Fig. 7b shows the occurrence rate for transmembrane current signal higher or lower than 10 pA. The threshold value of 10 pA is significantly higher than the average transmembrane currents when neither NPs nor FITC–dextran is present. In the absence of NPs, a high transmembrane current was not observed, whereas adding NPs to the system resulted in a significantly higher transmembrane current, suggesting that the NPs enhanced membrane permeability. The occurrence rate of high transmembrane current became higher at higher NP concentrations. Fig. 7c shows the translocation ratio of FITC–dextran across the BLM. Only negligible translocation was observed without NPs, whereas a significant translocation ratio (12–20%) was detected in the presence of NPs. This confirmed that the NPs facilitated the translocation of FITC–dextran across the BLM.

Fig. 8a shows the typical transmembrane current signals during the application of constant voltage at different NP concentrations. Persistent current signals were observed at all NP concentrations, suggesting the existence of transmembrane pores during this whole process. We estimated the diameter of these pores from the current signals. For simplicity, we assumed that there was only a single pore filled with electrolyte in the membrane, although membrane defects may occur at multiple locations. The diameter of this single pore was estimated using Hille's equation:³⁵V/I = 4ρL/πD² + ρ/D. V is the applied voltage, I is the measured current, ρ = 1.43 Ω m is the resistivity of the electrolyte solution (determined using the surface potential analyzer), L = 5.1 nm³⁶ is the length of the pore, and D is the estimated pore diameter. Fig. 8b shows the distribution of estimated D values at each NP concentration. D ranges from 7 to 23 nm, significantly smaller than the diameter of amine-PSL-NPs (ca. 50 nm, Table 1). Considering the limitation of the single-pore assumption, the size of actual pores should be smaller than the estimated D values. Consequently, we suppose that only FITC–dextran translocated across the BLM, not the NPs. Moreover, the estimated hydrodynamic diameter of folded dextran with a molecular weight of 5000 (4.2 nm)^37,38 is smaller than the aforementioned pore diameters, supporting the membrane crossing of FITC–dextran in this study. Fig. 8b also shows that the estimated pore diameter is smaller at higher NP concentrations. This is probably because a larger number of NPs adhering to the BLM inhibit the formation of larger transmembrane pores. Details of the dependence of pore size on the NP concentration are still unknown and should be further investigated.

Fig. 8 (a) Transmembrane current signals and (b) distribution of transmembrane pore diameter during the application of a constant voltage of 0.8 Δψ_appl,C at different NP concentrations. The pore diameter was estimated using Hille's equation.³⁵

We compared the estimated transmembrane pore diameter to those reported in the literature. Table 2 shows the estimated diameters of transmembrane pores resulting from the interaction with NPs or peptides.^{22,23,26,27,30,31} The pore diameter observed in this study was much larger than those from previous studies, suggesting the uniqueness of membrane permeability enhancement in the present case.

Table 2 Previously reported transmembrane pore diameters resulting from the interaction with NPs or peptides

BLM permeability enhancer	Pore diameter [nm]	Ref.
Quantum dots NPs	0.33–0.92	22
Quantum dots NPs	1.9	23
Gold NPs	0.20–0.40	26
Polystyrene NPs	0.58–2.72	27
Antimicrobial peptide	0.90–1.30	30
Insecticidal protein	0.80–1.40	31

---

We investigated changes in BLM properties under an external voltage in the context of membrane integrity. Table 3 presents the membrane resistance and capacitance before and after application of the constant voltage. Both the membrane resistance and capacitance remained unchanged after applying a constant voltage of 0.8 Δψ_appl,C, at which point the membrane-crossing of FITC–dextran was confirmed to occur (see Fig. 7c). This suggests that membrane integrity was retained despite the application of this constant voltage and the membrane crossing of FITC–dextran. In other words, the model delivery compound successfully crossed the membrane aided by the charged NPs and weak electric field without causing membrane breakdown.

Table 3 Membrane resistance and capacitance before and after applying an external voltage of 0.8 ΔΨ_appl,c at each NP concentration

NP concentration [μL^−1]	Membrane resistance before/after applying external voltage [GΩ]		Membrane capacitance before/after applying external voltage [pF]
	Before	After	Before	After
Without NP	0.8	0.9	68	69
10^6	0.4	0.4	67	67
10^8	1.2	1.2	62	63
10^9	1.8	1.7	71	71

---

Finally, we discussed the NP concentrations used in this study (10⁶ to 10⁹ particles per μL) in detail. First, surface coverage of NP on the membrane surface at 10⁶ to 10⁹ particles per μL was estimated. The surface coverage was estimated to check whether all the NPs were adhered to the inner surface of the aqueous droplet in the well. The surface coverage was also estimated by assuming that the inner surface of the aqueous droplet was cover with NPs in a close-packed single layer. The results suggest that the surface coverage can be 0.502% to 502% at 10⁶ to 10⁹ particles per μL. Details can be seen in the ESI† (Table S1). This estimation implies that membrane crossing of FITC–dextran can occur even at less than 100% surface coverage of NPs. Second, we compared the NP concentrations used in this study to the safe dose to real biological cells. Safe dose data were extracted from literature reports^39–41 using the same amine-PSL-NPs (Sigma Aldrich, L0780) as in this study. Details can be seen in the ESI† (Table S2). The results indicated that the NP concentrations of 10⁶ to 10⁹ particles per μL can fall within a range of no adverse effects on mammalian cell lines³⁹ and bacteria.^40,41

Conclusions

This study investigated membrane crossing of a model delivery compound (FITC–dextran with M_w of 3000–5000) under the assistance of charged NPs (amine-modified polystyrene nanoparticles with 50 nm in diameter) and a weak external electric field. The cell membrane was modeled by a BLM prepared by DCM. The BLM was broken down at a critical applied voltage of Δψ_appl,C = 372 mV, very similar to the previously reported values. We found that membrane breakdown was likely to occur at higher NP concentrations and longer exposure times (up to 10 min before saturation). The capacitance of surviving BLMs increased significantly at a higher NP concentration of 1.0 × 10¹⁰ particles per μL, which was attributed to membrane thinning and a higher surface charge on the BLM that could be caused by closer association of charged NPs with the BLM. Our results also suggested that the increase in membrane capacitance was mainly due to electrophoresis of charged NPs. Finally, we demonstrated that adding charged NPs under a weak external electric field could allow the model delivery compound to cross the membrane without membrane breakdown. We verified that FITC–dextran translocated across the BLM even at an applied voltage below Δψ_appl,C. Moreover, the membrane resistance and capacitance remained unchanged before and after constant voltage application. The diameter of transmembrane pore formed in our experiments was estimated to be 7 to 23 nm, considerably smaller than the NP diameter (50 nm) but larger than the hydrodynamic diameter of folded dextran (4.2 nm). These estimated sizes support the translocation of FITC–dextran across the BLM.

The results here provide proof of concept for the proposed cell membrane-crossing strategy using charged NPs and a weak electric field, which can lead to a new strategy for intracellular delivery systems.

Nevertheless, it is clear that there is a gap between the BLM system and real cell membrane. Even from the viewpoint of the membrane deformability, BLM is not perfect mimic of the real cell membrane. Thus, the effect of NP concentration on the pore size found in this study may change in real cell membranes and needs to be further investigated in in vitro tests.

Author contributions

Hideya Nakamura: conceptualization, formal analysis, funding acquisition, methodology, project administration, resources, supervision, visualization, writing – original draft, writing – review & editing. Takumi Okamura: data curation, investigation, visualization, writing – original draft. Masaya Tajima: data curation, investigation. Ryuji Kawano: methodology, resources. Misa Yamaji: methodology, resources. Shuji Ohsaki: resources, validation, writing – review & editing. Satoru Watano: resources, validation, writing – review & editing.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was mainly supported by the Japan Society for the Promotion of Science, KAKENHI Grant Numbers 18H03536, 19K22976, and 19KK0129.

Notes and references

1. C. E. Nelson and C. A. Gersbach, Engineering Delivery Vehicles for Genome Editing, Annu. Rev. Chem. Biomol. Eng., 2016, 7, 637–662.
2. M. P. Stewart, A. Sharei, X. Ding, G. Sahay, R. Langer and K. F. Jensen, In vitro and ex vivo strategies for intracellular delivery, Nature, 2016, 538, 183–192.
3. J. Fang, Y.-Y. Hsueh, J. Soto, W. Sun, J. Wang, Z. Gu, A. Khademhosseini and S. Li, Engineering Biomaterials with Micro/Nanotechnologies for Cell Reprogramming, ACS Nano, 2020, 14, 1296–1318.
4. A. K. Fajrial, Q. Q. He, N. I. Wirusanti, J. E. Slansky and X. Ding, A review of emerging physical transfection methods for CRISPR/Cas9-mediated gene editing, Theranostics, 2020, 10, 5532–5549.
5. M. Sun, J. Lee, Y. Chen and K. Hoshino, Studies of nanoparticle delivery with in vitro bio-engineered microtissues, Bioact. Mater., 2020, 5, 924–937.
6. X. Hu, Y. Zhang, T. Ding, J. Liu and H. Zhao, Multifunctional Gold Nanoparticles: A Novel Nanomaterial for Various Medical Applications and Biological Activities, Front. Bioeng. Biotechnol., 2020, 8, 990.
7. H. Nakamura and S. Watano, Direct Permeation of Nanoparticles across Cell Membrane: A Review, KONA Powder Part. J., 2018, 35, 49–65.
8. C. Chen, S. W. Smye, M. P. Robinson and J. A. Evans, Membrane electroporation theories: a review, Med. Biol. Eng. Comput., 2006, 44, 5–14.
9. K. Shimizu, H. Nakamura and S. Watano, MD simulation study of direct permeation of a nanoparticle across the cell membrane under an external electric field, Nanoscale, 2016, 8, 11897–11906.
10. H. Nakamura, K. Sezawa, M. Hata, S. Ohsaki and S. Watano, Direct translocation of nanoparticles across a model cell membrane by nanoparticle-induced local enhancement of membrane potential, Phys. Chem. Chem. Phys., 2019, 21, 18830–18838.
11. Y. Ikeda, H. Nakamura, S. Ohsaki and S. Watano, Direct translocation of a negatively charged nanoparticle across a negatively charged model cell membrane, Phys. Chem. Chem. Phys., 2021, 23, 10591–10599.
12. E. Rascol, J.-M. Devoisselle and J. Chopineau, The relevance of membrane models to understand nanoparticles-cell membrane interactions, Nanoscale, 2016, 8, 4780–4798.
13. L. Wu and X. Jiang, Recent developments in methodology employed to study the interactions between nanomaterials and model lipid membranes, Anal. Bioanal. Chem., 2016, 408, 2743–2758.
14. S. Howorka and Z. Siwy, Nanopore analytics: sensing of single molecules, Chem. Soc. Rev., 2009, 38, 2360.
15. R. P. Carney, Y. Astier, T. M. Carney, K. Voïtchovsky, P. H. J. Silva and F. Stellacci, Electrical Method to Quantify Nanoparticle Interaction with Lipid Bilayers, ACS Nano, 2013, 7, 932–942.
16. A. Negoda, K. J. Kim, E. D. Crandall and R. M. Worden, Polystyrene nanoparticle exposure induces ion-selective pores in lipid bilayers, Biochim. Biophys. Acta, Biomembr., 2013, 1828, 2215–2222.
17. Y. Guo, E. Terazzi, R. Seemann, J. B. Fleury and V. A. Baulin, Direct proof of spontaneous translocation of lipid-covered hydrophobic nanoparticles through a phospholipid bilayer, Sci. Adv., 2016, 2, e1600261.
18. J. Broda, J. Setzler, A. Leifert, J. Steitz, R. Benz, U. Simon and W. Wenzel, Ligand-lipid and ligand-core affinity control the interaction of gold nanoparticles with artificial lipid bilayers and cell membranes, Nanomedicine, 2016, 12, 1409–1419.
19. T. I. Rokitskaya and Y. N. Antonenko, Fullerenol C₆₀(OH)₂₄ increases ion permeability of lipid membranes in a pH-dependent manner, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 1165–1174.
20. I. U. Foreman-Ortiz, D. Liang, E. D. Laudadio, J. D. Calderin, M. Wu, P. Keshri, X. Zhang, M. P. Schwartz, R. J. Hamers, V. M. Rotello, C. J. Murphy, Q. Cui and J. A. Pedersen, Anionic nanoparticle-induced perturbation to phospholipid membranes affects ion channel function, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 27854–27861.
21. C. M. Basham, S. Spittle, J. Sangoro, J. El-Beyrouthy, E. Freeman and S. A. Sarles, Entrapment and Voltage-Driven Reorganization of Hydrophobic Nanoparticles in Planar Phospholipid Bilayers, ACS Appl. Mater. Interfaces, 2022, 14, 54558–54571.
22. S. Ramachandran, N. E. Merrill, R. H. Blick and D. W. Van Der Weide, Colloidal quantum dots initiating current bursts in lipid bilayers, Biosens. Bioelectron., 2005, 20, 2173–2176.
23. S. A. Klein, S. J. Wilk, T. J. Thornton and J. D. Posner, Formation of nanopores in suspended lipid bilayers using quantum dots, J. Phys.: Conf. Ser., 2008, 109, 012022.
24. M. R. R. de Planque, S. Aghdaei, T. Roose and H. Morgan, Electrophysiological Characterization of Membrane Disruption by Nanoparticles, ACS Nano, 2011, 5, 3599–3606.
25. C. Corredor, W.-C. Hou, S. A. Klein, B. Y. Moghadam, M. Goryll, K. Doudrick, P. Westerhoff and J. D. Posner, Disruption of model cell membranes by carbon nanotubes, Carbon, 2013, 60, 67–75.
26. R. Palankar, B. El Pinchasik, B. N. Khlebtsov, T. A. Kolesnikova, H. Möhwald, M. Winterhalter and A. G. Skirtach, Nanoplasmonically-induced defects in lipid membrane monitored by ion current: Transient nanopores versus membrane rupture, Nano Lett., 2014, 14, 4273–4279.
27. B. Lu, T. Smith and J. J. Schmidt, Nanoparticle–lipid bilayer interactions studied with lipid bilayer arrays, Nanoscale, 2015, 7, 7858–7866.
28. R. Kawano, Y. Tsuji, K. Sato, T. Osaki, K. Kamiya, M. Hirano, T. Ide, N. Miki and S. Takeuchi, Automated Parallel Recordings of Topologically Identified Single Ion Channels, Sci. Rep., 2013, 3, 1995.
29. A. Sharei, J. Zoldan, A. Adamo, W. Y. Sim, N. Cho, E. Jackson, S. Mao, S. Schneider, M.-J. Han, A. Lytton-Jean, P. A. Basto, S. Jhunjhunwala, J. Lee, D. A. Heller, J. W. Kang, G. C. Hartoularos, K.-S. Kim, D. G. Anderson, R. Langer and K. F. Jensen, A vector-free microfluidic platform for intracellular delivery, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 2082–2087.
30. H. Watanabe and R. Kawano, Channel Current Analysis for Pore-forming Properties of an Antimicrobial Peptide, Magainin 1, Using the Droplet Contact Method, Anal. Sci., 2016, 32, 57–60.
31. T. Kunthic, H. Watanabe, R. Kawano, Y. Tanaka, B. Promdonkoy, M. Yao and P. Boonserm, pH regulates pore formation of a protease activated Vip3Aa from Bacillus thuringiensis, Biochim. Biophys. Acta, Biomembr., 2017, 1859, 2234–2241.
32. P. Kramar, D. Miklavcic and A. M. Lebar, Determination of the lipid bilayer breakdown voltage by means of linear rising signal, Bioelectrochemistry, 2007, 70, 23–27.
33. M. Robello and A. Gliozzi, Conductance transition induced by an electric field in lipid bilayers, Biochim. Biophys. Acta, Biomembr., 1989, 982, 173–176.
34. I. Genco, A. Gliozzi, A. Relini, M. Robello and E. Scalas, Electroporation in symmetric and asymmetric membranes, Biochim. Biophys. Acta, Biomembr., 1993, 1149, 10–18.
35. O. S. Smart, J. Breed, G. R. Smith and M. S. Sansom, A novel method for structure-based prediction of ion channel conductance properties, Biophys. J., 1997, 72, 1109–1126.
36. R. Benz and K. Janko, Voltage-induced capacitance relaxation of lipid bilayer membranes Effects of membrane composition, Biochim. Biophys. Acta, Biomembr., 1976, 455, 721–738.
37. E. Perez and J. E. Proust, Effects of a non-adsorbing polymer on colloid stability: force measurements between mica surfaces immersed in dextran solution, J. Phys., Lett., 1985, 46, 79–84.
38. S. Tasker, G. Matthijs, M. C. Davies, C. J. Roberts, E. H. Schacht and S. J. B. Tendler, Molecular Resolution Imaging of Dextran Monolayers Immobilized on Silica by Atomic Force Microscopy, Langmuir, 1996, 12, 6436–6442.
39. Y. Liu, W. Li, F. Lao, Y. Liu, L. Wang, R. Bai, Y. Zhao and C. Chen, Intracellular dynamics of cationic and anionic polystyrene nanoparticles without direct interaction with mitotic spindle and chromosomes, Biomaterials, 2011, 32, 8291–8303.
40. J. Miyazaki, Y. Kuriyama, A. Miyamoto, H. Tokumoto, Y. Konishi and T. Nomura, Adhesion and internalization of functionalized polystyrene latex nanoparticles toward the yeast Saccharomyces cerevisiae, Adv. Powder Technol., 2014, 25, 1394–1397.
41. J. Miyazaki, Y. Kuriyama, H. Tokumoto, Y. Konishi and T. Nomura, Cytotoxicity and behavior of polystyrene latex nanoparticles to budding yeast, Colloids Surf., A, 2015, 469, 287–293.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp03281g

---