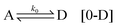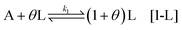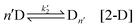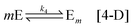Open Access Article
Open Access ArticleVariations in activation energy and nuclei size during nucleation explain chiral symmetry breaking
A.
Arango-Restrepo
 *a,
D.
Barragán
*a,
D.
Barragán
 b and
J. M.
Rubi
b and
J. M.
Rubi
 a
a
aDepartament de Física de la Matèria Condensada, Universitat de Barcelona, Avinguda Diagonal 647, 08028 Barcelona, Spain. E-mail: aarangor@unal.edu.co
bEscuela de Química, Universidad Nacional de Colombia, Carrera 65 No 59A-110, Bloque 16, Núcleo El Volador, 050034 Medellín, Colombia
First published on 20th October 2023
Abstract
We show that variations in enantiomer nuclei size and activation energy during the nucleation stage of crystallization are responsible for the chiral symmetry breaking resulting in excess of one of the possible enantiomers with respect to the other. By understanding the crystallisation process as a non-equilibrium self-assembly process, we quantify the enantiomeric excess through the probability distribution of the nuclei size and activation energy variations which are obtained from the free energy involved in the nucleation stage of crystallisation. We validate our theory by comparing it to Kondepudi et al. previous experimental work on sodium chlorate crystallisation. The results demonstrate that the self-assembly of enantiomeric crystals provides an explanation for chiral symmetry breaking. These findings could have practical applications for improving the production of enantiopure drugs in the pharmaceutical industry, as well as for enhancing our understanding of the origins of life since enantiomeric amino acids and monosaccharides are the building blocks of life.
1 Introduction
The universe and all its constituents are not necessarily symmetrical. In fact, at the birth of the universe, an asymmetry triggered the formation of a slightly higher amount of matter over antimatter and then allowed the formation of the known universe,1 and maybe also dictated its fate.2 Chiral symmetry breaking is a phenomenon that can be easily found in physical and chemical processes in our labs and industries.3 Chiral symmetry breaking is evidenced when the ratio between enantiomers (mirror image of each other) is not 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and takes place on scales as diverse as those of elementary particles and living beings.4–9
1, and takes place on scales as diverse as those of elementary particles and living beings.4–9
Chiral symmetry breaking in the NaClO3 crystallisation process has been the subject of much interest in recent years.10 When using thermodynamics at equilibrium, the free energy ΔGrev required for the formation of the possible enantiomers is practically the same so the corresponding probabilities ps ∝ exp(−ΔGrev/kBT), with kB the Boltzmann constant and T the temperature, are very similar, resulting in weak or none chiral symmetry breaking. However, experiments have shown that under non-equilibrium conditions, such as in the presence of temperature gradients, the shear rates and chemical reactions9,11,12 chiral symmetry-breaking may be induced, i.e., ps is not given only through ΔGrev. Furthermore, it has been shown by the formalism of non-equilibrium thermodynamics that there is a relationship between enantioselective catalysis and energy dissipation which plays an important role in chiral symmetry breaking.13 On the other hand, secondary nucleation and Viedma ripening are two well-known and complementary mechanisms that explain chiral symmetry breaking.10,14,15 In addition, the presence of an enantiomeric excess has also been attributed to differences in activation energies between the enantiomers, leading to different rates of formation.7,16 These variations in the nucleation stage, proposed by both secondary nucleation and Viedma ripening mechanisms, are influenced by shear rates affecting crystal and nuclei formation, which could be related to variations in activation energies during the nucleation stage. Therefore, non-equilibrium conditions during the crystallisation play a crucial role in determining the symmetry-breaking phenomenon and not only the initial conditions.
Experiments consisting of evaporating the solvent to obtain NaClO3 crystals,14 performed by stirring the sample, showed the existence of a disproportion in the concentrations of both enantiomeric crystals of NaClO3. In these experiments, histograms of the enantiomeric excess are obtained revealing symmetry breaking in which it is proposed kinetic arguments for understanding symmetry breaking. Enantiomeric crystals can be understood as structures arising from non-equilibrium self-assembly (NESA) processes in which the fundamental constituents are chiral molecules or chiral building blocks. A mechanism for understanding out-of-equilibrium crystallisation using NESA processes has previously been proposed.17 Since energy dissipation is related to the occurrence of NESA18 structures, we wonder whether there is a probability distribution, depending on the dissipated energy, that allows us to quantify the excess of enantiomeric crystals and thus chiral symmetry breaking.
In this paper, we aim to show that variations in the activation energies and size of nuclei of the enantiomeric precursors at the nucleation stage play a crucial role in symmetry breaking. We demonstrate that these variations are due to energy dissipation, and we show that the probability distribution of the variations is defined by the Gibbs free energy, which also considers the irreversibilities of the process. We use the crystallisation of sodium chlorate as a case study to validate our theory and reproduce experimental results presented in ref. 14 under both stirred and non-stirred conditions. Our results show that agitation affects not only the kinetics but also the thermodynamics of the crystallisation process. We prove that symmetry breaking is amplified when agitation increases until a certain threshold value. Finally, our results indicate that from a kinetic perspective, agitation breaks the symmetry, however, from thermodynamic and kinetic perspectives, the cause lies in the variations induced by energy dissipation.
2 Emergence of enantiomeric structures
2.1 A mechanism based on non-equilibrium self-assembly
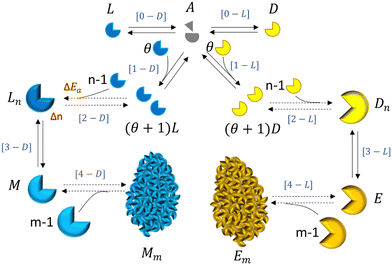
Our main proposal lies in modelling the mechanism of the formation of the enantiomeric structures as a non-equilibrium self-assembly (NESA) process based on activation, assembly and disassembly steps.19 In Fig. 1, we illustrate the mechanism for forming two enantiomeric structures from an achiral precursor A which might transform into a chiral precursor (levogyre L or dextrogyre D) or it might be induced by a chiral precursor (L or D) to become a chiral precursor (L or D). The chiral precursor L interacts with n − 1 other levogyre precursors to give rise to a first-order chiral structure Ln. The first-order chiral structure becomes activated M and finally interacts with other activated chiral structures to form the levogyre second-order structure Mm. The same mechanism holds for the dextrogyre structures. Both processes take place simultaneously and can produce a racemic mixture, a pure enantiomeric L or D solution or a mixture of enantiomers.The mechanism proposed in Fig. 1 involves the activation of the fundamental component (achiral compound, such as chiral molecules or simply dissolved salts) from thermal fluctuations[0] or by the interaction with a chiral compound or precursor (achiral molecules or liquid agglomerates),1 sequential assembly (formation of first-order chiral structure such as solid nuclei),2 second activation (first-order structure activation such available solid nuclei),3 and non-sequential assembly (second-order structure formation such as crystal formation).4 These subprocesses can be interpreted as self-replication and autocatalysis, [1] phase change, [2–3] and agglomeration, [4] respectively. Here we consider nucleation as processes [1] to [3], and crystal growth as process [4].
By considering a fundamental component (achiral component) A being activated in two different ways, L and D (chiral precursors), we have the first activation:
which requires high activation energies and is therefore unlikely. Here the change of free energy is zero. However, by taking into account a self-replication mechanism, due to the achiral component being induced by a chiral precursor, the activation kinetics is improved. The most general way to describe this step is to consider θ chiral precursors (L or D) inducing the activation of A into L or D. Therefore, the activation (self-replication) step is written as:
Notice that in this step, the production of L and D precursors might have different kinetic constants, due to variations in activation energies, coming from the number of neighbour molecules of L and D interacting with A.
The sequential assembly process is the formation of aqueous nuclei composed of n chiral precursors:
Strictly speaking, this step is performed sequentially, with activated chiral precursors being added one by one until a specific size is achieved. However, for simplicity, we adopt the process outlined in [2-D] and [2-L]. It should be noted that the size of the nuclei may vary depending on the conditions (indicated by n′). Furthermore, during this step, the aqueous nuclei assume a configuration that ensures the resulting solid nuclei possess clear chirality. In the reconfiguration, we encounter a crucial step where the activation energy can fluctuate easily, as the structure is not as stable as it would be in close proximity to a solid state. It is at this point that we consider fluctuations in the activation energy, which is evident in the kinetic constant denoted as
 . This key step involves variations in the activation energy and the size of the nuclei, which can occur due to the internal configuration of the aqueous nuclei, as well as the presence of gradients (temperature, density, salt), and shear rates at the location where the process is taking place.
. This key step involves variations in the activation energy and the size of the nuclei, which can occur due to the internal configuration of the aqueous nuclei, as well as the presence of gradients (temperature, density, salt), and shear rates at the location where the process is taking place.
The second activation is the transition of the nuclei from aqueous to solid state:
The last step is the second-order assembly by aggregation of nuclei which corresponds to a Smoluchowski aggregation. We simplify this process assuming that it can be viewed as the agglomeration of m nuclei:
where Mm and Em are the respective crystals for each configuration.
Our proposed mechanism will enable us to replicate experiments on chiral symmetry breaking using fundamental concepts of self-assembly and self-organization, which we hypothesize to be critical in demonstrating how energy dissipation and variations in thermodynamic variables induce chiral symmetry breaking and amplify it. This mechanism proposes that self-catalysis (sequential self-assembly) and phase change (second-order activation), accounting for the formation of the enantiomeric nuclei (nucleation), are the key processes to consider variations in thermodynamic variables leading to chiral symmetry-breaking. Additionally, we take into account the competition between the kinetics of producing enantiomeric crystals Mm and Em, as suggested in prior research,7,14 and the agitation considered in ref. 14, which play a role in the understanding of chiral symmetry breaking.
2.2 Mass balance
Let pi(Γ,t) be the probability distribution of finding the chemical compound i in the system at time t and state/configuration Γ along the sub-processes (process [0] to [4]). The probability is defined in a landscape large enough to carry out a thermodynamic analysis. The continuity equation for the probability in the Γ-space is given by, | (1) |
Assuming that processes [0] to [4] are uncoupled along each γj, the continuity equation can be rewritten as:19
 | (2) |
Carrying out a coarse-graining approach to eliminate the γ-coordinate, we obtain
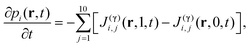 | (3) |
The number of moles Ni can be related to the probability through Ni = N0pi, where N0 is the initial amount of dissolved salt. The rate of the process per component is ṙi,j(t) = N0[J(γ)i,j(1,t) − J(γ)i,j(0,t)]. Multiplying eqn (3) by N0 and using the previous relations, we obtain the balance equation for the number of moles of the ith component
 | (4) |
The expressions for the rates ṙi,j are computed in the quasi-stationary regime.20 They include Arrhenius factors (kj(T) = ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) j
j![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Ea/RT)).21,22 The rates can describe processes (or reactions) which do not fulfill the law of mass action because of the presence of activity coefficients in the original kinetic expressions. Rates will be expressed in terms of the concentration Ci defined as Ci = Ni/V(t) in which the volume V(t) decreases linearly on time due to the evaporation of the solvent as done experimentally.14 The obtained rates for the NESA process for the formation of enantiomeric crystals are given by:
exp(Ea/RT)).21,22 The rates can describe processes (or reactions) which do not fulfill the law of mass action because of the presence of activity coefficients in the original kinetic expressions. Rates will be expressed in terms of the concentration Ci defined as Ci = Ni/V(t) in which the volume V(t) decreases linearly on time due to the evaporation of the solvent as done experimentally.14 The obtained rates for the NESA process for the formation of enantiomeric crystals are given by:
| R1 = k+L0CA − k−L0CL, | (5) |
| R2 = k+D0CA − k−D0CD, | (6) |
| R3 = k+L1CACL − k−L1CL2, | (7) |
| R4 = k+D1CACD − k−D1CD2, | (8) |
| R5 = k+L2CL2 − k−L2CLn, | (9) |
| R6 = k+D2CD2 − k−D2CDn, | (10) |
 | (11) |
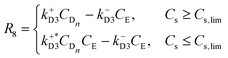 | (12) |
 | (13) |
 | (14) |
Since we are not considering the formation of intermediate structures with a number of elements less than n, we approximate the self-assembly rate (eqn (9) and (10)), as a kinetic of second-order in the enantiomeric concentration (CL and CD respectively). The second activation rate (eqn (11) and (12)) is a first-order kinetic expression in the enantiomeric aqueous nucleus concentration (CLn and (CDn respectively). The second-order activation may be constrained by a phase change, which implies the existence of a threshold value for the concentration of aqueous compound Cs,lim that needs to be exceeded, in which Cs is the sum of all the concentration of aqueous components in the system. Once this threshold is surpassed, an oversaturation (or supersaturation) force (proportional to k+L3CLn − k−L3CM and k+D3CDn − k−D3CE) comes into play, driving the subprocess. In addition, in this step, we can recognise a parallel activation (or secondary nucleation15) when the system is undersaturated (below the threshold Cs,lim) and is induced by the presence of first-order structures coming from the disassembly of second-order structures (e.g., due to mechanical stress as in the Viedma ripening mechanism15).
Regarding the aggregation process rate (eqn 13 and (14)), an auto-catalytic effect of the crystal formation is expected since the structures tend to minimize the surface area to become more stable. Furthermore, there is a threshold value for the precursor concentration (CM and CE) in which above the value, there is a combination between second-order kinetics in the precursor and a direct dependence of the crystal concentration. Notice that the process rate also depends linearly on the degree of agitation α as proposed in ref. 23 with α ≥ 0. The value of α accounts for the magnitude of shear rates in the system, but it does not account for the stirring modes. It is worth noting that agitation promotes crystal growth when the nuclei concentration exceeds Clim as it increases the likelihood of nuclei interacting with crystals. Conversely, agitation facilitates crystal dissolution and breakage when the nuclei concentration falls below Clim, which in the present case is negligible since the system is always oversaturated. Finally, from eqn (5)–(14), we can write the ṙi,j fluxes using the stoichiometry of the processes [0–4] (see Appendix).
3 Methods
3.1 NaClO3 crystallisation
In the context of crystallisation, thermodynamic formalism plays a pivotal role in elucidating the intricacies of the process. Crystallisation is fundamentally governed by the delicate interplay of energy considerations and molecular interactions. When examining the formation of enantiomeric crystals of NaClO3, we must delve into the thermodynamic underpinnings of the phenomenon. Fundamentally, crystallisation is the process in which solute species, like Na+ and ClO3− ions in this instance, transform from a chaotic, solvated state in a solution to a structured, solid-state crystal lattice. This transformation indicates a change in the system's Gibbs free energy, and the creation of crystalline structures is preferred when the free energy decreases.We explain how enantiomeric NaClO3 crystals are generated through the crystallisation process, based on the proposed general mechanism. In Fig. 2, we present a scheme for the crystallisation process of NaClO3 with the proposed sub-processes. Given that the fundamental constituents are the dissolved ions, Na+ and ClO3−, the transition (activation) to a chiral precursor, Levogyro (−) or Dextrogyro (+), ((±)(NaClO3(aq))), encounters kinetic impediments, resulting in an extremely high or effectively infinite activation energy. In the framework of this process [0], activation is explained as a consequence of thermal fluctuations, described as follows:
The nucleation process begins with Na+ and ClO3− ions interacting with small clusters of aqueous ions denoted as (n − 1)(±)NaClO3. It is important to note that these clusters of ions have a preferred internal structure, often with a chiral precursor. This preference for chirality is due to the underlying thermodynamic formalism, which reflects the energetic stability associated with certain molecular arrangements.
The molecular agglomerates, driven by thermodynamic considerations, gradually coalesce to form larger aqueous nuclei, denoted as (±)NaClO3(aq))n(aq). This assembly process highlights the progressive organisation of solute species in the aqueous medium. It is within these aqueous cores that the thermodynamic picture becomes increasingly evident, as the transition from disordered and solvated ions to ordered and structured molecular assemblies involves a reduction of the Gibbs free energy.
The water-based nuclei go through a final change where they transform from a liquid state to solid nuclei, specifically (±)NaClO3(s). This marks the final step of the nucleation process, where the natural forces driving crystallisation ultimately result in the creation of NaClO3 crystals (sub-process [4]) with clear structural and chiral properties. The final step can be written as
In the experiments carried out by Kondepudi et al.14 NaClO3 was carefully dissolved in water forming an undersaturated solution at 50 °C in which no impurities were present. The solution contained water (the solvent) and the ions Na+ and ClO3−. The solution was cooled to room temperature (25 °C). Then, several samples were taken and transferred to smaller recipients, where the solvent was evaporated to reach oversaturation. There, the crystallisation process took place (from Na+ and ClO3− to (±) NaClO3(c)) with the consequent formation of the enantiomeric crystals. The experiments were performed with and without stirring during the crystallisation process. Here, we try to describe from our simple and general mechanism the formation of the crystals with and without the presence of agitation. Additionally, we analyse the case of different stirring rates.
3.2 Physical and chemical properties
The activation energies, the forward kinetic constants and the change of the standard chemical potential for each process used in the numerical solution are presented in Table 1.| Processes | E a/kBT |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) +/
+/![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) +L0 +L0 |
ΔG0/kBT |
|---|---|---|---|
| [0L] & [0D] | 60 | 1 | 0 |
| [1L] & [1D] | 20 | 1 | 0 |
| [2L] & [2D] | 10 | 10 | −10 |
| [3L] & [3D] | 2 | 100 | −5 |
| [4L] & [4D] | 5 | 250 | −40 |
Here ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) − is defined through:
− is defined through: ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) −/
−/![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) +L0 = exp(ΔG0/RT). In the Table, the values of the kinetic constants consider the fact that the collision frequency of reactants of [4L] & [4D] (number of “crashes” between nuclei) must be higher than the frequencies of the other processes because of the big size and low concentration of the reactants. To determine the activation energy values, we employ the concept of electronic configuration, considering the stability of chemical bonds. The activation energy of processes [0L] & [0D] (activation) have the highest value because there is a low probability for electronic reconfiguration (formation or destruction of chemical bonds) to trigger a change between achiral and chiral components, without the influence of an external agent, while processes [1L] & [1D] (activation by self-replication) has lower activation energy because a chiral component may induce re-configurations in the electronic structure of the achiral component. In general, processes involving only electronic re-configuration ([0L] & [0D] and [1L] & [1D]) have the highest activation energy and zero free energy change, and processes involving only physical changes ([2L] & [2D], [3L] & [3D] and [4L] & [4D]) have low activation energy and negative free energy change (exergonic process, thermodynamically favoured).
+L0 = exp(ΔG0/RT). In the Table, the values of the kinetic constants consider the fact that the collision frequency of reactants of [4L] & [4D] (number of “crashes” between nuclei) must be higher than the frequencies of the other processes because of the big size and low concentration of the reactants. To determine the activation energy values, we employ the concept of electronic configuration, considering the stability of chemical bonds. The activation energy of processes [0L] & [0D] (activation) have the highest value because there is a low probability for electronic reconfiguration (formation or destruction of chemical bonds) to trigger a change between achiral and chiral components, without the influence of an external agent, while processes [1L] & [1D] (activation by self-replication) has lower activation energy because a chiral component may induce re-configurations in the electronic structure of the achiral component. In general, processes involving only electronic re-configuration ([0L] & [0D] and [1L] & [1D]) have the highest activation energy and zero free energy change, and processes involving only physical changes ([2L] & [2D], [3L] & [3D] and [4L] & [4D]) have low activation energy and negative free energy change (exergonic process, thermodynamically favoured).
3.3 Total entropy produced
The total entropy produced in the formation of enantiomers, Σ(η), is the integral over time of the entropy production rate σ(η): | (15) |
The entropy production rate of the process results from free energy differences between the initial and final state, and viscous dissipation (friction) due to the agitation of the system. According to mesoscopic non-equilibrium thermodynamics21 and micromixing analysis,24 it can be written in terms of the rates and agitation degree
 | (16) |
3.4 Probability distribution
We consider crystal formation as a non-equilibrium self-assembly process subject to changes in free energy and energy dissipation due to the action of external forces. The probability of observing a state η is given by18 | (17) |
| ΔG = ΔrG + ΔiG + ΔcG | (18) |
To obtain the configurational free energy change ΔcG, we assume that the process evolves by making efficient use of the available resources,26,27 for which an extreme value of the energy dissipated, at which ∂ΔEd/∂η|η* = 0, is the signature of an optimal design of the structure as for instance stated in dendritic crystals.28–30 Therefore, the energy cost to keep a configuration different from the hypothetical efficient configuration is ΔcG = |Ed(η) − Ed(η*)|. By performing an expansion of Ed around η*,18 we obtain:
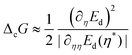 | (19) |
4 Results and discussion
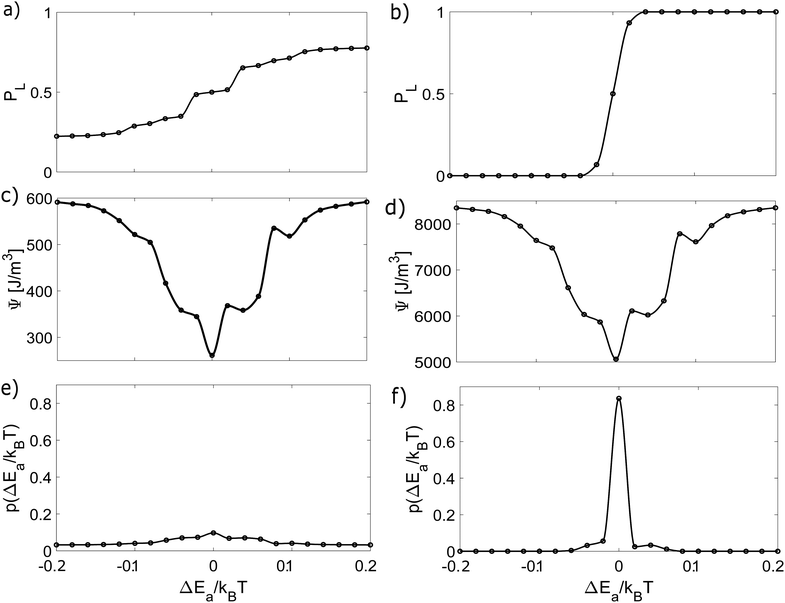
Using a deterministic model, we aim to reproduce the histograms for the enantiomeric excess obtained in ref. 14. In order to achieve such a goal, we use the probability distribution given by eqn (17). Therefore, we first solve the kinetics for every chemical compound numerically simultaneously (eqn (4)–(14)) using MATLABR2023a. For very long times, once re-dissolution is negligible due to evaporation as in the experiments ref. 14 we obtain the value for the concentration of both enantiomeric crystals and from it the probability of observing an enantiomer, for instance, L-enantiomer, defined as: | (20) |
In both figures, PL varies more sharply in the stirring case. These variations lead to higher energy dissipation and, consequently, to higher values of the free energy, giving rise to a spiky probability distribution, in contrast to the roughly constant shape of the non-stirred case. It is also clear that the presence of variations breaks the chiral symmetry, and as these variations increase, one enantiomer becomes more dominant over the other.
To estimate the degree of chiral symmetry breaking, we use the enantiomeric excess percentage. We generate a random variable following the distribution ρ for the variations in Ea and n. This should be analogous to performing several experiments without controlling the variations in Ea and n. Since our final goal is the building of the histograms for the enantiomeric excess, we use the biassed Ea and n variations following ρ and insert it into PL. Then we are able to obtain a set of data for the probability 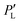 . Using this re-defined probability of observing an L-crystal, we obtain the enantiomeric excess percentage
. Using this re-defined probability of observing an L-crystal, we obtain the enantiomeric excess percentage
 | (21) |
 | ||
| Fig. 5 Histograms for the enantiomeric excess percentage. The left-hand column represents results considering variations in ΔEa while the right-hand column corresponds to variations in Δn. Histograms for: (a) and (b) no-stirring (α = 0). (c) and (d) low stirring (α = 2). (e) and (f) high stirring (α = 10). Blue histograms correspond to experimental results14 | ||
Our results for the variations in the activation energy, as shown in Fig. 5(a) and (e), are consistent with the histograms presented in ref. 14. This shows that our model not only accurately describes the experiments, but also that understanding crystallisation as a non-equilibrium self-assembly process with its associated free energy sheds light on the reason for the chiral symmetry breaking that lies in the dissipation-induced changes in the activation energy of nucleation, according to ref. 32.
It is clear that unimodal distributions describe systems with negligible symmetry-breaking, while bimodal distributions describe full symmetry-breaking. These distributions differ in the standard deviation of the enantiomeric excess, denoted as σe. In Fig. 6, we represent the order parameter δ = 1 − σe, which accounts for the degree of chiral symmetry-breaking.
 | ||
| Fig. 6 Order parameter for chiral symmetry breaking δ for variations in ΔEa and Δn as a function of the stirring rate α. | ||
We observe a similar behaviour of δ for both types of variations. For very low agitation (α ≤ 1), δ tends to zero, indicating negligible symmetry-breaking. For 1 < α ≤ 2, there is a transition from unimodal to bimodal distribution, resulting in quasi-uniform and trimodal distributions, as shown in Fig. 5(c) and (d). This transition takes place for 0 < δ ≤ 1/3 whereas for 2 < α ≤ 4.5, the system starts to exhibit enantiopure populations, corresponding to 1/3 < δ < 4/5. Finally, there is a threshold value for the agitation degree (α ≈ 4.5), beyond which δ exhibits a jump (from δ = 4/5 to δ = 9/10), and then remains essentially constant with increasing agitation.
Our findings are in agreement with prior studies conducted across various shear rates, and for the same agitation mode, and are consistent with the research conducted by Kim.33 In Kim's study, it was observed that as agitation speed increased, the initial induced enantiomeric excess exhibited a linear rise, while the final enantiomeric excess displayed a sigmoidal behavior, correlating with the initial excess. This indicates a sigmoidal relationship between enantiomeric excess and agitation speed, along with an asymptotic trend beyond a specific agitation speed threshold.
5 Conclusions
By considering crystallisation as a non-equilibrium self-assembly process, we can rationalize the relationship between thermodynamic variables variations (activation energy and nuclei size) and chiral symmetry breaking. This relationship arises because the variations in nuclei size and activation energy in the nucleation stage depend on the non-equilibrium free energy from the non-equilibrium self-assembly formalism, which is calculated from the irreversibilities in the process. Among the variations, those in the activation energy provide the best fit for the experimental results of ref. 14 and of previous theoretical proposals in terms of the enantiomeric excess.7,9,16,32We have shown that it is the degree of agitation, and not just the agitation itself, that determines the extent of chiral symmetry breaking. This relationship is closely linked to variations in both kinetics and energy dissipation. Although stirring is commonly understood to be a crucial factor in the observation and amplification of chiral symmetry breaking, it is important to note that this is not only due to changes in crystallisation kinetics but also to alterations in the non-equilibrium free energy that determine variations in the activation energy during nucleation.
Advances in the study of chiral symmetry breaking may have an impact in for example the production of efficient and safe medicines,31,34,35 the use of liquid crystals in biosensors and microlasers,35 the control of self-assembly for the production of advanced materials36 and synthetic biological tissues,37,38 and in providing a deeper understanding of the emergence of life.8,39
Author contributions
A. A.-R.: designed research, performed research, analysed data, wrote the paper. J. M. R.: designed research, analysed data, wrote the paper. D. B.: designed research, analysed data. All authors reviewed the manuscript.Conflicts of interest
There are no conflicts to declare.Appendix. Stoichiometry
From the kinetics (eqn (5)–(14)) and using the stoichiometry of processes [0]–[4] (10 subprocesses), we can rewrite the fluxes ṙi,j used in the mass balances. The ṙi,j flux gives the rate at which the component i is transformed in the jth process. Renaming components A, L, D, Ln, Dn, M, E, Mm, Em by 1–9 respectively, we obtain | (22) |
 | (23) |
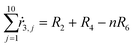 | (24) |
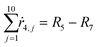 | (25) |
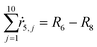 | (26) |
 | (27) |
 | (28) |
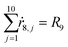 | (29) |
 | (30) |
| CA(0) = CA + CL + nCLn + nCM + mnCMm + CD + nCDn + nCE + mnCEm | (31) |
Acknowledgements
A. A.-R. and J. M. R. are grateful for the financial support of MICIU (Spanish Government) under grant No. PID2021-126570NB-I00.Notes and references
- A. Smith, Speed read: The Importance of Asymmetry, 2008, https://www.nobelprize.org/prizes/physics/2008/speedread/, Last accessed Wed. 10 Nov 2021 Search PubMed.
- E. W. Kolb and S. Wolfram, Astrophys. J., 1980, 239, 428–432 CrossRef CAS.
- G. An, P. Yan, J. Sun, Y. Li, X. Yao and G. Li, CrystEngComm, 2015, 17, 4421–4433 RSC.
- R. A. Hegstrom and D. K. Kondepudi, Sci. Am., 1990, 262, 108–115 CrossRef.
- P. Cintas and C. Viedma, Chirality, 2012, 24, 894–908 CrossRef CAS PubMed.
- T. Buhse, J.-M. Cruz, M. E. Noble-Terán, D. Hochberg, J. M. Ribó, J. Crusats and J.-C. Micheau, Chem. Rev., 2021, 121, 2147–2229 CrossRef CAS PubMed.
- J. M. Ribó, D. Hochberg, J. Crusats, Z. El-Hachemi and A. Moyano, J. R. Soc., Interface, 2017, 14, 20170699 CrossRef PubMed.
- H. Kuhn, Curr. Opin. Colloid Interface Sci., 2008, 13, 3–11 CrossRef CAS.
- D. K. Kondepudi and K. Asakura, Acc. Chem. Res., 2001, 34, 946–954 CrossRef CAS PubMed.
- L.-C. Sögütoglu, R. R. Steendam, H. Meekes, E. Vlieg and F. P. Rutjes, Chem. Soc. Rev., 2015, 44, 6723–6732 RSC.
- H. Niinomi, T. Sugiyama, M. Tagawa, S. Harada, T. Ujihara, S. Uda, K. Miyamoto and T. Omatsu, Cryst. Growth Des., 2018, 18, 4230–4239 CrossRef CAS.
- J. M. Ribó, J. Crusats, Z. El-Hachemi, A. Moyano, C. Blanco and D. Hochberg, Astrobiology, 2013, 13, 132–142 CrossRef PubMed.
- J. M. Ribó and D. Hochberg, Phys. Chem. Chem. Phys., 2020, 22, 14013–14025 RSC.
- D. K. Kondepudi, R. J. Kaufman and N. Singh, Science, 1990, 250, 975–976 CrossRef CAS PubMed.
- C. Viedma, Phys. Rev. Lett., 2005, 94, 065504 CrossRef PubMed.
- M. Rekharsky and Y. Inoue, J. Am. Chem. Soc., 2000, 122, 4418–4435 CrossRef CAS.
- A. Arango-Restrepo, D. Barragán and J. M. Rubi, Phys. Chem. Chem. Phys., 2018, 20, 4699–4707 RSC.
- A. Arango-Restrepo, D. Barragán and J. M. Rubi, J. Phys. Chem. B, 2021, 125, 1838–1845 CAS.
- A. Arango-Restrepo, J. M. Rubi and D. Barragán, J. Phys. Chem. B, 2018, 122, 4937–4945 CrossRef CAS PubMed.
- I. Pagonabarraga and J. M. Rubi, Physica A, 1997, 237, 205–219 CrossRef CAS.
- D. Reguera, J. M. Rubí and J. M. G. Vilar, J. Phys. Chem. B, 2005, 109, 21502–21515 CrossRef CAS PubMed.
- G. J. M. Koper, J. Boekhoven, W. E. Hendriksen, J. H. Van Esch, R. Eelkema, I. Pagonabarraga, J. M. Rubí and D. Bedeaux, Int. J. Thermophys., 2013, 34, 1229–1238 CrossRef CAS.
- G. D. Botsaris, E. G. Denk, G. S. Ersan, D. J. Kirwan, G. Margolis, M. Ohara, R. C. Reid and J. Tester, Ind. Eng. Chem., 1969, 61, 86–113 CrossRef CAS.
- H. D. Laufhütte and A. Mersmann, Chem. Eng. Technol., 1987, 10, 56–63 CrossRef.
- A. Bejan, G. Tsatsaronis and M. Moran, Thermal Design and Optimization, John Wiley and Sons. Inc. New York, 1996 Search PubMed.
- M.-O. Coppens, Curr. Opin. Chem. Eng., 2012, 1, 281–289 CrossRef CAS.
- E. Magnanelli, S. B. B. Solberg and S. Kjelstrup, Chem. Eng. Res. Des., 2019, 152, 20–29 CrossRef CAS.
- A. Bejan, Int. J. Therm. Sci., 1999, 38, 653–663 CrossRef CAS.
- L. M. Martyushev and P. S. Terentiev, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 041604 CrossRef CAS PubMed.
- Y. D. Bensah and J. Sekhar, Curr. Opin. Chem. Eng., 2014, 3, 91–98 CrossRef.
- M. Szurgot, Crystallization and Materials Science of Modern Artificial and Natural Crystals, InTech, Rijeka, Croatia, 2012, ch. Parity Violation in Unstirred Crystallization from Achiral Solutions Search PubMed.
- A. Arango-Restrepo, O. Arteaga, D. Barragán and J. M. Rubi, Phys. Chem. Chem. Phys., 2023, 25, 9238–9248 RSC.
- J. Ahn, D. H. Kim, G. Coquerel and W.-S. Kim, Cryst. Growth Des., 2018, 18, 297–306 CrossRef CAS.
- M. C. Nunez, M. E. Garcia-Rubino, A. Conejo-Garcia, O. Cruz-Lopez, M. Kimatrai, M. A. Gallo, A. Espinosa and J. M. Campos, Curr. Med. Chem., 2009, 16, 2064–2074 CrossRef CAS PubMed.
- J. Jeong, Z. S. Davidson, P. J. Collings, T. C. Lubensky and A. G. Yodh, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 1742–1747 CrossRef CAS PubMed.
- H.-T. Feng, C. Liu, Q. Li, H. Zhang, J. W. Y. Lam and B. Z. Tang, ACS Mater. Lett., 2019, 1, 192–202 CrossRef CAS.
- K. Jakab, et al. , Tissue Eng., Part A, 2008, 14, 413–421 CrossRef CAS PubMed.
- S. A. P. van Rossum, M. Tena-Solsona, J. H. van Esch, R. Eelkema and J. Boekhoven, Chem. Soc. Rev., 2017, 46, 5519–5535 RSC.
- F. Frank, Biochim. Biophys. Acta, 1953, 11, 459–463 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2023 |