Accounting for super-, plateau- and mesa-rate burning by lead and copper-based ballistic modifiers in double-base propellants: a computational study

Abstract

We present a first-principles computational study to understand the action of lead and copper-based ballistic modifiers in the combustion of double-base propellants (DBPs). We show that lead oxide clusters are easily broken down upon addition of small amounts of carbon and the resulting graphitic matrix, dispersed with weakly bound and exposed Pb sites, acts as a Lewis acid to bind small molecule Lewis bases such as NO₂ and CH₂O that form in the combustion flame. This accounts for super-rate burning, where the fuel burn rate is enhanced. We also show how carbon availability accounts for the plateau- and mesa-rate burning effects, where the fuel burn rate is suppressed. In contrast, cluster integrity on binding carbon to copper oxide is retained, and interaction with NO₂ and CH₂O is essentially negligible. Carbon binds more strongly to copper oxide, however, and we therefore propose that when carbon levels start to fall this results in the lead oxide clusters being starved of carbon, which leads to plateau and mesa burning. Taken together, the calculations support a general model that accounts for the super-, plateau- and mesa-rate ballistic modifier burning effects.

---

Introduction

Double-base propellant (DBP) systems are solid rocket propellants typically containing the energetic polymer nitrocellulose plasticised with nitroglycerin, that find application in missile and rocket propulsion due to their rapid energy release and expansion of smokeless gaseous combustion products.^1,2 Homogeneous DBPs have a simple one-dimensional combustion wave, and the burning rate r can be represented by Vieille's law, according to:

r = apⁿ (1)

where a is a constant dependent on the chemical composition and the initial propellant temperature, p is the combustion chamber pressure, and n is the pressure exponent of the burning rate.^1,3 The burning rate is therefore very sensitive to changes in pressure, as shown in Fig. 1(a). In order to counteract this effect, ballistic modifiers (also known as burn rate catalysts)⁴ are added to the propellant system, which alter the burning behaviour of the propellant in three distinct ways.⁵ First, in the low-pressure range it enhances combustion, in a process termed super-rate burning, where typically 0.8 < n < 2.0.^6,7 This heightened burn rate provides more thrust at the start of launch. Second, as the gas pressure increases, super-rate burning rapidly dissipates, to produce either a plateau (0 < n < 0.2) where the propellant burns with greater control as the dependency on pressure is reduced, or a decrease in burn rate (n < 0); the latter phenomenon is termed mesa-rate burning.^2,3,8 Finally, at higher gas pressures, the burn rate returns to approximately the level of the unmodified propellant.

Fig. 1 Burning rate-pressure relation (a) for non-catalysed and catalysed DBP (Copyright AIAA, 1974),⁹ and (b) influence by lead and copper oxide ballistic modifiers (Copyright Springer, 1995).¹⁰

The first ballistic modifiers that were identified were lead oxides and aliphatic lead salts,¹¹ and further addition of either carbon black or the use of aromatic lead salts was found to advantageously produce a larger plateau zone that extended to higher operating pressures.¹² To date, only lead-based compounds have been found to support all three burn-rate effects.¹³ The further addition of copper salts pushes super-rate burning to higher pressures that inevitably results in a pronounced mesa burning effect, as shown in Fig. 1(b);^10,14 the combined use of lead- and copper-based ballistic modifiers are considered as industry-standard formulations for DBPs.

The role of the ballistic modifier on the DBP combustion mechanism outlined above has recently been reviewed,¹³ and the literature consensus points towards involvement at the solid/gas boundary (known as the burning surface) of the propellant.^6,15,16 Several theories attempt to account for both the super-rate and plateau-burning mechanisms, with the most comprehensive being the carbon-soot theory. This postulates that the lead salts decompose below the burning surface¹⁷ and alter the alkoxyl radical decomposition pathway of the DBP to favour the formation of carbon-soot at the burning surface.^{9,13,15,16,18} The resulting carbon matrix incorporates dispersed Pb particles (of lead or lead oxide),^15,19 and is attributed to supporting super-rate burning.^13,16,18 The subsequent loss of the carbon matrix with increasing pressure dampens the catalytic effect and is therefore thought to induce the plateau-burning effect.^13,16,18

The continued dependence on lead additives in DBP formulations is problematic as this highly toxic element presents hazards in its use and disposal, and impending European Union regulations (REACH – registration, evaluation, authorisation and restriction of chemicals)²⁰ will soon ban their use. As no current alternative exists, the aims of this study are to use computational modelling to understand how lead and copper, present in the form of metal oxide clusters, interact with carbon and small molecules such as CH₂O and NO₂ that are known to form in the combustion flame. The results from the simulations allow us to build upon the carbon-soot theory, to offer atomistic interpretations that account for the onset of the super-, plateau- and mesa-burn rate effects.

The paper is organised as follows. In the first instance, a library of lead oxide clusters has been generated via ab initio random structure searching (AIRSS), to present a plausible range of structures that could form at the burning surface of a DBP combustion flame. The influence of adding increasing amounts of carbon atoms to the clusters is then reported, alongside an investigation into the binding and activation of CH₂O and NO₂. An analogous investigation is also reported for the stable copper oxide cluster Cu₅O₅, to establish how it differs from lead oxide. We then propose a catalytic burn rate profile that accounts for the unique ability of lead-based ballistic modifiers to create super-, plateau- and mesa-burn rate effects.

Computational methodology

Ab Initio Random Structure Searching (AIRSS)²¹ integrated with the DFT code CASTEP,²² was used to locate the lowest energy configurations for all clusters. For the initial generation of a library of metal oxide clusters, structures were generated through placement of atoms randomly within a sphere large enough to contain the whole cluster thus generated, which in turn was present in a 20 Å cubic periodic boundary box. The only constraints placed on atom positions were on the minimum distances between atom types (set to 2, 1.5 and 1.0 Å for Pb⋯Pb, Pb⋯O and O⋯O distances, respectively, to reduce the risk of nonsensical structures or O₂ repeatedly randomly forming). For the carbon binding study only the carbon atoms were randomly placed (within a minimum and maximum distance of 0.8 Å to 4.0 Å away from oxygen atoms) around selected stable metal oxide clusters. For each cluster type investigated by AIRSS at least 50 optimised structures were obtained.

For all CASTEP calculations, the ultrasoft pseudopotentials²³ were generated “on the fly”, with Γ-point Brillouin zone sampling. For the first round of structure searching, convergence criteria were set at 0.05 eV Å⁻¹, 0.1 GPa, 0.05 Å and 5 × 10⁻⁴ eV per atom for force, stress, ionic displacement and energy, respectively. The cut-off energy was set to 400 eV. Higher level optimisation calculations (energy cut-off 800 eV, optimisation criteria 0.01 eV Å⁻¹, 0.02 GPa, 0.005 Å, and 5 × 10⁻⁶ eV per atom, for force, stress, ionic displacement and energy, respectively) were then run for the lowest energy structures. For all calculations, the PBE GGA functional²⁴ was applied, along with the TS dispersion correction scheme.²⁵

Local force constants were calculated using LMODEA,^26–28 following geometry optimization and frequency calculation performed in Gaussian16 using the SDD/def2-TZV basis set and PBE0 functional with Grimme D3BJ dispersion.^29–31 The resulting optimisations were analysed in Multiwfn to obtain the HOMO–LUMO gaps and orbital contributions to the LUMO,³² using Stout-Politzer population analysis for the latter. The relative stability of the clusters was determined from their binding energy per atom, defined as:

where E(M), E(O), and E(M_xO_y) are the total energies of an isolated metal atom, an isolated oxygen atom and the M_xO_y metal oxide cluster, respectively. Variation in spin states for all clusters was probed, with the two most stable electron configurations investigated for all clusters within the ca. 250 kJ mol⁻¹ lowest energy structures. The energy rankings shown in the ESI† have been obtained from Gaussian16; the most stable spin state for each M_xO_yC₁₂ cluster has been utilised for the LMODEA analysis.

The same model chemistry was used for the CH₂O and NO₂ binding study, according to the following equation:

Binding energy (ΔG) = E(AB) − E(A) − E(B) (3)

where E(AB) is the total energy of the molecule-bound system, and E(A) and E(B) are the total energies of the separated fragments respectively. Negative values indicate favourable attachment. Basis set superposition errors (BSSE) have been accounted for using the standard counterpoise correction, as well as zero point thermal free energy corrections as calculated by Gaussian16.

Results and discussion

Building lead oxide cluster library

Stable lead oxide clusters (Pb_xO_y, where x ≤ 6, y ≤ x + 3) were created using AIRSS and DFT optimisation, with an example energy ranking plot shown in Fig. 2 for Pb₄O₄. The cubane structure was generated >20 times out of 80 obtained clusters, providing confidence that the global energy minima has been found. This methodology was pursued for the rest of the cluster series, with full results given in the ESI.† Metal oxide laser ablation and mass spectrometric vaporization studies indicate that (PbO)_x (x = 1–4) clusters are particularly stable^33–37 and this was echoed here through favourable calculated binding energies and HOMO–LUMO energy gaps (see ESI†). Due to its inherent stability, structures based on Pb₄O₄, which is also attributed as a building block for larger lead oxide clusters,³⁷ was taken forward for further analysis. In order to explore the effects of structure variation, due to the non-equilibrium conditions in a combustion flame, two further clusters with increasing oxygen content were also included (see Fig. 3).

Fig. 2 Relative energies of Pb₄O₄ clusters obtained by AIRSS/DFT vs. number of structures generated. Colour scheme: Pb (dark grey), O (red).

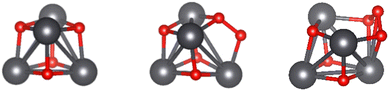Fig. 3 Global minimum energy structures of Pb₄O_4–6 series found by AIRSS/DFT. Colour scheme: Pb (dark grey), O (red).

Carbon binding study to Pb₄O_4–6

The carbon-soot theory postulates that the addition of lead-based ballistic modifiers to DBPs results in the growth of large amounts of carbon filaments at the burning surface, which flake off into the gas zone.^6,16 It is thought that the growth, and subsequent loss, of this carbon layer plays a key role in controlling the onset of plateau-burning.^7,13,18 To explore the effect of carbon on the Pb₄O_4–6 clusters we have added low numbers of carbon atoms, in three-atom units up to a total of twelve atoms, using AIRSS/DFT. The resulting energy ranking of structures formed was very broad (see ESI†), with no single lowest-energy structure created more than once, despite typically >50 optimised structures being obtained for each cluster type. An example is given in Fig. 4, where the energy landscape obtained for Pb₄O₄C₁₂ clusters obtained within a window of ca. 250 kJ mol⁻¹ of the lowest energy structure is presented. A common feature of all clusters formed is the insertion of carbon into Pb–O bonds to create short chains that terminate in C–O bonds. For the high carbon content clusters shown in Fig. 4, the lower energy structures feature graphitic carbon nets; this is in contrast to the lower carbon content (3–6 atoms) clusters that typically grew short-chain carbon wires, resulting in the Pb₄O₄ cubane structure remaining largely intact. The cluster series generated on addition of nine carbon atoms contained a mixture of carbon wires and graphitic nets (see ESI†). The Pb₄O_5-6 clusters followed the same trends (see ESI†). The lowest energy structures obtained for each cluster type are given in Fig. 5; for the high carbon content structures representatives of both the net and wire structures, along with approximate energy separations, are also given.

Fig. 4 Energy landscape of Pb₄O₄C₁₂ clusters found by AIRSS/DFT. Colour scheme: Pb (dark grey). C (gold), O (red).

Fig. 5 Low energy structures Pb₄O_4–6 clusters, and representative structures obtained by AIRSS/DFT upon subsequent addition of carbon atoms. Colour scheme: Pb (dark grey), C (gold), O (red).

While the amount of carbon included in these models is small compared to experimental levels,^19,38 it sets a level of expectation that the addition of more carbon would likely create graphitic-type structures. It is also evident from Fig. 5 that the formation of graphitic carbon structures results in the destruction of the metal oxide cluster, and the metal atoms are more exposed compared to the carbon-free structures. Pb⋯Pb bond distances typically increase from ca. 3.5 to 4–8 Å upon addition of twelve carbon atoms (see ESI†). This finding is in agreement with a solid-state modelling study of PbO, where oxygen abstraction was observed upon contact with an amorphous carbon layer.³⁹

The strengths of the individual bonds within the clusters can be gauged through local (mass independent) force constants for each bond type (Fig. 6 and ESI†).^26–28 This plot explains the general observations obtained in the AIRSS/DFT study, where oxygen extraction to create strong terminal C–O bonds, alongside strong C–C bonds, provides the thermodynamic driver for the reaction. Overall, weak Pb–O bonds are replaced by longer Pb–C bonds of comparable strength (1.0 ± 0.4 mDyn Å⁻¹), thus further exposing the metal atom sites.

Fig. 6 Plots of bond length vs. local force constants for the 29 most stable Pb₄O_4–6C₁₂ clusters.

Carbon binding study to copper oxide cluster Cu₅O₅

Next, we studied how copper oxide interacts with carbon. The lead oxide study described above showed that the primary findings were independent of cluster choice: adding carbon to different lead oxide clusters always resulted in similar observations of cluster degradation. Therefore, for this AIRSS/DFT study, a single stable cluster of copper oxide, Cu₅O₅, which had previously been reported both experimentally and computationally,^40,41 was employed as the baseline model. The full potential energy ranking of all structures generated by AIRSS/DFT is reported in the ESI;† trends that unite all low energy structures within a window of ca. 250 kJ mol⁻¹ are discussed here. Representative geometries of the lowest energy structures are given in Fig. 7; for the higher carbon content structures examples of both carbon wires and nets are given, along with an approximate energy separation between the structure types.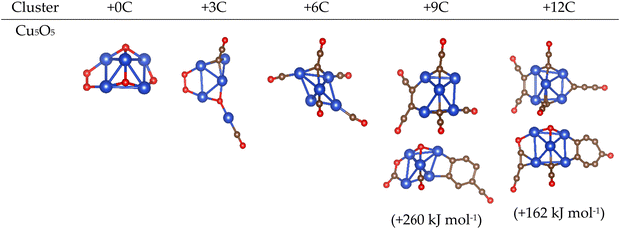

Fig. 7 Representative low energy structures for Cu₅O₅C_0–12 clusters obtained by AIRSS/DFT. Colour scheme: Cu (blue), C (gold), O (red).

In common with lead oxide, the addition of three carbon atoms resulted in oxygen abstraction from the copper oxide cluster (Fig. 7). Results diverge thereafter: whereas lead oxide clusters support the formation of graphitic carbon nets, for copper oxide further addition of carbon results in the formation of more carbon wires through further oxygen abstraction. Whilst graphitic-type structures were obtained upon addition of nine and twelve carbon atoms, carbon growth was generally observed to occur on the cluster surface. This is in contrast to the lead oxide clusters (Fig. 5) where graphitic carbon forms inside the cluster. Consequently Cu⋯Cu distances are largely unchanged by the build-up of the carbon structures (see ESI†).

Analysis of local force constants for the individual bond types found for the 26 low energy structures for Cu₅O₅C₁₂ are given in Fig. 8(a), and show that the thermodynamic drivers for carbon insertion are still C–O and C–C bond formation. In Fig. 8(b) the local force constants for the Pb–C and Cu–C bonds have been plotted for direct comparison. From this it is clear that the Cu–C bonds formed are, on average, stronger than Pb–C (1.6 ± 0.5 mDyn Å⁻¹vs. 1.0 ± 0.4 mDyn Å⁻¹).

Fig. 8 (a) Plots of bond length vs. local force constants for the 26 most stable Cu₅O₅C₁₂ clusters and (b) replotting of data for Cu–C and Pb–C bonds, for direct comparison.

Small molecule binding study to metal oxide clusters: NO₂ and CH₂O

The combustion chemistry at the burning surface is thought to be dominated by the reactions of aldehyde fragments, alkoxyl radicals and NO₂ to form the combustion products CO₂, N₂ and H₂O.^42,43 Herein, we focus on the potential for the metal oxide clusters to bind and activate CH₂O and NO₂, gauged through evaluation of binding energies and N–O/C–O bond weakening effects.

The empty p-orbital character in the LUMOs for Pb₄O₄ and Pb₄O₄C₁₂ shows that both have the potential to act as Lewis acids to bind small (Lewis base) molecules such as CH₂O and NO₂ (Fig. 9). This is balanced, however, against the location of prominent lone pairs on the lead atoms that originate from the HOMOs of the clusters, as shown by electron localisation function plots (ELFs), which are probability functions for pairs of electrons. These plots also show how cluster degradation exposes the Pb sites for small molecule binding. Small contributions from the Cu d-orbitals can be observed in the LUMO of Cu₅O₅, while the LUMO of Cu₅O₅C₁₂ is dominated by empty orbitals on C and O atoms on the outside of the cluster. The ELF plots show electron pairs are located over the carbon, oxygen framework.

Fig. 9 LUMOs (top) and ELFs (bottom) for (left to right) Pb₄O₄, Pb₄O₄C₁₂, Cu₅O₅ and Cu₅O₅C₁₂.

In total, three cluster types have been considered for the binding of small molecules to lead oxide clusters: the parent Pb₄O_4–6 structures from our cluster library, along with representative carbon-wire clusters obtained for Pb₄O₄C₉, and carbon-net clusters obtained for Pb₄O₄C₁₂. For the binding study of copper oxide, the only carbon-bound system investigated was the wire-type, as the net-type structures were consistently greater than 150 kJ mol⁻¹ higher in energy. In this way, a range of models are explored to probe the structural response to varying levels of available carbon. Results are presented in Fig. 10, with further details in the ESI.†

Fig. 10 Binding energies for NO₂ (top) and CH₂O (bottom) to lead oxide clusters (blue) and copper oxide clusters (red) with varying carbon content for Pb₄O₄ and Cu₅O₅.

The binding strength of NO₂ and CH₂O to the lead oxide clusters progressively decreases as the amount of carbon present falls. This is particularly significant for NO₂, where some binding sites in Pb₄O₄C₁₂ even result in N–O bond cleavage (see ESI†). No favourable binding sites for NO₂ could be found for Pb₄O₄ (although some were observed for Pb₄O₅ and Pb₄O₆, see ESI†). For CH₂O, binding to Pb₄O₄C₁₂ results in favourable adsorption, while binding to Pb₄O_4–6 is weak; this agrees with previous reports.^44,45 Reactions between lead oxide and formaldehyde have been previously reported.^46,47 The carbon-wire cluster Pb₄O₄C₉ shows intermediate binding energies for both NO₂ and CH₂O. Taken together these results suggest that carbon activates the lead oxide clusters for small molecule binding by destroying the cluster integrity to expose more open metal sites, and that the effect is dependent on the quantity of carbon present. Local-mode analysis confirms that the C–O and N–O bonds weaken on binding to any of the lead oxide clusters (see ESI†).

Fig. 10 also shows that the binding energies for both NO₂ and CH₂O to Cu₅O₅ are weak and largely invariant with carbon content. For CH₂O the most energetically favourable binding sites were across Cu–O bonds; copper oxide has previously been reported to oxidise formaldehyde.^48,49 For NO₂, as carbon is introduced to the structures, a preference for NO₂ binding to carbon sites is found compared to Cu binding.

Accounting for the super-rate, plateau- and mesa-burning effects by ballistic modifiers in DBPs

These calculations support a carbon-activated route for lead oxide clusters that influences the chemistry occurring in the combustion flame of DBPs. This information, along with observations from the literature, can now be brought together to postulate the variation in modifier activity via four important behaviours, as summarised in Fig. 11(a). The first denotes the low-pressure, super-rate burning effect (i), which reaches a peak (ii) with respect to activity of the modifier as the amount of carbon in the flame steadily increases to a maximum – an effect well documented in the literature.^14,38,50,51 After the maximum, the effect of the modifier diminishes as higher gas pressures are reached and the carbon levels fall (iii); this follows directly from the carbon-soot theory, i.e. the reduction of carbon levels from the burning surface is responsible for the drop in burn rate.^13,18,52 The final feature we construct on the burn rate profile is a sharp drop (iv) denoting an abrupt and complete loss of the carbon matrix, i.e. deactivation of the modifier. Summing this activity profile with the underlying burn rate of the propellant with respect to increasing pressure generates the total burn rate of the ballistic-modified DBP system, which supports super-, plateau- and mesa-burn rate effects (Fig. 11(b) and Fig. 1).

Fig. 11 Plots of (a) proposed modifier activity profile (orange line) against pressure for a burn rate modifier in a DBP, (b) the unmodified burn rate (blue line) and the resulting total burn rate (green line) showing super-rate, plateau- and mesa-burning effects. Plots (c) and (d) show variations in the activity profile resulting in subsequent loss of the mesa- and plateau-burn rate effects, respectively.

Applying this activity profile to the simulations we have performed, these results suggest that super-rate burning occurs due to high levels of carbon-activated lead oxide clusters catalysing exothermic reactions with small molecules such as NO₂ and CH₂O. This results in a rapid rise in temperature of the combustion flame. It is known that lead oxide alone is a poor ballistic modifier, requiring the addition of carbon-soot to the formulation to support the onset of super-rate burning.³⁸ Moreover, it is also well known that aromatic lead salts, such as lead salicylate, produce longer plateau-burning responses which extend to larger pressures, compared to aliphatic lead salts such as lead stearate.^{11,12,14,52,53} This long-standing observation can now be attributed to the presence of pre-formed stable aromatic carbon structures to activate lead oxide. Super-rate burning stops when carbon levels fall. The variation in NO₂ and CH₂O binding strengths to lead oxide with varying carbon content shown in Fig. 10 follows a similar profile to loss of catalytic activity in Fig. 11(a), and we therefore propose that this is the reason for the onset of the plateau in the burning profile. Lastly, we attribute the weak nature of the Pb−C bonds, compared to e.g. Cu−C (Fig. 8(b)) for the mesa-burn rate effect, as the carbon and lead part company and are lost from the flame. Thus the three burn-rate effects can all be accounted for by the build-up and loss of carbon, and its consequent effect on activating and deactivating lead oxide for small molecule binding.

This model for ballistic modifier behaviour also highlights some important observations that go some way towards explaining why the task of finding lead-free ballistic modifiers capable of supporting all three burn-rate effects has proven to be such a difficult task. Firstly, it explains why super-rate burning is relatively straightforward to achieve, as any additional effect from the ballistic modifier will simply boost the underlying propellant burn rate. Plateau- and mesa-burning, however, only occur due to a delicate balance of competing effects. Fig. 11(c) illustrates that the mesa-effect is lost if sudden modifier deactivation does not occur, while Fig. 11(d) makes the point that a true plateau-effect is only achieved if the rate of loss of modifier activity matches the rise in propellant burn rate.

This context also provides a platform to account for the variation in DBP burn rate when copper oxide is added as a second ballistic modifier (Fig. 1). Firstly, the super-rate burning effect is enhanced. This can be directly attributed to an increase in the amount of carbon present, an effect previously noted in the literature where the highest carbon content combustion flames were reported for a Pb/Cu ballistic modifier combination.¹⁰ Secondly, the loss of a plateau-effect and an early onset mesa-effect can now be interpreted as due to a much more rapid loss of carbon from the activated lead oxide clusters. Given that this work has highlighted the stronger nature of Cu−C bonds compared to Pb−C, we therefore propose that copper oxide provides a stronger thermodynamic sink for carbon as levels drop, effectively starving the lead oxide clusters of carbon, resulting in rapid deactivation for small molecule binding.

Conclusions

This computational study has provided evidence to understand the effects of lead and copper-based ballistic modifiers on the combustion chemistry of double-base propellants. Working within the assumption that the modifiers present as metal oxide clusters in the hot combustion flame, our calculations have shown that lead oxide clusters are activated for small molecule binding by the addition of carbon, while copper oxide is not. Our calculations also suggest a sliding scale of small-molecule binding and activation exists for lead oxide which is dependent on the amount of carbon present. We have also shown that copper oxide binds carbon more strongly than lead oxide; thus when carbon levels start to fall the lead oxide clusters will become starved of carbon, inducing deactivation for the binding of small molecules.

We have also derived a general activity profile for ballistic modifiers that builds on the carbon-soot theory and accounts for the super-, plateau- and mesa-rate burning effects. It also goes some way towards explaining why plateau- and mesa-rate burning are hard effects to achieve, and therefore why the search for lead-free alternatives has proven so challenging. We hope that these new insights hasten the search for non-toxic alternatives to lead-based ballistic modifiers for DBPs.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

All authors kindly acknowledge Mr Martin Sloan (UK MoD) for insightful discussions, and Prof. E. Kraka (Department of Chemistry, Southern Methodist University, Texas) for early access to their local mode analysis software, LMODEA. Research was sponsored by UK MoD through WSTC1085. This work has made use of the resources provided by EaSTCHEM Research Computing Facility and the Edinburgh Compute and Data Facility (ECDF) (https://www.ecdf.ed.ac.uk/). We are grateful for computational support from the UK Materials and Molecular Modelling Hub, which is partially funded by EPSRC (EP/T022213/1, EP/W032260/1 and EP/P020194/1), for which access was obtained via the UKCP consortium and funded by EPSRC grant ref EP/P022561/1.

References

1. H. Shekhar, Cent. Eur. J. Energ. Mater., 2012, 9, 353–364.
2. H. Austruy, in Solid Rocket Propulsion Technology, ed. A. Davenas, Elsevier Ltd, 1993, pp. 369–413.
3. N. Kubota, Propellants and Explosives: Thermochemical Aspects of Combustion, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2015.
4. J. Kalman, Propellants, Explos., Pyrotech., 2022, 47, e202200148.
5. D. R. Greatrix, Powered Flight: The Engineering of Aerospace Propulsion, Springer, London, 2012, pp. 323–379.
6. N. Kubota, T. J. Ohlemiller, L. H. Caveny and M. Summerfield, Symp. Combust., 1975, 15, 529–537.
7. N. Kubota, Symp. Combust., 1979, 17, 1435–1441.
8. G. Lengellé, J. Brulard and H. Moutet, Symp. Combust., 1977, 16, 1257–1269.
9. N. Kubota, T. J. Ohlemiller, L. H. Caveny and M. Summerfield, AIAA J., 1974, 12, 1709–1714.
10. A. P. Denisyuk, L. A. Demidova and V. I. Galkin, Combust., Explos. Shock Waves, 1995, 31, 161–167.
11. R. F. Preckel, ARS J., 1961, 31, 1286.
12. R. F. Preckel, AIAA J., 1964, 3, 346–347.
13. L. R. Warren, Z. Wang, C. R. Pulham and C. A. Morrison, Propellants, Explos., Pyrotech., 2021, 46, 13–25.
14. J. Duterque, J. Hommel and G. Lengelle, Propellants, Explos., Pyrotech., 1985, 10, 18–25.
15. J. Sharma, G. B. Wilmot, A. A. Campolattaro and F. Santiago, Combust. Flame, 1991, 85, 416–426.
16. D. J. Hewkin, J. A. Hicks, J. Powling and H. Watts, Combust. Sci. Technol., 1971, 2, 307–327.
17. H. Singh and R. K. Rao, Proc. Indian. Acad. Sci. U. S. A., 1984, 93, 93–97.
18. C. Youfang, Propellants, Explos., Pyrotech., 1987, 12, 209–214.
19. L. Shufen, Combust. Sci. Technol., 1998, 133, 395–401.
20. Lead REACH Consortium, https://ila-reach.org/.
21. C. K. Pickard and R. J. Needs, J. Phys.: Condens. Matter, 2021, 23, 053201.
22. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570.
23. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
24. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985.
25. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
26. E. Kraka, W. Zou and Y. Tao, WIREs Comput. Mol. Sci., 2020, 10, 1480.
27. D. Cremer and E. Kraka, Curr. Org. Chem., 2010, 14, 1524–1560.
28. W. Zou, R. Kalescky, E. Kraka and D. Cremer, J. Chem. Phys., 2012, 137, 084114.
29. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
30. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, 2016, Gaussian 16, Revision C.01, Gaussian, Inc., Wallin.
31. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
32. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
33. J. S. Ogden and M. J. Ricks, J. Chem. Phys., 1972, 56, 1658.
34. A. Popovič, A. Lesar, M. Guček and L. Bencze, Rapid Commun. Mass Spectrom., 1997, 11, 459–468.
35. G. V. Chertihin and L. Andrews, J. Chem. Phys., 1996, 105, 2561.
36. J. Drowart, R. Colin and G. Exsteen, Trans. Faraday Soc., 1965, 61, 1376–1383.
37. H. Liu, S. Wang, G. Zhou, J. Wu and W. Duan, J. Chem. Phys., 2007, 126, 134705.
38. A. P. Denisyuk, T. M. Kozyreva and V. G. Khubaev, Combust., Explos. Shock Waves, 1975, 11, 271–273.
39. L. R. Warren, C. R. Pulham and C. A. Morrison, Phys. Chem. Chem. Phys., 2020, 22, 25502–25513.
40. G. T. Bae, B. Dellinger and R. W. Hall, J. Phys. Chem. A, 2011, 115, 2087–2095.
41. M. Abdul Latif, J. W. J. Wu, R. Moriyama, M. Nakano, K. Ohshimo and F. Misaizu, ACS Omega, 2018, 3, 18705–18713.
42. R. A. Fifer, Fundamentals of Solid-Propellant Combustion, AIAA, 1984, vol. 90, pp. 177–237.
43. S. Meng, X. Fu, Z. Wang, L. Jiang and J. Wang, Combust. Flame, 2022, 236, 111768.
44. K. C. Salooja, Combust. Flame, 1967, 11, 247–254.
45. Q. Wang, C. Zhang, L. Shi, G. Zeng, H. Zhang, S. Li, P. Wu, Y. Zhang, Y. Fan, G. Liu, Z. Jiang, Z. Liu and Y. Sun, iScience, 2018, 9, 487–501.
46. S. Zou, J. Liu, H. Kobayashi, X. Hu, L. Xiao and J. Fan, Chem. Commun., 2014, 50, 6316–6318.
47. J. Tétreault, J. Sirois and E. Stamatopoulou, Stud. Conserv., 1998, 43, 17–32.
48. J. J. Byerley and W. K. Teo, Can. J. Chem., 1969, 47, 3355–3360.
49. Z. Jusys and A. Vaškelis, Langmuir, 1992, 8, 1230–1231.
50. V. A. Sizov, A. P. Denisyuk and L. A. Demidova, Combust. Sci. Technol., 2021, 00, 1–13.
51. Q. L. Yan, M. Gozin, F. Q. Zhao, A. Cohen and S. P. Pang, Nanoscale, 2016, 8, 4799–4851.
52. N. Kubota, PhD thesis, Princeton University, 1973.
53. H. Singh and K. R. K. Rao, AIAA J., 1977, 15, 1545–1549.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp03197g

---