Ultrafast dynamics in polymeric carbon nitride thin films probed by time-resolved EUV photoemission and UV-Vis transient absorption spectroscopy

Abstract

The ground- and excited-state electronic structures of four polymeric carbon nitride (PCN) materials have been investigated using a combination of photoemission and optical absorption spectroscopy. To establish the driving forces for photocatalytic water-splitting reactions, the ground-state data was used to produce a band diagram of the PCN materials and the triethanolamine electron scavenger, commonly implemented in water-splitting devices. The ultrafast charge-carrier dynamics of the same PCN materials were also investigated using two femtosecond-time-resolved pump–probe techniques: extreme-ultraviolet (EUV) photoemission and ultraviolet-visible (UV-Vis) transient absorption spectroscopy. The complementary combination of these surface- and bulk-sensitive methods facilitated photoinduced kinetic measurements spanning the sub-picosecond to few nanosecond time range. The results show that 400 nm (3.1 eV) excitation sequentially populates a pair of short-lived transient species, which subsequently produce two different long-lived excited states on a sub-picosecond time scale. Based on the spectro-temporal characteristics of the long-lived signals, they are assigned to singlet-exciton and charge-transfer states. The associated charge-separation efficiency was inferred to be between 65% and 78% for the different studied materials. A comparison of results from differently synthesized PCNs revealed that the early-time processes do not differ qualitatively between sample batches, but that materials of more voluminous character tend to have higher charge separation efficiencies, compared to exfoliated colloidal materials. This finding was corroborated via a series of experiments that revealed an absence of any pump-fluence dependence of the initial excited-state decay kinetics and characteristic carrier-concentration effects that emerge beyond few-picosecond timescales. The initial dynamics of the photoinduced charge carriers in the PCNs are correspondingly determined to be spatially localised in the immediate vicinity of the lattice-constituting motif, while the long-time behaviour is dominated by charge-transport and recombination processes. Suppressing the latter by confining excited species within nanoscale volumes should therefore affect the usability of PCN materials in photocatalytic devices.

---

1 Introduction

A major challenge for a successful transition to renewable-energy exploitation is the design and development of efficient and cheap photocatalytic materials.^1,2 Besides being catalytically efficient, suitable candidate materials and composites should ideally contain only Earth-abundant elements, be non-toxic, long-lived, and their production should be easily up-scalable.

Polymeric carbon nitrides (PCN) comprise a class of metal-free, two-dimensional (2D) materials that have been proposed as promising candidates for various energy conversion applications.³ These include hydrogen and oxygen evolution (HER, OER) in the water-splitting reaction,^4–8 CO₂ reduction to produce storable fuels,^9,10 and organic pollutant degradation,^11–13 with prospects to expand their use in photovoltaic, electronic, bioimaging, and sensing applications.^14–16 Depending on the synthetic conditions, the structure of PCN is based on either the s-triazine (1,3,5-triazine, C₃N₃H₃), heptazine (tri-s-triazine, 1,3,4,6,7,9,9b-heptaazaphenalene, C₆N₇H₃), or s-triazine and heptazine core heterocyclic aromatic units, composed of C and N atoms in ring structures.¹⁷ PCN has attracted significant attention due to its photocatalytic performance in the near-ultraviolet and visible (UV-Vis) spectral range, combined with a high flexibility in structural modification, chemical robustness, abundant availability and low cost.¹

Despite the advantages described above, the efficiency of PCN is limited by poor visible-light-harvesting capacity, typically small specific and morphology-dependent surface area (≤10 m² g⁻¹),¹⁸ moderately low quantum yield associated with rapid carrier recombination, and inefficient transport of the photogenerated charge carriers.^19–21 Attempts to improve this situation include structural and chemical modifications, as well as construction of PCN-based heterojunctions and dye sensitisation.^22–25 Despite this, the origin of the photocatalytic activity of PCN, and in particular the dynamics of photogenerated charges is still poorly understood. A number of questions correspondingly arise, which are interrelated (and non-exhaustive).

(A) Nature of the active species

It is clear that reductive reactions, such as HER, utilise negative charges on the catalyst–substrate interface, while oxidative reactions (e.g., OER) require positive charges. Therefore, the recombination of photo-generated electrons and holes must be suppressed in order to facilitate reasonable catalytic yields. Thus, most approaches in heterogeneous catalysis concentrate on efficient charge-separation processes, accompanied by spatial separation of reductive and oxidative reaction sites, including z-scheme reactions.²² It is typically assumed that high carrier mobility is advantageous since it should lead to faster separation and hence lower recombination probability. However, recent theoretical results show that charge separation – especially in the case of triazine/heptazine-based polymers – is not necessarily the ideal approach.²⁶ Hence, it is not a priori clear whether separated charges or excitons are the more desirable outcome of the photogeneration process.

(B) Semiconductor or molecular aggregate

Closely related to (A), heterogeneous catalysts/absorbers are typically assumed to be either metals or semiconductors. While the notion of any non-metallic, condensed material being a semiconductor is valid in the wider sense, it is not necessarily a practical model. In the case of PCN, carrier mobilities are generally found to be fairly low, indicative of hopping rather than band-like transport.²⁷ At the same time, the optical absorption and emission processes in the low photon-energy range appear to be dominated by the network-constituting motif.^27–29 This is especially true for heptazine-based materials like melon,²⁸ while it seems to be less pronounced for triazine-based networks.³⁰ Spectroscopic results indicate that low-energy (≲3.5 eV) excitations result in both localised (excitonic) and charge-separation states in varying proportions.^29,31 Depending on the photon energy of excitation light, PCN may therefore be more appropriately described within a transition regime between a molecular aggregate and (defective/amorphous) semiconductor.

(C) Absorption is not utilisation

While it is clear that every absorbed photon does not result in a catalytic reaction, given losses through trapping and recombination, the former questions imply that there are drastic qualitative differences between different photon energy ranges. The strategy of simply enhancing the visible absorption – e.g., via the formerly mentioned modifications – should therefore be carefully scrutinised.

(D) Choice of spectroscopic tools and correlation with catalytic activity

Previous studies have consistently shown that the correlation between specific surface area and catalytic activity is generally evident for PCN materials. Based on the assumptions mentioned above, one would also expect similar correlations for the lifetime and mobility of the excited species. Given the particulate morphology of most PCN materials, a direct measurement of the latter is often impossible or associated with substantial error margins. In order to access the “true” (i.e., intraparticle) properties of charge carriers, time-resolved optical spectroscopy techniques have been widely utilised as proxies, mainly in the form of time-resolved photoluminescence (TRPL) and transient absorption spectroscopy (TAS).^27,31–33 Both techniques integrate over the whole volume of photoexcited particles; their sensitivity to surface species therefore depends strongly on the specific surface area. Together with the above-mentioned low mobility of excited species, previous studies found minimal correlations between the kinetics of either TRPL or TAS traces and catalytic activity.^32,34 However, the obtained results allowed for the development of various microscopic excitation-transport-relaxation models. Some of these models yielded even quantitative predictions, e.g., for carrier lifetimes and mobilities, which were successfully correlated to catalytic activities.^22,27 Besides the lack of surface selectivity, neither TAS nor TRPL provide direct insight into the absolute energetics of the excited species, i.e. with respect to a well-defined energy reference. This, however, is a crucial quantity for the assessment and optimization of catalytic materials.

In this work, we apply steady-state and femtosecond time-resolved extreme-ultraviolet (EUV) photoemission spectroscopy (PES) to investigate the electronic structure and early-time dynamics of four PCN materials with different morphologies, as described below. The PES technique gives direct access to electron binding energies (BEs) of the ground electronic states of the investigated samples.³⁵ The time-resolved PES (TRPES) variant allows transient, excited-state electron BEs and population dynamics to be probed in addition. In the condensed-phase, these BEs primarily reveal energy gaps between the initial and photo-oxidised final states of the many-body quantum systems, but also include the effects of any static or dynamic sample surface potential on the detected electrons. The interpretation of (TR)PES spectra is therefore often not trivial;^35–37 more details will be discussed below.

In contrast to bulk spectroscopy techniques like TAS, the inherently shallow probing depth of EUV (TR)PES, of just a few nanometres, results in a high experimental surface-sensitivity.³⁸ In femtosecond TRPES experiments, this leads to the alleviation of the light-pulse-temporal-broadening effects observed in TAS for scattering samples, facilitating time resolutions below 100 fs. In order to connect the extended range of measurable quantities afforded by the EUV (TR)PES probe to the literature and current state of the art, femtosecond diffuse-reflectance TAS measurements have been performed on the same samples that were investigated in the TRPES experiments.

Since there are numerous PCNs with different morphologies, porosities, surface functional groups and electronic structure, which cannot be fully tracked by elaborate techniques such as TRPES or TAS, a “representative” choice of samples is important. All of the samples that are investigated here were synthesised using various flavours of the so-called bulk polycondensation method. This route generally yields crystal structures closely resembling melon,^39,40 as opposed to the idealised, fully condensed 2D structure of “g-C₃N₄”.⁴¹ Here, we included one of the few well-established PCN materials derived from a sol–gel route (sg-CN), providing repeatable results in terms of morphology, surface area, and catalytic activity.⁴² Another strategy to obtain high surface area, and thus enhanced photocatalytic activity, is the so-called exfoliation method, which may yield 2D, atomically-thin nanosheets.^43,44 We chose a number of samples, derived from a common bulk synthesis, that comprises atomically-thin porous sheets of oxygen-containing or amino co-functional groups, specifically engineered for enhanced HER.⁴⁵

Although many desired photocatalytic applications, such as water-splitting, involve both reductive and oxidative reactions, it is often beneficial to study the half-reactions separately. In the example of the HER in water-splitting, triethanolamine (TEOA) is often used as a sacrificial agent to quench the radical holes.⁴⁶ To enable this, the mutual energy levels of the photocatalyst and sacrificial agent need to be favourable. Therefore, in this work, we also investigated the ground state energetics of an aqueous solution of TEOA, applying liquid-jet, steady-state PES.^47,48

2 Experimental methods

2.1 Sample preparation

In the present work, four different PCN materials were investigated. Firstly, mesoporous PCN (sg-CN, also referred to in the literature as “sg-CN-6” or “CN-6”) was synthesised and provided by the group of Prof. Arne Thomas from the Technical University of Berlin. The sg-CN powder was synthesised at 550, according to the previously reported procedure.⁴² The sample used in the present study is from the same batch as the material used by Indra et al.³⁴ A second batch of three PCN powders was synthesised and provided by the group of Prof. Bin Zhang from the Tianjin University.⁴⁵ Here, the base “bulk” material (CNB) was synthesised by thermal polymerisation of melamine at 520 °C. From this sample, two exfoliated PCN species with different co-functionalisation were derived. Porous oxygen-rich carbon nitride nanosheets (CNPS–O) were produced by oxidation and etching of the initially produced CNB. Amino co-functionalised, atomically-thin porous PCN sheets (CNPS–NH₂) were synthesised using the same procedure as CNPS–O, with ammonia (NH₃) treatment subsequently implemented to further exfoliate and form –NH₂ groups on the resulting 2D porous nanosheets. Selected properties of the PCN samples are presented in Table 1. It can be seen that, compared to bulk-synthesised material,^18,45 both sol–gel synthesis and exfoliation strategies yield high specific surface areas, S_BET, above 100 m² g⁻¹, as determined by the Brunauer–Emmett–Teller (BET) method.^34,42,45 This is also reflected in the drastically decreasing bulk density, ρ_B, of the materials. Sheet thicknesses, d_sheet, as determined by atomic-force microscopy, tend towards the single-layer regime in CNPS–NH₂, while the other samples exhibit domain sizes in the interplanar direction on the order of 10 nm, comparable to those reported earlier for bulk-condensated PCN.³⁹

Table 1 Selected properties of the PCN samples investigated in this work. Data were taken from the indicated references. Film thicknesses, d_film, were determined from cross-sectional SEM images (see Fig. S1, ESI), and represent average values

Sample	S BET/m^2 g^−1	ρ B/g cm^−3	d sheet/nm	d film/μm
sg-CN^34,42	140	—	5	11.5
CNB^45	8	0.544	16	1.8
CNPS–O^45	48	0.134	10	2.8
CNPS–NH2^45	195	0.012	0.4	1.3

---

For each PCN sample, 10 mg of the respective powder was dispersed in 5 ml of distilled water (18 MΩ cm), followed by a sonication treatment at 35 kHz for two hours to obtain dispersions with a concentration of 2 mg ml⁻¹. 2.2 mm thick, 1 × 1 cm² surface area transparent low-iron sodalime-silica glass substrates with an electrically conductive fluorine-doped tin oxide (FTO) coating (7 Ω sq⁻¹, Solaronix S.A.) were implemented in the measurements. These substrates were sequentially sonicated for 15 minutes in isopropanol and hot distilled water (70 °C). The PCN films were deposited onto the pre-cleaned FTO substrates by drop-casting 20 μl of the respective PCN dispersions, and dried at room temperature. Fig. 1 shows some resulting, representative samples used in both the TRPES and TAS experiments. Additional scanning electron microscopy (SEM) images can be found in Fig. S1 of the ESI.† Room temperature UV-Vis diffuse reflectance spectra of the thin films were recorded using a UV/Vis/NIR spectrophotometer (PerkinElmer, Lambda 950), equipped with an integrating sphere detector module; representative results are shown in Fig. 5.

Fig. 1 Thin-film samples of mesoporous (sg-CN), bulk (CNB), oxygen-containing (CNPS–O) and amino co-functionalised nanosheet PCN (CNPS–NH₂), deposited on FTO-coated glass substrates.

For liquid-jet PES studies of aqueous TEOA, an aqueous solution (750 mM) was prepared at room temperature by dissolving the TEOA solute (≥99% purity, Carl Roth) in Milli-Q water (18.2 MΩ cm resistivity at 25 °C). Sodium chloride (50 mM) was admixed to this solution in order to suppress the effects of extrinsic potentials, such as the liquid-jet streaming potential and ionisation-induced sample charging, in the PES experiments.⁴⁸

2.2 Steady-state and ultrafast EUV TRPES

Fig. 2(a) shows a simplified scheme of the EUV-TRPES experiment. The PES experiments were conducted with the ex situ prepared PCN thin film samples inside an interaction chamber maintained at a residual pressure of 10⁻⁷ mbar. The samples were mounted in a stainless steel holder, which was in electrical contact with the electron spectrometer. The position of the sample in the interaction chamber was adjusted in front of the orifice of the electron spectrometer using a high-precision three-dimensional (3D) manipulator. The spectrometer axis was oriented perpendicular to the EUV beam propagation. The angle of the sample surface with respect to the incident EUV beam and to the spectrometer axis was set to 45°. In the steady-state PES experiments on aqueous TEOA solution, the sample was introduced into the interaction chamber as an in-vacuum vertical, free-flowing liquid-jet (LJ). The 750 mM solution was injected at an actively-stabilised 1 ml min⁻¹ flow rate through a 24 μm orifice diameter glass capillary nozzle, forming a jet that maintained a laminar flow over a length of a few millimetres. Following interaction with the EUV laser pulses, the liquid sample broke down into a droplet train, which was condensed and ultimately frozen in a liquid–nitrogen-cooled cryogenic trap. This allowed a residual pressure of 10⁻⁵–10⁻⁴ mbar to be maintained in the interaction chamber during the experiment. The jet was electrically grounded to the interaction chamber. A cooling system, connected to the liquid-jet rod, allowed the solution sample temperature to be stabilised at 7 °C, prior to injection into the interaction chamber. The position of the laminar region of the jet was adjusted in front of the spectrometer entrance orifice using the 3D sample manipulator.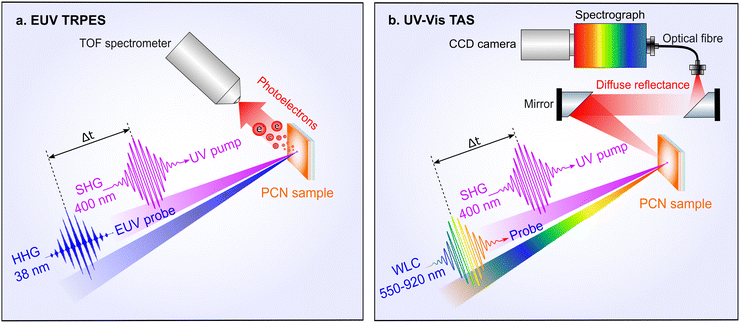

Fig. 2 Simplified schemes of the time-resolved spectroscopy setups. (a) Ultrafast EUV TRPES, (b) ultrafast UV-Vis TAS. See the main text for details.

Ultrashort laser pulses were generated from a femtosecond Ti:Sapphire laser amplifier system (Legend Elite Duo, Coherent Inc.), delivering 2.5 mJ pulse⁻¹ energies, 28 fs (full-width at half-maximum, FWHM) pulse durations, a central fundamental wavelength of 800 nm (1.55 eV photon energy), at a 5 kHz repetition rate. The laser system output was split by a beam splitter into two parts, where 1.5 mJ pulse⁻¹ energies were implemented to generate the EUV probe pulses via frequency up-conversion through the gas-phase high-order harmonic generation (HHG) process. This was achieved by focusing the 800 nm beam into a 4 mm-long, argon-filled gas cell. The argon (Ar) pressure was set to 50 mbar using a dosing valve and a gas feed-through to the gas cell. The cell was sealed with a thin aluminium foil, in which the entrance and exit apertures were created by the focused laser beam. The linearly polarised laser pulses were focused with a CaF₂ lens with a nominal, in-air focal length of 600 mm. The laser focus was positioned just after the exit of the Ar gas cell, to produce a near-IR focal spot size of ≈60 μm (FWHM). To optimise the HHG yield, the peak intensity of the laser pulse at the focus was varied in the range of 10¹⁴–10¹⁵ W cm⁻² by attenuating the high-harmonic-generating laser beam power. In the present experiments, the 21st (32.52 eV/38 nm) or 25th (38.75 eV/32 nm) harmonic of the fundamental frequency were spectrally selected using a reflective zone plate monochromator.⁴⁹ The zone plate is designed to first-order diffract and focus the desired high-order harmonic onto a monochromator slit. A 200 nm thick, meshless aluminium foil spectral filter (Luxel Corp.) was placed after the slit to filter any remaining 800 nm light, which may be scattered down the vacuum beamline. Subsequently, the selected harmonic was redirected and refocused into the sample interaction chamber using a gold-coated toroidal mirror. This resulted in a EUV-beam focal spot size of 60 μm (FWHM). A photon flux of 10⁶ photons pulse⁻¹ and pulse duration of ≈45 fs (FWHM) were respectively measured in the interaction chamber using a photodiode and by applying a cross-correlation technique.⁴⁹

A portion of the remainder of the laser output was used to generate photoexcitation pulses with a 400 nm central wavelength (3.1 eV photon energy). This was achieved using second harmonic generation (SHG) of the fundamental wavelength in a 150 μm thick β-BaB₂O₄ (BBO) non-linear crystal. The produced pump beam was sent through a variable-optical-delay, linear translation stage, allowing the time delay between the optical pump and EUV probe pulses to be tuned over a 2 ns range. Subsequently, the 400 nm beam was focused with a CaF₂ lens with a nominal focal length of 384 mm and reflected into the interaction region by an in-vacuum mirror placed slightly aside the EUV beam path, prior to the interaction region. This resulted in a ∼1° angle between the optical and EUV beams and an on-sample focal spot size of 150 × 210 μm (FWHM) at the sample. Since the sample surface is inclined by 45° within the plane spanned by the laser beams and the spectrometer axis, both the pump and probe spot are elliptical in shape at the sample surface. The pump and probe pulses were spatially overlapped on the sample in front of the orifice of the electron spectrometer. The pump pulse duration was broadened to ≈40 fs (FWHM) in the optical path, as determined from the optical-EUV cross-correlation photoemission (PE) signal. The peak intensity of the pump pulse at the focus was attenuated to suppress multiphoton ionisation, as well as to avoid photochemical degradation of the sample. Typically a pump pulse energy of ∼50 nJ pulse⁻¹, corresponding to a deposited pump pulse energy density of ≈140 μJ cm⁻² and a spatio-temporal peak intensity of 4.6 × 10⁹ W cm⁻² at the focus, was applied in the TRPES experiments on the PCN thin films. The pump and probe beam polarisation axes were oriented parallel to each other and to the spectrometer's time-of-flight axis. The TRPES spectra were recorded by scanning the pump–probe time delay over a range from −400 fs to +2500 fs in 20 fs steps. To improve the signal-to-noise levels, the delay range was swept through 15 times when recording each data set.

The photoelectron kinetic energy spectra were recorded using a commercial time-of-flight (TOF) electron spectrometer (THEMIS 600 EP, SPECS GmbH). The electrostatic lens system inside the spectrometer enables operation in different modes, characterised by different angle and energy acceptance windows and associated resolutions. For the experiments reported here, the spectrometer was operated in three lens modes. The steady-state PE spectra of the PCN thin films, as well as of the aqueous TEOA solution, were recorded using the so-called drift mode (DM). This provided a high energy resolution in a wide kinetic energy range, but with a limited planar photoelectron acceptance angle of ±1° with respect to the spectrometer axis. The transient PE spectra of the PCN thin films were recorded in the wide-angle mode (WAM) and in the low-angular dispersion mode (LADM). The WAM allows acquisition with a high signal-to-noise ratio, due to its large photoelectron acceptance planar angle of ±15°, but over a limited kinetic energy range of 7 eV in the measurements reported here. The LADM was applied to expand the kinetic energy range of the recorded transient spectra to 15 eV, with a lower ±7° angular acceptance and, hence, signal-to-noise ratio. At a kinetic energy of 20 eV, the spectrometer resolutions in the DM, LADM, and WAM were 25 meV, 80 meV, and 110 meV, respectively.

The central photon energy and the spectral bandwidth of the EUV light were inferred from the steady-state PE spectra of Ar gas, recorded prior to each data collection run (Fig. S2, ESI†). The typical spectral bandwidth of the monochromatised 21st and 25th harmonic of the laser, as recorded using the spectrometer LADM was 183 meV and 241 meV, respectively. The temporal overlap between the pump and EUV probe pulses, as well as the time resolution of the TRPES experiments, were defined from the reference cross-correlation (CC) measurements conducted with gas-phase (Ar gas) and solid-phase (thin gold wire) targets before each experiment.^50,51 In the steady-state PES and TRPES experiments, the absolute electron BE scale of the PCN samples was referenced with respect to the Fermi level, E_F, of the samples and the spectrometer via a gold-wire reference measurement. The electron BE scale of the 750 mM aqueous TEOA solution and ref. 50 mM aqueous NaCl solution was energy-referenced with respect to the local vacuum level, E_vac, as well as to E_F, as defined by the energy calibration procedure described in detail in Section 4 of the ESI.†

2.3 Ultrafast UV-Vis TAS

For the UV-Vis transient absorption spectroscopy (TAS) experiments, the setup used by Noda et al. was modified to adopt a diffuse-reflectance geometry.³⁰ A simplified scheme of the setup is shown in Fig. 2(b). The same laser system described in Section 2.2 was utilized for the pump and probe light generation, where the pump light generation was identical to that used with the PES setup. The 400 nm central wavelength pump pulse energies were varied using a half-wave plate and polariser combination. There, the pump beam with ≈45 fs (FWHM) pulse duration was loosely focused to a diameter of 600 μm (1/e²) in the light-sample interaction region. The resulting pump pulse energy density was varied between 42–2120 μJ cm⁻², corresponding to spatio-temporal peak pump pulse intensities of 3.3 × 10⁸ – 1.6 × 10¹⁰ W cm⁻², respectively.

The transient absorption changes were probed over the visible and near-infrared spectral range with a white light continuum (WLC). For this purpose, a commercial femtosecond optical parametric amplifier (OPA, Coherent OPerA Solo) was employed to produce a pump wavelength of 1300 nm with 120 μJ pulse energies. These NIR pulses were suitably attenuated and focused into a 3 mm-thick sapphire crystal to produce WLC probe light in a spectral range spanning 480–1650 nm.³⁰ The WLC probe pulse duration was estimated to be ≈60 fs (FWHM), as determined from the kinetic-model-based analysis of TAS data. The WLC probe beam was focused with a 200 mm focal length concave mirror into the interaction region, resulting in a focal spot size diameter of 300 μm (1/e²) at the sample surface. Care was taken to limit the WLC probe pulse energies to ∼2 nJ, corresponding to a peak intensity of ≈7 × 10⁷ W cm⁻².

The diffuse-reflectance geometry was realised by placing the samples horizontally, and using both pump and probe beams in near-vertical incidence. Although the probe pulses were not further polarised in these experiments, the WLC has predominantly the same linear polarisation as its respective pump pulse, and the polarisations of pump and probe beams were generally set to be parallel. In order to collect only the diffusely reflected part of the probe light, two off-axis parabolic mirrors were used, and the incident beams were steered through a hole in the first (collimating) mirror. It is important that the specular reflected beams leave the setup via this hole, such as not to introduce a non-pump–probe-interaction background to the TAS signals. The remaining diffusely reflected light was focused into a multimode fibre, spectrally dispersed using a Czerny–Turner spectrograph (Shamrock 303, Andor Technology), and detected with a multichannel detector (Newton DU920 P-BEX2-DD, Andor Technology). Since PCN emits substantial amounts of luminescence in the blue-green region, suitable long-pass filters were introduced to prevent detector saturation. This leads to an effective probe range spanning 550–920 nm. Transient spectra were recorded for pump–probe delays between −20 ps and +1800 ps using the optical delay stage, where the delay was imposed on the pump beam. A semi-logarithmic delay scheme was utilised, providing a dense linear sampling during the ultrafast period, and logarithmic sampling afterward.⁵²

3 Results

3.1 Ground state energetics of PCN

The electron BEs of the PCN thin films were determined on an absolute energy scale at the solid-vacuum interface using solid-state PES. Fig. 3 shows the steady-state EUV photoemission spectra of the PCN samples, where the origin of the energy axis is set as the Fermi level, E_F (see Section 4 of the ESI†). Here, and in the subsequent sections, we analyse the data both within molecular orbital (MO) and semiconductor band structure frameworks. The former involves fitting the spectra using a superposition of Gaussian bands, as given bywhere E is the electron BE, w_i is the full-width at half-maximum (FWHM) of feature i, E_i is the central peak position, and A_i is the peak amplitude.

Fig. 3 Steady-state EUV photoemission spectra of the sg-CN, CNB, CNPS–O, and CNPS–NH₂ thin films in the low BE region. The spectra were fitted by a superposition of Gaussian envelopes. The labels 1–4 are assigned to the decomposed emission bands of the PCNs obtained from the multi-component Gaussian fit (Table 2). The VBM position determined for each sample, as extracted from a tangent fit to the PCN signals and the associated low-BE x-axis crossing point (see Fig. S7, ESI†), is indicated by a blue arrow. The electron BE scale is presented with respect to E_F.

The spectra shown in Fig. 3 were fitted using eqn (1) and four Gaussian components, to roughly extract the energetic positions of the spectral bands associated with the lowest-energy ionizing transitions of the PCN samples (see Table 2 for the fit results). A minimum number of Gaussian features was employed in the fits. Due to the broad spectral structure of the photoemission spectra, it is possible that several individual photoemission bands of the PCN samples are represented by a single Gaussian envelope. Remarkably, the three emission bands in the lower BE range (peaks 1–3) could be fitted with the same central positions for all four samples, yielding 3.61 eV, 5.37 eV, 7.66 eV peak centres, respectively, with only the widths and amplitudes varying between the samples. The bands arising at BEs >10 eV (peak 4), which provide most of the total count rate, are best fitted using different parameters for each sample (see Table 2). The PE spectral profile of the CNPS–NH₂ sample is similar to the bare FTO-coated substrate (see Fig. S3, ESI†), although the CNPS–NH₂ higher-BE spectral features are significantly more intense. At low BEs, the underlying photoemission signal from the FTO substrate notably interferes with the analysis of the low-signal-level CNPS–NH₂ data. Thus, the widths and amplitudes of emission peaks 1–3 are larger for the CNPS–NH₂ thin films when compared to the sg-CN, CNB, and CNPS–O samples.

Table 2 Fit parameters of the Gaussian envelopes used to describe the photoemission bands of PCN thin films

Sample	Label	BE/eV	FWHM/eV
sg-CN	1	13.61 ± 0.38	2.09 ± 0.07
	2	15.37 ± 0.37	3.41 ± 0.06
	3	17.66 ± 0.31	2.73 ± 0.05
	4	11.90 ± 0.04	4.62 ± 0.06
CNB	1	13.61 ± 0.39	2.16 ± 0.08
	2	15.37 ± 0.34	2.62 ± 0.14
	3	17.66 ± 0.30	1.71 ± 0.09
	4	10.89 ± 0.29	6.33 ± 0.08
CNPS–O	1	13.61 ± 0.37	2.60 ± 0.06
	2	15.37 ± 0.34	2.95 ± 0.03
	3	17.66 ± 0.29	3.23 ± 0.03
	4	12.78 ± 0.31	5.98 ± 0.22
CNPS–NH2	1	13.61 ± 0.38	4.67 ± 0.22
	2	15.37 ± 0.39	3.84 ± 0.14
	3	17.66 ± 0.32	3.35 ± 0.04
	4	10.73 ± 0.02	3.62 ± 0.06

---

Based on previous studies, we tentatively assign the photoemission bands introduced above as follows. Inoki et al. observed similar photoemission bands, centred at BEs around 3.5 eV, 4.5 eV, and 7.0 eV in their ultraviolet photoemission spectroscopy studies on melon-based and so-called “parvus” carbon nitride thin films.⁵³ In the present study, the spectral bands of the PCN thin films are significantly broader compared to the previously reported results, which leads to a significant overlap of the photoemission bands in the valence spectra of the PCNs. This may be partially due to the comparably broad EUV-source bandwidth and the limited spectrometer energy resolution used in the present experiments. Apart from that, the electronic structure of PCN thin films depends on the local synthetic conditions of the obtained powdered PCN product. Studies on amorphous CN have shown that the energetic position and width of the photoemission bands in the valence spectra depends on the nitrogen content.⁵⁴ Souto et al. attempted to assign the origin of the main features of the valence photoemission spectra of amorphous CN films.⁵⁵ Accordingly, the two photoemission bands centred around 3.61 eV and 7.66 eV BEs can be associated with π-bonding and σ-bonding states, respectively, specifically due to delocalised C 2p electrons. The peak arising at 5.37 eV can be attributed to C–C π-bonding states as well as the localised nitrogen lone pair electrons. The broad photoemission bands centered at >10 eV BEs may be assigned to C–N σ-bonding states.⁵⁵

In addition to the approximate MO decomposition of the photoemission spectra, the position of the valence-band maximum (VBM) of the samples was extracted within a semiconductor electronic structure framework. The VBM values obtained using a tangent derivative-based method (Fig. S7, ESI†), are presented in Table 7, and are shown by the blue, vertical arrows in Fig. 3. For application in photocatalytic water-splitting, the position of the VBM of the PCNs should be low and correspond to a more positive potential than the redox potential of the desired oxidation process.

3.2 Ground state energetics of aqueous TEOA

The valence electronic structure of the TEOA sacrificial agent, which is used as a hole scavenger for PCN photocatalysts in order to achieve a high H₂ evolution rate in the water-splitting reaction, was interrogated at the liquid-vacuum interface using steady-state liquid-jet PES. The details of the analysis procedure are presented in ESI,† Section 4. Briefly, the pre-calibrated PE spectrum of the H₂O solvent was used to calibrate the BE axis,⁵⁶ followed by subtraction of a reference 50 mM aqueous NaCl, NaCl_(aq), solution spectrum from the spectrum of aqueous TEOA, TEOA_(aq), to obtain the PE spectrum of the TEOA solute. As in the majority of LJ-PES experiments, this energy-referencing treatment assumes that the solute (750 mM TEOA_(aq)) has a negligible effect on the electron BEs of the water solvent, which can lead to BE calibration errors on an up to few-hundred-meV scale.⁵⁶

Fig. 4 shows the difference photoemission signal between TEOA_(aq) solution and reference H₂O solvent spectra. The solvent-subtracted signal was fitted using a superposition of two Gaussian envelopes, described by eqn (1), to extract the energy positions of the peaks corresponding to the removal of an electron from the highest occupied molecular orbital (HOMO) and HOMO−1 of the TEOA solute during the photoionisation process. After such a subtraction, two TEOA_(aq) photoemission bands are resolved at 3.35 ± 0.54 eV and 5.44 ± 0.42 eV BEs with respect to E_F. By applying the tangent method, and assuming that the threshold ionisation energy of the TEOA solute is equivalent to its VBM (i.e., assuming a negligible reorganisation energy of aqueous TEOA following photoionisation), the VBM of the sample was also extracted from the recorded liquid-jet PES difference spectrum. The correspondingly extracted VBM value of the TEOA solute is 2.31 ± 0.38 eV. This value differs from the previously reported cyclic and differential pulse voltammetry studies,^57–59 where the irreversible oxidation potential for the TEOA_(aq) solution was found to vary between 0.5 V and 1.07 V (or eV) versus the standard hydrogen electrode (SHE), depending on both the TEOA concentration and the pH of the solution. To our knowledge, no PES studies of the TEOA solute have been carried out so far. A discussion on the difference between voltammetry and PES determinations of oxidation potentials and the PES-determined band alignment of the PCN samples with respect to the TEOA solute will be presented in Section 4.1.

Fig. 4 The difference between the H₂O solvent and the TEOA_(aq) solution spectra. Two low BE photoemission peaks of the TEOA solute are highlighted, as well as the VBM position determined from the derivative-based tangent intersection with the BE-axis (see Fig. S6, ESI†).

3.3 Optical transitions in PCN

The low-energy optical excitations in the thin-film PCN samples were determined using UV-Vis diffuse reflectance spectroscopy. The resulting absorption spectra are shown in Fig. 5. Assuming that the initial excitation is localised, we believe that a molecular electronic structure framework is more appropriate for describing optical transitions in PCN samples. All PCN samples exhibit the characteristic absorption increase in the near-UV (>2.8 eV, <440 nm). These absorption bands have been previously assigned to π → π* transitions of the heterocyclic aromatic constituents in the conjugated ring systems.^29,60,61 Photocatalytic and spectroscopic experiments indicate that these transitions lead to relatively efficient charge-separation, and thus provide the main contribution to the photocatalytic activity in the UV-Vis excitation range.^27,31,33,60 CNPS–O and CNPS–NH₂ show blue-shifted absorption edges, indicating larger HOMO–LUMO (or band) energy gaps as compared to CNB. This can possibly be attributed to quantum confinement,⁶² or a smaller solvatochromic effect, caused by the reduced number of neighbouring heptazine units,⁶³ both of which would ultimately be due to a smaller sheet thickness of the exfoliated samples. The shoulder in the sg-CN sample, which appears at about 2.5 eV, is a typical feature of increased synthesis temperatures.^32,60 It has been initially interpreted as being due to n → π* transitions involving lone pairs on the N atoms of the triazine/heptazine rings.^60,61 More recent theoretical studies indicate that such transitions may also be of π → π* character.²⁹ Both band-band transitions are dipole-forbidden for perfectly symmetric and planar s-triazine or heptazine units, but they become weakly allowed due to vibronic intensity borrowing from higher-lying bright states, and due to structural distortions.^29,61 Such deformations have been shown to become more prominent with higher polymerisation temperature, including effects caused by layer buckling and deviation of the ring units from a trigonal symmetry.^39,40

Fig. 5 Signal-onset regions of UV-Vis absorption spectra of the mesoporous (sg-CN), bulk (CNB), porous ultrathin nanosheets of oxygen-containing (CNPS–O) and amino co-functional groups (CNPS–NH₂) PCN thin films deposited on a FTO-coated glass substrate. The fits (dashed lines) represent a decomposition into Gaussian bands according to eqn (1) (see Table 3). Red arrows indicate the direct band gap energies determined from the data by employing the Tauc method (see Fig. S8, ESI†), and are summarised in Table 4.

In the following, we will quantify these observations using the same framework as used for the steady-state PE spectra. Firstly, within the aforementioned MO picture, the experimental UV-Vis absorption spectra were analysed by fitting a superposition of Gaussian envelopes described by eqn (1). It is noted that a Gaussian envelope is an approximation for the true vibronic envelope of an inhomogeneously-broadened condensed-phase transition. The minimum number of Gaussian envelopes needed to describe the experimental absorption spectra were fitted, which are deemed to correspond to the contributions of individual electronic transitions. As with the PES fits, it is not excluded that two electronic transitions, which cannot be clearly distinguished in the present spectra without the use of theoretical calculations, are modeled by a single Gaussian envelope here. The respective fit results are presented in Table 3. For CNB and CNPS–O, a good description is found using two bands each, centred at similar peak positions, albeit with slightly different amplitude ratios. Only the latter of these two peaks, at 3.22 eV, is needed to describe the spectrum of CNPS–NH₂. This behaviour may be interpreted either as a blue-shift of the π → π* transitions, or a big change in relative proportions between different transitions within this manifold. On the other hand, in sg-CN, the higher-energy spectral range can be described using one considerably broader band, in addition to another broad peak centred at 2.57 eV. This suggests that the two different applied synthesis methods have an effect not only on the morphology, but also on the electronic structure of the PCNs.

Table 3 Fit parameters of the Gaussian envelopes used to describe the low-energy absorption bands of the PCN samples

Sample	Label	E peak/eV	FWHM/eV
sg-CN	1	2.57 ± 0.01	0.53 ± 0.01
	2	3.21 ± 0.01	0.63 ± 0.01
CNB	1	2.97 ± 0.01	0.19 ± 0.01
	2	3.21 ± 0.01	0.39 ± 0.02
CNPS–O	1	2.97 ± 0.01	0.17 ± 0.01
	2	3.23 ± 0.01	0.33 ± 0.01
CNPS–NH2	1	3.22 ± 0.01	0.18 ± 0.01

---

As mentioned above, PCN is typically described within a semiconductor picture. However, it is not clear whether direct or indirect band gaps should be assumed, and consequently one can find values extracted using both assumptions in the literature. Here, we analyse the spectra using Tauc's method for amorphous semiconductors,⁶⁴ and apply the tangent method described above to extract both direct and indirect band gaps, E_g, according to

(αhν)^1/n = C(hν − E_g), (2)

where α is the optical absorption coefficient, hν is the photon energy and C is a proportionality constant. The parameter n depends on the nature of the electronic transition, with n = 1/2 for direct or n = 2 for indirect allowed electronic transitions, respectively.⁶⁵

The results for direct and indirect band gap values are given in Table 4, and the analysis procedure details are presented in the ESI.† Taking this into account, a pump pulse photon energy of 3.1 eV (400 nm) was chosen to initiate the photoinduced electron dynamics in the PCN thin films in the present studies.

Table 4 Band gap energies of the PCN samples for direct and indirect allowed electronic transitions, as determined from the Tauc plots

Sample	E g direct/eV	E g indirect/eV
sg-CN	2.88 ± 0.02	2.71 ± 0.03
CNB	2.95 ± 0.03	2.81 ± 0.01
CNPS–O	3.06 ± 0.01	2.96 ± 0.02
CNPS–NH2	3.13 ± 0.02	3.09 ± 0.01

---

3.4 Excited state TRPES study of PCN thin films

The early-time electron dynamics of the PCN thin films, following photoexcitation at a 400 nm central wavelength, were studied at the surface-vacuum interface using TRPES, both in the WAM and LADM of the spectrometer. The resulting 2D maps – presented here following subtraction of the time-independent, EUV-only PE spectra – are shown in Fig. 6. The relative magnitude of the PE yield is represented by the colour bar in the figures (note that the colour maps associated with the different data sets have been individually normalised). The electron BE scale in Fig. 6 is energy referenced with respect to E_F, as determined from the steady-state PES measurements using the reference Au-wire sample. To enhance visibility of the transient signal, the EUV emission spectrum of the unpumped sample, recorded at negative time delays and averaged over the range between −400 fs and −200 fs, was subtracted as a background spectrum from the data recorded at each time delay. The time zero position was corrected in each delay time scan, according to the peak of the pump–probe cross-correlation (CC) signal arising at early time delays. The CC widths have been respectively determined to be 80 ± 16 fs and 92 ± 13 fs for the WAM and LADM data sets shown here (see Fig. S10, ESI†).

Fig. 6 2D maps of the transient photoemission signal. The data is plotted as a function of the electron BE and pump–probe time delay for the PCN samples recorded in both the WAM (left panels) and LADM (right panels) of the spectrometer. For better visualisation of the transient signal, the time-independent background signal, recorded at negative pump–probe delays, has been subtracted from the data. The transient data was recorded with a pump–pulse fluence of 140 μJ cm⁻². The BE scale is energy-referenced with respect to the sample and spectrometer E_F.

To prevent significant multi-photon ionisation of the sample by the pump pulse and, thus, to reduce the space-charge effect that perturbs the photoemission spectra,^66,67 the pump pulse peak intensity was reduced. Nevertheless, one should note that to achieve reasonable integration times in TRPES experiments with kHz light sources, relatively high pulse fluences are often required. Due to the 5 kHz repetition rate laser source employed in the present experiments, the acquired photoemission signals exhibit a low signal-to-noise ratio. For this reason, the 2D maps in Fig. 6 show rebinned transient data over the BE-axis with bin sizes of 0.25 eV and 0.35 eV for the WAM and LADM, respectively. However, further integration of the transient signal over the different BE ranges gives much better statistics, as shown in the lower panels in Fig. 7.

Fig. 7 Global fit reproduction of the experimental background-subtracted transient photoemission spectra for the sg-CN thin films recorded in the WAM and LADM of the spectrometer with the use of the kinetic model described by eqn (3). The data is energy-referenced with respect to E_F of the sample and the spectrometer. The lower panels show the time dependence of the transient signal integrated over the different BE ranges encompassing the population of the short- and long-lived excited states in the sg-CN sample. The negative contribution to the transient signal, associated with depletion of the ground state, was subtracted from the data (grey circles) and the cumulative fit results (black curves) and is not presented here. A schematic depiction of the PCN photocycle at the surface-vacuum interface following 400 nm optical excitation is also shown in the upper right corner. The rate parameters described in eqn (3), k_1–3, are appended to this depiction.

Generally, the different samples and recording modes show similar features, which are:

1. A strong positive signal (red colour) around zero delay time, which is partially due to the CC.

2. Another positive signal, at negative BE (i.e., energies above E_F) and observed using the spectrometer WAM, with an apparent decay time of a few hundred femtoseconds.

3. A long-lived bleach signal (shown in blue), appearing rapidly at short delay times and from zero towards positive BEs, which is the most prominent feature in both the WAM and LADM data sets.

4. Another positive signal at higher BE, which emerges after a few hundred femtoseconds and is most obvious in the spectrometer LADM.

Features 3 and 4 persist beyond the time scale of the present measurements, out to ≈2.5 ps pump–probe delays. Note that for better visualisation of the positive signal from ionisation of the transient excited states, the relative magnitude of the colour scale of the PE yield differs in the 2D maps presented for the WAM and LADM data. Therefore, the negative values of the transient signal at positive time delays seemingly, but artificially, emerge at different BE ranges in the left and right panels of Fig. 6. Due to the lower collection efficiency, the positive transient signal in LADM is less readily identified in the electron BE range below about 2 eV in comparison to that collected in WAM. This also has an impact on the strength of the positive feature associated with the CC signal from the PCN samples in the vicinity of zero time delay. The energetic position of the CC signal in the transient photoemission spectra recorded in LADM extends over a range from approximately 11 eV to 0 eV BE, being most prominent in the higher BE range.

The analysis of the transient photoemission spectra was based on solving sets of kinetic equations that were used to model the time-dependent population of electronic states using a global fitting procedure. According to previous TRPL and TAS studies,^27,31,33,68 the decay of the initially populated 400 nm-excited state in PCN powders and colloids occurs within about 200 fs. The dynamics that occur on this timescale are also observed in the transient photoemission spectra of the PCN thin films, specifically as a prominent transient signal in the low BE range, that is particularly apparent in WAM. In addition, there is a clear indication of the subsequent population of an excited electronic state that decays within 1 ps, which was not previously observed. The transient signal prevailing in the photoemission spectra recorded in LADM indicates the population of a long-lived electronic state at higher BE. The long-lived dynamics in PCN colloids after light excitation have previously been attributed to the formation of a charge-transfer (CT) or singlet exciton (SE) state.^27,31,33 Thus, based on the observed spectroscopic features as well as previously reported results, the early-time electron dynamics of PCN thin films following 400 nm optical excitation can be represented in terms of a kinetic model that involves a sequential population of four excited electronic states. The proposed photocycle is schematically depicted in Fig. 7. It comprises the minimum number of electronic states required to describe the population dynamics and transition channels in the PCN samples, as based on a global analysis of the measured multidimensional data in both the WAM and LADM of the spectrometer.

According to the kinetic model, optical excitation of the dipole-allowed electronic transition at 3.1 eV central photon energy leads to photoexcitation from the electronic ground state (GS) to a first excited state (ES1). The excited state ES1 undergoes a fast relaxation process and populates a short-lived intermediate state (ES2). The sequential relaxation of the intermediate ES2 state leads to the formation of a long-lived metastable state (ES3), followed by further electronic relaxation processes on a timescale that significantly exceeds the time delay range implemented in the TRPES experiments. The present kinetic model will be extended in Section 3.5 below, based on the results of extended-time-delay-range TAS experiments, which reveal kinetics on much longer time scales. The rate-equation system for the electron population dynamics, probed using TRPES, has the following form:

Here, P(t) is the time-dependent excitation rate coefficient for the transition from the ground state, GS, to the initially populated state ES1, which is described by a Gaussian temporal envelope of the pump pulse, P(t) ∝ exp(−t²/σ_pump²), where σ_pump is the pump pulse width. The rate coefficients k_1–3 characterise the sequential transitions to the subsequent states ES2 to ES3 to the undefined, subsequently populated state, X, respectively. Initial conditions for the normalised state population densities are [GS] = 1, [ES1] = [ES2] = [ES3] = 0 at t → −∞.

Fig. 7 exemplarily shows the experimental background-subtracted transient data (top row) and the result of the global fit (middle row) for the sample sg-CN, recorded in WAM (left) and LADM (right). Details about the fit results for all PCN samples, including associated residual maps, can be found in Section 8 and Section 9 of the ESI.† It can be seen that the fit results (second row panels in Fig. 7) match the experimental data quite well. This is exemplified by the decompositions shown in the lower panels of Fig. 7. Here, the ultrafast decay of ES1 is prominently visible in the −2 to 1 eV BE interval in WAM. On the other hand, the build-up of the long-lived state, ES3, can be clearly modelled in the region 6.9–10.9 eV in the LADM data. Furthermore, the kinetic parameters, shown in Table 5, are consistent between the WAM and LADM results. Here the decay time constants represent inverse values of the corresponding transition rates: τ_i = k_i⁻¹. For the first excited state, ES1, we find a decay time τ₁ ≈ 165 fs, slightly faster than the reported literature values.^31,33,68 The relaxation into the longer-lived state ES3 from the intermediate ES2 state proceeds within τ₂ ≈ 700–730 fs. In comparison to that, the other three CN samples exhibit slightly faster relaxation of ES1 (135–155 fs), and slightly slower transitions from ES2 to ES3 (820–960 fs). The latter is also apparent from the comparably delayed onset of the respective blue/red features of these samples in the LADM (right column of Fig. 6). From these results, one may deduce a general trend towards faster relaxation of ES1 and slower build-up of ES3 with reduced domain size in the vertical (interplanar) direction of the PCN structure.

Table 5 Kinetic parameters obtained from the global fits to the transient photoemission spectra recorded in the WAM and LADM

Sample	Mode	τ 1/fs	τ 2/fs	τ 3/ps
sg-CN	WAM	166^+10−9	731^+67−56	>2.4
	LADM	165^+10−9	709^+39−35	>2.4
CNB	WAM	142^+11−9	824^+90−76	>2.4
	LADM	138^+8−7	830^+38−35	>2.4
CNPS–O	WAM	153^+9−8	877^+60−52	>2.4
	LADM	146^+13−11	903^+75−53	>2.4
CNPS–NH2	WAM	137^+7−6	953^+33−31	>2.4
	LADM	135^+8−7	960^+39−28	>2.4

---

Fig. 8 shows the state-associated spectra for the sg-CN sample, as extracted from the global fits to the spectrometer-WAM photoemission spectra. The state-associated spectra for all four PCN samples are shown in Fig. S15 of the ESI.† These spectra highlight an initial positive PE signal at negative BEs (ES1, ES2), together with a shift towards higher positive BE in ES3. This may be associated with the evolution of either the SE or CT states. Both cases are characterised by the presence of an outer-valence hole (left over by the former HOMO/VB electron), accompanied by an electron in a more weakly bound state, as compared to the GS. The PE spectrum of ES3 shows the signature of the hole as a loss of PES amplitude in the HOMO/VBM range, while the excited electron signal only appears to be observable at negative BE during the ES1/ES2 phases. Apparently, there is no discernible signal of the photo-excited, hole-separated electron in the ES3 spectrum; we speculate that this may be related to the limited (but best achievable) signal-to-noise ratio in our 5 kHz, EUV-probe experiments and the production of excited electron signatures with a broad range of BEs. Unfortunately, further interrogation of this intriguing behaviour requires the implementation of a significantly higher repetition rate, ultrashort-pulse EUV light source.

Fig. 8 State-associated spectra of the electronic states extracted from global fits to the photoemission spectra for the sg-CN sample recorded in the WAM, following photoexcitation at 3.1 eV. The BE scale is energy-referenced with respect to the sample and spectrometer E_F.

3.5 Transient diffuse reflectance spectra of PCN thin films

Diffuse reflectance TAS studies were performed to gain detailed insights into interfacial electron transfer processes and track the ultrafast photodynamics of the PCN thin films on time scales ranging from femtoseconds to nanoseconds. As opposed to the current implementation of the TRPES technique, the TAS experiments additionally allow the application of a range of pump fluences, so as to investigate the influences of higher excited-state concentrations on the immediate and subsequent kinetics of the system. The effect of wavelength-dependent pump–probe interaction due to the chirp of the probe pulse was modelled in a global fit routine.^30,52,69Fig. 9 exemplarily shows the 2D maps associated with chirp-corrected transient diffuse reflectance signals from the sg-CN thin films for an applied pump pulse fluence of 420 ± 50 μJ cm⁻², recorded as a function of probe wavelength and pump–probe time delay. The colour bar represents the relative magnitude of the absorbance change, ΔOD(t,λ), induced by the pump pulse. For better visualisation of both ultrafast and long-lived transient signals, the data are presented on a semilogarithmic time axis.⁵² The TA rises sharply at zero delay time, and generally relaxes very slowly, leaving a substantial signal at the maximum time delay of 1800 ps. The accompanying spectrum is very broad, covering the whole probed wavelength range (550–920 nm), and has no detectable distinct sharp features.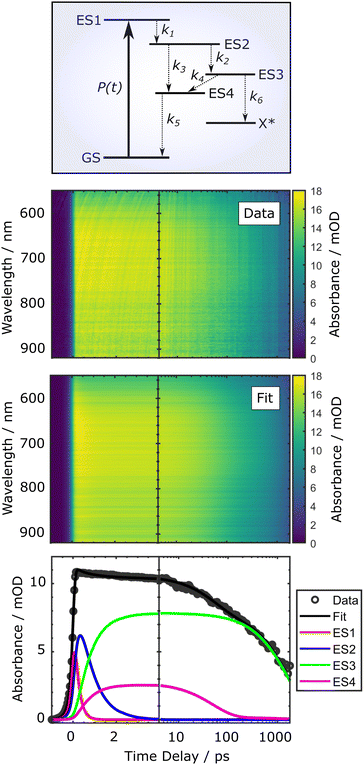

Fig. 9 Global fit reproduction of the experimental, chirp-corrected diffuse reflectance spectra for the sg-CN thin films recorded for pump pulse fluence of 420 ± 50 μJ cm⁻² with the use of the kinetic model described by eqn (4). The lower panel shows the time dependence of the TA signal integrated over the 550–920 nm wavelength range. This range encompasses the interfacial population dynamics of the 400 nm photoexcited states in the sg-CN sample. The upper panel shows a schematic depiction of the PCN photocycle at the bulk-surface interface following 400 nm optical excitation. The rate parameters described in eqn (4), k_1–6, are appended to this depiction.

In order to incorporate the prevailing long-lived dynamics observed in the TAS studies, as well as the ultrafast kinetics evident from the TRPES measurements, it was necessary to implement a more complex kinetic scheme. Here, we also take into account the observations and proposed explanations that have been reported in previous TRPL and TAS studies.^{27,28,31,33,68,70–72} According to those results, there are (at least) two additional processes that potentially contribute to the long-lived population dynamics in PCN materials. The first process, identified as prompt fluorescence, occurs on a time scale of hundreds of ps up to several ns. The second process is the so-called delayed fluorescence, which exhibits a spectral distribution similar to prompt fluorescence, but with emission occurring on time scales up to milliseconds. While the former process is typically associated with singlet excitons (SE), the latter involves spatial separation of species. This may be either due to the formation of triplet exciton (TE) states (via singlet fission), or the emergence of a charge-transfer (CT) state. Although the exact nature of the separation state is currently unclear, we will refer to it in the following as a CT state. Regardless, the recombination process of either TE or CT species will be of a diffusive nature, whose elemental steps (e.g., nearest-neighbour hopping) take place on the timescale of a few nanoseconds. This part of the model is corroborated by TRPL as well as TAS studies, showing the characteristic power-law type decay curves (I ∝ t^−α) associated with diffusion-limited recombination processes.^27,33

Taking this into account, we can extend the earlier model as depicted in Fig. 9: after formation of the intermediate ES2 state, two relaxation paths lead to the formation of metastable states ES3 and ES4, presumably corresponding to the CT and SE states, respectively. The formed ES3 (CT) state may undergo parallel transitions to the ES4 (SE) state, as well as alternative relaxation processes (here denoted as leading to X*). The latter manifest as delayed fluorescence (and/or long-lived TA) signals on time scales much longer than those measured in the TAS experiments, which can be characterised by the above mentioned power-law decays. As such, we can only observe the fastest part of this ensemble of diffusion-limited relaxations or other lifetime distributions.^27,33 State ES4 (SE) is assumed to relax to the ground state (GS) via an at least partially radiative channel, corresponding to the prompt or delayed fluorescence signal. The kinetic rate equations thus read:

The results of the global fit are shown in Fig. 9 for sg-CN, and the respective fit parameters of the kinetic model are given in Table 6 for a pump fluence of 420 ± 50 μJ cm⁻² for sg-CN, CNB, CNPS–O and CNPS–NH₂ samples. The effect of wavelength-dependent pump–probe interaction due to the chirp of the probe pulse was modelled in a global fit routine.^30,52,69 The TAS results presented below show the corrected data and fits, accordingly. A more detailed description of the global fit results for all samples can be found in the ESI,† Section 11. In Fig. 9, the fit results (middle panel) demonstrate a good reproduction of the measured TA data. This is also apparent in the lower panel in Fig. 9, where the transient signal is integrated over the full wavelength range. In general, we find that the relaxation time constants of ES1 and ES2 follow the trend of the TRPES results for the different samples. Namely, a speed-up of the decay of ES1 and a slowing-down of that of ES2 (combined rate constants k₂ + k₃ in eqn (4)) when going from bulk sg-CN and CNB towards exfoliated CNPS–O and CNPS–NH₂ samples. The relaxation of the supposed CT state ES3 becomes slightly faster (k₄ + k₆); however, given the probed time range, a definite assessment of the values is difficult. Notably, the supposed partial radiative decay (k₅) of ES4 does not show a distinct trend among the different samples.

Table 6 Kinetic parameters obtained from global fits to the transient diffuse reflectance spectra recorded with a pump pulse fluence of 420 ± 50 μJ cm⁻². Decay time constants are presented for the ES1, ES2, ES3, and ES4 states for the PCN thin films following 400 nm excitation at the surface-bulk interface

Sample	τ 1/fs	τ 2/fs	τ 3/ps	τ 4/ns	τ 5/ps	τ 6/ns	σ pump/fs	σ probe/fs
sg-CN	200^+10−9	0877^+79−65	2.87^+0.89−0.68	2.7^+1.9−1.8	50^+15−11	5.0^+3.6−3.5	65 ± 3	80 ± 5
CNB	102^+16−14	0392^+94−81	1.37^+0.38−0.36	2.7^+1.8−1.7	40^+13−10	5.0^+3.7−3.3	67 ± 5	82 ± 6
CNPS–O	103^+13−12	1560^+170−150	2.88^+0.92−0.78	2.3^+1.3−1.3	43^+14−11	3.6^+2.8−2.3	65 ± 5	84 ± 5
CNPS–NH2	101^+15−13	2660^+370−250	5.35^+1.64−1.43	2.6^+1.7−1.6	40^+12−10	3.8^+3.1−2.8	64 ± 6	82 ± 7

---

The influence of pump fluence on the electronic relaxation dynamics was monitored for excitation fluences of 40 ± 5, 140 ± 20, and 420 ± 50 μJ cm⁻² for the sg-CN, CNB, and CNPS–O samples, respectively. Due to the relatively low ΔOD(t,λ) values obtained for the TAS signal in the CNPS–NH₂ sample, higher excitation fluences of 420 ± 50, 1400 ± 200, and 2100 ± 300 μJ cm⁻² were applied in that case. Fig. 10 shows the normalised kinetic traces of the TAS signal of sg-CN, integrated over the 550–920 nm wavelength range as a function of pump fluence. The initial amplitude at zero time delay, t₀, is found to increase linearly with the pump fluence, as shown in the inset in Fig. 10. There is thus no evidence for a substantial contribution of multi-photon absorption, nor for saturation effects in the immediate excitation process. On the other hand, increased pump fluences result in a relative decrease of the transient signal in the delay time range from hundreds of picoseconds to nanoseconds. For the CNPS–NH₂ sample, this change is even more pronounced, when even higher excitation fluences are applied (see details in ESI,† Fig. S19).

Fig. 10 Decay kinetics of the normalised transient diffuse reflectance signal for the sg-CN sample integrated over the 550–920 nm wavelength range, shown for different 400 nm pump fluences. The inset shows the dependence of the initial amplitude of the raw transient signal on the excitation fluence at zero time delay. The data (circles) and the cumulative global fit results (curves) are presented on a linear time scale.

Pump fluence-dependent transient signal decay kinetics in PCN powders and colloids were previously observed in TRPL and TAS studies.^27,33,68 The TAS decay shapes reported in those works exhibit dependencies very similar to the one shown in Fig. 10, while the TRPL decay shapes are virtually unaffected by variations of the pump fluence. We will discuss these findings in more detail below. Here, based on the global analysis and kinetic modelling of the diffuse reflectance spectra, the excited state population time constants in the PCN thin films were used to determine the origin of the pump-pulse-fluence-induced changes to the population dynamics. The corresponding time constants, τ_1–6, for the sg-CN, CNB, CNPS–O and CNPS–NH₂ samples, as obtained using eqn (4), are summarised in ESI† (Table S2). Based on those results, it can be concluded that following 400 nm excitation, the early-time dynamics associated with the ES1, ES2 and ES3 states do not depend on the pump fluence. The associated reproducibility of the decay time constants over the implemented pump fluence range (within the error bars) confirms the reliability of the kinetic model used to describe the transient population of the excited electronic states in the PCN thin films. In contrast to the short lifetime population dynamics, the long lifetime population kinetics are found to be excitation-fluence dependent. In particular, the transition from the ES4 state to the GS state occurs faster at the higher excitation fluences. The decay time constant τ₄, which is appended to the relaxation channel from the ES3 (CT) state to the ES4 (SE) state, becomes shorter with increasing pump fluence. At the same time, the ES3 → X* transition, which occurs on a similar timescale, is lengthened. Thus, there is a competition between the two relaxation channels of the ES3 state. Note that the current delay-time limit of the TAS setup (1.8 ns) does not allow an exact determination of the time constants τ₄ and τ₆; the reported values therefore only correspond to the numerical result obtained from the fit. By increasing the delay time span in the TAS experiments to the ms range, a more reliable investigation of those long-lived decay components should be possible. However, as discussed below, one will then have to take into account the mentioned diffusive nature of excited species, leading to power-law type decays in the respective kinetic models.

4 Discussion

4.1 Ground state energetics of PCN and TEOA

The values obtained for the VBM position of the PCN thin films and TEOA solute from the steady-state EUV photoemission spectra were used to determine the VBM potentials with respect to the standard redox potentials of water. The determination of the band-edge potentials of the PCN thin films and the TEOA sacrificial agent allows an estimation of the catalyst-sacrificial agent interfacial energetics. Furthermore, it enables evaluation of the maximum redox potentials of the photogenerated electron–hole pairs in the photocatalyst, which plays a major role in driving an efficient photocatalytic water-splitting reaction. Fig. 11 shows a schematic diagram of the band-edge alignment of the PCN thin films as well as TEOA solute within a semiconductor band structure framework, as well as the redox electrochemical potentials of the HER (H⁺/H₂) and OER (O₂/H₂O). The energy scale is presented relative to the electrochemical potential in a solution containing a redox couple, equivalent to the Fermi level, E_F,redox, in eV, when E_F in a solid sample and E_F,redox are in equilibrium. The absolute potential of the electrochemical standard hydrogen electrode (SHE) in water, E⁰_SHE(H⁺/H₂)_H2O, is equal to 4.44 ± 0.02 eV at 298 K,⁷³ relative to the electron in vacuum close to the solution surface. This potential was set as zero of the energy scale. In a photocatalytic water-splitting reaction, solid-state PCN compounds are typically dispersed in an aqueous electrolyte solution with a specifically chosen pH (for TEOA_(aq) pH = 7.0). Thus, the pH of the solution must also be taken into account at the liquid–solid interface, as it can modify the redox potentials of the electrolyte as well as the photocatalyst and shift the energy levels. In such systems the redox potentials are referenced against the reversible hydrogen electrode (RHE), which changes with pH with respect to the SHE as E⁰_RHE = E⁰_SHE − 0.05916 eV × pH.⁷⁴

Fig. 11 Schematic of the band-edge alignment of the PCN thin films as compared to the TEOA solute within a semiconductor band structure framework. The respective water redox potentials (blue dashed lines) are also shown. The energy scale is presented relative to the electrochemical potential versus the RHE, equivalent to E_F,redox. The obtained E_VBM, E_CBM and E_g values, depicted in the figure, are summarised in Table 7.

In this work, the VBM energy positions, E_VBM, obtained for the PCN thin films from the solid-state PES experiments and presented as electron BEs relative to E_F, were used to calculate the electrochemical potential of the samples relative to the RHE at pH 7.0. The calculated E_VBM values for the sg-CN, CNB, CNPS–O, and CNPS–NH₂ thin films versus RHE are 1.56 ± 0.37 eV, 1.66 ± 0.34 eV, 2.24 ± 0.36 eV, and 1.26 ± 0.31 eV, respectively. Taking into account the E_g values, for the direct allowed electronic transitions in the PCN thin films, as determined from the Tauc plots (see Section 3.3), the CBM energy positions, E_CBM, for the solid samples versus RHE are estimated to be −1.32 ± 0.39 eV, −1.29 ± 0.37 eV, −0.82 ± 0.37 eV, and −1.87 ± 0.33 eV, respectively. The associated E_g values and the E_VBM energetic positions relative to the E_F are summarised in Table 7.

Table 7 The E_g values and the E_VBM and E_CBM energetic positions relative to E_F, used to determine the E_VBM and E_CBM values versus RHE for the PCN thin films

Sample	E g/eV	E VBM vs. E F/eV	E CBM vs. E F/eV	E VBM vs. RHE/eV	E CBM vs. RHE/eV
sg-CN	2.88 ± 0.02	1.98 ± 0.35	−0.90 ± 0.37	1.56 ± 0.37	−1.32 ± 0.39
CNB	2.95 ± 0.03	2.08 ± 0.32	−0.87 ± 0.35	1.66 ± 0.34	−1.29 ± 0.37
CNPS–O	3.06 ± 0.01	2.65 ± 0.34	−0.41 ± 0.35	2.24 ± 0.36	−0.82 ± 0.37
CNPS–NH2	3.13 ± 0.02	1.68 ± 0.29	−1.45 ± 0.31	1.26 ± 0.31	−1.87 ± 0.33

---

As can be seen from Fig. 11, for all four PCN samples, the thermodynamic condition for driving a single-step, overall water-splitting reaction is satisfied for both the HER and OER. Specifically, the mesoporous, sg-CN, and bulk, CNB, polymeric carbon nitride samples with the moderate E_g values of 2.88 eV and 2.95 eV, respectively, both possess a sufficiently large thermodynamic driving force for H₂ (0.91 eV for sg-CN and 0.88 eV for CNB) and O₂ (0.74 eV for sg-CN and 0.84 eV for CNB) evolution. The electronic band structure of the porous oxygen-rich carbon nitride nanosheets, CNPS–O, suggests that the presence of oxygen-containing group provides a stronger driving force for the OER (1.42 eV versus O₂/H₂O) and a weaker one for the HER (0.41 eV versus H⁺/H₂). The potential of the CBM of the amino functional group, atomically-thin porous carbon nitride nanosheets, CNPS–NH₂, is notably higher than those of the other samples (1.46 eV versus H⁺/H₂), which can provide a relatively large thermodynamic driving force for the HER.

Considering the TEOA VBM measurements, our LJ-PES data suggests, in contrast to the reported irreversible oxidation potential obtained from voltammetry studies,^57–59 that TEOA will be an ineffective sacrificial agent in PCN-driven HER. However, to fully address this issue, it is important to note that although these two quantities typically exhibit a linear relationship, they are by no means identical, especially for thin-film samples in an electrolyte.⁷⁵

Specifically for the LJ-PES experiments, several assumptions have been made: (1) a semiconductor electronic structure model has been applied to a molecular solute, (2) the TEOA solute has a negligible effect on the electronic structure of the H₂O solvent, and (3) the threshold ionisation energy of aqueous TEOA is equivalent to its VBM, disregarding the reorganisation energy of the TEOA molecule after photoionization (or oxidation). The latter may lead to a considerable overestimation of the oxidation potential.⁷⁶

Likewise, the accuracy of voltammetric studies is limited by various influences, such as scanning speed and appropriate choice of electrodes. Microscopic effects due to (de)protonation, decomposition or parasitic chemical reactions of the oxidised product, as well as diffusion in the Nernst layer can lead to an underestimation of the oxidation potentials.⁷⁷

Thus, further experiments that probe the true PCN–TEOA_(aq) interface would be required to resolve the true VBM alignment of aqueous TEOA with respect to different PCN materials. Furthermore, in the case of associated PES measurements, more robust energy-referencing methodologies would be needed to allow arbitrary solution BEs to be determined with respect to the Fermi level.^56,78

4.2 Excited state dynamics of PCN

Having established a favourable (static) energetic situation for photocatalytic reaction, we will now discuss some details of the kinetic processes that occur upon photoexcitation. These chemical kinetics turn out to be decisive for the performance of catalytic devices in general. For a photocatalytic device specifically, those kinetics are determined by the photoexcitation process and the subsequent steps: charge separation, thermalisation, and transport. While it is crucial to avoid undesirable pathways throughout the whole chain, an efficient device may be inviable if substantial losses occur already within the early-time dynamics. This work, therefore, focuses on a better understanding of the ultrafast dynamics, encompassing the charge separation and thermalisation processes.

Previous studies utilised a range of excitation wavelengths between 355 nm and 400 nm, thus presumably addressing the above-mentioned π → π* transition around 3.2 eV.^31,33,68 In all cases, it was concluded that a CT state emerges after ≈200 fs, alongside an SE state, to which the PL signals were assigned. Therein, the charge-separation efficiency was estimated to be between 5% and 65%, with a tendency towards higher values with larger photon energy.^31,68 In the present work, TRPES shows evidence for a more complex situation, involving an intermediate state, which only gradually evolves into the SE and CT states. The BE of the resulting state suggests that significant charge separation persists on a ps timescale and potentially that hole-separated electrons are generated with a broad range of BEs. According to the TAS results, the charge-separation efficiency can be calculated as k₂/(k₂ + k₃). The results range between 65 ± 11% and 78 ± 11%, with the higher values being found for the bulk CN materials. Although the confidence intervals on these numbers only allow us to make a rough estimate, we can conclude that the signals observed in the TRPES data for delay times >1 ps are most likely dominated by the CT state.

We find that the kinetic parameters observed in TRPES and TAS experiments are in overall good agreement. Slight differences, insofar as they may be considered significant, may be due to the generally worse temporal resolution of the TAS experiment. It is also currently unclear, how the difference between the surface- and bulk-sensitive techniques will affect the observations. Near-surface excited species, e.g. surface excitons or polarons, have a more two-dimensional character than their bulk counterparts. Correspondingly, they may exhibit different kinetic behaviours.⁷⁹ Additional effects, like ultrafast migration of excitation from the surface into the bulk, while not to be ruled out, are unlikely on the scale of several nanometers within the sub-picosecond range. As discussed below, such motion is rather expected on timescales in the nanosecond range.

Apart from that, it is noteworthy that the additional visible absorption band in sg-CN does not have an obvious impact on either the TRPES or TAS results. This may be due to the higher excitation photon energy utilised in this work, resulting in inefficient excitation of the states associated with this particular absorption feature. However, it also indicates that the states involved in this lower-energy transition do not act as dominant traps within the temporal window observed here.

Closely related to the question of charge-separation efficiency is the peculiar excitation-fluence dependence of the TAS and TRPL signals reported here and in previous works.^{27,28,31,33,68} In all of these studies, the TRPL decay shapes are found to be independent of the applied pump fluence, while in bulk CN, the TAS decays exhibit a speed-up with higher applied pump intensities. In contrast, Zhang et al. observed no such dependence for either TRPL or TAS signals in exfoliated CN colloids.³¹ Our present fit results to the TAS data indicate that the initial charge-separation process, occurring on up to few picosecond timescales, are largely unaffected by the excitation fluence. Substantial differences only occur on time ranges starting around 100 ps, which is when charges begin to migrate through the bulk of the CN material. This supports the interpretation that the initial excitation process is mainly localised at the heptazine motif, not involving band-like delocalisation. Increased bulk concentrations of the excited species can therefore only lead to changes in the decay kinetics on longer timescales, which is when transport processes become dominant.

Merschjann et al. found that for delay times exceeding about 1 ns, the TRPL decay is well described by a power law relation of the form I ∝ t^−α, with α = 3/2, independent of the applied variation of excitation fluence, which was tuned by a factor of 300 (0.73–220 μJ cm⁻²).²⁷ Due to the independence on pump fluence and the characteristic decay exponent, these authors ascribed the TRPL signals to a geminate recombination of separated charges, whose diffusive motion is weakly confined in a one-dimensional system. Since the waiting-time of the elemental steps of this diffusive transport scales exponentially with the stacking distance of the graphitic CN sheets, it was concluded that the transport proceeds mainly along the vertical direction of the CN structure.²⁷ The TRPL experimental findings were confirmed by Godin et al., who additionally showed that TAS signals could also be well described by a power law in the time range from nanoseconds to seconds.³³ In contrast to TRPL, the TAS decays exhibit an increasing exponent 0.11 < α < 0.20 for increasing excitation fluence (24–784 μJ cm⁻²), which is not commensurate with the TRPL decay exponent. This behaviour was attributed to electron trapping–detrapping processes within an exponential conduction-band tail, where higher excitation fluence leads to a larger filling of the exponential density of states.^80,81 This in turn should result in an altered ageing of the diffusion process, showing the characteristic change of the power-law exponent.⁸² Consequently, suppressing spatial charge transport by exfoliating CN sheets, thus confining carriers within single- or oligo-layered colloids, leads to faster recombination and also lifts the concentration dependence of the decay curves.^31,68 However, we note that so far, none of the above-mentioned models can fully explain the observed phenomena, especially the apparent distinction between emitting and non-emitting species, exhibiting different temporal behaviour. Further time-resolved experiments, as well as more sophisticated theoretical models are correspondingly needed to explain those peculiarities.

Finally, based on the assumption that the initial dynamics are predominantly localised on the heptazine motifs, we attempt to assign the early-time PES state-associated spectra to specific heptazine photoexcited states. Although we are not aware of experimental PES results for molecular heptazine, detailed reports on the valence excited and ionic states of molecular triazine exist, including assignments of associated electronic and vibrational state characters.^83,84 Recent theoretical works by Ehrmaier et al. confirm these experimental results and suggest that the nature and symmetry of those states and transitions are by and large analogous in triazine and heptazine, although the over-all energetics of the latter are shifted to lower values due to the more extended aromatic system.^8,29,85,86 Adopting the nomenclature of Ehrmaier,²⁹ the photocycle from Fig. 7 may be described as follows: photons of 3.1 eV energy resonantly photoexcite the ground state, GS (, S₀), of a heptazine PCN sub-unit to reach the optically-bright ES1 state (¹E′, S₄).²⁹ This state (S₄) is expected to undergo an ultrafast radiationless relaxation into ES2 (, S₁*), which should be optically dark and would be populated with a high degree of vibrational excitation.⁸⁶ From here, the substantial vibrational excess energy (up to ≈1 eV) opens two possible relaxation paths to ES3, both of which occur on a sub-picosecond timescale. The system will then undergo intra-state vibrational relaxation (IVR) toward the vibrationally-cold S₁ state (corresponding to the SE state, ES4, in Fig. 9). Furthermore, Ehrmaier et al. suggest that a transition can occur towards a CT state, in their case between molecular heptazine and a water molecule.⁸⁶ We speculate that a similar relaxation path is open between neighbouring heptazine motifs in the polymeric materials, thus leading to the population of the CT state, ES3, in the TAS photocycle shown in Fig. 9. Regardless of whether IVR, CT, or a combination of the two relaxation processes occur, the resulting states are expected to have lifetimes well in excess of a few picoseconds, since they will exhibit minimal electric-dipole coupling to the S₀ ground state. Such a mechanism could be assessed, and further details about the initial stages of the heptazine and PCN photocycles could be investigated, via additional calculations that utilise the techniques applied by Ehrmaier et al., albeit with a focus on the electronic structure and excited-state dynamics in PCN supercells.

As for the expected PES spectral signatures of the different excited states mentioned above, we consider the triazine molecular system and project the associated conclusions onto the heptazine molecule and PCN material systems considered here. In the specific case of triazine, photoexcitation and ionization is expected to lead to the following states and energetics.^83,84 The optically bright → ¹E′ transition at 7.65 eV can be related to the 1e′′ → 2e′′ molecular orbital transition. The associated excited state will Koopmans correlate with the first excited state of the triazine cation,^87,88 (1e′′)⁻¹ or D₁, which has an electron binding energy of 11.69 eV with respect to vacuum, resulting in an expected excited-state binding energy of 11.79–7.65 eV = 4.04 eV, with respect to the vacuum level.⁸⁴ Upon internal conversion from this excited state to the vibrationally excited S₁ state, a (6e′)⁻¹ (2e′′)¹ configuration is produced in comparison to the ground state. This state correlates with the ground state of the cation, (6e′)⁻¹ or D₀, with a binding energy of 10.01 eV with respect to vacuum.⁸⁴ Following vibrational relaxation, this state is then expected to result in an approximate excited-state binding energy of 10.01–3.70 eV = 6.31 eV,⁸⁴i.e., a more than 2 eV increase in binding energy following ultrafast internal conversion from the optically-bright state and subsequent IVR. If the analogy between triazine and heptazine holds, one can expect this situation to be mapped onto the PCN case, albeit with different absolute energetics. That is, a similar optically bright → ¹E′ transition pervades in the heptazine and PCN cases to populate the S₄ state, ES1, in this case with lower peak absorption energies of around 4.4 eV.²⁹ Like in the triazine case – and generally for higher-lying, singly-excited states of molecular systems – the heptazine and PCN S₄ states will correlate with electronically-excited ionized states, which are here expected to produce low-binding-energy electrons, as observed in the ES1 state-associated spectra. Following the generally expected ultrafast internal conversion from the electronically excited singlet state (S₄) to vibrationally-excited levels of S₁,^89,90 ES2 is formed and the related PCN state-associated-spectra exhibit a binding energy reduction of ≈1 eV, which together with the extracted time-constants are indicative of an electronic state switch. Generally, as vibrationally excited molecular excited states undergo IVR, associated excited-state electron binding energies are expected to increase. This is indeed observed: as the system relaxes from vibrationally-excited levels of S₁, in going from ES2 to ES3, a further electron-binding-energy reduction of ≈1 eV is discerned in the PCN state-associated spectra. A similar, albeit energetically offset, relaxation process as in the triazine case correspondingly seems to pervade in the PCN materials. We finally note that PES and particularly femtosecond-time-resolved PES measurements on molecular and solid heptazine samples would be particularly helpful in confirming such considerations, and more importantly in the development of a deeper understanding of the ionization mechanisms, early-time excited-state behaviours, and photocatalytic properties of PCN materials.

5 Conclusions

In summary, we have shown that TRPES is a promising tool to reveal the ultrafast kinetics of organic, solid-state photocatalysts. Here, we utilised the complementary combination of photoemission and optical absorption spectroscopy to investigate the electronic structure and charge-mobility dynamics of various kinds of polymeric carbon nitrides (PCN). Steady-state PES and UV-Vis absorption spectroscopy results were used to construct a band diagram for the four studied PCN systems: sg-CN; CNB, CNPS–O, and CNPS–NH₂. The results highlight the energetic driving forces for water-splitting processes at aqueous-PCN interfaces. Relatively, they also indicate that a significantly higher overpotential is achieved for the HER by the CNPS–NH₂ sample, which is one of the favourable ingredients in its superior performance as a water-splitting catalyst. Beyond that, liquid-jet PES experiments on aqueous triethanolamine (TEOA) solutions revealed the photoemission peaks associated with the valence states of the TEOA solute. These results suggest that TEOA will be an ineffective hole-scavenger when incorporated in PCN-based devices. However, to confirm this, technically challenging in-situ TRPES experiments on solid–liquid interfaces, involving TEOA sacrificial agents, would need to be performed.^91,92

The fs-time-resolved spectroscopy results show that 400 nm (3.1 eV) excitation sequentially populates a pair of short-lived transient species. Considerations of the molecular triazine PES and triazine and heptazine electronic structure literature suggest that these states respectively correspond to the optically-bright fourth-excited-singlet state and vibrationally excited first-excited singlet state of heptazine motifs within the overall PCN structures.^8,29,83–86 These states subsequently produce two different long-lived excited states on a sub-picosecond time scale, which were identified as singlet-exciton (SE) and charge-transfer (CT) states, with the associated charge-separation efficiencies inferred to be between 65% and 78% for the different studied materials. It was determined that the early-time processes in the differently synthesized PCNs do not differ qualitatively between sample batches. However, the materials of more voluminous character were found to have higher charge separation efficiencies, compared to exfoliated colloidal materials. Pump-fluence-dependent measurements of the initial excited-state decay kinetics corroborated this finding and reproduced the characteristic high-carrier-concentration effects that are known to emerge beyond few-picosecond timescales. The initial dynamics of the photoinduced charge carriers in the PCNs are correspondingly determined to be spatially localised in the immediate vicinity of the lattice-constituting motif, while the long-time behaviour is dominated by charge-transport and recombination processes. Correspondingly, it is concluded that recombination effects could be mitigated by confining the excited species within nanoscale volumes and that such an approach should therefore increase the effectiveness of PCN materials in photocatalytic devices.

Generally, the results reported here allowed us to garner a broader perspective of the electronic energetics, charge-carrier dynamics, and driving forces behind potential water-splitting devices, built around PCN materials. Further insights may be obtained using state-of-the-art, higher-repetition-rate and average power EUV light sources together with the TRPES technique.^93–97 Such an approach could significantly improve experimental signal-to-noise levels and allow PCN vacuum-solid interface energetics to be probed on both the ultrafast and longer timescales encompassed by photocatalytic cycles. Furthermore, high-time-resolution, in situ solid–liquid interface probes – as potentially afforded by diffuse-reflection TAS, time-resolved sum-frequency generation spectroscopy,^98–100 or high-time-resolution variants of solid–liquid interface TRPES – have the potential to extract dynamic electronic energetic information from functioning interfaces within heterogeneous catalytic systems.¹⁰¹ Such experiments promise to yield critical insights into the optimisation of PCN-based, and alternative, water-splitting devices. We hope that the insights accumulated through the time- and energy-resolved, interfacially-sensitive experiments reported here can go some way to motivate such important further work.

Author contributions

NK: data curation, investigation, validation, visualisation, writing – original draft. IYK: conceptualisation, resources, supervision, writing – review & editing. IW: project administration, supervision, writing – review & editing. CM: conceptualisation, data curation, resources, validation, visualisation, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to the research groups of Prof. Arne Thomas (Technical University Berlin, Germany) and Prof. Bin Zhang (Tianjin University, People's Republic of China) for providing the PCN materials used in this study, as well as to Dr Tristan Petit for establishing collaboration contacts. We would also like to thank Florian Gores for the important and constant technical support of the ULLAS femtosecond laser facility at the Helmholtz-Zentrum Berlin für Materialien und Energie GmbH. CM acknowledges support from the German Federal Ministry of Education and Researchs funding measure “CO2-WIN” (project “PRODIGY”).

Notes and references

1. L. Zhou, H. Zhang, H. Sun, S. Liu, M. O. Tade, S. Wang and W. Jin, Catal. Sci. Technol., 2016, 6, 7002–7023.
2. A. B. Djurišić, Y. He and A. M. C. Ng, APL Mater., 2020, 8, 030903.
3. L. Dai, Carbon-Based Metal-Free Catalysts: Design and Applications, Wiley-VCH Verlag GmbH & Co. KGaA, 2018.
4. X. Wang, K. Maeda, A. Thomas, K. Takanabe, G. Xin, J. M. Carlsson, K. Domen and M. Antonietti, Nat. Mater., 2009, 8, 76–80.
5. J. Wen, J. Xie, X. Chen and X. Li, Appl. Surf. Sci., 2017, 391, 72–123.
6. S. Ye, R. Wang, M.-Z. Wu and Y.-P. Yuan, Appl. Surf. Sci., 2015, 358, 15–27.
7. Y. Xu, M. Kraft and R. Xu, Chem. Soc. Rev., 2016, 45, 3039–3052.
8. J. Ehrmaier, W. Domcke and D. Opalka, J. Phys. Chem. Lett., 2018, 9, 4695–4699.
9. M. Marszewski, S. Cao, J. Yu and M. Jaroniec, Mater. Horiz., 2015, 2, 261–278.
10. S. Ilic, M. R. Zoric, U. P. Kadel, Y. Huang and K. D. Glusac, Annu. Rev. Phys. Chem., 2017, 68, 305–331.
11. W.-J. Ong, L.-L. Tan, Y. H. Ng, S.-T. Yong and S.-P. Chai, Chem. Rev., 2016, 116, 7159–7329.
12. W. K. Darkwah and K. A. Oswald, Nanoscale Res. Lett., 2019, 14, 234.
13. D. R. Paul and S. P. Nehra, Environ. Sci. Pollut. R, 2020, 28, 3888–3896.
14. J. Liu, H. Wang and M. Antonietti, Chem. Soc. Rev., 2016, 45, 2308–2326.
15. M.-H. Chan, R.-S. Liu and M. Hsiao, Nanoscale, 2019, 11, 14993–15003.
16. A. Pandikumar, C. Murugan and S. Vinoth, Nanoscale Graphitic Carbon Nitride: Synthesis and Applications, Elsevier Science, 2022.
17. E. Kroke, M. Schwarz, E. Horath-Bordon, P. Kroll, B. Noll and A. D. Norman, New J. Chem., 2002, 26, 508–512.
18. X. Wang, K. Maeda, X. Chen, K. Takanabe, K. Domen, Y. Hou, X. Fu and M. Antonietti, J. Am. Chem. Soc., 2009, 131, 1680–1681.
19. J. Liu, Y. Liu, N. Liu, Y. Han, X. Zhang, H. Huang, Y. Lifshitz, S.-T. Lee, J. Zhong and Z. Kang, Science, 2015, 347, 970–974.
20. S. Cao and J. Yu, J. Phys. Chem. Lett., 2014, 5, 2101–2107.
21. N. Fajrina and M. Tahir, Int. J. Hydrogen Energy, 2019, 44, 540–577.
22. F. K. Kessler, Y. Zheng, D. Schwarz, C. Merschjann, W. Schnick, X. Wang and M. J. Bojdys, Nat. Rev. Mater., 2017, 2, 17030.
23. M. Makaremi, S. Grixti, K. T. Butler, G. A. Ozin and C. V. Singh, ACS Appl. Mater. Interfaces, 2018, 10, 11143–11151.
24. F. Dong, Z. Zhao, T. Xiong, Z. Ni, W. Zhang, Y. Sun and W.-K. Ho, ACS Appl. Mater. Interfaces, 2013, 5, 11392–11401.
25. N. Zhang, L. Wen, J. Yan and Y. Liu, Chem. Pap., 2020, 74, 389–406.
26. W. Domcke, J. Ehrmaier and A. L. Sobolewski, ChemPhotoChem, 2018, 3, 10–23.
27. C. Merschjann, S. Tschierlei, T. Tyborski, K. Kailasam, S. Orthmann, D. Hollmann, T. Schedel-Niedrig, A. Thomas and S. Lochbrunner, Adv. Mater., 2015, 27, 7993–7999.
28. C. Merschjann, T. Tyborski, S. Orthmann, F. Yang, K. Schwarzburg, M. Lublow, M.-C. Lux-Steiner and T. Schedel-Niedrig, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 205204.
29. J. Ehrmaier, E. J. Rabe, S. R. Pristash, K. L. Corp, C. W. Schlenker, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2019, 123, 8099–8108.
30. Y. Noda, C. Merschjann, J. Tarábek, P. Amsalem, N. Koch and M. J. Bojdys, Angew. Chem., Int. Ed., 2019, 58, 9394–9398.
31. H. Zhang, Y. Chen, R. Lu, R. Li and A. Yu, Phys. Chem. Chem. Phys., 2016, 18, 14904–14910.
32. D. Hollmann, M. Karnahl, S. Tschierlei, K. Kailasam, M. Schneider, J. Radnik, K. Grabow, U. Bentrup, H. Junge, M. Beller, S. Lochbrunner, A. Thomas and A. Brückner, Chem. Mater., 2014, 26, 1727–1733.
33. R. Godin, Y. Wang, M. A. Zwijnenburg, J. Tang and J. R. Durrant, J. Am. Chem. Soc., 2017, 139, 5216–5224.
34. A. Indra, A. Acharjya, P. W. Menezes, C. Merschjann, D. Hollmann, M. Schwarze, M. Aktas, A. Friedrich, S. Lochbrunner, A. Thomas and M. Driess, Angew. Chem., Int. Ed., 2017, 56, 1653–1657.
35. S. Hüfner, Photoelectron spectroscopy: principles and applications, Springer, Berlin, Heidelberg, 3rd edn, 2003.
36. F. S. Roberts, S. L. Anderson, A. C. Reber and S. N. Khanna, J. Phys. Chem. C, 2015, 119(11), 6033–6046.
37. S. Malerz, F. Trinter, U. Hergenhahn, A. Ghrist, H. Ali, C. Nicolas, C.-M. Saak, C. Richter, S. Hartweg, L. Nahon, C. Lee, C. Goy, D. M. Neumark, G. Meijer, I. Wilkinson, B. Winter and S. Thurmer, Phys. Chem. Chem. Phys., 2021, 23, 8246–8260.
38. S. Suga, A. Sekiyama and C. Tusche, Photoelectron Spectroscopy, Springer International Publishing, 2021.
39. T. Tyborski, C. Merschjann, S. Orthmann, F. Yang, M.-C. Lux-Steiner and T. Schedel-Niedrig, J. Phys.: Condens Matter, 2013, 25, 395402.
40. F. Fina, S. K. Callear, G. M. Carins and J. T. S. Irvine, Chem. Mater., 2015, 27, 2612–2618.
41. D. M. Teter and R. J. Hemley, Science, 1996, 271, 53–55.
42. K. Kailasam, J. D. Epping, A. Thomas, S. Losse and H. Junge, Energy Environ. Sci., 2011, 4, 4668–4674.
43. Y. Sun, S. Gao, F. Lei and Y. Xie, Chem. Soc. Rev., 2015, 44, 623–636.
44. C. Tan, X. Cao, X.-J. Wu, Q. He, J. Yang, X. Zhang, J. Chen, W. Zhao, S. Han, G.-H. Nam, M. Sindoro and H. Zhang, Chem. Rev., 2017, 117, 6225–6331.
45. N. Meng, J. Ren, Y. Liu, Y. Huang, T. Petit and B. Zhang, Energy Environ. Sci., 2018, 11, 566–571.
46. V. Kumaravel, M. Imam, A. Badreldin, R. Chava, J. Do, M. Kang and A. Abdel-Wahab, Catalysts, 2019, 9, 276.
47. B. Winter, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 601, 139–150.
48. N. Kurahashi, S. Karashima, Y. Tang, T. Horio, B. Abulimiti, Y.-I. Suzuki, Y. Ogi, M. Oura and T. Suzuki, J. Chem. Phys., 2014, 140, 174506.
49. J. Metje, M. Borgwardt, A. Moguilevski, A. Kothe, N. Engel, M. Wilke, R. Al-Obaidi, D. Tolksdorf, A. Firsov, M. Brzhezinskaya, A. Erko, I. Y. Kiyan and E. F. Aziz, Opt. Express, 2014, 22, 10747–10760.
50. T. E. Glover, R. W. Schoenlein, A. H. Chin and C. V. Shank, Phys. Rev. Lett., 1996, 76, 2468–2471.
51. L. Miaja-Avila, C. Lei, M. Aeschlimann, J. L. Gland, M. M. Murnane, H. C. Kapteyn and G. Saathoff, Phys. Rev. Lett., 2006, 97, 113604.
52. U. Megerle, I. Pugliesi, C. Schriever, C. F. Sailer and E. Riedle, Appl. Phys. B, 2009, 96, 215–231.
53. H. Inoki, G. Seo and K. Kanai, Appl. Surf. Sci., 2020, 534, 147569.
54. P. Hammer, N. M. Victoria and F. Alvarez, J. Vac. Sci. Technol., A, 2000, 18, 2277–2287.
55. S. Souto, M. Pickholz, M. C. dos Santos and F. Alvarez, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 2536–2540.
56. S. Thürmer, S. Malerz, F. Trinter, U. Hergenhahn, C. Lee, D. M. Neumark, G. Meijer, B. Winter and I. Wilkinson, Chem. Sci., 2021, 12, 10558–10582.
57. A.-M. Manke, K. Geisel, A. Fetzer and P. Kurz, Phys. Chem. Chem. Phys., 2014, 16, 12029–12042.
58. Y. Pellegrin and F. Odobel, Cr Chim, 2017, 20, 283–295.
59. S. Mazzanti, B. Kurpil, B. Pieber, M. Antonietti and A. Savateev, Nat. Commun., 2020, 11, 1387.
60. A. B. Jorge, D. J. Martin, M. T. S. Dhanoa, A. S. Rahman, N. Makwana, J. Tang, A. Sella, F. Corà, S. Firth, J. A. Darr and P. F. McMillan, J. Phys. Chem. C, 2013, 117, 7178–7185.
61. M. Deifallah, P. F. McMillan and F. Corà, J. Phys. Chem. C, 2008, 112, 5447–5453.
62. A. P. Alivisatos, Science, 1996, 271, 933–937.
63. T. Tyborski, C. Merschjann, S. Orthmann, F. Yang, M.-C. Lux-Steiner and T. Schedel-Niedrig, J. Phys.: Condens Matter, 2012, 24, 162201.
64. J. Tauc, R. Grigorovici and A. Vancu, Phys. Status Solidi B, 1966, 15, 627–637.
65. E. A. Davis and N. F. Mott, Philos. Mag., 1970, 22, 0903–0922.
66. S. Hellmann, K. Rossnagel, M. Marczynski-Bühlow and L. Kipp, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 035402.
67. J. Graf, S. Hellmann, C. Jozwiak, C. L. Smallwood, Z. Hussain, R. A. Kaindl, L. Kipp, K. Rossnagel and A. Lanzara, J. Appl. Phys., 2010, 107, 014912.
68. K. L. Corp and C. W. Schlenker, J. Am. Chem. Soc., 2017, 139, 7904–7912.
69. S. A. Kovalenko, A. L. Dobryakov, J. Ruthmann and N. P. Ernsting, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 59, 2369–2384.
70. H. Zhang and A. Yu, J. Phys. Chem. C, 2014, 118, 11628–11635.
71. H. Wang, S. Jiang, S. Chen, X. Zhang, W. Shao, X. Sun, Z. Zhao, Q. Zhang, Y. Luo and Y. Xie, Chem. Sci., 2017, 8, 4087–4092.
72. L. Jing, R. Zhu, D. L. Phillips and J. C. Yu, Adv. Funct. Mater., 2017, 27, 1703484.
73. S. Trasatti, J. Electroanal. Chem. Interfacial Electrochem., 1986, 209, 417–428.
74. G. Jerkiewicz, ACS Catal., 2020, 10, 8409–8417.
75. B. Dandrade, S. Datta, S. Forrest, P. Djurovich, E. Polikarpov and M. Thompson, Org. Electron., 2005, 6, 11–20.
76. D. Ghosh, A. Roy, R. Seidel, B. Winter, S. Bradforth and A. I. Krylov, J. Phys. Chem. B, 2012, 116, 7269–7280.
77. F. Marken, A. Neudeck and A. M. Bond, Electroanalytical Methods, Springer Berlin Heidelberg, 2009, pp. 57–106.
78. B. Winter, S. Thürmer and I. Wilkinson, Acc. Chem. Res., 2023, 56, 77–85.
79. C. Franchini, M. Reticcioli, M. Setvin and U. Diebold, Nat. Rev. Mater., 2021, 6, 560–586.
80. A. J. Cowan, J. Tang, W. Leng, J. R. Durrant and D. R. Klug, J. Phys. Chem. C, 2010, 114, 4208–4214.
81. H. Ohkita and S. Ito, Polymer, 2011, 52, 4397–4417.
82. J. Nelson, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 155209.
83. C. Fridh, L. Åsbrink, B. Jonsson and E. Lindholm, Int. J. Mass Spectrom. Ion Phys., 1972, 8, 85–99.
84. D. Holland, D. Shaw, M. Stener, P. Decleva and S. Coriani, Chem. Phys., 2016, 477, 96–104.
85. J. Ehrmaier, M. J. Janicki, A. L. Sobolewski and W. Domcke, Phys. Chem. Chem. Phys., 2018, 20, 14420–14430.
86. J. Ehrmaier, T. N. V. Karsili, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2017, 121, 4754–4764.
87. T. Koopmans, Physica, 1933, 1, 104–113.
88. T. Helgaker, P. Jorgensen and J. Olsen, Molecular Electronic-Structure Theory, John Wiley and Sons, 2013.
89. M. Kasha, Discuss. Faraday Soc., 1950, 9, 14–19.
90. G. I. Cristina and M. Marazzi, Theoretical and Computational Photochemistry, Elsevier, 2023.
91. A. Knop-Gericke, V. Pfeifer, J.-J. Velasco-Velez, T. Jones, R. Arrigo, M. Hävecker and R. Schlögl, J. Electron. Spectrosc., 2017, 221, 10–17.
92. M. Favaro, P. C. Clark, M. J. Sear, M. Johansson, S. Maehl, R. van de Krol and D. E. Starr, Surf. Sci., 2021, 713, 121903.
93. J. Rothhardt, S. Hädrich, Y. Shamir, M. Tschnernajew, R. Klas, A. Hoffmann, G. K. Tadesse, A. Klenke, T. Gottschall, T. Eidam, J. Limpert, A. Tünnermann, R. Boll, C. Bomme, H. Dachraoui, B. Erk, M. D. Fraia, D. A. Horke, T. Kierspel, T. Mullins, A. Przystawik, E. Savelyev, J. Wiese, T. Laarmann, J. Küpper and D. Rolles, Opt. Express, 2016, 24, 18133.
94. C. Corder, P. Zhao, J. Bakalis, X. Li, M. D. Kershis, A. R. Muraca, M. G. White and T. K. Allison, Struct. Dyn., 2018, 5, 054301.
95. A. K. Mills, S. Zhdanovich, M. X. Na, F. Boschini, E. Razzoli, M. Michiardi, A. Sheyerman, M. Schneider, T. J. Hammond, V. Süss, C. Felser, A. Damascelli and D. J. Jones, Rev. Sci. Instrum., 2019, 90, 083001.
96. T. Saule, S. Heinrich, J. Schötz, N. Lilienfein, M. Högner, O. deVries, M. Plötner, J. Weitenberg, D. Esser, J. Schulte, P. Russbueldt, J. Limpert, M. F. Kling, U. Kleineberg and I. Pupeza, Nat. Commun., 2019, 10, 458.
97. J. Wang, F. Chen, M. Pan, S. Xu, R. Lv, J. Liu, Y. Li, S. Fang, Y. Chen, J. Zhu, D. Zhang, T. Qian, C. Yun, K. Zhao, H. Ding and Z. Wei, Opt. Express, 2023, 31, 9854.
98. F. Vidal and A. Tadjeddine, Rep. Progr. Phys., 2005, 68, 1095–1127.
99. J. Kubota and K. Domen, Anal. Bioanal. Chem., 2007, 388, 17–27.
100. A. M. Gardner, K. H. Saeed and A. J. Cowan, Phys. Chem. Chem. Phys., 2019, 21, 12067–12086.
101. L. Negahdar, C. M. A. Parlett, M. A. Isaacs, A. M. Beale, K. Wilson and A. F. Lee, Catal. Sci. Technol., 2020, 10, 5362–5385.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp03191h

‡ Present address: Advanced Research Center for Nanolithography, Science Park 106, 1098 XG Amsterdam, The Netherlands.

---