Pd and Pt metal atoms as electron donors in σ-hole bonded complexes

Abstract

Quantum calculations provide a systematic assessment of the ability of Group 10 transition metals M = Pd and Pt to act as an electron donor within the context of pnicogen, chalcogen, and halogen bonds. These M atoms are coordinated in a square planar geometry, attached to two N atoms of a modified phenanthrene unit, as well as two ligand atoms Cl, Br, or I. As the Lewis acid, a series of AF_n molecules were chosen, which could form a pnicogen bond (A = P, As, Sb), chalcogen bond (A = S, Se, Te) or halogen bond (A = Cl, Br, I) with M. These noncovalent bonds are fairly strong, varying between 6 and 20 kcal mol⁻¹, with the occupied d_z² orbital of M acting as the origin of charge transferred to the acid. Pt forms somewhat stronger bonds than Pd, and the bond strength rises with the size of the A atom of the acid. Within the context of smaller A atoms, the bond strength rises in the order pnicogen < chalcogen < halogen, but this distinction vanishes for the fifth-row A atoms. The nature of the ligand atoms on M has little bearing on the bond strength. Based on the Harmonic Oscillator Model of Aromaticity (HOMA) index, the ZB, YB and XB bonds were shown to have only a subtle effect on the ring electronic structures.

---

Introduction

Hydrogen bonds are extremely common in both chemistry and molecular biology. Their roles range from structural to those that allow directional adjustment of molecules via self-assembly processes, selective molecular recognition, and proton transfer.^1–4 The diversity of types and strengths of H-bonds motivated the IUPAC organization to devise a modern HB definition in 2011.⁵ In the context of hydrogen bonding research or noncovalent bonding in general, a less frequently addressed topic is the interaction of hydrogen or any other electrophilic agent with metals as electron donors. It was first suggested more than 60 years ago that metals can act as hydrogen bond acceptors based on solution-phase IR spectroscopy studies of ferrocenyl alcohols.^6–9 Further exploration of metal participation in H-bonds comprised several works where electron transfer from metals Co and Pt was observed through the appropriate orientation of their filled metal (M) d_z² orbital directed to the hydrogen-containing group, i.e. σ* orbital of the N–H amino group.^10–13 Other scenarios¹⁰ raised the possibility of π-back donation from the filled metal d orbital to the vacant σ*(C–H) orbital or even σ-donation in the reverse direction, namely, from the filled C–H orbital to the vacant M d-orbital (the latter is commonly referred to as an agostic bond¹⁴). The investigation by Groenewald et al.^15,16 revealed the presence of Au⋯H interactions between the metal atom in dialkylgold(I) or dimethylaurate and hydrogen from small ligands such as water, ammonia or hydrogen cyanide. The energy of such bonds was in the range 5–14 kcal mol⁻¹.

In 2019, the Au⋯H hydrogen bond was observed by NMR and IR and predicted theoretically in cationic gold(I) complexes featuring ditopic phosphine-ammonium (P, NH⁺) ligands.¹⁷ Its presence accounted for the stabilization of the most stable conformer (in relation to those without such H-bonds) by as much as 11 to 21 kcal mol⁻¹. The source of this interaction was attributed to a donor–acceptor second-order interaction energy [E(2)] of 12.8 kcal mol⁻¹ between d(Au) and the σ*(N–H) orbitals.¹⁷ Parallel spectroscopic and computational evidence was found in another gold(I) synthon, [Cl–Au–L]⁺ complex, where L refers to a protonated N-heterocyclic carbene.¹⁸ The Au⋯H–N bond detected therein was characterized by E(2) of 13 kcal mol⁻¹ between the Au lone-pair (LP) and the σ*(N–H) orbital, while the overall binding energy was assessed as 10 kcal mol⁻¹.¹⁸ The literature also contains reports of platinum to hydrogen interactions. Such a non-classical H-bond is explained mainly by charge transfer from the Pt d_z² orbital to σ*(X–H). In the model PtX₂L₂ complexes (X = Me, CN, OH, Br, Cl, F; L= NH₃, CO, PH₃) with HCl, the total interaction energy was strictly correlated with this interorbital interaction.¹⁹ Other studies demonstrating the binding of platinum(II) complexes to water are also known.^20–22

Donor–acceptor interactions of the sort described above are not limited to H-bonds but extend to other noncovalent interactions, especially those which have recently gathered popularity, labeled as σ-hole interactions. Already in 1992, Politzer and coworkers²³ theoretically predicted the positive electrostatic potential on the halogen ends in halogenated methanes and obtained their complexes with electron donors as benzene or p-xylene.

Further work^24–28 in 2007 established the connotation of halogen bonds (XBs) as the electrostatic attraction between the negatively charged area of a nucleophile (electron lone pair, π-electron system) and the positive region localized along the R–X extension (σ-hole) in the Lewis acid molecule.^29–32

The pace of this work continues to accelerate even today.^33–39 Over the years, the investigations of these interactions have moved beyond halogen atoms, hence the development of analogous chalcogen or pnicogen bonds which engender robust study.^36,40–44

The bulk of bonds of this type utilize either a lone pair of the nucleophile as the source of charge to be transferred, or a π-electron system, either localized as in ethylene, or aromatic. A new wrinkle in this bonding is the finding that there are occasions where metal atoms can serve as the electron source, despite their low electronegativity. As one example, Ivanov et al.⁴⁵ spotted two unconventional halogen bond schemes in the crystal structure databank in which the d_z², d_x²_–y² or d_xy orbitals of metal attacked the σ-hole zone of halogen atoms. A Au⋯I XB was noted with Au in its d¹⁰ configuration (refcode ABAPAV⁴⁶). A similar XB occurred with d⁸ metal – nickel. The Ni⋯I interaction in MEXBID⁴⁷ was dominant and its magnitude was assessed at 4.5 kcal mol⁻¹.⁴⁵ Frontera and co-workers^48,49 furthered this story by expansion of metal-involved XB motifs as I⋯Rh, Br⋯Pt, I⋯Pd, Br⋯Pd, Br⋯Ni, and Cl⋯Pt.⁴⁹ A XB with a palladium(II) electron donor was found by Katlenok et al.⁵⁰ The intramolecular I⋯Pt⋯I interaction was discovered by Bulatov and co-workers.⁵¹ The binding between I₂ and various d⁸ metals (Pd, Ni, Co, Rh, and Ir) has also been described in van Koten's pincer complex and its 19 alterations.⁵² Eliseeva et al.⁵³ found both a classical C–I⋯I XB and metal-including C–I⋯Pt in trans-[PtI₂(NCN(CH₂)₅)₂]·2CHI₃, again using the Pt d_z² orbital as the electron source. It was also reported by Li et al.⁵⁴ that Ni or Pt metal nanoparticles are able to interact with Na cations, HF or H₂O based on the local electrostatic contacts between positively and negatively charged areas of subunits from both groups. The correlation between the electrostatic potential and the binding energy of anticipated Lewis base–Lewis acid complexes has been confirmed there.

Although not quite as plentiful, there are literature reports of parallel M electron donors beyond the XBs mentioned above. A CSD survey by Frontera and Bauza⁵⁵ disclosed several square planar Pd/Pt coordination complexes with Se and Te chalcogen atoms as σ-hole donors. The strong directionality of these interactions was signaled by the orientation of the M d_z² orbital aimed at the σ-hole located at the chalcogen (Y) atom. Likewise, a chalcogen bond (YB), this time in the shape of the platinum(II) interaction with Se and Te centers was described by Rozhkov et al.⁵⁶ with support from MEP, NBO and NCI analyses. The authors came to the conclusion, in line with previous studies, that the LP(Pt) d_z² → σ*(Ch–C) interorbital interaction is crucial for directionality and stabilization. Finally, the metal-assisted pnicogen bond (ZB) was reported for the first time in the literature by Burguera et al.⁵⁷ by the observation of Sb⋯Pt(II) contacts within the crystal lattice. Again the results pointed to the repeated pattern of charge transfer from the occupied M d_z² orbital to the σ* orbital (in this case σ(Sb–Cl)*).

While results continue to accumulate that echo the claim that metal atoms can indeed function in the capacity of an electron donor in HBs and various σ-hole noncovalent bonds, the data remain fragmentary. Various studies examine pertinent systems, but usually focus on one particular sort of interaction, and usually for just one particular metal in a given setting, and with only one nucleophile. What is needed at this point is a comprehensive study that encompasses a wide range of different metals, substituents, and nucleophiles, which would permit the elucidation of a set of guiding principles. The work presented below comprises this sort of thorough study. Both Pd and Pt are considered within a square planar framework. Lying within a phenanothroline setting that bonds two N atoms to the metal, the other two substituents are varied from Cl to Br to I so as to cover a range of different electronegativities. The nucleophile approaching from above the M spans a set of different noncovalent bonds: halogen, chalcogen, and pnicogen. This wide spectrum of different bonding partners and noncovalent bond types is designed to cast a wide net to permit the extraction of the fundamental principles guiding the ability of metal atoms to serve as electron donors. The results ought to have implications for noncovalent bonds in general, as well as issues of coordination chemistry.

Computational details

Quantum calculations were performed with the def2-TZVP^58,59 basis set in the context of DFT^60,61 using the PBE0-D3 functional.⁶² Geometries were fully optimized with no restrictions, and their characters as true minima were verified by the absence of imaginary frequencies. All calculations were carried out using the Gaussian 16 set of codes (ver. C.01)⁶³ The interaction energy of each dyad (E_int) is defined as the difference between the energy of the complex and the sum of energies of monomers in the geometry they adopt within the optimized complex. E_int was corrected for basis set superposition error (BSSE) by the counterpoise (CP) protocol.⁶⁴ The BSSE correction was computed a posteriori. The binding energy (E_b) refers to the energies of the monomers in their fully optimized geometries, so is equal to the dimerization reaction energy.

Each Molecular Electrostatic Potential (MEP) was probed by the MultiWFN software (ver. 3.7)⁶⁵ so as to ascertain extrema or the MEP at a particular point. The topology of the electron density was analyzed according to the Quantum Theory of Atoms in Molecules (QTAIM).^66–68 QTAIM analyses were carried out with the use of the AIMAll software.⁶⁹ The Natural Bond Orbital (NBO) formulation was used to examine interorbital charge transfers and their energetic consequence.⁷⁰ NBO calculations were performed using NBO 7.0 software.⁷¹ Decomposition of the interaction energies was performed at the PBE0-D3/ZORA/TZ2P level of theory^72,73 using the ADF–EDA protocol according to the Morokuma–Ziegler scheme⁷⁴ embedded in ADF software.^75,76 The Harmonic Oscillator Model of Aromaticity (HOMA)⁷⁷ revealed aromaticity changes in the fused rings of the Pd/Pt-systems caused by complexation. The aromaticity calculations were carried out using the Multiwfn (ver. 3.7) program.⁶⁵

Visualizations were obtained with the Chemcraft (ver. 6.0.16)⁷⁸ and IQmol⁷⁹ programs. A survey of the Cambridge Structural Database via supporting CSD software Mercury and ConQuest^80,81 noted a number of structures wherein a Pd or Pt atom within a square planar coordination was approached by a potential Lewis acid atom from the pnicogen, chalcogen, or halogen family, as described below.

Results

As mentioned in the Introduction section, we began by reviewing CSDs to find structures with a motif suggestive of halogen bonds with metal atoms acting as electron donors. The CSD search criteria were as follows: a metal atom M (M = Pd, Pt) with four ligands attached to it (two halogen atoms and two other atoms such as nitrogen, phosphorus, oxygen or sulfur) was approached by a halogen atom (X = Cl, Br or I) connected to another atom M. The contact between M and X was constrained to a distance less than the sum of the vdW radii of these atoms. The angle M–X⋯M was also added as a search criterion, within the range of 140–180°. Additional technical restrictions were applied to the ConQuest software: only structures with 3D coordinates defined, non-disordered, with no errors and with R < 0.1 were allowed in the search. In this way, eight structures stabilized by the M–X⋯M halogen bond were identified.

Several sample structures drawn from the CSD are displayed in Fig. 1. The H atom positions in each were refined by a partial geometry optimization that left the non-H atoms in their X-ray positions. All share the primary feature that a halogen atom approaches a Pd or Pt atom from above the square planar local geometry in which it is ensconced. The metal is liganded by two O and two N atoms, with the latter atoms part of an aromatic ring. The latter ring is 5-membered for DAPYUQ⁸² and ZEWXUU,⁸³ while YAVCIJ⁸⁴ contains a hexagonal 6-membered ring. The approaching halogen atom is Br in DAPYUQ, and I in the other two. The central M is Pd for the former and Pt for the latter. Additional information regarding these three structures can be found in the ESI† (see Fig. S1–S3 and Table S1).

Fig. 1 View of dimers extracted from crystal structures following optimization of the H atom positions (PBE0-D3/def2-TZVP level of theory) taken from the Cambridge Structural Database (CSD).

With regards to the quantum chemical calculations, the metal-containing Lewis bases are modeled after the crystal systems. As shown in Fig. 2, the metal (Pd or Pt) is placed in a square planar bonding environment, attached to the two N atoms of a diazole ring within a modified phenanthrene structure, similar to that of DAPYUQ and ZEWXUU. The two other ligands L were taken as any of three different halogen atoms Cl, Br, or I. Three different AF_n Lewis acid types were allowed to approach M from above: ZF₃ in Fig. 2a where Z = P, As, or Sb, can engage in a Z⋯M pnicogen bond (ZB); YF₂ (Y= S, Se, Te) in Fig. 2b can likewise form a chalcogen bond (YB) and a halogen bond (XB) is possible for XF in Fig. 2c. Altogether, these various combinations add up to a total of 54 different complexes that were examined here.

Fig. 2 Geometrical parameters of (a) ZB, (b) YB, and (c) XB complexes. M = Pt or Pd; L = Cl, Br, I; X = Cl, Br, I; Y = S, Se, Te; Z = P, As, Sb. R denotes the interatomic distance between M and Z, Y and X. θ indicates a valence angle between M, Z or Y or X and fluorine atom.

Monomer properties

It is commonly observed that noncovalent bonds of these types contain a large electrostatic component, and the latter is related to the distribution of the molecular electrostatic potential (MEP) surrounding each monomer. One useful measure of this distribution is the maximum of the MEP on an isodensity surface surrounding the Lewis acid. The maximum for each Lewis acid is located along an extension of the A–F bond axis where A refers to the central atom, Z, Y, or X. This positive region is commonly referred to as a σ-hole since it is derived from a polarization of the A-F σ-bond orbital that leaves a deficit of density near the A atom. The depths of these σ-holes are listed in Table 1 as V_S,max, the maximum of the MEP on the 0.001 a.u. isodensity surface. The patterns conform to previous calculations of these quantities in that the σ-hole deepens as the central A atom grows larger. It is also evident that the hole deepens along the sequence Z < Y < X, which suggests that the ZB ought to be the weakest and XB the strongest.

Table 1 V _s,max values for optimized Lewis acid structures

Lewis acid	V S,max, kcal mol^−1
PF3	26.28
AsF3	37.99
SbF3	46.17
SF2	34.16
SeF2	44.09
TeF2	52.26
ClF	41.37
BrF	49.52
IF	57.43

---

The positive σ-hole will be interacting attractively with the negative region of the MEP that surrounds the Lewis base, specifically above the M atom. Although the MEP is negative in this region, the isodensity surface does not contain a minimum as such directly above the M atom, due in part to the negative areas associated with the L and N ligand atoms and their lone pairs. To provide an alternate gauge of the negative character of the MEP, this potential was evaluated for the base monomer at the position where the incoming A atom situates itself in each optimized complex. This quantity is reported as V in Table 2. There is some variation as one moves down either the Pd or Pt column, due primarily to the different intermolecular distances from one complex to the next, but there are several patterns that can be recognized, even if not strong ones. In the first place, the Pt systems on the right side of the table tend to have a somewhat more negative V. It also appears that the pair of Cl ligands in the upper section of Table 2 leads to a somewhat more negative V than do their Br cousins in the second segment, followed by I in the bottom third.

Table 2 Potential (V) for Lewis base (in the geometry of the complex) at the point corresponding to the position of the A atom on which the Sigma hole was located. V_S refers to the MEP at the point of density ρ = 0.001 a.u. All data are given in kcal mol⁻¹

Lewis base	V	V s	Lewis base	V	V s
Pd-complexes			Pt-complexes
Cl2(Phen)Pd⋯PF3	−13.00	−17.24	Cl2(Phen)Pt⋯PF3	−13.81	−20.81
Cl2(Phen)Pd⋯AsF3	−17.89	−21.23	Cl2(Phen)Pt⋯AsF3	−17.04	−22.13
Cl2(Phen)Pd⋯SbF3	−19.19	−22.61	Cl2(Phen)Pt⋯SbF3	−18.76	−24.32
Cl2(Phen)Pd⋯SF2	−13.43	−16.40	Cl2(Phen)Pt⋯SF2	−15.83	−20.49
Cl2(Phen)Pd⋯SeF2	−15.14	−17.53	Cl2(Phen)Pt⋯SeF2	−16.98	−21.13
Cl2(Phen)Pd⋯TeF2	−16.38	−19.40	Cl2(Phen)Pt⋯TeF2	−16.73	−21.56
Cl2(Phen)Pd⋯ClF	−12.45	−13.21	Cl2(Phen)Pt⋯ClF	−15.78	−17.81
Cl2(Phen)Pd⋯BrF	−12.77	−13.98	Cl2(Phen)Pt⋯BrF	−15.40	−18.35
Cl2(Phen)Pd⋯IF	−13.34	−15.43	Cl2(Phen)Pt⋯IF	−14.91	−19.21
Br2(Phen)Pd⋯PF3	−12.49	−16.52	Br2(Phen)Pt⋯PF3	−13.54	−20.42
Br2(Phen)Pd⋯AsF3	−16.52	−19.72	Br2(Phen)Pt⋯AsF3	−17.12	−22.67
Br2(Phen)Pd⋯SbF3	−17.47	−20.71	Br2(Phen)Pt⋯SbF3	−17.86	−23.37
Br2(Phen)Pd⋯SF2	−12.87	−15.67	Br2(Phen)Pt⋯SF2	−15.32	−19.93
Br2(Phen)Pd⋯SeF2	−14.52	−16.72	Br2(Phen)Pt⋯SeF2	−16.48	−20.53
Br2(Phen)Pd⋯TeF2	−15.41	−18.09	Br2(Phen)Pt⋯TeF2	−16.21	−20.84
Br2(Phen)Pd⋯ClF	−12.27	−12.88	Br2(Phen)Pt⋯ClF	−15.43	−17.37
Br2(Phen)Pd⋯BrF	−12.62	−13.65	Br2(Phen)Pt⋯BrF	−15.13	−17.94
Br2(Phen)Pd⋯IF	−13.14	−15.04	Br2(Phen)Pt⋯IF	−14.66	−18.80
I2(Phen)Pd⋯PF3	−11.80	−16.08	I2(Phen)Pt⋯PF3	−13.18	−20.34
I2(Phen)Pd⋯AsF3	−14.81	−18.38	I2(Phen)Pt⋯AsF3	−16.16	−21.97
I2(Phen)Pd⋯SbF3	−15.41	−18.96	I2(Phen)Pt⋯SbF3	−16.76	−22.47
I2(Phen)Pd⋯SF2	−12.57	−15.54	I2(Phen)Pt⋯SF2	−15.07	−19.87
I2(Phen)Pd⋯SeF2	−13.94	−16.31	I2(Phen)Pt⋯SeF2	−16.23	−20.37
I2(Phen)Pd⋯TeF2	−14.41	−17.15	I2(Phen)Pt⋯TeF2	−15.89	−20.59
I2(Phen)Pd⋯ClF	−12.59	−13.22	I2(Phen)Pt⋯ClF	−15.73	−17.63
I2(Phen)Pd⋯BrF	−12.83	−13.91	I2(Phen)Pt⋯BrF	−15.36	−18.18
I2(Phen)Pd⋯IF	−13.10	−15.08	I2(Phen)Pt⋯IF	−14.81	−18.97

---

In order to conform also with the usual prescription of locating and quantifying the minimum of the MEP on an isodensity surface with ρ = 0.001 au surrounding the base, this quantity is defined as V_S and is reported in the next columns of Table 2. Rather than evaluate the MEP at the location of the electron acceptor atom, V_S is equal to the MEP at that point along the M⋯A vector where ρ = 0.001 au. In the case where the central atom is Pt, the V_S values are more negative. Thus, for example, the V_S value calculated for LB in the geometry of the Cl₂(Phen)Pd⋯AsF₃ complex is −21 kcal mol⁻¹. When palladium was exchanged with platinum the value of this potential decreased by about 5% (to −22 kcal mol⁻¹). A noticeably larger difference was observed for Lewis bases in the geometry of Br₂(Phen)Pd⋯ClF and Br₂(Phen)Pt⋯ClF complexes where, in the case of the latter, the V_S is smaller by about 50%. As can be seen from the data presented, the substitution of halogen substituents around the central metal atom causes slight changes in the value of V_S. The greatest influence on the value of this parameter derives from the type of Lewis acid with which the complex is formed.

For six selected complexes (three containing a Pt atom and three with a Pd atom, two for each bond type considered), electrostatic potential values were calculated along the axis passing through the M and A atoms. Plots showing the relationship between the V value and the position on the M–A axis are included in the ESI† (see Fig. S4). These plots indicate the position of V and V_S whose values can be found in Table 2.

Since neither V nor V_S corresponds to a minimum on the surface of the electrostatic potential around LB, the values and positions of V_S,min near the metal atom for the six LB are given in Fig. S5 (ESI†). The values of these minima are more negative than the values of V or V_S. This suggests that in the case of any choice of the position of complexation, the Lewis acid would attach first precisely in the vicinity of halogen substituents. However, the subject under consideration in this paper is the complex in which it is LA that attaches directly to the metal atom (as is the case with complexes whose crystal structures are shown in Fig. 1).

Geometries of complexes

Several of the most important geometric parameters of the optimized dyads are listed in Table 3. The first column of data displays the R(M⋯A) intermolecular distance which varies between 2.6 and 3.5 Å. Because of the variability of both the A and M atoms it is perhaps more revealing to consider this distance after normalization, by dividing by the sum of the vdW radii of these two atoms. This latter sum is reported in the next column, followed by this ratio, which displays several intriguing patterns. In the first place, this ratio diminishes as either the Z or Y atom grows larger, indicative of a strengthening noncovalent bond. However, the opposite trend occurs for the halogen-bonded complexes, where it is Cl which lies closer to the metal atom in absolute as well as normalized terms. As another overall observation, these normalized distances do not vary much as one transitions from halogen to chalcogen to pnicogen bonds. The A⋯Pt distances are universally shorter than their Pd analogues, by 0.03 to 0.05, suggesting Pt engages in somewhat stronger bonding. Overall, these normalized bond distances are comfortably below the vdW sum, some less than 0.7, indicating they are moderate to strong noncovalent bonds. The next column of Table 3 refers to the degree of linearity of the M⋯AF alignment. The θ angles tend to be the largest for the smaller A atoms, implying that these larger atoms have a greater degree of angular flexibility that permits more nonlinearity. The distortions from linearity seem to be smallest for the YBs and largest for the ZBs.

Table 3 Structural parameters in complexes (distances in Å, angles in degs)

Complex	R, Å	ΣrvdW (M⋯A)	R/ΣrvdW	θ	r(FA)	Δr(FA)^a
a Between r(FA) in complex and isolated AFn.
Cl2(Phen)Pd⋯PF3	3.420	4.05	0.84	172.1	1.581	0.008
Cl2(Phen)Pd⋯AsF3	3.210	4.03	0.80	171.8	1.732	0.017
Cl2(Phen)Pd⋯SbF3	3.208	4.62	0.69	165.3	1.909	0.023
Cl2(Phen)Pd⋯SF2	3.160	4.04	0.78	178.7	1.606	0.015
Cl2(Phen)Pd⋯SeF2	3.044	3.97	0.77	175.0	1.756	0.026
Cl2(Phen)Pd⋯TeF2	3.132	4.14	0.76	166.2	1.920	0.030
Cl2(Phen)Pd⋯ClF	2.712	3.97	0.68	174.7	1.679	0.059
Cl2(Phen)Pd⋯BrF	2.814	4.01	0.70	172.7	1.812	0.058
Cl2(Phen)Pd⋯IF	2.998	4.19	0.72	169.4	1.953	0.048
Br2(Phen)Pd⋯PF3	3.444	4.05	0.85	171.7	1.580	0.007
Br2(Phen)Pd⋯AsF3	3.246	4.03	0.81	171.7	1.731	0.016
Br2(Phen)Pd⋯SbF3	3.246	4.62	0.70	165.6	1.908	0.022
Br2(Phen)Pd⋯SF2	3.185	4.04	0.79	178.2	1.605	0.014
Br2(Phen)Pd⋯SeF2	3.064	3.97	0.77	175.0	1.756	0.026
Br2(Phen)Pd⋯TeF2	3.145	4.14	0.76	166.7	1.921	0.031
Br2(Phen)Pd⋯ClF	2.716	3.97	0.68	173.7	1.679	0.059
Br2(Phen)Pd⋯BrF	2.820	4.01	0.70	171.6	1.813	0.059
Br2(Phen)Pd⋯IF	3.008	4.19	0.72	167.9	1.954	0.049
I2(Phen)Pd⋯PF3	3.469	4.05	0.86	172.1	1.580	0.007
I2(Phen)Pd⋯AsF3	3.296	4.03	0.82	172.1	1.731	0.016
I2(Phen)Pd⋯SbF3	3.290	4.62	0.71	166.5	1.908	0.022
I2(Phen)Pd⋯SF2	3.192	4.04	0.79	177.2	1.606	0.015
I2(Phen)Pd⋯SeF2	3.073	3.97	0.77	175.3	1.757	0.027
I2(Phen)Pd⋯TeF2	3.148	4.14	0.76	167.8	1.922	0.032
I2(Phen)Pd⋯ClF	2.707	3.97	0.68	172.6	1.684	0.064
I2(Phen)Pd⋯BrF	2.814	4.01	0.70	170.4	1.818	0.064
I2(Phen)Pd⋯IF	3.006	4.19	0.72	166.6	1.957	0.052
Cl2(Phen)Pt⋯PF3	3.376	4.19	0.81	175.7	1.583	0.010
Cl2(Phen)Pt⋯AsF3	3.152	4.17	0.76	174.5	1.736	0.021
Cl2(Phen)Pt⋯SbF3	3.149	4.76	0.66	167.8	1.914	0.028
Cl2(Phen)Pt⋯SF2	3.024	4.18	0.72	178.7	1.615	0.024
Cl2(Phen)Pt⋯SeF2	2.944	4.11	0.72	176.5	1.769	0.039
Cl2(Phen)Pt⋯TeF2	3.026	4.28	0.71	169.7	1.930	0.040
Cl2(Phen)Pt⋯ClF	2.649	4.11	0.64	177.2	1.707	0.087
Cl2(Phen)Pt⋯BrF	2.770	4.15	0.67	176.1	1.833	0.079
Cl2(Phen)Pt⋯IF	2.951	4.33	0.68	174.4	1.968	0.063
Br2(Phen)Pt⋯PF3	3.401	4.19	0.81	175.1	1.583	0.010
Br2(Phen)Pt⋯AsF3	3.180	4.17	0.76	174.3	1.736	0.021
Br2(Phen)Pt⋯SbF3	3.176	4.76	0.67	167.8	1.913	0.027
Br2(Phen)Pt⋯SF2	3.048	4.18	0.73	178.5	1.615	0.024
Br2(Phen)Pt⋯SeF2	2.961	4.11	0.72	176.4	1.768	0.038
Br2(Phen)Pt⋯TeF2	3.039	4.28	0.71	169.6	1.930	0.040
Br2(Phen)Pt⋯ClF	2.652	4.11	0.65	176.6	1.708	0.088
Br2(Phen)Pt⋯BrF	2.774	4.15	0.67	175.4	1.834	0.080
Br2(Phen)Pt⋯IF	2.957	4.33	0.68	173.6	1.968	0.063
I2(Phen)Pt⋯PF3	3.440	4.19	0.82	174.8	1.582	0.009
I2(Phen)Pt⋯AsF3	3.221	4.17	0.77	174.3	1.735	0.020
I2(Phen)Pt⋯SbF3	3.210	4.76	0.67	168.3	1.913	0.027
I2(Phen)Pt⋯SF2	3.073	4.18	0.74	178.0	1.614	0.023
I2(Phen)Pt⋯SeF2	2.972	4.11	0.72	176.5	1.769	0.039
I2(Phen)Pt⋯TeF2	3.048	4.28	0.71	169.8	1.931	0.041
I2(Phen)Pt⋯ClF	2.649	4.11	0.64	175.8	1.711	0.091
I2(Phen)Pt⋯BrF	2.775	4.15	0.67	174.5	1.837	0.083
I2(Phen)Pt⋯IF	2.962	4.33	0.68	172.4	1.971	0.066

---

With regard to the internal geometry of the Lewis acid units, the r(FA) distances referring to the F that lies diametrically opposite the M are contained in the penultimate column of Table 3. These values are followed in the last column by the stretch of this bond relative to the fully optimized monomer. These stretches are largest for the halogen-bonded complexes, followed in order by the YB and then the ZB. On the other hand, the sensitivity of this stretching to the size of the A atom is curious. Both the YF and ZF elongations grow in magnitude along with the size of the Y and Z atom, respectively. However, this pattern appears to reverse for the XBs, where enlarging the X atom causes this elongation to diminish.

The aromaticity changes in polycyclic aromatic compounds have been an object of experimental and theoretical studies.^85,86 It has been learned that the value of the aromaticity index for each individual ring depends on the topological environment. Terminal rings tend to exhibit a high aromaticity value, but this property diminishes as the number of rings increases.

The aromaticity in the metal-containing species was analyzed using the Harmonic Oscillator Model of Aromaticity – HOMA index. Table S2 (ESI†) indicates a lower level of aromaticity in the central ring of the various molecules, whether M = Pd or Pt. The HOMA index is a bit higher for Pt vs. Pd, and diminishes slightly as the ligands become heavier Cl >Br > I. This index is reported for the complexes with the Lewis acids in Table S3 (ESI†) which displays many of the same trends as in the uncomplexed monomers. Comparison with Table S2 (ESI†) demonstrates very little effect of the complexation on terminal ring aromaticities. There is a small perturbation of the central ring, where the aromaticity tends to increase slightly, but this rise amounts to only several percent at most. The amount of this increment rises slightly with the size of the approaching atom, irrespective of whether it is halogen, chalcogen, or pnicogen.

Energetics

The energetics involved with the formation of each of the complexes are reported in Table 4 where E_int compares the energy of each complex with the sum of the individual monomers, each in the geometry it adopts within the dimer. The basis set superposition error within this quantity has been corrected by the counterpoise procedure. The binding energy refers to the reaction which takes the pair of isolated and fully optimized monomer reactants to the dimer as the product.

Table 4 Interaction (E_int) with BSSE correction a posteriori and binding (E_b) energies (without BSSE correction), along with the deformation energy (E_def) of each complex, in kcal mol⁻¹, electron density at BCP, and E2 for transfer from the M d_z² orbital to empty orbital of the Lewis acid, total charge CT transferred from the base to acid, and natural charge of the M atom

Complex	E int	E b	E def	ρ BCP, au	E2 kcal mol^−1	CT^a, me	q(M), e
a Obtained by the NBO approach.
Cl2(Phen)Pd⋯PF3	−6.40	−7.03	0.34	0.011	1.3	2.7	0.665
Cl2(Phen)Pd⋯AsF3	−11.68	−12.10	0.85	0.017	5.4	30.5	0.656
Cl2(Phen)Pd⋯SbF3	−17.32	−17.12	1.44	0.020	7.5	52.6	0.649
Cl2(Phen)Pd⋯SF2	−7.36	−8.04	0.37	0.015	2.0	27.9	0.666
Cl2(Phen)Pd⋯SeF2	−11.69	−12.27	0.75	0.022	6.5	66.1	0.660
Cl2(Phen)Pd⋯TeF2	−16.14	−16.21	1.08	0.023	7.4	89.6	0.659
Cl2(Phen)Pd⋯ClF	−9.49	−9.15	1.25	0.036	10.6	152.5	0.703
Cl2(Phen)Pd⋯BrF	−12.28	−12.07	1.15	0.035	12.3	160.0	0.690
Cl2(Phen)Pd⋯IF	−13.98	−13.92	0.76	0.030	22.9	142.2	0.669
Br2(Phen)Pd⋯PF3	−6.51	−7.09	0.34	0.010	1.0	1.2	0.577
Br2(Phen)Pd⋯AsF3	−11.64	−12.05	0.82	0.016	4.9	28.4	0.567
Br2(Phen)Pd⋯SbF3	−17.10	−16.91	1.34	0.019	6.8	49.8	0.560
Br2(Phen)Pd⋯SF2	−7.37	−8.05	0.34	0.015	1.9	25.8	0.576
Br2(Phen)Pd⋯SeF2	−11.66	−12.25	0.71	0.021	6.6	64.6	0.568
Br2(Phen)Pd⋯TeF2	−16.06	−16.15	1.01	0.022	7.2	91.4	0.566
Br2(Phen)Pd⋯ClF	−9.64	−9.26	1.28	0.036	10.2	151.9	0.608
Br2(Phen)Pd⋯BrF	−12.50	−12.24	1.17	0.034	11.7	160.4	0.593
Br2(Phen)Pd⋯IF	−14.30	−14.16	0.78	0.029	21.8	143.4	0.573
I2(Phen)Pd⋯PF3	−6.56	−7.16	0.30	0.010	1.3	-0.2	0.448
I2(Phen)Pd⋯AsF3	−11.44	−11.87	0.74	0.014	4.4	26.8	0.440
I2(Phen)Pd⋯SbF3	−16.60	−16.49	1.19	0.017	6.1	48.9	0.433
I2(Phen)Pd⋯SF2	−7.42	−8.10	0.34	0.015	1.9	26.3	0.446
I2(Phen)Pd⋯SeF2	−11.72	−12.30	0.70	0.021	7.1	67.6	0.437
I2(Phen)Pd⋯TeF2	−16.07	−16.17	0.97	0.022	7.1	98.3	0.434
I2(Phen)Pd⋯ClF	−10.30	−9.71	1.48	0.037	10.4	162.5	0.476
I2(Phen)Pd⋯BrF	−13.26	−12.82	1.34	0.035	11.8	171.8	0.460
I2(Phen)Pd⋯IF	−15.07	−14.80	0.89	0.029	22.3	154.8	0.439
Cl2(Phen)Pt⋯PF3	−6.97	−7.42	0.40	0.014	3.1	12.0	0.662
Cl2(Phen)Pt⋯AsF3	−12.73	−12.87	0.99	0.023	12.9	52.5	0.656
Cl2(Phen)Pt⋯SbF3	−18.78	−18.30	1.56	0.027	19.6	79.6	0.649
Cl2(Phen)Pt⋯SF2	−8.82	−9.13	0.76	0.025	5.5	66.6	0.678
Cl2(Phen)Pt⋯SeF2	−14.43	−14.30	1.41	0.033	17.1	119.4	0.683
Cl2(Phen)Pt⋯TeF2	−19.34	−18.71	1.70	0.034	25.7	140.2	0.676
Cl2(Phen)Pt⋯ClF	−13.94	−12.13	2.63	0.050	23.2	241.0	0.763
Cl2(Phen)Pt⋯BrF	−16.76	−15.52	2.08	0.046	24.8	235.9	0.743
Cl2(Phen)Pt⋯IF	−18.08	−17.39	1.32	0.039	54.2	207.9	0.713
Br2(Phen)Pt⋯PF3	−7.10	−7.51	0.39	0.013	3.2	8.9	0.575
Br2(Phen)Pt⋯AsF3	−12.81	−12.94	0.96	0.022	11.6	48.1	0.568
Br2(Phen)Pt⋯SbF3	−18.81	−18.31	1.51	0.025	17.7	74.8	0.561
Br2(Phen)Pt⋯SF2	−8.79	−9.12	0.70	0.023	5.0	60.8	0.588
Br2(Phen)Pt⋯SeF2	−14.39	−14.27	1.37	0.032	15.8	114.2	0.592
Br2(Phen)Pt⋯TeF2	−19.35	−18.69	1.67	0.033	23.8	136.2	0.584
Br2(Phen)Pt⋯ClF	−13.97	−12.12	2.65	0.050	22.2	239.5	0.672
Br2(Phen)Pt⋯BrF	−16.85	−15.56	2.10	0.045	23.9	234.3	0.650
Br2(Phen)Pt⋯IF	−18.25	−17.49	1.33	0.038	52.2	206.1	0.618
I2(Phen)Pt⋯PF3	−7.24	−7.65	0.38	0.012	3.0	6.3	0.444
I2(Phen)Pt⋯AsF3	−12.77	−12.93	0.91	0.020	10.0	44.6	0.438
I2(Phen)Pt⋯SbF3	−18.63	−18.19	1.43	0.024	15.5	72.5	0.429
I2(Phen)Pt⋯SF2	−8.81	−9.17	0.67	0.022	4.5	57.0	0.455
I2(Phen)Pt⋯SeF2	−14.47	−14.34	1.38	0.031	15.7	113.8	0.458
I2(Phen)Pt⋯TeF2	−19.50	−18.79	1.71	0.032	22.5	137.2	0.448
I2(Phen)Pt⋯ClF	−14.45	−12.40	2.86	0.050	21.8	246.4	0.538
I2(Phen)Pt⋯BrF	−17.36	−15.94	2.24	0.045	23.0	240.1	0.514
I2(Phen)Pt⋯IF	−18.82	−17.97	1.42	0.038	50.4	211.2	0.480

---

As may be seen by a comparison between the first two columns of Table 4, these two energetic measures of the noncovalent bonds are quite similar to one another, obeying very similar trends. The bond is strengthened as the central A atom grows larger, and by quite a bit. For example, the interaction energy of the Br₂(Phen)Pd⋯PF₃ complex is nearly tripled when the P is replaced by Sb. The variation from ZB to YB to XB does not conform to a simple pattern. For example, bonds strengthen in the order Pd⋯P < Pd⋯S < Pd⋯Cl for the second-row A atoms, but this pattern reverses when the atoms are drawn from the fourth row: Pd⋯Sb > Pd⋯Te < Pd⋯I. The bonds employing Pt as the electron donor are somewhat stronger than their Pd parallels.

The next column of Table 4 displays the deformation energy which is defined as the difference in energy between each optimized monomer, and that of the same molecule in the geometry it adopts within the complex. This quantity is fairly small, 1 kcal mol⁻¹ or less, so has little impact on the trends within the data. One can see an interesting pattern in that this strain energy tends to grow for larger pnicogen or chalcogen atoms, but changes in the opposite direction, becoming smaller as the halogen atom enlarges.

Analyses

In addition to the energetics, another measure of the strength of each noncovalent bond is derived from the topology of the electron density. QTAIM analysis provides the electron density at each noncovalent bond critical point, which is reported in the next column of Table 4. This quantity places this set of bonds in the range where ρ_BCP varies between 0.01 and 0.05 au, placing them squarely in the category of moderate noncovalent bonds. A more complete set of parameters for each of these bond critical points is contained in Table S4 (ESI†); all BCP Laplacians are positive, affirming their character as covalent bonds. The full QTAIM diagram for each complex is provided as Table S5 (ESI†). Bond paths are located in some cases for auxiliary atom-atom pairs, but their BCP densities are substantially smaller than those of the ZB, YB, or XB of interest.

As another variant of the QTAIM analysis of the electron density topology, NCI presents a three-dimensional diagram of the reduced density gradient. The NCI diagrams of several of the Pd and Pt complexes in Fig. S6 and S7 (ESI†) respectively present further evidence of the noncovalent bonding between the M and A atoms. The transition of the color in the relevant interatomic region from green to light blue to darker blue is also consistent with the QTAIM ρ_BCP designations of the bond strength increasing from ZB to YB to XB.

As the z-axis in each complex was defined as the M⋯A direction, it is the d_z² orbital that most closely aligns with the empty orbital of the Lewis acid to which it may transfer some of its density. The energetic consequence of this transfer is measured by NBO as a second order perturbation energy E2. The orbital acting as the receptor of this charge was in many cases a lone vacant orbital, specifically the valence p_z orbital, and in other cases it is the σ*(AF) antibonding orbital that acts in this capacity. The values of E2 for the various complexes are contained in the next column of Table 4 where it is readily apparent that these transfers make a sizable contribution to each bond. Unlike some of the other parameters, E2 behaves in a very regular fashion, growing larger along with the size of the A atom. It is also clear that E2 is much larger for the XBs, followed by the YBs, and are smallest for the ZBs. Another unique aspect of this parameter is that there is a considerably greater degree of charge transfer for the Pt complexes in the bottom half of the table as compared to the Pd counterparts in the upper half. Indeed, the former are between 2 and 3 times larger than the latter.

The interaction between the Lewis acid and base will naturally lead to a certain amount of charge being transferred from the latter subunit to the former. This total CT was computed as the sum of natural atomic charges on each monomer, and is reported in the next column of Table 4. This quantity is largest for the XBs, followed in turn by the YBs and then the ZBs. In most cases, CT grows as the A atom enlarges, although there is an inversion noted in the transition from BrF to IF. There is also a tendency for the CT to be quite a bit larger for the Pt dyads than for their Pd analogues. The last column of Table 4 lists the natural charge assigned to the M atom in each complex. All of these charges fall into the range between 0.4 and 0.8, with little distinction between Pd and Pt. It would appear that this atomic charge is most positive when the base is conjoined with a XB, in keeping with the larger total charge transferred from the metal-bearing base unit. It is this positive charge which makes the activity of these M-bearing units as nucleophiles counterintuitive in some ways.

Another window into the nature of the bonding is opened by way of a decomposition of the total interaction energy into a number of physically meaningful components. This decomposition provides an electrostatic component E_ES arising from the Coulombic interaction between the full charge clouds of the two monomers, prior to any mutual polarization. The mutual effects of the two subunits on the orbitals within, a combination of polarization and charge transfer, is encompassed by E_OI, and the dispersion energy is included as well, as E_dis. The Pauli repulsion prevents the two monomers from collapsing into one another. All of these terms were calculated and included in Table 5. For each of the three attractive components, its percentage contribution to the total attractive energy (E_ES + E_OI + E_dis) is also included in the table.

Table 5 EDA/PBE0-D3/ZORA/TZ2P decomposition of the interaction energy of complexes into Pauli repulsion (E_Pauli), and attractive electrostatic (E_ES), dispersion (E_dis) and orbital interaction (E_OI) components. All energies in kcal mol⁻¹

Complex	E Pauli	E ES	%	E dis	%	E OI	%	E int
Cl2(Phen)Pd⋯PF3	8.76	−7.49	49	−3.96	26	−3.94	26	−6.62
Cl2(Phen)Pd⋯AsF3	16.54	−15.52	54	−4.35	15	−8.85	31	−12.18
Cl2(Phen)Pd⋯SbF3	25.37	−23.51	56	−4.51	11	−13.79	33	−16.44
Cl2(Phen)Pd⋯SF2	12.61	−9.42	45	−3.58	17	−8.01	38	−8.40
Cl2(Phen)Pd⋯SeF2	21.64	−16.60	47	−4.03	11	−14.69	42	−13.68
Cl2(Phen)Pd⋯TeF2	29.33	−23.02	50	−4.26	9	−18.87	41	−16.81
Cl2(Phen)Pd⋯ClF	30.43	−16.85	38	−2.62	6	−25.16	56	−14.20
Cl2(Phen)Pd⋯BrF	31.09	−19.16	40	−3.06	6	−26.11	54	−17.24
Cl2(Phen)Pd⋯IF	30.26	−20.64	44	−3.40	7	−23.14	49	−16.91
Br2(Phen)Pd⋯PF3	8.67	−7.33	48	−4.13	27	−3.95	26	−6.74
Br2(Phen)Pd⋯AsF3	15.98	−14.83	53	−4.63	16	−8.76	31	−12.25
Br2(Phen)Pd⋯SbF3	24.23	−22.26	55	−4.83	12	−13.57	33	−16.44
Br2(Phen)Pd⋯SF2	12.24	−9.09	44	−3.73	18	−7.87	38	−8.46
Br2(Phen)Pd⋯SeF2	21.28	−16.14	46	−4.21	12	−14.71	42	−13.78
Br2(Phen)Pd⋯TeF2	29.03	−22.43	49	−4.48	10	−19.04	41	−16.93
Br2(Phen)Pd⋯ClF	30.40	−16.75	37	−2.73	6	−25.35	57	−14.43
Br2(Phen)Pd⋯BrF	31.13	−19.10	39	−3.20	7	−26.44	54	−17.62
Br2(Phen)Pd⋯IF	30.43	−20.69	43	−3.56	7	−23.54	49	−17.36
I2(Phen)Pd⋯PF3	8.84	−7.38	47	−4.31	28	−3.92	25	−6.76
I2(Phen)Pd⋯AsF3	15.39	−14.22	52	−4.88	18	−8.36	30	−12.07
I2(Phen)Pd⋯SbF3	23.62	−21.42	54	−5.10	13	−13.19	33	−16.09
I2(Phen)Pd⋯SF2	12.63	−9.27	44	−3.86	18	−7.98	38	−8.49
I2(Phen)Pd⋯SeF2	22.08	−16.52	46	−4.39	12	−15.02	42	−13.86
I2(Phen)Pd⋯TeF2	30.13	−22.88	49	−4.68	10	−19.58	42	−17.02
I2(Phen)Pd⋯ClF	32.31	−17.95	38	−2.83	6	−26.63	56	−15.09
I2(Phen)Pd⋯BrF	33.03	−20.42	40	−3.31	6	−27.62	54	−18.33
I2(Phen)Pd⋯IF	32.46	−22.22	44	−3.67	7	−24.67	49	−18.10
Cl2(Phen)Pt⋯PF3	11.23	−9.17	50	−4.13	22	−5.10	28	−7.17
Cl2(Phen)Pt⋯AsF3	22.42	−19.42	55	−4.60	13	−11.46	32	−13.06
Cl2(Phen)Pt⋯SbF3	33.12	−28.71	57	−4.80	9	−17.16	34	−17.54
Cl2(Phen)Pt⋯SF2	21.37	−14.78	47	−3.71	12	−12.93	41	−10.05
Cl2(Phen)Pt⋯SeF2	33.26	−24.17	49	−4.21	9	−21.05	43	−16.17
Cl2(Phen)Pt⋯TeF2	40.82	−30.91	51	−4.60	8	−24.88	41	−19.57
Cl2(Phen)Pt⋯ClF	48.04	−27.13	41	−2.67	4	−36.44	55	−18.21
Cl2(Phen)Pt⋯BrF	45.30	−28.52	43	−3.12	5	−34.53	52	−20.87
Cl2(Phen)Pt⋯IF	42.80	−29.38	47	−3.51	6	−30.15	48	−20.24
Br2(Phen)Pt⋯PF3	10.91	−8.94	49	−4.28	23	−5.03	28	−7.34
Br2(Phen)Pt⋯AsF3	21.72	−18.77	54	−4.85	14	−11.34	32	−13.23
Br2(Phen)Pt⋯SbF3	32.19	−27.85	56	−5.07	10	−17.08	34	−17.81
Br2(Phen)Pt⋯SF2	20.52	−14.18	46	−3.85	13	−12.56	41	−10.07
Br2(Phen)Pt⋯SeF2	32.66	−23.60	48	−4.39	9	−20.95	43	−16.28
Br2(Phen)Pt⋯TeF2	40.47	−30.45	51	−4.80	8	−25.01	42	−19.79
Br2(Phen)Pt⋯ClF	47.85	−26.91	41	−2.78	4	−36.59	55	−18.44
Br2(Phen)Pt⋯BrF	45.21	−28.35	43	−3.26	5	−34.82	52	−21.21
Br2(Phen)Pt⋯IF	42.77	−29.26	46	−3.67	6	−30.47	48	−20.64
I2(Phen)Pt⋯PF3	10.52	−8.78	49	−4.47	25	−4.77	26	−7.51
I2(Phen)Pt⋯AsF3	20.95	−18.26	53	−5.08	15	−10.88	32	−13.28
I2(Phen)Pt⋯SbF3	31.61	−27.38	55	−5.30	11	−16.76	34	−17.84
I2(Phen)Pt⋯SF2	20.13	−14.11	47	−3.98	13	−12.18	40	−10.14
I2(Phen)Pt⋯SeF2	33.13	−24.00	48	−4.54	9	−21.03	42	−16.44
I2(Phen)Pt⋯TeF2	41.46	−31.22	51	−4.96	8	−25.38	41	−20.10
I2(Phen)Pt⋯ClF	49.30	−28.02	41	−2.88	4	−37.45	55	−19.05
I2(Phen)Pt⋯BrF	46.41	−29.46	43	−3.37	5	−35.42	52	−21.85
I2(Phen)Pt⋯IF	44.05	−30.55	47	−3.79	6	−31.05	47	−21.35

---

In general terms, the electrostatic attraction accounts for roughly half of the total. This percentage is greatest for the ZBs, and smallest for the XBs. One also may note that this same quantity rises as the A atom grows in size. E_OI is a bit more variable: it is smaller than E_ES for the ZBs and YBs, but larger for the XBs. The dispersion's contribution is quite variable. Although its magnitude grows slowly with the increasing size of the A atom, its percentage contribution drops as both E_ES and E_OI climb much more quickly. As another point of comparison, E_dis diminishes as one progresses from the pnicogen and then to the chalcogen and halogen bonds.

Correlations

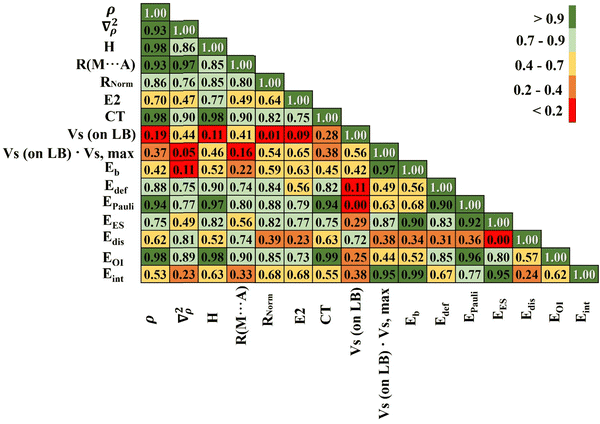
The foregoing has documented a number of different parameters that are all related in one way or another to the strength of the noncovalent bond. It is instructive to consider how all of these parameters correlate with one another. This overall correlation scheme is presented in Fig. 3 as a matrix diagram that indicates the absolute value of correlation coefficient (|R|) between each pair of parameters by way of a color scheme for ease of interpretation. Dark green indicates |R| > 0.9, and lighter colors, transitioning to orange and red, show deteriorating correlations, as explained by the inset to Fig. 3.

Fig. 3 Correlation coefficients of selected features for all complexes examined. The absolute values of the correlation coefficients are presented on a five-point scale: high values are green and low values are red.

The bottom row of Fig. 3 relates each of the various properties to the overall interaction energy. The binding energy E_b correlates very well, as one would expect, differing from E_int only by deformation energy. The other parameter with a correlation coefficient exceeding 0.9 is the electrostatic component, with |R| = 0.95. This correlation is much better than with the orbital interaction energy or the dispersion component. Also the product of V_s (from Table 2) and V_s,max (from Table 1) very well correlate with the value of the interaction energy. This additionally indicates that an important ingredient of this interaction is an electrostatic term (which is dominant in the case of complexes containing a pnicogen or chalcogen bond).

The correlations with the QTAIM quantities, H (the density of total electron energy), ρBCP, and ∇²ρ are surprisingly poor, and that with the MEP minimum on the base is only 0.60. The correlation between E_int and R_norm, in which the intermolecular distance is divided by the sum of vdW radii, is far superior to that for the simple and uncorrected R(M…A). For CT, unsurprisingly, the best correlation was found with E_oi. Moreover, CT correlates very well with electron density as well as the total energy density at the BCP (bond critical point). There is a good deal of internal agreement between the various measures of bond strength arising from QTAIM analysis, as shown by the dark green regions in the upper portion of the triangle in Fig. 3, which in turn are strongly correlated with the intermolecular distance R. Some of the QTAIM parameters also correlate well with the Pauli repulsion and orbital interaction component E_OI.

Part of the reason for some of the mediocre correlations is the mixing together of all three sorts of noncovalent bonds together in Fig. 3. There is a good deal of improvement if only one sort of bond is considered as for example the series of ZB complexes in Fig. 4. Most of the colors are either dark or light green as compared to numerous yellow and red boxes in Fig. 3. In this particular group of complexes there is a very high degree of correlation between E_int and the various energy components, with ∣R∣ > 0.97 for all with the exception of 0.80 for the dispersion energy. The correlations with the three QTAIM quantities are all excellent as well, as is that with the intermolecular distance and the MEP on the base, all with ∣R∣ exceeding 0.80. For complexes stabilized by the pnicogen bond, the correlation coefficient between E_int and the normalized distance is 0.97. Analogous data are presented in Fig. S8 and S9 (ESI†) for the chalcogen and halogen-bonded complexes, respectively. Although not quite as good as the pnicogen bond correlations in Fig. 4, there is still a substantial improvement when compared to Fig. 3 with all three bonding types mixed together.

Fig. 4 Correlation coefficients of selected features obtained for complexes containing a pnicogen bond. The absolute values of the correlation coefficient are presented on a five-point scale: high values are green and low values are red.

Discussion

The application of theoretical quantum calculations reveals a number of intriguing similarities and differences between Pd and Pt metals as electron donors as they engage in pnicogen, chalcogen and halogen bonds from their square planar coordination within a phenanthroline framework. The results can be placed in a broader context when compared with prior works dealing with the general concept of σ-hole donor⋯d⁸ transition metal interactions in molecular complexes.

The MEP protocol is commonly utilized to help predict the geometry of complexes and even the strength of noncovalent interactions, especially those based on σ-hole interactions. A study by Bauza and Frontera⁴⁸ of crystal fragments containing Ni, Pd and Pt atoms computed a negative MEP (from −25 to −43 kcal mol⁻¹) above these metal atoms which reinforces our contention that these systems can be considered as full-fledged Lewis bases. Their MEPs were considerably more negative than in the systems discussed above with negative potentials in the −12 to −19 kcal mol⁻¹ range. As in the prior work our own calculations found intermolecular distances that were smaller than the vdW radius sums. A more recent publication⁴⁹ computed halogen bond energies of Pt(II), Ni(II) and Pd(II) in square planar systems in the range between 2.5 and 6.4 kcal mol⁻¹ when the coordinates were extracted directly from crystal coordinates. These quantities are somewhat smaller than those computed here, attributed in part to our use of optimized distances. Nonetheless, their data were consistent with our findings that Pt binds more tightly than does Pd. As another point of similarity, the electron density at the BCP connecting the halogen atom to M is comparable to the values obtained here. A partitioning of their total interaction energies suggested a significant orbital contribution (37%) when the Pt d_z² orbital donates charge to iodopentafluorobenzene. The results obtained at the PBE0-D3/def2-TZVP level for models constructed based on X-ray structures are comparable to those obtained in our work.

Ivanov et al. recently described the behavior of metals as σ-hole acceptors in crystal structures taken from the CSD database.⁴⁵ The authors identified several crystal structures which contained X⋯d_z² [Pd^II] and X⋯d_z² [Pt^II] halogen bonds. The Br⋯Pt distance (3.365 Å) is slightly shorter and its directionality is subtly higher than that of I⋯Pt (3.439 Å) in refcodes LIHMIB⁸⁷ and UKEKIG⁸⁸ structures, respectively. The study suggested that the Br⋯Pt interaction is slightly weaker than I⋯Pt. The I⋯Pt interaction can be as strong as 15.0 kcal mol⁻¹ while the energy of the Br⋯Pd contact reaches up to 9.6 kcal mol⁻¹, a difference attributed to both the stronger nucleophilic character of Pt and deeper σ-hole at the I center.

In the study by Boyarskiy⁸⁹ several trans-[MCl₂(NCNMe₂)₂]·2CHX₃ (M = Pd, Pt and X= Br, I) complexes were investigated, and the metallic center was found to be a σ-hole acceptor. QTAIM results⁸⁹ revealed the presence of BCPs in trans-[MCl₂(NCNMe₂)₂]·2CHX₃ complexes between Pd and Br or I atoms (ρ at BCP varies between 0.012 and 0.013 au). Concerning the results reported in the current work for complexes with Pd, the ρ at BCPs varies between 0.010 and 0.050 au (see Tables S5 and S6, ESI†). The relationship between a classical C–I⋯I XB and I⋯[d_z²-Pt^II] metal-involving XB in trans-[PtI₂(NCN(CH₂)₅)₂]·2CHI₃ was discussed by Eliseeva et al.⁵³ In this complex, the source of stabilization is the charge transfer from the metal d_z² orbital. Therefore, the noted interactions are designated as C–I⋯[d_z²-Pt^II] metal-involving XBs, where Pt^II acts as a d_z²-nucleophile. DFT results obtained at the PBE-D3/jorge-TZP-DKH level of theory showed that the Pt⋯I distance is equal to 3.5131 Å which is longer than the I⋯Pt distances computed here which are in turn all less than 3.0 Å. QTAIM analysis placed these interactions in the same magnitude as typical I⋯I dihalogen bonds in the supramolecular assembly.

In the work of Freindorf et al.⁵² I₂ and d⁸ transition-metal van Koten's pincer complexes were studied. NBO analysis revealed that the largest interorbital energy transfer from the d_z² Pt orbital to σ*(I–I) reached 55.0 kcal mol⁻¹. Binding energies for all 20 studied complexes fluctuated between 11 and 36 kcal mol⁻¹. In our own calculations, the Cl₂(Phen)Pt⋯IF complex is characterized by similar E2 of 54.2 kcal mol⁻¹, albeit with a different interaction energy. Other systems exhibiting a I⋯Pd motif⁵⁰ include trans-(O,C)-[Pd(ppz)(μ-O∩N)]₂ and trans-(E,N)-[Pd(ppz)(μ-E∩N)]₂ where (E∩N is a deprotonated 2-substituted pyridine; E = S, Se; Hppz = 1-phenylpyrazole). The I⋯Pd and I⋯E interactions had similar strength but the former was controlled mainly by dispersion forces while the latter by the electrostatic component. I⋯Pt interactions have been found by Bulatova et al.⁹⁰ in the PtX₂COD⋯1,4-diiodotetrafluorobenzene (X = Cl, Br, I, COD= 1,5-cyclooctadiene) adducts. Metal-involved interactions acted in this case as secondary contacts as they were weaker than dihalogen bonds according to the combination of ELF plus QTAIM analyses. The ratio of the I⋯Pt distances versus the sum of the van der Waals radii of the iodine and platinum atoms was more than 1.

A chalcogen bond with a metal nucleophile has been investigated by Rozhkov et al.⁵⁶ in two isostructural cocrystal complexes between [Pt(ppy)(acac)] or [Pt(ppy)(tmhd)] and 2·2/3(4-NC₅F₄)₂Se and 2·(4-NC₅F₄)₂Te units. PBE0D3BJ calculations of the X-ray structures found NBO values of E(2) concerning donation from the Pt d_z² orbital to σ*(Se/Te-C) in the range of 3.6 to 11 kcal mol⁻¹, with total interaction energies between 7 and 12 kcal mol⁻¹. A study by Burguera et al. indicated that Sb also can act as an electron donor in the square planar Pt(II)-complexes creating a metal-assisted pnicogen bond scheme.⁵⁷ The NBO results for square planar complexes revealed a small orbital contribution (E2 = 1.07 kcal mol⁻¹) due to a donation from the Pt d_z² orbital to σ*(Sb–Cl). The QTAIM and NCI analyses confirmed the existence of a Pt⋯Sb interaction that is comparable to our complexes with platinum. The QTAIM data reported in that work are in agreement with values in the current study (see Tables S5 and S6, ESI†).

Conclusions

The Pd and Pt atoms in their square planar coordinations can function as efficient electron donors within the context of pnicogen, chalcogen, and halogen bonds. The electrostatic potential above these atoms is negative, despite their formal positive atomic charge, and so fully capable of attracting the positive σ-hole of the Lewis acid molecule. The HOMA index values reveal that the ZB, YB and XB bonds have a small but noticeable influence on the aromaticity changes in the rings. The binding reaction is facilitated by a certain amount of charge transfer from the occupied d_z² orbital of M to the σ*(AF) antibonding orbital of the Lewis acid. The interaction energies of these noncovalent bonds are substantial, in the 6–19 kcal mol⁻¹ range. Although these energies do not vary much from one class of bond to the other, there is a clear pattern of strengthening as the Lewis acid atom containing the σ-hole becomes heavier. Pt engages in somewhat stronger bonds than Pd does by some 10–50%. The binding is attributed in roughly equal parts to electrostatic attraction and orbital interactions, with a smaller contribution arising from dispersion.

Funding

This research was funded by the Polish Ministry of Science and Higher Education for the Faculty of Chemistry of Wroclaw University of Science and Technology under Grant No. 8211104160/K14W03D10 and by the US National Science Foundation under Grant No. 1954310.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work was financed in part by a statutory activity subsidy from the Polish Ministry of Science and Higher Education for the Faculty of Chemistry of Wroclaw University of Science and Technology and by the US National Science Foundation under Grant No. 1954310. A generous allotment of computer time from the Wroclaw Supercomputer and Networking Center is acknowledged.

References

1. G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421.
2. T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76.
3. S. Pullanchery, S. Kulik, B. Rehl, A. Hassanali and S. Roke, Science, 2021, 374, 1366.
4. T. Kato, N. Mizoshita and K. Kishimoto, Angew. Chem., Int. Ed., 2006, 45, 38–68.
5. E. Arunan, G. R. Desiraju, R. A. Klein, J. Sadlej, S. Scheiner, I. Alkorta, D. C. Clary, R. H. Crabtree, J. J. Dannenber, P. Hobza, H. G. Kjaergaard, A. C. Legon, B. Mennucci and D. J. Nesbitt, Pure Appl. Chem., 2011, 83, 1637–1641.
6. A. W. Baker and D. E. Bublitz, Spectrochim. Acta, 1966, 22, 1787–1799.
7. E. A. Hill and J. H. Richards, J. Am. Chem. Soc., 1961, 83, 4216–4221.
8. E. A. Hill and J. H. Richards, J. Am. Chem. Soc., 1961, 83, 3840–3846.
9. D. S. Trifan and R. Bacskai, J. Am. Chem. Soc., 1960, 82, 5010–5011.
10. L. Brammer, Dalton Trans., 2003, 3145–3157,  10.1039/B303006G.
11. F. Calderazzo, G. Fachinetti, F. Marchetti and P. F. Zanazzi, J. Chem. Soc., Chem. Commun., 1981, 181–183,  10.1039/C39810000181.
12. F. Cecconi, C. A. Ghilardi, P. Innocenti, C. Mealli, S. Midollini and A. Orlandini, Inorg. Chem., 1984, 23, 922–929.
13. L. Brammer, D. Zhao, F. T. Ladipo and J. Braddock-Wilking, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1995, 51, 632–640.
14. M. Brookhart, M. L. H. Green and G. Parkin, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6908–6914.
15. F. Groenewald, J. Dillen, H. G. Raubenheimer and C. Esterhuysen, Angew. Chem., Int. Ed., 2016, 55, 1694–1698.
16. F. Groenewald, H. G. Raubenheimer, J. Dillen and C. Esterhuysen, Dalton Trans., 2017, 46, 4960–4967.
17. M. Rigoulet, S. Massou, E. D. Sosa Carrizo, S. Mallet-Ladeira, A. Amgoune, K. Miqueu and D. Bourissou, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 46–51.
18. M. Straka, E. Andris, J. Vícha, A. Růžička, J. Roithová and L. Rulíšek, Angew. Chem., Int. Ed., 2019, 58, 2011–2016.
19. R. Sánchez-de-Armas and M. S. G. Ahlquist, Phys. Chem. Chem. Phys., 2015, 17, 812–816.
20. P. Vidossich, M. Á. Ortuño, G. Ujaque and A. Lledós, ChemPhysChem, 2011, 12, 1666–1668.
21. H. Ogasawara, B. Brena, D. Nordlund, M. Nyberg, A. Pelmenschikov, L. G. M. Pettersson and A. Nilsson, Phys. Rev. Lett., 2002, 89, 276102.
22. L. Brammer, J. M. Charnock, P. L. Goggin, R. J. Goodfellow, A. G. Orpen and T. F. Koetzle, J. Chem. Soc., Dalton Trans., 1991, 1789–1798,  10.1039/DT9910001789.
23. T. Brinck, J. S. Murray and P. Politzer, Int. J. Quantum Chem., 1992, 44, 57–64.
24. J. S. Murray, P. Lane, T. Clark and P. Politzer, J. Mol. Model., 2007, 13, 1033–1038.
25. J. S. Murray, P. Lane and P. Politzer, Int. J. Quantum Chem., 2007, 107, 2286–2292.
26. P. Politzer, P. Lane, M. C. Concha, Y. G. Ma and J. S. Murray, J. Mol. Model., 2007, 13, 305–311.
27. P. Politzer, J. S. Murray and M. C. Concha, J. Mol. Model., 2007, 13, 643–650.
28. P. Politzer, J. S. Murray and P. Lane, Int. J. Quantum Chem., 2007, 107, 3046–3052.
29. N. Liu, Q. Z. Li and S. A. C. McDowell, Front. Chem., 2020, 8, 608486.
30. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2010, 12, 7748–7757.
31. J. S. Murray and P. Politzer, WIREs Comput. Mol. Sci., 2011, 1, 153–163.
32. J. S. Murray, P. Lane, T. Clark, K. E. Riley and P. Politzer, J. Mol. Model., 2012, 18, 541–548.
33. T. S. Spilfogel, H. M. Titi and T. Friščić, Cryst. Growth Des., 2021, 21, 1810–1832.
34. N. Tarannam, R. Shukla and S. Kozuch, Phys. Chem. Chem. Phys., 2021, 23, 19948–19963.
35. S. Scheiner, Phys. Chem. Chem. Phys., 2023, 25, 7184–7194.
36. M. A. A. Ibrahim, N. A. M. Moussa, S. M. A. Saad, M. N. Ahmed, A. M. Shawky, M. E. S. Soliman, G. A. H. Mekhemer and A.-S. S. M. Rady, ACS Omega, 2022, 7, 11264–11275.
37. M. M. Szczęśniak and G. Chałasinski, Front. Chem., 2022, 10, 858946.
38. V. Tabernero, M. Teresa Muñoz, M. Palenzuela, R. M. Gomila, A. Frontera and M. E. G. Mosquera, Dalton Trans., 2023, 52, 551–555.
39. A. Frontera and A. Bauzá, Crystals, 2021, 11, 1205.
40. J. A. Fernández Riveras, A. Frontera and A. Bauzá, Phys. Chem. Chem. Phys., 2021, 23, 17656–17662.
41. S. Scheiner, Chem. Phys. Chem., 2023, e202200936.
42. K. T. Mahmudov, A. V. Gurbanov, V. A. Aliyeva, M. F. C. Guedes da Silva, G. Resnati and A. J. L. Pombeiro, Coord. Chem. Rev., 2022, 464, 214556.
43. R. M. Gomila and A. Frontera, Molecules, 2022, 27, 6597.
44. A. Frontera, Crystals, 2020, 10, 721.
45. D. M. Ivanov, N. A. Bokach, V. Y. Kukushkin and A. Frontera, Chem. – Eur. J., 2022, 28, e202103173.
46. S. H. Jungbauer and S. M. Huber, J. Am. Chem. Soc., 2015, 137, 12110–12120.
47. Z. M. Bikbaeva, D. M. Ivanov, A. S. Novikov, I. V. Ananyev, N. A. Bokach and V. Y. Kukushkin, Inorg. Chem., 2017, 56, 13562–13578.
48. A. Bauzá and A. Frontera, Supramolecular Assemblies Based on Electrostatic Interactions, ed. M. A. Aboudzadeh and A. Frontera, Springer International Publishing, Cham, 2022, pp. 203–241 DOI:10.1007/978-3-031-00657-9_7.
49. I. Benito, R. M. Gomila and A. Frontera, CrystEngComm, 2022, 24, 4440–4446.
50. E. A. Katlenok, A. V. Rozhkov, O. V. Levin, M. Haukka, M. L. Kuznetsov and V. Y. Kukushkin, Cryst. Growth Des., 2021, 21, 1159–1177.
51. E. Bulatov, T. Eskelinen, A. Y. Ivanov, P. M. Tolstoy, E. Kalenius, P. Hirva and M. Haukka, Chem. Phys. Chem., 2021, 22, 2044–2049.
52. M. Freindorf, S. Yannacone, V. Oliveira, N. Verma and E. Kraka, Crystals, 2021, 11, 4.
53. A. A. Eliseeva, M. A. Khazanova, A. M. Cheranyova, I. S. Aliyarova, R. I. Kravchuk, E. S. Oganesyan, A. V. Ryabykh, O. A. Maslova, D. M. Ivanov and S. A. Beznosyuk, Crystals, 2023, 13, 712.
54. G. Li, J. H. Stenlid, M. S. G. Ahlquist and T. Brinck, J. Phys. Chem. C, 2020, 124, 14696–14705.
55. A. Frontera and A. Bauza, Int. J. Mol. Sci., 2022, 23, 4188.
56. A. V. Rozhkov, E. A. Katlenok, M. V. Zhmykhova, A. Y. Ivanov, M. L. Kuznetsov, N. A. Bokach and V. Y. Kukushkin, J. Am. Chem. Soc., 2021, 143, 15701–15710.
57. S. Burguera, R. M. Gomila, A. Bauzá and A. Frontera, Inorganics, 2023, 11, 2.
58. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
59. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
60. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
61. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
62. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110(13), 6158–6170.
63. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian, Inc., Wallingford, CT, USA, 2016.
64. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
65. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
66. R. Bader, Atoms In Molecules. A Quantum Theory, Clarendon Press, Oxford, 1990.
67. R. F. W. Bader, J. Phys. Chem. A, 1998, 102, 7314–7323.
68. R. F. W. Bader and H. Essen, J. Chem. Phys., 1984, 80, 1943–1960.
69. A. T. Keith, AIMAll (Version 14.11.23), TK Gristmill Software, Overland Park, KS, USA, 2014.
70. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
71. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, P. Karafiloglou, C. R. Landis and F. Weinhold, NBO 7.0 Madison, Theoretical Chemistry Institute, University of Wisconsin, USA, 2018.
72. C. F. Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403.
73. E. v Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610.
74. K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325–340.
75. ADF 2014, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2014.
76. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
77. J. Kruszewski and T. M. Krygowski, Tetrahedron Lett., 1972, 3839.
78. G. A. Zhurko, https://www.chemcraftprog.com.
79. IQmol - free open-source molecular editor and visualization package, https://iqmol.org.
80. C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466–470.
81. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
82. M. Rimoldi, F. Ragaini, E. Gallo, F. Ferretti, P. Macchi and N. Casati, Dalton Trans., 2012, 41, 3648–3658.
83. R. J. H. Clark, F. P. Fanizzi, G. Natile, C. Pacifico, C. G. Vanrooyen and D. A. Tocher, Inorg. Chim. Acta, 1995, 235, 205–213.
84. K. Ha, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2012, 68, 1144.
85. J. Poater, M. Duran and M. Sola, Front. Chem., 2018, 6, 561.
86. T. M. Krygowski, M. Cyranski, A. Ciesielski, B. Swirska and P. Leszczynski, J. Chem. Inf. Comput. Sci., 1996, 36, 1135–1141.
87. S. V. Baykov, U. Dabranskaya, D. M. Ivanov, A. S. Novikov and V. P. Boyarskiy, Cryst. Growth Des., 2018, 18, 5973–5980.
88. D. M. Ivanov, A. S. Novikov, I. V. Ananyev, Y. V. Kirina and V. Y. Kukushkin, Chem. Commun., 2016, 52, 5565–5568.
89. S. V. Baykov, U. Dabranskaya, D. M. Ivanov, A. S. Novikov and V. P. Boyarskiy, Cryst. Growth Des., 2018, 18, 5973–5980.
90. M. Bulatova, D. M. Ivanov and M. Haukka, Cryst. Growth Des., 2021, 21, 974–987.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp03171c

---