Open Access Article
Open Access ArticleMolecular dynamics investigation of benzoic acid in confined spaces†
Luca
Sironi
 a,
Giovanni
Macetti
a,
Giovanni
Macetti
 a and
Leonardo
Lo Presti
a and
Leonardo
Lo Presti
 *ab
*ab
aUniversità degli Studi di Milano, Department of Chemistry, Via Golgi 19, 20133 Milano, Italy. E-mail: leonardo.lopresti@unimi.it
bIstituto Nazionale di Fisica Nucleare (INFN), Laboratori Nazionali di Frascati, Frascati, Italy
First published on 26th September 2023
Abstract
Classical molecular dynamics simulations are carried out to investigate the aggregation of supercooled benzoic acid in confined spaces. Nanocavities, nanotubes and nanolayers are defined by restricting the periodicity of the simulation to zero, one or two dimensions, with boundaries set by adjustable, general, and computationally cheap van der Waals barriers. The effect of different confinement geometries is explored. It is found that the confinement impacts the liquid collective dynamics, strengthening the correlations that affect the motion of distant molecules. Overall, confinement determines up to a tenfold increase of the viscosity of the liquid and strongly slows down the rotational correlation times. Aggregation mediated by interactions with the walls and partial polarization of the liquid are observed. Additionally, transitions to high-density liquid states occur when stiffer barriers are used. In general, a reduced accessible amount of phase space fosters the struggle for a closer packing to relieve unfavorable atom–atom contacts, while maximizing the attractive ones. In benzoic acid, this implies that the hydrogen bond network is organized more efficiently in high density states.
1. Introduction
The past twenty years witnessed impressive advances in nanotechnologies.1 Such achievements would have not been possible without the development of techniques to manipulate matter down to the nanoscale.1,2 In particular, nano-confinement is now attracting attention as a cheap and promising strategy to produce tailored materials through the fine control of the crystallization environment. This can be realized using either soft interfaces set up by micelles, droplets, vesicles, and other sub-micrometer structures,3 or hard scaffolds, including nanopores, nanochannels and the interstices among beads of block copolymers.3–5Confinement affects the inner dynamics of the liquid phase:6 the amount of surface molecules is significantly increased with respect to the unconfined liquid, and liquid-barrier interactions may be set up, fostering local ordering effects. For example, surface freezing is enhanced when n-alkanes are crystallized in hard microcapsules,3,7,8 producing nucleation centers that may nurture plastic phases before developing a fully ordered crystal. In addition, some packing modes may be suppressed or favored, resulting either in the selective crystallization of a specific polymorph,9 or in the stabilization of metastable phases.10 The design of micro- and nano-vessels with different volumes, shapes, and chemically specific walls, paves the way to endless opportunities in the synthesis of uniformly oriented molecular arrays,11,12 with applications that range from drugs and proteins to hybrid metal–organic scaffolds and energetic materials.13
At the same time, significant experimental efforts were spent on the investigation of the structure and dynamics of confined molecular liquids, including water,14 alcohols,15 and other organic solvents.16 The techniques employed were mainly X-ray scattering,17 neutron scattering18,19 and NMR,20 while various confinement conditions were tested, such as mesoporous silica (hydrophilic surface),21 ordered mesoporous carbon (hydrophobic surface),22 hybrid mesoporous systems.23 Confined crystallization is also a valuable tool to investigate the initial stages of nucleation at a length scale comparable to that of the nuclei themselves. Recent breakthroughs include the use of time-resolved TEM to monitor the formation of NaCl nuclei within carbon nanotubes,24 and of micro-Raman spectroscopy to study the early aggregation of glycine in solution.25–28 Unfortunately, understanding nucleation is an overwhelmingly complex problem, as both metastable structures and unstable intermediates, to which experimental probes are mostly blind, are involved in the process.
The design of complex experiments in these fields testifies to the increasingly pressing need to understand the behavior of condensed phases of matter in confined space, likely prompted by the vast landscape of technological implications such knowledge would bear. Synergy between experimental evidence and computational predictions may help to shed light on these issues. Computational methods indeed may give precious hints to disentangle complexity out of the experimental outcomes.
Classical molecular dynamics (MD) is here employed to study self-aggregation of small molecules in confined spaces. The aim is to understand how confinement impacts on the early stages of self-recognition, shedding light on the nature and dynamics of transient supramolecular clusters lying on possible paths toward crystallization.29 Benzoic acid (BZA, C7H6O2, M.W. 122.12 g mol−1, m.p. ∼395 K, Fig. 1) was chosen as a suitable test case, as it lacks conformational complexity and can easily form strong hydrogen bonds.30
General confinement conditions were set up through computationally cheap neutral van der Waals barriers; the new algorithm was embedded in the free MiCMoS software for condensed-phase studies of small organic molecules.31 The user may control the periodicity of the confined space, allowing the simulation of a nanolayer, a nanotube or a nanocavity, as well as the distance among the barriers and their stiffness. Up to 500 ps-long MD trajectories were run on a supercooled liquid at 350 K, under the assumption of local equilibrium, that is, that equilibrium conditions hold on a space-time scale larger than point fluctuations, but considerably small with respect to the real macroscopic system. This assumption is reasonable considering the dimensions adopted for the edge of the simulation box (5 nm or less, see below). As shown below, conditions of local equilibrium are generally satisfied, except for some examples discussed in detail in Section 3.5. The results are compared with those of the unconfined liquid.
2. Materials and methods
2.1 General parameters of the MD simulations
The topology of BZA corresponding to the experimental crystal structure at 300 K was used throughout (P21/c; Cambridge Structural Database reference code BENZAC0232). The MD simulations of the liquid phases were carried out at constant p, T and number of particles (NpT) conditions with the Milano Chemistry Molecular Simulation (MiCMoS) v2.1 suite of programs.31,33 When periodic boundary conditions were not applied, “NVT-like” simulations were performed instead, where the volume was restrained by applying force constants to the barriers (see Section 2.2 below and Section S1 in the ESI†). All the simulations were run in parallel mode, with 4–8 threads each. The same box34 containing 432 BZA molecules at 350 K was used as a starting point under the same assumptions of local equilibrium and manipulated, when necessary, with MiCMoS service modules to build smaller or larger boxes with the desired shape and dimensions (Section 2.2). It is important to note that liquid BZA at 350 K is not at thermodynamic equilibrium. We are implicitly assuming that the local equilibrium approximation is valid, though (see the Introduction). As this is generally the case in the spacetime scale of our simulations, structural properties can be safely extracted by averaging over the trajectories sampling these pseudo-stationary states.The temperature was high enough to keep liquid the BZA ensemble, as testified by the viscosity estimates (Sections 3.1 and 3.2). At the same time, deep supercooling ensures that (meta-)stable clusters are observable, as they are not destroyed at once by thermal smearing. The Lennard-Jones–Coulomb (LJC) force field35 was employed throughout, in conjunction with atomic charges fitted against the electrostatic potential of the isolated molecule at the MP2/6-31G(p,d) level of theory obtained with Gaussian16 package.36 Temperature and pressure (when applicable) were both controlled by Berendsen-like rescaling, with relaxation time τ = 0.6 ps and compressibility coefficient μ0 = 0.4 atm−1. Results of some test runs were also compared with those obtained using the stochastic Bussi–Donadio–Parrinello thermostat.37 A leap-frog integrator with time steps of 1 × 10−3 ps was employed. A 16.0 Å cutoff was applied to molecular centers of mass to compute intermolecular energies, with sums running on entire molecules to ensure electroneutrality.
The bulk liquid served as a reference against the confined phases (see below). A 500 ps–long trajectory was produced by evolving the starting box of 432 BZA molecules at 350 K (see above) under full periodic boundary conditions. The same system was also equilibrated at the same temperature with Gromacs (all-atom gromos54a7 force field38) to provide an independent estimate of some crucial bulk properties.39 Full details of the Gromacs calculations were deposited in the ESI† (Section S3).
2.2 The confinement algorithm
Confinement is obtained thanks to van der Waals barriers composed of massless neutral pseudo-atoms, or “pixels”, ordered on an equispaced grid. The C6, C12 Lennard-Jones parameters of the pixels can be chosen among all the atom types available in MiCMoS, while the pixel radius is user-defined. In this work, carbon atom parameters were used throughout, including the corresponding van der Waals radius (1.77 Å) for the pixel dimensions. If desired, the attractive part of the Lennard Jones potential can be switched off to decouple the effect of confinement from that of surface adsorption.Simulations are currently restricted to spaces bound by orthogonal barriers, but more general shapes will be introduced in future MiCMoS releases. By default, the starting simulation boxes have a roughly cubic shape. The starting distances are set automatically by the program, according to the desired packing efficiency, Cpack,40 given the number of molecules in the model. The number of pixels within each barrier is computed as the ratio between the edge of the square box boundary and the user-selected pixel diameter. By defining the number of molecules in their box, the user can always tune the starting barrier–barrier distances, that is, the confinement size for a given packing efficiency (see also Section S1, ESI†). If not otherwise specified, the maximum theoretical limit for random packing (Cpack = 0.66)41 is exploited, which for BZA corresponds generally to a confined liquid ∼42 Å thick. When dealing with 1-periodic (nanotube) or 2-periodic (nanolayer) systems, the user can also tune the distance between the barriers along the non-periodic direction(s). In that case, the starting simulation box is automatically reshaped to keep the desired packing efficiency.
Each pixel is always positioned tangentially to the simulation box surface and the whole barriers can stretch or compress along the periodic directions. To avoid their unphysical expansions or contractions, harmonic potentials were used as restraints in the pixels’ planes. These are useful especially at the beginning of the trajectory when the system is not fully equilibrated. A reference value of 3400 kJ mol−1 Å−2, corresponding roughly to an aromatic Csp2–Csp2 stretching, was used throughout. A user-defined empirical damping factor (s‖) is applied to the force constant (0.025 or 0.050 in this work). Symmetric barrier displacements in the direction orthogonal to the pixels’ planes are also allowed. This vibration is subject to the same harmonic restraints, but the user is free to use a different scaling factor (s⊥) with respect to the in-plane deformation, allowing anisotropic dynamics. Examples with anisotropic scaling parameters are described in Section 3.5.
The liquid can be conceptually partitioned into two distinct regions, depending on whether atom-barrier interactions are negligible or not (Fig. 2). We define the “barrier” region as the volume where the absolute atom-pixel interaction energy is >0.001 kJ mol−1, while the “bulk” one corresponds to absolute atom-pixel interaction energies ≤0.001 kJ mol−1.
The choice of the barrier as a grid of unreferenced pixels allows this model to be as general as possible and applicable to both soft and hard confinement scenarios. A similar strategy was employed by Chen and coworkers to simulate the nucleation of polyethylene, where van der Waals walls were composed of frozen particles arranged in a cubic stack with a lattice constant a = 2.835 Å.42 A full description of the confinement algorithm and the required parameter files is available in the ESI† (Section S1).
2.3 Reproducibility
Molecular geometry and MD input files are deposited in the ESI† (Section S2). The new algorithm for confined dynamics is included in the latest release of the MiCMoS package (v2.2), which can be downloaded free of charge upon registration at https://sites.unimi.it/xtal_chem_group/, under the specified citation and use conditions. This ensures complete reproducibility of all the calculations here described.3. Results
Hereinafter, we classify the barriers into two types according to the nature of their potential, namely as full van der Waals (attractive and repulsive) or repulsive-only, according to what parts of the Lennard-Jones potential are active. The discussion is organized as follows. In Sections 3.1–3.2, the nature of the barrier and the degree of confinement (nanolayer, nanotube or nanocavity) are studied by examining translational diffusion and rotational correlation. In Section 3.3, the structure of the liquid is studied in terms of radial distribution function (RDF), hydrogen bonds and local number density. Section 3.4 is devoted to the study of relative orientation between BZA molecules or between molecules and barriers. Finally, in Section 3.5, the role of the barrier stiffness is explored. The same scaling factors (s⊥ = s‖ = 0.025) were employed for both the directions parallel and orthogonal to the barriers, unless specified otherwise (see Methods).3.1 Translational diffusion
Translational diffusion is monitored through the mean square displacement (m.s.d., |r(t) − r(0)|2) of the molecular centers of mass from their initial (t = 0) positions. The diffusion coefficient D(t) at time t reads:33 | (1) |
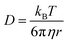 | (2) |
Results are summarized in Fig. 3, while the corresponding numerical entries are deposited in Table S2 (ESI†). The self-diffusion coefficient of the bulk liquid is of the order of 10−10 m2 s−1, which is one hundred times lower than that of other hydrocarbons (∼10−8 m2 s−1).43 Accordingly, the viscosity at 350 K is high, a result compatible with the ∼45 K supercooling. The MiCMoS estimate for η (0.00262(1) Pa s) agrees with the Gromacs prediction (0.00290(6) Pa s). Remarkably, both values are very close with data available in public repositories (0.00315 Pa s at 343.57 K)44 and outcomes from experimental measurements (0.00196 Pa s at 350 K, extrapolated from a linear regression in the 400–450 K range of T).45 The density of the unconfined liquid (Table S1, ESI†) is also correct: the MiCMoS prediction is lower by 4% than the Gromacs one (1.109(8) g cm−3vs. 1.156(1) g cm−3), which is in very good agreement with recent experimental data45 (1.150 g cm−3). This small discrepancy is in line with the expected MiCMoS performances.43
The confinement invariably results in a steep 73–85%-large decrease of the translational self-diffusion, with a consequent increase in viscosity (Fig. 3). Intuitively, the greater the degree of the confinement, that is, the number of non-periodic directions of the simulation box (NNP), the more hampered the translational diffusion. The effect is more evident when a fully repulsive barrier is employed (dashed curves in Fig. 3). This can be attributed to the molecules being forced away from the barriers, leading to a higher level of confinement and a reduced translational diffusion. Necessarily, molecules are squeezed in the free space between the barriers and the total density of the liquid tends to increase. Interestingly, the density increment in confined liquids with fully repulsive barriers (Table S2, ESI†) is on average half with respect to the ones with full van der Waals barriers (+1.7% against +3.5%). This increment is due to a 1–4% reduction of the volume of the simulation box with respect to the unconfined liquid at the equilibrium and it could be explained by the strengthening of specific directional intermolecular interactions, possibly due to partial ordering. In addition, barriers with full van der Waals potential provoke a higher density and a lower viscosity. A possible interpretation is that, on average, molecules are more correlated, allowing concerted movements that end up in a higher diffusion coefficient.
To shed light on this matter, the structure of the liquid must be studied in detail (Sections 3.3–3.5).
 (∼1.26) for the nanocavity simulations (52.8 Å). Full results are reported in the ESI† (Table S3). The same considerations made in Section 3.1 above for smaller boxes hold true. The densities are barely affected by the size of the confined space. However, when greater distances between barriers are set, self-diffusion coefficients increase while viscosities decrease, as expected. In other words, larger barrier-to-barrier distances make the system more alike to the unconfined liquid. More in detail, a 50% increment of the distance between the barriers implies, on average, a ∼35% increase of D, and a ∼26% decrease of η (Table S3, ESI†). The effect is barely appreciable for the repulsive-only nanocavity (NNP = 3), as confinement in all directions prevents most of the translational diffusion and molecules cannot set up attractive interactions with the barriers.
(∼1.26) for the nanocavity simulations (52.8 Å). Full results are reported in the ESI† (Table S3). The same considerations made in Section 3.1 above for smaller boxes hold true. The densities are barely affected by the size of the confined space. However, when greater distances between barriers are set, self-diffusion coefficients increase while viscosities decrease, as expected. In other words, larger barrier-to-barrier distances make the system more alike to the unconfined liquid. More in detail, a 50% increment of the distance between the barriers implies, on average, a ∼35% increase of D, and a ∼26% decrease of η (Table S3, ESI†). The effect is barely appreciable for the repulsive-only nanocavity (NNP = 3), as confinement in all directions prevents most of the translational diffusion and molecules cannot set up attractive interactions with the barriers.
In general, the dimensions of the confined space should produce potentially measurable effects on the liquid dynamics. Comparison of the bulk physicochemical parameters provided by independent estimates confirms the quality of the MiCMoS-LJC computational setup.
3.2 Molecular rotations
The dimensionless rotational correlation function C(t) reads:33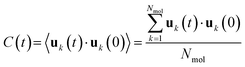 | (3) |
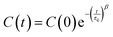 | (4) |
In the unconfined BZA liquid, one must wait at least 400–500 ps before reaching a significant loss of rotational correlation C(t) < 20%, Fig. S1, ESI†). The relaxation is even considerably slower in confined systems (Fig. S2, ESI†). Moreover, the choice of the reference axis has a significant impact on the relaxation time. If we consider the orientation vector v1 along the C1–C4 axis (Fig. 1), which roughly corresponds to the lowest-moment inertial axis and lies in the plane of the phenyl ring, the decay of C(t) is extremely slow, having a value between 70 and 80% for confined simulations after 500 ps and 40% for the unconfined one. On the contrary, when the axis is orthogonal to the phenyl ring (v2), C(t) slowly decreases down to 50–40% in 500 ps for confined simulations and below 20% for the unconfined one (Fig. S2, ESI†). This difference reflects an anisotropic rotational behavior of BZA and can be interpreted in terms of an easier rigid-body libration around the vector v1 and the internal rotation around the C1–C12 bond. These movements do not change the orientation of vector v1, but affect the vector v2, causing a quicker decay in the corresponding rotational correlation function. The behavior of rotational correlation functions for the unconstrained liquid is also qualitatively like that predicted by Gromacs estimates, even though the gromos54a7 force field invariably implies quicker decays (Fig. S1, ESI†). Comparison with Gromacs results gives an idea of possible errors in correlation functions.
The C(t) data was fitted with the KWW stretched exponential function (4). A nonlinear Levenberg–Marquardt least-squares algorithm, as implemented in Fityk 1.3.1,50 was used throughout. Refined estimates for C(0), τc and β are shown in Table S4 (ESI†). The unconfined liquid bears invariably the lowest correlation times, as it should be. The parameters τc‖, β‖ and τc⊥, β⊥ are the correlation times and Kohlrausch exponents associated respectively to the easy libration axis v1 and to the phenyl ring normal v2 (Fig. 1). τc‖'s are of the order of nanoseconds and countercorrelate with β‖: the higher the rotational correlation time, the lower the corresponding Kohlrausch exponent (Fig. S3, ESI†). This is intuitively understandable, as C1–C4 is the direction along which strong intermolecular hydrogen bonds are preferentially set up. Thus, large τc‖'s should mirror persistent hydrogen-bond interactions, as any reorientation would likely destroy short OH⋯O contacts. This slowdown effect is less appreciable for the vector perpendicular to the phenyl ring (v2), as no strong intermolecular interactions exist in this direction. Accordingly, no obvious τc⊥/β⊥ correlations are recognizable (Fig. S3, ESI†) and the characteristic τc⊥'s are much smaller (300–700 ps), reflecting faster orientational changes of the phenyl, partly due to libration around v1 (Fig. S2, ESI†).
The rotational diffusion is always slower in repulsive-only simulations. For example, in the nanolayer τc⊥ undergoes a ∼30% increase, from 390 to 508 ps, upon switching off the attractive barrier-solute potential (Table S4, ESI†). This effect is more evident for nanotubes, where τc⊥ increases from 309 ps to 724 ps, while only a ∼15% large increment, from 568 to 653 ps, is observed for nanocavities. In general, the nature of the barrier significantly affects the rotational correlation time of the confined liquid, but not the Kohlrausch exponent is not affected by the nature of the potential. All the simulations produce β exponents lower than 1, typically in the 0.5–0.7 range, with a few exceptions. Nanolayers have slightly higher β⊥ values with respect to all the other systems, including bulk liquid (∼0.65 vs. ∼0.55). It is difficult to attach a clear physical meaning to such figures, as testified by the rich and ongoing debate on the application of the KWW function to relaxation phenomena in liquids and glasses.48,49,51–53 However, it is worth noting our β⊥ estimates lie around βSR = 3/5 = 0.6, which is the value expected for relaxation dynamics slowed down by short-range forces in three-dimensional spaces.48 Likely, this further points out the pivotal role of short hydrogen bonds in determining the dynamics of the liquid at the molecular scale.
3.3 Structure of the liquid
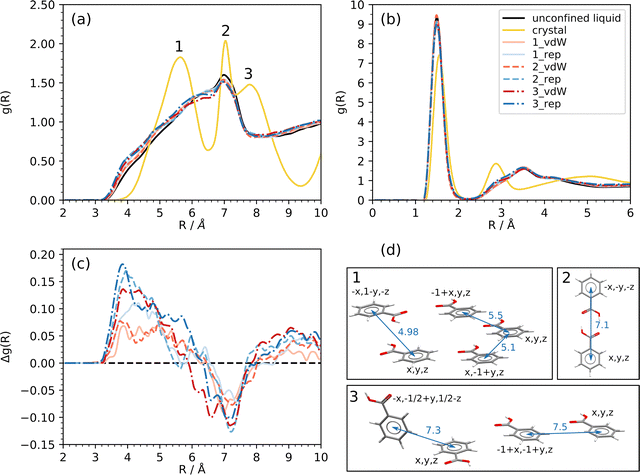
Cohesive energy is calculated as the sum of Coulomb and dispersion energies over all the molecule pairs, without considering the interaction with the barriers. The more non-periodic directions are included in the model, the lower the liquid cohesion is (Fig. 4). In other words, the enthalpy needed to take a molecule out of the liquid is lower as NNP raises. This behavior is due to lack of specific attractive interactions, like HBs, between BZA molecules at the boundaries. The effect is particularly clear for nanocavities (up to ∼5%, corresponding to +4 kJ mol−1 per molecule) while it does not depend on the potential used to model the barriers. As expected, the nanolayer exploits the same cohesion as the bulk liquid within ±0.7 kJ mol−1 per molecule.Fig. 5a and b compare the confined simulations (red and blue curves) with the free liquid (black curves) in terms of radial distribution function (RDF) g(R) of intermolecular OH⋯O contacts and center of mass (c.o.m.) distances. The curves for a MD run at equilibrium on a perfect BZA crystal (yellow lines) are also shown. All g(R) functions were averaged over the last 200 frames (100 ps) of each trajectory, after preliminary equilibration had ended. To compare the RDFs on equal ground, periodic boundary conditions were activated, if not already present, before computing the corresponding g(R)'s. Thus, all curves rely on consistent normalization of the distance density and are fully comparable. Any difference is due to the different properties of BZA in the confined or unconfined space.
All the liquids share the same hydrogen bond (HB) structure (Fig. 5b), which is dominated by an intense peak at ∼1.5 Å due to close –OH⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C contacts between the carboxy functions. This feature is slightly downshifted with respect to the analogue peak in the perfect crystal (yellow line). The next-neighbors produce a broad and unstructured band around ∼3.5 Å, which suggests the setup of networks of hydrogen-bonded molecules, albeit showing a lack of long-range ordered HB patterns. Also, the center of mass (c.o.m.) RDFs of confined systems are qualitatively like that of the bulk liquid (black line, Fig. 5a). All the g(R) functions display the same broad peak, where a sharp maximum at ∼7 Å emerges from a large left shoulder that extends down to R ∼ 3.5 Å. Comparison with the c.o.m. RDF in the crystal (yellow line) shows that the peak at ∼7 Å corresponds to hydrogen bonded BZA cyclic dimers (Fig. 5a and d, peak 2), while the unstructured band at lower R could be related to the random close packing of molecules that in the crystal are correlated by short range translation-dependent interactions (Fig. 5a and d, peak 1) and ring stacking. Interestingly, the in-crystal peak at ∼8 Å, which corresponds to long-range translation-related molecules, is not present at all in any of the liquids (Fig. 5a and d, peak 3).
C contacts between the carboxy functions. This feature is slightly downshifted with respect to the analogue peak in the perfect crystal (yellow line). The next-neighbors produce a broad and unstructured band around ∼3.5 Å, which suggests the setup of networks of hydrogen-bonded molecules, albeit showing a lack of long-range ordered HB patterns. Also, the center of mass (c.o.m.) RDFs of confined systems are qualitatively like that of the bulk liquid (black line, Fig. 5a). All the g(R) functions display the same broad peak, where a sharp maximum at ∼7 Å emerges from a large left shoulder that extends down to R ∼ 3.5 Å. Comparison with the c.o.m. RDF in the crystal (yellow line) shows that the peak at ∼7 Å corresponds to hydrogen bonded BZA cyclic dimers (Fig. 5a and d, peak 2), while the unstructured band at lower R could be related to the random close packing of molecules that in the crystal are correlated by short range translation-dependent interactions (Fig. 5a and d, peak 1) and ring stacking. Interestingly, the in-crystal peak at ∼8 Å, which corresponds to long-range translation-related molecules, is not present at all in any of the liquids (Fig. 5a and d, peak 3).
More subtle dissimilarities can be appreciated by looking at the point-by-point difference Δg(R) between the RDF of confined and unconfined liquids (Fig. 5c). A positive Δg(R) implies a higher probability of finding a molecule at distance R from any other in confined systems with respect to the unconfined liquid. A negative Δg(R) has the opposite meaning. The confinement invariably produces an increase of RDF at short distances, and a more prominent RDF depletion at longer ones. The differences are small, but consistent, with maxima of Δg(R) around 4 Å and minima around 7 Å. The higher the degree of confinement, the more appreciable is the depletion effect at ∼7 Å, according to the sequence nanolayer < nanotube < nanocavity. The trend is the same for both kinds of barriers, with full van der Waals ones (red curves in Fig. 5c) showing larger depletion effects. At low R, the trend is not so neat, but repulsive-only barriers (blue curves in Fig. 5c) produce a larger increase of Δg(R). These results could indicate a slight preference of confined systems to put BZA molecules in close contact at short-range with respect to the free liquid, at the expense of cyclic HB dimers at R ∼ 7 Å. Clearly, this is not due to a strengthening of HB contacts, but it could be related to more frequent stacking interactions among adjacent liquid layers, as it will be discussed in the next section.
The average structural information conducted by RDF is not sufficient to gain insights into the dynamics of the liquid. Quantitative information can be obtained by looking at OH⋯O contacts within a threshold distance along the H⋯O line of sight.54 As expected, most of them lie in the 1.55–1.75 Å range, well below the sum of van der Waals radii (2.680 Å), mirroring the tendency of COOH groups to set up strong cyclic HBs with themselves.30 We also analyzed the number of hydrogen bonds and their persistence along the trajectories (Fig. 6). In this case, a threshold distance equal to 0.9 times the sum of van der Waals radii was used to exclude long, weak contacts (Section S6, ESI†).53 This definition is rather conservative, as the same HB interaction may be destroyed and formed several times along the trajectory; however, it has the advantage of getting rid of ambiguities due to intermittent contacts. If the H⋯O contacts that fulfil this geometric requirement are counted, the average number of HBs per frame amounts to ∼433 (Fig. S4, ESI†) and is not significantly influenced by the nature of the barrier potential or the degree of confinement. As all the simulation boxes contain 432 molecules, this means that 1 HB per molecule is always present, on average, in both the free and the confined liquids. This is consistent with the high HB propensity of the COOH function.
 | ||
| Fig. 6 Percentage of OH⋯O contacts N(HB) within the threshold distance (0.9 × (rvdW,H + rvdW,O) = 2.412 Å) vs. the lifetime, tlife, which is defined as the time along which an OH⋯O contact continuously bears an H⋯O distance smaller than the threshold (<2.412 Å).55 The analysis was carried out based on the HBs in the last frame, whose lifetime was monitored across the whole trajectory. The numbers 1, 2, 3 and the abbreviations vdW and rep in the labels have the same meaning as in Fig. 5. | ||
The effect of confinement is evident when the HB lifetimes are studied. Operatively, a specific reference frame is chosen in the last part of the trajectory, typically the last one, and the HBs in such a frame are found. Then, their time evolution was monitored through the whole trajectory. Whenever the H⋯O distance becomes higher than the above-described cutoff, the bond was considered as broken, and a count was placed in the corresponding lifetime bin. We verified that the choice of the reference frame has essentially no effect on the distribution of the HB lifetimes, provided that the system is fully equilibrated, at least locally.
Many HBs are destroyed in 2 ps or less, but there is also a consistent number of contacts which survive more than 200 ps (Fig. 6). The percentage of HBs in the unconfined liquid (black bar) is significantly lower than in the confined counterpart when considering the 0–2 ps interval, while it is significantly higher in the 50–100, 100–200 and 200–500 ps intervals. The net effect is that there is also a higher percentage of HBs that survive more than 50 ps in the free liquid. This proves that there is a larger formation/breaking frequency of HBs when barriers are present. In addition, tlife is also roughly the same at all degrees of confinement.
3.4 Molecular orientations
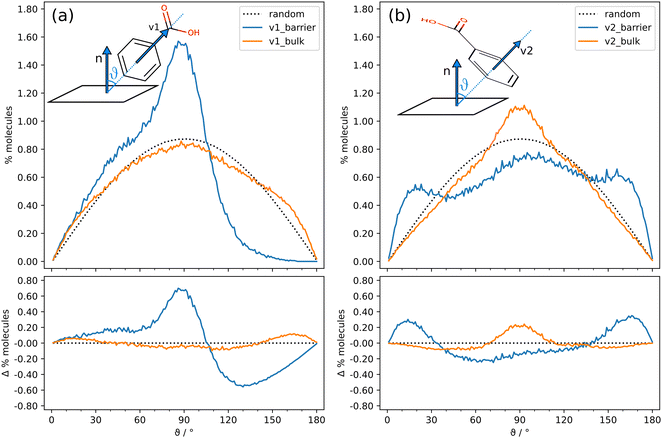
The angle between two random vectors in space has a symmetric distribution between 0 and 180°, with a maximum at 90°. However, the confinement induces a partial ordering in the liquid, resulting in significant differences with respect to a completely random distribution. Suitable descriptors of the BZA orientation are vector v1, approximately parallel to the molecular dipole moment, and vector v2, orthogonal to the phenyl ring, together with the angles φ between v1 or v2 vectors of adjacent molecules (Fig. 1). Antiparallel v1 vectors have φ close to 180° and may be associated to cyclic hydrogen bonded dimers (Fig. 5d, box 2) or dipole–dipole interactions (Fig. 5d, box 1, left), while φ ∼ 120° could be associated to cyclic trimers. Instead, both parallel (φ ∼ 0°) and antiparallel (φ ∼ 180°) v2 vectors indicate that the phenyl rings are arranged in parallel planes.Fig. 7 reports the probability density distribution of molecule vectors v1 (Fig. 7a) and v2 (Fig. 7b) and the difference with respect to a random probability density distribution for the repulsive-only nanocavity simulation. Each point comes from the space average of all the molecules with centers of mass within 10 Å from each other, and from the corresponding time average over 600 frames (300 ps).
The same analysis was conducted in the “barrier” (blue) and “bulk” (orange) regions of the nanocavity, as defined in Fig. 2. An excess of cyclic dimers (main peak shifted towards 180°) and trimers (shoulder at ∼120°) occurs in the “bulk” space (Fig. 7a). In the “barrier” space the shoulder is absent, indicating that only an excess of cyclic dimers occurs, but an additional peak close to zero degrees is neatly recognizable, which is likely due to stacking interactions. This can be appreciated by looking at the v2 vector distribution (Fig. 7b), where the difference maxima lie close to 0° and 180° and indicate a general tendency of BZA to arrange in parallel planes. This tendency is present throughout the liquid but is neatly more evident about the barrier.
Fig. 8 shows the probability density distribution of vectors v1 and v2 with respect to the barrier normal. θ is the corresponding orientation angle. In other words, Fig. 8 analyses the average molecular orientation with respect to the fixed boundaries. These distributions allow to highlight possible polarization effects, which would determine an uneven population of the available orientational degrees of freedom. As above, the average is carried out over the last 600 frames (300 ps). Far from the barriers, BZA adopts a random arrangement (Fig. 8a), with an almost totally symmetrical distribution. Close to the barriers, the distribution is no longer symmetric (blue lines) and molecules preferentially align v1 orthogonal to the barrier normal (θ ∼ 90°). There are indeed almost no COOH groups pointing towards the barriers (θ ∼ 180°). This can be explained with the tendency of BZA molecules to maximize the number of hydrogen bonds. Consequently, favorite orientations imply v2 parallel (θ ∼ 0°) or antiparallel (θ ∼ 180°) to the barrier normals, i.e., the phenyl rings are parallel to the barriers. This is probably due to the optimization of the packing efficiency. Interestingly, the “bulk” curve also exhibits a prominent peak at 90°. This is due to the cubic shape of the nanocavity: molecules lying parallel to any pair of barriers, are necessarily orthogonal to the other ones.
The results are similar when full van der Waals barriers are employed (Fig. S7 and S8, ESI†). This is expected: the parallel arrangements of phenyl rings close to the barriers maximizes the dispersive interaction energy. More surprising is that the same geometry is preferentially adopted by the molecules when the barrier is only repulsive. A possible explanation is that the mechanism for the setup of the molecular packing is different in the two cases. When repulsive-only potential is employed, the driving force is probably the pressure exerted by the next molecular layers onto the BZA units in direct contact with the barriers. In this case, partial ordering is achieved to alleviate the steric pressure, rather than to maximize attractive dispersive interactions.
3.5 Barrier stiffness and liquid–liquid transitions
In confined crystallization experiments, rigid walls frequently lead to templating effects.56 Moreover, it has been shown that rigid surfaces enhance the kinetic barrier that opposes nucleation with respect to softer ones.57 To explore the effect of the barrier rigidity, we repeated the simulations described above after doubling the scaling constant (s = 0.050). For the nanolayer, an anisotropic scaling was also considered, where an easier relaxation along the boundary normal was allowed using s⊥ = 0.010.A notable outcome is the dependence of the nanolayer viscosity η on s⊥ for repulsive-only barriers: η under anisotropic scaling (s⊥ = 0.010, s‖ = 0.050) is 12.0 × 10−3 Pa s, while isotropic scaling (s⊥ = s‖ = 0.050) predicts an η value of 7.0 × 10−3 Pa s, which is significantly lower albeit still ∼3 times higher than the unconfined liquid. Thus, the stiffer the confinement along the normal, the less viscous the layered liquid. This counterintuitive effect cannot be due to a different thickness of the liquid layers,58 as the equilibrium barrier–barrier distance differs, on average, only by 1 Å (∼2% of the total barrier–barrier distance) in the two simulation boxes. Rather, it must be ascribed to the fully repulsive nature of the barriers: if barrier relaxation is not allowed, molecule-barrier repulsions are not damped, and individual molecules approaching the boundaries are easily pushed away, increasing their probability of leaving HB aggregates. This effect reduces the dynamical correlation among individual molecules, whose enhanced mobility translates into a reduction of viscosity. In fact, if a full van der Waals potential is employed to describe interactions with barriers, isotropic and anisotropic scaling give more similar results, both close to 6 × 10−3 Pa s (Table S6, ESI†).
An oscillating behavior between two liquid states with different densities was detected in the nanocavity-confined liquids with stiff boundaries. To confirm this result and ensure reproducibility, we run 3 trajectories with repulsive-only barriers and 3 trajectories with full van der Waals barriers, starting from an identical input. In the current parallel implementation of MiCMoS, numerical approximations carried out by different threads cause random fluctuations in forces, which allow the system to evolve in slightly different ways. If the local equilibrium approximation holds true, like in the unconfined BZA liquid, the outcomes of such trajectories are identical, with average differences in bulk density and cohesive energy not exceeding 0.001 g cm−3 and 0.3 kJ mol−1 per molecule, i.e., well below the standard deviations (0.03 g cm−3 and 2 kJ mol−1 per molecule) and the expected numerical accuracy. In the proximity of a transition, however, the local equilibrium approximation is no longer valid, and the microscopic behavior is determined by fluctuations at the nanoscale. As for the present case, all the trajectories tested show the occurrence of one or more transitions between the same liquid states, but their onset and time sequence are non-deterministic in nature.
Fig. 9 shows the liquid densities and cohesive energies, together with the corresponding Coulomb and dispersive terms (Ecoh = ECoul + EvdW)33 of selected trajectories where the transition is more evident. We chose these specific examples as both states last long enough to extract meaningful information on their properties. Other examples are shown in Fig. S10 and S11 (ESI†). The two states are the same irrespective of the potential (repulsive-only or full van der Waals); in the examples discussed here, the high-density one (HD, ρ = 1.17(1) g cm−3) spans from 134 to 500 ps for the repulsive barrier (blue curves) and from 0 to 255 ps for the full van der Waals one (red curves). The low-density state (LD, ρ = 1.13(1) g cm−3) is found in the complementary time intervals. The cohesive energy of the HD state is invariably less negative than the LD one by about 4 kJ mol−1 per molecule and undergoes very large fluctuations (upper left panel of Fig. 9). The reason can be traced back to the enhancement of the electrostatic interactions in the HD state, while the dispersive Lennard-Jones interactions follow the opposite trend (Fig. 9, right). Thus, changes of the ECoul and EvdW terms partially cancel out, but the dispersion energy prevails due to its greater magnitude and dictates the behavior of the total cohesive energy. Such results could be rationalized with the setup of a stronger HB network in the HD state, as suggested by the more negative electrostatic energies. On average, stronger HBs and electrostatics imply that molecules are kept in closer contact. Thus, the repulsive potential energy becomes more positive due to the enhanced van der Waals repulsion. Large fluctuations of Ecoh and density in the HD state likely indicate that this liquid is not in a stable state. In fact, we also observe the reverse transition in other trajectories, irrespective of the nature of the barrier potential (Fig. S10 and S11, ESI†).
Microscopic information on the nature of the HD and LD states can be deduced by studying the structural descriptors of the liquid before and after the transition. Fig. 10 compares the radial distribution function g(R) of OH⋯O contacts, as averaged over 200 frames (100 ps) in either state.
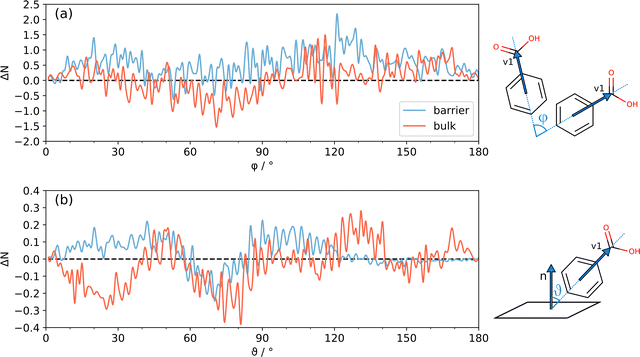
The curve of the unconfined liquid at the same T is also shown for the sake of comparison. In the HD state, the peak of g(R) at ∼1.5 Å that corresponds to short cyclic HBs (Fig. 5) is more intense and downshifted by ∼0.2 Å with respect to LD, indicating a preference toward stronger HB contacts in this state, also in line with the interpretation of the energy decomposition (Fig. 9). Obviously, molecular recognition in other molecular systems, for example those not able to form strong HBs, must rely on different non-covalent interactions, like stacking of aromatic rings and high-order electrostatics. Systems incapable of forming HBs may undergo transitions between even other liquid states, which imply packing modes different from BZA. Fig. S13 (ESI†) shows the distribution (φ) of the orientation vector v1 (Fig. 1) with those of the surrounding molecules, both in the “barrier” and “bulk” regions (Fig. S13a and b, ESI†), plus the one (θ) of v1 with the nanocavity barriers (Fig. S13c and d, ESI†). At variance with Fig. 7 and 8, the molecular orientations are shown in terms of average number instead of percentage of molecules, to better highlight the absolute differences. Fig. 11 shows the corresponding HD–LD point-by-point differences. In Fig. 11a, the barrier and bulk curves are qualitatively similar. The HD state favors φ values in the 120–140° interval and, to a minor extent, in the 20–40° one, but only when BZA is within the interaction distance from the barrier (6.4 Å, Fig. 2). The difference in the distributions is small but detectable and systematic; moreover, it comes from an extensive space-time average, meaning that it likely reflects a true genuine physical effect. Overall, it implies that cyclic hydrogen bonded trimers (Fig. S12, ESI†) are preferred in the region close to the walls. More in detail, the average number of cyclic trimers in proximity of the barriers increases from 15(3) in the LD state (30–130 ps) to 23(2) in the HD one (400–500 ps). To the sake of comparison, the same values in the whole simulation box read 21(5) (LD) and 32(2) (HD).
In Fig. 11b, again, the differences between the two states are small but systematic. Close to the barriers, both flat (θ ∼ 90°) and vertical (θ ∼ 20–60°) geometries are slightly more populated in the HD liquid. On the contrary, the difference for the molecules in the bulk shows an opposite behavior in these intervals. Overall, the HD state is characterized by an excess of cyclic trimers (see above), while the positive ΔN regions in the HD–LD difference around θ ∼ 40–60° and 120–140° may be interpreted as the preferential vertical arrangement of cyclic trimers.
4. Conclusions
In this work, a general algorithm was developed for classical molecular dynamics simulations of liquids in confined spaces and embedded into the free Milano Chemistry Molecular Simulation (MiCMoS) platform. The new code allows the modeling of flat van der Waals generic barriers, to ensure applicability to the widest possible range of cases. Accordingly, the user may select the Lennard Jones parameters, the degree of confinement (nanolayer, nanotube, nanocavity), the stiffness of the barriers in various directions, and their distance. Different confinement models were applied to supercooled benzoic acid (BZA) liquids, with the aim of understanding how and why the inner dynamics is affected by interactions with the impassable barriers. The trajectories were also examined to see whether and to what extent confinement influences self-aggregation in BZA.In agreement with the Literature, we found that the viscosity of the liquid increases steeply with the number of non-periodic directions (NNP) in the simulation box, following the concomitant reduction of the translational diffusion coefficient. In general, the barriers foster the setup of correlations that involve both translational and rotational degrees of freedom. Rotational correlation times are very high, reflecting a damped orientational relaxation due to the setup of strong HBs. In any case, the nature of the barrier potential affects the rotational dynamics, with repulsive-only barriers scoring the largest correlation times. On the contrary, the Kohlrausch exponents, which express the correlation strength, mostly lie in the 0.5–0.7 range. This is close to the ideal 0.6 value that characterizes correlations due to short-range forces, which can be interpreted as mediated by long-living hydrogen bonds among COOH groups.
From a structural viewpoint, the differences among the various confinement geometries are minimal, with partial local ordering but no evidence of long-range ordering phenomena. The picture changes if the stiffness of the barrier is increased. Transitions between a high density (HD) and low density (LD) liquid states were found to occur in nanocavities with stiff barriers. The driving force resides in more attractive electrostatic interactions in the HD state. However, the concomitant enhancement of molecule–molecule repulsions makes the HD state metastable, as the system switches from one state to another in a non-deterministic way. The more negative Coulomb energy implies that HBs are the main actors in this process. Structural differences with respect to the LD state are a genuine byproduct of the confinement and consist in (i) a slight preference toward hydrogen bonded cyclic trimers and (ii) the preferential setup of parallel orientation of the main molecular plane with respect to the barrier.
The MD simulations here discussed are valid on a qualitative scale, as it should be expected for a purely classical model run on a small spacetime scale in conditions of local equilibrium. Thus, it is impossible to say whether the metastable HD state could be somehow related to the high-density nanoregions that, according with the multi-step nucleation theory, are predicted to lie on the path to nucleation. In the current computational setup, the HD liquid is transient, with an expected lifetime of hundreds of picoseconds. Probably, this time is still too short to have a reasonable chance to observe symmetrization, if any. In any case, the present simulations not only demonstrate that confinement alone may trigger a transition to different states, but also provides a quantitative description of what is going on at the molecular scale, which is not easily accessible by standard analytical methods. We expect that the results are molecule-dependent, as systems with different chemical functions with respect to BZA rely on different recognition modes. As a bonus, we demonstrated that several system parameters, in principle amenable to experimental verification, like densities, viscosities and rotational correlation times, can be extracted seamlessly from the trajectories with a minimum computational cost.
Current limitations of our algorithm reside in the shape of the confined space, which must have square or rectangular section if NNP > 1, and in the hydrophobicity of the barriers. Future developments are straightforward, though, and include allowing circular sections for nanotubes and nanocavities, as well as the addition of “hotspots” at specific sites on the barrier surface, which may serve as both HB donors (OH and NH groups) or acceptors (O, N, halogens).
Author contributions
Luca Sironi: formal analysis, data curation, software, validation, visualization, writing – review and editing; Giovanni Macetti: formal analysis, software, supervision, visualization, writing – review and editing; Leonardo Lo Presti: conceptualization, methodology, resources, supervision, writing – original draft.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
Thanks are due to Prof. Angelo Gavezzotti for continuous encouragement and inspiration. The Chemistry Department at Università degli Studi di Milano is also acknowledged for funding this research through the PSR 2022 program (PSR2021_DIP_005_PI_AMING).References
- T. W. Odom, Celebrating 20 years of Nano Letters, Nano Lett., 2021, 21, 1–2 CrossRef CAS PubMed.
- N. Baig, I. Kammakakam, W. Falath and I. Kammakakam, Nanomaterials: a review of synthesis methods, properties, recent progress, and challenges, Mater. Adv., 2021, 2, 1821–1871 RSC.
- Y. Su, G. Liu, B. Xie, D. Fu and D. Wang, Crystallization features of normal alkanes in confined geometry, Acc. Chem. Res., 2014, 47, 192–201 CrossRef CAS.
- A. Adawy, Z. Amghouz, J. C. M. van Hest and D. A. Wilson, Sub-Micron Polymeric Stomatocytes as Promising Templates for Confined Crystallization and Diffraction Experiments, Small, 2017, 13, 1700642 CrossRef PubMed.
- Y. Liu, Y. Wu, J. Yao, J. Yin, J. Lu, J. Mao, M. Yao and F. Luo, Confined Crystallization and Melting Behaviors of 3-Pentadecylphenol in Anodic Alumina Oxide Nanopores, ACS Omega, 2021, 6, 18235–18247 CrossRef CAS PubMed.
- K. Koga, H. Tanaka and X. C. Zeng, First-order transition in confined water between high-density liquid and low-density amorphous phases, Nature, 2000, 408, 564–567 CrossRef CAS PubMed.
- D. Fu, Y. Liu, G. Liu, Y. Su and D. Wang, Confined crystallization of binary n-alkane mixtures: Stabilization of a new rotator phase by enhanced surface freezing and weakened intermolecular interactions, Phys. Chem. Chem. Phys., 2011, 13, 15031–15036 RSC.
- B. Xie, G. Liu, S. Jiang, Y. Zhao and D. Wang, Crystallization behaviors of n-octadecane in confined space: Crossover of rotator phase from transient to metastable induced by surface freezing, J. Phys. Chem. B, 2008, 112, 13310–13315 CrossRef CAS PubMed.
- S. Milita, C. Dionigi, F. Borgatti, W. Porzio and F. Biscarini, Monitoring the crystallization process of nano-confined organic molecules by synchrotron X-ray diffraction, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 411–413 CrossRef CAS.
- M. Beiner, Nanoconfinement as a tool to study early stages of polymer crystallization, J. Polym. Sci., Part B: Polym. Phys., 2008, 46, 1556–1561 CrossRef CAS.
- J. M. Carr, D. S. Langhe, M. T. Ponting, A. Hiltner and E. Baer, Confined crystallization in polymer nanolayered films: A review, J. Mater. Res., 2012, 27, 1326–1350 CrossRef CAS.
- L. Zhu, S. Z. D. Cheng, B. H. Calhoun, Q. Ge, R. P. Quirk, E. L. Thomas, B. S. Hsiao, F. Yeh and B. Lotz, Crystallization temperature-dependent crystal orientations within nanoscale confined lamellae of a self-assembled crystalline - Amorphous diblock copolymer, J. Am. Chem. Soc., 2000, 122, 5957–5967 CrossRef CAS.
- Z. Yang, C. Huang, F. Gong, X. Zhao, C. Lin, L. Ding, J. Zhang, Y. Li and F. Nie, Energetic nanoarray structures by confined crystallization for enhanced energy-release efficiency, Chem. Eng. J., 2021, 403, 126408 CrossRef CAS.
- A. K. Giri, F. Teixeira and M. N. D. S. Cordeiro, Structure and kinetics of water in highly confined conditions: A molecular dynamics simulation study, J. Mol. Liq., 2018, 268, 625–636 CrossRef CAS.
- V. V. Chaban and O. N. Kalugin, Structure and dynamics in methanol and its lithium ion solution confined by carbon nanotubes, J. Mol. Liq., 2009, 145, 145–151 CrossRef CAS.
- C. Alba-Simionesco, G. Dosseh, E. Dumont, B. Frick, B. Geil, D. Morineau, V. Teboul and Y. Xia, Confinement of molecular liquids: Consequences on thermodynamic, static and dynamical properties of benzene and toluene, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 12, 19–28 CrossRef CAS PubMed.
- H. Weiss, H. W. Cheng, J. Mars, H. Li, C. Merola, F. U. Renner, V. Honkimäki, M. Valtiner and M. Mezger, Structure and Dynamics of Confined Liquids: Challenges and Perspectives for the X-ray Surface Forces Apparatus, Langmuir, 2019, 35, 16679–16692 CrossRef CAS PubMed.
- H. Abe, F. Nemoto, K. Hiroi, K. Ohishi and S. Takata, Spontaneous formations of nanoconfined water in ionic liquids by small-angle neutron scattering, J. Mol. Liq., 2022, 346, 117035 CrossRef CAS.
- V. F. Sears, Cold Neutron Scattering by Molecular Liquids: III, Methane, 2011, 45, 237–254, DOI:10.1139/p67-025.
- G. Buntkowsky, H. Breitzke, A. Adamczyk, F. Roelofs, T. Emmler, E. Gedat, B. Grünberg, Y. Xu, H. H. Limbach, I. Shenderovich, A. Vyalikh and G. Findenegg, Structural and dynamical properties of guest molecules confined in mesoporous silica materials revealed by NMR, Phys. Chem. Chem. Phys., 2007, 9, 4843–4853 RSC.
- X. Kong, F. B. Surani and Y. Qiao, Effects of addition of ethanol on the infiltration pressure of a mesoporous silica, J. Mater. Res., 2005, 20, 1042–1045 CrossRef CAS.
- K. Morishige and K. Mikawa, Tensile effect on crystal nucleation of methanol and ethanol confined in pores, J. Phys. Chem. C, 2012, 116, 3618–3622 CrossRef CAS.
- M. Boudot, D. R. Ceratti, M. Faustini, C. Boissière and D. Grosso, Alcohol-assisted water condensation and stabilization into hydrophobic mesoporosity, J. Phys. Chem. C, 2014, 118, 23907–23917 CrossRef CAS.
- T. Nakamuro, M. Sakakibara, H. Nada, K. Harano and E. Nakamura, Capturing the Moment of Emergence of Crystal Nucleus from Disorder, J. Am. Chem. Soc., 2021, 143, 1763–1767 CrossRef CAS PubMed.
- Z. Liao and K. Wynne, Mesoscopic amorphous particles rather than oligomeric molecular aggregates are the cause of laser-induced crystal nucleation, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2207173119 CrossRef PubMed.
- T. B. M. Adachi, J. Brazard and O. Urquidi, Reply to Liao and Wynne: The size of crystal nucleus remains an open question, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2207713119 CrossRef CAS PubMed.
- Z. Liao and K. Wynne, A Metastable Amorphous Intermediate Is Responsible for Laser-Induced Nucleation of Glycine, J. Am. Chem. Soc., 2022, 144, 6727–6733 CrossRef CAS PubMed.
- O. Urquidi, J. Brazard, N. LeMessurier, L. Simine and T. B. M. Adachi, In situ optical spectroscopy of crystallization: One crystal nucleation at a time, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2122990119 CrossRef CAS PubMed.
- G. Macetti, L. Sironi and L. Lo Presti, Classical Molecular Dynamics Simulation of Molecular Crystals and Materials: Old Lessons and New Perspectives, Reference Module in Chemistry, Molecular Sciences and Chemical Engineering, 2023 DOI:10.1016/B978-0-12-821978-2.00107-0.
- A. Gavezzotti and L. Lo Presti, Building Blocks of Crystal Engineering: A Large-Database Study of the Intermolecular Approach between C–H Donor Groups and O, N, Cl, or F Acceptors in Organic Crystals, Cryst. Growth Des., 2016, 16, 2952–2962 CrossRef CAS.
- A. Gavezzotti, L. Lo Presti and S. Rizzato, Molecular dynamics simulation of organic materials: structure, potentials and the MiCMoS computer platform, CrystEngComm, 2022, 24, 922–930 RSC.
- R. Feld, M. S. Lehmann, E. W. Muir and J. C. Speakman, The crystal structure of Benzoic Acid: A redetermination with X-rays at room temperature; a summary of neutron-diffraction work at temperatures down to 5 K, Z. Kristallogr. – New Cryst. Struct., 1981, 157, 215–231 CrossRef CAS.
- L. Lo Presti, S. Rizzato, G. Macetti and L. Sironi, MiCMoS Users’ Manual - MIlano Chemistry MOlecular Simulation v2.1, 2022, 1–158 Search PubMed.
- L. Lo Presti, S. Rizzato and A. Gavezzotti, Kinetic-Bias Model for the Dynamic Simulation of Molecular Aggregation. The Liquid, Solute, Solvated-Nanodrop, and Solvated-Nanocrystal States of Benzoic Acid, Cryst. Growth Des., 2022, 22, 1857–1866 CrossRef CAS.
- A. Gavezzotti, L. Lo Presti and S. Rizzato, Mining the Cambridge Database for theoretical chemistry. Mi-LJC: a new set of Lennard-Jones–Coulomb atom–atom potentials for the computer simulation of organic condensed matter, CrystEngComm, 2020, 22, 7350–7360 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian16 (Revision A.03), 2016 Search PubMed.
- G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- W. Huang, Z. Lin and W. F. Van Gunsteren, Validation of the GROMOS 54A7 force field with respect to β-peptide folding, J. Chem. Theory Comput., 2011, 7, 1237–1243 CrossRef CAS PubMed.
- A. Gavezzotti and L. Lo Presti, Dynamic simulation of liquid molecular nanoclusters: structure, stability and quantification of internal (pseudo)symmetries, New J. Chem., 2019, 43, 2077–2084 RSC.
- A. Gavezzotti, The Calculation of Molecular Volumes and the Use of Volume Analysis in the Investigation of Structured Media and of Solid-State Organic Reactivity, J. Am. Chem. Soc., 1983, 105, 5220–5225 CrossRef CAS.
- A. Zaccone, Explicit Analytical Solution for Random Close Packing in d = 2 and d = 3, Phys. Rev. Lett., 2022, 128, 028002 CrossRef CAS PubMed.
- S. Chen, W. Chen, Y. Ren, J. Sun, J. Wang and Y. Yang, Molecular Dynamics Simulation of the Nascent Polyethylene Crystallization in Confined Space: Nucleation and Lamella Orientation, Macromolecules, 2022, 55, 7368–7379 CrossRef CAS.
- A. Gavezzotti and L. Lo Presti, Molecular dynamics simulation of organic crystals: introducing the CLP-dyncry environment, J. Appl. Crystallogr., 2019, 52, 1253–1263 CrossRef CAS.
- Cheméo - Chemical & Physical Properties by Cheméo, https://www.chemeo.com/, (accessed 28 March 2023).
- T. Sun and A. S. Teja, Density, viscosity, and thermal conductivity of aqueous benzoic acid mixtures between 375 K and 465 K, J. Chem. Eng. Data, 2004, 49, 1843–1846 CrossRef CAS.
- R. Kohlrausch and U. das Dellmann'sche Elektrometer, Ann. Phys. Chem., 1847, 148, 353–405 CrossRef.
- W. Graham and D. C. Watts, Non-Symmetrical Dielectric Relaxation Behaviour Arising from a Simple Empirical Decay Function, Trans. Faraday Soc., 1970, 66, 80–85 RSC.
- J. C. Phillips, Stretched exponential relaxation in molecular and electronic glasses, Rep. Prog. Phys., 1996, 59, 1133 CrossRef CAS.
- K. L. Ngai, Alternative explanation of the difference between translational diffusion and rotational diffusion in supercooled liquids, J. Phys. Chem. B, 1999, 103, 10684–10694 CrossRef CAS.
- M. Wojdyr, Fityk: A general-purpose peak fitting program, J. Appl. Crystallogr., 2010, 43, 1126–1128 CrossRef CAS.
- E. Aydiner, A Simple Model for Stretched Exponential Relaxation in Three-Level Jumping Process, Phys. Status Solidi B, 2019, 256, 1900103 CrossRef CAS.
- J.-P. Hansen and S. Yip, Molecular dynamics investigations of slow relaxations in supercooled liquids, Transp. Theory Stat. Phys., 1995, 24, 1149–1178 CrossRef CAS.
- N. Neuber, O. Gross, M. Frey, B. Bochtler, A. Kuball, S. Hechler, F. Yang, E. Pineda, F. Westermeier, M. Sprung, F. Schäfer, I. Gallino, R. Busch and B. Ruta, Disentangling structural and kinetic components of the α-relaxation in supercooled metallic liquids, Commun. Phys., 2022, 5, 316 CrossRef CAS.
- L. Lo Presti, On the significance of weak hydrogen bonds in crystal packing: a large databank comparison of polymorphic structures, CrystEngComm, 2018, 20, 5976–5989 RSC.
- J. D. Dunitz and A. Gavezzotti, Attractions and Repulsions in Molecular Crystals: What Can Be Learned from the Crystal Structures of Condensed Ring Aromatic Hydrocarbons?, Acc. Chem. Res., 1999, 32, 677–684 CrossRef CAS.
- F. C. Meldrum and C. O’Shaughnessy, Crystallization in Confinement, Adv. Mater., 2020, 32, 2001068 CrossRef CAS PubMed.
- F. Eslami and J. A. W. Elliott, Thermodynamic investigation of the barrier for heterogeneous nucleation on a fluid surface in comparison with a rigid surface, J. Phys. Chem. B, 2011, 115, 10646–10653 CrossRef CAS PubMed.
- S. Granick, Motions and Relaxations of Confined Liquids, Science, 1991, 253, 1374–1379 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Full description of the confinement algorithm. Molecular geometry and MD input files. Gromacs simulation of the bulk liquid phase. Translational diffusion. Molecular rotations. Hydrogen bonds. Local number density. Molecular orientations. Stiff barriers and liquid–liquid transitions. See DOI: https://doi.org/10.1039/d3cp02886k |
| This journal is © the Owner Societies 2023 |