Open Access Article
Open Access ArticleSingle-photon ionization of SiC in the gas phase: experimental and ab initio characterization of SiC+†
B.
Gans
 *a,
J.
Liévin
b,
P.
Halvick
*a,
J.
Liévin
b,
P.
Halvick
 c,
N. L.
Chen
c,
N. L.
Chen
 a,
S.
Boyé-Péronne
a,
S.
Boyé-Péronne
 a,
S.
Hartweg‡
a,
S.
Hartweg‡
 d,
G. A.
Garcia
d,
G. A.
Garcia
 d and
J.-C.
Loison
d and
J.-C.
Loison
 c
c
aInstitut des Sciences Moléculaires d'Orsay, CNRS, Université Paris-Saclay, F-91405 Orsay, France. E-mail: berenger.gans@universite-paris-saclay.fr
bSpectroscopy, Quantum Chemistry and Atmospheric Remote Sensing, Université Libre de Bruxelles, CP 160/09, B-1050 Bruxelles, Belgium
cInstitut des Sciences Moléculaires, CNRS, Université de Bordeaux, F-33400 Talence, France
dSynchrotron SOLEIL, L'Orme des Merisiers, St. Aubin, F-91192 Gif sur Yvette, France
First published on 18th August 2023
Abstract
We report the first experimental observation of single-photon ionization transitions of the SiC radical between 8.0 and 11.0 eV performed on the DESIRS beamline at the SOLEIL synchrotron facility. The SiC radical, very difficult to synthesize in the gas phase, was produced through chemical reactions between CHx (x = 0–3) and SiHy (y = 0–3) in a continuous microwave discharge flow tube, the CHx and SiHy species being formed by successive hydrogen-atom abstractions induced by fluorine atoms on methane and silane, respectively. Mass-selected ion yield and photoelectron spectra were recorded as a function of photon energy using a double imaging photoelectron/photoion coincidence spectrometer. The photoelectron spectrum enables the first direct experimental determinations of the X+ 4Σ− ← X 3Π and 1+ 2Π ← X 3Π adiabatic ionization energies of SiC (8.978(10) eV and 10.216(24) eV, respectively). Calculated spectra based on Franck–Condon factors are compared with the experimental spectra. These spectra were obtained by solving the rovibrational Hamiltonian, using the potential energy curves calculated at the multireference single and double configuration interaction level with Davidson correction (MRCI + Q) and the aug-cc-pV5Z basis set. MRCI + Q calculations including the core and core–valence electron correlation were performed using the aug-cc-pCV6Z basis set to predict the spectroscopic properties of the six lowest electronic states of SiC+. Complete basis set extrapolations and relativistic energy corrections were also included in the determination of the energy differences characterizing the photoionization process. Using our experimental and theoretical results, we derived semi-experimental values for the five lowest ionization energies of SiC.
1. Introduction
In addition to its significance in semi-conductor physics,1 silicon carbide (SiC) is supposed to be a key species in interstellar media. For instance, SiC would be the main dust species, with amorphous carbon grains, in a cool atmosphere of the C-rich asymptotic giant branch (AGB) stars.2,3 As a matter of fact, it was detected in the circumstellar envelopes of carbon-rich evolved stars such as IRC +10.216.4 However, although the detection of the 11.3 μm emission feature commonly observed in AGB stars is attributed to the presence of SiC dustgrains,5 this transition has never been observed in the interstellar medium (ISM). The possible destruction of SiC (molecules or clusters) has been proposed,6 but the responsible mechanisms remain an open question. A potentially efficient process for SiC destruction is photoionization since SiC+ and ionized SiC clusters are much more reactive than neutral species.5 Up to now, only two spectrometric studies using electron impact ionization have been performed in the 60's, probably because its gas-phase production is a challenge. The derived experimental ionization potential (IP) of SiC is very approximate (9.2 ± 0.4 eV7 and 9.0 eV8 with probably large error bars). The most accurate IP value in the literature seems to be the one derived from the Active Thermochemical Tables,9 8.930 ± 0.035 eV, based on several standard composite calculations. To our knowledge, almost no spectroscopic information on SiC+ is available in the literature except in a few theoretical papers.10,11 Indeed, when carborundum (crystalline SiC) is heated or vaporized by a pulsed Nd-YAG laser, the major constituents of the vapor are Si, SiC2, Si2C but very few SiC.12,13 In this work, we have used a radical source based on a microwave discharge flow-tube reactor coupled with the SAPHIRS setup of the DESIRS beamline (SOLEIL synchrotron)14–16 to chemically produce SiC in the gas phase. The source is based on the reaction of fluorine atoms (F) with a mixture of methane (CH4) and silane (SiH4). We were able to produce a significant amount of C, CH, Si and SiH, and then SiC likely through Si + CH and C + SiH reactions. Using a double imaging photoelectron/photoion coincidence (i2PEPICO) spectrometer providing mass-selectivity, we succeeded in measuring for the first time the ion yield and photoelectron spectra of the SiC radical following a single photon excitation with VUV (vacuum ultra violet) synchrotron radiation. The photoelectron spectrum of the SiC radical has been analyzed through Franck–Condon factor calculations based on the low-lying electronic potential energy curves of SiC and SiC+ obtained in this work by means of large-scale ab initio calculations. The two lowest electronic states of SiC and the six lowest electronic states of SiC+, potentially contributing to the observed photoionization spectra, are included in these calculations. The first two 2Π states of SiC+, which are known to be strongly perturbed by their avoided crossing,10,17 cannot be described by the simple harmonic oscillator model to perform Franck–Condon simulations. We have therefore computed and diagonalized the Hamiltonian matrices representing SiC and SiC+ vibrational motions and calculated the Franck–Condon factors from the obtained wave functions. Such anharmonic calculations were carried out for all states of SiC and SiC+. The equilibrium properties (bond length, rotational and vibrational constants) have been predicted to help further spectroscopic studies. The term energies of the excited states of SiC+ and the corresponding ionization energies have been computed at a high level of ab initio theory including core–core and core–valence correlation energies, complete basis set extrapolations and relativistic corrections. These results are compared with the corresponding experimental results and with previous calculations.10,11,17–212. Methodologies
2.1 Experimental details
The experiments were performed at the SOLEIL French synchrotron facility on the DESIRS beamline22 and have been described in detail previously.15,23 SiH4 (1 × 1013 molecules cm−3) and CH4 (1 × 1013 molecules cm−3) seeded in helium carrier gas (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
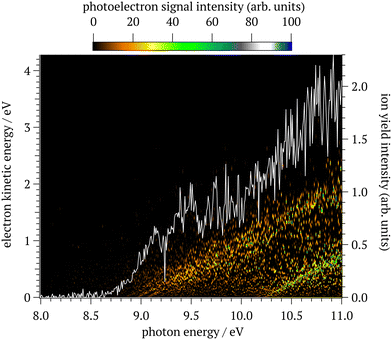
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000) were introduced into the flow-tube reactor (total pressure of 4 × 10−1 mbar) to react with the F atoms (around 2 × 1013 atoms cm−3) produced upstream by a microwave discharge on F2. F atoms react with CH4 and SiH4 along successive H-atom abstraction reactions to generate a series of CHx (x = 0–3) and SiHy (y = 0–3) radicals. By adjusting the experimental conditions such as the concentration of the F atom, gas flows or injector distance, the production of SiCHn radicals (n = 0–4), including SiC radicals, was optimized considering the compromise between selectivity and quantity. The flow-tube gas mixture was twice skimmed before arriving in the interaction chamber (pressure of 2 × 10−7 mbar) and crossing at a right angle the monochromatized synchrotron radiation in the center of the double imaging photoelectron/photoion spectrometer DELICIOUS3.14 The photon resolution in the 8–11 eV energy range was about δλ = 2.16 Å corresponding to δE from 11 to 21 meV. The photoions and the photoelectrons were extracted by a 88.7 V cm−1 DC field in opposite directions and detected by two VMI (velocity-map-imaging) detectors. The signals acquired along the measurement were corrected by the photon flux evolution independently recorded on a Si photodiode (AXUV, IRD). The coincidence scheme led to ion-mass filtered photoelectron images which were then Abel inverted to extract the mass-selected photoelectron spectra (PES), recorded in our case for the SiC radical (see Fig. 1).
1000) were introduced into the flow-tube reactor (total pressure of 4 × 10−1 mbar) to react with the F atoms (around 2 × 1013 atoms cm−3) produced upstream by a microwave discharge on F2. F atoms react with CH4 and SiH4 along successive H-atom abstraction reactions to generate a series of CHx (x = 0–3) and SiHy (y = 0–3) radicals. By adjusting the experimental conditions such as the concentration of the F atom, gas flows or injector distance, the production of SiCHn radicals (n = 0–4), including SiC radicals, was optimized considering the compromise between selectivity and quantity. The flow-tube gas mixture was twice skimmed before arriving in the interaction chamber (pressure of 2 × 10−7 mbar) and crossing at a right angle the monochromatized synchrotron radiation in the center of the double imaging photoelectron/photoion spectrometer DELICIOUS3.14 The photon resolution in the 8–11 eV energy range was about δλ = 2.16 Å corresponding to δE from 11 to 21 meV. The photoions and the photoelectrons were extracted by a 88.7 V cm−1 DC field in opposite directions and detected by two VMI (velocity-map-imaging) detectors. The signals acquired along the measurement were corrected by the photon flux evolution independently recorded on a Si photodiode (AXUV, IRD). The coincidence scheme led to ion-mass filtered photoelectron images which were then Abel inverted to extract the mass-selected photoelectron spectra (PES), recorded in our case for the SiC radical (see Fig. 1).
The 28SiC signal was thus recorded as a function of electron kinetic and photon energy from which the slow photoelectron spectrum (SPES) was extracted following previously published methodology.16,24 The SPES electron resolution for an electron bandwidth of 70 meV was measured at 22 meV at 7.4 eV using the Si(1D) → Si+ (2P) atom ionization transitions, which gives a total energy resolution of 26 meV at 9 eV when convolved with the photon resolution. The calibration of the energy scale was achieved with an absolute accuracy of ±4 meV using the Si (Si(1D) → Si+ (2P) and Si(3P) → Si+ (2P)) and CH3 ionization transitions along with the third order ionization of the He atom. Note that the 88.7 V cm−1 extraction field leads to a field-induced downshift of the ionization energies of approximately 7 meV.25
Concerning the chemistry occurring in the radical source, the mass spectrum reported in Fig. 2 is an integrated mass spectrum over the 8–11 eV photon energy for the SiH4 + CH4 + F scheme and exhibits the composition of the reactor. The most intense peaks in this mass spectrum correspond to SiHy+(y = 0–3), SiFHz+ (z = 0–3), and CH3+. We can also see weaker peaks, indicating the production of CHx+ (x = 1–2), Si2Hm+ (m = 0–4) and SiCHn+(n = 0–4) compounds. The latter ones are induced by the presence of both SiHy(y = 0–3) and CHx(x = 0–3) radicals in the reactor. In Fig. 2, the production of SiC is much lower than the other SiCHn=2–4 compounds. Among the CHx species, the CH3 radical is clearly the major species and we suspect that SiHy + CH3 reactions lead to the SiCHn (n = 2–4) + H channels but not to the production of SiC or SiCH. Nevertheless, all the species produced by the radical source and the remaining precursors will not interfere with the study of SiC in this work, thanks to the mass selectivity of the coincidence detection technique. It is worth pointing out that the complex chemistry, which leads to the production of SiC, results in a large number of different side products as illustrated in Fig. 2.
2.2 Ab initio calculations
The ab initio calculations have been carried out using the MOLPRO suite of programs26–28 using the internally contracted multireference configuration interaction method (MRCI),29 with energies corrected by the Davidson unlinked clusters contribution (MRCI+Q).30 The molecular orbitals (MOs) were optimized by means of complete active space self-consistent field (CASSCF) calculations31 using two different active spaces (ASs) also adopted in the MRCI calculations.In the first AS, the five low-lying MOs (four σ and one π) correlating to 1s, 2s and 2p of silicon and 1s of carbon are kept closed, and 8 active electrons (7 for SiC+) are distributed in the six valence MOs (four σ and two π). This AS corresponding to the usual frozen core approximation will be referred to below as V, meaning that all valence electrons are correlated. The aug-cc-pV5Z basis set (AV5Z for short) has been used in all V calculations.32–34
The second AS adds the core–core and core–valence correlation energies arising from the outer core of silicon (2s and 2p) and from the 1s orbital of carbon. The 1s inner core orbital of silicon, lying too deep to interact appreciably with the valence shells, has been kept frozen. This AS will be referred below to as CV, meaning that it correlates both core and valence electrons. Such calculations use the aug-cc-pCV6Z basis set (ACV6Z for short), optimized for the description of both core and valence correlation.35–37 CV calculations are, of course, more expensive computationally than the V ones, with a factor of 180 in the size of the MRCI configuration spaces and a factor of 100 in the corresponding computing times. V/AV5Z was used for calculating the potential energy curves (PECs) over a wide range of internuclear distances from 1 to 4 Å and with a tight grid of 0.01 Å, allowing the description of excited vibrational levels and the Franck–Condon simulation. On the other hand, CV/ACV6Z calculations were performed over a more restricted range of 0.5 Å around the equilibrium geometries to predict equilibrium spectroscopic properties and characteristic energy differences.
The equilibrium properties of all states (re, Be, αe, ωe, and ωexe) were calculated from a Dunham 8th order polynomial fit of the calculated PECs, using the DIATOMIC code in MOLPRO. The electric dipole moment at equilibrium μe has also been calculated as the expected value of the dipole moment operator, using the center of mass as the origin of the coordinate system.
The terms energies of the excited electronic states and the adiabatic ionization energies have been obtained from the difference of energies extrapolated to the complete basis set (CBS) limits of the ACVnZ basis set series (n = Q, 5, and 6).32,33,35–38 This extrapolation has been carried out at the ACV6Z equilibrium geometry of each electronic state. The CASSCF (ECASSCF) and dynamical correlation (ECorr = EMRCI+Q − ECASSCF) CBS energies were obtained using the ECASSCF(CBS) + A × exp(−B × n) and ECorr(CBS) + C × n−3 functionals, respectively.39 The contributions of the scalar relativity (SR) and the spin–orbit (SO) coupling to the characteristic energies have also been evaluated, the former by means of the exact two-component relativistic Fock operator40,41 using the ACV6Z-X2C basis set,27 and the latter by a diagonalization of the full Breit-Pauli spin–orbit Hamiltonian in the zeroth-order Λ–S basis set of the MRCI eigenfunctions.42 All electronic states correlating to the first dissociation limits of SiC and SiC+ were involved in this basis set, i.e. two Σ+, one Σ−, two Π, and one Δ states of singlet, triplet and quintet spin species for SiC, and one Σ+, two Σ−, two Π, and one Δ states of doublet and quartet spin species for SiC+. Indirect SO coupling being found to be small at the equilibrium geometry of all calculated states, there was no need for adding higher zeroth order states in the SO calculation. In order to improve the accuracy of the zeroth-order energies, the MRCI + Q energies were used on the diagonal of the SO matrix. Vibrational zero point energy (ZPE) corrections were calculated using the Dunham ωe and ωexe values.
2.3 Simulation of the photoelectron spectrum
For all the electronic states of SiC and SiC+ that have been calculated ab initio, the radial nuclear Hamiltonian, including both the MRCI+Q/AV5Z potential and the centrifugal potential, has been represented in a discrete variable representation based on 201 imaginary exponential functions43 in the interval 1.06–3.17 Å of the radial coordinate. This allowed to compute the 20 lowest vibrational energies with an accuracy better than 10−2 cm−1. Neither the spin nor the electronic angular momentum has been considered in this calculation. For each electronic state, all rovibrational energies and vibrational wave functions with 0 ≤ v ≤ 9 and 0 ≤ N ≤ 29 have been calculated, except for the 1+ 2Π state where more wave functions have been calculated, namely 0 ≤ v ≤ 19, the vibrational energy spacings being much smaller for this state. Since all the vibrational wave functions were expanded in the same orthonormal basis set, the overlap integrals were then easily calculated using dot products and then squared to give Franck–Condon factors. Computing the radial part of the rovibrational functions allowed us to include the centrifugal effect in the Franck–Condon factors. However, applying the selection rules on rotational transitions implies to take into account the couplings of the rotational angular momentum with the electronic spin, the electronic angular momentum, and the angular momentum of the ejected electron. Since all these angular momenta have been neglected in the present work, we shifted towards a simple and rough approximation. Only the rotational transitions with |ΔN| < 5 were included in the calculations of the Franck–Condon factors. The simulated spectra were obtained by specifying the rovibrational levels of SiC for selected vibrational and rotational temperatures, and the transition intensities were convolved with a Gaussian function to account for the experimental resolution.The adiabatic transition energies obtained by the CBS extrapolations corrected from the ZPE were used to fix the energy of the origin bands (v+ = 0 ← v = 0) of the calculated spectra.
3. Results and discussion
3.1 Ab initio results
The main configurations of the electronic states calculated in this work, i.e. the two and six lowest states of SiC and SiC+, respectively, are given below:| SiC(X 3Π): […](7σ)1(2π)3 |
| SiC(a 1Σ+): […](7σ)0(2π)4 |
| SiC+(X+ 4Σ−): […](7σ)1(2π)2 |
| SiC+(1+ 2Δ, 1+ 2Σ−, 1+ 2Σ+): […](7σ)1(2π)2 |
| SiC+(1+ 2Π, 2+ 2Π): […](7σ)2(2π)1/[…](7σ)0(2π)3 |
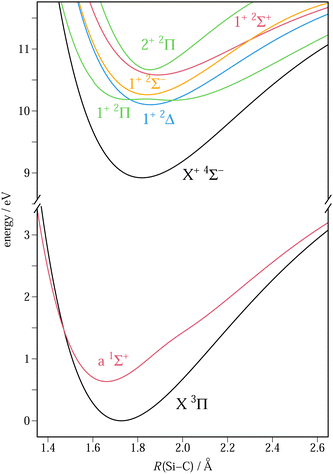 | ||
| Fig. 3 Potential energy curves of SiC (lower part of the figure) and SiC+ (upper part of the figure) computed at the MRCI + Q/AV5Z level of theory. | ||
The double-well in the PEC of the lowest 2Π state of SiC+ results from the avoided crossing occurring with the second 2Π state. Both states are described by a mixing of the two electronic configurations given above, and a two-state averaged CASSCF calculation has been performed to obtain the corresponding PECs. A more detailed discussion about the double-well shape and its consequences on the spectrum is proposed in the ESI.† We also point out the multireference character of the a 1Σ+ state of SiC, which required a state-averaged CASSCF orbital optimization involving the three lowest 1Σ+ states to converge its equilibrium properties.
The spectroscopic properties at equilibrium (re, Be, αe, ωe, and ωexe) derived from the calculated PECs are given in Table 1. The second anharmonic constants ωeye, also provided by the Dunham analysis, are not reported because they are found to be small (<5 × 10−3 cm−1) and subject to numerical uncertainty. Also note that the rovibrational properties are not provided for the pair of 2Π states of SiC+ perturbed by the avoided crossing in the region of the minima, which prevents the use of the standard Dunham analysis. We refer to the next section for a correct vibrational treatment of these states by diagonalization of the rovibrational Hamiltonian.
| Ref.a | r e/Å | B e/cm−1 | 103αe/cm−1 | ω e/cm−1 | ω e x e/cm−1 | μ e/D | ΔESOb/cm−1 | |
|---|---|---|---|---|---|---|---|---|
| a This work otherwise specified. AV5Z and ACV6Z refer to MRCI + Q/V and CV calculations, respectively. b The Ω values of the lowest and highest SO components, respectively, are given in parentheses. c Properties are listed for both minima of the double-well potential, with those corresponding to the lowest energy underlined. | ||||||||
| SiC | ||||||||
| X 3Π | AV5Z | 1.7269 | 0.67311 | 5.608 | 957.29 | 5.92 | −1.450 | 74.5 (2, 0−) |
| ACV6Z | 1.7176 | 0.68042 | 5.584 | 970.16 | 5.78 | −1.230 | ||
| Exp.44 | 1.7182 | 0.67976 | 5.38 | 965.16 | 5.910 | |||
| Calc.19 | 1.7187 | 0.67963 | 5.661 | 965.79 | 6.04 | 72.4 (2, 0+) | ||
| Calc.20 | 1.7187 | 0.6796 | 5.580 | 967.21 | 5.72 | |||
| Calc.17 | 1.726 | 954 | −1.62 | 100 (2, 0+) | ||||
| a 1Σ+ | AV5Z | 1.6604 | 0.72811 | 7.265 | 1016.37 | 10.09 | −2.130 | |
| ACV6Z | 1.6483 | 0.73882 | 6.959 | 1043.08 | 9.28 | −2.108 | ||
| Calc.19 | 1.6546 | 0.73311 | 7.82 | 1008.45 | 11.76 | |||
| Calc.21 | 1.6551 | 0.73285 | 8.296 | 1006.94 | 13.05 | |||
| Calc.17 | 1.68 | 975 | −2.14 | |||||
| SiC + | ||||||||
| X+ 4Σ− | AV5Z | 1.8190 | 0.60666 | 5.203 | 837.57 | 5.33 | −1.184 | 0.15 (1/2, 3/2) |
| ACV6Z | 1.8101 | 0.61264 | 5.175 | 846.75 | 5.26 | −1.037 | ||
| Calc.11 | 1.83 | 817 | −1.190 | 0.0 | ||||
| 1+ 2Δ | AV5Z | 1.8561 | 0.58265 | 6.274 | 752.12 | 6.70 | −1.008 | 6.3 (5/2, 3/2) |
| ACV6Z | 1.8466 | 0.58870 | 6.279 | 760.63 | 6.65 | −0.810 | ||
| Calc.11 | 1.88 | 723 | −0.950 | 87 (5/2, 3/2) | ||||
| 1+ 2Πc | AV5Z | 1.7591/![[1 with combining low line]](https://www.rsc.org/images/entities/char_0031_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif) ![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[4 with combining low line]](https://www.rsc.org/images/entities/char_0034_0332.gif) ![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif) ![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) |
0.64867/![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif) ![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif) ![[2 with combining low line]](https://www.rsc.org/images/entities/char_0032_0332.gif) ![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif) ![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif) ![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif) |
— | — | — | −1.689/−![[1 with combining low line]](https://www.rsc.org/images/entities/char_0031_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif) ![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif) ![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif) ![[2 with combining low line]](https://www.rsc.org/images/entities/char_0032_0332.gif) |
60.5 (3/2, 1/2)/![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif) ![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif) ![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif) (1/2, 3/2) (1/2, 3/2) |
| ACV6Z | ![[1 with combining low line]](https://www.rsc.org/images/entities/char_0031_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif) ![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif) ![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif) ![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif) /1.9283 /1.9283 |
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif) ![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif) ![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif) ![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif) ![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif) ![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif) /0.53983 /0.53983 |
— | — | — | −![[1 with combining low line]](https://www.rsc.org/images/entities/char_0031_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif) ![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif) ![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif) ![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif) /−1.428 /−1.428 |
||
| Calc.11 | 1.99 | — | ![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif) ![[4 with combining low line]](https://www.rsc.org/images/entities/char_0034_0332.gif) (3/2, 1/2) (3/2, 1/2) |
|||||
| 1+ 2Σ− | AV5Z | 1.8422 | 0.59150 | 6.096 | 776.13 | 6.54 | −1.527 | |
| ACV6Z | 1.8323 | 0.59793 | 6.090 | 785.56 | 6.46 | −1.421 | ||
| Calc.11 | 1.86 | 759 | −1.45 | |||||
| 1+ 2Σ+ | AV5Z | 1.8907 | 0.56157 | 7.070 | 678.29 | 7.51 | −0.818 | |
| ACV6Z | 1.8799 | 0.56800 | 6.984 | 689.67 | 7.35 | −0.689 | ||
| Calc.11 | 1.91 | 651 | −0.73 | |||||
| 2+ 2Π | AV5Z | 1.8498 | 0.58664 | — | — | — | −1.656 | 5.8 (3/2, 1/2) |
| ACV6Z | 1.8544 | 0.58375 | — | — | — | −1.609 | ||
| Calc.11 | 1.87 | — | 30 (3/2, 1/2) | |||||
The values of the dipole moment at equilibrium geometry, μe, are also provided in the Table. They correspond to the projection of the dipole moment vector on the internuclear axis pointing from Si to C. The negative values indicate that the partial atomic charges decrease from Si to C, as illustrated by the Mulliken charges Si+0.154C−0.154 and Si+0.808C+0.192, calculated for the ground states of SiC and SiC+, respectively. The last column of the Table reports the spin–orbit (SO) energy splitting ΔESO at equilibrium, and the Ω values of the lowest and highest SO components.
A comparison between the V/AV5Z and CV/ACV6Z results confirms the expected contraction of the molecular structure with the introduction of the core electrons in the correlation treatment. There is a shortening of the bond distances of about 0.01 Å, a rise in the vibrational frequencies of about 10 cm−1, and a rise in the modulus of the dipole moment of 0.1–0.2 D. More important changes are, however, observed for states which have a strong multireference character, and for which the core effect may act differently on the main configurations of the multireference and consequently change their interaction. This happens in the case of the double-well potential of the lowest 2Π state, as shown in Table 1, which reports the equilibrium properties of both minima, those corresponding to the lowest energy being underlined. As can be seen, the relative stability of the minima inverts when going from AV5Z to ACV6Z, the global minimum being the one at the larger (1.94 Å) and smaller (1.74 Å) distances, respectively. This difference changes the vibrational overlaps characterizing the 1+ 2Π ← X 3Π ionization and has therefore been taken into account in the Franck–Condon simulations (see the ESI†). We also point out the change of spin–orbit splitting along the 1+ 2Π curve. The small and large distance minima are indeed characterized by inverted and regular splittings, respectively. This is explained by Hund's rule applied to the configurations having a dominant weight at these minima, i.e. […](7σ)0(2π)3 and […](7σ)2(2π)1, respectively. The splitting inverts in the vicinity of the maximum separating the two wells, where equal configuration weights and a small ΔESO value of 2 cm−1 are observed. A similar splitting interconversion also happens in the 2+ 2Π state, as a result of the orthogonality of the wavefunctions. The minimum, lying in the region of equal configuration weights, explains the small value of ΔESO (5.8 cm−1). The latter result disagrees with the value of 30 cm−1 obtained by Pramanik et al.,11 probably because of a shift of the interconversion geometry in their calculations. We also observe, for unknown reasons, a large discrepancy for the ΔESO value of the 1+ 2Δ state (87 cm−1 to be compared with our smaller value of 6.3 cm−1).
The comparison with spectroscopic experiments is unfortunately limited to the X 3Π ground state of SiC,44 for which there is a good agreement with our CV results. For SiC, a comparison can be made with previous calculations, which also introduced the core–valence correlation, but as an additive correction. The agreement with our results is good for the X 3Π state,19,20 but some discrepancies are observed for the a 1Σ+ state.19,21 Electron core potential calculations using a medium size basis set have also been performed on both SiC and SiC+.11,17 These V calculations of lower level underestimate the strength of the molecular bonding in both systems. Since there is no high-level ab initio results available to date for SiC+, we recommend our ACV6Z constants for the future spectroscopic investigation of this cation.
Theoretical predictions of the adiabatic ionization energies (IE) and of the term energies (T), calculated as explained in Section 2.2, are provided in Tables 2 and 3, respectively. Both Tables report in the first two energy columns the results of ic-MRCI + Q geometry optimizations performed at the V/AV5Z and CV/ACV6Z levels, respectively. The next column gives the result of a CBS extrapolation carried out with the ACVnZ basis set series (n = Q, 5, 6) and the following columns successively add to the CBS values the contributions of the scalar relativity (SR) and of the spin–orbit (SO). The last column finally introduces the vibrational zero-point energies (ZPE) and provides v+ = 0 ← v = 0 predictions (IE0 and T0) to be compared to experimental values.
| IE (AV5Z)a | IE (ACV6Z)a | IE (CBS)b | IE (CBS + SR)c | IE (CBS + SR + SO)c | IE0 (CBS + SR + SO + ZPE)c | |
|---|---|---|---|---|---|---|
| a From V/AV5Z and CV/ACV6Z MRCI + Q geometry optimizations. b From CV/ACVnZ CBS limit extrapolations. c CBS results with the inclusion of SR, SO and ZPE contributions; see the text for details. | ||||||
| X+ 4Σ− | 8.920 | 8.885 | 8.896 | 8.886 | 8.892 | 8.884 |
| 1+ 2Δ | 10.101 | 10.078 | 10.098 | 10.088 | 10.093 | 10.080 |
| 1+ 2Π | 10.172 | 10.144 | 10.162 | 10.158 | 10.160 | 10.132 |
| 1+ 2Σ− | 10.262 | 10.235 | 10.253 | 10.243 | 10.248 | 10.237 |
| 1+ 2Σ+ | 10.581 | 10.551 | 10.570 | 10.561 | 10.566 | 10.549 |
| 2+ 2Π | 10.665 | 10.651 | 10.671 | 10.665 | 10.669 | 10.678 |
| T e (AV5Z)a | T e (ACV6Z)a | T e (CBS)a | T e (CBS + SR)a | T e (CBS + SR + SO)a | T 0 (CBS + SR + SO + ZPE)a | other calc.b | |
|---|---|---|---|---|---|---|---|
| a See Table 2. b Previous calculations including SO. | |||||||
| SiC | |||||||
| a 1Σ+ | 5107 | 5081 | 5151 | 5178 | 5216 | 5260 | 537017 |
| 486719 | |||||||
| SiC+ | |||||||
| 1+ 2Δ | 9509 | 9630 | 9691 | 9689 | 9686 | 9643 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27811 27811 |
| 1+ 2Π | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 089 089 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 163 163 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 213 213 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 258 258 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 228 228 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 065 065 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 68111 68111 |
| 1+ 2Σ− | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 809 809 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 888 888 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 945 945 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 940 940 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 940 940 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 909 909 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 49811 49811 |
| 1+ 2Σ+ | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 385 385 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 437 437 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 503 503 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504 504 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 505 505 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 426 426 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67511 67511 |
| 2+ 2Π | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 059 059 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 244 244 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 312 312 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 341 341 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 337 337 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 468 468 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31311 31311 |
The evolution of the IE values, from left to right in Table 2, exhibits an oscillating pattern, due to positive and negative mutually compensating contributions. The core and core–valence correlation (difference between V and CV energies) and the scalar relativity are enhanced in the cation by the contraction of the electron density on the atomic cores, and thus introduce negative contributions (in average −26 meV and −8 meV, respectively). In contrast, the CBS, promoted in the neutral species by the additional electron, induces positive contributions (in average +18 meV). For the SO contributions, we have calculated, for the states of SiC and SiC+ involved in each photoionization transition, the energy difference between the lowest Ω state and the corresponding Λ–S non-relativistic state. These contributions to IE are small (in average +4 meV). They mainly come from the Λ ≠ 0 states, with the largest one coming from the X 3Π ground state of SiC. This explains why all corrections are positive. Let us note that weak indirect SO couplings are also taken into account for Λ = 0 states. Finally, the ZPE, which is larger in SiC, decreases the IE value by 11 meV in average, providing vibrationally corrected IE0 values. For the first ionization, our value of 8.884 eV agrees with the previously reported experimental appearance potential (9.0–9.2 ± 0.4 eV)7,8 and the values obtained in this work (see Section 3.3). Previous theoretical works provide a vertical IE value of 8.7 eV10,18 and an adiabatic value of 8.76 eV.17
Regarding the term energies, all contributions are positive, except those concerning the ZPE. The evolution with respect to the level of theory is less important than for IE because it implies energy differences between states corresponding to an equal number of electrons. The largest effect comes from the core–valence correlation (18 meV in average), followed by the CBS (8 meV), while the relativistic effects (SR and SO) are quite small. The ZPE corrected values provide T0 values, recommended for guiding further spectroscopic studies. Values from previous calculations including the SO contribution are given for comparison.11,17,19
3.2 SiC Photoelectron spectrum
Fig. 4(a) displays our experimental SPES spectrum (upper grey spectrum) for the m/z = 40 channel. The photoionizing transition involving the ground states of SiC (X 3Π) and SiC+ (X+ 4Σ−) is unambiguously observed around 9 eV. This transition consists of several bands corresponding to the vibrational progression and assigned by their Δv value. From the positions of the (v–v+) = (1–0), (0–0), and (0–1) bands, we derive that the vibrational fundamentals of the SiC and SiC+ electronic ground states are 940(50) cm−1 and 830(50) cm−1, respectively. These values are in good agreement with our ACV6Z calculations (958.60 cm−1 and 836.23 cm−1, respectively, obtained from the molecular constants of Table 1) and with the experimental work on neutral SiC of Butenhoff and Rohlfing44 (953.2(2) cm−1). In Fig. 4(a), we clearly see other transitions around 10.2 eV.To assign this spectrum, we have modeled the photoionization spectra by calculating the Franck–Condon factors using the vibrational wave functions obtained from the electronic energy curves of the states calculated at the MRCI + Q/AV5Z level. The calculated spectra are shown in Fig. 4(b–g), each transition being normalized to its maximum. The rotational temperature for the simulations was assumed equal to the translational temperature of our beam (180 K), which can be experimentally measured from the ion images, while the 2000 K vibrational temperature has been chosen to best reproduce the hot bands of the X+ 4Σ− ← X 3Π transition. The vibrational temperature is only indicative and is probably not well defined in our experiment. The simulated transitions were then convolved with a Gaussian line shape (FWHM = 26 meV) to simulate the observed bandwidth. The relative energy scale of the calculated v+ = 0 ← v = 0 transitions has been built using the ab initio IE(CBS + SR) adiabatic energies provided in Table 2. We did not take the SO contributions into account, as our experimental spectrum do not resolve the SO splitting. In order to get the best agreement with the experimental spectrum, we shifted by +87 meV the IE(CBS + SR) value of the only unambiguous transition (X+ ← X) involving the ground SiC(X 3Π) and SiC+ (X+ 4Σ−) states:
| IEth(X+ ← X) = IE(X+ ← X; CBS + SR) + 87 meV | (1) |
| IEth(Y+ ← X) = IEth(X+ ← X) + IE(Y+ ← X; CBS + SR) − IE(X+ ← X; CBS + SR) | (2) |
In Fig. 4(a), another transition can be identified using our calculations: the one involving the 1+ 2Π electronic state of SiC+ which has a particular shape due to the double-well structure of this state. All the other transitions from the neutral ground state depicted in Fig. 4 can, a priori, contribute to the experimental spectrum, but an unambiguous assignment is not possible.
Transitions from the X 3Π and a 1Σ+ states of SiC to the 2+ 2Π state of SiC+ have not been considered in our simulations because they have negligible probabilities (see our estimations in the ESI†).
Finally, we have to discuss about possible transitions from the first excited state of the neutral SiC, namely a 1Σ+. Indeed, considering the high exothermicity of the potential reaction sequences producing SiC in our system (most likely the Si + CH reaction and eventually Si + CH2 reaction both starting from SiH4 + CH4 + F), metastable states of neutral SiC can be populated. From the electronic configurations given in Section 3.1, it is expected that only the SiC+ (1+ 2Π) ← SiC(a 1Σ+) transition is allowed. The corresponding calculated spectrum is presented in panel g of Fig. 4. We can see that this transition is not present (or negligible) in the experimental spectrum. This can be rationalized by a low population of the a 1Σ+ state and/or the low ionization probability of the corresponding transition (see our estimation in the ESI†).
Because the resolving power at the FWHM selected for this experiment (m/Δm ≈ 650) is not sufficient to separate isobars, we checked that neither the allene (H2CCCH2) nor the propyne (CH3 CCH), with both m/z = 40.0639 close to that of SiC equal to m/z = 40.0962, contributed to the experimental spectrum. The photoelectron spectra and IEs of these two molecules are well known (IE = 9.69 eV and 10.37 eV for allene and propyne, respectively).45,46 No notable lines are present around 9.7 eV and thus allene is not present. Around 10.37 eV, the PES of CH3 CCH can possibly participate in some minor lines above 10.37 eV but the main features located at 10.24 eV are therefore unambiguously assigned to SiC.
The photoelectron spectrum has been simulated considering an identical ejection probability for each electron involved in the photoionization process and using relative probabilities for the different ionization transitions estimated to 1.0/1.0/0.8/0.5/0.5/0.0 for the transitions from X 3Π towards the X+ 4Σ−, 1+ 2Δ, 1+ 2Π, 1+ 2Σ−, 1+ 2Σ+, and 2+ 2Π states of SiC+, respectively, and to 0.1 for the transition from a 1Σ+ towards the 1+ 2Π state. As detailed in the ESI,† these probabilities, normalized to the main X+ ← X ionization, take the weights of the main configurations in the MRCI wave functions of the states of SiC and SiC+ involved in these transitions and the corresponding spin and orbital degeneracies into account.
Despite an underestimation of the SiC+ (X+ 4Σ−) ← SiC(X 3Π) transition intensities, we can consider that there is a good agreement between the experimental spectrum and the calculated spectrum shown in Fig. 5. Note that deviations from the calculated relative intensities might exist due to continuum resonances such as autoionizations.
 | ||
| Fig. 5 Experimental photoelectron spectrum of SiC (upper grey curve) compared with our calculated spectrum (lower purple curve). The calculated spectrum corresponds to the sum of the calculated spectra displayed in Fig. 4 weighted by relative photoionization probabilities. See the text for details. | ||
3.3 IE determination
As discussed previously, we can derive two IEs from our experimental spectrum. Indeed, only the X+ 4Σ− ← X 3Π and, to a lesser extent, the 1+ 2Π ← X 3Π transitions are clearly identified. Thus experimentally, we can provide the spectral position of the X+ 4Σ−(v+ = 0) ← X 3Π(v = 0) band at 8.968 eV and the maximum of the feature which includes the 1+ 2Π(v+ = 0) ← X 3Π(v = 0) band (see panel d) shown in Fig. 4 at 10.236 eV. Note that this latter value does not correspond exactly to the 0–0 transition (see panel d) of Fig. 4, which will be taken into account in the error bar. After the Stark-induced-shift correction (+7 meV, see Section 2.1), the corresponding IEs are 8.975(6) eV and 10.243(20) eV, respectively. These two values, directly extracted from our spectrum, do not take into account the rotational structures of the bands and the SO couplings. In this section, we propose semi-experimental values of the 5 lowest IEs using our experimental values, our calculations, and by estimating, in simple terms, the effect of the SO couplings.| • IE(X+ 4Σ−(v+ = 0) ← X 3Π(v = 0)) = 8.973 eV, |
| • IE(1+ 2Δ(v+ = 0) ← X 3Π(v = 0)) = 10.169 eV, |
| • IE(1+ 2Π(v+ = 0) ← X 3Π(v = 0)) = 10.215 eV, |
| • IE(1+ 2Σ−(v+ = 0) ← X 3Π(v = 0)) = 10.326 eV, and |
| • IE(1+ 2Σ+(v+ = 0) ← X 3Π(v = 0)) = 10.637 eV. |
| • IE(X+ 4Σ−1/2(v+ = 0) ← X 3Π2(v = 0)) = 8.978 eV, |
| • IE(1+ 2Δ5/2(v+ = 0) ← X 3Π2(v = 0)) = 10.173 eV, |
| • IE(1+ 2Π3/2(v+ = 0) ← X 3Π2(v = 0)) = 10.216 eV, |
| • IE(1+ 2Σ−1/2(v+ = 0) ← X 3Π2(v = 0)) = 10.331 eV, and |
| • IE(1+ 2Σ+1/2(v+ = 0) ← X 3Π2(v = 0)) = 10.642 eV, |
Note that the case involving the 1+ 2Π state is again peculiar because of its double-well curve. As mentioned in Section 3.1, the small and large distance minima are characterized by inverted and regular SO splittings, respectively. As our highest-level calculation (MRCI + Q/ACV6Z) seems to indicate that the minima at short distance are the most stable, we used the corresponding SO splitting (see Table 1).
In conclusion, all the SO corrections are mainly the result of the SO coupling occurring in the neutral ground state (X 3Π) except for the IE of the 1+ 2Π3/2(v+ = 0) ← X 3Π2(v = 0) transition. Indeed, in that case, the SO corrections are similar in the neutral and cationic states and thus their effects compensate each other.
4. Conclusions
In this article, we presented a study of SiC photoionization combining high-level ab initio calculations and synchrotron-based experiment performed in the gas phase. The experimental photoelectron spectrum of pure SiC was measured for the first time in the gas phase over the 8 to 11 eV range, thanks to the coupling of a flow-tube reactor with a double imaging electron/ion detection setup, which allows isolating the weak signal of SiC species out of the numerous side products. The observed structures are assigned using our calculations and ionization energies have been derived. We have clearly identified the signature of ionization from the ground triplet state of SiC to the low-lying states of SiC+, involving its quartet ground state, but also its four lowest doublet states. Among them is the 1+ 2Π state which is responsible for a band structure of peculiar shape observed in our spectra, and which results from its double-well potential. We have provided for the first time semi-experimental ionization energies involving the excited states of the cation. Although the spin–orbit was not resolved in our spectra, we were able to integrate it, thanks to the results of our calculations. From our tentative SO corrections on the IEs, one can deduce that our initial experimental values (see introduction of Section 3.3), which neglect the SO couplings, have underestimated uncertainties. Thus, our recommended adiabatic IE values for X+ 4Σ−(v+ = 0) ← X 3Π(v = 0) and the 1+ 2Π(v+ = 0) ← X 3Π(v = 0) transitions are 8.978(10) eV and 10.216(24) eV.Another contribution of the calculations has been to characterize the electronic structure of SiC+ and to provide useful data for future spectroscopic investigations of this cation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was performed on the DESIRS Beamline at SOLEIL synchrotron under proposal number #20200996. We are grateful to the whole staff of SOLEIL for running the facility. Ning L. Chen acknowledges the support from the Paris Ile-de-France Region (DIM ACAV+, SPIRAULI project) for her PhD grant. This work has also received financial support from the French “Agence Nationale de la Recherche” (ANR) under grant no. ANR-21-CE29-0017-01 (Project ZEPHIRS). This work was supported by the Programme National de Physique et Chimie du Milieu Interstellaire (PCMI) of CNRS/INSU with INC/INP cofunded by CEA and CNES. J. L. thanks the Fonds de la Recherche Scientifique-FNRS (IISN grant No. 4.4504.10) for financial support, and the Consortium des Équipements de Calcul Intensif (CÉCI), funded by the Fonds de la Recherche Scientifique de Belgique (F.R.S.-FNRS) under grant number 2.5020.11 and by the Walloon Region, for computational resources.Notes and references
- K. Daviau and K. K. M. Lee, Crystals, 2018, 8, 217 CrossRef.
- S. Cristallo, A. Nanni, G. Cescutti, I. Minchev, N. Liu, D. Vescovi, D. Gobrecht and L. Piersanti, Astron. Astrophys., 2020, 644, A8 CrossRef CAS.
- M. Lugaro, B. Cseh, B. Világos, A. I. Karakas, P. Ventura, F. Dell'Agli, R. Trappitsch, M. Hampel, V. D'Orazi, C. B. Pereira, G. Tagliente, G. M. Szabó, M. Pignatari, U. Battino, A. Tattersall, M. Ek, M. Schönbächler, J. Hron and L. R. Nittler, Astrophys. J., 2020, 898, 96 CrossRef CAS.
- J. Cernicharo, C. A. Gottlieb, M. Guelin, P. Thaddeus and J. M. Vrtilek, Astrophys. J., 1989, 341, L25 CrossRef CAS.
- D. Gobrecht, Front. Astron. Space Sci., 2021, 8, 662545 CrossRef.
- T. Chen, C. Y. Xiao, A. Li and C. T. Zhou, Mon. Not. R. Astron. Soc., 2022, 509, 5231 CrossRef CAS.
- J. Drowart, G. De Maria and M. G. Inghram, J. Chem. Phys., 1958, 29, 1015–1021 CrossRef CAS.
- G. Verhaegen, F. E. Stafford and J. Drowart, J. Chem. Phys., 1964, 40, 1622–1628 CrossRef CAS.
- B. Ruscic and D. H. Bross, Active Thermochemical Tables (ATcT) values based on ver. 1.124 of the Thermochemical Network, Argonne National Laboratory (2019); available at ATcT.anl.gov, 2022, https://atct.anl.gov/.
- P. J. Bruna, C. Petrongolo, R. J. Buenker and S. D. Peyerimhoff, J. Chem. Phys., 1981, 74, 4611–4620 CrossRef CAS.
- A. Pramanik, S. Chakrabarti and K. K. Das, Chem. Phys. Lett., 2008, 450, 221–227 CrossRef CAS.
- P. F. Bernath, S. A. Rogers, L. C. O’Brien, C. R. Brazier and A. D. McLean, Phys. Rev. Lett., 1988, 60, 197–199 CrossRef CAS PubMed.
- A. C. Borin, J. P. Gobbo, R. D. S. Batista and L. G. M. de Macedo, Chem. Phys., 2005, 312, 213–222 CrossRef CAS.
- G. A. Garcia, B. K. de Miranda, M. Tia, S. Daly and L. Nahon, Rev. Sci. Instrum., 2013, 84, 053112 CrossRef CAS PubMed.
- G. A. Garcia, B. Gans, X. Tang, M. Ward, S. Batut, L. Nahon, C. Fittschen and J. C. Loison, J. Electron Spectrosc. Relat. Phenom., 2015, 203, 25–30 CrossRef CAS.
- B. Gans, F. Holzmeier, J. Krüger, C. Falvo, A. Röder, A. Lopes, G. A. Garcia, C. Fittschen, J.-C. Loison and C. Alcaraz, J. Chem. Phys., 2016, 144, 204307 CrossRef CAS PubMed.
- A. Pramanik and K. K. Das, J. Mol. Spectrosc., 2007, 244, 13–23 CrossRef CAS.
- A. I. Boldyrev, J. Simons, V. G. Zakrzewski and W. von Niessen, J. Phys. Chem., 1994, 98, 1427–1435 CrossRef CAS.
- D. H. Shi, W. Xing, J. F. Sun and Z. L. Zhu, Eur. Phys. J. D, 2012, 66, 262 CrossRef.
- W. Xing, D. Shi and J. Sun, J. Quant. Spectrosc. Radiat. Transfer, 2019, 227, 86–93 CrossRef CAS.
- M. Zhang and K. Wang, J. Quant. Spectrosc. Radiat. Transfer, 2019, 233, 13–20 CrossRef CAS.
- L. Nahon, N. De Oliveira, G. A. Garcia, J. F. Gil, B. Pilette, O. Marcouillé, B. Lagarde and F. Polack, J. Synchrotron Radiat., 2012, 19, 508–520 CrossRef CAS PubMed.
- X. Tang, G. A. Garcia, J.-F. Gil and L. Nahon, Rev. Sci. Instrum., 2015, 86, 123108 CrossRef PubMed.
- J. C. Poully, J. P. Schermann, N. Nieuwjaer, F. Lecomte, G. Grégoire, C. Desfrançois, L. P. G. A. Garcia, L. Nahon, D. Nandi and M. Hochlaf, Phys. Chem. Chem. Phys., 2010, 12, 3566–3572 RSC.
- W. A. Chupka, J. Chem. Phys., 1993, 98, 4520–4530 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, WIREs Comput. Mol. Sci., 2012, 2, 242–253 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Hesselmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107 CrossRef CAS PubMed.
- H.-J. Werner, P. J. Knowles, P. Celani, W. Györffy, A. Hesselmann, D. Kats, G. Knizia, A. Köhn, T. Korona, D. Kreplin, R. Lindh, Q. Ma, F. R. Manby, A. Mitrushenkov, G. Rauhut, M. Schütz, K. R. Shamasundar, T. B. Adler, R. D. Amos, S. J. Bennie, A. Bernhardsson, A. Berning, J. A. Black, P. J. Bygrave, R. Cimiraglia, D. L. Cooper, D. Coughtrie, M. J. O. Deegan, A. J. Dobbyn, K. Doll, M. Dornbach, F. Eckert, S. Erfort, E. Goll, C. Hampel, G. Hetzer, J. G. Hill, M. Hodges, T. Hrenar, G. Jansen, C. Köppl, C. Kollmar, S. J. R. Lee, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, B. Mussard, S. J. McNicholas, W. Meyer, T. F. Miller III, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. A. Peterson, K. Pflüger, R. Pitzer, I. Polyak, M. Reiher, J. O. Richardson, J. B. Robinson, B. Schröder, M. Schwilk, T. Shiozaki, M. Sibaev, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, J. Toulouse, M. Wang, M. Welborn and B. Ziegler, MOLPRO, version 2022, a package of ab initio programs, see https://www.molpro.net.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803 CrossRef CAS.
- E. R. Davidson and D. W. Silver, Chem. Phys. Lett., 1977, 52, 403–406 CrossRef CAS.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- T. V. Mourik, A. K. Wilson and T. H. Dunning, Mol. Phys., 1999, 96, 529–547 CrossRef.
- T. V. Mourik and T. H. Dunning, Int. J. Quantum Chem., 2000, 76, 205–221 CrossRef.
- A. K. Wilson, T. van Mourik and T. H. Dunning, J. Mol. Struct. THEOCHEM, 1996, 388, 339–349 CrossRef CAS.
- K. A. Peterson and T. H. Dunning, J. Chem. Phys., 2002, 117, 10548–10560 CrossRef CAS.
- A. J. C. Varandas, J. Chem. Phys., 2007, 126, 244105 CrossRef CAS PubMed.
- W. Kutzelnigg and W. Liu, J. Chem. Phys., 2005, 123, 241102 CrossRef PubMed.
- D. Peng and M. Reiher, Theor. Chem. Acc., 2012, 131, 1081 Search PubMed.
- A. Berning, M. Schweizer, H.-J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823–1833 CrossRef CAS.
- G. G. Balint-Kurti, R. N. Dixon and C. C. Marston, Int. Rev. Phys. Chem., 1992, 11, 317–344 Search PubMed.
- T. J. Butenhoff and E. A. Rohlfing, J. Chem. Phys., 1991, 95, 3939–3943 CrossRef CAS.
- Z. Z. Yang, L. S. Wang, Y. T. Lee, D. A. Shirley, S. Y. Huang and W. A. Lester, Chem. Phys. Lett., 1990, 171, 9–13 CrossRef CAS.
- C. Baker, D. W. Turner and W. C. Price, Proc. R. Soc. London, Ser. A, 1968, 308, 19–37 CAS.
- R. Signorell and F. Merkt, Mol. Phys., 1997, 92, 793–804 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Further details regarding the 1+ 2Π electronic state potential energy curve of SiC+ and our photoionization probability estimations. See DOI: https://doi.org/10.1039/d3cp02775a |
| ‡ Current address: Institute of Physics, University of Freiburg, 79104 Freiburg, Germany. |
| This journal is © the Owner Societies 2023 |