Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Phenol, the simplest aromatic monohydroxy alcohol, displays a faint Debye-like process when mixed with a nonassociating liquid†
Lars
Hoffmann
 ,
Joachim
Beerwerth
,
Joachim
Beerwerth
 ,
Kevin
Moch
,
Kevin
Moch
 and
Roland
Böhmer
and
Roland
Böhmer

Fakultät Physik, Technische Universität Dortmund, 44221 Dortmund, Germany
First published on 1st September 2023
Abstract
Solvated in propylene carbonate, viscous phenol is studied using dielectric spectroscopy and shear rheology. In addition, several oxygen-17 and deuteron nuclear magnetic resonance (NMR) techniques are applied to specifically isotope labeled equimolar mixtures. Quantum chemical calculations are used to check the electrical field gradient at phenol's oxygen site. The chosen combination of NMR methods facilitates the selective examination of potentially hydrogen-bond related contributions as well as those dominated by the structural relaxation. Taken together the present results for phenol in equimolar mixtures with the van der Waals liquid propylene carbonate provide evidence for the existence of a very weak Debye-like process that originates from ringlike supramolecular associates.
1. Introduction
Hydrogen bonding is at the core of molecular associations in all sorts of condensed matter. Depending on the kind of moieties that are in the hydrogen bonding “soup”1 and subject to the geometrical constraints imposed by the molecular architecture, a wealth of different aggregates can emerge in solids and liquids. The formation of hydrogen bonding patterns has been studied intensively in self-associating liquids such as linear and branched monohydroxy alcohols.2 Due to the typically small hydrogen bonding strength,3 transient supramolecular patterns often evolve4 that can be modulated by changes in external parameters such as temperature, pressure, external field, or the degree of dilution.5,6The monohydroxy alcohols are probably among the molecularly simplest glassforming liquids for which, depending on the position of the OH group on the aliphatic backbone, ring- or chain-type association patterns are favored. For a long time it was thought that phenyl groups are effective in reducing the impact of hydrogen bonding, not the least because the presence of the relatively bulky aromatic rings can act as a source of considerable steric hindrance for the association of OH groups.7 Recent scrutiny, involving systematic variations of the “sidegroup” that is attached to the phenyl ring, shows that matters are more complex: In addition to steric effects and O–H⋯O hydrogen bonding,3,8 also the π–π interactions among the phenyl rings,9 as well as O–H⋯π based associations need to be taken into consideration,10–15 albeit not always conforming to the classical notion of “π stacking”.16 Owing to their ability to supercool easily and to form glasses, recently the isomeric phenyl propanols received particular attention: Using light-scattering-assisted,17 shear mechanical,18 as well as high-field electrical experiments,19 an important finding for these liquids is that, at least in their highly viscous state, a supramolecular Debye-type process exists that is slower than the structural relaxation.
For a long-time, the Debye process in monohydroxy alcohols was considered a phenomenon that is only accessible via dielectric spectroscopy.5 In these liquids, the amplitude of the Debye relaxation can be about 100 times larger than that of the structural relaxation,20 but also three times smaller than the latter.6,21,22 It has been recognized that the Debye process leaves its mark in other quantities such as an OH-related mode as detected using NMR relaxometry4 and neutron spin-echo techniques23 as well as in a polymer-like viscosity enhancement.24
Without reference to these latter observations, but rather by comparison with results from light scattering, more recently it has been suggested that a Debye process could be featured in the dielectric response also of nonassociating glass forming liquids.25 This recent suggestion underscores that for an identification of a Debye process that is akin to that in associating liquids, in particular to that in aliphatic monohydroxy alcohols, it is advisable to rely not just on dielectric measurements. Therefore, in addition to dielectric spectroscopy, in the present work we will apply shear rheology and several nuclear magnetic resonance (NMR) techniques to check whether or not in a mixed liquid in which the only associating component is phenol (PhOH), the simplest aromatic monohydroxy alcohol, a hydrogen-bond related Debye process does exist.
From the present perspective, a comparison with other members of the homologous C6H5–(CH2)n–OH series is particularly intriguing.11,17 While initially it was thought that due to effects of sterical hindrance the Debye-type relaxation might not generally be observable in liquids like 1-phenyl-2-propanol,7 recent evidence shows that also here a Debye relaxation does exist, but it weakens as the OH group gets closer to the phenyl ring.17 These findings raise the question whether in the n = 0 (monohydroxybenzene) limit, i.e., for PhOH, the sterical hindrance becomes overwhelming so that the formation of hydrogen bonded structures is precluded or whether the hydrogen bond interactions are sufficiently effective, so that a Debye process is observable nevertheless.
X-ray diffraction and infrared absorption techniques were exploited to map out the interplay between dispersive and hydrogen bond interactions in the C6H5–(CH2)n–OH series upon systematically varying the length of the linear alkyl chain (n = 1–5, 7) that is attached to the ring moiety.11 Obviously, the n = 0 case, PhOH, where the OH group is directly attached to the aromatic ring, was not considered in this context, so far. Presumably, this is because C6H5–X with X = OH, which melts near 314 K,26 but also the substances with X = SH or SeH, display a pronounced crystallization tendency.27 At ambient pressure, the molecules in crystalline PhOH form three-fold hydrogen bonded helices.28 Along them the OH-related dipole moments are aligned in an antiparallel fashion.29 With reference to the fact that the ambient-pressure structure of PhOH is built from trimeric repeat units, a Raman study of the pure liquid, emphasizes the important role that intermolecular hydrogen bonding plays in stabilizing three-membered phenol clusters.30 When PhOH is compressed to 0.16 GPa, two-fold ribbon-like structures evolve, along which the dipole moments are arranged in a parallel fashion.29,31
Glass formation has been reported for phenol dissolved in relatively concentrated mixtures with hydrogen bonded liquids such as ethanol,32 glycerol/water solutions,33 or deep eutectic choline chloride binaries.34,35 Furthermore, when embedded in a host of solvents near and above room temperature, PhOH was examined using vibrational spectroscopy also under more highly diluted conditions.30,36–38 PhOH does not form vitrifying mixtures with other simple aromatic ring molecules such as toluene32 or (as a result from the present work also not with) 2-picoline, while for PhOH diluted in an ortho-terphenyl/benzene solution glass formation could apparently be enforced by shock freezing to liquid nitrogen temperature.39
Attempts that we undertook to vitrify pure PhOH by quenching from about 350 to 77 K with rates exceeding 15 K s−1 failed. Therefore, with the goal to examine the relaxational contributions associated with the phenolic hydrogen bonds nevertheless, for PhOH a nonassociating mixing partner devoid of hydroxyl groups is to be sought. In this context, it should be emphasized that studies of supramolecular association in aliphatic monohydroxy alcohols often exploit dilution with a mixing partner that is unable to sustain hydrogen bonds: Typically, in 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixtures and sometimes even for smaller alcohol concentrations, the Debye process can persist almost unaltered, albeit reduced in intensity.6,40–47
50 mixtures and sometimes even for smaller alcohol concentrations, the Debye process can persist almost unaltered, albeit reduced in intensity.6,40–47
The solvent that is suitable to dilute PhOH should exhibit a good ambient-pressure glassforming propensity48 to avoid the need for the application of high cooling or heating rates. Furthermore, we presumed that in order to ensure miscibility, the mixing partner should be polar and possess a molecular weight comparable to that of PhOH. Conforming to these provisos, in the present work we will show that propylene carbonate (PC) is a suitable choice. This van der Waals glass former, with a glass transition temperature Tg of about 160 K,49,50 was studied already by, e.g., dielectric spectroscopy,51–54 shear rheology,55 and NMR.56 Furthermore, PC was studied by numerous other techniques as well.57–60 PhOH, a very weak acid, and PC, a very weak base,61 are not expected to react with each other.62 A potential drawback of choosing PC as a mixing partner may be its large dipole moment of about 5 D,63–65 while for PhOH some solution studies indicate an “infinite dilution” value of “only” 1.5 D. The sizeable dependence of PhOH's dipole moment on concentration and solvent could be taken as a hint for self-association effects.66,67
The dipolar response of PhOH mixtures with PC are thus expected to comprise significant contributions also from the van der Waals liquid. To enable an additional perspective on the relaxation properties of PhOH in PC that is not sensitive on the molecular dipole moments, apart from dielectric spectroscopy, we performed shear mechanical measurements. Furthermore, to achieve a fully selective detection of the various components in the mixture, we will exploit isotope edited NMR. In other words, for the present NMR studies unlabeled substances were mixed with ring-deuterated PC, ring-deuterated PhOH, or 17O labeled PhOH. Thus, while the PC-d3 and the PhOH-d3 molecules can be expected to be most sensitive to the structural relaxation, the oxygen-17-labeled probe is closest to and should therefore be most sensitive to the dynamics at the hydrogen bonding site.
2. Experimental details
Fully protonated PC and PhOH (nominal purities ≥99%) were acquired from Alfa Aesar and Sigma Aldrich, respectively. PC-d3 was taken from the batch used in ref. 56. Phenol-2,4,6-d3 (PhOH-d3, ≥98 atom% D) was purchased from Sigma Aldrich. The Ph17OH sample (17O enrichment 35.8 atom%, purity ≥98%) was obtained from Eurisotop. To prepare samples with the desired molar fraction, xPhOH, directly in the dielectric cell or in the NMR glass tube, PhOH was first weighed under a fume hood. Then, the appropriate amount of PC was pipetted into the cell or tube where during stirring in or shaking of these containers, PhOH quickly dissolved in PC. To remove potentially adverse effects of paramagnetic O2, the filled NMR tubes were degassed via the freeze–pump–thaw method and hermetically flame-sealed afterwards.For the rheological measurements of a sample with xPhOH = 0.5 we employed an MCR 502 rheometer from Anton-Paar. A premixed PC:PhOH solution was pipetted onto the lower shear plate of a 4 mm parallel-plate geometry. To control and stabilize the temperature to within 0.2 K, an EVU20 unit and a CTD450 oven were used. Dielectric spectroscopy experiments were carried out on fully protonated PC:PhOH mixtures (or an equimolar mixture of PhOH and 2-picoline, data not shown) using a Novocontrol Alpha Analyzer in conjunction with a Quatro temperature controller from Novocontrol Co. The utilized sapphire/invar cell was stabilized to the desired temperatures to within ±0.1 K.
The NMR experiments were conducted using home-built equipment. The 2H spectrometer was operated at a Larmor frequency of ωD = 2π× 45.6 MHz. The 17O/1H double-resonance spectrometer was operated at ωO = 2π × 54.2 MHz and ωH = 2π × 400.1 MHz in conjunction with a probe head from NMR Service Co. Below 200 K, 1H decoupling employed a power level corresponding to a Rabi frequency of 167 kHz in order to effectively remove unwanted hydroxyl-proton impacts on the oxygen magnetization. The oxygen-17 spectra are referenced with respect to liquid 1H217O at 291 K. The 2H pulses were tD,π/2 = 2.0 to 2.5 μs long and for the excitation of the central (−1/2 ↔ +1/2) 17O transition tO,π/2 was 1.5 μs. During each NMR experiment the temperature stability was typically better than ±0.2 K.
3. Results and analyses
Below, in Section 3A we will first present dielectric measurements on PC:PhOH mixtures and show how their spectra can be decomposed into a Debye-like and another contribution. Then, based on rheology, we will determine the so-called viscosity enhancement which is able to signal the presence of even weak supramolecular modes. Section 3B focuses on PC:PhOH's NMR spectra. These are required, for instance, for the detailed analysis of the 17O spin relaxation times that are dealt with in Section 3C. On a similar basis, Section 3D provides time-scale information by employing deuteron NMR. For aliphatic monohydroxy alcohols, close to the site where hydrogen bonding occurs, the correlation times (determined using 17O NMR) are found to be longer than those at the alkyl rest (accessible, e.g., using 2H NMR) that probes the structural relaxation.4,5,68 Sections 3C and D aim at gathering all the (mostly time scale) information that is needed to check whether or not PC:PhOH displays a pattern similar to that which characterizes the well-established Debye liquids.A. Dielectric spectroscopy and shear rheology
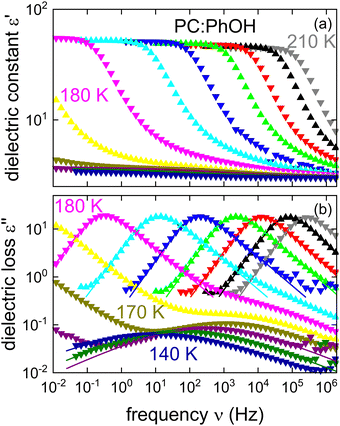
Fig. 1 shows the real and the imaginary part of the complex dielectric function ε* = ε′ − iε′′ of PC:PhOH. Upon cooling, well defined steps in ε′, cf.Fig. 1(a), and well defined asymmetric loss peaks in ε′′, cf.Fig. 1(b), shift through the accessible frequency window. Above about 175 K the spectral shapes remain more or less invariant, implying that frequency temperature superposition is approximately fulfilled. Then at lower temperatures, steps and peaks which refer to the dominant relaxation of PC:PhOH are no longer detected. Now, another process that is characterized by an enormously large spectral width and a very small relaxation strength is visible. This symmetrically broadened relaxation can be assigned to a Johari–Goldstein process.As indicated by the solid lines in Fig. 1, the peaks and steps referring to the dominant relaxation are nicely describable using a Cole–Davidson function, i.e., by a Havriliak–Negami function
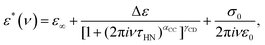 | (1) |
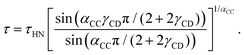 | (2) |
For the dominant relaxation of PC:PhOH (apart from αCC = 1) we find γCD = 0.6 ± 0.05, a value typical for many neat supercooled liquids.70 However, for binary mixtures often times one also observes an enhanced broadening, hence smaller γCD.71 In this context, we note that for the dielectrically detected α-process of neat PC an exponent γCD = 0.66 was reported.51
A direct comparison of the dielectric function of PC at 180 K with that for the equimolar PhOH mixture is shown in Fig. 2. Here, one recognizes that the alcohol addition slows the dominant dynamics of the mixture by about 5 decades. This finding suggests that if PhOH could be vitrified in pure form, its effective Tg would be much larger than that of neat PC.49,50Fig. 2 also includes a dielectric spectrum recorded for a binary mixture featuring a molar PhOH fraction of 75%. The appearance of a strongly reduced relaxation strength in that sample and of a peak frequency similar to that of the 50% mixture indicate a limited miscibility beyond this latter PhOH fraction. A comparison of the relaxation strengths also including several other compositions (see the inset of Fig. 2) confirms the overall trend and furthermore that the equimolar sample does not show signs of segregation.
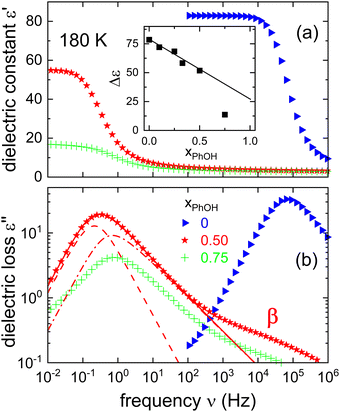 | ||
| Fig. 2 Isothermal comparison of (a) the real and (b) the imaginary part of the dielectric function ε* as measured for different molar fractions xPhOH at 180 K. For this temperature, the inset shows the relaxation strengths as a function of xPhOH. For xPhOH ≤ 0.5 we find that Δε displays a linear trend, while for xPhOH = 0.75 the reduced Δε is indicative for a partial crystallization. The line in the inset is calculated using eqn (23) and the information given below that equation. The dashed and the dash-dotted lines in frame (b) result from a decomposition of the main peak in terms of a Debye-like (γCD,D = 1) and an α-type contribution (γCD,α = 0.53), respectively. The decomposition is not entirely unique, but with the chosen γCD,α, the time constants of the two processes differ by a factor of about 3.3. | ||
So far we assumed that the relaxation strength essentially originates from a monomodal main peak. However, also another interpretation is possible by assuming a recently suggested decomposition into a Debye-like (D) and an α-type contribution that was applied in analyses of various phenyl alcohols.17–19 For comparison purposes, the results of such a decomposition are included in Fig. 2 (see also Fig. S1 in the ESI†).
As already pointed out, from Fig. 1(b) it is obvious that PC:PhOH exhibits a well-defined secondary process. To describe the broad peaks referring to this so called β relaxation, eqn (1) was used again but now in the Cole–Cole limit with αCC = 0.33 ± 0.03 and γCD ≈ 1. The appearance of a Johari–Goldstein relaxation in PC:PhOH is remarkable because in neat PC such a feature could be resolved via broadband dielectric spectroscopy only after excessive physical aging.72 Yet, for glassformers like toluene or meta-fluoroaniline, which involve substituted aromatic rings, the existence of a prominent Johari–Goldstein relaxation is well known.73,74
In the search for dynamical signatures of supramolecular structures, also shear rheology plays an important role. Therefore, we carried out measurements of the complex shear modulus G* = G′ + iG′′ and in Fig. 3(b) we show G′′(ν) for PC:PhOH at different temperatures. The slowdown of the dynamics that occurs with decreasing temperature leads to a down-shift of the loss peak frequencies that reflect an increase of the associated time constants τG.
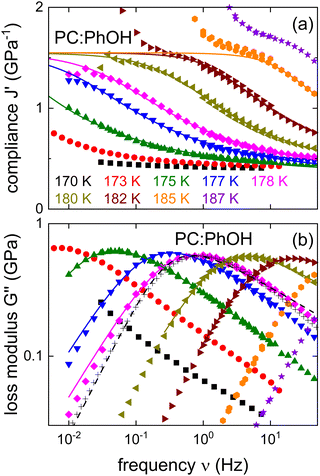 | ||
| Fig. 3 Shear mechanical response of PC:PhOH, here represented as (a) real part of the compliance and (b) imaginary part of the loss modulus. The solid lines represent fits and calculations using eqn (3) and the parameters given in the text. The black crosses mark appropriately shifted data for DC704 (for T = 218 K) a simple liquid devoid of supramolecular modes.75,76 For 178 K the dashed line represents a Cole–Davidson curve normalized to the maximum of G′′. The low-frequency upturns seen in J′ above about 1.5 GPa−1 reflect the low-torque resolution limit of our rheometer. | ||
While the evolution of G′′(ν) looks similar to that revealed by the dielectric loss, one has to realize that in Fig. 1 we plot ε*, i.e., the dielectric susceptibility, while in Fig. 3(b) a modulus is presented. For a more consistent comparison, it is advisable to use the mechanical equivalent of ε*, i.e., the mechanical compliance J* = J′ − iJ′′ = 1/G*. From Fig. 3(a) one recognizes well defined steps in J′(ν), akin to the situation for ε′(ν). Peaks in J′′(ν), that one may naively expect in analogy to the situation for ε′′(ν), are not observed. This is because, similar to the dc conductivity in ε′′(ν), for the compliance the viscous flow leads to a 1/ν divergence in J′′(ν). This contribution is so prevalent that it completely masks any peaks in the loss part of the compliance.
Nevertheless, analogous to the dielectric data, one may try to describe the mechanical ones using, e.g., a Havriliak–Negami function here written as
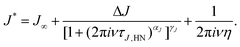 | (3) |
| z0 = 2πνmaxη′(ν → 0)/G∞. | (4) |
B. 17O and 2H NMR spectra
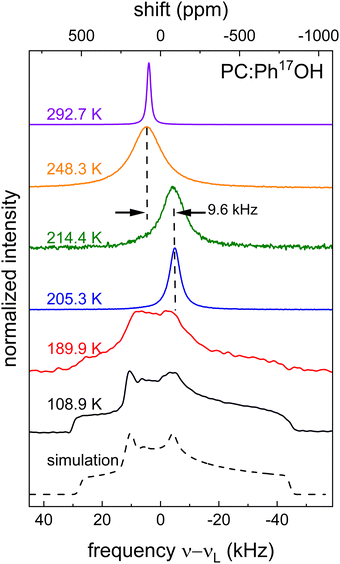
Using NMR, information regarding molecular dynamics can for instance be gathered by tracking motional narrowing effects. Furthermore, from the low-temperature spectra, the quadrupolar coupling constant CQ = eQVzz/h and the asymmetry parameter η = (VXX − VYY)/VZZ become accessible. These quantities involve the components |VZZ| ≥ |VYY| ≥ |VXX| of the electrical field gradient tensor at the nuclear site and are necessary for the analysis of the spin-relaxation times that will be discussed in Section 3C, below.Fig. 4 shows 17O central-transition spectra that were recorded for PC:Ph17OH in a wide temperature range. Near ambient temperature a motionally narrowed spectrum is observed, indicating that here the motional correlation times are short on the scale of τ ≈ 1/ωO ≈ 2.9 ns that is set by the inverse Larmor frequency. Then, upon cooling the absorption spectra broaden, shift their center of gravity, narrow again, and eventually broaden into a well-structured pattern. As the analysis of these data will reveal, this seemingly unintuitive sequence of temperature dependent effects is in fact characteristic for slowing dynamics as probed by nuclei that are subjected to strong quadrupolar interactions.
Above about 250 K, the spectra are peaked near 4.6 kHz, corresponding to an isotropic chemical shift δiso = 86 ppm in the high-temperature limit. Due to the appearance of very short T2 times (≲10 μs), see Section 3C, below, spectra could not be recorded between about 250 and 215 K. From the data below this latter temperature it is evident that the spectra have undergone a so-called dynamic frequency shift.78 This shift amounts to about 9.6 kHz, see Fig. 4, corresponding to Δδ = 177 ppm.
In the framework of second-order perturbation theory, the dynamic frequency shift can be calculated to be78
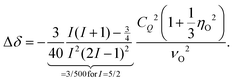 | (5) |
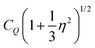 of 9.3 MHz results for spin I = 5/2 nuclei. To disentangle the values of CQ and ηO, the low-temperature spectrum shown in Fig. 4 can be simulated using a suitable combination of these parameters. The dashed line in Fig. 4 reflects a spectrum simulated by means of WSolids79 using parameters that within experimental uncertainty are compatible with the quadrupolar product inferred from Δδ.
of 9.3 MHz results for spin I = 5/2 nuclei. To disentangle the values of CQ and ηO, the low-temperature spectrum shown in Fig. 4 can be simulated using a suitable combination of these parameters. The dashed line in Fig. 4 reflects a spectrum simulated by means of WSolids79 using parameters that within experimental uncertainty are compatible with the quadrupolar product inferred from Δδ.
In addition to recording 17O spectra, also 2H spectra were sampled. To achieve spectral selectivity we investigated suitably labeled PC:PhOH mixtures, i.e., PC:PhOH-d3 and PC:PhOH-d3. It turns out that we do not detect lineshape changes of the type observed, e.g., in binary mixtures comprising constituents of significantly differing molecular weight.80 Therefore, as Fig. S2 in the ESI† we provide only low-temperature spectra for PC-d3 and PhOH-d3 in the corresponding mixtures. From these spectra we determine the 2H quadrupolar coupling constants which are often expressed in terms of the anisotropy parameter  .81 For neat PC-d3 an anisotropy parameter δPC/2π = 125 kHz and a vanishing asymmetry parameter were reported.56 In the mixture we find the same values. For PhOH (in fact for ring-deuterated phenol-d5) only rough estimates are given in the literature.82,83 For the PhOH-d3 component in the presently studied mixture we find δPhOH/2π = 135 ± 3 kHz and ηPhOH = 0.05 ± 0.02. Expectedly the anisotropy parameter given here is somewhat larger than for aliphatic deuterons, but well within the range expected for aromatic deuterons.84,86
.81 For neat PC-d3 an anisotropy parameter δPC/2π = 125 kHz and a vanishing asymmetry parameter were reported.56 In the mixture we find the same values. For PhOH (in fact for ring-deuterated phenol-d5) only rough estimates are given in the literature.82,83 For the PhOH-d3 component in the presently studied mixture we find δPhOH/2π = 135 ± 3 kHz and ηPhOH = 0.05 ± 0.02. Expectedly the anisotropy parameter given here is somewhat larger than for aliphatic deuterons, but well within the range expected for aromatic deuterons.84,86
C. Oxygen spin relaxation and line widths
Spin–lattice relaxation times T1 were monitored using saturation or inversion recovery techniques. For the measurement of the spin–spin relaxation times T2 and if necessary for refocusing when recording T1, 90°–180° (Hahn-echo) and 90°–90° (solid-echo) pulse sequences were applied for the 17O and the 2H experiments, respectively.To determine T1 and T2 for the equimolar mixture of PC and Ph17OH, we measured the longitudinal magnetization recovery Mz(t) and the transverse magnetization decay Mxy(t), respectively, in a wide temperature range. The corresponding magnetization curves were fitted using the stretched exponential functions
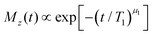 | (6) |
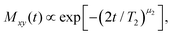 | (7) |
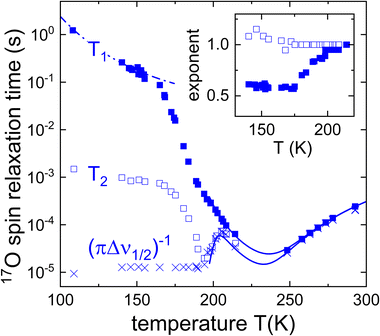 | ||
Fig. 5 Spin–lattice relaxation times T1 (filled symbols) and spin–spin relaxation times T2 (open symbols) of an equimolar mixture of Ph17OH and PC. The crosses (×) refer to  . Below 200 K, the T2 times and the spectra were measured under continuous-wave proton decoupling. At higher temperatures decoupling was not applied. The inset depicts the Kohlrausch exponents corresponding to the spin relaxation times. The lines are fits using eqn (8), (13), and (14). The dash-dotted line reflects the calculated T1 contribution that arises from the β-relaxation, see the Discussion section. . Below 200 K, the T2 times and the spectra were measured under continuous-wave proton decoupling. At higher temperatures decoupling was not applied. The inset depicts the Kohlrausch exponents corresponding to the spin relaxation times. The lines are fits using eqn (8), (13), and (14). The dash-dotted line reflects the calculated T1 contribution that arises from the β-relaxation, see the Discussion section. | ||
For temperatures below 215 K, Fig. 5 shows that while T2 exhibit a nonmonotonic behavior upon cooling, T1 displays a monotonous increase which is somewhat more steep between 185 and 165 K and then tends to become flatter. The region of steeper increase is reminiscent of similar effects observed using 2H NMR, where the analogous phenomenon was assigned to a crossover from rate averaging over a distribution of T1 times at high temperatures to time averaging at low temperatures.85 In other words, at high T ergodicity restoring effects take place on the T1 scale and lead to an exponential spin–lattice relaxation; conversely, at lower T where this effect ceases to be operative on the scale of T1, spin lattice relaxation is expected to proceed in a nonexponential fashion.86 Indeed, the exponent μ1(T) for PC:Ph17OH conforms exactly to this behavior, see the inset of Fig. 5.
Regarding the applicability of the interpretation just given for μ1(T), one should keep in mind that for halfinteger quadrupolar spins, in principle, spin–lattice relaxation proceeds in a nonexponential fashion.87–89 Yet, even in the slow-motion regime the expected deviations from exponentiality are small and can roughly be parameterized using a Kohlrausch exponent μ1 = 0.95, see Appendix A. Disregarding these minor deviations, the spin–lattice relaxation rate can be expressed as90,91
 | (8) |
 | (9) |
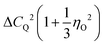 . For I = 1 the numerical factor is KQ = 3π2/20.
. For I = 1 the numerical factor is KQ = 3π2/20.
In eqn (8) the spectral density function J(ω) depends on the molecular correlation time. For typical glassforming liquids, a distribution of correlation times needs to be taken into account. For the structural relaxation, we will use a Cole–Davidson spectral density93
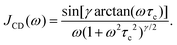 | (10) |
In the regime of fast and intermediate motion, ωτc ≲ 1, the spin–spin relaxation is “nearly exponential”94 as well so that one can define a rate
 | (11) |
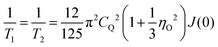 | (12) |
Outside the intermediate motion regime, where in the presence of a strong quadrupolar coupling essentially only the central transition is excited, the first-order quadrupolar contribution to the effective transverse relaxation rate is95
 | (13) |
 is ≈ 0.53.
is ≈ 0.53.
As τc gets longer towards the μs scale, also T2 tends to become longer so that for the transverse relaxation eventually the second-order quadrupolar contribution96–98
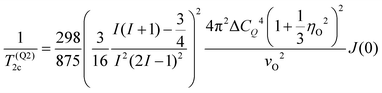 | (14) |
Returning to the line width, in the range in which τc < τexc the overall width is expected to be given by
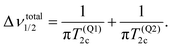 | (15) |
 | (16) |
 | (17) |
According to ref. 99 a local minimum in T2 (corresponding to a local maximum line width) will appear at a temperature at which the motional correlation time is τc,T2min ≈ 1/(2.56M21/2) ≈ 40 μs. The corresponding time constant is included in the Arrhenius plot that is presented in Section 4, below.
Using the theoretical framework outlined in the present section, for T ≥ 200 K we fitted eqn (8) to the spin–lattice relaxation times with the quadrupolar coupling set to CQ = 8.6 MHz, and the asymmetry parameter to ηO = 0.7 and assumed that the time constants follow the Vogel–Fulcher law that is displayed in the Arrhenius plot in Section 4, below. From the fit curve in Fig. 5, we can read out that the minimal oxygen T1 relaxation time that would be expected to appear at 237 K. Taking into account the underlying time constants derived from the T1 values together with the estimated Cole–Davidson parameter γCD = 0.36 ± 0.04 as well as CQ and ηO as given above, we calculated the T2 values according to eqn (13) and (14) and present the results in Fig. 5 as well.
For the current parameters (but with γ = 1), eqn (16) and (17) would yield 1.4 kHz and 0.3 μs, respectively. If γ < 1, then eqn (15) has to be analyzed numerically (see also Fig. S3 in the ESI†) and for the current γ exponent we find (Δνtotal1/2)min = 5.4 kHz and τc,T2max = 0.6 μs.
The line widths Δν1/2(T) from the experimentally recorded spectra such as those shown in Fig. 4 are included in Fig. 5 in the form of effective spin–spin relaxation times,  . From Fig. 5 one recognizes that
. From Fig. 5 one recognizes that  (which lacks the refocusing effects inherent in the present acquisition of T2) agrees with T2 down to about 190 K. Upon further cooling, Δv1/2(T) approaches its rigid-lattice value and thus becomes temperature independent.
(which lacks the refocusing effects inherent in the present acquisition of T2) agrees with T2 down to about 190 K. Upon further cooling, Δv1/2(T) approaches its rigid-lattice value and thus becomes temperature independent.
D. Deuteron spin relaxation and stimulated echoes
Like for the 17O labeled mixture, also for PC-d3:PhOH and for PC:PhOH-d3, longitudinal and transverse magnetization curves were recorded and analyzed using eqn (6) and (7), respectively. The corresponding spin relaxation times are presented in Fig. 6 (together with the data for PC:Ph17OH) for the two differently 2H labeled equimolar mixtures. The Kohlrausch exponents are given as Fig. S4 in the ESI.† The 2H spin–lattice relaxation times display temperature dependent patterns that are similar to those seen for 17O. However, due to the relatively small quadrupolar 2H couplings, for the deuteron probes the T1 minima can be fully resolved. Since PC-d3 and PhOH-d3 show somewhat different quadrupolar parameters, see Section 3B, the two axes in Fig. 6 were shifted to achieve a good overlap in the high-temperature regime. This way any remaining differences in the (scaled) spin relaxation times should reflect differences in the temperature dependence or distribution width of the correlation times.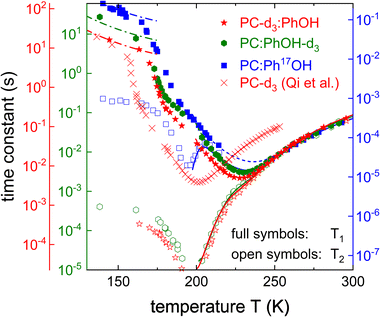 | ||
| Fig. 6 Spin–lattice and spin–spin relaxation times of PC:PhOH-d3, PC:PhOH-d3, and PC:Ph17OH. For neat PC-d3T1 was measured at a slightly lower Larmor frequency (40.2 MHz).56 The y-axes are shifted so that the high-temperature flanks of all spin relaxation times superimpose. Thus, the axes for the deuterated substances differ by a factor 2.26, those for phenol in PC:PhOH-d3 and in PC:Ph17OH by a factor of 235. The dashed lines (barely visible due to excellent agreement with the data) are fits to T1 using eqn (8) for T ≥ 200 K. The solid lines describing the 2H T2 times were calculated according to eqn (11). The dash-dotted lines reflect the calculated T1 contribution arising from the β-relaxation, see Section 4, below. | ||
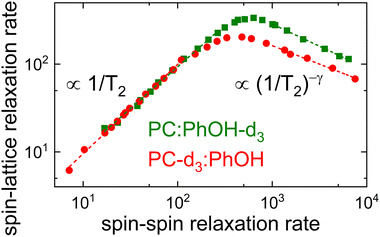
The difference in the distribution width is nicely brought out in a plot of 1/T1vs. 1/T2,100 see Fig. 7. In this representation, the limiting slopes refer directly to those of the corresponding frequency dependent NMR susceptibility. For instance assuming a Cole–Davidson form, a power law with an exponent +1 will be observed on the left flank and on the right flank the exponent will be −γ. Fig. 7 shows that for PC-d3:PhOH one has γ = 0.42 and for PC:PhOH-d3 one has γ = 0.51. This means that in the mixture, PC senses a somewhat broader distribution of correlation times than PhOH.
Using these Cole–Davidson exponents γ (and ηD = 0), eqn (8) was fitted to the experimentally determined longitudinal relaxation times for T ≥ 200 K. Fig. 6 shows that good agreement is achieved when setting the quadrupolar coupling to ΔCQ = 144 kHz for PC-d3:PhOH and to ΔCQ = 180 kHz for PC:PhOH-d3. From the Vogel–Fulcher laws underlying these fits, see the ESI,† and using eqn (11), we calculated the solid T2 lines shown in Fig. 6 which describe the transverse relaxation times very well down to the T1 minimum.
To assess the molecular correlation times also the procedure outlined in ref. 56 is often applied: Here, not only the fluctuating part of the quadrupolar coupling, but also the smallest measured longitudinal relaxation time (T1,min) plays an important role. For PC:PhOH-d3 one has T1,min = 3.0 ms at 230 ± 3 K and T1,min = 4.9 ms for PC-d3:PhOH at 228 ± 3 K. The correlation times at the T1 minimum depend slightly on the exponent γ according to the empirical expression, ωD〈τc(γ)〉 ≈ 0.425 + 0.467γ − 0.548γ2 + 0.385γ3 − 0.113γ4 that is applicable if T1 is of the form given by eqn (8).101 For the given γ exponents this expression yields 1.95 ns for the PhOH-d3 component and 1.8 ns the PC-d3 component. Thus despite the slightly different maximum positions apparent from Fig. 7 the resulting time scale agree within experimental uncertainty.
Using spin relaxometry the molecular correlation function is probed most efficiently on the nanosecond scale (T1) or on the microsecond scale (T2). To monitor dynamical process directly on millisecond (and longer) time scales, deuteron stimulated-echo spectroscopy can be exploited to measure the (rotational) correlation functions of the quadrupolarly perturbed frequency81,102
 | (18) |
Suitably phase cycled stimulated-echo pulse sequences allow one to record the two-time orientational correlation function81,102
 | (19) |
In Fig. 8 we show experimentally determined F2(tp,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tm) curves for the two differently deuteron labeled PC:PhOH mixtures as a function of temperature for a fixed evolution time. For both samples one recognizes that upon cooling the decay of the stimulated-echo amplitude shifts to longer times and becomes more stretched. For a quantitative analysis of these data we took the independently measured spin–lattice relaxation times into account and employed the stretched exponential function
tm) curves for the two differently deuteron labeled PC:PhOH mixtures as a function of temperature for a fixed evolution time. For both samples one recognizes that upon cooling the decay of the stimulated-echo amplitude shifts to longer times and becomes more stretched. For a quantitative analysis of these data we took the independently measured spin–lattice relaxation times into account and employed the stretched exponential function
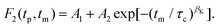 | (20) |
 | ||
| Fig. 8 Stimulated cos-cos echo functions measured for (a) PC-d3:PhOH and (b) PC:PhOH-d3. A three-pulse sequence with an evolution time of tp = 20 μs was used. The lines are fits using eqn (20). | ||
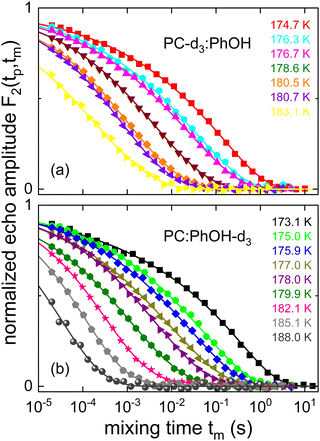
While temperature dependent data are presented in Fig. 8 for a fixed evolution time, Fig. 9 shows stimulated-echo decays for PC-d3:PhOH taken at T = 180.5 K for a range of evolution times. From least-squares fits based on eqn (20), we find that the correlation time τc(tp) strongly depends on tp, see Fig. 10.
 | ||
| Fig. 9 Evolution time dependent stimulated cos-cos echo functions recorded for PC-d3:PhOH. The lines represent fits using eqn (20). For tp ≤ 10 μs a four-pulse sequence was utilized. | ||
 | ||
| Fig. 10 Evolution time dependent cos–cos time constants as measured for PC-d3:PhOH and for PC:PhOH-d3. The solid line is adapted from ref. 104 and reflects simulations based on a motional model featuring a bimodal jump-angle distribution. | ||
This figure also includes data for the complementarily deuteron labeled sample, PC:PhOH-d3. One recognizes that both mixtures exhibit very similar τc(tp) dependences. The solid line in Fig. 10 reflects simulations based on a simple model which involves a bimodal distribution of small-angle (2°) and large-angle (30°) jumps, where on average the former are 50 times more frequent. Simulations with this reorientational scenario, after adjusting the scale for τc(tp) → 0, were previously found suitable also for other glass formers including PC-d3.56,104
4. Discussion
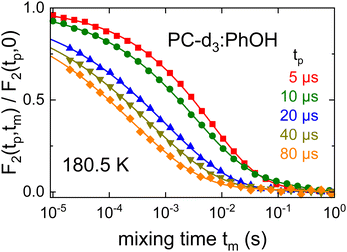
Based on the results from the various experimental methods, Section 4A collects the evidence for the occurrence of a Debye process in PC:PhOH. Insights regarding the molecular conformation and arrangement as obtained from NMR and from dielectric spectroscopy are discussed in Sections 4B1 and 4B2, respectively. Then, Section 4C deals with the implications of these considerations regarding the supramolecular association in PC:PhOH. Finally, Section 4D is concerned with the finding of a clearly discernible secondary relaxation in these mixtures.In order to facilitate the further discussion, the temperature dependent relaxation times of PC:PhOH that we determined in the previous sections are collected in the Arrhenius plot shown as Fig. 11. This includes the time constants obtained from dielectric and mechanical spectroscopy, from the spin-relaxation times, as well as from stimulated-echo spectroscopy. Except for the data relating to the β process, overall and typical for glass forming liquids, a curved temperature dependence is obvious from this representation. Such a dependence can be described using the Vogel–Fulcher law
τ = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[B/(T − T0)], exp[B/(T − T0)], | (21) |
 | ||
| Fig. 11 Dielectric, mechanical, and NMR-based relaxation times of PC:PhOH with xPhOH = 0.5. Half-filled triangles mark the results from the decomposition of the dielectric spectra as illustrated in Fig. 2. The τG time scales represented without a central dot are determined using frequency-temperature superposition, the others from observed shear loss peaks. Most stimulated-echo (STE) decays were recorded for evolution times of 20 μs, those represented by filled triangles pointing to the right for tp = 5 μs. Lines are fits using Vogel–Fulcher or Arrhenius laws. The dashed lines reflect the Vogel–Fulcher fits used to describe the T1 curves. Their parameterization as well as those of the dash-dotted and solid lines is given in the text or as ESI.† For comparison with the PC:PhOH data, this plot features dielectric, rheological, as well as NMR-based time scales as determined for neat PC taken from ref. 51–53 and 55. | ||
A. Evidence for the Debye process in PC:PhOH
The pattern displayed in Fig. 11 is reminiscent of that observed for aliphatic monohydroxy alcohols and like for those hydrogen bonded liquids it provides evidence for the existence of a Debye process also in PC:PhOH:4,5(i) The relaxation times originating from the dominant dielectric loss peaks (cf. the dash-dotted line in Fig. 11) are longer than those from the NMR based time scales.
(ii) The correlation times detected using 17O NMR at the hydroxyl group are intermediate.
(iii) Statement (ii) is corroborated not only by the deuteron spin relaxation data but by the stimulated-echo results as well (also in the tp → 0 limit, cf. the solid line in Fig. 11).
(iv) The shear rheological results display a small, yet significant viscosity enhancement.
(v) Upon approaching the glass transition temperature, the timescales from the Debye-like and the structural modes approach each other.
In order to appreciate statement (i) better a few comments are warranted: In general, the observed timescale separation seen in Fig. 11 is much larger than the maximum factor of three that is expected when dealing with different Legendre polynomial ranks, i.e., when comparing dielectric and NMR time scales.103 Following previous work,17–19 the identification of a Debye process can be based on the spectral decomposition illustrated in Fig. 2, see also Fig. S1 in the ESI.† Since, like for other examples,106 such a decomposition is not immediately obvious from the raw spectra, the application of additional experimental methods is required to allow for an unambiguous detection of a Debye process.
Despite decade-long beliefs to the contrary, that the Debye process in monohydroxy alcohols manifests solely in dielectric spectroscopy,5 NMR experiments provided the first evidence that this notion needs substantial revision: the Debye relaxation leaves its mark in an OH-related timescale that is intermediate between those of the Debye and of the structural process.4 Further confirmed by findings in pure and diluted monohydroxy alcohols,46,107 the observations summarized in items (ii) and (iii) underscore that PC:PhOH closely resembles the pattern revealed by well-established Debye liquids. In PC:PhOH the separation of the OH-related time scale from the other modes is, however, less pronounced than it is in liquids that display a strong Debye process.
In line with these findings, as indicated in item (iv), the rheological investigation of PC:PhOH (see Fig. 3) reveals a viscosity enhancement, see eqn (4), relative to that of nonassociating liquids and thus the existence of a supramolecular mode. The spectral comparison with a nonassociating liquid shows that this additional contribution is readily visibly, but relatively small in amplitude. Consequently, the quantitative assessment of the viscosity enhancement, carried out in Section 3A, yields a scaled zero-shear viscosity z0 that is only slightly larger than 1. By comparison with other supramolecular liquids,77 this means that in PC:PhOH the underlying rheological mode is relatively weak, a statement that corroborates the finding from the decomposition of the dielectric spectra, cf.Fig. 2. Further vindicating the existence of a faint Debye-like process, the time scales determined from the shear compliance (often taken as a measure for the structural relaxation time) almost coincide with the shorter time scale inferred from the decomposition of the dielectric loss spectra.
As item (v) highlights, another observation from Fig. 11 agrees with that for many aliphatic monohydroxy alcohols:20 The Debye and the structural relaxation timescales approach each other upon cooling down to the glass transition temperature.20 Taken together, the combination of the results from the various methods all indicate a weak Debye-like process to be present in PC:PhOH.
B. Molecular conformation and arrangement
In order to further scrutinize the quadrupolar parameters at the oxygen site, analogous to previous work,110,111 for crystalline phenol,28,29 we carried out quantum chemical calculations using the CASTEP 19.11 code.112 These involved the PBE functional113 as well as a cut-off energy of 800 eV and employed a Monkhorst–Pack grid with a spacing of 0.03 Å−1.114 Further details regarding the density functional calculations are given in the ESI.†
For the ambient-pressure phase in which the planar PhOH molecules form three-fold hydrogen bonded helical chains28 we find CQ = −8.67 MHz and ηO = 0.82, thereby confirming the coupling parameters from earlier work33 (see also the ESI†). In the high-pressure phase which is stable at 0.16 GPa,29 the PhOH molecules are nonplanar with a dihedral CCOH angle of almost 20°. For this phase in which the PhOH molecules are arranged in hydrogen bonded ribbons, our calculations reveal significantly larger quadrupolar parameters (CQ = −9.0 MHz and ηO = 0.96). Thus, the comparison with the experimentally determined parameters, see Fig. 4, suggests that in the present binary liquid the PhOH molecules are characterized by a planar structure.
 | (22) |
For PC the magnitude of the electrical dipole moment (μPC ≈ 5 D) is generally agreed upon.64 However, the dipole moments reported for PhOH in the gas phase,37,38,116,117 in the low-viscosity liquid state,118 in aqueous119,120 and other solutions,121 as well as for the crystal at ambient28 and high pressures29 range from 1.2 D in the gas phase, to about 1.5…2.5 D in solution, and 3.5 D in the ambient pressure crystal. Interestingly, the dipole moment for geometry-optimized PhOH trimers was found to be even larger (3.75 D).30
In view of the large uncertainty regarding the magnitude of μPhOH in liquid mixtures that contain PhOH,119–121 in the following analysis we can only expect to extract the product of gK and μ2 in a reliable way. This quantity can be estimated from69
 | (23) |
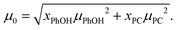 | (24) |
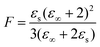 | (25) |
Now, based on this result, the determination of gK rests on assumptions regarding μPhOH and vice versa. For instance, taking μPhOH = 1.5 or 2.5 D, the minimum or maximum values, respectively, reported for phenol in various solutions,119–121 one arrives at 0.66 ≤ gK ≤ 0.81 or at 0.66 ≤ gK ≤ 0.70. Tentatively assuming a chainlike association, characterized by, e.g., gK = 2, which would however be at variance with the findings for neat PC54 even at high temperatures,126 one would have μPhOH ≈ 1.7 D and (also at variance with the experimental value) μPC ≈ 2.8 D. These considerations show that in the present mixtures a chain-like arrangement of the PhOH molecules can be ruled out.
C. Hydrogen bonding and dilution effects in aromatic and aliphatic Debye liquids
As discussed above, the observed 17O quadrupolar coupling constant of phenol as well as the Kirkwood factors which characterize PC:PhOH favor an interpretation in terms of the existence of ring-like molecular associates or dipole arrangements with antiparallel orientations. Like for monohydroxy alcohols displaying ring-like supramolecular associations,6 it is not surprising that for PC:PhOH only a relatively weak hydrogen-bond mediated viscosity enhancement is found.For phenyl propanols12–14 it was emphasized that the tendency to form molecular associates transiently4 held together by O–H⋯O bonds is impeded by the propensity of these molecules to form O-H⋯π15 and π–π configurations. Additionally, it has to be taken into account that PC cannot be involved in the formation of supramolecular structures so that this van der Waals glass former merely acts as a diluent in the PC:PhOH mixture. Hence, we anticipate that similar to the pure ambient-pressure liquid,30 also when mixed with PC, the PhOH molecules predominantly form three-membered O–H⋯O bonded clusters and ring-like structures. From X-ray diffraction experiments, similar bonding motifs were in fact detected for aliphatic monohydroxy alcohols displaying small Debye processes, while for alcohols featuring large Debye processes chain-like clustering prevails.6,47,127 To check which supramolecular bonding structures are present in the PC:PhOH mixtures, in the future these should be scrutinized using suitable scattering experiments.
D. Secondary relaxation
So far, the discussion focused on the structural relaxation or on processes which are slower than that. As can be seen in Fig. 11 PC:PhOH exhibits a β relaxation, i.e., a faster process as well. At first sight, this is remarkable since without long-time aging,72 neat PC does not show a discernible β process. For aromatic glass formers it is not clear what to expect: Substances such as meta-fluoroaniline and toluene do exhibit a strong β relaxation while others, such as 2-picoline, do not.128,129The Johari–Goldstein relaxation times that we obtain for PC:PhOH follow an Arrhenius law
τ = τ0,β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Eβ/kBT). exp(Eβ/kBT). | (26) |
We will now demonstrate that the signature of the β process can be found also from NMR, i.e., in the low-temperature T1 data. To see this, for T < Tg where the α process ceases to lead to significant spin–lattice relaxation and where thus the β process prevails, based on eqn (8) and (10) we calculated T1. As input parameters, we used τβ from dielectric spectroscopy in conjunction with a Cole–Cole spectral density with an exponent αCC = 0.2 so that the only free parameter is the fluctuating part of the coupling constants. To obtain the dash-dotted lines in Fig. 6 (2H data) that reflect these calculation we used 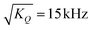 . Analogously, for the 17O data we obtain
. Analogously, for the 17O data we obtain  . Reduced quadrupolar couplings (here: 5 to 7% of the full ones) are in fact expected in the framework of models for secondary relaxations: Here, the molecular segments perform motions in an angularly restricted range, typically pictured to occur within a cone.86,130 From the cited works cone semiangles κ in the 5 to 20° range were found for various glass formers. Indeed, from the relaxation strengths Δεβ and Δε referring to the β and the dominant relaxation, respectively, of PC:PhOH using the empirical relationship131,132 sin2κ = Δεβ/Δε it is possible to assess κ on the basis of the dielectric data as well. Assuming that Δεα is constant not only above Tg, see Fig. 1, but also below Tg, for xPhOH = 0.5 for between 140 to 170 K we find κ ≈ 6 to 8° (or 8 to 11° if the relaxation strength relating only to the α-type contribution is taken, cf.Fig. 2).
. Reduced quadrupolar couplings (here: 5 to 7% of the full ones) are in fact expected in the framework of models for secondary relaxations: Here, the molecular segments perform motions in an angularly restricted range, typically pictured to occur within a cone.86,130 From the cited works cone semiangles κ in the 5 to 20° range were found for various glass formers. Indeed, from the relaxation strengths Δεβ and Δε referring to the β and the dominant relaxation, respectively, of PC:PhOH using the empirical relationship131,132 sin2κ = Δεβ/Δε it is possible to assess κ on the basis of the dielectric data as well. Assuming that Δεα is constant not only above Tg, see Fig. 1, but also below Tg, for xPhOH = 0.5 for between 140 to 170 K we find κ ≈ 6 to 8° (or 8 to 11° if the relaxation strength relating only to the α-type contribution is taken, cf.Fig. 2).
The observation of a β process in binary systems in which one of the glassformers does not show this phenomenon in its neat form is not unprecedented: Mixtures of toluene and 2-picoline do indeed feature a secondary relaxation which was reported to strongly resemble that found for neat glassformers128 so that in ref. 128 it was concluded that “all molecular species contribute to the secondary relaxation of the mixtures”. The present results suggest that in PC:PhOH we encounter the same situation, i.e., that also here both molecular constituents contribute to the secondary relaxation.
5. Conclusions
In this work, we studied the relaxation dynamics of phenol. Since in its pure form, PhOH cannot be brought into the amorphous form, even by quenching with large cooling rates, we studied solutions with PC, an excellent van der Waals glass former, mostly focusing on equimolar mixtures. To this end we employed a large array of techniques including dielectric spectroscopy and shear rheology, NMR line shape analysis including quantum chemical calculations, spin relaxometry using 2H and 17O as nuclear probes, as well as deuteron stimulated-echo spectroscopy. The present combination of experimental techniques allowed us to probe the dynamics of glass forming PC:PhOH over a large temperature range. Furthermore, the applied deuteron editing enabled a selective detection of the spin relaxation and stimulated-echo behavior of the two molecular components that form PC:PhOH: we find that within the mixture, the two components display essentially the same structural and secondary dynamics, demonstrating that PC is a well suited mixing partner for the present purpose. However, since PC, unlike PhOH, is unable to sustain hydrogen bonds, the van der Waals glass former cannot be directly involved in the formation of supramolecular structures that give rise to the Debye-like process. For PC:PhOH the latter is identified on the basis of the following findings: by examining the behavior at the hydroxyl site using 17O NMR, we find that this moiety displays slightly longer correlation times than inferred from deuteron NMR for the PhOH ring, an observation that hints at a weak hydrogen-bond induced molecular association. Corroborating this finding, the dielectric relaxation times turn out to be somewhat longer than those determined using 2H NMR, even after taking into account that the different techniques probe different Legendre orders of the underlying reorientational correlation function. 17O NMR, a method that here probes the dynamics at phenol's hydroxyl site reveals an intermediate dynamic, akin to the situation in aliphatic monohydroxy alcohols. Analogous to those latter liquids, from our shear rheology study on PC:PhOH evidence for an, albeit weak viscosity enhancement is obtained. Thus, taking together the results from the diverse array of the present experiments and analyses we obtain evidence for the presence of a faint Debye-like process stemming from phenol. In this sense our studies reveal that this process not only occurs in phenyl alkanols with sizeable side chains, but also in a mixture of a nonassociating liquid with the simplest aromatic alcohol.Conflicts of interest
There are no conflicts of interest to declare.Appendix
Appendix A: Multi-exponential spin–lattice relaxation of I = 5/2 nuclei: selective and nonselective conditions
Generally, 17O spin–lattice relaxation proceeds in a nonexponential fashion and the time dependent part of the multi-exponential magnetization recovery can be written as | (27) |
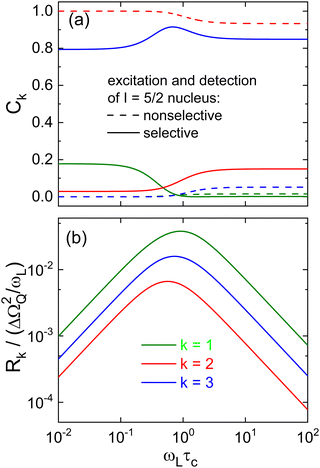
Therefore, based on the eigenvalues and eigenvectors of the relaxation matrix derived from ref. 134, we solved eqn (2.4a) in conjunction with eqn (A20), both from that reference, and summarize our numerical results in Fig. 12. A close inspection shows that the relative amplitudes Ck calculated using this approach and marked as “nonselective” in Fig. 12(a) as well as the calculated rates, see Fig. 12(b), reproduce the previously published ones.87–89
While the rates do of course not dependent on specific excitation and detection conditions, the relative amplitudes Ck do. This is seen in Fig. 12(a) where the amplitudes referring to selective and nonselective conditions are shown. In particular, for the selective case in the slow-motion regime where ωLτc ≫ 1, a fit of Mz(t) using eqn (6) – after the relevant coefficients were plugged into eqn (27) – yields a Kohlrausch exponent μ1 = 0.95. In other words, under the conditions which are most relevant for the present work, the deviations from nonexponential spin–lattice relaxation are minor.
Acknowledgements
This work was financially supported by the Deutsche Forschungsgemeinschaft under project no. 286881352.References
- C. R. Ashworth, R. P. Matthews, T. Welton and P. A. Hunt, Doubly ionic hydrogen bond interactions within the choline chloride–urea deep eutectic solvent, Phys. Chem. Chem. Phys., 2016, 18, 18145 RSC.
- W. Dannhauser, Dielectric Study of Intermolecular Association in Isomeric Octyl Alcohols, J. Chem. Phys., 1968, 48, 1911 CrossRef CAS.
- G. A. Jeffrey, An Introduction to Hydrogen Bonding, Oxford University Press, Oxford, 1997 Search PubMed.
- C. Gainaru, R. Meier, S. Schildmann, C. Lederle, W. Hiller, E. A. Rössler and R. Böhmer, Nuclear-magnetic-resonance measurements reveal the origin of the Debye process in monohydroxy alcohols, Phys. Rev. Lett., 2010, 105, 258303 CrossRef CAS PubMed.
- R. Böhmer, C. Gainaru and R. Richert, Structure and dynamics of monohydroxy alcohols - milestones towards their microscopic understanding, 100 years after Debye, Phys. Rep., 2014, 545, 125 CrossRef.
- S. P. Bierwirth, J. Bolle, S. Bauer, C. Sternemann, C. Gainaru, M. Tolan and R. Böhmer, Scaling of suprastructure and dynamics of pure and mixed Debye liquids, in The scaling of relaxation processes, ed. A. Loidl, F. Kremer, Springer, Cham, 2018, ch. 5, pp. 121–171 Search PubMed.
- O. E. Kalinovskaya, J. K. Vij and G. P. Johari, Mechanism of the major orientation polarization in alcohols, and the effects of steric hindrance-, and dilution-induced decrease on H-bonding, J. Phys. Chem. A, 2001, 105, 5061 CrossRef CAS.
- E. Arunan, G. R. Desiraju, R. A. Klein, J. Sadlej, S. Scheiner, I. Alkorta, D. C. Clary, R. H. Crabtree, J. J. Dannenberg, P. Hobza, H. G. Kjaergaard, A. C. Legon, B. Mennucci and D. J. Nesbitt, Pure Appl. Chem., 2011, 83, 1637 CrossRef CAS.
- R. Thakuria, N. K. Nath and B. K. Saha, The Nature and Applications of π–π Interactions: A Perspective, Cryst. Growth Des., 2019, 19, 523 CrossRef CAS.
- A. Nowok, K. Jurkiewicz, M. Dulski, H. Hellwig, J. G. Małecki, K. Grzybowska, J. Grelska and S. Pawlus, Influence of molecular geometry on the formation, architecture and dynamics of H-bonded supramolecular associates in 1-phenyl alcohols, J. Mol. Liq., 2021, 326, 115349 CrossRef CAS.
- N. Soszka, B. Hachuła, M. Tarnacka, E. Kamińska, J. Grelska, K. Jurkiewicz, M. Geppert-Rybczyńska, R. Wrzalik, K. Grzybowska, S. Pawlus, M. Paluch and K. Kamiński, The impact of the length of alkyl chain on the behavior of benzyl alcohol homologues – the interplay between dispersive and hydrogen bond interactions, Phys. Chem. Chem. Phys., 2021, 23, 23796 RSC.
- A. Nowok, M. Dulski, J. Grelska, A. Z. Szeremeta, K. Jurkiewicz, K. Grzybowska, M. Musiał and S. Pawlus, Phenyl Ring: A Steric Hindrance or a Source of Different Hydrogen Bonding Patterns in Self-Organizing Systems?, J. Phys. Chem. Lett., 2021, 12, 2142 CrossRef CAS PubMed.
- N. Soszka, B. Hachuła, M. Tarnacka, J. Grelska, K. Jurkiewicz, M. Geppert-Rybczyńska, R. Wrzalik, K. Grzybowska, S. Pawlus, M. Paluch and K. Kamiński, Aromaticity effect on supramolecular aggregation. Aromatic vs. cyclic monohydroxy alcohols, Spectrochim. Acta A, 2022, 276, 121235 CrossRef CAS PubMed.
- A. Nowok, M. Dulski, K. Jurkiewicz, J. Grelska, A. Z. Szeremeta, K. Grzybowska and S. Pawlus, Molecular stiffness and aromatic ring position – Crucial structural factors in the self-assembly processes of phenyl alcohols, J. Mol. Liq., 2021, 335, 116426 CrossRef CAS.
- C. M. Baker and G. H. Grant, Modeling Aromatic Liquids: Toluene, Phenol, and Pyridine, J. Chem. Theory Comput., 2007, 3 CrossRef CAS PubMed , 530 find relatively little oxygen electron density above or below the aromatic ring, suggesting that the formation of O–H⋯π hydrogen bonds is rare.
- C. R. Martinez and B. L. Iverson, Rethinking the term ‘‘pi-stacking”, Chem. Sci., 2012, 3, 2191 RSC.
- T. Böhmer, J. P. Gabriel, T. Richter, F. Pabst and T. Blochowicz, Influence of Molecular Architecture on the Dynamics of H-Bonded Supramolecular Structures in Phenyl-Propanols, J. Phys. Chem. B, 2019, 123, 10959 CrossRef PubMed.
- M. Mikkelsen, J. P. Gabriel and T. Hecksher, Dielectric and Shear Mechanical Spectra of Propanols: The Influence of Hydrogen-Bonded Structures, J. Phys. Chem. B, 2023, 127, 371 CrossRef CAS PubMed.
- J. P. Gabriel, E. Thoms and R. Richert, High electric fields elucidate the hydrogen-bonded structures in 1-phenyl-1-propanol, J. Mol. Liq., 2021, 330, 115626 CrossRef CAS.
- S. Bauer, K. Burlafinger, C. Gainaru, P. Lunkenheimer, W. Hiller, A. Loidl and R. Böhmer, Debye relaxation and 250 K anomaly in glass forming monohydroxy alcohols, J. Chem. Phys., 2013, 138, 094505 CrossRef CAS PubMed.
- S. P. Bierwirth, C. Gainaru and R. Böhmer, Coexistence of two structural relaxation processes in monohydroxy alcohol–alkyl halogen mixtures: Dielectric and rheological studies, J. Chem. Phys., 2018, 149 CrossRef CAS PubMed , 044509, see the data for 4-methyl-4-heptanol and 3-methyl-3-heptanol.
- S. P. Bierwirth, G. Honorio, C. Gainaru and R. Böhmer, Linear and nonlinear shear studies reveal supramolecular responses in supercooled monohydroxy alcohols with faint dielectric signatures, J. Chem. Phys., 2019, 150, 104501 CrossRef PubMed.
- P. Sillrén, A. Matic, M. Karlsson, M. Koza, M. Maccarini, P. Fouquet, M. Götz, T. Bauer, R. Gulich, P. Lunkenheimer, A. Loidl, J. Mattsson, C. Gainaru, E. Vynokur, S. Schildmann, S. Bauer and R. Böhmer, Liquid 1-propanol studied by neutron scattering, near-infrared, and dielectric spectroscopy, J. Chem. Phys., 2014, 140, 124501 CrossRef PubMed.
- C. Gainaru, R. Figuli, T. Hecksher, B. Jakobsen, J. C. Dyre, M. Wilhelm and R. Böhmer, Shear-Modulus Investigations of Monohydroxy Alcohols: Evidence for a Short-Chain-Polymer Rheological Response, Phys. Rev. Lett., 2014, 112, 098301 CrossRef CAS PubMed.
- F. Pabst, A. Helbling, J. Gabriel, P. Weigl and T. Blochowicz, Dipole-dipole correlations and the Debye process in the dielectric response of nonassociating glass forming liquids, Phys. Rev. E, 2020, 102, 010606 CrossRef CAS PubMed.
- S. P. Thomas, R. Sathishkumar and T. N. G. Row, Organic alloys of room temperature liquids thiophenol and selenophenol, Chem. Commun., 2015, 51, 14255 RSC.
- V. D. Aleksandrov and V. A. Postnikov, Supercooling in the crystallization of phenol, Russ. J. Phys. Chem., 2005, 79, 1192 CAS.
- V. E. Zavodnik, V. K. Bel'skii and P. M. Zorkii, Crystal structure of phenol at 123° K, J. Struct. Chem., 1988, 28, 793 CrossRef.
- D. R. Allan, S. J. Clark, A. Dawson, P. A. McGregor and S. Parsons, Pressure-induced polymorphism in phenol, Acta Cryst. B, 2002, 58, 1018 CrossRef PubMed.
- A. Singh, D. Gangopadhyay, R. Nandi, P. Sharma and R. K. Singh, Raman signatures of strong and weak hydrogen bonds in binary mixtures of phenol with acetonitrile, benzene and orthodichlorobenzene, J. Raman Spectrosc., 2016, 47, 712 CrossRef CAS.
- K. Jones, J. M. D. Lane and N. W. Moore, A reactive molecular dynamics study of phenol and phenolic polymers in extreme environments, AIP Conf. Proc., 2020, 2272, 070018 CrossRef CAS.
- C. A. Angell, J. M. Sare and E. J. Sare, Glass Transition Temperatures for Simple Molecular Liquids and Their Binary Solutions, J. Phys. Chem., 1978, 82, 2622 CrossRef CAS.
- V. K. Michaelis, B. Corzilius, A. A. Smith and R. G. Griffin, Dynamic nuclear polarization of 17O: Direct polarization, J. Phys. Chem. B, 2013, 117, 14894 CrossRef CAS PubMed.
- W. Guo, Y. Hou, S. Ren, S. Tian and W. Wu, Formation of Deep Eutectic Solvents by Phenols and Choline Chloride and Their Physical Properties, J. Chem. Eng. Data, 2013, 58, 866 CrossRef CAS.
- B. Doherty and O. Acevedo, OPLS Force Field for Choline Chloride-Based Deep Eutectic Solvents, J. Phys. Chem. B, 2018, 122, 9982 CrossRef CAS PubMed.
- G. M. Førland, Y. Liang, O. M. Kvalheim, H. Høiland and A. Chazy, Associative behavior of benzyl alcohol in carbon tetrachloride solutions, J. Phys. Chem. B, 1997, 101, 6960 CrossRef.
- M. A. Czarnecki, Y. Morisawa, Y. Katsumoto, T. Takaya, S. Singh, H. Sato and Y. Ozaki, Solvent effect on the competition between weak and strong interactions in phenol solutions studied by near-infrared spectroscopy and DFT calculations, Phys. Chem. Chem. Phys., 2021, 23, 19188 RSC.
- S. Singh, M. Majer, M. A. Czarnecki, Y. Morisawa and Y. Ozaki, Solvent Effect on Assembling and Interactions in Solutions of Phenol: Infrared Spectroscopic and Density Functional Theory Study, Appl. Spectrosc., 2022, 76, 28 CrossRef CAS PubMed.
- A. Nalepa, K. Möbius, M. Plato, W. Lubitz and A. Savitsky, Nitroxide Spin Labels—Magnetic Parameters and Hydrogen-Bond Formation: A High-Field EPR and EDNMR Study, Appl. Magn. Reson., 2019, 50, 1 CrossRef CAS.
- H. Nadolny, A. Volmari and H. Weingärtner, Orientational Dynamics of Hydrogen-Bonded Liquids - A Comparative Study of Dielectric and Nuclear Magnetic Relaxation in n-Butanol-Tetrachloromethane Mixtures, Ber. Bunsenges. Phys. Chem., 1998, 102, 866 CrossRef CAS.
- L.-M. Wang, S. Shahriari and R. Richert, Diluent Effects on the Debye-Type Dielectric Relaxation in Viscous Monohydroxy Alcohols, J. Phys. Chem. B, 2005, 109, 23255 CrossRef CAS PubMed.
- T. El Goresy and R. Böhmer, Diluting the hydrogen bonds in mixtures of n-butanol with n-bromobutane: A dielectric study, J. Chem. Phys., 2008, 128, 154520 CrossRef CAS PubMed.
- S. Pawlus, M. Paluch and M. Dzida, Molecular dynamics changes induced by solvent in 2-ethyl-1-hexanol, Phys. Rev. E, 2011, 84, 031503 CrossRef PubMed.
- M. Preuß, C. Gainaru, T. Hecksher, S. Bauer, J. C. Dyre, R. Richert and R. Böhmer, Experimental studies of Debye-like process and structural relaxation in mixtures of 2-ethyl-1-hexanol and 2-ethyl-1-hexyl bromide, J. Chem. Phys., 2012, 137, 144502 CrossRef PubMed.
- A. R. Abdel Hamid, R. Lefort, Y. Lechaux, A. Moréac, A. Ghoufi, C. Alba-Simionesco and D. Morineau, Solvation Effects on Self-Association and Segregation Processes in tert-Butanol−Aprotic Solvent Binary Mixtures, J. Phys. Chem. B, 2013, 117, 10221 CrossRef CAS PubMed.
- S. Bauer, K. Moch, P. Münzner, S. Schildmann, C. Gainaru and R. Böhmer, Mixed Debye-type liquids studied by dielectric, shear mechanical, nuclear magnetic resonance, and near-infrared spectroscopy, J. Non-Cryst. Solids, 2015, 407, 384 CrossRef CAS.
- T. Büning, J. Lueg, J. Bolle, C. Sternemann, C. Gainaru, M. Tolan and R. Böhmer, Connecting structural and dynamical signatures of supramolecular Debye liquids, J. Chem. Phys., 2017, 147, 234501 CrossRef PubMed.
- G. Szklarz, K. Adrjanowicz and M. Paluch, Cooling-Rate versus Compression-Rate Dependence of the Crystallization in the Glass-Forming Liquid, Propylene Carbonate, Cryst. Growth Des., 2018, 18, 2538 CrossRef CAS.
- C. A. Angell, L. Boehm, M. Oguni and D. L. Smith, Far IR spectra and heat capacities for propylene carbonate and propylene glycol, and the connection to the dielectric response function, J. Mol. Liq., 1993, 56, 275 CrossRef CAS.
- S. Takahara and O. Yamamuro, Calorimetric Study of 3-Bromopentane: Correlation between Structural Relaxation Time and Configurational Entropy, J. Phys. Chem., 1995, 99, 9589 CrossRef CAS.
- L. J. Jorat, G. A. Noyel and J. R. Huck, Dielectric study of propylene carbonate/toluene mixtures and dipole moment of supercooled propylene carbonate, IEEE Trans. Electr. Insul., 1991, 26, 763 CrossRef CAS.
- F. Stickel, E. W. Fischer and R. Richert, Dynamics of glass-forming liquids. II. Detailed comparison of dielectric relaxation, dc-conductivity, and viscosity data, J. Chem. Phys., 1996, 104, 2043 CrossRef CAS.
- U. Schneider, P. Lunkenheimer, R. Brand and A. Loidl, Broadband dielectric spectroscopy on glass-forming propylene carbonate, Phys. Rev. E, 1999, 5, 6924 CrossRef PubMed.
- J. Barthel, R. Buchner, C. G. Hölzl and M. Münsterer, Dynamics of Benzonitrile, Propylene Carbonate and Butylene Carbonate: the Influence of Molecular Shape and Flexibility on the Dielectric Relaxation Behaviour of Dipolar Aprotic Liquids, Z. Phys. Chem., 2000, 214, 1213 CAS.
- C. Gainaru, T. Hecksher, N. B. Olsen, R. Böhmer and J. C. Dyre, Shear and dielectric responses of propylene carbonate, tripropylene glycol, and a mixture of two secondary amides, J. Chem. Phys., 2012, 137, 064508 CrossRef PubMed.
- F. Qi, K. U. Schug, S. Dupont, A. Döβ, R. Böhmer and H. Sillescu, Structural relaxation of the fragile glass-former propylene carbonate studied by nuclear magnetic resonance, J. Chem. Phys., 2000, 112, 9455 CrossRef CAS.
- K. Schröter and E. Donth, Comparison of shear response with other properties at the dynamic glass transition of different glassformers, J. Non-Cryst. Solids, 2002, 307–310, 270 CrossRef.
- V. M. Syutkin, V. L. Vyazovkin, V. V. Korolev and S. Y. Grebenkin, Length and Time Scales of Structural Heterogeneities in Deeply Supercooled Propylene Carbonate, Phys. Rev. Lett., 2012, 109, 137801 CrossRef CAS PubMed.
- J. S. Bender, M. C. Zhi and M. T. Cicerone, The polarizability response of a glass-forming liquid reveals intrabasin motion and interbasin transitions on a potential energy landscape, Soft Matter, 2020, 16 RSC , 5588 and refs cited therein.
- M. Bonetti and A. Dubois, Isochronal superpositioning in the equilibrium regime of superpressed propylene carbonate to ∼1.8 GPa: A study by diffusivity measurement of the fluorescent probe Coumarin 1, Eur. Phys. J. E, 2019, 42, 97 CrossRef PubMed.
- K. Izutsu, I. M. Kolthoff, T. Fujinaga, M. Hattori and M. K. Chantooni, Acid-base equilibriums of some acids in propylene carbonate, Anal. Chem., 1977, 49, 503 CrossRef CAS.
- S.-C. Kao, Y.-C. Lin, I. Ryu and Y.-K. Wu, Revisiting Hydroxyalkylation of Phenols with Cyclic Carbonates, Adv. Synth. Catal., 2019, 361 CrossRef CAS , 3639 show that reactions of PhOH with PC require the prolonged presence of high temperatures in conjunction with suitable catalysts.
- R. Kempa and W. H. Lee, 392. The dipole moments of some cyclic carbonates, J. Chem. Soc., 1958, 1936, 10.1039/jr9580001936.
- A. Brodin and P. Jacobsson, Dipolar interaction and molecular ordering in liquid propylene carbonate: Anomalous dielectric susceptibility and Raman non-coincidence effect, J. Mol. Liq., 2011, 164, 17 CrossRef CAS.
- J. I. Kim, A Critical Study of the Ph4AsPh4B Assumption for Single Ion Thermodynamics in Amphiprotic and Dipolar-Aprotic Solvents; Evaluation of Physical Parameters Relevant to Theoretical Consideration, Z. Phys. Chem. N.F., 1978, 113, 129 CrossRef CAS.
- S. Balamuralikrishnan and A. U. Maheswari, Dipole moment studies of some substituted anilines with phenols, J. Mol. Liq., 2006, 124, 19 CrossRef CAS.
- M. D. Magee and S. Walker, Dielectric Studies. Part XXXI. Analysis of the Dielectric Data of Phenol and its Polymerized Forms, Can. J. Chem., 1971, 49, 1106 CrossRef CAS.
- C. Lederle, W. Hiller, C. Gainaru and R. Böhmer, Diluting the hydrogen bonds in viscous solutions of n-butanol with n-bromobutane: II. A comparison of rotational and translational motions, J. Chem. Phys., 2011, 134, 064512 CrossRef PubMed.
- Broadband Dielectric Spectroscopy, ed. F. Kremer and A. Schönhals, Springer, Berlin, 2003 Search PubMed.
- R. Böhmer, K. L. Ngai, C. A. Angell and D. J. Plazek, Non-exponential relaxations in strong and fragile glass-formers, J. Chem. Phys., 1993, 99, 4201 CrossRef.
- T. Blochowicz and E. A. Rössler, Beta Relaxation versus High Frequency Wing in the Dielectric Spectra of a Binary Molecular Glass Former, Phys. Rev. Lett., 2004, 92, 225701 CrossRef CAS PubMed.
- U. Schneider, R. Brand, P. Lunkenheimer and A. Loidl, The Excess Wing in the Dielectric Loss of Glass Formers: A Johari–Goldstein β-Relaxation?, Phys. Rev. Lett., 2000, 84, 5560 CrossRef CAS PubMed.
- A. Kudlik, S. Benkhof, T. Blochowicz, C. Tschirwitz and E. Rössler, The dielectric response of simple organic glass formers, J. Mol. Struct., 1999, 479, 201 CrossRef CAS.
- S. Hensel-Bielówka, M. Paluch and K. L. Ngai, Emergence of the genuine Johari–Goldstein secondary relaxation in m-fluoroaniline after suppression of hydrogen-bond-induced clusters by elevating temperature and pressure, J. Chem. Phys., 2005, 123, 014502 CrossRef PubMed.
- T. Hecksher, N. B. Olsen, K. A. Nelson, J. C. Dyre and T. Christensen, Mechanical spectra of glass-forming liquids. I. Low-frequency bulk and shear moduli of DC704 and 5-PPE measured by piezoceramic transducers, J. Chem. Phys., 2013, 138, 12A543 CrossRef PubMed.
- M. Mikkelsen, K. L. Eliasen, N. Lindemann, K. Moch, R. Böhmer, H. A. Karimi-Varzaneh, J. Lacayo-Pineda, B. Jakobsen, K. Niss, T. Christensen and T. Hecksher, Piezoelectric shear rheometry: Further developments in experimental implementation and data extraction, J. Rheol., 2022, 66, 983 CrossRef CAS.
- S. P. Bierwirth, C. Gainaru and R. Böhmer, Communication: Correlation of terminal relaxation rate and viscosity enhancement in supramolecular small-molecule liquids, J. Chem. Phys., 2018, 148, 221102 CrossRef CAS PubMed.
- L. Werbelow and R. E. London, Dynamic frequency shift, Concepts Magn. Reson., 1996, 8, 325 CrossRef CAS.
- K. Eichele, WSolids1 Solid-State NMR Simulation, http://anorganik.uni-tuebingen.de/klaus/links/index.php.
- see, e.g., T. Körber, B. Pötzschner, F. Krohn and E. A. Rössler, Reorientational dynamics in highly asymmetric binary low-molecular mixtures—A quantitative comparison of dielectric and NMR spectroscopy results, J. Chem. Phys., 2021, 155, 024504 CrossRef PubMed.
- K. Schmidt-Rohr and H. W. Spiess, Multidimensional Solid-State NMR and Polymers, Academic Press, London, 1994 Search PubMed.
- M. A. Janusa, X. Wu, F. K. Cartledge and L. G. Butler, Solid-state deuterium NMR spectroscopy of d5-phenol in white portland cement: a new method for assessing solidification/stabilization, Environ. Sci. Technol., 1993, 27, 1426 CrossRef CAS.
- L. S. Loo, R. E. Cohen and K. K. Gleason, Deuterium Nuclear Magnetic Resonance of Phenol-d5 in Nylon 6 under Active Uniaxial Deformation, Macromolecules, 1999, 32, 4359 CrossRef CAS.
- E. Rössler and H. Sillescu, 2H NMR Study of supercooled toluene, Chem. Phys. Lett., 1984, 112, 94 CrossRef.
- B. Geil and G. Hinze, Influence of data treatment on the shape of 2H NMR T1 curves, Chem. Phys. Lett., 1993, 216, 51 CrossRef CAS.
- W. Schnauss, F. Fujara and H. Sillescu, The molecular dynamics around the glass transition and in the glassy state of molecular organic systems: A 2H-nuclear magnetic resonance (NMR) study, J. Chem. Phys., 1992, 97, 1378 CrossRef CAS.
- T. Bull, S. Forsén and D. Turner, Nuclear magnetic relaxation of spin 5/2 and spin 7/2 nuclei including the effects of chemical exchange, J. Chem. Phys., 1979, 70, 3106 CrossRef CAS.
- C.-W. Chung and S. Wimperis, Measurement of spin-5/2 relaxation in biological and macromolecular systems using multiple-quantum NMR techniques, Mol. Phys., 1992, 76, 47 CrossRef CAS.
- J. Zhu and G. Wu, Quadrupole central transition 17O NMR spectroscopy of biological macromolecules in aqueous solution, J. Am. Chem. Soc., 2011, 133, 920 CrossRef CAS PubMed.
- H. W. Spiess, Rotation of molecules and nuclear spin relaxation, Dynamic NMR Spectroscopy, Springer, Berlin, 1978, see in particular chapter 4.1.1, Table 4.4 Search PubMed.
- G. Wu, 17O NMR studies of organic and biological molecules in aqueous solution and in the solid state, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 114–115 CAS , 135 and references cited therein.
- J. Shen, V. Terskikh and G. Wu, A Quadrupole-Central-Transition 59Co NMR Study of Cobalamins in Solution, Chem. Phys. Chem., 2019, 20, 268 CrossRef CAS PubMed.
- P. A. Beckmann, Spectral densities and nuclear spin relaxation in solids, Phys. Rep., 1988, 171, 85 CrossRef.
- B. Halle and H. Wennerström, Nearly exponential quadrupolar relaxation. A perturbation treatment, J. Magn. Reson., 1981, 44, 89 CAS.
- G. Wu, An approximate analytical expression for the nuclear quadrupole transverse relaxation rate of half-integer spins in liquids, J. Magn. Reson., 2016, 269, 176 CrossRef CAS PubMed.
- A. Baram, Z. Luz and S. Alexander, Resonance Line Shapes for Semi-Integer Spins in Liquids, J. Chem. Phys., 1973, 58, 4558 CrossRef CAS.
- L. Werbelow, Adiabatic Nuclear Magnetic Resonance Linewidth Contributions for Central Transitions of I > 1/2 Nuclei, J. Chem. Phys., 1996, 104, 3457 CrossRef CAS.
- J. Shen, V. Terskikh and G. Wu, Observation of the Second-Order Quadrupolar Interaction as a Dominating NMR Relaxation Mechanism in Liquids: The Ultraslow Regime of Motion, J. Phys. Chem. Lett., 2016, 7, 3412 CrossRef CAS PubMed.
- S. H. Chung, K. R. Jeffrey and J. R. Stevens, Dynamics of sodium ions in NaClO4 complexed in poly(propylene-oxide): A 23Na nuclear magnetic resonance study, J. Chem. Phys., 1998, 108, 3360 CrossRef CAS.
- M. Becher, T. Körber, A. Döβ, G. Hinze, C. Gainaru, R. Böhmer, M. Vogel and E. A. Rössler, NMR spin relaxation in viscous liquids: relaxation stretching of single-particle probes, J. Phys. Chem. B, 2021, 125, 13519 CrossRef CAS PubMed.
- H. Nelson, A. Ihrig, R. Kahlau, P. Kibies, S. M. Kast and R. Böhmer, Dielectric and deuteron magnetic resonance studies of guest reorientation and defect dynamics in six clathrate hydrates with ring-type guests, J. Non-Cryst. Solids, 2015, 407, 431 CrossRef CAS.
- R. Böhmer, G. Diezemann, G. Hinze and E. Rössler, Dynamics of supercooled liquids and glassy solids, Prog. Nucl. Magn. Reson. Spectrosc., 2001, 39, 191 CrossRef.
- G. Diezemann, R. Böhmer, G. Hinze and H. Sillescu, Reorientational dynamics in simple supercooled liquids, J. Non-Cryst. Solids, 1998, 235–237, 121 CrossRef CAS.
- R. Böhmer and G. Hinze, Reorientations in supercooled glycerol studied by two-dimensional time-domain deuteron nuclear magnetic resonance spectroscopy, J. Chem. Phys., 1998, 109, 241 CrossRef.
- P. Lunkenheimer, S. Kastner, M. Köhler and A. Loidl, Temperature development of glassy α-relaxation dynamics determined by broadband dielectric spectroscopy, Phys. Rev. E, 2010, 81, 051504 CrossRef CAS PubMed.
- Y. Z. Chua, A. R. Young-Gonzales, R. Richert, M. D. Ediger and C. Schick, Dynamics of Supercooled Liquid and Plastic Crystalline Ethanol: Dielectric Relaxation and AC Nanocalorimetry Distinguish Structural α- and Debye Relaxation Processes, J. Chem. Phys., 2017, 147, 014502 CrossRef CAS PubMed.
- S. Schildmann, A. Reiser, R. Gainaru, C. Gainaru and R. Böhmer, Nuclear magnetic resonance and dielectric noise study of spectral densities and correlation functions in the glass forming monoalcohol 2-ethyl-1-hexanol, J. Chem. Phys., 2011, 135, 174511 CrossRef CAS PubMed.
- C. Scheringer, Die Kristallstruktur des Phenols, Z. Kristallogr., 1963, 119, 273 CrossRef CAS.
- X. Kong, M. Shan, V. Terskikh, I. Hung, Z. Gan and G. Wu, Solid-state 17O NMR of pharmaceutical compounds: Salicylic acid and aspirin, J. Phys. Chem. B, 2013, 117, 9643 CrossRef CAS PubMed.
- J. Beerwerth, M. Storek, D. Greim, J. Lueg, R. Siegel, B. Cetinkaya, W. Hiller, H. Zimmermann, J. Senker and R. Böhmer, Two-site jumps in dimethyl sulfone studied by one- and two-dimensional 17O-NMR spectroscopy, J. Magn. Reson. B, 2018, 288, 84 CrossRef CAS PubMed.
- J. Beerwerth and R. Böhmer, Low-temperature phase transitions and reorientational dynamics studied by 11B NMR in glassy crystal ortho-carborane, J. Non-Cryst. Solids: X, 2023, 18, 100180 CAS.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, First principles methods using CASTEP, Z. Kristallogr., 2005, 220, 567 CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- J. G. Kirkwood, The Dielectric Polarization of Polar Liquids, J. Chem. Phys., 1939, 7, 911 CrossRef CAS.
- N. W. Larsen, Microwave spectra of the six mono-13C-substituted phenols and of some monodeuterated species of phenol. Complete substitution structure and absolute dipole moment, J. Mol. Struct., 1979, 51, 175 CrossRef CAS.
- R. C. Barreto, K. Coutinho, H. C. Georg and S. Canuto, Combined Monte Carlo and quantum mechanics study of the solvatochromism of phenol in water. The origin of the blue shift of the lowest π–π* transition, Phys. Chem. Chem. Phys., 2009, 11, 1388 RSC.
- D. A. Mooney, F. Müller-Plathe and K. Kremer, Simulation studies for liquid phenol: properties evaluated and tested over a range of temperatures, Chem. Phys. Lett., 1998, 294, 135 CrossRef CAS.
- M. Kołaski, A. Kumar, N. J. Singh and K. S. Kim, Differences in structure, energy, and spectrum between neutral, protonated, and deprotonated phenol dimers: Comparison of various density functionals with ab initio theory, Phys. Chem. Chem. Phys., 2011, 13, 991 RSC.
- D. Paik, H. Lee, H. Kim and J.-M. Choi, Thermodynamics of π–π Interactions of Benzene and Phenol in Water, Int. J. Mol. Sci., 2022, 23, 9811 CrossRef CAS PubMed.
- Y. P. Morozova, O. N. Chaikovskaya and O. K. Bazyl, Influence of Solvents on the Spectral and Luminescent Properties of Phenol, Russ. Phys. J., 2003, 46, 62 CrossRef CAS.
- N. L. Allinger, J. Allinger and N. A. LeBel, Conformational Analysis. VIII. The Dipole Moments of cis- and trans-2-Bromo-4-t-butylcyclohexanone, J. Am. Chem. Soc., 1960, 82, 2926 CrossRef CAS.
- H. J. Hageman and E. Havinga, The conformation of non-aromatic ring compounds. Part 39. Dipole Moments and Conformational Properties of some trans-1,2-Dihalogenocyclohexanes and their alkyl derivatives, Recl. Trav. Chim. Pays-Bas, 1969, 88, 97 CrossRef CAS.
- J. P. Conde and J. Moura-Ramos, Study of conformational equilibrium by dipole moment measurements: A source of experiments in physical organic chemistry, J. Chem. Educ., 1986, 63, 823 CrossRef CAS.
- Z. J. Lu, E. Manias, D. D. Macdonald and M. Lanagan, Dielectric Relaxation in Dimethyl Sulfoxide/Water Mixtures Studied by Microwave Dielectric Relaxation Spectroscopy, J. Phys. Chem. A, 2009, 113, 12207 CrossRef CAS PubMed.
- L. Simeral and R. L. Amey, Dielectric properties of liquid propylene carbonate, J. Phys. Chem., 1970, 74, 1443 CrossRef CAS.
- S. P. Bierwirth, T. Büning, C. Gainaru, C. Sternemann, M. Tolan and R. Böhmer, Supramolecular X-ray signature of susceptibility amplification in hydrogen-bonded liquids, Phys. Rev. E, 2014, 90, 052807 CrossRef CAS PubMed.
- M. Vogel, C. Tschirwitz, G. Schneider, C. Koplin, P. Medick and E. Rössler, A 2H NMR and dielectric spectroscopy study of the slow β-process in organic glass formers, J. Non-Cryst. Solids, 2002, 307–310, 326 CrossRef CAS.
- C. Gainaru, R. Kahlau, E. A. Rössler and R. Böhmer, Evolution of excess wing and β-process in simple glass formers, J. Chem. Phys., 2009, 131, 184510 CrossRef PubMed.
- M. Vogel and E. Rössler, Slow β process in simple organic glass formers studied by one and two-dimensional 2H nuclear magnetic resonance. II. Discussion of motional models, J. Chem. Phys., 2001, 115, 10883 CrossRef CAS.
- A. Döβ, M. Paluch, H. Sillescu and G. Hinze, From strong to fragile glass formers: secondary relaxation in polyalcohols, Phys. Rev. Lett., 2002, 88, 95701 CrossRef PubMed.
- A. Döβ, M. Paluch, H. Sillescu and G. Hinze, Dynamics in supercooled polyalcohols: Primary and secondary relaxation, J. Chem. Phys., 2002, 117, 6582 CrossRef.
- A. G. Redfield, The theory of relaxation processes, Adv. Magn. Reson., 1965, 1, 1 Search PubMed.
- I. Furó and B. Halle, Spin relaxation of I > 1 nuclei in anisotropic systems. II. Inversion recovery and even rank polarization decay, J. Chem. Phys., 1989, 91, 42 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02774k |
| This journal is © the Owner Societies 2023 |