Towards the generation of potential energy surfaces of weakly bound medium-sized molecular systems: the case of benzonitrile–He complex†
Eya
Derbali
a,
Yosra
Ajili
*a,
Bilel
Mehnen
 b,
Piotr S.
Żuchowski
b,
Piotr S.
Żuchowski
 b,
Dariusz
Kędziera
b,
Dariusz
Kędziera
 *c,
Muneerah Mogren
Al-Mogren
d,
Nejm-Edine
Jaidane
a and
Majdi
Hochlaf
*c,
Muneerah Mogren
Al-Mogren
d,
Nejm-Edine
Jaidane
a and
Majdi
Hochlaf
 *e
*e
aLaboratoire de Spectroscopie Atomique, Moléculaire et Applications LSAMA, Université de Tunis Al Manar, Tunis, Tunisia. E-mail: yosra-aji@hotmail.fr
bInstitute of Physics, Faculty of Physics, Astronomy and Informatics, Nicolaus Copernicus University in Toruń, Grudziadz Street 5, 87-100 Toruń, Poland
cFaculty of Chemistry, Nicolaus Copernicus University in Toruń, ul. Gagarina 7, PL 87-100 Toruń, Poland. E-mail: teodar@chem.umk.pl
dDepartment of Chemistry, College of Sciences, King Saud University, PO Box 2455, Riyadh 11451, Saudi Arabia
eUniversité Gustave Eiffel, COSYS/IMSE, 5 Bd Descartes 77454, Champs sur Marne, France. E-mail: majdi.hochlaf@univ-eiffel.fr
First published on 20th September 2023
Abstract
Currently, the explicitly correlated coupled cluster method is used routinely to generate the multi-dimensional potential energy surfaces (mD-PESs) of van der Waals complexes of small molecular systems relevant for atmospheric, astrophysical and industrial applications. Although very accurate, this method is computationally prohibitive for medium and large molecules containing clusters. For instance, the recent detections of complex organic molecules (COMs) in the interstellar medium, such as benzonitrile, revealed the need to establish an accurate enough electronic structure approach to map the mD-PESs of these species interacting with the surrounding gases. As a benchmark, we have treated the case of the polar molecule benzonitrile interacting with helium, where we use post-Hartree–Fock and symmetry-adapted perturbation theory (SAPT) techniques. Accordingly, we show that MP2 and distinguishable-cluster approximation (DCSD) cannot be used for this purpose, whereas accurate enough PESs may be obtained using the corresponding explicitly correlated versions (MP2-F12 or DCSD-F12) with a reduction in computational costs. Alternatively, computations revealed that SAPT(DFT) is as performant as CCSD(T)-F12/aug-cc-pVTZ, making it the method of choice for mapping the mD-PESs of COMs containing clusters. Therefore, we have used this approach to generate the 3D-PES of the benzonitrile–He complex along the intermonomer Jacobi coordinates. As an application, we have incorporated the analytic form of this PES into quantum dynamical computations to determine the cross sections of the rotational (de-)excitation of benzonitrile colliding with helium at a collision energy of 10 cm−1.
I. Introduction
Studies of the spectroscopy and dynamics of clusters containing small and medium-sized molecules, A–B, are important for chemical, industrial, environmental, atmospheric planetary and astrophysical applications. From a theoretical point of view, the characterization of such weakly bound systems requires the generation of their multi-dimensional potential energy surfaces (mD-PESs), which are incorporated into nuclear motion treatments to derive their spectroscopy and/or into scattering computations to deduce the corresponding (de-)excitation cross sections and rate collisions. When A and B are atoms or small molecular systems, typically diatomics and/or He and/or H2, these mD-PESs can be mapped using accurate ab initio post-Hartree–Fock techniques, where one needs to go beyond the Born–Oppenheimer (BO) approximation and consider relativistic, nonadiabatic and quantum electrodynamic (QED) effects.1 More routinely, one can use the standard single and double-coupled cluster with the perturbative treatment of triple excitations (CCSD(T)) method,2–4 extrapolated to the complete basis set (CBS) limit5 and even the CCSDT and CCSDT(Q)6 approaches, where triple excitations are treated iteratively and the quadruple excitations are considered perturbatively. Although relatively very accurate, such procedures are computationally costly and cannot be applied in van der Waals (vdW) molecular systems composed of more than 3–5 atoms.In the last decade, Hochlaf and co-workers7–11 validated the use of explicitly correlated single and double-coupled clusters with the perturbative treatment of triple excitations (CCSD(T)-F12) approach in conjunction with a relatively small basis set (of aug-cc-pVTZ quality) for mapping such mD-PESs. A rapid convergence to the CBS limit was achieved with this small basis set through the implicit introduction of the interelectronic distance into the wave function expansion.12 Established in 2010, this procedure is currently used systematically by several groups all over the world (cf. recent ref. 13–18). Notably, Faure and co-workers used the CCSD(T)-F12/CBS method to generate the intermonomer interaction potential between propylene oxide and helium. They showed that such computations remain feasible but costly.17 Also, they used this PES in scattering calculations to determine the rotational collisional (de-)excitation rates of propylene oxide by He and to discuss the validity of local thermal equilibrium (LTE) in the case of the interstellar chiral propylene oxide.19 Single-point computations using CCSD(T)-F12/aug-cc-pVTZ remain possible for medium-sized molecular clusters,20 let's say formed by 10–15 atoms, whereas this procedure becomes prohibitively costly to generate their mD-PESs where typically >105 single point energies should be computed for difference non-equivalent nuclear configurations.17
The CCSD(T) method has a steep scaling with the basis set size scaling as N7. This can be overcome by using the symmetry-adapted perturbation theory (SAPT). The SAPT method has been successfully applied to many weakly bound systems, starting from the simplest one to very complex. This method was developed for the many-electron wave function and combined with the Møller–Plesset expansion21–23 or CCSD theory.24,25 More recently, efficient implementations of SAPT were combined with density fitting techniques, leading to vastly improved performance for SAPT theory based on wave function theory.26 The marriage between SAPT and density functional theory (DFT) was enormously successful in lowering the overall scaling down to N5, which combined with density fitting allows the extension of its capabilities to systems with tens of atoms. Recently, Metz et al.27 developed an algorithm for the automated generation of the site-site potential, which is based on SAPT(DFT). The method relies on the key advantages of SAPT, which possesses accurate analytical long-range behavior that can be seamlessly connected to the valence-overlap region. This allows the limiting of mD-PES sampling exclusively to the vicinity of minima and transition state points and thus reduces the number of sampled geometries by a factor of 10–100.
In the astrophysical context, there is a rapid increase in the complexity of detected molecules, in particular of complex organic molecules (COMs), such as benzonitrile.28–31 There is, therefore, an urgent need for new collision data for these COMs interacting with the most abundant surrounding gases, i.e., He, H or H2. This, in turn, necessitates the development of their mD-PESs interacting with He or H or H2. Consequently, alternatives to the computationally expensive CCSD(T) method are required since its scaling behaviour is unaffordable, even with modest basis sets that are feasible using explicitly correlated methods. Tentatively, DFT was used to generate mD-PESs of weakly bound complex potentials containing large molecular systems. For instance, Liu et al.32 were just performing counterpoise-corrected DFT calculations to get the interaction potential between C60-Rg (Rg = Ar, He). Such PESs allowed the analysis of the collision-induced C60 rovibrational relaxation probed by state-resolved nonlinear spectroscopy. Nevertheless, among the current DFT's weaknesses is the reliable description of mD-PESs because of the lack of suitable exchange–correlation functionals. Consequently, DFT-based mD-PESs are not accurate enough to be used to derive the state-to-state rotational (de-)excitations in astrophysical or atmospheric contexts. For the Be dimer, Bartlett and co-workers33 showed that DFT provides a potential that is about 30% too deep as compared to the highly accurate coupled-cluster method. This is not enough to probe collision effects at the ISM temperature (i.e. 5–10 K). Moreover, accurate behavior at long-range intermonomer separations is mandatory. This is not straightforward with DFT. A suitable choice of a long-range parameter present in some DFT functionals34 or using a combination of the short-range exchange correlation and long-range exact exchange energy is not enough.35 Alternatively, the generation of accurate mD-PESs of weakly bound complexes composed by COMs can be done using machine learning-based approaches as established recently for monohydrates of organic molecules.36 Nevertheless, these approaches are still under benchmarking as stated in the recent blind HyDRA challenge for computational vibrational spectroscopy.
In this study, we have considered the benzonitrile–He complex, which serves as a prototype system representative of such interactions. For instance, in 2015 Cui et al.37 proposed a Gaussian Process model to extrapolate the scattering data for medium-sized molecules from another molecule-related species without explicitly computing the mD-PES of the benzonitrile–He complex. They showed that such data for benzonitrile colliding with He can be obtained from those of the benzene–He system upon substituting –H with –CN. Nevertheless, they had to construct a PES for the benzene–He vdW system using a semi-empirical bond-additive method since pure ab initio methodologies were too costly. Moreover, this work and several previous works showed that the interaction potentials of COMs containing vdW clusters are strongly anisotropic, invalidating simple considerations for the precise generation of their mD-PESs for spectroscopy and scattering. Such anisotropies induce transitions and populate molecular levels important for interpreting astrophysical surveys and laboratory observations.31,38
We have compared the performance of the CCSD(T)-F12 method with the less computationally demanding MP2, DSCD, MP2-F12 and DSCD-F12 methods, as well as with the SAPT family of techniques. We have assessed their effectiveness by examining the interactions between benzonitrile, a complex aromatic polar molecule (μ = 4.5152(68) D39), and helium, a key astrophysical collider. We also used the AutoPES protocol27 to generate the benzonitrile–He global PES and adopt it to the Jacobi coordinate system (cf.Fig. 1), which will allow the performance of close-coupling scattering cross section calculations. In-depth investigations of the performance of the SAPT method have enabled us to provide recommendations regarding the optimal settings to use for this method and its applicability for the generation of medium-sized molecules (e.g. COMs) bearing vdW clusters.
II. Benchmarks
As discussed in the Introduction, previous works7,8,11,40 showed that the explicitly correlated method of CCSD(T)-F12 in conjunction with the aug-cc-pVTZ basis set41,42 is accurate enough to make a satisfactory description of the vdW interaction energy since it leads to potentials as accurate as those obtained using the conventional CCSD(T) method extrapolated to the CBS limit. Nevertheless, we looked for an alternative that is less costly for medium-sized molecules (e.g. COMs) containing vdW clusters. As a benchmark, we considered the benzonitrile–He complex, where the electronic calculations were conducted considering the benzonitrile molecule as a rigid rotor, using the experimental geometry of this molecule in its vibrational ground state as determined by Császár and Forgarasi43 (Table S1, ESI†). The ground state of the benzonitrile–He complex correlates to the benzonitrile (X1A1) + He (1S) dissociation limit at infinite intermonomer separation, where the interaction potential vanishes.Two sets of computations were carried out: (i) using ab initio post-Hartree–Fock techniques as implemented in the MOLPRO electronic structure suite of programs44 and (ii) using the SAPT 2020 package.45 Therefore, we computed one-dimensional cuts of the benzonitrile–He PES along the R Jacobi coordinate, where different values were assigned to the θ and ϕ angles corresponding to some selected relative positions of He with respect to benzonitrile as specified in Fig. 2. Some of these positions correspond to stationary points on this mD-PES (either minima or transition states, vide infra). We also chose some positions that are not stationary points to make sure that our findings are relevant to all nuclear configurations. This is mandatory for the validation of the electronic structure methodology to be used for the generation of the mD-PES of the benzonitrile–He complex. The CCSD(T)-F12/aug-cc-pVTZ level will be used as a reference for the computations of benzonitrile–He potentials and for validation. Strictly speaking, one needs to compare mD-PESs and not solely one dimensional cuts for validation. Nevertheless, we believe that these one-dimensional cuts of this mD-PES allow the capture of any possible major deviations between our CCSD(T)-F12/aug-cc-pVTZ reference potentials and those computed with the other approaches.
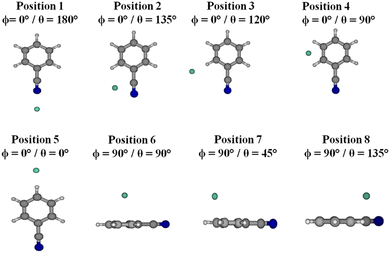 | ||
| Fig. 2 Different positions of the He atom with respect to benzonitrile considered in the present work. | ||
a. Ab initio post Hartree–Fock methods
For the selected configurations presented in Fig. 2, electronic calculations of the interaction energies of the benzonitrile–He complex were made for intermolecular distances R ranging from 2.5 to 100 Å as specified in the ESI† (Table S2) for 6 values of θ angles [0°, 45°, 90°, 135°, 120° and 180°] and with 2 orientations of the He atom toward the benzonitrile molecule corresponding to ϕ = 0° (i.e. planar configuration) and ϕ = 90° (i.e. out-of-plane configuration). The intermolecular distance R plays a crucial role in the calculations, so the grid of points was chosen to probe both the short and long parts of the potential.The counterpoise procedure of Boys and Bernardi46 was used, where the basis set superposition error (BSSE) was corrected at all geometries by the following scheme:
| V(R, θ, ϕ) = Ebenzonitrile–He(R, θ, ϕ) − Ebenzonitrile(R, θ, ϕ) − EHe(R, θ, ϕ) | (1) |
An evaluation of the size of this effect was performed for the global minimal structure. It was found to account for ∼16%. Thus, this correction is needed for the accurate generation of this PES.
For electronic structure computations, both standard and explicitly correlated approaches were used. As conventional methods, we used MP2 and the distinguishable-cluster approximation (DCSD).47 For explicitly correlated computations, we used the MP2-F1248 and CCSD(T)-F1249,50 methods and the recently implemented explicitly correlated version of the distinguishable-cluster approximation (DCSD-F12) approach.51 The atoms were described using the aug-cc-pVTZ basis set together with MOLPRO's default choices for the density fitting and resolution of the identity basis sets.52
Fig. 3 presents the radial cuts of the mD-PES of benzonitrile–He as computed at the CCSD(T)-F12/aug-cc-pVTZ, DCSD-F12/aug-cc-pVTZ, MP2-F12/aug-cc-pVTZ, DCSD/aug-cc-pVTZ and MP2/aug-cc-pVTZ levels of theory. These cuts were done for the selected configurations as specified in Fig. 2. The corresponding characteristics (i.e. minimal R and potential well depth, V) are listed in Table S3 (ESI†). This table and figure show that the CCSD(T)-F12 approach gives the deepest potential wells, except for positions 4 and 6. Although DCSD-F12 and MP2-F12 explicitly correlated methods lead to potentials closer to those obtained by CCSD(T)-F12, they are unable to achieve a good description of the interaction of benzonitrile and He as well as the MP2 and DCSD standard approaches. Nevertheless, DCSD-F12 and MP2-F12 can be viewed as good ab initio alternatives to CCSD(T)-F12 when the size of the molecular system is too large to be treated by CCSD(T)-F12. Besides, Table S3 (ESI†) shows that the Gaussian process model proposed by Cui et al.37 leads to distinctly less deep potentials, whatever the position of He with respect to benzonitrile. Differences between both sets of data are in the 5–30% range.
 | ||
| Fig. 3 One-dimensional cuts of the benzonitrile–He complex PES along the R (in Å) coordinate for selected configurations as computed at different levels of theory. The atoms were described by the aug-cc-pVTZ basis set. (a)–(h) Correspond to positions 1–8 as defined in Fig. 2, respectively. See Table S3 (ESI†) for the corresponding minimal distances and well depths of the benzonitrile–He complex PES. | ||
b. SAPT methods
The SAPT method relies on the partitioning of the total Hamiltonian of the A–B complex into monomers and the interaction potential H = HA + HB + λV, where A = benzonitrile and B = He. HA + HB is the zeroth order Hamiltonian and V is the perturbation. This defines the energy expansion in terms of the power series of V. In SAPT, corrections are distinctly partitioned into two classes of components: polarization terms and exchange corrections. Polarization terms up to the first two orders in λ represent electrostatic, dispersion, and induction terms. The exchange terms appear due to symmetry forcing and appear in each order of SAPT and are the most important repulsive terms in the valence overlap region. When using many-electron SAPT, one faces the problem of using exact eigen functions of HA and HB Hamiltonians, which are impossible to obtain, even for medium-sized systems. Thus, approximate wave function for monomers A and B are needed. The most basic approximation is to use the Hartree–Fock wave function to describe the monomers. This corresponds to taking the zeroth order Hamiltonian as FA + FB where FA and FB are the Fock operators for a given monomer.21 Such an approach is often referred to as SAPT0 and is generally known to be of low quality. For aromatic systems, SAPT0, for instance, overestimates the dispersion interactions.53 Substantially better approximations can be obtained once the intramonomer correlation effects are included. To this end, the corrections to SAPT, which include intramonomer correlation to the second order, based on Møller–Plesset expansion, were developed in ref. 22, 24 and 54.Herein, we follow the hierarchy of approximations to many-electron SAPT introduced by Hohenstein and Sherrill,55 which are built on top of the supermolecular Hartree–Fock interaction energy, EHF. The SAPT2+ approximation is defined as follows:
| ESAPT2+ = EHF + E(2)disp(2) + E(2)corr,ind(2) + E(1)corr,elst(2) + E(1)corr,elst(2) | (2) |
Similarly, one can introduce the approximation that includes key third-order corrections56,57 in the operator V, as well as third-order intramonomer correlation:58
| ESAPT2+3 = ESAPT2+ + E(3)SAPT + E(1)corr,elst(3) | (3) |
| δ(2)HF = EHF − (E(10)elst + E(10)exch + E(20)ind,resp + E(20)exch–ind,resp) | (4) |
Apart from the SAPT based on wave function theory, one of the most important approximations introduced into the many-electron SAPT is the Kohn–Sham description of monomers61–63 in which the DFT response theory is used for the induction and dispersion terms, whereas the first order was deduced from Kohn–Sham orbitals obtained with the asymptotic correction of the exchange–correlation potential. This approach is referred to as SAPT(DFT). It was recently demonstrated that the accuracy of SAPT(DFT) approaches that of CCSD(T) with the numerical cost reduced by 2 orders of magnitude (N5 as compared to N7). Therefore, we also used SAPT(DFT) to compute the interaction energies between benzonitrile and He. These energies were calculated within the density-fitted symmetry-adapted perturbation theory (DF-SAPT(DFT), denoted here as SAPT(DFT)) up to the second order, based on the asymptotically corrected PBE0 functional. The aug-cc-pVQZ basis sets41,42 were employed for all atoms. For density fitting auxiliary basis sets, aug-cc-pVQZ/RI and aug-cc-pVQZ/JK were used for nitrogen and carbon atoms, while for helium, the JK basis was derived via the AutoAux procedure as implemented in ORCA.64–66
As a default setting, a mid-bond with the M1 basis set, taken from the SAPT library, was included for every geometry for which the interaction energy was computed. This was placed in the 1/r6-weighted average of the atomic positions between monomers. SAPT(DFT) calculations necessitate a gradient-regulated asymptotic correction (GRAC)67 of exchange–correlation functionals. The parameters needed for such procedures are ionization energies. The standard protocol in AutoPES includes the calculation of the neutral-cation energy difference using the PBE0/aug-cc-pVQZ calculation. The obtained values that were used in SAPT(DFT) calculations were 24.8497 eV for helium and 9.5450 eV for benzonitrile.
A common problem in SAPT is the treatment of third- and higher-order corrections. It is debatable whether this term should be added or not, and under what circumstances. Given that the mD-PES of benzonitrile is mapped using SAPT(DFT), it is crucial to assess its accuracy and examine it in the context of other approximations. The comparison with wave functions-based SAPT is particularly instructive, as both approximations depend on the truncation of the perturbation series at the 2nd order, and optionally include a supermolecular Hartree–Fock evaluation to account for the contributions of higher orders.
Using SAPT, we performed some benchmark computations where the He is in the plane of benzonitrile (position 2 and position 3) or on top of the aromatic ring (position 6), which exhibited different types of interactions between monomers. In Fig. 4, we present a comparison of wave function-based SAPT approaches and SAPT(DFT) against the reference value provided by CCSD(T)-F12. Both wave functions SAPT and SAPT(DFT) performed remarkably well across all cases, with exceptions noted where the appropriate δHF terms (see eqn (5) and (6)) were neglected. Benzonitrile exhibited significant polarity, resulting in substantial effects beyond the second order in the interaction potential. The term in question is negative for all studied geometries and can reach values as low as −20 cm−1 for R corresponding to the inner turning point. The smallest deviation from the reference CCSD(T)-F12 was observed for SAPT(DFT) and SAPT2+3 approximations. Given the high efficiency of the implementation of the SAPT2+3 approximation, it can be considered an excellent alternative in instances where DFT lacks credibility.
c. SAPT vs. supermolecular calculations
Fig. 4 shows a comparison of interaction energies calculated using SAPT(DFT) and CCSD(T)-F12 with cost-efficient, wave function-based explicitly correlated methods MP2-F12/aug-cc-pVTZ and DCSD-F12/aug-cc-pVTZ. Interestingly, the DCSD-F12 method, which effectively accounts for dynamical electronic correlation at the singles and doubles levels, performed worse than MP2. This unexpected result can be attributed to a fortuitous error cancellation in MP2 and the absence of triply excited terms, which are crucial for dispersion interactions. An examination of SAPT dispersion energies can provide additional insights into this behavior: E(20)disp corresponds to the one present in the MP2 approximation, E(2)disp(2) includes linked triply excited configurations, present in CCSD(T), which can be separated from E(2)disp(SDQ) (dispersion energy with excitations corresponding to single, double and unlinked quadruple excitations; see ref. 22 for a detailed discussion of these terms). E(2)disp(SDQ) corresponds roughly to the interaction energy at the DCSD or CCSD level. In Fig. 5, we present the histogram for the deviation of E(20)disp and E(2)disp(SDQ) dispersions with respect to full E(2)disp(2) sampled for uniformly chosen 330 geometries, which correspond to negative interaction energies and slightly repulsive wall potentials (up to 100 cm−1). Clearly, SDQ dispersion systematically underestimates the full dispersion; therefore, DCSD-F12 is always shallower than CCSD(T)-F12. The distribution of errors is very narrow with a mean of 0.87 (median 0.88) and σ of 0.03. In contrast, the interaction energy, E(20)disp, has a fairly broad distribution of deviations with a mean of 0.97 (median 0.98) and σ of 0.07. Thus, it is not surprising that MP2-F12 can occasionally overestimate CCSD(T)-F12 but its overall performance is good.These benchmarks reveal that SAPT(DFT) performs quite well for both types of configurations between benzonitrile and He. The good performance of SAPT(DFT) compared to CCSD(T)-F12 is accompanied by a strong reduction of computational costs (cf. Table S4, ESI†). It turns out that SAPT(DFT) should be considered a good alternative for the generation of accurate enough mD-PESs for medium-sized molecules containing van der Waals complexes.
III. Generation of the 3D-PES of the benzonitrile–He complex
a. Automatically generated PES
A 3D-PES for the interaction between rigid benzonitrile and helium was generated using the AutoPES code,27,68 interfaced with SAPT,69,70 ORCA64 and Dalton.71 The SAPT(DFT) interaction energy with δ(2)HF correction was considered. AutoPES constructs a site-site potential as described previously in ref. 27. Thus, the number of fitting potential parameters depends on the number of sites. The quality of the fit is screened by four values of the root mean square error (RMSE) for the interaction energy. The first RMSE was calculated for points where the interaction energy is below half of the deepest minimum value. The second RMSE was calculated for all points within the attractive region. The third RMSE was for points with energy less than 3500 cm−1, and the final RMSE value corresponds to points with energy less than 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1.
000 cm−1.
The AutoPES procedure was initiated with a bare benzonitrile molecule and a helium atom, progressively enabling electrostatic, polarization, induction plus dispersion, and repulsive exponential components for all atoms to be taken into account. This procedure yields a 3D-PES built on 420 points, modeled with 45 fitted parameters. The quality of the fit was evaluated with RMSEs of 10.93 cm−1 for 75 points, 10.97 cm−1 for 285 points, 57.91 cm−1 for 418 points, and 113.18 cm−1 for all 420 points. The deepest potential minimum had a potential depth of −87.92 cm−1. Nevertheless, these RMSEs are relatively large for this initial fit. Therefore, we proceeded to incorporate off-atomic sites. The approach to determine optimal off-atomic sites was twofold: Initially, we selected potential off-atomic sites located on benzonitrile bonds and along lines passing through the phenyl group's C–C bond centers. Subsequently, we identified which of these sites enhanced the fit quality. The most advantageous sites were persistently included in the input, with the off-atomic site search repeated until an RMSE of approximately 1% in the well was obtained. For these off-atomic sites, we included electrostatic and exponential energy components. By adding 15 off-atomic sites, we achieved a satisfactory fit. Afterwards, we ran AutoPES again with the obtained off-atomic sites. The resulting PES spans over 1493 points with 85 parameters. The final fit was characterized by RMSEs of 1.15 cm−1 for 160 points for interaction energies below half of the global minimum value, 1.28 cm−1 for 969 points for energies ≤0 cm−1, 17.69 cm−1 for 1471 points for energies <3500 cm−1, and 111.60 cm−1 for 1493 points for energies <35000 cm−1. This fit is given in an analytical form and can be incorporated into molecular dynamical computations in any coordinate system. In our case, we used Jacobi coordinates, which can be easily obtained after applying a simple transformation procedure.
The analytical fit of the PES generated by AutoPES occasionally exhibits holes at very short atom–atom distances. The AutoPES algorithm randomly tests for and eliminates holes in the fit up to 5000 cm−1. However, this automated procedure was not sufficient because of the strong anisotropy of the interaction between benzonitrile and He. Therefore, we implemented a home-made hole-elimination procedure, which relies on the extrapolation of energy on the potential wall, when the helium atom, for a given R, is too close to any atom of the benzonitrile molecule, i.e., when He is closer than the boundary distance of 1.4 times the sum of the covalent radii of the helium atom and the closest benzonitrile atom. In such a case, we determine the intermonomer distance for which the distance between the helium atom and the nearest benzonitrile atom is equal to the boundary distance. Then, we deduce from the PES fit the interaction energies in the vicinity of this distance. The corrected PES is obtained by two-point extrapolation in R using the exponential formula
α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−βR) exp(−βR) | (5) |
The key step in implementing the potential to the Jacobi set of coordinates is the expansion into spherical harmonic series. To get the right expansion coefficient at a given R one needs to sample all possible orientations of the complex. In the case of strongly anisotropic PES, this is very challenging, since for many relative orientations the interaction energy might be very high or even non-physical, as the helium atom might appear between the atoms of benzonitrile even for the value of R that corresponds to the global minimum. We followed the procedure suggested by Wernli et al.72 for the HC3N molecule interacting with H2 or He and used the regularization procedure to flatten the potential for high interaction energies:
Eint_reg = EMAX/2 + EMAX/π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) atan(π(Eint/EMAX − 0.5)) atan(π(Eint/EMAX − 0.5)) | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1.
000 cm−1.
The validity of this procedure was discussed in previous works. In particular, it does not affect the quality of the PESs for low-energy collisions (E < 5000 cm−1). The subroutines and the fitted coefficients of this 3D-PES are given in the ESI.†
b. Analytical representation
For dynamical calculations, an analytical form of the 3D-PES is required to be implemented later in the MOLSCAT package.73 Thus the generated 3D-PES was refitted following this formula: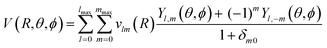 | (7) |
To compute the vlm(R) coefficients, a least-squares procedure was carried out for each point in the radial grid. In the expansion, all values of m (0 < m < l) were considered for a given angular momentum l ranging from 0 to 18, whereas we considered lmax = mmax = 18. This gives a total of 100 vlm(R) coefficients to be determined. These vlm(R) are given in the ESI.†
The quality of this new fit is controlled by minimizing the value of the root mean square as defined by
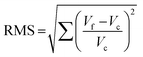 | (8) |
To ensure the reproduction of the auto-PES generated points, a relative error of less than 0.5% for all radial values was assumed. This 3D-PES can be sent upon request.
c. Stationary points on the 3D-PES of benzonitrile–He
By examining the 3D-PES of the benzonitrile–He complex, we located ten stationary points with particular configurations of the interaction of benzonitrile with He. These configurations are displayed in Fig. 6 where they are denoted as GM, LM1–LM5 and TS1–TS4. The minima are ordered from the deepest potential well of −99.15 cm−1 to the shallower well of −50.78 cm−1. The structural and energetic characteristics of these stationary points are listed in Table 1.| Structure | GM | LM1 | LM2 | LM3 | LM4 | LM5 | TS1 | TS2 | TS3 | TS4 |
|---|---|---|---|---|---|---|---|---|---|---|
| R | 3.15 | 3.55 | 4.15 | 4.35 | 4.75 | 5.35 | 4.95 | 5.75 | 3.45 | 3.95 |
| θ | 77 | 115 | 126 | 127 | 79 | 26 | 105 | 52 | 107 | 121 |
| ϕ | 90 | 90 | 90 | 0 | 0 | 0 | 0 | 0 | 90 | 90 |
| V | −99.15 | −79.25 | −65.20 | −55.15 | −52.38 | −50.78 | −27.94 | −26.68 | −59.82 | −54.16 |
GM corresponds to the global minimum. It has a non-planar configuration where He is interacting with the π orbital of the aromatic ring. It is located at ϕ = 90°, θ = 77°, R = 3.15 Å and a potential well depth of V = −99.15 cm−1. LM1, LM2, LM3, LM4 and LM5 are local minima on this PES. They are associated with well depths of −79.25, −65.20, −55.15, −52.38 and −50.78 cm−1, respectively. These minima are separated by transition states denoted as TS1, TS2, TS3 and TS4 and located at planar and non-planar configurations with potential energies of −27.94, −26.68, −59.82 and −54.16 cm−1, respectively. Also, it is worth noting the strong anisotropy of this 3D-PES with respect to the radial coordinate since quite different R minimal distances are found for GM, LM1–LM5 and TS1–TS4 (Table 1 and Fig. S1, ESI†).
d. Description of the 3D-PES
Fig. 7 shows 2D contour plots of the 3D-PES of the benzonitrile–He vdW system along two Jacobi coordinates for planar (ϕ = 0°) and non-planar (ϕ = 90°) configurations. In particular, we plot the 2D-cuts of the interaction potential for GM configuration. Again, this figure confirms that this 3D-PES is very anisotropic with respect to θ and ϕ angles, as well as along the intermonomer coordinate R. This strong anisotropy is expected to lead to significant values for the collisional rates of the benzonitrile rotational (de)-excitation by He. Fig. 7 shows that this 3D-PES is extremely flat along the R, θ and ϕ coordinates, which favors the occurrence of large amplitude motions in this potential. | ||
| Fig. 7 2D contour plots of the 3D-PES of benzonitrile–He cluster. In (a) ϕ = 90°; in (b) ϕ = 0°; in (c) R = 3.15 Å; and in (d) θ = 77°. Energies are in cm−1. | ||
Close examination of Fig. 7a allows the location of the global minimum (GM) and two shallower local minima (LM1 and LM2), which are connected by the two transition states denoted TS3 and TS4. Besides, one can find three local minima LM3, LM4 and LM5 in Fig. 7b. These minimal positions of the He atom towards benzonitrile are separated by TS1 and TS2 transition states. Accordingly, the potential barriers connecting these stationary points are low so that large amplitude motions of He allow the conversion of one isomer into another. The rotation of He with respect to the Z-axis leads straightforwardly from GM to LM1 and LM2 structures, whereas rotation along the ϕ angle populates LM3, LM4 and LM5 planar minima starting from the non-planar GM structure. These intracluster isomerizations go through the transition states specified in Table 1 and Fig. 6. For instance, LM3 to GM isomerization may evolve either viaTS1 or TS3.
IV. Application
We applied our newly generated 3D-PES of the benzonitrile–He interacting system by incorporating it into dynamical computations to deduce the cross sections for the rotational (de-)excitation of benzonitrile colliding with He. Such computations are challenging due to the strong anisotropy of this 3D-PES and because of the high density of the rotational levels of benzonitrile. The dynamics of the benzonitrile–He system is a benchmark system for COMs interacting with the surrounding interstellar gases.a. Rotational structure of benzonitrile
Benzonitrile is an asymmetric top-type rotator. Its rotational Hamiltonian, Hrot, is expressed as follows:| Hrot = Ajx2 + Bjy2 + Cjz2 − DJj(j + 1)−DJKj(j + 1)k2 − DKk4 | (9) |
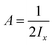 ,
, 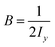 and
and  . DJ, DJH and DK are first-order centrifugal distortion corrections.
. DJ, DJH and DK are first-order centrifugal distortion corrections.
The rotational levels of the asymmetric top benzonitrile molecule are labeled as jka,kc, where j denotes the angular momentum and ka and kc are the projections of j along the a and c inertial axes, which coincide with the Z and Y axes (Fig. 1). To deduce the rotational energy levels, 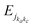 , of benzonitrile, we used the ground state experimental rotational and distortional constants as determined by Wlodarczak et al.74 These correspond to A = 0.1886393, B = 0.0515982, C = 0.0405082, DJ = 1.5106117 × 10−9, Dk = 3.1110856 × 10−8 and DJK = 1.059066 × 10−8 (all values are in cm−1). For the nine detected transitions by McGuire et al.,30 Table S5 (ESI†) gives the comparison between the calculated and observed frequencies, where a good agreement validated the rotational Hamiltonian and constants used presently.
, of benzonitrile, we used the ground state experimental rotational and distortional constants as determined by Wlodarczak et al.74 These correspond to A = 0.1886393, B = 0.0515982, C = 0.0405082, DJ = 1.5106117 × 10−9, Dk = 3.1110856 × 10−8 and DJK = 1.059066 × 10−8 (all values are in cm−1). For the nine detected transitions by McGuire et al.,30 Table S5 (ESI†) gives the comparison between the calculated and observed frequencies, where a good agreement validated the rotational Hamiltonian and constants used presently.
Calculations were limited to the first 46 levels of the benzonitrile molecule up to jka,kc = 909 for rotational energy Erot ≤ 5 cm−1 with a cutoff for ka values at ka ≤ 3. The respective energetic diagram is presented in Fig. 8. This figure shows that the spacing between the rotational states is small due to the small rotational constant values. This results in a very high density of rotational states, close to each other. Accordingly, the rotational structure of this asymmetric top COM is very complex.
 | ||
| Fig. 8 The lowest 46 rotational levels of benzonitrile up to jka,kc = 909 for rotational energy Erot ≤ 5 cm−1 with a cutoff for ka values at ka ≤ 3. The energies of these levels were derived using a model Hamiltonian and the ground state experimental rotational and distortional constants as determined by Wlodarczak et al.74 | ||
b. Cross section calculations
Quantum scattering calculations were performed using the MOLSCAT 2022 package.75 These computations were done at the close coupling level. Considering the small values of the rotational constants of benzonitrile that lead to a high density of rotational states and the relatively deep potential well (∼99 cm−1) of the 3D-PES of benzonitrile–He, the present collision calculations were challenging in terms of computational costs (both computing time and disk space requirements). The size of the coupled equations and the required computational cost for their resolution increased rapidly with the size of the basis set.Preliminary dynamical computations were carried out for a single collisional energy E = 10 cm−1. Prior to that, we performed a series of convergence tests. First, we adjusted the radial values (Rmin and Rmax), which define the limits for integrating the coupled equations. These radial parameters were chosen far enough into the classically forbidden region at short and long ranges, respectively. As given in Table S6 (ESI†), these tests showed that Rmin = 1.05 Å and Rmax = 21.16 Å ensuring that radial values below these limits do not contribute effectively to the collisional calculations. Table S6 (ESI†) shows also that a STEPS parameter of 70 is enough to ensure convergence of the cross sections at E = 10 cm−1.
The reduced mass of the benzonitrile–He colliding system is μ = 3.8530471093 amu. The close-coupling equations were resolved using the Manolopoulos diabatic modified log-derivative (LDMD) propagator76 starting from Rmin = 1.05 Å up to Rmax = 21.16 Å and STEPS = 70. Besides, the rotational basis for the benzonitrile was tested for 9 ≤ jmax ≤ 15. The maximum values of the total angular momentum JTOT were set large enough (i.e. JTOT = 23) to ensure the convergence of the cross sections to be within 0.01 Å2. These tests are shown in Fig. S2 (ESI†), where the cross section convergence with respect to jmax values is extremely slow. This is accompanied by a drastic increase in the computational cost (both memory and CPU time) for these dynamical computations.
In Fig. 9, we plot the cross sections for the rotational de-excitation of benzonitrile by collision with He for transitions populating the ground state 000 as a function of the initial level j for collisional energy E = 10 cm−1. From this figure, we can conclude that the largest cross section corresponds to the 202–000 transition. This is consistent with the radial expansion of the 3D-PES (vlm(R) terms) as presented in Fig. S3 (ESI†), which shows that the largest anisotropic term (in magnitude) corresponds to v20(R) with l = 2. One can also notice the remarkable intensities of the 330–000 and 220–000 transitions as already observed for other asymmetric top molecules interacting with helium.17,77 The computed cross section pattern is typical for rotational inelastic cross sections for asymmetric top molecules and is consistent with the results obtained by Faure and co-workers17,77 for propylene oxide and methyl formate colliding with helium, respectively.
V. Conclusion
As a case study, we investigated the intermonomer interactions between benzonitrile and He to benchmark an accurate methodology that is not costly for electronic structure computations of intermonomer potentials of medium-sized molecules (e.g. COMs) interacting with surrounding gases, such as He, H and H2 in interstellar media. Diverse ab initio and SAPT methodologies were tested. Computations showed that explicitly correlated MP2-F12 and DCSD-F12 ab initio approaches in conjunction with aug-cc-pVTZ are less accurate than CCSD(T)-F12/aug-cc-pVTZ but can be used for the generation of mD-PESs of such vdW complexes when CCSD(T)-F12/aug-cc-pVTZ computations are prohibitive. SAPT(DFT) is viewed as a good alternative, and the SAPT2 + 3 approximation can be considered as a good alternative when DFT cannot be used. We expect that the presently established electronic structure methodology for generating the mD-PESs of medium and large-sized systems containing weakly bound clusters will be used routinely as is the case for CCSD(T)-F12, which has been benchmarked for small molecular systems in the last decade.As an application, we mapped the 3D-PES of benzonitrile–He weakly bound complex in Jacobi coordinates. This 3D-PES is very anisotropic along these coordinates. It was subsequently incorporated into quantum close coupling scattering computations to deduce the rotational (de-)excitation of benzonitrile colliding with He at E = 10 cm−1. These dynamical calculations are also challenging due to the strong anisotropy of benzonitrile–He 3D-PES and the high density of benzonitrile rotational levels even at low collision energies.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors extend their appreciation to the Researchers Supporting Project number (RSPD2023R808) King Saud University, Riyadh, Saudi Arabia. BM, PZ and DK acknowledge the National Science Center for support (Sonata Bis 9, grant no. 2019/34/E/ST4/00 407). The authors are also grateful for financial support from the Programme National “Physique et Chimie du Milieu Interstellaire” (PCMI) of the Centre National de la Recherche Scientifique (CNRS)/Institut National des Sciences de l’Univers (INSU) and the Institut de Chimie (INC)/Institut de Physique (INP), co-funded by the Commissariat à l’Energie Atomique (CEA) and Centre National d’Etudes Spatiales (CNES). We thank the COST Action CA21101 – Confined Molecular Systems: From a new generation of materials to the stars (COSY) of the European Community for support.References
- J. Tennyson, J. Chem. Phys., 2016, 145, 120901 CrossRef PubMed.
- C. Hampel, K. Peterson and H.-J. Werner, Chem. Phys. Lett., 1992, 190, 1 CrossRef CAS.
- M. J. O. Deegan and P. J. Knowles, Chem. Phys. Lett., 1994, 227, 321 CrossRef CAS.
- P. J. Knowles, C. Hampel and H.-J. Werner, J. Chem. Phys., 1993, 99, 5219 ( J. Chem. Phys. , 2000 , 112 , 3106 ) CrossRef CAS , Erratum.
- E. Roueff and F. Lique, Chem. Rev., 2013, 113, 8906 CrossRef CAS PubMed.
- Y. J. Bomble, J. F. Stanton, M. Kállay and J. J. Gauss, Chem. Phys., 2005, 123, 054101 Search PubMed.
- F. Lique, J. Klos and M. Hochlaf, Phys. Chem. Chem. Phys., 2010, 12, 15672 RSC.
- Y. Ajili, K. Hammami, N.-E. Jaidane, M. Lanza, Y. N. Kalugina, F. Lique and M. Hochlaf, Phys. Chem. Chem. Phys., 2013, 15, 10062 RSC.
- Y. N. Kalugina, I. A. Buryak, Y. Ajili, A. A. Vigasin, N.-E. Jaidane and M. Hochlaf, J. Chem. Phys., 2014, 140, 234310 CrossRef PubMed.
- M. Mogren Al Mogren, O. Denis-Alpizar, D. Ben Abdallah, T. Stoecklin, P. Halvick, M.-L. Senent and M. Hochlaf, J. Chem. Phys., 2014, 141, 044308 CrossRef PubMed.
- M. Hochlaf, Phys. Chem. Chem. Phys., 2017, 19, 21236 RSC.
- L. Kong, F. A. Bischoff and E. F. Valeev, Chem. Rev., 2012, 112, 75 CrossRef CAS PubMed.
- S. Demes, F. Lique, A. Faure and C. Rist, J. Chem. Phys., 2020, 153, 094301 CrossRef CAS PubMed.
- E. Quintas-Sánchez, R. Dawes and O. Denis-Alpizar, Mol. Phys., 2021, 119, e1980234 CrossRef.
- L. Wang, X.-L. Zhang, Y. Zhai, M. Nooijen and H. Li, J. Chem. Phys., 2020, 153, 054303 CrossRef CAS PubMed.
- M. Qin, H. Zhu and H. Fan, J. Chem. Phys., 2017, 147, 084309 CrossRef PubMed.
- A. Faure, P. J. Dagdigian, C. Rist, R. Dawes, E. Quintas-Sánchez, F. Lique and M. Hochlaf, ACS Earth Space Chem., 2019, 3, 964 CrossRef CAS.
- A. Ben Krid, Y. Ajili, D. Ben Abdallah, M. Dhib, H. Aroui and M. Hochlaf, J. Chem. Phys., 2021, 154, 094304 CrossRef CAS PubMed.
- K. Dzenis, A. Faure, B. A. McGuire, A. J. Remijan, P. J. Dagdigian, C. Rist, R. Dawes, E. Quintas-Sánchez, F. Lique and M. Hochlaf, Astrophys. J., 2021, 926, 3 CrossRef.
- Z. Chen, K.-C. Lau, G. A. Garcia, L. Nahon, D. K. Božanić, L. Poisson, M. Mogren Al-Mogren, M. Schwell, J. S. Francisco, A. Bellili and M. Hochlaf, J. Am. Chem. Soc., 2016, 138, 16596 CrossRef CAS PubMed.
- B. Jeziorski and M. Van Hemert, Mol. Phys., 1976, 31, 713 CrossRef CAS.
- S. Rybak, B. Jeziorski and K. Szalewicz, J. Chem. Phys., 1991, 95, 6576 CrossRef CAS.
- B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887 CrossRef CAS.
- R. Moszynski, B. Jeziorski, S. Rybak, K. Szalewicz and H. L. Williams, J. Chem. Phys., 1994, 100, 5080 CrossRef CAS.
- T. Korona, J. Chem. Theory Comput., 2009, 5, 2663 CrossRef CAS PubMed.
- E. G. Hohenstein and C. D. Sherrill, J. Chem. Phys., 2010, 133, 104107 CrossRef PubMed.
- M. P. Metz, K. Piszczatowski and K. Szalewicz, J. Chem. Theory Comput., 2016, 12, 5895 CrossRef CAS PubMed.
- https://www.astrochymist.org/astrochymist_ism.html .
- B. A. McGuire, Astrophys. J., Suppl. Ser., 2022, 259, 30 CrossRef.
- B. A. McGuire, P. B. Carroll, R. A. Loomis, I. A. Finneran, P. R. Jewell, A. J. Remijan and G. A. Blake, Science, 2016, 352, 1449 CrossRef CAS PubMed.
- B. A. McGuire, A. M. Burkhardt, S. Kalenskii, C. N. Shingledecker, A. J. Remijan, E. Herbst and M. C. McCarthy, Science, 2018, 359, 202 CrossRef CAS PubMed.
- L. R. Liu, P. B. Changala, M. L. Weichman, Q. Liang, J. Toscano, J. Klos, S. Kotochigova, D. J. Nesbitt and J. Ye, PRX QUANTUM, 2022, 3, 030332 CrossRef.
- V. F. Lotrich, R. J. Bartlett and I. Grabowski, Chem. Phys. Lett., 2005, 405, 43 CrossRef CAS.
- M. de Oliveira Bispo and D. A. da Silva Filho, J. Mol. Mod., 2022, 28, 121 CrossRef PubMed.
- J. G. Ángyán and I. C. Gerber, Phys. Rev. A., 2005, 72, 012510 CrossRef.
- T. L. Fischer, M. Bödecker, S. M. Schweer, J. Dupont, V. Lepère, A. Zehnacker-Rentien, M. A. Suhm, B. Schröder, T. Henkes, D. M. Andrada, R. M. Balabin, H. K. Singh, H. P. Bhattacharyya, M. Sarma, S. Käser, K. Töpfer, L. I. Vazquez-Salazar, E. D. Boittier, M. Meuwly, G. Mandelli, C. Lanzi, R. Conte, M. Ceotto, F. Dietrich, V. Cisternas, R. Gnanasekaran, M. Hippler, M. Jarraya, M. Hochlaf, N. Viswanathan, T. Nevolianis, G. Rath, W. A. Kopp, K. Leonhard and R. A. Mata, Phys. Chem. Chem. Phys., 2023, 25, 22089 RSC.
- J. Cui, Z. Li and R. V. Krems, J. Chem. Phys., 2015, 143, 154101 CrossRef PubMed.
- V. F. Lotrich, R. J. Bartlett and I. Grabowski, Chem. Phys. Lett., 2005, 405, 43 CrossRef CAS.
- K. Wohlfart, M. Schnell, J. W. Grabow and J. Küpper, J. Mol. Spec., 2008, 247, 119 CrossRef CAS.
- A. Badri, L. Shirkov, N.-E. Jaidane and M. Hochlaf, Phys. Chem. Chem. Phys., 2019, 21, 15871 RSC.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796 CrossRef CAS.
- A. G. Császár and G. Fogarasi, Spectroc. Acta A, 1989, 45A, 845 CrossRef.
- MOLPRO version, 2015, https://www.molpro.net.
- SAPT2020 by R. Bukowski et al. See https://www.physics.udel.edu/~szalewic/SAPT/SAPT.html for more details.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553 CrossRef CAS.
- D. Kats, J. Chem. Phys., 2014, 141, 061101 CrossRef PubMed.
- H.-J. Werner, T. B. Adler and F. R. Manby, J. Chem. Phys., 2007, 126, 164102 CrossRef PubMed.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- D. Kats, D. Kreplin, H.-J. Werner and F. R. Manby, J. Chem. Phys., 2005, 142, 064111 CrossRef PubMed.
- K. E. Yousaf and K. A. Peterson, J. Chem. Phys., 2008, 129, 184108 CrossRef PubMed.
- J. Šponer and P. Hobza, Chem. Phys. Lett., 1997, 267, 263 CrossRef.
- R. Moszynski, B. Jeziorski and K. Szalewicz, Int. J. Quant. Chem., 1993, 45, 409 CrossRef CAS.
- E. G. Hohenstein and C. D. Sherrill, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 304 CAS.
- K. Patkowski, K. Szalewicz and B. Jeziorski, J. Chem. Phys., 2006, 125, 154107 CrossRef PubMed.
- J. M. Waldrop and K. Patkowski, J. Chem. Phys., 2006, 154, 024103 CrossRef PubMed.
- T. M. Parker, L. A. Burns, R. M. Parrish, A. G. Ryno and C. D. Sherrill, J. Chem. Phys., 2014, 140, 094106 CrossRef PubMed.
- A. J. Misquitta, R. Bukowski and K. Szalewicz, J. Chem. Phys., 2000, 112, 5308 CrossRef CAS.
- R. Moszynski, T. G. H. Heijmen and B. Jeziorski, Mol. Phys., 1996, 88, 741 CAS.
- A. J. Misquitta, B. Jeziorski and K. Szalewicz, Phys. Rev. Lett., 2003, 91, 033201 CrossRef PubMed.
- A. J. Misquitta, R. Podeszwa, B. Jeziorski and K. Szalewicz, J. Chem. Phys., 2005, 123, 214103 CrossRef PubMed.
- A. Heßelmann and G. Jansen, Chem. Phys. Lett., 2003, 367, 778 CrossRef.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8, e1327 Search PubMed.
- G. L. Stoychev, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2017, 13, 554 CrossRef CAS PubMed.
- R. van Leeuwen and E. J. Baerends, Phys. Rev. A, 1994, 49, 2421 CrossRef CAS PubMed.
- M. P. Metz and K. Szalewicz, J. Chem. Theory Comput., 2020, 16, 2317 CrossRef CAS PubMed.
- R. Bukowski, W. Cencek, P. Jankowski, M. Jeziorska, B. Jeziorski, M. P. Metz, R. Moszynski, K. Patkowski, R. Podeszwa, F. Rob, S. Rybak, K. Szalewicz, H. L. Williams, R. J. Wheatley, P. E. S. Wormer and P. Zuchowski, “SAPT2016: An ab initio program for symmetry-adapted perturbation theory.” See https://www.physics.udel.edu/~szalewic/SAPT/index.html.
- J. Garcia, R. Podeszwa and K. Szalewicz, J. Chem. Phys., 2020, 152, 184109 CrossRef CAS PubMed.
- K. Aidas, et al. , WIREs Comput. Mol. Sci., 2014, 4, 269 CrossRef CAS PubMed.
- M. Wernli, L. Wiesenfeld, A. Faure and P. Valiron, Astron. Astrophys., 2007, 464, 1147 CrossRef CAS.
- J. M. Hutson and S. Green, 1994, MOLSCAT computer code, version 14. Collaborative Computational Project No. 6 of the Engineering and Physical Sciences Research Council, UK.
- G. Wlodarczak, J. Burie, J. Demaison, K. Vormann and A. G. Császár, J. Mol. Spectrosc., 1989, 134, 297 CrossRef CAS.
- J. M. Hutson and C. R. Le Sueur, Comput. Phys. Commun., 2019, 241, 9 CrossRef CAS.
- D. E. Manolopoulos, J. Chem. Phys., 1986, 85, 6425 CrossRef CAS.
- A. Faure, K. Szalewicz and L. Wiesenfeld, J. Chem. Phys., 2011, 135, 024301 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02720a |
| This journal is © the Owner Societies 2023 |





