Protein network centralities as descriptor for QM region construction in QM/MM simulations of enzymes

Abstract

The construction of a suitable QM region is the most crucial step in setting up hybrid quantum mechanics/molecular mechanics (QM/MM) simulations for enzymatic reactions. The QM region should ideally include all important amino acids residues, while being as small as possible to save computational effort. Most available methods for systematic QM region construction are based either on the distance of single amino acids to the active site or on their electrostatic effect. Such approaches might miss non-electrostatic and long-range allosteric interactions. Here, we present a proof of concept study for the application of protein network analysis to tackle this problem. Specifically, we explore the use of the protein network centralities as descriptor for QM region construction. We find that protein network centralities, in particular the betweenness centrality, can be a useful descriptor for systematic QM region construction. We show that in combination with our previously developed point charge variation analysis, they can be used to identify important residues that are missed in purely electrostatic approaches.

---

The hybrid quantum mechanics/molecular mechanics (QM/MM) approach¹ is widely used for the investigation of enzymatic reactions.^2–6 It combines the quantum-mechanical (QM) accuracy for the active center with the molecular-mechanical (MM) efficiency for its protein environment.^7–10

For simulation scientists, setting up a QM/MM calculation requires many manual choices. Most important is the selection of the QM region.^11–15 A suitable QM subsystem should ideally take into account all effects which have to be investigated in the quantum-mechanical calculation, while its size should be as small as possible to minimize the computational effort.

Several different approaches for the systematic construction of suitable QM regions have been reported in the past (for a recent review, see ref. 16). In the simplest case, only catalytic or active site residues are included. This can be extended by including further residues based on their distance to the active site. However, this approach on the one hand might miss important residues and on the other hand include residues which do not have a significant effect. Therefore, systematic methods have been developed to exclusively detect high-impact residues. Commonly, these consider the electrostatic effect of single amino acids on the active site. Examples of such approaches include charge deletion analysis (CDA),^17,18 charge shift analysis (CSA),¹⁴ and Fukui shift analysis (FSA).¹⁹ Point charge variation analysis (PCVA),²⁰ recently developed by us based on uncertainty quantification of the electrostatic effect of single amino acids on the QM/MM reaction energy, also falls into this category.

However, such approaches based solely on distance criteria or the electrostatic effect might miss residues that play an important steric role or take part in covalent interactions along allosteric pathways in enzymes. This is particularly relevant if the structure of the active site changes along the reaction path, which is not captured by a purely electrostatic analysis. Hix et al. used an analysis of evolutionary conserved residues in protein families to identify such residues and to systematically construct QM regions based on this information.²¹ However, this approach relies on the availability of protein sequence data for families of proteins that are related to a system of interest.

Here, we present a novel approach to detect residues with a high allosteric effect based on graph theory for proteins. Specifically, we propose and explore the use of the protein network centralities as descriptor for systematic QM region construction. This can be combined with one of the aforementioned methods based on electrostatic effects. In the present work, we will focus on the comparison and combination with our previously developed PCVA approach.^20,22

Graph theory can be applied to proteins to investigate long-range interactions and dynamics. A common approach is to represent the amino acids as nodes connected by edges which are weighted by the distance or other more complex descriptors such as interaction energies or correlated motion. In the literature numerous examples can be found in which network approaches are used to describe protein dynamics,^23–25 for the construction of coarse-graining models of proteins,^26–28 or to partition proteins into fragments for quantum-chemical subsystem methods.^29–32

Here, we follow an approach that has previously been employed for finding and characterizing allosteric pathways in proteins.^33–35 A graph representation is constructed using the graph generation part of the WISP (Weighted Implementation of Suboptimal Paths) script developed by Wart et al.³⁶ The C_α atoms are chosen as nodes, which are connected by edges, to which weights (corresponding to a distance in “network space” between the nodes) are assigned according to

w_ij = −log|C_ij| (1)

with

That is, nodes i and j are connected by a short edge (w_ij → 0) if the fluctuations Δr(t) = r(t) − 〈r(t)〉 of their C_α atoms along a molecular dynamics trajectory are highly correlated (C_ij → +1) or anticorrelated (C_ij → −1). Conversely, a long distance is assigned to edges (w_ij → ∞) between nodes if their fluctuations are uncorrelated. This graph is further simplified by removing edges between residues without any atom pair distance below the contact map cutoff p_cutoff = 4.5 Å as described in ref. 36.

The resulting graph can be analyzed using network analysis tools. An important concept in network analysis is the so-called centrality. In this concept, ranks are assigned to nodes within a network graph according to their position and in consequence, the centrality acts as an indicator for the importance of a node (i.e., of a single amino acid) in the network.

Three different centrality approaches will be considered in this work. The degree centrality^37,38 (d) is the simplest approach and corresponds to the number of connections of a specific node. A more complex concept is called betweenness centrality^37,39 (b) which quantifies how often a node is crossed on the shortest pathway between two other nodes. The third concept, the eigenvector centrality^35,37 (e), quantifies the influence of a certain node by assigning a relative score which takes into account that a connection to a high-scoring node contributes more to the score than a connection to nodes with a lower score.

We applied this approach to catechol O-methyltransferase (COMT) since it is a well-understood system regarding systematic QM region construction. The graph was constructed based on a classical MD trajectory (see Computational Details) using WISP³⁶ as described above. Based on this graph, we calculated the d-, b-, and e-centralities for each single amino acid. These are visualized in Fig. 1, where a representation of the residue–active site center-of-mass distances is included for comparison.

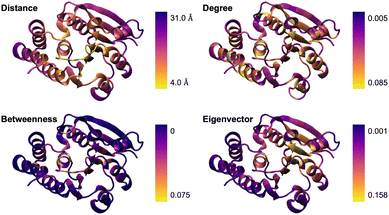Fig. 1 Visual comparison of residue–active site center-of-mass distances and of the degree, betweenness, and eigenvector centralities for catechol O-methyltransferase (COMT).

The simple d-centrality does not follow a clear trend regarding the correlation between residue position and assigned centrality value. The b- and e-centrality approaches assign low centrality values to surface residues, which matches the expected behavior since the corresponding nodes rarely appear in paths along the graph and are not able to form connections to other high-scoring nodes. Overall, the centrality value distribution for b-centrality reasonably matches the distance distribution, which still is an important measure in QM region construction. This indicates that betweenness is the most sensible approach to be used in the following.

Centrality rankings for each centrality descriptor are listed in Table S1 in the ESI† and can be compared to the indicator ranking from our single amino acid PCVA (saaPCVA) approach.^20,22 The saaPCVA indicator combines the electrostatic effect of each amino acid on the QM/MM reaction energy with its inverse center-of-mass distance and was used in our previous work to systematically construct QM regions.

There are clearly remarkable differences between the three centrality rankings. To pick one example, VAL170 is ranked 14th and 18th in the e- and d-centrality, respectively, but was assigned to rank 83 in the b-centrality. Based on the comparison with the PCVA ranking, b-centrality seems to be most promising as it is able to detect a few residues also ranked very high by the PCVA scheme such as ALA66 or ASP140, and it additionally assigns high ranks to residues which are expected to be quite important and which have been previously detected by the CSA and FSA approaches of Kulik and co-workers^14,19 such as GLU63 or TYR70.

Several residues such as MET75 or MET136 ranked very high by b-centrality can be found in the midfield of the PCVA ranking at rank 79 and 81, respectively. Additionally, their low scores in CSA and FSA (MET136 is not considered in CSA) indicate a small electrostatic effect. Nevertheless, both methionine side chains are positioned towards the active site and especially MET75 is proximal to SER71, which was considered to have an important effect on SAM.¹⁹ Since the network analysis approach aims at identifying additional residues which do not primarily apply a high electrostatic effect, but are crucial in allosteric interactions, we assume these amino acids to be interesting to be included in the QM region.

To further verify these observations, we constructed atom-economical 16-residue QM regions based on the three centrality rankings by including the corresponding highest-ranked residues and performed QM/MM calculations analogous to the previous assessment of the atom-economical PCVA-constructed QM regions.^20,22 Since d-centrality often assigns the same value to more than one residue, in this case, the QM region contains 17 residues to cover all equally-ranked residues. The different QM regions are visualized at the bottom of Fig. 2, and their composition is listed in the ESI† in Table S3. Comparisons to previous PCVA results concerning QM/MM reaction energies and VDD ligand charges are shown in Fig. 2. Here, it emerges that the b-centrality performs much better than the d- or e-centrality. The reaction energy (Fig. 2B and D) using the b-centrality (about −13.5 kcal mol⁻¹) is closer to the best estimate at −10.5 kcal mol⁻¹ than for the d-centrality (−4 kcal mol⁻¹) and the e-centrality (−7 kcal mol⁻¹). Regarding VDD charges (Fig. 2A and C), the atom-economical QM region constructed based on the b-centrality is able to reproduce the best estimate charges for Mg²⁺ and CAT, similar to PCVA. In contrast, the QM regions based on the d- and e-centrality assign an about 0.2 higher charge for Mg²⁺ and CAT compared to the best estimate. Regarding the VDD charge of the SAM ligand, none of the methods is able to assign a charge near to the best estimate, as previously observed for PCVA.²⁰ Nevertheless, using the b-centrality ranking pushes the charge from around zero to a positive charge of about 0.6, indicating the ability to detect SAM-impacting residues, even though the charge is overestimated here. Overall, the b-centrality seems to be the most promising centrality descriptor for QM region construction.

Fig. 2 Ligand VDD charges and reaction energies from QM/MM calculations for COMT using QM regions of increasing size constructed using PCVA (upper part, adapted from ref. 20) and for atom-economical 16-residue QM regions constructed using PCVA as well as centrality-based descriptors (middle part). In the bottom part, the different QM regions are visualized without ligands. (A) Convergence of Mg²⁺ (blue), SAM (magenta) and CAT (yellow) VDD charges with increasing QM region size. (B) Convergence of the QM/MM reaction energy for the methyl transfer reaction in COMT with increasing QM region size. Best estimate results (corresponding to QM region 9′) are indicated by a solid horizontal line. (C) Ligand VDD charges for atom-economical 16-residue QM regions (indicated by dashed vertical line in A) constructed using different centrality-based descriptors. (D) QM/MM reaction energies for atom-economical 16-residue QM regions (indicated by dashed vertical line in B) constructed using different centrality-based descriptors.

With these results in mind, we constructed two different atom-economical, 16-residue QM regions in a hybrid PCVA/b-centrality approach. One QM region, referred to as b-half, was constructed by including the highest-ranked eight residues from PCVA and the b-centrality approach, respectively. If a residue detected by one scheme is already ranked higher in the other scheme, it is replaced by the next lower-ranked residue in this scheme. The second QM region, referred to as b-norm, is constructed by normalizing the two descriptors with respect to each other. Since the differences in the assigned PCVA indicators and b-centralities, respectively, of the highest-ranked residues are quite large, the first 5 residues of each scheme are included analogously to the b-half scheme, and all other descriptors for rank 6 and lower are normalized with respect to the rank 5 value. The six remaining places in the 16-residue QM region are then awarded to the six residues with the highest normalized value of any of the two descriptors.

These two QM regions are again compared to the best estimate with respect to VDD ligand charges and the QM/MM reaction energy (see Fig. 2C and D). Regarding VDD charges, b-half and b-norm perform similar to PCVA for Mg²⁺ and CAT. In contrast to PCVA, both b-half and b-norm are able to predict a positive ligand charge for SAM, where b-norm still overestimates the charge while b-half underestimates it. Nevertheless, for b-half the SAM charge of about 0.1 is closer to the best estimate than for all PCVA or centrality-based approaches considered so far. Concerning the reaction energy, b-norm, delivers an energy of about −20 kcal mol⁻¹ which is close to the PCVA but about 10 kcal mol⁻¹ below the best estimate. Here, the b-half approach outperforms all other methods with −9.5 kcal mol⁻¹, nearly perfectly reproducing the best estimate.

These results give first hints that protein network centralities, in particular the betweenness centrality, can be a useful descriptor for the systematic construction of QM regions. Besides residues that have a large electrostatic effect (and which are also detected by other schemes such as PCVA), the b-centrality ranking detects specific residues that have large non-electrostatic effects. As shown above, the inclusion of such residues in systematically constructed atom-economical QM regions can improve the agreement with our best estimate, both for ligand charges and for reaction energies.

To further ensure the applicability of the centrality-based and hybrid methods, we additionally applied the identical procedure to the triosephosphate isomerase (TIM), which was also subject to our previous investigations.²² These results are shown and discussed in Section S3 of the ESI† and confirm the general trends observed for COMT, even though the agreement for the QM/MM calculations using a 16-residue, atom-economical QM region with the best estimate is worse.

Overall, we have shown that protein network centralities, in particular the betweenness centrality, are a promising descriptor for the systematic construction of QM regions. The b-centrality allows one to identify residues that have important non-electrostatic or allosteric effects on the active site, and that are thus missed by descriptors that only consider the direct, electrostatic effect, such as our previously developed PCVA scheme. Therefore, we propose to augment QM regions constructed using PCVA with residues that have a high b-centrality, for which two simple schemes have been proposed.

In future work, we plan to further refine these hybrid schemes. To this end, it will be crucial to further rationalize the usefulness of protein network centralities as descriptor for QM region construction by systematically analyzing the electrostatic and non-electrostatic effects that contribute to the error in QM/MM reaction energies.

More generally, network analysis offers a promising framework for systematic QM region construction. Here, we employed the construction of graphs based on the correlated motion of the amino acid residues, which allows for the identification of allosteric pathways. Other schemes for the construction of graphs, e.g. based on electrostatic interactions, could be considered and subjected to the tools of network analysis to minimize the error introduced by QM/MM schemes. Work along these lines is currently in progress in our group.

Computational details

For the calculation of centrality descriptors, molecular dynamics (MD) simulations were performed using GROMACS 2019.3^40,41 with the AMBER99SB-ILDN⁴² force field. The different substrates were parametrized using Antechamber^43,44 and acpype.^45,46 The systems were minimized and equilibrated (see Section S1 in the ESI†) to obtain the initial structures used in our previous work.^20,22 These were used as starting point for a productive 100 ns MD simulation resulting in 10 000 frames as basis for graph construction.

The analysis of results was achieved with Python. Network analysis and centrality calculations were also performed in Python using the WISP script³⁶ for correlation matrix and contact map construction and the networkx module^47,48 for calculating d-, b- and e-centralities. Plots were generated with Matplotlib^49,50 and structures were visualized using Visual Molecular Dynamics (VMD).⁵¹

QM regions using PCVA were constructed as shown in our previous work (using the standard variant).^20,22 Residues included in the differently-sized QM regions for each system are listed in the ESI† (see Section S2) with the corresponding QM region charge and the number of atoms and link atoms.

All QM/MM calculations used the minimized and equilibrated initial structures (see above) obtained in our previous work,^20,22 from which geometry optimizations were performed for reactants and products. All QM/MM calculations were performed using the Amsterdam Modeling Suite (AMS Version 2020.203),⁵² using PBE⁵³ and a DZ and a TZP Slater-type orbital basis set⁵⁴ for geometry optimizations and single point calculations, respectively. For the MM region the ForceField engine of AMS was used with the AMBER95 force field,⁵⁵ which was extended by parameters for the substrates. All charges are calculated from the Voronoi deformation density (VDD)⁵⁶ of the reactant structures only. Further details are given in the ESI† (see Section S1).

Data availability

Data for this paper, including the Python script for WISP and centrality analysis, the PDB files of the starting structures, the modified AMBER95 force field for the use with AMS, substrate, and ion AMS fragment files, as well as the AMS input files for all geometry optimizations and single point calculations, are available at Zenodo at https://10.5281/zenodo.8023313.

Author contributions

Felix Brandt: conceptualization (equal), investigation (lead), software (lead), visualization (lead), writing – original draft (lead), writing – review and editing (equal). Christoph R. Jacob: conceptualization (equal), writing – review and editing (equal).

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. A. Warshel and M. Levitt, Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme, J. Mol. Biol., 1976, 103, 227–249.
2. M. W. van der Kamp and A. J. Mulholland, Combined Quantum Mechanics/Molecular Mechanics (QM/MM) Methods in Computational Enzymology, Biochemistry, 2013, 52, 2708–2728.
3. K. Swiderek, I. Tunon and V. Moliner, Predicting enzymatic reactivity: from theory to design, WIREs Comput. Mol. Sci., 2014, 4, 407–421.
4. M. G. Quesne, T. Borowski and S. P. de Visser, Quantum Mechanics/Molecular Mechanics Modeling of Enzymatic Processes: Caveats and Breakthroughs, Chem. – Eur. J., 2016, 22, 2562–2581.
5. S. F. Sousa, A. J. M. Ribeiro, R. P. P. Neves, N. F. Brás, N. M. F. S. A. Cerqueira, P. A. Fernandes and M. J. Ramos, Application of quantum mechanics/molecular mechanics methods in the study of enzymatic reaction mechanisms, WIREs Comput. Mol. Sci., 2017, 7, e1281.
6. S. Ahmadi, L. B. Herrera, M. Chehelamirani, J. Hostaš, S. Jalife and D. R. Salahub, Multiscale modeling of enzymes: QM-cluster, QM/MM, and QM/MM/MD: A tutorial review, Int. J. Quantum Chem., 2018, 118, e25558.
7. M. J. Field, P. A. Bash and M. Karplus, A combined quantum mechanical and molecular mechanical potential for molecular dynamics simulations, J. Comput. Chem., 1990, 11, 700–733.
8. J. Gao in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, VCH, New York, 1995, vol. 7, pp. 119–185.
9. G. Groenhof in Biomolecular Simulations: Methods and Protocols, Methods in Molecular Biology, ed. L. Monticelli and E. Salonen, Humana Press, Totowa, NJ, 2013, pp. 43–66.
10. U. Ryde in Methods in Enzymology, Computational Approaches for Studying Enzyme Mechanism Part A, ed. G. A. Voth, Academic Press, 2016, vol. 577, pp. 119–158.
11. C. V. Sumowski and C. Ochsenfeld, A Convergence Study of QM/MM Isomerization Energies with the Selected Size of the QM Region for Peptidic Systems, J. Phys. Chem. A, 2009, 113, 11734–11741.
12. D. Flaig, M. Beer and C. Ochsenfeld, Convergence of Electronic Structure with the Size of the QM Region: Example of QM/MM NMR Shieldings, J. Chem. Theory Comput., 2012, 8, 2260–2271.
13. G. Jindal and A. Warshel, Exploring the Dependence of QM/MM Calculations of Enzyme Catalysis on the Size of the QM Region, J. Phys. Chem. B, 2016, 120, 9913–9921.
14. H. J. Kulik, J. Zhang, J. P. Klinman and T. J. Martínez, How Large Should the QM Region Be in QM/MM Calculations? The Case of Catechol O-Methyltransferase, J. Phys. Chem. B, 2016, 120, 11381–11394.
15. R. Mehmood and H. J. Kulik, Both Configuration and QM Region Size Matter: Zinc Stability in QM/MM Models of DNA Methyltransferase, J. Chem. Theory Comput., 2020, 16, 3121–3134.
16. K.-S. Csizi and M. Reiher, Universal QM/MM approaches for general nanoscale applications, WIREs Comput. Mol. Sci., 2023, e1656.
17. P. A. Bash, M. J. Field, R. C. Davenport, G. A. Petsko, D. Ringe and M. Karplus, Computer simulation and analysis of the reaction pathway of triosephosphate isomerase, Biochemistry, 1991, 30, 5826–5832.
18. R.-Z. Liao and W. Thiel, Convergence in the QM-only and QM/MM modeling of enzymatic reactions: A case study for acetylene hydratase, J. Comput. Chem., 2013, 34, 2389–2397.
19. M. Karelina and H. J. Kulik, Systematic Quantum Mechanical Region Determination in QM/MM Simulation, J. Chem. Theory Comput., 2017, 13, 563–576.
20. F. Brandt and C. R. Jacob, Systematic QM Region Construction in QM/MM Calculations Based on Uncertainty Quantification, J. Chem. Theory Comput., 2022, 18, 2584–2596.
21. M. A. Hix, E. M. Leddin and G. A. Cisneros, Combining Evolutionary Conservation and Quantum Topological Analyses To Determine Quantum Mechanics Subsystems for Biomolecular Quantum Mechanics/Molecular Mechanics Simulations, J. Chem. Theory Comput., 2021, 17, 4524–4537.
22. F. Brandt and Ch. R. Jacob, Efficient automatic construction of atom-economical QM regions with point-charge variation analysis, Phys. Chem. Chem. Phys., 2023, 25, 14484–14495.
23. C. Böde, I. A. Kovács, M. S. Szalay, R. Palotai, T. Korcsmáros and P. Csermely, Network analysis of protein dynamics, FEBS Lett., 2007, 581, 2776–2782.
24. M. Fossépré, L. Leherte, A. Laaksonen and D. P. Vercauteren, in Biomolecular Simulations in Structure-Based Drug Discovery, ed. F. L. Gervasio and V. Spiwok, John Wiley & Sons, Ltd, 2018, pp. 105–161.
25. L. Franke and C. Peter, Visualizing the Residue Interaction Landscape of Proteins by Temporal Network Embedding, J. Chem. Theory Comput., 2023, 19, 2985–2995.
26. M. Chakraborty, C. Xu and A. D. White, Encoding and selecting coarse-grain mapping operators with hierarchical graphs, J. Chem. Phys., 2018, 149, 134106.
27. P. I. Diggins, C. Liu, M. Deserno and R. Potestio, Optimal Coarse-Grained Site Selection in Elastic Network Models of Biomolecules, J. Chem. Theory Comput., 2019, 15, 648–664.
28. M. A. Webb, J.-Y. Delannoy and J. J. de Pablo, Graph-Based Approach to Systematic Molecular Coarse-Graining, J. Chem. Theory Comput., 2019, 15, 1199–1208.
29. M. von Looz, M. Wolter, Ch. R. Jacob and H. Meyerhenke in Lecture Notes in Computer Science, Experimental Algorithms, ed. A. V. Goldberg and A. S. Kulikov, Springer International Publishing, 2016, pp. 353–368.
30. M. Zheng, N. W. Moriarty, Y. Xu, J. R. Reimers, P. V. Afonine and M. P. Waller, Solving the scalability issue in quantum-based refinement: Q|R#1, Acta Cryst. D, 2017, 73, 1020–1028.
31. A. Kumar, N. DeGregorio and S. S. Iyengar, Graph-Theory-Based Molecular Fragmentation for Efficient and Accurate Potential Surface Calculations in Multiple Dimensions, J. Chem. Theory Comput., 2021, 17, 6671–6690.
32. M. Wolter, M. von Looz, H. Meyerhenke and Ch. R. Jacob, Systematic Partitioning of Proteins for Quantum-Chemical Fragmentation Methods Using Graph Algorithms, J. Chem. Theory Comput., 2021, 17, 1355–1367.
33. A. Romero-Rivera, M. Garcia-Borràs and S. Osuna, Role of Conformational Dynamics in the Evolution of Retro-Aldolase Activity, ACS Catal., 2017, 7, 8524–8532.
34. M. A. Maria-Solano, J. Iglesias-Fernández and S. Osuna, Deciphering the Allosterically Driven Conformational Ensemble in Tryptophan Synthase Evolution, J. Am. Chem. Soc., 2019, 141, 13049–13056.
35. C. F. A. Negre, U. N. Morzan, H. P. Hendrickson, R. Pal, G. P. Lisi, J. P. Loria, I. Rivalta, J. Ho and V. S. Batista, Eigenvector centrality for characterization of protein allosteric pathways, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E12201–E12208.
36. A. T. Van Wart, J. Durrant, L. Votapka and R. E. Amaro, Weighted Implementation of Suboptimal Paths (WISP): An Optimized Algorithm and Tool for Dynamical Network Analysis, J. Chem. Theory Comput., 2014, 10, 511–517.
37. M. E. J. Newman, The New Palgrave Dictionary of Economics, Palgrave Macmillan, UK, London, 2016, pp. 1–8.
38. L. C. Freeman, Centrality in social networks conceptual clarification, Social Networks, 1978, 1, 215–239.
39. L. C. Freeman and A. Set, of Measures of Centrality Based on Betweenness, Sociometry, 1977, 40, 35–41.
40. D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, GROMACS: Fast, flexible, and free, J. Comput. Chem., 2005, 26, 1701–1718.
41. Gromacs Version 2019.6, 2020 DOI:10.5281/zenodo.3685922, http://www.gromacs.org/.
42. K. Lindorff-Larsen, S. Piana, K. Palmo, P. Maragakis, J. L. Klepeis, R. O. Dror and D. E. Shaw, Improved side-chain torsion potentials for the Amber ff99SB protein force field, Proteins: Struct., Funct., Bioinf., 2010, 78, 1950–1958.
43. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25, 1157–1174.
44. J. Wang, W. Wang, P. A. Kollman and D. A. Case, Automatic atom type and bond type perception in molecular mechanical calculations, J. Mol. Graphics Model., 2006, 25, 247–260.
45. A. W. Sousa da Silva and W. F. Vranken, ACPYPE - AnteChamber PYthon Parser interfacE, BMC Res. Notes, 2012, 5, 367.
46. Acpype, 2021, https://github.com/alanwilter/acpype.
47. A. A. Hagberg, D. A. Schult, and P. J. Swart, in Proceedings of the 7th Python in Science Conference (SciPy2008), ed. G. Varoquaux, T. Vaught, and J. Millman, Pasadena, CA USA, 2008, pp. 11–15.
48. networkx Version 2.6.3, 2021, https://networkx.org.
49. J. D. Hunter, Matplotlib: A 2D Graphics Environment, Comput. Sci. Eng., 2007, 9, 90–95.
50. Matplotlib Version 3.4.2, 2021 DOI:10.5281/zenodo.4743323, https://matplotlib.org.
51. W. Humphrey, A. Dalke and K. Schulten, VMD – Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14, 33–38.
52. Software for Chemistry and Materials, Amsterdam, Ams, Amsterdam Modelling Suite, 2020, http://www.scm.com.
53. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865.
54. E. Van Lenthe and E. J. Baerends, Optimized Slater-type basis sets for the elements 1-118, J. Comput. Chem., 2003, 24, 1142–1156.
55. W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules, J. Am. Chem. Soc., 1995, 117, 5179–5197.
56. C. Fonseca Guerra, J.-W. Handgraaf, E. J. Baerends and F. M. Bickelhaupt, Voronoi deformation density (VDD) charges: Assessment of the Mulliken, Bader, Hirshfeld, Weinhold, and VDD methods for charge analysis, J. Comput. Chem., 2004, 25, 189–210.

---

Footnote

† Electronic supplementary information (ESI) available: Extended computational details, additional results for triosephosphate isomerase (TIM), supplementary tables showing descriptor rankings as well as the compositions of the different considered QM regions. See DOI: https://doi.org/10.1039/d3cp02713a

---