Elucidating local diffusion dynamics in nickel-rich layered oxide cathodes

Abstract

Elucidating Li-ion transport properties is essential for designing suitable methodologies to optimise electrochemical performance in Ni-rich cathodes for high energy density Li-ion batteries. Here, we report the local-scale Li-diffusion characteristics of a series of nickel-rich layered oxide cathodes, prepared via microwave methods, using muon spin relaxation methods. Our results detail the effects of cation dopants, selected for structure stability, on transport properties in candidate nickel-rich chemistries. We find that the local diffusion properties improve with increasing nickel content. Our results demonstrate that these observations are dependant on substitutional effects.

---

1. Introduction

Ni-rich layered oxide materials are attractive high energy density cathodes for Li-ion batteries for electric vehicle (EV) applications.^1–3 Building on the archetypal transition metal layered oxide cathodes LiCoO₂ and LiNi_1/3Mn_1/3Co_1/3O₂ (NMC111), the development of Ni-rich layered oxides affords higher specific capacities at stable voltages.^4–6 The layered oxides LiMO₂ (M = Ni, Mn, Co) adopt the rhombohedral R3̄m space group, isostructural with α-NaFeO₂. Transition metal and lithium ions are located in octahedral 3b and 3a sites respectively, where oxygen anions occupy the 6c sites to form a cubic close-packed array with M and Li arranged in separate, alternating layers.⁷ Upon increasing the Ni-content, LiNi_0.8Mn_0.1Co_0.1O₂ (NMC811) delivers higher discharge capacities than LiNi_0.6Mn_0.2Co_0.2O₂ (NMC622) when cycled under identical conditions, but NMC622 benefits from enhanced stabilities owing to its lower nickel content.^8–10

Ni-rich variants require that synthetic parameters be carefully considered to deliver high quality materials.^11,12 Co-precipitation from stoichiometric amounts of transition metal salts by addition of base is the typical approach for preparing a metal hydroxide precursor, followed by calcination with a lithium source to deliver the final Li-containing layered oxide.¹³ Controlled temperatures and treatment times, alongside an oxygen-rich atmosphere, are critical during the calcination process to stabilize Ni³⁺, failure of which can result in excess Ni²⁺ and the promotion of anti-site mixing between 3a Li⁺ and 3b Ni²⁺ which can be detrimental to the cycling performance.^14–16 Doping with electrochemically inactive cations such as Al³⁺ or Mg²⁺ is one route to stabilising cycling performance, with dopants predicted to sit in the 3b and 3a sites respectively.^17,18 The presence of Al³⁺ on Ni sites is thought to improve thermal stability and mitigate anti-site mixing while small quantities of Mg²⁺ occupying sites in the Li layer imparts structural stability through pillaring.^19–24 There is also a need to develop more sustainable synthetic approaches, aimed at limiting synthesis energy demands while still producing high-quality materials with tailored particle morphologies. One example of this is the development of microwave-assisted strategies which can afford faster, lower temperature routes to energy storage materials.^25–28 These faster synthetic routes can also allow for morphology tailoring which may influence structural stability and Li⁺ diffusion processes.

Underpinning the whole cycling process is the motional behavior of Li⁺ ions through the structure. In NMCs, 2-dimensional Li⁺ diffusion takes place in the interlayer.²⁹ Here, there are two pathways available for Li⁺ diffusion represented in Fig. 1. These can be understood by considering a hop of length a from one Li site to a neighboring site. For fully lithiated materials, this pathway is unviable and a second pathway of length a/√3 must be considered where Li⁺ moves into an interstitial site within the interlayer.

Fig. 1 Projection onto the lithium containing ab plane for LiMO₂ (M = Ni, Mn, Co) showing the two different jump paths available for Li⁺ diffusion. Pathway 1 involves a jump to an adjacent Li site with a distance of a and the pathway 2 involves a jump to an interstitial site with distance a/√3.

Here, we investigate the influence of dopants on Li⁺ diffusion properties in NMC622 and NMC811 cathodes prepared by faster microwave methods. Traditional approaches to ion transport measurement includes impedance or titration methods which probe macro-scale diffusional properties but can be susceptible to sample processing conditions and surface effects.^30,31 Here, we apply muon spin relaxation (μ⁺SR) as a local probe of ion diffusion in doped Ni-rich cathodes which offers advantages over traditional approaches and has been successfully applied previously to study battery materials.^{25,28,32–40} For example, paramagnetic species do not complicate μ⁺SR due to the fact that electronic and nuclear contributions to the relaxation process can be separated.⁴¹ Operating on a time scale of 10⁻⁵ to 10⁻⁸ s, μ⁺SR is perfectly primed to probe the consecutive short range jumps between interstitial sites in a structure that characterize Li⁺ diffusion.³⁴

2. Experimental section

Synthetic procedures

Microwave assisted sol–gel synthesis of NMC622, NMC811 and doped NMC811 powders. Stoichiometric amounts of Ni(CH₃CO₂)₂·4H₂O, Mn(CH₃CO₂)₂·4H₂O, Co(CH₃CO₂)₂·4H₂O and Li(CH₃CO₂) (10 mol% excess of Li) powders were weighed out dissolved in deionised H₂O. Appropriate amounts of Al(NO₃)₃·9H₂O or Mg(CH₃CO₂)₂·4H₂O were dissolved in this step for the doped samples to obtain 1 mol% dopant in total. To this, a solution of fully dissolved citric acid (with a transition metal to citric acid molar ratio of 1 : 2) was added and the resultant sol was stirred magnetically on a stirrer-hot plate at 150 °C in order to evaporate the solvent, with a viscous gel obtained at the end. The gel was then pre-dried at ≈300 °C in a heating mantle to obtain a black coloured ash. The ash was transferred to an alumina crucible and heated in air at 450 °C for 14 hours to remove carbon species originating from the acetate groups and the citric acid. The precursor was transferred to an alumina crucible and heated in a CEM Phoenix microwave furnace (2.45 GHz) and heated at 850 °C for 2 hours. Black powders of NMC were obtained and stored in an Ar filled glovebox prior to use.

Materials characterisation

Powder X-ray diffraction and Rietveld refinements. Powder X-ray diffraction (PXRD) characterization of the NMC samples was carried out using a Rigaku MiniFlex diffractometer in reflection mode using Cu Kα radiation operated at 40 kV and 15 mA. Data were collected in a 2θ range 10 to 70° in step sizes of 0.02°. Rietveld refinements were carried out using GSAS-II.⁴² The refinement was carried out in the general following order: (i) background, (ii) scale factor, (iii) cell parameters, (iv) sample displacement, (v) profile parameters, (vi) Ni occupancy in Li sites where the total Ni content was constrained to 0.8 in NMC811 or 0.6 in NMC622.

Muon spin relaxation measurements. Muon experiments were carried out on the EMU instrument at ISIS Neutron and Muon Source. Powders of NMC622, NMC811 and doped NMC811 (ca. 0.5–1 g for each sample) were transferred to titanium sample holders with a titanium foil window where titanium is chosen as it is a weak depolarizer of muons. Samples were exposed to a beam of spin polarized, positively charged muons, resulting in muon implantation within the sample.⁴³ After rapid thermalization, muons preferentially stop at electronegative sites within the structure.³⁴ For transition metal layered oxides the muon implantation site is predicted to be close to O²⁻ anions in the structure, where muons sit in interstitial sites with a typical bond length of d_μ–O ≈ 1.12 Å with all stopping sites roughly equivalent from an electrostatic viewpoint.³⁹ While implanted, the muon spin direction experiences both a local field distribution (Δ) caused by surrounding static nuclear magnetic environments and a fluctuation rate (ν) induced by the motion of surrounding nuclei.³² For lithium ion cathodes, ν is largely affected by Li⁺ diffusion. These effects cause a depolarization of the muon spin ensemble over time. With a mean lifetime of 2.2 μs the implanted muon decays into a positron and two neutrinos via a three-body process governed by the weak interaction. As a result of the violation of parity conservation, the positron is emitted preferentially in the same direction as the muon spin direction at the instant of decay.^43,44 The time evolution of the positron asymmetry thus, can be directly linked to the time evolution of the muon spin relaxation which in itself reveals the ion dynamics in the system. Eqn (1) demonstrates how positron asymmetry A(t) can be determined through counting detected positrons in forward (N_F) and backward detector (N_B) banks placed around the sample such thatwhere α is a correction factor to compensate for efficiency discrepancies between the two detector banks.⁴⁴

Measurements were carried out over a temperature range of 100 K to 400 K to encapsulate a low temperature baseline where the ionic motion is too slow to be observed and the thermally activated region where Li⁺ cations overcome the energetic barriers opposing ionic transport and move on timescales the muon can probe. At each temperature, measurements were performed at zero field (ZF) and with applied longitudinal fields (LFs) of 5 G and 10 G. For all samples discussed here, the data were fit using a baseline asymmetry to account for the background (A_bg) and an exponentially relaxing signal accounting for initial fast relaxation from localised 3d electrons on the cations multiplying the dynamical form of the Gaussian Kubo–Toyabe (KT) relaxation function (A_KT) that describes the dynamic nuclear magnetic fields such that

A₀P(t) = A_bg + A_KTG_KT(Δ, ν, t, H_LF)e^−λt (2)

where A_bg and A_KT are the respective amplitudes of the two components and G_KT is the dynamic form of the KT function with a Gaussian distribution, which is sensitive to the trend of the static field distribution width at the muon stopping site (Δ) and the field fluctuation rate (ν) with time (t) and the applied longitudinal field (H_LF). The field fluctuation rate here is caused from the local field seen by the muon from nearby Li⁺ ion diffusion. For each sample, eqn (2) was fit to all three datasets (ZF, 5 G LF and 10 G LF) simultaneously to isolate the contributions to the asymmetry signal from Li⁺ hopping and lead to more reliable determinations of ν and Δ parameters. The relaxation rate λ was determined at 300 K for each sample and was fixed for subsequent fitting. Data fitting was completed using the WiMDA program.⁴⁵

3. Results and discussion

The time evolution of the decay positron asymmetry from data collected at 300 K for the NMC811, NMC622 and the 1 mol% Al- and Mg-doped NMC811 samples (with respective targeted stoichiometries of LiNi_0.79Al_0.01Mn_0.1Co_0.1O₂ and Li_0.99Mg_0.01Ni_0.8Mn_0.1Co_0.1O₂) are shown in Fig. 2 with corresponding fits represented by solid lines. All fitting parameters for the samples are shown in Tables S1–S4 (ESI†). From inspection of the asymmetry, all four samples undergo similar behavior described by the product of the two relaxation processes outlined by the applied relaxation function (eqn (2)). The form of the data suggests the convolution of the Gaussian field distribution coming from the nuclear magnetic moments and a Lorentzian field distribution that is likely to come from the paramagnetic moments. The temperature dependent Li⁺ ionic motion is apparent in the form of the data at longer times. While the possibility of μ⁺ diffusion cannot be excluded, recent μ⁻SR studies (where the negatively charged muon is immobile) have shown there is minimal difference between the field fluctuation rates for positive and negative muons to the field fluctuation rate in spinel materials.^46,47 Furthermore, the correlation found between the field fluctuation rate from μ⁺SR and the diffusion coefficient from electrochemical techniques indicates that the predominant nuclear contribution to the muon spin relaxation also originates from Li⁺ diffusion in layered oxides.³¹ Therefore, we assume the changes seen for ν in the thermally activated region for all materials studied are a consequence of changes in Li⁺ diffusion properties.

Fig. 2 Decay positron asymmetry obtained for μ⁺SR measurements conducted at 300 K for (a) NMC811, (b) NMC622, (c) A-NMC811 and (d) Mg-NMC811 powders. Data at zero field and applied longitudinal fields of 5 G and 10 G are shown alongside fits to the data using the dynamic Kubo–Toyabe function.

As the temperature increases to 400 K (Fig. S1, ESI†), more dynamic behavior persists for all four samples, indicating faster Li⁺ diffusion at higher temperatures. This observation is consistent with high temperature μ⁺SR data reported for other layered oxides.^32,38,39,48 When longitudinal fields of 5 G and 10 G are applied, the relaxation decreases with increasing field strength owing to gradual decoupling of the muon spin from the static nuclear environment. We observe that NMC622 shows a less dynamical environment (characterized by the more Kubo–Toyabe like appearance of the fits obtained) than NMC811 and suggests more sluggish Li⁺ diffusion in these lower Ni-content compositions.

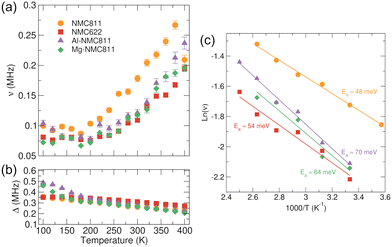
Fig. 3(a) and (b) shows the temperature dependence of the field fluctuation rate (ν) and the static field distribution width (Δ) parameters respectively for each sample. The temperature dependence of ν follow a similar trend where an initial flat (static) region is followed by an increase in ν as the temperature is raised due to the onset and gradual increase of thermally activated Li⁺ diffusion processes. For NMC811 this occurs at ≈200 K with the fluctuation rate rising sharply to a maximum ≈0.26 MHz. The fall in ν observed at 400 K for NMC811 has been observed previously and is likely due to the Li⁺ diffusion becoming too fast to detect at these elevated temperatures.^25,36 The more sluggish increase in ν seen for NMC622 in Fig. 3(a) suggests that once the energetic barriers for ionic motion are overcome, NMC811 displays a faster frequency of Li⁺ hopping than NMC622 across the thermally activated temperature range. For Al-NMC811 and Mg-NMC811, ν values obtained suggest that the dopant cations may hinder Li⁺ ionic diffusion. This effect has been highlighted by Kang and Ceder as a possible concern in designing doped compositions.⁴⁹

Fig. 3 Temperature dependence of the (a) field fluctuation rate (v) and (b) the local field distribution at the muon stopping site (Δ) for μ⁺SR data collected for NMC811, NMC622, Al-NMC811 and Mg-NMC811 samples between 100 to 400 K. Arrhenius analysis (c) over the thermally activated region yields the activation energy E_a.

At higher temperatures, all samples display similar behavior for the Δ temperature dependence. The gradual decrease is explained by a motional narrowing effect as a result of more rapid lithium diffusion as the temperature increases.³⁸ Values of Δ for NMC811 are slightly lower than those for NMC622. The muon active isotope of Ni (⁶¹Ni, 1.1% abundant, nuclear magnetic moment −0.75 μ μ_N⁻¹) has a lower nuclear magnetic moment compared to Mn (⁵⁵Mn, 100%, +3.45 μ μ_N⁻¹) and Co (⁵⁹Co, 100%, +4.63 μ μ_N⁻¹) and resultant internal nuclear fields will thus be weaker for higher Ni-content samples.⁵⁰ However, larger Δ values at lower temperatures are observed for both doped samples compared to NMC811. Both ²⁷Al (100% and +3.64 μ μ_N⁻¹) and ²⁵Mg (10% and −0.86 μ μ_N⁻¹) possess a nuclear magnetic moment which would introduce additional contributions to the local field experienced by the muon. However, as dopant levels are low, the observed effects cannot solely be explained by this. The increased value of Δ and ν below 150 K in both Mg- and Al-doped samples indicates the likelihood of additional electronic contributions from the dopant ions at low temperatures. Magnetic transition effects have been noticed at similar temperatures on commercial NMC811 and have been found to be highly sample dependent.⁵¹ During data fitting the relaxing asymmetry is found to decrease noticeably at low temperatures for the doped samples but not NMC622 and NMC811 (Tables S1–S4, ESI†), further indicating the likelihood of a magnetic transition below 150 K as a result of the inclusion of Mg and Al ions.⁵² Changes to the overall structure caused by dopant incorporation are likely to further explain the differences in Δ observed. Rietveld refinements (Fig. S3 and Table S5, ESI†) reveal changes in the a lattice parameter (indicative of changes to the average oxidation state in the TM layer), the c lattice parameter (indicative of changes in the layer spacings) and the Ni/Li mixing percentages, means that there is likely to be a complex interplay between these parameters that serves to alter the muon stopping site relative to the nuclear moments and induce changes in Δ. However, this effect is lost at higher temperatures, indicating that additional effects from motional narrowing are further likely to have an impact.

Activation energies for thermally activated Li⁺ diffusion can be calculated from an Arrhenius plot shown in Fig. 3(c). Activation energies for NMC811 and NMC622 of 48 (±2) and 54 (±6) meV respectively compare well with similar studies conducted on Li_xNi_1/3Mn_1/3Co_1/3O₂ materials³⁹ and μ⁺SR studies of NMC622 and NMC811 samples synthesized by a hydrothermal flow method.⁵³ For higher Ni-content materials, the calculated Li⁺ diffusion barriers are sensitive to the identity of the transition metal with higher Ni-content found to reduce the activation barrier.^54,55 The reasons for enhanced diffusion properties as Ni content increases in NMC materials is likely to stem from structural and electronic changes in the structure as elucidated by Wang et al.⁵⁶ For example, lattice expansion, particularly along the c-axis, is likely to facilitate easier Li⁺ hopping along the diffusion pathways, resulting in reduced barriers to Li⁺ diffusion. Furthermore, additional factors relating to the Li⁺-TM electrostatic interactions should also be considered. Increasing the Ni-content is achieved by reducing Mn⁴⁺ content which in turn decreases the strength of the interactions between the Li⁺ and the TMO₂ layer; a factor which further serves to reduce the Li⁺ diffusion barriers. It is worth noting that as a volume-averaged probe, μ⁺SR signals are dominated by intragrain, short-range Li⁺ diffusion (hops), and impeding contributions from grain boundaries and other extrinsic factors do not play a substantial role as they would in techniques such as electrochemical impedance spectroscopy. As a result, activation energies reported for μ⁺SR measurements reflect the nature of the unit cell length-scale this technique probes i.e. energies represent the fundamental energy required to motivate singular ionic hops.^34,37

To obtain diffusion coefficients, D_Li, the ionic hops that enable Li⁺ motion (Fig. 1) must be considered and eqn (3) is applied.

where N_i is the number of accessible Li⁺ sites in the available path, Z_v,i is the vacancy fraction of the destination sites, s_i is the jump distance between adjacent Li⁺ sites in the ith path and ν is the field fluctuation rate discussed previously. For layered oxides where higher neighbouring jumps are not considered, for path 1: N₁ = 6, Z_v,1 = (1-lithium occupancy) and s₁ = a and for path 2: N₂ = 3, Z_v,2 = 1 and s₂ = a/√3. For the samples studied here, it was assumed that the material was fully lithiated i.e. lithium occupancy = 1 and thus only path 2 involving hops to interstitial sites was considered. The value for a in these calculations is the a lattice parameter that is calculated from Rietveld refinements of the NMC materials. The obtained refinements and structural parameters are given in Fig. S3 and Table S5 respectively (ESI†).

Diffusion coefficients at 300 K for NMC811 and NMC622 were calculated as 1.6 ± 0.1 × 10⁻¹¹ cm² s⁻¹ and 1.0 ± 0.1 × 10⁻¹¹ cm² s⁻¹ respectively, under the assumption of first and second nearest neighbouring jumps Table 1. These values indicate that Li⁺ diffusion is faster in NMC811 compared to NMC622. For comparison, D_Li at 300 K for an NMC111 sample was reported as 3.5 × 10⁻¹² cm² s⁻¹ by Månsson et al., highlighting further the improvement in ion transport properties with increasing Ni- that we observe. These results further corroborate the enhanced Li⁺ diffusivity properties of higher Ni-content NMCs previously found through electrochemical methods.^54,56 For Al-NMC811 and Mg-NM811, activation energies of 70 (±9) and 64 (±4) meV were estimated respectively. Compared to NMC811 (E_a = 48 ± 2 meV) the results here suggest that the presence of dopant cations can introduce a higher energy barrier for singular ionic hops thus may play a role in hindering Li⁺ diffusion. Diffusion coefficients were calculated as 1.1 ± 0.1 × 10⁻¹¹ cm² s⁻¹ at 300 K for both Al-NMC811 and Mg-NMC811. Higher activation energies coupled with lower diffusion coefficients signal hindered Li⁺ diffusion in NMC811 upon the introduction of even small quantities of dopants. The presence of Mg²⁺ within the Li⁺ containing layer likely block diffusional pathways, with the higher charge density of Mg²⁺ contributing a further impedance to ionic motion. The contraction in the c parameter observed for the Al-NMC811 could lower the Li⁺ diffusion through shrinkage of the layer spacing which hinders ionic transport across the layer.^49,55 To examine any effect the material microstructure may have on the local scale diffusional properties, we carried out muon studies on commercial NMC811 and NMC622 materials (Fig. S4, S5 and Table S7, ESI†). Our results demonstrate a negligible effect indicating the μ⁺SR method is not sensitive to differing particle morphology for these samples.

Table 1 Values of E_a and D_Li at 300 K calculated for NMC811, NMC622, Al-NMC811 and Mg-NMC811 samples as obtained from μ⁺SR experiments

Sample	Composition	E a (meV)	D Li at 300 K (cm^2 s^−1)
NMC811	LiNi0.8Mn0.1Co0.1O2	48 (±2)	1.6 ± 0.1 × 10^−11
NMC622	LiNi0.6Mn0.2Co0.2O2	54 (±6)	1.0 ± 0.1 × 10^−11
Al-NMC811	LiNi0.79Al0.01Mn0.1Co0.1O2	70 (±9)	1.1 ± 0.1 × 10^−11
Mg-NMC811	Li0.99Mg0.01Ni0.8Mn0.1Co0.1O2	64 (±4)	1.1 ± 0.1 × 10^−11

---

4. Conclusions

In conclusion, we demonstrate μ⁺SR as an excellent technique to study microscopic lithium diffusion in nickel-rich cathodes. We find that even small quantities of structurally and thermally stabilizing dopants can hinder ion diffusion in these materials. These insights are useful for considering the design of new nickel-rich cathodes, where the desired stability introduced by such dopants is considered in tandem with possible implications to electrochemical performance.

Author contributions

BIIJ: conceptualisation, investigation, formal analysis, writing – original draft, writing – review and editing, visualisation, funding acquisition. IM: validation, writing – review and editing. PJB: methodology, formal analysis, resources, writing – review and editing, funding acquisition. SAC: conceptualisation, resources, writing – review and editing, supervision, funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge the ISIS Neutron and Muon Source and the Facility Access Panel for the award of beamtime (DOI: https://doi.org/10.5286/ISIS.E.RB1920560-1). Electron microscopy was performed in the Sorby Centre for Electron Microscopy at the University of Sheffield. This project was supported through the Faraday Institution projects FutureCat (FIRG017) and Degradation (FIRG001).

References

1. X. Wang, Y.-L. Ding, Y.-P. Deng and Z. Chen, Adv. Energy Mater., 2020, 10, 1903864.
2. S. G. Booth, A. J. Nedoma, N. N. Anthonisamy, P. J. Baker, R. Boston, H. Bronstein, S. J. Clarke, E. J. Cussen, V. Daramalla, M. D. Volder, S. E. Dutton, V. Falkowski, N. A. Fleck, H. S. Geddes, N. Gollapally, A. L. Goodwin, J. M. Griffin, A. R. Haworth, M. A. Hayward, S. Hull, B. J. Inkson, B. J. Johnston, Z. Lu, J. L. MacManus-Driscoll, X. M. D. I. Labalde, I. McClelland, K. McCombie, B. Murdock, D. Nayak, S. Park, G. E. Pérez, C. J. Pickard, L. F. J. Piper, H. Y. Playford, S. Price, D. O. Scanlon, J. C. Stallard, N. Tapia-Ruiz, A. R. West, L. Wheatcroft, M. Wilson, L. Zhang, X. Zhi, B. Zhu and S. A. Cussen, APL Mater., 2021, 9, 109201.
3. P. S. Grant, D. Greenwood, K. Pardikar, R. Smith, T. Entwistle, L. A. Middlemiss, G. Murray, S. A. Cussen, M. J. Lain, M. J. Capener, M. Copley, C. D. Reynolds, S. D. Hare, M. J. H. Simmons, E. Kendrick, S. P. Zankowski, S. Wheeler, P. Zhu, P. R. Slater, Y. S. Zhang, A. R. T. Morrison, W. Dawson, J. Li, P. R. Shearing, D. J. L. Brett, G. Matthews, R. Ge, R. Drummond, E. C. Tredenick, C. Cheng, S. R. Duncan, A. M. Boyce, M. Faraji-Niri, J. Marco, L. A. Roman-Ramirez, C. Harper, P. Blackmore, T. Shelley, A. Mohsseni and D. J. Cumming, J. Phys.: Energy, 2022, 4, 042006.
4. W. Li, E. M. Erickson and A. Manthiram, Nat. Energy, 2020, 5, 26–34.
5. A. Manthiram, J. C. Knight, S.-T. Myung, S.-M. Oh and Y.-K. Sun, Adv. Energy Mater., 2016, 6, 1501010.
6. J. Xu, F. Lin, M. M. Doeff and W. Tong, J. Mater. Chem. A, 2017, 5, 874–901.
7. Y. Koyama, N. Yabuuchi, I. Tanaka, H. Adachi and T. Ohzuku, J. Electrochem. Soc., 2004, 151, A1545.
8. S.-M. Bak, E. Hu, Y. Zhou, X. Yu, S. D. Senanayake, S.-J. Cho, K.-B. Kim, K. Y. Chung, X.-Q. Yang and K.-W. Nam, ACS Appl. Mater. Interfaces, 2014, 6, 22594–22601.
9. Y. Ding, Z. P. Cano, A. Yu, J. Lu and Z. Chen, Electrochem. Energy Rev., 2019, 2, 1–28.
10. R. Jung, M. Metzger, F. Maglia, C. Stinner and H. A. Gasteiger, J. Electrochem. Soc., 2017, 164, A1361.
11. M. D. Tikekar, S. Choudhury, Z. Tu and L. A. Archer, Nat. Energy, 2016, 1, 16114.
12. D. Y. Wang, J. Xia, L. Ma, K. J. Nelson, J. E. Harlow, D. Xiong, L. E. Downie, R. Petibon, J. C. Burns, A. Xiao, W. M. Lamanna and J. R. Dahn, J. Electrochem. Soc., 2014, 161, A1818.
13. T. Entwistle, E. Sanchez-Perez, G. J. Murray, N. Anthonisamy and S. A. Cussen, Energy Rep., 2022, 8, 67–73.
14. Y. Bi, W. Yang, R. Du, J. Zhou, M. Liu, Y. Liu and D. Wang, J. Power Sources, 2015, 283, 211–218.
15. Y. Koyama, H. Arai, I. Tanaka, Y. Uchimoto and Z. Ogumi, Chem. Mater., 2012, 24, 3886–3894.
16. H. Yu, Y. Qian, M. Otani, D. Tang, S. Guo, Y. Zhu and H. Zhou, Energy Environ. Sci., 2014, 7, 1068–1078.
17. K. Min, S.-W. Seo, Y. Y. Song, H. S. Lee and E. Cho, Phys. Chem. Chem. Phys., 2017, 19, 1762–1769.
18. T. Weigel, F. Schipper, E. M. Erickson, F. A. Susai, B. Markovsky and D. Aurbach, ACS Energy Lett., 2019, 4, 508–516.
19. Z. Huang, Z. Wang, X. Zheng, H. Guo, X. Li, Q. Jing and Z. Yang, Electrochim. Acta, 2015, 182, 795–802.
20. H. Li, P. Zhou, F. Liu, H. Li, F. Cheng and J. Chen, Chem. Sci., 2019, 10, 1374–1379.
21. S. Madhavi, G. V. Subba Rao, B. V. R. Chowdari and S. F. Y. Li, J. Power Sources, 2001, 93, 156–162.
22. S. W. Woo, S. T. Myung, H. Bang, D. W. Kim and Y. K. Sun, Electrochim. Acta, 2009, 54, 3851–3856.
23. Q. Xie, W. Li and A. Manthiram, Chem. Mater., 2019, 31, 938–946.
24. C. Zhang, J. Wan, Y. Li, S. Zheng, K. Zhou, D. Wang, D. Wang, C. Hong, Z. Gong and Y. Yang, J. Mater. Chem. A, 2020, 8, 6893–6901.
25. T. E. Ashton, J. V. Laveda, D. A. MacLaren, P. J. Baker, A. Porch, M. O. Jones and S. A. Corr, J. Mater. Chem. A, 2014, 2, 6238–6245.
26. J. V. Laveda, V. Chandhok, C. A. Murray, G. W. Paterson and S. A. Corr, Chem. Commun., 2016, 52, 9028–9031.
27. M. Amores, S. A. Corr and E. J. Cussen, J. Electrochem. Soc., 2017, 164, A6395.
28. M. Amores, T. E. Ashton, P. J. Baker, E. J. Cussen and S. A. Corr, J. Mater. Chem. A, 2016, 4, 1729–1736.
29. A. Van der Ven, J. Bhattacharya and A. A. Belak, Acc. Chem. Res., 2013, 46, 1216–1225.
30. S. Ohno, T. Bernges, J. Buchheim, M. Duchardt, A.-K. Hatz, M. A. Kraft, H. Kwak, A. L. Santhosha, Z. Liu, N. Minafra, F. Tsuji, A. Sakuda, R. Schlem, S. Xiong, Z. Zhang, P. Adelhelm, H. Chen, A. Hayashi, Y. S. Jung, B. V. Lotsch, B. Roling, N. M. Vargas-Barbosa and W. G. Zeier, ACS Energy Lett., 2020, 5, 910–915.
31. I. Mcclelland, S. G. Booth, N. N. Anthonisamy, L. A. Middlemiss, G. E. Pérez, E. J. Cussen, P. J. Baker and S. A. Cussen, Chem. Mater., 2023, 35, 4149.
32. J. Sugiyama, K. Mukai, Y. Ikedo, H. Nozaki, M. Månsson and I. Watanabe, Phys. Rev. Lett., 2009, 103, 147601.
33. J. V. Laveda, B. Johnston, G. W. Paterson, P. J. Baker, M. G. Tucker, H. Y. Playford, K. M. Ø. Jensen, S. J. L. Billinge and S. A. Corr, J. Mater. Chem. A, 2018, 6, 127–137.
34. I. McClelland, B. Johnston, P. J. Baker, M. Amores, E. J. Cussen and S. A. Corr, Annu. Rev. Mater. Res., 2020, 50, 371–393.
35. I. McClelland, S. G. Booth, H. El-Shinawi, B. I. J. Johnston, J. Clough, W. Guo, E. J. Cussen, P. J. Baker and S. A. Corr, ACS Appl. Energy Mater., 2021, 4, 1527–1536.
36. J. Sugiyama, H. Nozaki, M. Harada, K. Kamazawa, Y. Ikedo, Y. Miyake, O. Ofer, M. Månsson, E. J. Ansaldo, K. H. Chow, G. Kobayashi and R. Kanno, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 054111.
37. P. J. Baker, I. Franke, F. L. Pratt, T. Lancaster, D. Prabhakaran, W. Hayes and S. J. Blundell, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 174403.
38. J. Sugiyama, Y. Ikedo, K. Mukai, H. Nozaki, M. Månsson, O. Ofer, M. Harada, K. Kamazawa, Y. Miyake, J. H. Brewer, E. J. Ansaldo, K. H. Chow, I. Watanabe and T. Ohzuku, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 224412.
39. J. Sugiyama, K. Mukai, M. Harada, H. Nozaki, K. Miwa, T. Shiotsuki, Y. Shindo, S. R. Giblin and J. S. Lord, Phys. Chem. Chem. Phys., 2013, 15, 10402–10412.
40. B. I. J. Johnston, P. J. Baker and S. A. Cussen, J. Phys. Mater., 2021, 4, 044015.
41. R. S. Hayano, Y. J. Uemura, J. Imazato, N. Nishida, T. Yamazaki and R. Kubo, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 20, 850–859.
42. B. H. Toby and R. B. Von Dreele, J. Appl. Crystallogr., 2013, 46, 544–549.
43. S. J. Blundell, Contemp. Phys., 1999, 40, 175–192.
44. L. Nuccio, L. Schulz and A. J. Drew, J. Phys. D: Appl. Phys., 2014, 47, 473001.
45. F. L. Pratt, Phys. B, 2000, 289–290, 710–714.
46. I. Umegaki, K. Ohishi, T. Nakano, S. Nishimura, S. Takeshita, A. Koda, K. Ninomiya, M. K. Kubo and J. Sugiyama, J. Phys. Chem. C, 2022, 126, 10506–10514.
47. J. Sugiyama, K. Ohishi, O. K. Forslund, M. Månsson, S. P. Cottrell, A. D. Hillier and K. Ishida, Z. Phys. Chem., 2022, 236, 799–816.
48. M. Månsson, H. Nozaki, J. M. Wikberg, K. Prša, Y. Sassa, M. Dahbi, K. Kamazawa, K. Sedlak, I. Watanabe and J. Sugiyama, J. Phys.: Conf. Ser., 2014, 551, 012037.
49. K. Kang and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 094105.
50. N. J. Stone, At. Data Nucl. Data Tables, 2005, 90, 75–176.
51. P. Mukherjee, J. A. M. Paddison, C. Xu, Z. Ruff, A. R. Wildes, D. A. Keen, R. I. Smith, C. P. Grey and S. E. Dutton, Inorg. Chem., 2021, 60, 263–271.
52. C. T. Kaiser, V. W. J. Verhoeven, P. C. M. Gubbens, F. M. Mulder, I. De Schepper, A. Yaouanc, P. Dalmas De Réotier, S. P. Cottrell, E. M. Kelder and J. Schoonman, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, R9236–R9239.
53. T. E. Ashton, P. J. Baker, C. Sotelo-Vazquez, C. J. M. Footer, K. M. Kojima, T. Matsukawa, T. Kamiyama and J. A. Darr, J. Mater. Chem. A, 2021, 9, 10477–10486.
54. H.-J. Noh, S. Youn, C. S. Yoon and Y.-K. Sun, J. Power Sources, 2013, 233, 121–130.
55. Y. Wei, J. Zheng, S. Cui, X. Song, Y. Su, W. Deng, Z. Wu, X. Wang, W. Wang, M. Rao, Y. Lin, C. Wang, K. Amine and F. Pan, J. Am. Chem. Soc., 2015, 137, 8364–8367.
56. S. Wang, M. Yan, Y. Li, C. Vinado and J. Yang, J. Power Sources, 2018, 393, 75–82.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02662k

---