 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Solid state 1H, 7Li, and 13C NMR studies on new ionic plastic crystals of crown ether–Li-TFSA complexes†
Akira
Kobayashi
a,
Jun
Yamagami
b,
Subham
Ranjan
 a,
Satoshi
Takamizawa
a,
Satoshi
Takamizawa
 ab and
Hisashi
Honda
ab and
Hisashi
Honda
 *ab
*ab
aGraduate School of Nanobioscience, Yokohama City University, Kanazawa-ku, Yokohama, 236-0027, Japan
bFaculty of Science, Yokohama City University, Kanazawa-ku, Yokohama, 236-0027, Japan
First published on 26th September 2023
Abstract
This study provides the first evidence that a Li ion can form ionic plastic crystals using crown ether with a bis-(trifluoromethanesulphonyl) amide (TFSA) anion. 1H, 7Li, and 13C nuclear-magnetic-resonance (NMR) measurements of the 15-crown-5–Li-TFSA complex revealed that the constituents underwent isotropic reorientation in the plastic crystalline phase. The NMR data of the 12-crown-4–Li-TFSA salt showed that the complex is a rotator crystal (the complexes are denoted as [Li 15C5] and [Li 12C4] in this paper). The X-ray diffraction (XRD) reflection patterns of the [Li 15C5] crystal recorded in the highest-temperature solid phase (plastic phase) could be indexed to a cubic structure. Conversely, [Li 12C4] could be fitted to a trigonal structure. In this study, [M (3n)Cn] (M = Li, Na, K; n = 4–6) complexes were also prepared, and NMR, DSC, XRD, and electrical conductivity measurements were performed. Based on these results, we additionally revealed that the [Na 15C5] and [K (15C5)2] complexes are also new rotator crystals. Single-crystal XRD measurements also revealed that the [Na 15C5] compound has two stable sites in the crystal. Activation energies of molecular motions in the [M (3n)Cn] crystals were estimated using 1H NMR relaxation time (T1 and T2) measurements. The electrical conductivity measurements of [Li 12C4], [Li 15C5], and [Na 15C5] showed high ionic conductivities (∼10−2 S cm−1).
Introduction
Some compounds (fullerene, adamantane, tetrachloromethane, etc.) have a mesophase between the solid and liquid phases,1–6 although many chemicals (such as H2O) directly transform from a solid state to a liquid state by heating at ambient pressure. Mesophases can generally be classified into three categories: plastic, rotator, and liquid crystals. In the liquid crystal phase, the orientation of the constituents is ordered; however, their gravity point is disordered (fused). Conversely, in the plastic crystal phase, the orientation of the constituents is disordered in three dimensions and the gravity point is ordered (solidifying). Thus, plastic crystals are often referred to as crystals with liquid characteristics. If the constituents perform an uniaxial rotation in the crystal (orientational disorder in two dimensions), it is called the rotator phase. Owing to the similarities between plastic and rotator crystals, a few researchers treat rotator crystals as plastic crystals. In this literature, the word ‘plastic crystal’ is distinguished from the rotator crystal. In plastic crystals, the isotropic reorientation motion of constituents results in small entropy changes at the melting point (ΔmpS). A relationship of ΔmpS < 21 J K−1 mol−1 has been reported (in the literature, ΔmpS < 5 cal deg−1 is described),7 and many plastic crystals satisfy this condition. In addition to isotropic reorientation, the constituents can jump to lattice defects with low activation energies. This translational motion causes plasticity in solid materials. Based on this property, ionic plastic crystals can often be applied in the development of new solid electrolytes as replacements for current organic and polymer solvents. In contrast, there have been scarce reports on the utilization of rotator crystals in the advancement of novel solid electrolytes. It can be considered that the constituents in the rotator phase typically perform translational jumps within a plane perpendicular to the axis of uniaxial rotation (2D diffusion). Bis-(trifluoromethanesulphonyl) amide (TFSA) (Fig. 1) can form ionic liquids with cations.8–13 Therefore, ionic plastic crystals have been investigated in TFSA salts with alkylammonium, bis-quaternary ammonium, pyrrolidinium, etc.14–16 It has also been reported that ionic conductivities reach 10−2 S cm−1 when a Li-TFSA salt is doped into plastic crystals, ionic liquids, polymers, etc.17–22Many researchers have actively developed ionic conductors using plastic crystals; however, plastic crystals formed by alkali metal ions have been rarely reported without MNO2 (M = K, Rb, and Cs).23–26 We have proposed that both globular cations and anions undergo isotropic reorientation if the Coulomb force acting among the ions is sufficiently weak, similar to a molecular plastic crystal. Based on this idea, we have found many new ionic plastic crystals in tetraalkylammonium salts26–31 and 4-aza-1-azoniabicyclo[2.2.2]octane, 1-alkyl (denoted as [N-R DABCO], R = Me, Et) compounds32 with [BEt3Me]− and [BEt4]− counter anions. Here, the alkyl groups of the cation and anion act as spacers between the N and B atoms which can be assumed to be the centres of charge. In addition, a novel chemical family of [n-CxH(2x+1)NEt3][BEt3Me], which has plastic (x = 1–5), rotator (x = 6, 7), and ionic liquid crystals (8 ≤ x ≤ 16), has been developed.33 Based on this proposal, it is expected that plastic crystals constructed using alkali metal ions can be obtained if a clathrate compound with alkali metal ions is prepared.
It is well known that crown ethers can form complexes with alkali metal ions. Abu-Lebdeh et al. reported that Li-TFSA salts form ionic plastic crystals with crown ethers of 12-crown-4 and 18-crown-634 (We have abbreviated [(3n)-crown-n ether–M-TFSA] complexes as [M (3n)Cn] (M = Li, Na, K; n = 4–6) in this paper, e.g. [Li 12C4], [Li 18C6], and [K (12C4)2]). Abu-Lebdeh et al. based their assignment of plastic crystals only on the DSC results: ΔmpS values of 44.5 J K−1 mol−1 at 418 K ([Li 12C4]) and 4.5 J K−1 mol−1 at 332 K ([Li 18C6]). The former is larger than the proposed value of 21 J K−1 mol−1; however, the authors explained that the flexibility of the anion chains results in a large ΔmpS value.34 Another research group measured the IR spectra, Raman spectra, DSC curves, and ionic conductivities of [Li 12C4], [Li 15C5], and [Li 18C6].35 These studies show that [Li 12C4] and [Li 18C6] crystals have a high ionic conductivity of 10−5∼10−4 S cm−1; however, no information about molecular motions has been reported. An essential characteristic of plastic crystals is ‘isotropic reorientation’; hence, the utilization of nuclear magnetic resonance (NMR) data is imperative for investigating plastic crystals.
In this study, solid-state 1H, 7Li, and 13C NMR spectra and relaxation times were measured as a function of temperature in powdered samples of [M (3n)Cn] (M = Li, Na, K; n = 4–6) salts to obtain information on molecular motions. In the case of solid-state 1H NMR spectra, information about the interactions among the constituents is obtained because the line widths of the signals are mainly determined by dipole–dipole interactions between the 1H nuclei. The line breadth is frequently estimated using the second moment of the spectrum (M2). A relationship of M2 < 1 G2 is often reported in plastic crystals because of the constituents' jump to lattice defects in addition to isotropic reorientation.36,37 The 1H NMR spin–lattice relaxation time (T1) and spin–spin relaxation time (T2) provided information about the motion frequencies and diffusion of the constituents, respectively. In the case of the 7Li nucleus (I = 3/2), a central transition signal accompanied by two satellite peaks beside itself (a first-order line pattern of a nucleus with I = 3/2) can be recorded in ordinal crystals.38 However, it can be expected that a 7Li signal without satellite peaks is detected in plastic crystals (the quadrupole coupling constant (QCC) is zero) because the isotropic reorientation of the constituents results in an isotropic electric field gradient (EFG) at the nucleus. In solid-state 13C NMR spectra of ordinal compounds, line shapes with chemical shift anisotropy (CSA) are generally recorded. However, averaging the three components of the chemical shift (CS) tensor (σxx, σyy, and σzz) results in a Lorentz-type line shape in the spectrum if the constituents exhibit isotropic reorientation in the crystal (plastic phase). Solid-state NMR measurements of other crown ether complexes have been reported, including 13C CP/MAS (CP: cross-polarisation and MAS: magic angle spinning) NMR absorption curves of 18-crown-6 crystals and 18-crown-6–2LiOPh, –NaNCS·H2O, and –KSCN complexes,39 and 7Li NMR spectra of 12-crown-4–LiCl, –LiBr, and –LiNO3 complexes.40 The latter literature reveals that a crystal of the 12-crown-4–LiCl complex shows typical 7Li NMR line shapes for first-order quadrupolar interactions with a QCC of 60 kHz at 300 K. Previous studies show that two 13C NMR signals recorded at 69 and 70.5 ppm (240 K) reduced to one signal at 325 K in a crystal of the 18-crown-6–KSCN complex and explain this result in terms of exchange speed between two different conformational structures of the crown ether ring. Based on these data, it is expected that the 12-crown-4–LiCl and 18-crown-6–KSCN complexes do not form plastic crystals. In addition to these two studies, a model of the merry-go-round rotation of crown ether rings has been proposed by 2H NMR measurements of partially deuterated 15-crown-5–NaI, 15-crown-5–NaClO4, and 21-crown-7–KI solids.41 In the case of 1H NMR spectra, only a few studies have been reported on crown ether crystals. Gotoh et al. reported the narrow solid-state 1H NMR spectra with a M2 of ∼0 for 15-crown-5 and 18-crown-6 with Na and K in graphite intercalation compounds and revealed their molecular dynamics.42 As described above, NMR spectroscopy is a powerful tool for determining the motional modes of crown ether complexes in crystals.
For our target samples, Shriver et al. reported Tmp values of 370, 352, and 302 K for [Li 12C4], [Li 15C5], and [Li 18C6], respectively.35 By contrast, Abu-Lebdeh et al. reported Tmp values of 418 and 332 K for [Li 12C4] and [Li 18C6], respectively.34 Additionally, Shriver et al. showed a glass transition at 223 K in the [Li 18C6] crystal; however, this glass transition was not observed in the study reported by Abu-Lebdeh et al. (they detected a first-order transition at 243 K). In the case of the other complexes of [M (3n)Cn] (M = Na, K. n = 4–6), we could not obtain DSC data; therefore, we prepared complexes of [M (3n)Cn] (M = Li, Na, K; n = 4–6) and performed DSC measurements. In this study, we used the symbols Ttr1 and Ttr2 to indicate the phase-transition temperatures within the solid phase upon moving from higher to lower temperatures, and the symbols Δtr1S and Δtr2S at each transition temperature. The characteristics of Phase I, Phase II, etc. indicate the solid phase starting from a high temperature.
X-ray diffraction (XRD) measurements of powder and single-crystal samples provide beneficial information for plastic crystal studies because ionic plastic crystals normally have NaCl- and CsCl-type cubic structures (occasionally, tetragonal, trigonal, etc.43). It has been reported that 12-crown-4 can form not only [Li 12C4] but also [Li (12C4)2].44 A sandwich structure is also expected in [Na (12C4)2] and [K (15C5)2] because the ionic radii of Na+ at 95–120 pm and K+ at 133–144 pm are slightly larger than the cavity radius of 12-crown-4 at 72–81 pm and 15-crown-5 at 86–110 pm, respectively.45
In this study, we prepared [M (3n)Cn] (M = Li, Na, K.; n = 4–6) and performed solid-state NMR, DSC, XRD, and conductivity measurements.
Results and discussion
DSC
The DSC thermograms of each crown ether complex are plotted in Fig. 2 and Fig. S1 (ESI†). Since plastic crystals frequently have metastable phases, each sample was heated from ca. 200 K to just above the melting temperature (the first heating run), successively cooled from the temperature to ca. 200 K, and heated again from ca. 200 K (the second heating run). Because the same curves as those in the first heating scan were recorded in the second heating run, as displayed in Fig. S1 (ESI†), the phase transition temperatures and enthalpy changes were determined from the data of the second heating scan. The transition temperatures (Ttr1, Ttr2, …) and entropy changes (Δtr1S, Δtr2S, …) obtained from the DSC measurements are listed in Table 1. The melting temperatures were checked using test-tube observations. In the case of [Na (12C4)2], [K (15C5)2], and [Li 18C6], these compounds decomposed below each melting temperature. The decomposition temperatures were determined by thermogravimetric (TG) measurements. For [Li 12C4], the DSC curves were similar to those reported for Tmp = 418 K, Ttr1 = 362 K, Ttr2 = 164 K, and ΔmpS = 44.5 J K−1 mol−1.34 In the reported studies, these temperatures were estimated by each peak top of the DSC curves; in contrast, we determined the temperatures by each rising edge of each signal. Therefore, a slight difference from the reference value was tolerated. In the case of [Li 18C6], a reference showed endothermic peaks at 243 K, 302 K, and Tmp = 322 K;34 in contrast, another paper reported a glass transition at 220 K and Tmp = 309 K.35 Our data, however, showed no endothermic signal in the temperature range of 300–330 K as shown in Fig. S1 (ESI†), although preparation was attempted many times. Since previous reports also show different results (one reports glass transition and the other shows first-order transition at around 243 K),34,35 it can be considered that [Li 18C6] has some stable states, and another state was obtained in this study. In the case of [Li 15C5], Tmp has only been reported at 356 K.35 This value was similar to our data; however, we also recorded Ttr1 at 337 K. In addition, an exothermic peak was detected at 300 K. This signal was also recorded in the first heating run, as displayed in Fig. S1 (ESI†). Because plastic crystals frequently have metastable states and show exothermic peaks during the heating process,26–33 it can be considered that this exothermic peak corresponds to a phase transition from a metastable state to a stable state. In general, plastic crystals show small ΔmpS values (< 21 J K−1 mol−1);7 however, slightly larger ΔmpS values were obtained for [Li 15C5], as displayed in Table 1. In contrast, other complexes such as [Li 12C4] and [Na 15C5] showed large ΔmpS values.| Δtr3S | Δtr2S | Δtr1S | ΔmpS | |
|---|---|---|---|---|
| *Dec.: Decomposed. | ||||
| [Li 12C4] | 8.8 ± 0.1 (170 ± 1) | 7.3 ± 0.1 (351 ± 1) | 31.6 ± 0.1 (400 ± 1) | |
| [Na (12C4)2] | 19.5 ± 0.5 (436 ± 1) | Dec. (ca. 460) | ||
| [Li 15C5] | −11.5 ± 0.5 (300 ± 1) | 18.8 ± 0.1 (337 ± 1) | 29.2 ± 0.1 (358 ± 1) | |
| [Na 15C5] | 7.8 ± 0.1 (358 ± 1) | 13.1 ± 0.1 (361 ± 1) | 3.6 ± 0.1 (374 ± 1) | 35.7 ± 0.5 (405 ± 1) |
| [K (15C5)2] | 1.23 ± 0.01 (219 ± 1) | 0.57 ± 0.05 (356 ± 1) | Dec. (ca. 440) | |
| [Li 18C6] | The second order transition (213 ± 1) | Dec. (ca. 385) | ||
| [Na 18C6] | 79.4 ± 0.1 (381 ± 1) | |||
| [K 18C6] | 57.9 ± 0.1 (425 ± 1) | |||
XRD
The powder XRD patterns of the complexes recorded at various temperatures are shown in Fig. 3. The reflection patterns detected in Phase I of [Li 15C5] could be indexed to a cubic structure (a space group of Pn![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) with a lattice constant of a = 1381 ± 5 pm. This result suggests that both the crown ether and the TFSA anion perform isotropic reorientation in the crystal because these molecules have no C3-axis in themselves. Thus, [Li 15C5] could be used as a new ionic plastic crystal. In the case of Phases II and III of [Li 15C5], powder patterns similar to those of Phase I were recorded; therefore, it can be expected that the overall motion of the constituents also occurs in the low-temperature solid phases. In contrast, the powder patterns recorded in Phase I of [Li 12C4] and [Na 15C5] can be fitted by the trigonal structure of P3. Lattice constants of a = 928 ± 5, c = 892 ± 5, a = 977 ± 5, and c = 1799 ± 5 were obtained for [Li 12C4] and [Na 15C5], respectively. In the case of the [Li 18C6] crystal, the crystal structure of Phase I could not be uniquely determined. Because the sample showed that the fluidity and the XRD pattern were similar to that observed in liquid crystals, it can be considered that Phase I of [Li 18C6] is a liquid crystalline phase. The other complexes showed complex diffraction patterns, and a unique crystal structure could not be assigned.
) with a lattice constant of a = 1381 ± 5 pm. This result suggests that both the crown ether and the TFSA anion perform isotropic reorientation in the crystal because these molecules have no C3-axis in themselves. Thus, [Li 15C5] could be used as a new ionic plastic crystal. In the case of Phases II and III of [Li 15C5], powder patterns similar to those of Phase I were recorded; therefore, it can be expected that the overall motion of the constituents also occurs in the low-temperature solid phases. In contrast, the powder patterns recorded in Phase I of [Li 12C4] and [Na 15C5] can be fitted by the trigonal structure of P3. Lattice constants of a = 928 ± 5, c = 892 ± 5, a = 977 ± 5, and c = 1799 ± 5 were obtained for [Li 12C4] and [Na 15C5], respectively. In the case of the [Li 18C6] crystal, the crystal structure of Phase I could not be uniquely determined. Because the sample showed that the fluidity and the XRD pattern were similar to that observed in liquid crystals, it can be considered that Phase I of [Li 18C6] is a liquid crystalline phase. The other complexes showed complex diffraction patterns, and a unique crystal structure could not be assigned.
1H NMR spectra
Solid-state NMR measurements were performed to assign the motional modes of each compound. The 1H NMR spectra of the complexes are shown in Fig. 4. Narrow line widths are observed, although these signals accumulate without MAS modulation. In general, 1H NMR lines with narrow line widths are difficult to obtain without a high-speed MAS method in ordinal crystals because of the large dipole–dipole interactions among the 1H nuclei. Because Lorentz-type lines with narrow linewidths were detected in Phase I of the [Li 15C5] and [Li 18C6] compounds, it can be considered that the constituents undergo overall motion with large amplitudes (isotropic reorientation). In the case of Phases II and III of [Li 15C5], line envelopes could be fitted by two components: narrow and broad lines, as shown in Fig. S2 (ESI†) and Fig. 4 shows that the amount of the broad component increased in lower-temperature solid phases. Because H atoms are included only in crown ethers, it can be considered that there are two kinds of 15-crown-5 molecules in Phases II and III: one performs isotropic reorientation, similar to the detection in Phase I, and the other undergoes another motion with lower freedom of motion compared with isotropic reorientation. The motion contributing to a broad linewidth is discussed in the following section of 13C NMR. In the case of the [Li 12C4] salt, our 1H NMR spectrum could be separated into two components: one had a narrow linewidth and the other was broad, as plotted in Fig. S2 (ESI†). Because the NMR spectrum area corresponds to the number of sites, it can be considered that a large amount of crown ether cannot undergo isotropic reorientation in Phase I of [Li 12C4]. This is inconsistent with a previous report in which the [Li 12C4] complex was concluded to be a plastic crystal based on DSC measurements.34 A more detailed discussion of [Li 12C4] is provided in later sections. For other complexes, broad 1H NMR line envelopes were recorded (Fig. 4). In the case of [Na 15C5], two peaks were detected at ca. +8 and −3 ppm in Phase I, although the peak tops of the other samples were obtained at approximately 2 ppm. This result suggests that there are two types of crown ether with different electron densities. This discussion is presented in the following sections. In the case of [Na (12C4)2], our DSC data showed that Phase I was obtained above 436 K. Unfortunately, such high temperatures exceeded the temperature limit of our NMR apparatus; therefore, no spectrum was observed for Phase I of [Na (12C4)2]. | ||
| Fig. 4 1H NMR spectra of [M (3n)Cn] (M = Li, Na, K.; n = 4–6) crystals as a function of temperature. | ||
Molecular motion in crystals is often linked to the M2 values of the 1H NMR absorption lines. The M2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Obs values were estimated using the following relationship:36,37
Obs values were estimated using the following relationship:36,37
 | (1) |
Here, ω0 and f(ω0 − ω) are the angular frequency (rad s−1) of the peak top and line height at ω0 − ω, respectively. We analysed the lines using Lorentz functions, as displayed in Fig. S2 (ESI†) in which some data are displayed. The M2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Obs values estimated from each analysed line are summarised in Table 2. The theoretical M2
Obs values estimated from each analysed line are summarised in Table 2. The theoretical M2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cal values can be estimated using the following relationship:36,37
Cal values can be estimated using the following relationship:36,37
 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Obs (G2). These values were determined by analysing the 1H NMR lines
Obs (G2). These values were determined by analysing the 1H NMR lines
| Phase | Δν/kHz |
M
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Obs/G2 Obs/G2 |
||
|---|---|---|---|---|
| [Li 12C4] | I | 0.60 ± 0.01 | 0.39 ± 0.01 | Isotropic rotation |
| 11.2 ± 0.5 | 4.66 ± 0.05 | Uniaxial rotation | ||
| II | 6.8 ± 0.5 | 4.12 ± 0.05 | Uniaxial rotation | |
| 28.8 ± 0.5 | 8.05 ± 0.05 | |||
| [Na (12C4)2] | II | 16.6 ± 0.5 | 8.93 ± 0.05 | |
| [Li 15C5] | I | 0.18 ± 0.01 | 0.12 ± 0.01 | Isotropic rotation |
| II | 0.49 ± 0.01 | 0.32 ± 0.01 | Isotropic rotation | |
| 17.5 ± 0.5 | 9.3 ± 0.05 | |||
| III | 0.55 ± 0.01 | 0.36 ± 0.01 | Isotropic rotation | |
| 23.8 ± 0.5 | 11.7 ± 0.5 | |||
| [Na 15C5] | I | 9.4 ± 0.5 | 5.51 ± 0.05 | Uniaxial rotation |
| 8.8 ± 0.5 | 5.20 ± 0.05 | Uniaxial rotation | ||
| II | 10.3 ± 0.5 | 5.97 ± 0.05 | Uniaxial rotation | |
| 10.3 ± 0.5 | 5.97 ± 0.05 | Uniaxial rotation | ||
| III | 13.3 ± 0.5 | 7.46 ± 0.05 | ||
| 13.3 ± 0.5 | 7.48 ± 0.05 | |||
| [K (15C5)2] | I | 7.2 ± 0.5 | 4.34 ± 0.05 | Uniaxial rotation |
| II | 13.5 ± 0.5 | 7.53 ± 0.05 | ||
| [Li 18C6] | I | 0.18 ± 0.01 | 0.12 ± 0.01 | Isotropic rotation |
| [Na 18C6] | I | 1.90 ± 0.05 | 1.22 ± 0.05 | Isotropic rotation |
| 23.9 ± 0.5 | 11.7 ± 0.05 | |||
| [K 18C6] | I | 0.90 ± 0.05 | 0.59 ± 0.01 | Isotropic rotation |
| 19.7 ± 0.5 | 10.2 ± 0.5 |
Here, γI, γS, I, S, N, h, θ, and r are the gyromagnetic ratios of nuclei I (1H) and S (7Li, 23Na, etc.), nuclear spin quantum number of 1H (I = 1/2) and S, number of nuclei counted in the calculation, Plank's constant, angle between the static magnetic field and I–I and I–S vectors, and length of I–I and I–S vectors, respectively. In this study, the M2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cal values were estimated for one cation; only intramolecular interactions were calculated (in the case of [Na (12C4)2]+ and [K (15C5)2]+, sandwich structures reported in previous studies44 are assumed). The results are summarised in Table 3. In this table, each M2
Cal values were estimated for one cation; only intramolecular interactions were calculated (in the case of [Na (12C4)2]+ and [K (15C5)2]+, sandwich structures reported in previous studies44 are assumed). The results are summarised in Table 3. In this table, each M2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cal value with M ions is similar to that without M ions. This result can be explained by the effects of small γS values of Li, Na, and K, and large M–H distances compared with those between H and H separations. Our M2
Cal value with M ions is similar to that without M ions. This result can be explained by the effects of small γS values of Li, Na, and K, and large M–H distances compared with those between H and H separations. Our M2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cal values were similar to those reported for 15-crown-5 and 18-crown-6.42 Because the contributions of intermolecular interactions can be roughly estimated to be approximately 0.5–1.5 G2, the observed M2 value of 0.12 G2 in the Phase I of [Li 15C5] can be assigned to isotropic reorientation. The M2
Cal values were similar to those reported for 15-crown-5 and 18-crown-6.42 Because the contributions of intermolecular interactions can be roughly estimated to be approximately 0.5–1.5 G2, the observed M2 value of 0.12 G2 in the Phase I of [Li 15C5] can be assigned to isotropic reorientation. The M2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Obs value of <1.5 G2 is also assigned to isotropic reorientation, and the 1H NMR lines recorded in the Phase I of [Li 18C6] and the narrow component in Phases II and III of [Li 15C5] and in Phase I of [Na 18C6] and [K 18C6] can be assigned to the isotropic reorientation of the crown ether molecule. In contrast, it can be attributed to the Phase I of [Li 12C4], Phases I and II of [Na 15C5], and Phase I of [K (15C5)2] being rotator phases, as compared with the M2
Obs value of <1.5 G2 is also assigned to isotropic reorientation, and the 1H NMR lines recorded in the Phase I of [Li 18C6] and the narrow component in Phases II and III of [Li 15C5] and in Phase I of [Na 18C6] and [K 18C6] can be assigned to the isotropic reorientation of the crown ether molecule. In contrast, it can be attributed to the Phase I of [Li 12C4], Phases I and II of [Na 15C5], and Phase I of [K (15C5)2] being rotator phases, as compared with the M2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Obs and M2
Obs and M2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Calc values of uniaxial rotation.
Calc values of uniaxial rotation.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cal values in G2. The values were estimated for one cation (only the intramolecular interaction was calculated)
Cal values in G2. The values were estimated for one cation (only the intramolecular interaction was calculated)
| Models | [M 18C6]+ | [M 15C5]+ | [M 12C4]+ | |
|---|---|---|---|---|
| a [Na (12C4)2]+. b [K (15C5)2]+. | ||||
| Without alkali metal ions | Rigid | 15.05 | 16.53 | 15.70 |
| Uniaxial rotation | 1.46 | 4.06 | 5.62 | |
| Isotropic rotation | 0.00 | 0.00 | 0.00 | |
| Li | Rigid | 15.05 | 16.53 | 15.70 |
| Uniaxial rotation | 1.49 | 4.12 | 5.65 | |
| Isotropic rotation | 0.00 | 0.00 | 0.00 | |
| Na | Rigid | 15.05 | 16.53 | 18.13a |
| Uniaxial rotation | 1.47 | 4.09 | 7.77a | |
| Isotropic rotation | 0.00 | 0.00 | 0.00 | |
| K | Rigid | 15.05 | 17.42b | |
| Uniaxial rotation | 1.46 | 4.36b | ||
| Isotropic rotation | 0.00 | 0.00 | ||
Because the relationship M2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Obs < 1 is often obtained in plastic crystals, it can be expected that the constituents undergo self-diffusion in Phase I of [Li 15C5] and [Li 18C6] in addition to isotropic rotational motion. In the lower-temperature phases of [Li 15C5], the narrow components of M2
Obs < 1 is often obtained in plastic crystals, it can be expected that the constituents undergo self-diffusion in Phase I of [Li 15C5] and [Li 18C6] in addition to isotropic rotational motion. In the lower-temperature phases of [Li 15C5], the narrow components of M2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Obs = 0.32 (Phase II) and 0.36 G2 (Phase III) can also be assigned to diffusion. In contrast, the broad components of 9.3 and 11.7 G2 could hardly be linked to isotropic reorientation. Based on these results, it can be illustrated that a few crown ethers can perform isotropic reorientation; however, most molecules perform motions with smaller degrees of freedom compared with isotropic reorientation in Phases II and III of [Li 15C5]. This model is consistent with our conductivity data, as described in the later section (the [Li 15C5] crystal showed large conductivity). In the case of Phase I of [Li 12C4] which was reported to be in the plastic crystalline phase,34 one component with an M2
Obs = 0.32 (Phase II) and 0.36 G2 (Phase III) can also be assigned to diffusion. In contrast, the broad components of 9.3 and 11.7 G2 could hardly be linked to isotropic reorientation. Based on these results, it can be illustrated that a few crown ethers can perform isotropic reorientation; however, most molecules perform motions with smaller degrees of freedom compared with isotropic reorientation in Phases II and III of [Li 15C5]. This model is consistent with our conductivity data, as described in the later section (the [Li 15C5] crystal showed large conductivity). In the case of Phase I of [Li 12C4] which was reported to be in the plastic crystalline phase,34 one component with an M2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Obs value of 0.39 G2 can be linked to isotropic reorientation and diffusion (the [Li 12C4] crystal also showed high conductivity). However, the main component with an M2
Obs value of 0.39 G2 can be linked to isotropic reorientation and diffusion (the [Li 12C4] crystal also showed high conductivity). However, the main component with an M2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Obs value of 4.66 G2 cannot be attributed to isotropic reorientation.
Obs value of 4.66 G2 cannot be attributed to isotropic reorientation.
13C NMR spectra
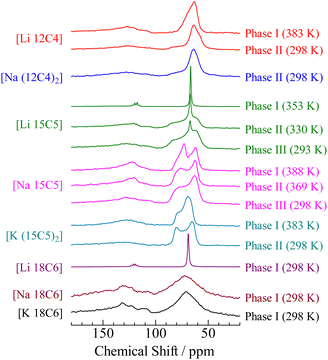
The 1H NMR spectra provide information about the averaging of the dipole–dipole interactions by molecular motion. In contrast, the line shapes of the 13C NMR spectra were mainly determined by CSA because the magnetic dipole moments of the 1H nuclei were decoupled in this measurement. The 13C NMR spectra observed for the crystals of [M (3n)Cn] (M = Li, Na, K. n = 4–6) are shown in Fig. 5. If the 13C NMR spectra were observed in solution, two peaks could be detected: one was assigned to the crown ethers (∼70 ppm) and the other was linked to the anion (∼120 ppm). In our apparatus, the dipole moments of 19F nuclei could not be decoupled. Therefore, it can be expected that signals assigned to the anion show a large linewidth unless the anion undergoes motions with a large degree of freedom of motion, for example, isotropic reorientation. In the case of Phase I of [Li 15C5] and [Li 18C6], the quartet signals attributed to spin coupling with 19F (I = 1/2) were detected at approximately 120 ppm, in addition to the narrow lines without CSA at approximately 70 ppm. Based on these results, it can be concluded that both crown ether molecules and anions exhibit isotropic reorientation in Phase I of the [Li 15C5] and [Li 18C6] complexes. This result is consistent with the 1H NMR spectra. In the case of Phase I of [Li 12C4], a line envelope with CSA was recorded at approximately 70 ppm. In addition, a broad peak was recorded at approximately 120 ppm. These results also support that [Li 12C4] should not be classified as a plastic crystal, although the previous paper reported that [Li 12C4] is a plastic crystal.34 The line shape detected at ca. 70 ppm could be fitted by powder patterns of axial-symmetric CSA (σxx = σyy ≠ σzz) rather than static-type line envelopes (σxx ≠ σyy ≠ σzz) as demonstrated in Fig. S3 (ESI†); therefore, it can be regarded that the 12-crown-4 molecule performs a uniaxial motion in Phase I. This assignment is consistent with our results (an M2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Obs value of 4.66 G2 and a P3 crystal structure). In the 1H NMR spectrum, the sharp component can be assigned to isotropic reorientation; however, the 13C NMR line shape can be fitted without its component. Because the amount of the component is small, as described above, it can be considered that its contribution to the 13C NMR spectrum is small. In Phase II, the spectrum can be fitted by two components: an axial-symmetric CSA and a static-type line envelope. This result is consistent with the M2 results. The estimated CSA values are presented in Table 4. Based on these results, it can be concluded that the [Li 12C4] complex was a rotator crystal rather than a plastic crystal. This determination was also supported by our 7Li NMR spectra, as discussed in the next section.
Obs value of 4.66 G2 and a P3 crystal structure). In the 1H NMR spectrum, the sharp component can be assigned to isotropic reorientation; however, the 13C NMR line shape can be fitted without its component. Because the amount of the component is small, as described above, it can be considered that its contribution to the 13C NMR spectrum is small. In Phase II, the spectrum can be fitted by two components: an axial-symmetric CSA and a static-type line envelope. This result is consistent with the M2 results. The estimated CSA values are presented in Table 4. Based on these results, it can be concluded that the [Li 12C4] complex was a rotator crystal rather than a plastic crystal. This determination was also supported by our 7Li NMR spectra, as discussed in the next section.
 | ||
| Fig. 5 13C NMR spectra of [M (3n)Cn] (M = Li, Na, K.; n = 4–6) crystals as a function of temperature. | ||
| Phase | σ zz | σ yy | σ xx | |
|---|---|---|---|---|
| [Li 12C4] | I | 76 ± 1 | 61 ± 1 | — |
| II | 86 ± 1 | 63 ± 1 | — | |
| 68 ± 1 | 60 ± 1 | 55 ± 1 | ||
| [Na (12C4)2] | II | 86 ± 1 | 64 ± 1 | 63 ± 1 |
| 69 ± 1 | 62 ± 1 | 58 ± 1 | ||
| [Li 15C5] | I | 66.7 ± 0.5 | — | — |
| II | 67.1 ± 0.5 | — | — | |
| 87 ± 1 | 64 ± 1 | 58 ± 1 | ||
| III | 67.2 ± 0.5 | — | — | |
| 87 ± 1 | 63 ± 1 | 56 ± 1 | ||
| [Na 15C5] | I | 79 ± 1 | 73 ± 1 | 71 ± 1 |
| 70 ± 1 | 62 ± 1 | 60 ± 1 | ||
| II | 84 ± 2 | 76 ± 2 | 69 ± 2 | |
| 71 ± 2 | 62 ± 2 | 60 ± 2 | ||
| III | 86 ± 2 | 77 ± 2 | 71 ± 2 | |
| 72 ± 2 | 63 ± 2 | 58 ± 2 | ||
| [K (15C5)2] | I | 81 ± 2 | 79 ± 2 | 73 ± 2 |
| II | 74 ± 2 | 69 ± 2 | 64 ± 2 | |
| [Li 18C6] | I | 69.9 ± 0.5 | — | — |
| [Na 18C6] | I | 89 ± 4 | 72 ± 4 | 56 ± 4 |
| [K 18C6] | I | 82 ± 3 | 71 ± 3 | 56 ± 3 |
In Phases II and III of [Li 15C5], the 13C NMR signals recorded at approximately 70 ppm could be fitted by two components, as shown in Fig. S3 (ESI†). One is a Lorentz-type adsorption line and the other is a CSA-type function. This result is consistent with the 1H NMR spectra displayed in Fig. 3, where the two components form the 1H NMR line envelope. At ca. 120 ppm, a quartet signal was detected in phases II and III. The intensity decreased from Phase I, and the component with a narrow linewidth recorded at ∼70 ppm was also reduced. Based on these results, the number of cations and anions performing isotropic reorientation was reduced in the lower-temperature phase. This tendency is also consistent with the 1H NMR spectra.
In the case of [Na 18C6] and [K 18C6], broad signals were recorded at around 70 and 120 ppm, respectively; therefore, it can be concluded that these compounds form ordinal crystals in each highest-temperature solid phase. This conclusion is consistent with the 1H NMR and XRD results. Unfortunately, we could not observe any NMR spectrum of Phase I of [Na (12C4)2] because of the limited temperature of our apparatus. In the case of [Na 15C5], two signals were recorded at approximately 62 and 73 ppm. This difference was also detected in 18-crown-6–KSCN complexes.41 Buchanan explained that there are two different conformational structures of the crown ether ring in the crystal; therefore, we prepared a single crystal of [Na 15C5] and single crystal XRD (SCXRD) measurements were conducted. The results are described in the following section on SCXRD.
7Li NMR spectra
Since the nuclear spin quantum number of 7Li is 3/2, quadrupole effects contributing to 7Li NMR spectra are generally observed, and the spectra show satellite peaks beside the central signal if the nucleus experiences the anisotropic charge distribution spatially.38 The separation between the satellites (Δ in Hz) depends on the QCC values. If both the Li–crown-ether cation and the TFSA anion undergo isotropic reorientation, a Lorentz-type function accompanied with no satellite peaks is detected in the 7Li NMR spectrum. The results obtained for [Li 12C4], [Li 15C5], and [Li 18C6] are shown in Fig. 6. A signal with half-height full linewidths (Δν) of 1.4 and 1.1 kHz was recorded in Phase I of [Li 15C5] and [Li 18C6], respectively. Because no signal was accompanied by satellite peaks, it can be regarded that the constituents perform isotropic reorientation. This result is consistent with the 1H and 13C NMR data. In contrast, the Δν value of 4.2 kHz was recorded in Phase I of [Li 12C4]. In this phase, the 1H and 13C NMR spectra showed that the crown ether molecules underwent uniaxial rotation rather than isotropic reorientation. Therefore, it can be assumed that the linewidth includes the satellite peaks. This assumption yields a QCC value of 8.4 kHz. In Phase II of [Li 12C4], the satellite signals could be fitted by the typical line shape of a first-order quadrupolar interaction with nonzero asymmetry parameters (η). The analysed lines of the satellite signals are also plotted in Fig. 6. The estimated QCC value of 22.4 kHz was significantly smaller than that of 60–68 kHz reported in the 12-crown-4–LiCl complex.40 In previous studies, it was reported that the Li ion undergoes an anisotropic vibration in the crown ether, and the motion causes larger QCC values. In this study, η = 0.40 could be estimated in Phase II. This value indicates the presence of crown ether molecules without a uniaxial rotation. The 1H and 13C NMR spectra were fitted by two components, as shown in Fig. 4 and 5, respectively. Based on these facts, it can be concluded that each broad component recorded in the 1H and 13C NMR spectra is related to 7Li satellite peaks. In the case of Phase II and III of [Li 15C5], satellite signals were recorded as shown in Fig. 6. This result is consistent with the 1H and 13C NMR data. Since the line shapes were complex, the line envelope could not be fitted by unique functions. | ||
| Fig. 6 7Li NMR spectra of [Li (3n)Cn] (n = 4–6) crystals as a function of temperature. Expanded signals are displayed at the right side. The blue solid line is analysing curves. | ||
1H NMR relaxation times
To obtain information about ionic motion, relaxation time measurements were performed. An inversion recovery method was applied to estimate the 1H NMR T1. In this method, the magnetic recovery curves can be fitted using the following function:37,38 | (3) |
Here, Meq and M(τ) are the magnitudes of the magnetisations along the static magnetic field at thermal equilibrium and at an interval of τ, respectively. The magnetic recovery curve is shown in Fig. 7. Using eqn (3), a T1 value could be determined from the slope of the recovery curve. The recovery curves obtained at each temperature for each complex could be fitted by one component; therefore, one type of motion (isotropic reorientation, uniaxial rotation, etc.) mainly contributes to the relaxation process of 1H nuclear spins. The temperature dependence of 1H NMR T1 values obtained for each complex is plotted in Fig. 8. For [Li 15C5], the T1 values increased with increasing temperature in the plastic phase (Phase I). This tendency is similar to that reported for [NR4][BEt3R']-type plastic crystals.26–30 In contrast to Phase I, a T1 minimum was obtained in Phase II. If the 1H relaxation process is caused by the fluctuation of dipole–dipole interactions between spins, the T1 values can be described by the following relationship:37
 | (4) |
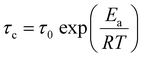 | (5) |
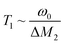 | (6) |
 | ||
| Fig. 8 Temperature dependences of 1H NMR T1 and T2 obtained in [Li 12C4] (● and ○), [Li 15C5] (● and ○), [Li 18C6] (● and ○), and [Na 15C5] (● and ○), respectively. | ||
Substituting the T1 minimum value of 660 ms into eqn (6) and (2), the r value of approximately 250 pm was estimated. This value corresponds to the H–H distance between neighbouring CH2 groups; therefore, it can be considered that the T1 relaxation detected in Phase II of [Li 15C5] is caused by isotropic reorientation. This assignment is supported by the fact that the T1 relaxation speed in Phase I was slightly higher owing to the phase transition at Ttr1. Using eqn (4) and (5), Ea values of 25 ± 1 and 34 ± 1 kJ mol−1 were estimated for the isotropic reorientation motion in Phase I and Phase II of [Li 15C5], respectively. In the case of [Li 18C6], the Ea value of 26 ± 1 kJ mol−1 was obtained. These values are larger than those reported for [NR4][BEt3R′] (R, R′ = Me, Et)-type plastic crystals.26–30 This difference from [NR4][BEt3R′] can be explained by the size of the constituents. For the other samples, the T1 slopes gave Ea values as listed in Table 5. Since T1 minima were recorded in Phase II of [Li 15C5] and Phase I of [Li18C6], τ0 values of 6.2 × 10−14 s and 2.1 × 10−14 s were also estimated using eqn (4) and (5), respectively.
| Phase I | Phase II | Phase III | |
|---|---|---|---|
| Isotropic: isotropic reorientation, Uniaxial: uniaxial rotation, DA: difficult of analysing. | |||
| [Li 12C4] | 17 (Uniaxial) | 21 (Uniaxial) | |
| [Li 15C5] | 25 (Isotropic) | 34 (Uniaxial) | |
| [Na 15C5] | 22 (Uniaxial) | DA | 21 (Uniaxial) |
| [Li 18C6] | 26 (Isotropic) | ||
To estimate the Ea values of the ion jump, 1H NMR T2 was used. The spin echo method was applied at each temperature. The results are also shown in Fig. 8. T2 relaxation is a function of the correlation time of the self-diffusion motion, and its value can be described by the following relationships:39
 | (7) |
 | (8) |
These relationships indicate that T2 increases with temperature (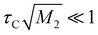 ) and is independent of temperature (
) and is independent of temperature ( ). In Phase I of [Li 15C5] and [Li 18C6], the T2 increment was obtained; therefore, it can be regarded that the crown ether molecules undergo self-diffusion in each crystal. Using eqn (7), Ea values of 202 ± 1 and 34 ± 3 kJ mol−1 were estimated for Phase I of [Li 15C5] and [Li 18C6], respectively. The large difference between these complexes can be explained by the fluidity of the [Li 18C6] compound. For [Li 12C4] and [Na 15C5] and Phase II of [Li 15C5], T2 values were independent of temperature. This suggests that the correlation times of the self-diffusion of the molecules are long compared with those in Phase I of [Li 15C5].
). In Phase I of [Li 15C5] and [Li 18C6], the T2 increment was obtained; therefore, it can be regarded that the crown ether molecules undergo self-diffusion in each crystal. Using eqn (7), Ea values of 202 ± 1 and 34 ± 3 kJ mol−1 were estimated for Phase I of [Li 15C5] and [Li 18C6], respectively. The large difference between these complexes can be explained by the fluidity of the [Li 18C6] compound. For [Li 12C4] and [Na 15C5] and Phase II of [Li 15C5], T2 values were independent of temperature. This suggests that the correlation times of the self-diffusion of the molecules are long compared with those in Phase I of [Li 15C5].
SCXRD
The 1H and 13C NMR spectra of [Na 15C5] show two peaks as shown in Fig. 4 and 5, respectively. This result indicates that crown ether molecules have two types of environments in the crystal. To reveal this fact, a single crystal of the [Na 15C5] complex was prepared using a slow evaporation method using diethyl ether, and the SCXRD analysis was performed. The obtained crystals were well-formed, colourless, block-shaped crystals. SCXRD studies revealed that in crystal packing, the molecules form a 2D tape via short and weak interactions C–H⋯O (3.538 Å, 155.02°), C–H⋯N (3.599 Å, 144.56°), and C–H⋯O (3.37 Å, 129.01°) along the bc plane in a monoclinic crystal system with the space group C2/c with Z = 8 at 293 K (Fig. S4, ESI†). However, the crown ether rings exhibited conformational disorder even at a low temperature of 253 K (Fig. 9), with the labile attachment of crown ether and Na+. The weak intermolecular interactions can favour spatially loose crystal packing, allowing increased molecular movements, resulting in conformational disorder in the crown ether ring. SCXRD measurements revealed that the occupancy of one state was slightly larger than that of the other, and the ratio difference in occupancy decreased with the increasing temperature (28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72 at 253 K was changed to 32
72 at 253 K was changed to 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 68 at room temperature). Based on our analysis, it can be concluded that the crown ether molecule jumps between two stable states, rather than two exact sites in the crystal. Since we obtained rare results (1H and 13C NMR spectra showed two signals), the detailed discussion will present in another paper.
68 at room temperature). Based on our analysis, it can be concluded that the crown ether molecule jumps between two stable states, rather than two exact sites in the crystal. Since we obtained rare results (1H and 13C NMR spectra showed two signals), the detailed discussion will present in another paper.
Electrical conductivity
To detect the translational motion of ions, electrical conductivity measurements were performed as a function of temperature. The results are plotted in Fig. S5 (ESI†). The obtained σ values of [Li 12C4] reaching 6.85 × 10−4 S cm−1 are similar to those reported in the literature.34 In the case of [Li 15C5], the σ value rapidly increased with the increasing temperature and reached 2.52 × 10−4 S cm−1. This value is similar to those of some Li compounds.16–22,46–52 A σ jump was detected at a Ttr1 of 337 K. Discontinuities were also recorded at the Ttr of some complexes. This phenomenon is often observed in first-order phase transitions. In the case of [Li 18C6], the crystal was very soft; therefore, we could not make any pellets. In [K 18C6], the σ values could not be recorded because of the high resistance values. Phase I of [Na (12C4)2] and Phase III of [Li 15C5] were outside the temperature ranges of our apparatus; therefore, no σ values could be obtained.The function ln (σT) can be described by the following relationship:
 | (9) |
Plotting ln(σT) as a function of T−1 (Fig. 10), the activation energies (Ea![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) diff) listed in Table 6 were obtained. For [Li 15C5] and [Na 18C6], σ values rapidly increased just below the melting temperature. Therefore, we estimated Ea
diff) listed in Table 6 were obtained. For [Li 15C5] and [Na 18C6], σ values rapidly increased just below the melting temperature. Therefore, we estimated Ea![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) diff values in the high- and low-temperature ranges of Phase I. Activation energies of 620 and 127 kJ mol−1 were obtained in the high- and low-temperature ranges of the plastic phase of [Li 15C5], respectively. The former value is much larger than 202 kJ mol−1 estimated by the 1H T2 measurement; in contrast, the latter is small. Conductivity measurements detect the self-diffusion of ions (the crown ether molecule motion can rarely be estimated); in contrast, the motion of crown ether molecules contributes to 1H NMR T2 values. As described in the previous section, the effects of the Li magnetic moment on the M2 values are little. Because T2 is related to M2 as shown in eqn (7), it can be considered that the effects of the motion of Li ions on the 1H T2 relaxation process are negligible. The 13C NMR spectrum recorded in Phase II of [Li 15C5] showed that the anion rarely underwent isotropic reorientation, as displayed in Fig. 5. In contrast, the intensity of the satellite peaks of the 7Li NMR signal was lower than that of [Li 12C4], as shown in Fig. 8. Based on these results, it can be concluded that the Ea
diff values in the high- and low-temperature ranges of Phase I. Activation energies of 620 and 127 kJ mol−1 were obtained in the high- and low-temperature ranges of the plastic phase of [Li 15C5], respectively. The former value is much larger than 202 kJ mol−1 estimated by the 1H T2 measurement; in contrast, the latter is small. Conductivity measurements detect the self-diffusion of ions (the crown ether molecule motion can rarely be estimated); in contrast, the motion of crown ether molecules contributes to 1H NMR T2 values. As described in the previous section, the effects of the Li magnetic moment on the M2 values are little. Because T2 is related to M2 as shown in eqn (7), it can be considered that the effects of the motion of Li ions on the 1H T2 relaxation process are negligible. The 13C NMR spectrum recorded in Phase II of [Li 15C5] showed that the anion rarely underwent isotropic reorientation, as displayed in Fig. 5. In contrast, the intensity of the satellite peaks of the 7Li NMR signal was lower than that of [Li 12C4], as shown in Fig. 8. Based on these results, it can be concluded that the Ea![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) diff values of 620 and 127 kJ mol−1 are the translational motions of the TFSA anion and Li cation, respectively.
diff values of 620 and 127 kJ mol−1 are the translational motions of the TFSA anion and Li cation, respectively.
 | ||
| Fig. 10 Arrhenius plots of electrical conductivity. [Li 12C4] (○), [Na (12C4)2] (○), [Li 15C5] (○), [Na 15C5] (○), [K (15C5)2] (○), and [Na 18C6] (○). | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) diff in kJ mol−1 estimated by conductivity measurements
diff in kJ mol−1 estimated by conductivity measurements
| Phase I | Phase II | Phase III | |
|---|---|---|---|
| a Value in the low temperature range of Phase II. b Value in the high temperature range of Phase I. | |||
| [Li 12C4] | 107 ± 10 | 55 ± 5 | — |
| [Na (12C4)2] | — | 111 ± 10, 36 ± 5a | |
| [Li 15C5] | 620 ± 50b, 127 ± 10 | 68 ± 5 | — |
| [Na 15C5] | 220 ± 10 | 103 ± 10 | 67 ± 5 |
| [K (15C5)2] | 66 ± 5 | 24 ± 3 | |
| [Na 18C6] | 340 ± 10b, 46 ± 5 | ||
Experimental
Sample preparation
Because the products showed hygroscopicity, all treatments were performed in a glove box in which air was completely substituted by N2 gas. 2.5 mmol of crown ethers of [12C4], [15C5], and [18C6] (Tokyo Kasei) and Li-TFSA (Tokyo Kasei) were mixed in 20 mL of dichloromethane solvent (Kantou Kagaku). In the case of [Na (12C4)2] and [K (15C5)2] preparation, 5.0 mmol of [12C4] and [15C5] were added to the same volume of the solvent with the same amount (2.5 mmol) of Na-TFSA (Kantou Kagaku) and K-TFSA (Wako Jyunyaku), respectively. In the other samples of [Na 15C5], [Na 18C6], and [K 18C6], the same amounts of crown ethers and M-TFSA were mixed in the same volume of the solvent. The mixed solution was stirred at room temperature for 24 h. After filtering the residue from each solution, the solutions were evaporated at 80 °C. The solids were then washed with a large amount of diethyl ether (Kantou Kagaku). The crystals were dried under vacuum.Measurements
Differential scanning calorimetry (DSC) measurements were performed using a Hitachi Hightech DSC-7020 calorimeter. All samples were placed in aluminium pans (h = 5 mm and ϕs. Heating and cooling rates of 10 K min−1 were employed. In this study, some compounds were decomposed by heating; therefore, a thermogravimetric (TG) analysis was performed using a Hitachi Hightech STA7300 calorimeter.XRD powder patterns were recorded using a Bruker D8 ADVANCE diffractometer equipped with a Cu anticathode. A TTK450 probe was employed at various temperatures. The powder patterns were plotted in the scan range of 6–40° with an angular step size of 0.02°. Single-crystal X-ray diffraction (SCXRD) data of [Na 15C5] were collected using a Bruker D8 VENTURE (PHOTON III 14) and a nitrogen-flow temperature controller using graphite monochromated Mo-Kα radiation (λ = 0.71073 Å) at 293 and 253 K. Intrinsic phasing methods (SHELXT)53 were used to solve the structure, and full-matrix least-squares calculations on F2 (SHELXL)54,55 were used to refine the structure. The non-hydrogen atoms were refined anisotropically. Mercury CSD was used to measure the distances and angles in the structural analysis.
Solid-state 1H, 7Li, and 13C NMR spectra were recorded at Larmor frequencies of 600.13, 233.23, and 150.92 MHz, respectively, using a Bruker Avance 600 spectrometer (14.10 T). The samples were sealed in handmade glass tubes with an outer diameter of approximately 4 mm. The spectra were obtained by Fourier transform (FT) of the free induction decay (FID) signals recorded after π/2 (1H and 13C) and π/4 (7Li) pulses with recycling times of 5 s (1H and 7Li) and 20 s (13C). The 1H, 7Li, and 13C NMR chemical shifts were calibrated relative to the external references of water (δ = 4.80 ppm), LiCl aqueous solution of 1 mol dm−3 (δ = 0 ppm) and glycine (δ = 43.16 ppm), respectively. Glycine signals were observed with an MAS rate of 5 kHz, using the cross-polarisation (CP) method. T1 and T2 values were obtained by inversion recovery (pulse sequence: π–τ–π/2) and spin-echo (π/2–τ–π–τ) methods, respectively. The sample temperature was controlled using a Bruker VT-3000 instrument. The whole data accumulation started after 10 min of waiting at each temperature.
Electrical conductivity measurements at 1 kHz were performed at temperatures ranging from 298 K to just below each melting point using a two-terminal method employing an Agilent Technologies E4980A Precision LCR meter equipped with an Al sheet. The powdered sample was pressed into a disc with a diameter of 1 cm and a thickness of approximately 1 mm at 20 kPa. Because the specimens were hygroscopic, the air around the probe was replaced with dry N2 gas.
To analyse the NMR data, density functional theory (DFT) simulations were performed using the Gaussian 16 computer program. We used a B3LYP/6-311 + G** function for the estimation of shielding tensors because it is in agreement with the experimental 13C NMR peaks and linewidths of alkylammonium and alkylboronate ions.26–28 The atomic coordinates of each cation and anion were optimised using the B3LYP/6-311 + G**function. The calculated CS values were determined by the difference in the shielding tensor estimated in a tetramethyl silane (TMS) molecule, and the same function was applied to optimise the atomic coordinates and estimate the shielding tensor of TMS.
Conclusions
This study provides the first evidence that Li ions can form ionic plastic crystals using crown ether with TFSA. The 1H, 7Li, and 13C NMR spectra showed that the constituents underwent isotropic reorientation in the plastic crystalline phase (337–358 K) of [Li 15C5]. 1H NMR T1 measurements also revealed that the activation energy of the motion was 25 kJ mol−1. This value is larger than that reported for [NR4][BEt3R′] (R, R′ = Me, Et)-type plastic crystals.26–30 This difference could be explained by the sizes of the constituents. The [Li 15C5] crystal had a cubic structure in Phase I and a small ΔmpS value of 29.2 J mol−1 K−1. The temperature dependences of the 1H NMR T2 values and electrical conductivity indicated that the 15-crown-5 molecule underwent self-diffusion with an Ea![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) diff value of 202 kJ mol−1, and the Li ion and the counter ion underwent translational motion with Ea
diff value of 202 kJ mol−1, and the Li ion and the counter ion underwent translational motion with Ea![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) diff values of 127 and 620 kJ mol−1, respectively.
diff values of 127 and 620 kJ mol−1, respectively.
In Phase I of the [Li 18C6] complex, our 1H, 7Li, and 13C NMR measurements revealed that the constituents underwent isotropic reorientation. However, this complex exhibited fluidity. In addition, the XRD patterns could not be indexed to any cubic structure, and the pattern was similar to that of the liquid crystal. Based on these facts, we conclude that the complex cannot be classified as a plastic crystal. The 1H NMR T1 and T2 observations revealed that the 18-crown-6 molecule exhibited isotropic reorientation and self-diffusion with Ea values of 26 and 34 kJ mol−1, respectively.
[Li 12C4] has been reported to be a plastic crystal, based on DSC measurements.34 However, 1H, 7Li, and 13C NMR spectra revealed that the 12-crown-4 molecule underwent uniaxial rotation in the highest-temperature solid phase. Thus, we conclude that this complex is a rotator crystal rather than a plastic crystal. The crystal had high σ values reaching 6.85 × 10−4 S cm−1 in Phase I. This value is similar to that reported in the literature.34
We also treated Na and K complexes. Based on the results of the 1H and 13C NMR spectra, it can be considered that the [Na 15C5] and [K (15C5)2] compounds are new rotator crystals. In the former complex, SCXRD measurements revealed that 15-crown-5 had two stable sites in the crystal.
Author contributions
A. K.: investigation, formal analysis, and methodology; J. Y: investigation, formal analysis, and methodology; S. R.: formal analysis, methodology, and writing – review and editing; S. T.: conceptualization, supervision, and writing – review and editing; H. H.: conceptualization, supervision, project administration, and writing – original draft.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partly supported by the JSPS KAKENHI Grant Number JP23K04693.References
- W. I. F. David, Appl. Radiat. Isot., 1995, 46, 519–524 CrossRef CAS
.
- Y. Jin, A. Xenopoulos, J. Cheng, W. Chen, B. Wunderlich, M. Diack, C. Jin, R. L. Hettich, R. N. Compton and G. Guiochon, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1994, 257, 235–250 CrossRef CAS
.
- G. Burns, F. H. Dacol and B. Welber, Solid State Commun., 1979, 32, 151–155 CrossRef CAS
.
- M. Debeau and P. Depondt, J. Chim. Phys., 1985, 82, 233–238 CrossRef CAS
.
- S. Ganguly Somnath, J. R. Fernandes and C. N. R. Rao, Adv. Mol. Relax. Interact. Processes, 1981, 20, 149–163 CrossRef
.
- K. Kobashi and R. D. Etters, Mol. Phys., 1982, 46, 1077–1083 CrossRef CAS
.
- J. Timmermans, J. Phys. Chem. Solids, 1961, 18, 1–8 CrossRef CAS
.
- H. Sakaebe and H. Matsumoto, Electrochem. Commun., 2003, 5, 594–598 CrossRef CAS
.
- H. Usui, H. Matsui, N. Tanabe and S. Yanagida, J. Photochem. Photobiol., A, 2004, 164, 97–101 CrossRef CAS
.
- W. A. Henderson and S. Passerini, Chem. Mater., 2004, 16, 2881–2885 CrossRef CAS
.
- T. Sato, T. Maruo, S. Marukane and K. Takagi, J. Power Sources, 2004, 138, 253–261 CrossRef CAS
.
- M. Egashira, S. Okada, J. Yamaki, D. A. Dri, F. Bonadies and B. Scrosati, J. Power Sources, 2004, 138, 240–244 CrossRef CAS
.
- M. Yoshizawa-Fujita, H. Yamada, S. Yamaguchi, H. Zhu, M. Forsyth, Y. Takeoka and M. Rikukawa, Batteries Supercaps, 2020, 3, 884–891 CrossRef CAS
.
- M. Matsuki, T. Yamada, S. Dekura, H. Kitagawa and N. Kimizuka, Chem. Lett., 2018, 47, 497–499 CrossRef CAS
.
- C. Shi, S. Li, W. Zhang, L. Qiu and F. Yan, J. Mater. Chem. A, 2013, 1, 13956–13962 RSC
.
- A. Martinelli, A. Matic, P. Jacobsson and L. Börjesson, J. Phys. Chem. B, 2009, 113, 11247–11251 CrossRef CAS PubMed
.
- L. Zhang, L. Chai, L. Zhang, M. Shen, X. Zhang, V. S. Battaglia, T. Stephenson and H. Zheng, Electrochim. Acta, 2014, 127, 39–44 CrossRef CAS
.
- S. Ferrari, E. Quartarone, P. Mustarelli, A. Magistris, M. Fagnoni, S. Protti, C. Gerbaldi and A. Spinella, J. Power Sources, 2010, 195, 559–566 CrossRef CAS
.
- M. Nádherná, J. Reiter, J. Moskon and R. Dominko, J. Power Sources, 2011, 196, 7700–7706 CrossRef
.
- I. Quinzeni, S. Ferrari, E. Quartarone, C. Tomasi, M. Fagnoni and P. Mustarelli, J. Power Sources, 2013, 237, 204–209 CrossRef CAS
.
- L. Aguilera, J. Scheers and A. Matic, Phys. Chem. Chem. Phys., 2016, 18, 25458–25464 RSC
.
- D. R. MacFarlane and M. Forsyth, Adv. Mater., 2001, 13, 957–966 CrossRef CAS
.
- M. Kenmotsu, H. Honda, H. Ohki, R. Ikeda, T. Erata, A. Tasaki and Y. Furukawa, Z. Naturforsch., 1994, 49a, 247–252 CrossRef
.
- H. Honda, M. Kenmotsu, H. Ohki, R. Ikeda and Y. Furukawa, Ber. Bunsenges. Phys. Chem., 1995, 99, 1009–1014 CrossRef CAS
.
- H. Honda, S. Ishimaru, N. Onoda-Yamamuro and R. Ikeda, Z. Naturforsch., 1995, 50a, 871–875 CrossRef
.
- T. Hayasaki, S. Hirakawa and H. Honda, Bull. Chem. Soc. Jpn., 2013, 86, 993–1001 CrossRef CAS
.
- T. Hayasaki, S. Hirakawa and H. Honda, Am. Chem. Sci. J., 2014, 4, 745–758 CrossRef
.
- T. Hayasaki, S. Hirakawa and H. Honda, Z. Naturforsch., 2014, 69a, 433–440 CrossRef
.
- S. Hirakawa and H. Honda, Z. Naturforsch., 2015, 70, 521–528 CrossRef CAS
.
- Y. Kotani and H. Honda, Bull. Chem. Soc. Jpn., 2019, 92, 768–778 CrossRef CAS
.
- K. Nagai and H. Honda, Z. Naturforsch., A: Phys. Sci., 2022, 77, 899–908 CrossRef CAS
.
- S. Hirakawa, Y. Kotani, T. Hayasaki and H. Honda, Bull. Chem. Soc. Jpn., 2015, 88, 1735–1745 CrossRef CAS
.
- Y. Yamada, E. Kashimoto and H. Honda, Bull. Chem. Soc. Jpn., 2019, 92, 1289–1298 CrossRef CAS
.
- A. Abouimrane, P. Alarco, Y. Abu-Lebdeh, I. Davidson and M. Armand, J. Power Sources, 2007, 174, 1193–1196 CrossRef CAS
.
- R. E. A. Dillon and D. F. Shriver, Chem. Mater., 1999, 11, 3296–3301 CrossRef CAS
.
-
Principles of Magnetic Resonance, ed. C. P. Slichter, Springer-Verlag, New York, 3rd edn, 1992 Search PubMed
.
-
Nuclear Magnetic Resonance and Relaxation, ed. B. Cowan, Cambridge University Press, Cambridge, 1997 Search PubMed
.
-
Transient Techniques in NMR of Solids, ed. B. C. Gerstein, C. R. Dybowski, Academic Press, London, 1985 Search PubMed
.
- G. W. Buchanan, Prog. Nucl. Magn. Reson. Spectrosc., 1999, 34, 327–377 CrossRef
.
- T. Pietrass and P. K. Burkert, Magn. Reson. Chem., 1993, 31, 709–713 CrossRef CAS
.
- G. Buchanan, M. Gerzain and C. Ratcliffe, Canadian J. Chem., 1999, 77, 1911–1921 CrossRef CAS
.
- K. Gotoh, S. Kunimitsu, H. Zhang, M. M. Lerner, K. Miyakubo, T. Ueda, H. Kim, Y. Han and H. Ishida, J. Phys. Chem. C, 2018, 122, 10963–10970 CrossRef CAS
.
-
Plastistically Crystalline State, ed. J. N. Sherwood, John Willy & Sons, New York, 1979 Search PubMed
.
- R. E. A. Dillon, C. L. Stern and D. F. Shriver, Solid State Ionics, 2000, 133, 247–255 CrossRef CAS
.
- R. M. Izatt, J. S. Brashaw, S. A. Nielsen, J. D. Lamb, J. J. Christensen and D. Sen, Chem. Rev., 1985, 85, 271–339 CrossRef CAS
.
- P. C. Barbosaa, M. M. Silva, M. J. Smith, A. Goncalves, E. Fortunato, S. C. Nunes and V. Z. Bermudez, Electrochim. Acta, 2009, 54, 1002–1009 CrossRef
.
- A. Swiderska-Mocek and D. Naparstek, Solid State Ionics, 2014, 267, 32–37 CrossRef CAS
.
- L. Aguilera, J. Scheers and A. Matic, Phys. Chem. Chem. Phys., 2016, 18, 25458–25464 RSC
.
- M. Moriya, D. Kato, W. Sakamoto and T. Yogo, Chem. Commun., 2011, 47, 6311–6313 RSC
.
- K. Yang, Z. Liao, Z. Zhang, L. Yang. and S. Hirano, Mater. Lett., 2019, 236, 554–557 CrossRef CAS
.
- S. Li, K. Yang, Z. Zhang, L. Yang and S. Hirano, Ind. Eng. Chem. Res., 2018, 57, 13608–13614 CrossRef CAS
.
- L. Jin, P. C. Howlett, J. M. Pringle, J. Janikowski, M. Armand, D. R. MacFarlane and M. Forsyth, Energy Environ. Sci., 2014, 7, 3352–3361 RSC
.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed
.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed
.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed information about thermal, NMR, crystallographic, and electric conductivity studies (pdf). DSC data: Fig. S1. 1H NMR spectra: Fig. S2. 13C NMR spectra: Fig. S3. Crystallographic data: Fig. S4. Electrical conductivity: Fig. S5. CCDC 2237016 and 2265322. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3cp02614k |
| This journal is © the Owner Societies 2023 |





