Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effects of surfactant adsorption on the wettability and friction of biomimetic surfaces†
Erik
Weiand
 *abc,
Francisco
Rodriguez-Ropero
*abc,
Francisco
Rodriguez-Ropero
 d,
Yuri
Roiter
d,
Yuri
Roiter
 d,
Peter H.
Koenig
d,
Stefano
Angioletti-Uberti
d,
Peter H.
Koenig
d,
Stefano
Angioletti-Uberti
 bce,
Daniele
Dini
bce,
Daniele
Dini
 abc and
James P.
Ewen
abc and
James P.
Ewen
 *abc
*abc
aDepartment of Mechanical Engineering, Imperial College London, South Kensington Campus, SW7 2AZ London, UK. E-mail: erik.weiand19@imperial.ac.uk; j.ewen@imperial.ac.uk
bInstitute of Molecular Science and Engineering, Imperial College London, South Kensington Campus, SW7 2AZ London, UK
cThomas Young Centre for the Theory and Simulation of Materials, Imperial College London, South Kensington Campus, SW7 2AZ London, UK
dCorporate Functions Analytical and Data & Modeling Sciences, Mason Business Center, The Procter and Gamble Company, Mason, 45040 Ohio, USA
eDepartment of Materials, Imperial College London, South Kensington Campus, SW7 2AZ London, UK
First published on 8th August 2023
Abstract
The properties of solid–liquid interfaces can be markedly altered by surfactant adsorption. Here, we use molecular dynamics (MD) simulations to study the adsorption of ionic surfactants at the interface between water and heterogeneous solid surfaces with randomly arranged hydrophilic and hydrophobic regions, which mimic the surface properties of human hair. We use the coarse-grained MARTINI model to describe both the hair surfaces and surfactant solutions. We consider negatively-charged virgin and bleached hair surface models with different grafting densities of neutral octadecyl and anionic sulfonate groups. The adsorption of cationic cetrimonium bromide (CTAB) and anionic sodium dodecyl sulfate (SDS) surfactants from water are studied above the critical micelle concentration. The simulated adsorption isotherms suggest that cationic surfactants adsorb to the surfaces via a two-stage process, initially forming monolayers and then bilayers at high concentrations, which is consistent with previous experiments. Anionic surfactants weakly adsorb via hydrophobic interactions, forming only monolayers on both virgin and medium bleached hair surfaces. We also conduct non-equilibrium molecular dynamics simulations, which show that applying cationic surfactant solutions to bleached hair successfully restores the low friction seen with virgin hair. Friction is controlled by the combined surface coverage of the grafted lipids and the adsorbed CTAB molecules. Treated surfaces containing monolayers and bilayers both show similar friction, since the latter are easily removed by compression and shear. Further wetting MD simulations show that bleached hair treated with CTAB increases the hydrophobicity to similar levels seen for virgin hair. Treated surfaces containing CTAB monolayers with the tailgroups pointing predominantly away from the surface are more hydrophobic than bilayers due to the electrostatic interactions between water molecules and the exposed cationic headgroups.
1 Introduction
The adsorption of surfactants on heterogeneous solid surfaces is important for the performance of a wide range of industrial and domestic formulations, from fluids for oil extraction1 and lubricants2 to laundry detergents3 and cosmetics.4 Despite this, the vast majority of experimental and computational studies of surfactant adsorption are conducted using flat homogeneous substrates.5 It has been shown that nanoscale surface roughness and chemical heterogeneity can strongly impact surfactant performance, so it is important to include these substrate effects in the surfactant design and formulation process.5Human hair is one such heterogeneous surface where surfactant adsorption plays an important role in modifying interfacial behaviour. The outer layer of hair, the epicuticle, is protected by a fatty acid monolayer that is primarily composed of 18-methyleicosanoic acid (18-MEA).6 This layer is crucial to maintaining the hydrophobicity, low friction, and satisfactory look and feel of hair.6 The 18-MEA layer is covalently bound to the underlying cysteine layer via thioester bonds,7 and can be partially removed when hair is damaged through chemical treatments such as bleaching,8 exposed to ultraviolet light,9 or even rubbed vigorously.10 These damage processes expose oxidised cysteic acid residues, which results in the formation of negatively charged regions on the hair surface.11 Microscopically damaged regions12 are randomly arranged on the epicuticles, leading to heterogeneous surfaces.13 Due to stronger electrostatic interactions between water molecules and the negatively charged sulfonate groups than nonpolar 18-MEA chains, bleached hair is hydrophilic, while virgin hair is hydrophobic.10,14,15
Hair has no natural self-repair mechanism for the 18-MEA layer apart from the exposure of fresh cuticles through delamination,16,17 which only occurs following strong chemical hair treatments18 or extended weathering.17 Therefore, one of the main functions of hair care formulations19 is to repair the damaged 18-MEA monolayer.4 Hair care products, such as shampoos and conditioners, contain a wide range of anionic, cationic, zwitterionic, and non-ionic surfactants to aid the maintenance and grooming processes.20 The main function of shampoos is to clean the hair,20 while conditioners repair hair damage to make it easier to comb and improve its feel, shine, and softness.21 Shampoos contain mostly anionic surfactants due to their superior cleaning performance20,22 and they have been shown to successfully remove dirt and sebum from the hair surface.22 Conditioners typically contain cationic surfactants or polymers, which form strong ionic bonds with negatively-charged regions on the hair surface and act as a repairing agent that remain bound after rinsing and drying.21 Many experimental studies have investigated the adsorption of anionic surfactants,23,24 cationic surfactants23,25–27 and cationic polymers28–32 on hair.
Chemically damaged and bleached hair shows much higher friction than virgin hair.33–40 This is due to the removal of the protective 18-MEA layer and its replacement with anionic sulfonate groups.41 Atomic force microscopy (AFM) experiments showed that the application of a commercial hair conditioner reduced the friction of chemically damaged and bleached hair to levels comparable to virgin hair through adsorption onto the damaged patches.36 More recent AFM experiments suggested that friction reduction of chemically damaged hair due to treatment with a commercial conditioner was evident below a normal load threshold of 5 nN (corresponding to a mean Hertz pressure, σ ≈ 120 MPa for a 15 nm SiN tip), above which friction was similar to untreated damaged hair.38 In addition to formulated conditioners, reductions in hair friction have also been observed with simple cationic surfactants. It has been shown that the friction between a single bleached hair and hard rubber can be decreased by increasing the concentration of cetyltrimethylammonium bromide (CTAB).33 Friction reduction of single hair–hair contacts was also observed using AFM as the concentration of tetradecyltrimethylammonium bromide (TTAB) was increased.39 Friction reductions with CTAB has also been observed at larger scales in rubbing experiments with a model finger on hair bundles.42 In addition to friction reduction, cationic surfactants and polymers can also be added to formulations to make hydrophilic bleached hair more hydrophobic.10,15,39,43–47 Dynamic and static wetting experiments on bleached hair showed that the water contact angle can be increased through the deposition of cationic surfactants.6,15,48
Theoretical and numerical models can help in providing insights to surfactant interactions with hair surfaces that are otherwise inaccessible through experiments. Mean-field theory approaches, such as self-consistent field theory (SCF) have been used to predict self-assembly of polymers and surfactants and their adsorption to hair-like surfaces.49–51 These tools ultimately provide useful insights into the equilibrium structure of surfactants in bulk solution and near substrates across a wide range of concentrations and molecular architectures. However, system dynamics and non-equilibrium systems as well as the three-dimensional structure cannot be accurately captured with the common mean-field approaches. These factors can be accounted for using molecular simulation techniques, such as molecular dynamics (MD) and dissipate particle dynamics (DPD). For example, DPD has been used to study the adsorption of nonionic n-alkyl poly(ethylene oxide) surfactants on planar hydrophobic surfaces as a model for virgin hair.52 The adsorption of non-ionic surfactants on chemically heterogeneous surfaces, comparable to those found on damaged hair, has also been studied with DPD.53 Recently, the adsorption and desorption under shear of cetrimonium chloride (CTAC) and fatty alcohols on 18-MEA monolayers grafted to a planar surface as a model for virgin hair were investigated using DPD.54 MD simulations with atomistic resolution have also been used to study the adsorption of fatty acids onto the 18-MEA-covered ultrahigh sulfur proteins.55
We recently proposed a coarse-grained molecular model to study the wettability of virgin and bleached hair using MD simulations.56 We also used these models to investigate the friction between two hair surfaces at various levels of chemical damage under dry and wet conditions using non-equilibrium molecular dynamics (NEMD) simulations.41 Recently, a similar coarse-grained MD framework was used to study the adsorption and friction of large biomacromolecules mixed with ionic surfactants on hair surfaces.57
In this work we study the adsorption of cationic and anionic surfactants onto virgin and bleached hair surfaces using coarse-grained MD simulations. We simulate surfactant adsorption isotherms with bulk systems at concentrations above the critical micelle concentration (cmc). Subsequently, we investigate the friction of hair surfaces with adsorbed cationic surfactants using squeeze-out and NEMD simulations at a wide range of contact pressures and sliding velocities. Our NEMD simulation results are compared to previous hair friction experiments with various cationic surfactants. Finally, we carry out nanodroplet wetting simulations to compare the contact angle on surfaces with adsorbed cationic surfactants to previous results on bare model hair surfaces. The methodology introduced in this work is expected to be applicable to screening of a wide range of different ionic surfactants with regards to their surface affinity, aggregation at heterogeneous surfaces, wetting and ultimately their effect on friction between hairs and other soft matter interfaces.
2 Methodology
2.1 Surfactant bulk solutions
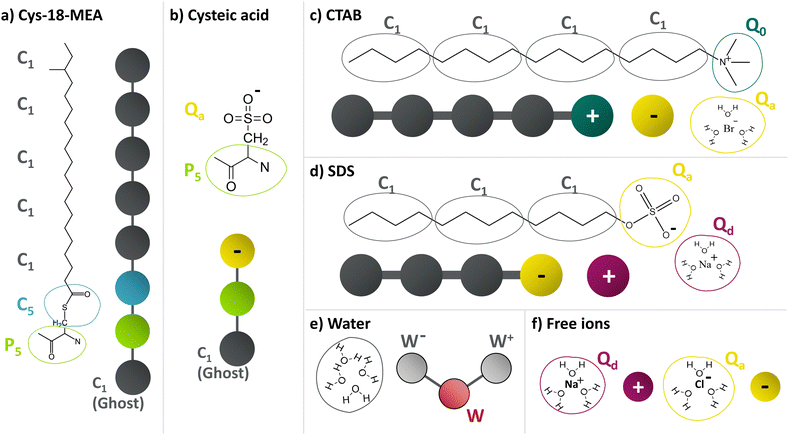
We carry out MD simulations of the self-assembly of ionic surfactants in aqueous solution to establish equilibrated bulk systems for subsequent surface adsorption simulations. We use CTAB as a model cationic surfactant and sodium dodecyl sulfate (SDS) as a model anionic surfactant. We also consider systems with excess salt (NaCl) to study the effect on self-assembly and adsorption. An overview of all the molecules considered and their coarse-grained bead types is shown in Fig. 1. We employ the MARTINI 2 model58,59 in conjunction with the polarizable MARTINI water model introduced by Yesylevskyy et al.60 throughout. This combination has been validated previously for the structure, wettability, and friction of virgin and bleached hair surfaces.41,56 All bulk systems presented in this work were prepared using PACKMOL61 for both the pre-assembled micelles and randomly distributed molecules and Moltemplate62 for assembly of the systems.CTAB is described as a linear chain of four apolar C1 beads with a terminal positively-charged Q0 bead and negatively-charged Qa bead representative of the bromide counterions.63–65 For CTAB, we consider bulk concentrations in the range of c0 = 120–973 mM, where c0 is the concentration prior to any adsorption. The equilibrium bulk concentration is further denoted by ce and can potentially differ from the initial concentration due to surfactant adsorption and therefore depletion from the finite-size bulk.66 SDS is modelled as three apolar C1 and a terminal negatively-charged Qa bead with a positively-charged sodium counterion (Qd).63,67,68 Initial SDS concentrations in the range of c0 = 173–701 mM are considered.
All simulations were performed in the open-source code LAMMPS.69 We use the velocity-Verlet70 integration scheme with a timestep of 5 fs.58 The fully periodic bulk systems are equilibrated to atmospheric pressure (p = 1 atm) for 0.1 ns in the isothermal–isobaric (NPT) ensemble and are then run in the canonical ensemble (NVT) at T = 300 K for at least 100 ns. We used a global Nosé–Hoover thermostat71,72 and barostat73 with a damping coefficient of 1 ps for the temperature and 3 ps for the pressure.
The standard MARTINI shifted Lennard-Jones (LJ) potentials58 are used for all non-bonded interactions between non-aqueous, charge-neutral beads. The LJ contributions are smoothly shifted to zero between the cut-off radius rLJ,cut = 0.9 and rLJ,shift = 1.2 nm.58 All remaining non-bonded interactions are treated in accordance with the extensions introduced by the polarizable water model.60 Short-range electrostatic interactions between charged beads are considered through direct coulombic potentials below the switching radius of rC,cut = 1.2 nm. Long-range electrostatic interactions are calculated using the particle–particle particle–mesh (PPPM) method at a relative energy tolerance of 10−5.74 The importance of accurate long-range electrostatics to correctly capture the self-assembly and adsorption behaviour of ionic surfactant solutions was highlighted in previous studies using the MARTINI force field.63,66 Bonds and angles are treated using harmonic potentials as in the original MARTINI framework.58 The SHAKE algorithm75 is applied to constrain all polarizable water bonds to r = 0.14 nm.
We performed additional simulations with pre-assembled micelles to assess how a variation in micelle aggregation number would affect the micelle stability and adsorption to the hair surface. Aggregation numbers of Nag = 82 for CTAB and Nag = 45 for SDS were chosen in accordance with experiments and previous coarse-grained simulations with standard MARTINI water.63,76–79 The pre-assembled micelles were generated using PACKMOL.61 For the pre-assembled micelles, we consider low and intermediate concentrations for both CTAB (c0 = 120 mM and c0 = 509 mM) and SDS (c0 = 170 mM and c0 = 584 mM) used in the self-assembled systems. Micelle stability simulations were run in a fully periodic system for at least 100 ns. Afterwards, we transferred the bulk systems to the hair surfaces and conducted adsorption simulations, as described below.
2.2 Surface properties
Coarse-grained MARTINI models are used to describe the surface of virgin and bleached hair.56 In this study, we consider two surfaces with different degrees of alkyl and sulfonate groups with a combined packing density of 2.73 nm−2. For virgin hair, we use a random arrangement of 75% alkyl groups and 25% sulfonate groups. For medium bleached hair, we use a random arrangement of 15% alkyl groups and 85% sulfonate groups. These groups are grafted to a flat graphene sheet made up of MARTINI C1 beads.80 The graphene sheet serves as a simple representation of the protein layers below and conveniently serves as a base to apply normal forces and sliding velocities to the contact. The MARTINI bead types for the surface-grafted molecules are shown in Fig. 1(a and b). The 18-MEA molecules are represented by a P5 bead, bonded to a C5 bead, bonded to five C1 beads for the alkyl groups.81 The oxidised cysteic acid molecules are represented by a P5 bead, bonded to a Qa bead with a charge of −1 for the sulfonate group and a free Qd bead with a charge of +1 for the sodium counterion. A detailed model description of the MARTINI parameters and their validation for hair surface wettability can be found elsewhere.56 The x × y dimensions of both periodic surfaces are 24 × 21 nm for the adsorption simulations. The surface properties of the two hair models are given in Table 1.| Property | Symbol | Virgin hair | Med. bleached hair |
|---|---|---|---|
| a Adapted from ref. 41 under a Creative Commons Attribution 3.0 Unported Licence. | |||
| Surface snapshotsa |

|

|
|
| 18-MEA grafting density | ρ MEA | 2.05 nm−2 | 0.41 nm−2 |
| SO3− grafting density | ρ SO3− | 0.68 nm−2 | 2.32 nm−2 |
| Surface charge density | ρ c | −11.0 μC cm−2 | −37.2 μC cm−2 |
| Surface energy | γ | 20.4 mJ m−2 | 23.5 mJ m−2 |
| RMS roughness | σ | 1.77 nm | 0.94 nm |
| Fractal dimension | D f = 3 − H | 2.59 | 2.78 |
The surface energies (polar + non-polar) were calculated using the Owens–Wendt82 method from previously reported contact angle measurements from coarse-grained MD simulations using the same hair surfaces with water (polar) and n-hexadecane (non-polar) droplets.56 The surface energy is larger for bleached hair than virgin hair, mainly due to the increase in the polar contribution. The surface energies in Table 1 are in good agreement with those obtained from wetting experiments on real virgin hair (18.9 mJ m−2) and bleached hair (29.8 mJ m−2).48 The virgin hair surface energy is somewhat overestimated in the simulations compared to the experiments, while the bleached hair surface energy is underestimated. The underestimation of the surface energy of the medium bleached hair surface is probably due to the systematically lower water-vapour surface tension of the polarizable MARTINI water model.60 On the other hand, the n-hexadecane-vapour surface tension with the MARTINI force field is close to experiments.56,83
The surface charge densities from the simulations are somewhat larger than those from previous experimental measurements of the surface charge density of virgin (−1.5 μC cm−2) and bleached (−10.0 μC cm−2) hair.11 However, the density of cysteic acid groups on bleached hair is in good agreement with estimates (ρSO3− = 2.2 nm−2) from another experimental study.12 This suggests that the surface charge measured in the experiments11 is lower than the simulations due to partial screening of the negative charges by the K+ counterions present in solution. The screening effect by Na+ counterions is not considered in the simulations surface charge density values reported in Table 1. The charge density for the medium bleached hair surface is very similar to that measured for an SDS monolayer at the hexadecane–water interface (−37.9 μC cm−2).84
We also determined the root-mean-square (RMS) roughness of our model surfaces by obtaining a discrete time-averaged topography map of the surface. The surface was discretized by treating the coarse-grained beads as hemispheres with a radius equivalent to half the Lennard-Jones potential energy minimum σ/2 and using a grid spacing of Δx = 0.071 nm−1. The RMS roughness of our model surfaces (24 nm × 21 nm) is somewhat larger for virgin hair than medium bleached hair. On the other hand, experimental AFM measurements with a 200 × 200 nm scan area suggested that the RMS roughness of hair increased slightly from 1.48 nm for a region where the 18-MEA layer was intact (virgin hair), to 1.74 nm in a region where the 18-MEA layer had been removed by bleaching.85 This discrepancy between the experiments and simulations is likely a result of the simplified atomically-smooth surfaces used in the simulations. In reality, the underlying disordered protein layer55 is likely to be rougher than the graphene layer used to represent it in the simulations. Despite this opposite trend, the RMS roughnesses for both model surfaces are quite close to the experimental values using a small scanning area.85 AFM experiments with larger scan areas (10 μm × 10 μm) showed higher RMS roughness values, which also increased from 10 nm for virgin hair and hair bleached for 10 minutes to 13 nm for hair bleached for 20 minutes (mean of three locations).86 These larger area scans also included features such as cuticle edges, which are not considered in the current simulations.
The fractal dimension of the hair surfaces was estimated using a surface roughness spectral approach as described by Persson.87 Approximate experimental fractal dimension of Df = 2.20 for virgin hair (2 × 2 μm scan area),85 and Df = 2.71 for bleached hair (7 × 7 μm)13 were estimated from AFM images available in the literature. The increase in fractal dimension for the bleached hair model compared to virgin hair is in good agreement with these experimental estimates. This observation suggests that the bleached hair surfaces are more irregular than virgin ones,88 which is due to the formation of lipid islands as an increasing proportion of alkyl groups are replaced by sulfonate groups.56 Previous MD simulations of hydrophobic surfaces have shown that wettability is sensitive to the nanoscale RMS roughness, but not the fractal dimension.89 However, for the current biomimetic surfaces, where hydrophobic groups in virgin hair are replaced by hydrophilic groups in bleached hair, the wettability is expected to be affected by both of these parameters.
2.3 Surfactant adsorption
A single hair surface is brought into contact with the equilibrated bulk solution, similar to previous coarse-grained MD66,90 and DPD52–54 adsorption studies on different surfaces. The bulk solution is placed approximately 3 Å above the surface to avoid initial overlap of the beads. Excess counterions in the bulk corresponding to the number of hair surface charges were randomly removed for systems with CTAB and added for systems with SDS to maintain an overall charge-neutral system. We also investigated the effect of counterion condensation by considering an initially charge-neutral surface (counterions adsorbed). The configurational differences arising from the initial distribution of couterions are discussed in full in the ESI† (Section S3 and Fig. S2, S3).The transfer to the surface breaks the periodicity of the bulk solution in the direction normal to the hair surface (z), so care was taken to ensure that surfactant micelles in the bulk were not sliced. For large surfactant concentrations (c0 > 300 mM), no separating plane could be found that would not divide at least one micelle. Adsorption simulations were run in the canonical ensemble (NVT) at a temperature of T = 300 K. Periodic boundary conditions were applied in the x and y directions, while the systems were finite the z direction. A repulsive 12-6 Lennard-Jones wall potential was added at the top of the simulation cell in the z-direction. Long-range electrostatic interactions were evaluated using a slab implementation91 of the PPPM method.74 All other simulation parameters follow those presented for the bulk systems.
2.4 Friction
We also investigated the effect of cationic surfactants on friction between two hair surfaces using NEMD simulations.92 The methodology for the NEMD simulations is similar to that previously described for water-lubricated hair surfaces.41 First, squeeze-out simulations between two hair surfaces are performed in a water bath to establish equilibrium contact thickness and composition for a given normal stress, σ. The cationic surfactant is pre-adsorbed on the surfaces in the configurations obtained from the adsorption simulations. We select two surface adsorption densities, Γ, based on our adsorption study for the virgin and medium bleached hair surface models. The surfaces were duplicated and reflected at an initial distance of 10 nm between the surfaces. This is sufficiently large to accommodate the adsorption structures from both surfaces and an initial water film.A normal stress of σ = 5–50 MPa is applied between two hair surfaces of equal surface damage. This range is consistent with our previous estimate of physiologically relevant contact pressures between two hairs.41 No excess surfactants are present in the bath since we do not expect the surface coverage of surfactants to increase during squeeze-out due to micelle entrapment or further physical adsorption. Very few CTAB molecules were squeezed out from the contact due to the strong affinity to the surfaces. Therefore, only the number of water molecules in the contact varied significantly with respect to the normal load applied during squeeze-out.
NEMD simulations were then performed to investigate the friction between two hair surfaces based on the composition and thickness obtained from the surfactant-containing squeeze-out simulations. Two hair surfaces with equal surface damage are slid against each other in the x-direction at a constant sliding velocity vs. We consider sliding velocities of 0.01–1 m s−1, which are deemed realistic for typical hair manipulations (brushing and combing).93,94 During squeeze-out and sliding, a constant contact pressure (5–50 MPa) is maintained by applying an average normal force to the coarse-grained beads of the upper graphene sheet, while keeping the lower graphene sheet fixed in z.41 Using a global Nosé–Hoover thermostat71,72 in the NEMD simulations could artificially influence the behaviour of the confined fluid molecules.92 Therefore, temperature is controlled by applying a one-dimensional Langevin thermostat95 to the grafted P5 beads in the direction perpendicular to compression and sliding (y) set at T = 300 K with a time relaxation constant of 1 ps. This leads to a negligible temperature rise (<1 K) within the contact for the sliding velocities applied. Production NEMD simulations are run for at least 200 ns. For the lowest sliding velocities considered, simulations are run up to 500 ns to sample at least 5 nm of surface displacement.41
2.5 Contact angle
The wettability of the CTAB-treated hair surfaces is investigated by the deposition of water nanodroplets. CTAB molecules are not present in the water droplet and negligible desorption occurs during the wetting simulations. Thus, we consider the effect of the surfactant on the solid–liquid and solid–vapour surface tensions, but not the liquid–vapour surface tension.96 This is equivalent to experimentally measuring the contact angle of pure water on hair previously treated with a cationic surfactant.15The methodology for the wetting simulations is the same as we described previously for base virgin and bleached hair surfaces.56 This was based on a previous study of the wetting of graphene by water and various surfactants using the MARTINI model.97 The diameter of the initially hemispherical droplet is d = 20 nm, containing 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 121 polarizable water molecules.56 In our previous study, this droplet size was found to be sufficiently large to be representative of the contact angle of macroscale droplets.56 Larger hair surfaces with simulation box lengths of
121 polarizable water molecules.56 In our previous study, this droplet size was found to be sufficiently large to be representative of the contact angle of macroscale droplets.56 Larger hair surfaces with simulation box lengths of 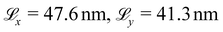 were used for the wetting simulations to accommodate droplets with low contact angles. The model surfaces were equilibrated for 10 ns in the canonical (NVT) ensemble, followed by a production run with the droplet added for a further 10 ns. We apply a global Nosé–Hoover thermostat71,72 with a damping coefficient of 1 ps. We measure the water nanodroplet contact angle at the interface using 10 block averages of 1 ns.
were used for the wetting simulations to accommodate droplets with low contact angles. The model surfaces were equilibrated for 10 ns in the canonical (NVT) ensemble, followed by a production run with the droplet added for a further 10 ns. We apply a global Nosé–Hoover thermostat71,72 with a damping coefficient of 1 ps. We measure the water nanodroplet contact angle at the interface using 10 block averages of 1 ns.
3 Results and discussion
3.1 Surfactant bulk self-assembly
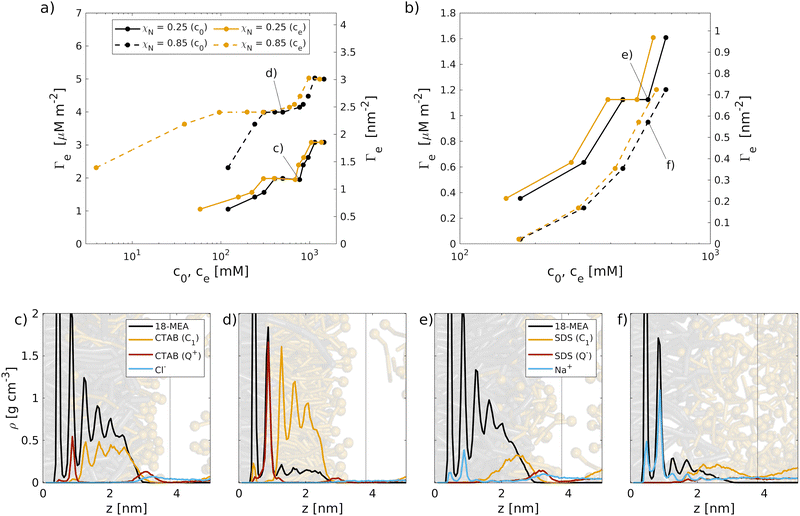
The formation of micelles is expected for both cationic (CTAB) and anionic surfactants (SDS) in water in the range of concentrations used in the current study.63 Examples of the bulk systems containing CTAB and SDS are shown in Fig. 2. Spherical micelles are observed in all of our systems, apart from the system with the highest CTAB concentration (c = 963 mM), where the onset of a transition from spherical micelles to hexagonally-ordered structures is observed. The formation of non-spherical micelles at high CTAB concentrations is in agreement with the phase diagrams from experiments99,100 and MD simulations with the MARTINI force field.63 For SDS, the concentrations considered here are below the phase boundary limit of the hexagonal phase at ambient conditions.63,99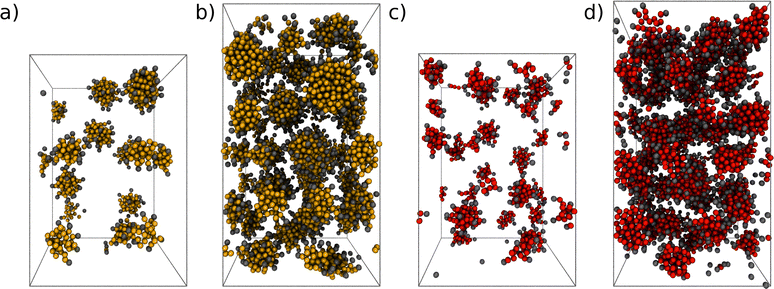 | ||
| Fig. 2 Snapshots of self-assembled micellar systems at equilibrium: CTAB at (a) c0 = 120 mM, (b) c0 = 497 mM and SDS at (c) c0 = 174 mM, and (d) c0 = 664 mM. Ionic headgroups are coloured in gray. Counterions are not shown here for clarity. Rendered with VMD.98 | ||
We investigated the implications of using the polarizable MARTINI water model60 on the aggregation behaviour of the surfactants. Aggregation numbers as a function of the bulk concentration are provided in the ESI† (Table S1). The size of surfactant micelles with the polarizable water model is underpredicted in comparison to both experiments and the standard non-polarizable MARTINI 2 water model.64 For CTAB at c = 90 mM, aggregation numbers around Nagg = 70 were reported with the standard MARTINI water model,64 compared to experimental aggregation number measurements up to Nagg ≈ 150 above the second cmc (m = 0.24 mol kg−1) obtained using nuclear magnetic resonance (NMR) spectroscopy.101 Finite-size effects102 were briefly checked by comparing self-assembly simulations for systems with box lengths of 11.9 × 10.3 nm and 23.8 × 20.6 nm. No significant differences in micelle aggregation numbers between these systems were observed. It has been recently observed that the polarizable MARTINI force field tends to underpredict the micelle aggregation numbers of other surfactants, such as zwitterionic dodecylphosphocholine (DPC) compared to both experiments and the standard MARTINI water model.102 At the same time, the use of the polarizable force field was found to be detrimental to producing micelles of zwitterionic surfactants that are in structural accordance with experiments.103 It is also worth noting that a systematic underestimation of the aggregation numbers of CTAB and SDS compared to experiments was reported for the standard water model on multiple occasions.63,64,102 This is in contrast to larger-than-experimental aggregation numbers of SDS above c = 100 mM found during self-assembly simulations with standard MARTINI water but with adjusted Lennard-Jones parameters for the beads representing the SDS hydrocarbon tails.104 We conclude that capturing the experimental aggregation numbers of specific surfactant types likely requires fine-tuning of the force field parameters when using either polarizable or non-polarizable water models. This is beyond the scope of the current study, where we are more interested in the adsorption of surfactants on solid surfaces.
We conducted additional bulk and adsorption simulations of larger pre-assembled CTAB (Nagg = 82) and SDS (Nagg = 45) micelles to investigate if the reduced micelle size due to the force field parameters would have a significant effect on surface adsorption. These micelle sizes were selected based on previous experiments76–79 and molecular simulations with standard MARTINI water.63 The pre-assembled micelles were stable in bulk simulations over more than 100 ns. The adsorption densities and kinetics from pre-assembled and self-assembled micelles were very similar across a wide range of surfactant concentrations, as shown for CTAB in the ESI† (Fig. S1). This indicates that the aggregation number does not seem to be an important consideration for the adsorption of ionic surfactants since the micelles tend to break up in the proximity of the surface. We therefore only discuss the results using bulk systems with self-assembled micelles in the remainder of this study.
3.2 Surfactant adsorption onto hair surfaces
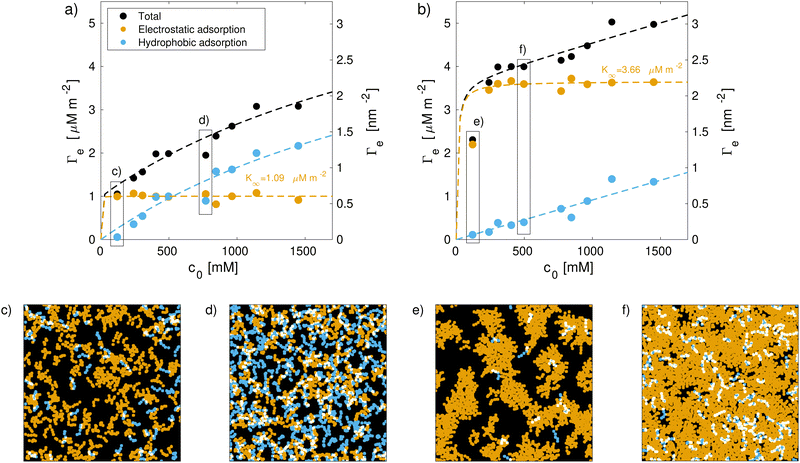
The adsorption isotherms of CTAB can be divided into three characteristic regions. (i) At low concentrations, a sharp increase in surface coverage is observed, which is due to electrostatic adsorption of the cationic surfactants to the negatively charged sulfonate sites. (ii) A region of saturation is found at intermediate concentrations (virgin: ce = 300–690 mM, medium bleached: ce = 95–300 mM) where all anionic surface charges are saturated by adsorbed cationic surfactant molecules. Here, surfactants are predominantly arranged in a combined monolayer with the grafted 18-MEA lipids. The positively charged terminal bead are oriented towards the surface, as evident from the mass density profiles in Fig. 3(c and d). For virgin hair, the region of saturation is shifted towards higher concentrations. A secondary peak for the charged CTAB beads in Fig. 3(c) suggests an onset of hydrophobic-driven adsorption at the end of the saturation plateau. (iii) When further increasing the surfactant bulk concentration, a sharp increase in the adsorption densities is observed on both virgin and medium bleached hair surfaces. Here, hydrophobic-driven adsorption leads to the formation of a secondary surfactant layer on top of the existing mixed monolayer of CTAB and covalently-bound 18-MEA.
Overall, the adsorption densities on virgin hair are reduced compared to medium bleached hair surfaces, as fewer negatively charged damage sites are available on the virgin hair surface. Previous experiments of hair fibres treated with hair conditioners also found higher levels of cationic surfactants on bleached than on virgin hair fibres.25,105,106
It is also worth noting that the initial distribution of counterions on either the surface or in the bulk can affect the structure and to some extent the adsorption density of the cationic surfactants. When all counterions are initially adsorbed on the surface, the adsorbed structure might appear more disordered and micelle-like as opposed to the layered structures discussed here. Further details are discussed in the ESI† (Section S3).
The multi-stage adsorption behaviour observed here is in qualitative agreement with experimental investigations of cationic surfactant adsorption on hair. Ran et al.27 previously reported a multi-stage behavior of the cationic surfactant dimethylpabamidopropyl laurdimonium tosylate (DDABDT) on virgin hair samples. Two plateaus regions were identified and attributed to monolayer and bilayer configurations of the surfactants on the surface.27 Tyrode et al.107 also reported multi-stage adsorption isotherms for CTAB on hydrophilic silicon surfaces. They also identified two plateau regions, the first at a CTAB coverage of around 1 nm−2 and the second at around 3 nm−2, which is the same range seen in Fig. 3 for our model hair surfaces. These works considered surfactant concentrations below and slightly above the cmc, whereas in our simulations the concentrations are all above the cmc due to the significant computational cost of these large-scale explicit solvent simulations.63 Nonetheless, the plateau adsorption densities reported in this work are similar to those observed experimentally for comparable cationic surfactants on virgin hair27 and CTAB on other hydrophilic surfaces.107 We therefore expect that, despite the higher surfactant concentrations and finite-size limitations of the MD adsorption simulations, they provide a useful pathway for obtaining similar equilibrium adsorption configurations as seen experimentally for subsequent MD simulations of friction and wetting.
For virgin hair, SDS primarily adsorbs as a monolayer with the anionic group extending into the bulk, while the hydrophobic tail interacts with the 18-MEA lipids on the surface, as shown in Fig. 3(e). For medium bleached hair, the mass density profiles and corresponding snapshot in Fig. 3(f) suggest a more disordered behavior, where surfactants adsorb to the few remaining 18-MEA lipids in a hemimicellar configuration. No preferential orientation of the anionic headgroups is evident from the snapshots. The interface between adsorbed surfactants and the bulk SDS molecules in solution is also considerably less well-resolved on medium bleached hair than on virgin hair.
The shape of the adsorption isotherms for SDS are in qualitative agreement with previous MD simulations of SDS adsorption at the water–air interface.110 No plateau region is identified in the accessible concentration range due to the low affinity of SDS to the anionic surfaces. At higher bulk concentrations, further increases in the SDS surface coverage would be expected for both virgin and medium bleached hair, eventually reaching a plateau region.110 However, at such high bulk concentrations, effects such as liquid–liquid phase transitions from spherical micelles to hexagonally-ordered structures would need to be considered,63 which are beyond the scope of the present study.
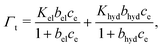 | (1) |
For virgin hair surfaces, a cross-over in the orientation of CTAB is observed. At low concentrations, electrostatic adsorption dominates as the a few negatively charged sites on the surface are quickly saturated by the cationic surfactants. Above c0 ≈ 500 mM, hydrophobic processes dominate the equilibrium surface coverage and the majority of free surfactants adsorb with their hydrophilic headgroup exposed towards the bulk.
For medium bleached model hair surfaces, the surfactants predominantly adsorb as a monolayer with the cationic group facing towards the negatively charged sites on the hair surface. With increasing surfactant concentration, the contributions from a secondary layer on top of both adsorbed CTAB and few remaining 18-MEA lipids start to become significant. A fraction of 22% of the hydrophobic-driven bilayer component is found at the highest concentration considered here (ce = 1.3 M). The increase in hydrophobic-driven surface coverage is approximately linear with c0 for both degrees of hair damage across all concentrations considered. Hydrophobic or physical adsorption thus becomes the rate-determining process at high concentrations, where electrostatic adsorption has saturated. This is in line with our initial hypothesis explaining the three observed regions in the total adsorption isotherm: (i) at low concentrations, increases in Γ are mostly caused by the electrostatic component. (ii) At intermediate concentration, this components saturates and (iii) the hydrophobic-driven contribution becomes significant. This adsorption behaviour is accurately described using the general two-step Langmuir model.114
We also calculated the orientation and distribution of SDS adsorbed on the hair surfaces, as shown in the ESI† (Fig. S4). SDS molecules are primarily oriented with the hydrophobic tail facing towards the surfaces on virgin hair at all concentrations studied. Adsorption of SDS is localised in the regions of high 18-MEA coverage with damaged regions of anionic cysteic acid groups remaining uncovered. On medium bleached hair, SDS molecules agglomerate in a hemi-micellar configuration around the few remaining patches of 18-MEA on the surface. This is demonstrated by the increase in the fraction of SDS molecules favoring a preferential orientation of their anionic site towards the surface.
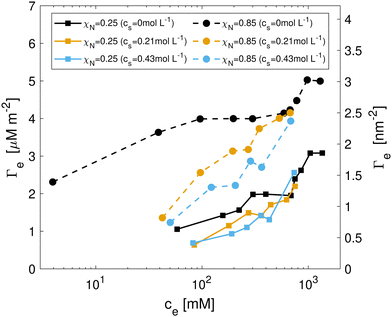 | ||
| Fig. 5 CTAB adsorption at different levels of excess salt concentrations (cs = cNa+ + cCl−) for virgin and medium bleached model hair surfaces. | ||
CTAB adsorption densities were much less sensitive to background salt concentration on virgin hair. This supports our previous suggestion that CTAB adsorption on virgin hair is primarily driven by hydrophobic interactions, where charge screening will not play a significant role.
The type of counterions may also affect the structure and kinetics of ionic surfactant adsorption and aggregation on solid substrates.117,118 Therefore, it may be interesting to studying different monovalent and divalent ions and their interactions with the surface charges and surfactants in future studies. However, atomistic force fields are likely to be required for that purpose as the MARTINI 2 force field cannot differentiate between hydrated monovalent ions.
3.3 Friction with adsorbed cationic surfactants
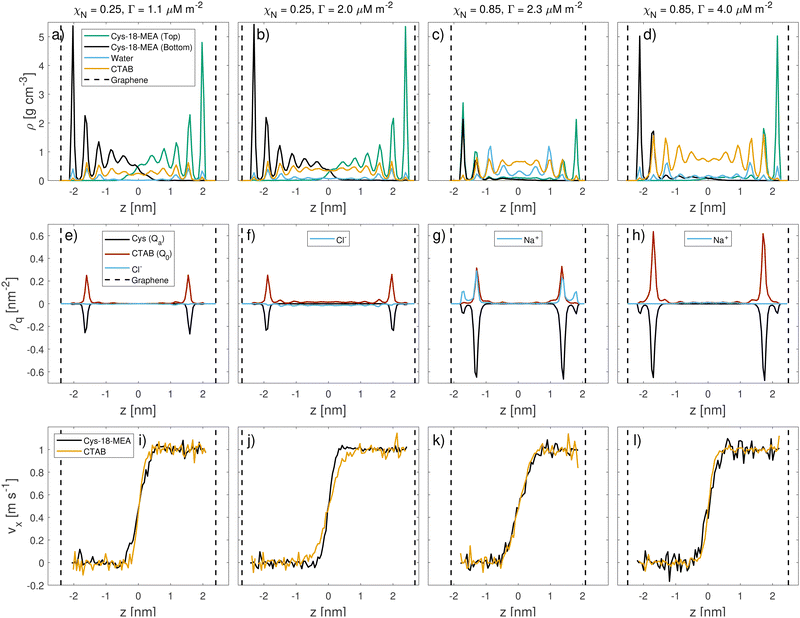
On the other hand, CTAB is not expected to damage the hair surface, so its effects on friction can be fully captured by the current simulation framework. We selected two points from each CTAB adsorption isotherm, corresponding to points (c)–(f) in Fig. 4 to be representative of the adsorption structures low (c0 = 120 mM) and high (c0 = 770 mM) CTAB concentrations. This translates to adsorption densities of Γ = 1.1 μM m−2 and Γ = 2.0 μM m−2 on virgin as well as Γ = 2.3 μM m−2 and Γ = 4.0 μM m−2 on medium bleached model hair surfaces. The surfaces with adsorbed surfactants were duplicated and reflected before squeeze-out simulations were applied to determine the number of water molecules remaining in the contact for a given normal load, as shown in the ESI† (Table S2). The number of water molecules in the contact is below the amount observed for pristine 18-MEA monolayers in water41 and does not show a strong dependence with respect to the normal stress, σ.
Representative snapshots of the systems studied in the NEMD simulations are shown in Fig. 6. We first investigated the friction behavior as a function of sliding velocity vs at σ = 10 MPa. Fig. 7(a and b) show the shear stress, τ, as a function of sliding velocity for virgin and medium bleached hair with CTAB adsorbed on both surfaces. Friction results for the same surfaces lubricated by water without adsorbed CTAB molecules41 are also shown for reference. We applied an extended stress-augmented thermal activation (SATA) model120 to the shear stress versus sliding velocity data for vs ≥ 0.1 m s−1. This model was extended from the earlier SATA model for monolayer friction due to Briscoe and Evans,121 as discussed in our previous study.41 Data points at low velocities, vs < 0.1 m s−1, are excluded from the fits due to the shear stress plateau.41
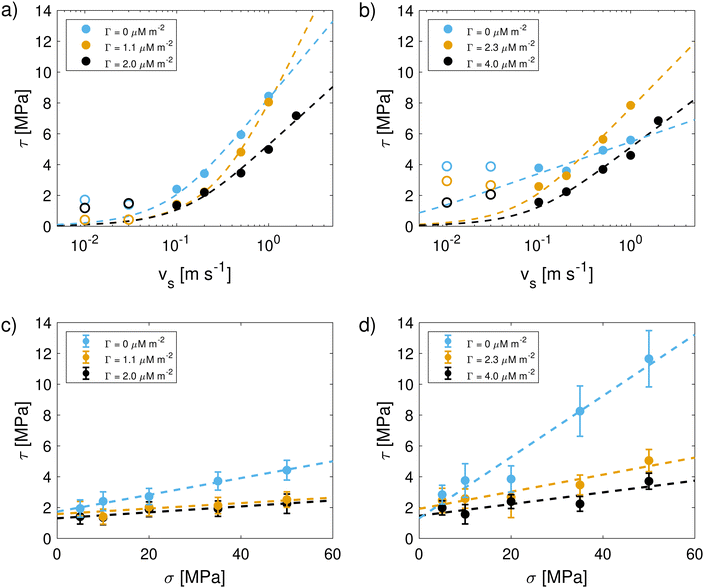 | ||
| Fig. 7 Shear stress as a function of sliding velocity vs for (a) virgin and (b) medium bleached hair surfaces with pure water (from ref. 41) and pre-adsorbed CTAB at low and high coverage at a constant normal stress of 10 MPa. The high-velocity data (vs ≥ 0.1 m s−1) is fit to an extended SATA model.120 Open symbols represent data points excluded from fitting. Normal-load variation for (c) virgin and (d) medium bleached hair surfaces at a constant sliding velocity vs = 0.1 m s−1. | ||
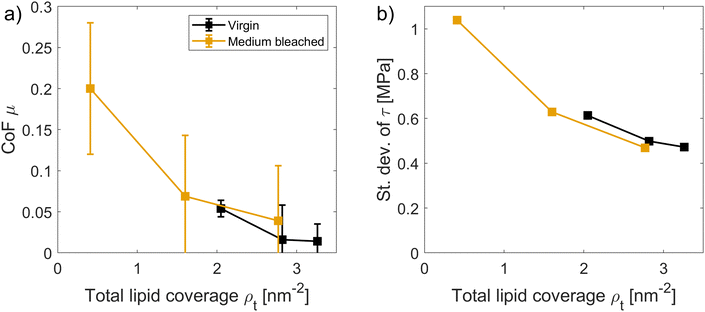
The addition of CTAB generally leads to reduction in the shear stress of hair–hair contacts compared to pure water across all considered sliding velocities. This observation is in agreement with previous experiments with CTAB on bleached hair.33 An exception to this behaviour is observed at vs = 1 m s−1 for medium bleached hair, where the shear stress for surfaces with intermediate CTAB coverage is higher than in contacts with pure water. On virgin hair, intermediate degrees of CTAB coverage provide the lowest shear stress, τ(Γ = 1.1 μM m−2) < τ(Γ = 2.0 μM m−2) < τ(Γ = 0 μM m−2). A cross-over in the shear stress between moderate and high surfactant coverage is observed around vs = 0.1 m s−1. Above this threshold, the shear stress at moderate coverage approaches the levels observed in pure water contacts. On medium bleached hair, the shear stress is generally reduced monotonically with increasing CTAB coverage, i.e., τ(Γ = 4.0 μM m−2) < τ(Γ = 2.3 μM m−2) < τ(Γ = 0 μM m−2). These results suggest that, at physiologically relevant sliding velocities,93,94 moderate coverages of CTAB adsorption tend to be more effective for providing friction reductions on virgin hair, while a larger coverage is favorable on bleached hair. This is due to the reduction of 18-MEA on bleached surfaces, which can be balanced by increased adsorption densities of the cationic surfactant on the hair surface. The combined surface coverage of the 18-MEA lipids and adsorbed CTAB ρt are 2.82 nm−2 and 3.26 nm−2 for virgin hair at low and high CTAB coverage respectively. On moderately bleached hair, the total surface coverage amounted to 1.60 nm−2 and 2.77 nm−2 for low and high surfactant coverage. We previously estimated the grafting density of a fully-functionalised layer of the 18-MEA on hair at 2.73 nm−2,56 which is in close agreement with the reported densities for virgin hair surfaces with low CTAB coverage, as well as for medium bleached hair with high CTAB coverage. The total adsorption densities are summarized in Table 2.
| Virgin hair | CTAB coverage, Γ = | 0 nm−2 | 0.77 nm−2 | 1.21 nm−2 |
|---|---|---|---|---|
| CTAB + lipid coverage | ρ t | 2.05 nm−2 | 2.82 nm−2 | 3.26 nm−2 |
| Friction coefficient | μ | 0.054 ± 0.010 | 0.018 ± 0.023 | 0.019 ± 0.012 |
| Contact angle | θ | 102.2 ± 0.9° | 106.1 ± 0.6° | 79.6 ± 0.6° |
| Medium bleached hair | CTAB coverage, Γ = | 0 nm−2 | 1.19 nm−2 | 2.36 nm−2 |
|---|---|---|---|---|
| CTAB + lipid coverage | ρ t | 0.41 nm−2 | 1.60 nm−2 | 2.77 nm−2 |
| Friction coefficient | μ | 0.20 ± 0.08 | 0.055 ± 0.034 | 0.038 ± 0.040 |
| Contact angle | θ | 49.8 ± 0.9° | 71.6 ± 2.7° | 106.5 ± 0.8° |
We analysed the structure of the contact during sliding to investigate the molecular-scale mechanisms linked to friction reduction with CTAB. Mass density, charge density and velocity profiles of the contact at vs = 1 m s−1 are shown in Fig. 8. We also report additional combined mass density profiles for the 18-MEA and CTAB at different sliding velocities in the ESI† (Fig. S6). Mass density profiles and interdigitation are insensitive to the sliding velocity, which is consistent with previous NEMD simulations of other systems containing adsorbed surfactants.120,122 For virgin hair, there is some interdigitation between the 18-MEA lipid monolayers grafted to the sliding surfaces. Interdigitation of the 18-MEA layers is less pronounced at higher CTAB coverages, suggesting that it is more effective in separating the two surfaces compared to sodium counterions. For medium bleached hair, there is much less interdigitation of the 18-MEA monolayers than for virgin hair.41 Nonetheless, there is reduced interdigitation of the remaining 18-MEA on the surface by high coverage CTAB films. The interface mostly consists of the hydrophobic tails of the cationic surfactant containing small amounts of residual water (ρw ≈ 5.4–8.1 nm−2).
During sliding, the structure of confined CTAB molecules differs considerably from that on single hair surfaces (Fig. 3). For the single surfaces, we observed CTAB bilayer on the virgin hair surface at high coverages, where a significant amount of surfactant molecules were oriented with their cationic group facing towards the bulk solution. Conversely, once a dynamic equilibrium is reached during sliding simulations, most CTAB molecules are oriented with the hydrophobic tail facing the centre of the contact, as shown in Fig. 8. We analyzed the mass density profiles at the beginning and at equilibrium of both compression and sliding simulations, as shown in the ESI† (Fig. S7). The bilayer is observed after compression of the two surfaces for up to 10 ns. For prolonged compression in the absence of shear for up to 70 ns, surfactant diffusion leads to a distribution of the bilayer in the contact, as previously observed in diffusion experiments of ionic surfactants confined between mica surfaces.123 Once the constant shear is applied, any remaining bilayer contributions are redistributed within the first 5–10 ns of sliding, independent of the sliding velocity. Previous experiments with carboxylic acid surfactants on mica surfaces have also shown that multilayers are easily removed and show similar friction behaviour to monolayers.121 Surface force balance experiments with CTAC on mica surfaces showed a transition from adsorbed micelles to bilayers under compression and shear.124 The tendency for surfactants to desorb from the hair surface under shear has also been reported both experimentally38 and in DPD simulations.54
The charge density profiles in Fig. 8 highlight the dominant electrostatic interactions inside the contact during sliding. Surface charges are locally neutralized by free cationic surfactants and counterions, where relevant. For virgin hair, CTAB fully adsorbs to the charged sites on the surface for both degrees of coverage. On medium bleached surfaces with low CTAB coverage, the number of cationic surfactants is insufficient to fully neutralize the surface charges. In this case, positively charged counterions (Na+ with its first hydration shell) equally contribute to local charge neutralisation near the surfaces. At high CTAB coverage, CTAB again predominantly occupies the negatively charged sites on the surface. The centre of the contact is generally sparse in charged beads. When CTAB molecules are present at the interface, the surface charges on the opposing surfaces are separated by a larger distance, as shown in ESI† (Fig. S8). This makes trapping of the cations between the sliding anionic surfaces125 less likely for CTAB than when the charges are neutralised by sodium counterions.41
Fig. 8 also shows the velocity profiles for CTAB and the 18-MEA molecules during sliding. The velocity profiles of CTAB and the 18-MEA overlap for all contacts, with minor deviations for virgin hair at high CTAB coverage (Γ = 2.0 μM m−2). This overlap suggests that there is no significant slip of the CTAB monolayer relative to the grafted 18-MEA lipids. Shear is confined to a small region (d ≈ 1 nm) near the contact centre for all degrees of damage and CTAB coverages. On virgin hair at Γ = 2.0 μM m−2, a slightly wider CTAB region is sheared compared to that for 18-MEA. No slip of cationic surfactants is observed near the cysteic acid groups on the surfaces, which suggests that the attractive forces between electrostatically-adsorbed surfactants and the anionic sulfonate groups on the surface are strong enough to counteract any shear-driven desorption. The charge density and velocity profiles for virgin hair at high surfactant coverage suggest that there are some CTAB molecules from the bilayer component that are not adsorbed to either of the sliding surfaces. Here, the combined CTAB and lipid surface coverage is above that expected for a pristine 18-MEA monolayer, suggesting that the surface is somewhat over-saturated. We briefly investigated the mobility fraction126 of cationic surfactants at the interface shown in the ESI† (Fig. S9). During sliding, there is a much higher mobility fraction of the CTAB surfactants on virgin hair surfaces at Γ = 2.0 μM m−2 than the other surface-coverage combinations, which confirms our hypothesis of an over-saturation. The mobility fraction is not sensitive to the sliding velocity for any of the surfaces or CTAB coverages. The mean-square-displacement (MSD) of cationic beads (Q0) on CTAB in the directions normal to the sliding direction (y and z) also confirmed an increased mobility of surfactants for virgin hair at high CTAB concentrations (Fig. S10 in the ESI†). These investigations show that excess surfactants from the secondary hydrophobically-adsorbed layer can desorb in the presence of a wide range of shear rates.
We also investigated the order within the adsorbed CTAB films. Fig. S11 in the ESI,† shows the change in nematic order of CTAB molecules with sliding velocity for the various surfaces and coverages. The CTAB chains form fluid-like rather than solid-like monolayers, with a maximum nematic order parameter of approximately 0.6 for the high coverage bleached hair system.126 The nematic order only weakly increases with the sliding velocity.
For virgin hair, the addition of CTAB to the contact leads to significant reductions in the CoF compared to water for both surfactant coverages. The Derjaguin offset, τ0, is comparable for pure water and the CTAB-containing solutions. Nikogeorgos et al.38 used AFM to study the friction of the cuticle surface of virgin and damaged hair at vs = 4 μm s−1. Under wet conditions, they reported a small increase in the coefficient of friction (+10%) of virgin hair treated with a conditioner containing cationic surfactants and silicone polymers compared to the untreated fibre.38 Conversely, AFM experiments of virgin hair–hair contacts by Mizuno et al.39 conducted at vs = 4–20 μm s−1 showed a consistent decrease in friction as the concentration of cationic surfactant TTAB was increased. From pure water to a TTAB concentration of 0.2 cmc, the CoF was reduced by approximately 50% in their experiments. Between 0.2 and 1 cmc, the CoF increased slightly, while at concentrations above the cmc, the CoF remained relatively constant.39 This is consistent with our NEMD results at physiologically relevant sliding velocities (vs = 0.1 m s−1), where the magnitudes of the shear stress for both CTAB coverages are comparable. The CoF values for virgin hair (μ ≈ 0.6) and treated virgin hair (μ ≈ 0.3) reported by Mizuno et al.39 are considerably higher than the values reported in this study. This is likely due to the crossed fibre experimental setup, where interactions between topographical features of the hair such as cuticle edges are also measured. Dhopatkar et al.127 also observed reductions in the CoF for CTAB solutions with increased concentrations lubricating hydrophobic polymer surfaces. They reported a large reduction in CoF from 0.1 cmc (μ ≈ 1.5) to 1 cmc (μ ≈ 0.5) and further friction reductions up to 10 cmc (μ ≈ 0.2). Generally, the surfactant structure on the surface rather than the bulk concentration is dominating the friction since none of the micelles remained intact on the surfaces in our adsorption simulations. Friction reductions due to conditioners on undamaged hair have also been observed in macroscopic tress combing experiments at elevated sliding velocities (vs = 0.1–20 mm s−1).128 Overall, the friction behaviour of virgin hair treated by cationic surfactants and polymers observed in experiments is in good agreement with our NEMD simulations.
On the medium bleached hair surfaces, we observe more pronounced reductions in the CoF due to CTAB adsorption. The highest reduction in the CoF (∼80%) is observed for high degrees of CTAB coverage, Γ = 4.0 μM m−2. No clear differences in adhesive contributions to friction by means of the Derjaguin offset τ0 are identified from the simulations. Our simulations are in excellent agreement with the trend observed in friction experiments on chemically damaged and bleached hair surfaces. Scott and Robbins observed a large decrease in the CoF in a rubber-on-bleached-hair contact moving from pure water (μ = 0.54) to a 0.5 wt% CTAB solution (μ = 0.25).33 The treatment of KOH-damaged hair with a cationic surfactant and silicone polymer formulation decreased the CoF by up to 65%, as reported from AFM measurements under wet conditions at low normal loads (FN < 5 nN).38 At higher normal loads, the CoF was similar to untreated KOH-damaged hair, suggesting that the formulation was removed from the hair surface. This mechanism would not be captured in our simulations due to the periodic surfaces. Moreover, the estimated contact pressure in the hair-AFM tip contact experiments (σ ≈ 120 MPa) is substantially higher than in our simulations and in real hair–hair contacts.41 The CoF from the NEMD simulations of bleached hair treated with CTAB (μ = 0.041) is comparable to that for virgin hair with pure water (μ = 0.054). This observation is in good agreement with the findings by Nikogeorgos et al.,38 who also found very similar friction for KOH-treated bleached hair to virgin hair. The CoF values in our NEMD simulations are somewhat higher than those observed in experiments of CTAC bilayers on atomically-smooth mica surfaces (μ ≈ 0.001).124 This can be attributed to the comparatively rough, chemically heterogenous nature of our simulated surfaces. We observe a large decrease in the standard deviation of the friction signal for hair with cationic surfactants (error bars in Fig. 7c and d), which suggests that stick-slip phenomena are partially eliminated. This is consistent with observations from AFM experiments, where the signal uncertainty was found to be largest for KOH-damaged hair, followed by conditioned KOH-damaged and finally untreated virgin hair.38
We also related the total surface coverage ρt from surfactants and 18-MEA, as summarized in Table 2, to the CoF at vs = 0.1 m s−1. Fig. 9 shows a consistent decrease in friction as well as in the amplitude of the shear stress oscillation (prevalence of stick-slip) with increasing lipid coverage for both virgin and medium bleached hair surfaces. The overlap between the two profiles at different degrees of damage clearly motivates that the presence of the hydrophobic tails (from either the 18-MEA or CTAB) exposed on each surface dominates the friction reductions, as the surface heterogeneity is reduced and damaged surface patches are repaired.
3.4 Wettability with adsorbed cationic surfactants
Finally, wetting simulations at the two surface coverages of CTAB are performed for the model surfaces representative of virgin and medium bleached hair. Nanodroplets of pure water are placed on the surfaces with pre-adsorbed surfactants, following the methodology described in ref. 56. The equilibrium contact angles obtained from the wetting of these droplets gives an indication on how efficiently the hydrophobicity of virgin hair can be restored by treatment with cationic surfactants. Fig. 10 depicts the contact angles for the four configurations considered here. Contact angles from hair surfaces without surfactants from ref. 56 are also included for comparison. Table 2 further shows a summary of contact angles at the various degrees of CTAB coverage.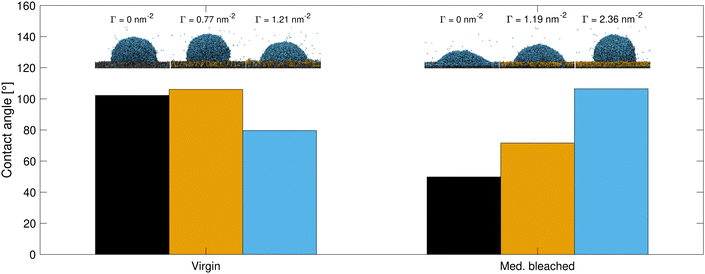 | ||
| Fig. 10 Water contact angles for untreated (from ref. 56) and CTAB-treated hair surfaces as a function of CTAB coverage. Snapshots show the equilibrium nanodroplets on bare and surfactant-coated surfaces. | ||
On virgin hair, moderate CTAB adsorption (Γ = 1.1 μM m−2) leads to a moderate increase of the contact angle to θ = 106.1° compared to the bare surfaces, θ = 102.2°. The majority of free surfactant molecules adsorbs to the few damaged patches on the surface, therefore increasing the contact angle to nearly the value reported for a pristine monolayer (θ = 120°).56 At elevated surfactant concentrations on virgin hair, the contact angle decreases to θ = 79.6°. This decrease in θ is attributed to the adsorbed CTAB bilayer. In this bilayer configuration, a significant fraction of CTAB molecules is oriented with their hydrophilic cationic sites exposed towards the water droplet, thus increasing the affinity of water to the surface. The decrease in contact angle on virgin hair is in good agreement with experimental wetting measurements of virgin hair with adsorbed proteolipids.15 The agreement with these wetting experiments also suggest that the observed bilayer might be resistant to being rinsed off when being locally wetted at macroscopic timescales and in the absence of strong shear stresses.
Unconditioned bleached model hair surfaces show an increase in wettability, as highlighted in ref. 56 and previous experimental studies on hair wetting.48,129 This is typically attributed to the surface oxidation and subsequent increase in the polar component of the surface energy.48,129 The presence of cationic surfactants on the surface restores the hydrophobicity of the medium bleached surface (θ = 49.8°), as indicated by the increase in contact angles to θ = 71.6° and θ = 106.5° for low and high CTAB coverage, respectively. On surfaces representative of bleached hair, nearly all cationic surfactants adsorb through electrostatic interactions with their cationic site facing towards the cysteic acid groups on the surface and exposing their hydrophobic tail to the bulk. At high concentrations, the observed contact angle exceeds that observed on bare virgin hair surfaces. The increase in contact angle observed in our MD simulations is in agreement with experimental results on conditioned bleached hair reported by Schulze Zur Wiesche et al.15 Treatment of bleached and permed hair with K-peptide and K-protein also led to moderate increases in advancing contact angle from dynamic wetting force measurements.129 In contrast, virgin hair wetting was largely unaffected by treatment with these molecules.129 The observed increase in water contact angle and decrease in the CoF on bleach damaged hair surfaces treated with CTAB demonstrate that cationic surfactants can restore the hydrophobicity and low friction properties of the virgin hair surface.
4 Conclusions
In this study, we have investigated the adsorption, friction and wettability of ionic surfactants on virgin and chemically bleached model hair surfaces using coarse-grained MD simulations. For virgin hair, which contains 75% 18-MEA alkyl groups and 25% sulfonate groups, adsorption of cationic surfactants occurs through both electrostatic and hydrophobic-driven adsorption. At low concentrations, CTAB forms a complete monolayer where the cationic headgroups point towards the surface due to electrostatic attraction to the anionic sulfonate groups. At higher concentrations, CTAB forms a bilayer due to hydrophobic interactions with the tailgroups of the adsorbed CTAB molecules.On medium bleached hair, which contains 15% alkyl groups and 85% sulfonate groups, CTAB adsorption is dominated by electrostatic attraction between the anionic sulfonate groups and the cationic headgroup of the surfactant. At low concentrations, CTAB forms a partial monolayer, while a complete monolayer is formed at higher concentrations. We also highlighted that the background salt concentration significantly reduces CTAB adsorption to the surface at lower CTAB concentrations. The shape and plateau surface concentrations in our multi-stage adsorption isotherms are in qualitative agreement with experimental studies of cationic surfactant adsorption on hair, despite the increased bulk concentrations required in our simulations. Adsorption of the anionic surfactant SDS is solely driven by hydrophobic interactions of the tailgroups with the grafted 18-MEA alkyl layer due to the like-charged nature of surfactant headgroups and the surface sulfonate groups. Adsorption densities for SDS were found to be significantly lower compared to CTAB.
We subsequently investigated the tribological response of adsorbed CTAB molecules on virgin and bleached model hair surfaces using NEMD simulations. Cationic surfactants reduce friction on both virgin and bleached hair to below the value of the untreated virgin hair surface. On virgin hair, an intermediate CTAB coverage was found to be most effective at lowering friction at low sliding velocities. At physiologically relevant sliding velocities, no strong difference in friction was observed for the two degrees of surfactant coverage considered. Excess cationic surfactants residing in a secondary layer on virgin hair surfaces were found to desorb during sliding. On bleached hair, increased adsorption densities are necessary to achieve low friction comparable to untreated virgin hair, due to increased surface heterogeneity caused by the lower coverage of alkyl groups and a higher coverage of sulfonate groups on the surface. Friction reductions of up to 80% were observed on bleached hair at high surfactant coverage.
Water nanodroplet wetting simulations confirmed that cationic surfactants effectively restore the hydrophobic character of untreated hair after bleaching. On virgin hair, moderate levels of CTAB adsorption further increased the hydrophobicity of the surface due to electrostatic adsorption of surfactants to the few available damaged sites on the surface. Excessive CTAB adsorption on virgin hair led to a decrease in contact angle induced by the formation of a bilayer on the surface. On medium bleached hair, the contact angle monotonically increased with higher adsorption densities due to the formation of a CTAB monolayer with increasing surface coverage. Our results are in excellent agreement with experimental friction and wetting measurements on hair and show why hair conditioners based on cationic surfactants are effective at repairing chemically damaged hair fibres.
Our simulations also highlight that the structure of surfactants during sliding of two hair surfaces in contact is perturbed in comparison to the structure on a single hair surface. We expect the results of this study to be applicable to further screening of more complex and multi-component hair care formulations, including the interactions of charged polymers and polymer–surfactant complexes with hair and in the presence of excess background electrolytes.
Author contributions
E. W. methodology, investigation, data curation, formal analysis, visualization, writing – original draft; J. P. E. conceptualization, methodology, supervision, writing – original draft; Y. R. conceptualization, writing – review & editing; P. H. K. conceptualization, project administration, writing – review & editing; F. R.-R. conceptualization, project administration, writing – review & editing; S. A.-U. conceptualization, supervision, writing – review & editing; D. D. conceptualization, funding acquisition, resources, supervision, project administration, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
E. W. thanks the Engineering and Physical Sciences Research Council (EPSRC) and Proctor and Gamble for PhD funding through an iCASE studentship (EP/T517690/1). J. P. E. was supported by the Royal Academy of Engineering (RAEng) through their Research Fellowships scheme. D. D. thanks Shell and the RAEng for support via a Research Chair in Complex Engineering Interfaces as well as the EPSRC for funding through an Established Career Fellowship (EP/N025954/1). We acknowledge the use of the Imperial College London Research Computing Service (DOI: 10.14469/hpc/2232) and the UK Materials and Molecular Modelling Hub, which is partially funded by the EPSRC (EP/T022213/1, EP/W032260/1 and EP/P020194/1). We thank Steven H. Page (Retired, Procter and Gamble) for useful discussions.Notes and references
- Z. Liu, G. Zhao, M. Brewer, Q. Lv and E. J. Sudhölter, Adv. Colloid Interface Sci., 2021, 294, 102467 CrossRef CAS PubMed.
- C. McFadden, C. Soto and N. D. Spencer, Tribol. Int., 1997, 30, 881–888 CrossRef CAS.
- D. Bajpai and V. K. Tyagi, J. Oleo Sci., 2007, 56, 327–340 CrossRef CAS PubMed.
- G. S. Luengo, A. L. Fameau, F. Léonforte and A. J. Greaves, Adv. Colloid Interface Sci., 2021, 290, 102383 CrossRef CAS PubMed.
- A. Striolo, Curr. Opin. Chem. Eng., 2019, 23, 115–122 CrossRef.
- S. Tokunaga, H. Tanamachi and K. Ishikawa, Cosmetics, 2019, 6, 31 CrossRef CAS.
- M. Okamoto, K. Ishikawa, N. Tanji and S. Aoyagi, Surf. Interface Anal., 2012, 44, 736–739 CrossRef CAS.
- Y. Masukawa, H. Tsujimura, H. Tanamachi, H. Narita and G. Imokawa, Exog. Dermatol., 2004, 3, 273–281 CrossRef CAS.
- T. Habe, N. Tanji, S. Inoue, M. Okamoto, S. Tokunaga and H. Tanamachi, Surf. Interface Anal., 2011, 43, 410–412 CrossRef CAS.
- R. A. Lodge and B. Bhushan, J. Appl. Polym. Sci., 2006, 102, 5255–5265 CrossRef CAS.
- F. M. Maddar, D. Perry, R. Brooks, A. Page and P. R. Unwin, Anal. Chem., 2019, 91, 4632–4639 CrossRef CAS PubMed.
- M. Korte, S. Akari, H. Kühn, N. Baghdadli, H. Möhwald and G. S. Luengo, Langmuir, 2014, 30, 12124–12129 CrossRef CAS PubMed.
- T. I. Morozova, N. A. García, J.-L. Barrat, G. S. Luengo and F. Léonforte, ACS Appl. Mater. Interfaces, 2021, 13, 30086–30097 CrossRef CAS PubMed.
- R. Molina, F. Comelles, M. R. Juliá and P. Erra, J. Colloid Interface Sci., 2001, 237, 40–46 CrossRef CAS PubMed.
- E. Schulze Zur Wiesche, A. Körner, K. Schäfer and F.-J. Wortmann, J. Cosmet. Sci., 2011, 62, 237–249 Search PubMed.
- J. A. Swift and J. R. Smith, Scanning, 2000, 22, 310–318 CrossRef CAS PubMed.
- J. A. Swift, J. Soc. Cosmet. Chem., 1999, 50, 23–47 Search PubMed.
- K. Kizawa, T. Inoue, Y. Masahito, P. Kleinert, H. Troxler, C. W. Heizmann and Y. Iwamoto, J. Cosmet. Sci., 2005, 56, 219–226 CAS.
- L. Fernández-Peña and E. Guzmán, Cosmetics, 2020, 7, 26 CrossRef.
- P. A. Cornwell, Int. J. Cosmet. Sci., 2018, 40, 16–30 CrossRef CAS PubMed.
- B. Bhushan, Prog. Mater. Sci., 2008, 53, 585–710 CrossRef CAS.
- M. F. R. G. Dias, Int. J. Trichol., 2015, 7, 2–15 CrossRef PubMed.
- K. Ohbu, T. Tamura, N. Mizushima and M. Fukuda, Colloid Polym. Sci., 1986, 264, 798–802 CrossRef CAS.
- F. Pan, Z. Lu, I. Tucker, S. Hosking, J. Petkov and J. R. Lu, J. Colloid Interface Sci., 2016, 484, 125–134 CrossRef CAS PubMed.
- G. V. Scott, C. R. Robbins and J. D. Barnhurst, J. Soc. Cosmet. Chem., 1969, 20, 135–152 CAS.
- B. C. Beard and J. Hare, J. Surfactants Deterg., 2002, 5, 145–159 CrossRef CAS.
- G. Ran, Y. Zhang, Q. Song, Y. Wang and D. Cao, Colloids Surf., B, 2009, 68, 106–110 CrossRef CAS PubMed.
- J. Jachowicz, M. Berthiaume and M. Garcia, Colloid Polym. Sci., 1985, 263, 847–858 CrossRef CAS.
- V. André, R. Nörenberg, P. Hössel and A. Pfau, Macromol. Symp., 1999, 145, 169–179 CrossRef.
- S. T. Regismond, Y. M. Heng, E. D. Goddard and F. M. Winnik, Langmuir, 1999, 15, 3007–3010 CrossRef CAS.
- A. V. Svensson, L. Huang, E. S. Johnson, T. Nylander and L. Piculell, ACS Appl. Mater. Interfaces, 2009, 1, 2431–2442 CrossRef CAS PubMed.
- M. Rincón-Fontán, L. Rodríguez-López, X. Vecino, J. M. Cruz and A. B. Moldes, RSC Adv., 2016, 6, 63064–63070 RSC.
- G. V. Scott and C. R. Robbins, J. Soc. Cosmet. Chem., 1980, 31, 179–200 CAS.
- R. L. McMullen and S. P. Kelty, Scanning, 2001, 23, 337–345 CrossRef CAS PubMed.
- S. Breakspear, J. R. Smith and G. S. Luengo, J. Struct. Biol., 2005, 149, 235–242 CrossRef CAS PubMed.
- C. LaTorre and B. Bhushan, Ultramicroscopy, 2005, 105, 155–175 CrossRef CAS PubMed.
- C. LaTorre and B. Bhushan, J. Vac. Sci. Technol., A, 2005, 23, 1034–1045 CrossRef CAS.
- N. Nikogeorgos, I. W. Fletcher, C. Boardman, P. Doyle, N. Ortuoste and G. J. Leggett, Biointerphases, 2010, 5, 60 CrossRef CAS PubMed.
- H. Mizuno, G. S. Luengo and M. W. Rutland, Langmuir, 2010, 26, 18909–18915 CrossRef CAS PubMed.
- E. Max, W. Häfner, F. Wilco Bartels, A. Sugiharto, C. Wood and A. Fery, Ultramicroscopy, 2010, 110, 320–324 CrossRef CAS PubMed.
- E. Weiand, J. P. Ewen, Y. Roiter, P. H. Koenig, S. H. Page, F. Rodriguez-Ropero, S. Angioletti-Uberti and D. Dini, Nanoscale, 2023, 15, 7086–7104 RSC.
- M. Sano, H. Mayama and Y. Nonomura, J. Surfactants Deterg., 2023, 26, 185–193 CrossRef CAS.
- Y. K. Kamath, C. J. Dansizer and H.-D. Weigmann, J. Appl. Polym. Sci., 1985, 30, 925–936 CrossRef CAS.
- E. Oshimura, H. Abe and R. Oota, J. Cosmet. Sci., 2007, 58, 347–357 CAS.
- Y. Nagahara, Y. Nishida, M. Isoda, Y. Yamagata, N. Nishikawa and K. Takada, J. Oleo Sci., 2007, 56, 289–295 CrossRef CAS PubMed.
- H. Tanamachi, S. Inoue, N. Tanji, H. Tsujimura, M. Oguri, S. M. S. Ishita and F. Sazanami, J. Cosmet. Sci., 2009, 60, 31–44 CAS.
- M. Okamoto, N. Tanji, T. Habe, S. Inoue, S. Tokunaga and H. Tanamachi, Surf. Interface Anal., 2011, 43, 298–301 CrossRef CAS.
- T. Gao, Y. He, P. Landa and J.-M. Tien, J. Cosmet. Sci., 2011, 62, 127–137 Search PubMed.
- S. Banerjee, C. Cazeneuve, N. Baghdadli, S. Ringeissen, F. A. M. Leermakers and G. S. Luengo, Soft Matter, 2015, 11, 2504–2511 RSC.
- S. Banerjee, C. Cazeneuve, N. Baghdadli, S. Ringeissen, F. Léonforte, F. A. M. Leermakers and G. S. Luengo, J. Phys. Chem. B, 2017, 121, 8638–8651 CrossRef CAS PubMed.
- E. Guzmán, L. Fernández-Peña, G. S. Luengo, A. M. Rubio, A. Rey and F. Léonforte, Polymers, 2020, 12, 624 CrossRef PubMed.
- K. Sindelka and M. Lisal, Mol. Phys., 2021, 119, e1857863 CrossRef.
- J. Klebes, S. Finnigan, D. J. Bray, R. L. Anderson, W. C. Swope, M. A. Johnston and B. O. Conchuir, J. Chem. Theory Comput., 2020, 16, 7135–7147 CrossRef CAS PubMed.
- K. Sindelka, A. Kowalski, M. Cooke, C. Mendoza and M. Lisal, J. Mol. Liquids, 2023, 375, 121385 CrossRef CAS.
- J. M. Sanders, B. J. Coscia, A. Fonari, M. Misra, P. G. M. Mileo, D. J. Giesen, A. R. Browning and M. D. Halls, Langmuir, 2023, 39, 5263–5274 CrossRef CAS PubMed.
- E. Weiand, J. P. Ewen, P. H. Koenig, Y. Roiter, S. H. Page, S. Angioletti-Uberti and D. Dini, Soft Matter, 2022, 18, 1779–1792 RSC.
- B. J. Coscia, J. C. Shelley, A. R. Browning, J. M. Sanders, R. Chaudret, R. Rozot, F. Léonforte, M. D. Halls and G. S. Luengo, Phys. Chem. Chem. Phys., 2023, 25, 1768–1780 RSC.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. De Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS PubMed.
- S. J. Marrink and D. P. Tieleman, Chem. Soc. Rev., 2013, 42, 6801–6822 RSC.
- S. O. Yesylevskyy, L. V. Schäfer, D. Sengupta and S. J. Marrink, PLoS Comput. Biol., 2010, 6, 1–17 CrossRef PubMed.
- L. Martinez, R. Andrade, E. G. Birgin and J. M. Martinez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef CAS PubMed.
- A. I. Jewett, D. Stelter, J. Lambert, S. M. Saladi, O. M. Roscioni, M. Ricci, L. Autin, M. Maritan, S. M. Bashusqeh, T. Keyes, R. T. Dame, J. E. Shea, G. J. Jensen and D. S. Goodsell, J. Mol. Biol., 2021, 433, 166841 CrossRef CAS PubMed.
- S. D. Anogiannakis, P. C. Petris and D. N. Theodorou, J. Phys. Chem. B, 2020, 124, 556–567 CrossRef CAS PubMed.
- S. Illa-Tuset, D. C. Malaspina and J. Faraudo, Phys. Chem. Chem. Phys., 2018, 20, 26422–26430 RSC.
- S. Liu, D. Wu and X. Yang, Mol. Simul., 2016, 42, 31–38 CrossRef CAS.
- S. Wang and R. G. Larson, Langmuir, 2015, 31, 1262–1271 CrossRef CAS PubMed.
- S. Jalili and M. Akhavan, Colloids Surf., A, 2009, 352, 99–102 CrossRef CAS.
- Y. Ruiz-Morales and A. Romero-Martínez, J. Phys. Chem. B, 2018, 122, 3931–3943 CrossRef CAS PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in 't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- L. Verlet, Phys. Rev., 1967, 159, 98 CrossRef CAS.
- S. Nosé, Mol. Phys., 1984, 52, 255–268 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4189 CrossRef CAS.
- R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, CRC Press, New York, 1989 Search PubMed.
- J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- P. Lianos and R. Zana, Chem. Phys. Lett., 1980, 72, 171–175 CrossRef CAS.
- C. Ma, G. Li, Y. Xu, H. Wang and X. Ye, Colloids Surf., A, 1998, 143, 89–94 CrossRef CAS.
- J. Rassing, P. J. Sams and E. Wyn-Jones, J. Chem. Soc., Faraday Trans. 2, 1974, 1247–1258 RSC.
- A. Patist, S. G. Oh, R. Leung and D. O. Shah, Colloids Surf., A, 2001, 176, 3–16 CrossRef CAS.
- D. Wu and X. Yang, J. Phys. Chem. B, 2012, 116, 12048–12056 CrossRef CAS PubMed.
- Y. Atsmon-Raz and D. P. Tieleman, J. Phys. Chem. B, 2017, 121, 11132–11143 CrossRef CAS PubMed.
- D. K. Owens and R. C. Wendt, J. Appl. Polym. Sci., 1969, 13, 1741–1747 CrossRef CAS.
- M. Ndao, J. Devémy, A. Ghoufi and P. Malfreyt, J. Chem. Theory Comput., 2015, 11, 3818–3828 CrossRef CAS PubMed.
- D. Glikman and B. Braunschweig, ACS Nano, 2021, 15, 20136–20147 CrossRef CAS PubMed.
- N. Wang, R. Barfoot, M. Butler and C. Durkan, ACS Biomater. Sci. Eng., 2018, 4, 3063–3071 CrossRef CAS PubMed.
- R. Humphry, N. Wang and C. Durkan, J. Mech. Behav. Biomed. Mater., 2022, 126, 105001 CrossRef CAS PubMed.
- B. N. Persson, Tribol. Lett., 2014, 54, 99–106 CrossRef.
- D. Avnir, D. Farin and P. Pfeifer, Nature, 1984, 308, 261–263 CrossRef CAS.
- C. Yang, U. Tartaglino and B. N. Persson, Phys. Rev. Lett., 2006, 97, 116103 CrossRef CAS PubMed.
- V. V. Ginzburg, A. K. Van Dyk, T. Chatterjee, A. I. Nakatani, S. Wang and R. G. Larson, Macromolecules, 2015, 48, 8045–8054 CrossRef CAS.
- I. C. Yeh and M. L. Berkowitz, J. Chem. Phys., 1999, 111, 3155–3162 CrossRef CAS.
- J. P. Ewen, D. M. Heyes and D. Dini, Friction, 2018, 6, 349–386 CrossRef CAS.
- S. New, G. Daniels and C. L. Gummer, Int. J. Cosmet. Sci., 2018, 40, 461–466 CrossRef CAS PubMed.
- W. Newman, G. L. Cohen and C. Hayes, J. Soc. Cosmet. Chem., 1973, 24, 773–782 Search PubMed.
- T. Schneider and E. Stoll, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 17, 1302–1322 CrossRef CAS.
- B. Bera, O. Carrier, E. H. Backus, M. Bonn, N. Shahidzadeh and D. Bonn, Langmuir, 2018, 34, 12344–12349 CrossRef CAS PubMed.
- D. Sergi, G. Scocchi and A. Ortona, J. Chem. Phys., 2012, 137, 094904 CrossRef PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics Modell., 1996, 14, 33–38 CrossRef CAS PubMed.
- K. Fontell, Mol. Cryst. Liq. Cryst., 1981, 63, 59–82 CrossRef CAS.
- N. K. Raman, M. T. Anderson and C. J. Brinker, Chem. Mater., 1996, 63, 59–82 Search PubMed.
- M. Tornblom, U. Henriksson and M. Ginley, J. Phys. Chem., 1994, 98, 7041–7051 CrossRef.
- J. J. Harris, G. A. Pantelopulos and J. E. Straub, J. Phys. Chem. B, 2021, 125, 5068–5077 CrossRef CAS PubMed.
- J. F. Kraft, M. Vestergaard, B. Schiøtt and L. Thøgersen, J. Chem. Theory Comput., 2012, 8, 1556–1569 CrossRef CAS PubMed.
- S. D. Peroukidis, D. G. Tsalikis, M. G. Noro, I. P. Stott and V. G. Mavrantzas, J. Chem. Theory Comput., 2020, 16, 3363–3372 CrossRef CAS PubMed.
- A. Harvey, C. Carr and A. Pereira, J. Cosmet. Sci., 2004, 55, 265–279 CAS.
- L. Labarre, O. Squillace, Y. Liu, P. J. Fryer, P. Kaur, S. Whitaker, J. M. Marsh and Z. J. Zhang, Int. J. Cosmet. Sci., 2023, 45, 224–235 CrossRef CAS PubMed.
- E. Tyrode, M. W. Rutland and C. D. Bain, J. Am. Chem. Soc., 2008, 130, 17434–17445 CrossRef CAS PubMed.
- R. D. C. C. Wagner and I. Joekes, Colloids Surf., B, 2005, 41, 7–14 CrossRef CAS PubMed.
- B. Singh and S. Umapathy, J. Biophoton., 2011, 4, 315–323 CrossRef CAS PubMed.
- C. Yang and H. Sun, J. Phys. Chem. B, 2014, 118, 10695–10703 CrossRef CAS PubMed.
- L. Lajtar, J. Narkiewicz-Michalek and W. Rudzinski, Langmuir, 1994, 10, 3754–3764 CrossRef CAS.
- B. Li and E. Ruckenstein, Langmuir, 1996, 12, 5052–5063 CrossRef CAS.
- S. Wu, L. Shi, L. B. Garfield, R. F. Tabor, A. Striolo and B. P. Grady, Langmuir, 2011, 27, 6091–6098 CrossRef CAS PubMed.
- R. Atkin, V. S. Craig, E. J. Wanless and S. Biggs, J. Colloid Interface Sci., 2003, 266, 236–244 CrossRef CAS PubMed.
- S. Llamas, E. Guzmán, F. Ortega, N. Baghdadli, C. Cazeneuve, R. G. Rubio and G. S. Luengo, Adv. Colloid Interface Sci., 2015, 222, 461–487 CrossRef CAS PubMed.
- J. A. Faucher, E. D. Goddard and R. B. Hannan, Textile Res. J., 1977, 47, 616–620 CrossRef CAS.
- M. Suttipong, N. R. Tummala, A. Striolo, C. S. Batista and J. Fagan, Soft Matter, 2013, 9, 3712–3719 RSC.
- N. R. Tummala, B. P. Grady and A. Striolo, Phys. Chem. Chem. Phys., 2010, 12, 13137–13143 RSC.
- J. Jachowicz, S. Maxey and C. Williams, Langmuir, 1993, 9, 3085–3092 CrossRef CAS.
- M. Doig, C. P. Warrens and P. J. Camp, Langmuir, 2013, 30, 186–195 CrossRef PubMed.
- B. J. Briscoe and D. C. Evans, Proc. R. Soc. London, Ser. A, 1982, 380, 389–407 CAS.
- J. P. Ewen, C. Gattinoni, N. Morgan, H. A. Spikes and D. Dini, Langmuir, 2016, 32, 4450–4463 CrossRef CAS PubMed.
- A. D. Berman, S. D. Cameron and J. N. Israelachvili, J. Phys. Chem. B, 1997, 101, 5692–5697 CrossRef CAS.
- G. Silbert, N. Kampf and J. Klein, Langmuir, 2014, 30, 5097–5104 CrossRef CAS PubMed.
- G. Kagata, J. P. Gong and Y. Osada, J. Phys. Chem. B, 2003, 107, 10221–10225 CrossRef CAS.
- A. Z. Summers, C. R. Iacovella, M. R. Billingsley, S. T. Arnold, P. T. Cummings and C. McCabe, Langmuir, 2016, 32, 2348–2359 CrossRef CAS PubMed.
- N. Dhopatkar, A. P. Defante and A. Dhinojwala, Sci. Adv., 2016, 2, e1600763 CrossRef PubMed.
- O. Ajayi, A. Davies and S. Amin, Cosmetics, 2021, 8, 77 CrossRef CAS.
- C. Barba, S. Scott, A. Roddick-Lanzilotta, R. Kelly, A. M. Manich, J. L. Parra and L. Coderch, Fibers Polym., 2010, 11, 1055–1061 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02546b |
| This journal is © the Owner Societies 2023 |