A theoretical study of the reaction of borata derivatives of benzene, anthracene and pentacene with CO₂

Abstract

A theoretical study of the reaction between several borataacenes (1-methylboratabenzene, 9-methyl-9-borataanthracene and cis and trans diboratapentacene) and CO₂ has been carried out at the M06-2X computational level. The influence of a counterion (potassium cation), the cation complexation by 18-crown-6-ether and solvent effects have been explored. The computational results predict anti/syn selectivity as found experimentally in the cis- and trans-diboratapentacene reaction with CO₂ (Baker et al., J. Am. Chem. Soc., 2023, 145, 2028).

---

1. Introduction

CO₂ removal from the atmosphere and its application are important challenges in science nowadays.¹ From a chemical point of view, several systems are able to sequestrate and activate CO₂.² Amines,^3–5 ionic liquids and eutectic solvents,^6–8 carbenes,^9–14 guanidines,^15–17 phosphines,^18–21 frustrated Lewis pairs (FLPs)^22–27 and metal organic frameworks (MOFs),^28–30 among others, fulfill these tasks.

Polycyclic aromatic hydrocarbons (PAHs) containing at least one boron atom, boraacenes, are known to be able to react with CO₂.^31,32 For instance, anionic 9,10-diboraanthracene is well known to react with small molecules, in particular with CO₂.^33,34 The neutral 9,10-diboraanthracene also reacts with CO₂.³⁵ It is possible to stabilize it with nitrogen heterocyclic carbenes (NHCs).^35–37 The synthesis of 9-aza-10-boraanthracene has been recently reported³⁸ and our theoretical studies show that the analogous dibenzophosphaborines are able to capture CO₂.³²

Recently, Barker et al. have synthesized and studied the reactivity of diboratapentacene (DBP) with CO₂.³⁹ They synthesized the dianionic cis and trans isomers in the form of a potassium salt. Initially, only the antireaction with two CO₂ molecules was found. However, when the potassium cations form complexes with 18-crown-6-ether, the syn addition of two CO₂ molecules occurs.

In this article, we study the reaction mechanism of the cis- and trans-diboratapentacene with CO₂, starting with simplified model systems such as 1-methylboratabenzene, BBZN, and 9-methyl-9-borataanthracene, BA (Fig. 1). The presence/absence of the neutralizing cation (K⁺), the complexation of the cation with crown-ethers, and the solvent effect have been analyzed using density-functional theory (DFT) computational methods and several computational methods. For each reaction, the molecular electrostatic potentials (MESP) of the isolated borataacenes and the corresponding potassium salt have been calculated and analyzed. In addition, all the stationary points (minima and transition states – TSs) that connect the isolated monomers with the CO₂ adducts have been characterized using the M06-2X/def2TZVP computational level. In general, the reactions of the isolated borataacenes with CO₂ show a lower number of stationary points as compared to the corresponding potassium salt.

Fig. 1 Systems studied in the present article.

2. Computational details

The geometry of the systems has been optimized using the M06-2X DFT functional⁴⁰ and the def2TZVP⁴¹ basis set except for those systems that include the 18-crown-6-ether where the def2SVP basis set has been used. Frequency calculations at the same computational level used for the geometry optimization have been performed to verify that the geometries obtained correspond to minima or TS. Using the geometry of the TS, IRC calculations have been carried out to confirm that the TSs are connected to the expected minima. The geometries of all stationary points are gathered in Table S1 of the ESI† material. Calculations using a different functional (PBE0/def2TZVP) and at the DLPNO-CCSD(T)/def2TZVP computational level in selected stationary points provide very similar energetic results to those obtained at the M06-2x/def2TZVP level (Table S2, ESI†), which give confidence in the results presented here.

The effect of the solvent in the reactions has been addressed with the SMD model⁴² and tetrahydrofuran (THF) parameters; THF is the solvent used in the experimental study of the reactions of 5,12- and 5,7-diboratapentacene dianions with CO₂.³⁹ Since the X-ray structures of the 5,12- and 5,7-diboratapentacene monomers and adducts show 1.5 molecules of THF per diboratapentacene molecule, in some cases, systems with two molecules of THF interacting with the potassium cation on top of the SMD model have been calculated. The results of the combination of explicit and implicit solvent models are very similar to those obtained only with the implicit SMD one (Table S3, ESI†). All computations have been carried out using the Gaussian-16 scientific software.⁴³

The topological properties of the electron density of the energetic stationary points have been analyzed within the quantum theory of atoms in molecules (QTAIM)^44,45 and the AIMAll program.⁴⁶ In this methodology, the critical points of the electron density are defined as and classified using the sign of the eigenvalues of ∇²ρ, i.e. the number of the positive and/or negative curvatures of the electron density at a given point of zero gradient.

The molecular electrostatic potential (MESP) on the 0.001 au electron density has been analyzed using the Multiwfn program⁴⁷ and represented with Jmol.⁴⁸ Regions with MESP negative values indicate that positively charged groups will favorably interact with the borataacenes while for those regions with positive MESP values, the favorable interaction will be with negatively charged groups. It is expected that the oxygen of CO₂ will interact with MESP positive regions of the systems displayed in Fig. 1, while the carbon atom will interact with MESP negative regions of these borataacene systems.

3. Results and discussion

This section has been divided into six parts. In the first and second parts, 1-methylborabenzene and 9-borataanthracene and their reactivity with CO₂ have been explored. In the third and fourth parts, the two diborapentacene anions and their corresponding potassium salts were considered. Finally, sections five and six deal, respectively, with the solvent effect and the complexation of the cation with 18-crown-6-ether molecules.

3.1. 1-Methylboratabenzene and its reaction with CO₂

1-Methylboratabenzene (BBZN) is a known compound for which the X-ray structure in the form of salt with trimethylphenylammonium has been described [Cambridge Structural Database (CSD)⁴⁹ refcode YIYBEN⁵⁰]. The calculated and experimental geometries of BBZN present a planar 6-membered ring with B–C bond distances larger than the C–C ones (see Table S4, ESI†). The crystal structure shows the absence of symmetry in their B–C_ortho and C_meta–C_para bonds due to the asymmetry of the crystal environment. The presence of the potassium cation in the calculations slightly elongates the bond distances of the aromatic ring when compared to the isolated structure calculated in the gas phase (Table S4, ESI†) while the B–CH₃ bond is shortened.

The MESPs of the BBZN anion and BBZN-K neutral salt are shown in Fig. 2. In the case of the isolated BBZN system, all the values obtained are negative as expected for an anion, being the two faces of the system equivalent. A MESP minimum (−551.4 kJ mol⁻¹) above and below the center of the ring is located, while the less negative values, in this case maxima, are located in the periphery of the molecule. The presence of a cation in BBZN-K breaks the symmetry of the compound, and the two faces are no longer identical. The cation is located above the center of the six-membered ring where the minimum of the isolated BBZN was located. Around the cation, a spherical positive potential with a maximum of +367.6 kJ mol⁻¹ is calculated. The opposite face presents a negative minimum with a value of −183.8 kJ mol⁻¹, below the center of the ring.

Fig. 2 MESPs of BBZN and BBZN-K on the 0.001 a.u. electron density isosurface. The location of the minima and maxima are indicated with cyan and black small spheres and their values are indicated in kJ mol⁻¹.

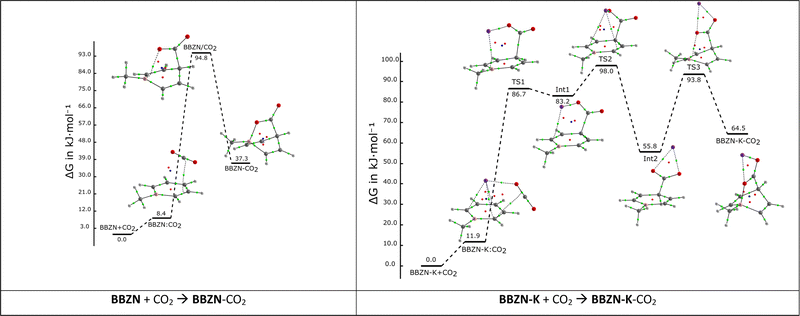
The free energy reaction profiles of BBZN + CO₂ and BBZN-K + CO₂ at 298.15 K are shown in Fig. 3 and the corresponding electronic energy profiles are shown in Fig. S1 (ESI†). The former (BBZN + CO₂) shows only three stationary points: a pre-reactive complex with a binding energy of −28 kJ mol⁻¹ (Fig. S1, ESI†) but less stable than the parent compounds by 8.4 kJ mol⁻¹ considering ΔG, a TS and an adduct with relative free energies (electronic energies) with respect to the isolated BBZN and CO₂ of +95 kJ mol⁻¹ (+42 kJ mol⁻¹) and +37 kJ mol⁻¹ (−23 kJ mol⁻¹), respectively. The adduct formation produces a significant bending in the boratabenzene ring to accommodate the simultaneous new bonds with CO₂. This deformation has been computed to be 354 kJ mol⁻¹.

Fig. 3 Free energy profiles at 298.15 K for the reactions of BBZN + CO₂ → BBZN-CO₂ (left) and BBZN-K + CO₂ → BBZN-K-CO₂ (right) with the corresponding molecular graphs of the stationary points. Green, red and blue small spheres indicate the location of the bond, ring and cage critical points.

In the free energy profile of BBZN-K + CO₂, the presence of a cation stabilizes two intermediates along the reaction coordinate. These intermediates are less stable than the entrance channel by 83 and 56 kJ mol⁻¹ (44 and 14 kJ mol⁻¹ considering the electronic energy, Fig. S1, ESI†). The three TSs characterized in this case show relative energies of +87, +98 and +94 kJ mol⁻¹ and the adduct is also less stable than the entrance channel by 64 kJ mol⁻¹ (9 kJ mol⁻¹ considering the electronic energy). TS1 shows the formation of the C–C bond and the displacement of the potassium atom. The potassium moves from interacting with the six-membered ring and the CO₂ group to only with the CO₂ group in TS2. The last TS, TS3, corresponds to the beginning of the formation of the O–B bond. The energetic values of this profile indicate that the reaction in the presence of potassium will be slightly slower than without it (TS with more positive values) and less favorable thermodynamically. Using the Eyring equation⁵¹ and considering the more energetic TS to calculate the rate constant of the reaction, it was found that k = 1.53 × 10⁻⁴ s⁻¹ for the reaction without the cation, and k = 4.21 × 10⁻⁵ s⁻¹ with the potassium cation.

It is interesting to notice that the shape of the free energy profile of the reactions shown along the main article is very similar to the corresponding one with the electronic energy, shown in the ESI,† but adding to the last one the entropic penalty derived from the reduction of the number of molecules along the reactions (in average 46 kJ mol⁻¹ in the reactions shown in Fig. 3 and Fig. S1, ESI†).

From the molecular graphs of Fig. 3, it can be observed that the first bond created, when CO₂ interacts with BBZN or BBZN-K, is the C–C bond between the carbon of the CO₂ and the carbon in the para of BBZN. The bond is already created in the first TS. By looking at the electron density at the bond-critical point (ρ_BCP) of the C–C bond, the BBZN/CO₂ TS shows a 74% of the value obtained in the final adduct and 42%, 77% and 90% for TS1, TS2, TS3 when compared to the adduct of the reaction with BBZN-K, respectively. In contrast, the boron oxygen bond only shows up in the last TS of the reaction, being the ρ_BCP values of 21 and 25% in the BBZN/CO₂ and TS3 of BBZN-K/CO₂ with respect to their values in the corresponding adducts, respectively.

3.2. 9-Borataanthracene and its reaction with CO₂

The X-ray structures of two 9-borataanthracenes with a phenyl substituent in the boron atom are available in the CSD database, refcodes: GAFXUG and GAGGIE.⁵² In both cases, the counter cations (lithium-tetramethylethylenediamine and zirconium-pentamethyl-cyclopentadienyl, respectively) interact with the central aromatic ring where the boron atom is located. The experimental and calculated geometries are shown in Fig. S2 (ESI†) and they show similar parameters. The borataanthracene tricyclic structure is planar in our calculation and in the GAFXUG refcode while in the GAGGIE one it is slightly distorted from planarity probably due to the packing effect of the counterion. The B–C bonds in the six membered ring show a distance of 1.53 Å approx. and the C–C bonds are shorter as it was observed in the boratabenzene structure previously discussed.

The MESPs of BA and BA-K are shown in Fig. 4. In the case of BA, two symmetric minima are found above/below the center of the middle ring with a value of −459.2 kJ mol⁻¹ while the maxima are located in the periphery as in the case of BBZN. In the BA-K system, the potassium atom is located on one of the minima found for the isolated BA while in the opposite face a minimum with a value of −134.7 kJ mol⁻¹ is found. The minima found in BA and BA-K could be available for the interaction with the carbon atom of CO₂.

Fig. 4 MESPs of BA and BA-K on the 0.001 a.u. electron density isosurface. The locations of the minima and maxima are indicated with cyan and black small spheres and their values are indicated in kJ mol⁻¹.

The reaction of BA + CO₂ proceeds with the formation of a BA:CO₂ pre-reactive complex with the CO₂ located above the central ring (Fig. 5a) and an electronic energy stabilization of 36 kJ mol⁻¹ (Fig. S3, ESI†), followed by a TS with a relative free energy of 49 kJ mol⁻¹ with respect to the isolated monomers, yielding a very stable adduct (ΔG_rel = −50 kJ mol⁻¹) (Fig. 5a). The BA system is highly distorted due to the formation of the adduct with CO₂ showing a deformation energy of 294 kJ mol⁻¹.

Fig. 5 Free energy profiles at 298.15 K of reactions BA + CO₂ → BA-CO₂ (left) and BA-K + CO₂ → BA-K-CO₂ (right)with the molecular graphs of the stationary points.

In the case of the BA-K +CO₂ reaction, two pre-reactive complexes have been obtained (Fig. S4, ESI†). The most stable (a binding energy of −27.6 kJ mol⁻¹) and precursor of the reaction shows the interaction of one oxygen atom of CO₂ with the potassium cation, BA-K:CO₂(1). The less stable one (−8 kJ mol⁻¹) shows the CO₂ interacting with BA in the opposite face of the potassium cation, BA-K:CO₂(2). This complex will not be considered further in this study.

In the case of the boratabenzene, the presence of the potassium cation stabilizes an additional intermediate and the corresponding TS before reaching the final product (Fig. 5b). The relative free energies of TS1, Int1 and TS2 are 52, 20 and 39 kJ mol⁻¹, respectively. Therefore, the first TS will be the limiting step and the stability of the final product (ΔGrel = −41 kJ mol⁻¹) will be the driving force of the reaction.

In the case of BBZN and BBZN-K, the C–C bond between BBZN and CO₂ is formed already in the first TS. The value of ρ_BCP in the C–C bond of the BA/CO₂ TS shows a value that corresponds to a 33% of the final adduct while in TS1 of BA-K/CO₂ it is a 20% of the corresponding final adduct. These percentages are lower than the ones obtained in the case of BBZN and BBZN-K. It can then be considered that these TSs are earlier than the ones of BA, which agrees with the lower TS energies observed in the case of BA and BA-K reactions. In the reaction with BA and BA-K, no B-O BCP is localized in the last TS, again agreeing with the early stage of the TSs.

3.3. Cis and trans-diborapentacene dianions

5,12-Dimethyl-5,12-diboratapentacene (trans-DBP) and 5,7-dimethyl-5,7-diboratapentacene (cis-DBP) potassium salts (Refcode: NEWBAW, NEWBEA, NEWBIE, NEWBOK)³⁹ and the corresponding CO₂ adducts are available in the CSD database (Refcode: NEWCOL, NEWCUR, and NEWDAY).³⁹ Superpositions of experimental and optimized structures are available in Fig. S5 (ESI†). In general, the calculated results reproduce appropriately the results obtained in the crystal structure with the exception of potassium cations, since in the X-ray structures these cations interact with several molecules.

The calculated MESPs of the two isolated diboratapentacene cis and trans isomers are very similar (Fig. 6). Moreover, due to the symmetry plane of the molecule, the two faces of DBP are equivalent. The central ring has a larger minimum than the lateral rings. This is in agreement with the experimental observation that the central rings are more aromatic than the lateral ones.³⁹

Fig. 6 MESPs of cis-DBP and trans-DBP (M06-2X/def2TZVP wave function; isosurface 0.001 a.u.; range [−660.0 and −365.0] kJ mol⁻¹.).

The reaction of CO₂ with cis-DBP and trans-DBP can yield two mono-adducts (one per DBP molecule) and four di-adducts (two per DBP molecule, one with the two molecules of CO₂ in the same face of the DBP molecule, syn, and another with the two molecules in opposite faces, anti). Our calculations suggest that the reactions proceed stepwise and the mono-adducts are formed first and are intermediates in the formation of the di-adducts as confirmed by a 2D scan (Fig. S6, ESI†).

The free reaction profile of the addition of CO₂ is very similar to that of cis-DBP and trans-DBP (Fig. 7 and Fig. S7, ESI†), being very favorable for the formation of the di-adducts with no significant preferences for the anti and syn addition of the CO₂ molecules. The molecular graphs of the stationary points along the reaction show similar characteristics to the ones obtained for the reactions with BA and BA-K. The C–C bonds are formed in very early stage in different TS, and a BCP between oxygen and boron is only localized in the final adducts. The adduct formation with the first CO₂ molecule produces free energy stabilization values of 79 and 95 kJ mol⁻¹ with respect to the isolated molecules in the cis- and trans-DBP, respectively. The insertion of the second CO₂ molecule yields products that are around 150 kJ mol⁻¹ more stable than the entrance channel. In both reactions, the barrier from the pre-reactive complex and the first TS is smaller than 21 kJ mol⁻¹. In addition, it is interesting to notice that save the first complex and TS1, the relative free energy of all the stationary points are below the entrance channel and indicates that the reaction will proceed spontaneously once the TS1 is overcome.

Fig. 7 Free energy reaction profiles of the anti addition of two CO₂ molecules to the trans-DBP(left) and cis-DBP (right), with the corresponding molecular graphs of the stationary points.

3.4. Cis and trans-diborapentacene potassium salts

The four potential neutral potassium diboratapentacene salts (Fig. 8), two for each diboratapentacene isomer, have been optimized with the potassium atoms in the same, syn, or opposite faces, anti. The relative energies of these molecules show that the anti isomers (potassium atoms in the opposite faces) are more stable than the syn ones by around 30 kJ mol⁻¹. This energy difference can be explained by the electrostatic repulsion of the potassium cations when they are located in the same face of the diboratapentacene systems which is reduced when they are in opposite ones. In the rest of this section, only the structure with potassium atoms in anti will be considered.

Fig. 8 Optimized DBP-K monomers (M06-2X/def2TZVP).

The MESPs of the cis-DBP-K-anti and trans-DBP-K-anti (Fig. 9) are very similar: a positive region associated with the potassium atoms and a negative one on the opposite face of the DBP. Thus, the Sigma hole of the CO₂ can interact with the basic carbon atom of DBP, and the lone pair of one oxygen atom can interact with the potassium cation to form the pre-reactive complexes, like in the case of the BA-K complex.

Fig. 9 MESP monomers with cations (M06-2X/def2TZVP); electron density isosurface 0.001 a.u.; range [−30.0 and +30.0] kJ mol⁻¹.

In agreement with the MESP, the first step of the reaction of cis-DBP-K and trans-DBP-K proceeds with the formation of a complex where the CO₂ interacts with one of the potassium cations, as in the case of the BA-K:CO₂ complex, with an interaction energy of 39 kJ mol⁻¹ (Fig. 10 and Fig. S8, ESI†). As in the case of the BA-K systems, the adduct formation with the first CO₂ molecule evolves with the presence of an intermediate and two TSs, yielding a mono-adduct which are slightly less stable than the corresponding ones obtained with the isolated dianions (ΔG_rel = −74 and −91 kJ mol⁻¹ for the adducts of the cis-DPB-K and trans-DBP-K systems, respectively).

Fig. 10 Free energy reaction profiles of cis- (green) and trans-DBP-K (black) with two CO₂ molecules.

The reaction with the second CO₂ molecule starts with the corresponding pre-reactive complex in the opposite face where the first CO₂ has been added since it corresponds to the location of the potassium cation that has not interacted with CO₂ yet. As previously described, an intermediate is located before reaching the final product with two CO₂ molecules added to DBP and the corresponding two TSs. The final molecules are very stable (ΔG_rel = −121 and −135 kJ mol⁻¹ for the cis and trans-DBP-K systems) but about 25 kJ mol⁻¹ less stable than the corresponding molecules in the absence of the potassium cations.

The corresponding syn products of the addition of two CO₂ molecules (Fig. S9, ESI†), not observed experimentally, are 58.0 and 53.3 kJ mol⁻¹ less stable than the anti ones obtained for the cis and trans-DBP-K molecules, respectively.

3.5. Solvent effect on the reaction (THF)

In order to evaluate the effect of the solvent in the reaction, all the stationary points were reoptimized using a continuous model of solvent with the THF parameters since this solvent was used experimentally. The corresponding results are shown in Fig. 11 and compared to the previous results in the gas phase.

Fig. 11 Relative free energy (kJ mol⁻¹) of the different single CO₂ adducts in vacuum and in solution (THF) with respect to the isolated borata derivatives + CO₂.

As it can be observed in Fig. 11, the solvation in THF favors the adducts with cations with respect to those in the gas phase, while the anionic systems are destabilized with the exception of the AB-CO₂ adduct that is 3.4 kJ mol⁻¹ more stable in THF than in the gas phase. These results indicate that in the systems that includes the cations, the solvation of the adducts is more favorable than the solvation of the reactants while in the anions, it is the opposite, the solvation of the reactants is more important than the solvation of the adducts. These results can be easily rationalized using the thermodynamic cycle included in the ESI† (Fig. S10).

The solvation has an interesting geometric effect in the case of the DBP-K systems. The adducts of 2-cis-DBP-K and 2-trans-DBP-K have the two cations interacting simultaneously with the CO₂ molecules and the π-system of the DBP in the gas phase. The inclusion of the solvent produces the migration of one of the cations towards outer regions and the single interaction with one of the CO₂ molecules (Fig. 12). In addition, a second conformation is observed in THF, but not in the gas phase, with a relative energy of +15 kJ mol⁻¹, which resembles the structures found in the crystal structure.

Fig. 12 Adduct structures of cis-DBP-K in the gas phase and THF solution.

3.6. Effect of the presence of 18-crown-6-ether molecules

The presence of 18-crown-6-ether molecules has been shown to influence the stereochemistry of the CO₂ addition to the diboratapentacene molecules. In the absence of the crown ether, the anti addition is obtained while in its presence the syn addition is obtained.³⁹

The 18-crown-6-ether molecule surrounds the potassium cations and reduces the positive region of the MESP (no “blue” regions around the potassium atom) while the minima associated with the diborataacenes is now located in the extreme aromatic ring in the opposite face of the potassium-crown ether situation as can be seen in Fig. S11 (ESI†).

When the first CO₂ is added to the diborataacenes, the potassium and the surrounding crown ether that are in the same face of the DBP move to interact with the CO₂ molecule allowing the second molecule to interact in the same face producing the syn product (Fig. 13). The opposite face is before the addition of the second CO₂ molecule fully covered by the potassium cation and the corresponding crown ether and does not allow the interaction of the second CO₂ molecule with this face of the DBP preventing the formation of the anti adducts. The last step of this reaction is the reorganization of the potassium cation and the corresponding crown ether to interact with the last CO₂ added.

Fig. 13 Proposed mechanism for the generation of the syn adduct in the presence of crown ethers. The structures shown have been optimized at the M06-2X/def2SVP computational level.

4. Conclusions

A theoretical study of the reaction of boratabenzene, boratanaphthalene and cis and trans diboratapentacene with CO₂ has been carried out at the M06-2X/def2TZVP level of theory. Borataacenes have been considered as anions and as neutral salts in the presence of potassium cations. All the stationary points connecting the isolated monomers to the CO₂ adducts have been characterized. The reaction with the anions are simpler, and in general they involve the formation of a pre-reactive complex and a TS that connects with the adduct for each CO₂ molecule. The reaction in the presence of the potassium counterion provides several intermediates due to the simultaneous bond formation of CO₂ with the borataacene and the movement of the cation from its initial disposition, interacting with the π-cloud of the borataacene and interacting with the added CO₂ molecule.

Based on the free energy variation at room temperature, all the reactions studied are favorable, except for the formation of BBZN-CO₂ and BBZN-K-CO₂ that are 37.3 and 64.5 kJ mol⁻¹ less stable than the isolated monomers. In the gas phase, the incorporation of the CO₂ molecule in the anions is more favorable when the potassium counterion is present.

The inclusion of THF as a solvent in our models increases the stability of the adducts formed in the neutral salts when compared to the results obtained in the gas phase, while the adducts of the anions are slightly destabilized.

The stabilization of the adducts is parallel to the size of the borataacenes since the deformation energy decreases as the size of the acene increases.

The quantum chemical results of this work are in good agreement with the experiments.

Author contributions

MF did the calculations and tabulated the results. MF and IA wrote the first draft of the article. All the authors revised and improved the article.

Conflicts of interest

The authors declare that they have no conflicts of interest.

Acknowledgements

This work was carried out with financial support from the Ministerio de Ciencia, Innovación y Universidades (Projects PID2021-125207NB-C32). Thanks are given to the Centro de Supercomputación de Galicia (CESGA), CTI (CSIC) and the Irish Centre for High-End Computing (ICHEC, Dublin) for their continued computational support.

References

1. D. P. Keller, A. Lenton, E. W. Littleton, A. Oschlies, V. Scott and N. E. Vaughan, Curr. Clim. Change Rep., 2018, 4, 250–265.
2. E. S. Sanz-Pérez, C. R. Murdock, S. A. Didas and C. W. Jones, Chem. Rev., 2016, 116, 11840–11876.
3. L. A. Darunte, K. S. Walton, D. S. Sholl and C. W. Jones, Curr. Opin. Chem. Eng., 2016, 12, 82–90.
4. G. Rim, F. Kong, M. Song, C. Rosu, P. Priyadarshini, R. P. Lively and C. W. Jones, JACS Au, 2022, 2, 380–393.
5. J. J. Lee, C. Sievers and C. W. Jones, Ind. Eng. Chem. Res., 2019, 58, 22551–22560.
6. Y. Zhang, X. Ji and X. Lu, Renewable Sustainable Energy Rev., 2018, 97, 436–455.
7. M. Farsi and E. Soroush, in Advances in Carbon Capture, ed. M. R. Rahimpour, M. Farsi and M. A. Makarem, Woodhead Publishing, 2020, pp. 89–105 DOI:10.1016/B978-0-12-819657-1.00004-9.
8. V. Alizadeh, L. Esser and B. Kirchner, J. Chem. Phys., 2021, 154, 094503.
9. P. Chen, T. Xiong, Y. Pan and Y. Liang, Asian J. Org. Chem., 2022, 11, e202100738.
10. H. A. Duong, T. N. Tekavec, A. M. Arif and J. Louie, Chem. Commun., 2004, 112–113,  10.1039/B311350G.
11. I. Alkorta, M. M. Montero-Campillo and J. Elguero, Chem. Eur. J., 2017, 23, 10604–10609.
12. S. Soroudi and M. Z. Kassaee, J. Phys. Org. Chem., 2022, 35, e4323.
13. J. E. Del Bene, I. Alkorta and J. Elguero, J. Phys. Chem. A, 2017, 121, 8136–8146.
14. I. Alkorta, M. M. Montero-Campillo and J. Elguero, Chem. – Eur. J., 2017, 23, 10604–10609.
15. S. Anila and C. H. Suresh, Phys. Chem. Chem. Phys., 2021, 23, 13662–13671.
16. R. D. d E. Santo, R. M. Capitão and E. R. P. González, in Guanidines as Reagents and Catalysts II, ed. P. Selig, Springer International Publishing, Cham, 2017, pp. 27–74 DOI:10.1007/7081_2015_167.
17. C. A. Seipp, N. J. Williams, M. K. Kidder and R. Custelcean, Angew. Chem., Int. Ed., 2017, 56, 1042–1045.
18. F. Buß, P. Mehlmann, C. Mück-Lichtenfeld, K. Bergander and F. Dielmann, J. Am. Chem. Soc., 2016, 138, 1840–1843.
19. I. Alkorta, C. Trujillo, G. Sánchez-Sanz and J. Elguero, Inorganics, 2018, 6, 110.
20. G. Sánchez-Sanz, I. Alkorta, J. Elguero and C. Trujillo, Chem. Phys. Chem., 2019, 20, 3195–3200.
21. C. B. Musgrave Iii, A. Prokofjevs and W. A. Goddard Iii, J. Phys. Chem. Lett., 2022, 13, 11183–11190.
22. A. E. Ashley and D. O’Hare, Top. Curr. Chem., 2012, 334, 191–217.
23. M. Ferrer, I. Alkorta, J. Elguero and J. M. Oliva-Enrich, J. Phys. Chem. A, 2021, 125, 6976–6984.
24. T. Wang, M. Xu, A. R. Jupp, Z.-W. Qu, S. Grimme and D. W. Stephan, Angew. Chem., Int. Ed., 2021, 60, 25771–25775.
25. R. Pal, M. Ghara and P. K. Chattaraj, Catalysts, 2022, 12, 201.
26. M. Ferrer, I. Alkorta, J. M. Oliva-Enrich and J. Elguero, Struct. Chem., 2023, 34, 1591–1601.
27. T. A. R. Horton, M. Wang and M. P. Shaver, Chem. Sci., 2022, 13, 3845–3850.
28. H. Demir, G. O. Aksu, H. C. Gulbalkan and S. Keskin, Carbon Capture Sci. Technol., 2022, 2, 100026.
29. J. H. Choe, H. Kim and C. S. Hong, Mater. Chem. Front., 2021, 5, 5172–5185.
30. G. Benedetto, B. M. Cleary, C. T. Morrell, C. G. Durbin, A. L. Brinks, J. Tietjen and K. A. Mirica, J. Chem. Educ., 2023, 100, 1289–1295.
31. M. Ferrer, I. Alkorta, J. Elguero and J. M. Oliva-Enrich, Sci. Rep., 2023, 13, 2407.
32. M. Ferrer, I. Alkorta, J. Elguero and J. M. Oliva-Enrich, Chem. Phys. Chem., 2022, 23, e202200204.
33. A. Lorbach, M. Bolte, H.-W. Lerner and M. Wagner, Chem. Commun., 2010, 46, 3592–3594.
34. G. Berionni, Chem. Sci., 2023, 14, 5241–5242.
35. I. Cortés, J. J. Cabrera-Trujillo and I. Fernández, ACS Org. Inorg. Au, 2022, 2, 44–52.
36. J. W. Taylor, A. McSkimming, C. F. Guzman and W. H. Harman, J. Am. Chem. Soc., 2017, 139, 11032–11035.
37. M. Dietz, M. Arrowsmith, A. Gärtner, K. Radacki, R. Bertermann and H. Braunschweig, Chem. Commun., 2021, 57, 13526–13529.
38. Y. Ishikawa, K. Suzuki and M. Yamashita, Organometallics, 2019, 38, 2597–2601.
39. J. E. Barker, A. D. Obi, D. A. Dickie and R. J. Gilliard, Jr., J. Am. Chem. Soc., 2023, 145, 2028–2034.
40. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
41. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
42. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
43. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson and H. Nakatsuji, et al., Gaussian 16; Revision, A.03, Gaussian, Inc., Wallingford, CT, USA, 2016.
44. R. F. W. Bader, Atoms In Molecules: A Quantum Theory, Clarendon Pr., 1990.
45. P. L. A. Popelier, Atoms In Molecules. An introduction, Prentice Hall, Harlow, England, 2000.
46. T. A. Keith, AIMAll, 19.10.12 Version (aim.tkgristmill.com).
47. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
48. Jmol: an open-source Java viewer for chemical structures in 3D. http://www.jmol.org/.
49. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B, 2016, 72, 171–179.
50. G. E. Herberich, B. Schmidt and U. Englert, Organometallics, 1995, 14, 471–480.
51. H. Eyring, J. Chem. Phys., 2004, 3, 107–115.
52. R. A. Lee, R. J. Lachicotte and G. C. Bazan, J. Am. Chem. Soc., 1998, 120, 6037–6046.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02516k

---