Open Access Article
Open Access ArticleCorrelation vs. exchange competition drives the singlet–triplet excited-state inversion in non-alternant hydrocarbons†
M. E.
Sandoval-Salinas
 ab,
G.
Ricci
ab,
G.
Ricci
 c,
A. J.
Pérez-Jiménez
c,
A. J.
Pérez-Jiménez
 a,
D.
Casanova
a,
D.
Casanova
 *de,
Y.
Olivier
*de,
Y.
Olivier
 *c and
J. C.
Sancho-García
*c and
J. C.
Sancho-García
 *a
*a
aDepartment of Physical Chemistry, University of Alicante, E-03080 Alicante, Spain. E-mail: jc.sancho@ua.es
bSchool of Physical and Chemical Science, Queen Mary University of London, London, UK
cUnité de Chimie Physique Théorique et Structurale, & Laboratoire de Physique du Solid, Namur Institute of Structured Matter, Université de Namur, B-5000 Namur, Belgium. E-mail: yoann.olivier@unamur.be
dDonostia International Physics Center (DIPC), E-20018 Donostia, Euskadi, Spain. E-mail: david.casanova@ehu.es
eIKERBASQUE-Basque Foundation for Science, E-48009 Bilbao, Euskadi, Spain
First published on 14th July 2023
Abstract
In this work, we focus on the understanding of the driving force behind the S1–T1 excited-state energy inversion (which would thus violate Hund's rule, making the S1 state lower in energy than the T1 state) of two non-benzenoid non-alternant hydrocarbons, composed of odd-membered rings. The molecules considered here have identical chemical composition but different atomic configuration in space. The delicate interplay between structural and electronic factors that might induce inversion and its energy extension, only by a few meV, is systematically investigated here by state-of-the-art calculations. Qualitative and quantitative accurate predictions are obtained employing post-HF methods, thanks to the balanced and careful inclusion of electron correlation effects. The obtained results might guide and rationalize new searches for molecules violating Hund's rule, concomitantly demonstrating the importance of key contributions from the theoretical method of choice.
1. Introduction
The molecules dicyclohepta[cd,gh]pentalene (1) and dicyclopenta[ef,ki]heptalene (2) are non-benzenoid non-alternant hydrocarbons, see Fig. 1, historically predicted as candidates violating Hund's rule in their lowest singlet (S1) and triplet (T1) excited states.1,2 Thus, hypothetically situating S1 lower in energy with respect to T1, contrarily to most of the known conjugated systems.3 The simplest combination of cycloheptatriene (a 7-membered ring) and cyclopentadiene (a 5-membered ring) indeed constitutes the azulene molecule, which can thus be viewed as the building block of compounds 1 and 2. However, it has been experimentally confirmed by photodetachment photoelectron spectroscopy that azulene does not violate Hund's rule.4 On the other hand, the violation of Hund's rule has been very recently predicted from theoretical calculations5 only for compound 1 and not for 2, but experiments to corroborate this finding are still missing, as far as we know, which has prompted us to systematically investigate in detail these systems given their structural similarity. Interestingly, the violation of Hund's rule for excited states of compounds 1 and/or 2 would arise without the need to introduce heteroatoms into their structure, as opposed to the recently synthesized heptazine derivatives for which a negative ΔEST was demonstrated.6 The latter study first screened a large set (around 35 × 103) of compounds to identify viable candidates for this excited-state energy inversion, to then narrow down the set of candidates to only 3% of the original number. They finally selected a pair of molecules to be synthesized and experimentally analyzed by temperature-dependent transient photoluminescence spectroscopy, constituting a clear advance from an experimental point of view and showing how challenging and costly can be the whole process to optimize molecules expected to behave in this way.Actually, the different calculations so far performed on nitrogen and/or boron-doped materials not only anticipated this effect long ago for heterodoped compounds, but also allowed the understanding of the physical effects driving this excited-state inversion.7–16 Invigorated by this set of experimental and theoretical advances, possibly fostered by the promise of a superior light-emitting efficiency of these organic compounds under, e.g., electroluminescence stimuli, a recent and massive screening of heteroatom-doped candidates confirmed that the energy inversion of the S1 and T1 excited states was not exclusive of cyclazine or heptazine, but could occur in tens of other closely related compounds.17 Furthermore, following this line of work,18 a large number of pure all-carbon systems (hydrocarbons) were also recently screened employing high-level calculations,5 concluding that the excited-state energy inversion is not limited to heteroatom-doped systems. One of the main outcomes of the latter study, to be emphasized in the present context, was the prediction of the violation of Hund's rule for compound 1 but not for compound 2, which therefore disagrees with previous investigations2 and opens the door to deeper investigations to unveil the physical reason(s) for such a difference, given the structural and chemical similarity of both molecules.
The relevance of understanding whether excited-state inversion on non-benzenoid alternant hydrocarbons is viable or not relies on their potential application for the development of organic light-emitting diodes (OLEDs)19 or for photocatalytic applications,20 given the recent interest attracted by this family of molecules showing the excited-state inversion,21 together with advances in parallel for synthesizing adequately substituted hydrocarbons containing rings with an odd number of C atoms to exhibit luminescence.22,23 As a matter of illustration of the envisioned technological improvements, the enhanced luminescence and associated quantum yields upon the harvesting of (initially dark) triplet excitons could be the driving force for other discoveries and applications, noticing the unusual downconversion experienced by triplet to singlet excitons following a Reverse Intersystem Crossing Process (RISC). Actually, the use of these molecules for real-world applications would need the exploration of substituted derivatives (i.e., reducing the symmetry of the compounds) to concomitantly display the aforesaid excited-state energy inversion together with non-vanishing oscillator strength values.5
Therefore, these findings have prompted us to investigate in more detail the relationships between the chemical structure and Hund's rule violation for excited states of compounds 1 and 2, as well as their building block, the azulene molecule. With the help of theoretical methods, we will address here the interplay of exchange and correlation effects, to correctly interpret the results from the electronic structure point of view, as well as the role played by symmetry or aromaticity effects, from the structural point of view, as done recently.5,24
2. Computational details
The geometries of azulene and compounds 1 and 2 are fully optimized (with no symmetry restrictions) at the ωB97XD/def2-TZVP level of theory.25 We calculate the vertical excitation singlet (S1 ← S0) and triplet (T1 ← S0) energies, resulting in the energy difference ΔEST = E(S1 ← S0) − E(T1 ← S0), employing a variety of wavefunction methods. First, configuration interactions (CI) with single (S) and partially introduced double (D) substitutions, or CIS and CIS(D),26 respectively, as well as the spin-component-scaled (SCS-) version of the latter, SCS-CIS(D),27 will be applied, followed by a second-order approximate Coupled Cluster singles and doubles method CC228,29 and second-order Algebraic Diagrammatic Construction ADC(2),30 together with their corresponding SCS-based versions, named SCS-CC2 and SCS-ADC(2), respectively. The latter corrects excitation energies by introducing different opposite-spin (COS = 6/5) and same-spin (CSS = 1/3) coefficients, which are obtained after a reparameterization against some training sets.31The restricted active space (RAS) method is selected here to obtain reference results due to its excellent trade-off between accuracy and computational cost for any spin-dependent multi-state calculation.32–34 First, a Configuration Interaction (RAS-CI35–37) is obtained through the hole-particle formalism. A Spin-Flip (RAS-SF38–40) flavor is next applied, using a triplet state as a high-spin reference and incorporating by default mostly the non-dynamical (long-range) correlation energy. Then, an additional exchange–correlation energy functional is coupled (RAS-CI-srDFT or simply RAS-srDFT in the following) to incorporate some of the missing dynamic (short-range) correlation energy.41 As the active space of n electrons in m orbitals needed for any of these RAS-based calculations, denoted here simply as [n,n], we will use minimal[2,2], moderate ([4,4] and [6,6]), and large ([8,8] and [10,10]) active spaces in all cases to understand the influence of the correlation energy added by increasing the active space size. All of these results are compared with the equation-of-motion coupled-cluster single and doubles method, or EOM-CCSD,42 which has recently been shown to be a very accurate method for electronic excitations too.43
Time-dependent density functional theory (TD-DFT) will also be applied complementarily due to its wide use for excited-state calculations. To isolate the dependence of the TD-DFT results with respect to the functional form, we keep the parameter-free PBE exchange (Ex[ρ]) and correlation (Ec[ρ]) functionals fixed, and systematically vary the weight (cx) of the EXact-eXchange (EXX) term to form the corresponding hybrid expression as:
| Exc[ρ] = Ex[ρ] + Ec[ρ] = cxEEXXx + (1 − cx)Ex[ρ] + Ec[ρ], | (1) |
| EDHxc[ρ] = Ex[ρ] + ccEPT2c + (1 − cc)Ec[ρ], | (2) |
The cost-effective 6-311G(d) basis set will be employed for all the excited-state calculations, with the ESI† (see Fig. S1) showing the negligible effect beyond the 6-31G(d) basis set, compared with the larger aug-cc-pVDZ or the def2-TZVP ones, at e.g. the RAS-SF level. Nucleus-independent Chemical Shifts (NICS) were evaluated for each of the rings at the ωB97XD/6-311G(d) level25 using the gauge-independent atomic orbital (GIAO) method.57 The TD-DFT, CIS and (SCS-)CIS(D) calculations are done with the ORCA 5.0 package,58 (SCS-)CC2 and (SCS-)ADC(2) with the TURBOMOLE 7.4 package,59 while NICS, RAS[n,n]-CI, RAS[n,n]-SF, RAS[n,n]-srDFT, and EOM-CCSD calculations employed the Q-CHEM 6.0 package.60
3. Results and discussion
3.1 General remarks
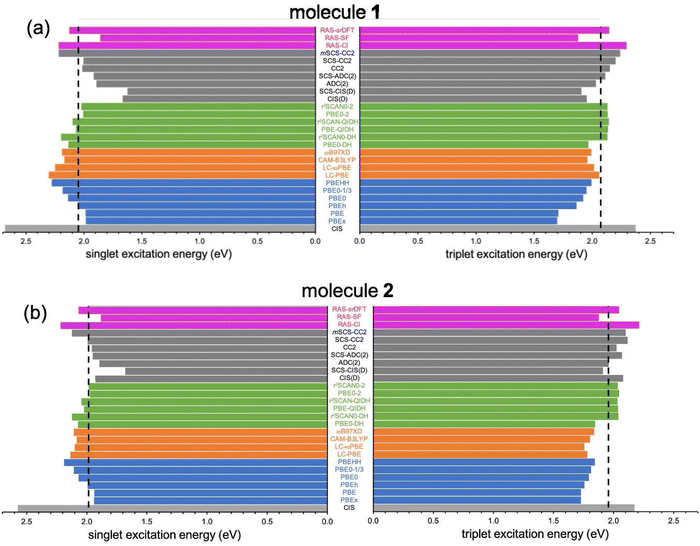
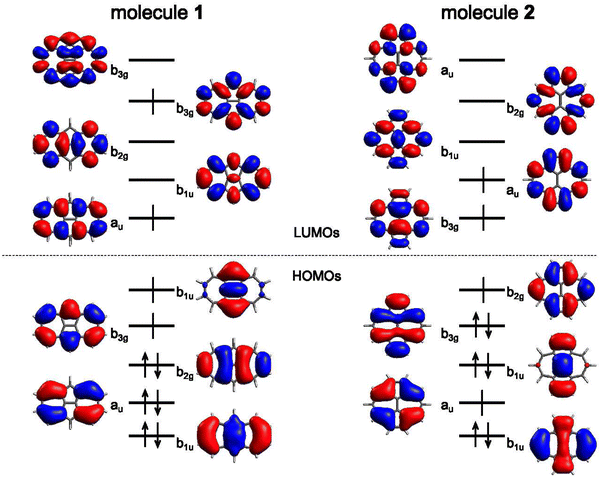
In the following, we explore the performance of a variety of wavefunction and TD-DFT approaches in the computation of singlet and triplet excitation energies for molecules 1 and 2. Moreover, we use the accuracy of the different methods in the calculation of singlet and triplet excitation energies to rationalize the physical effects controlling the singlet–triplet gap, concretely, in 1 and 2, also serving as a general reminder of the necessary requirements to observe their inversion.Ground state optimized structures of 1 and 2 correspond to the D2h symmetry point group. The lowest-lying singlet (S1) and triplet (T1) excited states of the two non-alternant hydrocarbons are (almost) exclusively composed by a HOMO to LUMO (π → π*) electronic excitation (i.e., from the highest occupied molecular orbital or HOMO to the lowest unoccupied molecular orbital or LUMO), regardless of the employed computational method. Interestingly, despite that the frontier molecular orbitals of 1 and 2 have different symmetries (see Fig. 2), S1 and T1 in both cases belong to the B1g irreducible representation. Therefore, the optical transition to S1 at the Franck–Condon region is symmetry forbidden, i.e., would display a zero oscillator strength.
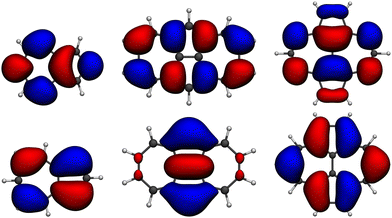 | ||
| Fig. 2 Isocontour plots (σ = 0.02 e bohr−3) of the LUMO (top) and HOMO (bottom) of the molecules studied: azulene, 1, and 2 (from left to right) computed at the HF/6-311G(d) level. | ||
EOM-CCSD/6-311G(d) results reveal that the computed vertical energies to S1 and T1 for 1 are 2.053 and 2.078 eV, respectively, hence suggesting a singlet–triplet inversion of −25 meV, in good agreement with previous calculations5 at the EOM-CCSD/aug-cc-pVDZ level (ΔEST = −14 meV). On the other hand, in 2, the excited singlet lies slightly above the lowest triplet (ΔEST = 23 meV), with transition energies obtained at 1.991 and 1.968 eV, respectively, thus indicating a different state ordering for 1 and 2.
3.2 The role of orbital localization, exchange, and aromaticity
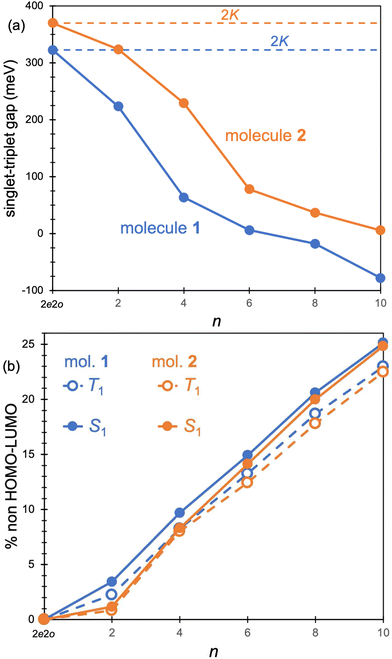
The origin of the small singlet–triplet gap in these π-conjugated molecules (ΔEST < 100 meV) emerges from the small exchange energy, which relates to the properties of the two frontier orbitals (mostly) describing the S1 ← S0 and T1 ← S0 electronic transitions. Note that HOMO and LUMO of both biazulenes exhibit a disjoint-like nature (Fig. 2), thus resulting in a small spatial overlap, which is known to promote low ΔEST values.61 Actually, we have calculated Tozer's Λ index,62 a measure of spatial overlap for a given excitation ranging between 0 (no overlap) and 1 (full overlap), at the HF/6-311G* level, to find values of Λ = 0.466 and Λ = 0.566 for 1 and 2, respectively, thus indicating a smaller overlap for compound 1 than for compound 2, as well as for azulene for which Λ = 0.589.This situation resembles the electronic structure of disjoint non-Kekulé diradicals, in which both semioccupied orbitals are represented over different sets of atoms. Then, by decreasing the electronic repulsion, the triplet is less favored over the singlet; i.e., the gap between both states narrows.63 Indeed, in a simplified two-electrons in two-orbitals (2e2o) model, i.e., CAS-CI(2,2), S1 and T1 states correspond (entirely) to the spin adapted single electron occupation of HOMO and LUMO for compounds 1 and 2. For disjoint orbitals, as those HOMO and LUMO found in 1 and 2, the small exchange integral  between the HOMO (ϕi ≡ ϕHOMO) and the LUMO (ϕj ≡ ϕLUMO) gives rise to low exchange energy and thus to low ΔEST gap, since ΔE2e2oST = 2K, computed as 323 and 370 meV for 1 and 2, respectively.
between the HOMO (ϕi ≡ ϕHOMO) and the LUMO (ϕj ≡ ϕLUMO) gives rise to low exchange energy and thus to low ΔEST gap, since ΔE2e2oST = 2K, computed as 323 and 370 meV for 1 and 2, respectively.
The description of S1 and T1 in 1 and 2 by the simple CIS method nearly corresponds to the 2e2o model (HOMO to LUMO amplitudes greater than 0.98 for both cases). CIS overestimates both excitation energies (see Table 1 and Fig. 3), especially for S1, which might be attributed to the lack of electron correlation.64 In fact, CIS can be seen as a mean-field approach for excited states, similar to HF for the electronic ground state. The CIS singlet–triplet energy gap can be approximately related to the exchange interaction, ΔEST ≈ 2K, because CIS includes configuration interaction effects beyond the 2e2o scheme. Since K > 0, CIS always locates S1 above T1, with a 308 meV gap for 1 and higher (399 meV) for 2.
| Method | 1 | 2 | ||||
|---|---|---|---|---|---|---|
| S1 ← S0 | T1 ← S0 | ΔEST | S1 ←S0 | T1 ←S0 | ΔEST | |
| a Taken from ref. 5. | ||||||
| CIS | 2.684 | 2.376 | 308 | 2.576 | 2.177 | 399 |
| PBEx | 1.985 | 1.701 | 284 | 1.942 | 1.732 | 210 |
| PBE | 1.989 | 1.711 | 278 | 1.941 | 1.732 | 209 |
| PBEh | 2.050 | 1.867 | 183 | 1.994 | 1.761 | 233 |
| PBE0 | 2.139 | 1.924 | 215 | 2.070 | 1.798 | 272 |
| PBE0-1/3 | 2.186 | 1.953 | 233 | 2.110 | 1.816 | 294 |
| PBEHH | 2.279 | 1.996 | 283 | 2.190 | 1.847 | 343 |
| LC-PBE | 2.305 | 2.061 | 244 | 2.266 | 1.943 | 323 |
| LC-ωPBE | 2.252 | 2.019 | 233 | 2.221 | 1.903 | 318 |
| CAM-B3LYP | 2.171 | 1.962 | 209 | 2.087 | 1.808 | 279 |
| ωB97XD | 2.190 | 1.995 | 195 | 2.110 | 1.842 | 268 |
| PBE0-DH | 2.136 | 1.970 | 166 | 2.075 | 1.849 | 226 |
| r2SCAN0-DH | 2.198 | 2.134 | 64 | 2.125 | 2.044 | 81 |
| PBE-QIDH | 2.072 | 2.138 | −66 | 2.027 | 2.039 | −12 |
| r2SCAN-QIDH | 2.101 | 2.145 | −44 | 2.048 | 2.035 | 13 |
| PBE0-2 | 2.010 | 2.137 | −127 | 1.977 | 2.049 | −72 |
| r2SCAN0-2 | 2.025 | 2.134 | −109 | 1.988 | 2.038 | −50 |
| CIS(D) | 1.667 | 1.957 | −290 | 1.932 | 2.083 | −151 |
| SCS-CIS(D) | 1.625 | 1.910 | −285 | 1.683 | 1.914 | −231 |
| ADC(2) | 1.895 | 2.034 | −139 | 1.899 | 1.963 | −64 |
| SCS-ADC(2) | 1.918 | 2.114 | −196 | 1.952 | 2.071 | −119 |
| CC2 | 2.017 | 2.155 | −138 | 1.960 | 2.028 | −68 |
| CC2a | 2.033 | 2.155 | −123 | — | — | — |
| SCS-CC2 | 2.007 | 2.204 | −197 | 1.996 | 2.120 | −124 |
| mSCS-CC2 | 2.219 | 2.243 | −24 | 2.126 | 2.102 | 24 |
| EOM-CCSD | 2.053 | 2.078 | −25 | 1.991 | 1.968 | 23 |
| EOM-CCSDa | 2.066 | 2.079 | −14 | — | — | 42 |
| RAS[10,10]-CI | 2.219 | 2.297 | −78 | 2.221 | 2.215 | 6 |
| RAS[10,10]-SF | 1.860 | 1.880 | −20 | 1.886 | 1.881 | 5 |
| RAS[10,10]-srDFT | 2.128 | 2.149 | −21 | 2.071 | 2.048 | 23 |
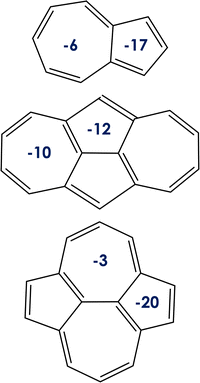 | ||
| Fig. 3 Nucleus-independent chemical shift values (NICS, in ppm) for the rings of the (from top to bottom) azulene, 1, and 2 systems. | ||
Taking into account previous studies,12,13 the strength of the exchange interaction in both systems seems sufficiently weak to be influenced by correlation effects and revert the sign of ΔEST, as obtained from EOM-CCSD calculations on 1. Actually, the ΔEST values recently computed for cyclazine and heptazine at the CIS level, two molecules known to violate Hund's rule,65,66 are 340 and 400 meV, respectively,13i.e., of the same order as those obtained for molecules 1 and 2. On the other hand, despite the disjoint-like character of the HOMO and LUMO in azulene (Fig. 2), it shows a considerably larger 2K value (624 meV at the CIS level), which might thus preclude the inversion of its S1 and T1 energies. Complementarily, sophisticated DFT/MRCI calculations4 predicted a ΔEST value for azulene of 69 meV, small but positive, in agreement with the arguments exposed here.
Note that the orbital localization, aimed at minimizing the exchange integral, is a consequence of symmetry,24 which in some instances is triggered by aromaticity. We use the Nucleus-Independent Chemical Shifts (NICS) to describe the aromaticity of ground state of azulene, and compounds 1 and 2. The NICS values (see Fig. 3) indicate the local aromaticity of all the 5- and 7-membered rings of the compounds under study. Moreover, the values for molecules 1 and 2 fully reflect their D2h nuclear symmetry. Comparing azulene with compounds 1 and 2, the 7-membered ring is always less aromatic than the 5-membered ring, in agreement with previous results.5 Local aromaticities of cycloheptatriene and cyclopentadiene are understood as the consequence of electron sharing, so they both fulfill the (4n+ 2)π-electron Hückel rule for aromaticity. Nevertheless, the lowest ππ* excited states (those S1 and T1 here) in most cases follow the Baird's rule, being classified as aromatic/antiaromatic those cycles with (4n)π/(4n + 2)π-electrons.67 We thus highlight that the localization of the orbitals involved in the S1 and T1 excited state transition is a prerequisite but not a sufficient condition for the excited-state inversion and that aromaticity (in view of Baird's rule for excited states) cannot be used by itself as a criterion for rationalizing or predicting the excited-state energy inversion without further and deeper investigation. Additionally, NICS calculations performed at the DFT level with different exchange–correlation functionals (i.e., CAM-B3LYP, LC-ω PBE, ωB97X-D, PBE0, PBE and PBEh) do not show any clear correlation between state aromaticity and computed S1/T1 gaps (see the ESI†). On the other hand, although it would be interesting to explore differences in excited singlet and triplet aromaticities with correlated wavefunctions, e.g. CASSCF, these calculations are beyond the scope of the present study.
3.3 The critical role of the correlation energy
The results discussed above clearly indicate that weak exchange interaction, although required, it is not a sufficient condition to invert the energy ordering of S1 and T1. Hence, it seems necessary to consider electron correlation effects beyond the mean-field (CIS) solution. For this, we turn our attention to the impact of electron correlation in the computation of singlet–triplet energies within TD-DFT in various flavors and a manifold of wavefunction-based methods.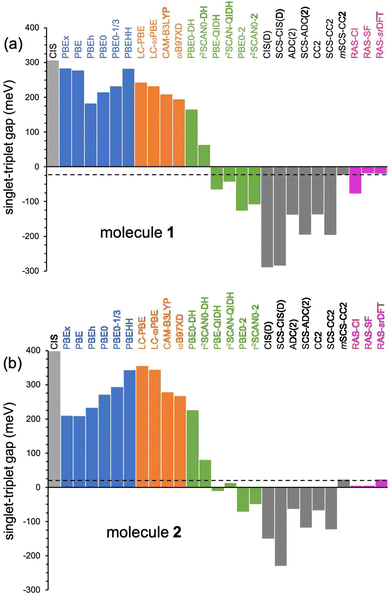 | ||
| Fig. 5 Singlet–triplet energy gaps (in meV) for 1 (a) and 2 (b) computed with different methods with the 6-311G(d) basis set. Horizontal dashed lines indicate the EOM-CCSD (reference) values. | ||
Next, we analyze the performance of double-hybrid functionals for excited-state calculations.68,69 In this sense, we would like to remark that excitation energies with these methods, ΩDH, are obtained in a two-step procedure as: ΩDH = Ω + ccΔ(D), with cc being the weight given in eqn (2) to the perturbative term, which translates to a (D)-like correction to excited states70 of any type. Additionally, their recent application to N-doped organic molecules showing the equivalent excited-state inversion has confirmed their accuracy in the computation of small S1/T1 energy gaps.14 In general, the DH excitation energies for both biazulenes are slightly larger than the EOM-CCSD values (Table 1 and Fig. 4), with ΔEST approaching the reference energy gaps (especially for larger cc values) and linearly decreasing with the cc coefficient. Hence, indicating the importance of wavefunction-like second-order perturbative corrections in order to capture the differential correlation effects between the excited singlet and triplet states. Interestingly, the ΔEST value for compound 1 always remains lower than that for compound 2, although PBE0-DH (PBE-QIDH and PBE0-2) both predicted to be positive (negative).
The use of the r2SCAN exchange–correlation functional instead of PBE attenuates the values in all cases, bringing them closer to the reference results, with r2SCAN-QIDH providing ΔEST values of −44 and 13 meV for compounds 1 and 2, respectively, in close agreement with the reference results. Note that the newest r2SCAN correlation functional recovers more exact constraints than the PBE original one, and it is thus expected to behave more accurately once a pair of (cx, cc) values is determined.71 By analyzing now the contribution of the ccΔ(D) correction for the successful r2SCAN-QIDH model, this amounts to −314 and −224 meV (−251 and −159 meV) for the S1 and T1 excited states of 1 (2), respectively, indicating a slightly more pronounced impact of the second-order perturbative-like correlation correction for the former molecule but always larger for S1 than for T1 in both cases.
| ΔEST = ΔECISST + ΔEcST | (3) |
We have also applied (SCS-)CC2 and (SCS-)ADC(2) methods to this challenging energy difference (see Table 1 and Fig. 4), since they have shown to be very accurate in the evaluation of excitation energies of related compounds.72 First of all, CC2 values for S1 ← S0 (T1 ← S0) excitation energies are 2.017 eV (2.155 eV) for compound 1, in perfect agreement with previous CC2/aug-cc-pVDZ results from ref. 5 of 2.033 eV (2.155 eV) confirming the small influence of basis set effects. The resulting ΔEST values at the CC2 level are too negative (−138 meV) than the EOM-CCSD reference result taken from literature5 (−14 meV) or the one calculated here (−25 meV), and the same holds from the application of the ADC(2) method. The spin-scaled CC2 and ADC(2) predict even more negative gaps, with ΔEST approximately −200 meV.
Additionally, all of these methods predict a negative ΔEST value for compound 2, ranging between −64 and −124 meV. Strikingly, at all of these levels of theory, a negative ΔEST energy difference is also predicted for azulene, contrary to experimental (49 meV) and other theoretical results (69 meV) for this molecule.4 Note that even the very costly CC3 method (results available in ref. 73) predicts a negative ΔEST value of −40 meV, with the 6-31G+(d) basis set, for azulene. Our own EOM-CCSD calculations, done here as a sanity check, predict a lower triplet state with a 51 meV gap instead, in close agreement with the experimental estimate of 49 meV (see the ESI†).
To rationalize the results obtained by the SCS-CC2 method, we first note that when moving from CC2 (COS = CSS = 1.0) to SCS-CC2 (COS = 6/5 and CSS = 1/3), T1 is destabilized by 49 meV, 92 meV and 51 meV for compounds 1, 2, and azulene, respectively, essentially due to the lowering of the same-spin interaction associated with a decrease of the exchange interaction, while S1 undergoes a stabilization of −10 meV and −46 meV for compound 1 and azulene, respectively, and a destabilization of 36 meV for compound 2. This leads to the wider negative gap predicted by including the SCS scheme for the three compounds, suggesting that the original values chosen for COS and CSS are, in fact, not the optimal ones for these compounds. In light of this, we computed the excitation energies and the ΔEST values of the three compounds by systematically changing these two parameters (grid of 0.05) to meet the values obtained at the EOM-CCSD level (see the ESI†). For this modified SCS-CC2 (mSCS-CC2), the ΔEST value is −24 meV (24 meV) for compound 1 (2), with fine-tuned parameters COS = 0.75 and CSS = 0.40 (COS = 0.80 and CSS = 0.50). Not surprisingly, the S1 excitation energy is more sensitive to COS (and thus to the coulomb correlation effect) than T1 (see Fig. S5 for 1 and 2, ESI†) due to the dominant opposite-spin configurations of its wavefunction. Hence, reducing COS leads to a large reduction in the S1–T1 gap. For consistency, we would like to remark that: (i) mSCS-CC2 provided an excited state nature consistent with all other methods employed in this work, e.g., both S1 and T1 are dominated by a HOMO to LUMO transition; (ii) the same procedure is also extended to azulene, for which a ΔEST value of 47 meV is found for COS = 0.90 and CSS = 0.10. This demonstrates that the pristine CC2 (COS = 1.0) and SCS-CC2 (COS = 1.2) clearly overestimates the role of the coulomb correlation and a tuning of the parameters deems appropriate here.
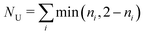 . Both compounds exhibited relatively small NU values, 0.76 for 1 and 0.68 for 2, considerably lower than the NU = 1.42 value displayed by cyclazine also obtained at the RAS-SF level,7 but still higher than the values for typical emitters that are not prone to excited-state inversion (e.g. the PXZ-TRZ molecule75 has NU = 0.06). The NU values of the excited singlet and triplet states for the two studied biazulenes are slightly higher that 2, which indicates that they mostly correspond to configurations with two unpaired electrons with minor contributions from higher n-tuple excitations. These terms, i.e., double, triple, etc. excited configurations, are those providing for electron correlation effects neutralizing the exchange interaction (ΔEcST in eqn (3)) These results are in agreement with the HOMO-to-LUMO configuration being the main term describing the S1 and T1 states in both compounds.
. Both compounds exhibited relatively small NU values, 0.76 for 1 and 0.68 for 2, considerably lower than the NU = 1.42 value displayed by cyclazine also obtained at the RAS-SF level,7 but still higher than the values for typical emitters that are not prone to excited-state inversion (e.g. the PXZ-TRZ molecule75 has NU = 0.06). The NU values of the excited singlet and triplet states for the two studied biazulenes are slightly higher that 2, which indicates that they mostly correspond to configurations with two unpaired electrons with minor contributions from higher n-tuple excitations. These terms, i.e., double, triple, etc. excited configurations, are those providing for electron correlation effects neutralizing the exchange interaction (ΔEcST in eqn (3)) These results are in agreement with the HOMO-to-LUMO configuration being the main term describing the S1 and T1 states in both compounds.
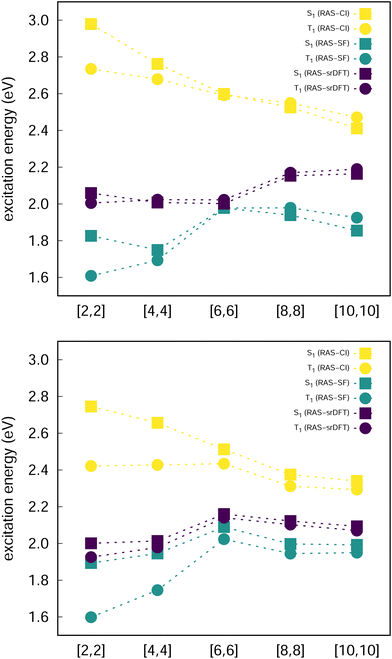
Excited state energies computed at the RAS-CI, RAS-SF and RAS-srDFT levels are presented in Fig. 6 as a function of the active space size, with Table 1 including the results with the largest [10,10] one. The RAS[n,n]-CI results for compound 1 clearly show the importance of the active space size to consistently decrease both S1 ← S0 and T1 ← S0 excitation energies, thus progressively approaching the EOM-CCSD values, and concomitantly passing from a positive to a negative value for ΔEST. A similar trend is found for compound 2, but always keeping a positive sign for ΔEST in agreement with EOM-CCSD results too. The application of the RAS[10,10]-srDFT method yielded very accurate results, confirming the key role played by a large and balanced introduction of correlation effects, with a close agreement with EOM-CCSD reference results: a negative ΔEST value (singlet–triplet inversion is predicted) for compound 1 (−21 meV) together with a slightly positive ΔEST value for compound 2 (23 meV). Looking again (see Table 1 and Fig. 6) at the individual excitation energies S1 ← S0 and T1 ← S0, we can confirm that this accuracy in the calculation of ΔEST for both systems does not come from any error cancellation, since RAS[10,10]-srDFT values for both compounds and for both excitation energies differ by less than 0.1 eV compared with reference EOM-CCSD results.
The increase of the ΔEcST < 0 magnitude shrinking the singlet–triplet gap can be related to the differential mixing of electronic configurations beyond the 2e2o model (HOMO-to-LUMO terms), which increases with n (Fig. 7). Moreover, the contribution of these additional terms is larger in S1 than in T1, which might explain the fact that correlation effects have a larger impact in the excitation of the singlet than the triplet state. Larger active orbital spaces increase the possibility to mix in additional electron correlations, which further reduce the S1 energy with respect to T1.
These extra contributions mostly correspond to double excitations with respect to the HF determinant and can be classified into two types: (i) configurations with two unpaired electrons obtained as double excitations from or to a single orbital, and (ii) double excitations resulting in four unpaired electrons. In fact, the configurations beyond 2e2o with the largest weight in the excited singlet and triplet states of 1 and 2 exhibit four unpaired electrons and can be seen as single excitation with respect to the HOMO-to-LUMO term (Fig. 8). It is important to notice that closed-shell-like configurations, e.g., two-electron HOMO-to-LUMO excitation, belong to the totally symmetric irreducible representation (Ag) and are thus symmetry forbidden in B1g excited states, i.e., S1 and T1. We also identify triple excitations contributing to the wavefunctions of the excited singlet and triplet states, but with a considerably lower weight.
4. Conclusions
We have systematically investigated the physical reasons driving the (lowest-energy) singlet (S1) and triplet (T1) excited-state energy inversion of a biazulene hydrocarbon (1), which constitutes another example of Hund's rule violation, placing the S1 lower in energy than the T1 excited state, that is, leading to a negative energy difference ΔEST < 0. To better understand the reasons for that, we have designed and investigated another biazulene compound (2), chemically identical to 1 just differing in the spatial arrangement of atoms, for which that inversion is not calculated. Therefore, the inversion happens only for molecule 1 as a consequence of a delicate trade-off between exchange and correlation contributions to those S1 and T1 excited states. We found that RAS[10,10]-srDFT calculations led to results closely agreeing with reference EOM-CCSD values but, most importantly, have also allowed us to carefully disentangle and understand the reasons for having a ΔEST < 0 value for 1: a delicate balance between a larger weight of double excitations for S1 than T1 (correlation effects) together with a relatively small exchange energy. The situation for molecule 2 differs in the sense that these double excitations are slightly attenuated with respect to 1, but also due to the fact that the exchange energy was slightly larger, thus representing a not-so-ideal starting point for the excited-state energy inversion.Not surprisingly, the majority of the rest of the methods considered in this work fail to cope with the aforementioned exchange and correlation balance, leading to qualitative and/or quantitative wrong results for either one or the two molecules, with the notable exception of TD-DFT calculations performed with the recently proposed r2SCAN-QIDH double-hybrid functional, thus representing these apparently simple molecules a real challenge for excited-state calculations. Overall, the conscious and systematic use of quantum-chemical methods is key to rationalize these complex phenomena arising from meV excited-state energy differences, thus revealing all their potential to tackle any challenging situation.
Data availability statement
The data that support the findings of this study are available in the ESI† of this article or available upon request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work in Alicante is supported by project PID2019-106114GB-I00 (“Ministerio de Ciencia e Innovación”). M. E. S.-S. acknowledges the funding by the United Kingdom Research and Innovation (U. K. R. I.) under the U.K. government's Horizon Europe funding guarantee (grant number EP/X020908/1). Y. O. acknowledges the funding by the “Fonds de la Recherche Scientifique-FNRS” under Grant n. F.4534.21 (MIS-IMAGINE). G. R. acknowledges a grant from the “Fonds pour la formation a la Recherche dans l'Industrie et dans l’Agriculture” (F.R.I.A.) of the F.R.S.-F.N.R.S. Computational resources were also provided by the “Consortium des Équipements de Calcul Intensif” (CÉCI), funded by the “Fonds de la Recherche Scientifiques de Belgique” (F.R.S.-F.N.R.S.) under grant no. 2.5020.11. D. C. acknowledges funding by projects PID2019-109555GB-I00 and RED2018-102815-T (“Ministerio de Ciencia e Innovación”) and from project no. PIBA19-0004 (“Eusko Jaularitza”).References
- A. Toyota and T. Nakajima, Violation of Hund's multiplicity rule in the lowest excited singlet–triplet pairs of cyclic bicalicene and its higher homologues, J. Chem. Soc., Perkin Trans. 2, 1986,(11), 1731–1734 RSC.
- A. Toyota, Violation of Hund's rule in the lowest excited singlet–triplet pairs of dicyclohepta [cd, gh] pentalene and dicyclopenta [ef, kl] heptalene, Theor. Chim. Acta, 1988, 74, 209–217 CrossRef CAS.
- A. Köhler and D. Beljonne, The singlet–triplet exchange energy in conjugated polymers, Adv. Funct. Mater., 2004, 14(1), 11–18 CrossRef.
- S. Vosskötter, P. Konieczny, C. M. Marian and R. Weinkauf, Towards an understanding of the singlet–triplet splittings in conjugated hydrocarbons: azulene investigated by anion photoelectron spectroscopy and theoretical calculations, Phys. Chem. Chem. Phys., 2015, 17(36), 23573–23581 RSC.
- J. T. Blaskovits, M. H. Garner and C. Corminboeuf, Symmetry-Induced Singlet–Triplet Inversions in Non-Alternant Hydrocarbons, Angew. Chem., Int. Ed., 2023, e202218156 Search PubMed.
- N. Aizawa, Y. J. Pu, Y. Harabuchi, A. Nihonyanagi, R. Ibuka and H. Inuzuka, et al., Delayed fluorescence from inverted singlet and triplet excited states, Nature, 2022, 609(7927), 502–506 CrossRef CAS PubMed.
- M. E. Sandoval-Salinas, A. Carreras and D. Casanova, Triangular graphene nanofragments: open-shell character and doping, Phys. Chem. Chem. Phys., 2019, 21(18), 9069–9076 RSC.
- P. de Silva, Inverted Singlet–Triplet Gaps and Their Relevance to Thermally Activated Delayed Fluorescence, J. Phys. Chem. Lett., 2019, 10(18), 5674–5679 CrossRef CAS PubMed.
- J. Ehrmaier, E. J. Rabe, S. R. Pristash, K. L. Corp, C. W. Schlenker and A. L. Sobolewski, et al., Singlet–Triplet Inversion in Heptazine and in Polymeric Carbon Nitrides, J. Phys. Chem. A, 2019, 123(38), 8099–8108 CrossRef CAS PubMed.
- S. Pios, X. Huang, A. L. Sobolewski and W. Domcke, Triangular boron carbon nitrides: An unexplored family of chromophores with unique properties for photocatalysis and optoelectronics, Phys. Chem. Chem. Phys., 2021, 23, 12968–12975 RSC.
- A. L. Sobolewski and W. Domcke, Are heptazine-based organic light-emitting diode chromophores thermally activated delayed fluorescence or inverted singlet–triplet systems?, J. Phys. Chem. Lett., 2021, 12(29), 6852–6860 CrossRef CAS PubMed.
- J. Sanz-Rodrigo, G. Ricci, Y. Olivier and J. C. Sancho-Garcia, Negative singlet–triplet excitation energy gap in triangle-shaped molecular emitters for efficient triplet harvesting, J. Phys. Chem. A, 2021, 125(2), 513–522 CrossRef CAS PubMed.
- G. Ricci, E. San-Fabián, Y. Olivier and J. C. Sancho-García, Singlet–triplet excited-state inversion in heptazine and related molecules: assessment of TD-DFT and ab initio methods, Chem. Phys. Chem., 2021, 22(6), 553–560 CrossRef CAS PubMed.
- J. C. Sancho-García and E. San-Fabián, Organic emitters showing excitedstates energy inversion: An assessment of MC-PDFT and correlation energy functionals beyond TD-DFT, Computation, 2022, 10(2), 13 CrossRef.
- S. Ghosh and K. Bhattacharyya, Origin of the Failure of Density Functional Theories in Predicting Inverted Singlet–Triplet Gaps, J. Phys. Chem. A, 2022, 126(8), 1378–1385 CrossRef CAS PubMed.
- L. Tučková, M. Straka, R. R. Valiev and D. Sundholm, On the origin of the inverted singlet–triplet gap of the 5th generation light-emitting molecules, Phys. Chem. Chem. Phys., 2022, 24(31), 18713–18721 RSC.
- R. Pollice, P. Friederich, C. Lavigne, G. dos Passos Gomes and A. Aspuru-Guzik, Organic molecules with inverted gaps between first excited singlet and triplet states and appreciable fluorescence rates, Matter, 2021, 4(5), 1654–1682 CrossRef CAS.
- N. C. Forero-Martinez, K. H. Lin, K. Kremer and D. Andrienko, Virtual screening for organic solar cells and light emitting diodes, Adv. Sci., 2022, 9(19), 2200825 CrossRef CAS PubMed.
- J. Li, L. Tao, Y. Wang, Y. Yao and Q. Guo, Heptazine-Based π-Conjugated Materials for Light-Emitting, Front. Chem., 2021, 9, 482 Search PubMed.
- P. Audebert, E. Kroke, C. Posern and S. H. Lee, State of the Art in the Preparation and Properties of Molecular Monomeric s-Heptazines: Syntheses, Characteristics, and Functional Applications, Chem. Rev., 2021, 121(4), 2515–2544 CrossRef CAS PubMed.
- J. Li, Z. Li, H. Liu, H. Gong, J. Zhang and Y. Yao, et al., Organic molecules with inverted singlet–triplet gaps, Front. Chem., 2022, 10, 1039 Search PubMed.
- J. Wang, F. Gordillo, J. M. Beloqui, A. Diaz-Andres, X. Miao and D. Casanova, et al., Synthesis of a Dicyclohepta[a, g]heptalene-Containing Polycyclic Conjugated Hydrocarbon and the Impact of Non-Alternant Topologies, Angew. Chem., Int. Ed., 2022, 62(10), e202217124 Search PubMed.
- P. Mathey, F. Lirette, I. Fernández, L. Renn, T. Weitz and J. F. Morin, Annulated Azuleno[2,1,8-ija]azulenes: Synthesis and Properties, Angew. Chem., 2023, 135(11), e202216281 CrossRef.
- G. Ricci, J. C. Sancho-García and Y. Olivier, Establishing design strategies for emissive materials with an inverted singlet–triplet energy gap (INVEST): a computational perspective on how symmetry rules the interplay between triplet harvesting and light emission, J. Mater. Chem. C, 2022, 10(35), 12680–12698 RSC.
- J. D. Chai and M. Head-Gordon, Systematic optimization of long-range corrected hybrid density functionals, J. Chem. Phys., 2008, 128(8), 084106 CrossRef PubMed.
- Y. M. Rhee and M. Head-Gordon, Scaled second-order perturbation corrections to configuration interaction singles: Efficient and reliable excitation energy methods, J. Phys. Chem. A, 2007, 111(24), 5314–5326 CrossRef CAS PubMed.
- L. Goerigk and S. Grimme, Assessment of TD-DFT methods and of various spin scaled CIS(D) and CC2 versions for the treatment of low-lying valence excitations of large organic dyes, J. Chem. Phys., 2010, 132(18), 184103 CrossRef.
- O. Christiansen, H. Koch and P. Jørgensen, The second-order approximate coupled cluster singles and doubles model CC2, Chem. Phys. Lett., 1995, 243(5–6), 409–418 CrossRef CAS.
- A. Hellweg, S. A. Grün and C. Hättig, Benchmarking the performance of spin-component scaled CC2 in ground and electronically excited states, Phys. Chem. Chem. Phys., 2008, 10(28), 4119–4127 RSC.
- M. Wormit, D. R. Rehn, P. H. Harbach, J. Wenzel, C. M. Krauter and E. Epifanovsky, et al., Investigating excited electronic states using the algebraic diagrammatic construction (ADC) approach of the polarisation propagator, Mol. Phys., 2014, 112(5–6), 774–784 CrossRef CAS.
- S. Grimme, Improved second-order Møller–Plesset perturbation theory by separate scaling of parallel-and antiparallel-spin pair correlation energies, J. Chem. Phys., 2003, 118(20), 9095–9102 CrossRef CAS.
- N. Orms and A. I. Krylov, Singlet–triplet energy gaps and the degree of diradical character in binuclear copper molecular magnets characterized by spin-flip density functional theory, Phys. Chem. Chem. Phys., 2018, 20(19), 13127–13144 RSC.
- M. E. Sandoval-Salinas, A. Carreras, J. Casado and D. Casanova, Singlet fission in spiroconjugated dimers, J. Chem. Phys., 2019, 150(20), 204306 CrossRef PubMed.
- D. Casanova and A. I. Krylov, Spin-flip methods in quantum chemistry, Phys. Chem. Chem. Phys., 2020, 22(8), 4326–4342 RSC.
- D. Casanova and M. Head-Gordon, Restricted active space spin-flip configuration interaction approach: theory, implementation and examples, Phys. Chem. Chem. Phys., 2009, 11(42), 9779–9790 RSC.
- D. Casanova, Efficient implementation of restricted active space configuration interaction with the hole and particle approximation, J. Comput. Chem., 2013, 34(9), 720–730 CrossRef CAS PubMed.
- D. Casanova, Restricted active space configuration interaction methods for strong correlation: Recent developments, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12(1), e1561 CAS.
- A. I. Krylov, Spin-flip configuration interaction: an electronic structure model that is both variational and size-consistent, Chem. Phys. Lett., 2001, 350(5), 522–530 CrossRef CAS.
- Y. Shao, M. Head-Gordon and A. I. Krylov, The spin–flip approach within time-dependent density functional theory: Theory and applications to diradicals, J. Chem. Phys., 2003, 118(11), 4807–4818 CrossRef CAS.
- A. I. Krylov, Spin-flip equation-of-motion coupled-cluster electronic structure method for a description of excited states, bond breaking, diradicals, and triradicals, Acc. Chem. Res., 2006, 39(2), 83–91 CrossRef CAS PubMed.
- D. Casanova, Short-range density functional correlation within the restricted active space CI method, J. Chem. Phys., 2018, 148(12), 124118 CrossRef PubMed.
- A. I. Krylov, Equation-of-motion coupled-cluster methods for open-shell and electronically excited species: The hitchhiker's guide to Fock space, Annu. Rev. Phys. Chem., 2008, 59, 433–462 CrossRef CAS PubMed.
- P. F. Loos, F. Lipparini, M. Boggio-Pasqua, A. Scemama and D. Jacquemin, A mountaineering strategy to excited states: Highly accurate energies and benchmarks for medium sized molecules, J. Chem. Theory Comput., 2020, 16(3), 1711–1741 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes, J. Chem. Phys., 2003, 119(23), 12129–12137 CrossRef CAS.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110(13), 6158–6170 CrossRef CAS.
- C. A. Guido, E. Brémond, C. Adamo and P. Cortona, Communication: One third: A new recipe for the PBE0 paradigm, J. Chem. Phys., 2013, 138, 021104 CrossRef PubMed.
- J. Sancho-García, Treatment of singlet–triplet splitting of a set of phenylene ethylenes organic molecules by TD-DFT, Chem. Phys. Lett., 2007, 439(1–3), 236–242 CrossRef.
- H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, A long-range correction scheme for generalized-gradient-approximation exchange functionals, J. Chem. Phys., 2001, 115(8), 3540–3544 CrossRef CAS.
- O. A. Vydrov and G. E. Scuseria, Assessment of a long-range corrected hybrid functional, J. Chem. Phys., 2006, 125(23), 234109 CrossRef PubMed.
- T. M. Henderson, A. F. Izmaylov, G. Scalmani and G. E. Scuseria, Can shortrange hybrids describe long-range-dependent properties?, J. Chem. Phys., 2009, 131(4), 044108 CrossRef PubMed.
- E. Brémond and C. Adamo, Seeking for parameter-free double-hybrid functionals: the PBE0-DH model, J. Chem. Phys., 2011, 135(2), 024106 CrossRef PubMed.
- É. Brémond, J. Sancho-García, Á. Pérez-Jiménez and C. Adamo, Communication: double-hybrid functionals from adiabatic-connection: the QIDH model, J. Chem. Phys., 2014, 141(3), 031101 CrossRef PubMed.
- J. D. Chai and S. P. Mao, Seeking for reliable double-hybrid density functionals without fitting parameters: the PBE0-2 functional, Chem. Phys. Lett., 2012, 538, 121–125 CrossRef CAS.
- J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, Accurate and numerically efficient r2SCAN meta-generalized gradient approximation, J. Phys. Chem. Lett., 2020, 11(19), 8208–8215 CrossRef CAS PubMed.
- E. Brémond, M. Rodríguez-Mayorga, Á. J. Pérez-Jiménez, C. Adamo and J. C. Sancho-García, Assessment of the nonempirical r2SCAN-QIDH double-hybrid density functional against large and diverse datasets, J. Chem. Phys., 2023 Search PubMed , submitted for publication.
- Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. R. Schleyer, Nucleus-independent chemical shifts (NICS) as an aromaticity criterion, Chem. Rev., 2005, 105(10), 3842–3888 CrossRef CAS PubMed.
- F. Neese, Software update: The ORCA program systemVersion 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12(5), e1606 Search PubMed.
- TURBOMOLE V7.0 2015, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; available from https://www.turbomole.com.
- E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao and N. Mardirossian, et al., Software for the frontiers of quantum chemistry: An overview of developments in the Q-Chem 5 package, J. Chem. Phys., 2021, 155(8), 084801, DOI:10.1063/5.0055522 Available from.
- S. Koseki, T. Nakajima and A. Toyota, Violation of Hund's multiplicity rule in the electronically excited states of conjugated hydrocarbons, Can. J. Chem., 1985, 63(7), 1572–1579 CrossRef CAS.
- M. J. Peach, P. Benfield, T. Helgaker and D. J. Tozer, Excitation energies in density functional theory: An evaluation and a diagnostic test, J. Chem. Phys., 2008, 128(4), 044118 CrossRef PubMed.
- M. Abe, Diradicals, Chem. Rev., 2013, 113(9), 7011–7088 CrossRef CAS PubMed.
- J. D. Morgan III and W. Kutzelnigg, Hund's rules, the alternating rule, and symmetry holes, J. Phys. Chem., 1993, 97(10), 2425–2434 CrossRef.
- W. Leupin and J. Wirz, Low-lying electronically excited states of cycl[3.3.3]azine, a bridged 12π-perimeter, J. Am. Chem. Soc., 1980, 102(19), 6068–6075 CrossRef CAS.
- W. Leupin, D. Magde, G. Persy and J. Wirz, 1,4,7-Triazacycl[3.3.3]azine: basicity, photoelectron spectrum, photophysical properties, J. Am. Chem. Soc., 1986, 108(1), 17–22 CrossRef CAS.
- N. C. Baird, Quantum organic photochemistry. II. Resonance and aromaticity in the lowest 3ππ* state of cyclic hydrocarbons, J. Am. Chem. Soc., 1972, 94(14), 4941–4948 CrossRef CAS.
- S. Grimme and F. Neese, Double-hybrid density functional theory for excited electronic states of molecules, J. Chem. Phys., 2007, 127(15), 154116 CrossRef PubMed.
- A. Ottochian, C. Morgillo, I. Ciofini, M. J. Frisch, G. Scalmani and C. Adamo, Double hybrids and time-dependent density functional theory: An im-plementation and benchmark on charge transfer excited states, J. Comput. Chem., 2020, 41(13), 1242–1251 CrossRef CAS PubMed.
- M. Head-Gordon, R. J. Rico, M. Oumi and T. J. Lee, A doubles correction to electronic excited states from configuration interaction in the space of single substitutions, Chem. Phys. Lett., 1994, 219(1–2), 21–29 CrossRef CAS.
- E. Brémond, M. Savarese, Á. J. Pérez-Jiménez, J. C. Sancho-García and C. Adamo, Systematic improvement of density functionals through parameterfree hybridization schemes, J. Phys. Chem. Lett., 2015, 6(18), 3540–3545 CrossRef PubMed.
- D. Hall, J. C. Sancho-García, A. Pershin, G. Ricci, D. Beljonne and E. Zysman- Colman, et al., Modeling of Multiresonant Thermally Activated Delayed Fluorescence Emitters Properly Accounting for Electron CorrelationIs Key!, J. Chem. Theory Comput., 2022, 18(8), 4903–4918 CrossRef CAS PubMed.
- P. F. Loos and D. Jacquemin, A Mountaineering Strategy to Excited States: Highly Accurate Energies and Benchmarks for Bicyclic Systems, J. Phys. Chem. A, 2021, 125(47), 10174–10188 CrossRef CAS PubMed.
- M. Head-Gordon, Characterizing unpaired electrons from the oneparticle density matrix, Chem. Phys. Lett., 2003, 372(3), 508–511 CrossRef CAS.
- H. Tanaka, K. Shizu, H. Miyazaki and C. Adachi, Efficient green thermally activated delayed fluorescence (TADF) from a phenoxazine–triphenyltriazine (PXZ–TRZ) derivative, Chem. Commun., 2012, 48(93), 11392–11394 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: (i) The basis set dependence of the S1 ← S0 and T1 ← S0 excitation energies for compounds 1 and 2 at the RAS[6,6]-SF level; (ii) results at the TD-DFT, (SCS-)CC2 and (SCS-)ADC(2) levels for azulene; (iii) evolution of the excitation energies for azulene at all the RAS-based levels of theory as a function of the active space size; (iv) information about the calculation of Tozer's index; (v) detailed information about the derivation of the mSCS-CC2 method; (vi) results of NICS values at various DFT levels for S0 and T1 excited states of compounds 1 and 2; and (vii) optimized cartesian coordinates of the compounds. See DOI: https://doi.org/10.1039/d3cp02465b |
| This journal is © the Owner Societies 2023 |