Decoding the infrared spectra changes upon formation of molecular complexes: the case of halogen bonding in pyridine⋯perfluorohaloarene complexes

Abstract

A recently developed computational scheme is employed to interpret changes in the infrared spectra of halogen-bonded systems in terms of intermolecular interaction energy components (electrostatic, exchange, induction, dispersion) taking pyridine⋯perfluorohaloarene complexes as examples. For all complexes, we find a strong linear correlation between the different terms of the interaction-induced changes of the IR band associated with an intermolecular halogen bond stretching mode and the corresponding terms of the interaction energy, which implies that the interaction components play similar roles in both properties. This is not true for other vibrational modes localized in one of the monomers studied here, for which the corresponding interaction-induced changes in IR bands may present a completely different decomposition than the interaction energy.

---

Intermolecular interactions have a key role in the physicochemical properties of matter, such as solubility, reactivity, or all types of spectroscopic signatures, to name a few. Over the last decades, several theoretical frameworks have been developed to analyze the effect of the different intermolecular forces on the properties of the matter,^1–10 allowing the understanding of their fundamental aspects in a plethora of molecular systems covering a wide palette of interaction types and strengths. Nowadays the methodology to analyze intermolecular interactions is an important part of modern interpretive chemistry and it is used to understand the physical origin of the experimental manifestations of intermolecular interactions. Myriads of atomic and molecular complexes have been studied using energy decomposition analyses, thus enriching the rationalization of the basic interaction types that govern the structure, stability, and properties of molecular complexes and their organization at larger scales.

Spectroscopic techniques, with infrared (IR) spectroscopy at the forefront, are frequently used to substantiate the formation of molecular complexes. The popularity of IR spectroscopy is due to its high interpretive power, e.g., the presence of hydrogen bonds in molecular complexes can be identified easily by the change of the frequency of the bands associated with the vibrational modes of functional groups involved in the intermolecular interaction,^11,12 a feature listed by IUPAC¹³ as a criterion to call the interaction hydrogen bond (similar applies for halogen bonds).¹⁴ Spectroscopic IR studies are often paralleled by computational efforts in the framework of the theory of intermolecular interactions to link the strength of the interactions with specific interaction types (exchange, electrostatic, induction, dispersion).^15,16 However, none of the performed studies attempted to analyze the changes in the intensity and frequency of the peaks of IR spectra in terms of interaction types since the available decomposition schemes were primarily developed for interaction energies. To overcome this limitation, we recently developed a new scheme to interpret the nature of the changes in infrared spectra occurring upon the formation of a molecular complex.¹⁷ This new scheme, called infrared spectra decomposition analysis (IRS-DA) allows the association of the simultaneous changes in the intensity and frequency of each peak of the IR spectra occurring upon complex formation with the different interaction types (i.e. exchange, electrostatic, induction, dispersion). Specifically, IRS-DA decomposes the changes in the ratio between intensity and frequency squared for each normal mode upon AB complex formation from monomers A and B. IRS-DA provides information regarding the interplay of interaction types, i (exchange, electrostatic, induction, dispersion), and their manifestation through changes in the band position and intensity of normal mode a:

Note that for bands that undergo negligible frequency changes upon complex formation, or for which , the above equation can be simplified to:

ΔIⁱ_a = Iⁱ_a(AB) − Iⁱ_a(A) −Iⁱ_a(B) (2)

thus allowing for direct decomposition of ΔI_a into interaction types i. The net change in IR intensity for mode a (ΔI_a) can be expressed as the sum of all considered interaction types i.

In this communication, we report the first analysis of IR intensity changes upon the formation of halogen-bonded (XB) complexes, using the molecular complexes formed by pyridine (pyr) and perfluorohaloarenes (C₆F₅X, where X is Cl, Br, or I) as examples (Fig. 1). As demonstrated in our previous work, halogen bond formation in complexes containing pyridine can be identified using spectroscopic techniques, including IR spectroscopy.¹⁸ In particular, the measured IR spectrum of a 1 : 1 mixture of pyridine and C₆F₅I featured a new band at 195 cm⁻¹ not present in the IR spectra of the pure liquids pyridine or C₆F₅I. This new band was assigned to the intermolecular C–I⋯N stretching, in agreement with the theoretical IR spectra obtained at the MN15/aug-cc-pVDZ(PP) level¹⁸ and previous measurements for the cocrystal.¹⁹ Thanks to the newly developed IRS-DA method it is now possible to link the formation of this band with individual intermolecular interaction types.¹⁷ XB complexes are nowadays in the limelight due to the unique properties of halogen bonding and its wide range of applications,²⁰ such as in crystal engineering²¹ of emissive materials,^22,23 sensing enhancement²⁴ or in medicine.^25–27 The term halogen bond is applied to a directional intermolecular interaction involving an electrophilic region (so-called σ-hole) associated with a halogen atom and a nucleophilic second atom. The σ-hole was described theoretically already a long time ago,²⁸ and has been invoked as an explanation for many phenomena. However, it was only very recently possible to visualize the σ-hole directly by Kelvin probe force microscopy.²⁹ Halogen bonding resembles hydrogen bonding (HB) in many aspects, including, in strongly interacting molecules, intermolecular migration of the heavy halogen atom, similar to proton transfer in certain hydrogen-bonded complexes.³⁰ Given the widespread interest in XB complexes and their possible coexistence with hydrogen bonding, as exemplified in supramolecular synthons,³¹ we consider the analysis of changes in spectroscopic vibrational signatures in terms of interaction types very timely. Intermolecular interactions influence the location and topology of the potential energy minima and the electron density distribution of the molecules that form the complexes, which in turn affects both the position and the intensity of the bands in the IR spectra.

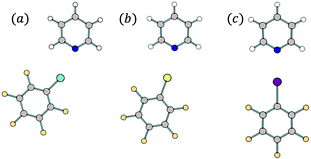Fig. 1 Optimized structures of the studied halogen-bonded complexes, composed of pyridine and (a) C₆F₅Cl, (b) C₆F₅Br or (c) C₆F₅I.

In order to perform the analysis of ΔI_a upon complex formation in terms of interaction types i we choose the general framework of decomposition of the interaction energy at the second-order Møller–Plesset perturbation theory (MP2) level based on the variational-perturbational decomposition scheme (VP-EDS).^32–36 According to VP-EDS, the total interaction energy of a dimer is partitioned into several interaction energy terms as defined in the symmetry-adapted perturbation theory (SAPT).^32–35 At the MP2 level, the total VP-EDS interaction energy of the complex calculated by a supermolecular approach in the dimer-centered-basis set (DCBS)³⁷ is partitioned into the Hartree–Fock (HF) (ΔE^HF_int) and the electron correlation interaction energy correction (ΔE^MP2_corr):

The HF term encompasses the electrostatic interactions of the charge densities of the unperturbed subsystems, ε⁽¹⁰⁾_el, the exchange repulsion (ΔE^HL_ex), and the charge delocalization (ΔE^HF_del). The last two terms account for exchange effects due to the Pauli antisymmetry principle and induction, respectively. The second-order electron correlation term includes the electron correlation correction to the first-order electrostatic interaction, ε⁽¹²⁾_el,r, the second-order dispersion interaction, ε⁽²⁰⁾_disp, and the remaining second-order electron correlation effects (ΔE⁽²⁾_ex).^34,36,38

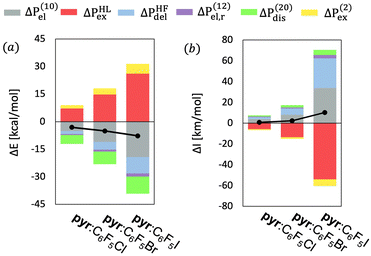
We will start the analysis of the pyr:C₆F₅X complexes with the partitioning of the intermolecular interaction energy (ΔE). Fig. 2a and Table S1 (ESI†) show the MP2 interaction energies and their components for the three complexes ordered according to the increasing value of the total interaction energy. As expected, the absolute value of the VP-EDS/MP2 interaction energy is largest for the complex containing iodine, and it decreases with increasing electronegativity (χ) of atom X, (i.e., ΔE(I) > ΔE(Br) > ΔE(Cl)). The partitioning of the interaction energy for the three pyr:C₆F₅X complexes reveals a large destabilizing exchange-repulsion contribution, which is canceled by the sum of the electrostatic and delocalization terms, thus predicting only very weak binding at the uncorrelated level (Table S1, ESI†). Thus, the observed stability of the studied complexes is mostly due to the sum of the electron correlation terms, especially Δε⁽²⁰⁾_disp and ΔE⁽²⁾_ex, to the total interaction energies.

Fig. 2 Partitioning of (a) the interaction energy (ΔP = ΔE) and (b) the excess IR intensity (ΔP = ΔI) of the intermolecular vibrational stretching mode (ν^int_a) for the pyr:C₆F₅X complexes at the equilibrium geometries at the MP2/aug-cc-pVDZ-PP level of theory. The black dots combined with black lines indicate the total excess properties.

Fig. 2a shows that the interplay of the interaction energy components for the three pyr:C₆F₅X complexes is very similar, i.e. the relative weight of the different interaction terms contributing to ΔE for the three different halogen bonds resembles each other to a large extent (see also Fig. S1, ESI†). We may thus conclude that the stability of these different XB complexes with the nitrogen atom in pyridine as the nucleophilic partner has a similar physical origin, in the sense that the different elements of the intermolecular interaction lead to comparable relative contributions to the total excess energy. We note that a similar conclusion can be drawn from the good linear fits with negligible y-intercept between the ΔE and ΔEⁱ terms of D:C₆F₅X (where D represents a fluoroborate-based dye containing pyridine, see Fig. S2, ESI†)¹⁸ and the corresponding terms of pyr:C₆F₅I, as shown in Fig. S3 and Table S2 (ESI†).

Furthermore, the partition of ΔE for these six complexes follows the same trends observed in previous studies of small halogen-bonded dimers performed by our group, indicating that the nature of halogen bonding is similar for complexes of different chemical composition.³⁹ Table S3 (ESI†) presents the R² of the linear fits between partition terms of the intermolecular interaction energy of all the XB and HB complexes studied in this work and three complexes in π–π stacking arrangement studied in the ref. 17 The complexes presenting the same type of non-covalent interaction share a very similar physical origin (i.e., R² > 0.89). On the contrary, this is not true for systems that present different types of non-covalent interactions (i.e., R² as low as 0.39).

The difference IR spectrum of pyr:C₆F₅I displayed in Fig. 3 reveals significant changes in the IR spectra of the individual constituents upon complexation. Our IRS-DA analysis will be focussed on four representative bands attributed to (a) the intermolecular vibrational stretching mode (ν^int_a); (b) the C–I stretching, which implies a change in the halogen bond distance (ν^C–X_b); and two vibrational modes that involve movements of the atoms of only one monomer: (c) a distortion of the ring of the C₆F₅ I, (ν_c^C₆F₅I) and (d) a rocking in-plane bending of the hydrogens of the pyridine, (ν^pyr_d). We have also analyzed the changes of the IR bands upon complex formation associated with the four equivalent vibrational modes of the complexes pyr:C₆F₅Br and pyr:C₆F₅Cl (Fig. S4 and S5, ESI†).

Fig. 3 Difference IR spectrum obtained by subtracting the simulated IR spectra of pyridine and C₆F₅I from the IR spectrum of pyr:C₆F₅I complex, as well as the displacements of: (a) an intermolecular vibrational stretching mode (ν^int_a), (b) a C–X stretching mode of C₆F₅I, which involves a change in the halogen bond distance (ν^C–X_b), (c) one local vibrational mode of C₆F₅I (ν_c^C₆F₅I) and (d) one local vibrational mode of pyridine (ν^pyr_c).

The mode ν^int_a is only present in the complex and arises due to the halogen bonding. Therefore, we will first focus our analysis on the physical origin of ΔI for this peak. For ν^C–X_b, ν_c^C₆F₅I and ν^pyr_d, the frequency shifts upon complex formation are very small, which according to eqn (2) permits the direct decomposition of IR intensity changes. We note that the displacements of the two first modes include large variations of the halogen-bond distance, which is not the case for the latter two. Thus, ν^int_a and ν^C–X_b have a direct effect on the intermolecular interaction, in contrast with ν_c^C₆F₅I and ν^pyr_d. Even though the observed vibrational frequency shifts upon complex formation observed for modes localized on C₆F₅X (ν^C–X_b, ν_c^C₆F₅I) are much smaller than that for mode ν^int_a, in all three cases we found a strong linear correlation between Δ[small nu, Greek, macron] and intermolecular interaction energy terms (see Table S4, ESI†).

Fig. 2b shows the partition of ΔI_a for the intermolecular vibrational stretching mode ν^int_a of the three pyr:C₆F₅X complexes ordered according to increasing values of the total interaction energy (see also Tables S5–S7, ESI†). Similarly to the pattern found for the interaction energy, the largest IR intensity changes are found for the complex with X = I and they decrease with increasing electronegativity of the halogen atom X. Indeed, as shown in Table S8 (ESI†), for this normal mode a good linear correlation with a very small y-intercept exists between the computed values of ΔE and ΔI_a for the three complexes (R² = 0.93). Also, mimicking the decomposition of ΔE, the partitioning of the intensity of the band associated to ν^int_a of pyr:C₆F₅I reveals that the increment of ΔI_a is mainly due to the sum of electrostatic and delocalization terms partially canceled by a large negative Pauli exchange-repulsion contribution. But now the total ΔI_a value is fairly well (up to ≈ 80%) described at the HF level. Nevertheless, as for ΔE, the electron correlation terms, especially the dispersion and second-order exchange contributions, also play an important role in ΔI_a of this normal mode. However, we should point out that the relative weight of the dispersion contribution decreases when the electronegativity of the halogen increases, again in agreement with the interaction energies.

Fig. 4 and Fig. S6, S7 (ESI†) show that for ν^int_a there is indeed a nice linear correlation with a small y-intercept between the values of the terms of the ΔE decomposition and those of the ΔI_a decomposition (i.e. R² > 0.89), indicating that both excess properties have the same physical nature in the sense defined above. The goodness-of-fit improves with the strength of the intermolecular interaction, giving the best linear correlation for the pyr:C₆F₅I complex. Similar good linear fits between the decomposition terms of the ΔE and ΔI are observed for the ν^C–X_b band of pyr:C₆F₅Br and pyr:C₆F₅I (see Table S8 and Fig. S8–S10, ESI†). On the contrary, we do not find a good linear correlation for pyr:C₆F₅Cl, possibly due to the strong deviation of the C–X–N angle from 180 (161), which reduces the coupling of ν^C–X_b vibration with the halogen bond distance. ν_c^C₆F₅X and ν^pyr_d bands also show a high linear correlation between the values of ΔE and ΔI. However, the decomposition of ΔI for those normal modes, which do not affect the halogen-bond distance, is very different from the decomposition of ΔI for ν^int_a and ν^C–X_b. For ν_c^C₆F₅X and ν^pyr_d, the relative weights and even the signs of the terms of ΔI change depending on the complex and normal mode (Tables S5–S7 and Fig. S11, ESI†). For instance, the largest contribution for ν_c^C₆F₅Cl, ν_c^C₆F₅Br, and ν_c^C₆F₅I is ΔI_el⁽¹⁰⁾, ΔI_ex^HL and ΔI_del^HF, respectively. Therefore, while for those vibrational modes that induce large variations of the halogen-bond distance the partitions of ΔI are strongly correlated with their ΔE counterparts, no such correlation is found for the other vibrational modes studied here.

Fig. 4 Linear fits between interaction-type contributions for the interaction energy (ΔP = ΔE) and the corresponding terms of the excess IR intensity (ΔP = ΔI) for ν^int_a for the pyr:C₆F₅I complex. Energies are given in kcal mol⁻¹ and intensities in km mol⁻¹.

To investigate if this observation can be generalized to other molecular complexes, the decompositions of ΔE and ΔI for three vibrational modes of two small halogen-bonded complexes (HCN:IF and HCN:BrF) and of three small hydrogen-bonded systems (HCN:HCl, HCN:HNC and HCN:HCN) were analyzed (Fig. S12–S16 and Tables S9–S14, ESI†). As summarized in Table S15 (ESI†), for the intermolecular stretching of the five complexes the decomposition terms of ΔI are linearly correlated with the decomposition terms of ΔE (R² > 0.83). On the other hand, for the local vibrational modes the analogous linear correlation is usually not found, (i.e. the coefficients of determination (R²) are between 0.20 and 0.80).

In summary, thanks to our recent development of a new computational scheme to decompose the IR spectra of molecular complexes in terms of intermolecular interaction energy components, we have shown for different types of systems and intermolecular bonds that the partitions of ΔE and ΔI are strongly linearly correlated, with a very small y-intercept, for the vibrational modes which involve substantial variations of the intermolecular bond length. Therefore, for such modes, the physical origin of the changes in the corresponding IR bands in terms of interaction types is similar to the interaction energy, which implies that both excess properties have equivalent physical nature. This is not true for other vibrational modes localized in one of the monomers studied here, for which the corresponding interaction-induced changes in IR bands may present a completely different decomposition than the interaction energy.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

A. I. R., B. O., and R. Z. acknowledge support from the National Science Centre, Poland (Grant 2019/35/B/ST5/00656). J. M. L. thanks the funds from the Spanish government MICINN (PGC2018-098212-B-C22), Generalitat de Catalunya (2021SGR00623), and Donostia International Physics Center (DIPC-INV-003133). The COST Action CA21101 is also acknowledged. The authors thank Wroclaw Centre for Networking and Supercomputing for computational resources and Miss Elizaveta F. Petrusevich for the preparation of the GTOC.

References

1. K. Morokuma, J. Chem. Phys., 1971, 55, 1236–1244.
2. T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10.
3. K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325–340.
4. P. S. Bagus, K. Hermann and C. W. Bauschlicher, J. Chem. Phys., 1984, 80, 4378.
5. W. J. Stevens and W. H. Fink, Chem. Phys. Lett., 1987, 139, 15–22.
6. E. D. Glendening and A. Streitwieser, J. Chem. Phys., 1994, 100, 2900.
7. Y. Mo, J. Gao and S. D. Peyerimhoff, J. Chem. Phys., 2000, 112, 5530.
8. P. Su and H. Li, J. Chem. Phys., 2009, 131, 014102.
9. P. R. Horn and M. Head-Gordon, Phys. Chem. Chem. Phys., 2016, 18, 23067.
10. A. Aldossary, M. Gimferrer, Y. Mao, A. K. D. Honxia Hao, P. Salvador, T. Head-Gordon and M. Head-Gordon, J. Phys. Chem. A, 2023, 127, 1760–1774.
11. A. Buckingham, J. Del Bene and S. McDowell, Chem. Phys. Lett., 2008, 463, 1–10.
12. T. Fornaro, D. Burini, M. Biczysko and V. Barone, J. Phys. Chem. A, 2015, 119, 4224–4236.
13. E. Arunan, G. R. Desiraju, R. A. Klein, J. Sadlej, S. Scheiner, I. Alkorta, D. C. Clary, R. H. Crabtree, J. J. Dannenberg, P. Hobza, H. G. Kjaergaard, A. C. Legon, B. Mennucci and D. J. Nesbitt, Pure Appl. Chem., 2011, 83, 1637–1641.
14. G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711–1713.
15. Q. Zhang, M. Chen, M. Zhou, D. M. Andrada and G. Frenking, J. Phys. Chem. A, 2015, 119, 2543–2552.
16. D. Ojha, K. Karhan and T. Kühne, Sci. Rep., 2018, 8, 2045–2322.
17. A. Iglesias-Reguant, H. Reis, M. Medved, J. M. Luis and R. Zalesny, Phys. Chem. Chem. Phys., 2023, 25, 11658–11664.
18. A. Iglesias-Reguant, J. Zielak-Milewska, T. Misiaszek, R. Zalesny, J. M. Luis and B. Osmialowski, J. Org. Chem., 2022, 87, 15159–15165.
19. V. Vasylyeva, L. Catalano, C. Nervi, R. Gobetto, P. Metrangolo and G. Resnati, CrystEngComm, 2016, 18, 2247–2250.
20. F. Meyer and P. Dubois, CrystEngComm, 2013, 15, 3058–3071.
21. G. R. Desiraju, J. Am. Chem. Soc., 2013, 135, 9952–9967.
22. W. Wang, Y. Zhang and W. J. Jin, Coord. Chem. Rev., 2020, 404, 213107.
23. J. K. Salunke, N. A. Durandin, T.-P. Ruoko, N. R. Candeias, P. Vivo, E. Vuorimaa-Laukkanen, T. Laaksonen and A. Priimagi, Sci. Rep., 2018, 8, 14431.
24. K. M. Bak, S. C. Patrick, X. Li, P. D. Beer and J. J. Davis, Angew. Chem., Int. Ed., 2023, 62, e202300867.
25. P. Auffinger, F. A. Hays, E. Westhof and P. S. Ho, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 16789–16794.
26. R. Wilcken, M. O. Zimmermann, A. Lange, A. C. Joerger and F. M. Boeckler, J. Med. Chem., 2013, 56, 1363–1388.
27. W.-S. Zou, S. Lin, J.-Y. Li, H.-Q. Wei, X.-Q. Zhang, D.-X. Shen, J.-Q. Qiao, H.-Z. Lian, D.-Q. Xie and X. Ge, New J. Chem., 2015, 39, 262–272.
28. T. Clark, M. Hennemann and J. Murray, et al. , J. Mol. Model., 2007, 13, 291–296.
29. B. Mallada, A. Gallardo, M. Lamanec, B. de la Torre, V. Spirko, P. Hobza and P. Jelinek, Science, 2021, 374, 863–867.
30. S. Yu, J. S. Ward, K.-N. Truong and K. Rissanen, Angew. Chem., Int. Ed., 2021, 60, 20739–20743.
31. N. Bedekovic, L. Fotovic, V. Stilinovic and D. Cincic, Cryst. Growth Des., 2022, 22, 987–992.
32. M. Gutowski, F. V. Duijneveldt, G. Chałasiński and L. Piela, Mol. Phys., 1987, 61, 233–247.
33. W. A. Sokalski, S. Roszak and K. Pecul, Chem. Phys. Lett., 1988, 153, 153–159.
34. S. M. Cybulski, G. Chałasiński and R. Moszyński, J. Chem. Phys., 1990, 92, 4357–4363.
35. G. Chałasiński and M. M. Szcześniak, Chem. Rev., 1994, 94, 1723–1765.
36. G. Chałasiński and M. M. Szcześniak, Mol. Phys., 1988, 63, 205–224.
37. F. B. van Duijneveldt, J. G. C. M. van Duijneveldt-van de Rijdt and J. H. Van Lenthe, Chem. Rev., 1994, 94, 1873–1885.
38. R. Moszyński, S. Rybak, S. Cybulski and G. Chałasiński, Chem. Phys. Lett., 1990, 166, 609–614.
39. M. Medved, A. Iglesias, H. Reis, R. Góra, J. M. Luis and R. Zaleśny, Phys. Chem. Chem. Phys., 2020, 22, 4225–4234.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02412a

---