Why do polyarginines adsorb at neutral phospholipid bilayers and polylysines do not? An insight from density functional theory calculations and molecular dynamics simulations

Abstract

Adsorption of cell-penetrating peptides (CPPs) at cellular membranes is the first and necessary step for their subsequent translocation across cellular membranes into the cytosol. It has been experimentally shown that CPPs rich in arginine (Arg) amino acid penetrate across phospholipid bilayers more effectively than their lysine (Lys) rich counterparts. In this work, we aim to understand the differences in the first translocation step, adsorption of Arg₉ and Lys₉ peptides at fully hydrated neutral phosphatidylcholine (PC) and phosphatidylethanolamine (PE) lipid bilayers and evaluate in detail the energetics of the process using molecular dynamics (MD) simulations and free energy calculations of adsorption of the single peptide. We show that the adsorption of Arg₉ is energetically feasible, with the free energy of adsorption being ∼−5.0 kcal mol⁻¹ at PC and ∼−5.5 kcal mol⁻¹ at PE bilayers. In contrast, adsorption of Lys₉ is not observed at PC bilayers, and their adsorption at PE bilayers is very weak, being ∼−0.5 kcal mol⁻¹. We show by energy decomposition and analysis of peptide hydration along the membrane that significantly stronger electrostatic interactions of Arg₉ with lipid phosphate groups, together with the greater loss of peptide hydration (and in turn stronger hydrophobic interactions) along the membrane translocation path, are the main driving factors governing the adsorption of Arg-rich peptides at neutral lipid bilayers in contrast to Lys-rich peptides. Finally, we also compare the energetics in lipid/bilayer systems with the density functional theory (DFT) calculations of the corresponding model systems in the continuum water model and reveal the energetic differences in different environments.

---

Introduction

Cells are the smallest key building blocks of all living matter surrounded by a few nanometers thin cell membrane ubiquitous for cell integrity, transport across the cell, and its function.¹ Lipids and various membrane proteins are integral building blocks of the membrane – while membrane proteins perform vital cellular functions, the surrounding lipids provide an optimal environment and scaffold needed for proteins to act properly, precisely controlling the transmembrane transport.²

Due to the semipermeable character of phospholipid bilayers, the spontaneous passive translocation of charged species across protein-free membranes is very slow, since the charged species must transfer across the strongly hydrophobic interior around phospholipid hydrocarbon tails, which is energetically very costly.^3,4 However, the transport of ions, such as ATP,⁵ Na⁺, or K⁺,⁶ is vital for many cellular functions and is, therefore, actively facilitated by the control of embedded membrane proteins whose function is driven by the energy released by ATP hydrolysis. Additionally, other active translocation processes, such as endocytosis or exocytosis, are also fueled by ATP and regulated by the sophisticated membrane protein machinery.^7,8

However, it has been shown in the last few decades that some of the charged species can easily passively translocate phospholipid bilayers without endocytosis and energy provided by ATP hydrolysis.⁹ In particular, Arg-rich peptides, containing more than 5 Arg units, have been shown to translocate across cellular membranes in contrast to equally charged Lys-rich peptides,^10–14 which is often referred to as the “arginine magic” in the literature.¹⁵ This unique behavior of polyarginines can possibly be ascribed to the unique properties of the main component of the Arg side chain, the guanidinium (Gdm⁺) cation. It has been shown previously that Gdm⁺ cations tend to make like-charge ion pairs in water, despite their positive charge and Coulomb repulsion between them.^16,17 Moreover, it has been shown that deca-arginines also tend to make aggregates in water, in contrast to deca-lysines.¹⁸ In addition, it has also been shown that nona- and deca-arginines tend to aggregate and adsorb to the neutral phospholipid bilayers in contrast to nona- and deca-lysines.^19,20 Recent experiments have also shown that octa-arginines can spontaneously translocate across giant PC unilamellar vesicles, but the mechanism of translocation is very vaguely described at the molecular level.^21–23

Since the first step of the translocation process of any species across the cellular membrane is adsorption to the outer leaflet of the phospholipid bilayer, mostly composed of neutral zwitterionic lipids such as PC,²⁴ in this work we decided to quantitatively assess the adsorption of nona-arginines (R₉) and nona-lysines (K₉) at the 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) and 1-palmitoyl-2-oleoyl-phosphatidylethanolamine (POPE) lipid bilayers using molecular dynamics (MD) simulations and accompanying free energy calculations. In the previous work, we have shown a qualitative difference between the adsorption of poly-Arg and poly-Lys,^19,20,25 where Arg-rich peptides adsorb more favorably than Lys-rich peptides. We report here for the first time the adsorption energetics obtained by PMF calculations of the adsorption of a single peptide, in contrast to free energies obtained from unbiased calculations, where we have shown that peptide concentration and ionic strength play an important role in peptide adsorption energetics.²⁵ Moreover, since Arg-rich peptides are predicted to aggregate in water¹⁸ as well as at the membranes,^19,20 it is important to calculate the adsorption energy of a single peptide at infinite dilution to eliminate both the aggregation and ionic strength effect. Similar work has been reported in the literature for single R₈ at PC, PE, and PG membranes,²⁶ but with a different, pore-forming coordinate instead of a z-axis which does not necessarily predict the adsorption energetics of Arg-rich peptides at membranes.

Using the described methods, in combination with energy decomposition analysis of key energy interactions between lipids and peptides in the membrane interior, we try to answer the simple question – why do polyarginines adsorb to neutral membranes and polylysines do not? One of the first logical assumptions is that positively charged Arg residues interact more strongly with the negatively charged phospholipid phosphate groups than Lys residues, simply due to the different geometry as the Gdm⁺ cation present in the Arg side chain can make both monodentate and bidentate bonding to phosphates via one or two hydrogen bonds, whereas the ammonium (–NH₃⁺) group in Lys can interact with phosphates only with a single hydrogen bond. However, this hypothesis has not been confirmed by NMR experiments and accompanying MD simulations, and it has been shown that Arg interacts with aspartate differently than with glutamate amino acid (+1.9 vs. +0.5 kcal mol⁻¹) in water, whereas the binding of Lys is almost identical (+1.0 and +0.9 kcal mol⁻¹) for both amino acids, respectively, and all the interactions between the compounds were destabilizing.²⁷ This surprising behavior where Arg interacts with Glu in a qualitatively different fashion, being much more destabilizing than in the interaction with Asp, has been explained by the entropic factors arising from one methylene group less in Glu compared to Asp, thus reducing the ability of Glu to adapt to a larger number of favorable double hydrogen bonded salt bridge conformations and in turn more stable interaction, compared to Asp. Interestingly, a similar effect has not been observed for Lys, where these subtle entropic effects do not play a decisive role due to only entropically more favored single hydrogen bonded salt bridge interactions, in turn resulting in similar destabilization of the studied complexes. However, we should mention here that the overall destabilization of salt bridge interactions in experiments (as well as MD simulations) occurs due to completely hydrated salt bridges at the peptide concentrations used in the work, which is usually not favorable for the stabilization of the complexes.²⁷ Therefore, a simple premise that Arg containing the –Gdm⁺ group interacts more strongly (or less destabilizing) than Lys containing the –NH₃⁺ group with negatively charged phosphates in phospholipid bilayers (which is a more heterogeneous and less hydrated medium than water), remains to be quantitatively verified, which is one of the goals of the present study.

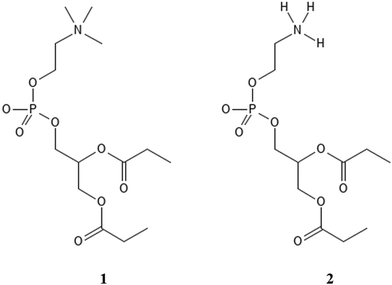
A complementary set of density functional theory (DFT) calculations of stabilization of POPC and POPE proxy models (1 and 2, Scheme 1) with Gdm⁺ and NH₄⁺ in continuum water models was performed to elucidate the general interaction patterns and the effect of the environment, serving as a guide for the analysis of peptide-membrane interactions in MD simulations.

Scheme 1 Proxy systems representing POPC lipid (1) and POPE lipid (2).

Computational methods

Density functional theory (DFT) calculations

DFT calculations of total electronic energies of interactions of POPC and POPE proxy systems (1 and 2, Scheme 1), with Gdm⁺ and NH₄⁺ ions (Fig. 1 and 2) were performed using the PCM continuum water model with SMD Coulombic atomic radii using a dielectric constant of 78.4.²⁸ Geometry optimization was conducted at the M062X/aug-cc-pVDZ level of theory with subsequent single point calculations using the aug-cc-pVTZ basis set.²⁹ M062X functionals were applied as they were initially benchmarked against arginine-halide clusters, showing excellent performance compared to the MP2 method.³⁰ Complex formation with Gdm⁺ and NH₄⁺ ions, using proxy models 1 and 2, was performed for a set of specific configurations, reflecting the interactions between the ions and proxy lipid headgroups, i.e. choline (POPC) and ammonium (POPE) group. The complexes resembling separately the interaction of Gdm⁺ and NH₄⁺ with the choline group and with the phosphate group (in both monodentate and bidentate forms) of POPC and POPE proxy systems 1 and 2, respectively, were manually generated by arranging ions and proxy systems in the corresponding binding-like initial configurations (Fig. 1 and 2), and the energy stabilization of the resulting complexes was calculated as the total energy difference between the energy of the complex and the sum of the corresponding energy of participating molecules. All DFT calculations were performed using the Gaussian 16 set of codes.³¹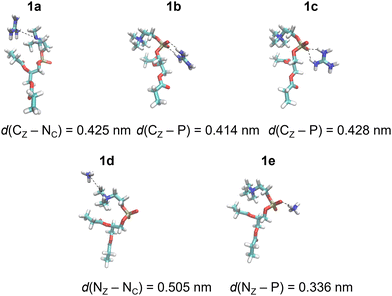

Fig. 1 Gdm⁺ and NH₄⁺ complexes with POPC proxy 1 in the SMD water model calculated at the M1 level of theory (Table 1).

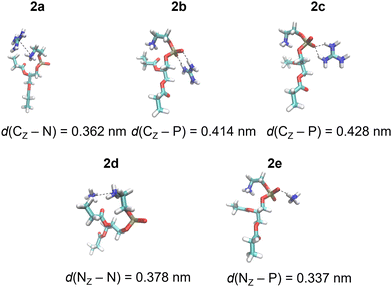Fig. 2 Gdm⁺ and NH₄⁺ complexes with POPC proxy 2 in the SMD water model calculated at the M1 level of theory (Table 1).

Molecular dynamics (MD) simulations

Atomistic molecular dynamics (MD) simulations were employed to systematically investigate the membrane interactions of R₉ and K₉ at POPC and POPE bilayer systems, respectively. A single R₉ or K₉ peptide is added to the water solution of hydrated lipid bilayers, and chloride counterions were added to neutralize the systems. The initial peptide structures were linear at the beginning of the simulations, but very rapidly (after several ns) assumed different secondary structures in water (random-coiled for R₉ peptides, and mostly linear for K₉ peptides). During translocation across lipid interior, these changes were dictated by the interactions with the lipid phosphate groups, and the peptides did not exhibit any particular secondary structure. The simulation boxes of all studied systems contained ∼13 700 water molecules. The membrane bilayer consisted of 100 POPC or POPE lipids in each leaflet. Since commonly used MD force fields, such as AMBER³² or CHARMM,³³ lack the proper description of electronic polarizability, we decided to use a different approach and apply so-called “scaled-charge” force fields built in-house, where all ionic charges were decreased by 25% percent, which leads to the correct description of electrostatic energy between oppositely charged ions.^34,35 This approach has been successfully used in several simulations of ionic pairs in water, where ionic interactions were benchmarked against neutron diffraction measurements and have shown a qualitatively different and more accurate description of the electrostatics in the studied systems.^36,37 The described approach has also been proposed and validated for ion-lipid and peptide–lipid interactions²⁵ in the recently available CHARMM36-based ProsECCo force field,³⁸ which was used in this work.

ProsECCo models were applied for lipids and proteins, and the chloride counterion parameters were incorporated through the electronic continuum correction (ECC) approach. This adjustment addresses the issue of charged molecules overbinding to zwitterionic bilayers. Specifically, the partial charges in the ProsECCo models, namely those of the phosphate and choline groups of POPC and POPE, as well as the charged groups of arginine and lysine (i.e., termini and side-chains) were scaled down by 25%, resulting in the decrease of charges from +1e to +0.75e. Similarly, the charge of chloride counterions was decreased from −1e to −0.75e. The corresponding partial charges of used peptides, lipids, and Cl⁻ ions are provided in Table S1 (ESI†). No other changes were made to the CHARMM36 lipid or peptide parameters, and MD simulations were used without NBFIX correction.³⁹ All systems were solvated using the CHARMM-specific TIP3P (“TIPS3P”) water.^40,41 Buffered Verlet lists were used to track atomic neighbors, while a cut-off of 1.2 nm was used for the Lennard-Jones potential. van der Waals interactions were treated using a cut-off of 1.2 nm, with the forces smoothly attenuated to zero between the distances of 1.0 and 1.2 nm. The smooth particle mesh Ewald method⁴² was used to describe long-range electrostatic interactions. The systems were first minimized and equilibrated for at least 20 ns. For production runs, we used the Parrinello–Rahman barostat⁴³ with a semi-isotropic pressure coupling and at 1 bar in combination with the Nosé–Hoover thermostat at 310 K.⁴⁴ The time constants for coupling were set at 5 ps and 1 ps for the barostat and the thermostat, respectively. Lipid molecules, peptides, and solvents (water and chloride counterions) were coupled separately to the thermostats. All covalent bonds in peptides and lipids involving hydrogens were constrained using the P-LINCS algorithm,⁴⁵ whereas the SETTLE algorithm⁴⁶ was used for water molecules. Production unbiased MD simulation runs were performed for 200 ns using a time step of 2 fs.

Free energy calculations of peptide adsorption to membranes are obtained for all systems by placing the R₉ or K₉ center of mass at ∼4.5 nm from the bilayer center in the water phase. After the initial pulling of the peptide along the z-axis using a rate of 0.001 nm ps⁻¹, we generated a set of ∼40 different configuration windows separated by 0.1 nm between the peptide and lipid center of mass along the z-axis. After that, a harmonic umbrella potential of 1000 kJ mol⁻¹ nm⁻² was applied between the peptide center of mass and the lipid bilayer center of mass. Biased MD simulations were then performed for 100 ns per umbrella window with the first 20 ns omitted from further analysis. The distance between molecules was monitored during umbrella sampling simulations, which were used to calculate the potential of mean force (PMFs) applying the WHAM procedure, while error bars for free energies were estimated using the bootstrap method with 200 bootstraps.⁴⁷

Energy decomposition was performed using the gmx_energy tool for each umbrella window separately, extracting corresponding Coulombic and Lennard-Jones (LJ) contributions for energy interactions between peptide vs. choline and phosphate groups in POPC lipids, and peptide vs. ammonium and phosphate groups in POPE lipids, respectively. Importantly, we chose to compare the energetic contributions at 0.5–0.8 nm from the bilayer center (depending on the system), not at energy minima, due to two reasons – first, the comparison of energy deeper in the hydrophobic center reveals more pronounced differences in energetics in this region. Second, it is not possible to compare energy differences in energy minimum directly because it either does not exist in the case of K₉-POPC or is very broad and weakly pronounced in the case of K₉-POPE. All MD simulations were performed using the GROMACS 2018.4 program package.⁴⁸

Results and discussion

DFT calculations

DFT calculations were performed for a set of complexes between Gdm⁺ and NH₄⁺ with proxy systems 1 and 2 (Scheme 1, Fig. 1 and 2), representing different investigated Arg/Lys – POPC/POPE interactions. Total electronic stabilization energies were calculated as an energy difference between separated species Gdm⁺, NH₄⁺, and proxies 1 and 2, and their corresponding complexes in the SMD water continuum model. Distances were extracted considering the central carbon atom of the Gdm⁺ group (C_Z), the nitrogen atom of the ammonium group (N_Z), the nitrogen atom of the choline group (N_C), and the phosphorus atom (P) of the phosphate group in proxies 1 and 2, respectively (Fig. 1 and 2). The interaction of Gdm⁺ with the choline group of 1 (mimicking primarily the hydrophobic Arg/POPC choline interaction) results in a complex, 1a (Fig. 1, top left panel) with the electronic stabilization of −3.1 kcal mol⁻¹ at the M2 level of theory (Table 1). A relatively short interaction between Gdm⁺ and choline groups in 1a with a calculated non-negligible several kcal mol⁻¹ energy stabilization indicates an important hydrophobic component of the total energetic interaction. At the observed distance between the choline group and Gdm⁺ cation which is anisotropically hydrated only in-plane,¹⁶ no water molecules are expected to be present between the hydrophobic planes of Gdm⁺ and choline group, therefore indicating a hydrophobic effect as a key component in the stabilization of the complex. On the other hand, the interactions in 2a (Fig. 1, bottom left panel) are much weaker (although with the shorter distance between the Gdm⁺ cation and ammonium group), indicating a lack of hydrophobic interaction, leading to the loss of the total electronic stabilization of the complex, being +0.2 kcal mol⁻¹ (Table 1, M2). The lack of hydrophobic interaction between NH₄⁺ and the choline group is not unexpected, since the NH₄⁺ ion is spherically hydrated and water molecules are likely present in the explicit water environment between NH₄⁺ and choline group, similar to the reported ab initio MD simulations of NH₄⁺–NH₄⁺ ions in the explicit water environment, in contrast to Gdm⁺–Gdm⁺ ions.¹⁶

Table 1 Total electronic stabilization energies (in kcal mol⁻¹) of specific complexes of Gdm⁺ and NH₄⁺ with POPC proxy system 1 and POPE proxy system 2 (Scheme 1, Fig. 1 and 2), respectively, in the SMD continuum water model obtained by DFT calculations using M062X/aug-cc-pVDZ (M1) and M062X/aug-cc-pVTZ//M062x/aug-cc-pVDZ (M2) levels of theory. Distance between the central carbon atom of the Gdm⁺ group (C_Z) and the nitrogen atom of the ammonium group (N_Z) vs. the nitrogen atom of the choline group (N_C), and the phosphorus atom (P) of the phosphate group in proxies 1 and 2 in the corresponding energy minima, respectively, is given in nm

	Label	M1	M2	Distance
a Bidentate complex. b Monodentate complex.
POPC – proxy 1
Gdm^+-choline	1a	−4.2	−3.1	0.425
Gdm^+-phosphate^a	1b	−10.7	−9.5	0.414
Gdm^+-phosphate^b	1c	−8.2	−7.5	0.428
NH4^+-choline	1d	−0.9	−0.6	0.505
NH4^+-phosphate	1e	−7.5	−6.9	0.336
POPE – proxy 2
Gdm^+-ammonium	2a	−0.6	0.2	0.362
Gdm^+-phosphate^a	2b	−8.1	−6.9	0.414
Gdm^+-phosphate^b	2c	−4.7	−4.2	0.428
NH4^+-ammonium	2d	−4.4	−3.5	0.378
NH4^+-phosphate	2e	−3.2	−3.0	0.337

---

Next, we perform the analysis of the binding geometries of NH₄⁺ ions with choline and ammonium groups 1 and 2 (complexes 1d and 2d, Fig. 1 and 2), representing Lys-POPC choline and Lys-POPE ammonium interactions, respectively. The distance between the NH₄⁺ group and choline in complex 1d is 0.13 nm longer compared to complex 2d between the NH₄⁺ and the ammonium group. Accordingly, the stabilization of 1d is much weaker than that of 2d (−0.6 vs. −3.5 kcal mol⁻¹, Table 1, method M2). This is quite surprising, because the interaction between Gdm⁺ and the ammonium group in complex 1d is very weak, whereas pure hydrophilic interaction between NH₄⁺ ions and ammonium group in system 2d is more energetically favored (which is expected to be strictly repulsive in explicit water¹⁶). Conspicuously, the interaction between the NH₄⁺ ions and ammonium group in 2d shows a quite short distance between ammonium groups (Fig. 2, bottom left panel) in contrast to the Gdm⁺ ion and ammonium group in 1d. This suggests an unexpected (and quite unrealistic) possibility of the stabilizing contact ion pair between ammonium cations in the continuum water model in this specific geometry configuration.

Another possible interaction of Gdm⁺ ions with 1 and 2 is with their phosphate groups (Fig. 1 and 2), simulating Arg/POPC phosphate and Arg/POPE phosphate interactions. The complexation can occur in two ways – via a bidentate binding mode simultaneously interacting with two oxygen phosphates (complexes 1b and 2b) and a monodentate binding mode with a single oxygen phosphate (complexes 1c and 2c). Importantly, complexes 1e and 2e which mimic Lys/POPC and Lys/POPE interactions with phosphate group proxies 1 and 2 result in monodentate complexes only, due to the small size of the NH₄⁺ cation. The geometric analysis reveals that the bidentate binding mode of Gdm⁺ in 1b and 2b, results in shorter Gdm⁺ carbon distance vs. monodentate binding (1c and 2c) by 0.14 nm. Interestingly, the distances between Gdm⁺ and phosphate ions in systems 1b and 1cvs.2b and 2c in both binding configurations, respectively, are virtually identical. However, this is not completely reflected in their binding energetics. Specifically, the stabilization of complex 1b is −9.5 vs. −6.9 kcal mol⁻¹ in system 2b (Table 1, method M2), suggesting a stronger bidentate Gdm⁺ binding in the POPC proxy model vs. the POPE proxy model. This is even more pronounced for the corresponding monodentate complexes 1c and 2c, where the differences in complexation stabilization are −7.5 vs. −4.2 kcal mol⁻¹ (Table 1, method M2). Overall, the comparison of energetics between Gdm⁺ ions with proxies 1 and 2 suggests that Arg/POPC interactions are stronger than the corresponding Arg/POPE interactions in the continuum water model as evidenced by both stronger hydrophobic Gdm⁺-choline as well as Gdm⁺-phosphate interactions in systems 1a–1c and 2a–2c (Table 1, method M2).

On the other hand, the energy stabilization in Lys/POPC choline proxy complex 1d is much weaker than in the corresponding Lys/POPE ammonium proxy complex 2d (−0.6 vs. −3.5 kcal mol⁻¹, Table 1, method M2). Conversely, Lys/POPE phosphate interactions represented by the proxy complex 1e are significantly stronger than Lys/POPE phosphate interactions in the proxy complex 2e (−6.9 vs. −3.0 kcal mol⁻¹). In contrast to Arg/POPC and Arg/POPE proxy models, differences in various complex stabilities in proxy Lys/POPC and Lys/POPE are more difficult to interpret due to the opposite energetic stabilization trends.

In the end, we should mention that the estimation of free energy stabilization is technically possible in SMD continuum water models using simplified thermodynamic algorithms based on vibrational analysis.⁴⁹ However, they are not performed here due to the extensive computational cost of the vibrational analysis of the optimized complexes, especially using the aug-cc-pVTZ basis set. Additionally, many possible configurations present in explicit water environments are not represented properly in the simplified continuum model, thus questioning the validity of free energy calculations on single structures due to incomplete evaluation of entropic contribution caused by the inability of the model to fully represent numerous configurations represented in the solution. Therefore, we compared only the total electronic energies of complexes to obtain better qualitative insight into the interaction patterns of the studied systems and approximate energetics of binding, disregarding partial enthalpic and entropic contributions theoretically available by using the SMD model. A detailed free energy study of interactions that are directly relevant for peptide/membrane interactions, including all enthalpic and entropic contributions in an explicit water solvent, is performed using classical MD simulations and is described below.

MD simulations

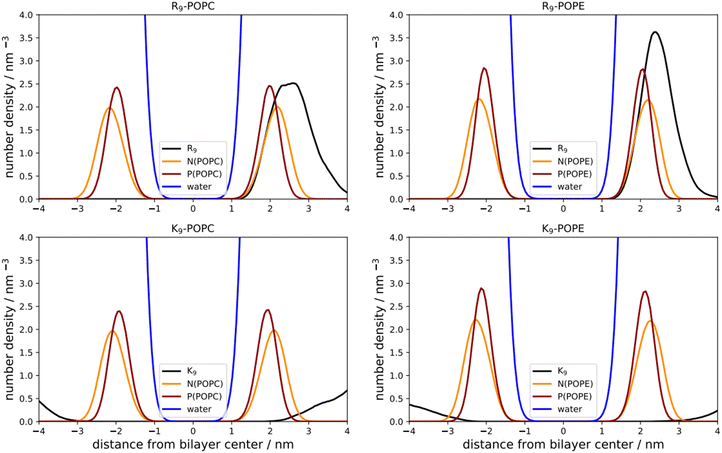
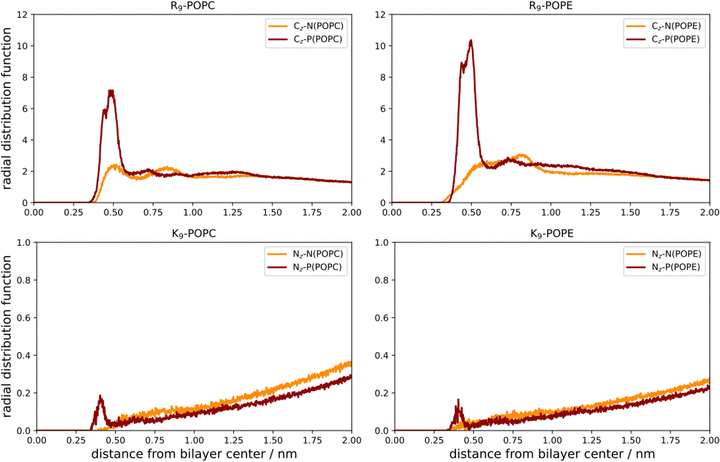
As a first step, we performed direct unbiased MD simulations of R₉ and K₉ at POPC and POPE lipid bilayers, respectively, to obtain the density profiles of the species in the system (Fig. 3). We also calculated the corresponding radial distribution functions (RDFs) between the key groups in peptides and lipids to assess their binding geometry and affinity to the selected lipid bilayer groups (Fig. 4).

Fig. 3 Number density profiles of peptides, N(POPC), P(POPC), and water (black, orange, dark red, and blue line, top and bottom left panels); N(POPE), P(POPE) atom and water (black, orange, dark red, and blue line, top and bottom right panels), respectively.

Fig. 4 Radial distribution functions (RDFs) between R₉-C_Z atoms and N(POPC, orange) and P(POPC, dark red), and R₉-C_Z atoms vs. N(POPE, orange) and P(POPE, dark red), respectively, are depicted in the left top and bottom panels. Radial distribution functions (RDFs) between K₉-N_Z atoms and N(POPC, orange) and P(POPC, dark red), as well as K₉-N_Z atoms vs. N(POPE, orange) and P(POPE, dark red), respectively, are presented in the bottom left and right panels). RDFs are given vs. the corresponding distance between the groups.

The number density profiles of all investigated systems are shown in Fig. 3. It is evident that R₉ peptides adsorb to both POPC and POPE, demonstrated by a larger peptide number density at membranes vs. bulk, in contrast to K₉ peptides which show no signs of binding and depletion from the bilayer. An enhanced number density profile of R₉ at POPE (Fig. 3, top right panel) shows a sharper maximum in the number density peak vs. R₉/POPC interaction (Fig. 3, top left panel), thus indicating more favorable peptide adsorption. This is additionally supported by the analysis of the corresponding RDFs shown in Fig. 4, where a higher RDF maximum is observed for the interaction between the R₉ and POPE phosphate group (Fig. 4, top right panel) than in the R₉ and POPC phosphate group (Fig. 4, top left panel). Importantly, the presence of two peaks at different distances in RDF maxima in R₉-POPC and R₉-POPE indicates a certain degree of both monodentate and bidentate binding of Gdm⁺ to a lipid phosphate group, in agreement with different binding geometries of Gdm⁺ with phosphate complexes 1b and 1c in the continuum SMD water model (Fig. 1, top middle and top right panel). The interactions between R₉ and POPC choline group as well as R₉ and POPE ammonium group, (Fig. 5, bottom left and right panel, respectively), are also qualitatively different with significantly smaller corresponding RDF peaks and are not decisive for the overall energy balance. Importantly, the larger stabilization of R₉ at POPE vs. POPC disagrees with DFT calculations in Arg/POPC and Arg/POPE proxy systems in continuum SMD water models, which predict that the interaction of Gdm⁺ with proxy 1 (simulating POPC) is more favorable (Table 1, M2).

Fig. 5 Free energy calculations and the corresponding PMFs for the R₉/POPC system (top left panel), Coulombic (C_Z-phosphate and C_Z-choline), and Lennard-Jones total energy contributions (C_Z-phosphate and C_Z-choline, top middle panel), and the calculated number of closest water molecules within 0.6 nm of R₉ along the POPC bilayer (top right panel). Free energy calculations and the corresponding PMFs for the R₉/POPE system (bottom left panel), Coulombic (C_Z-phosphate and C_Z-ammonium), and Lennard-Jones total energy contributions (C_Z-phosphate and C_Z-ammonium, bottom middle panel), and the calculated number of closest water molecules within 0.6 nm of R₉ along the POPE bilayer (bottom right panel). Total energetic contributions are estimated at ∼ 0.5 nm from the membrane center. All values are given as a function of peptide vs. lipid bilayer center of mass distances.

On the other hand, density profiles of K₉ at POPC and POPE bilayers show no peptide enhancement close to the membrane surface (Fig. 3, bottom left and right panels) and very small or negligible peaks in the corresponding RDFs (Fig. 4, bottom left and right panel), suggesting no favorable interactions between K₉ peptides with either POPC and POPE phosphate group or POPC choline and POPE ammonium group, respectively. These results suggest that the interaction of K₉ peptides with POPC and POPE is destabilizing, in contrast to water continuum model calculations, which predict the existence of stable complexes between NH₄⁺ and proxies 1 and 2 (1d–1e and 2d–2e, Table 1, method M2).

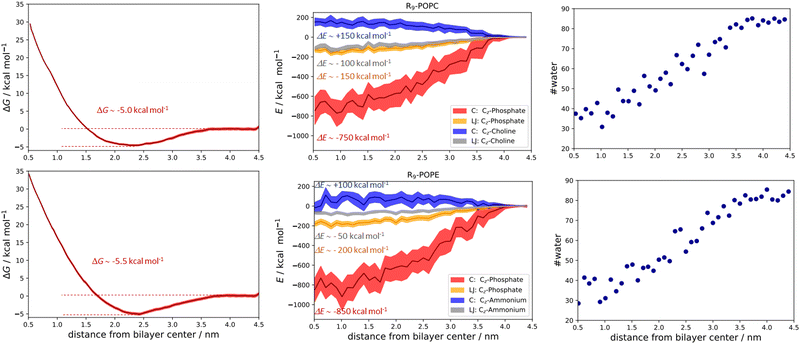
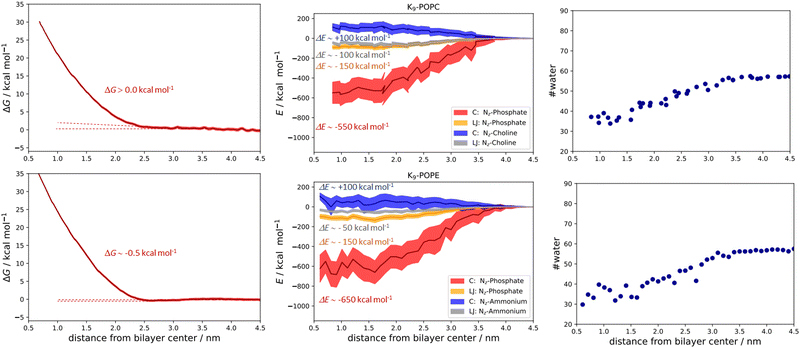
The qualitative description of interactions by the analysis of number density profiles and RDF calculations shown in the above section is further quantitatively assessed using the free energy of binding calculations (Fig. 5). In the first example, the R₉/POPC free binding energy is presented in Fig. 5 (top left panel), where we observe the free energy minimum at ∼0.23 nm from the membrane center, amounting to the free energy of stabilization being ∼−5.0 kcal mol⁻¹. This clearly indicates favorable binding of R₉ and POPC and is also evidenced by inspection of key total energy components of the interaction (Fig. 5, top middle panel). In particular, a destabilizing Coulombic interaction between positively charged R₉ and POPC choline groups is present throughout the whole membrane, with a maximum of ∼+150 kcal mol⁻¹ close to the POPC bilayer center (Fig. 5, top middle panel). However, this energy destabilization is counteracted by stabilizing LJ interactions of R₉ and choline and phosphate POPC group (being ∼−100 and −150 kcal mol⁻¹) and strong Coulombic electrostatic interaction of R₉ with the POPC phosphate group of ∼−750 kcal mol⁻¹.

The free energy of binding between R₉ and POPE and the corresponding PMF is presented in the bottom left panel of Fig. 5. Interestingly, the free energy minimum is a bit sharper and moves slightly away from the membrane center at the distance of ∼0.24 nm (compared to ∼0.23 nm for POPC). Moreover, the interaction is a little more stabilizing than the R₉/POPC interaction by ∼−0.5 kcal mol⁻¹, being ∼−5.5 kcal mol⁻¹. The Coulombic interaction between R₉ and POPE ammonium is by ca. −50 kcal mol⁻¹ less destabilizing compared to R₉/POPC choline interaction, being ∼+100 kcal mol⁻¹ at the distance of ∼0.5 nm from the POPE membrane center, and the LJ interactions between the R₉ and POPE ammonium group are up to ∼50 kcal mol⁻¹ less stabilizing across the membrane compared to the R₉/POPC choline interaction (Fig. 5, bottom middle panel). This is intuitively expected, because the interaction between the spherically hydrated ammonium POPE group and the anisotropically hydrated Gdm⁺ cation should not result in favorable hydrophobic stabilization, in agreement with the corresponding continuum water calculations (1a and 2a, Table 1, M2). The LJ interaction between R₉ and POPE phosphate group is similar in strength to R₉/POPC phosphate interactions, but the electrostatic interaction between R₉ and POPE phosphate group is more stabilizing by an additional ∼100 kcal mol⁻¹ (−850 vs. −750 kcal mol⁻¹, Fig. 5 middle panels), which compensates weaker hydrophobic stabilization between R₉ and POPE ammonium group. Additionally, we also observed that the decrease of R₉ peptide hydration in POPC and POPE (calculated as the number of water molecules with 0.6 nm of the peptide) is quite pronounced, ranging from ∼90 water molecules in bulk vs. ∼30 water molecules close to the membrane center (Fig. 5, top and bottom right panels). Since the strength of electrostatic interaction is inversely proportional to the dielectric constant of the environment, (which is significantly larger in water, where ε_r ∼ 78.5 vs. membrane interior where ε_r ∼ 2), a hydrophobic effect, demonstrated as the pronounced decrease in R₉ hydration, also contributes to the stabilization of R₉ at POPC and POPE membranes. The overall energy balance of Coulombic and Lennard-Jones interactions in R₉/POPC and R₉/POPE, together with a similar hydration loss, slightly favors the latter, contributing to its observed greater energy stabilization at the membrane. Specifically, the differences observed in the interaction of positively charged Gdm⁺ cations of R₉ with POPC or POPE phosphate groups (−750 vs. −850 kcal mol⁻¹ close to membrane center) are likely responsible for the observed slight increase of free energy of binding of R₉ at POPE vs. R₉ at POPC (−5.5 vs. −5.0 kcal mol⁻¹, Fig. 5).

In the case of binding in K₉ at POPC and K₉ at POPE, we also observed some small but illustrative energetic differences. First, the free energy of binding between K₉ and POPC is fully repulsive, and no free energy minimum is found along the z-axis of the POPC bilayer (Fig. 6, top left panel). Second, in the case of K₉-POPE binding, a very shallow free energy minimum of ∼−0.5 kcal mol⁻¹ (which is at odds with the error bar of calculations) is observed. Although the binding of K₉ to POPE is very weak at best, it points to subtle differences in the binding revealed in the analysis of the energetics. Coulombic interactions between K₉ and POPE ammonium group are destabilizing as expected (Fig. 6, top middle panel). Here, we also see destabilization in LJ interactions between the K₉ and POPE choline group (Fig. 6, bottom middle panel) by ∼50 kcal mol⁻¹ compared to K₉ and POPC choline group, similar to the corresponding interactions in R₉/POPC and R₉/POPE (Fig. 5, top and bottom middle panels). Interestingly, LJ interactions between K₉ and POPC choline group are close in value to the interactions of R₉ and POPC choline group (∼−100 kcal mol⁻¹, Fig. 5 and 6 top middle panels), indicating a similar hydrophobic stabilization of –NH₃⁺ and –Gdm⁺ groups with the lipid choline group, despite the different hydration of Gdm⁺ and NH₄⁺ cations in bulk water.¹⁶ LJ interactions between K₉ and POPC and POPE phosphate groups are stabilizing being ∼−150 kcal mol⁻¹ for both systems (Fig. 6, top and bottom middle panel). The interactions of the K₉ group and POPE phosphate group are stronger by ∼100 kcal mol⁻¹ in the case of K₉/POPE vs. K₉/POPC (−650 vs. −550 kcal mol⁻¹), thus indicating why K₉ adsorbs at POPE very weakly (if at all), in contrast to fully repulsive K₉-POPC interaction (Fig. 5, bottom left panel). Finally, overall weaker peptide stabilization in K₉/POPC and K₉/POPE systems vs. corresponding R₉ systems is witnessed in a less pronounced hydrophobic effect, i.e. the change of peptide hydration along the membrane. In the case of K₉ peptides, the loss of hydration along the membrane is 25 molecules (contrasted to 60 water molecules for R₉ peptides, Fig. 5) within 0.6 nm of the peptide (55 water molecules in bulk vs. 30 water molecules close to the membrane center) and is similar for both K₉/POPC and K₉/POPE systems (Fig. 6, top right and bottom right panel). The observed overall loss of hydration is significantly smaller in K₉/POPC and K₉/POPE systems than in R₉/POPC and R₉/POPE systems, resulting in weaker hydrophobic stabilization. In addition to stronger phosphate binding in the case of the R₉ systems, the observed differences in the hydrophobic effect strength evidence why polylysines adsorb with less affinity than polyarginines at neutral zwitterionic POPC and POPE membranes (Fig. 5 and 6). We should stress here that calculated free energies of adsorption of a single peptide do not correspond to the data obtained at finite peptide concentrations using unbiased MD simulations,²⁵ where we have shown that adsorption energetics depends on the peptide concentration and weakens with its increase. Moreover, unbiased MD simulations for the single peptides do not allow estimating the free energies of binding using number density ratios, because a single peptide would be confined only to the adsorbed state and no exchange between unadsorbed and adsorbed state is recorded which is essential for the quantitative estimate of adsorption free energy.²⁵ In addition, when compared to the available free energy calculations of R₈ at POPC and POPE membranes using a non-optimal pore-forming coordinate (which is better suited for penetration energetics, not adsorption), there is a lack of agreement, and the latter simulations predict no binding of R₈ at the POPE bilayer, in contrast to the results shown in this work.²⁶

Fig. 6 Free energy calculations and the corresponding PMFs for the K₉-POPC system (top left panel), Coulombic (N_Z-phosphate and N_Z-choline), and Lennard-Jones total energy contributions (N_Z-phosphate and N_Z-choline, top middle panel), and the calculated number of closest water molecules within 0.6 nm of K₉ along the POPC bilayer (top right panel). Free energy calculations and the corresponding PMFs for the K₉/POPE system (bottom left panel), Coulombic (N_Z-phosphate and N_Z-ammonium), and Lennard-Jones total energy contributions (N_Z-phosphate and N_Z-ammonium, bottom middle panel), and the calculated number of closest water molecules within 0.6 nm of K₉ along the POPE bilayer (bottom right panel). Total energetic contributions are estimated at ∼0.8 (for POPC) and ∼0.6 nm (for POPE) from the membrane center. All values are given as a function of peptide vs. lipid bilayer center of mass distances.

Still, we should mention here that the evaluation of energetic decomposition of only a few selected total energy interactions and their comparison to free energies of binding is not fully justified due to the lack of entropic effects in analyzed total energy interactions. However, the analysis of key energetic contributions and differences in peptide hydration in the membrane interior helps to qualitatively assess the quantitative free energy binding differences between polyarginines and polylysines at neutral PC and PE membranes, respectively.

Conclusions

In summary, a combination of DFT calculations and MD simulations in this work is used to show in detail how R₉ peptides adsorb to neutral POPC and POPE membranes in contrast to K₉ peptides, which are either fully repulsed from the membrane as in POPC, or at best very weakly stabilized in the K₉/POPE system. Specifically, the binding of R₉ with the lipid phosphate groups occurs via both monodentate and bidentate interaction modes, in contrast to K₉ which does not interact with the lipid bilayer. We rationalized in detail the energetic differences between R₉/POPC and R₉/POPE and compared them to K₉/POPC and K₉/POPE interactions and peptide hydration along the membrane, respectively, and found that the electrostatic interaction of R₉ with the lipid phosphate group is significantly stronger than the corresponding K₉ lipid/phosphate interaction. Together with the more pronounced hydration loss of R₉ peptides vs. K₉ peptides, and in turn stronger hydrophobic effect, these two factors are dominant in the overall energy interaction pattern, thus answering the title question of why polyarginines bind to neutral membranes in contrast to polylysines. Subtle binding energy differences between R₉/POPC and R₉/POPE as well as K₉/POPC and K₉/POPE systems, respectively, are also explained at the molecular level, indicating why the strongest stabilization is observed in the case of R₉/POPE interaction.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors acknowledge the Croatian Science Foundation for funding (IP-2019-04-3804). We also thank the computer cluster Isabella based in SRCE – the University of Zagreb, University Computing Centre for computational resources. A grammar check was performed using the Grammarly application. We also appreciate constructive discussion with Phil E. Mason.

References

1. J. M. Berg, J. L. Tymoczko and L. Stryer, Biochemistry, W.H. Freeman, New York NY, 5th edn, 4. print, 2002.
2. Ü. Coskun and K. Simons, Cell Membranes: The Lipid Perspective, Structure, 2011, 19, 1543–1548.
3. F. Kamp, H. V. Westerhoff and J. A. Hamilton, Movement of Fatty Acids, Fatty Acid Analogues, and Bile Acids across Phospholipid Bilayers, Biochemistry, 1993, 32, 11074–11085.
4. F. Kamp and J. A. Hamilton, pH gradients across phospholipid membranes caused by fast flip-flop of un- ionized fatty acids, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 11367–11370.
5. E. Pebay-Peyroula, C. Dahout-Gonzalez, R. Kahn, V. Trézéguet, G. J. M. Lauquin and G. Brandolin, Structure of mitochondrial ADP/ATP carrier in complex with carboxyatractyloside, Nature, 2003, 426, 39–44.
6. J. H. Kaplan, Biochemistry of Na,K-ATPase, Annu. Rev. Biochem., 2002, 71, 511–535.
7. S. Kumari, S. Mg and S. Mayor, Endocytosis unplugged: Multiple ways to enter the cell, Cell Res., 2010, 20, 256–275.
8. S. Mukherjee, R. N. Ghosh and F. R. Maxfield, Endocytosis, Physiol. Rev., 1997, 77, 759–803.
9. N. J. Yang and M. J. Hinner, Getting across the cell membrane: an overview for small molecules, peptides, and proteins, Methods Mol. Biol., 2015, 1266, 29–53.
10. D. J. Mitchell, L. Steinman, D. T. Kim, C. G. Fathman and J. B. Rothbard, Polyarginine enters cells more efficiently than other polycationic homopolymers, J. Pept. Res., 2000, 56, 318–325.
11. C. Yao, Z. Kang, B. Yu, Q. Chen, Y. Liu and Q. Wang, All-Factor Analysis and Correlations on the Transmembrane Process for Arginine-Rich Cell-Penetrating Peptides, Langmuir, 2019, 35, 9286–9296.
12. N. Sakai and S. Matile, Anion-Mediated Transfer of Polyarginine across Liquid and Bilayer Membranes, J. Am. Chem. Soc., 2003, 125, 14348–14356.
13. E. G. Stanzl, B. M. Trantow, J. R. Vargas and P. A. Wender, Fifteen years of cell-penetrating, guanidinium-rich molecular transporters: Basic science, research tools, and clinical applications, Acc. Chem. Res., 2013, 46, 2944–2954.
14. H. D. Herce, A. E. Garcia and M. C. Cardoso, Fundamental molecular mechanism for the cellular uptake of guanidinium-rich molecules, J. Am. Chem. Soc., 2014, 136, 17459–17467.
15. M. Vazdar, J. Heyda, P. E. Mason, G. Tesei, C. Allolio, M. Lund and P. Jungwirth, Arginine ‘magic’: Guanidinium Like-Charge Ion Pairing from Aqueous Salts to Cell Penetrating Peptides, Acc. Chem. Res., 2018, 51, 1455–1464.
16. M. Vazdar, F. Uhlig and P. Jungwirth, Like-charge ion pairing in water: An ab initio molecular dynamics study of aqueous guanidinium cations, J. Phys. Chem. Lett., 2012, 3, 2021–2024.
17. M. Vazdar, J. Vymětal, J. Heyda, J. Vondrášek and P. Jungwirth, Like-charge guanidinium pairing from molecular dynamics and ab initio calculations, J. Phys. Chem. A, 2011, 115, 11193–11201.
18. G. Tesei, M. Vazdar, M. R. Jensen, C. Cragnell, P. E. Mason, J. Heyda, M. Skepö, P. Jungwirth and M. Lund, Self-association of a highly charged arginine-rich cell-penetrating peptide, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 11428–11433.
19. A. D. Robison, S. Sun, M. F. Poyton, G. A. Johnson, J. P. Pellois, P. Jungwirth, M. Vazdar and P. S. Cremer, Polyarginine Interacts More Strongly and Cooperatively than Polylysine with Phospholipid Bilayers, J. Phys. Chem. B, 2016, 120, 9287–9296.
20. M. Vazdar, E. Wernersson, M. Khabiri, L. Cwiklik, P. Jurkiewicz, M. Hof, E. Mann, S. Kolusheva, R. Jelinek and P. Jungwirth, Aggregation of oligoarginines at phospholipid membranes: Molecular dynamics simulations, time-dependent fluorescence shift, and biomimetic colorimetric assays, J. Phys. Chem. B, 2013, 117, 11530–11540.
21. T. Morishita, K. Aburai, K. Sakai, M. Abe, I. Nakase, S. Futaki, H. Sakai and K. Sakamoto, Key process and factors controlling the direct translocation of cell-penetrating peptide through bio-membrane, Int. J. Mol. Sci., 2020, 21, 1–18.
22. K. Sakamoto, T. Kitano, H. Kuwahara, M. Tedani, K. Aburai, S. Futaki, M. Abe, H. Sakai, H. Ohtaka and Y. Yamashita, Effect of Vesicle Size on the Cytolysis of Cell-Penetrating Peptides (CPPs), Int. J. Mol. Sci., 2020, 21, 7405.
23. K. Sakamoto, T. Morishita, K. Aburai, D. Ito, T. Imura, K. Sakai, M. Abe, I. Nakase, S. Futaki and H. Sakai, Direct entry of cell-penetrating peptide can be controlled by maneuvering the membrane curvature, Sci. Rep., 2021, 11, 1–9.
24. J. H. Lorent, K. R. Levental, L. Ganesan, G. Rivera-Longsworth, E. Sezgin, M. Doktorova, E. Lyman and I. Levental, Plasma membranes are asymmetric in lipid unsaturation, packing and protein shape, Nat. Chem. Biol., 2020, 16, 644–652.
25. M. T. H. Nguyen, D. Biriukov, C. Tempra, K. Baxova, H. Martinez-Seara, H. Evci, V. Singh, R. Šachl, M. Hof, P. Jungwirth, M. Javanainen and M. Vazdar, Ionic Strength and Solution Composition Dictate the Adsorption of Cell-Penetrating Peptides onto Phosphatidylcholine Membranes, Langmuir, 2022, 38, 11284–11295.
26. S. F. Verbeek, N. Awasthi, N. K. Teiwes, I. Mey, J. S. Hub and A. Janshoff, How arginine derivatives alter the stability of lipid membranes: dissecting the roles of side chains, backbone and termini, Eur. Biophys. J., 2021, 50, 127–142.
27. A. D. White, A. J. Keefe, J. R. Ella-Menye, A. K. Nowinski, Q. Shao, J. Pfaendtner and S. Jiang, Free energy of solvated salt bridges: A simulation and experimental study, J. Phys. Chem. B, 2013, 117, 7254–7259.
28. A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions, J. Phys. Chem. B, 2009, 113, 6378–6396.
29. T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1998, 90, 1007.
30. M. Walker, A. J. A. Harvey, A. Sen and C. E. H. Dessent, Performance of M06, M06-2X, and M06-HF density functionals for conformationally flexible anionic clusters: M06 functionals perform better than B3LYP for a model system with dispersion and ionic hydrogen-bonding interactions, J. Phys. Chem. A, 2013, 117, 12590–12600.
31. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
32. D. A. Case, T. E. Cheatham, T. Darden, H. Gohlke, R. Luo, K. M. Merz, A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, The Amber biomolecular simulation programs, J. Comput. Chem., 2005, 26, 1668–1688.
33. J. B. Klauda, R. M. Venable, J. A. Freites, J. W. O’Connor, D. J. Tobias, C. Mondragon-Ramirez, I. Vorobyov, A. D. MacKerell and R. W. Pastor, Update of the CHARMM All-Atom Additive Force Field for Lipids: Validation on Six Lipid Types, J. Phys. Chem. B, 2010, 114, 7830–7843.
34. I. Leontyev and A. Stuchebrukhov, Accounting for electronic polarization in non-polarizable force fields, Phys. Chem. Chem. Phys., 2011, 13, 2613–2626.
35. I. V. Leontyev and A. A. Stuchebrukhov, Electronic continuum model for molecular dynamics simulations of biological molecules, J. Chem. Theory Comput., 2010, 6, 1498–1508.
36. M. Vazdar, P. Jungwirth and P. E. Mason, Aqueous guanidinium-carbonate interactions by molecular dynamics and neutron scattering: Relevance to ion-protein interactions, J. Phys. Chem. B, 2013, 117, 1844–1848.
37. J. Melcr, H. Martinez-Seara, R. Nencini, J. Kolafa, P. Jungwirth and O. H. S. Ollila, Accurate Binding of Sodium and Calcium to a POPC Bilayer by Effective Inclusion of Electronic Polarization, J. Phys. Chem. B, 2018, 122, 4546–4557.
38. R. Nencini, C. Tempra, D. Biriukov, J. Polák, D. Ondo, J. Heyda, S. O. Ollila, M. Javanainen, H. Martinez-Seara, R. Nencini, C. Tempra, D. Biriukov, J. Polák, D. Ondo, J. Heyda, S. O. Ollila, M. Javanainen and H. Martinez-Seara, Prosecco: polarization reintroduced by optimal scaling of electronic continuum correction origin in MD simulations, Biophys. J., 2022, 121, 157a.
39. J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. L. De Groot, H. Grubmüller and A. D. MacKerell, CHARMM36m: An Improved Force Field for Folded and Intrinsically Disordered Proteins, Nat. Methods, 2017, 14, 71.
40. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1998, 79, 926.
41. S. R. Durell, B. R. Brooks and A. Ben-Naim, Solvent-induced forces between two hydrophilic groups, J. Phys. Chem., 1994, 98, 2198–2202.
42. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, A smooth particle mesh Ewald method, J. Chem. Phys., 1998, 103, 8577.
43. M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: A new molecular dynamics method, J. Appl. Phys., 1981, 52, 7182–7190.
44. D. J. Evans and B. L. Holian, The Nose–Hoover thermostat, J. Chem. Phys., 1998, 83, 4069.
45. B. Hess, P-LINCS: A Parallel Linear Constraint Solver for Molecular Simulation, J. Chem. Theory Comput., 2007, 4, 116–122.
46. S. Miyamoto and P. A. Kollman, Settle: An analytical version of the SHAKE and RATTLE algorithm for rigid water models, J. Comput. Chem., 1992, 13, 952–962.
47. J. S. Hub, B. L. De Groot and D. Van Der Spoel, G-whams-a free Weighted Histogram Analysis implementation including robust error and autocorrelation estimates, J. Chem. Theory Comput., 2010, 6, 3713–3720.
48. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindah, Gromacs: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25.
49. Thermochemistry in Gaussian|Gaussian.com, https://gaussian.com/thermo/ (accessed 26 March 2023).

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02411c

‡ Present address: Selvita d.o.o. Prilaz baruna Filipovića 29, 10000 Zagreb, Croatia.

---