Fragment-based approach for the efficient calculation of the refractive index of metal–organic frameworks

Abstract

Increasing demands on materials in the field of optical applications require novel materials. Metal–organic frameworks (MOFs) are a prominent class of hybrid inorganic–organic materials with a modular layout. This allows the fine-tuning of their optical properties and the tailored design of optical systems. In the present theoretical study, an efficient method to calculate the refractive index (RI) of MOFs is introduced. For this purpose, the MOF is split into disjoint fragments, the linkers and the inorganic building units. The latter are disassembled until metal ions are obtained. The static polarizabilities are calculated individually using molecular density functional theory (DFT). From these, the MOF's RI is calculated. To obtain suitable polarizabilities, an exchange–correlation functional benchmark was performed first. Subsequently, this fragment-based approach was applied to a set of 24 MOFs including Zr-based MOFs and ZIFs. The calculated RI values were compared to the experimental values and validated using HSE06 hybrid functional DFT calculations with periodic boundary conditions. The examination of the MOF set revealed a speed up of the RI calculations by the fragment-based approach of up to 600 times with an estimated maximal deviation from the periodic DFT results below 4%.

---

Introduction

The refractive index (RI) is one of the determining optical properties when considering a material for application in optical systems. Anti-reflective coatings require materials with low RI values, whereas mirrors and filters require a combination of materials with high as well as low RI values, to name just two examples.^1–3 The development of high refractive index polymers (HRIPs) with full transparency in the visible spectral range is still challenging.^4,5

In the last years, the use of metal–organic frameworks (MOFs) as materials for optical applications and the examination of the RI of MOFs has gathered increasing attention.^6–13 MOFs are a class of porous organic–inorganic hybrid materials built up by inorganic building units (IBUs) connected by organic ligands serving as linkers.^14,15 This modular design and the inherent porosity allows the fine tuning of the electronic and optical properties of MOFs in a broad range by incorporating different metal centers, linkers and guest molecules.^{10,11,16–18}

The development of novel MOF-based optical materials and systems requires precise knowledge about their optical properties with a focus on the RI. Today, more than 90 000 MOFs are experimentally accessible.¹⁹ To assess suitable MOFs for possible applications from this large set, computational screenings are a convenient approach.²⁰ The precise calculation of the optical properties of MOFs requires the use of hybrid density functional theory (DFT) exchange–correlation (XC) functionals and periodic boundary conditions (PBC) making these calculations computationally demanding and time consuming.^12,13,21 This computational effort prevents the fast screening of MOFs regarding their RI. Thus, other methods are required to allow a fast screening of the RI of MOFs.

There are several methods reported enabling the high-throughput screening of materials and their RI for optical applications. Afzal et al. established an efficient protocol to calculate the RI of polymers.^22,23 The protocol is based on the linear correlation of the size of an oligomer and its polarizability. This correlation is used to extrapolate the polarizability of a polymer chain. Additionally, the number density is calculated via a machine learning model enabling the prediction of the RI of a polymer. Ligorio et al. used a partitioning scheme provided by the quantum theory of atoms in molecules (QTAIM) to reduce the computational effort of RI calculations of crystalline molecular materials.²⁴ Therefore, calculations with molecular aggregates were carried out, followed by a partitioning of the polarizabilities to obtain the polarizability of a single interacting molecule. This allows the calculation of the RI of the molecular materials without computationally demanding fully periodic DFT calculations. Ernst et al. also used a partitioning scheme provided by QTAIM to calculate the RI of metal–organic networks built up by chains of amino acids and metal ions.²⁵ They used clusters of the secondary building units of this metal–organic network chains and calculated the atomic polarizabilities of the atoms of the asymmetric unit. Those polarizabilities were used to calculate the RI of the crystalline materials.

All aforementioned approaches are suitable for molecular materials or materials formed by (coordination) polymer chains and were developed for dense materials. In contrast, MOFs are built up by IBUs coordinated by linkers in two or three dimensions forming porous layers or frameworks. Using the approaches described in literature, the evaluation of extended MOF clusters is necessary to obtain a suitable representation of the interacting atoms forming the material. This translates into systems with several hundred atoms leading to the loss of the initial reduction of the computational demands by the omission of the PBC.

Here, we present a method allowing the evaluation of the RI of MOFs with substantial reduced computational effort. Our approach is based on a fragmentation scheme for MOFs combined with molecular DFT to obtain the static polarizability and RI. More precisely, the MOF is fragmented into metal ions, ligands and linkers, which static polarizabilities are calculated individually. We note that neglecting the metal–ligand bond is a substantial approximation. Furthermore, cutting this bond is often viewed with great skepticism as a fragmentation method for energy calculations.^26–28 However, the proposed fragmentation scheme in this work, benefits from the fact, that the polarizability and optical properties of the investigated MOFs are dominated by their linkers.^{10–13,17,29,30} In the following step, the calculated static polarizabilities of the fragments are used to obtain the static polarizability of the corresponding MOF. Therefore, the polarizabilities of the isolated fragments are added up with respect to the composition of the MOF relying on the additivity hypothesis.³¹ This approach is known as orientated gas model and has been successfully applied to calculate the optical properties of molecular crystals, crystalline materials and metal–organic networks.^25,32,33 Furthermore, the additivity of the polarizability has been used successfully to calculate the RI of minerals.^34,35 Finally, the polarizability of the MOF is used to estimate the corresponding RI by applying the Lorenz-Lorentz equation.^36,37 The use of the Lorenz-Lorentz equation to calculate the static as well as the frequency-dependent RI with polarizabilities obtained by DFT is well established and is not limited to isotropic systems.^38,39 In addition, using the Lorenz-Lorentz equation in combination with polarizabilities obtained by DFT yields RIs in good agreement with experiments for gases, liquids, and materials.^23,40–42

The developed fragment-based approach is validated with periodic hybdrid DFT calculations based on fully relaxed MOF structures to obtain reliable electronic structures and optical properties using our previously published approach.^12,13 In a first step of this study, we performed a benchmark to select a suitable exchange–correlation (XC) functional for the molecular DFT calculations. Afterwards the fragment approach was tested with 24 MOFs. The selected MOFs are transparent in the near IR and visible region of the light and possess a band gap larger than 3 eV. Hence, they are suited for a broad range of optical applications.

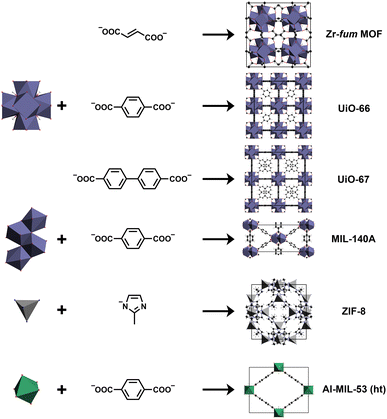
The MOFs selected for this study (see Table 1) mainly belong to the groups of Zr-based MOFs and zeolitic imidazolate frameworks (ZIFs). Their design principles can be found in Fig. 1. The Zr-based MOFs were chosen due to of their well-known high chemical and thermal stability promoting the use of this MOF family for practical applications.⁴³ As representatives of Zr-based MOF materials, UiO-66 and derivatives, MIL-140A and derivatives, Zr-fum MOF, and UiO-67 were chosen.^44–46 UiO-66 and its derivatives are very prominent Zr-based MOFs built up by the typical Zr₆O₄OH₄ IBU coordinated by 1,4-benzenedicarboxylate (bdc) forming an expanded cubic closed-packed structure (see Fig. 1). These MOFs have already been considered as materials for optical applications.^{12,13,44,47–51} Analog to the UiO-family, the Zr-fum MOF is based on the typical Zr₆-containing IBU and show the same topology as well, but features fumarate (fum) as linker leading to a denser framework.⁴⁶ The MIL-140A frameworks are also Zr-based MOFs built up by the bdc linker, but have an one-dimensional IBU leading to a different topology and higher density compared to the UiO-family MOFs.⁴⁵ In contrast, ZIFs are based on the topology of zeolites and are formed by imidazolate (im) linkers coordinating transition metal ions.⁵² ZIFs and especially ZIF-8 have already been examined for and used in different optical applications, e.g. as thin films of optical quality or coatings in optical sensor systems. Hence, we also applied our fragment approach to nine different ZIFs.^11,53–56 ZIF-8 is one of the most prominent ZIFs consisting of zinc ions coordinated by 2-methylimidazolate (mim) linkers crystallizing with the SOD topology (see Fig. 1).⁵² Besides ZIF-8, four additional zinc-based ZIFs featuring the SOD topology all built up by different imidazolate derivatives (SOD-ZIF-71, ZIF-90, ZIF-318 and SALEM-2) were assessed.^57–60 Furthermore, three ZIFs next to SALEM-2 consisting of the im linker and zinc ions (ZIF-1, ZIF-10, ZIF-64) with different topologies and densities were included.^52,61 In addition, ZIF-72 formed by zinc ions and 4,5-dichloroimidazolate (dcim) analog to SOD-ZIF-71 was also part of this study.⁶¹ Apart from the Zr-based MOFs and ZIFs, the high temperature (ht) phase of the well-known Al-MIL-53 MOF (see Fig. 1) was also studied to show the transferability of our approach for non-transition metal containing MOFs.⁶²

Table 1 Overview of all selected MOFs with their linkers, IBUs, compositions (A = IBU and B = linker) and nets (RCSR).⁶³ MIL-140A and Al-MIL-53 possess a one-dimensional IBU (*)

	MOF	Linker		IBU	Composition	Net
Zr-based	UiO-66	bdc	1,4-Benzenedicarboxylate	[Zr6O4(OH)4]^12+	AB6	fcu
	UiO-66-NO2	bdc-NO2	2-Nitrobenzene-1,4-dicarboxylate
	UiO-66-F	bdc-F	2-Fluorobenzene-1,4-dicarboxylate
	UiO-66-F4	bdc-F4	2,3,5,6-Tetrafluorobenzene-1,4-dicarboxylate
	UiO-66-Cl	bdc-Cl	2-Chlorobenzene-1,4-dicarboxylate
	UiO-66-Br	bdc-Br	2-Bromorobenzene-1,4-dicarboxylate
	UiO-66-I	bdc-I	2-Iodorobenzene-1,4-dicarboxylate
	UiO-67	bpdc	Biphenyl-4,4′-dicarboxylate
	Zr-fum MOF	fum	Fumarate
	MIL-140A	bdc		[ZrO]^2+ *	AB	bsn
	MIL-140A-NO2	bdc-NO2
	MIL-140A-F	bdc-F
	MIL-140A-Cl	bdc-Cl
	MIL-140A-Br	bdc-Br
ZIFs	ZIF-8	mim	2-Methyl-imidazolate	Zn^2+	AB2	sod
	ZIF-318	cf 3 im	2-Trifluoromethyl-imidazolate
	ZIF-90	Ica	Imidazolate-2-carboxyaldehyde
	SOD-ZIF-71	dcim	4,5-Dichloroimidazolate
	SALEM-2	im	Imidazolate
	ZIF-1	im		Zn^2+	AB2	crb
	ZIF-10	im				mer
	ZIF-64	im				crb
	ZIF-72	dcim				lcs
	Al-MIL-53 (ht)	bdc		[Al(OH)]^2+ *	AB	bpq

---

Fig. 1 Zr-based MOFs, ZIF-8 with SOD topology and Al-MIL-53 (ht). The Zr-fum MOF, UiO-66 and UiO-67 share the typical Zr₆-containing IBU and the expanded cubic closed-packed structure. MIL-140A is based on the bdc linker analogously to UiO-66, but has a one-dimensional IBU. ZIF-8 is based on the mim linker and show the SOD topology. Al-MIL-53 (ht) is built up by a one-dimensional IBU based on corner-sharing octahedra and the bdc linker.

Finally, we compared the experimental determined RI value of ZIF-8 with the calculated value obtained by using our fragment-based approach as well as our protocol with PBC calculations to highlight the adequacy of the present fragment-based approach.

Methods

Periodic DFT calculations

Kohn–Sham density functional theory calculations with PBC were used to validate the fragment-based approach and ensure that the studied MOFs are transparent in the visible region by analyzing their band structures in detail.⁶⁴ Therefore, a previously published protocol was applied to obtain reliable electronic structures and RI values.^12,13 The calculations were performed using the CASTEP code (version 20.1) employing a plane-wave basis set in combination with pseudopotentials.⁶⁵ All MOFs were modelled with primitive cells. The convergence of the plane-wave kinetic energy cutoff and the Brillouin zone sampling were examined with respect to the lattice parameters (see ESI‡ Section S1). The pseudopotentials were generated on-the-fly using the Koelling–Harmon method to incorporate relativistic effects into the generated pseudopotentials.⁶⁶ The PBEsol exchange–correlation (XC) functional was applied to fully relax the structures using ‘‘on-the-fly’’ generated ultra-soft pseudopotentials.⁶⁷

Subsequently three different XC functionals were assessed with regard to the experimental lattice parameters of the MOFs to obtain precise structural models for further characterization (see ESI‡ Section S1). The experimental reference values were chosen with a focus on single crystal (SC) XRD experiments carried out at low temperatures. To determine suitable XC functionals, full cell relaxations were performed using the parameters described above. The benchmark included the generalized gradient approximation (GGA) functional of Perdew, Burke, and Ernzerhof (PBE) with D2 and TS dispersion correction, respectively, the PBE expansion for solids (PBEsol) as well as its dispersion corrected form (PBEsol-TS), and the rSCAN meta-GGA (mGGA) functional.^67–72

Using the optimized models, single point HSE06 hybrid DFT calculations were performed to obtain the band structures, the corresponding density of states (DOS) and the dispersion of the refractive index.⁷³ All calculations were carried out using the determined Brillouin zone sampling and planewave kinetic energy cutoff. The optical properties were calculated applying the tools provided within CASTEP to evaluate the electronic structure, obtain the complex dielectric function and subsequently the dispersion of the index of refraction.⁷⁴

Fragmentation scheme for MOFs

A fragmentation scheme was developed to overcome the computationally demanding DFT calculations with PBC to evaluate the RI of a MOF. This scheme yields MOF fragments allowing computationally less expensive molecular DFT calculations to compute polarizabilities and subsequently the calculation the RI of the corresponding MOF.

The developed fragmentation scheme consists of two steps to break down a MOF into fragments. In a first step, the IBU of a MOF is identified and all coordinative IBU-linker bonds are broken heterolytically (see Fig. 2). This results in anionic linker fragments and a cationic IBU residue. In the case of IBUs formed by metal ions e.g. ZIF-8, this first step is sufficient to obtain the MOF fragments, because the cationic IBU residue is only a metal cation (see Fig. 2). Therefore, the fragments of such MOFs are anionic linker ions and cationic metal ions. On the contrary, MOFs with a more complex IBU, e.g. UiO-66, require a second step to achieve a sufficient fragmentation ensuring a low computational demand. In this second step, all metal–ligand bonds of the IBU are broken heterolytically (see Fig. 2). As a result, metal cations and anionic ligands are obtained. Finally, the fragmentation of MOFs with complex IBUs results in anionic linker ions, cationic metal ions and anionic ligand ions.

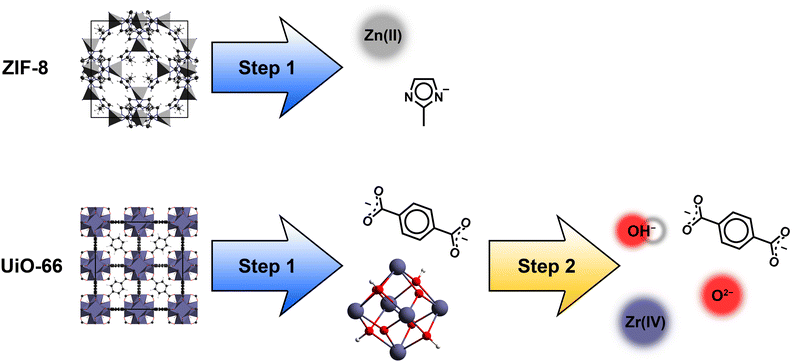Fig. 2 Fragmentation scheme for MOFs with 2 steps: heterolytic breaking of IBU-linker bonds (step 1) and afterwards heterolytic breaking of residual metal-ligand bonds (step 2).

Refractive index calculations with MOF fragments

In the MOF fragmentation scheme described above, ionic MOF fragments are employed in isolated molecular DFT calculations. These molecular DFT calculations were performed using the ORCA program (version 4.2.1) with the libXC and libint2 libraries and the def2-QZVP basis set.^75–79 In the first step of all calculations, the structure of the obtained multi-atom fragments were fully relaxed, the details of the calculation parameters are given in the ESI‡ in Section 3. Afterwards the static polarizability of all fragments was calculated using the coupled-perturbed (CP) SCF method integrated in the ORCA program. The CP SCF method allows the calculation of the polarizability as analytic second derivative of the electronic energy with respect to an applied electric field.^80–82 For further calculations the isotropic polarizability of the fragments was used.

The Lorenz-Lorentz formula relates the polarizability α and the RI n of a substance by taking the number density N into account:^36,37,83

Using the molecular formula of a MOF and number of formula units per unit cell Z, the total polarizability of the unit cell of a MOF is calculated taking into account the isotropic polarizability of its fragments. An example calculation is given in the ESI‡ Section 6. The number density of a MOF corresponds to the reciprocal volume of the unit cell of a MOF. Ideally, the unit cell volume V is obtained from low temperature SC XRD experiments to suit the polarizabilities calculated with energy minimized MOF fragments and avoid temperature dependent influences on the RI calculation.

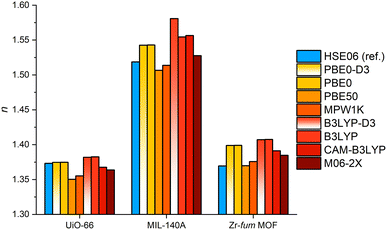
To determine a suitable XC functional for the molecular DFT calculations, benchmark calculations were performed with five hybrid GGA (hGGA) and one hybrid mGGA (hmGGA) XC functional. Following the study of Afzal et al. the PBE0 and B3LYP (hGGA) functionals with D3 dispersion correction were tested.^84–86 In addition, both functionals were also assessed without the D3 dispersion correction. According to the study of Ligorio et al., the CAM-B3LYP hGGA and M06-2X hmGGA XC functionals were selected.^87,88 Furthermore, we included the MPW1K and PBE50 hGGA XC functionals.^89,90 Both functionals were part of a benchmark study by Hait et al. focusing in the polarizability of small inorganic species.⁹¹ It was shown by Hait et al., that these two functionals were only outperformed by a double hybrid GGA XC functional demanding high computational effort. The Zr-based MOFs UiO-66, MIL-140A and Zr-fum MOF were chosen as test set. Using the six mentioned XC functionals, the static RIs of the three MOFs were calculated and compared to reference RI values. The reference values were taken from the RI dispersion curves at 589 nm (D line of sodium vapor) of these MOFs obtained from calculations with our DFT protocol using PBC and the HSE06 hGGA XC functional. Furthermore, materials for optical applications should not show any absorption in the visible region and thus their RI shows only a small frequency dependence making a comparison with static RI values feasible.²²

Finally, the static RI of 24 MOFs was calculated using the fragment-based approach with the MPW1K XC functional. The RI values were compared to the ones obtained from DFT calculations with PBC and experimental values.

Results and discussion

This study is concerned with the development of a fragment-based approach for the calculation of the RI of MOFs. This approach should overcome the computationally demanding DFT calculations employing PBC. We first determined a suitable XC functional for the fragment-based approach by examining hGGA and hmGGA functionals with benchmark calculations to validate this novel approach with reference calculations and experimental values.

XC functional benchmark

To assess a suitable XC functional for the fragment-based calculation of the RI of MOFs, five hGGA and one hmGGA functional were benchmarked. Therefore, the fragment-based approach was applied to the Zr-based MOFs UiO-66, MIL-140A and Zr-fum MOF. The MOF UiO-66 is a well-known and widely studied MOF and was chosen as a representative compound.^44,92 The Zr-fum MOF features the same topology and IBU as UiO-66 but in contrast it contains the considerably smaller fum linker leading to a denser and less porous framework.⁴⁶ The MOF MIL-104A consist also the bdc linker but possess a one-dimensional IBU forming a denser framework. This allows short-range dispersive interactions between the linkers leading to π-stacking of these.⁴⁵ This collection of MOFs with different linkers showing interacting and isolated arrangements in the frameworks as well as zero- and one-dimensional IBUs, and different patterns of oxo-ligands inside of these IBUs forms a diverse set for the benchmark study. The investigated MOFs are transparent in the visible region as shown by hGGA band structure calculations (see ESI‡ Section 7). The RI reference values were taken from RI dispersion curves (see ESI‡ Section 8) at 589 nm obtained from DFT calculations with PBC using our published simulation protocol.^12,13

The comparison of the static RI values calculated with the fragment-based approach and the reference values (see Fig. 3) shows, that the fragment-based approach is in general a suitable method to calculate the RI of MOFs independently from the choice of the XC functional. All examined XC functionals reproduce the trend of the reference values with acceptable accuracy and allow a qualitative assessment of the RI of the evaluated MOFs. The use of the B3LYP functional with D3 dispersion correction results in the largest mean relative error (MRE) of about 2.5% corresponding to a mean absolute error (MAE) of about 0.035 in the RI (see ESI‡ Section 4, Fig. S37). Comparing the results obtained with the B3LYP and PBE0 functionals with and without D3 dispersion correction, neglectable differences in the polarizabilities and RIs are observed in the case of the PBE0 functional. In the case of the B3LYP functional, small differences in the polarizability of the bdc linker occur due to the altered molecular geometry by the dispersion correction. This is only visible for MIL-140A, because the IBU of MIL-140A is much smaller compared to the Zr₆-containing IBU of both other MOFs. This results in an increased influence of the polarizability of the linker and thus its molecular geometry on the total polarizability of the MOF. Overall, in contrast to the method for polymers proposed by Afzal et al., no dispersion corrected functionals are needed here. In addition, the benchmark shows that the M06-2X hmGGA functional has the most consistent performance with a MRE smaller than 1% and the smallest standard deviation of all tested XC functionals (see ESI‡ Section 4 and Fig. S37). PBE50 and MPW1K functionals show the smallest deviation compared to the HSE06 calculations with PBC, but in the case of PBE50 with a tendency to underestimate the RI. Overall, the MPW1K functional leads to the smallest errors of all tested functionals with a MRE of about 0.7% with the second smallest standard deviation of the benchmark with about 0.5% (see ESI‡ Section 4 and Fig. S37). Therefore, the MPW1K functional was selected to perform the subsequent calculations.

Fig. 3 XC functional benchmark with three Zr-based MOFs. The static RI values obtained with the fragment-based approach (redish) are compared with the reference values at 589 nm obtained using DFT calculations with PBC (blue).

Although, the fragment-based approach neglects all contributions of the metal–ligand and metal–linker bonds to the polarizability of a MOF as well as the possible interaction of closely packed linker molecules, this benchmark suggest that the chosen fragmentation scheme is valid to obtain more than a coarse qualitative estimate of the RI by using the MPW1K XC functional. Furthermore, a comparison of the CPU times for UiO-66 using the fragment-based approach and the reference calculation with PBC underlines the possible speed up of the RI evaluation by applying the fragment-based approach (see ESI‡ Section 7 and Tables S5, S6). This comparison reveals a more than 170 times faster calculation of the RI by the fragment-approach with the MPW1K XC functional for UiO-66 with a relative error of about 1.3% and an absolute error of about 0.02 in the RI. This result has encouraged to apply the fragment-based approach using the MPW1K functional to 21 further MOFs.

UiO-type MOFs and Zr-fum MOF

The fragment-based approach was applied to UiO-66, its monohalogenated derivatives UiO-66-X (F, Cl, Br, I), tetrafluoro derivative UiO-66-F₄ and nitro derivative UiO-66-NO₂.^44,93–96 Additionally, UiO-67 and the Zr-fum MOF were evaluated.^44,46 Both share the UiO-66 topology and IBU, but contain a longer (4,4′-biphenyl-dicarboxylate, bpdc) and a shorter (fum) linker compared to the bdc linker of UiO-66, respectively. To ensure the transparency in the visible region band structure calculations were performed at hGGA level (see ESI‡ Section 8).^12,13 Starting with the Zr-fum MOF, the band gaps decrease from 4.41 eV to 3.16 eV for the UiO-66-I MOF (see ESI‡ Section 8, Fig. S38 and Table S11). The substitution of the acetylenic group of the fum linker with the phenylene group in the bdc linker results in a reduced band gap of 4.25 eV.¹² The introduction of a second phenylene group to the linker leads to the bpdc linker of UiO-67 resulting in a further reduced band gap of 3.51 eV (see ESI‡ Fig. S40). In the same manner, the functionalization of the bdc linker leads to a reduction of the band gap. In the series of UiO-66 derivatives, UiO-66-F MOF shows the largest band gap of 3.96 eV followed by the nitro, tetrafluoro, chloro, bromo and iodo compounds.¹³ While the substitution of the acetylenic group in the fum linker with phenylene groups increases the polarizability of the resulting linker (see ESI‡ Table S4), the RI of UiO-66 is only slightly larger compared to the Zr-fum MOF and the RI of UiO-67 even decreases (see Fig. 4 and ESI‡ Fig. S56). This is caused by the different cell volumes and the resulting number densities. The introduction of larger linkers to the expanded cubic closed-packed structures leads to expansion of the framework. This partly compensates the increasing polarizability of the linkers. The fragment-based approach reproduces these trends in the RI values reliably with a minimum error of about 0.6% for the Zr-fum MOF and a maximum error of about 3.8% for the UiO-67 (see ESI‡ Table S12 in Section 10).

Fig. 4 Comparison of the RI of Zr-fum MOF, UiO-66 and UiO-67 (corresponding linkers are shown) calculated with the reference approach with PBC (blue) and the fragment-based approach (orange).

The introduction of functional groups to the bdc linker results in UiO-66 derivatives with tuned optical properties sharing the topology of UiO-66 as well as its cell parameters and thus its number density.^12,13 As a result, the incorporation of linkers into the framework with a lower or higher polarizability than the pristine bdc linker leads directly to lower or higher RI values of the resulting MOFs (see Fig. 5 and ESI‡ Fig. S56). This effect of the linker functionalization is well reproduced by the fragment-based approach with the smallest error of about 0.3% for the UiO-66-F₄ and the largest error of about 1.5% for the UiO-66-F MOF (see ESI‡ Table S12).

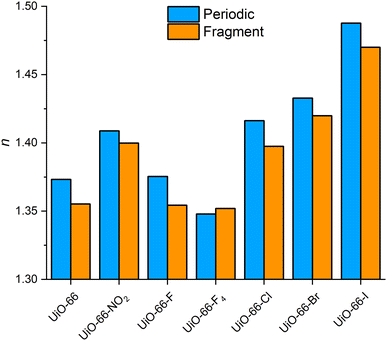Fig. 5 Comparison of the RI of different UiO-66 derivatives calculated with the reference approach with PBC (blue) and the fragment-based approach (orange).

MIL-140A and derivatives

MIL-140A MOF is a Zr-based MOF incorporating the bdc linker and containing a one-dimensional IBU.⁴⁵ This compound is denser compared to UiO-66 allowing short-range dispersive interactions, π-stacking of the linker, and showing a higher number density. The linker interactions result in a large number of delocalized states at the valence band maximum (VBM) (see ESI‡ Section 8 and Fig. S41), but do not affect the transparency in the visible region (E_g = 4.04 eV). According to the higher number density, MIL-140A has a higher RI compared to UiO-66 (see Fig. 2 and ESI‡ Fig. S64). Although the fragment-based approach founds on isolated linker fragments without the consideration of intermolecular interactions between the MOF fragments, the RI value of MIL-140A is reproduced in good agreement with an error of about 0.3%.

Analog to UiO-66, the functionalization of the bdc linker allows the tuning of the electronic structure and optical properties of MIL-140A (see ESI‡ Section 8).⁹⁷ Additionally, the MIL-140A framework allows the incorporation of functionalized bdc linkers without notable changes in the lattice parameters (see ESI‡ Table S1). Thus, the use of functionalized bdc derivatives with increased or decreased polarizabilities results directly in an increase or decrease of the RI of the MIL-140A derivatives compared to the pristine MIL-140A MOF, respectively (see ESI‡ Section 9 and Fig. S58). This allows the tuning of the RI of MIL-140A frameworks in the remarkable range between about 1.51 (MIL-140A-F) and 1.58 (MIL-140A-Br). The fragment-based approach reproduces this trend (see Fig. 6 and ESI‡ Table S12) yielding a minimal error of about 0.4% for the MIL-140A-F and a maximal error of about 2.3% for MIL-140-Br.

Fig. 6 Comparison of the RI of different MIL-140A derivatives calculated with the reference approach with PBC (blue) and the fragment-based approach (orange).

ZIFs

The ZIF-8 MOF is a prominent representative of the ZIF family formed by zinc ions and mim with SOD topology.⁵² ZIF-8 shows a band gap of 5.27 eV (see ESI‡ Fig. S46 and Table S11) and is therefore suitable for optical applications in the visible range as well as in the near infra-red (IR) and ultra-violet (UV) regions.^53,54 The use of differently substituted imidazolate linkers allow the formation of ZIF-8 analog SOD-type ZIFs (see Fig. 7). ZIF-318 and SALEM-2 were modelled as ideal, phase-pure ZIFs without the partial incorporation of the mim linker observed in the experiment.^59,60 The band gaps of ZIF-318, ZIF-90, SOD-ZIF-71 and SALEM-2 are larger than 4 eV (see ESI‡ Section 8). In contrast to the Zr-based MOFs discussed above, these ZIF-8 analogues vary slightly in their lattice parameters causing different number densities (see ESI‡ Table S1 and S12).^57–60 Nevertheless, the introduction of linkers with higher or lower polarizability results directly in materials with a higher or lower RI, respectively (see Fig. 7 and Fig. S59, ESI‡). This allows the tuning of the RI within a given topology in a broad range between 1.26 and 1.39 (at the sodium D-line), while maintaining the transparency in a wide spectrum. The fragment-based approach reproduces this variation of the RI due to the linker functionalization with reasonable precision and a minimal error of about 1% and maximal error of about 3%. Moreover, the fragment-based approach is in very good agreement with the experimental value for ZIF-8 at 589 nm with an error of about 0.7%. Additionally, a comparison of the CPU times for ZIF-8 (see ESI‡ Section 7 and Table S7, S8) reveals a more than 600 times faster calculation of the RI by the fragment-based approach. This underlines the capability of the fragment-based approach to predict the RI of MOFs efficiently.

Fig. 7 Comparison of the RI of ZIFs with SOD topology (corresponding linkers are shown): calculated values with the reference approach with PBC (blue) and the fragment-based approach (orange) and experimental value¹¹ (green) for ZIF-8 (mim), ZIF-318 (cf₃im), ZIF-90 (ica), SOD-ZIF-71 (dcim) and SALEM-2 (im).

In addition to SALEM-2 with SOD topology, further ZIFs based on zinc ions and the im linker with different topologies exist, e.g. ZIF-1, ZIF-10 and ZIF-64. The different topologies of those ZIFs involve different lattice parameters (see ESI‡ Table S1). Due to the identical chemical composition, the electronic structures and band gaps are very similar (see ESI‡ Section 3) with band gaps of about 5.3 eV. Within this set of MOFs, two pairs of MOFs consisting of SALEM-2 and ZIF-10 as well as ZIF-1 and ZIF-64 (same net, see Table 1) can be distinguished. Each of these pairs have comparable densities leading to analogous RI values (see ESI‡ Fig. S60 and Table S12). This is well reproduced by the fragment-based approach (see ESI‡ Fig. S66) with a minimal error of about 0.5% for ZIF-10 and a maximal error of about 3.7% for ZIF-64.

Analog to the zinc-im-system, there are also several ZIFs formed by zinc ions and the dcim linker with different topologies. Here, ZIF-72 was studied next to SOD-ZIF-71.⁶¹ The band gap of ZIF-72 is only slightly larger (5.18 eV) compared to SOD-ZIF-71 (5.03 eV) (see ESI‡ Table S11 and Fig. S54), but ZIF-72 has a higher density leading to higher RI values with about 1.48 compared to 1.39 of SOD-ZIF-71 at 589 nm (see ESI‡ Fig. S61). The fragment-based approach allows a detailed description of this differences in the RI values (see ESI‡ Fig. S67) with only an error of about 1.2% and 1.0% for SOD-ZIF-71 and ZIF-72, respectively (see ESI‡ Table S12).

Al-MIL-53 (ht)

All afore mentioned MOFs are based on transition metals. To test the fragment-based approach for p-element metals, the ht phase of the well-known Al-MIL-53 MOF was examined. The Al-MIL-53 framework is formed by an one-dimensional Al-based IBU and bdc linkers.⁶² The MOF is transparent in the visible region with a band gap of 4.48 eV (see ESI‡ Fig. S55). The RI value at 589 nm of Al-MIL-53 (ht) is slightly larger (1.33) compared to ZIF-8 (1.32) and lower than the value of UiO-66 (1.37) (see ESI‡ Fig. S62). The dispersion of the RI in the visible region is larger compared to ZIF-8, but very similar to UiO-66. The fragment-based approach allows a reliable calculation of the RI of this p-element-based MOF with an error of about 2.9% (see Fig. 8). Finally, the fragment-based approach allows a more than 70 times faster calculation of the RI (see ESI‡ Section 7 and Table S9, S10).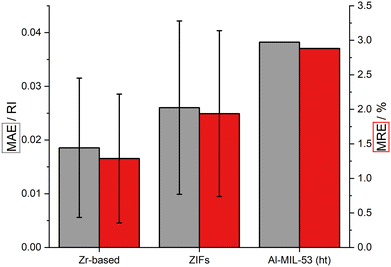

Fig. 8 Comparison of the RI calculated via fragment approach and periodic HSE06 calculation: MAE (gray) and MRE (red) of the examined Zr-based MOFs, ZIFs and Al-MIL-53 (ht).

Comparison of the different MOF sets

In this study, 24 MOFs were examined regarding their RI by applying a fragment-based approach. Of this group, 14 MOFs are Zr-based, 9 MOFs are ZIFs and one MOF is based on aluminum ions. The comparison of the RI of the Zr-based MOFs obtained with the fragment-based approach with reference calculations under PBC shows a mean relative error (MRE) of 1.29% (see Fig. 8) with a minimal and maximal error of 0.30% and 3.75%, respectively. The MRE corresponds to a mean absolute error (MAE) of the RI of about 0.02. The comparison of the calculated RI values of the ZIFs results in a MRE of about 1.9% with a minimal and maximal error of 0.50% and 3.76%, respectively, and a MAE of the RI of about 0.03 (see Fig. 8). The RI of the Al-based MOF was calculated with a relative error of 2.88% and an absolute error of the RI of about 0.04.

The fragment-based approach was developed on the basis of a XC functional benchmark including three different Zr-based MOFs. The results discussed above underline the transferability of the chosen simulation parameters for the fragment-based approach. This approach allows the efficient calculation of the RI of MOFs with a reasonable error compared to demanding DFT calculations with PBC. The MRE of the Zr-based MOFs and ZIFs are below 2% with maximal values below 4%. In the case of the Al-based MOF, the use of the fragment-based approach results in an error below 3%. This points out the capability of the fragment-based approach to predict the RI of MOFs not only qualitatively but also quantitatively. Trends in the RI within a class of MOFs due to linker functionalization as well as effects due to different topologies are also reproduced well. Overall, the fragment-based approach is a promising method to predict the RI of MOFs efficiently with a maximal expected error of approximately 4%.

Conclusions

An efficient approach for the calculation of the RI of MOFs was developed. The approach is based on a fragmentation scheme for MOFs coupled with molecular DFT calculations. This fragment-based simulation approach allows the calculation of the RI of MOFs circumventing demanding DFT calculations with PBC diminishing the CPU times severely by up to 600 times.

The fragmentation scheme consists of two fundamental steps resulting in anionic linker fragments, cationic metal ions and further anionic ligands in the case of more complex IBUs. Subsequently, molecular DFT calculations are performed to obtain energy minimized fragments and compute their isotropic polarizabilities. Using these polarizabilities, the sum of the polarizabilities of a formula unit of a MOF can be calculated. This polarizability, the number of formula units per unit cell, and the unit cell volume is then used to calculate the RI of a MOF by applying the Lorenz-Lorentz equation.

To obtain suitable polarizabilities of the MOF fragments, a XC functional benchmark was performed. Therefore, six hGGA and hmGGA XC functionals were assessed using three Zr-based MOFs. As reference, DFT hGGA (HSE06) calculations with PBC were used. The use of the MPW1K functional in combination with the def2-QZVP basis set yielded a MRE below 1% and was chosen for further molecular DFT calculations.

Subsequently, the fragment-based approach was applied to a set 24 MOFs consisting of 14 Zr-based MOFs, nine ZIFs and one Al-based MOF. The fragment-based approach quantitatively reproduced the trends observed in the RI of the Zr-based MOFs caused by varying lengths of a linker within a given topology as well as different functionalized linkers. Furthermore, the effect of the density of a framework on the RI by using the same linker in two different MOFs (UiO-66 and MIL-140A) was successfully calculated. The MRE for this set of Zr-based MOFs was below 1.5%. The calculations were accelerated by a factor of more than 170 compared to the DFT calculation with PBC. Moreover, the fragment-based approach allowed the calculation of the index of refraction of ZIF-8 and further ZIFs with SOD topology in good agreement with the reference calculations. Here, a reduction of the CPU times of approximately 600 times for ZIF-8 was observed. In addition, the effect of different topologies on the RI of ZIFs within a given metal–linker-system was tested with the fragment-based approach resulting in a precise description of the trends. The MRE for the examined set of ZIFs was below 2% underlining the transferability of the approach. Moreover, the RI value of ZIF-8 obtained with the fragment-based approach was compared to the experimental value revealing an error of less than 1% proving the capability of the fragment-based approach. Finally, the fragment-based approach was used to calculate the RI of the ht phase of Al-MIL-53 to include a non-transition metal-based MOF. Here, the fragment-based approach gave a relative error below 3% while reducing the CPU time more than 70 times. This highlights the reliability and robustness of the developed approach and hints the general applicability of the fragmentation scheme and the chosen combination of XC functional and basis set. All in all, the largest observed relative error of all MOFs was below 4% suggesting an estimated relative error for the prediction of RI values of maximal 4% while massively reducing the required computational effort and thus the calculation time.

Additionally, this study highlights the versatility of MOF as materials for optical applications due to their modular design. Within the chosen set of 24 MOFs, a broad range of RI values between 1.24 (ZIF-10) and 1.58 (MIL-140A-Br) was observed with full transparency in the visible spectral region. In combination with the presented fragment-based approach for the calculation of the RI, this promotes further studies of MOFs as materials for optical applications, e.g. the automated screening of MOF databases and the design of novel MOFs. Aiming for very low and high RI values, this allows the improvement of existing optical systems like coatings of mirrors and lenses as well as the design of novel optical systems like waveguiding elements, optical filters or in Fabry–Pérot devices.

Finally, we propose from our study that future work should focus on the extension of the presented fragment-based approach allowing the calculation of frequency-dependent polarizabilities. This should allow the efficient calculation of absorption spectra as well as the dispersion of the RI.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the LUH compute cluster, which is funded by the Leibniz University Hannover, Germany, the Lower Saxony Ministry of Science and Culture and the German Research Association (DFG). This work is funded by the DFG under Germany's Excellence Strategy within the Cluster of Excellence PhoenixD (EXC 2122, Project ID 390833453).

References

1. H. K. Raut, V. A. Ganesh, A. S. Nair and S. Ramakrishna, Energy Environ. Sci., 2011, 4, 3779.
2. C. Rodríguez, S. Günster, D. Ristau and W. Rudolph, Opt. Express, 2015, 23, 31594.
3. H.-Y. Pan, X. Chen and X.-L. Xia, Renewable Sustainable Energy Rev., 2022, 161, 112361.
4. E. K. Macdonald and M. P. Shaver, Polym. Int., 2015, 64, 6.
5. D. H. Kim, W. Jang, K. Choi, J. S. Choi, J. Pyun, J. Lim, K. Char and S. G. Im, Sci. Adv., 2020, 6, eabb5320.
6. T. N. Nguyen, F. M. Ebrahim and K. C. Stylianou, Coord. Chem. Rev., 2018, 377, 259.
7. Y. Zheng, F.-Z. Sun, X. Han, J. Xu and X.-H. Bu, Adv. Optic. Mater., 2020, 8, 2000110.
8. K.-T. Hsu, P. Thanasekaran, T.-W. Hsu, C.-H. Su, B.-C. Chang, Y.-H. Liu, C.-H. Hung and K.-L. Lu, CrystEngComm, 2021, 23, 824.
9. H. Li, L. Zhang, H. He, Y. Yang, Y. Cui and G. Qian, Sci. China Mater., 2021, 64, 698.
10. W. Yin, C.-A. Tao, F. Wang, J. Huang, T. Qu and J. Wang, Sci. China Mater., 2018, 61, 391.
11. N. C. Keppler, K. D. J. Hindricks and P. Behrens, RSC Adv., 2022, 12, 5807.
12. M. Treger, A. Hannebauer, A. Schaate, J. L. Budde, P. Behrens and A. M. Schneider, Phys. Chem. Chem. Phys., 2023, 25, 6333.
13. M. Treger, A. Hannebauer, P. Behrens and A. M. Schneider, Phys. Chem. Chem. Phys., 2023, 25, 15391.
14. J. L. Rowsell and O. M. Yaghi, Microporous Mesoporous Mater., 2004, 73, 3.
15. S. R. Batten, N. R. Champness, X.-M. Chen, J. Garcia-Martinez, S. Kitagawa, L. Öhrström, M. O’Keeffe, M. Paik Suh and J. Reedijk, Pure Appl. Chem., 2013, 85, 710.
16. M. A. Syzgantseva, C. P. Ireland, F. M. Ebrahim, B. Smit and O. A. Syzgantseva, J. Am. Chem. Soc., 2019, 141, 6271.
17. K. Hendrickx, D. E. P. Vanpoucke, K. Leus, K. Lejaeghere, A. van Yperen-De Deyne, V. van Speybroeck, P. van der Voort and K. Hemelsoet, Inorg. Chem., 2015, 54, 10701.
18. M. D. Allendorf, M. E. Foster, F. Léonard, V. Stavila, P. L. Feng, F. P. Doty, K. Leong, E. Y. Ma, S. R. Johnston and A. A. Talin, J. Phys. Chem. Lett., 2015, 6, 1182.
19. S. M. Moosavi, A. Nandy, K. M. Jablonka, D. Ongari, J. P. Janet, P. G. Boyd, Y. Lee, B. Smit and H. J. Kulik, Nat. Commun., 2020, 11, 4068.
20. Y. J. Colón and R. Q. Snurr, Chem. Soc. Rev., 2014, 43, 5735.
21. B. Ni, W. Sun, J. Kang and Y. Zhang, J. Phys. Chem. C, 2020, 124, 11595.
22. M. A. F. Afzal, C. Cheng and J. Hachmann, J. Chem. Phys., 2018, 148, 241712.
23. M. A. F. Afzal and J. Hachmann, Phys. Chem. Chem. Phys., 2019, 21, 4452.
24. R. F. Ligorio, A. Krawczuk and L. H. R. Dos Santos, J. Phys. Chem. A, 2020, 124, 10008.
25. M. Ernst, L. H. R. Dos Santos and P. Macchi, CrystEngComm, 2016, 18, 7339.
26. M. A. Collins and R. P. A. Bettens, Chem. Rev., 2015, 115, 5607.
27. D. Hua, H. R. Leverentz, E. A. Amin and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 251.
28. J. Hellmers, E. D. Hedegård and C. König, J. Phys. Chem. B, 2022, 126, 5400.
29. M. R. Ryder, Z. Zeng, K. Titov, Y. Sun, E. M. Mahdi, I. Flyagina, T. D. Bennett, B. Civalleri, C. S. Kelley and M. D. Frogley, et al. , J. Phys. Chem. Lett., 2018, 9, 2678.
30. R. Warmbier, A. Quandt and G. Seifert, J. Phys. Chem. C, 2014, 118, 11799.
31. D. S. Chemla, J. L. Oudar and J. Jerphagnon, Phys. Rev. B: Solid State, 1975, 12, 4534.
32. K. Wu and C. Chen, J. Cryst. Growth, 1996, 166, 533.
33. K. Wu, J. G. Snijders and C. Lin, J. Phys. Chem. B, 2002, 106, 8954.
34. R. D. Shannon and R. X. Fischer, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235111.
35. R. D. Shannon and R. X. Fischer, Am. Mineral., 2016, 101, 2288.
36. L. Lorenz, Ann. Phys. Chem., 1880, 247, 70.
37. H. A. Lorentz, Ann. Phys. Chem., 1880, 245, 641.
38. S. T. Ang, A. Pal and S. Manzhos, J. Chem. Phys., 2018, 149, 44114.
39. A. Pal, S. Arabnejad, K. Yamashita and S. Manzhos, J. Chem. Phys., 2018, 148, 204301.
40. S. S. Park, S. Lee, J. Y. Bae and F. Hagelberg, Chem. Phys. Lett., 2011, 511, 466.
41. C. Haichuan, J. Guozhu, Z. Liang and H. Yinshu, Phys. Chem. Liq., 2014, 53, 435.
42. S. Maekawa, K. Moorthi and Y. Shigeta, J. Comput. Chem., 2016, 37, 2759.
43. Y. Bai, Y. Dou, L.-H. Xie, W. Rutledge, J.-R. Li and H.-C. Zhou, Chem. Soc. Rev., 2016, 45, 2327.
44. J. H. Cavka, S. Jakobsen, U. Olsbye, N. Guillou, C. Lamberti, S. Bordiga and K. P. Lillerud, J. Am. Chem. Soc., 2008, 130, 13850.
45. V. Guillerm, F. Ragone, M. Dan-Hardi, T. Devic, M. Vishnuvarthan, B. Campo, A. Vimont, G. Clet, Q. Yang and G. Maurin, et al. , Angew. Chem., 2012, 124, 9401.
46. G. Wißmann, A. Schaate, S. Lilienthal, I. Bremer, A. M. Schneider and P. Behrens, Microporous Mesoporous Mater., 2012, 152, 64.
47. J. H. Cavka, S. Jakobsen, U. Olsbye, N. Guillou, C. Lamberti, S. Bordiga and K. P. Lillerud, J. Am. Chem. Soc., 2008, 130, 13850.
48. S. J. Garibay and S. M. Cohen, Chem. Commun., 2010, 46, 7700.
49. M. Kandiah, M. H. Nilsen, S. Usseglio, S. Jakobsen, U. Olsbye, M. Tilset, C. Larabi, E. A. Quadrelli, F. Bonino and K. P. Lillerud, Chem. Mater., 2010, 22, 6632.
50. B. Ni, W. Sun, J. Kang and Y. Zhang, J. Phys. Chem. C, 2020, 124, 11595.
51. Y. Huang, C.-A. Tao, R. Chen, L. Sheng and J. Wang, Nanomaterial, 2018, 8, 676.
52. K. S. Park, Z. Ni, A. P. Côté, J. Y. Choi, R. Huang, F. J. Uribe-Romo, H. K. Chae, M. O'Keeffe and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10186.
53. L. Zheng, N. Keppler, H. Zhang, P. Behrens and B. Roth, Adv. Mater. Technol., 2022, 7, 2200395.
54. K.-J. Kim, P. Lu, J. T. Culp and P. R. Ohodnicki, ACS Sens., 2018, 3, 386.
55. W. Vandezande, K. P. F. Janssen, F. Delport, R. Ameloot, D. E. de Vos, J. Lammertyn and M. B. J. Roeffaers, Anal. Chem., 2017, 89, 4480.
56. G. Lu and J. T. Hupp, J. Am. Chem. Soc., 2010, 132, 7832.
57. M. E. Schweinefuss, S. Springer, I. A. Baburin, T. Hikov, K. Huber, S. Leoni and M. Wiebcke, Dalton Trans., 2014, 43, 3528.
58. W. Morris, C. J. Doonan, H. Furukawa, R. Banerjee and O. M. Yaghi, J. Am. Chem. Soc., 2008, 130, 12626.
59. S. S. Mondal, M. Hovestadt, S. Dey, C. Paula, S. Glomb, A. Kelling, U. Schilde, C. Janiak, M. Hartmann and H.-J. Holdt, CrystEngComm, 2017, 19, 5882.
60. O. Karagiaridi, M. B. Lalonde, W. Bury, A. A. Sarjeant, O. K. Farha and J. T. Hupp, J. Am. Chem. Soc., 2012, 134, 18790.
61. R. Banerjee, A. Phan, B. Wang, C. Knobler, H. Furukawa, M. O'Keeffe and O. M. Yaghi, Science, 2008, 319, 939.
62. T. Loiseau, C. Serre, C. Huguenard, G. Fink, F. Taulelle, M. Henry, T. Bataille and G. Férey, Chemistry, 2004, 10, 1373.
63. M. O'Keeffe, M. A. Peskov, S. J. Ramsden and O. M. Yaghi, Acc. Chem. Res., 2008, 41, 1782.
64. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
65. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567.
66. D. D. Koelling and B. N. Harmon, J. Phys. C: Solid State Phys., 1977, 10, 3107.
67. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
68. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
69. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
70. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 73005.
71. W. A. Al-Saidi, V. K. Voora and K. D. Jordan, J. Chem. Theory Comput., 2012, 8, 1503.
72. A. P. Bartók and J. R. Yates, J. Chem. Phys., 2019, 150, 161101.
73. J. Paier, M. Marsman, K. Hummer, G. Kresse, I. C. Gerber and J. G. Ángyán, J. Chem. Phys., 2006, 125, 249901.
74. A. J. Morris, R. J. Nicholls, C. J. Pickard and J. R. Yates, Comput. Phys. Commun., 2014, 185, 1477.
75. F. Neese, WIREs Comput. Mol. Sci., 2012, 2, 73.
76. F. Neese, WIREs Comput. Mol. Sci., 2018, 8, e1327.
77. S. Lehtola, C. Steigemann, M. J. Oliveira and M. A. Marques, SoftwareX, 2018, 7, 1.
78. E. F. Valeev, Libint: A library for the evaluation of molecular integrals of many-body operators over Gaussian functions, can be found under https://libint.valeyev.net/, 2019.
79. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
80. J. A. Pople, R. Krishnan, H. B. Schlegel and J. S. Binkley, Int. J. Quantum Chem., 1979, 16, 225.
81. N. C. Handy, D. J. Tozer, G. J. Laming, C. W. Murray and R. D. Amos, Isr. J. Chem., 1993, 33, 331.
82. B. G. Johnson and M. J. Fisch, J. Chem. Phys., 1994, 100, 7429.
83. H. Kragh, Substantia, 2018, 2, 7.
84. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158.
85. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
86. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
87. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51.
88. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
89. B. J. Lynch, P. L. Fast, M. Harris and D. G. Truhlar, J. Phys. Chem. A, 2000, 104, 4811.
90. Y. A. Bernard, Y. Shao and A. I. Krylov, J. Chem. Phys., 2012, 136, 204103.
91. D. Hait and M. Head-Gordon, Phys. Chem. Chem. Phys., 2018, 20, 19800.
92. S. Øien, D. Wragg, H. Reinsch, S. Svelle, S. Bordiga, C. Lamberti and K. P. Lillerud, Cryst. Growth Des., 2014, 14, 5370.
93. F. Vermoortele, M. Vandichel, B. van de Voorde, R. Ameloot, M. Waroquier, V. van Speybroeck and D. E. de Vos, Angew. Chem., Int. Ed., 2012, 51, 4887.
94. S. Biswas, J. Zhang, Z. Li, Y.-Y. Liu, M. Grzywa, L. Sun, D. Volkmer and P. van der Voort, Dalton Trans., 2013, 42, 4730.
95. Z. Hu, Y. Peng, Z. Kang, Y. Qian and D. Zhao, Inorg. Chem., 2015, 54, 4862.
96. M. Kandiah, M. H. Nilsen, S. Usseglio, S. Jakobsen, U. Olsbye, M. Tilset, C. Larabi, E. A. Quadrelli, F. Bonino and K. P. Lillerud, Chem. Mater., 2010, 22, 6632.
97. W. Liang, R. Babarao and D. M. D'Alessandro, Inorg. Chem., 2013, 52, 12878.

---

Footnotes

† Dedicated to the memory of Professor Peter Behrens.

‡ Electronic supplementary information (ESI) available: Details of DFT calculations, polarizabilities of the MOF fragments and calculated refractive indices. See DOI: https://doi.org/10.1039/d3cp02356g

---