Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Characteristic nuclear spin-induced optical rotation in oxygen-containing organic molecules†
Eelis
Kamula
,
Juha
Vaara
 and
Petr
Štěpánek
and
Petr
Štěpánek
 *
*
NMR Research Unit, Faculty of Science, University of Oulu, Oulu, FI-90014, Finland. E-mail: petr.stepanek@oulu.fi
First published on 2nd October 2023
Abstract
Nuclear spin-induced optical rotation (NSOR) is a nuclear magneto-optic effect that manifests itself as a rotation of the plane of polarization of linearly polarized light. The effect is induced by ordered nuclear magnetic moments within a molecule. NSOR is sensitive to specific, localized interactions. Hence, the connection between the local chemical environment and the corresponding NSOR signal is crucial to understand. Despite the fact that contributions to better understand the connection have been made, the general systematics still remain unknown. In this paper, NSOR in oxygen compounds is investigated systematically to better understand the impact of oxygen atoms on the NSOR signal. NSOR signals are computed using density-functional theory methods for five different classes of oxygen compounds. The ability of NSOR to distinguish different molecules and individual nuclei in the molecules is studied and the information provided by NSOR is compared to conventional NMR spectroscopy. The results reveal that NSOR is capable of chemical distinction between nuclei and molecules, and by using NMR and NSOR together it is possible to distinguish nuclei near the oxygen atom.
1 Introduction
Spectroscopic methods provide insight into the molecular structure and dynamics and are essential for the development of new chemical substances and materials with desirable properties. New spectroscopic techniques are constantly being invented as each spectroscopy provides its own unique insight due to the different interactions between the probing radiation and the investigated molecule.A group of emerging techniques is the so-called nuclear magneto-optic spectroscopy (NMOS). NMOS is based on nuclear magneto-optic (NMO) effects, molecular interactions between the nuclear spins and the electromagnetic radiation of light, mediated by the electrons of the molecule. They are analogous to the so-called classical magneto-optic effects1 with the difference that, instead of the external magnetic field, an internal field due to the magnetization of nuclear spins causes the NMO effects. Since the NMO interactions involve both localized nuclei and the outer, polarizable part of the electron cloud, the NMO techniques have potential to provide a unique combined response unavailable by other contemporary spectroscopic methods.
Of the five hitherto proposed NMOS methods2–6 currently the most experimentally advanced and the one attracting the most attention2,7–11 is nuclear spin-induced optical rotation (NSOR). NSOR is an effect of rotation of the plane of polarization of linearly polarized light as it passes through the sample that has nuclear spins partially oriented along the direction of the propagation of the light beam. It is the only experimentally observed NMO effect so far, and its theoretical background has also received the most attention.7,12–17 The magnitude of the NSOR signal is measured as the angle by which the plane of polarization is rotated from its original orientation, upon passing through the sample. Due to the complex interaction between the electron cloud, the electromagnetic radiation and the nuclear spins, the magnitude of this rotation in the NSOR signal is difficult to predict without the use of quantum-chemical calculations. However, certain trends have been observed, such as shown in a recent study of hydrocarbons.17 Therein it was demonstrated that, in a group of structurally similar molecules, NSOR exhibits comparable magnitudes of the signals for nuclei in similar chemical environments within the molecular structure. This suggests a possibility to empirically map NSOR signals against structural features of molecules, in analogy to characteristic vibrational frequencies in infrared and Raman spectroscopies, or chemical shifts in NMR.18
In this work we extend the computational NSOR investigation towards families of organic molecules containing oxygen: alcohols, ethers, aldehydes, ketones and carboxylic acids. These are selected because the oxygen moieties are common in many organic and biomolecules and are, thus, an important target for spectroscopic measurements. Furthermore, oxygen is an electron-rich atom and a part of common spectroscopically active chromophores,19 such as the –OH and –COOH groups in molecules.
We investigate the NSOR signals of 1H, 13C and 17O nuclei in a set of these oxygen-containing molecules, including conformational effects and different ways of describing the solvent. The results suggest that nuclei in similar chemical environments within the oxygen-containing molecules give rise to characteristic NSOR signals, similarly as in the case of hydrocarbons.17 Since the observable signals are in the experimental NSOR set-ups modulated at the Larmor frequency of the nuclei, they also contain the chemical-shift information similarly to the standard one-dimensional NMR. NSOR thus arguably contains more information than an equivalent induction-detected one-dimensional NMR experiment.
2 Theory
Natural optical activity occurs in chiral materials due to different phase velocities of the left- and right-circular components of electromagnetic radiation.1 In contrast, classical magneto-optic effects, such as Faraday optical rotation, occur in all molecules regardless of their chirality, when an external magnetic field is applied. In an experiment where light travels through a path length l in a sample placed in an external magnetic field along the laboratory z axis, the electric field vector of the light beam rotates and the optical rotation angle ϕ is given by6 | (1) |
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) denotes the number density of molecules in the sample and
denotes the number density of molecules in the sample and  denotes the imaginary part of the motionally averaged antisymmetric dipolar polarizability
denotes the imaginary part of the motionally averaged antisymmetric dipolar polarizability  of the molecule.
of the molecule.
In the absence of an external magnetic field, the net magnetization of a sample of spin-polarized nuclei can be utilized for generating the optical rotation. This gives rise to NSOR, manifesting itself as a rotation of the electric-field vector of linearly polarized light. In electronically closed-shell molecules the effect is caused by two simultaneous physical phenomena. One contribution arises from the hyperfine interaction between the nuclear spins and electrons within the molecular electronic structure. The other factor is the partial orientation of the nuclear spins, creating a bulk magnetization that undergoes Larmor precession around a magnetic field directed perpendicularly to the light beam.2 Due to this precession the magnetization is aligned periodically with the wave vector of the linearly polarized light. This interaction modifies the dynamic polarizability of the electron cloud of the molecule with the result that the optical properties of the molecule undergo a change. For a liquid-phase sample implying isotropically tumbling molecules, the antisymmetric polarizability in eqn (1) can, in the case of NSOR, be written for a magnetic nucleus K as6
 | (2) |
 , τ and ν refer to Cartesian coordinate components. ε is the Levi-Civita symbol. For practical eletronic-structure calculation the molar NSOR angle can be expressed as6
, τ and ν refer to Cartesian coordinate components. ε is the Levi-Civita symbol. For practical eletronic-structure calculation the molar NSOR angle can be expressed as6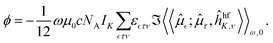 | (3) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) and the hyperfine interaction ĥhfK, which in nonrelativistic theory of closed-shell systems involves the paramagnetic nuclear spin-electron orbit (orbital hyperfine) operator ĥPSOK. The electric dipole operator is19
and the hyperfine interaction ĥhfK, which in nonrelativistic theory of closed-shell systems involves the paramagnetic nuclear spin-electron orbit (orbital hyperfine) operator ĥPSOK. The electric dipole operator is19 | (4) |
 | (5) |
![[l with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006c_0302.gif) K,i = −iħ[(ri − RK) × ∇i] describes the angular momentum of electron i with respect to the position RK of the nucleus K.
K,i = −iħ[(ri − RK) × ∇i] describes the angular momentum of electron i with respect to the position RK of the nucleus K.
3 Methods
3.1 Labelling system for nuclei
The NSOR signals from each 13C and 1H nuclei were labelled based on two structural criteria (Fig. 1). The first criterion is the distance from the oxygen atom in the molecule. The distance is calculated in bonds. The atom that is directly bound to the oxygen is one bond away, the next atom is two bonds away and so on. The second criterion characterises the bonding situation of the atom by the number of carbon–carbon bonds connected to it. This separates the carbons into five different groups. Carbons at the end of a carbon chain are bound to one other carbon and they are labelled as E-type carbons (end of chain). Carbon atoms in the middle of the carbon chain are bound to two other carbons and they are labelled as C-type (chain) carbons. Carbons that are bound to three other carbons are referred to as T-type (tertiary) carbons and carbons that make four bonds with other carbons are Q-type (quaternary) carbons. These are labeled so because all the present molecules only contain single bonds between carbons. In ethers the carbon in the methoxy group makes no bonds with other carbons and it is, consequently, labelled as M-type (methoxy) carbon.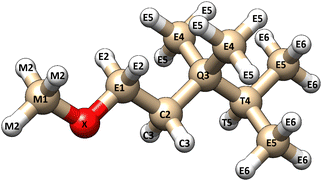 | ||
| Fig. 1 A visual illustration of the labelling system of the nuclei. Each atom is labelled based on their distance (in bonds) from the oxygen atom (X) and the number of carbon–carbon bonds to the atom in question. The letters M, E, C, T and Q refer to 0, 1, 2, 3 and 4 carbon–carbon bonds, respectively (corresponding to methoxy, end-of-chain, chain, tertiary, and quaternary). Protons have the same letter as the carbon they are bound to. The figure was rendered using UCSF Chimera.21 | ||
The signals from protons are labelled based on the distance from the oxygen atom and the above-explained class of the carbon centre they are bound to. For example, a proton that is four bonds away from the oxygen and is bound to an E-type carbon, would be an E4-type proton. In alcohols, the proton in the hydroxyl group is an X-type proton.
The oxygens are marked as X atoms. The oxygen signals are labelled based on the molecule class which are alcohol, aldehyde, ether and ketone.
The trends of NSOR for the different structural motifs were investigated using a large set of molecules. The complete sets of molecules were built in Molden22 as single conformers. The number of different structural motifs was kept similar, meaning that the carbon atoms near the oxygen atom make all possible number of bonds at each position in the chain in all four different molecule groups (E, C, T, Q). The molecules were selected such that there is a representation of combinations of structural motifs with respect to both the distance of the atom from the oxygen and their bonding situation.
The full list of investigated molecules is in Table S1 in ESI.†
3.2 Geometry optimization
First, a conformation search was performed to check how NSOR depends on conformation of a molecule. One alcohol, one ether, one ketone and one aldehyde were chosen to calculate NSOR in different-energy conformers. Each molecule was first optimized using the extended tight-binding program package xtb,23 then 15 lowest-energy conformers for each of them were generated using xtb's utility program CREST (Conformer-Rotamer Ensemble Sampling Tool).24 All of these conformers were then optimized in Turbomole25 using the hybrid DFT functionals PBE026 and B3LYP27,28 with the resolution-of-identity (RI)29 and dispersion correction D430 using the def-TZVP basis set.31 The energies for all conformers produced by CREST and the different DFT methods were recorded and the ordering of the energies was investigated. The ordering of energies are reported in Table S2 (ESI†). For the evaluation of the effect of conformation, three lowest-energy conformers separately from xTB, PBE0 and B3LYP calculations were chosen for the NSOR calculation. NSOR signals for this group of molecules were computed for 13C nuclei up to the distance of three bonds from the oxygen atom.For the main calculations, the entire set of molecules was used. The geometry optimization procedure started with xtb and continued with CREST to produce low-energy conformers. The conformers were sorted according to energy using CREGEN32 and finally the lowest-energy conformer was fine-tune optimized at the B3LYP/def-TZVP level of theory with the dispersion correction D4 in Turbomole, along with the conductor-like screening model (COSMO).33 The methanol solvent parameters were used in all optimizations. After the optimization procedure, harmonic vibrational frequencies were calculated in Turbomole to verify that a local geometry minimum had been found.
To investigate the effect of the solvent model, some calculations were also carried out in vacuum or within PCM with an additional explicit solvent molecule. Since one of the common interactions that oxygen moieites participate in is the formation of hydrogen bond, the probe molecule to investigate the effect of explicit solvent was chosen to be water. It is acknowledged that methanol would be more consistent choice here as it is used in implicit model. However, as the goal was to investigate mainly the effect of the hydrogen bond, water was a more convenient probe as it has fewer degrees of freedom and has smaller steric influence.
For NSOR calculations in vacuum and with the explicit solvent molecule, the geometries were taken from the implicit solvent optimizations without further optimization to not introduce possible changes in NSOR due to different geometry. For the same reason, in explicit solvent calculations, only the position of the water molecule was optimized while the parent molecule was fixed in space. This means that our approach allows us to assess separately only the direct solvent effects. However, the possibly significant15,34 conformational effects induced by the solvent are not included in this model. For alcohols and aldehydes the explicit solvent calculations were conducted in two ways. In half of the calculations, the water molecule was placed so that it approached the oxygen atom of the functional group of the parent molecule, whereas the other half was done so that the water approached the hydrogen atom of the functional group. For ethers, the explicit solvent calculations were not conducted due to the fact that the oxygen is well-embedded in the parent molecule, making it more difficult for the water molecule to approach it. The optimizations of the water molecule were performed at the same level of theory as in the implicit solvent calculations. Some of the geometries ended up with one or two imaginary-frequency modes. The modes are the ones where the water molecule is slightly coupled to the –OH group of the main molecule. The magnitudes of the imaginary modes are typically around 100i cm−1. As the parent molecule was fixed in space, this is as good optimization as possible and these geometries were then used for the NSOR calculations.
3.3 NSOR calculations
NSOR signals in the conformer search were calculated in DALTON35 with the polarizable continuum model (PCM),36 using DFT with the BHandHLYP functional27,28 and co2 basis set.16 The BHandHLYP functional was chosen due to its relatively good performance for NSOR calculations when compared with systematic ab initio coupled clusters singles and doubles (CCSD) approach,7,9 while allowing computations for rather large systems. The co2 basis set is a completeness-optimized basis set for NSOR.37 It was designed and benchmarked in order to provide a reasonably sized basis set that features both a good description of the electronic structure near the nucleus, as well as flexibility in the polarization further away, which is important for optical properties. The NSOR constants in implicit solvent and in vacuum, as well as with an explicit solvent molecule, were calculated at the same level of theory. Methanol was used as an implicit solvent in all the NSOR calculations. The parameters of the solvent cavity are reported in Table S3 (ESI†). The units for the NSOR signals are μrad dm3 (mol cm)−1. In the text, the abbreviation μrad is used, but all reported signals are normalized to concentration, nuclear polarization and unit path length. The proton signals from each carbon are averaged to get only one signal for each chemically equivalent group of nuclei. All NSOR calculations were carried out at the wavelength of 405 nm, which is a standard wavelength in many commercial laser diodes and, hence, often used in NSOR experiments.3.4 The effect of degree of oxidation on NSOR
We also investigated the direct effect of increasing the formal oxidation state of the oxygen-bearing carbon atoms on NSOR in a selected series of molecules (from alcohol to carboxylic acid). These trends in NSOR with oxidation were investigated in alcohols, aldehydes and carboxylic acids. The structures were built such that the carbon skeleton in each molecule class is the same, meaning that the carbon structure from the alcohol was taken and the hydroxyl group was replaced first by a formyl group (forming aldehyde) and then by a carboxyl group (forming carboxylic acid) in such a way that the number of carbons in the molecule does not change. This was done with three different carbon skeletons of varying structure. The optimization procedure was similar to the one followed in the implicit solvent calculations. A few of the alcohol geometries ended up with one imaginary-frequency mode. The magnitudes of the imaginary vibrational modes are 5i cm−1 and 20i cm−1 and, hence, they can be considered as numerical inaccuracies and tighter geometry optimization criteria would have had negligible effect on the result of the NSOR calculation. NSOR signals were obtained in the same way as in the implicit solvent calculations.3.5 NMR calculations
A comparison of NSOR angles and NMR chemical shifts was conducted for all the investigated atom types at the distances of one and two bonds from the oxygen atom. The comparison was done between vacuum calculations and for several examples of each class of molecule (alcohol, ether, ketone, aldehyde, carboxylic acid). The geometries used in the NMR calculations are the same as in the NSOR calculations. The chemical shifts were calculated in Turbomole without any solvent model at the same level of theory as the NSOR signals.4 Results and discussion
4.1 Effect of conformation
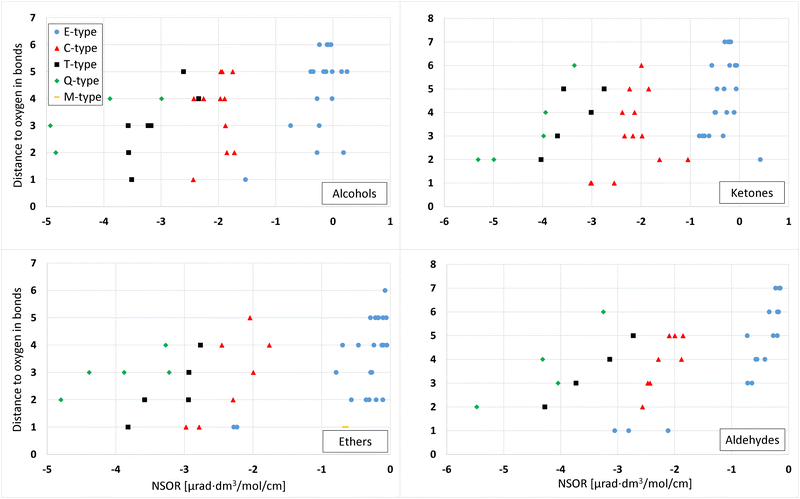
The effect of the conformation of a molecule on the energy and NSOR for nuclei in up to 3 bonds' distance from oxygen was investigated using one molecule from each different molecule class (aldehyde, ketone, alcohol, ether).Fig. 2 shows the main gross features of 13C NSOR from the conformation search and the effect of conformation for each molecule class. The comparison of energies are in Fig. S1 and S2 in ESI.† The figure contains the lowest-energy conformer from calculation using xtb, PBE0 and B3LYP for each molecule class. The signals are spread between −7 and 0.5 μrad dm3 mol−1 cm−1 and rather widely spread out for each molecule class. However, the NSOR of different atom types follows a rough pattern of Q ≥ T ≥ C ≥ E.
 | ||
| Fig. 2 Effect of conformation on the 13C NSOR in alcohols, ketones, ethers, and aldehydes. In each figure, the y axis shows the distance to the oxygen atom in bonds. The signals are slightly vertically offset so they are easier to see. The x axis shows the NSOR angle in μrad (mol dm−3 cm)−1. E-, C-, T- and Q-type carbons (see Fig. 1) are denoted by circle, triangle, square and diamond, respectively. | ||
In all molecule classes the atom types form quite compact groups and, only occasionally individual signals are not included in the main groups, with more significant differences. The choice of the quantum-chemical method in geometry optimization and selection of conformers has only a small effect on NSOR.
In 4-(1-ethyl-2-methylpropyl)-3,4,5-trimethyl-3-octanol (top left) the signals from each nucleus are in a small area, except a couple of signals in Q-type carbon. However, also those two signals have a very slight deviation from the group where most of the values are. In general, the differences are smaller than in other molecule classes.
In the case of 3-ethyl-4-(1-methylpropyl)-2-octanone (top right) the signals are a bit wider spread out than in the case of alcohol, but still very compactly in a single area. T2-type carbons form two distinct groups but they are very close to each other. Also one C1 carbon is a bit outside of the main group but still very close to other signals.
In the case of 4,4-dimethyl-2-isopropoxypentane (bottom left) there is a bit more deviation in the signals than in the other figures, but the deviations still remain small. At the distance of one bond, the group of C1-type carbons is composed of signal from two different nuclei, which makes it look like there is more deviation than there really is. Other nuclei have some spread as well but in general the signals are quite tightly located in a small area.
2,4,6,6-Tetramethylheptanal (bottom right) has similar trends as the other molecule classes. In general the differences are small. In the case of E3 nucleus, a couple of signals are significantly different compared to the main cluster. Since the magnitudes of the signals are around −1 μrad, a difference of 0.42 μrad is relatively quite significant.
In all classes of molecules, the different geometry optimizations and the selection among the energetically most favorable conformers generate similar NSOR. The values are very close to each other, often even on top of each other. There are individual cases where some signals have more different values compared to each other, but the results are qualitatively similar. The generally most important factor is the atom type and its distance from oxygen. The class of molecule and the method chosen for the geometry optimization have much smaller effects.
In addition, we have performed a series of partial optimizations on a set of four model molecules (2-methylbutanol, 2-methylbutanal, 3-methylpentan-2-one, 1-methoxy-2-methylbutane). In these calculations we constrained the dihedral angle O–C–C–C from the moiety to assess the effect of the conformations that do not correspond to the local energy minima. The results show that while there is some variation in the NSOR, the values of each atom type remain in a relatively narrow range. Even when some close lying signals change their order due to this variation, there are no excursions outside of the region of typical values that would contradict the general trends observed from the analysis of the large set. This justifies using the optimized structures as an approximation to discussion of the broad features of NSOR. The results are reported in Fig. S3–S10 in ESI.† Fig. S11–S14 (ESI†) show the structures and also indicate the fixed dihedral angle.
4.2 Effect of different oxygen moieties on NSOR
Proton signals from ketones (top right) range from about 1.4 to 1.85 μrad, thus falling in the same range with those of alcohols. E- and C-type nuclei generate larger NSOR angles as the distance to the oxygen grows. There are very few T signals so it is not clear if this happens in the T types. T-type NSOR seems to be larger than E- and C-types, but due to the small amount of data it is not possible to say if this is true in general.
Ether signals (bottom left) are, again, found in a range that encompasses both alcohols and ketones from about 1.4 to 1.8 μrad. The M-type proton cannot be distinguished from the E-type protons. There are E signals that are smaller, larger and also quite similar to the M-type signal. There are no clear trends, all the signals are mixed.
Aldehyde angles (bottom right) range from about 1.35 to 1.8 μrad, again in the range of other classes of molecules. Most of the signals are between 1.5 and 1.6 μrad. The signals are mixed up, there are not any clear trends.
In general, NSOR signals from 1H nuclei in oxygen compounds are quite mixed up. The signals fall to similar ranges despite the different molecule classes, atom types and distances to the oxygen centre. There are no clearly identifiable groups due to the relatively large spread of signals and the overlap of ranges of signals of different atom types.
Alcohol values (top left) are between −5 and 0.5 μrad, and most of the values are negative. The E1 signal seems clearly different compared to the E signals further from the oxygen.
Ketones (top right) give angles from −5.5 to 0.5 μrad, i.e., the range overlaps with that observed for the alcohols, as found for the 1H signals (see above). The C1 and C2 nuclei give clearly different NSOR values from each other with C1-NSOR being stronger than C2-NSOR. Interestingly for C-type nuclei the trend of NSOR with distance does not seem monotonic as the signals from C2 nuclei have substantially smaller NSOR than both C1 and C3–C6. Ether values (bottom left) again range from about −5 to 0 μrad. E1-type signals are clearly different from other E-type signals. The M1-type signal is similar to E-type signals at two-bond distance from oxygen and further. Finally, aldehyde (bottom right) shows similar trends as the other molecule types. NSOR goes from −5.5 to 0 μrad. The atoms bound directly to the oxygen (E1) show clearly distinct values from the ones at distances further from the oxygen.
4.3 Effect of solvent model
Fig. 5 shows the correlation between NSOR signals in vacuo and in the implicit solvent model for 13C and 1H nuclei in alcohols. In general, the inclusion of implicit solvent increases the values of NSOR and there is a very good linear correlation between values calculated in vacuo and the implicit solvent. Interestingly, this solvent-induced increase is in contrast to the previous investigation of NSOR of water clusters, where the presence of explicit water molecules decreased the NSOR values.15 | ||
| Fig. 5 Correlation between calculated NSOR signals calculated in vacuo and in the implicit solvent model (methanol) for 13C (upper subfigure) and 1H (lower subfigure) nuclei in alcohols. | ||
In 13C (upper subfigure), NSOR in solvent approximately equals NSOR in vacuum multiplied by a constant >1. The absolute differences are small, but signals close to zero might experience large relative changes up to 30%, but the stronger signals have smaller relative changes, usually around 10% to 20%. All C-, T- and Q-type values reside under the diagonal and almost all E-type values are either on the diagonal or under it. There is virtually no spread in the signals, they are all practically perfectly on one line. Almost all values are negative, only a few E-type signals are positive. The coefficient of determination R2 ≈ 0.9994. A linear least-squares fit has a slope of 1.20 and an intercept of −0.02.
In the case of 1H (lower subfigure), the correlation has both a scaling factor >1 and is also notably offset compared the vacuum calculations. A linear least-squares regression line gives a slope of 1.10 and an intercept of 0.16 with R2 ≈ 0.9954.
Fig. 5 shows trends similar to those of saturated and unsaturated hydrocarbons,17 where n-heptane was used as solvent in the PCM model and 13C and 1H NSOR were calculated at the same level of theory as in this paper. The magnitude of the solvent effect seems more moderate in the present case with methanol as a solvent, as compared to the 25% reported previously. The trends that 13C has a more linear dependence and 1H is offset are the same in both cases. This is not surprising as we are looking mostly at atoms far from the oxygen group, where the molecules are structurally quite similar.
13C and 1H in ketones, ethers and aldehydes show dependence on the implicit solvent model that is practically identical to that of the above-discussed alcohol case. The correlations for 13C and 1H nuclei are linear and offset, respectively. The linear least-squares fit gives similar slopes and intercepts for all molecule types. The plots for other molecule types are given in Fig. S15 and S16 in ESI.†
For comparison we also performed calculations with a combination of explicit solvent molecule and implicit solvent cavity. Fig. 6 shows the correlation between the NSOR angles with an explicit solvent molecule and only with the implicit solvent for 1H nuclei in different molecule types. The common features in all cases is that the correlation is quite linear. In most cases there is only a small difference between the implicit and explicit model. However, in some cases there are significant deviations, indicating that the use of only the implicit solvent may not be sufficient for quantitative accuracy in all cases.
In the case of alcohols (top) the correlation is linear and there is only a moderate spread. Most of the values are on the diagonal or close to it. E-types lie on the diagonal most often, in other atom types there are more off-diagonal values. The off-diagonal values are evenly distributed under and over the diagonal and there are no clear trends on which direction the solvent molecule changes the NSOR. The (O)- and (H)-type signals, which refer to the atom nearest to the explicit solvent molecule, are almost equal in most cases. Signals for X-type 1H nuclei are plotted in Fig. S17 in ESI.†
In ketones (middle) the correlation is linear. Only a couple of E- and C-type signals are clearly above the diagonal. Others are on the diagonal or very close to it. One T-type signal is below the diagonal and two T-type signals are above the diagonal. As signals are on both sides of the diagonal there is no clear trend how the solvent molecule changes NSOR. The plot suggests that the explicit solvent molecule has practically no effect on NSOR in E- and C-type 1H nuclei in ketones. In T-type nuclei the effect is more significant. Interestingly, the T signals that are showing the largest shifts are from a single molecule and at the distance of six bonds from the oxygen. This suggests that the effect of the explicit solvent can reach quite far and can be related to the particular molecule or its conformation.
Aldehydes (bottom) have majority of the values close to the diagonal, meaning that the explicit solvent molecule did not have a large effect on NSOR for these nuclei. However, there are some clearly off-diagonal values as well. The off-diagonal values are evenly divided under and over the diagonal and there are no clear trends on which direction the solvent molecule changes the NSOR. Close to the diagonal, the (O)- and (H)-signals from the same nuclei are in most cases close to each other, indicating that the orientation of the water molecule has a smaller effect than its overall presence. Further from the diagonal, the orientation of the water molecule is more relevant. In this case many of the signals with largest changes are close to the aldehyde group, with distances between 2 and 4.
Fig. 7 shows the correlations between NSOR angles with implicit solvent and in the presence of explicit solvent molecule for 13C nuclei in different molecule types. The correlations are again in all cases quite linear with some differences between the orientation of the explicit solvent molecule.
The correlation in alcohols (top) is quite linear. The Q- and T-type signals are almost exactly on the diagonal. However, in the E and C types there is some spread. The E signals have large relative offsets of the same order of magnitude as the signals themselves. The other signals are larger so the relative offsets are smaller. There are signals on both sides of the diagonal. The explicit solvent gives rise to possibly more localized interactions due to the explicit solvent molecule, which might lead to more spread in the signals. However, in most cases the (O)- and (H)-signals from the same nucleus are very close to each other, indicating that the orientation of the water molecule does not have a large effect on NSOR.
In ketones (middle) the explicit solvent molecule has little effect on NSOR. The dependence is quite linear with some spread in the signals on both sides of the diagonal. The Q-type signals are almost perfectly on the diagonal. Three T-type signals are on the diagonal and two signals are above it. The C- and E-type nuclei have spread on both sides of the diagonal. As the atom type progresses from E towards Q, the relative spread reduces due to the larger absolute values of the signals.
Aldehydes (bottom) have somewhat linear correlation. All Q types are on the diagonal or very close to it. There are signals on both sides of the diagonal, leaving it unclear how the explicit solvent molecule affects NSOR. However, there are more signals under the diagonal than above it. The (O)- and (H)-signals from the same nuclei are very close to each other, indicating that the orientation of the water molecule does not matter much. The relative spread in E type nuclei is larger than in other atom types. Overall the differences are larger than in the previous cases, over 10% of the signal for some nuclei.
In general, ketones and aldehydes are more sensitive to the explicit solvent than alcohol. Overall the changes can be quite large. The largest relative changes happen in nuclei whose signals are close to zero. Q-type nuclei are not so sensitive to the explicit solvent since their signals are typically much larger than E-signals, for example.
Explicit solvation has a clear impact on the signals and hence it is important to take into account. There are not very clear indications that either (O) or (H) approach would have larger impact on the signal. Both approaches affect the NSOR intensity. The 1H signals seem to be relatively more sensitive to the explicit solvation than the 13C ones.
4.4 17O-NSOR
Fig. 8 shows the NSOR signals from 17O nuclei in different molecule types in the implicit solvent. Alcohols are clearly different from other molecule classes, which give similar NSOR. Alcohol signals range from −7.88 to −6.38 μrad, whereas the second smallest signals from ketones range from −4.52 to −3.59 μrad. In ethers the NSOR values go from −4.14 to −2.27 μrad. Aldehydes give values from −4.36 to −2.14 μrad. | ||
| Fig. 8 NSOR signals from 17O nuclei in different molecule classes in the implicit solvent (methanol). | ||
In all other molecule types the distribution of the signals is somewhat uniform except in ethers. Ethers clearly divide into two different groups. The left-most values in ethers range from −4.14 to −3.85 μrad and the right-most values from −2.82 to −2.27 μrad. In all cases with larger NSOR around −4 μrad, the ethers contain a methoxy group. In the other group where signals land between −3 and −2 μrad, none of the molecules contains a methoxy group. Five of the molecules contain an ethoxy group and the rest have a larger alkoxy group. This strongly suggests that 17O-NSOR is able to distinguish ethers containing methoxy group from other ethers where both of the carbon chains are longer than one carbon atom.
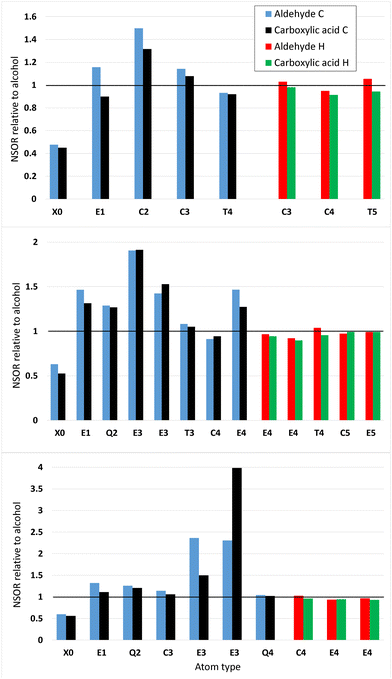
4.5 Trends in NSOR with oxidation
Fig. 9 shows the NSOR from aldehydes and carboxylic acids obtained by oxidizing 4-ethyl-5,5-dimethylheptane (top), 7-ethyl-2,2,3-trimethyl-6-(2-methyl-2-butyl)nonane (middle) and 2,2,4,4,5,5-hexamethylheptane (bottom), with respect to the alcohol baseline. These three systems were chosen so that there is a variety of different types of nuclei. In each figure, the relative value for each nucleus in the alcohol compound is set equal to one. The molecular structures of the carbon skeletons can be found from Fig. S18–S20 (ESI†). Fig. S21 (in ESI†) shows the NSOR signals in μrad dm3 mol−1 cm−1. Names of the molecules are reported in Table S4 in ESI.†Oxidized 4-ethyl-5,5-dimethylheptane (top) shows that the aldehyde has stronger NSOR than carboxylic acid in all atom types for both 1H and 13C. Oxygen signals are weaker than in alcohol. As expected, the 13C-signals are stronger at distances ranging from one to three bonds than at the distance four. The 1H-signals are quite close to one, i.e., close to the values of alcohols, as expected based on the previous figures on 1HSOR.
Nuclei from oxidized 7-ethyl-2,2,3-trimethyl-6-(2-methyl-2-butyl)nonane (middle) are more mixed up. Oxygen signals are clearly weaker than in the alcohol. The carbon signals are mostly stronger than in alcohol and there are no big differences between aldehyde and carboxylic acid. The 1H-signals are again quite close to one.
2,2,4,4,5,5-Hexamethylheptanal (bottom) has a weaker 17O NSOR than the corresponding alcohol. The oxidized carbon structure shows some interesting individual features. One E3-type 13C has a very strong aldehyde signal compared to the alcohol case. The corresponding nucleus from the carboxylic acid also displays much stronger signal than the alcohol, but not nearly as strong as the aldehyde. On the other hand, another E3-type 13C has extremely strong carboxylic acid signal and very strong aldehyde signal, which is, however, much weaker than the carboxylic acid signal. In all other nuclei except this one, the aldehyde produces stronger signal than the carboxylic acid. The 1H-signals are close to unity.
4.6 Optical contrasts for nuclear magnetic resonance
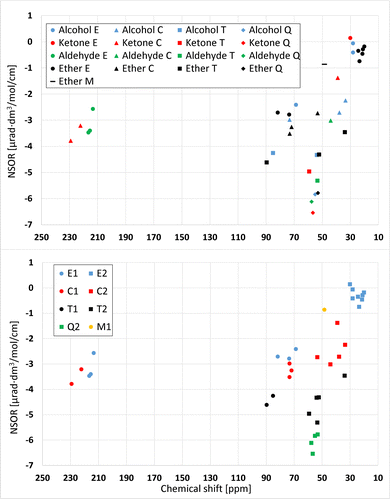
Fig. 10 shows a relation plot of NMR chemical shifts and NSOR of 13C and 1H nuclei in oxygen compounds. In the upper subfigure, all nuclei are either one or two bonds away from the oxygen. The chemical shift given in parts per million (ppm) on the x axis is referenced to the carbon signal from tetramethylsilane. In the upper figure different molecule types are denoted by different colors and different atom types by different shapes. The group of signals closest to zero that consists of five ether signals, two alcohols signals and one ketone signal, is quite compact. The NSOR dimension cannot separate the signals because they are mixed in that direction. However, adding the chemical shift scale separates the ether signals from the alcohols and ketone, but the distinction is not very large. The two alcohol signals can be separated with NSOR. Similarly, the two ether signals at about (73, −2.8) and (81, −2.7) cannot be clearly separated with NSOR but the NMR dimension creates a distinction between them.The E- and C-type signals from all molecule types around −3 μrad are mixed, but adding the NMR dimension very clearly separates the aldehyde E- and ketone C-signals from the rest of the NSOR values. There is also difference between the aldehyde E- and ketone C-signals in NMR direction. The aldehydes are around 215 ppm and ketones between 220 and 230 ppm.
The lower subfigure shows the correlation of NMR chemical shifts and NSOR of 13C nuclei at distances of one and two bonds from the oxygen atom from another angle. These are the same signals as in the upper subfigure, but this time grouped according to the atom type. Different atom types are denoted here by different colors and different distances by different shapes. Different colors create distinct groups. The group close to zero contains only E-type atoms, and for example Q-type nuclei are compactly in a small area. Q2- and T2-atoms produce similar NMR shifts around 50–60 ppm, and hence cannot be distinguished based on chemical shifts, but adding the NSOR dimension separates the two atom types from each other. Q-type nuclei generate clearly larger NSOR than those of the T type. There is also one T2-signal clearly outside of the groups, with the NMR shift of about 34 ppm and NSOR angle of about −3.5 μrad dm3 mol−1 cm−1. In the NSOR dimension the angles of these T2 nuclei are similar to T1, but in the NMR dimension the distinction between T1 and T2 is clear. The T1 have shifts around 85 to 90 ppm, and the T2 have shifts from 50 to 60 ppm. This means that, with one dimension, the three groups, T1, T2 and Q2, cannot be distinguished from each other but using both NMR and NSOR they can be.
The M1 signal is different compared to E-type signals and other signals at the distance of one bond from the oxygen. It has both a smaller chemical shift and a smaller NSOR angle. In general, the signals at distance one are on the left side of the graph and signals at the distance of two bonds are on the right side. We speculate that this might happen due to the electron withdrawal from the M-site by the oxygen compared to the E-sites. NMR calculations were not conducted for protons because of the fact that protons generate similar NSOR regardless of atom type and distance to the oxygen. Hence, their relative spread does not allow to easily distinguish them with NSOR. Hence, adding the NMR dimension to proton NSOR would not provide any useful information.
5 Conclusions
Nuclear spin-induced optical rotation (NSOR) of 1H, 13C and 17O nuclei was investigated with density functional theory for several kinds of oxygen compounds (alcohols, ethers, ketones, aldehydes). The effects of implicit and explicit solvents were studied. NSOR signals were compared to computationally obtained NMR shifts at the same level of theory as the NSOR signals. The aim was to see if NSOR is able to distinguish molecules or individual atoms in molecules. Some promising results were obtained.The effect of conformation is in general quite small, but occasionally there might be larger relative changes between signals from different methods. The effect of conformation was briefly assessed in saturated and unsaturated hydrocarbons,17 where it was found that the molecular conformation can affect the NSOR intensity noticeably. The saturated parts of molecules were less sensitive to changes due to conformation. The effect of conformation on the unsaturated parts of the molecule appeared more pronounced.
The 13C nuclei yield characteristic NSOR in all molecule types. In vacuum, 1H nuclei give NSOR from about 1.35 to 1.85 μrad dm3 mol−1 cm−1 and the NSOR angles are similar regardless of the atom type and distance to the oxygen. Only protons in the hydroxyl groups generate distinct NSOR signals, ranging from 0.1 to 0.3 μrad dm3 mol−1 cm−1. 13C nuclei give NSOR between −5.5 and 0.5 μrad dm3 mol−1 cm−1. Typically, as the number of carbon–carbon bonds to the atom in question decreases, also NSOR decreases. NSOR is strongest near the oxygen atom.
The addition of the implicit solvation by the PCM model increases both 1H and 13C NSOR by a significant amount. For 1H the correlation between vacuum and PCM results is offset for all molecule types. The correlation between 13C NSOR in vacuum and with the inclusion of PCM is linear. The PCM model always enhances NSOR, regardless of molecule type, atom type and distance to the oxygen atom.
The addition of an explicit solvent molecule can either increase or decrease NSOR as compared to the PCM model. In general, alcohols are the least sensitive molecules to the explicit solvent. Aldehydes are the most sensitive. The changes are in general relatively largest for nuclei whose signals are small, that is, E-type atoms. Interaction with both hydrogen or oxygen part of the oxygen moiety can induce significant changes to signals.
Carboxylic acids generate NSOR similar to the other oxygen compounds. Often aldehydes have the largest NSOR, carboxylic acids the second largest and alcohols the smallest. The signals from aldehyde and carboxylic acid are usually close to each other and the alcohol signal is further away. In many cases the transition from alcohol to carboxylic acid enhances NSOR but the transition from aldehyde to carboxylic acid does not. This suggests that the effect might be due to the addition of the doubly bound oxygen in ketones and carboxylic acids, which is absent in alcohols.
Adding the NMR dimension separates the E1 signals in aldehydes and C1 signals in ketones from the rest of the signals. NMR cannot separate T2 from Q2, but adding the NSOR dimension distinguishes them. The results suggest that NMR and NSOR could be combined to create a more powerful spectroscopic tool and to obtain additional information about chemical structures. Both NMR and NSOR can be in principle obtained within the same experimental setup.
NSOR of 17O nuclei is clearly the strongest in alcohols. Ketones, ethers and aldehydes generate weaker NSOR than alcohols. Those three molecule types all generate similar NSOR, ranging from about −4.5 to −2 μrad dm3 mol−1 cm−1. Interestingly, 17O NSOR divides ethers into two groups, depending on whether or not the ether contains a methoxy group. If an ether contains a methoxy group, it generates a stronger NSOR than an ether that does not contain a methoxy group.
The results suggest that the NSOR effect correlates to some extent with the underlying molecular structure motifs. The NSOR phenomenon could be experimentally used as a basis for a viable spectroscopic method. The effect still needs much more investigation, but the results presented here provide new insight into it.
Author contributions
E. K.: calculations and analysis, manuscript writing; J. V.: discussions, manuscript commenting; P. Š: study design, manuscript writing and commenting.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank for the financial support to the Academy of Finland (Grants 316180 (P. Š.) and 331008 (J. V.)) and Magnus Ehrnrooth foundation (grant Optical contrasts in nuclear magnetic resonance). The support from the Kvantum institute (University of Oulu) is acknowledged. The authors wish to acknowledge CSC – IT Center for Science, Finland, for computational resources.References
- L. D. Barron, Molecular light scattering and optical activity, Cambridge University Press, 2nd edn, 2004 Search PubMed.
- I. M. Savukov, S. Lee and M. V. Romalis, Nature, 2006, 442, 1021–1024 CrossRef CAS PubMed.
- T. Lu, M. He, D. Chen, T. He and F. Liu, Chem. Phys. Lett., 2009, 479, 14–19 CrossRef CAS.
- L. Fu, A. Rizzo and J. Vaara, J. Chem. Phys., 2013, 139, 181102 CrossRef PubMed.
- L. Fu and J. Vaara, ChemPhysChem, 2014, 15, 2337–2350 CrossRef CAS PubMed.
- J. Vaara, A. Rizzo, J. Kauczor, P. Norman and S. Coriani, J. Chem. Phys., 2014, 140, 134103 CrossRef PubMed.
- J. Shi, S. Ikäläinen, J. Vaara and M. V. Romalis, J. Phys. Chem. Lett., 2013, 4, 437–441 CrossRef CAS PubMed.
- I. M. Savukov, H. Chen, T. Karaulanov and C. Hilty, J. Magn. Reson., 2013, 232, 31–38 CrossRef CAS PubMed.
- P. Štěpánek and A. M. Kantola, J. Phys. Chem. Lett., 2019, 10, 5458–5462 CrossRef PubMed.
- Y. Zhu, Y. Gao, S. Rodocker, I. Savukov and C. Hilty, J. Phys. Chem. Lett., 2018, 9, 3323–3327 CrossRef CAS PubMed.
- Y. Zhu, C. Hilty and I. Savukov, Angew. Chem., Int. Ed., 2021, 60, 8823–8826 CrossRef CAS PubMed.
- S. Ikäläinen, P. Lantto, P. Manninen and J. Vaara, J. Chem. Phys., 2008, 129, 124102 CrossRef PubMed.
- S. Ikäläinen, M. V. Romalis, P. Lantto and J. Vaara, Phys. Rev. Lett., 2010, 105, 153001 CrossRef PubMed.
- S. Ikäläinen, P. Lantto and J. Vaara, J. Chem. Theory Comput., 2012, 8, 91–98 CrossRef PubMed.
- T. S. Pennanen, S. Ikäläinen, P. Lantto and J. Vaara, J. Chem. Phys., 2012, 136, 184502 CrossRef PubMed.
- J. Vähäkangas, P. Lantto and J. Vaara, J. Phys. Chem. C, 2014, 118, 23996–24005 CrossRef.
- P. Štěpánek, Phys. Chem. Chem. Phys., 2020, 22, 22195–22206 RSC.
- J. M. Hollas, Modern spectroscopy, John Wiley & Sons Ltd, 3rd edn, 1996 Search PubMed.
- P. W. Atkins and R. S. Friedman, Molecular quantum mechanics, Oxford University Press, 4th edn, 2005 Search PubMed.
- J. Olsen and P. Jørgensen, J. Chem. Phys., 1985, 82, 3235–3264 CrossRef CAS.
- E. F. Pettersen, T. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and R. E. Ferrin, J. Comput. Chem., 2004, 13, 1605–1612 CrossRef PubMed.
- G. Schaftenaar and J. H. Noordik, J. Comput.-Aided Mol. Des., 2000, 14, 123–134 CrossRef CAS PubMed.
- Semiempirical extended tight-binding program package xtb. See https://xtb-docs.readthedocs.io/en/latest/setup.html.
- Conformer-rotamer ensemble sampling tool based on the semiempirical extended tight-binding program package xtb's utility program CREST. See https://xtb-docs.readthedocs.io/en/latest/crest.html.
- TURBOMOLE V7.5 2020, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; Available from https://www.turbomole.org.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- R. Ahlrichs, Phys. Chem. Chem. Phys., 2004, 6, 5119–5121 RSC.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Phys. Chem., 1994, 100, 5829 CrossRef.
- Ensemble sorting tool based on the semiempirical extended tight-binding program package xtb's utility program CREGEN. See https://xtb-docs.readthedocs.io/en/latest/crestcmd.html#ensemble-sorting.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- T. S. Pennanen, P. Lantto, M. Hakala and J. Vaara, Theor. Chem. Acc., 2011, 129, 313–324 Search PubMed.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansík, H. J. Aa. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. K. H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Sałek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284 Search PubMed.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- P. Manninen and J. Vaara, J. Comput. Chem., 2006, 27, 434–445 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Complete list of investigated molecules, comparison of relative energies, detail about effects of solvent model and its parameters, detail of calculations of carboxylic acid. See DOI: https://doi.org/10.1039/d3cp02352d |
| This journal is © the Owner Societies 2023 |