The effect of methyl group rotation on ¹H–¹H solid-state NMR spin-diffusion spectra

Abstract

Fast magic-angle spinning (MAS) NMR experiments open the way for proton-detected NMR studies and have been explored in the past years for a broad range of materials, comprising biomolecules and pharmaceuticals. Proton-spin diffusion (SD) is a versatile polarization-transfer mechanism and plays an important role in resonance assignment and structure determination. Recently, the occurrence of negative cross peaks in 2D ¹H–¹H SD-based spectra has been reported and explained with higher-order SD effects, in which the chemical shifts of the involved quadruple of nuclei need to compensate each other. We herein report negative cross peaks in SD-based spectra observed for a variety of small organic molecules involving methyl groups. We combine experimental observations with numerical and analytical simulations to demonstrate that the methyl groups can give rise to coherent (SD) as well as incoherent (Nuclear Overhauser Enhancement, NOE) effects, both in principle manifesting themselves as negative cross peaks in the 2D spectra. Analytical calculations and simulations however show that higher-order coherent contributions dominate the experimentally observed negative peaks in our systems. Methyl groups are prone to the observation of such higher order coherent effects. Due to their low-frequency shifted ¹H resonances, the chemical-shift separation relative to for instance aromatic protons in spatial proximity is substantial (>4.7 ppm in the studied examples) preventing any sizeable second-order spin-diffusion processes, which would mask the negative contribution to the peaks.

---

Introduction

Proton-detected solid-state NMR spectroscopy under fast magic-angle spinning (MAS) conditions (>60 kHz) has developed into a key technique to study biomaterials (for a recent review see ref. 1), pharmaceuticals (for selected examples see ref. 2–4), as well as materials (for a recent review see ref. 3). Besides the high gyromagnetic ratio of protons, and thus the high sensitivity of the NMR experiments, protons serve as highly sensitive reporters for noncovalent interactions, which are essential in a variety of molecular-recognition events. An increase in MAS frequencies is achieved by decreasing the outer diameter of the cylindrical ZrO₂ rotors, leading to the development of rotors with a diameter of only 0.5 mm.⁵ Such rotors allow MAS frequencies up to 150–170 kHz.^6,7 An important advantage of experiments performed in those rotors is the small sample amount needed (<1 mg), which is particularly of interest when studying biomolecules, which are difficult to express with isotope labelling. The gain in resolution of ¹H-detected spectra is related to a decrease in homogeneous line broadening caused by the strong proton–proton dipolar coupling network.⁸ Combining fast MAS with very high static magnetic-field strengths, such as the recently commercially available 28.2 T superconducting NMR magnets,⁹ is expected to further decrease homogeneous linewidths, as illustrated by first examples.^10,11

It has been recognized early on that spin diffusion (SD) provides an effective source for transferring polarization between dipolar-coupled nuclei¹² and is, thus, of high importance for employing NMR in structure-determination techniques. SD can be subdivided into spatial and spectral spin diffusion, where the first process describes the transfer of polarization between chemically equivalent nuclei driven by non-equilibrium longitudinal magnetization,¹³ and in the second represents polarization transfer between spins with different resonance frequencies.¹⁴ The Hamiltonian promoting the polarization transfer can be described by a zero-quantum flip-flop term Î_i⁺Î_j⁻ + Î_i⁻Î_j⁺ interchanging the polarization of the two coupled nuclei denoted by i and j.¹⁵ The required energy conservation is often provided by the coupling to a dipolar coupling network.¹⁴ In static NMR, the efficiency of the SD process depends on (i) the dipolar coupling strength, (ii) the intensity of the zero-quantum (ZQ) spectrum at frequency zero, which decreases in case of a large chemical-shift difference of the two nuclei, and (iii) the orientation of the dipolar coupling tensor with respect to the external field (via the second-order Legendre polynomial).^14,16 Under MAS, SD can be described as a second-order process either using average Hamiltonian theory (AHT) or Floquet theory and thus becomes less efficient at higher MAS frequencies, while being less prone to dipolar truncation effects compared to first-order recoupling sequences. The latter property is an essential requirement for determining long-range distance restraints, for instance in NMR-driven protein structure determinations (for a recent review on amyloid fibrils see ref. 17). The spin operator is proportional to 2Î_lz(Î_m⁺Î_n⁻ + Î_m⁻Î_n⁺) in such a formalism. However, even at MAS frequencies exceeding 100 kHz and high static magnetic-field strengths (>20 T), SD of protons has still been shown to be efficient enough to probe spatial proximities.⁶

¹H–¹H SD experiments have been used in a broad context, for instance to probe spatial proximities in small, typically organic, molecules in the solid state,^18,19 to determine distance restraints that can be used in “NMR crystallography”²⁰ or to distinguish different phases.²¹ As a matter of fact, SD in the form of proton-driven SD, also plays a crucial role in biomolecular NMR to probe spatial proximities and access distance restraints, such as in dipolar assisted rotational resonance (DARR)²² or XHHY spectra, in which X and Y represent ¹³C, ¹⁵N or ³¹P.²³

Typically, the well-known NOESY-type three-pulse sequence²⁴ is used to record ¹H–¹H 2D correlation spectra. In the mixing period, however, polarization transfer can be achieved not only through SD, but also via chemical exchange and through cross-relaxation effects, of which the latter is also the source of the nuclear Overhauser effect (NOE).²⁵ Cross relaxation in contrast to SD is an incoherent polarization-transfer mechanism in which stochastic motions generate the polarization transfer.²⁶ Of note, cross peaks caused by NOE are typically negative in case of fast motion and respective short correlation times τ_c (τ_c ≪ 1/(2ω₀), with ω₀ denoting the proton Larmor frequency), which is often the case for small organic molecules in solution. In the solid state, cross relaxation can only occur if local motions modulate the dipolar couplings stochastically on a fast time scale. In addition, the spectral resolution of proton-detected solid-state NMR spectra need to be sufficiently high, which is most easily achieved using fast MAS experiments.¹ First reports on the potential presence of negative cross peaks in ¹H–¹H 2D solid-state NMR spectra potentially caused by NOE effects have been published very recently.^4,11,27 These examples all involve methyl groups that can potentially have fast rotational correlation times that are required to obtain negative cross peaks. They comprise an active pharmaceutical ingredient,⁴ a lanthanide–calixarene complex and β-aspartyl L-alanine²⁷ for which such negative cross-peaks can be envisioned between methyl groups and high frequency-shifted chemical entities. Furthermore, heteronuclear NOE effects in the solid state have been reported before. This includes for instance transient NOE effects observed on the quadrupolar ¹¹B spin in the BH₃⋯PPh₃ adduct,²⁸ in which the fast motion required for the NOE is probably caused by fast rotation of the –BH₃ unit around the C₃ symmetry axis. Also, a number of studies on ¹³C–¹H heteronuclear NOEs have been reported, in most cases for molecules comprising fast rotating methyl groups.²⁹

Quite recently, negative cross peaks in ¹H–¹H SD-based spectra recorded at 60 kHz MAS have been identified and explained by coherent third-order terms in the effective NMR Hamiltonian.¹⁸ Similar observations were already made in ¹⁹F–¹⁹F SD-based spectra and have been explained by a kinetic model.³⁰ We herein present several examples of small organic molecules, for which such negative peaks appear in ¹H–¹H SD-based spectra, in all cases involving methyl group protons. We systematically investigate by numerical and analytical calculations of coherent, as well as NOE-based incoherent effects, the respective contributions of those mechanisms to the negative cross peaks observed.

Results and discussion

Negative cross peaks in ¹H–¹H SD-based spectra explained by coherent effects

We first observed the effect of negative cross peaks in ¹H–¹H SD-based spectra of O-phospho-L-serine^31,32 (for the chemical structure and a snapshot from the crystal structure see Fig. 1a). Fig. 1b shows the ¹H–¹H 2D homonuclear correlation spectrum recorded at 100 kHz MAS and 16.4 T magnetic-field strength showing negative cross peaks with respect to the sign of the diagonal peaks between the CH₂ and the COOH and PO₃OH protons, observed at 4.2 ppm and 16.8 ppm, as well as 4.2 ppm and 12.7 ppm. A further weak negative cross peak is observed between the H_α and COOH protons at 5.2 ppm and 16.8 ppm, respectively. The spectrum recorded at 60 kHz MAS is depicted in Fig. 1c, clearly showing broader resonances, but more intense cross peaks caused by a more efficient SD, as expected at the lower MAS frequency. The previously reported observation of negative cross peaks due to a coherent third-order contribution requires that the resonance frequencies, ω_i, of the four involved spins k, l, m and n fulfil the condition¹⁸

(ω_k − ω_l) + (ω_m − ω_n) ∼ 0. (1)

In our case, the condition is indeed fulfilled for the quadruple of spins comprising the COOH (16.8 ppm), PO₃OH (12.7 ppm), NH₃⁺ (8.3 ppm) and CH₂^a (4.2 ppm) protons. In this case, the differences of chemical shifts amount to ω_COOH − ω_PO3OH = 4.1 ppm and ω_NH3 − ω_CH2 = 4.1 ppm. For further possible four-spin combinations see Table S1 (ESI†). Therefore, negative cross peaks for the CH₂^a/COOH and CH₂^a/PO₃OH pairs are observed, whereas the one between CH₂^a/NH₃ still remains positive, most likely caused by an insufficient suppression of the second-order SD term due to the smaller chemical-shift difference. The observations are thus very similar to the ones made on histidine·HCl·H₂O.¹⁸ In contrast and as expected, such negative cross peaks remain absent in a radiofrequency-driven recoupling (RFDR)³³ spectrum recorded at 100 kHz MAS (Fig. 1d), in which instead such cross peaks possess the same sign as the diagonal (for comparisons of SD-based and RFDR experiments at fast MAS see for instance ref. 34).

Fig. 1 Negative cross peaks in SD-based spectra based on a coherent SD mechanism. (a) Chemical structure of O-phospho-L-serine 1 together with the hydrogen bond network present in the crystal structure (CCDC access code 1441044). ¹H–¹H SD spectra of O-phospho-L-serine 1 recorded at (b) 100 kHz MAS and (c) 60 kHz MAS with a mixing time of 50 ms. Both spectra have been recorded at 16.4 T. Positive contour levels are shown in blue and red, negative ones in cyan. (d) ¹H–¹H RFDR spectrum of 1 recorded at 100 kHz MAS and 16.4 T. Note that in the ¹H–¹H RFDR spectrum, the cyan peaks are caused by signal truncation in the indirect dimension.

Negative cross peaks in ¹H–¹H SD-based spectra involving methyl groups.

We recently investigated a calixarene–lanthanide complex, in which we also observed negative cross peaks in spin-diffusion spectra.¹¹ In this case, the negative cross peaks involved methyl groups and deshielded aromatic as well as imino protons. The observation that (i) methyl groups are involved and (ii) the ¹H chemical-shift differences between the methyl group and proton pairs for which such cross peaks have been observed is rather large (>4.6 ppm), led us to study their origin in order to disentangle the role of coherent and incoherent cross-relaxation (NOE-type) contributions to the observed peaks.

We thus investigated five additional examples of small organic molecules, in which methyl group and deshielded protons could potentially lead to negative cross peaks in ¹H–¹H SD-based spectra. In addition to the previously mentioned O-phospho-L-serine 1, we studied racemic α-trifluoromethyl lactic acid (in the following denoted as α-TLA) 2, a cyclic sulfoximine (specifically, 2-methyl-3H-2λ⁴-benzo[c]isothiazole 2-oxide,³⁵ in the following denoted as sulfoximine 3, recently already studied by solid-state NMR³⁶), a dimeric (cymene)ruthenium dichloride complex 4, a bora[4]pyramidane 5,³⁷ as well as durene 6. The chemical structures of these five compounds are shown in Fig. 2 together with the 1D ¹H MAS spectra recorded at 60 kHz spinning frequency and 16.4 T as well as their resonance assignments (we refer to Fig. S1 (ESI†) for the nomenclature used in the resonance assignments. For MAS-dependent ¹H spectra of 1 see Fig. S2, ESI†). Table 1 summarizes the ¹H chemical-shift differences and averaged shortest crystallographic distances between the methyl-group protons and the high-frequency shifted protons involved in the negative cross peaks.

Fig. 2 1D ¹H MAS spectra of the compounds investigated in this study. (a) O-phospho-L-serine 1, (b) racemic α-TLA 2, (c) sulfoximine 3, (d) RuCl₂-cymene 4, (e) bora[4]pyramidane 5 and (f) durene 6. The assignment of the ¹H resonances is reported for each system. For the nomenclature adopted in the assignment of 3 and 4 see Fig. S2 (ESI†). All spectra were recorded at 60 kHz MAS and 16.4 T static magnetic-field strength. + denotes a minor impurity.

Table 1 Chemical-shift differences between methyl group protons and deshielded protons, for which negative cross peaks in SD-based spectra have been observed (2, 3 and 4) or have been expected (5 and 6). Reported are also the (averaged) shortest CH₃–H distances (^a: intermolecular distances) determined from the published crystal structures (CCDC access codes: 2 666328, 3 2264046,³⁸4 1895287, 5 2108769 and 6 1146814) and the resulting estimate for the ¹H–¹H dipolar couplings (calculated with R: NMR Tool³⁹)

Compound	Δδ(CH3⋯H)/ppm	Crystallographic d(CH3⋯H)/Å	^1H dipolar coupling/kHz
α-TLA (2)	10	3.33^a	3.3
Sulfoximine (3)	4.7	Harom (4) = 3.84^a	Harom (4) = 2.1
		Harom (7) = 3.66^a	Harom (7) = 2.5
RuCl2-cymene (4)	5.7	CH3^b⋯Harom^a (5) = 4.87	Harom^a (5) = 1.0
		CH3^b⋯Harom^a (9) = 4.99	Harom^a (9) = 1.0
Bora[4]pyramidane (5)	5.7	3.28	3.4
Durene (6)	5.3	2.97	4.6

---

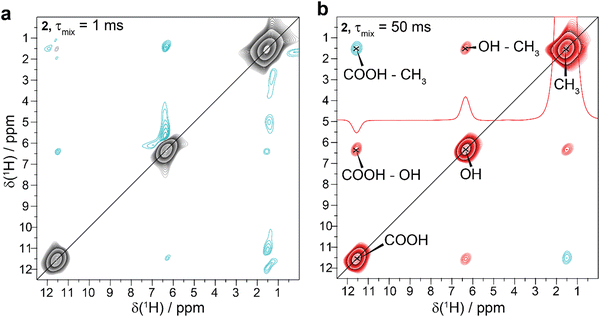
We measured 2D ¹H–¹H SD spectra with variable mixing times of all these compounds to determine whether the spectra show negative cross peaks. Fig. 3b and 4 show representative SD spectra (τ_mix = 50 ms) for the samples 2 to 6. Negative cross peaks involving methyl groups are present for racemic α-TLA 2 (Fig. 3), sulfoximine 3 (asymmetric with respect to the diagonal caused by non-equilibrium initial magnetization conditions, Fig. 4a and Fig. S3, ESI†) and RuCl₂-cymene 4 (originating from the isolated CH₃^b group, Fig. 4b). All of these substances are characterized by the fact that they have additional resonances in between the methyl group and the downfield shifted resonances that show the negative cross peaks. In these cases, the mentioned compensated isotropic chemical-shift condition for a coherent third-order SD process is approximately fulfilled, although broadened possibly by the rotation of the involved methyl groups leading to more efficient chemical-shift compensation (see Table S1, ESI,†vide infra). For a more detailed discussion of the spectra of 2 and 3 see ESI.†

Fig. 3 Negative cross peaks in α-TLA. 2D ¹H–¹H SD spectra of racemic α-TLA 2 recorded with (a) 1 ms and (b) 50 ms mixing times. In panel (b) also the 1D trace along the F2 dimension of the 2D SD spectrum is reported. All spectra have been recorded at 60 kHz MAS frequency and at 16.4 T static magnetic-field strength. Note in panel (a) that the spectrum shows FID truncation in the indirect dimension.

Fig. 4 The presence and absence of negative cross peaks in 2D ¹H–¹H SD spectra. 2D ¹H–¹H SD spectra recorded with 50 ms mixing time for (a) 3, (b) 4, (c) 5 and (d) 6. All spectra have been recorded at 60 kHz MAS frequency and 16.4 T static magnetic-field strength. Note in panel c that the spectrum shows FID truncation in the indirect dimension for the methyl resonance. + denotes a minor impurity.

Positive cross-peaks in case of two chemically-distinct types of proton spins

For two of the investigated systems, bora[4]pyramidane 5 (Fig. 4c) and durene 6 (Fig. 4d), no negative cross peaks could be observed. These compounds are characterized by the absence of any additional resonances between the methyl group and the downfield-shifted resonances that could allow for chemical-shift compensation required for the third-order spin diffusion. Also, increasing the mixing time does not result in the observation of negative cross peaks for these two compounds. Since the resonance condition for a coherent SD mechanism can obviously not be fulfilled in these examples comprising only two chemically-distinct types of proton spins, possible incoherent effects are too small to lead to negative cross peaks in the spectrum.

Considering our findings altogether, it is apparent that for the observation of negative cross peaks for the samples investigated here the following qualitative characteristics are favourable: (i) a methyl group at low-ppm values, (ii) deshielded proton resonances to slow down second-order SD, (iii) two additional “mediating” spins with a chemical-shift value ranging in-between the two mentioned groups allowing for chemical-shift compensation within a quadruple of spins (resonance conditions required to observe third-order SD).

SD build-up behaviour accessed by mixing-time depended 2D spectra

Fig. 5 shows the dependence of the cross-peak intensity on the mixing time in the SD-based spectra for the negative cross peaks. The absolute values are normalized with respect to their relative CH₃ diagonal peaks at τ_mix = 1 ms. Negative intensities progressively become more negative for incrementing the mixing time up to τ_mix = 50 ms for α-TLA 2 (for further analysed peaks see Fig. S4, ESI†), and RuCl₂-cymene 4 (for a 2D ¹H–¹H SD spectrum see Fig. S5, ESI†) and reach a negative maximum at τ_mix = 50 ms for sulfoximine 3. Upon further increase in the mixing time, we observe a slow decrease of the negative peak intensity for sulfoximine towards zero, which however does not become positive even for long mixing times (see Fig. S6, ESI† for the spectrum with τ_mix = 1.5 s). Similar observations can be made for α-TLA 2 (Fig. S7a–c, ESI†), for which the cross peaks remain negative up to τ_mix = 1 s and disappear by a further increase in the mixing time to 2.5 s (mixing time length approaching the timescale of longitudinal relaxation T₁ of α-TLA). On the contrary, while a negative-profile trend is also observed for RuCl₂-cymene, the cross peak becomes positive at long mixing times (see Fig. S6b, ESI† for the spectrum with τ_mix = 800 ms).

Fig. 5 Mixing time dependence of negative cross peak (normalized with respect to the methyl-group diagonal peak at t_mix = 1 ms) integrated intensities in ¹H–¹H SD spectra for α-TLA 2 (a), sulfoximine 3 (b) and RuCl₂-cymene 4 (c) at 60 kHz MAS frequency and 16.4 T static magnetic-field strength.

The observation that negative cross peaks remain negative (sulfoximine and α-TLA) or become positive (RuCl₂-cymene) at long mixing times can be explained with relayed second-order SD polarization transfer that can either fully or only partially compensate the direct third-order SD process depending on the relative magnitude and efficiency of the two processes. One open question here is whether negative NOE could also influence the polarization transfer in such systems. We will address this discussion through numerical and analytical simulations in the following.

Analytical and numerical calculations of incoherent effects on SD spectra

To assess the contribution of NOE transfer in addition to third-order SD, we have performed analytical and numerical simulations of the polarization transfer under a stochastic methyl rotation. To analytically calculate the cross relaxation, we assume an AX₃ spin system with four protons where the three chemically-equivalent protons representing the methyl group undergo fast hopping between the three equivalent sites. Longitudinal auto and cross relaxation-rate constants can be found in the literature⁴⁰ and are given below.The spectral-density functions and can be calculated based on the geometry of the spin system and the jump model. We have implemented such an analytical calculation of the three relaxation-rate constants using the structure of sulfomixine 3, where the positions of the four protons were obtained from a crystal structure.³⁸ The closest distance between the separate proton (aromatic H5/6 proton) and a proton of the methyl group was found to be at 2.7 Å. The closest aromatic H4/7 proton has a slightly larger distance of about 3 Å to the nearest proton in the methyl group. The proton coordinates used for the calculations as well as the analytical expressions for the spectral-density functions can be found in the ESI.† We can then calculate the three relaxation-rate constants as a function of the three-site jump correlation time for the experimentally-used proton Larmor frequency of 700 MHz which is shown in Fig. 6.

Fig. 6 (a) Plot of the analytically calculated relaxation-rate constants (blue, auto relaxation of H, eqn (2)) and (orange, cross relaxation H₃ to H, eqn (4)), (b) (blue, auto relaxation of H₃, eqn (3)), as a function of the three-site jump correlation time in sulfoximine 3 at a proton Larmor frequency of 700 MHz. The cross relaxation-rate constant changes sign from negative to positive around τ_j ≈ 8.5 × 10⁻⁹ s. The positive maximum of the cross relaxation-rate constant is reached around τ_j ≈ 8.7 × 10⁻¹¹ s with a value of about 0.02 s⁻¹.

As expected, the cross-relaxation rate constant changes sign around a correlation time of τ_j ≈ 8.5 × 10⁻⁹ s leading to negative polarization transfer for shorter correlation times. The maximum of the cross-relaxation rate constant is reached around τ_j ≈ 8.7 × 10⁻¹¹ s with a value of about 0.02 s⁻¹. Fig. 7 shows the magnitude and the time scale of the build-up of the cross-relaxed magnetization for several correlation times around the maximum value of the rate constant.

Fig. 7 Calculated cross relaxation from the methyl-group protons to the aromatic H_5/6 proton for different values of the jump correlation time, τ_j of the methyl protons in sulfoximine 3. The cross relaxed magnetization is as expected negative with a build-up that happens on the order of several 100 ms. The level reached is approximately 0.3% of the initial methyl-group intensity.

The cross-relaxed magnetization builds up on a time scale of several 100 ms and reaches a negative maximum of about 0.3% of the initial methyl-group magnetization. This is much lower and slower than the experimentally observed build-up of the negative magnetization (see Fig. 5).

To double check the analytical calculations, we also performed numerical simulations of a four-spin system with the same geometry as used for the analytical calculations including again the three methyl protons and the closest aromatic proton. A three-site exchange model was applied to the three protons of the methyl group to simulate the relaxation process in Liouville space. The complete laboratory-frame Hamiltonian including the Zeeman interaction and all terms of the not truncated dipolar Hamiltonian was included in the Hamiltonian as well as an exchange process that describes the stochastic exchange event. Such simulations contain all possible relaxation pathways that are allowed under dipolar auto- and cross-correlated relaxation in a four-spin system. For more simulation details, see the ESI.† The result of such a simulation is shown in Fig. 8 (blue curve).

Fig. 8 Numerically simulated polarization transfer from the methyl group to the aromatic H_5/6 proton. Blue curve: cross relaxation from the methyl-group protons to the aromatic H_5/6 proton of sulfoximine 3 in a four-spin system (three methyl protons undergoing stochastic jumps and one aromatic proton) for a methyl jump correlation time of τ_j = 8.7 × 10⁻¹¹ s. The build-up of the negative cross-relaxed magnetization happens again as in the analytical calculations on the time scale of several 100 ms. Orange line: Third-order spin diffusion and cross relaxation from the methyl group to the aromatic H_5/6 proton of sulfoximine 3 in a six-spin system (three methyl protons undergoing stochastic jumps and one aromatic proton and two methylene protons) for a methyl jump correlation time of τ_j = 8.7 × 10⁻¹¹ s. The build-up of the negative polarization happens on a much faster time scale (10 ms) and is much higher than in the case of cross relaxation.

The cross relaxation happens again on the time scale of several 100 ms and the magnitude of the cross-relaxed magnetization is on the order of 0.2% which agrees well with the analytical calculations. The relaxation time of the protons was T₁ = 2.85 s which is slightly shorter than the T₁ found in the analytical calculations which was about 3 s (see Fig. 6). Experimentally, a relaxation time of the methyl protons of 3.5 s was found. This could be due to different relaxation pathways allowed in this simulation, small differences in the proton–proton distances, a different jump-rate correlation time, or a more complex dynamic process of the methyl group. A faster build-up in such simulations can only be achieved by decreasing the distance between the methyl-group and the aromatic protons substantially, to unrealistic values of 1.5 Å or less (see Fig. S8, ESI† for such numerical simulations assuming different geometries and distances between the methyl and aromatic protons). Alternatively, relayed cross relaxation through an intermediate proton could be possible, but it seems unlikely that this would happen on such a much faster time scale.

There are, however, clear differences between the analytical and the numerical simulation. In the numerical simulations, there is an initial very fast positive polarization transfer between the methyl and the additional proton. The source of this transfer is not yet understood. There is also a stronger damping of the transferred polarization at longer times in the numerical simulation and differences in the numerical values between the analytical and numerical simulations. They can, most likely, be attributed to the differences in describing the relaxation in the two approaches. While the analytical calculations are limited to two magnetization modes and assume that powder averaging of the rate constants is allowed, the analytical calculations take into account all magnetization modes in an AX₃ spin system that are allowed under dipolar auto-correlated and cross-correlated relaxation⁴⁰ and do a proper powder averaging of the density operator instead of the rate constant. We believe that these differences can explain the differences between the two simulation methods. However, the qualitative agreement is quite good and shows that cross relaxation between the methyl group and the aromatic proton in sulfomixine is much slower than experimentally observed and leads to much slower transferred magnetization.

The orange curve in Fig. 8 shows the results of a simulation in a six-spin system including the three methyl protons, the H_5/6 aromatic proton and the two methylene protons with a jump correlation time of τ_j = 8.7 × 10⁻¹¹ s. The protons were selected such that one of the distances between the methylene and the methyl and the aromatic proton is as short as possible (about 2.7 Å). The chemical shifts were set such that the third-order resonance condition for spin diffusion was fulfilled (see the ESI† for simulation details). One can clearly see that the build-up of the negative polarization happens on a much faster time scale of 10 ms and reaches much larger values than the polarization transfer by cross relaxation only. Since this result is much closer to the experimental results, we conclude that the negative polarization transfer from the methyl groups to the aromatic protons is mostly determined by the third-order spin diffusion process. The simulations however give significantly lower transfer minima than the experiment. This is most likely due to the possibility of many polarization transfer pathways by a subset of six spins in the experiment while in the simulation we have only selected one such subset.

Conclusions

Negative cross peaks in spin-diffusion spectra can originate from either coherent (third-order spin diffusion) or incoherent (cross-relaxation based) polarization transfer. We have demonstrated that it is possible to disentangle the two possible polarization-transfer mechanisms determining the observation of negative cross peaks in 2D ¹H–¹H SD-based spectra. We show using several small organic molecules containing fast rotating methyl groups, a collection of possible key factors for the manifestation of third-order SD Hamiltonian terms as negative cross peaks in SD spectra recorded at fast MAS frequencies (60 kHz). While both polarization-transfer pathways are possible and lead to negative cross peaks, our study shows that for the samples studied here, negative cross can be explained best by the dominating coherent effects (which experimentally are the most probable observation), caused by third- order terms in the NMR Hamiltonian, but not from NOE effects typically explored by solution-state NMR. Analytical and numerical simulations show, that the experimentally-observed fast build-up of negative cross peak intensity is in better agreement with coherent effects, with potentially minor additional contributions from NOE-type polarization transfer. A better separation of the two effects could be achieved using temperature-dependent experiment. They are, however, not easily implemented at fast MAS frequencies due to the limited temperature range of commercial probes. We note that this behaviour could be further explored in multidimensional pulse sequences comprising SD-steps, such as homonuclear 3D HHH experiment, to follow the polarization of fast rotating methyl groups, for instance also in proteins, to simplify their resonance assignment. We expect similar observations for ¹⁹F-detected NMR experiments at fast MAS, in which fast rotating –CF₃ groups should also lead to analogue effects, with the larger chemical-shift dispersion for ¹⁹F slowing down second-order spin diffusion more efficiently than observed for protons. This is currently further investigated in our laboratories.

Materials and methods

Sample preparation

O-Phospho-L-serine 1, α-TLA 2, RuCl₂-cymene 4 and durene 6 are commercially available and have been purchased from Afla Aesar (α-TLA) and Sigma Aldrich (all others). Sulfoximine 3 has been prepared as reported in ref. 35. Details of the synthesis of the bora[4]pyramidane 5 are given in ref. 37.

Solid-state NMR

Proton-detected solid-state NMR spectra of 1 were acquired at 16.4 T static magnetic-field strength on an 0.7 mm triple-resonance MAS probe (Bruker Biospin). The MAS frequency for the 2D ¹H–¹H spectra was set to 100 kHz, while for the series of 1D ¹H spectra was set to 42 kHz, 50 kHz, 60 kHz, 70 kHz, 80 kHz, 90 kHz and 100 kHz. All other proton-detected spectra have been recorded on a Bruker 1.3 mm double-resonance MAS probe (Bruker Biospin). The MAS frequency for the 2D ¹H–¹H spectra was set to 50 kHz and 60 kHz, while the 1D ¹H spectra were acquired at 60 kHz MAS (see Table S3, ESI†). For the acquisition of the 2D SD spectra of α-TLA 2 a NOESY three-pulse sequence²⁴ with final additional refocusing echo was employed in order to flatten the baseline and improve peak fitting accuracy.

All spectra were processed with the software topspin (versions 3.6.4 and 4.1.3, Bruker Biospin). 2D ¹H–¹H spectra were processed with a shifted (α-TLA 2 and bora[4]pyramidane 5: 2.0, O-phospho-L-serine 1: 2.5, all others: 3.0) squared cosine apodization function and were cut in the direct dimension to 10 ms. For all 2D ¹H–¹H spectra, zero filling was applied in the indirect dimension up to double the amount of points.

Spectra of 1 were referenced setting the CH_2b resonance to 4 ppm, according to literature values.³² All other experiments were referenced relative to the DSS scale using an external calibration on adamantane (methylene resonance set to 40.49 ppm) recorded in the same probe directly before the measurements. All measurements were carried out with temperature control (temperatures determined from an external calibration on KBr). For the target samples temperatures during acquisition and further experimental parameters we refer to Table S3 (ESI†).

Analysis of the spectra was carried out with the software CcpNmr (version 2.4.2).⁴¹

Data analysis

Internuclear distances for the samples in Table 1 were extracted from the respective crystal structures using the software Diamond.⁴² The values for the crystallographic distances (d(CH₃⋯H)/Å) reported in Table 1 represent the averaged shortest CH₃⋯H intermolecular distances. Dipolar coupling values were calculated with the program R.³⁹

Peak fitting and intensities

In order to extract the integrated intensities for sulfoximine 3, the 2D SD spectra were processed without apodization function and zero filling was applied in both dimensions. The spectra were then loaded in Matlab and the fits calculated using a home-written script performing peak fitting with a Voigt profile. In the case of α-TLA 2 and RuCl₂-cymene 4 the peak intensities have been extracted with the automatic peak-picking routine in CcpNMR and plotted after normalization with respect to the CH₃ peak at short mixing time.

Spin-dynamics simulations

Numerical simulations of a four- to six-spin system including a three-site jump dynamics on the methyl protons was implemented in the spin-simulation environment GAMMA⁴³ using Liouville space simulations and exchange among the three methyl protons. More details can be found in the ESI.†

Analytical calculations of the auto and cross relaxation between the methyl protons and the remote proton were implemented in Mathematica using a three-site jump model as well as the geometry of sulfoximine, and calculating the spectral-density function for such a model. More details can be found in the ESI.†

Author contributions

E. B., D. J. L., N. T. and T. W. have recorded the solid-state NMR spectra. M. E. has performed analytical calculations and simulations. All authors have analysed and interpreted the data and contributed to the writing of the manuscript. M. E. and T. W. have designed and supervised the research.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

T. W. acknowledges support from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation, project number 455240421 and Heisenberg fellowship, project number 455238107) and the Max Planck Society. T. W. and C. B. appreciate funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – Exzellenzcluster 2186 “The Fuel Science Center”. We are thankful to BSc Leeroy Hendrickx for the support with preliminary measurements on sulfoximine. We thank Prof. Dr Gerhard Erker, Dr Gerald Kehr and Dr Qiu Sun (all Westfälische Wilhelms-Universität Münster, Germany) for providing the bora[4]pyramidane sample and Dr Alexis Bordet (Max Planck Institute for Chemical Energy Conversion) for providing a sample of RuCl₂-cymene. The research stay of D. J. L. at RWTH Aachen University was supported by a short-term research exchange grant from the IDEA League. Open Access funding provided by the Max Planck Society.

References

1. T. Le Marchand, T. Schubeis, M. Bonaccorsi, P. Paluch, D. Lalli, A. J. Pell, L. B. Andreas, K. Jaudzems, J. Stanek and G. Pintacuda, Chem. Rev., 2022, 122, 9943–10018.
2. X. Lu, Y. Tsutsumi, C. Huang, W. Xu, S. R. Byrn, A. C. Templeton, A. V. Buevich, J.-P. Amoureux and Y. Su, Phys. Chem. Chem. Phys., 2020, 22, 13160–13170; C. M. Quinn, R. Zadorozhnyi, J. Struppe, I. V. Sergeyev, A. M. Gronenborn and T. Polenova, Anal. Chem., 2021, 93, 13029–13037.
3. Y. Nishiyama, G. Hou, V. Agarwal, Y. Su and A. Ramamoorthy, Chem. Rev., 2023, 123, 918–988.
4. D. A. Hirsh, A. V. Wijesekara, S. L. Carnahan, I. Hung, J. W. Lubach, K. Nagapudi and A. J. Rossini, Mol. Pharm., 2019, 16, 3121–3132.
5. A. Samoson, J. Magn. Reson., 2019, 306, 167–172.
6. M. Schledorn, A. A. Malär, A. Torosyan, S. Penzel, D. Klose, A. Oss, M. L. Org, S. Wang, L. Lecoq, R. Cadalbert, A. Samoson, A. Böckmann and B. H. Meier, ChemBioChem, 2020, 21, 2540–2548.
7. E. C.-Y. Yuan, S.-J. Huang, H.-C. Huang, J. Sinkkonen, A. Oss, M.-L. Org, A. Samoson, H.-C. Tai and J. C. C. Chan, Chem. Commun., 2021, 57, 4110–4113.
8. E. Brunner, D. Freude, B. C. Gerstein and H. Pfeifer, J. Magn. Reson., 1990, 90, 90–99; U. Sternberg, R. Witter, I. Kuprov, J. M. Lamley, A. Oss, J. R. Lewandowski and A. Samoson, J. Magn. Reson., 2018, 291, 32–39; I. Schnell and H. W. Spiess, J. Magn. Reson., 2001, 151, 153–227; V. E. Zorin, S. P. Brown and P. Hodgkinson, J. Chem. Phys., 2006, 125, 144508.
9. P. Wikus, W. Frantz, R. Kümmerle and P. Vonlanthen, Supercond. Sci. Technol., 2022, 35, 033001.
10. E. Nimerovsky, K. T. Movellan, X. C. Zhang, M. C. Förster, E. Najbauer, K. Xue, R. Dervişoǧlu, K. Giller, C. Griesinger, S. Becker and L. B. Andreas, Biomolecules, 2021, 11, 752; M. Callon, A. A. Malär, S. Pfister, V. Rimal, M. E. Weber, T. Wiegand, J. Zehnder, M. Chavez, R. Cadalbert, R. Deb, A. Dapp, M. L. Fogeron, A. Hunkeler, L. Lecoq, A. Torosyan, D. Zyla, R. Glockshuber, S. Jonas, M. Nassal, M. Ernst, A. Böckmann and B. H. Meier, J. Biomol. NMR, 2021, 75, 255–272.
11. E. Bartalucci, A. A. Malar, A. Mehnert, J. B. Kleine Buning, L. Gunzel, M. Icker, M. Borner, C. Wiebeler, B. H. Meier, S. Grimme, B. Kersting and T. Wiegand, Angew. Chem., Int. Ed., 2023, 62, e202217725.
12. N. Bloembergen, Physica, 1949, 15, 386–426.
13. A. Abragam, The Principles of Nuclear Magnetism, Clarendon Press Oxford, 1961.
14. D. Suter and R. R. Ernst, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 25, 6038–6041.
15. P. Robyr, B. H. Meier and R. R. Ernst, Chem. Phys. Lett., 1989, 162, 417–423.
16. M. Ernst and B. H. Meier, in Studies in Physical and Theoretical Chemistry, ed. I. Ando and T. Asakura, Elsevier, 1998, vol. 84, pp. 83–121.
17. B. H. Meier and A. Böckmann, in Protein Aggregation: Methods and Protocols, ed. A. S. Cieplak, Springer US, New York, NY, 2023, pp. 53–62 DOI:10.1007/978-1-0716-2597-2_5.
18. V. Agarwal, J. Magn. Reson., 2020, 311, 106661.
19. B. Elena and L. Emsley, J. Am. Chem. Soc., 2005, 127, 9140–9146; D. L. Bryce, IUCrJ, 2017, 4, 350–359; T. Kobayashi, K. Mao, P. Paluch, A. Nowak-Król, J. Sniechowska, Y. Nishiyama, D. T. Gryko, M. J. Potrzebowski and M. Pruski, Angew. Chem., Int. Ed., 2013, 52, 14108–14111.
20. P. Hodgkinson, Prog. Nucl. Magn. Reson. Spectrosc., 2020, 118–119, 10–53.
21. G. R. Goward, M. F. H. Schuster, D. Sebastiani, I. Schnell and H. W. Spiess, J. Phys. Chem. B, 2002, 106, 9322–9334; G. N. Reddy, A. Huqi, D. Iuga, S. Sakurai, A. Marsh, J. T. Davis, S. Masiero and S. P. Brown, Chem. – Eur. J., 2017, 23, 2315–2322.
22. K. Takegoshi, S. Nakamura and T. Terao, Chem. Phys. Lett., 2001, 344, 631–637; K. Takegoshi, S. Nakamura and T. Terao, Chem. Phys. Lett., 1999, 307, 295–302.
23. A. Lange, S. Luca and M. Baldus, J. Am. Chem. Soc., 2002, 124, 9704–9705; T. Wiegand, M. Schledorn, A. A. Malär, R. Cadalbert, A. Däpp, L. Terradot, B. H. Meier and A. Böckmann, ChemBioChem, 2020, 21, 324–330.
24. S. Macura and R. R. Ernst, Mol. Phys., 2002, 100, 135–147.
25. D. Neuhaus and M. P. Williamson, The Nuclear Overhauser Effect in Structural and Conformational Analysis, Wiley-VCH, 2000.
26. W. A. Anderson and R. Freeman, J. Chem. Phys., 1962, 37, 85–103; D. Neuhaus and M. P. Williamson, The Nuclear Overhauser Effect in Structural and Conformational Analysis, VCH, 1989.
27. B. P. Tatman, W. T. Franks, S. P. Brown and J. R. Lewandowski, J. Chem. Phys., 2023, 158, 184201.
28. S. E. Ashbrook, N. G. Dowell, I. Prokes and S. Wimperis, J. Am. Chem. Soc., 2006, 128, 6782–6783.
29. A. Findlay and R. K. Harris, J. Magn. Reson., 1990, 87, 605–609; J. L. White and P. Mirau, Macromolecules, 1993, 26, 3049–3054; J. L. White, Solid State Nucl. Magn. Reson., 1997, 10, 79–88; J. S. Higgins, A. H. Hodgson and R. V. Law, J. Mol. Struct., 2002, 602–603, 505–510; J. Cui, J. Li, X. Peng and R. Fu, J. Magn. Reson., 2017, 284, 73–79; J. M. del Amo, V. Agarwal, R. Sarkar, J. Porter, S. Asami, M. Rübbelke, U. Fink, Y. Xue, O. F. Lange and B. Reif, J. Biomol. NMR, 2014, 59, 241–249; D. Daube, V. Aladin, J. Heiliger, J. J. Wittmann, D. Barthelmes, C. Bengs, H. Schwalbe and B. Corzilius, J. Am. Chem. Soc., 2016, 138, 16572–16575.
30. L.-S. Du, M. H. Levitt and C. P. Grey, J. Magn. Reson., 1999, 140, 242–249.
31. A. Iuga and E. Brunner, Magn. Reson. Chem., 2004, 42, 369–372; L. Duma, D. Abergel, P. Tekely and G. Bodenhausen, Chem. Commun., 2008, 2361–2363,  10.1039/B801154K.
32. A. A. Malär, L. A. Völker, R. Cadalbert, L. Lecoq, M. Ernst, A. Böckmann, B. H. Meier and T. Wiegand, J. Phys. Chem. B, 2021, 125, 6222–6230.
33. A. E. Bennett, R. G. Griffin, J. H. Ok and S. Vega, J. Chem. Phys., 1992, 96, 8624–8627.
34. M. K. Pandey, S. Vivekanandan, K. Yamamoto, S. Im, L. Waskell and A. Ramamoorthy, J. Magn. Reson., 2014, 242, 169–179; M. K. Pandey, S. Vivekanandan, K. Yamamoto, S. Im, L. Waskell and A. Ramamoorthy, J. Magn. Reson., 2014, 245, 178; A. Ramamoorthy and J. Xu, J. Phys. Chem. B, 2013, 117, 6693–6700.
35. P. Lamers, L. Buglioni, S. Koschmieder, N. Chatain and C. Bolm, Adv. Synth. Catal., 2016, 358, 3649–3653.
36. E. Bartalucci, C. Schumacher, L. Hendrickx, F. Puccetti, I. d'Anciaes Almeida Silva, R. Dervisoglu, R. Puttreddy, C. Bolm and T. Wiegand, Chem. – Eur. J., 2023, 29, e202203466.
37. Q. Sun, C. G. Daniliuc, X. Yu, C. Mück-Lichtenfeld, G. Kehr and G. Erker, J. Am. Chem. Soc., 2022, 144, 7815–7821.
38. R. R. Puttreddy, K.-N. Truong, K. Rissanen and C. Bolm, CCDC 2264046: Experimental Crystal Structure Determination, 2023 DOI:10.5517/ccdc.csd.cc2fzxr3.
39. K. Eichele, WSolids1 vers. 1.21.7, Universität Tübingen, 2021.
40. L. G. Werbelow and D. M. Grant, in Advances in Magnetic and Optical Resonance, ed. J. S. Waugh, Academic Press, 1977, vol. 9, pp. 189–299.
41. W. F. Vranken, W. Boucher, T. J. Stevens, R. H. Fogh, A. Pajon, M. Llinas, E. L. Ulrich, J. L. Markley, J. Ionides and E. D. Laue, Proteins: Structure, Function, and Bioinformatics, 2005, 59, 687–696; T. Stevens, R. Fogh, W. Boucher, V. Higman, F. Eisenmenger, B. Bardiaux, B.-J. van Rossum, H. Oschkinat and E. Laue, J. Biomol. NMR, 2011, 51, 437–447; R. Fogh, J. Ionides, E. Ulrich, W. Boucher, W. Vranken, J. P. Linge, M. Habeck, W. Rieping, T. N. Bhat, J. Westbrook, K. Henrick, G. Gilliland, H. Berman, J. Thornton, M. Nilges, J. Markley and E. Laue, Nat. Struct. Mol. Biol., 2002, 9, 416–418.
42. Diamond 3.2-Crystal and Molecular Structure Visualization, demonstration version, Crystal Impact.
43. S. A. Smith, T. O. Levante, B. H. Meier and R. R. Ernst, J. Magn. Reson. A, 1994, 106, 75–105.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02323k

---