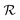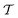Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Colossal room-temperature electrocaloric strength aided by hydrostatic pressure in lead-free multiferroic solid solutions
César
Menéndez
a,
Riccardo
Rurali
b and
Claudio
Cazorla
 *c
*c
aSchool of Chemistry, The University of Sydney, NSW 2006, Australia
bInstitut de Ciència de Materials de Barcelona, ICMAB–CSIC, Campus UAB, 08193 Bellaterra, Spain
cDepartament de Física, Universitat Politècnica de Catalunya, 08034 Barcelona, Spain. E-mail: claudio.cazorla@upc.edu
First published on 12th June 2023
Abstract
Solid-state cooling applications based on electrocaloric (EC) effects are particularly promising from a technological point of view due to their downsize scalability and natural implementation in circuitry. However, EC effects typically involve materials that contain toxic substances and require relatively large electric fields (∼100–1000 kV cm−1) that cause fateful leakage current and dielectric loss problems. Here, we propose a possible solution to these practical issues that consists of concertedly applying hydrostatic pressure and electric fields on lead-free multiferroic materials. We theoretically demonstrate this strategy by performing first-principles simulations on supertetragonal BiFe1−xCoxO3 solid solutions (BFCO). It is shown that hydrostatic pressure, besides adjusting the occurrence of EC effects to near room temperature, can reduce enormously the intensity of driving electric fields. For pressurized BFCO, we estimate a colossal room-temperature EC strength, defined as the ratio of the adiabatic EC temperature change by an applied electric field, of ∼1 K cm kV−1, a value that is several orders of magnitude larger than those routinely measured in uncompressed ferroelectrics.
One of the limiting factors of modern microelectronic devices is their tremendous heat dissipation density, which needs to be mitigated through cooling in order to ensure appropriate performance. Current refrigeration technologies, however, rely on compression cycles of environmentally harmful gases and cannot be scaled down to microchip dimensions. Electrocaloric (EC) cooling is a highly promising solid-state refrigeration technology for the thermal management of chips and microcircuitry owing to its high efficiency, environmental friendliness, and easy miniaturization.1 EC refrigeration exploits the reversible thermal change of ferroelectric materials resulting from phase transitions induced by external electric field variations. A large EC isothermal entropy change, ΔSEC, of ∼10 J K−1 kg−1 and an adiabatic temperature change, ΔTEC, of ∼1–10 K have been measured in ferroelectric materials like BaTiO3,2,3 Pb(Zr,Ti)O34 and HfO2,5 to cite few examples.
Nonetheless, unfortunately, the largest EC effects observed to date normally involve materials that contain toxic substances like lead and require large electric fields that are energetically costly and produce adverse leakage currents and dielectric losses.6–8 Recently, several materials design strategies have been proposed to overcome these common EC problems. For instance, by exploiting electrostatic coupling and interface effects in lead-free ferroelectric relaxor heterostructures, an unprecedentedly large EC adiabatic temperature shift of ≈23 K has been realized near room temperature for moderate electric bias (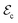 ∼ 100 kV cm−1).9 Nevertheless, the magnitude of such EC effects can be strongly influenced by the specific details of the heterostructure synthesis process and thus in practice ΔTEC may strongly fluctuate from one sample to another. Another recent EC advancement has been reported for the layered hybrid perovskite ferroelectric [(CH3)2CHCH2NH3]2PbCl4,10 in which a sharp first-order ferroelectric phase transition associated with a high-entropy change occurs instead of the continuous phase transformation associated with a low-entropy change that is characteristic of inorganic ferroelectric perovskites.11 In this case, a giant ΔTEC of 11.1 K has been measured at room temperature for a small electric field of 29.7 kV cm−1. However, the implicated material still contains lead and the degree of reversibility associated with such giant EC effects appears to be quite limited.
∼ 100 kV cm−1).9 Nevertheless, the magnitude of such EC effects can be strongly influenced by the specific details of the heterostructure synthesis process and thus in practice ΔTEC may strongly fluctuate from one sample to another. Another recent EC advancement has been reported for the layered hybrid perovskite ferroelectric [(CH3)2CHCH2NH3]2PbCl4,10 in which a sharp first-order ferroelectric phase transition associated with a high-entropy change occurs instead of the continuous phase transformation associated with a low-entropy change that is characteristic of inorganic ferroelectric perovskites.11 In this case, a giant ΔTEC of 11.1 K has been measured at room temperature for a small electric field of 29.7 kV cm−1. However, the implicated material still contains lead and the degree of reversibility associated with such giant EC effects appears to be quite limited.
In this work, we propose a completely different approach for the enhancement of EC effects that consists of the application of multiple external fields on lead-free multiferroic materials able to undergo sharp first-order phase transitions. (Previous experimental and theoretical studies have already explored a similar approach although considering lead-containing materials and/or non-abrupt phase transitions.12–18) In particular, we demonstrate by means of computational first-principles methods that the sequential operation of hydrostatic pressure and electric fields in BiFe1−xCoxO3 solid solutions (BFCO) can trigger large and inverse EC effects of ΔSEC ≈ 5 J K−1 kg−1 and ΔTEC ≈ −5 K at room temperature. Moreover, aided by pressure BFCO displays a colossal EC strength of ∼1 K cm kV−1, defined as |ΔTEC|/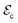 ,19 which surpasses by several orders of magnitude the typical values reported for uncompressed ferroelectrics.
,19 which surpasses by several orders of magnitude the typical values reported for uncompressed ferroelectrics.
Results
Phase competition in BFCO under pressure
At room temperature and zero pressure, BiFe1−xCoxO3 solid solutions (BFCO) can be stabilized in two different polymorphs, depending on the relative content of Fe/Co atoms, exhibiting rhombohedral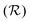 and tetragonal
and tetragonal 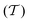 symmetries.20–22 For relative cobalt contents of 0 ≤ x ⪅ 0.25, the BFCO ground state is the
symmetries.20–22 For relative cobalt contents of 0 ≤ x ⪅ 0.25, the BFCO ground state is the 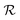 phase, which is analogous to the ground state of bulk BiFeO3.20–23 This rhombohedral phase presents an electric polarization of 60–80 μC cm−2 that is oriented along the pseudocubic direction [111] (Fig. 1a) and G-type antiferromagnetic spin ordering (AFM-G, the net magnetic moment of each transition metal ion is antiparallel to those of its six first nearest neighbours). For larger relative cobalt contents, 0.25 < x, the BFCO ground state corresponds to the
phase, which is analogous to the ground state of bulk BiFeO3.20–23 This rhombohedral phase presents an electric polarization of 60–80 μC cm−2 that is oriented along the pseudocubic direction [111] (Fig. 1a) and G-type antiferromagnetic spin ordering (AFM-G, the net magnetic moment of each transition metal ion is antiparallel to those of its six first nearest neighbours). For larger relative cobalt contents, 0.25 < x, the BFCO ground state corresponds to the 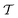 phase, which is analogous to the ground state of bulk BiCoO3.20–22,24,25 According to theoretical calculations, this tetragonal phase presents a giant electric polarization of 160–180 μC cm−2 oriented along the pseudocubic direction [001] (Fig. 1a),20–22 and hence sometimes it is referred to as “supertetragonal”, and C-type antiferromagnetic spin ordering (AFM-C, the net magnetic moment of each transition metal ion is parallel to those of its two first nearest neighbours located along the polar axis and antiparallel to those of its other four first nearest neighbours).
phase, which is analogous to the ground state of bulk BiCoO3.20–22,24,25 According to theoretical calculations, this tetragonal phase presents a giant electric polarization of 160–180 μC cm−2 oriented along the pseudocubic direction [001] (Fig. 1a),20–22 and hence sometimes it is referred to as “supertetragonal”, and C-type antiferromagnetic spin ordering (AFM-C, the net magnetic moment of each transition metal ion is parallel to those of its two first nearest neighbours located along the polar axis and antiparallel to those of its other four first nearest neighbours).
Under increasing temperature and for relative cobalt contents of x ≲ 0.25, the supertetragonal  phase can be stabilized over the
phase can be stabilized over the  phase owing to its larger vibrational entropy.20–22 Such a T-induced phase transition is clearly of first-order type (or discontinuous) since the volume change associated with it is huge (∼10%). Barocaloric effects are driven by hydrostatic compression; however, to the best of our knowledge, there are no experimental studies on BFCO under pressure. Here, we amend for such a lack of information by carrying out accurate first-principles calculations based on density functional theory (DFT, Methods).22,26Fig. 1b shows the estimated hydrostatic pressure that is necessary to drive the
phase owing to its larger vibrational entropy.20–22 Such a T-induced phase transition is clearly of first-order type (or discontinuous) since the volume change associated with it is huge (∼10%). Barocaloric effects are driven by hydrostatic compression; however, to the best of our knowledge, there are no experimental studies on BFCO under pressure. Here, we amend for such a lack of information by carrying out accurate first-principles calculations based on density functional theory (DFT, Methods).22,26Fig. 1b shows the estimated hydrostatic pressure that is necessary to drive the  phase transition at low temperatures (i.e., disregarding entropy and also likely quantum nuclear effects, which tend to slightly overestimate pt) and for compositions in the interval 0.25 ≤ x ≤ 0.50. This transition pressure is found to steadily, and significantly, decrease upon increasing Fe content. For instance, pt amounts to 1.4 GPa at x = 0.50 and 0.3 GPa at x = 0.25. As expected, the closer the cobalt content is to the
phase transition at low temperatures (i.e., disregarding entropy and also likely quantum nuclear effects, which tend to slightly overestimate pt) and for compositions in the interval 0.25 ≤ x ≤ 0.50. This transition pressure is found to steadily, and significantly, decrease upon increasing Fe content. For instance, pt amounts to 1.4 GPa at x = 0.50 and 0.3 GPa at x = 0.25. As expected, the closer the cobalt content is to the  –
– morphotropic phase boundary (xc ≈ 0.25), the easier results to switch from the supertetragonal phase to the rhombohedral phase with pressure.
morphotropic phase boundary (xc ≈ 0.25), the easier results to switch from the supertetragonal phase to the rhombohedral phase with pressure.
Simulating temperature effects in materials using first-principles methods is computationally very intensive and laborious. However, temperature effects are critical for the assessment of possible caloric phenomena and consequently cannot be neglected in the present study. We employed the quasi-harmonic approximation (QHA)22,26 to calculate ab initio Gibbs free energies for BFCO in the  and
and  phases under broad pressure, temperature and electric field conditions, thus allowing for the estimation of barocaloric and electrocaloric effects associated with first-order phase transitions (Methods).
phases under broad pressure, temperature and electric field conditions, thus allowing for the estimation of barocaloric and electrocaloric effects associated with first-order phase transitions (Methods).
Fig. 1c shows the p–T phase diagram calculated for BFCO at a composition of x = 0.50, hereafter referred to as BFCO0.5. Therein, it is appreciated that pt consistently increases upon increasing temperature, reaching a value of 1.24 GPa at room temperature. In spite of such a relatively large pressure, in what follows we present the multicaloric results obtained for bulk BFCO0.5 at and near room temperature since from a computational point of view this solid solution is highly affordable (i.e., the size of the corresponding simulation cells is among the smallest thus making the QHA free energy calculations feasible). In practice, much smaller pressures of the order of several 0.1 GPa can be attained by reducing the relative content of Co ions (Fig. 1b) without probably affecting the main conclusions presented in the next section (see the Discussion section).
Barocaloric performance of BFCO0.5
We start by analyzing the barocaloric effects induced by hydrostatic pressure in bulk BFCO0.5 in the absence of electric fields. Fig. 2a and b show the compression required to induce the phase transition as a function of temperature, pt, and the accompanying relative volume change. The estimated phase transition volume change is negative and very large as it amounts to ∼8% in absolute value. Such a huge relative volume change augurs a large phase transition entropy change, as it can be inferred from the Clausius–Clapeyron (CC) relationship
phase transition as a function of temperature, pt, and the accompanying relative volume change. The estimated phase transition volume change is negative and very large as it amounts to ∼8% in absolute value. Such a huge relative volume change augurs a large phase transition entropy change, as it can be inferred from the Clausius–Clapeyron (CC) relationship  . However, after performing the calculations and assuming that ΔSBC ≈ ΔSt (Methods), it was found that the ensuing barocaloric isothermal entropy shifts were actually quite modest (Fig. 2c). For instance, at room temperature, we obtained |ΔSBC| = 1.7 J K−1 mol−1 (5.4 J K−1 kg−1), which is about one order of magnitude smaller than the giant barocaloric entropy changes found in superionic and plastic crystals (∼100 J K−1 kg−1).27–35 Under decreasing temperature, |ΔSBC| slightly increases (e.g., 2.8 J K−1 mol−1 at T = 200 K); however, the estimated values still are quite reduced. The reason for these outcomes is that pt barely changes with temperature in the explored thermodynamic range (i.e., the temperature derivative of the phase transition pressure amounts only to ∼10−3 GPa K−1, Fig. 2a).
. However, after performing the calculations and assuming that ΔSBC ≈ ΔSt (Methods), it was found that the ensuing barocaloric isothermal entropy shifts were actually quite modest (Fig. 2c). For instance, at room temperature, we obtained |ΔSBC| = 1.7 J K−1 mol−1 (5.4 J K−1 kg−1), which is about one order of magnitude smaller than the giant barocaloric entropy changes found in superionic and plastic crystals (∼100 J K−1 kg−1).27–35 Under decreasing temperature, |ΔSBC| slightly increases (e.g., 2.8 J K−1 mol−1 at T = 200 K); however, the estimated values still are quite reduced. The reason for these outcomes is that pt barely changes with temperature in the explored thermodynamic range (i.e., the temperature derivative of the phase transition pressure amounts only to ∼10−3 GPa K−1, Fig. 2a).
The revealed minute T-induced pt variation, on the other hand, implies sizeable changes in the phase transition temperature, Tt, as induced by small pressure shifts (since dTt/dp = [dpt/dT]−1), thus suggesting possibly large barocaloric thermal shifts in bulk BFCO0.5. Fig. 2d shows the barocaloric adiabatic temperature changes, ΔTBC, estimated as a function of temperature (Methods). At room temperature (T = 200 K), ΔTBC was found to amount to 4.7 K (6.5 K) which, although it cannot rival with the barocaloric adiabatic temperature changes reported for superionic and plastic crystals (∼10 K),27–35 it shows promise in the context of electrocaloric effects (∼1–10 K).
The barocaloric results presented above were obtained using the Clausius–Clayperon (CC) method, which is not exact.27 Aimed to assess the extent of the employed approximations, we mimicked with theory quasi-direct barocaloric experiments27,31 where entropy curves are estimated as a function of pressure and temperature and from which ΔSBC and ΔTBC can be straightforwardly determined (Fig. 3a and b).35 Moreover, using this quasi-direct estimation approach it is also possible to determine, for a given pressure shift, Δp, the temperature span, Tspan, over which barocaloric effects can be operated (Fig. 3b). In view of the huge dTt/dp of ∼103 K GPa−1 estimated for BFCO0.5, giant Tspan values are anticipated.36
Fig. 3c shows the results of our quasi-direct barocaloric descriptor estimations. At room temperature and T = 200 K, we obtained adiabatic temperature changes of 2.0 ± 2.5 and 4.0 ± 2.5 K, respectively. Within the numerical uncertainties, these results are compatible with our previous estimations obtained using the CC method; however, it goes without saying that the reported error bars are unacceptably too large. The reasons for the relatively huge numerical uncertainties on ΔTBC are the small ΔSt and great p-induced Tt shifts involved in the quasi-direct estimation (Fig. 3a). Thus, unfortunately, in the present case, it is not possible to discern the actual precision of the barocaloric adiabatic temperature changes obtained using the approximate CC method. Nevertheless, the estimation of Tspan is still possible given its noticeably large size (Fig. 3a and b). By considering an outset compression of 1.18 GPa, we obtained a Tspan of ≈ 60 K for a small pressure shift of 0.06 GPa (calculated by adding up all the ΔTspan increments shown in Fig. 3c). This result is very encouraging since it indicates that, in spite of the relative smallness of ΔSBC and ΔTBC, barocaloric effects in BFCO0.5 could be operated over unusually ample temperature ranges.
Electrocaloric performance of pressurized BFCO0.5
The electric polarization, P, of BFCO0.5 in the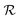 and
and  phases is significantly different; for instance, P in the supertetragonal phase is more than two times larger than that in the rhombohedral phase,22 adding up to polarization module differences of >100 μC cm−2 (Fig. 4b). Such a huge electric polarization disparity seems very promising from an electrocaloric (EC) point of view, as it can be inferred from the electric Clausius–Clapeyron relationship
phases is significantly different; for instance, P in the supertetragonal phase is more than two times larger than that in the rhombohedral phase,22 adding up to polarization module differences of >100 μC cm−2 (Fig. 4b). Such a huge electric polarization disparity seems very promising from an electrocaloric (EC) point of view, as it can be inferred from the electric Clausius–Clapeyron relationship  , where ΔSt represents the entropy change associated with the field-induced phase transition and
, where ΔSt represents the entropy change associated with the field-induced phase transition and 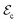 is the necessary electric field to switch from the
is the necessary electric field to switch from the 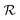 phase to the
phase to the  phase. Fig. 4a shows the
phase. Fig. 4a shows the 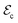 estimated for a fixed pressure of 1.25 GPa as a function of temperature (Methods), which has been selected to ensure appropriate stabilization of the
estimated for a fixed pressure of 1.25 GPa as a function of temperature (Methods), which has been selected to ensure appropriate stabilization of the  phase under conditions T ≤ 300 K. As clearly appreciated therein, the critical electric field steadily decreases upon increasing temperature, ranging from 43 kV cm−1 at 200 K to ≈2 kV cm−1 at room temperature.
phase under conditions T ≤ 300 K. As clearly appreciated therein, the critical electric field steadily decreases upon increasing temperature, ranging from 43 kV cm−1 at 200 K to ≈2 kV cm−1 at room temperature.
Fig. 4c–e show the electrocaloric isothermal entropy and adiabatic temperature changes, ΔSEC and ΔTEC, estimated for compressed BFCO0.5 using the CC approach (Methods). In this case, the sign of the EC descriptors indicates that the caloric effect is inverse, that is, ΔTEC<0. This result follows from the fact that the high-entropy phase  presenting the largest electric polarization is stabilized via the application of the external electric bias, namely, ΔSEC > 0 (conversely, in customary direct electrocaloric effects, the ferroelectric phase that is stabilized through the electric field corresponds to the low-entropy phase, thus ΔSEC<0 and consequently ΔTEC > 0). As expected, the size and temperature dependence of |ΔSEC| and |ΔTEC|, which are directly related among them through the temperature and heat capacity (Fig. 4d, Methods), are very much similar to those of |ΔSBC| and |ΔTBC| since the underlying phase transitions are equivalent. For instance, at T = 200 K, we estimated an electrocaloric adiabatic temperature change of −6.9 K and at a room temperature of −4.8 K, to be compared with the analogous barocaloric shifts of +6.5 and +4.7 K. These ΔTEC values are very much promising, specially when considering the small size of the required driving electric fields (that is,
presenting the largest electric polarization is stabilized via the application of the external electric bias, namely, ΔSEC > 0 (conversely, in customary direct electrocaloric effects, the ferroelectric phase that is stabilized through the electric field corresponds to the low-entropy phase, thus ΔSEC<0 and consequently ΔTEC > 0). As expected, the size and temperature dependence of |ΔSEC| and |ΔTEC|, which are directly related among them through the temperature and heat capacity (Fig. 4d, Methods), are very much similar to those of |ΔSBC| and |ΔTBC| since the underlying phase transitions are equivalent. For instance, at T = 200 K, we estimated an electrocaloric adiabatic temperature change of −6.9 K and at a room temperature of −4.8 K, to be compared with the analogous barocaloric shifts of +6.5 and +4.7 K. These ΔTEC values are very much promising, specially when considering the small size of the required driving electric fields (that is,  ).
).
Fig. 4f encloses results for the electrocaloric strength of BFCO0.5, ΛEC, expressed as a function of temperature; this quantity is defined as the ratio of ΔTEC to the corresponding electric bias.19 At T = 200 K, the attained adiabatic temperature change is highest; however, the required switching electric field is also largest, thus the resulting electrocaloric strength is smaller than the one obtained at higher temperatures. Still, the calculated ΛEC amounting to 0.2 K cm kV−1 is already comparable to the record experimental values reported for oxide and hybrid organic–inorganic perovskites.2,3,10 Remarkably, under increasing temperature, the electrocaloric strength of BFCO0.5 noticeably increases reaching a maximum, and a colossal value of 2.2 K cm kV−1 at T = 300 K. These figures will be put into context in a next section; in what follows, we explain how the dual response of BFCO0.5 to mechanical and electric stimuli may be exploited in practical solid-state cooling cycles.
Proposed  multicaloric cycle.
multicaloric cycle.
Single stimulus solid-state cooling cycles typically consist of four thermodynamic steps, two involving the adiabatic switching on and off of the applied external field and the other two constant-field heat transfer processes with the environment and the system to be refrigerated.35 In the present work, we propose an original multi-stimuli solid-state cooling cycle consisting of eight thermodynamic steps that has been designed to minimize the applied electric field, thus maximizing ΛEC, and with a cumulative multicaloric performance of |ΔTMC| = |ΔTBC| + |ΔTEC| and |ΔSMC| = |ΔSBC| + |ΔSEC|.
Fig. 5 shows the envisaged multi-stimuli solid-state cooling cycle comprising hydrostatic pressure and electric fields being applied on multiferroic lead-free BFCO solid solutions near room temperature. The cycle starts with multiferroic BFCO in the supertetragonal  phase at temperature T. Subsequently, hydrostatic pressure is adiabatically applied on BFCO so that it transforms into the
phase at temperature T. Subsequently, hydrostatic pressure is adiabatically applied on BFCO so that it transforms into the  phase and experiences a temperature increase of |ΔTBC|. In the third step, heat is released to the ambient, δQBC, and the initial temperature of the cycle is restored; compressed BFCO still remains in the
phase and experiences a temperature increase of |ΔTBC|. In the third step, heat is released to the ambient, δQBC, and the initial temperature of the cycle is restored; compressed BFCO still remains in the  phase. Next, an electric field is adiabatically applied on compressed BFCO so that it transforms into the
phase. Next, an electric field is adiabatically applied on compressed BFCO so that it transforms into the  phase, thus experiencing a temperature decrease of |ΔTEC|. In the fifth step, heat is absorbed by the system, δQEC, and the initial temperature of the cycle is restored; compressed and electrically biased BFCO remains in the
phase, thus experiencing a temperature decrease of |ΔTEC|. In the fifth step, heat is absorbed by the system, δQEC, and the initial temperature of the cycle is restored; compressed and electrically biased BFCO remains in the  phase. Subsequently, the electric field is adiabatically removed thus BFCO transforms into the
phase. Subsequently, the electric field is adiabatically removed thus BFCO transforms into the  phase and experiences a temperature increase of |ΔTEC|. In the seventh step, heat is released to the ambient, δQEC, and the initial temperature of the cycle is restored; compressed BFCO remains in the
phase and experiences a temperature increase of |ΔTEC|. In the seventh step, heat is released to the ambient, δQEC, and the initial temperature of the cycle is restored; compressed BFCO remains in the  phase. Finally, hydrostatic pressure is adiabatically released so that BFCO transforms back into the
phase. Finally, hydrostatic pressure is adiabatically released so that BFCO transforms back into the  phase and experiences a temperature decrease of |ΔTBC|. Then, heat is absorbed by the system, δQBC, and the initial temperature of the cycle is restored, thus completing an entire multi-stimuli cycle.
phase and experiences a temperature decrease of |ΔTBC|. Then, heat is absorbed by the system, δQBC, and the initial temperature of the cycle is restored, thus completing an entire multi-stimuli cycle.
Upon the completion of a multi-stimuli cycle, multiferroic BFCO is able to remove an amount of heat equal to |δQBC| + |δQEC|, or equivalently, T (|ΔSBC| + |ΔSEC|), from the targeted system to be refrigerated and release it to the ambient (thus cooling it down). The described multi-stimuli cycle lends itself to several useful variations. For instance, the state reached in the seventh step is thermodynamically equivalent to that attained in the third step; therefore, one could recursively perform the electrocaloric subcycle consisting of steps (3)–(6) which entails the application and removal of an electric bias under fixed hydrostatic pressure (dashed lines in Fig. 5). Likewise, if the multi-stimuli cooling cycle started with multiferroic BFCO in the rhombohedral  phase instead of the
phase instead of the  phase (e.g., due to some compositional synthesis constraints), then the sequential application of hydrostatic pressure and electric fields explained above should be swapped.
phase (e.g., due to some compositional synthesis constraints), then the sequential application of hydrostatic pressure and electric fields explained above should be swapped.
Discussion
Table 1 summarizes some representative materials for which EC effects at or near room temperature have been experimentally measured and reported in the literature. The selected compounds belong to three different families of ferroelectric materials, namely, oxides (e.g., HfO2 and BaTiO3), hybrid organic–inorganic perovskites ([(CH3)2CHCH2NH3]2PbCl4) and polymers (terpolymer). In terms of largest |ΔTEC|, the oxides Y-HfO25 and BNBT-BCZT9 and the elastomer terpolymer/PMN-PT38 emerge as the most promising materials since they display colossal values of 20–30 K. Nevertheless, these record materials require quite large electric fields to realize their full EC potential , hence with no exception their associated electrocaloric strengths turn out to be quite mediocre, namely, ΛEC ∼ 0.01 K cm kV−1.
, hence with no exception their associated electrocaloric strengths turn out to be quite mediocre, namely, ΛEC ∼ 0.01 K cm kV−1.
 , of compressed BFCO0.5 is significantly larger than the experimental ΛEC of other uncompressed ferroelectric compounds
, of compressed BFCO0.5 is significantly larger than the experimental ΛEC of other uncompressed ferroelectric compounds
| T (K) | (kV cm−1) | ΔTEC (K) | (K cm kV−1) | Ref. | |
|---|---|---|---|---|---|
| Y-HfO2 | 358 | 3500 | 24.8 | 0.01 | 5 (Expt.) |
| 0.93PMN-0.07PT | 298 | 723 | 9.0 | 0.01 | 37 (Expt.) |
| (NH4)2SO4 | 220 | 400 | 4.5 | 0.01 | 42 (Expt.) |
| Terpolymer/PMN-PT | 303 | 1800 | 31.0 | 0.02 | 38 (Expt.) |
| Ba0.65Sr0.35TiO3 | 293 | 130 | 3.1 | 0.02 | 40 (Expt.) |
| BaZr0.2Ti0.8O3 | 313 | 145 | 4.5 | 0.03 | 39 (Expt.) |
| BNBT-BCZT | 370 | 620 | 23.0 | 0.04 | 9 (Expt.) |
| PbZr0.46Sn0.46Ti0.08O3 | 317 | 30 | 1.6 | 0.05 | 4 (Expt.) |
| 0.73Pb(Mg1/3Nb2/3)O3–0.27PbTiO3 | 300 | 10 | 2.5 | 0.25 | 41 (Expt.) |
| BaTiO3 | 400 | 4.0 | 0.9 | 0.23 | 2 and 3 (Expt.) |
| [(CH3)2CHCH2NH3]2PbCl4 | 302 | 30 | 11.1 | 0.37 | 10 (Expt.) |
| BFCO0.5 (pressurized) | 300 | 2.2 | −4.8 | 2.18 | This work (Theory) |
Ferroelectric materials exhibiting moderate or even small |ΔTEC| but attained under smaller electric fields 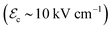 , on the other hand, become the clear winners in terms of largest ΛEC. For instance, the archetypal perovskite oxide BaTiO3 renders an adiabatic temperature change of roughly 1 K driven by a minute electric field of 4 kV cm−1, thus leading to a huge electrocaloric strength of 0.23 K cm kV−1.2,3 Likewise, 0.73Pb(Mg1/3Nb2/3)O3–0.27PbTiO3 renders a remarkable value of 0.25 K cm kV−141 and the hybrid organic–inorganic perovskite [(CH3)2CHCH2NH3]2PbCl4 holds a record ΛEC of 0.37 K cm kV−1, which results from a small electric field of 30 kV cm−1 and an adiabatic temperature change of 11.1 K.10 It is worth noting that all these figures correspond to experimental data.
, on the other hand, become the clear winners in terms of largest ΛEC. For instance, the archetypal perovskite oxide BaTiO3 renders an adiabatic temperature change of roughly 1 K driven by a minute electric field of 4 kV cm−1, thus leading to a huge electrocaloric strength of 0.23 K cm kV−1.2,3 Likewise, 0.73Pb(Mg1/3Nb2/3)O3–0.27PbTiO3 renders a remarkable value of 0.25 K cm kV−141 and the hybrid organic–inorganic perovskite [(CH3)2CHCH2NH3]2PbCl4 holds a record ΛEC of 0.37 K cm kV−1, which results from a small electric field of 30 kV cm−1 and an adiabatic temperature change of 11.1 K.10 It is worth noting that all these figures correspond to experimental data.
Table 1 also encloses the EC results that we have theoretically estimated in this study for pressurized BFCO0.5 at room temperature. According to our QHA-DFT calculations, compressed multiferroic BFCO solid solutions have the potential to surpass all previously known EC materials in terms of largest ΛEC. In particular, we predict an outstanding electrocaloric strength of 2.18 K cm kV−1 that arises from an adiabatic temperature change of 4.8 K and an electric bias of ≈2 kV cm−1. This theoretically estimated ΛEC value is from one to two orders of magnitude larger than those experimentally measured in uncompressed ferroelectrics. The key mechanism in achieving such a colossal figure is to employ an ancillary field, in our case hydrostatic pressure, to bring the system towards the verge of a ferroelectric phase transition so that it is possible to drive it with a minuscule electric field.
In the specific case considered here, the pressure required to achieve a colossal ΛEC value of 2.18 K cm kV−1 is higher than 1 GPa. Obviously, this compression is too large to be considered for practical applications. Nevertheless, as it was argued at the beginning of the Results section, it is possible to significantly reduce the size of this ancillary pressure to the order of several 0.1 GPa by decreasing the relative content of cobalt ions down to a critical composition of ≈0.25, without substantially affecting the main conclusions presented above. In particular, we calculated the vibrational properties of a multiferroic BFCO solid solution with a cobalt content of exactly 25%, BFCO0.25, both in the 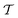 and
and 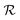 phases. At room temperature and under no pressure, the entropy difference between the two crystal structures was equal to 1.3 J K−1 mol−1 (disregarding thermal expansion effects), which matches within the numerical uncertainties the |ΔSBC| of 1.7 ± 0.4 J K−1 mol−1 calculated for compressed BFCO0.5 under the same thermodynamic conditions (Fig. 2c). Moreover, the relative volume change and electric polarization difference between the
phases. At room temperature and under no pressure, the entropy difference between the two crystal structures was equal to 1.3 J K−1 mol−1 (disregarding thermal expansion effects), which matches within the numerical uncertainties the |ΔSBC| of 1.7 ± 0.4 J K−1 mol−1 calculated for compressed BFCO0.5 under the same thermodynamic conditions (Fig. 2c). Moreover, the relative volume change and electric polarization difference between the  and
and  phases respectively amount to ≈9% and ≈110 μC cm−2, which in this case also turn out to be very much similar to the corresponding values estimated for BFCO0.5 under equivalent thermodynamic conditions.
phases respectively amount to ≈9% and ≈110 μC cm−2, which in this case also turn out to be very much similar to the corresponding values estimated for BFCO0.5 under equivalent thermodynamic conditions.
It is also worth noting that the ΛEC enhancement approach proposed in this study, and theoretically demonstrated for BFCO0.5, in principle should be generalizable to many other well-known EC materials since most of them are responsive to pressure as well (even though the magnitude of the resulting BC effects may be quite small in comparison to those achieved in state-of-the-art barocaloric materials). Take the archetypal ferroelectric compound BaTiO3 as an example. The ferro- to paraelectric phase transition temperature in this material can be effectively shifted with pressure, namely, dTt/dp ≈ −25 K GPa−1;43 thus, its room-temperature EC performance could be potentially improved with our proposed strategy.12,16 Finally, to mention that recent developments in the synthesis of ferroelectric membranes and thin films may also allow for the enhancement of the ΛEC figure-of-merit by combining electric fields with other types of mechanical stimuli like uniaxial44 and biaxial45 stress.
In conclusion, we have proposed a new strategy for the enhancement of the electrocaloric strength of ferroelectric materials that consists of concertedly applying pressure and electric fields. We have theoretically proved our new concept on multifunctional BFCO solid solutions, an intriguing family of compounds displaying a discontinuous phase transition between two multiferroic states. In particular, for compressed BFCO0.5, we estimated a record ΛEC parameter of 2.18 K cm kV−1 at room temperature resulting from an adiabatic temperature change of 4.8 K and an electric bias of ≈2 kV cm−1. This electrocaloric strength turns out to be colossal since it is about one order of magnitude larger than those experimentally measured in uncompressed ferroelectrics (∼0.1 K cm kV−1). The demonstrated ΛEC enhancement strategy can be applied to other types of ferroelectric materials, not necessarily magnetic, and be modified at convenience on the mechanical component. Thus, the combination of multiple stimuli opens new horizons in the field of caloric materials and solid-state refrigeration by expanding the design of possible cooling cycles and boosting caloric performance descriptors. We hope that the present theoretical study will motivate new experimental works on the engineering of original and environmentally friendly solid-state cooling devices.
Methods
Spin-polarized DFT calculations were performed with the generalized gradient approximation proposed by Perdew, Burke and Ernzerhof (PBE) as it is implemented in the VASP package.46,47 The “Hubbard-U” scheme due to Dudarev et al. was employed in the PBE calculations for treating better the Co (Fe) 3d electrons, adopting a U value of 6 (4) eV.22–25,48 The “projected augmented wave” method49 was used to represent the ionic cores considering the following electronic states as valence: Co 4s13d8, Fe 3p64s13d7, Bi 6s25d106p3, and O 2s22p4. An energy cut-off of 800 eV and a Γ-centered k-point grid of 4 × 6 × 6 were employed for a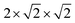 simulation cell containing 20 atoms,50 thus obtaining zero-temperature energies converged to within 0.5 meV per formula unit. Geometry relaxations were performed for an atomic force threshold of 0.005 eV Å−1. Electric polarizations were accurately estimated with the hybrid HSE06 functional51 and the Berry phase formalism.52–54
simulation cell containing 20 atoms,50 thus obtaining zero-temperature energies converged to within 0.5 meV per formula unit. Geometry relaxations were performed for an atomic force threshold of 0.005 eV Å−1. Electric polarizations were accurately estimated with the hybrid HSE06 functional51 and the Berry phase formalism.52–54
Ab initio free energies were estimated within the quasi-harmonic approximation (QHA)23,26,55 as a function of p and T. Phonon frequencies were calculated using the small displacement method.55 The following technical parameters provided QHA free energies converged to within 5 meV per formula unit: 160-atom supercells, atomic displacements of 0.01 Å, and q-point grids of 16 × 16 × 16 for integration within the first Brillouin zone. The effects of chemical disorder were addressed by generating all possible atomic Co–Fe and magnetic spin arrangements (ferromagnetic–FM– and antiferromagnetic–AFM– of type A, C, and G) for a 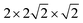 supercell containing 40 atoms. Quasi-harmonic free energies were calculated only for the lowest-energy configurations. Our spin-polarized DFT calculations were performed for bulk BiFe0.5Co0.5O3.
supercell containing 40 atoms. Quasi-harmonic free energies were calculated only for the lowest-energy configurations. Our spin-polarized DFT calculations were performed for bulk BiFe0.5Co0.5O3.
Within the QHA,23,26,55 the Gibbs free energy of a given crystal phase, Gharm, is expressed as follows:
| Gharm(p, T) = E(p) + pV(p, T) + Fharm(p, T), | (1) |
 | (2) |
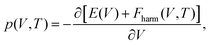 | (3) |
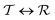 phase transition occurs at a given pressure, Tt, the condition
phase transition occurs at a given pressure, Tt, the condition  was employed.
was employed.
Likewise, the entropy of the crystal can be obtained through the following expression:
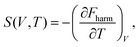 | (4) |
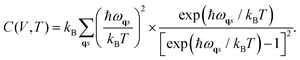 | (5) |
In the absence of electric fields, the isothermal entropy change associated with barocaloric effects was approximately estimated using the Clausius–Clapeyron (CC) method like:34
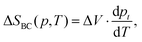 | (6) |
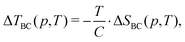 | (7) |
In the presence of electric fields, and assuming zero pressure, the thermodynamic potential that describes a particular phase is the Gibbs free energy defined as  , where E and Fharm are the same terms that appear in eqn (1), P is the electric polarization and
, where E and Fharm are the same terms that appear in eqn (1), P is the electric polarization and 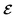 is the applied electric field. In this case, the thermodynamic condition that determines the
is the applied electric field. In this case, the thermodynamic condition that determines the 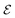 -induced phase transition is
-induced phase transition is  . The value of the corresponding critical electric field then can be estimated as
. The value of the corresponding critical electric field then can be estimated as
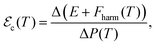 | (8) |
Once the value of  and its dependence on temperature are determined through eqn (8), the isothermal entropy change associated with electrocaloric effects can be approximately estimated using the CC method as25
and its dependence on temperature are determined through eqn (8), the isothermal entropy change associated with electrocaloric effects can be approximately estimated using the CC method as25
 | (9) |
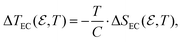 | (10) |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge financial support by the MCIN/AEI/10.13039/501100011033 under grants PID2020-119777GB-I00 and TED2021-130265B-C22, the “Ramón y Cajal” fellowship RYC2018-024947-I and the Severo Ochoa Centres of Excellence Program (CEX2019-000917-S), and by the Generalitat de Catalunya under grant no. 2017 SGR 1506. Computational support was provided by the Red Española de Supercomputación (RES) under the grants FI-2022-1-0012, FI-2022-1-0006, FI-2022-2-0003 and FI-2022-3-0014.References
- Y. Liu, J. F. Scott and B. Dkhil, Direct and indirect measurements on electrocaloric effect: Recent developments and perspectives, Appl. Phys. Rev., 2016, 3, 031102 Search PubMed
.
- E. Stern-Taulats, P. Lloveras, M. Barrio, E. Defay, M. Egilmez, A. Planes, J.-L. Tamarit, L. Mañosa, N. D. Mathur and X. Moya, Inverse barocaloric effects in ferroelectric BaTiO3 ceramics, APL Mater., 2016, 4, 091102 CrossRef
.
- X. Moya, E. Stern-Taulats, S. Crossley, D. González-Alonso, S. Kar-Narayan, A. Planes, L. Mañosa and N. D. Mathur, Giant electrocaloric strength in single-crystal BaTiO3, Adv. Mater., 2013, 25, 1360 CrossRef CAS
.
- P. D. Thacher, Electrocaloric effects in some ferroelectric and antiferroelectric Pb(Zr,Ti)O3 compounds, J. Appl. Phys., 1968, 39, 1996 CrossRef CAS
.
- S. Samanta, G. Anoop, W. Seol, S. M. Park, H. Joh, J. O. Choi, D. Ahn, S. Unithrattil, H. Kim, J. Yeom, S. Hong and J. Y. Jo, Large electrocaloric effect with high thermal and electric field cycling stability in solution-processed Y:HfO2 thin films, J. Mater. Chem. A, 2022, 10, 9960 RSC
.
- A. S. Mischenko, Q. Zhang, J. F. Scott, R. W. Whatmore and N. D. Mathur, Giant electrocaloric effect in thin-film PbZr0.95Ti0.05O3, Science, 2006, 311, 1270 CrossRef CAS
.
- B. Neese, B. Chu, S.-G. Lu, Y. Wang, E. Furman and Q. Zhang, Large electrocaloric effect in ferroelectric polymers near room temperature, Science, 2008, 321, 821 CrossRef CAS
.
- B. Asbani, Y. Gagou, J.-L. Dellis, M. Trcek, Z. Kutnjak, M. Amjoud, A. Lahmar, D. Mezzane and M. El Marssi, Lead-free Ba0.8Ca0.2TexTi1−xO3 ferroelectric ceramics exhibiting high electrocaloric properties, J. Appl. Phys., 2017, 121, 064103 CrossRef
.
- S. E. Shirsath, C. Cazorla, T. Lu, L. Zhang, Y. Y. Tay, X. Lou, Y. Liu, S. Li and D. Wang, Interface-charge induced giant electrocaloric effect in lead free ferroelectric thin-film bilayers, Nano Lett., 2020, 20, 1262 CrossRef CAS
.
- X. Liu, Z. Wu, T. Guan, H. Jiang, P. Long, X. Li, C. Ji, S. Chen, A. Sun and J. Luo, Giant room temperature electrocaloric effect in a layered hybrid perovskite ferroelectric: [(CH3)2CHCH2NH3]2PbCl4, Nat. Commun., 2021, 12, 5502 CrossRef CAS
.
- R. E. Cohen, Origin of ferroelectricity in perovskite oxides, Nature, 1992, 358, 136 CrossRef CAS
.
- Y. Liu, J. Wei, P.-E. Janolin, I. C. Infante, X. Lou and B. Dkhil, Giant room-temperature barocaloric effect and pressure-mediated electrocaloric effect in BaTiO3 single crystal, Appl. Phys. Lett., 2014, 104, 162904 CrossRef
.
- S. Patel, A. Chauhan, R. Vaish and C. S. Lynch, Large barocaloric effect and pressure-mediated electrocaloric effect in Pb0.99Nb0.02 (Zr0.95Ti0.05)0.08O3 ceramics, J. Am. Ceram. Soc., 2017, 100, 4902 CrossRef CAS
.
- A. Chauhan, S. Patel, S. Wang, N. Novak, B.-X. Xu, P. Lv, R. Vaish and C. S. Lynch, Enhanced performance of ferroelectric materials under hydrostatic pressure, J. Appl. Phys., 2017, 122, 224105 CrossRef
.
- Y.-K. Wang, Q.-L. Zhao, J. J. Di, G.-P. He, L. Zhao, T.-T. Su, M.-Y. Zhang, J. Zhang, X. Liang and D. Bu, Thermodynamic analysis of stress-mediated barocaloric effect, electrocaloric effect, and energy storage of PbZrO3 antiferroelectric film, Phys. Status Solidi A, 2021, 218, 2000651 CrossRef CAS
.
- Y. Liu, G. Zhang, Q. Li, L. Bellaiche, J. F. Scott, B. Dkhil and Q. Wang, Towards multicaloric effect with ferroelectrics, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 214113 CrossRef
.
- S. Lisenkov, B. K. Mani, C.-M. Chang, J. Almand and I. Ponomareva, Multicaloric effect in ferroelectric PbTiO3 from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 224101 CrossRef
.
- L. Liang, Y. L. Li, L.-Q. Chen, S. Y. Hu and G.-H. Lu, Thermodynamics and ferroelectric properties of KNbO3, J. Appl. Phys., 2009, 106, 104118 CrossRef
.
- S.-G. Lu, X. Lin, J. Li, D. Li, Y. Yao, T. Tao and B. Liang, Enhanced electrocaloric strengths at room temperature in (SrxBa1−x)(Sn0.05Ti0.95)O3 lead-free ceramics, J. Alloys Compd., 2021, 871, 159519 CrossRef CAS
.
- M. Azuma, S. Niitaka, N. Hayashi, K. Oka, M. Takano, H. Funakubo and Y. Shimakawa, Rhombohedral-tetragonal phase boundary with high Curie temperature in (1−x)BiCoO3–xBiFeO3 solid solution, Jpn. J. Appl. Phys., 2008, 47, 7579 CrossRef CAS
.
- H. Hojo, K. Oka, K. Shimizu, H. Yamamoto, R. Kawabe and M. Azuma, Development of bismuth ferrite as a piezoelectric and multiferroic material by cobalt substitution, Adv. Mater., 2018, 30, 1705665 CrossRef
.
- C. Menéndez and C. Cazorla, Giant thermal enhancement of the electric polarization in ferrimagnetic BiFe1−xCoxO3 solid solutions near room temperature, Phys. Rev. Lett., 2020, 125, 117601 CrossRef
.
- C. Cazorla and J. Íñiguez, Insights into the phase diagram of bismuth ferrite from quasiharmonic free-energy calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 214430 CrossRef
.
- C. Cazorla, O. Diéguez and J. Íñiguez, Multiple structural transitions driven by spin-phonon couplings in a perovskite oxide, Sci. Adv., 2017, 3, e1700288 CrossRef
.
- C. Cazorla and J. Íñiguez, Giant direct and inverse electrocaloric effects in multiferroic thin films, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 98, 174105 CrossRef CAS
.
- C. Cazorla and J. Boronat, Simulation and understanding of atomic and molecular quantum crystals, Rev. Mod. Phys., 2017, 89, 035003 CrossRef
.
- A. Aznar, P. Lloveras and M. Romanini,
et al., Giant barocaloric effects over a wide temperature range in superionic conductor AgI, Nat. Commun., 2017, 8, 1851 CrossRef PubMed
.
- C. Cazorla and D. Errandonea, Giant mechanocaloric effects in fluorite-structured superionic materials, Nano Lett., 2016, 16, 3124 CrossRef CAS
.
- A. K. Sagotra, D. Errandonea and C. Cazorla, Mechanocaloric effects in superionic thin films from atomistic simulations, Nat. Commun., 2017, 8, 963 CrossRef
.
- A. K. Sagotra, D. Chu and C. Cazorla, Room-temperature mechanocaloric effects in lithium-based superionic materials, Nat. Commun., 2018, 9, 3337 CrossRef PubMed
.
- P. Lloveras, A. Aznar and M. Barrio,
et al., Colossal barocaloric effects near room temperature in plastic crystals of neopentylglycol, Nat. Commun., 2019, 10, 1803 CrossRef CAS
.
- B. Li, Y. Kawakita and S. Ohira-Kawamura,
et al., Colossal barocaloric effects in plastic crystals, Nature, 2019, 567, 506 CrossRef CAS
.
- C. Cazorla, Refrigeration based on plastic crystals, Nature, 2019, 567, 470 CrossRef CAS
.
- K. Sau, T. Ikeshoji, S. Takagi, S.-I. Orimo, D. Errandonea, D. Chu and C. Cazorla, Colossal barocaloric efects in the complex hydride Li2B12H12, Sci. Rep., 2021, 11, 11915 CrossRef CAS PubMed
.
- C. Cazorla, Novel mechanocaloric materials for solid-state cooling applications, Appl. Phys. Rev., 2019, 6, 041316 Search PubMed
.
- J. Li, D. Dunstan, S. Lou, A. Planes, L. Mañosa, M. Barrio, J.-L. Tamarit and P. Lloveras, Reversible barocaloric effects over a large temperature span in fullerite C60, J. Mater. Chem. A, 2020, 8, 20354 RSC
.
- T. M. Correia, J. S. Young, R. W. Whatmore, J. F. Scott, N. D. Mathur and Q. Zhang, Investigation of the electrocaloric effect in a PbMg1/3Nb2/3O3–PbTiO3 relaxor thin film, Appl. Phys. Lett., 2009, 95, 182904 CrossRef
.
- C. Huang, H.-B. Yang and C.-F. Gao, Giant electrocaloric effect in cracked ferroelectrics, J. Appl. Phys., 2018, 123, 154102 CrossRef
.
- X.-S. Qian, H. J. Ye, Y. Zhang, H. Gu, X. Li, C. A. Randall and Q. M. Zhang, Giant electrocaloric response over a broad temperature range in modified BaTiO3 ceramics, Adv. Funct. Mater., 2014, 24, 1300 CrossRef CAS
.
- X. Q. Liu, T. T. Chen, Y. J. Wu and X. M. Chen, Enhanced electrocaloric effects in spark plasma-sintered Ba0.65Sr0.35TiO3 -based ceramics at room temperature, J. Am. Ceram. Soc., 2013, 96, 1021 CrossRef CAS
.
- B. Lu, X. Jian, X. Lin, Y. Yao, T. Tao, B. Liang, H. Luo and S.-G. Lu, Enhanced electrocaloric effect in 0.73Pb(Mgi1/3Nb2/3)O3 -0.27PbTiO3 single crystals via direct measurement, Crystals, 2020, 10, 451 CrossRef CAS
.
- S. Crossley, W. Li, X. Moya and N. D. Mathur, Large electrocaloric effects in single-crystal ammonium sulfate, Philos. Trans. R. Soc., A, 2016, 374, 20150313 CrossRef
.
- S. A. Hayward and E. K. H. Salje, The pressure-temperature phase diagram of BaTiO3: a macroscopic description of the low-temperature behaviour, J. Phys.: Condens. Matter, 2002, 14, L599 CrossRef CAS
.
- Y. Zang, C. Di and Z. Geng,
et al., Giant thermal transport tuning at a metal/ferroelectric interface, Adv. Mater., 2022, 34, 2105778 CrossRef CAS
.
- Y. Liu, L. C. Phillips, R. Mattana, M. Bibes, A. Barthélémy and B. Dkhil, Large reversible caloric effect in FeRh thin films via a dual-stimulus multicaloric cycle, Nat. Commun., 2016, 7, 11614 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS
.
- C. Menéndez, D. Chu and C. Cazorla, Oxygen-vacancy induced magnetic phase transitions in multiferroic thin films, npj Comput. Mater., 2020, 6, 76 CrossRef
.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef
.
- C. Cazorla and M. Stengel, Electrostatic engineering of strained ferroelectric perovskites from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 214108 CrossRef
.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS
.
- R. D. King-Smith and D. Vanderbilt, Theory of polarization of crystalline solids, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 1651 CrossRef CAS
.
- R. Resta, Macroscopic polarization in crystalline dielectrics: the geometric phase approach, Rev. Mod. Phys., 1994, 66, 899 CrossRef CAS
.
- L. Bellaiche and D. Vanderbilt, Intrinsic piezoelectric response in perovskite alloys: PMN-PT versus PZT, Phys. Rev. Lett., 1999, 83, 1347 CrossRef CAS
.
- A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1 CrossRef CAS
.
- L. Mañosa and A. Planes, Materials with giant mechanocaloric effects: Cooling by strength, Adv. Mater., 2017, 29, 1603607 CrossRef PubMed
.
| This journal is © the Owner Societies 2023 |



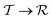
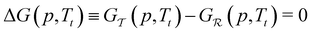



![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif)