The magnetically induced current density of the [12]infinitene dianion

Abstract

The magnetically induced current–density susceptibility (MICD) of the [12]infinitene dianion and the induced magnetic field around it have been calculated at the density functional theory level. Separation of the MICD into diatropic and paratropic contributions shows that the MICD is dominated by the diatropic contribution in contrast to the notion that it is antiaromatic, which was reported in a recently published article. The MICD of the [12]infinitene dianion exhibits several through-space MICD pathways, whereas it sustains only weak local paratropic current-density contributions. We identified four main current-density pathways of which two are similar to the ones for neutral [12]infinitene. It is difficult to judge from calculations of the nucleus independent shielding constants and the induced magnetic field around the [12]infinitene dianion whether it sustains diatropic or paratropic ring currents.

---

1 Introduction

The synthesis of the lemniscular [12]infinitene was reported in 2022.¹ Calculations of the magnetically induced current density showed that the molecule sustains two independent ring currents along the edges formed by 24 carbon atoms.^2,3 The ring currents flow along the outer loop on one side of the molecule and continues to the inside on the other side of the molecule. The two ring currents circulate in the classical diatropic direction even though the number of conjugated orbitals is even. This is at a first sight surprising because the aromaticity rule for doubly Möbius-twisted molecules is the same as for planar conjugated molecules.^4–12 Thus, an even number of occupied conjugated orbitals would suggest that the molecule is antiaromatic. However, since [12]infinitene sustains two almost independent and parallel ring currents, the aromatic character follows the cylindrical aromaticity rule.¹² The magic numbers of conjugated orbitals of cylindrical aromatic molecules are 1, 2, 4, 6, 8, 10, … corresponding to σ_g, σ_u, π_u, π_g, δ_g, δ_u, … orbitals. The magic number of conjugated orbitals is even when more than one orbital contribute to the conjugation because when the parity is considered the two first conjugated orbitals are σ orbitals with a m quantum number of m = 0, that is, they have no nodes along the perimeter but different parities in the direction along the symmetry axis of the cylinder. For example, the B₂₀ “wedding ring” is aromatic even though it has 10 conjugated orbitals because the two first ones are σ_g and σ_u.^13,14 The rest of the conjugated orbitals appears pairwise with degenerate orbitals for ±m. The topology of the lemniscular [12]infinitene is a doubly-twisted ring.

The ring current of [12]infinitene does not vanish because the area inside the bigger loop is larger than the one enclosed by the inner loop. The external magnetic field induces a diatropic ring current, that is, a ring current in the classical direction. The ring current is forced to continue in the non-classical direction along the inner loop on the other side of the lemniscular structure. The ring current in the smaller loop flows in the non-classical direction even though it is diatropic.

Tropicity is a global property that can be determined only by following the vector field of the current density around the whole vortex.¹⁵ For simple ring-shaped molecules the tropicity can be determined locally from the direction of the current density passing through a plane that cuts the ring. Since the classical direction dominates, the ring current is diatropic around the whole circuit.

The dication is expected to be cylindrical antiaromatic because it has formally only two electrons in the outermost shell with space for four electrons in the two degenerate orbitals. Calculations on the dication showed that it has a smaller gap of 2.52 eV between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) than the HOMO–LUMO gap of 5.43 eV for neutral [12]infinitene.² The smaller HOMO–LUMO gap suggests that the dication is antiaromatic also in practice. Calculations on the dication of [12]infinitene yielded a current density that is indeed dominated by a paratropic current density that passes through the space from one strand to the other in the middle of the molecule at the crossing point.² Seen from above, the paratropic current density consists of two ring currents flowing in the paratropic direction along the edge of the projected coronene structures.

The magnetic response of the dianion of [12]infinitene has been studied very recently.¹⁶ The calculations suggested that the dianion is antiaromatic as also the orbital counting rule would suggest. However, very small HOMO–LUMO gaps of 2.09 eV and 0.20 eV were reported for the neutral [12]infinitene and for its dianion, respectively. The HOMO–LUMO gap of neutral [12]infinitene is more than a factor of two smaller than the one of 5.43 eV that we obtained in our study.² In the recent study of the [12]infinitene dianion, Olea Ulloa and Muñoz-Castro assumed that the molecular structure belongs to the D₂ point group, which is not the energetically lowest one. Therefore, the calculated magnetic response for the dianion might be wrong.

The [12]infinitene molecule has received attention in Chemical Engineering News¹⁷ and Chemistry World¹⁸ since the synthesis was reported in 2022. Computational studies of molecular properties of [12]infinitene have also been published.^19,20

Here, we calculate the magnetic response and the magnetically induced current density susceptibility, which is often called current density, for the [12]infinitene dianion. In the next section, we described the employed computational methods. The main results are discussed in Section 3 and concluded in Section 4.

2 Computational methods

The molecular structure of the [12]infinitene dianion was optimized at the density functional theory (DFT) level using the CAM-B3LYP functional²¹ and triple-ζ polarization quality basis sets (def2-TZVP).²² Dispersion interaction was considered by using the D3(BJ) semi-empirical term in the Hamiltonian.²³ The negatively charged dianion was stabilized by using the COSMO solvation model.^24,25 The electronic structure calculations were performed with the Turbomole program.^26–28 The optimized molecular structure shown in Fig. 1 belongs to the C₂ point group, which was verified by calculating the vibrational frequencies numerically with the NumForce script of Turbomole. The Cartesian coordinates of the optimized molecular structure are given in the ESI.† The gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) is 2.83 eV at the CAM-B3LYP level, which are similar to the HOMO–LUMO gap of 2.52 eV for the dication calculated at the B3LYP level. Single-point B3LYP^29–31 calculations were performed for comparing the HOMO–LUMO gap of the dianion with the ones obtained in our previous calculations on [12]infinitene and its dication. A smaller HOMO–LUMO gap of 1.15 eV was obtained for the [12]infinitene dianion in a single-point B3LYP/def2-TZVP calculation using COSMO and the molecular structure optimized at the CAM-B3LYP/def2-TZVP level. The HOMO–LUMO gap of neutral [12]infinitene is 5.43 eV at the B3LYP level.²

Fig. 1 The molecular structure of the [12]infinitene dianion seen along the symmetry axis (above) and from the side (below). In the upper picture, the C₂ axis at the center of the molecule pointing towards the readers is parallel to the external magnetic field. The pictures have been made with VESTA³² and PowerPoint.

Nuclear magnetic shielding constants were calculated at the CAM-B3LYP level²¹ using the def2-TZVP basis sets.²² The density matrix in atomic orbital basis and the magnetically perturbed density matrices were obtained in the nuclear magnetic shielding calculations with Turbomole.³³ The calculated magnetic shielding constants are given in the ESI.†

The density matrix, the magnetically perturbed density matrices, the Cartesian coordinates of the molecular structure and the basis-set information were used as input data in the calculations of the magnetically induced current-density susceptibility (MICD) using the GIMIC program.^12,34–37 Gauge-including atomic orbitals were used in the calculations of the nuclear magnetic shielding constants and the magnetically induced current density susceptibility.^38,39

The MICD was analyzed by calculating ring-current strengths that are obtained by integrating the MICD passing through a plane intersecting chemical bonds or cutting through the molecule.^12,34,35,37 The magnetic field was applied along the C₂ symmetry axis through the strands. The unit for the ring-current (susceptibility) strengths is nA/T. The tropicity of the current density in discrete points was determined by following the vector field around the vortex using the Runge–Kutta algorithm.^15,40,41 The MICD is visualized using the Paraview program.⁴²

The induced magnetic field (in ppm)^43–45 was calculated in discrete points around the molecule using the Aromagnetic⁴⁶ program that can be used for calculating and visualizing one-dimensional profiles of the induced magnetic field and two-dimensional isolines and isosurfaces of the induced magnetic field and nucleus independent chemical shifts (NICS).^47–49 In the visualization of the induced magnetic field, it is assumed that the strength of the external magnetic field along the C₂ symmetry axis is 1 T. The z component of induced magnetic field is then the most important contribution.

3 Results and discussion

3.1. Magnetic shielding functions

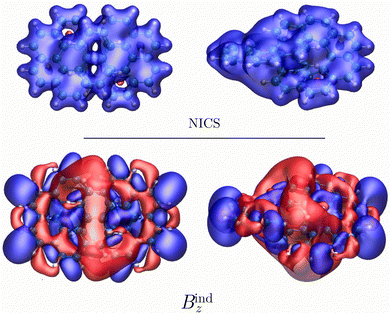
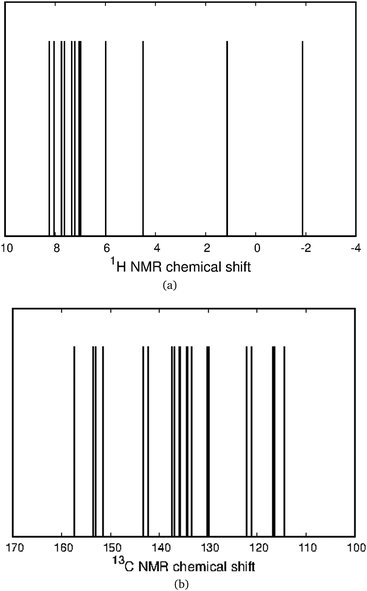
The aromaticity character of the [12]infinitene dianion is difficult to determine by calculating only the magnetic shielding function or the induced magnetic field in the vicinity of the molecule. In neutral [12]infinitene, it was possible to identify well-defined shielding and deshielding cones that agreed with the expected ones from the calculated magnetically induced current density. Calculations of the nuclear independent chemical shift (NICS) function^50–55 and the z component of the induced magnetic field (B^ind_z)^{43–45,56,57} with the magnetic field oriented along the z axis yielded a completely different magnetic response as seen in Fig. 2. While the NICS isosurface exhibits shielding behavior around the molecular frame suggesting a local aromatic character, B^ind_z consists of a complex mixture of shielding and deshielding contributions. The calculated magnetic response explains why the NICS(0) and B^ind_z (0) values vary so much from one ring to another. It is generally important to verify the aromatic character that is obtained from NICS values by performing calculations of magnetic shielding functions. For multiring molecules as the one studied here, it is necessay to calculate the MICD to determine the ring-current pathways.^58–60

Fig. 2 The NICS isosurface is shown in the upper picture. The picture below shows the isosurface of B^ind_z. The shielding (−5 ppm) and deshielding (+5 ppm) cones are shown in blue and red, respectively. The external field is parallel to the z axis, which is also the symmetry axis.

The calculated ¹H NMR and ¹³C NMR chemical shifts for the [12]infinitene dianion are shown in Fig. 3. The peaks in the ¹H NMR spectrum suggest that the molecule is aromatic, that is, dominated by diatropic current density contributions. The peaks in the calculated ¹³C NMR spectrum appear in about the same range as obtained in the previous study.¹⁶ However, the interpretation and the calculated induced magnetic field around the molecule differ in the two studies.

Fig. 3 The calculated (a) ¹H NMR and (b) ¹³C NMR chemical shifts (in ppm) of the [12]infinitene dianion. The shielding constants of the tetramethylsilan (TMS) reference are 31.89 ppm and 188.55 ppm for H and C, respectively.

3.2. Diatropic and paratropic current-density contributions

The magnetically induced current density of the [12]infinitene dianion is very complex with several through-space current-density pathways. Two independent global ring current pathways are shown in Fig. 4. More pictures of the current density are shown in the ESI.†

Fig. 4 The streamlines of the two independent figure-eight-shaped global ring currents are drawn in green and blue, respectively. The picture has been made with paraview.⁴²

Determination of the tropicity of current-density pathways is difficult for lemniscular-shaped molecules.¹⁵ Locally diatropic (paratropic) current density and returning paratropic (diatropic) current density flow in the same direction. To avoid mixing of diatropic and returning paratropic contributions to the current density (or vice versa), we separate the tropicities by using the Runge–Kutta method.^15,40,41

The diatropic and paratropic contributions are animated in the ESI.† Separating the diatropic and paratropic contributions to the current density shows that almost the whole current density in the [12]infinitene dianion is diatropic, which is unexpected because the dianion has 25 occupied conjugated orbitals and a doubly Möbius-twisted cylindrical aromatic topology. Thus, based on the orbital or electron counting rule, the [12]infinitene dianion should be antiaromatic and dominated by paratropic current-density contributions. The current density obtained in the GIMIC calculation suggests that the dianion is aromatic with strong through-space current-density pathways in the middle of the molecule near the crossing point of the two strands.

3.3. Current-density pathways

There are many current-density pathways. We can identify four significant pathways, whereas a more thorough inspection reveals many branching points of the global current-density flux. There are two independent figure-eight-shaped current-density pathways that flow on the outside of one half of the molecule and continues along the conjugated framework to the inside of the other half as shown in Fig. 4. These pathways are the same as the ones we obtained for neutral [12]infinitene.² There are 24 carbon atoms along one of the figure-eight-shaped pathways. Considering the two extra electrons of the dianion suggests aromaticity. However, since there are two parallel current-density pathways of this kind, the current density would be expected to be paratropic. Thus, counting the number of orbitals or electrons in the bond conjugation may lead to wrong conclusions. The molecule does not follow the counting rules because of the through-space current-density shortcuts.

Another important current-density pathway is shown in Fig. 5. The diatropic current density along the outer edge also splits into two through-space branches. One continues along the outer edge of the molecule implying that it flows through the space from one strand to the other in the middle of the molecule as illustrated with the purple line in Fig. 5. The current density has many through-space pathways in the middle of the molecule where it passes from one strand to the other at the overlapping projected naphthalene moieties. The through-space current-density pathways are seen in the lower-right picture of Fig. 5. More pictures are shown in the ESI.†

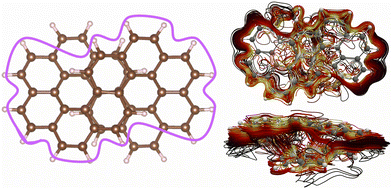Fig. 5 The global ring current around the whole molecule is illustrated with the purple line in the left picture. The detailed spaghetti plot is shown from the top (upper right) and from the side (lower right). The color scheme in the spaghetti plot corresponds to the strength of the current density with white being the strongest and then yellow and then red, the weakest ones are black. The current-density pictures have been made with paraview.⁴²

The second significant through-space current-density pathway is shown in Fig. 6. It splits and merges in the middle of the molecule. The current-density pathway is illustrated with the red and blue lines in Fig. 6. The diatropic current density on the outer edge of one half of the molecule shown in red approaches the centre of the molecule where it passes from the upper strand to the lower and then it continues in the diatropic direction along the outer edge of the other half as shown with the blue line in Fig. 6. This current-density pathway is marked in orange when it approaches the centre of the molecule where it passes from the upper strand to the lower one and continues in the diatropic direction shown in dark blue. The through-space current density is seen in the lower-right picture of Fig. 6. The strength of the through-space current is relatively weak as compared to the complicated current-density flux seen in the upper-right picture.

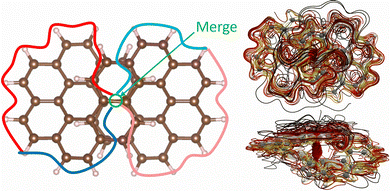Fig. 6 A global through-space current-density pathway is illustrated in the left picture. A more detailed spaghetti plot is shown from the top view in upper-right picture and from the side in the lower-right picture. The color scheme in the right pictures corresponds to the strength of the current density with white being the strongest, then yellow and red. The weakest ones are shown in black. The current-density pictures have been made with paraview.⁴²

3.4 Strengths of current-density pathways

The strengths of the current-density pathways can be estimated by integrating the current density passing through planes intersecting chemical bonds or parts of the molecular rings. The position of the integration planes are shown in Fig. 7. The planes are perpendicular to the reader as illustrated in the upper picture. The integration domains of plane A and plane B are shown with the red and the green line, respectively. The planes extend in the other direction from very far below the molecule to very far above it where the current density vanishes. Plane C and plane D are illustrated with the blue and purple dashed line, respectively. In the other direction, they begin in the center of the molecule and continues to very far away from the molecule.

Fig. 7 The positions of the integration planes for determining the strength of the current-density pathways are shown with the colored lines in the upper picture. The division of the plane in the middle of the molecule into C and D planes is shown in the lower one. The pictures have been made with VESTA³² and PowerPoint.

The strengths of the current-density pathways are difficult to determine accurately due to the strong through-space current-density pathways that are shown with a two-dimensional profile picture in Fig. 8. The plane in Fig. 8 is perpendicular to the C₂ symmetry axis and the direction of the external magnetic field. The red peaks in the upper picture show where the current density passes from one strand to the other in the plane halfway between the two strands. The blue peaks are due to the local current density at the carbon atoms where the plane reaches the molecular frame.

Fig. 8 The strength of the through-space current density is illustrated. The side view is shown in the upper picture and it is shown from the top in the lower picture, where it is combined with the molecular structure.

The strength of the current density passing on the outside of the molecule through plane A is 14.0 nA/T and the one passing on the outside of the molecule through plane B is 8.5 nA/T. The rest of the current-density pathway of 5.5 nA/T continues to the inside of the other side of the molecule forming the figure-eight-shaped current-density pathway.

The strength of the current density at the outer edge at the other end of an extended plane B is 16.4 nA/T showing that the ring current branches from the outer edge towards the inner one before it reaches the middle of the molecule with the overlapping naphthalene moieties. See the profiles of the current density in the ESI.† The strength of current-density pathway along the edge at plane C is 6.1 nA/T, which is less than the expected 8.5 nA/T. The difference is due to undefined through-space current-density pathways in the middle of the molecule. The strength of the current density of 9.6 nA/T passing through plane D is slightly larger than 8.5 nA/T for the same reason. The sum of the through-space current-density pathways in the middle of the molecule is about 3.5 nA/T.

Integration of the current density passing through planes A–D suggests that the current density is dominated by a global diatropic pathway whose strength is about 16 nA/T. It branches in a complicated fashion. The strengths of the individual branches of the current density are of about the same magnitude that is less than 10 nA/T.

4 Conclusions

We have calculated and analyzed the magnetic response of the [12]infinitene dianion. The current-density calculations show that it sustains strong diatropic through-space current-density pathways. We have identified four main current-density pathways. Two of them are similar to the ones for the neutral [12]infinitene molecule. The figure-eight-shaped diatropic current-density pathway on the outside of the molecular frame on one half of the molecule continues to the inside of the other half. The two current-density pathways are independent. There is one current-density pathway around the outer edge of the entire molecule. It passes through the space along the edge in the middle of the molecule. There are strong current-density pathways in the stacked naphthalene moieties with through-space current-density pathways between them. The current-density pathways from the outer edges merge in the middle and pass through the space to the other strand where they split into two edge current-density pathways.

Separation of diatropic and paratropic contributions to the current density shows that the current density is completely dominated by diatropic contributions. The complicated topology of the molecule leads to diatropic current-density contributions that flow locally in the paratropic direction. The [12]infinitene dianion can be considered aromatic since it sustains mainly global diatropic current-density pathways, whose strengths are about as strong as the ring current of benzene.⁶¹

The z component of the induced magnetic field also show that the current density of the [12]infinitene dianion is very complex since it is very difficult to judge whether it sustains diatropic or paratropic current density based on the magnetic response. Calculations of the NICS function around the molecule suggest that the benzene rings are locally aromatic, whereas calculations of the induced magnetic field with the external magnetic field along the symmetry axis suggest that the current density is complex consisting of many global pathways.

The current-density calculations indicate that the [12]infinitene dianion is globally aromatic with strong through-space current-density pathway, which is not in agreement with the conclusions drawn in a recent study of the magnetic response of the [12]inifinite dianion.¹⁶

Author contributions

DS suggested current-density studies of the [12]infinitene dianion. All authors performed calculations. QW and MO-I visualized the current density and the induced magnetic field, respectively. All authors discussed results and contributed to the final manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been supported by the Academy of Finland through project number 340583, by the Magnus Ehrnrooth Foundation, Waldemar von Frenckell's foundation, and the Swedish Cultural Foundation in Finland. QW thanks the China Scholarship Council for a pre-doctoral fellowship. We acknowledge computational resources from the CSC – IT Center for Science, Finland.

References

1. M. Krzeszewski, H. Ito and K. Itami, J. Am. Chem. Soc., 2022, 144, 862–871.
2. M. Orozco-Ic, R. R. Valiev and D. Sundholm, Phys. Chem. Chem. Phys., 2022, 24, 6404–6409.
3. G. Monaco, R. Zanasi and F. F. Summa, J. Phys. Chem. A, 2022, 126, 3717–3723.
4. E. Heilbronner, Tetrahedron Lett., 1964, 5, 1923–1928.
5. H. S. Rzepa, Org. Lett., 2008, 10, 949–952.
6. S. M. Rappaport and H. S. Rzepa, J. Am. Chem. Soc., 2008, 130, 7613–7619.
7. R. Herges, Chem. Rev., 2006, 106, 4820–4842.
8. H. S. Rzepa, Chem. Rev., 2005, 105, 3697–3715.
9. G. R. Schaller and R. Herges, Chem. Commun., 2013, 49, 1254–1260.
10. P. W. Fowler and H. S. Rzepa, Phys. Chem. Chem. Phys., 2006, 8, 1775–1777.
11. L. N. Wirz, M. Dimitrova, H. Fliegl and D. Sundholm, J. Phys. Chem. Lett., 2018, 9, 1627–1632.
12. D. Sundholm, H. Fliegl and R. J. Berger, WIREs Comput. Mol. Sci., 2016, 639–678.
13. B. Kiran, S. Bulusu, H. J. Zhai, S. Yoo, X. C. Zeng and L. S. Wang, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 961–964.
14. M. P. Johansson, J. Phys. Chem. C, 2009, 113, 524–530.
15. Q. Wang, M. Dimitrova, S. Taubert and D. Sundholm, Phys. Chem. Chem. Phys., 2023, 25, 12469–12478.
16. C. Olea Ulloa and A. Muñoz-Castro, Phys. Chem. Chem. Phys., 2023, 25, 8190–8197.
17. L. Howes, Chem. Eng. News, 2022, 100(12) , https://cen.acs.org/physical-chemistry/computational-chemistry/Infinitene-might-aromatic/100/i12.
18. K. Tustain, Chem. World, 2022 , https://www.chemistryworld.com/news/infinity-shaped-molecule-displays-unexpected-aromaticity/4015412.article.
19. V. M. Freixas, S. Tretiak and S. Fernandez-Alberti, J. Phys. Chem. Lett., 2022, 13, 8495–8501.
20. C. Olea Ulloa, R. Guajardo-Maturana and A. Muñoz-Castro, Polyhedron, 2023, 234, 116323.
21. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
22. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
23. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
24. A. Schäfer, A. Klamt, D. Sattel, J. C. W. Lohrenz and F. Eckert, Phys. Chem. Chem. Phys., 2000, 2, 2187–2193.
25. A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805.
26. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
27. F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, WIREs Comput. Mol. Sci., 2014, 4, 91–100.
28. S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodynski and J. M. Yu, J. Chem. Phys., 2020, 152, 184107.
29. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
30. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
31. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
32. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
33. K. Reiter, F. Mack and F. Weigend, J. Chem. Theory Comput., 2018, 14, 191–197.
34. J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963.
35. H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518.
36. D. Sundholm, M. Dimitrova and R. J. F. Berger, Chem. Commun., 2021, 57, 12362–12378.
37. J. Jusélius, D. Sundholm and co-workers, GIMIC, Gauge-Including Magnetically Induced Currents, a stand-alone program for the calculation of magnetically induced current density., https://github.com/qmcurrents/gimic (accessed 19 March 2023).
38. R. Ditchfield, Mol. Phys., 1974, 27, 789–807.
39. K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 119, 8251–8260.
40. C. D. T. Runge, Math. Ann., 1895, 46, 167–178.
41. W. Kutta, Z. Angew. Math. Phys., 1901, 46, 435–453.
42. J. Ahrens, B. Geveci and C. Law, ParaView: An End-User Tool for Large Data Visualization, Visualization Handbook, Elsevier, 2005, ISBN-13: 978-0123875822, see also: http://www.paraview.org.
43. G. Merino, T. Heine and G. Seifert, Chem. – Eur. J., 2004, 10, 4367–4371.
44. T. Heine, R. Islas and G. Merino, J. Comput. Chem., 2007, 28, 302–309.
45. R. Islas, T. Heine and G. Merino, Acc. Chem. Res., 2012, 45, 215–228.
46. M. Orozco-Ic, J. L. Cabellos and G. Merino, Aromagnetic, 2016, Cinvestav-Mexico.
47. M. Orozco-Ic, C. A. Celaya and D. Sundholm, RSC Adv., 2020, 10, 18124–18130.
48. M. Orozco-Ic, J. Barroso, N. D. Charistos, A. Muñoz-Castro and G. Merino, Chem. – Eur. J., 2019, 26, 326–330.
49. M. Orozco-Ic, M. Dimitrova, J. Barroso, D. Sundholm and G. Merino, J. Phys. Chem. A, 2021, 125, 5753–5764.
50. P. von Ragué Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. van Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318.
51. J. Jusélius and D. Sundholm, Phys. Chem. Chem. Phys., 1999, 1, 3429–3435.
52. P. von Ragué Schleyer, M. Manoharan, Z.-X. Wang, B. Kiran, H. Jiao, R. Puchta and N. J. R. van Eikema Hommes, Org. Lett., 2001, 3, 2465–2468.
53. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. von Ragué Schleyer, Chem. Rev., 2005, 105, 3842–3888.
54. R. Gershoni-Poranne and A. Stanger, Chem. – Eur. J., 2014, 20, 5673–5688.
55. R. Gershoni-Poranne and A. Stanger, Aromaticity: Modern Computational Methods and Applications, ed. I. Fernández López, Elsevier, 2021, ch. 4, pp. 99–154 DOI:10.1016/B978-0-12-822723-7.00004-2.
56. S. Klod and E. Kleinpeter, J. Chem. Soc. Perkin Trans. 2, 2001, 1893–1898.
57. N. D. Charistos, A. G. Papadopoulos and M. P. Sigalas, J. Phys. Chem. A, 2014, 118, 1113–1122.
58. P. Lazzeretti, Phys. Chem. Chem. Phys., 2004, 6, 217–223.
59. G. Acke, S. Van Damme, R. W. A. Havenith and P. Bultinck, Phys. Chem. Chem. Phys., 2019, 21, 3145–3153.
60. D. Inostroza, V. García, O. Yañez, J. J. Torres-Vega, A. Vásquez-Espinal, R. Pino-Rios, R. Báez-Grez and W. Tiznado, New J. Chem., 2021, 45, 8345–8351.
61. H. Fliegl, D. Sundholm, S. Taubert, J. Jusélius and W. Klopper, J. Phys. Chem. A, 2009, 113, 8668–8676.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates of the optimized molecular structure, isotropic magnetic shielding constants, and pictures of magnetically induced current densities, profiles of the current density passing through integration planes, and magnetic shielding functions are reported. Animations of the current-density plots are also provided. See DOI: https://doi.org/10.1039/d3cp02214e

---