Potential of nanostructured carbon materials for iodine detection in realistic environments revealed by first-principles calculations

Abstract

In the context of effective detection of iodine species (I₂, CH₃I) formed in nuclear power plants and nuclear fuel reprocessing facilities, we perform a comparative study of the potential sensing performance of four expectedly promising 2D materials (8-Pmmn borophene, BC₃, C₃N, and BC₆N) towards the iodine-containing gases and, with the view of checking selectivity, towards common inhibiting gases in the containment atmosphere (H₂O and CO), applying methods of dispersion-corrected density functional theory with periodic boundary conditions. A covalent bond is formed between the CO molecule and boron in BC₃ or in 8-Pmmn borophene, compromising the anticipated applicability of these materials for iodine detection. The presence of nitrogen atoms in BC₆N-2 prevents the formation of a covalent bond with CO; however, the closeness of adsorption energies for all the four gases studied does not distinguish this material as specifically sensitive to iodine species. Finally, the energies of adsorption on C₃N yield a significant and promising discrimination between the adsorption energies of (I₂, CH₃I) vs. (CO, H₂O), revealing possibilities for this material's use as an iodine sensor. The conclusions are supported by simulations at finite temperature; underlying electronic structures are also discussed.

---

1 Introduction

The release of volatile iodine fission products such as I₂ and CH₃I from nuclear power plants or fuel reprocessing facilities^1–3 is dangerous for human health. Indeed, ¹²⁹I and ¹³¹I are highly volatile isotopes which must be captured very quickly after release because of their relatively easy assimilation by the thyroid, which seriously affects human metabolism.^4,5 They are also likely to form iodomethane (CH₃I) upon reaction with any volatile organic compounds present around.⁶ All these volatile species present in the nuclear facilities⁷ can be released into the environment either by direct leakage of the containment or by the opening of their venting systems used to depressurize the containment in order to keep its integrity. Therefore, many efforts are made to confine these species and limit their spread in the environment.^6,7 Many efforts are made to confine these species and limit their spread in the environment. In this context, the development of sensors for accurate detection of iodine species is of utmost importance for the safety of the population.

The suitability for iodine detection of various materials such as metal–organic frameworks,^8,9 polymers,¹⁰ or metal-oxide sensors¹¹ for iodine detection has been explored. Even if these sensors demonstrate good sensitivity, the fact that their operating temperatures need to be quite high makes them expensive to employ and to maintain.¹¹ In addition, the sensor operation at elevated temperatures may degrade the long-term stability, reduce the sensitivity, and even modify the morphology of the sensor.¹² Therefore, new alternatives, i.e., carbon nanomaterials, have been explored as gas sensors to overcome these limitations.^13–16

During the past decades, the research on carbon-based two-dimensional nanomaterials, e.g., graphene and graphene-like materials, has attracted tremendous attention due to their exceptional physical and chemical properties.^17,18 Notably, their huge surface-to-area ratio, high chemical and mechanical stability along with the tunability of their band gaps make these materials promising as sensors to detect different gases. In fact, graphene¹⁹ and carbon nanofibers^20,21 have already been tested for iodine detection.

The adsorption of diatomic halogen molecules, including iodine, on graphene and graphite has been investigated by dispersion-corrected density functional theory (DFT) – see, e.g., Kim et al.²² and Price et al.²³ for recent reviews on corresponding methods and applications. Rudenko et al.²⁴ confirmed that the van der Waals (vdW) interactions contribute significantly to the interaction between the iodine molecules and graphene. In addition, analysis of the electronic structure showed the presence of an ionic interaction due to charge transfer from graphene to the iodine molecules. Similarly, Arabieh et al.²⁵ revealed that the interaction between iodine and 2D pristine boron nitride (BN) is mainly driven by vdW forces. This work also demonstrated that the presence of defects significantly increases the reactivity of the iodine molecule.

Following the same path, we opted to study the 8-Pmmn borophene in a preliminary screening, in anticipation that a substitution of carbon atoms in graphene with boron (resulting in BC₃), nitrogen (resulting in C₃N) or both (resulting in BC₆N) would enhance the sensing properties of graphene towards iodine gas. Since the valences of boron and nitrogen are “symmetric” with respect to that of carbon and the atom sizes are close, in combined doping they easily accommodate into carbon structures. In fact, Beniwal et al.²⁶ reported a successful synthesis of 2D hexagonal graphenic BCN monolayers. For BC₆N, two different structures, referred to as BC₆N-1 and BC₆N-2, have been inspected within a theoretical study by Mortazavi et al.,²⁷ whereby the latter structure, with B and N immediately neighbouring on the lattice, was predicted to be lower in energy by 0.14 eV per atom. This conclusion was confirmed in a study by Shi et al.²⁸ on three (hence all possible for an 8-atom unit cell) configurations. Therefore, we confined our simulation of BC₆N to this particular structure.

The properties of graphene-like BC₃, C₃N and BC₆N-2 monolayers have been studied,^29–31 and their potential for use as gas sensors has been discussed.^32–35 For example, Ma et al.³⁵ reported that the pristine C₃N monolayer is a good room-temperature NO₂ sensor with high selectivity, sensitivity, and good reversibility. Moreover, they revealed that boron doping replacing nitrogen atoms in the C₃N monolayer significantly enhances the adsorption strength and the charge transfer. This further improves the sensing selectivity of C₃N towards NO₂ molecules.

Despite all these promising manifestations of graphene-like materials, they have not yet been tested for iodine detection, and we believe that they deserve deep investigation. An additional consideration for shaping the current work is the fact that most of the reported studies for iodine detection have only focused on the I₂ molecule and not on other iodine-containing species, e.g., CH₃I.

It is noteworthy that the nuclear containment atmosphere is mainly composed of water steam.³⁶ Moreover, other gaseous compounds such as CO can be formed during a severe accident.^37,38 These two gases (CO and H₂O) are known to be able to compete with the adsorption of iodine species^39–42 which is likely to perturb or bias the performance of the sensor. To the best of our knowledge, no systematic experimental or theoretical works have been devoted to the evaluation of nanostructured carbon-based materials to selectively detect iodine species in the presence of other gases.⁴³

The accuracy of DFT calculations is sufficient to discriminate adsorption enthalpies of competing molecules on surfaces.^44–47 Therefore, we used this approach to compare the adsorption of I₂, CH₃I, H₂O and CO over 8-Pmmn borophene, BC₃, C₃N and BC₆N 2D materials.

The article is organized as follows: first, we outline our computational methods, after which the results obtained with the DFT tools are presented and discussed, while focusing on the sensing performances of the listed materials towards the iodine molecule. Finally, we present the main conclusions of our study.

2 Simulation details

In order to reliably compare the adsorption energies of different molecules on an, in principle, infinite sheet, we need to take care of the following issues:

(i) When applying a simulation method with periodic boundary conditions (which is not absolutely necessary, but convenient and largely acceptable, in order to not become biased by ambiguities related to the sheet termination, if the latter is chosen as a limited fragment), a large enough lateral supercell has to be chosen, in order to minimize the interference between periodically placed molecules. In principle, the results need to be tested for convergence against an increase of the supercell size.

(ii) Dispersion interactions are expected to play an important role in adsorption processes, affecting equilibrium geometries and electron energies; they ought to be – at least – included into the analysis with the help of one of “reliable” (practically recognized) method, although careful inspection of the performance of different possible schemes would be even better.

(iii) A priori, the preferential adsorption site or the ground-state configuration of an adsorbed molecule might be far from evident, hence a big number of trial initial configurations may need to be inspected.

Our first-principles calculations were carried out using the Vienna Ab initio Simulation Package (VASP),^48,49 which is based on the plane wave pseudopotential approach and uses ultrasoft pseudopotentials or a projected augmented wave (PAW) technique to cope with the core states.^50,51 The specific form of the exchange–correlation (XC) functional used was the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) parametrization.⁵²

For the DFT calculations, the planewave cutoff was set to 800 eV. The integration over the Brillouin zone was sampled by a 12 × 12 × 1 Γ-centered k-point Monkhorst–Pack grid using a Gaussian integration method with a width of 0.2 eV for 2 × 2 supercell size in the cases of BC₃, BC₆N-2 and C₃N, and 2 × 3 supercell in the case of 8-Pmmn borophene. These cutoff values were justified by convergence tests staged in order to check that total energy differences between distinct positions of molecules remain stable to the accuracy relevant for the present work.

Unit cells of all the structures considered were fully relaxed, yielding the lattice constants of 5.17 Å, 4.97 Å, 4.86 Å and (4.51 Å) × (3.25 Å) for BC₃, C₃N and BC₆N-2 and 8-Pmmn borophene, respectively; these values are in good agreement with previously published results.^27,53,54 In order to reliably resolve the energy difference relevant to the present work, it was essential to use the “Accurate” calculation mode within VASP, setting further on the 10⁻⁷ eV threshold for self-consistency criterion in solving the Kohn–Sham equations; the relaxation loop is stopped when the forces on all atoms get smaller than 0.02 eV Å⁻¹. Dispersion interactions in most cases have been taken into account following the Grimme-D2 scheme;⁵⁵ however, other correction schemes, e.g. the DFT-D3 method of Grimme with Becke–Jonson damping,⁵⁶ Many-body dispersion energy method⁵⁷ and Tkatchenko–Scheffler⁵⁸ method with iterative Hirshfeld partitioning⁵⁹ have also been applied, in cases of adsorption on CN₃, for comparison.

For calculation of the densities of states (DOSs) and partial densities of states (PDOSs), a 20 × 20 × 1 k-points mesh was applied.

The adsorption energy (E_ad) of a molecule considered (m) on each 2D sheet (s) at different positions was calculated according to the equation:

E_ad = E_m/s − E_s − E_m, (1)

where E_m/s is the energy of the 2D sheet with the adsorbed molecule, E_s is the energy of the pristine 2D sheet and E_m is the energy of the isolated molecule calculated in a box with the same size of the system.

In each of these parts, dispersion contribution to the energy is straightforwardly identified, on top of the “conventional” DFT result, of the type E = E^DFT + E^disp. Since the energy is additive within each term, one can identify the dispersion contribution within the full adsorption energy:

E^disp_ad = E^disp_m/s − (E^disp_s + E^disp_m). (2)

Beyond the values of adsorption energy, the redistribution of charge in the course of adsorption might be revealing in the discussion of trends. In order to minimize the dependence on a particular calculation code, the “absolute” charge transfer will be expressed according to the Bader analysis,⁶⁰ in the spirit of the above expressions for energy:

ΔQ = Q_m/s − (Q_s + Q_m). (3)

Along with this, the difference charge density as continuous spatial function will be communicated:

Δρ(r) = ρ_m/s(r) − [ρ_s(r) + ρ_m(r)]. (4)

There is a subtlety in the definition of differential energies and charges. If the latter are compared between two separately relaxed and hence not identical structures (molecule on the substrate vs. free substrate plus free molecule), the charge distributions are compared for the same placement of atoms, i.e., ρ_s(r) corresponds to self-consistent charge density in the adsorption geometry, with the molecule removed, and ρ_m(r) stands for the charge density of a free molecule, brought into its equilibrium adsorbed position.

As a complement to static (T = 0) DFT calculations, dynamical simulations have been done using Born–Oppenheimer ab initio molecular dynamics (AIMD) within the NVT ensemble (using the same supercell as for static calculations), during a simulation time of 200 ps with a time step of 1 fs. The temperature was set to 305 K and controlled using the Nosé–Hoover thermostat.^61,62

The planewave cutoff and the k-grid for the Brillouin zone were reduced to 500 eV and 6 × 6 × 1, respectively, in order to reduce the computational cost, while keeping the same threshold for self-consistency in solving the Kohn–Sham equations.

From these dynamical simulations, the internal energies of adsorption were extracted by averaging the internal energy of each system and its components separately (2D sheets and molecules) over the last 100 ps of the simulation. The internal energy of adsorption is expressed as follows:

E^AIMD_ad = 〈E^AIMD_m/s〉 − [〈E^AIMD_s〉 + 〈E^AIMD_m〉], (5)

where 〈E^AIMD_m/s〉 is the average of the internal energy of the 2D sheet with the adsorbed molecule, 〈E^AIMD_s〉 is the average of the internal energy of the pristine 2D sheet, and 〈E^AIMD_m〉 is the average of the internal energy of the isolated molecule.

3 Results and discussion

The main idea of the present work was to probe several layer materials with respect to their aptitude to adsorb the iodine-containing molecules, I₂ and CH₃I, likely to emerge in the case of severe nuclear accident, in the presence of so-called contaminant molecules in the confinement building, e.g., CO and H₂O, in view of identifying a substrate which will clearly discriminate the former two from the latter two by their corresponding adsorption energies.

In the following, the results are outlined substrate by substrate. The full data are available in the Electronic Supplementary Information (ESI†). In the main text we cover the results selectively – not only those which served our ultimate goal, but also “negative” ones which were nevertheless instructive, in one context or the other.

Every substrate offered a number of adsorption positions – hollow site, atop an atom, etc. – subject to symmetry constraints of the lattice in question. In combination with possible initial orientations of the gas molecule, this yields a multitude of initial trial configurations. They are numbered in an arbitrary way and specified in the figures and tables. For adsorption of all the trial molecules, 54 configurations in total were tried on BC₃ and 53 configurations on C₃N.

As a rule, scenarios of conjugate-gradient structure relaxation starting from these trial configurations ended up in just a few final configurations (adsorption site/orientation of a molecule/possible deformation of the substrate), for which the adsorption energy and electronic properties are reported.

Out of the four 2D materials probed, three were hexagonal monolayers with 8 atoms per unit cell; the fourth one (borophene) represented a “thick” structured layer of rectangular symmetry, with 8 atoms per unit cell as well. In order to minimize spurious interaction between (translated, by force of periodic boundary conditions) adsorbed molecules, sufficiently large lateral supercells must be chosen. In our simulations, as the unit cells were already relatively large, we used 2 × 2 supercells for all hexagonal systems and 2 × 3 supercells for borophene.

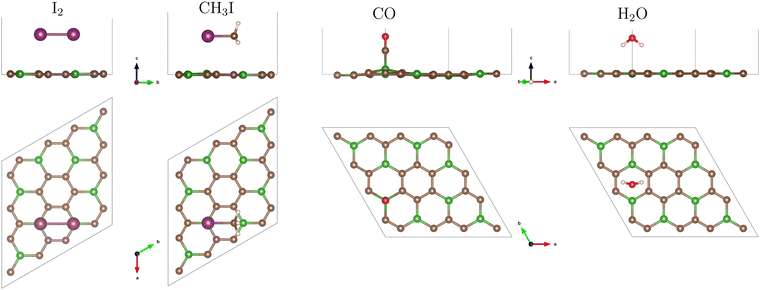
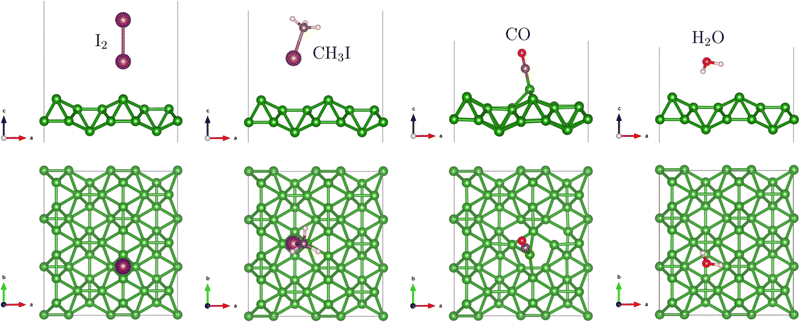
The relevant adsorption positions of all considered molecules on all studied 2D materials are presented in Fig. S1–S4 of the ESI.† The adsorption energies for these positions are calculated and assembled in Table S1 of the ESI.† For each combination substrate/molecule, the relaxed structure of the most preferable position, i.e. that with the strongest adsorption energy, is shown in Fig. 1, 3, 4 and 5, and the corresponding adsorption energies and interaction distances (vertical separations) are specified in Table 1.

Fig. 1 Top and side views of the relaxed conformations (corresponding to the largest adsorption energy, among the trial structures studied) of I₂, CH₃I, CO and H₂O molecules adsorbed on the BC₃ monolayer. Brown spheres: carbon, green: boron, large purple: iodine, red: oxygen. See the text for detail.

Fig. 2 PDOS of carbon (upper panel) and boron atoms (lower panels) in the case of adsorption of CO on BC₃. See the text for details.

Fig. 3 Top and side views of the relaxed conformations (corresponding to the largest adsorption energy, among the trial structures studied) of I₂, CH₃I, CO and H₂O molecules adsorbed on Pmmn-8 borophene. Brown spheres: carbon, green spheres: boron atoms. See the text for details.

Fig. 4 Top and side views of the relaxed conformations (corresponding to the largest adsorption energy, among the trial structures studied) of I₂, CH₃I, CO and H₂O molecules adsorbed on the BC₆N-2 monolayer. Brown spheres: carbon, green spheres: boron, silver spheres: nitrogen atoms. See the text for details.

Fig. 5 Top and side views of the relaxed conformations (corresponding to the largest adsorption energy, among the trial structures studied) of I₂, CH₃I, CO and H₂O molecules adsorbed on the C₃N monolayer. Brown spheres: carbon, silver spheres: nitrogen atoms. See the text for details.

Table 1 Calculated adsorption energies and minimal interaction distances for molecules over substrates, in the configurations shown in Fig. 1, 3, 4 and 5

Substrate	Adsorption energy (eV)				Interaction distance^a (Å)
	I2	CH3I	CO	H2O	I2	CH3I	CO	H2O
a Minimal height separating the atoms of the molecule from the atoms of the substrate.
BC3	−0.491	−0.437	−0.746	−0.207	3.20	2.54	1.53	2.33
8-Pmmn borophene	−0.663	−0.351	−0.651	−0.236	2.51	2.80	1.40	1.73
BC6N-2	−0.400	−0.265	−0.122	−0.172	3.08	3.29	3.06	2.41
C3N	−0.801	−0.335	−0.152	−0.194	3.38	2.53	2.95	2.41

---

The overview of adsorption energies helps to understand the expectations of the present study, with respect to selectivity of different substrates towards the molecules tested, and our logic behind the quest for a “good” substrate material. The trial of BC₃ was motivated by several recent works.^34,63,64 It revealed a noticeable selectivity towards iodine-containing molecules as compared to water; however, the adsorption of carbon monoxide turned out to be much stronger than that of all other molecules, with a danger to contaminate, or to bias, the prospective sensor. Guided by an idea of importance to have boron in the substrate, we tried the ultimate case of borophene, which revealed an enhanced sensitivity towards pure iodine, albeit not for CH₃I, whereas a strong sensitivity toward CO persisted. Saturation of the BC₃ substrate with nitrogen, in the form of balanced co-doping towards BC₆N, gave the first promises of clear positive discrimination of (I₂, CH₃I) against (CO, H₂O). Finally, an idea to get rid of boron whatsoever, turning to C₃N substrate, produced a reasonable combination of outstanding selectivity towards I₂ molecules and a fair selectivity towards CH₃I, as compared to both CO and H₂O. In the following, we discuss some interesting results from simulations on the first three substrate systems, even if they did not fully respond to expectations, and address in more detail the performance of C₃N.

3.1 Adsorption on BC₃

The I₂ molecule, tentatively placed over the BC₃ sheet in 15 different trial configurations (Fig. S1 of the ESI†), stabilises in several end configurations, with their corresponding adsorption energies given in Table S1 of the ESI.† The strongest adsorption energy (−0.49 eV) is found in “flat” configuration, the iodine atoms being situated over opposite boron atoms of a C₄B₂ hexagon, see Fig. 1. Very close energies (−0.44 to −0.42 eV) correspond to nearly upright yet tilted placement of I₂ above a C–B bond. Further on, there is a group of “flat” configurations with adsorption energies −0.38 to −0.33 eV, the iodine atoms being stabilised over centers of adjacent C₄B₂ hexagons, or over a boron atom and the center of its “next-neighboring” C₆ hexagon. Finally, “weak” adsorption energies (−0.29 to −0.27 eV) correspond to “flat” configurations over a C₆ or C₄B₂ hexagon, anchored over the opposite C–C bonds and avoiding the boron atoms in the latter case. About the same adsorption energy, −0.27/−0.26 eV, corresponds to the cases of upright placement of I₂ over the center of a C₆ hexagon, or atop a B atom.

The CH₃I molecule, for which 19 trial initial configurations have been tested (see Fig. S1 of the ESI†), prefers to be adsorbed (with the energy −0.41 eV) in a “flat” position (the I–C bond parallel to the substrate), with iodine atom atop boron, see Fig. 1. The “next-choice” configurations (adsorption energies −0.35 to −0.31 eV) are equally “flat”, with I “head” over the C₄B₂ hexagon. Placing the iodine atom over a C₆ hexagon results in a slightly weaker adsorption energy (−0.28 eV). Of comparable adsorption energies (−0.28 to −0.26 eV) are also positions with upright orientation of the molecule, iodine downwards, over different competing sites: carbon atom, C–C or C–B bond, C₄B₂ hexagon, or (−0.21 eV) over a boron atom. Finally, the least favourable (−0.19 to −0.18 eV) are upright iodine-up positions, the carbon of the methyl group being placed over C or B atoms or C–C or C–B bonds. Summarizing, an CH₃I molecule can “glide” on its methyl tail but gets trapped if its iodine head approaches boron, and gets fixed in a flat position, anchored to two boron atoms in the substrate.

In the adsorption of carbon monoxide, dominating configuration is the upright one, with the carbon end of the molecule being atop a boron atom at a distance of 1.53–1.58 Å, yielding an adsorption energy of −0.75 eV. Other final configurations, flat or tilted or oxygen downwards, are almost indiscriminately characterized by a much larger distance from the substrate (about 3 Å) and much smaller adsorption energies (−0.11 to −0.06 eV). The abovementioned strongest-bound (oxygen-up) configuration brings about a substantial distortion in the substrate, the underlying boron atom being pulled upwards by ≃0.53 Å, so that the C(molecule)–B–C(substrate) angle makes 101°, as can be seen in Fig. 1. DFT calculations for CO (among other molecules) adsorption on BC₃ have been recently reported by Mehdi Aghaei et al.³⁴ (who used PBE with D2 Grimme correction) and by Zhang et al.⁶⁵ (who used VASP with PBE, not mentioning any inclusion of dispersion interactions). Agreement between our present calculation and the two cited ones is excellent in what regards the orientation of the molecule, interatomic distances and angles. Namely, the “anchor” boron atom raises above the substrate layer by 0.5 Å and binds the carbon atom on top of it at 1.53–1.54 Å. Our adsorption energies are however almost two times smaller than those reported in ref. 34 and 65 (−1.34 and −1.30 eV, correspondingly). In the latter of these works, the buckling of the BC₃ layer is much stronger than in our case, consistently with a larger adsorption energy.

The remarkable adsorption of CO on BC₃ deserves some more detailed discussion, so we briefly mention the calculated PDOS shown in Fig. 2. There is clear evidence of chemical bonding between the (downwards directed) carbon atom of the CO molecule and the underlying boron atom in the substrate. This bonding involves 2s and 2p_z states of the atoms concerned, that could have been a priori anticipated and is indeed evidenced by a similar pattern of peaks in the corresponding PDOS. It is noteworthy that the patterns of 2s and 2p_z PDOS at boron atoms distant from the adsorbed molecule (see the bottom panel of Fig. 2) is completely different; the marked peaks are situated at different energies. However, the spectrum of 2p_x, p_y states is very similar for the boron atom beneath the adsorbed molecule and that far away; obviously the in-plane hybridizations are not strongly affected by the adsorbed molecule.

We note in this relationship that the perturbations in the substrate layer caused by the adsorption of other molecules (I₂, CH₃I and H₂O) is negligible, which hints at an absence of noteworthy hybridization between the orbitals of the molecules and those of the substrate atoms.

In the case of water molecules, the largest adsorption energy (−0.21 eV) corresponds to a symmetric hydrogens-down/oxygen-up placement over the center of a C₄B₂ hexagon. A slightly weaker adsorption (−0.15 eV) occurs over the C₆ hexagon. In both cases, turning the molecule upside down (hydrogens-up/oxygen-down) results in a metastable configuration, with adsorption energy reduced by 0.09 eV (−0.12 eV over C₄B₂, −0.06 eV over C₆). All the start configurations tested end up in one of these four possibilities. We note that the turnover of the molecule does not cost much energy, and the discrimination of different adsorption sites is not very pronounced. In fact, the same span of adsorption energies, −0.21 to −0.06 eV, will cover the cases of water molecule adsorption over other substrates to be considered in the following subsections.

Summarizing the situation with BC₃, the adsorption energies of I₂ and CH₃I on this substrate seem interestingly large, exceeding (in configurations which correspond to the largest adsorption energies) that of water by a factor of two. (The adsorption of iodine-containing molecules tends to happen on top of the boron atom in the substrate. Both I₂ and CH₃I molecules, in their respective configurations with the strongest adsorption energy, place themselves flat over the substrate, roughly spanning the distance between two closest boron atoms in the substrate – cf.Fig. 1). The problem is that the carbon monoxide, in its optimal adsorption configuration, bonds, in its turn, two times more strongly than the iodine-containing molecules, therefore the latter cannot be discriminated over the background of CO. Moreover, the CH₃I molecule may happen to be adsorbed, at several metastable sites, with about the same energy as the water molecule, hence even the discrimination against water looks problematic. For this reason, we conclude that BC₃, a rising star in a number of interesting applications,^{27,29,63–65} is hardly promising for the detection of iodine-containing molecules.

In the hope that this would be different for other substrates, we turned to the study of Pmmn8-borophene and BC₆N-2 in the following subsections.

3.2 Adsorption on borophene

Pmmn-8 borophene is singled out among other substrates explored in our work in that its structure is neither hexagonal nor flat, and thicker than one atomic layer. In fact its surface consists of parallel ridges, separated by valleys, see Fig. 3. We will not discuss the adsorption in detail, because borophene failed to offer a satisfactory solution to the iodine selectivity problem, yet we provide an overview of the results briefly, for completeness. The configuration of the I₂ molecule with the strongest adsorption energy (−0.66 eV) is upright, anchored at the ridge (over a B–B bond along the ridge). The distance between the iodine atom and the closest boron atom underneath is 2.7 Å. The position parallel to the first one, upright over a valley (atop a B–B bond bridging the opposite slopes across the valley) yields the adsorption energy of −0.48 eV; the distance between iodine and the closest underlying boron atom is 3.3 Å. Two “flat” positions are along (atop) the ridge, with an adsorption energy −0.38 eV, the closest I–B distance being 3.51 Å, and along the valley between the two ridges, with the adsorption energy being −0.54 eV and the closest I–B distance of 3.86 Å. The most stable adsorption configuration found for CH₃I is upright as for I₂ yet slightly tilted and drifted, with its iodine “head”, onto the valley, attaining the adsorption energy of −0.35 eV.

Carbon monoxide molecules adsorb preferentially (adsorption energy of −0.65 eV) in oxygen-up (tilted) configuration, atop a boron atom in the ridge. This atom protrudes upwards, by about as much as the “contact” boron atom in BC₃. The B–C distance is 1.51 Å, again like in the case of adsorption on BC₃.

The strongest-energy (−0.24 eV) adsorption position of the water molecule is above the valley, in hydrogens-down orientation. A number of metastable configurations have been found, with adsorption energies −0.17 to −0.12 eV. Similar to the case of BC₃, the adsorption energy of H₂O is (in the major part of adsorption configurations) weaker than that of I₂ and CH₃I, which satisfies the target condition of our study. However, again in similarity with the case of BC₃, the CO molecule tends to make a stronger bond with the borophene sheet than the iodine-containing molecules do, in the case when it is adsorbed, with its carbon side, on top of a boron atom (Table S1 and Fig. S2 of the ESI†). Even if the difference between the adsorption energies (on borophene) of, from the one hand, CO and, from the other hand, I₂ and CH₃I is smaller than in the case of adsorption on BC₃, this does not yet make borophene a good sensor for I₂ and CH₃I. It is interesting to mention that the adsorption of CO on borophene leads also to a significant distortion in the borophene sheet (Fig. 3), which can be considered as a sign of the formation of a covalent bond between the molecule and the substrate.

3.3 Adsorption on BC₆N-2

We have seen that boron has a good affinity for iodine-containing species in contrast to that for water. However, when confronted with carbon monoxide, the boron atom in BC₃ and in borophene materials exhibits an enhanced tendency to share electrons with a fourth carbon atom whenever it comes into its vicinity, and to covalently bond with it, changing its (boron's) hybridization scenario. We hoped to cope with this problem in the next system tested, that contained some amount of nitrogen, an element with an extra electron in its valence band over that of carbon, which may fill the requirement of the boron atom in the sheet. Specifically, we considered BC₆N-2 in which the nitrogen atom is directly bonded to the boron atom (Fig. S3 of the ESI†) as a markedly preferential system, among the isomers previously simulated.^27,28 As we anticipated, the DFT calculations confirmed that the formation of a covalent bond with CO is prevented by the presence of nitrogen in the sheet (Fig. 4). However, let us discuss the adsorption preferences of different molecules in the same order as before. The preferential position of adsorbed I₂ (with energy −0.40 eV) is upright (as shown in Fig. 4), atop a carbon atom bonded with boron. Another competitive configuration (−0.39 eV) is upright atop the boron atom. On the contrary, the I₂ molecule initially placed atop a nitrogen atom escapes from this position. “Flat” configurations come about as “second choice” for adsorption, with slightly weaker energies (−0.35 to −0.33 eV). The I₂ molecule with about the same probability may lay over opposing carbon atoms in the C₅B hexagon, or over opposing either (C and B) or (C and N) atoms in a C₄BN hexagon.

The CH₃I molecule, similarly to I₂ as shown in Fig. 4, also preferentially adsorbs in the upright position, iodine atom down, over a carbon atom bonded with boron (with the adsorption energy − 0.27 eV), or otherwise atop B or N atoms (with adsorption energies −0.26 and −0.23 eV, correspondingly). The inverted configurations, with the methyl group turned to the substrate, are metastable with slightly weaker adsorption energies (−0.21 to −0.19 eV).

The carbon monoxide molecule stabilises in a tilted carbon-down configuration, over a substrate C atom bonded to B (at a distance of 3.14 Å, with an adsorption energy −0.12 eV), or immediately over a boron atom. Several not clearly discriminated end configurations with slightly different positions and tiltings come up with about the same adsorption energies, −0.12 to −0.11 eV. The upturned tilted position, with oxygen towards the substrate, is equally possible with an adsorption energy of −0.08 eV; in these cases the oxygen is anchored at the N atom in the substrate. This makes sense because the nitrogen is more electronegative than boron, and the oxygen end of the CO molecule is slightly positively charged, which is shown in the experimental work of Rosenblum et al.⁶⁶ We note in this relationship that the measured dipole moment of CO⁶⁷ is in good agreement with accurate calculations,⁶⁸ including modern DFT ones.³⁴ “Good news” in the context of our study is that in no configuration does the CO molecule bond to the substrate as strongly as was the case with previously discussed substrates, and moreover the “adsorption energy landscape” of carbon monoxide is quite smooth and not much depends on the position and orientation.

Stable adsorption configurations of the water molecule, which span the range of adsorption energies −0.17 to −0.15 eV, are characterized by “hydrogen-down” orientation atop the boron atom, or over C₅B, or over the C₄BN hexagon. In the “absence” of boron, when the molecule is docked over the C₅ N hexagon, the absorption energy is only slightly weaker, −0.14 eV. The “oxygen-down” orientation is also possible over a C atom close to B, with the energy −0.07 eV.

As a result, the adsorption energies of CO and H₂O for all the considered sites are systematically smaller than those of I₂ and CH₃I (cf. Table S1 of the ESI†). Consequently, the BC₆N-2 can be considered as good candidate for sensing I₂ and CH₃I molecules.

These results encourage us to push the investigation one step further by checking the adsorption on a 2D material where boron atoms are totally substituted by nitrogen atoms. This leads us to consider the C₃N sheet in the next section.

3.4 Adsorption on C₃N

3.4.1 General considerations and adsorption configurations. The adsorption of I₂, CH₃I, CO and H₂O on C₃N gives very promising results, as our DFT calculation reveals that the (absolute) adsorption energies for both iodine-containing molecules are in almost all cases larger than for the two iodine-free ones, over a wide range of possible initial positions (see Fig. S4 and Table S1 of the ESI†). The structures identified as those with the largest (the most negative) adsorption energy for each adsorbing molecule are shown in Fig. 5.

In more detail, the trial configurations of the I₂ molecule, initially placed over different sites of the substrate, end up either in “flat” or in “upright” (probably slightly tilted) geometry. The former span the range of adsorption energies from −0.80 to −0.73 eV; the latter from −0.60 to −0.51 eV; hence the two “families” of solutions are clearly separated. Among the “flat” solutions, those with the lowest energy correspond to the iodine atoms placing themselves either approximately over the centers of adjacent C₄N₂ hexagons, or roughly over opposite nitrogen atoms in the same hexagon. The placement of iodine atoms atop opposite C–C bonds in a hexagon, or over carbon atoms, have a disadvantage in what concerns the adsorption energy (measuring in these cases −0.78 to −0.73 eV); nevertheless one can conclude that the “adsorption relief” for the flat I₂ molecule stuck to (or, moving over) the C₃N layer is relatively even.

Among the “upright” positions of I₂, the strongest adsorption energy (−0.60 eV) is attributed to placements at a carbon atom or at a C–C bond, whereas the weakest energy (−0.51 eV) corresponds to anchoring at a N atom. Somehow simplifying, one can conclude that an I₂ dimer seeks to share its coupling over two nitrogen atoms in the substrate, whereas a terminal iodine atom in the upright molecule, on the contrary, avoids nitrogen in the substrate.

The CH₃I molecule may be adsorbed on a number of sites in different configurations, which can be sorted out into three groups, according to the molecule's orientation. The strongest adsorption energies (−0.31 to −0.34 eV) correspond to “flat” geometry (the I–C bond being roughly parallel to the C₃N plane), whereby the position of the iodine “head” – over C, N or hollow site – is relatively unimportant (with a slight preference nevertheless towards docking the iodine atom atop of carbon).

Adsorption of CH₃I in an upright configuration (I atom towards the surface) is equally possible, with slightly weaker adsorption energy (−0.28 to −0.24 eV). The strongest energies (−0.28 eV) correspond to the cases of the molecule's iodine “head” being docked over a carbon atom, a C–C bond, or a C₆ hexagon. The weakest adsorption energies are over a C₄N₂ hexagon (−0.25 eV) or atop a nitrogen atom (−0.24 eV).

Finally, an adsorption in upright iodine-up configurations is also possible, with yet lower energy (−0.22 to −0.18 eV). Of these possibilities, the weakest adsorption (−0.18 eV) occurs over a center of C₆ hexagon; all other possibilities are very close in energy (−0.21 to −0.22 eV). It is remarkable that, having three distinct groups of possible CH₃I dockings, the adsorption energies in all of them remain (even if just slightly) larger than in the “best” configurations for the “competing” molecules, CO and H₂O.

For carbon monoxide, some of the trial initial configurations end up in relaxed positions with adsorption energies −0.15 through −0.07 eV, hence markedly weaker than for iodine-containing molecules. The strongest coupling occurs in almost “flat” configurations (the oxygen end slightly higher, the carbon end hangs over the hollow C₆ site, off-centered towards a C–C bond). Otherwise, upright (or slightly tilted) oxygen-up configurations are possible over different sites, with adsorption energies −0.13 to −0.10 eV, and upright carbon-up configurations, also over different sites, with adsorption energies −0.09 to −0.07 eV.

Finally, the water molecule would preferably stabilise itself in asymmetric “hydrogens-down” configuration over a hollow C₆ or C₄N₂ site or atop a carbon atom, with adsorption energies −0.19 to −0.17 eV. Another dense set of favourable configurations (with adsorption energies −0.12 to −0.07 eV) is “oxygen-down”, again either over hollow sites, or – here – atop a nitrogen atom. The hydrogens-down position over a nitrogen atom in the substrate is a kind of intermediate one between the abovementioned two groups, with an adsorption energy of −0.13 eV.

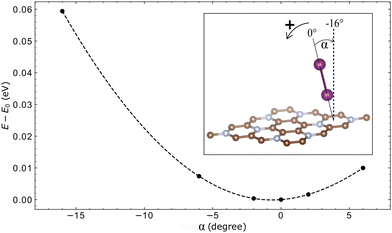
It is noteworthy that some molecules, when adsorbed, stabilise themselves in a low-symmetry inclined position. In order to verify that this indeed corresponds to the genuine energy minimum, and to estimate its “flatness”, we scanned in one of such cases, that of the I₂ molecule adsorbed on C₃N, its total energy as a function of deviation from the nominal equilibrium angle; see Fig. 6. The total energy profile turned out to be well “centered” and symmetric with respect to this inclined configuration.

Fig. 6 Effect of deviating the inclination of the I₂ on C₃N with respect to its relaxed position given by the DFT calculation. E₀ is the energy of the relaxed system. The inset shows the system at its relaxed position and specifies the inclination angle of I₂.

One can expect from these results that CO and H₂O molecules do not show any marked preference for a particular adsorption geometry, and the adsorption energies are “uniform” over different sizes and not large in their magnitude. One can anticipate certain volatility of adsorption configurations for these gases and, in principle, their mobility over the substrate. This reduces the risk of CO and H₂O getting stuck at some positions, degrading the sensing capability of substrate for iodine-containing molecules. These latter show clear preference for particular adsorption configurations, which are characterized by considerable adsorption energies.

The adsorption energies of I₂, at different sites and in different configurations, are larger than those of CO or H₂O by 0.36–0.73 eV, while for the case of CH₃I, this difference ranges between ≃0 and 0.27 eV. The relaxed structures of the positions with the strongest adsorption energy for each molecule are shown in Fig. 5. We noticed that, like the case of BC₆N-2, no covalent bond was formed between the CO and the C₃N. On the other hand, no significant distortion in the C₃N was observed after the adsorption of the molecules.

3.4.2 Role of dispersion interactions. It could be anticipated that dispersion interactions will be important in shaping the adsorption energies in different configurations. Consequently, the existing diversity of practical methods to implement these interactions in a DFT calculation may contribute to confusion and biasing the results. All the energies reported so far have been obtained with the DFT-D2 method of Grimme,⁵⁵ as indicated in Section 2. In the present section, dealing with our potentially interesting results for adsorption on the most promising (for the purposes of iodine sensitivity) substrate, we provide a more detailed analysis, based also on the use of the DFT-D3 method of Grimme with Becke–Jonson damping,⁵⁶ Many-Body Dispersion energy method,⁵⁷ and Tkatchenko–Scheffler⁵⁸ method with iterative Hirshfeld partitioning.⁵⁹ The obtained results are presented in Fig. 7.

Fig. 7 Adsorption energies (in eV) in the most preferable positions of I₂, CH₃I, CO, and H₂O molecules on the C₃N sheet. D2, D3(BJ), MBD and TS/HI are the DFT+D2 method of Grimme, DFT+D3 method of Grimme with Becke-Jonson damping, Many-Body Dispersion energy method, and Tkatchenko–Scheffler method with iterative Hirshfeld partitioning, respectively.

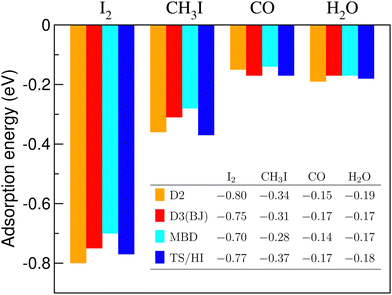
One can note a reasonable consistency of results for the molecules and dispersion-energy schemes considered. It seems important that the order of the adsorption energies throughout the row of the molecules considered remains the same, irrespective of the scheme applied. We cannot judge the true accuracy of the methods without comparing them to experimental results. However, we refer to this comparison as an argument in favour of credibility of our results concerning equilibrium energies and conformations.

A relevant question is how large the net contribution of dispersion interactions, expressed according to Eq. (2), is in the total adsorption energy of the molecules. Fig. 8 shows these contributions (calculated with the DFT-D2 method of Grimme) for the four molecules adsorbed on C₃N. For the two iodine-containing molecules, for comparison, the estimations of the adsorption energy from MD calculations, according to Eq. (5), and the corresponding dispersion contributions in them are also given.

Fig. 8 Contribution of the dispersion energy correction (E^disp_ad) in the total adsorption energy (E_ad) for four molecules, computed at the PBE+D2 level of theory. The corresponding estimates from AIMD calculations are added for I₂ and CH₃I.

A remarkable observation is that the dispersion part makes all the adsorption energy in the case of CO and H₂O adsorption, and exceeds the resulting adsorption energy for CH₃I. In other words, according to a “conventional” DFT calculation, the CH₃I molecule would “flow away” from the C₃N substrate, whereas carbon monoxide and water molecules won't show any adsorbing tendency at this surface. In the case of the I₂ molecule, the situation is different and the dispersion part makes just slightly more than the half of the resulting adsorption energy. This means that “chemistry” is important in this case, and will be discussed further on.

3.4.3 Effect of adsorption on the electronic properties of C₃N. The previously discussed trends in the adsorption energies (at least, in what regards the DFT parts) are manifestations of underlying changes in the electronic structure in the course of adsorption. Fig. 9 depicts the summary of partial densities of states (PDOS) and total density of states (DOS) for a supercell cut out of the C₃N monolayer, with the four different molecules adsorbed on it (in their respective lowest-energy configurations, shown in Fig. 5). The DOS within the substrate are not visibly affected by interaction with adsorbed molecules; however, in principle, these tiny modifications in the band structure of the substrate, resulting from superposition with molecules' electronic states (also slightly modified) bring about tiny preferences in the total energy for one or other structure conformation. In a brief overview, we cannot do more than to make notes on how exactly the molecules' energy levels split and superpose with the substrate DOS. These results, obviously, correspond to pure DFT (GGA) calculations (since the dispersion interactions are included via a correction to total energy and do not yield and specific displacement of energy levels), with all usual shortcomings related to addressing the electronic structures of molecules within the DFT. Different DOS are aligned by the corresponding Fermi levels, and set to zero in the common energy scale. The attribution of p_x, p_y, and p_z projections in the PDOS relates to the global Cartesian system as chosen in Fig. 5, i.e., x along the a lattice vector, y perpendicular to it in the layer, and z normal to the layer. (Additional markers ‖,⊥ refer to the axis of the molecule in question.) The resulting (near) degeneracies of p levels, highlighted by choosing mirror up/down directions of corresponding PDOS axes in some panels of Fig. 9, may therefore vary, due to different orientations of molecules in Fig. 5.

Fig. 9 Total density of states for the four molecules (indicated at the top of each column) adsorbed on C₃N substrate (bottom panel in each column) and partial densities of states in adsorbed molecules (in the panels above it). Zero energy delimits the occupied states (shown shaded in the bottom panel).

According to our calculation, the band gap of the C₃N sheet is 0.35 eV which is in agreement with a recent computational result based on the same method of calculation.⁶⁹ This is (expectedly) underestimated with respect to hybrid-functional (HSE06) calculation⁷⁰ (1.042 eV) and to the reported experimental value⁷¹ (2.67 eV). We already mentioned that the “chemical” part in the adsorption energy, which can be grasped in a “pure” DFT calculation, is negligible in the case of CH₃I, CO and H₂O molecules. Consequently, no appreciable traces in the electronic structure can be anticipated upon adsorption. One can otherwise express this as physisorption being the principal mechanism.

For the case of I₂, the situation is a bit different. The system of energy levels of the I₂ molecule includes (occupied) 5s states, split into bonding/antibonding combinations and situated at ≃−13/−11.5 eV, respectively, in Fig. 9 [I₂]. The 5p states directed along the molecule axis undergo a relatively strong σ hybridization, yielding energy levels at ≃−4 and ≃0 eV in Fig. 9 [I₂], which are marked p_x(‖), according to the choice of the coordinate system. Moreover, a weaker π-bonding splits the (doubly degenerate) 5p states extended in the perpendicular directions to the I–I axis, labelled p_y(⊥) and p_z(⊥). The corresponding peaks at ≃−2.3 and ≃−1.2 eV bracket the Dirac cone (at −2 eV) in the electronic structure of the substrate. Therefore, prominent peaks of molecular origin superpose with “sensitive” places of the substrate DOS: just at the top of the valence band and flanking the Dirac cone.

The counting of electrons to be placed onto a system of 5s+ 5p hybridized states in a I₂ molecule would leave the highest (5p σ-antibonding) state empty, and so it stays also on adsorption. In fact, the sharp peak in the DOS at (just above) 0 eV is empty (indicated by color in Fig. 9 [I₂]) and plays a role of acceptor level in a semiconductor. Somewhat counter-intuitively, during adsorption, this level is not populated with electrons, but, on the contrary, the I₂ molecule loses its charge to the benefit of the substrate. This can be evidenced by the Bader analysis,^60,72–75 according to which 0.43 electrons flow away from the basins associated with the I₂ molecule, comparing the cases of the latter being free and adsorbed on C₃N (cf. Table S3 of the ESI†).

The attribution of Bader charges is an unambiguously defined (hence comparable throughout calculation methods) yet not necessarily a physically (chemically) enlightening procedure. A different representation of charge flow can be given by a map of differential charge density, comparing the cases of adsorbed molecule on a substrate and a superposition of these two entities calculated in their separation. These charge density differences (CDD) are shown in Fig. 10 by conveniently chosen isosurfaces. We note that for the figure depicting the I₂ molecule, the isolevel (chosen arbitrarily but so as to emphasize non-trivial features) is set much higher than would be good for other molecules, in accordance with the generally higher amount of charge transfer. One can see from Fig. 10 [I₂] that the charge flow mostly depopulates 5p states of iodine (to a slight profit of 5s states) and more or less uniformly enriches the substrate atoms below the adsorbed molecule, the main recipients, also at some distance, being the nitrogen atoms. In simple terms, this can be considered as a manifestation of relative electronegativities, that of nitrogen (3.04, in the Pauling scale) being larger than for iodine (2.66) and carbon (2.55). As a result, the adsorption energy includes an important chemical (DFT) part (cf. previous discussion around Fig. 7), of partially ionic origin. This observation will not hold anymore for other adsorbed molecules.

Fig. 10 Charge density difference (CDD) due to the adsorption of molecules on the C₃N sheet. Isosurfaces corresponding to an inflow of electron density (negative charge) are shown in red, those to an outflow (loss of electrons; extra positive charge) are shown in blue. The absolute value of the (+/−) differential charge density (in units of e Å⁻³) are indicated in each panel.

For the CH₃I molecule, the hybridisation of I 5s and C 2s levels produces two peaks split by ≃2.5 eV – cf.Fig. 9 [CH₃I]. A much larger splitting (≃7 eV) occurs due to σ bonding between I 5p_y and C 2p_y (along the molecule axis) states, followed by smaller (≃4.5 eV) splitting induced by π hybridisation between I 5p_⊥ and C 2p_⊥ states. PDOS are almost identical within each pair of (p_x,p_z) states (perpendicular to the molecule's axis but either parallel or normal to the substrate layer); this reveals indifference of the molecule's electronic states to the presence of the substrate. Except in the case of I₂, all the molecular states place themselves relatively far from the band gap, either below or above (the closest being the empty σ level at ≃1.5 eV). The net charge transfer, according to the difference of Bader charges, is 0.00. The CDD isosurfaces shown in Fig. 10 [CH₃I] (note a very low isolevel value chosen) reveal a disappearingly small relocation of electron density from In 5p states perpendicular to the C–I axis (the highest occupied among the molecular states, cf. upper panel of Fig. 9 [CH₃I]) onto the substrate underneath. From “chemical” considerations, this interaction does not result in any bonding. As shown in Fig. 8, the dispersion energy correction dominates in the resulting adsorption energy, compensating for a slightly “underbonding” character of DFT prediction.

From Fig. 8, the net “chemical” contribution in the adsorption energy is also absent for the two remaining molecules, CO and H₂O; correspondingly the CDD isosurfaces shown for them in Fig. 10 can only be chosen almost at a level of numerical noise, without a chance to draw any enlightening conclusions from their shape. The net values of the Bader charge transfer are −0.04e for CO and −0.02e for H₂O, hence formally from the molecule to the substrate but on the brink of disappearance (cf. Table S3 of the ESI†).

Some words can be however said about the superposition of the molecular levels with the substrate DOS for these two systems.

The peaks of the other molecules are relatively far from the Fermi energy which explains the vdW nature of interaction between these molecules and the sheet, therefore we cannot expect a great impact on the electronic properties of the sheet in these cases. For more details, the PDOS plots for each orbital of the constituting atoms of each structure are presented in Fig. S5–S8 of the ESI.†

4 Conclusions

Summarizing, we simulated from first principles (applying periodic boundary conditions) the adsorption of I₂, CH₃I, CO, and H₂O molecules on BC₃, borophene, BC₆N-2, and C₃N 2D materials in a search for a sensor or detector which would readily adsorb iodine-containing molecules and so help to discriminate them from other atmospheric ones. BC₃ and borophene, even if suggested by some considerations, did not prove themselves promising in this context. The major problem consisted in that a strong covalent bond was formed between the CO molecule, oriented upright with carbon end downwards, and the underlying boron atom, thus resulting in a “contamination” of the prospective sensor. In BC₆N-2, the presence of nitrogen atoms prevents the formation of the covalent bond with CO; however, the energy difference between the adsorption energies of I₂ and CH₃I, from one side, and those of CO and H₂O, from the other side, is not convincingly large; therefore, even if this system can, in principle, be used for sensing I₂ and CH₃I gases, its selectivity might be in need of improvement. Finally, the results from the adsorption on C₃N seem very promising in that the difference between the adsorption energies of (I₂, CH₃I) vs. (CO, H₂O) is significant. Our calculations reveal that the “pure DFT” part of adsorption energy (e.g., due to chemical bonding) is appreciable, out of the systems considered, only in the case of adsorption of the I₂ molecule, which was accompanied by a redistribution of charge (of about half an electron, estimated from calculations of Bader charges) from the molecule towards the substrate. About 60% of the resulting adsorption energy (in the case of I₂ adsorption on C₃N) and nearly the whole energy in the case of CH₃I, CO and H₂O adsorption are due to dispersion interaction, which can be included in the calculation on top of the “conventional” interactions grasped by the DFT. A variety of practical methods (at different levels of accuracy) suggested to grasp the effect of dispersion interactions have been applied within the present work; they did not result in big scattering of estimations for the adsorption energy in each given system. For a detailed discussion of the trends (energies in different adsorption geometries etc.), the results obtained with a semi-empirical Grimme D2 method have been therefore considered.

Understanding the complexity of a read adsorption process, we took care of including possibly many (in principle, “all” in view of symmetry of perfect surfaces) initial configurations as starting conditions of the conjugate-gradient search towards a few metastable adsorption configurations, which could have been thus identified. Aware of limitations of this “static” (zero-temperature) approach, we attempted molecular dynamics simulations for two systems, I₂ and CH₃I on C₃N, which reinforced the conclusion on stability of molecules “dancing” in the adsorbed state.

The order-of-magnitude consistency of adsorption energy estimates from these (exploratory/trial) dynamic and from (systematic/controllable) static simulations is encouraging; yet these are only far approximations from different sides to the physics of the process. As obvious improvements of the present approach, one should consider vibrations and zero-point energy corrections. Moreover, a model of the monolayer substrate is likely to be in a need of adjustment to the conditions of practical realisation. In particular, the effect of water coverage is worth examining, because under realistic conditions this molecule is expected to be much more abundant than the others studied here. However, on the basis of the results obtained so far one can suggest verification of our findings in experiments, in view of practical use of C₃N for iodine sensing.

Author contributions

K. Zhour: formal analysis, investigation, validation, visualization, writing – original draft. A. Daouli: data curation, investigation. A. Postnikov: formal analysis, visualization, writing – review & editing. A. Hasnaoui: supervision. M. Badawi: conceptualization, methodology, project administration, supervision, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

A. D., A. H. and M. B. acknowledge financial support from the Ministry of Europe and Foreign Affairs of France, Ministry of Higher Education, Research and Innovation of Morocco and the French Institute of Rabat within the PHC TOUBKAL 2022, grant Number: 12345AB. K. Z. and A. P. thank the mesocenter of calculation EXPLOR at the Université de Lorraine (project 2019CPMXX0918) for access to computation facilities.

Notes and references

1. B. Clément, L. Cantrel, G. Ducros, F. Funke, L. Herranz, A. Rydl, G. Weber and C. Wren, State of the art report on iodine chemistry, Organisation for economic co-operation and development technical report, 2007.
2. D. R. Haefner and T. J. Tranter, Methods of Gas Phase Capture of Iodine from Fuel Reprocessing Off-Gas: A Literature Survey, Idaho National Lab. (INL), Idaho Falls, ID (United States) Technical Report, 2007.
3. B. Xerri, S. Canneaux, F. Louis, J. Trincal, F. Cousin, M. Badawi and L. Cantrel, Comput. Theor. Chem., 2012, 990, 194–208.
4. A. J. González, Health Phys., 2007, 93, 571–592.
5. J. R. Goldsmith, C. M. Grossman, W. E. Morton, R. H. Nussbaum, E. A. Kordysh, M. R. Quastel, R. B. Sobel and F. D. Nussbaum, Environ. Health Perspect., 1999, 107, 303–308.
6. J. Huve, A. Ryzhikov, H. Nouali, V. Lalia, G. Augé and T. J. Daou, RSC Adv., 2018, 8, 29248–29273.
7. B. J. Riley, J. D. Vienna, D. M. Strachan, J. S. McCloy and J. L. Jerden Jr., J. Nucl. Mater., 2016, 470, 307–326.
8. L. J. Small and T. M. Nenoff, ACS Appl. Mater. Interfaces, 2017, 9, 44649–44655.
9. M. L. Daz-Ramrez, B. Vargas, J. R. Álvarez, B. Landeros-Rivera, M. Rivera-Almazo, C. Ramos, J. G. Flores, E. Morales, R. Vargas and J. Garza, et al. , Dalton Trans., 2020, 49, 6572–6577.
10. M. Xu, T. Wang, L. Zhou and D. Hua, J. Mater. Chem. A, 2020, 8, 1966–1974.
11. C. Muhire, A. T. Reda, D. Zhang, X. Xu and C. Cui, Chem. Eng. J., 2021, 133816.
12. Y.-F. Sun, S.-B. Liu, F.-L. Meng, J.-Y. Liu, Z. Jin, L.-T. Kong and J.-H. Liu, Sensors, 2012, 12, 2610–2631.
13. P. Dariyal, S. Sharma, G. S. Chauhan, B. P. Singh and S. R. Dhakate, Nanoscale Adv., 2021, 3, 6514–6544.
14. I. Raya, H. H. Kzar, Z. H. Mahmoud, A. Al Ayub Ahmed, A. Z. Ibatova and E. Kianfar, Carbon Lett., 2021, 1–26.
15. F. R. Baptista, S. A. Belhout, S. Giordani and S. J. Quinn, Chem. Soc. Rev., 2015, 44, 4433–4453.
16. S. G. Ramaraj, M. Muruganathan, O. G. Agbonlahor, H. Maki, Y. Onda, M. Hattori and H. Mizuta, Carbon, 2022, 190, 359–365.
17. K. R. Nandanapalli, D. Mudusu and S. Lee, Carbon, 2019, 152, 954–985.
18. Q. Tang, Z. Zhou and Z. Chen, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 360–379.
19. S. M. Scott, T. Hu, T. Yao, G. Xin and J. Lian, Carbon, 2015, 90, 1–8.
20. R. Kumar, J. Mittal and M. Jaiswal, Diamond Relat. Mater., 2021, 120, 108551.
21. E. Cho, A. Perebikovsky, O. Benice, S. Holmberg, M. Madou and M. Ghazinejad, Sensors, 2018, 18, 1486.
22. M. Kim, W. J. Kim, E. K. Lee, S. Lebègue and H. Kim, Int. J. Quantum Chem., 2016, 116, 598.
23. A. J. A. Price, K. R. Bryenton and E. R. Johnson, J. Chem. Phys., 2021, 154, 230902.
24. A. N. Rudenko, F. J. Keil, M. I. Katsnelson and A. I. Lichtenstein, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 035427.
25. M. Arabieh and Y. T. Azar, Appl. Surf. Sci., 2018, 434, 604–612.
26. S. Beniwal, J. Hooper, D. P. Miller, P. S. Costa, G. Chen, S.-Y. Liu, P. A. Dowben, E. C. H. Sykes, E. Zurek and A. Enders, ACS Nano, 2017, 11, 2486–2493.
27. B. Mortazavi, M. Shahrokhi, M. Raeisi, X. Zhuang, L. F. C. Pereira and T. Rabczuk, Carbon, 2019, 149, 733–742.
28. L.-B. Shi, M. Yang, S. Cao, Q. You, Y.-J. Zhang, M. Qi, K.-C. Zhang and P. Qian, J. Mater. Chem. C, 2020, 8, 5882–5893.
29. H. Tanaka, Y. Kawamata, H. Simizu, T. Fujita, H. Yanagisawa, S. Otani and C. Oshima, Solid State Commun., 2005, 136, 22–25.
30. S. Yang, W. Li, C. Ye, G. Wang, H. Tian, C. Zhu, P. He, G. Ding, X. Xie and Y. Liu, et al. , Adv. Mater., 2017, 29, 1605625.
31. X. Liu, X. Ma, H. Gao, X. Zhang, H. Ai, W. Li and M. Zhao, Nanoscale, 2018, 10, 13179–13186.
32. S. M. Aghaei, A. Aasi, S. Farhangdoust and B. Panchapakesan, Appl. Surf. Sci., 2021, 536, 147756.
33. V. Babar, S. Sharma and U. Schwingenschlögl, J. Phys. Chem. C, 2020, 124, 5853–5860.
34. S. Mehdi Aghaei, M. M. Monshi, I. Torres, S. M. J. Zeidi and I. Calizo, Appl. Surf. Sci., 2018, 427(part A), 326–333.
35. D. Ma, J. Zhang, X. Li, C. He, Z. Lu, Z. Lu, Z. Yang and Y. Wang, Sens. Actuators, B, 2018, 266, 664–673.
36. L. E. Herranz, T. Lind, K. Dieschbourg, E. Riera, S. Morandi, P. Rantanen, M. Chebbi and N. Losch, Proceedings of the 10th International Topical Meeting on Nuclear Thermal-Hydraulics, Operation and Safety (NUTHOS-10), Okinawa, Japan, December 14-18, 2014, 2015, pp. NUTHOS10-1106.
37. D. Jacquemain, S. Guentay, S. Basu, M. Sonnenkalb, L. Lebel, J. Ball, H. J. Allelein, M. Liebana, B. Eckardt, N. Losch, L. Ammirabile, D. Gryffroy, L. Sallus, A. Kroes, T. Rensonnet, A. Anden, S. Gyepi-Garbrah, A. Viktorov, J. Duspiva, T. Routamo, S. Guieu, A. Hotta, H. Nakamura, J. H. Song, K. S. Ha, C. Filio, M. V. Kuznetsov, L. Kubisova, T. Nemec, W. Frid, D. Loy, D. Pellini, T. Zieger, L. Herranz Puebla, A. Amri and M. Kissane, OECD/NEA/CSNI Status Report on Filtered Containment Venting, Organisation for economic co-operation and development technical report, 2014.
38. J. J. Foit, Nucl. Eng. Des., 1997, 170, 73–79.
39. M. Chebbi, S. Chibani, J.-F. Paul, L. Cantrel and M. Badawi, Microporous Mesoporous Mater., 2017, 239, 111–122.
40. S. Chibani, I. Medlej, S. Lebègue, J. G. Ángyán, L. Cantrel and M. Badawi, ChemPhysChem, 2017, 18, 1642–1652.
41. S. Chibani, M. Chebbi, S. Lebègue, T. Bucko and M. Badawi, J. Chem. Phys., 2016, 144, 244705.
42. S. Chibani, M. Chebbi, S. Lebègue, L. Cantrel and M. Badawi, Phys. Chem. Chem. Phys., 2016, 18, 25574–25581.
43. F. R. Baptista, S. A. Belhout, S. Giordani and S. J. Quinn, Chem. Soc. Rev., 2015, 44, 4433–4453.
44. V. Van Speybroeck, K. Hemelsoet, L. Joos, M. Waroquier, R. G. Bell and C. R. A. Catlow, Chem. Soc. Rev., 2015, 44, 7044.
45. B. A. De Moor, M.-F. Reyniers, O. C. Gobin, J. A. Lercher and G. B. Marin, J. Phys. Chem. C, 2011, 115, 1204–1219.
46. F. Göltl, A. Grüneis, T. Bucko and J. Hafner, J. Chem. Phys., 2012, 137, 114111.
47. G. Piccini, M. Alessio, J. Sauer, Y. Zhi, Y. Liu, R. Kolvenbach, A. Jentys and J. A. Lercher, J. Phys. Chem. C, 2015, 119, 6128–6137.
48. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
49. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
50. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
51. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
52. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
53. K. Zhour and A. Postnikov, Phys. Status Solidi B, 2021, 258, 2100131.
54. K. Zhour, J. M. Otero-Mato, F. El Haj Hassan, H. Fahs, M. Vaezzadeh, E. López-Lago, L. J. Gallego and L. M. Varela, J. Mol. Liq., 2021, 321, 114759.
55. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
56. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
57. A. Tkatchenko, R. A. DiStasio Jr., R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402.
58. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
59. T. Bucko, S. Lebègue, J. G. Ángyán and J. Hafner, J. Chem. Phys., 2014, 141, 034114.
60. R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15.
61. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
62. W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695.
63. J. Beheshtian, A. Ahmadi Peyghan and M. Noei, Sens. Actuators, B, 2013, 181, 829–834.
64. A. Bafekry, S. Farjami Shayesteh, M. Ghergherehchi and F. M. Peeters, J. Appl. Phys., 2019, 126, 144304.
65. H. Zhang, Y. Tang, H. Chai, W. Chen, M. Zhao and X. Dai, Mol. Phys., 2019, 117, 125–135.
66. B. Rosenblum, A. H. Nethercot and C. H. Townes, Phys. Rev., 1958, 109, 400–412.
67. J. S. Muenter, J. Mol. Spectrosc., 1975, 55, 490–491.
68. G. E. Scuseria, M. D. Miller, F. Jensen and J. Geertsen, J. Chem. Phys., 1991, 94, 6660–6663.
69. A. Bafekry, M. Neek-Amal and F. M. Peeters, Phys. Rev. B, 2020, 101, 165407.
70. X. Zhou, W. Feng, S. Guan, B. Fu, W. Su and Y. Yao, J. Mater. Res., 2017, 32, 2993–3001.
71. J. Mahmood, E. K. Lee, M. Jung, D. Shin, H.-J. Choi, J.-M. Seo, S.-M. Jung, D. Kim, F. Li and M. S. Lah, et al. , Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 7414–7419.
72. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
73. E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908.
74. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354.
75. M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 134, 064111.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02205f

‡ Present address: Institut für Physikalische Chemie, Universität Münster, Germany.

---