Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dioctyl sodium sulfosuccinate surfactant self-assembly dependency of solvent hydrophilicity: a modelling study†
Maisa
Vuorte
 ab,
Aapo
Lokka
ab,
Alberto
Scacchi
ab,
Aapo
Lokka
ab,
Alberto
Scacchi
 abc and
Maria
Sammalkorpi
abc and
Maria
Sammalkorpi
 *abd
*abd
aDepartment of Chemistry and Materials Science, School of Chemical Engineering, Aalto University, P.O. Box 16100, FI-00076 Aalto, Finland. E-mail: maria.sammalkorpi@aalto.fi
bAcademy of Finland Center of Excellence in Life-Inspired Hybrid Materials (LIBER), Aalto University, P.O. Box 16100, FI-00076 Aalto, Finland
cDepartment of Applied Physics, School of Science, Aalto University, P.O. Box 11000, FI-00076 Aalto, Finland
dDepartment of Bioproducts and Biosystems, School of Chemical Engineering, Aalto University, P.O. Box 16100, FI-00076 Aalto, Finland
First published on 21st September 2023
Abstract
The self-assembly of dioctyl sodium sulfosuccinate (AOT) model surfactant in solvent environments of differing polarity is examined by means of dissipative particle dynamics (DPD) bead model parametrized against Hildebrand solubility parameters from atomistic molecular dynamics (MD) simulations. The model predicts that in hydrophobic solvents (e.g. dodecane) the surfactant forms small (Nagg ∼ 8) reverse micellar aggregates, while in a solvent corresponding to water lamellar assembly takes place, in good agreement with literature structural parameters. Interestingly, solvents of intermediate polarity lead to formation of large, internally structured aggregates. In these, the surfactant headgroups cluster within the aggregate, surrounded by a continuous phase formed by the hydrocarbon tails. We show that the partitioning of the headgroups between the aggregate surface layer and the inner clustered phase depends primarily on solvent polarity, and can be controlled by the solvent, but also system composition. Finally, we compare the DPD assembly response to simplified effective interaction potentials derived at dilute concentration limit for the interactions. The comparison reveals that the simplified effective potential descriptions provide good level of insight on the assembly morphologies, despite drastic, isotropic interactions simplification involved.
1 Introduction
Surfactants and their assemblies have widespread technological applications, including the use as detergent and wetting agents,1 emulsifiers,2,3 microreactors,4–6 and in nanoparticle synthesis.7–10 Intermolecular interactions drive surfactant self-assembly into diverse morphologies, including spherical, rod-like, hexagonal, and lamellar phases, tunable via environmental factors such as surfactant concentration, solvent chemistry, temperature, and additives, such as water, salt or co-surfactants.11Dioctyl sodium sulfosuccinate (AOT) is an anionic model surfactant, known especially for forming well-characterized reverse micellar systems in apolar solvents, tunable via solvent chemistry, surfactant concentration and, particularly, water to surfactant ratio.12–16 Experimentally, AOT self-assemblies have been characterized using dynamic light scattering (DLS),17–19 small-angle X-ray scattering (SAXS),17,18,20 small-angle neutron scattering (SANS),15,21,22 nuclear magnetic resonance spectroscopy (NMR),16 fluorescence labeling,23 as well as, viscosity experiments.24,25 However, obtaining detailed molecular level description of these structures is challenging due to the dynamic and heterogeneous nature of the aggregates. This contributes to the experimentally derived structural parameters, especially at the low hydration limit, having a large scatter.14,16 Consequently, some uncertainty of AOT assembly and assembly characteristics at molecular level in different environments and solution conditions persists.
In non-polar solvents, such as hydrocarbons, AOT forms reverse micelles, characterized significantly in prior works.15,24,26–28 AOT reverse micelles with aqueous cores have technological applications in, e.g., nanoparticle synthesis,10,29,30 as microreactors, and as extraction systems.31,32 On the other hand, in dry hydrocarbon solvents, AOT forms monodisperse, slightly aspherical aggregates with aggregation numbers corresponding to 20–30 AOT molecules, depending on the molar volume of the solvent.14,24,33,34 Additionally, aggregation propensity of AOT has been shown to depend strongly on the polarity of the solvent, as well as the presence of trace water in the system.35,36 Particularly, the shape and size of the reverse micelles depend on the water-to-surfactant ratio.37,38 The high sensitivity to trace water is also well-known for other reverse micellar systems.39–43
AOT–water self-assembling systems have received comparably less attention. In purely aqueous systems, AOT displays a range of interesting self-assembly morphologies that depend on concentration and temperature.44–48 The lamellar mesophase has been most well documented,45,48–51 however, bi-continuous cubic phases and inverse hexagonal phases have also been observed at high AOT concentrations.33,45 Additionally, small AOT micelles have been reported in experiments corresponding to isotropic solutions at low concentration,52–54 although there remains a lack of consensus on micellar shape in these conditions. Importantly, the self-assembly response of AOT–water systems can be significantly tuned via addition of salt, that is, changing the dielectric screening constant of the solvent.55–57
Complementing the experimental characterization works reviewed above that provide information on the average AOT aggregate assembly structure, computer simulations, particularly molecular modelling techniques, are a powerful tool for determining the assembly morphology and dynamics of surfactant aggregates at a molecular level. Extensive computational studies of AOT self-assembly, with particular focus on AOT reverse micelles,38,58–61 exist in literature. The shape and fluctuations of small and larger preformed AOT reverse micelle aggregates, at dry and with various water loadings, have been extensively studied at both atomistic13,38,58,61–63 and coarse grained59,60,64–66 detail. Capturing larger scale self-assembly behaviour, such as the formation of AOT lamellar phases in water, is often beyond the time and length scale limitations of classical MD. On the other hand, atomistic MD simulations have been used to capture water and surfactant dynamics, and interface fluctuations in individual bilayers.50,67 Additionally, some work on overall bulk self assembly structures at atomistic detail level exist.68
Mesoscale simulation techniques, such as dissipative particle dynamics (DPD) simulations, bridge the gap between atomistic and macroscopic models in terms of the observable length and time scales.69–71 The trade-off is the abstraction of chemical features and molecular scale interactions, such as hydrogen bonding and solvent shell formation. However, well argumented DPD parametrization schemes of surfactant micellar systems have provided a good match to experimental observables.72–77 Furthermore, the approach has also enabled establishing scaling laws.78
Here, we construct a coarse-grained (CG) DPD model for AOT surfactant and explicit hydrocarbon solvent. The model is based on a bottom-up parametrization approach which relies on atomistic MD simulation data. In the model construction, we target such degree of coarse-graining NCG that achievable assembly length and time scales become sufficient to examine large scale assembly changes. The simplified, CG surfactant can be considered to model AOT, because via systematic tuning of the model interaction parameters, the equilibrium assembly response of the AOT surfactant–solvent binary systems in aqueous and hydrocarbon solvents is achieved. We map the assembly response in varying solvent polarities with examined range covering solvents from an apolar hydrocarbon solvent, to polar water solvent, as well as intermediate solvent polarities. The resulting equilibrium self-assembly phases are characterised with comparison to existing experimental data to verify the model response. The self-assembly response is analyzed for assembly characteristics and system dependencies with the purpose of gaining solvent dependent control over the assembly response. In addition to the known apolar hydrocarbon solvent and water solvent responses, the characterization covers self-assembly phases in solvents on intermediate polarity, for which the AOT self-assembly response in largely unknown. Finally, to map the limits of model simplification, we extract the corresponding dilute limit effective interactions potentials for selected AOT systems and compare them and their finite concentration assembly response in the DPD simulations.
2 Computational methods
2.1 Dissipative particle dynamics
DPD, first formulated by Groot and Warren,79 is a common CG particle-based simulation technique. The chemical system is described as interacting particles each corresponding to groups of atoms within a molecule or a region of solvent (i.e. cluster of solvent molecules). In addition to soft interaction potentials, DPD relies on dissipative forces calculated pairwise additively between the particles. The time evolution of the system of particles, commonly referred to as DPD beads, is obtained by integration of Newton's equations of motion. The DPD approach leads to conservation of momentum and preservation of hydrodynamics. The total force acting on a single DPD bead i69,75 is formulated as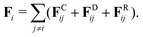 | (1) |
The repulsive soft-core potential, corresponding to the conservative force, allows using a significantly longer time step than in classical MD simulations. This translates into increased computational speed, as well as temporal and spatial resolution. The use of a soft-core potential is justified by the softness of effective interactions between groups of several hard-core (Lennard-Jones type) atoms.80 The DPD conservative force is given by
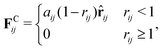 | (2) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij = rij/rij is referred to as
ij = rij/rij is referred to as ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij. In this, rij = ri − rj and rij = |rij|.
ij. In this, rij = ri − rj and rij = |rij|.
The random FRij and dissipative FDij forces are formulated as
FDij = −γωD(rij)(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij·vij) ij·vij)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij, ij, | (3) |
FRij = σωR(rij)ξijΔt−1/2![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij, ij, | (4) |
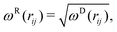 | (5) |
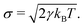 | (6) |
In this, T is the absolute temperature and kB the Boltzmann constant. Notably, the friction coefficient γ influences viscosity and hydrodynamic modes dissipation in DPD; if modelling dynamical properties of the different solutions, γ becomes an important parameter to consider in the model, see e.g. ref. 81–85. Here, the focus was on equilibrium structure, and a value of γ = 4.5 was used.79 Assembly structure is mainly dependent on the conservative force parameters.86 In standard DPD, all interacting beads, regardless of bead type or model chemical species, have the same mass mi and diameter rc. Typically, and without loss of generality, DPD simulations employ reduced units, so that rc = mi = kBT = 1.
2.2 Surfactant model parametrization
In the parametrization, we focus on tuning the repulsion parameters aij, which relate to the chemical nature of the modelled system and govern the equilibrium assembly response. Notably, if dynamical viscoelastic properties of the solutions are targeted, also the friction coefficient γ and the fluctuations decay should be considered. The CG DPD representation of the AOT molecule consists of two hydrophobic tail beads (T) linked by a hydrophilic head bead (H), see Fig. 1. The solvent is described by a monomeric solvent bead (S).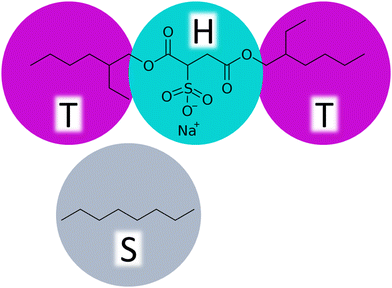 | ||
| Fig. 1 CG DPD bead representations of the AOT surfactant and the octane solvent used as the model hydrocarbon solvent in this study. | ||
The self-repulsion parameter aii is typically obtained by matching to isothermal compressibility κT. For water at T = 298 K, with coarse-graining degree NCG = 1, and DPD density ρ = 3, aii = 25 kBT. The same value is commonly used for also polymer blends, see e.g., ref. 79. To avoid losing generality of the model, we use the same compressibility value for the entirety of the examined range. aii scales linearly with NCG, as does the bead diameter rc = (ρNCGvm)1/3, where vm is the molecular volume of – in most cases – water. Therefore, the repulsive potential becomes steeper for larger beads, and the potential approaches hard-sphere-like behaviour. Following this approach, at an upper limit – in practice at NCG,limit < 1087 – the solvent freezes. It should be noted that DPD mappings with high NCG disregard the compressibility matching while matching other parameters, such as density and pressure. This allows DPD approaches to model also significantly higher NCG values than strictly allowed by the compressibility consideration. Since here we have NCG = 8, the choice aii = 25 kBT is well motivated. The cross-repulsion parameters aij were obtained via mapping the interactions to the Flory–Huggins mixing parameter χij as
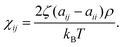 | (7) |
Here ζ = 0.101 ± 0.001 for DPD bead density ρ ≥ 3. In the current work, the Flory–Huggins mixing parameter is calculated from Hildebrand solubility parameters88 as
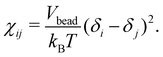 | (8) |
In this, Vbead is the DPD bead volume, while δi and δj are the Hildebrand solubility parameters for components i and j, respectively. The Hildebrand solubility parameter δ is defined based on cohesive energy Ecoh, that is, the energy difference between the condensed phase and the gas phase of a component. Here, Ecoh was determined based on all-atom MD simulations. In these, the CHARMM-C36 force field89,90 and the compatible Tip3p all-atom water model91,92 were used. The MD simulations were performed using the Gromacs v2020.393–95 simulation package. For the atomistic detail simulations values, separate condensed phase simulations consisting of 180 octane, 172 2-methylheptane, 122 sulfosuccinic acid, and 1265 water molecules, were first energy minimized for 1000 steps using the steepest-descent method.
The molecular species were chosen such that parameters for DPD parametrization corresponding to apolar hydrocarbon solvent (octane), polar solvent (water), and the AOT molecule composed of a head bead and two tail beads can be obtained. Notably, as all bead types in standard DPD are identical in mass and volume, the resulting beads correspond to the mass-equivalent of 8 water molecules of the parametrized species. In the model, the headgroup of the AOT molecule is considered as bound with the Na+ counterion.
Equilibration was achieved via 5 ns NPT ensemble simulations with timestep Δt = 2 fs. In these, temperature was controlled using the stochastic velocity rescale thermostat developed by Bussi et al.,96 with reference temperature T = 300 K and τT = 0.5 ps. A target pressure of p = 1.0 bar was maintained by isotropic Berendsen barostat97 with τP = 2.0 ps and compressibility of 4.5 × 10−5 bar−1.
Next, the non-bonded energy terms (Coulombic and Lennard-Jones contributions) were sampled during a 2 ns NVT ensemble simulation at T = 300 K. Additionally, single molecule gas phase, i.e. vacuum (in vacuo) simulations of individual sulfosuccinic acid, 2-methylheptane, and octane molecules, as well as, the 8 water molecules considered for single DPD bead, were set up using the exact simulation box dimensions of the condensed phase NVT run. This choice was made so that the system volume dependent part of the particle mesh Ewald method,98 used for electrostatic interactions, would be for same sized box. Non-bonded energy terms were sampled during a 2 ns NVT ensemble run at T = 300 K. Ecoh was then calculated as the difference in non-bonded energies of the condensed phase and the in vacuo simulations. Notably, reliable values of Ecoh require a well equilibrated condensed phase simulation. The solubility parameter can then be calculated as 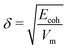 , where Vm is the molar volume. For tabulated non-bonded energies and solubility parameters, see Table S1 in the ESI.† The resulting DPD conservative repulsion parameters aij are presented in Table 1.
, where Vm is the molar volume. For tabulated non-bonded energies and solubility parameters, see Table S1 in the ESI.† The resulting DPD conservative repulsion parameters aij are presented in Table 1.
| Tail | Head | Solvent | |
|---|---|---|---|
| Tail | 25 | 73 | a TS |
| Head | 73 | 25 | a HS |
| Solvent | a TS | a HS | 25 |
Intramolecular T–H bonds in the three bead CG representation of the AOT molecule, Fig. 1, are described by a simple harmonic potential FBij = K(r − r0)2![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij, where the spring constant K = 20 kBTrc−1 and the inter-bead bond equilibrium length r0 = rc.
ij, where the spring constant K = 20 kBTrc−1 and the inter-bead bond equilibrium length r0 = rc.
2.3 System set-up and analysis
Simulations were performed in a cubic box of (60 rc)3 with rc ≈ 0.9 nm. Periodic boundary conditions were applied in all dimensions. With ρ = 3, this corresponds to 648000 beads per simulation box. For the initial configuration of each system, 14547 AOT (equivalent to a molar concentration of 150 mM or 6.7 w/w%) were randomly distributed within the simulation box. This particular concentration is selected for this study because it is an extremely common concentration used in various different types of experimental setups involving AOT, both in fundamental research and technological processes, see e.g. ref. 99–102. Additionally, the selected concentration exceeds critical micellization concentration (CMC) throughout the examined solvent polarity range.47,103,104 The remainder of the box was subsequently filled with monomeric solvent. Simulations were performed using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) MD program.105 Molecular visualization were produced using VMD.106 Each simulation was run for 5 × 106 steps with a time step Δt = 0.01. For data analysis, the last 5 × 105 simulation steps were used. During the beginning part of the trajectory, the structural and assembly characteristics equilibrated, as measured by cluster size distributions and order parameter time evolution analysis.Solvent was varied in the simulations by varying aTS and aHS, such that their values were scaled in steps, to correspond to a solvent environment from an apolar hydrocarbon solvent (system α1) to polar water (α12). The corresponding AOT miscibility parameter pairs aij are summarized in Table 2. Sensitivity of the assembly response to balance between aTS and aHS in the scaling was examined for systems α1, α3, α6, and α9, by variation of the solvent–surfactant interactions. Table 3 summarizes the range of sensitivity analysis and provides the sampled parameter values. All other interactions were kept constant. The detailed results of the sensitivity simulations can be found in the ESI.†
| a ij | α 1 | α 2 | α 3 | α 4 | α 5 | α 6 | α 7 | α 8 | α 9 | α 10 | α 11 | α 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Head–solvent | 71 | 67 | 66 | 61 | 56 | 51 | 46 | 41 | 36 | 31 | 25 | 21 |
| Tail–solvent | 25 | 30 | 31 | 38 | 44 | 51 | 58 | 63 | 70 | 76 | 83 | 89 |
| a ij | α 1s1 | α 1s2 | α 3s1 | α 3s2 | α 6s1 | α 6s2 | α 9s1 | α 9s2 | α 11s1 | α rep |
|---|---|---|---|---|---|---|---|---|---|---|
| Head–solvent | 60 | 80 | 56 | 76 | 41 | 61 | 29 | 33 | 25 | 80 |
| Tail–solvent | 25 | 25 | 31 | 31 | 51 | 51 | 76 | 76 | 80 | 80 |
The number of aggregates and aggregate sizes were determined using the DBSCAN clustering algorithm,108 which works on the assumption that clusters are dense regions in space separated by regions of lower density. The sklearn DBSCAN clustering function109 was used with parameters eps = 2 rc and min_samples = 25. eps defines the maximum distance between two beads to be considered a part of a cluster, accounting for periodic boundary conditions. min_samples defines the minimum number of points to form a core point.
The internal structure of the assemblies was characterized using the order parameter
 | (9) |
3 Results and discussion
Fig. 2 provides a visual summary of the AOT surfactant self-assembly response observed in different solvents. In the modelling, the solvent is varied by the differing miscibility of the AOT surfactant headgroup and tails with the solvent, as captured by the aHS and aTS parameters. Data shows significant assembly response changes due to solvent polarity ranging from the α1 (hydrocarbon solvent) system, that forms oligomeric aggregates and has free AOT dissolved in the solvent phase, to the aqueous solvent α12, which results in formation of well-defined lamellae.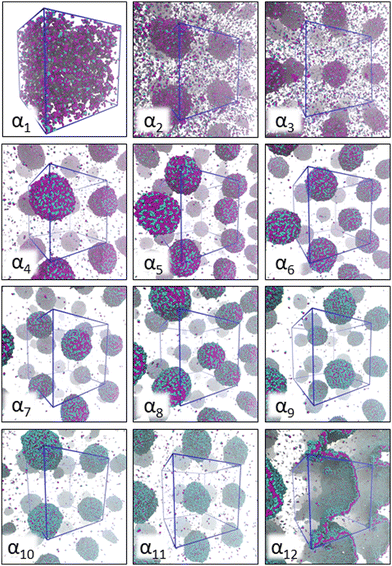 | ||
| Fig. 2 Simulation snapshots corresponding to AOT self-assembly (150 mM concentration) in the 12 different solvent compositions αi studied here. The corresponding aHS and aTS parameter combinations are summarized in Table 2. The AOT head beads are shown in cyan and tail beads in purple. For all systems, the visualization corresponds to the final simulation frame. The solvent beads are omitted in the visualization for clarity, and the boundaries of the periodic simulation box are marked as blue lines. For all systems except α1, where only very small aggregates form, periodic images are used to visualize the aggregates. | ||
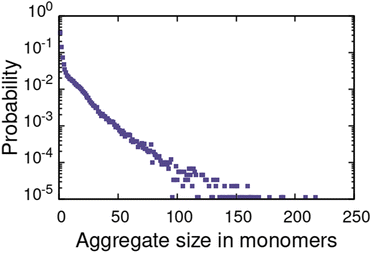
For the α1 (hydrocarbon solvent) system, very small AOT aggregates with average size Nagg = 7.8 form, see Fig. 3 for the aggregate size distribution. The observed aggregate size is smaller than the Nagg ≈ 10–30 previously reported for AOT reverse micelles in near water-less hydrocarbon solutions,15,24,33,110–112 including benzene (Nagg = 9–12),111,112 iso-octane (Nagg = 16–21),112,113 cylohexane (Nagg = 14–22)15,112 and dodecane (Nagg = 29).110 However, the notable variance in reported aggregation number for reportedly “water-less” systems, reflects the challenge of accurately quantifying the sizes of small non-hydrated reverse aggregates experimentally. Also, the presence of even trace amounts of water in the system greatly affect the size, morphology, and dynamics of the formed reverse micelles.112,114 The exponential distribution of aggregate sizes, see Fig. 3, resulting from open association aggregation process, makes the average aggregate size a poor descriptor of the system.115,116 Additionally, a significant portion of the AOT remains monomerically dissolved in the solvent phase, see Fig. 4.
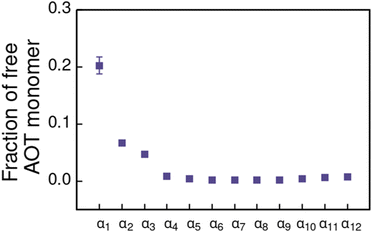 | ||
| Fig. 4 Fraction of free AOT surfactant monomers in solvents of different polarity. The solvent polarity variation is modelled by αi, see Table 2 for corresponding aHS and aTS parameter combinations. | ||
Further analysis of the formed aggregates by the radial distribution function for AOT head-beads gHH(r) in Fig. 7 indicates that the formed aggregates are spheroidal with an average diameter of the AOT headgroup core of approximately 2.4 rc ≈ 2.2 nm. This is slightly larger than the 1.7–1.9 nm previously reported based on scattering experiments14,15 and scaling laws15,117 for low hydration AOT reverse micelles. The discrepancy is likely explained by the difference in the actual molar volumes corresponding to the molecular regions mapped to the head and tail beads, respectively. As mentioned, beads in DPD are assumed to be equal in volume and in mass. Another source of disagreement is the soft nature of the DPD potential, which allows for bead overlap.
Further comparison of the AOT apolar solvent self-assembly response is complicated by most existing recent characterizations of AOT reverse micellization in solvents comparable to the apolar hydrocarbon solvent, here mainly concerning systems where water is present, at 3 to 20 water molecules per AOT concentration.13,58,63 These studies indicate that AOT reverse micelles undergo morphological changes in shape and size from elongated, highly dynamic filament-like aggregates at low water content (∼3 water molecules per AOT), to stabilized spherical reverse micelles at high water content (>7 water molecules per AOT). In the current work, we considered only dry hydrocarbon solvents as DPD level description of water leads to significant coarse-graining which can be expected to decrease modelling accuracy. Typically, an atomistic detail or hybrid modelling approach is needed, see e.g. ref. 118.
Although not covered by this work, as trace water is commonly present in AOT–apolar solvent systems, it is worthwile to consider literature further: In spherical reverse micelles with a sizeable water core, most of the water behaves as bulk water, and remains distanced from the AOT headgroup–tail interface. At lower water content, most of the water is interfacial, and aggregate growth occurs primarily via water bridging along one major axis, resulting in elongated aggregates.13,27,38,119 Previous modelling studies also reveal that the degree of micelle asphericity and elongation at low water content is larger for aggregates allowed to self-assemble from isotropic mixture than those relaxing from pre-built initial aggregates.13,58,63 The findings can be expected to generalize to AOT aggregation in the absence of water, especially if other polar impurities or additives are present. For example, several non-aqueous polar solvents, such as short-chain alcohols, form reverse micelles120–123 and act as cosurfactants.123,124 For example, AOT/non-polar solvent/alcohol tertiary systems have revealed that alcohol molecules, such as methanol, not only bind to AOT headgroups, but can also solvate AOT hydrocarbon tails and disperse in the apolar solvent phase.122,123 Similar findings for alcohol acting both as cosurfactant and cosolvent exist for other surfactant species.125
Increasing polarity of the solvent results first into reduced miscibility of the AOT surfactant. This shows as the sharp reduction of free monomers in Fig. 4, but also the formation of large, well-defined individual aggregates, as can be seen from the simulations configurations visualizations in Fig. 2. The phase separation resulting from reduced miscibility of the AOT surfactant is also apparent in the sudden increase in the tail bead order parameter value cT, see Fig. 5. Specifically, the higher head and tail order parameter values compared to the reverse micelle phase suggest compartmentalization and ordering within the larger aggregate. This internal ordering is evident from the aggregate cross-sections presented in Fig. 6, where the formation of AOT headgroup rich regions within a continuous phase of AOT tails is evident. The change in head bead order parameter cH is less pronounced, due to similar clustering of the AOT head beads being present already in the reverse micellar phase corresponding to α1. Both tail and head order parameters plateau at a maximum value for solvents corresponding to α4 and higher polarity. Furthermore, the assembly response taking place in intermediate polarity solvents allows a sparser AOT headgroup packing than in the tightly packed reverse micelle aggregates of the apolar solvent. This shows as the initial peak of head–head radial distribution function gHH(r) shifting to higher values of r in Fig. 7. Formation of the large aggregates also introduces a second, broad peak in the gHH(r) data at r ∼ 2.8 rc. This is related to the inter-spacing of the AOT headgroup rich clusters within the aggregate.
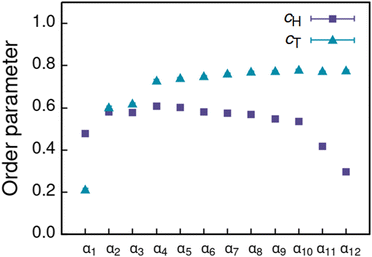 | ||
| Fig. 5 Order parameter c calculated for head (cH) and tail (cT) beads of the AOT assemblies formed in solvents of differing polarity indicated by αi, see Table 2 for corresponding aHS and aTS parameter combinations. | ||
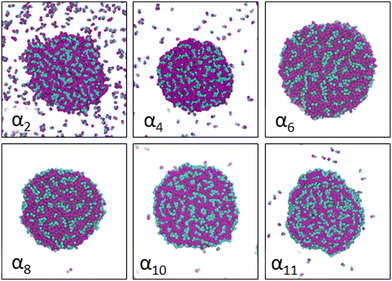 | ||
| Fig. 6 Cross-section cuts of representative self-assembled AOT aggregates at different solvent conditions αi, see Table 2 for corresponding aHS and aTS parameter combinations. The AOT head beads are shown in cyan and tail beads in purple and all cuts are made along the (x,y)-plane through the center of mass of the major visualized aggregate. Solvent beads are omitted in the visualizations for clarity. | ||
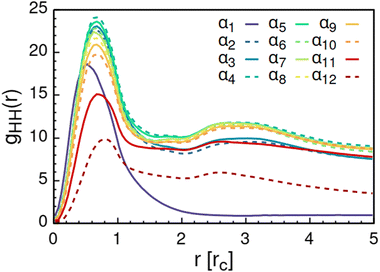 | ||
| Fig. 7 Radial distribution function gHH(r) calculated between the AOT head beads. The variable αi refers to solvent polarity variation, see Table 2 for corresponding aHS and aTS parameter combinations. | ||
As solvent polarity is increased further, the hydrophilic AOT headgroups migrate to the surface of the aggregate. This is evident from the shift of the first peak in the head–solvent radial distribution function gHS(r) to smaller values of r, and a notable increase in the peak height, see Fig. 8. This behaviour is reversed in the tail–solvent radial distribution function gTS, with the AOT head beads shielding interaction of the hydrophobic tails with the hydrophilic solvent, see Fig. 9. Furthermore, the order parameter dependencies on the solvent polarity in Fig. 5 reveal that partitioning of the AOT headgroups between intra-aggregate clusters and the aggregate surface causes a sharp decrease of the head order parameter cH in the solvent polarity range corresponding to that between α10 and α11 systems. This corresponds to the assembly response switching to a layered, onion-like surface structure for the elevated polarity solvents, see the cross section visualizations for parameter set α11 in Fig. 6. Finally, in highly polar solvents, such as system α12, AOT forms a lamellar phase, resulting in further decrease of head order parameter cH value, Fig. 5. As the AOT tailgroups form the inner, well-organized region of the lamella, the tail order parameter cT retains its high value. Additionally, at high solvent polarities, a slight increase in the fraction of free AOT surfactant can be observed. However, the amount of free AOT could in the simulations be affected by the compressibility characteristics of the simulation and the periodicity of the simulation box.
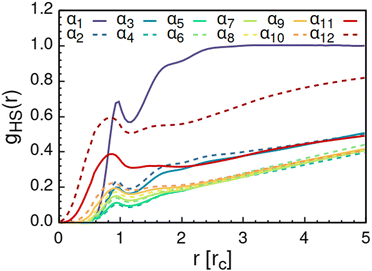 | ||
| Fig. 8 Radial distribution function gHS(r) calculated between the AOT head beads and the solvent beads. The examined systems αi differ in solvent polarity, see Table 2 for corresponding aHS and aTS parameter combinations. | ||
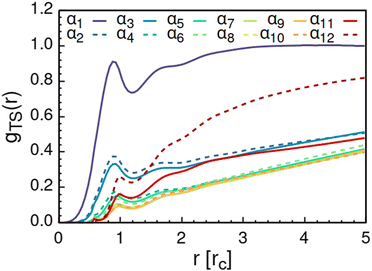 | ||
| Fig. 9 Radial distribution function gTS(r) calculated between the AOT tail beads and the solvent beads. The examined systems αi differ in solvent polarity, see Table 2 for corresponding aHS and aTS parameter combinations. | ||
Phase diagrams for AOT/water systems are well established in literature:55,56,126,127 AOT/water binary systems at ambient temperatures undergo phase changes from isotropic mixture, to lamellar phase, to bi-continuous cubic phase, and finally, to inverse hexagonal phase with increasing AOT concentration. In our simulations, at 150 mM/6.7 w/w% AOT, the system should be in the meta-stable coexistence region of the isotropic and lamellar phases.55,126 Indeed, we observe a rippled, yet stable, lamellar structure with some free AOT monomers in the hydrophilic, water-like solvent phase. Similar rippled AOT bilayers in the metastable region of the phase diagram have been previously reported, both experimentally45,128–130 and computationally.50 Experimentally, values of 1.8–1.96 nm for AOT bilayer thicknesses have been measured in water.45,49,128 Visually, the simulations assemblies correspond to approximately two DPD beads, which is consistent with the experimental values. Deviations can, however, be expected due to the lack of angle potentials within the DPD AOT model employed here combined with the ability of the DPD beads to overlap. Especially at high packing density, such as in the lamellar phase, this may result in nonphysical molecular conformations when mapped to an atomistic representation. We note that the employed DPD approach omits, e.g., electric double layer effects and solvation layer changes in the presence of charges. Spacing between the AOT headgroups in each lamella leaflet is ∼0.75 rc ≈ 0.68 nm, which is in good agreement with values of 0.64–0.67 nm from previously published experimental measurements.45,128 This means that even in the absence of proper electrostatic interactions description in the DPD bead model, particularly the model lacking accuracy in describing the repulsive interactions between the negatively charged sulfonate headgroups, the model presented here correctly reproduces the packing characteristics of the AOT bilayer.
To summarise the assembly characterization in terms of varying solvent, the here presented DPD parametrization for AOT surfactant in solvents of differing polarity reproduces in good agreement with literature structural observables for the isotropic reverse micelle phase (α1) and the lamellar phase in water (α12), corresponding to the two extrema of the examined solvent polarities. The agreement covers aggregation numbers and AOT bilayer topology, bilayer thickness, and headgroup spacing. This means that even a simplified DPD parametrization, with large enough degree of coarse-graining to achieve assembly phase level modelling, can capture response typical to model surfactant such as AOT.
For the solvent phases of intermediate polarity (α2–α11) literature sources on matching AOT–solvent binary systems are sparse and therefore accuracy of the model is challenging to judge. In these systems, we observe AOT agglomeration into singular large aggregates with internal compartmentalization of AOT headgroups within a continuous phase formed by the AOT hydrophobic tails. The response is a direct outcome of the competition between the miscibility and immiscibility characteristics in a dual-natured molecule, such as the surfactant. The response is well known for e.g., block-copolymers. With increasing polarity of the surrounding solvent medium, AOT headgroups form a hydrophilic outer layer for the aggregates. Notably, solubility of AOT monomers in bulk solvent decreases sharply with increased solvent polarity.
To further quantify the differences rising from the interactions with different solvents, we also performed simulations consisting of only two CG AOTs and the solvent beads in the DPD simulation box. In this low-density (LD) limit, it is possible to calculate the effective interaction potentials between the centres of mass (CM) of the AOTs, ϕeffCM, via the LD limit CM radial distribution function gLDCM as
| βϕeffCM(r) = −ln(gLDCM(r)), | (10) |
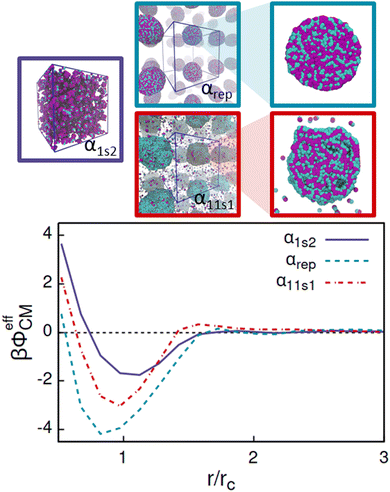 | ||
| Fig. 10 Low-density limit effective potentials between pairs of AOTs, βϕeffCM, for the cases α1s2, αrep, and α11s1, and the corresponding finite density equilibrium configurations. | ||
Comparing the effective potentials and the DPD simulated 150 mM AOT concentrations in Fig. 10 reveals that the strongest attraction, αrep, leads, as expected, strong aggregation and well-defined assembly structure. The intermediate attraction well, combined with the second long ranged repulsion barrier, α11s1, rises from the system assembling to deformed, flexible aggregates with significant portion of the AOT remaining soluble as monomers and oligomers. Most interestingly, the weakest effective attraction, with no barrier, corresponds to the small clustered aggregates and high solubility of the AOT. The comparison shows that such effective potentials can by their form and attraction strength indeed be connected with the equilibrium assembly structures. For example, the α1s2 system results in a significant attraction well region with depth ≈−1.8kBT in the effective potential. Such form clearly indicates that at low enough temperature, the effective system will phase separate according to basic thermodynamic considerations. However, the corresponding equilibrium configuration exhibits small clusters instead. Furthermore, the probability distribution of the cluster size decreases quite monotonically as the function of aggregate size, data presented in the ESI† as Fig. S3. This signifies that the binary AOT–solvent system is in a thermodynamic state outside the binodal line (assuming that such line exists in the surfactant system) in the miscibility region, but forming correlated clusters due to the attraction. On the other hand, the case αrep shows the highest attraction strength with a minimum of the potential of ≈−4.2kBT. At the concentration used to run the bulk DPD simulations, the AOT system exhibits a strong phase separation, in which the AOTs aggregate to a single large cluster in the bulk DPD simulations. This means that the thermodynamic state point chosen here lies below the miscibility line and inside the phase coexistence region of the phase diagram. Within the cluster, due to the symmetric interaction between head and solvent, and tail and solvent, heads and tails are well mixed (see Fig. 10). Finally, in α11s1, the relatively strong attraction combined with the second repulsion range results in a rather interesting assembly response: here the attraction strength is enough to enforce phase separation, as shown in Fig. 10. Additionally, compared to α1s2, a much higher number of free AOTs exist in solution. This is expected, since for decreased attraction strength, at fixed temperature, the concentration corresponding to the coexisting dilute phase moves to higher values (respectively, the dense phase concentration is decreased), see e.g. ref. 131. Interestingly, the cluster also exhibits an internal layered structure. These features correspond to a second length-scale emerging in the system. For the assembly, the second length scale characterises the spacing between the lamellae. The response can be connected with the repulsive tail in the effective interaction potential, on the order of ≈2 rc, but also depends on other system conditions.
The three example cases, for which we considered the assembly response via effective isotropic interactions based model, show that the functional form of ϕeffCM clearly gives relevant insight on the expected assembly phase for surfactant systems. Hypothetically, knowing precisely the effective pair potential allows the calculation of an effective phase diagram. This can be done in different ways, including simulations of spherical particles interacting via ϕeffCM(r) or via energy minimization of the corresponding free energy. The level of phase response predictability of this CG approach can be expected to correlate with the degree of symmetry of the real interactions between the surfactants.
Further insight to the properties of ϕeffCM can be obtained by considering the corresponding second virial coefficient B in the quadratic virial expansion, reading
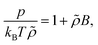 | (11) |
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) is the number density of the CG surfactants. For our surfactant systems,
is the number density of the CG surfactants. For our surfactant systems, ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) AOT = 0.067 rc−3. B can be calculated directly via
AOT = 0.067 rc−3. B can be calculated directly via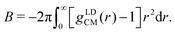 | (12) |
Next we present a critical overview of the DPD model and possible improvements to it. In this work, the DPD conservative repulsion parameters were derived based on determining Hildebrand solubility parameters from atomistic detail MD simulations data and employing the Flory–Huggins solubility theory to back-map the solubility parameters to DPD interactions. The Hildebrand solution theory is viable for non-polar molecules, but fails to accurately describe molecules with high polarity, hydrogen bonding capability, or charged moieties, such as the AOT sulfonate headgroups. For such cases, use of alternative solubility parameter descriptions, such as the Hansen solubility parameter, have been proposed.72,136 However, these do not have a similar physical basis as the Hildebrand solubility theory, and are therefore limited by the accuracy of group contribution methods mapping or availability of suitable experimental data for empirical estimation of the cohesion energy contributions. Anderson et al.137 have proposed tuning of DPD interaction parameters to reproduce experimental water–octanol partition coefficients. While this approach accurately reproduces, e.g., CMC for polyoxyethylene derived surfactants in water, average aggregate size is not accurately reproduced. This is mainly due to the dependence of the DPD parametrization on molecular bond length. Transferability of the approach by Anderson et al. to surfactants in apolar solvent without distinct CMC behaviour remains currently unexplored. Hence, for this work, we chose the Hildebrand approach and obtained with it assembly response that matches to a good degree to available literature data and expected response. Further advances could be made by expanding the work to other solubility estimates.
We focused the examination of the model performance on the literature reported structural assembly characteristics. The current parametrization could clearly be fine tuned to match experimental observables such as CMC, partition coefficients,137 or structural data, such as radial distribution function of binary systems.84 However, additional tuning may deteriorate the response in some other sense, and we decided against this in a general model. For example, increasing DPD bond stiffness often leads to better match to MD derived structural data at the cost of significantly reducing time step length and therefore limiting available simulation time.84,138 Additionally, surfactant headgroup charge contributes to observed self-assembly morphology, aggregate size, and aggregate dynamics in both water and hydrocarbon solutions.139–142 While incorporation of headgroup charge through, e.g., charge smearing approaches would be a viable option,143,144 this implies a uniform dielectric screening environment, which is not the case in a highly structured system, especially in internally structured aggregates such as those described in this work. Smearing of the headgroup charge also affects equilibrium self-assembly structures.78 Finally, most surfactants with strongly polar or charged headgroups are hygroscopic, which implies trace amounts of water present even in “dry” binary systems.145 Explicit description of the charged headgroup and its counterion would require addressing the degree of hydration of the counterion and surfactant headgroup.
Furthermore, the DPD model described here utilizes bonded potentials only for the AOT head–tail bonds, similar to previously published DPD surfactant models.75,146 Increased conformational accuracy could clearly be achieved by matching the parameters for the bonded potentials, especially the spring constant and equilibrium bond length, to, e.g., atomistic simulations data. Most commonly, radial distribution function of the centers of mass of a group of atoms is targeted.84 Furthermore, introduction of additional angle and dihedral terms may be important for accurate modelling of, e.g., surfactant systems, for which properties such as CMC and partitioning have been shown to depend on chain rigidity and equilibrium bond length.147,148 Here, the lack of angle terms in the AOT structure could contribute to the difference in thickness of the AOT bilayer in comparison to priorly reported values. The CG description also results in failure to capture hydrogen bonding related contributions to solvation and aggregate formation, demonstrated in our previous works to influence reverse micellar aggregation in apolar solvents with hydrogen bonding ability.115,116
In the model parametrization, the Na+ counterion is considered effectively bound to the headgroup of AOT surfactant, resulting in a lack of charged interactions and an explicit description of ionic species in the DPD bead model, but also allowing larger degree of coarse-graining which gives access to extended length and time scales, Fig. 2. This means that electrostatics interaction-mediated aggregate growth, as well as AOT sulfonate headgroup repulsion, are captured only marginally by the effective parameters in this level of CG model. The anionic sulfonate headgroup dominates the water/AOT interface interactions in both the AOT reverse micelles and lamellar structures, with a full solvation shell of ∼6 water molecules per sulfonate headgroup.48,149 Especially for dry reverse micelles, such as those corresponding to system α1 of this work, AOT sulfonate headgroup repulsion plays an important role in stabilising aggregates of finite size. Additionally, reverse micelles may gain net charge from micelle collision events.150 Such phenomena are not captured by this model. While attempts to include electrostatic interactions between charged beads via distributed charges exist,78,143,151,152 the parametrization of these interactions for specific DPD systems remains challenging.
4 Conclusions
We have presented, and verified against literature, a bottom-up DPD parametrization for sodium sulfosuccinate (AOT) surfactant in solvents of varying polarity, from apolar hydrocarbon solvent (octane) to polar solvent (water). The parametrization of the model is based on mapping Hildebrand solubility parameters, obtained based on atomistic MD simulations, and mapped to DPD conservative force repulsion parameters via Flory–Huggins solution theory. Additionally, we assessed the sensitivity of the derived DPD parametrization and compared the ability of simple, effective isotropic modelling approaches to capturing the AOT assembly response, reporting that, although the finite density phase response bears clear dependency on the solid concentration, such effective interaction potential derived from the low density limit response can be used as a simplified tool to predict the possible assembly structures.Despite considering a relatively large degree of coarse-graining, NCG = 8, the DPD model presented here reproduces well structural phases of AOT in apolar and polar solvents, where comparable literature data is available. Additionally, the model allows large-scale assembly modelling and characterization of the changes, not accessible at lower NCG. While additional tuning of the model is likely to be required for investigation of, e.g., viscoelastic response and dynamical properties, more complex ternary systems, or systems perturbed via an external field (e.g. electric field), the current model describes binary AOT–solvent systems on time and length scales currently unattainable via atomistic models. The predicted AOT self-assembly response can be used to design surfactant–solvent systems of desired assembly response. Furthermore, the diverse assembly morphologies in the solvents of intermediate polarities indicate that advanced functionalities from AOT assembly could be achieved by solvent variation.
Data availability
The data associated with the manuscript is available at https://doi.org/10.23729/7fd6b380-69f6-4658-8f7a-d2ac7ba89e50.Conflicts of interest
The authors have no conflicts of interest to disclose.Acknowledgements
This work was supported by the Academy of Finland through its Centres of Excellence Programme (2022-2029, LIBER) under project no. 346111 (M. S.), Novo Nordisk Foundation under project no. NNF22OC0074060 (M. S.) and the Project HPC-EUROPA3 (INFRAIA-2016-1-730897) (A. S.), with the support of the EC Research Innovation Action under the H2020 Programme. M. S. thanks Prof. Jaakko Timonen for asking the questions that motivated examining AOT aggregation response via modelling approaches and the ensuing discussions. A. S. gratefully acknowledges Prof. Uwe Thiele for scientific discussions and hosting of his research visit at the Institute of Theoretical Physics, WWU Münster, as well as the computer resources and technical support provided by HLSR Stuttgart. Computational resources by CSC IT Centre for Finland, RAMI – RawMatters Finland Infrastructure, and Aalto Science-IT project are also gratefully acknowledged. We are grateful for the support by FinnCERES Materials Bioeconomy Ecosystem.References
- N. M. Kovalchuk and M. J. Simmons, Curr. Opin. Colloid Interface Sci., 2021, 51, 101375 CrossRef CAS
.
- S. Tcholakova, N. Denkov and A. Lips, Phys. Chem. Chem. Phys., 2008, 10, 1608–1627 RSC
.
- A. I. Mohamed, A. S. Sultan, I. A. Hussein and G. A. Al-Muntasheri, J. Chem., 2017, 2017, 5471376 Search PubMed
.
- V. Uskoković and M. Drofenik, Surf. Rev. Lett., 2005, 12, 239–277 CrossRef
.
- S. Mukherjee, P. Chowdhury, W. F. DeGrado and F. Gai, Langmuir, 2007, 23, 11174–11179 CrossRef CAS PubMed
.
- P. Walde, Q. Peng, N. W. Fadnavis, E. Battistel and P. L. Luisi, Eur. J. Biochem., 1988, 173, 401–409 CrossRef CAS PubMed
.
- J. Najeeb, U. Farwa, F. Ishaque, H. Munir, A. Rahdar, M. F. Nazar and M. N. Zafar, Environ. Res., 2022, 208, 112644 CrossRef CAS PubMed
.
- W. Zhang, X. Qiao, J. Chen and H. Wang, J. Colloid Interface Sci., 2006, 302, 370–373 CrossRef CAS PubMed
.
- J. P. Cason, M. E. Miller, J. B. Thompson and C. B. Roberts, J. Phys. Chem. B, 2001, 105, 2297–2302 CrossRef CAS
.
- M. S. Orellano, C. Porporatto, J. J. Silber, R. D. Falcone and N. M. Correa, Carbohydr. Polym., 2017, 171, 85–93 CrossRef CAS PubMed
.
- S. Ghosh, A. Ray and N. Pramanik, Biophys. Chem., 2020, 265, 106429 CrossRef CAS PubMed
.
- R. D. Falcone, J. J. Silber and N. M. Correa, Phys. Chem. Chem. Phys., 2009, 11, 11096–11100 RSC
.
- V. Vasquez, B. Williams and O. Graeve, J. Phys. Chem. B, 2011, 115, 2979–2987 CrossRef CAS PubMed
.
- M. Kotlarchyk, S.-H. Chen, J. S. Huang and M. W. Kim, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 29, 2054 CrossRef CAS
.
- M. Kotlarchyk, J. S. Huang and S. H. Chen, J. Phys. Chem., 1985, 89, 4382–4386 CrossRef CAS
.
- A. Maitra, J. Phys. Chem., 1984, 88, 5122–5125 CrossRef CAS
.
- S. Sharifi, M. Amirkhani, J. M. Asla, M. R. Mohammadi and O. Marti, Soft Nanosci. Lett., 2012, 2, 8–12 CrossRef CAS
.
- N. B. Behzadi and S. Sharifi, Phys. Chem. Liq., 2014, 52, 428–435 CrossRef CAS
.
- K. Małycha, A. Burakowski, J. Gliński, H. Niu, S.-L. Bai and K. Orzechowski, J. Mol. Liq., 2021, 330, 115335 CrossRef
.
- H. Gochman-Hecht and H. Bianco-Peled, J. Colloid Interface Sci., 2005, 288, 230–237 CrossRef CAS PubMed
.
- E. W. Kaler, J. F. Billman, J. L. Fulton and R. D. Smith, J. Phys. Chem., 1991, 95, 458–462 CrossRef CAS
.
- S.-H. Tung, Y.-E. Huang and S. R. Raghavan, Soft Matter, 2008, 4, 1086–1093 RSC
.
- R. E. Riter, E. P. Undiks and N. E. Levinger, J. Am. Chem. Soc., 1998, 120, 6062–6067 CrossRef CAS
.
- T. Kinugasa, A. Kondo, S. Nishimura, Y. Miyauchi, Y. Nishii, K. Watanabe and H. Takeuchi, Colloids Surf., A, 2002, 204, 193–199 CrossRef CAS
.
- J. Smeets, G. Koper, J. Van Der Ploeg and D. Bedeaux, Langmuir, 1994, 10, 1387–1392 CrossRef CAS
.
- M. Hasegawa, T. Sugimura, Y. Shindo and A. Kitahara, Colloids Surf., A, 1996, 109, 305–318 CrossRef CAS
.
- D. Cringus, A. Bakulin, J. Lindner, P. Vöhringer, M. S. Pshenichnikov and D. A. Wiersma, J. Phys. Chem. B, 2007, 111, 14193–14207 CrossRef CAS PubMed
.
- A. S. Klymchenko and A. P. Demchenko, Langmuir, 2002, 18, 5637–5639 CrossRef CAS
.
- J. Eastoe, M. J. Hollamby and L. Hudson, Adv. Colloid Interface Sci., 2006, 128, 5–15 CrossRef PubMed
.
- P. Popovetskiy, Colloid J., 2020, 82, 144–151 CrossRef CAS
.
- M. Jalali-Jivan, F. Garavand and S. M. Jafari, Adv. Colloid Interface Sci., 2020, 283, 102227 CrossRef CAS PubMed
.
- V. Uskoković and M. Drofenik, Adv. Colloid Interface Sci., 2007, 133, 23–34 CrossRef PubMed
.
- P. Ekwall, L. Mandell and K. Fontell, J. Colloid Interface Sci., 1970, 33, 215–235 CrossRef CAS
.
- T. K. De and A. Maitra, Adv. Colloid Interface Sci., 1995, 59, 95–193 CrossRef CAS
.
- H.-F. Eicke and H. Christen, Helv. Chim. Acta, 1978, 61, 2258–2263 CrossRef CAS
.
- S. Muto and K. Meguro, Bull. Chem. Soc. Jpn., 1973, 46, 1316–1320 CrossRef CAS
.
- M. Van Dijk, J. Joosten, Y. Levine and D. Bedeaux, J. Phys. Chem., 1989, 93, 2506–2512 CrossRef CAS
.
- A. V. Martinez, L. Dominguez, E. Małolepsza, A. Moser, Z. Ziegler and J. E. Straub, J. Phys. Chem. B, 2013, 117, 7345–7351 CrossRef CAS PubMed
.
- S. Vierros and M. Sammalkorpi, J. Chem. Phys., 2015, 142, 094902 CrossRef CAS PubMed
.
- S. Vierros and M. Sammalkorpi, Phys. Chem. Chem. Phys., 2015, 17, 14951–14960 RSC
.
- P. A. Penttila, S. Vierros, K. Utriainen, N. Carl, L. Rautkari, M. Sammalkorpi and M. Österberg, Langmuir, 2019, 35, 8373–8382 CAS
.
- L. K. Shrestha, M. Dulle, O. Glatter and K. Aramaki, Langmuir, 2010, 26, 7015–7024 CrossRef CAS PubMed
.
- L. K. Shrestha, R. G. Shrestha, K. Oyama, M. Matsuzawa and K. Aramaki, J. Phys. Chem. B, 2009, 113, 12669–12679 CrossRef CAS PubMed
.
- P. L. Hubbard, K. M. McGrath and P. T. Callaghan, Langmuir, 2006, 22, 3999–4003 CrossRef CAS PubMed
.
- K. Fontell, J. Colloid Interface Sci., 1973, 44, 318–329 CrossRef CAS
.
- M. Gradzielski, H. Hoffmann, J.-C. Panitz and A. Wokaun, J. Colloid Interface Sci., 1995, 169, 103–118 CrossRef CAS
.
- B. S. Rauniyar and A. Bhattarai, J. Mol. Liq., 2021, 323, 114604 CrossRef CAS
.
- D. E. Moilanen, E. E. Fenn, D. Wong and M. Fayer, J. Am. Chem. Soc., 2009, 131, 8318–8328 CrossRef CAS PubMed
.
- C. Boissiere, J. Brubach, A. Mermet, G. De Marzi, C. Bourgaux, E. Prouzet and P. Roy, J. Phys. Chem. B, 2002, 106, 1032–1035 CrossRef CAS
.
- A. H. Poghosyan, M. P. Adamyan and A. A. Shahinyan, Colloids Surf., A, 2019, 578, 123578 CrossRef CAS
.
- S. K. Kumar, A. Tamimi and M. D. Fayer, J. Am. Chem. Soc., 2013, 135, 5118–5126 CrossRef CAS PubMed
.
- J. Rogers and P. Winsor, Nature, 1967, 216, 477–479 CrossRef CAS
.
- E. Y. Sheu, S. H. Chen and J. S. Huang, J. Phys. Chem., 1987, 91, 3306–3310 CrossRef CAS
.
- S. Mandal and S. De, Mater. Chem. Phys., 2016, 183, 410–421 CrossRef CAS
.
- J. Wolanin, L. Barre, C. Dalmazzone and D. Bauer, Colloids Surf., A, 2018, 559, 218–225 CrossRef CAS
.
- J. Bergenholtz and N. J. Wagner, Langmuir, 1996, 12, 3122–3126 CrossRef CAS
.
- M. A. Kamal and A. Pal, Colloids Surf., A, 2021, 611, 125788 CrossRef
.
- G. Eskici and P. H. Axelsen, J. Phys. Chem. B, 2016, 120, 11337–11347 CrossRef CAS PubMed
.
- G. Mudzhikova and E. Brodskaya, Colloid J., 2006, 68, 729–737 CrossRef CAS
.
- E. N. Brodskaya and G. V. Mudzhikova, Mol. Phys., 2006, 104, 3635–3643 CrossRef CAS
.
- J. Chowdhary and B. M. Ladanyi, J. Phys. Chem. B, 2009, 113, 15029–15039 CrossRef CAS PubMed
.
- A. Gardner, V. Vasquez, A. Clifton and O. Graeve, Fluid Phase Equilib., 2007, 262, 264–270 CrossRef CAS
.
- S. Abel, F. Sterpone, S. Bandyopadhyay and M. Marchi, J. Phys. Chem. B, 2004, 108, 19458–19466 CrossRef CAS
.
- A. Siddiqi and C. Herdes, Fluid Phase Equilib., 2022, 559, 113469 CrossRef CAS
.
- A. Soper and K. Edler, Biochim. Biophys. Acta, Gen. Subj., 2017, 1861, 1652–1660 CrossRef CAS PubMed
.
- E. Negro, R. Latsuzbaia, A. De Vries and G. Koper, Soft Matter, 2014, 10, 8685–8697 RSC
.
- A. Poghosyan and Y. S. Mamasakhlisov, Colloids Surf., A, 2022, 642, 128681 CrossRef CAS
.
- A. Bhat, M. T. Harris and V. W. Jaeger, J. Phys. Chem. B, 2021, 125, 13789–13803 CrossRef CAS PubMed
.
- P. Espanol and P. B. Warren, J. Chem. Phys., 2017, 146, 150901 CrossRef PubMed
.
- P. Hoogerbrugge and J. Koelman, Europhys. Lett., 1992, 19, 155 CrossRef
.
- J. Koelman and P. Hoogerbrugge, Europhys. Lett., 1993, 21, 363 CrossRef CAS
.
- A. Khedr and A. Striolo, J. Chem. Theory Comput., 2018, 14, 6460–6471 CrossRef CAS PubMed
.
- L. Zhen, K. Liu, D. Huang, X. Ren and R. Li, J. Dispersion Sci. Technol., 2016, 37, 941–948 CrossRef CAS
.
- D. Nivón-Ramrez, L. I. Reyes-Garca, R. Oviedo-Roa, R. Gómez-Balderas, C. Zuriaga-Monroy and J.-M. Martnez-Magadán, Colloids Surf., A, 2022, 128867 CrossRef
.
- C. Yang, X. Chen, H. Qiu, W. Zhuang, Y. Chai and J. Hao, J. Phys. Chem. B, 2006, 110, 21735–21740 CrossRef CAS PubMed
.
- S. J. Gray, M. Walker, R. Hendrikse and M. R. Wilson, Soft Matter, 2023, 19, 3092–3103 RSC
.
- M. Vuorte and M. Sammalkorpi, Soft Matter, 2023, 19, 5538–5550 RSC
.
- R. Mao, M.-T. Lee, A. Vishnyakov and A. V. Neimark, J. Phys. Chem. B, 2015, 119, 11673–11683 CrossRef CAS PubMed
.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS
.
- B. M. Forrest and U. W. Suter, J. Chem. Phys., 1995, 102, 7256–7266 CrossRef CAS
.
- M. Panoukidou, C. R. Wand and P. Carbone, Soft Matter, 2021, 17, 8343–8353 RSC
.
- D. Visser, H. C. Hoefsloot and P. D. Iedema, J. Comput. Phys., 2006, 214, 491–504 CrossRef
.
- F. Lahmar and B. Rousseau, Polymer, 2007, 48, 3584–3592 CrossRef CAS
.
- P. Pieczywek, W. Płaziński and A. Zdunek, Sci. Rep., 2020, 10, 1–14 CrossRef PubMed
.
- A. Boromand, S. Jamali and J. M. Maia, Comput. Phys. Commun., 2015, 196, 149–160 CrossRef CAS
.
- E. Zohravi, E. Shirani and A. Pishevar, Mol. Simul., 2018, 44, 254–261 CrossRef CAS
.
- W. Dzwinel and D. A. Yuen, Int. J. Mod. Phys. C, 2000, 11, 1–25 CrossRef
.
- A. Maiti and S. McGrother, J. Chem. Phys., 2004, 120, 1594–1601 CrossRef CAS PubMed
.
- J. B. Klauda, R. M. Venable, J. A. Freites, J. W. OConnor, D. J. Tobias, C. Mondragon-Ramirez, I. Vorobyov, A. D. MacKerell and R. W. Pastor, J. Phys. Chem. B, 2010, 114, 7830–7843 CrossRef CAS PubMed
.
- R. B. Best, X. Zhu, J. Shim, P. E. Lopes, J. Mittal, M. Feig and A. D. MacKerell, J. Chem. Theory Comput., 2012, 8, 3257–3273 CrossRef CAS PubMed
.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS
.
- A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, B. Nguyen, D. T. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, J. Watanabe, M. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef CAS PubMed
.
- H. Bekker, H. Berendsen, E. Dijkstra, S. Achterop, R. Vondrumen, D. van der spoel, A. Sijbers, H. Keegstra and M. Renardus, 4th International Conference on Computational Physics (PC 92), 1993, pp. 252–256.
- D. van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed
.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25 CrossRef
.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed
.
- H. J. Berendsen, J. van Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS
.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS
.
- A. Bricard, J.-B. Caussin, N. Desreumaux, O. Dauchot and D. Bartolo, Nature, 2013, 503, 95–98 CrossRef CAS PubMed
.
- G. Raju, N. Kyriakopoulos and J. V. I. Timonen, Sci. Adv., 2021, 7, eabh1642 CrossRef PubMed
.
- T. Cherian, F. Sohrabi, C. Rigoni, O. Ikkala and J. V. I. Timonen, Sci. Adv., 2021, 7, eabi8990 CrossRef CAS PubMed
.
- Y.-L. Chen, C.-K. Su and B.-H. Chiang, Process Biochem., 2006, 41, 752–758 CrossRef CAS
.
- G. N. Smith, P. Brown, S. E. Rogers and J. Eastoe, Langmuir, 2013, 29, 3252–3258 CrossRef CAS PubMed
.
- A. I. Mitsionis and T. C. Vaimakis, Chem. Phys. Lett., 2012, 547, 110–113 CrossRef CAS
.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen,
et al.
, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS
.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed
.
-
A. Barton, CRC Handbook of Solubility Parameters and Other Cohesion Parameters: Second Edition, CRC Press, 2017 Search PubMed
.
- M. Ester, H.-P. Kriegel, J. Sander and X. Xu, Int. Conf. Knowledge Discovery and Data Mining, 1996, p. 6.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed
.
- J. Peri, J. Colloid Interface Sci., 1969, 29, 6–15 CrossRef CAS
.
- K. Tamura and Z. Schelly, J. Am. Chem. Soc., 1981, 103, 1013–1018 CrossRef CAS
.
- M. Ueda and Z. Schelly, Langmuir, 1988, 4, 653–655 CrossRef CAS
.
- K. Kon-no and A. Kitahara, J. Colloid Interface Sci., 1971, 35, 636–642 CrossRef CAS
.
- T. K. Jain, M. Varshney and A. Maitra, J. Phys. Chem., 1989, 93, 7409–7416 CrossRef CAS
.
- S. Vierros, M. Österberg and M. Sammalkorpi, Phys. Chem. Chem. Phys., 2018, 20, 27192–27204 RSC
.
- M. Vuorte, S. Vierros, S. Kuitunen and M. Sammalkorpi, J. Colloid Interface Sci., 2020, 571, 55–65 CrossRef CAS PubMed
.
- R. Urano, G. A. Pantelopulos and J. E. Straub, J. Phys. Chem. B, 2019, 123, 2546–2557 CrossRef CAS PubMed
.
- S. Vierros and M. Sammalkorpi, ACS Omega, 2019, 4, 15581–15592 CrossRef CAS PubMed
.
- D. E. Moilanen, E. E. Fenn, D. Wong and M. Fayer, J. Phys. Chem. B, 2009, 113, 8560–8568 CrossRef CAS PubMed
.
- R. E. Riter, J. R. Kimmel, E. P. Undiks and N. E. Levinger, J. Phys. Chem. B, 1997, 101, 8292–8297 CrossRef CAS
.
- R. E. Ridley, E. Alvarado, A. A. Mrse, V. R. Vasquez and O. A. Graeve, Langmuir, 2020, 36, 11274–11283 CrossRef CAS PubMed
.
- P. Setua, D. Seth and N. Sarkar, Phys. Chem. Chem. Phys., 2009, 11, 8913–8922 RSC
.
- R. Lu, R. Zhu, R. Zhong and A. Yu, J. Photochem. Photobiol., A, 2013, 252, 116–123 CrossRef CAS
.
- L. M. Nazário, T. A. Hatton and J. P. Crespo, Langmuir, 1996, 12, 6326–6335 CrossRef
.
- S. Vierros and M. Sammalkorpi, Phys. Chem. Chem. Phys., 2018, 20, 6287–6298 RSC
.
- J. Rogers and P. Winsor, J. Colloid Interface Sci., 1969, 30, 247–257 CrossRef CAS
.
- J. Leng, M. Joanicot and A. Ajdari, Langmuir, 2007, 23, 2315–2317 CrossRef CAS PubMed
.
- D. Park, J. Rogers, R. Toft and P. Winsor, J. Colloid Interface Sci., 1970, 32, 81–89 CrossRef CAS
.
- G. Chidichimo, C. La Mesa, G. Ranieri and M. Terenzi, Mol. Cryst. Liq. Cryst., 1987, 150, 221–236 Search PubMed
.
- R. Faiman, I. Lundström and K. Fontell, Chem. Phys. Lipids, 1977, 18, 73–83 CrossRef CAS
.
- J.-P. Hansen and L. Verlet, Phys. Rev., 1969, 184, 151 CrossRef CAS
.
- R. P. Sear and W. M. Gelbart, J. Chem. Phys., 1999, 110, 4582–4588 CrossRef CAS
.
- A. Scacchi, M. Sammalkorpi and T. Ala-Nissila, J. Chem. Phys., 2021, 155, 014904 CrossRef CAS PubMed
.
- A. J. Archer and N. B. Wilding, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 031501 CrossRef PubMed
.
- T. F. Farage, P. Krinninger and J. M. Brader, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 042310 CrossRef CAS PubMed
.
- S. Venkatram, C. Kim, A. Chandrasekaran and R. Ramprasad, J. Chem. Inf. Model., 2019, 59, 4188–4194 CrossRef CAS PubMed
.
- R. L. Anderson, D. J. Bray, A. S. Ferrante, M. G. Noro, I. P. Stott and P. B. Warren, J. Chem. Phys., 2017, 147, 094503 CrossRef PubMed
.
- F. Sepehr and S. J. Paddison, Chem. Phys. Lett., 2016, 645, 20–26 CrossRef CAS
.
- D. Stigter, J. Phys. Chem., 1974, 78, 2480–2485 CrossRef CAS
.
- M. Laatikainen, W. Srithammavut, B. Toukoniitty, I. Turunen and T. Sainio, Adsorption, 2015, 21, 409–417 CrossRef CAS
.
- J. Faeder and B. M. Ladanyi, J. Phys. Chem. B, 2005, 109, 6732–6740 CrossRef CAS PubMed
.
- M. Senske, Y. Xu, A. Bäumer, S. Schäfer, H. Wirtz, J. Savolainen, H. Weingärtner and M. Havenith, Phys. Chem. Chem. Phys., 2018, 20, 8515–8522 RSC
.
- R. D. Groot, J. Chem. Phys., 2003, 118, 11265–11277 CrossRef CAS
.
- M. González-Melchor, E. Mayoral, M. E. Velázquez and J. Alejandre, J. Chem. Phys., 2006, 125, 224107 CrossRef PubMed
.
- Q. Guo, V. Singh and S. H. Behrens, Langmuir, 2010, 26, 3203–3207 CrossRef CAS PubMed
.
- S.-L. Yuan, Z.-T. Cai, G.-Y. Xu and Y.-S. Jiang, Chem. Phys. Lett., 2002, 365, 347–353 CrossRef CAS
.
- A. Vishnyakov, M.-T. Lee and A. V. Neimark, J. Phys. Chem. Lett., 2013, 4, 797–802 CrossRef CAS PubMed
.
- J. Saathoff, J. Chem. Phys., 2018, 148, 154102 CrossRef PubMed
.
- E. Prouzet, J.-B. Brubach and P. Roy, J. Phys. Chem. B, 2010, 114, 8081–8088 CrossRef CAS PubMed
.
- H. F. Eicke, M. Borkovec and B. Das-Gupta, J. Phys. Chem., 1989, 93, 314–317 CrossRef CAS
.
- H. Eslami, M. Khani and F. Müller-Plathe, J. Chem. Theory Comput., 2019, 15, 4197–4207 CrossRef CAS PubMed
.
- H. Wang, X. Tang, D. M. Eike, R. G. Larson and P. H. Koenig, Langmuir, 2018, 34, 1564–1573 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Solubility parameters of fine-grained bead molecules, additional molecular visualizations, and structural analysis related to the sensitivity analysis systems (Table 3). Cohesion energies and solubility parameters calculated from condensed phase and in vacuo simulations of octane, 2-methylheptane, sulfosuccinic acid, and water. Additionally, visualizations corresponding to the sensitivity analysis trajectories and comparison of the fraction of free AOT surfactant in the original solvent variation and in the sensitivity analysis systems are presented. Aggregate size distribution for α1a2 system is also presented. See DOI: https://doi.org/10.1039/d3cp02173d |
| This journal is © the Owner Societies 2023 |