Theoretical investigation of solvent and oxidation/deprotonation effects on the electronic structure of a mononuclear Ru-aqua-polypyridine complex in aqueous solution

Abstract

Mononuclear polypyridine ruthenium (Ru) complexes can catalyze various reactions, including water splitting, and can also serve as photosensitizers in solar cells. Despite recent progress in their synthesis, accurately modeling their physicochemical properties, particularly in solution, remains challenging. Herein, we conduct a theoretical investigation of the structural and electronic properties of a mononuclear Ru-aqua polypyridine complex in aqueous solution, considering five of its possible oxidation/protonation states species: [Ru^II(H₂O)(py)(bpy)₂]²⁺, [Ru^II(OH)(py)(bpy)₂]⁺, [Ru^III(H₂O)(py)(bpy)₂]³⁺, [Ru^III(OH)(py)(bpy)₂]²⁺ and [Ru^IV(O)(py)(bpy)₂]²⁺, where py = pyridine and bpy = 2,2′-bipyridine. At first, we investigate the impact of proton-coupled and non-coupled electron transfer reactions on the geometry and electronic structure of the complexes in vacuum and in solution, using an implicit solvent model. Then, using a sequential multiscale approach that combines quantum mechanics and molecular mechanics (S-QM/MM), we examine the explicit solvent effects on the electronic excitations of the complexes, and compare them with the experimental results. The complexes were synthesized, and their absorption spectra measured in aqueous solution. To accurately describe the QM interactions between the metal center and the aqueous ligand in the MM simulations, we developed new force field parameters for the Ru atom. We analyze the solvent structure around the complexes and account for its explicit influence on the polarization and electronic excitations of the complexes. Notably, accounting for the explicit solvent polarization effects of the first solvation shells is essential to correctly describe the energy of the electronic transitions, and the explicit treatment of the hydrogen bonds at the QM level in the excitation calculations improves the accuracy of the description of the metal-to-ligand charge-transfer bands. Transition density matrix analysis is used to characterize all electronic transitions in the visible and ultraviolet ranges according to their charge-transfer (CT) character. This study elucidates the electronic structure of those ruthenium polypyridyl complexes in aqueous solution and underscores the importance of precisely describing solvent effects, which can be achieved employing the S-QM/MM method.

---

1 Introduction

Since the development of the coordination chemistry of polypyridyl metal complexes¹ in the 1940's and 1960's, ruthenium (Ru) complexes have attracted attention in different areas of chemistry, with wide technological applications since their properties can be designed for different purposes depending on the coordinated ligands. Complexes characterized by high electronic delocalization have applications in nonlinear optics,² magnetism,³ liquid crystals,⁴ and molecular sensors,⁵ whereas sulfoxide-coordinated complexes are useful in chemotherapy for the treatment of cancer.⁶ In fact, N-heterocyclic ligand complexes are useful as DNA cleavage agents for therapeutic purposes,⁷ as photosensitizers in solar cells^8–11 and artificial photosynthesis,¹² and as catalysts.¹³ For example, Ru-aqua polypyridyl complexes can generate high valence species by successive coupled electron-/proton-transfer reactions¹⁴ able to promote oxidation of organic compounds¹⁵ and inorganic substrates.¹⁶

In 1982, It was reported the first complex capable of carrying out the oxidation of water, a water oxidation catalyst (WOC).¹⁷ This complex, known as Blue Dimer, cis,cis-[(bpy)₂(H₂O)Ru(μ-O)Ru(H₂O)(bpy)₂]⁴⁺ where bpy = 2,2′-bipyridine, is an oxo-ligand bridged di-nuclear Ru-complex. This catalyst inspired the next developments as demonstrated by the hegemony of WOCs with two metal centers until 2005, when Zong and Thummel demonstrated that mononuclear complexes can exhibit higher electrocatalytic activity,¹⁸ whose mechanism was elucidated in 2008 using the [Ru(H₂O)(bpm)(tpy)]²⁺ (bpm = 2,2′-bipyrimidine and tpy = 2,2′;6′,2′′-terpyridine) complex as catalyst.¹⁹ The catalytic active species was demonstrated to be the high valence [Ru^V(O)(bpm)(tpy)]³⁺ species, generated by reaction with a Ce^IV oxidizing agent (cerium ammonium nitrate, CAN), where the O–O bond was formed by water nucleophilic attack (WNA) to the Ru^V = O moiety.²⁰ However, following studies carried out with the [Ru(pic)(bda)] (bda²⁻ = 2,2′-bipyridine-6,6′-dicarboxylate and pic = 4-picoline) complex family indicated that the water oxidation reaction mechanism activated complex was in fact binuclear. In other words, a catalytic active intermediate should be formed in situ by the interaction of two M-O units (I2M).²¹ In addition, bulky axial ligands such as isoquinoline and phthalazine were very effective in enhancing the high catalytic activity of some of those compounds.²¹ Currently, there are several mononuclear catalysts able to mediate the four-electron oxidation of water to dioxygen.^22,23

Considered one of the precursors in the application of transition metal complexes in artificial photosynthesis, the cis-[Ru^II(H₂O)(py)(bpy)₂]²⁺ complex²⁴ (where py = pyridine, see Fig. 1), prepared in the early 1980s, was one of the first polypyridine complexes capable of two sequential proton-coupled electron-transfer processes generating a high oxidation state species, at a potential as low as 0.95 V.²⁴ More recently, in 2019, this complex was adopted as a electrocatalyst model, in a study by X-ray photoelectron spectroscopy (XPS) in connection with the liquid-jet approach, aiming the characterization of the relevant intermediate species involved in the electrocatalytic water splitting process,²⁵ with minimal interference on the reaction mechanism. Herein, we focus on the investigation of the electronic and optoelectronic properties of five different oxidation/protonation species of this complex, namely: [Ru^II(H₂O)(py)(bpy)₂]²⁺, [Ru^II(OH)(py)(bpy)₂]⁺, [Ru^III(H₂O)(py)(bpy)₂]³⁺, [Ru^III(OH)(py)(bpy)₂]²⁺ and [Ru^IV(O)(py)(bpy)₂]²⁺.

Fig. 1 Chemical structure of the [Ru(py)(bpy)₂X] complexes. The N-atoms of pyridine (py) and bipyridine (bpy₁, bpy₂), and the X ligand (O-atom of H₂O, OH⁻ and O²⁻), are all coordinated to a central Ru atom in a pseudo-octahedral site. Depending on the complex, the X position can be singularly occupied by an aqua, a hydroxo, or an oxo ligand.

In the last decades, the development of new reliable and efficient Ru compounds and the understanding of the mechanism of the electrocatalytic water cleavage reaction have undoubtedly been benefited by classical molecular dynamics,^26–28 but the recent advances in computational chemistry also, such as quantum molecular dynamics simulations with the Density Functional Theory (DFT),^29–36 and hybrid simulations combining molecular dynamics and DFT.^37–42 However, implementing the classical atomistic simulations, that should be a powerful tool for researchers to access the structure and dynamics of Ru-complexes, still is a challenging task. In fact, the presence of a transition metal such as Ru still represents a challenge to the parametrization of the bonded and non-bonded interactions in the complexes, although it is well established that classical molecular simulation is able to deal with large organic systems in the microsecond scale.^43–45 All parameters in a force field are highly sensitive to the oxidation and spin state of the metal, to the nature of the ligands coordinated to the metal center, and to the effects of microsolvation in potentially proton donor or acceptor regions; etc.^46–50 Thus, defining the force field of the metal and the complex represent the major challenges given the high variability on the charge-transfer and degree of delocalization dependent on solvent effects, as well as the covalent and ionic character of the metal-ligand interactions.

In fact, a fine theoretical description of such systems has been precluded by the difficulties in parameterization and modeling due to the strong intramolecular covalent interactions as well as solvent effects, especially in the case of aqua complexes prone to strong solvent effects and proton-coupled electron-transfer reactions in protic solvents, especially in aqueous solution. In this work, we present a theoretical/experimental study about the solvent effects on the structural and electronic properties of the five different species obtained by successive proton-coupled redox processes of [Ru^II(H₂O)(py)(bpy)₂]²⁺ complex in aqueous solution. The effects of the solvent and oxidation/deprotonation reactions (namely ET = electron-transfer, PT = proton-transfer, and PCET = proton-coupled electron-transfer reactions) on the structural conformation, electronic density distribution and the frontier molecular orbitals, as well as their electronic transitions in the UV-visible range, were investigated. Such study was carried out adjusting the force field (FF) parameters of the metal center using QM-based calculations of the complexes’ interaction potential, making possible a more quantitative evaluation of the solvent structure around and the key role of the intermolecular hydrogen bonds formed by the coordinated water ligand derived species (OH⁻ and O²⁻) and free water molecules for a more precise description of their structural, electronic and optical properties.

2 Methodology

A careful theoretical study on the solvent effects on the structural and electronic properties of five species derived from the [Ru^II(H₂O)(py)(bpy)₂] complex in aqueous solution is presented. At first, we investigated the effects of the solvent, and the effects of the oxidation/deprotonation reactions (namely ET: electron-transfer, PT: proton-transfer, PCET: proton-coupled electron-transfer reactions) in the structural conformation, electronic density distribution and in the frontier molecular orbitals. Next, using a hybrid approach combining molecular mechanics simulations with quantum mechanics calculations sequentially (S-QM/MM method),⁵¹ we explored the solvent effects in the electronic transitions of the complexes in the visible and ultraviolet regions. Such simulations were made possible from the adjustment of force field (FF) parameters of the metallic center using QM-based calculations of the complexes’ interaction potential. Thus, the new set of FF parameters are also one of the contributions of this work to the literature of Ru-aqua complexes. From the simulations, the solvent structure surrounding the complexes were elucidated in their atomistic details and statistically uncorrelated configurations^52–55 were extracted to compose the QM calculations of the opto-electronic properties. Such calculations, in turn, were also performed within a QM/MM scheme, where the solute and part of the solvent were treated at the QM level, and the remaining solvent molecules were considered as an electrostatic embedding. Within this framework, the role of the intermolecular hydrogen bonds formed between the coordinated aqua ligand and the water molecules in solution to the opto-electronic properties were elucidated.

Quantum mechanics (QM) calculations were carried out within the Density Functional Theory (DFT)^56,57 framework using the hybrid B3LYP functional^58,59 in the restricted Kohn–Sham formalism for the closed-shell systems, [Ru^II(H₂O)(py)(bpy)₂]²⁺ and [Ru^II(OH)(py)(bpy)₂]⁺, and in the unrestricted Kohn–Sham formalism for the open-shell doublets [Ru^III(H₂O)(py)(bpy)₂]³⁺ and [Ru^III(OH)(py)(bpy)₂]²⁺, and triplet [Ru^IV(O)(py)(bpy)₂]²⁺ systems. Other spin densities were addressed before as being less energetically stable.²⁵ The basis set aug-cc-pVDZ^60,61 was adopted for C, O, N and H atoms and the basis set with pseudopotential aug-cc-pVDZ-PP⁶² was adopted for Ru. This basis set combination was denominated (aug)-cc-pVDZ-(PP-Ru). The molecular structures of the complexes were obtained from geometry optimization processes and their dynamical stability confirmed by checking the vibrational frequencies calculated at the same level of theory.

The solvent distribution around the complexes was simulated using the Monte Carlo method considering a Ru-complex surrounded by 4000 water molecules in a cubic box, with an initial side length of about 50 Å. During the simulations, the intramolecular conformation of the solute was held fixed in its optimized geometry, except for the aqua ligand derived species interacting with a water molecule, which was simulated as any other solvent molecule. The isothermal–isobaric (NPT) ensemble was employed at room temperature (298.15 K) and pressure (1 atm). The simulations consisted of a thermalization stage of 8 × 10⁸ Monte Carlo steps, followed by an equilibrium sampling of 16 × 10⁸ Monte Carlo steps.

The interatomic interactions were modeled by the Lennard-Jones (LJ) and Coulomb potentials. The LJ parameters for N, C and H atoms were extracted from the OPLS-AA force field⁶³ using the pyridine molecule and the TIP3P model⁶⁴ was adopted for water molecules. The Ru LJ parameters were tuned to correctly describe the QM energy profile of Ru and the coordinated water molecule in the aqua complexes, prioritizing the equilibrium distance and the binding energy. The potential energy profile of the aqua complexes was obtained from a QM energy scan calculation varying the distance of the coordinated water molecule and the Ru ion around the equilibrium position, in 15 equally separated distances from 1.8 to 3.3 Å. The Counter Poise Correction^65,66 was adopted to correct any basis set superposition errors. Herein, the QM calculations were realized at the same theory level adopted in the geometry optimizations of all Ru-complex species, as described above. The use of the restricted or unrestricted Kohn–Sham formalisms to calculate the dissociation of the coordinated water molecule in Ru^IIH₂O was investigated (see Tables S5 and S6, ESI†), and very similar energy profiles were obtained with both formalisms.

The atomic charges of the Coulomb term were obtained using the fit of the QM electrostatic potential of the Ru-complex with the CHELPG (Charges from the Electrostatic Potential on a Grid) procedure.⁶⁷ The polarization of the Ru-complex due to the aqueous solution was included in the QM calculation by the Polarizable Continuum Model (PCM).⁶⁸ This procedure for evaluating the atomic charges of the polarized solute in aqueous solution has been shown to be better than the standard procedure based on atomic charges calculations of the solute in vacuum at the QM level suggested by the common force fields, i.e. HF/6-31G(d).^69–72 Standard procedures such as Metropolis sampling technique, image method, periodic boundary condition, cut-off-radius, and long-range correction⁷³ were adopted as before.⁷⁴ All interactions were explicitly computed considering a cut-off-radius about 22 Å.

Furthermore, a sequential multi-scale approach combining quantum mechanics and molecular mechanics (S-QM/MM)^51,75,76 was utilized to obtain the theoretical electronic spectra of all five ruthenium complex species in solution. After performing the Monte Carlo simulation, a total of 100 statistically uncorrelated Monte Carlo configurations were selected. Then, the Time Dependent Density Functional Theory (TD-DFT) was used to calculate the first 50 electronic transitions of the complexes in each Monte Carlo configuration, with solvent effects treated at different levels of approximation. The solvent effects were accounted under three different approximations: (i) as an electrostatic embedding composed of the atomic point charges of the 1000 closest solvent molecules (X + PC); (ii), and as before but considering the water molecules that makes hydrogen bonds with the complex as part of the QM region (X + HB + PC); and (iii) treating the solvent as a continuous dielectric with the Polarizable Continuum Model (X + PCM).

The QM calculations were performed using the Gaussian 09 package.⁷⁷ The Monte Carlo simulations were performed with the DICE program.⁷⁸ The electronic excitations were assigned based on the analyzes of the corresponding transition density matrices, using the Theoretical Density, Orbital Relaxation, and Exciton analysis package (TheoDORE).^79–82 In order to improve clarity and facilitate the reading, now on a simplified nomenclature will be adopted for the complexes. The closed-shell systems will be identified as [Ru^II(H₂O)]²⁺ and [Ru^II(OH)]⁺, and the open-shell systems as [Ru^III(H₂O)]³⁺, [Ru^III(OH)]²⁺ and [Ru^IV(O)]²⁺.

In order to compare the calculated spectra with the experimental results, all Ru-complex species were generated upon oxidation and/or deprotonation reactions of the [Ru^II(H₂O)]²⁺ complex, and the Ultraviolet-Visible spectra were measured in the laboratory, as described in the ESI.†

3 Results and discussion

In the first three sections, the effects of the solvent on the structural and electronic properties, and the effects of the oxidation/deprotonation reactions (namely ET, PT, PCET reactions) (1) in the structural conformation, (2) in the atomic charge distributions and (3) in the frontier molecular orbitals of all five ruthenium complex species, will be discussed based on implicit PCM solvent model. Next, it will be presented (4) the parametrization of new non-bonded parameters for Ru, (5) the analysis of the solvent structure around the complexes obtained from the atomistic MM simulations, and (6) the investigation of the explicit solvent effects on the electronic transitions of the Ru-complex species in the framework of the S-QM/MM approach.

3.1 Structural conformation

All species are composed by a central Ru atom hexa-coordinated with two bipyridines (bpy₁ and bpy₂), a pyridine (py) and a water derived ligand (a water molecule, a hydroxide ion, or an oxide ion), whose metal ion can be found in different oxidation states, varying from 2 to 5, depending on the environment conditions.²⁵ These complexes have some structural similarities with the [Ru^II(bpy)₃]²⁺ complex,^83–86 where the coordinated water derived ligand and the pyridine are replaced by a third bipyridine ligand, as shown in ESI.† In the gas phase, from geometry optimization, the relative positioning of bpy₁ and bpy₂ is very similar in all those Ru-complex species (Fig. 2), where the N₁₉–Ru–N₂₅ and N₁₁–Ru–N₃ angles are in the 76.2° to 78.9° interval; N₁₁–Ru–N₁₉, N₁₁–Ru–N₂₅, and N₃–Ru–N₂₅ in the 88.1° to 100.4°; N₃–Ru–N₁₉ in the 173.1° to 176.2°; and O–Ru–N₃ and O–Ru–N₁₉ are in the 85.1° to 97.4° interval. In contrast, the relative positioning of the pyridine and the water molecule is quite dependent on the characteristics of the Ru-complex species. The [Ru^II(H₂O)]²⁺ and [Ru^II(OH)]⁺ species exhibited the O–Ru–N₄₅–C dihedral (where C is the closest pyridine carbon to oxygen) respectively at 16.6° and 29.1°; whereas they were respectively shifted to −26.6° and −30.4° in the oxidized [Ru^III(H₂O)]³⁺ and [Ru^III(OH)]²⁺ species. Interestingly, a further oxidation to [Ru^IV(O)]²⁺ species bring those atoms almost to the same plane and the dihedral angle goes down to only 1.4° as consequence of the removal of the steric effects of the hydrogen atoms of water, or hydroxide, and the closest pyridine ligand in the Ru-complex species.

Fig. 2 Superposition of the optimized structures of the Ru-complex species (at B3LYP/(aug)-cc-pVDZ(PP-Ru) level) in vacuum (green color) and in aqueous solution (using PCM model, in red color). Root mean square deviation (RMSD) of the vacuum and solution geometries (RMSD^V/S) is shown for each species.

Polypyridine ligands confer characteristic spectroscopic and redox properties to the Ru-complex species, that can also be influenced by environment conditions. From vacuum to aqueous solution, the bond length changes induced by the implicit solvent are not so significant. For example, we observed the reduction of all Ru–N bond lengths of all Ru-complex species and reduction (increase) of the Ru–O bond length in those with a coordinated water (hydroxide or oxide) ligand, however the changes are smaller than 0.03 Å. Dihedral angles involving the pyridine or any of the water derived ligands and the metal ion are the most affected by the solvent, undergoing changes from 8 to 53 degrees. In contrast, dihedral angles involving the bipyridine and the metal ion changed at most 3 degrees, thus demonstrating their higher structural stability and low sensitivity to solvent effects (Detailed information is available in ESI†). Fig. 2 shows the superposition of the optimized geometries of all Ru-complex species in vacuum and in aqueous solution, as well as the root mean square deviation (RMSD) values of the vacuum (VAC) and solution (SOL) geometries. The RMSD^VAC/SOL is 0.16, 0.14, 0.11, 0.09 and 0.01 for [Ru^III(H₂O)]³⁺, [Ru^II(OH)]⁺, [Ru^IV(O)]²⁺, [Ru^III(OH)]²⁺ and [Ru^II(H₂O)]²⁺, respectively. Therefore, on average, the [Ru^II(H₂O)]²⁺ complex undergoes the smallest conformational changes due to solvent effects, while the species with the highest total charge, [Ru^III(H₂O)]³⁺, undergoes the largest conformational changes. On the other hand, the less charged species [Ru^II(OH)]⁺ is almost as sensitive to the solvent as the most charged one, being a counterintuitive result considering the major contribution of the solute-solvent electrostatic interactions. This demonstrates that the extent of structural changes induced by solvent effects may not be only correlated to their total charges, but also to specific solute/solvent interactions, as addressed later on.

The oxidation of the metal ion always increases its electron withdrawing character inducing an increase of the acidity of coordinated water or hydroxo ligand leading to their deprotonation. Accordingly, the oxidized/deprotonated Ru-complex species can be generated by reaction with a strong enough oxidizing agent by mechanisms limited by an electron-transfer step, that can be followed or preceded by acid–base equilibrium, more specifically a proton transfer (PT), or a proton-coupled electron-transfer (PCET) mechanism. Such reactions cause structural changes in the Ru-complex species, but the most relevant ones take place in the coordination sphere of the metal complex. Among the oxidized/deprotonated species, the bond lengths of Ru with the three bipyridine N-atoms (N₃, N₁₉ and N₂₅) varied from 2.060 to 2.134 Å in vacuum and from 2.058 to 2.106 Å in aqueous solution. The Ru to pyridine N-atom (N₄₅) bond length is slightly longer, and varied from 2.150 to 2.163 Å in vacuum and from 2.140 to 2.159 Å in aqueous solution. The Ru–N₁₁ and Ru–O bonds are the most affected by the oxidation/deprotonation reactions but exhibiting opposite behavior. Whether in vacuum or in solution, the Ru–O bond is longer in [Ru^II(H₂O)]²⁺ and gradually was shortened along the sequence [Ru^III(H₂O)]³⁺, [Ru^II(OH)]⁺, [Ru^III(OH)]²⁺ and [Ru^IV(O)]²⁺. On the other hand, following this trend, the Ru–N₁₁ bond length was gradually increased (see Fig. 3) as expected for a significant Trans Influence.⁸⁷

Fig. 3 Ru–N and Ru–O bond lengths for the Ru-complex species in vacuum (open symbols) and in aqueous solution (filled symbols). The bond lengths were obtained by geometry optimizations at B3LYP/(aug)-cc-pVDZ(PP-Ru) level, using the PCM model to implement solvent effects.

Additionally, the angles and dihedrals associated with the bipyridine ligands and the metal center are less sensitive to PT, ET, or PCET reactions, demonstrating once again the structural stability conferred to the Ru-complex species by these ligands. On the other hand, the pyridine and the water derived ligands are very sensitive to those types of reactions, that can induce dihedral rotation changes of up to 50 degrees. Some of such changes can be seen in Fig. 2, and in more details in the ESI.†

3.2 Atomic charges distribution

In addition to the structural changes discussed above, the atomic charges distribution on the complexes was shown to be very sensitive to solvation effects, as well as changes in the metal ion oxidation state and associated protonation/deprotonation reactions. Accordingly, the most important changes in the electronic density distribution were captured and analyzed using the CHELPG⁸⁸ atomic charge calculation scheme in which atomic charges are fitted to reproduce the molecular electrostatic potential around the Ru-complex species. At first, there is a clear separation between the charges on the Ru-atom, more positive and close to 1 atomic unit (a.u.); negative charges on the nitrogen atoms, ranging from around −0.5 and 0.0 a.u.; and the negative charge on the oxygen atom lower than approximately −0.5 a.u. Although there is no direct correspondence between the atomic charge on pyridine N₁₁ and the Ru–N₁₁ or Ru–O bond lengths, it is always the most negative for the Ru-complex species in solution with 1+ and 2+ total charge, and the less negative for the species with the highest total charge (3+). Somehow, it can be a clue for the solvent contributions to the Trans Influence, since the charges on Ru(III) ion in vacuum and in solution are more vulnerable to the polarization of the medium, being more positive in solution when coordinated to a water molecule (0.41 a.u.), and more negative when coordinated to a hydroxide ion (−0.18 a.u.). Nevertheless, only a minor shift of the density of polarized charges could be observed in the other Ru-complex species, that varied at most 0.03 a.u. relative to the corresponding charges in vacuum. Analyzing the sum of the atomic charges of the bpy₁, bpy₂ and py ligands (Fig. 4), it can be seen that the solvent polarization makes the polypyridine ligands less positive in the aqua complexes, and more positive in the hydroxo and oxo complexes. Therefore, the medium polarization effects greatly shift the electron density dynamic such that the Ru atom can act as an electron donor or acceptor when coordinated to H₂O or OH⁻, whereas the polypyridine ligands act as electron acceptors or donors, respectively.

Fig. 4 Ru-complex species electronic charge distribution in vacuum (normal) and in aqueous solution (bold and underlined), separated per groups: water derived ligands in red; polypyridines (bpy₁ + bpy₂ + py) in black; ruthenium ion in green. Atomic charges were calculated at B3LYP/(aug)-cc-pVDZ/(PP-Ru) level using the CHELPG fitting scheme and the PCM model to describe the solvent.

Effects of PT, ET, and PCET reactions can also be observed on the charge distribution of the Ru-complex species, see Fig. 4. The mono-oxidation of [Ru^II(H₂O)]²⁺ in solution causes variations of +0.36 a.u. in the metal center, +0.61 a.u. in the polypyridine ligands (bpy₁ + bpy₂ + py) and +0.03 a.u. in the ligand water molecule electronic density. For [Ru^II(OH)]⁺ the variations are +0.39, +0.37 and +0.24 a.u., respectively. Therefore, less than 40% of the electronic density lost in the monoelectronic oxidation of these Ru-complex species comes from their metal center. On the other hand, the mono-deprotonation of [Ru^II(H₂O)]²⁺ (or [Ru^III(H₂O)]³⁺) in solution causes variations of −0.61 (−0.58), +0.35 (+0.11) and −0.74 (−0.53) a.u. in the charge densities on the metal center, polypyridine (bpy₁ + bpy₂ + py) and water derived ligands, respectively. Therefore, the loss of 1 proton leads to changes in the electronic distribution which depend on the oxidation state of the Ru-complex species, where the greatest variations are observed in the metal center and in the water derived ligands. Notably, when the [Ru^II(H₂O)]²⁺ (or [Ru^III(H₂O)]³⁺) complex is deprotonated in solution, the Ru charge density decreases from 0.94 to 0.33 a.u. (1.30 to 0.72 a.u.).

Furthermore, the charge variations due to the oxidation, or deprotonation, reactions can also drastically depend on the solvent effects. For example, the mono-deprotonation of [Ru^III(H₂O)]³⁺ in vacuum causes a variation of −0.59 a.u. in the total charge density on the polypyridine ligands, which represents the largest shift in the opposite direction (by +0.11 a.u.) as compared with that observed in aqueous solution. This is a direct consequence of the electron density shift due to polarization effect of the medium, since the polypyridine ligands behave as electron density acceptor or donor in the aqua and hydroxo complex species, respectively. In PCET reactions a compensatory movement of the electronic density is observed, and the atomic charge variations are less abrupt. For example, the mono-oxidation/deprotonation of [Ru^III(H₂O)]³⁺ to [Ru^IV(O)]²⁺ species causes variations of 0.29, −0.09, and −0.20 a.u. in the metal center, polypyridine ligands (bpy₁ + bpy₂ + py) and water derived ligands charge densities, respectively. Other possible PCET reactions can be seen in Fig. 4.

The deprotonation of the water molecule coordinated to the metal center leads to a remarkable reduction in the length of the Ru–O bond. This is expected since the loss of a proton enhance the electronic density on the oxygen atom and its basicity, as well as its covalent interaction with the electron deficient metal center. Similarly, the oxidation of the Ru also entails a reduction in the Ru–O distance since it leads to a decrease in the ionic radius and an increase in the positive charge on Ru, thus enhancing the ionic and the covalent interactions. Consequently, the combination of both effects (deprotonation and oxidation) induce a dramatic Ru–O bond length decrease from 2.24 Å in [Ru^IIH₂O]²⁺ to 1.92 Å in the [Ru^IIIOH]²⁺ complex. This means that the associated potential/bond energy is much more negative (and the bond much stronger) upon oxidation coupled with deprotonation. This is perfectly consistent with the fact that the atomic charge densities, adjusted to represent the electrostatic potential of Ru and O atoms, becomes more separated after any of these processes. The calculated atomic charges for all Ru-complex species, in vacuum and in solution are available in ESI.†

3.3 Frontier molecular orbitals

The analysis of the occupied and unoccupied frontier molecular orbitals (FMOs) reveals the effect of the solvent and the ET/PT/PCET reactions on the electronic density, with important consequences in the electronic transitions of the Ru-complex species. The energy level diagram of the FMOs in vacuum and in aqueous solution are depicted in Fig. 5, where HOMO stands for “Highest Occupied Molecular Orbital”, SOMO for “Singly Occupied Molecular Orbital” (with half-filled HOMO), and LUMO stands for “Lowest Unoccupied Molecular Orbital”. The HOMO and SOMO orbitals have a high contribution of d orbitals centered at Ru (d_Ru) and a small contribution of ligands π orbitals (π_L), mainly from the water derived ligand. 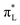LUMO, on the other hand, have a high contribution of both and orbitals. The closed shell species ([Ru^II(H₂O)]²⁺ and [Ru^II(OH)]⁺) have LUMO with high contribution from both bipyridine ligands whereas the open-shell species ([Ru^III(H₂O)]³⁺, [Ru^IV(O)]²⁺, [Ru^III(OH)]⁺) have major contribution from a single bipyridine, bpy₁ or bpy₂, respectively for Ru^III and Ru^IV species. This reveals a predominant metal-to-ligand charge-transfer character of the H(or S)OMO:LUMO electronic transitions in both closed-shell species, but that is drastically reduced in the open-shell systems in higher oxidation state, as expected.

Fig. 5 Energy level diagram of the frontier molecular orbitals and spin orbitals of the Ru-complex species in vacuum (vac) and in aqueous solution (sol). H(or S)OMO:LUMO energy gap indicated in the diagram and orbitals (sol) plotted (isovalue of 0.04) below.

As general trend, the FMOs energies are remarkably destabilized (it becomes less negative) by the solvent, and the magnitude of this destabilization is proportional to the total charge of the complexes: 2.32 eV for the complex with charge 1+; ranging from 5.15 to 5.31 eV for the complexes with charge 2+, and 7.96 eV for the complex with charge 3+. Such destabilizing orbitals effect can happen, for example, when the FMOs dipole moments do not have the same direction as the molecular dipole moment, thus inducing a destabilizing effect.⁸⁹ Conversely, the H(or S)OMO and LUMO orbitals stability are also connected to the total charges of the Ru-complex species. In solution, the H(or S)OMO (and LUMO) energies are −5.02 (−2.44), −6.11 (−2.73), −7.12 (−2.96), −7.05 (−3.03), −7.92 (−3.37) eV for [Ru^II(OH)]⁺, [Ru^II(H₂O)]²⁺, [Ru^III(OH)]²⁺, [Ru^IV(O)]²⁺ and [Ru^III(H₂O)]³⁺, respectively. Thus, the higher the total charge of the complex, more negative tend to be the FMOs. Besides, the H(or S)OMO–LUMO energy differences in vacuum (and in solution) are 2.39 (2.59), 3.46 (3.38), 3.95 (4.02), 4.02 (4.16), and 4.48 (4.55) for [Ru^II(OH)]⁺, [Ru^II(H₂O)]²⁺, [Ru^IV(O)]²⁺, [Ru^III(OH)]²⁺ and [Ru^III(H₂O)]³⁺, respectively. Therefore, the solvent effects cause the reduction of the H(or S)OMO–LUMO energy gap of [Ru^II(H₂O)]²⁺ and its increase for the other species. Similarly to H(or S)OMO and LUMO values, the energy gap also follows the total charge trend of the complexes.

Specially for closed-shell systems, the HOMO–LUMO energy gap can be associated to the system electronic excitability, resistance to charge transfer, and other properties. The chemical potential (μ), for example, characterizes the tendency of electrons to escape from the valence band and the chemical hardness (η) measures the internal charge transfer resistance of the system.⁹⁰ According to the Maximum Hardness Principle, molecular systems in equilibrium must be in a state of maximum hardness⁹⁰ and transition states must be in a state of minimum hardness.⁹¹ According to the definitions given by Parr and Pearson^92–94 and the Koopmans theorem, μ = (ε_L + ε_H)/2 and η = (ε_L − ε_H)/2, where ε_L and ε_H are the energy of LUMO and HOMO respectively.⁸⁹ For [Ru^II(H₂O)]²⁺ (and [Ru^II(OH)]⁺), μ is worth −9.70 (−6.15) and −4.42 (−3.73) eV in vacuum and in solution, respectively. It means that the solvation or the abstraction of a proton makes the chemical potential less negative, facilitating the removal of electrons from the complexes, thus making easier any chemical process. These are expected, since the loss of a proton decreases the electrostatic attraction between nucleus and electron in the complexes thus decreasing the resistance to electron transfer, since electrons will need less energy to escape. Otherwise, the chemical hardness (η) for [Ru^II(H₂O)]²⁺ (and [Ru^II(OH)]⁺) is 1.73 (1.69) and 1.19 (1.29) eV in vacuum and in solution, respectively. Therefore, the solvation makes the chemical hardness a little less positive for both closed-shell Ru-complex species, indicating that they have lower resistance to charge transfer processes in aqueous solution. Moreover, the increase/decrease of η upon mono-deprotonation of [Ru^II(H₂O)]²⁺ in vacuum/solution demonstrates a predominant role of the solvent in determining the charge transfer resistance of the complex under PT reactions. A table containing the values of the FMOs for all Ru-complex species is available in ESI.†

3.4 Optimized non-bonded parameters for Ru

The electronic properties of metal complexes are very susceptible to their oxidation and spin states, to the chemical nature of the ligands, and also to the environment conditions (pH, polarity, etc.). The molecular mechanics simulation of such systems in solution is highly dependent on the choice of suitable bonded and non-bonded force field parameters for the metal center and ligands, whose development is still a challenging task. In the last decades, a few non-bonded parameters for Ru-complexes, based on the Lennard-Jones plus Coulomb (LJC) potential (ε, σ, q), have been proposed (see Table 1). Allinger et al.,⁹⁵ Adlhart et al.⁹⁶ and Rappé et al.⁹⁷ presented LJ parameters for Ru without mentioning its oxidation state, and more recently Sebesta et al.⁴⁶ was the first to propose different sets of parameters for both Ru^II and Ru^III. Even though different sets of parameters for transition metals in many different oxidation states have been proposed by Sebesta et al., the parameterization procedure used by the authors does not consider the metals in a polypyridine coordination environment. Moreover, it has not been found in the Literature any parametrization proposal for Ru coordinated to polypyridine ligands simultaneously with an aqua, a hydroxo or an oxo ligand.

Table 1 Lennard Jones and Coulomb parameters for Ru atom

Reference	ε (kcal mol^−1)	σ (Å)	q (a.u.)
Allinger et al. (for Ru^II)^95 from MM3 force field	0.438	2.08	—
Adlhart et al. (for Ru^II)^96 from sybyl/tripos 5.2 force field	0.560	2.64	—
Rappé et al. (for Ru^II)^97 from UFF force field	0.056	2.64	—
Sebesta et al. (for Ru^II)^46	0.418	2.618	0.872
Sebesta et al. (for Ru^III)^46	1.644	2.523	0.790
Our (for Ru^II)	0.39	1.81	0.94
Our (for Ru^III)	0.39	1.99	1.30
Our (for Ru^IV)	0.39	1.81	1.01

---

The work of Allinger et al.⁹⁵ is quite general and comprises more than 100 atoms of the periodic table, including the Ru atom. The authors presented a broad set of LJ parameters developed for the MM3 force field. Adlhart et al.⁹⁶ presented LJ parameters for Ru from a modified version of the sybyl/tripos 5.2⁹⁸ force field. As mentioned by the authors, the LJ parameters were developed to be used in a QM/MM study of olefin-metathesis reaction catalyzed by Ru carbene complexes. Rappé et al.⁹⁷ developed the famous Universal Force Field (UFF) where the authors presented a full periodic table force field for molecular mechanic simulations, that includes LJ parameters for Ru. Sebesta et al.,⁴⁶ in turn, brings up the first parameterization study for Ru considering two different oxidation states (Ru^II and Ru^III). The authors employed the supramolecular approximation⁹⁹ to adjust the LJC parameters for various transition metals considering a neutral metal complex and a “test” molecule. [M(NH₃)_xCl_y] and [M(H₂O)_x(SH)_y] type structures were adopted as neutral complexes, where M is a transition metal and x or y indicate a variable number of ligands. As test molecules, they adopted NH₃, CH₄ and H₂O. The non-bonded parameters were then obtained to provide the best description of the metal-ligand quantum interaction energies.

The coordination of the metal with a water molecule, a hydroxide or an oxide ion can completely modify the electronic structure of the complex. For metal complexes with a coordinated aqua ligand, it is mandatory also consider the interaction of the metal center with the water molecules in solution to properly describe the intra and intermolecular non-bonded interactions of the complexes. In this work, we propose a set of non-bonded parameters for Ru in the oxidation states II, III and IV (“Our” in Table 1), based on the accurate description of the QM energy profile of Ru and the coordinated water molecule in the polypyridyl coordination environment of the studied closed-shell Ru-complex species. Fig. 6 shows the LJC energy profile of the water ligand in the [Ru^II(H₂O)]²⁺ and [Ru^IIIH₂O]³⁺ complexes obtained with the LJC parameters presented in Table 1 in comparison with the QM energy profile calculated with B3LYP/(aug)-cc-pVDZ(PP-Ru). From the literature, the set of parameters proposed by Allinger et al. is the one that provides the LJC energy profiles closest to the QM ones, but with less negative minimum energy (E_min), by 4.7 kcal mol⁻¹ for Ru^II, by 1.8 kcal mol⁻¹ for Ru^III; and distorted r₀ by 0.2 Å for Ru^II, and by 0.1 Å for Ru^III. Moreover, the set of parameters proposed by Sebesta et al. is the one that provides the LJC energy profiles furthermost to the QM ones, with even less negative E₀ (1.9 kcal mol⁻¹ for Ru^II, and 17.9 kcal mol⁻¹ for Ru^III) and even more distorted r₀ (0.5 Å for Ru^II, and 0.7 Å for Ru^III). LJC energies profiles intermediary to the LJC profiles of Allinger et al. and Sebesta et al. were obtained when the parameterizations proposed by Rappé et al. and Adlhart et al. was considered.

Fig. 6 Energy profile for the Ru-complex and interaction of the aqua and hydroxo ligands in [Ru^II(H₂O)]²⁺ (a) and [Ru^III(H₂O)]³⁺ (b) complexes.

Our set of LJC parameters, obtained with the precision of two digits, gave the best agreement of the LJC and QM energy profiles, with an excellent description of the minimum energy (E₀) and equilibrium distance r₀ for both Ru^II and Ru^III, reaching a deviation of only 1.4 and 0.8 kcal mol⁻¹ for the QM minimum energies of the Ru^II and Ru^III complexes, respectively. Also, we fitted exactly the QM minimum distance in both oxidation states. Equal ε values were obtained for Ru^II, Ru^III and Ru^IV, and different σ values were obtained for Ru^II, Ru^III and Ru^IV. The fitted σ value for Ru^III is 0.2 Å larger than for Ru^II and Ru^IV complexes. Moreover, a more positive charge for Ru^III and Ru^IV than Ru^II were obtained by fitting the electrostatic potential of the Ru-complex species using the CHELPG method. Even though the charge of Ru^II is expected to be more positive after a mono-oxidation, as we have obtained, the parameters proposed by Sebesta et al. do not follow this tendency, since a charge of Ru^III smaller than Ru^II is proposed by them. Last, but not less important, as long as we have adopted B3LYP without long range dispersion corrections, the LJ parameters adjusted for Ru accurately describe only the region near the Ru–O equilibrium distance.

3.5 Solvent structure around the complexes

Analyzing the Monte Carlo simulations of the complexes in solution, the solvent structure around the complexes was mapped by the minimum distance distribution function (MDDF)¹⁰⁰ (Fig. 7a). The first peaks, observed in r < 2 Å, refer to the micro-solvation region, where the formation of hydrogen bonds between the complexes and the solvent occurs. For larger distances, it is observed the formation of a first solvation layer with peak at 2.7 Å and minimum at 4.1 Å, integrating up to 25 water molecules (Fig. 7b), and a second solvation layer with peak varying between 5.5 and 5.7 Å, and minimum around 7 Å, integrating up to 200 water molecules. The radial distribution functions (RDFs) between the Ru and O atoms of the complexes and the O and H atoms of the solvent, g(r)^Ru–Ow, g(r)^Ru–Hw, g(r)^O–Ow and g(r)^O–Hw (Fig. 7) show how the solvent is structured in a micro-solvation region around the Ru-complex species, where hydrogen bonds take place. In the case of the aqua complexes, the position of the first peak in g(r)^O–Ow precedes the position of the first peak in g(r)^O–Hw, and the opposite is true for complexes coordinated with a hydroxo or an oxo ligand. This is notoriously an effect of the different types of hydrogen bonds made by different Ru-complex species, which can either donate or accept protons from the water molecules in the solvent as detailed below.

Fig. 7 (a) Minimum density distribution function (MDDF) of the Ru-complex species in aqueous solution. (b) Snapshot of the Monte Carlo simulation showing the [Ru^II(H₂O)]²⁺ complex surrounded by the solvent water molecules in the first solvation shell. (c–h) Radial distribution functions between Ru, O, and the oxygen (Ow) and hydrogen (Hw) atoms of the solvent molecules for [Ru^II(H₂O)]²⁺ (c) and (d), [Ru^II(OH)]⁺ (e) and (f) and [Ru^IV(O)]²⁺(g) and (h). The characteristic distances indicating the beginning of each RDF, the position of the first peak and the position of the first valley are indicated in the graphs by the labels r₀, r₁ and r₂, respectively. The RDFs of Ru-complex species in the 3+ oxidation state are shown in ESI.†

In the aqua complexes, the integral of any RDFs involving Ru, Ow, and Hw, up to a distance of 3.6 Å, is exactly equal to 1, which demonstrates that during the Monte Carlo simulations only the coordinated water molecule interacts directly with the metallic center. The average distance, during the simulations, between the oxygen of the coordinated water molecule and the Ru atom was 2.3 ± 0.1 Å (r₁ in g(r)^Ru–Ow), for the species in the oxidation states II or III, that is slightly larger than the distances obtained from the optimized geometries in solution (2.214 Å for [Ru^II(H₂O)]²⁺ and 2.148 Å for [Ru^III(H₂O)]³⁺. This is a consequence of the explicit treatment of the specific interactions in the simulations, which compete with the metallic center increasing the Ru–O bond.

In the hydroxo or oxo complexes, these moieties were treated as part of the solute (fixed in the optimized geometry relative positions), and therefore, their atoms were not counted in g(r)^Ru–Ow and g(r)^Ru–Hw. Concerning these complexes, the intensity of the first peak in g(r)^O–Hw is smaller for [Ru^III(OH)]²⁺, indicating that in the 3+ oxidation state, the hydroxide complex attracts less hydrogens of water molecules in solution. In other words, compared to [Ru^III(OH)]²⁺, the [Ru^II(OH)]⁺ complex can stablish a larger number of hydrogen bonds as a proton acceptor. Lastly, in the [Ru^IV(O)]²⁺ complex, the position of the first peak in g(r)^O–Hw (r₁ = 1.8 Å) is prior to the position of the first peak in g(r)^O–Ow (r₁ = 2.8 Å). This is an expected result since the oxide ion has a negative charge that necessarily attracts protons from the solution, making hydrogen bonds as a proton acceptor. In any complex, hydrogen bonds are stablished only between the coordinated aqua, hydroxo or oxo ligand and water molecules in solution, never involving the metallic center directly.

To account for the number of hydrogen bonds (N_HB) formed by the Ru-complex species, the criteria r < 3.5 Å and Θ < 40° were adopted for the maximum distance between electronegative atoms X and Y participating in the hydrogen bond, and the XYH angle of formation. Additionally, an energetic criterion was adopted according to which only hydrogen bonds with an interaction energy (E_HB) of at least −0.01 kcal mol⁻¹ are computed. Two types of hydrogen bonds were observed, the O–H⋯Ow type, where the Ru-complex donates a proton to a water molecule in solution and the O⋯Hw–Ow type, where the Ru-complex accept a proton from a water molecule in solution, see Fig. 8. The average number (N), distance (r), angle (θ) and energy (E_HB) of the accounted hydrogen bonds are listed in Table 2. Histograms showing the distributions of r, θ and E_HB are presented in ESI.†

Fig. 8 Illustration of the hydrogen bonds realized by the Ru-complex species in solution obtained from the superposition of 100 statistically uncorrelated Monte Carlo configurations. Red indicates Ru-complex species as hydrogen donor and gray as acceptor.

Table 2 Average number (N), distance (r), angle (θ) and energy (E_HB) of the hydrogen bonds made by the Ru-complex species with water molecules (Hw₂Ow) in solution, as a proton donor (O–H⋯Ow) and as a proton acceptor (O⋯Hw–Ow)

	O–H⋯Ow				O⋯Hw–Ow
	N	r (Å)	θ (degree)	E (kcal mol^−1)	N	r (Å)	θ (degree)	E (kcal mol^−1)
[Ru^II(H2O)]^2+	2	2.9 ± 0.2	14.9 ± 8.8	−9.2 ± 3.0	0.03	3.1 ± 0.2	20.5 ± 11.1	−0.9 ± 0.7
[Ru^III(H2O)]^3+	2.1	2.8 ± 0.2	14 ± 8.8	−13.5 ± 3.4	0.01	3.3 ± 0.1	33.9 ± 5.3	−2.5 ± 1.7
[Ru^II(OH)]^+	0.4	3.2 ± 0.2	15.2 ± 9.1	−1.9 ± 1.2	2	2.8 ± 0.2	11.6 ± 6.9	−7.9 ± 2.1
[Ru^III(OH)]^2+	1	2.9 ± 0.2	10.4 ± 6.3	−8.0 ± 2.3	1.3	2.9 ± 0.2	13.8 ± 8.0	−4.3 ± 1.9
[Ru^IV(O)]^2+	0	0	0	0	1.1	2.8 ± 0.2	15.7 ± 9.0	−3.7 ± 2.2

---

In the Ru-complex species with a coordinated water molecule, the O–H⋯Ow hydrogen bonds are preponderant, whereas hydrogen bonds, in which the Ru-complex acts as proton acceptor, is a very rare event (N_HB < 0.05). On the other hand, Ru-complex species with a coordinated hydroxide can make hydrogen bonds both as proton donor and acceptor as well. The [Ru^II(OH)]⁺ complex makes on average 0.4 hydrogen bonds as a donor and 2 hydrogen bonds as an acceptor. The [Ru^III(OH)]²⁺ complex makes on average 1 hydrogen bond as a donor and another 1.3 hydrogen bonds as an acceptor. Therefore, the O⋯Hw–Ow hydrogen bonds are preferred by the hydroxo complexes. Finally, the [Ru^IV(O)]²⁺ complex makes on average 1.1 hydrogen bonds only as an acceptor.

The distribution of hydrogen bond distances is generally unimodal (see histograms in ESI†), ranging from approximately 2.4 to 3.5 Å, with mean values in the 2.8 and 2.9 Å range. The distribution of bond angles also has unimodal character, ranging from 0 to 40 degrees and with average values in the range of 10.4 and 33.9 degrees. The energy distributions are unimodal for the [Ru^II(H₂O)]²⁺, [Ru^III(H₂O)]³⁺ and [Ru^IV(O)]²⁺ complexes, but bimodal for [Ru^II(OH)]⁺ and [Ru^III(OH)]²⁺ species. This behavior can be assigned to the two types of hydrogen bonds (O–H⋯Ow, and O⋯Hw–Ow) realized by these Ru-complex species, which have different energy distributions. The [Ru^III(H₂O)]³⁺ complex establishes the most intense hydrogen bonds with the solvent, with an average energy of −13.5 kcal mol⁻¹, followed by [Ru^II(H₂O)]²⁺, with an average energy of −9.2 kcal mol⁻¹. The [Ru^II(OH)]⁺ and [Ru^III(OH)]²⁺ complexes establish hydrogen bonds with an average energy of −1.9 and −8.0 kcal mol⁻¹ (OH⋯Ow) and −7.9 and −4.3 kcal mol⁻¹ (O⋯Hw–Ow), respectively. The weakest hydrogen bonds are realized by the [Ru^IV(O)]²⁺ complex, with an average energy of −3.7 kcal mol⁻¹. All values with respective standard deviations are listed in Table 2.

In general, the Coulomb interaction plays a fundamental role in the formation of hydrogen bonds in solution. Small shifts of the atomic charges in a molecule can completely change the characteristics of the hydrogen bonds formed.^101,102 The H-bonds made by [Ru^II(H₂O)]²⁺ are on average 70% less intense than that realized by the [Ru^III(H₂O)]³⁺ species. This behavior is justified by the higher total charge and smaller size of the complex in the 3+ oxidation state. Considering hydroxo complexes, for example, the differences in the number and average energy of OH⋯Ow and O⋯Hw–Ow type hydrogen bonds are mainly related to the atomic charge densities on the oxygen and hydrogen atoms of the hydroxo ligand. The atomic charges on the oxygen atom are −0.89 and −0.76, and on the hydrogen atom are 0.29 and 0.39, for [Ru^II(OH)]⁺ and [Ru^III(OH)]²⁺, respectively. Notably, the charge on the O-atom is more negative in the 2+ oxidation state thus attracting more protons from solution, and the charge on the H-atom is larger in the 3+ oxidation state, thus attracting more strongly the O-atom of the water molecules in solution. Furthermore, the number of H-bonds and the modulus of the O⋯Hw–Ow interaction energy by the hydroxo and oxo complexes increases as a function of the O-atom negative charge, which is −0.57, −0.76, and −0.89 for [Ru^IV(O)]²⁺, [Ru^III(OH)]²⁺, and [Ru^II(OH)]⁺, respectively. Furthermore, we will see in the next section that H-bonds play an important role in defining the electronic excitation energies of the complexes.

3.6 UV-vis absorption spectroscopy

The ultraviolet-visible (UV-vis) absorption spectra of the studied complexes in aqueous solution (Fig. 10 and ESI†) show absorption bands in the ultraviolet (λ < 400 nm) and in the visible (400 nm < λ < 700 nm) ranges, whose intensities follow the increasing trend of the transition energies. The absorption bands in the visible region are generally characterized by electronic transitions that involve charge-transfer from metal d orbitals to ligand π orbitals (MLCT: metal-to-ligand charge-transfer) and transitions centered in the metal d orbitals (MC: metal centered). The following electronic transitions take place in the ultraviolet region: (i) charge-transfer transitions from ligand π or σ orbitals to metal d orbitals (LMCT: ligand-to-metal charge-transfer), (ii) charge-transfer transitions involving ligands π orbitals (LLCT: ligand-to-ligand charge-transfer), and also (iii) transitions centered on ligand π orbitals (LC: ligand centered).¹⁰³ For the Ru-complex species with 2+ oxidation state, three absorption bands with well-defined maxima were observed at 472, 336, and 290 nm for [Ru^II(H₂O)]²⁺; at 506, 366, and 293 nm for [Ru^II(OH)]⁺ species. Accordingly, the deprotonation of the coordinated water molecule leads to a red-shift of all absorption bands. In the complexes in the 3+ and 4+ oxidation states, such absorption bands in the visible region lost intensity or disappeared, while the absorption peak of the most intense band, in the ultraviolet region, was slightly blue-shifted to 303, 302 and 304 nm for [Ru^III(H₂O)]³⁺, [Ru^III(OH)]²⁺ and [Ru^IV(O)]²⁺, respectively. This type of absorption spectra profile, with a more intense band in the ultraviolet and less intense bands in the longer wavelength regions, is typical of Ru-polypyridine complexes.¹⁰³

In order to assign the measured UV-Vis absorption spectra, the electronic excitations of the Ru-complex species were calculated using the TD-DFT theory with the B3LYP functional and the (aug)-cc-pVDZ(PP-Ru) basis sets. In preliminary tests (ESI†) it was demonstrated that this combination of methods and basis sets provides the best theoretical/experimental spectral matching with one of the lowest computational cost. In addition to B3LYP, the following methods were also tested: single-excitation CI, M06-2X, BHANDH, CAM-B3LYP, LC-ωPBE, and PBE0. Among these, the B3LYP and PBE0 methods showed the best performance, but with PBE0 energy values slightly overestimated. The following basis set types were considered: (i) all-electron basis sets for non-metallic atoms, combined with basis sets with effective core potential for Ru; (ii) all-electron basis sets for metallic and non-metallic atoms; and (iii) all-electron basis sets with Douglas-Kroll-Hess type zero-order relativistic correction. Interestingly, the inclusion of relativistic effects via effective potential was shown to be adequate to calculate the electronic transition energies of our Ru-complex species. Furthermore, as shown in Fig. 9, the solvent effects were investigated using both the traditional Polarizable Continuum Model (PCM)⁶⁸ and the S-QM/MM approach. Two approximations have been considered in the last case, namely: (i) treating the solvent molecules as point charges (PC approximation) and (ii) treating the solvent molecules that make hydrogen bonds with the Ru-complex species by quantum mechanics and the remaining as point charges (HB + PC approximation). The spectra of [Ru^II(H₂O)]²⁺ and [Ru^II(OH)]⁺ calculated in vacuum and in solution, using the three solvent effects approximation levels (see ESI† for other complexes), are shown in Fig. 9:

Fig. 9 Theoretical UV-Vis absorption spectra of the [Ru^II(H₂O)]²⁺ and [Ru^II(OH)]⁺ complexes, in vacuum and in aqueous solution. Electronic transitions calculated with the TD-DFT method, using B3LYP/(aug)-cc-pVDZ(PP-Ru). Solvent effects treated according to the PCM, PC and HB + PC approaches. Experimental spectra (Exp) are presented for comparison. The number are the calculated (in black) and experimental (in color) values of the maximum wavelength in nm. Conv = convoluted spectrum obtained from calculated electronic excitations where Excit = calculated electronic excitations with intensity defined by the calculated oscillator strength.

The energies and intensities of the calculated electronic excitations in solution are in good agreement with the experimental data, where the transitions in the visible range showed to be more sensitive to the solvent effects. From the convolution of the calculated electronic excitations with Lorentzian functions with 0.25 eV of width at half-height, the following theoretical values were obtained for the longer wavelength absorption peak of [Ru^II(H₂O)]²⁺ (and [Ru^II(OH)]⁺) species: 432 (520) nm in vacuum and 444 (510), 442 (482) and 456 (491) nm in solution using the PCM, PC and HB + PC approximations, respectively. Comparing with the experimental values of this absorption band (472 nm for [Ru^II(H₂O)]²⁺ and 506 nm for [Ru^II(OH)]⁺), the inclusion of solvent effects and the improvement of their description by considering explicitly the solvent molecules as point charges (PC approximation) and additional inclusion of a quantum mechanical treatment of the solvent molecules that realize hydrogen bonds with the complexes (HB + PC), contributed to a more accurate description of the UV-Vis spectra of these complexes.

Previous studies have shown the importance of the vibrational motion of ligands and solvent for understanding and modelling the optical properties and dynamics of Ru-complex species with bpy ligands.^104–109 The necessity of including at least the first solvation shell in the QM calculations has also been emphasized for the calculation of electronic properties of Ru complexes.^106,110 In our work, especially for [Ru^II(H₂O)]²⁺, we have also investigated the impact of including a larger number of explicit solvent molecules, going beyond hydrogen bonds. We took into account the complete first solvation shell when calculating the first five electronic excitations, albeit considering only five Monte Carlo configurations. Fig. S10 (ESI†) illustrates that the incorporation of the first solvation shell does not significantly improve the agreement with experimental results in terms of the energy of the excitations. Additionally, regardless of whether we employed the B3LYP or PBE0 functionals, our conclusions remained consistent. However, it is worth noting that the B3LYP functional exhibited a closer alignment with experimental observations. Therefore, treating only the hydrogen bonds at the quantum mechanical (QM) level and employing the electrostatic embedding approach to account for the remaining solvent molecules represents a reasonable compromise to describe and characterize the electronic spectra of the studied Ru-aqua complexes in aqueous solution.

In order to advance in the understanding of these UV-Vis absorption spectra, the assignment of the calculated electronic excitations was realized according to their spatial distribution on the molecular structure of the Ru-complex species (Fig. 10f–j). Further quantitative assessment was obtained by analyzing the transition density matrices from the TD-DFT calculations using a fragment-based analysis, as implemented in the Theoretical Density, Orbital Relaxation, and Exciton analysis (TheoDORE) package.^79–82 The complexes were fragmented into 5 groups of atoms (bpy1, bpy2, py, aqueous group and the Ru atom) and the transitions were quantitatively assigned based on their MLCT, MC, LMCT, LLCT, and LC contributions. See Fig. 10(f)–(j).

Fig. 10 (a)–(e) Theoretical UV-Vis electronic excitations (colored vertical lines) of the Ru-complex species in aqueous solution calculated over 100 statistically uncorrelated solute/solvent configurations extracted from Monte Carlo simulations, using the TD-DFT theory with B3LYP/(aug)-cc-pVDZ/(PP-Ru). Solvent effects treated with the HB + PC approach within the scope of the sequential QM/MM method, and using solvent configurations extracted from the simulations. Experimental spectra are presented for comparison. (f)–(j) Average map of the MC (pink), MLCT (red), LMCT (blue), LC (green) and LLCT (yellow) contributions of the calculated electronic excitations, obtained from the analysis of the transition density matrices.

For [Ru^II(H₂O)]²⁺ and [Ru^II(OH)]⁺, the absorption bands with peaks at 472, 336 nm and 506, 366 nm, respectively, are mainly composed by MLCT-type transitions (about 60%), and in lesser degree by LLCT and LC transitions (∼30%). Also, there is an increase of the LLCT and LC contributions in the UV region below 300 nm, that goes up to 56%, and a reduction of the MLCT transitions to 30%, indicating that the UV band around 290 nm is mainly composed by transitions centered in the pyridyl ligands. The oxidation of the [Ru^II(H₂O)]²⁺ species to [Ru^III(H₂O)]³⁺ causes a drastic reduction of the contributions of the MLCT transitions down to 16% since the Ru(III) ion is a much stronger electron acceptor than Ru(II), thus increasing the LMCT contribution to 32%, considering the first 30 transitions. The MLCT contributions dropped to 18% around 300 nm while the LC and LLCT contributions were enhanced to almost 70%.

In [Ru^III(OH)]²⁺, the MCLT contributions (34%) play an important role until up to 300 nm, competing with the LC and LLCT contributions (up to 35%), and the LMCT contributions (15%). In the 300 nm region, the MLCT contributions were estimated in 24% while the LC, LLCT and LMCT contributions added up to 71%. In the case of the [Ru^IV(O)]²⁺ complex, the LC and LLCT contributions corresponded to 47% of the first 30 transitions, and this number rose to 69% when the last 20 transitions were considered. In contrast, the MLCTs contributed with 25% for the first 30 transitions and only 21% for the last 20 transitions. The LMCT contributions corresponded to 17% of the contributions in the first set and only 7% in the second set of electronic transitions. Thus, the [Ru^IV(O)]²⁺ complex has the second highest percentage of LMCT contributions among the first 30 transitions, second only to the [Ru^III(H₂O)]³⁺ complex. In general, the contribution of MC transitions is relatively low among all type of transitions in any of those Ru-complex species, being less than 16% of the total.

In more detailed contribution maps (see ESI†), it is possible to observe that the MLCT contributions involve predominantly the transfer of electron density from the metal to the bipyridine ligands (bpy1 and bpy2), and to a lesser extent, from the metal to the pyridine ligand. In contrast, in the LMCT contributions, the electronic density is transferred predominantly from the bipyridine ligands to the ruthenium ion. There are also LMCT contributions involving the pyridine, the bipyridines and the water derived ligands in a minor extent. On the other hand, the bipyridine ligands concentrate almost all of the LLCT contributions. Specifically, in the [Ru^II(OH)]⁺ and [Ru^IV(O)]²⁺ complexes, it is also observed that the water derived ligands donates a small portion of its electronic density to the other ligands. Over the entire calculated spectrum, the OH-LCT and O-LCT contributions were both computed to be around 20%, as detailed in the ESI.†

4 Conclusions

We conducted a comprehensive and systematic investigation on the solvent effects on the molecular and electronic structures of the mononuclear [Ru(OH₂)]²⁺ complex and its four oxidation/deprotonation derivatives in aqueous solution. Various approximations for the solute/solvent interactions were employed, including implicit (PCM) and explicit (S-QM/MM) solvent models, which combined classical Monte Carlo simulations and Quantum Mechanics calculations within the DFT and TD-DFT frameworks.

Our findings reveal that the solvation, oxidation, and deprotonation of the [Ru–OH₂]²⁺ species lead to structural changes primarily in the Ru coordination sphere, with the distances and angles between the metal center and the water derived ligands or pyridine ligand atoms being the most sensitive. Global geometric changes resulting from solvation do not correlate with the total charge of the ruthenium complex species, as evidenced by the shortening of the Ru–N and Ru–O bond distances in the aqua complexes and lengthening in hydroxo and oxo complexes. Conversely, the oxidation of the Ru(II) complexes increases the Ru–N bond lengths, especially the bond opposite to the O-atom, whereas shortening the Ru–O bond length, which is more pronounced in hydroxo complexes. In contrast, deprotonation of the aqua/hydroxo ligand consistently leads to a shortening of the Ru–O bond and elongation/contraction of the opposite Ru–N bond, with the pyridine ligand being less sensitive to such effects than to the oxidation of the metal center. Notably, the bipyridine ligands remained insensitive to electron or proton-transfer processes.

Alongside geometric changes, oxidation and deprotonation processes have opposite effects on the electron density at the metal site. The conversion of the aqua into the hydroxo ligand and then into the oxo ligand lead to the transfer of electronic density and decrease of the positive charge on Ru-atom, whereas its oxidation tends to increase it. The polarization of the Ru-complex species due to the presence of the aqueous solution leads to larger variations in the electronic density on the metal center and water-derived ligands. Among all of the atoms in the [Ru(OH₂)]²⁺ complex, the Ru atom is the most sensitive to oxidation and deprotonation processes, undergoing the largest changes in the electronic density distribution.

The frontier molecular orbitals of the complexes, HOMO or SOMO and LUMO have predominantly d(metal) and π*(bipyridines) orbital character, respectively. This implies that the electronic transitions between these orbitals have metal-to-ligand charge-transfer (MLCT) character. Notably, the solvent tend to destabilize the frontier molecular orbitals relative to vacuum as the total charge of the complex increases. Furthermore, analysis of the effect of solvation, oxidation, and deprotonation processes on the HOMO–LUMO energy gap suggests that the migration of electronic density is lower in the more highly charged complexes, but tends to increase when the aqua ligand is successively deprotonated to the hydroxo and oxo ligands.

The solvation shell surrounding the complexes in solution displays similarity, with differences only found in the microsolvation region where intermolecular hydrogen bonding plays a significant role. In the aqua complexes, the Ru–O distance is primarily influenced by hydrogen bonding rather than the oxidation state of the complex. Meanwhile, the hydroxo complexes form a higher number of hydrogen bonds compared to the other species, with the strongest hydrogen bond being present in the complex with the highest total charge.

The UV-Vis absorption spectra of the [Ru(OH₂)]²⁺ complex and its oxidation/deprotonation species were simulated using the B3LYP/(aug)-cc-pVDZ/(PP-Ru) theory level, which provided the best description at the lowest computational cost. The UV-Vis spectra of the Ru-complex species were found to be more sensitive to solvent effects in the visible region, where closed-shell species exhibit broad MLCT absorption bands and solution pH-sensitive electronic transitions, wich lose intensity or disappear when the complex is oxidized, while LC and LLCT bands prevail in the ultraviolet region. The MLCT bands in the visible have a predominant contribution of metal-to-bipyridine charge-transfer transitions and are best described when the complex/solvent hydrogen bonds are treated at the QM level and the other water molecules are treated as point charges. The theoretical and experimental UV spectra were found to be in excellent agreement, validating the LJC parameters developed for the Ru-atom and the S-QM/MM protocol employed in this work.

Conflicts of interest

The authors declare that there are no conflicts of interest.

Acknowledgements

Authors gratefully acknowledge support from: the São Paulo State Research Foundation (FAPESP grants no. 2017/50129-0, 2017/11631-2, 2018/21489-1, 2018/04523-1 and 2021/09016-3), Shell and the strategic importance of the support given by ANP (Brazil's National Oil, Natural Gas and Biofuels Agency) through the R&D levy regulation, National Council of Scientific and Technological Development (CNPq grants no. 401581/2016-0, 303137/2016-9 and 304651/2021-4), CAPES/STINT grants no. 88881.465527/2019-01 and High Performance Computing of USP (HPC-USP) for computational resources. L. R. F. thanks CAPES for the fellowship (88882.160173/2017-01). CMA thanks the Swedish Research Council (VR) (grants no. 2020-05223), Swedish Energy Agency (grant no. 45420-1) and STandUP for Energy Collaboration.

References

1. D. A. Buckingham, A. M. Sargeson, F. P. J. Dwyer and D. P. Mellor, Chelating agents and metal chelates, ed. F. P. Dwyer and D. P. Mellor, Academic Press, New York, 1964, pp. 283–329.
2. L. Boubekeur-Lecaque, B. J. Coe, K. Clays, S. Foerier, T. Verbiest and I. Asselberghs, Redox-switching of nonlinear optical behavior in Langmuir-Blodgett thin films containing a ruthenium(II) ammine complex, J. Am. Chem. Soc., 2008, 130, 3286–3287.
3. M. Mikuriya, D. Yoshioka and M. Handa, Magnetic interactions in one-, two-, and three-dimensional assemblies of dinuclear ruthenium carboxylates, Coord. Chem. Rev., 2006, 250, 2194–2211.
4. M. A. S. Aquino, Diruthenium and diosmium tetracarboxylates: synthesis, physical properties and applications, Coord. Chem. Rev., 1998, 170, 141–202.
5. T. Kizaki, T. Abe, T. Matsumoto and S. Ogo, A pH-stable Ruthenium(II)-based Sensing System for Dissolved Dinitrogen, Chem. Lett., 2010, 39, 128–129.
6. D. de Oliveira, Silva, Perspectives for novel mixed diruthenium-organic drugs as metallopharmaceuticals in cancer therapy, Anti-Cancer Agents Med. Chem., 2010, 10, 312–323.
7. Y.-J. Liu, C.-H. Zeng, J.-H. Yao, F.-H. Wu, L.-X. He and H.-L. Huang, Synthesis, Structure, DNA-Binding Properties, and Cytotoxicity of Ruthenium(II) Polypyridyl Complexes, Chem. Biodiversity, 2010, 7, 1770–1783.
8. W.-C. Chang, H.-S. Chen, T.-Y. Li, N.-M. Hsu, Y. S. Tingare, C.-Y. Li, Y.-C. Liu, C. Su and W.-R. Li, Highly Efficient N-Heterocyclic Carbene/Pyridine-Based Ruthenium Sensitizers: Complexes for Dye-Sensitized Solar Cells, Angew. Chem., 2010, 122, 8337–8340.
9. F. Perrella, X. Li, A. Petrone and N. Rega, Nature of the Ultrafast Interligands Electron Transfers in Dye-Sensitized Solar Cells, JACS Au, 2022, 3, 70–79.
10. M. K. Nazeeruddin, C. Klein, P. Liska and M. Grätzel, Synthesis of novel ruthenium sensitizers and their application in dye-sensitized solar cells, Coord. Chem. Rev., 2005, 249, 1460–1467.
11. F. Perrella, A. Petrone and N. Rega, Direct observation of the solvent organization and nuclear vibrations of [Ru(dcbpy)₂(NCS)₂]⁴⁻,[dcbpy = (4,4′-dicarboxy-2,2′-bipyridine)], via ab initio molecular dynamics, Phys. Chem. Chem. Phys., 2021, 23, 22885–22896.
12. S. Berardi, S. Drouet, L. Francàs, C. Gimbert-Suriñach, M. Guttentag, C. Richmond, T. Stoll and A. Llobet, Molecular artificial photosynthesis, Chem. Soc. Rev., 2014, 43, 7501–7519.
13. C. Bruneau and P. H. Dixneuf, Ruthenium catalysts and fine chemistry, Springer Science & Business Media, 2004, vol. 11.
14. S. Miyazaki, T. Kojima, T. Sakamoto, T. Matsumoto, K. Ohkubo and S. Fukuzumi, Proton-Coupled Electron Transfer in Ruthenium(II)-Pterin Complexes: Formation of Ruthenium-Coordinated Pterin Radicals and Their Electronic Structures, Inorg. Chem., 2008, 47, 333–343.
15. T. Punniyamurthy, S. Velusamy and J. Iqbal, Recent advances in transition metal catalyzed oxidation of organic substrates with molecular oxygen, Chem. Rev., 2005, 105, 2329–2364.
16. R. H. Holm, Metal-centered oxygen atom transfer reactions, Chem. Rev., 1987, 87, 1401–1449.
17. S. W. Gersten, G. J. Samuels and T. J. Meyer, Catalytic oxidation of water by an oxo-bridged ruthenium dimer, J. Am. Chem. Soc., 1982, 104, 4029–4030.
18. R. Zong and R. P. Thummel, A new family of Ru complexes for water oxidation, J. Am. Chem. Soc., 2005, 127, 12802–12803.
19. J. J. Concepcion, J. W. Jurss, M. K. Brennaman, P. G. Hoertz, A. O. T. Patrocinio, N. Y. Murakami Iha, J. L. Templeton and T. J. Meyer, Making oxygen with ruthenium complexes, Acc. Chem. Res., 2009, 42, 1954–1965.
20. J. J. Concepcion, M.-K. Tsai, J. T. Muckerman and T. J. Meyer, Mechanism of water oxidation by single-site ruthenium complex catalysts, J. Am. Chem. Soc., 2010, 132, 1545–1557.
21. B. Zhang and L. Sun, Ru-bda: Unique molecular water-oxidation catalysts with distortion induced open site and negatively charged ligands, J. Am. Chem. Soc., 2019, 141, 5565–5580.
22. M. D. Karkas, O. Verho, E. V. Johnston and B. Åkermark, Artificial photosynthesis: molecular systems for catalytic water oxidation, Chem. Rev., 2014, 114, 11863–12001.
23. T. A. Matias, A. F. Keppler and F. H. Bartoloni, In need of a second-hand? The second coordination sphere of ruthenium complexes enables water oxidation with improved catalytic activity, Dalton Trans., 2020, 49, 16034–16046.
24. B. A. Moyer and T. J. Meyer, Properties of the oxo/aqua system (bpy)₂(py) RuO²⁺/(bpy)₂(py)Ru(OH₂)²⁺, Inorg. Chem., 1981, 20, 436–444.
25. J. L. Silva, I. Unger, T. A. Matias, L. R. Franco, G. Damas, L. T. Costa, K. C. F. Toledo, T. C. R. Rocha, A. N. de Brito, C. M. Saak, K. Coutinho, K. Araki, O. Björneholm, B. Brena and C. M. Araujo, X-ray Photoelectron Fingerprints of High-Valence Ruthenium-Oxo Complexes along the Oxidation Reaction Pathway in an Aqueous Environment, J. Phys. Chem. Lett., 2019, 10, 7636–7643.
26. S. Zhan, R. Zou and M. S. G. Ahlquist, Dynamics with Explicit Solvation Reveals Formation of the Prereactive Dimer as Sole Determining Factor for the Efficiency of Ru (bda) L2 Catalysts, ACS Catal., 2018, 8, 8642–8648.
27. S. Zhan, J. A. de Gracia Trivino and M. S. G. Ahlquist, The carboxylate ligand as an oxide relay in catalytic water oxidation, J. Am. Chem. Soc., 2019, 141, 10247–10252.
28. S. Basri, S. K. Kamarudin, W. R. W. Daud and Z. Yaakub, Nanocatalyst for direct methanol fuel cell (DMFC), Int. J. Hydrogen Energy, 2010, 35, 7957–7970.
29. J. M. de Ruiter, H. J. M. de Groot and F. Buda, Energetic Effects of a Closed System Approach Including Explicit Proton and Electron Acceptors as Demonstrated by a Mononuclear Ruthenium Water Oxidation Catalyst, ChemCatChem, 2018, 10, 4594–4601.
30. N. Govindarajan and E. J. Meijer, Modeling the Catalyst Activation Step in a Metal–Ligand Radical Mechanism Based Water Oxidation System, Inorganics, 2019, 7, 62.
31. N. Govindarajan, V. Sinha, M. Trincado, H. Grützmacher, E. J. Meijer and B. de Bruin, An In-Depth Mechanistic Study of Ru Catalysed Aqueous Methanol Dehydrogenation and Prospects for Future Catalyst Design, ChemCatChem, 2020, 12, 2610–2621.
32. D. Mei, V.-A. Glezakou, V. Lebarbier, L. Kovarik, H. Wan, K. O. Albrecht, M. Gerber, R. Rousseau and R. A. Dagle, Highly active and stable MgAl2O4-supported Rh and Ir catalysts for methane steam reforming: A combined experimental and theoretical study, J. Catal., 2014, 316, 11–23.
33. Y. Cao, Y. Gao, H. Zhou, X. Chen, H. Hu, S. Deng, X. Zhong, G. Zhuang and J. Wang, Highly efficient ammonia synthesis electrocatalyst: single Ru atom on naturally nanoporous carbon materials, Adv. Theory Simul., 2018, 1, 1800018.
34. B. S. Akpa, C. D’Agostino, L. F. Gladden, K. Hindle, H. Manyar, J. McGregor, R. Li, M. Neurock, N. Sinha and E. H. Stitt, et al., Solvent effects in the hydrogenation of 2-butanone, J. Catal., 2012, 289, 30–41.
35. S. Bandaru, N. J. English and J. M. D. MacElroy, Implicit and explicit solvent models for modeling a bifunctional arene ruthenium hydrogen-storage catalyst: A classical and ab initio molecular simulation study, J. Comput. Chem., 2014, 35, 683–691.
36. V. Sinha, N. Govindarajan, B. de Bruin and E. J. Meijer, How Solvent Affects C–H Activation and Hydrogen Production Pathways in Homogeneous Ru-Catalyzed Methanol Dehydrogenation Reactions, ACS Catal., 2018, 8, 6908–6913.
37. Z. Chen, J. J. Concepcion, X. Hu, W. Yang, P. G. Hoertz and T. J. Meyer, Concerted O atom–proton transfer in the O–O bond forming step in water oxidation, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 7225–7229.
38. V. Kunz, J. O. Lindner, M. Schulze, M. I. S. Röhr, D. Schmidt, R. Mitrić and F. Würthner, Cooperative water oxidation catalysis in a series of trinuclear metallosupramolecular ruthenium macrocycles, Energy Environ. Sci., 2017, 10, 2137–2153.
39. M. Hölscher and W. Leitner, DFT Investigation of the Potential of [H-M {(NHCH2CH2) 3X}] Catalysts (M = Mo, Ru, Os; X = N, P) for the Reduction of N2 to NH3 by H2, Eur. J. Inorg. Chem., 2006, 4407–4417.
40. P. Diamantis, J. F. Gonthier, I. Tavernelli and U. Rothlisberger, Study of the redox properties of singlet and triplet tris (2,2’-bipyridine) ruthenium(II)([Ru(bpy)₃]²⁺) in aqueous solution by full quantum and mixed quantum/classical molecular dynamics simulations, J. Phys. Chem. B, 2014, 118, 3950–3959.
41. X. Zeng, H. Hu, X. Hu, A. J. Cohen and W. Yang, Ab initio quantum mechanical/molecular mechanical simulation of electron transfer process: Fractional electron approach, J. Chem. Phys., 2008, 128, 124510.
42. R. Bianco, P. J. Hay and J. T. Hynes, Theoretical Study of Water Oxidation by the Ruthenium Blue Dimer. II. Proton Relay Chain Mechanism for the Step [bpy2 (HOO) RuIVORuIV (OH) bpy2] 4 + ?[bpy₂(O^2–) RuIVORuIII (OH2) bpy₂]⁴⁺, J. Phys. Chem. B, 2013, 117, 15761–15773.
43. A. Pérez, F. J. Luque and M. Orozco, Dynamics of B-DNA on the microsecond time scale, J. Am. Chem. Soc., 2007, 129, 14739–14745.
44. L. R. Franco, P. Park, H. Chaimovich, K. Coutinho, I. M. Cuccovia and F. S. Lima, Simulations reveal that antimicrobial BP100 induces local membrane thinning, slows lipid dynamics and favors water penetration, RSC Adv., 2022, 12, 4573–4588.
45. P. Park, L. R. Franco, H. Chaimovich, K. Coutinho, I. M. Cuccovia and F. S. Lima, Binding and Flip as Initial Steps for BP-100 Antimicrobial Actions, Sci. Rep., 2019, 9, 1–14.
46. F. Sebesta, V. Slma, J. Melcr, Z. Futera and J. V. Burda, Estimation of transition-metal empirical parameters for molecular mechanical force fields, J. Chem. Theory Comput., 2016, 12, 3681–3688.
47. X. Li, Y. Tu, H. Tian and H. Ågren, Computer simulations of aqua metal ions for accurate reproduction of hydration free energies and structures, J. Chem. Phys., 2010, 132, 104505.
48. L. Zhao, L. Liu and H. Sun, Semi-ionic model for metal oxides and their interfaces with organic molecules, The, J. Phys. Chem. C, 2007, 111, 10610–10617.
49. C. E. S. Bernardes, J. N. Canongia Lopes and M. E. M. da Piedade, All-atom force field for molecular dynamics simulations on organotransition metal solids and liquids. Application to M (CO) n (M = Cr, Fe, Ni, Mo, Ru, or W) compounds, J. Phys. Chem. A, 2013, 117, 11107–11113.
50. J. Torras and C. Aleman, Determination of new Cu⁺, Cu²⁺, and Zn²⁺ Lennard-Jones ion parameters in acetonitrile, J. Phys. Chem. B, 2013, 117, 10513–10522.
51. K. Coutinho and S. Canuto, Solvent effects from a sequential Monte Carlo-quantum mechanical approach, Adv. Quantum Chem., 1997, 28, 89–105.
52. K. Coutinho and S. Canuto, The sequential Monte Carlo-quantum mechanics methodology. Application to the solvent effects in the Stokes shift of acetone in water, THEOCHEM, 2003, 632, 235–246.
53. S. Canuto and K. Coutinho, From hydrogen bond to bulk: Solvation analysis of the n-π* transition of formaldehyde in water, Int. J. Quantum Chem., 2000, 77, 192–198.
54. K. Coutinho and S. Canuto, Solvent effects in emission spectroscopy: A Monte Carlo quantum mechanics study of the n← π* shift of formaldehyde in water, J. Chem. Phys., 2000, 113, 9132–9139.
55. K. Coutinho, S. Canuto and M. C. Zerner, A Monte Carlo-quantum mechanics study of the solvatochromic shifts of the lowest transition of benzene, J. Chem. Phys., 2000, 112, 9874–9880.
56. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864; W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
57. R. M. Dreizler and E. K. Gross, Density functional theory: an approach to the quantum many-body problem, Springer Science & Business Media, 2012.
58. A. D. Becke, Becke's three parameter hybrid method using the LYP correlation functional, J. Chem. Phys., 1993, 98, 5648–5652.
59. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
60. T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023.
61. R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions, J. Chem. Phys., 1992, 96, 6796–6806.
62. K. A. Peterson, D. Figgen, M. Dolg and H. Stoll, Energy-consistent relativistic pseudopotentials and correlation consistent basis sets for the 4 d elements Y–Pd, J. Chem. Phys., 2007, 126, 124101.
63. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids, J. Am. Chem. Soc., 1996, 118, 11225–11236.
64. W. L. Jorgensen, W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926; W. L. Jorgensen, W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926.
65. S. F. Boys and F. de Bernardi, The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors, Mol. Phys., 1970, 19, 553–566.
66. S. Simon, M. Duran and J. J. Dannenberg, How does basis set superposition error change the potential surfaces for hydrogen-bonded dimers?, J. Chem. Phys., 1996, 105, 11024–11031.
67. C. M. Breneman and K. B. Wiberg, Determining atom-centered monopoles from molecular electrostatic potentials. The need for high sampling density in formamide conformational analysis, J. Comput. Chem., 1990, 11, 361–373.
68. S. Miertuš, E. Scrocco and J. Tomasi, Electrostatic interaction of a solute with a continuum. A direct utilizaion of AB initio molecular potentials for the prevision of solvent effects, Chem. Phys., 1981, 55, 117–129.
69. M. V. A. Damasceno, B. J. C. Cabral and K. Coutinho, Theor. Chem. Acc, 2012, 7, 7.
70. R. C. Barreto, K. Coutinho, H. C. Georg and S. Canuto, Combined Monte Carlo and quantum mechanics study of the solvatochromism of phenol in water. The origin of the blue shift of the lowest π–π* transition, Phys. Chem. Chem. Phys., 2009, 11, 1388–1396.
71. V. Manzoni, M. L. Lyra, R. M. Gester, K. Coutinho and S. Canuto, Study of the optical and magnetic properties of pyrimidine in water combining PCM and QM/MM methodologies, Phys. Chem. Chem. Phys., 2010, 12, 14023–14033.
72. V. Manzoni, M. L. Lyra, K. Coutinho and S. Canuto, Comparison of polarizable continuum model and quantum mechanics/molecular mechanics solute electronic polarization: Study of the optical and magnetic properties of diazines in water, J. Chem. Phys., 2011, 135, 144103.
73. M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford University Press, 2017.
74. K. J. de Almeida, K. Coutinho, W. B. de Almeida, W. R. Rocha and S. Canuto, A Monte Carlo–quantum mechanical study of the solvatochromism of pyrimidine in water and in carbon tetrachloride, Phys. Chem. Chem. Phys., 2001, 3, 1583–1587.
75. K. Coutinho, R. Rivelino, H. C. Georg and S. Canuto, in Solvation Effects on Molecules and Biomolecules: Computational Methods and Applications, ed. S. Canuto, Springer Netherlands, Dordrecht, 2008, pp. 159–189.
76. H. M. Cezar, S. Canuto and K. Coutinho, Understanding the absorption spectrum of mesityl oxide dye in solvents of different polarities, J. Mol. Liq., 2020, 307, 112924.
77. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2016.
78. H. M. Cezar, S. Canuto and K. Coutinho, DICE: A Monte Carlo Code for Molecular Simulation including the Configurational Bias Monte Carlo Method, J. Chem. Inf. Model., 2020, 60, 3472–3488.
79. F. Plasser, TheoDORE: A toolbox for a detailed and automated analysis of electronic excited state computations, J. Chem. Phys., 2020, 152, 84108.
80. P. Kimber and F. Plasser, Toward an understanding of electronic excitation energies beyond the molecular orbital picture, Phys. Chem. Chem. Phys., 2020, 22, 6058–6080.
81. F. Plasser and H. Lischka, Analysis of excitonic and charge transfer interactions from quantum chemical calculations, J. Chem. Theory Comput., 2012, 8, 2777–2789.
82. S. Mai, F. Plasser, J. Dorn, M. Fumanal, C. Daniel and L. Gonzalez, Quantitative wave function analysis for excited states of transition metal complexes, Coord. Chem. Rev., 2018, 361, 74–97.
83. G. D. Hager and G. A. Crosby, Charge-transfer exited states of ruthenium(II) complexes. I. Quantum yield and decay measurements, J. Am. Chem. Soc., 1975, 97, 7031–7037.
84. E. M. Kober and T. J. Meyer, Concerning the absorption spectra of the ions M(bpy)32+ (M = Fe, Ru, Os; bpy = 2,2’-bipyridine), Inorg. Chem., 1982, 21, 3967–3977.
85. F. Felix, J. Ferguson, H. U. Guedel and A. Ludi, The electronic spectrum of tris(2,2’-bipyridine) ruthenium (2+), J. Am. Chem. Soc., 1980, 102, 4096–4102.
86. E. Gallhuber, G. Hensler and H. Yersin, Magnetic-field effects in the low-temperature polarized emission and absorption spectra of single-crystal tris (2,2’-bipyridine) ruthenium (2+) bis (hexafluorophosphate)([Ru(bpy)3](PF6)2), J. Am. Chem. Soc., 1987, 109, 4818–4822.
87. T. A. Matias, F. N. Rein, R. C. Rocha, A. L. B. Formiga, H. E. Toma and K. Araki, Effects of a strong $π$-accepting ancillary ligand on the water oxidation activity of weakly coupled binuclear ruthenium catalysts, Dalton Trans., 2019, 48, 3009–3017.
88. C. M. Breneman and K. B. Wiberg, Determining atom-centered monopoles from molecular electrostatic potentials. The need for high sampling density in formamide conformational analysis, J. Comput. Chem., 1990, 11, 361–373.
89. E. Sánchez-Marcos, J. Maraver, M. F. Ruiz-López and J. Bertran, Electrostatic interactions as a factor in the determination of the HOMO in the liquid state, Can. J. Chem., 1986, 64, 2353–2358.
90. R. G. Pearson, Recent advances in the concept of hard and soft acids and bases, J. Chem. Educ., 1987, 64, 561.
91. S. Gutierrez-Oliva, J. R. Letelier and A. Toro-Labbe, Energy, chemical potential and hardness profiles for the rotational isomerization of HOOH, HSOH and HSSH, Mol. Phys., 1999, 96, 61–70.
92. R. G. Parr and R. G. Pearson, Absolute hardness: companion parameter to absolute electronegativity, J. Am. Chem. Soc., 1983, 105, 7512–7516.
93. Z. Zhou and R. G. Parr, New measures of aromaticity: absolute hardness and relative hardness, J. Am. Chem. Soc., 1989, 111, 7371–7379.
94. R. G. Pearson, Chemical hardness, Wiley Online Library, 1997.
95. N. L. Allinger, X. Zhou and J. Bergsma, Molecular mechanics parameters, THEOCHEM, 1994, 312, 69–83.
96. C. Adlhart and P. Chen, Ligand Rotation Distinguishes First-and Second-Generation Ruthenium Metathesis Catalysts, Angew. Chem., Int. Ed., 2002, 41, 4484–4487.
97. A. K. Rappé, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations, J. Am. Chem. Soc., 1992, 114, 10024–10035.
98. M. Clark, R. D. Cramer III and N. Van Opdenbosch, Validation of the general purpose Tripos 5.2 force field, J. Comput. Chem., 1989, 10, 982–1012.
99. P. Hobza and R. Zahradnik, Intermolecular interactions between medium-sized systems. Nonempirical and empirical calculations of interaction energies. Successes and failures, Chem. Rev., 1988, 88, 871–897.
100. H. C. Georg, K. Coutinho and S. Canuto, Solvent effects on the UV-visible absorption spectrum of benzophenone in water: A combined Monte Carlo quantum mechanics study including solute polarization, J. Chem. Phys., 2007, 126, 34507.
101. L. R. Franco, K. C. F. Toledo, T. A. Matias, P. A. Benavides, H. M. Cezar, C. M. Araujo, K. Coutinho and K. Araki, Unraveling the acid–base characterization and solvent effects on the structural and electronic properties of a bis-bidentate bridging ligand, Phys. Chem. Chem. Phys., 2022, 24, 10222–10240.
102. L. R. Franco, I. Brandão, T. L. Fonseca and H. C. Georg, Elucidating the structure of merocyanine dyes with the ASEC-FEG method. Phenol blue in solution, J. Chem. Phys., 2016, 145, 194301.
103. E. A. Seddon and K. R. Seddon, The chemistry of ruthenium, Elsevier, 2013.
104. G. Prampolini, F. Ingrosso, J. Cerezo, A. Iagatti, P. Foggi and M. Pastore, Short-and long-range solvation effects on the transient UV–vis absorption spectra of a Ru(II)–polypyridine complex disentangled by nonequilibrium molecular dynamics, J. Phys. Chem. Lett., 2019, 10, 2885–2891.
105. A. Chantzis, T. Very, A. Monari and X. Assfeld, Improved treatment of surrounding effects: UV/vis absorption properties of a solvated Ru(II) complex, J. Chem. Theory Comput., 2012, 8, 1536–1541.
106. F. Perrella, A. Petrone and N. Rega, Understanding Charge Dynamics in Dense Electronic Manifolds in Complex Environments, J. Chem. Theory Comput., 2023, 19, 626–639.
107. G. Prampolini, F. Ingrosso, A. Segalina, S. Caramori, P. Foggi and M. Pastore, Dynamical and Environmental Effects on the Optical Properties of an Heteroleptic Ru (II)–Polypyridine Complex: A Multilevel Approach Combining Accurate Ground and Excited State QM-Derived Force Fields, MD and TD-DFT, J. Chem. Theory Comput., 2018, 15, 529–545.
108. J. D. Gaynor, A. Petrone, X. Li and M. Khalil, Mapping Vibronic Couplings in Intramolecular Charge Transfer of a Solar Cell Dye with Polarization-Selective Two-Dimensional Electronic-Vibrational Spectroscopy, J. Phys. Chem. Lett., 2018, 9, 6289–6295.
109. F. Perrella, F. Coppola, N. Rega and A. Petrone, An Expedited Route to Optical and Electronic Properties at Finite Temperature via Unsupervised Learning, Molecules, 2023, 28, 3411.
110. J. L. Silva, I. Unger, T. A. Matias, L. R. Franco, G. Damas, L. T. Costa, K. C. F. Toledo, T. C. R. Rocha and A. N. de Brito, C.-M. Saak and others, X-ray Photoelectron Fingerprints of High-Valence Ruthenium–Oxo Complexes along the Oxidation Reaction Pathway in an Aqueous Environment, J. Phys. Chem. Lett., 2019, 10, 7636–7643.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02154h

---