Structural and chemical properties of NiO_x thin films: the role of oxygen vacancies in NiOOH formation in a H₂O atmosphere

Abstract

NiO_x films grown from 50 nm thick Ni on Si(111) were put in contact with oxygen and subsequently water vapor at elevated temperatures. Near ambient pressure (NAP)-XPS and -XAS reveal the formation of oxygen vacancies at elevated temperatures, followed by H₂O dissociation and saturation of the oxygen vacancies with chemisorbing OH. Through repeated heating and cooling, OH-saturated oxygen vacancies act as precursors for the formation of thermally stable NiOOH on the sample surface. This is accompanied by a significant restructuring of the surface which increases the probability of NiOOH formation. Exposure of a thin NiO_x film to H₂O can lead to a partial reduction of NiO_x to metallic Ni accompanied by a distinct shift of the NiO_x spectra with respect to the Fermi edge. DFT calculations show that the formation of oxygen vacancies and subsequently Ni⁰ leads to a state within the band gap of NiO which pins the Fermi edge.

---

1. Introduction

Due to the undeniable progress of global warming, the utilization of sustainable energy sources with zero emission of greenhouse gases such as carbon dioxide is imperative. As part of an overall strategy, this can be realized, to some extent, by regeneratively produced hydrogen. The obvious advantages of hydrogen are the facts that it is storable and can thus be potentially distributed by existing infrastructure. Furthermore, it can either be used to generate heat by direct combustion or electrical energy in fuel cells.

Hydrogen can be produced through water splitting in an electrochemical device by water electrolysis in which hydrogen and oxygen are generated on the cathode (reduction, hydrogen evolution reaction (HER)) and the anode (oxidation, oxygen evolution reaction (OER)), respectively. Hence, this process consists of two half-reactions such that the overall efficiency is determined by the half-cell with the slowest reaction rate or kinetics. This is usually considered to be the OER half-reaction following the equation 6H₂O → O₂ + 4H₃O⁺ + 4e⁻ with a four-electron charge transfer at the liquid–solid interface.¹ Recently, as a replacement for high-cost noble metals, such as Ru, Ir or Pt, nickel-based oxides have come into focus again as an anode material for the OER in alkaline electrolytes due to their relative abundance and low cost as well as their reactivity and efficiency in the electrolytic process. Bode et al. established that the catalytically active phase changes according to NiO → (β,α)-Ni(OH)₂ ↔ (β, γ)-NiOOH during electrochemical cycling in the anodic potential range.² However, as they already stated 50 years ago, there is still no unambiguous picture with regard to the details of the involved reaction mechanisms or the state of the electrodes during the electrochemical reaction. The reason for this is that with the improved methods available since then, it became apparent that the catalytic performance of nickel oxide strongly depends on structural and chemical properties complicating the scientific case. Not only has it been shown that the efficiency of water splitting on nickel oxide single crystals is affected by the crystal's surface orientation^3–6 but also that defects, phase boundaries, kinks, and step-edges on the surface, which are usually present, act as reaction centers.^5,7–9 The latter is also the reason for referring to Ni oxide as NiO_x rather than NiO. Also, additional side reactions involving Ni and O species can lead to additional intermediate phases, mass transport issues, or even dissolution or structural transformation processes in the interface region of the catalyst including the sub-surface.¹⁰ The influences of the intrinsic properties and reaction mechanisms of the catalyst and its performance are still under investigation. This includes the transformation of NiO_x to Ni-(oxy)-hydroxides,^11,12 as well as determining the structure of Ni-(oxy)-hydroxides under various conditions, which is still under debate.^13–16

Apparently, defects, also in the form of oxygen or Ni vacancies, can play an important role in the observed catalytic activity and may also be crucial for the understanding of mechanisms responsible for the transformation between NiO_x and Ni-(oxy)-hydroxides.^17,18 We have recently shown that NiO_x films exposed to 0.5 mbar of O₂ readily form oxygen vacancies at elevated temperatures.¹⁹ Furthermore, the obtained results point to OH chemisorption at the vacancies, which may act as a precursor to NiOOH formation, while on the other hand, Ni vacancies, usually present only at room temperature on NiO_x, appear not to be involved at all. In the present study, NiO_x thin films were first thermally treated in an atmosphere of 0.5 mbar O₂ to deliberately create oxygen vacancies and other structural defects such as step-edges to facilitate the dissociation of water. Subsequently, they were exposed to H₂O at different temperatures. The samples were characterized in situ by real-time NAP-XPS and NAP-XAS in combination with ex situ SEM and EDX. The detailed examination of the interaction of oxygen vacancy-rich NiO_x with H₂O presented here provides new information on H₂O dissociation and subsequent NiOOH formation and builds the basis for a further study in which we investigate the OER at NiO_x/liquid electrolyte interfaces using electrochemical cells in operando.

2. Experimental section

2.1. Sample preparation

As a starting point, polished standard (111)-orientated phosphor-doped n-type silicon wafers with a resistivity of 0.5 Ω cm⁻¹ and a size of 10 mm by 10 mm were used. The substrates were cleaned and etched using buffered HF and NH₄F solutions resulting in an ultra-flat and hydrogen-terminated Si surface.^20,21 Afterwards, a 200 ± 20 nm thick nickel film was deposited on the n-Si(111):H substrate using a sputter coater (Cressington 208HR; Ni sputter target by Kurt J. Lesker, 99.99% purity) which is operated under a 0.08 mbar Ar atmosphere for 2 min at room temperature (RT). The NiO_x films were prepared by thermal oxidation at up to 270 °C heated by an external infrared laser (Limo, 808 nm wavelength; cw-mode) at an oxygen partial pressure of 0.5 mbar O₂ (Westfalen, purity 6.0) for different durations on stream. For some samples, this was followed by heating–cooling cycles in an atmosphere of 0.5 mbar O₂. The indicated samples were exposed to H₂O vapor at 0.5 mbar. The H₂O was cleaned of residual gases through freeze–pump–thaw cycles. Details: film Fig. 1, 2 and 7(c): oxidation at 270 °C for 46 min/total oxygen exposure of 200 min; film Fig. 3–5: oxidation at 250 °C for 23 min/total oxygen exposure of 326 min, H₂O exposure of 483 min; film Fig. 6: oxidation at 240 °C for 39 min/total oxygen exposure of 106 min, H₂O exposure of 241 min; film Fig. 7(a) and (d): total oxygen exposure of 155 min; H₂O exposure of 431 min; film Fig. 7(b): total oxygen exposure of 272 min; H₂O exposure of 264 min. The sample temperature was measured at the surface using a K-type thermocouple clamped between the sample surface and a coverlid. Heating–cooling rates of ≈20 °C min⁻¹ were applied. Gas flows were adjusted using mass flow controllers (Bronkhorst GmbH) in combination with a differential pumping stage regulating the final pressure in the analysis chamber.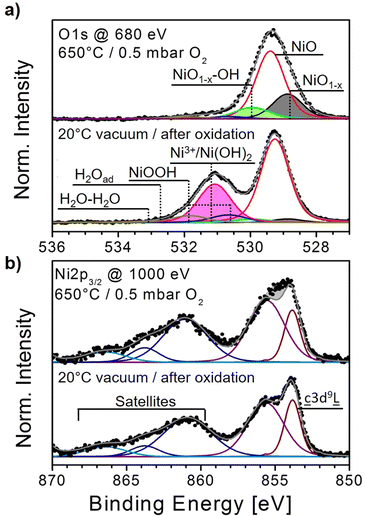

Fig. 1 NiO_x film heated in the 0.5 mbar O₂ atmosphere. (a) O1s fits of spectra recorded at RT in a vacuum directly after oxidation and during subsequent treatment at 650 °C in O₂. Different O1s oxygen species are indicated. The peaks at 531.2, 528.9 and 530 eV are highlighted. (b) Ni2p_3/2 spectra corresponding to (a) fitted only with NiO components. The fits were performed according to the peak components listed in the ESI,† Table S1. Note that the photon energies for the O1s and Ni2p_3/2 spectra in (a) and (b) represent the same information depth.

Fig. 2 (a) Evolution of the Ni and O fractions during heating to 650 °C in 0.5 mbar O₂. (b) Evolution of the residuum intensity derived from subtracting the fit of pure NiO from the measured spectrum (e.g., grey area in Fig. 1(b)) with temperature. (c) Evolution of the relative intensities derived from the fits of O1s spectra with temperature. The fits were performed according to the peak components listed in the ESI,† Table S1. (d) Heating profile. Preparation steps in which the sample was in a vacuum are indicated by dashed lines and “Vac.” and “V.”, respectively.

Fig. 3 NiO_x film during heating–cooling cycles in the 0.5 mbar H₂O atmosphere. (a) Bottom to top: O1s fits of spectra recorded at T_max,1 = 510 °C, T_min,2 = 50 °C, T_max,3 = 510 °C and after subsequent cooling and evacuation at RT. (b) Ni2p_3/2 spectra corresponding to (a). The residuum between the fitted NiO components and the measured spectrum are marked in grey. The fits were performed according to the components listed in the ESI,† Table S1.

Fig. 4 (a) Evolution of the Ni and O fractions during heating–cooling cycles in the 0.5 mbar H₂O atmosphere. (b) Evolution of the intensity residuum derived from subtracting the fit of pure NiO from the measured spectrum (e.g., grey areas in Fig. 3(b)) with temperature. (c) Evolution of the relative intensities derived from the fits of O1s spectra with temperature. Note that in this figure, for better visibility, the relative intensities of both NiOOH peaks as well as OH_ad and H₂O are combined. (d) Heating profile. Preparation steps in which the sample was in a vacuum are indicated by dashed lines and “V.”.

Fig. 5 (a) and (b) XA spectra of the Ni L₃- and O K-edge of the NiO_x sample at RT, at the first T_max and after the first cooling under 0.5 mbar H₂O partial pressure, corresponding to the results presented in Fig. 3 and 4. (c) Close-up of peak d in Fig. 5(b). (d) XA spectra of the O K-edge recorded at RT in a vacuum before H₂O exposure, after the second T_max and after final cooling, respectively. The features indicated as a–f are discussed in the text.

Fig. 6 XP spectra recorded during annealing in the 0.5 mbar H₂O atmosphere: (a) Ni2p_3/2 and (b) O1s. The black lines indicate a shift of the respective spectrum with respect to the Fermi-edge and thus the Ni-metal peak visible in the Ni2p_3/2 spectrum at 490 °C and after cooling to 20 °C. (c) (Top panel) Valence band spectra corresponding to (a). (c) (Bottom panel) Calculated total DOS for zero, one and two oxygen vacancies, respectively. Shifts and states close to the FE are indicated by dashed arrows. Differences in peak intensities are highlighted.

Fig. 7 Ex situ SEM micrographs of (a) a NiO_x sample after one (inset: enlarged scale) and (b) after three heating–cooling cycles to 510 °C in 0.5 mbar H₂O atmosphere. (c) SEM micrograph of NiO_x after heating to 650 °C in 0.5 mbar O₂ as shown in Fig. 1 and 2. (d) EDX spectra of the SEM micrographs presented in (a) and the ESI,† Fig. S5(b) with prominent O K- and Ni L-edges of nickel oxide as well as the Si K-edge, representing the underlying Si substrate. The result of the evaluation of the composition is given in the text.

2.2. Sample characterization

In situ experiments in O₂ and H₂O atmospheres were performed at the BELCHem beamline (UE56-2/PGM-1) located at the synchrotron radiation facility BESSY II (Berlin) in a dedicated NAP-XPS analysis system built around a SPECS Phoibos 150 analyzer. Details of the UHV system are described in detail elsewhere.^22,23 The XP spectra were recorded in normal photoemission geometry with a probing area of ≈150 μm × 80 μm corresponding to the profile of the incident X-ray beam. The overall spectral resolution of the NAP-XPS system is about 0.2 eV at a pass energy of 10 eV which was always used. The binding energy (BE) was calibrated using the valence band onset of metallic Ni with a pronounced Fermi edge with an accuracy of around 0.05 eV. In order to get an overview of the sample, survey spectra were recorded using a photon energy of hν = 1020 eV. The Ni2p core levels were measured with hν = 1000 eV only, while the O1s core levels were recorded with excitation energies of 680, 880 and 1000 eV to allow for depth profiling. All samples were screened for C and Si at various photon energies. Further details on the sample characterization addressing potential de-wetting, XPS fit analysis and quantification based on XPS are given in the ESI.†

In parallel to XPS, XA spectra were recorded. Therefore, the analyzer was adjusted to measure the partial electron yield at fixed kinetic energies of E_kin = 300 eV for the O K-edge and E_kin = 500 eV for the Ni L-edge, while the excitation energy was steadily varied in 0.05 eV steps with a dwell time of 0.1 s. The energy range for the O K-edge was 520 eV to 560 eV, whereas for the Ni-L edge, the energy range of 840 eV to 880 eV was chosen. Both the O K- and the Ni L-edges were normalized to the simultaneously recorded mirror currents (mirror coating: Pt). For further details, see the ESI.†

SEM micrographs were taken using a high-resolution ZEISS field emission-based microscope (LEO Gemini) with an integrated energy dispersive X-ray spectroscopy (EDX) system based on a fluorescence detector from Bruker (XFlash). The maximum lateral resolution is estimated to be in the range of about 10 nm depending on the structure and morphology of the films. In this work, several NiO_x samples were examined. This includes films before and after multiple heating–cooling cycles in O₂ as well after one and two heating–cooling cycles in the H₂O atmosphere, respectively.

2.3. DFT calculations

In the framework of the full-potential linearized augmented plane wave (FLAPW) method, the density functional theory (DFT) calculations have been performed using the Wien2k code.²⁴ Using the PBE functional by minimizing the total energy of the cubic crystal of NiO (space group Fm3̄m) to the volume, the theoretical lattice constant (a = 4.166 Å) was determined from the experimental lattice constant.^25,26 In the calculation, 500 k-points in the Brillouin zone (BZ), G_max = 14 (a.u.)⁻¹ (norm of the largest vector in the charge density Fourier expansion) and R_MT × k_max = 8.5 were used, where R_MT and k_max are the minimum muffin-tin radius and the maximum k-vector in the plane-wave expansion of the wave function, respectively. The TB-mBJ potential has been used for the calculation of the DOS and XAS on a relaxed 2 × 2 × 2 supercell with 50 K points in the Brillouin zone. This supercell contained 32 Ni and 32 O atoms (Ni_RMT= 1.86, O_RMT= 1.60) with an antiferromagnetic spin configuration on alternating (111) planes (type-II antiferromagnetism) with the values of G_max = 14 (a.u.)⁻¹ and R_MT × k_max = 8.5.²⁷

3. Results

3.1. Oxygen vacancy formation on NiO_x films

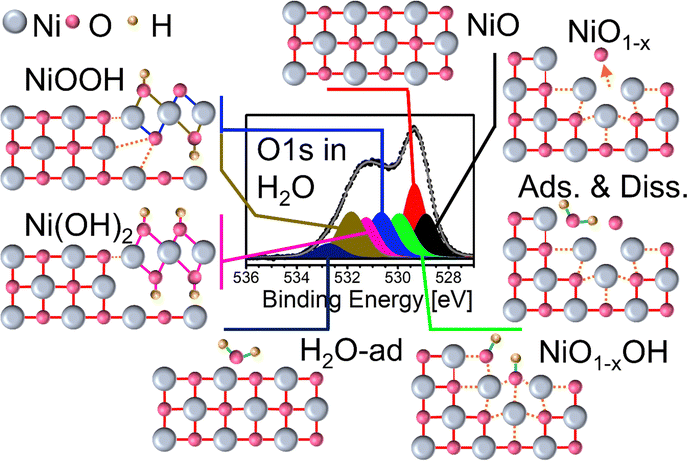
First, to understand the impact of oxygen and Ni vacancies and other defects on the formation of Ni-(oxy-) hydrates, we have to describe the conditions for the formation as well as the stability of such vacancies. Furthermore, the sample treatment required for their creation may have an impact on the structure of the NiO_x surface. Fresh NiO_x films can be prepared by heating a clean Ni metal film stepwise from room temperature (RT) to up to 270 °C under an oxygen partial pressure of 0.5 mbar. The transition from the metal to oxide then takes place between 190 °C and 240 °C. Characteristic, fitted O1s and Ni2p_3/2 XP spectra recorded after oxidation at RT are shown in the bottom panels of Fig. 1(a) and (b), respectively. Note that the same color code will always be used throughout unless noted otherwise. The fit of the Ni2p_3/2 spectrum shows a complex series of peaks and satellites as a result of the photoemission process. The NiO main line at ≈853.7 eV is commonly assigned to a c3d⁹L final state (L: ligand hole; c: core hole), while the extended satellite region above 860 eV is attributed to the c3d¹⁰L² and c3d⁸ states.^28,29 In contrast, the origin of the shoulder at the high binding energy side of the main peak is still under discussion. It is most commonly attributed to Ni³⁺ or “Ni₂O₃” formed due to Ni vacancies in the NiO lattice, but it may stem from multiplet splitting or non-local screening effects.^29–32 Also, surface-related effects such as island nucleation or sputter-induced defects contribute to this peak as recent experimental and theoretical studies of NiO suggest.^33–36 For the interpretation of the results presented in this work, all of these aspects need to be considered. A detailed description of the fit model including the complex Ni2p satellite structure, based on Biesinger's et al. work, is given in the ESI.† ^37,38

In the O1s region, the most intense peak, attributed to NiO, is located at 529.4 eV (Fig. 1(a)), bottom panel).^39,40 At higher binding energies (BE), several additional peaks are fitted, of which the most prominent one is located at about 531.2 eV. This peak is assigned to Ni-deficient NiO or Ni³⁺, which is labeled by some as Ni₂O₃ and both of which we will be used synonymously in the following discussion.^30,40–42 The BE of this peak is very close to the one assigned to Ni(OH)₂ which can make it difficult to separate both of their contributions from each other.^43,44 Two other peaks at 530.65 eV and 531.88 eV, respectively, are added to the fit and assigned to NiOOH, reflecting the different electronic configurations of its two oxygen atoms.^40,42,45 Both peaks will become very prominent during H2O exposures in the following experiments. Similarly, peaks related to single and multi-layer H₂O adsorption can be added on the high binding energy (BE) side of the spectrum.^40,42 Finally, two other weak peaks at 528.9 eV and 530 eV are fitted to the spectrum, indicated as NiO_1−x. and Ni_1−x–OH, respectively, which we relate to oxygen vacancies. As reported in detail in our study of oxygen vacancy formation on NiO_x thin films, such vacancies can readily form by thermal treatment in an oxygen atmosphere.¹⁹ Increasing the sample temperature leads to the removal of oxygen atoms from the lattice, just as in the common reduction process in a vacuum. Yet, in the presence of O₂, a balance between removal and replenishment of oxygen atoms depends on temperature. For example, when the NiO_x film shown in Fig. 1 is heated to 650 °C in 0.5 mbar of O₂, both the O1s and the Ni2p_3/2 spectra gradually but visibly change (full set in the ESI,† Fig. S3). The impact of heating on the O1s region consists of a considerable intensity loss at high BEs, while the NiO main peak appears to be broader. Simultaneously, the main feature in the Ni2p_3/2 spectrum loses its peak-and-shoulder-like shape, becoming rather flat. The fits reveal that at 650 °C, the O1s spectrum loses almost all Ni³⁺- and OH-bond-related peaks, while the two components at 528.9 eV and 530 eV flanking the NiO main peak become quite pronounced (Fig. 1(a), top panel). On the other hand, the fits of the Ni2p_3/2 spectrum recorded at 650 °C with NiO components only obviously lead to a residuum, marked as a grey area in the plot, which, by simply subtracting the fit envelope of pure NiO from the measured spectrum, can be used as a measure of deviation from the “as prepared” oxide spectrum (Fig. 1(b), top panel).

The evolution of the O- and Ni-fractions with increasing temperature derived from XPS as well as the relative intensities of the O1s and Ni2p_3/2 fit components and residuum, respectively, can be followed as shown in Fig. 2(a)–(c). Between RT and ≈200 °C, OH-bond-related peaks vanish quickly, which is accompanied by a loss of oxygen, while all other peaks remain largely unaffected. This suggests that these peaks are related to OH-species formed by residual water and carbon bonds. Indeed, the corresponding C1s signal is already completely quenched at 250 °C and does not appear again in an oxygen atmosphere (not shown). From approximately 200 °C onward, the Ni2p_3/2 residuum increases, which is seemingly related to an increase of the relative intensities of the NiO_1−x and NiO_1−x–OH peaks. The relative intensities of both peaks reach maxima of about 0.22 and 0.1, respectively, at about 500 °C. This apparent intensity saturation is reflected by the behaviour of the Ni2p_3/2 residuum, which reaches a maximum level at around the same temperature, suggesting that 500 °C may be a key temperature. DFT calculations of bond lengths, charge densities and BEs revealed that the NiO_1−x peak can be directly related to the formation of oxygen vacancies, which leads to a relaxation of the atoms around a vacancy influencing the charge density and, consequently, the XPS BE of these neighboring atoms.¹⁹ Hence, the peak at 528.9 eV was labeled NiO_1−x. The other peak at 530 eV is ascribed to the presence of oxygen vacancies with chemisorbed OH, thus representing NiO_1−x–OH.¹⁹ We will address the latter peak in detail below.

Furthermore, the O1s peak attributed to Ni₂O₃ or Ni vacancies continuously decreases throughout the whole experiment. Even after cooling at the end of the experiment, the original intensity is clearly not reached again. This behavior indicates that most Ni vacancies are irrevocably healed by the thermal treatment. In addition, the changes in the composition of Ni and O suggest a stronger loss of oxygen, reaching a maximum at ≈500 °C (Fig. 2(a)). Interestingly, beyond this temperature, the sample appears to gain oxygen again. This can be related to increasing fractions of: (a) the NiO_1−x–OH peak and (b) NiOOH starting just above 400 °C stemming from the dissociation of residual H₂O. Finally, after cooling and evacuating O₂, the NiOOH bond fraction increases slightly more which points to an involvement of oxygen vacancies in the formation of Ni oxy-hydroxide. However, at this stage, a contribution from residual gas adsorption cannot be excluded. Simultaneously, after cooling, the intensities of both the NiO_1−x and NiO_1−x–OH together with the Ni2p_3/2 residuum are almost completely quenched. Remarkably, the corresponding Ni2p_3/2 spectrum is virtually identical to the one prior to heating, while the O1s spectrum has changed (ESI,† Fig. S3). This behavior suggests that the observed dynamics of the Ni2p_3/2 spectra are not related to Ni³⁺ but are rather related to oxygen vacancies.

In our study of oxygen vacancies on NiO_x thin films, we have also shown that by applying multiple heating–cooling cycles to only 350 °C, oxygen vacancy formation is reversible to a certain extent (ESI,† Fig. S4). We observed that while the Ni2p_3/2 residuum fully vanishes, both the NiO_1−x and NiO_1−x–OH peaks retain some intensity even after cooling, which suggests a more defective surface than the as-prepared NiO_x film.¹⁹ However, the methods applied were only sensitive to the electronic environment and the bond states. As it turns out, repeated heating and cooling treatments in oxygen affect the morphology of the NiO_x sample as well. ESI,† Fig. S5(a) to (d) depict ex situ SEM micrographs of NiO_x samples before, after two and after three annealing cycles to 350 °C and subsequent cooling in 0.5 mbar of O₂. The as prepared NiO_x film shown in ESI† Fig. S5(a) appears mainly flat with only a small number of visible step edges or terraces most likely as NiO(100), the most stable NiO orientation.^46–51 Moreover, rather inhomogeneous, protruding areas are present which suggests the presence of more than one surface orientation. Their hexagonal and triangular shapes as well as the triangular holes within may indicate the presence of NiO(111).^44,52 A more detailed discussion is given in the ESI.† The morphology changes after several annealing cycles in O₂. The flat sample areas become visibly terraced that are detectable even with SEM, as indicated by the red arrows in ESI† Fig. S5(b) and by carbon deposited after air exposure in ESI† Fig. S5(c) and (d). The visibility of the steps with SEM can be explained by step bunching which has been observed before using TEM in situ during Ni oxidation.⁵³ The step bunching is possible because of a high mobility of Ni atoms on the NiO terraces. This can also explain the healing of Ni vacancies in the NiO films observed during heating to 650 °C. If Ni atoms can migrate, the vacancies can also move through the simple hopping of Ni atoms, most likely in the direction of step edges. This defective state of the NiO_x achieved through heating–cooling cycles provides an ideal surface for the dissociation of H₂O.

3.2. Oxygen vacancy-rich NiO_x in contact with water vapor at elevated temperatures

In preparation of the interaction of oxygen vacancies with H₂O, a fresh NiO_x sample was heated three times to 350 °C and subsequently cooled to RT in 0.5 mbar O₂ in order to create a defect-rich surface similar to those presented in ESI† Fig. S5. This sample was subsequently exposed to 0.5 mbar H₂O and treated to three further heating–cooling cycles with a maximum temperature of T_max = 510 °C to achieve the maximum number of oxygen vacancies according to the results presented in Fig. 2(c).

The evolution of the Ni2p_3/2 spectra throughout the heating–cooling cycles shows a similar behavior as previously observed for annealing in O₂.¹⁹ During each heating cycle with increasing temperature, the pronounced peak-and-shoulder-like structure of the Ni2p_3/2 main feature flattens, which is almost entirely reversed to the original shape during each cooling cycle (Fig. 3(b); for more temperature steps, see the ESI,† Fig. S6(a). Again, by simply subtracting the fit envelope of pure NiO from the measured spectrum, the resulting residuum, marked as a grey area in the plot, can be used as a measure of deviation from the RT oxide spectrum. The biggest deviations appear at each T_max = 510 °C as depicted in Fig. 4(b) with its BE centred around 855 eV. Interestingly, this is also the Ni2p_3/2 BE region for which NiOOH and Ni(OH)₂ are expected at ≈854.6–856 eV_x.^54,55 In ESI† Fig. S6(a), on close inspection, the Ni2p_3/2 main feature's point of maximum intensity at T_max seems to shift from ∼854 to ∼856 eV throughout the cycles. A shift like this would be in agreement with the presence of NiOOH. On the other hand, the Ni2p_3/2 spectra always reverse back to the peak-and-shoulder-like shape of NiO after cooling, although the ratio between the high- (“peak”) and low-intensity part (“shoulder”) of the main feature seems to decrease slightly (ESI,† Fig. S6(a)).

The evolution of the O1s spectra is even more dynamic than what was observed during heating in O₂. In Fig. 3(a), the fitted O1s spectra recorded at and after the first T_max as well as at and after the third T_max (in vacuum) are depicted (see also ESI† Fig. S6b). In comparison, the spectrum recorded at the first T_max = 510 °C and its components’ distribution are very similar to those obtained by heating to high temperatures in O₂. On both sides of the NiO main peak, rather strong NiO_1−x and NiO_1−x–OH peaks become visible. However, the OH-bond-related peaks on the high BE side of the main NiO peak exhibit slightly higher intensities compared to heating in O₂ (see ESI† Fig. S3b). The evolution of the O- and Ni-fractions with increasing temperature derived from XPS as well as the relative intensities of the O1s fit components, respectively, can be followed as shown in Fig. 4(a) and (c). The relative intensity plot shows that both the NiO_1−x and NiO_1−x–OH peaks reach a relative intensity of ≈0.2. This value for NiO_1−x, is in the expected range for maximum vacancy formation obtained in O₂ at ≈500 °C (Fig. 2(c)). On the other hand, the relative intensities of the NiO_1−x–OH peak are higher than those observed during heating in O₂ to 350 °C or even above 500 °C (ESI,† Fig. S4(f) and Fig. 2(c)). As expected, both peaks are – almost – entirely quenched after the first cooling to 50 °C (i.e., the starting point of the second cycle). Simultaneously, the O- and Ni-fractions of the sample reflect the formation and replenishment of oxygen vacancies with a significant loss of oxygen at the first T_max = 510 °C and subsequent gain upon cooling. After this, the similarity to heating in oxygen ends.

During the following cycles, both the evolution of the Ni2p_3/2 intensity residuum as well as the relative intensities of the NiO_1−x and NiO_1−x–OH peaks still follows the same pattern as in the first cycle. However, the O- and Ni-fractions derived from XPS start to change drastically with changing temperature, while during the first 1 ½ cycles, the Ni-/O-fractions increase/decrease at each T_max when oxygen vacancies are formed and decrease/increase when vacancies are replenished, and during the second cooling and subsequent evacuation, a permanent increase of oxygen is observed. This uptake of oxygen is closely related to the relative O1s intensity changes plotted in Fig. 4(c). First, after an initial intensity decrease due to the removal of residual adsorbates, a rearrangement of the spectral composition is observed already during the first heating ramp, which continues throughout the following cycles. This becomes particularly apparent when following the relative intensity changes of the NiO and Ni₂O₃/Ni(OH)₂ peaks. In O₂, the latter's intensity varied diametrically to the oxygen vacancy-related peaks (ESI,† Fig. S4f), which is also true for the first heating–cooling cycle in H₂O. After that, in H₂O, the Ni₂O₃/Ni(OH)₂ peak remains weak throughout the rest of the experiment, similar to what was observed when heating above 500 °C in O₂ (Fig. 2(c)). Equally, the main NiO O1s peak decreases visibly with the increasing number of cycles. Furthermore, the combined relative intensity of the two NiOOH components increases strongly during the second cooling and even preserves a significant partial intensity at the following T_max. Both the loss of NiO and Ni₂O₃/Ni(OH)₂ intensities and the simultaneous gain of NiOOH intensity reflect the observed overall oxygen gain and point to the formation of mainly NiOOH, partially at the expense of NiO, with ongoing heating–cooling cycles. Note that the combined intensity of peaks related to H₂O adsorbates is only prominent at low temperatures as one can expect. Regarding the formation of Ni(OH)₂, the situation is less distinct. Since both Ni₂O₃ and Ni(OH)₂ share almost the same O1s binding energy and are not resolved in our fits, the formation of the latter species is not easily confirmed. In particular, since after the first heating–cooling cycle, the relative intensity of the combined peak remains low and varies only slightly, making it difficult to determine its nature as either Ni₂O₃ or Ni(OH)₂. However, when considering the results displayed in Fig. 2(c), where a constant decrease of the Ni₂O₃ contribution with increasing temperature was observed and did not recover upon cooling, it is very likely that in the present experiment, the remaining relative intensity can be assigned to small amounts of Ni(OH)₂.

In the data presented so far, the spectra of the O1s and Ni2p regions were recorded at photon energies of hν = 680 and hν = 1000 eV, respectively, corresponding to a kinetic energy of the photoelectrons of E_kin = 150 eV. This means their photoelectron escape depth is close to its minimum of ≈7 Å and the recorded spectra are mostly surface sensitive.⁵⁶ To investigate the extent of NiOOH bond formation towards the bulk of the NiO_x film, O1s depth profiling at a kinetic energy of the photoelectrons of E_kin = 470 eV (hν = 1000 eV; escape depth ≈ 10 Å) was performed. While the general shape of the depth sensitive spectra remains very similar to the surface sensitive spectra, the former show less intensities in the high BE region (ESI,† Fig. S6b). Given that the side of the spectra is dominated by OH-bonds, this suggests that the formation of OH-bonds does not reach very far into the bulk. This is also confirmed by the evolution of the relative intensities of the fitted components depicted in ESI† Fig. S7. At both photon energies, the evolution is strikingly similar apart from the actual values of the relative intensities of the NiOOH and NiO peaks, respectively. Compared to the relative intensities obtained from the spectra recorded at the lower photon energy, those obtained from the higher photon energy spectra show a higher relative intensity of the NiO peak, while the relative intensity of the NiOOH peak is lower. In summary, the XPS results show a gradual change of the electronic structure with increasing information depth, which suggests that the formation of NiOOH happens mostly on the surface, not yet strongly affecting the bulk.

The formation of oxygen vacancies was also monitored via XAS during the heating–cooling cycles. In Fig. 5(a), the Ni L₃-edge of the NiO_x sample exposed to 0.5 mbar H₂O is compared at RT, 500 °C and after cooling to RT, respectively. Fig. 5(a) corresponds to the XPS results shown in Fig. 3(b). The spectra consist of three peaks a, b and c. According to multiplet calculations, they reflect the typical signature of bulk NiO in a high spin Ni²⁺ state.^57–60 Features a and b in the Ni-L₃ spectra correspond to Ni²⁺ related 2p⁶3d⁸ → 2p⁵3d⁹ transitions which are dominated by multiplet effects. Feature c is attributed to excitations leading to final states of 2p⁵3d¹⁰L̲.⁵⁹ Note that Ni L-spectra are split into two groups at around 854 eV (L₃) and 872 eV (L₂), not shown here, due to spin–orbit interactions of the 2p⁵ core-levels (2p⁵_3/2 and 2p⁵_1/2 → 2p⁴_3/2 and 2p⁴_1/2) similar to XPS. While the spectra recorded at RT are virtually identical, the spectrum recorded at T_max exhibits a shift/broadening of peaks a and b towards lower photon energies which also leaves the dip between both peaks less pronounced. Also, peak c remains unaffected. The observed behaviour resembles the evolution of the Ni2p_3/2 spectra recorded at the same temperatures (ESI,† Fig. S6a). Recent studies by Preda et al. showed that the presence of NiO_x under-coordinated with oxygen, e.g., at the rims of oxide nuclei, leads to a lower energy position of peaks a and b during the initial stages of NiO film growth. With increasing film thickness, reducing contributions from oxygen under-coordinated sites, both peaks shift towards higher energies.⁵⁷ Hence, in our case, the presence of oxygen vacancies, which can be considered an oxygen under-coordination of NiO_x, can explain the observed shifts towards lower energies.

The corresponding O K-edge spectra are shown in Fig. 5(b) and (c). The spectra recorded at RT in H₂O appear almost identical, similar to what was observed for their Ni L₃-edge counterparts. In the region displayed here, they consist of three peaks d, e and f. Peaks e and f can be attributed to mixed unoccupied O2p-Ni4sp states, while peak d is associated with unoccupied Ni e_g states.^19,57,60 Compared to the vacuum spectra shown in Fig. 5(d), small but visible intensity dips at 534, 535.85 eV and 537.1 eV appear. These dips are caused by absorption in the H₂O atmosphere and vanish upon evacuation. Upon heating to T_max, a pronounced shift of the peaks e and f as well as a distinct broadening of the low energy side of peak d sets in, displayed as a close-up shown in Fig. 5(c), which can be directly related to the formation of oxygen vacancies. Missing surface oxygen atoms and oxygen vacancies in the bulk lead to a broken symmetry which then leads to the appearance of additional peaks around 532 eV, causing a distinct broadening of this feature.^19,57,61 As expected from the XPS results presented in Fig. 2(c) and 4(c), the broadening of peak d appears to be only dependent on temperature. This distinction is clearly visible when comparing the broadening in vacuum, O₂ and H₂O as a function of T as given in the ESI,† Fig. S8 and S9. Since the spectra recorded at RT as shown in Fig. 5(b) are slightly distorted by the features stemming from H₂O gas phase absorption, it is not easy to see any changes which may be related to OH-bond formation. Here, the vacuum spectra obtained before H₂O exposure, after the second T_max and after the final cooling provide better information (Fig. 5(d)). Indeed, both the intermediate and final spectra show slightly higher intensities in the regions of peaks e and f compared to the initial spectrum which can be related to the formation of small amounts of NiOOH and/or Ni(OH)₂,⁶² agreeing well with the XPS results. In conclusion, XAS clearly evidences the presence of oxygen vacancies during heating in the H₂O atmosphere and supports the XPS finding that the formation of thermally stable NiOOH happens on or close to the sample surface under the given conditions.

3.3. Progressive oxygen vacancy formation on NiO_x thin films

In the experiments presented so far, the loss of oxygen by heating in O₂ and H₂O is limited to the formation of oxygen vacancies and appears to be fully reversible. Also, apart from the evolution of their individual components described above, the binding energy positions of the Ni2p_3/2 and O1s XP spectra appear to be largely fixed. This changes drastically when a freshly oxidized NiO_x film (i.e., with a smaller total oxygen exposure) is used for the annealing procedure in 0.5 mbar H₂O. As shown in Fig. 6, the heating not only leads to oxygen vacancy formation and subsequent chemisorption of OH onto the vacancies, clearly visible by the distinct changes in spectral shapes of the O1s and Ni2p_3/2 spectra, but also leads to the appearance of a metallic Ni peak that allows us to monitor spectral shifts with respect to the FE. With increasing temperature, a significant upshift of the entire Ni2p_3/2, O1s and the VB spectra with respect to the original NiO_x spectral position is observed (Fig. 6). The shapes of the Ni2p_3/2 and O1s spectra for each temperature step are virtually identical to those presented in the ESI,†Fig. 6 during and after the first heating–cooling cycle, i.e., at the first T_max and after the first cooling step (note: for the O1s recorded at 1000 eV). The only differences consist of slightly higher intensities between 531.5 eV and 534 eV in the O1s region attributed to adsorbing H₂O and, of course, the evolving metallic Ni2p_3/2 peak. In Fig. 6(a), the black vertical line marks the maximum of the strongest component of the Ni2p_3/2 peak. Up to 115 °C, the position of this peak remains unchanged, while a significant shift towards higher binding energies is observed above 150 °C. At about 240 °C, it reaches a maximum shift of 0.5 ± 0.1 eV towards higher binding energies and remains stable even upon cooling down. The same shift is seen in the O1s spectra shown in Fig. 6(b) with a comparable maximum of 0.5 ± 0.1 eV. Obviously, the experimental conditions applied here lead to a partial reduction of the thin NiO_x films which then causes the observed shift. This partial reduction in the H₂O atmosphere can be explained by the limited supply of oxygen atoms, replacing missing oxygen at vacancy sites. Since the dissociation of H₂O leads to the formation of OH rather than O, which contributes to the intensity of the NiO_1−x–OH component, mostly oxygen diffusing from the bulk will replace the missing oxygen. This reservoir is rather limited compared to a thick oxide film, e.g., as shown in Fig. 3.^3,63 Indeed, one can consider the emerging metal peak as a very controlled way of (partial) reduction. A similar behavior with shifts of up to 0.75 eV was observed by Reinert et al. and also by Greiner et al.^64,65 In both works, NiO(100) was deliberately partially reduced to Ni⁰ by heating the sample in UHV to above 250 °C and 180 °C, respectively. Greiner et al. argue that due to the lack of a lower oxidation state than Ni²⁺, this behavior is caused by the presence of oxygen vacancies and/or the removal of Ni₂O₃, which most likely leads to a change in the position of the FE of the oxide. On the other hand, Reinert et al. partially reduced their samples with the aim to induce electron doping. They suggest that Ni⁰ in NiO(100) may pin the Fermi edge depending on the amount of oxygen vacancies. It turns out that both effects contribute to the observed shifts. By calculating the total DOS of a 2 × 2 × 2 supercell (Ni₃₂O₃₂) using DFT and introducing one (Ni₃₂O₃₁) and two oxygen vacancies (Ni₃₂O₃₀), respectively, we can directly compare them to the experimentally determined DOS close to the Fermi edge. Fig. 6(c) shows the measured DOSs, i.e., the VB, versus the calculated one as derived from the convolution of the DOS curve with a Gaussian function. The main features of the theoretical DOSs are dominated by Ni3d-states superimposed by O2p- and minor Ni4p-states. Since DOS calculations do not consider cross-section issues related to excitation energies as for XPS, the spectral features at about 6 eV may be overstressed. However, the features in the upper VB region at around 2 eV fit quite well to the experimental data. By introducing oxygen vacancies in the 2 × 2 × 2 supercell, the calculations reveal a distinct shift of the whole VB by 0.5 eV already for the presence of one vacancy. This is caused by the appearance of an additional state in the bottom region of the band gap which becomes even more pronounced upon introducing a second oxygen vacancy (double arrows in Fig. 6(c)). Simultaneously, the DOS around 2 eV undergoes a change in shape, which reflects the flattening of the corresponding features in the experimental spectra attributed to oxygen vacancy formation. This comparison of theoretical and experimental data not only confirms the formation of oxygen vacancies again but also clearly indicates that the formation of a sufficient number of oxygen vacancies leads to the presence of metallic Ni domains which indeed pin the FE, leading to a shift of the NiO_x spectra. For thicker NiO_x films, neither heating in the O₂ nor H₂O atmosphere led to a visible reduction to the Ni metal.

3.4. Effect of temperature on the morphology of the NiO_x film

Unlike the surface-related spectral changes observed with XPS and XAS, the change in morphology of the NiO_x surface after repeated heating–cooling cycles in the H₂O atmosphere is immense. Compared to SEM micrographs of the NiO_x film taken after heating–cooling cycles or after heating to 650 °C in O₂ (ESI,† Fig. S5(b) and S7(c), the surface morphology has changed after single annealing at 510 °C in H₂O (Fig. 7(a)). Now, the sample surface appears grainy, without step edges forming small crystallites up to a size of ≈10–20 nm. After three heating–cooling cycles in H₂O, these crystallites become even bigger forming a 3-dimensional topography (Fig. 7(b)). Apparently, the presence of oxygen vacancies alone cannot be the only reason for the transformation into a micro-crystalline surface with 3-dimensional structures. Certainly, the annealing will have an impact since it is known that under certain conditions, sample temperatures above 400 °C can change the surface morphology and structure of NiO_x towards a higher degree of roughness.^46,66,67 O and Ni atoms can be very mobile at elevated temperatures in an O₂ atmosphere.⁵³ Moreover, when water is split at the NiO_x surface according to the reaction H₂O → OH⁻ + H⁺, the diffusion of hydrogen along defect structures, e.g., step edges or holes as shown in ESI† Fig. S5(b) may be involved, leading to more complex NiO/Ni structures.⁶⁸ Of course, this hypothesis needs further experimental proof beyond the scope of this work. On the other hand, given that the transformation towards micro-crystallites on the sample surface seems to happen in H₂O but not in O₂, the formation of Ni-(oxy)-hydroxide may have a strong influence. Their unit cells and orientations of the atoms within differ from that of NiO. Hence, it is feasible to assume that Ni-(oxy)-hydroxide formation will lead to significant strain and restructuring of surface topography. Also, the formation of (oxy)-hydroxides may be greater than what is detected by XPS because with these methods, only the apparent surface is covered. XPS only monitors the outermost facets of the grains, neglecting potentially oxy-hydroxide terminated grain boundaries that are at an angle to the surface so that the effective escape depth of photoelectrons becomes too large. In this regard, complementary information is provided by EDX measurements as displayed in Fig. 7(d), covering a larger volume of the sample. The spectra refer to the micrographs in ESI† Fig. S5(b) and S7(a), respectively. While the Ni signal appears unaffected, the O signal is notably larger after annealing in H₂O than before. The averaged [Ni]/[O] concentration of the NiO_x film as deduced from the image in ESI† Fig. S5(b) before heating in H₂O is 0.8 ± 0.1 according to the peak evaluation routine of the built-in EDX measurement software. This value is in between the one of stoichiometric NiO ([Ni]/[O] = 1.0) and stoichiometric Ni₂O₃ ([Ni]/[O] = 0.66), thus fitting well to Ni-deficient NiO discussed in Fig. 1(a) and 2(c). After the H₂O treatment, the averaged [Ni]/[O] concentration of the NiO_x film is 0.61 ± 0.1 which is closer to Ni(OH)₂ or NiOOH ([Ni]/[O] = 0.5), confirming the trends derived from XPS quantification.

4. Discussion

A schematic overview of the results presented above and discussed in the following discussion is presented in Fig. 8. Our findings suggest that several prerequisites have to be met to instigate NiOOH and Ni(OH)₂ formation. It is well known that H₂O dissociation on NiO(100) surfaces is not significant unless defects are introduced, e.g. by pre-sputtering, and unless “non-lattice” oxygen is present, e.g. by co-dosing small quantities of O₂.^6,17,69,70 One prerequisite is met by treating the NiO_x films with repeated heating–cooling cycles in O₂, which leads to a defect-rich, stepped surface. The formation of oxygen vacancies fulfills the second requirement because oxygen atoms separated from the NiO lattice are, in principle, freely available and would further support H₂O dissociation. Our results suggest that H₂O dissociation in the H₂O atmosphere is indeed quite effective. First, this can be seen by the evolution of the peak labeled NiO_1−x–OH at 530 eV. As shown in Fig. 4(c), the maximum of oxygen vacancies on NiO_x is reached at 510 °C as expected from the results obtained in the O₂ atmosphere (Fig. 2(c)). Obviously, the relative intensity evolution of the NiO_1−x–OH peak follows that of the NiO_1−x peak at 528.9 eV even reaching the same relative intensity at 510 °C. Since the NiO_1−x–OH component is located on the high binding energy side of the NiO peak closer towards the OH-bond related peak positions, an association with –OH chemisorption at oxygen vacancies is plausible. This was tested by performing DFT-based calculations of the XPS BE of OH adsorbing at an oxygen vacancy. The adsorption leads to an increase of the BE by 1.6 eV with respect to the main NiO peak which is in agreement with the observed BE shift. Oxygen atoms created by the formation NiO_1−x oxygen vacancies at the surface are readily available to react with any partner in its vicinity. Hence, at least a fraction of them can support the dissociation of H₂O adsorbed at step edges and other defects which results in the formation of OH molecules. Such OH can chemisorb at the step edges or immediately occupy any vacant sites such as the oxygen vacancies. A contribution of OH chemisorption on step-edges to the NiO_1−x–OH peak cannot be excluded since its bond state would be quite similar to OH chemisorbing at an oxygen vacancy. On the other hand, any contribution of adsorbing H₂O to this peak is highly unlikely because dissociative adsorption, i.e., as OH, is energetically much more favored on defect-rich surfaces.^18,70 It is expected that OH desorbs at about 200 °C in a vacuum.^6,71 Yet, the relative intensity of the NiO_1−x–OH peak at 530 eV remains quite stable under 0.5 mbar H₂O pressure even at higher temperatures. Apparently, due to the constant supply of OH and H provided by water dissociation and atomic oxygen stemming from the oxygen vacancies, the OH chemisorbed at an oxygen vacancy site, represented by the NiO_1−x–OH peak, can be considered metastable under the given condition. Furthermore, the chemisorbed hydroxyl seems to act as a precursor for the formation of thermally stable NiOOH and, to a much smaller extent, also Ni(OH)₂ during cooling (Fig. 4(c)). The NiOOH formation starts during cooling to ≤350 °C already after the first heating. The newly formed bonds mostly survive even re-heating to 510 °C in H₂O. However, a certain induction phase appears to be required as only after the second heating–cooling cycle, stronger NiOOH formation is observed despite already fully available oxygen atoms from the vacancies. This suggests that the other prerequisite, the structural transformation of the surface from flat and terraced to micro-crystalline structure observed via SEM, is a gradual process and a certain surface roughness/defect density is required to further trigger water dissociation. Indeed, our SEM results show that there is a tremendous difference in the surface topography between oxygen treated and one-time H₂O-treated samples and, in particular, three-times H₂O-treated samples (ESI,† Fig. S5 and S7). This points to Ni-(oxy)-hydroxide formation being a self-promoting process. More Ni-(oxy)-hydroxide is formed, straining and restructuring the surface topography of NiO due to the different unit cells, and the more the topography changes, the more Ni-(oxy)-hydroxide is formed. We are currently investigating this using XPS under EC conditions.

Fig. 8 Schematic overview of the fitted XPS peaks and their assignment to their respective species. From top counterclockwise: Bulk NiO; NiO_x with step-edge and oxygen vacancy (NiO_1−x); water adsorption on defect-rich NiO_x; OH chemisorption after water dissociation (Ni_1−x–OH); water adsorption on NiO; co-existing NiO_x and Ni(OH)₂ and NiOOH, respectively.

Finally, if the NiO film is comparatively thin and heated in H₂O, the partial reduction of NiO_x can proceed beyond the creation of oxygen vacancies towards the formation of Ni metal islands. This can happen because it is less likely for dissociating H₂O to produce single oxygen atoms and thus H₂O has less potential to sustain NiO than O₂ has. Furthermore, the amount of accessible oxygen atoms diffusing from the bulk to the surface is limited for a thin oxide film.^3,63 Hence, in order to initiate NiOOH formation on a larger scale, thick oxide films appear to be a better choice. This may be different under EC conditions. In the activation process of NiO_x electrodes for the OER even for small particles oxidizing conditions are (a) applied by a sufficient voltage which can easily be repeated numerous times and does not need to be as carefully tuned as the temperature in the model experiments presented in the present study,⁷² and (b) due to the electrolyte, the oxygen supply is much more efficient as in water vapor.

Another interesting result is the behavior of the Ni2p_3/2 main peak and its high BE shoulder. The shape of these combined features, measured by the Ni2p_3/2 residuum, is heavily influenced by the presence of oxygen vacancies visible by the flattening of its normally peak-and-shoulder-like appearance. However, in an O₂ atmosphere, the replenishing of oxygen vacancies leads to a full recovery of the original shape. In an H₂O atmosphere, its behavior is similar, which suggests that the shoulder on the high BE side of the Ni2p_3/2 main peak is very likely related to non-local screening effects than caused by a chemical shift due to the presence of Ni-oxygen bonds as often suggested. To fully confirm this conclusion, this needs to be addressed by detailed theoretical studies which are beyond the scope of the present work. However, there are two small deviances: In the H₂O atmosphere, the Ni2p_3/2 main feature's point of maximum intensity at T_max shifts slightly from ≈854 to ≈856 eV throughout the heating–cooling cycles. Since the intensity ratio between the high- and low-intensity part of the peak-and-shoulder-like main feature seems to change slightly as well after cooling (ESI,† Fig. S3(a)), this may indicate the presence of NiOOH features also in the Ni2p_3/2 region.^54,55 Obviously, the two effects are rather small. Hence, the onset of NiOOH formation is obviously much easier tracked by monitoring the O1s region where the NiOOH formation has a direct effect on the BEs.

5. Conclusions

Under the applied conditions, XPS, XAS, SEM and DFT calculations clearly evidence the presence of oxygen vacancies at elevated temperatures in the O₂ as well as H₂O atmosphere, represented by an O1s peak at 528.9 eV (NiO_1−x). In the oxygen atmosphere at elevated temperatures, the oxygen and Ni vacancies contribute to the high mobility of Ni atoms, which leads to the formation of a defect-rich, stepped surface. In the H₂O atmosphere, the combination of H₂O adsorbing at such defects and step edges and the generation of free oxygen atoms via oxygen vacancies can instigate the dissociation of water. Subsequently, this leads to the saturation of the oxygen vacancies and step edges with chemisorbing OH. Under the applied conditions, this is a metastable precursor state, indicated by an O1s peak at 530 eV (NiO_1−x–OH), which finally, during cooling, leads to the formation of thermally stable NiOOH located on or close to the sample surface which is also accompanied by a major restructuring of the surface. This superposition of oxygen vacancies, free oxygen atoms, dissociative H₂O adsorption and surface roughness/defects is crucial to understand and subsequently improve the phase transitions occurring during the activation process of NiO_x electrodes in the OER. It may even play a crucial role in the OER itself both of which are currently under investigation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The financial support through the project “fundamentals of electro-chemical phase boundaries at semiconductor/electrolyte interfaces” GEP-HE funded by the German Federal Ministry of Education and Research BMBF under contract 13XP5023A and by the European Union under the a-leaf project (732840-A-LEAF) as well as through the “PrometH₂eus” project funded by the BMBF under contract FKZ 03HY105E is gratefully acknowledged. We thank HZB for the allocation of synchrotron radiation beamtime at the BESSY II UE56_2-PGM-1 beamline and for financial support. Open Access funding provided by the Max Planck Society. We like to thank Wiebke Frandsen and Travis Jones for their support.

References

1. P. T. Babar, A. C. Lokhande, M. G. Gang, B. S. Pawar, S. M. Pawar and J. H. Kim, J. Ind. Eng. Chem., 2018, 60, 493–497.
2. H. Bode, K. Dehmelt and J. Witte, Electrochim. Acta, 1966, 11, 1079–1087.
3. R. P. Furstenau, G. McDougall and M. A. Langell, Surf. Sci., 1985, 150, 55–79.
4. R. Poulain, A. Klein and J. Proost, J. Phys. Chem. C, 2018, 122, 22252–22263.
5. J. M. McKay and V. E. Henrich, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32(10), 6764–6772.
6. D. Cappus, C. Xu, D. Ehrlich, B. Dillmann, C. A. Ventrice, K. Al Shamery, H. Kuhlenbeck and H.-J. Freund, Chem. Phys., 1993, 177, 533–546.
7. J. C. de Jesus, J. Carrazza, P. Pereira and F. Zaera, Surf. Sci., 1998, 397, 34–47.
8. W.-L. Jang, Y.-M. Ming and W.-S. Hwang, Vacuum, 2009, 83, 596–598.
9. T. Zhang, M.-Y. Wu, D.-Y. Yan, J. Mao, H. Liu, W.-B. hu, X.-W. Du, T. Ling and S.-Z. Qiao, Nano Energy, 2018, 43, 103–109.
10. N. Weidler, J. Schuch, F. Knaus, P. Stenner, S. Hoch, A. Maljusch, R. Schäfer, B. Kaiser and W. Jaegermann, J. Phys. Chem. C, 2017, 121, 6455–6463.
11. Y. Ren, W. K. Chim, L. Guo, H. Tanoto, J. Pan and S. Y. Chiam, Sol. Energy Mater. Sol. Cells, 2013, 116, 83–88.
12. S. Corby, M.-G. Tecedor, S. Tengeler, C. Steinert, B. Moss, C. A. Mesa, H. F. Heiba, A. A. Wilson, B. Kaiser, W. Jaegermann, L. Francas, S. Giminez and J. R. Durrant, Sustainable Energy Fuels, 2020, 4, 5024–5030.
13. J. C. Conesa, J. Phys. Chem. C, 2016, 120, 18999–19010.
14. M. J. Eslamibidgoli, A. Groß and M. Eikeling, Phys. Chem. Chem. Phys., 2017, 19, 22659–22669.
15. A. J. Tkalych, K. Yu and E. A. Carter, J. Phys. Chem. C, 2015, 119, 24315–24322.
16. J.-Y. Jung, J.-Y. Yu, S. Yoon, B. Yoo and J.-H. Lee, Adv. Sustainable Syst., 2018, 2, 1800083.
17. D. Cappus, M. Menges, C. Xu, D. Ehrlich, B. Dillmann, C. A. Ventrice, J. Libuda, M. Bäumer, S. Wohlrab, F. Winkelmann, H. Kuhlenbeck and H.-J. Freund, J. Electron Spectrosc. Relat. Phenom., 1994, 68, 347–355.
18. W. Zhao, M. Bajdich, S. Carey, A. Vojvodic, J. K. Norskov and C. T. Campbell, ACS Catal., 2016, 6, 7377–7384.
19. R. Blume, W. Calvet, A. Ghafari, T. Mayer, A. Knop-Gericke and R. Schlögl, ChemPhysChem, 2023 , submitted.
20. H. Angermann, W. Henrion, A. Röseler and M. Rebien, Mater. Sci. Eng., B, 2000, 73, 178–183.
21. G. S. Higashi, Y. J. Chabal, G. W. Trucks and K. Raghavachari, Appl. Phys. Lett., 1990, 56, 656.
22. H. Bluhm, M. Hävecker, A. Knop-Gericke, E. Kleimenov, R. Schlögl, D. Teschner, V. I. Bukhtiyarov, D. F. Ogletree and M. Salmeron, J. Phys. Chem. B, 2004, 108, 14340–14347.
23. A. Knop-Gericke, E. Kleimenov, M. Hävecker, R. Blume, D. Teschner, S. Zafeiratos, R. Schlögl, V. I. Bukhtiyarov, V. V. Kaichev, I. P. Prosvirin, A. I. Nizovskii, H. Bluhm, A. Barinov, P. Dudin and M. Kiskinova, in Advances in Catalysis, ed. B. C. Gates, H. Knözinger, Elsevier Inc., New York, 2009, vol. 52, pp. 213–272.
24. P. Blaha, K. Schwarz, P. Sorantin and S. B. Trickey, Comput. Phys. Commun., 1990, 59(2), 399–415.
25. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
26. S. Sasaki, K. fujino and Y. Takeuchi, Proc. Jpn. Acad., Ser. B, 1979, 55(2), 43–48.
27. F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401.
28. A. F. Carley, S. D. Jackson, J. N. O’Shea and M. W. Roberts, Surf. Sci., 1999, 440, L868–L874.
29. M. A. van Veenendaal and G. A. Sawatzky, Phys. Rev. Lett., 1993, 70, 2459–2462.
30. P. Sahoo, D. K. Misra, J. Salvador, J. P. A. Makongo, G. S. Chaubey, N. J. Takas, J. B. Wiley and P. F. P. Poudeu, J. Solid State Chem., 2012, 190, 29–35.
31. L. Sangaletti, L. E. Depero and F. Parmigiani, Solid State Commun., 1997, 103(7), 421–424.
32. Y. S. Chen, J. F. Kang, B. Chen, B. Gao, L. F. Liu, X. Y. Liu, Y. Y. Wang, L. Wu, H. Y. Yu, J. Y. Wang, Q. Chen and E. G. Wang, J. Phys. D: Appl. Phys., 2012, 45, 065303.
33. I. Preda, R. J. O. Mossanek, M. Abbate, L. Alvarez, J. Mendez, A. Gutierrez and L. Soriano, Surf. Sci., 2012, 606, 1426–1430.
34. L. Soriano, I. Preda, A. Gutierrez, S. Palacin, M. Abbate and A. Vollmer, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 233417.
35. S. Uhlenbrock, C. Scharfschwerdt, M. Neumann, G. Illing and H.-J. Freund, J. Phys.: Condens. Matter, 1992, 4, 7973–7978.
36. R. J. O. Mossanek, I. Preda, M. Abbate, J. Rubio-Zuazo, G. R. Castro, A. Vollmer and A. Gutierrez, Chem. Phys. Lett., 2011, 501, 437–441.
37. M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. M. Lau, A. R. Gerson and R. St. C. Smart, Appl. Surf. Sci., 2011, 257, 2717–2730.
38. A. P. Grosvenor, M. C. Biesinger, R. St. C. Smart and N. S. McIntyre, Surf. Sci., 2006, 600, 1771–1779.
39. H. Kuhlenbeck, G. Odörfer, R. Jaeger, G. Illing, M. Menges, Th Mull and H.-J. Freund, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1969–1986.
40. M. Fingerle, S. Tengeler, W. Calvet, W. Jaegermann and T. Mayer, J. Electrochem. Soc., 2020, 167, 136514.
41. M. Napari, T. N. Huq, R. L. Z. Hoye and J. L. MacManus-Driscoll, InfoMat, 2020, 3, 1–41.
42. M. Fingerle, S. Tengeler, W. Calvet, T. Mayer and W. Jaegermann, J. Electrochem. Soc., 2018, 165, H3148–H3153.
43. N. D. Hoa, P. V. Tong, C. M. Hung, N. V. Duy and N. V. Hieu, Int. J. Hydrogen Energy, 2018, 43(19), 9446–9453.
44. N. Kitakatsu, V. Maurice, C. Hinnen and P. Marcus, Surf. Sci., 1998, 407, 36–58.
45. F. Ullrich, S. Hillebrandt, S. Hietzschold, V. Rohnacher, T. Marszalek, W. Kowalsky, R. Lovrincic, S. Beck, E. Mankel and A. Pucci, ACS Appl. Energy Mater., 2018, 1, 3113–3122.
46. V. Patil, S. Pawar, M. Chougule, P. Godse, R. Ratnakar, S. Sen and P. Joshi, J. Surf. Eng. Mater. Adv. Technol., 2011, 1, 35–41.
47. M. S. Jamal, S. A. Shahahmadi, P. Chelvanathan, H. F. Alharbi, M. R. Karim, M. A. Dar, M. Luqman, N. H. Alharthi, Y. S. Al-Harthi, M. Aminuzzaman, N. Asim, K. Sopian, S. K. Tiong, N. Amin and Md Akhtaruzzaman, Results Phys., 2019, 14, 102360.
48. Z. Luo, L. Liu, X. Yang, X. Luo, P. Bi, Z. Fu, A. Pang, W. Li and Y. Yi, ACS Appl. Mater. Interfaces, 2020, 12, 39098–39107.
49. M. Sterrer and H.-J. Freund, in Surface and Interface Science, ed. K. Wandelt, Wiley-VCH, Weinheim, Germany, 2013, vol. 3, pp. 229–278.
50. M. A. Langell and M. H. Nassir, J. Phys. Chem., 1995, 99, 4162–4169.
51. M. A. Munoz-Marquez, R. E. Tanner and D. P. Woodruff, Surf. Sci., 2004, 565, 1–13.
52. L. Liu, S. Wang, S. Liu, Q. Guo and J. Guo, Surf. Sci., 2018, 667, 8–12.
53. X. Chen, J. Wang, X. Sun, D. Zakharov, S. Hwang and G. Zhou, Microsc. Microanal., 2021, 27(Suppl 1), 1958–1959.
54. M. C. Biesinger, B. P. Payne, L. W. W. Lau, A. Gerson and R. St. C. Smart, Surf. Interface Anal., 2009, 41, 324–332.
55. B. P. Payne, M. C. Biesinger and N. S. McIntyre, J. Electron Spectrosc. Relat. Phenom., 2009, 175, 55–65.
56. G. A. Somorjai, Introduction to Surface Chemistry and Catalysis, Wiley, New York, 1994.
57. I. Preda, M. Abbate, A. Gutierrez, S. Palacin, A. Vollmer and L. Soriano, J. Electron Spectrosc. Relat. Phenom., 2007, 156–158, 111–114.
58. F. M. F. De Groot, J. C. Fuggle, B. T. Thole and G. A. Sawatzky, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42(9), 5459–5468.
59. G. van der Laan, J. Magn. Magn. Mater., 1999, 192, 297–304.
60. L. Soriano, M. Abbate, J. Vogel, J. C. Fuggle, A. Fernandez, A. R. Gonzalez-Elipe and M. Sacchi, Chem. Phys. Lett., 1993, 208(6), 460–464.
61. L. Soriano, A. Gutierrez, I. Preda, S. Palacin, J. M. Sanz, M. Abbate, J. F. Trigo, A. Vollmer and P. R. Bressler, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 193402.
62. K. Chungguang, Y. Zhang, L. Han, H. L. Xin, C.-J. Sun, D. Nordlund, S. Qiao, X.-W. Du and F. Lin, J. Mater. Chem. A, 2020, 8, 10747.
63. J. A. Rodriguez, J. C. Hanson, A. I. Frenkel, J. Y. Kim and M. Perez, J. Am. Chem. Soc., 2002, 124, 346–354.
64. F. Reinert, P. Steiner, S. Hüfner, H. Schmitt, J. Fink, M. Knupfer, P. Sandl and E. Bertel, Z. Phys. B, 1995, 97, 83–93.
65. M. T. Greiner, M. G. Helander, Z.-B. Wang, W.-M. Tang and Z.-H. Lu, J. Phys. Chem. C, 2010, 114, 19777–19781.
66. N. R. Aswathy, J. Varghese and R. Vinodkumar, J. Mater. Sci.: Mater. Electron., 2020, 31, 16634–16648.
67. F. Hajakbari, M. Taheri Afzali and A. Hojabri, Acta Phys. Pol., A, 2017, 131, 417–419.
68. K. V. Manukyan, A. G. Avestiyan, C. E. Shuick, H. A. Chatilyan, S. Rouvimov, S. L. Kharatyan and A. S. Mukasyan, J. Phys. Chem. C, 2015, 119, 16131–16138.
69. P. A. Thiel and T. E. Madey, Surf. Sci. Rep., 1987, 7, 211–385.
70. D. J. Simpson, T. Bredow and A. R. Gerson, Theor. Chem. Acc., 2005, 114, 242–252.
71. S. Anderson and J. W. Davenport, Solid State Commun., 1978, 28, 677–681.
72. C. Lin, Y. Zhao, H. Zhang, S. Xie, Y.-F. Li, X. Li, Z. Jiang and Z.-P. Liu, Chem. Sci., 2018, 9, 6803–6812.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02047a

---