Charge delocalization and aromaticity of doubly reduced double-walled carbon nanohoops

Abstract

Cycloparaphenylenes (CPPs) exhibit selective host capabilities, featuring the ability to incorporate smaller CPPs to form double-walled host–guest complexes. Moreover, CPPs can also be stabilized by global aromaticity under twofold oxidation or reduction, involving electronic conjugation along with the overall structural backbone. Herein we explore the structural modifications, bonding, electron delocalization and magnetic properties of doubly reduced double-walled CPP complexes with DFT methods, in the isolated and aggregate [n + 5]CPP⊃[n]CPP²⁻ (n = 5–8) species. Our results show that the hosts undergo structural, bonding and delocalization deformations towards quinoidal configurations and exhibit global long-ranged shielding cones similar to global aromatic free dianionic CPPs, accounting for charge delocalization on the outer nanohoops, whereas the guests preserve local aromatic benzenoid configurations, resulting in global and local aromatic circuits within the host–guest aggregate. This observation suggests that in multi-layered related species electronic delocalization will be retained at the outer structural surface. The aromaticity of the hosts is manifested in the strong upfield shifts of the guests ¹H-NMR signals. Hence, CPP complexes can be extended to doubly reduced species stabilized by global host aromaticity expanding our understanding of doubled-walled nanotubes at the nanoscale regime.

---

Introduction

Macrocyclic aromatic carbon structures with curved π-surfaces exhibit exceptional structural and electronic properties with flourishing applications in nanomaterials, organic–electronic devices and supramolecular chemistry.^1–9 Among such structures, cycloparaphenylenes (CPPs), also called nanohoops, are a unique class of polycyclic aromatic hydrocarbons (PAHs) consisting of para-connected benzene rings forming an in-plane macrocyclic π system. They can be conceived as the smallest unit of armchair carbon nanotubes (CNTs), embodying the prospect for “bottom-up” organic synthesis of such single-walled nanomaterials.^10–13 Due to the pioneering work of Jasti,^4,7,14–17 Itami^11,13,18,19 and Yamago^20–23 groups, among others,^24,25 over the last decade, the selective synthesis of numerous [n]CPPs on a gram-scale is now attainable, allowing for further exploration of their chemistry.

One of the remarkable properties of [n]CPPs is the large interior space of the radial π-system which is capable of selectively binding smaller π-structures stabilized by π–π or CH–π interactions, establishing them as exemplary hosts with adjustable selectivity according to the number of benzene rings. Thus, numerous host–guest complexes with [n]CPPs serving as hosts have been experimentally characterized or theoretically predicted in recent years incorporating fullerenes,^16,26–33 planar and curved PAHs^34–36 or even smaller CPPs^37,38 as guests. The latter, termed “Russian doll”³⁹ or “Planetary orbit”⁴⁰ complexes, can be conceived as the shortest double-walled carbon nanotubes (DWCNTs).³⁷ Initially they were theoretically investigated by Fomine³⁹ and Bachrach⁴⁰ who predicted that [n]CPPs can be selectively bound by [n + 5]CPPs, forming [n + 5]CPP⊃[n]CPP complexes, experimentally confirmed in 2017 by Yamago with NMR spectroscopy for n = 5–8 and 10,³⁷ while Wang et al. recently prepared the [12]CPP⊃[6]CPP complex,³⁸ enabling the investigation of DWCNTs at the molecular level.

[n]CPPs display a local aromatic character of each benzene ring and they can be described as a collection of n Clar's π-sextets,⁴¹ while the whole macrocycles can be regarded as non-aromatic benzenoid structures.^42–46 However, upon twofold oxidation^47–50 or reduction^51–53 the [n]CPPs turn on global in-plane macrocyclic aromaticity adopting a quinoidal structural configuration. Thus, the doubly charged species are able to sustain global macrocyclic diatropic currents under the effect of a perpendicular external magnetic field.⁴² In turn, the π currents produce a globally induced magnetic field^54–58 which is manifested with global long-ranged shielding cones^44–46 providing reasonable interpretation of the ¹H-NMR chemical shift variations in the aromatic macrocycles, as well as in host–guest aggregates. Hence, charged [n]CPPs stabilized by global aromaticity are of special interest in redox chemistry, with promising potential applications in organic electronic devices, energy storage materials and supramolecular chemistry,^1,8,59 paving the way for novel host–guest complexes with unique selective guest binding capabilities.

Herein we set out to explore doubly reduced double-walled nanohoop complexes [n + 5]CPP⊃[n]CPP²⁻ (n = 5–8) by means of density functional theory (DFT) focusing on geometrical deformation, bonding, electron delocalization, induced magnetic fields^54–58 and ¹H-NMR chemical shifts, in order to investigate the charge delocalization and aromaticity of these complexes, as well as to provide useful information for experimental characterization. We show that the charge is exclusively delocalized on the hosts enabling a global aromatic character of the outer nanohoops, resulting in strong upfield chemical shifts of the strongly shielded guests, which tend to preserve their local benzenoid structures. The variations in host aromaticity affect the ¹H-NMR chemical shifts of the inner guests, which are strongly shifted upfield.

Computational methods

Geometry optimizations were performed using Gaussian⁶⁰ employing Grimme's standalone pure functional B97D3 with D3BJ dispersion corrections,⁶¹ along with the all-electron triple-ζ basis set with one polarization function (def2TZVP). B97D3 was chosen because it has been shown that it performs with very good agreement to CCSD(T) or other hybrid functionals for nonbonded π–π interactions of polycyclic hydrocarbons and CPP complexes,^62–66 providing accurate results with reduced computational cost. The stability of the wavefunctions of charged complexes was tested⁶⁷ using stable = opt keyword. All structures were verified as local minima on the potential energy surface by analytical frequencies calculations which yielded real vibrational frequencies. Molecular orbitals’ energy levels were recalculated with the ωB97XD⁶⁷ functional with the same basis set, because pure DFT functionals underestimate the HOMO–LUMO gaps, whereas hybrid functionals provide more accurate predictions.⁶⁸

Chemical shielding calculations were performed with the ADF2019^69,70 program. NICS calculations at the centers of the complexes were computed at the PBE/TZ2P level. ¹H-NMR chemical shifts were calculated using the hybrid PBE0 functional⁷¹ and triple-ζ slater basis set with one polarization function TZP, using benzene as the reference (δ_benzene = 7.36 ppm),⁷² according to the formula:

δ_calc = σ_benzene − σ_calc + δ_benzene

The induced magnetic field was derived from chemical shielding tensor calculations within the GIAO formalism⁷³ according to the formula B^ind_i = σ_ij(r)B^ext_j (i, j = x, y, z). The chemical shieldings were calculated in square grids of points with edges of 17.5 Å and step size 0.5 Å employing the Perdew–Burke–Ernzerhof (PBE) functional⁷⁴ with the double-ζ stater basis set with one polarization function (DZP). Dissection of the 2D induced magnetic field to π and σ + cores, as well as host–guest π-contributions were achieved with the natural chemical shielding (NCS) approach⁷⁵ using the NBO6.0 program,⁷⁶ taking into consideration the contributions of the respective localized natural bond orbitals (NBO) with a distinctive π or σ character. Moreover, CMO analysis of the induced magnetic field was performed at the same level, taking into consideration the magnetic response of frontier canonical orbitals. Still, the calculation and dissection of B^ind in 3D is computationally rigorous for large systems and alternatively the pseudo-π approach has been employed for the 3D visualization of the π response by representing the π orbitals with the corresponding σ orbitals of a hydrogen molecular model with the geometry of the carbon skeleton.^77–79 Additional calculations of the total full electron 3D magnetic response were carried out with Gaussian at the PBE/SVP level and mapped visualizations on VDW surfaces were made with the VMD program.⁸⁰ Input preparation, output processing, NBO and CMO dissection and 2D/3D visualization of the induced magnetic field were performed with our custom PyMAF program.⁸¹

Mayer bond orders^82,83 and 6-center Delocalization Index⁸⁴ (MCI) were calculated with the Multiwfn program.⁸⁵ MCI was calculated with the ωB97XD functional adopting the pseudo-π approach^86,87 within the fuzzy-atom space (FAS) partitioning,⁸⁸ using modified parameters to minimize errors in the atomic overlap matrix.

Results and discussion

Geometrical characteristics and local electron delocalization

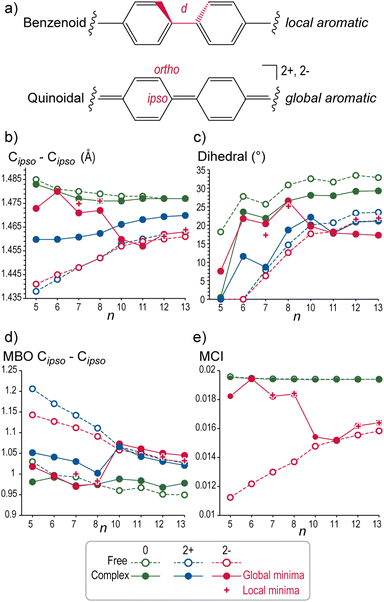
The optimized structures of [n + 5]CPP⊃[n]CPP^q (n = 5–8, q = 0, 2+, 2−) complexes are presented in Fig. 1 and Fig. S1 (ESI†). All dianionic ground state complexes were found to have stable closed-shell restricted wavefunctions. On the other hand, the ground states of the dicationic complexes were found to be open-shell triplet states. A characteristic structural feature of such complexes is the inclination angle between the host and the guest. According to the literature, when the inclination angle is zero (0°) adopting a parallel orientation between the host and the guest, the complex is termed “Russian doll”, whereas for non-zero inclination angles the complex is termed “Planetary orbit”.^37,39,40 The inclination angles are estimated from the fitted planes of host and guest ipso carbons, as described by Bachrach.⁴⁰ Our calculations detected three stable configurations for neutral [10]CPP⊃[5]CPP with inclination angles of 0°, 14.5° and 50.8°, where the Russian-doll configuration is the global minimum, as it was found to be more stable by 3.3 kcal mol⁻¹ and 1.9 kcal mol⁻¹ with respect to the planetary orbit configurations respectively. For the dianion [10]CPP⊃[5]CPP²⁻ only a planetary orbit configuration was located with an inclination angle of 13.8°. For the neutral higher complexes (n = 6, 7, and 8) only planetary orbit configurations were located, where the inclination angles computed at the B97D3/def2TZVP level of theory (32.7°, 26.4° and 23.2° for n = 6, 7, and 8 respectively) are in good agreement with those reported by Bachrach⁴⁰ at the CPCM(THF)/ωB97X-D/6-31G(d) level. For the dianions with n = 7 and 8 both Russian-doll and planetary orbit configurations were found with the former being more stable by 0.36 kcal mol⁻¹ and 1.61 kcal mol⁻¹ for n = 7 and 8 respectively. For the dications with n = 6, 7 and 8 only planetary orbit configurations were located with similar small inclination angles (10.5°, 10.3° and 10.8° for n = 6, 7, and 8 respectively), whereas for n = 5 a Russian-doll configuration was located.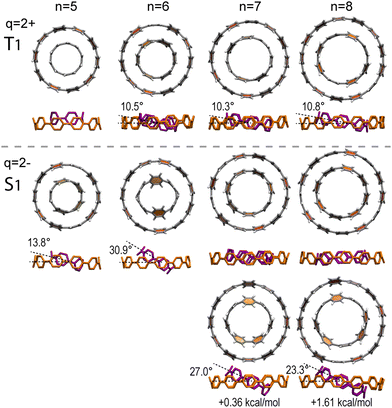

Fig. 1 Optimized geometries (B97D3/def2TZVP) of triplet state (T1) dicationic and singlet state (S1) dianionic complexes [n + 5]CPP⊃[n]CPP^q (n = 5–8; q = 2+, 2−).

The characteristic geometric modification of global aromatic doubly charged [n]CPPs^q (q = 2+, 2−) is a shift towards the quinoidal structure compared to the local aromatic benzenoid structure of the neutral counterparts (Fig. 2a), primarily expressed with the shortening of C_ipso–C_ipso bonds and secondary with the shortening of C_ortho–C_ortho bonds, as well as the elongation of C_ipso–C_ortho bonds. The trend of C_ipso–C_ipso modification with regard to the nanohoop size and the charge of both free and complexed [n]CPPs is presented in Fig. 2b, while the optimized averaged C–C bond lengths are given in Table S1 (ESI†). For free [n]CPPs both the dianions and the dications undergo the same shortening of C_ipso–C_ipso bond lengths characteristic of quinoidal configuration, which decreases as the size of the nanohoop increases, from 0.05 Å (n = 5) to 0.01 Å (n = 13). Upon neutral complex formation, the C–C bond lengths of both the hosts and the guests remain essentially unchanged compared to free neutral molecules. However, variations are expected and observed for the doubly charged complexes. The guests in the dianions (n = 5–8) retain very similar bond lengths with the neutral complexes. In contrast, the hosts in the dianions (n = 10–13) undergo the same shortening with the quinoidal free dianions. On the other hand, in the dications the C_ipso–C_ipso lengths of both the guests and the hosts are shortened halfway towards the quinoidal free dications.

Fig. 2 (a) Benzenoid and quinoidal configurations of [n]CPPs with highlighted dihedral angle, ipso and ortho carbons, (b) averaged C_ipso–C_ipso bond lengths (Å), (c) averaged dihedral angles, (d) averaged Mayer bond orders (MBO) of C_ipso–C_ipso bonds and (e) averaged multi-center delocalization indices (MCI) of phenylene rings of free [n]CPPs (n = 5–8, 10–13) (dotted lines), guests [n]CPPs and hosts [n + 5]CPPs (n = 5–8) of [n + 5]CPP⊃[n]CPP complexes (solid lines) at 0 (green) and 2− (red) and 2+ (blue) charge states.

To obtain more insight into the bonding characteristics we computed the Mayer Bond Orders (MBO) given in Table S3 (ESI†), while the trend of C_ipso–C_ipso bonds is presented in Fig. 2d. The MBOs of C_ipso–C_ipso of neutral free molecules vary in the range of 1.00 ± 0.02 and slightly decrease with increasing size, whereas for the charged molecules the MBO values are distinctly higher by an average value of ∼0.10 and decrease more sharply with increasing size. The MBO values of neutral complexes, as well as the guests of dianionic complexes are very close to the corresponding free molecules, denoting the persistence of the benzenoid character. However, the guests of dicationic complexes present higher MBO values than their neutral and dianionic counterparts. In contrast, the hosts of both dicationic and dianionic complexes display similar MBOs with the free dianions, denoting a shift towards quinoidal structures.

Another characteristic structural modification of the doubly charged [n]CPPs species, is the decrement of the dihedral angles between adjacent phenylenes, compared to the neutral counterparts, tending toward a vertical orientation with respect to the macrocycle plane.⁵¹ The trends and values of the averaged optimized dihedral angles are presented in Fig. 2b and Table S2 (ESI†) respectively. Concerning the neutral complexes, both hosts and guests display a similar small decrement of an averaged 4° in their dihedral angles compared to the corresponding free [n]CPPs, except for the guest [5]CPP which displays a negligible angle in the Russian-doll configuration (0.5°) which increases to 11.9° in the planetary orbit configuration. The guests of the dianions display a very small decrement in the dihedral angles compared to the guests of the neutral complexes (Δ = 1.8°, 4.5° and 1.6° for planetary orbit n = 6, 7 and 8 respectively and Δ = 1.5° and 0.1° for Russian-dolls with n = 7 and 8, respectively), while in the dications the decrement is more pronounced (Δ = 12.0°, 13.2° and 7.9° for n = 6, 7 and 8 respectively). In contrast, the hosts are much more affected by the double charge, leading to similar dihedrals in the dianions and the dications compared to the corresponding free charged [n]CPPs.

The preceding analysis of geometrical and bonding characteristics reveals a quinoidal character for the hosts of the doubly reduced complexes suggesting a global aromatic character, whereas the guests retain their benzenoid structures implying the persistence of local aromaticity. On the other hand, in the triplet state dications both the hosts and the guests are geometrically affected to a lesser degree towards a quinoidal character. Hereafter we will focus on the closed-shell dianionic species, since investigation of the open-shell aromaticity of nanohoops requires a specialized approach⁸⁹ which is out of the scope of the current paper.

It has been shown by geometric, magnetic and electron delocalization criteria that local aromaticity decreases in the presence of global aromaticity in CPPs.⁴⁵ To evaluate the variations of electron delocalization and local aromaticity we calculated the Multicenter Delocalization Index (MCI) for the six-membered rings. The MCI values for all rings are given in Table S4 (ESI†) and the trends are presented in Fig. 2e. It is evident that electron delocalization of phenylene rings remains unaffected upon neutral complex formation and is invariant to the macrocycle size. On the other hand, global aromatic free dianions display substantially reduced delocalization of phenylenes, which increases with macrocycle size. The trends of the MCI for the hosts and guests of the dianionic complexes are very similar to those of the C_ipso–C_ipso lengths. For the guests the MCI values are in the range of neutral counterparts. In contrast the hosts display MCI values very close to the free dianions. Hence the guests of the dianions preserve the local aromatic character of neutral counterparts, whereas the hosts adopt the reduced local aromatic character of global aromatic free dianions.

Finally, the planetary orbit and Russian doll configurations for n = 7 and 8 display similar or identical values concerning structural, bonding and delocalization indices, denoting that the configuration of the complexes does not affect the aromaticity of the system.

Induced magnetic fields of [5]CPP^q and [10]CPP^q (q = 0, 2−)

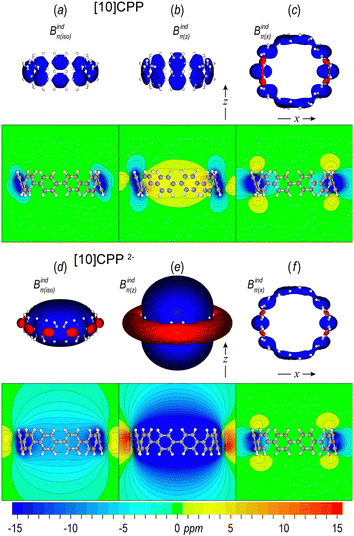
When an aromatic ring, such as benzene, is placed inside a uniform magnetic field with the ring plane oriented perpendicular to the field (tilt angle 0°), then the delocalized π electrons induce a clockwise ring current, which subsequently induces a secondary magnetic field forming a long-ranged shielding cone above and below the ring, complemented by a weaker torus-shaped deshielding zone outside the ring plane. This out-of-plane response can be visualized as 3D isosurfaces or 2D maps of the z component of the induced magnetic field B^ind_z, which is equivalent to NICS_zz.^90,91 As the tilt angle increases to a final parallel orientation of the ring (tilt angle 90°), the in-plane response (B^ind_x or B^ind_y) forms a short-ranged shielding area surrounding the ring, while the weak paratropic zone always remains outside the ring.^45,58 Furthermore, the isotropic response B^ind_iso, which is equivalent to iso-chemical shielding surfaces (ICSS),⁹² accounts for the averaged orientation to the external field due to molecular tumbling and can be directly related to ¹H-NMR experiments. However, in curved hydrocarbons the σ electrons can contribute significantly to the shielding⁹³ and therefore only the π contributions must be considered to evaluate the aromatic character of such systems. Hereafter we explore the π magnetic response of free neutral and doubly reduced [5]CPP and [10]CPP molecules and extend our investigation to [10]CPP⊃[5]CPP and higher complexes.

The magnetic response of the π system of [10]CPP in terms of the induced magnetic field B^ind_π(i), (i = iso, z, x) is shown in Fig. 3 and it is depicted with isosurfaces calculated with the pseudo-π model and as 2D maps derived with all electron calculations and dissected to π contributions employing NBO analysis. The isotropic response B^ind_π(iso) (Fig. 3a) displays local shielding areas depicted with a blue color surrounding each phenylene ring, representing the local aromatic character and can be interpreted by inspecting the out-of-plane response and the in-plane response B^ind_π(x). The out-of-plane response B^ind_π(z) (Fig. 3b) displays local short-ranged shielding areas in the vicinity of each phenylene ring, because the external field is parallel to the rings,⁵⁸ while a weak paratropic area, depicted with yellow in the 2D map, is observed inside the macrocycle (NICS_πzz = 4.5 ppm) as a result of the cumulative effect of weak local paratropic contributions of each ring. The in-plane response B^ind_π(x) (Fig. 3c) displays local long-ranged shielding cones at the phenylene rings that are oriented perpendicular to the applied field (tilt angle 0°), while the shielding cones are contracted as the tilt angle increases and the rings become parallel to the applied field. For the dianion [10]CPP²⁻ the in-plane response of B^ind_π(x) (Fig. 3f) has identical shape with the neutral and slightly contracted extension, indicating that the local aromatic character of each ring under a parallel orientation of the external field is preserved regardless of the charge state. However, the out-of-plane component B^ind_π(z) (Fig. 3e) displays a global, strong, and long-ranged shielding cone on the whole macrocycle (NICS_πzz = −24.2 ppm), representing global macrocyclic aromaticity. As a result, the isotropic response B^ind_π(iso) (Fig. 3d) is dominated by the out-of-plane component and displays a weaker global shielding cone (NICS_πiso = −7.2 ppm).

Fig. 3 Isosurfaces of pseudo-π and contour maps of π contributions to the isotropic (B^ind_π(iso)), out-of-plane (B^ind_π(z)) and in-plane (B^ind_π(x)) components of the induced magnetic field of neutral [10]CPP (a–c) and dianion [10]CPP²⁻ (d–f). Isosurface isovalue ±5 ppm. Blue: shielding; red: deshielding.

The same behavior is observed for [5]CPP (Fig. S2, ESI†) with local shielding cones on phenylene rings in the neutral state and a global long-ranged shielding cone for the out-of-plane response B^ind_π(z) of the dianion (NICS_πzz −31.5 ppm), leading to a global shielding isotropic response (NICS_πiso = −7.9). However, the out-of-plane response B^ind_π(z) of neutral [5]CPP displays a short-ranged global deshielding cone (NICS_πzz = 23.8 ppm) leading to weak global paratropicity of the isotropic response B^ind_π(iso) (NICS_πiso = 7.9 ppm). Although a global deshielding cone is a characteristic feature of antiaromatic molecules, in this case it is attributed to the cumulative paratropic effect of each ring inside the macrocycle, which is enhanced compared to the corresponding response of [10]CPP due to the small diameter of [5]CPP.

Induced magnetic fields of [n + 5]CPP⊃[n]CPP complexes

The out-of-plane response of neutral and doubly reduced complexes [10]CPP⊃[5] is shown in Fig. 4a and b. The magnetic response of neutral [10]CPP⊃[5]CPP (Fig. 4a) displays local shielding cones on phenylene rings and a global paratropic cone inside the guest (NICS_πzz = 35.0 ppm and NICS_πiso = 12.6 ppm) showing that the local aromatic character of the host and the guest is precisely retained, as the magnetic response of the complex is the sum of the magnetic response of neutral [10]CPP and [5]CPP (Fig. S4, ESI†). On the other hand, the out-of-plane response of the dianion (Fig. 4b) displays a global long-ranged shielding cone at the host which diminishes and becomes weakly paratropic inside the guest (NICS_πzz = 3.6 ppm). Accordingly, the isotropic response (Fig. S3a and b, ESI†) displays weak but long-ranged global shielding cones at the host and very weak paratropicity inside the guest (NICS_πzz = 2.0 ppm). This behavior clearly suggests that under twofold reduction the host becomes aromatic, while the guest seems to retain its local aromatic character, contributing paratropically at the center of the macrocycle. Otherwise, if the guest was aromatic, then the diatropicity would be greatly enhanced at the vicinity of the inner nanohoop. Hence, the extra charge appears to be delocalized mainly on the host [10]CPP.

Fig. 4 π contributions to the out-of-plane component of the induced magnetic field, B^ind_π(z), of [10]CPP⊃[5]CPP^q (q = 0, 2−) complexes (a and b) and NBO-dissected contributions of hosts (c and d) and guests (e and f). Isosurface isovalue ±5 ppm. Blue: shielding; red: deshielding.

The magnetic response of the complex is the cumulative result of host and guest responses. Hence, to gain insight into the origin and the variations in aromaticity, we dissected the total π response of each complex to distinct responses of host and guest macrocycles, by selecting the respective π-NBO (or σ-NBO for the pseudo-π model) contributions to chemical shielding, since each NBO is localized on a specific macrocycle in the complex. The results of NBO host–guest dissection are presented in Fig. 4c–f for the out-of-plane response and in Fig. S3c–f (ESI†) for the isotropic response. Furthermore, we compare the B^ind_π(z) of each macrocycle in the complexes, as well as the total π response, with the B^ind_π(z) of the corresponding free neutral or doubly reduced [10]CPP²⁻ and neutral [5]CPP, as well as their cumulative result, keeping the geometries of the macrocycles as they have been deformed in the complex (Fig. S3 and S4, ESI†). For the neutral complex the dissected magnetic responses of the host and the guest (Fig. 4c and e) are identical to free neutral [10]CPP and [5]CPP respectively, as expected. Accordingly, the total π magnetic response of the neutral complex is identical to the cumulative result of [5]CPP + [10]CPP (Fig. S4, ESI†). On the other hand, the host of the dianion (Fig. 4d) induces a strong shielding cone comparable to free [10]CPP²⁻, sustaining a B^ind_π(z) value of −4 ppm at 10.2 Å above the center, while for the free [10]CPP²⁻ this diatropicity is found at 11.0 Å. Moreover, the paratropic response of the guest (Fig. 4f) is slightly weaker than free [5]CPP. Accordingly, the total π response of the dianion [10]CPP⊃[5]CPP²⁻ is only marginally weaker than the cumulative result of [5]CPP + [10]CPP²⁻ (Fig. S5, ESI†).

The preceding analysis of [10]CPP⊃[5]CPP showed that the pseudo-π model provides a very accurate qualitative picture of the π magnetic response of the complexes, which is consistent with all-electron calculations of the total π response, as well as with the NBO dissection to host–guest contributions. Hence, we calculated the pseudo-π magnetic response of the higher complexes [n + 5]CPP⊃[n]CPP (n = 6–8) and dissected the complex response to host–guest contributions, as shown in Fig. 5. The higher complexes show the same magnetic behavior with [10]CPP⊃[5]CPP, with local shielding cones at the neutral states, and global shielding cones on the hosts of the doubly reduced complexes. The guests of the dianions display local shielding cones on phenylene rings, preserving the local aromatic character.

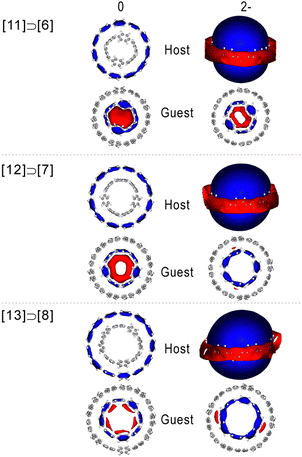Fig. 5 Host and guest dissected pseudo-π contributions of planetary orbit [n + 5]CPP⊃[n]CPP^q (n = 6–8; q = 0, 2−) complexes. Isosurface isovalue ±5 ppm. Blue: shielding; red: deshielding.

CMO analysis

According to CMO analysis, the variations of the magnetic response can be interpreted by analyzing the contributions of frontier orbitals.^56,57 In general, the highest lying orbitals shape the overall magnetic response via paratropic contributions induced from occupied-to-virtual MO rotational excitations, whereas the lower orbitals induce a diatropic response. The excitations obey the selection rules and the magnitude of the paratropic response depends on the energy gap and the overlap of the respective rotated orbitals.^57,94 In antiaromatic molecules the HOMO → LUMO rotational excitation is symmetry allowed resulting in the characteristic strong paratropicity, whereas in aromatic molecules these excitations are usually forbidden. In contrast to planar PAHs, [n]CPPs exhibit increasing HOMO–LUMO gaps with the number of rings, which is also evident in neutral complexes, where the HOMOs are localized on the guest (Fig. S6, ESI†). In the doubly reduced complexes, the electronic structure is modulated such that the HOMOs are localized on the host, leading to a drastic decrease of the HOMO–LUMO gap, which in contrast to neutral species decreases with increasing size (Fig. 6). The small HOMO–LUMO gaps are compatible with antiaromatic molecules, but in such electronic configurations the strong paratropic response of HOMOs is cancelled due to their nodal structure which forbids the respective HOMO → LUMO rotational excitation by symmetry. Accordingly, in the dianions the major contributing rotational allowed excitation is the HOMO−1 → LUMO, displaying a weaker magnetic response with regard to the neutral counterparts due to a smaller overlap.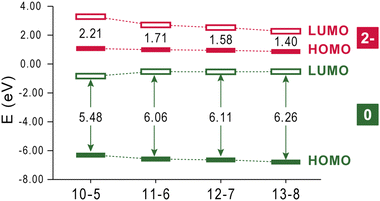

Fig. 6 Frontier orbital energy levels of neutral and doubly reduced [n + 5]CPP⊃[n]CPP^q (n = 5–8; q = 0, 2−) complexes (calculated at ωB97XD/def2TZVP).

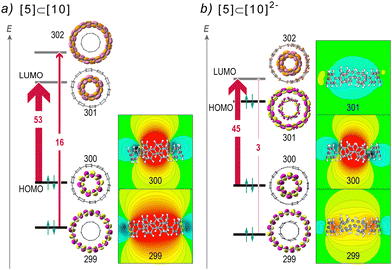
In Fig. 7 the magnetic response of frontier orbitals and the corresponding rotational excitations of [10]CPP⊃[5]CPP complexes are presented. In neutral [10]CPP⊃[5]CPP the HOMO and LUMO are localized exclusively on the guest, whereas the HOMO−1 and LUMO+1 are on the host. These orbitals correspond to the HOMO and LUMO of free [5]CPP and [10]CPP respectively and therefore they display similar paratropic magnetic responses. Specifically, a strong global deshielding cone is induced on the guest from HOMO → LUMO excitation (NICS_zz^HOMO→LUMO ≈ 53 ppm), whereas the HOMO−1 → LUMO+1 excitation induces a global deshielding cone on the host (NICS_zz^{HOMO−1→LUMO+1} ≈ 16 ppm, Fig. 7a). In the doubly reduced complex the HOMO → LUMO excitation is forbidden by symmetry and the dianion presents diminished paratropicity due to a smaller overlap of the remaining allowed excitations. Specifically, in the dianion the HOMO is mainly localized on the host and presents a weak diatropic response, while the HOMO−1 → LUMO and HOMO−2 → LUMO excitations contribute paratropically by 45 ppm and 3 ppm on the guest and the host respectively, resulting in a strong deshielding cone at the guest and a very weak deshielding cone at the host (Fig. 7b). Consequently, the dianion retains much of the paratropicity in the guest, whereas in the host the paratropic contributions are marginal, resulting in the strong global diatropic response discussed above.

Fig. 7 Relative energy levels of frontier CMOs of (a) neutral [10]CPP⊃[5]CPP and (b) dianion [10]CPP⊃[5]CPP²⁻, major π → π* rotational excitations (red arrows) and maps of CMO contributions to B^ind_πz. Values in red correspond to contributions of rotational excitations at the center of the complex (PBE/TZ2P, ppm). The width of the arrows is proportional to . The external field is applied perpendicular to the complex (z axis).

¹H-NMR chemical shifts

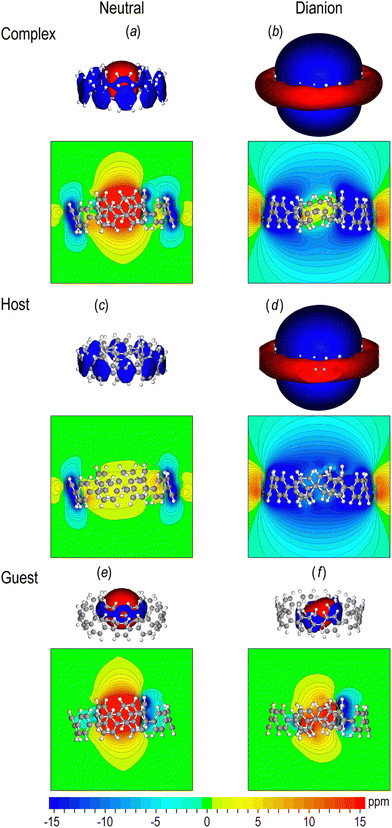
The varying aromaticity of neutral and dianionic complexes is expected to be manifested in the hydrogen chemical shifts, providing a useful interpretation of the respective ¹H-NMR experimental signals in host–guest aggregates. In Fig. 8a and b the isotropic chemical shielding of a full electron kernel is mapped on the VDW surfaces of neutral and doubly reduced [10]CPP⊃[5]CPP. In the neutral complex the hydrogens of the guest are deshielded, due to the deshielding cone of [5]CPP. In contrast, the hydrogens of the guests in the dianion are strongly shielded from the global shielding cone of the hosts.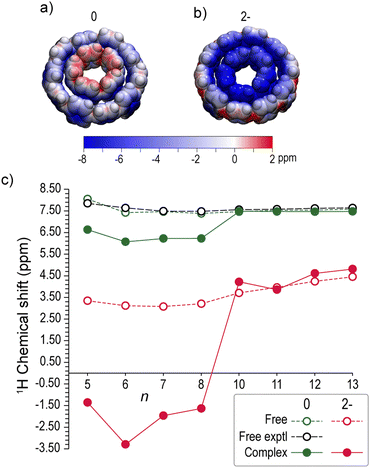

Fig. 8 Isotropic chemical shielding mapped on 90% VDW surfaces of (a) neutral and (b) dianion [10]CPP⊃[5]CPP^0/2− (blue: shielding; red: deshielding). (c) Calculated average ¹H chemical shifts of free [n]CPPs (n = 5–8, 10–13) (dotted lines), guests [n]CPPs and hosts [n + 5]CPPs (n = 5–8) of [n + 5]CPP⊃[n]CPP complexes (solid lines) at 0 (green) and 2− (red) charge states. Experimental values (black) taken from ref. 4.

The trends of the average calculated ¹H-NMR chemical shifts are depicted in Fig. 8c and their values are given Table S5 (ESI†). The calculated chemical shifts of neutral free [n]CPPs lying in the range 7.4–8.1 ppm are in very good agreement with experimental values⁴ with an average deviation Δ ≈ 0.1 ppm. The calculated shifts of free dianions are substantially upfield shifted by ∼3.9 ppm, ranging from 3.1 ppm to 4.5 ppm. The upfield shift of doubly reduced [n]CPPs, owing to their global aromatic character, is in line and somewhat larger than the experimental data (∼5.36 ppm).⁵¹

Upon neutral complex formation the hosts are essentially unaffected (Δ < 0.07 ppm for n = 10–13), while the guests are shifted upfield by ∼1.2 ppm, whereas the experimental data of Yamago³⁷ showed a marginal upfield shift for the guests (Δ ≈ 0.1 ppm). Concerning the doubly reduced complexes, very clear trends of upfield shifting are observed, differentiating the hosts from the guests. In the dianions, the hosts are upfield shifted by ∼3.1 ppm ranging from 3.9 ppm to 4.8 ppm, very close to the free [n]CPP²⁻ (n = 10–13) counterparts. The aromaticity of the hosts is manifested in the chemical shifts of the guests which are upfield shifted as they are experiencing strong shielding from the host. Indeed, the guests of the dianions are strongly shifted by ∼8.5 ppm taking negative values, ranging from −3.3 ppm to −1.4 ppm.

Conclusions

In summary, the doubly reduced double-walled cycloparaphenylene complexes [n + 5]CPP⊃[n]CPP²⁻ (n = 5–8) have been investigated with DFT methods and compared to the neutral counterparts as well as with the free [n]CPPs focusing on structural, bonding, electron delocalization and magnetic properties, in order to account for their variation in charge delocalization, aromaticity and ¹H-NMR spectroscopy properties. According to structural deformations, bonding and local electron delocalization variations, the hosts of the dianions adopt the quinoidal configuration of the corresponding global aromatic free [n]CPP²⁻, suggesting that the extra electrons are delocalized on the outer nanohoop of the complex enabling a global aromatic character, while the guests preserve the benzenoid geometry of the neutral state.

Under the effect of an external magnetic field, the hosts induce a global long-ranged shielding cone, representing a global aromatic character, similar to the corresponding free dianions [n]CPP²⁻. Since the magnetic response of the complex is the cumulative effect of both the host and the guest, the NBO dissection of the complex response to host and guest contributions reveals the individual behavior of each nanohoop. Hence in the dianions the hosts retain the global long-ranged shielding cone of the free [n]CPPs²⁻ denoting an exclusive delocalization of the extra charge on the outer nanohoop, whereas the guests preserve the local shielding cones of each phenylene ring, denoting the persistence of local aromaticity of neutral free species. The distinctive magnetic behavior of doubly reduced complexes is rationalized by the modulated electronic configuration which forbids strong paratropic contributions from HOMO → LUMO excitations and allows excitations from lower orbitals to LUMO, with weaker contributions due to smaller overlaps. Thus, in host–guest “Russian doll” or “Planetary orbit” dianionic species, the global aromatic behavior is retained in the outer structural layer, suggesting that further electronic delocalization in multi-layered related species will be contained at the outer structural surface.

The aromaticity of the hosts is manifested in the ¹H-NMR chemical shifts of the guests experiencing a strong shielding, which are upfield shifted in the dianions by ∼8 ppm with respect to the free neutral counterparts. These predictions could be helpful for the experimental identification of doubly reduced nanohoop complexes with ¹H-NMR spectroscopy, extending our understanding of double-walled nanotubes at the nanoscale regime.

Finally, we introduce and propose to aromaticity researchers a new approach for the investigation of complex carbon aggregates by the dissection of the induced magnetic field to individual host and guest π-contributions using NBO analysis, which can be very accurately and effectively modelled employing the computationally lightweight pseudo-π method.

Our group is currently working on an investigation of the properties and aromaticity of open-shell nanohoops and their complexes.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

A. M.-C. is thankful for the financial support of FONDECYT/ANID Grant 1221676. R. L. and N. D. C. acknowledge that some results presented in this work were produced using the AUTH Compute Infrastructure and Resources. N. D. C. acknowledges Prof. Michael Sigalas for the fruitful discussions.

References

1. E. J. Leonhardt and R. Jasti, Emerging applications of carbon nanohoops, Nat. Rev. Chem., 2019, 3, 672–686.
2. D. Lu, Q. Huang, S. Wang, J. Wang, P. Huang and P. Du, The Supramolecular Chemistry of Cycloparaphenylenes and Their Analogs, Front. Chem., 2019, 7, 668.
3. Y. Xu and M. von Delius, The Supramolecular Chemistry of Strained Carbon Nanohoops, Angew. Chem., Int. Ed., 2020, 59, 559–573.
4. E. R. Darzi and R. Jasti, The dynamic, size-dependent properties of [5]–[12]cycloparaphenylenes, Chem. Soc. Rev., 2015, 44, 6401–6410.
5. Á. J. Pérez-Jiménez and J. C. Sancho-García, Theoretical Insights for Materials Properties of Cyclic Organic Nanorings, Adv. Theory Simul., 2020, 3, 2000110.
6. S. E. Lewis, Cycloparaphenylenes and related nanohoops, Chem. Soc. Rev., 2015, 44, 2221–2304.
7. M. R. Golder and R. Jasti, Syntheses of the Smallest Carbon Nanohoops and the Emergence of Unique Physical Phenomena, Acc. Chem. Res., 2015, 48, 557–566.
8. S. Eder, D. Yoo, W. Nogala, M. Pletzer, A. Santana Bonilla, A. J. P. White, K. E. Jelfs, M. Heeney, J. W. Choi and F. Glöcklhofer, Switching between Local and Global Aromaticity in a Conjugated Macrocycle for High-Performance Organic Sodium-Ion Battery Anodes, Angew. Chem., 2020, 132, 13058–13064.
9. D. Wu, W. Cheng, X. Ban and J. Xia, Cycloparaphenylenes (CPPs): An Overview of Synthesis, Properties, and Potential Applications, Asian J. Org. Chem., 2018, 7, 2161–2181.
10. T. J. Sisto, L. N. Zakharov, B. M. White and R. Jasti, Towards pi-extended cycloparaphenylenes as seeds for CNT growth: investigating strain relieving ring-openings and rearrangements, Chem. Sci., 2016, 7, 3681–3688.
11. H. Omachi, S. Matsuura, Y. Segawa and K. Itami, A modular and size-selective synthesis of [n]cycloparaphenylenes: A step toward the selective synthesis of [n,n] single-walled carbon nanotubes, Angew. Chem., Int. Ed., 2010, 49, 10202–10205.
12. Y. Segawa, A. Yagi, K. Matsui and K. Itami, Design and Synthesis of Carbon Nanotube Segments, Angew. Chem., Int. Ed., 2016, 55, 5136–5158.
13. H. Omachi, Y. Segawa and K. Itami, Synthesis of cycloparaphenylenes and related carbon nanorings: a step toward the controlled synthesis of carbon nanotubes, Acc. Chem. Res., 2012, 45, 1378–1389.
14. R. Jasti, J. Bhattacharjee, J. B. Neaton and C. R. Bertozzi, Synthesis, Characterization, and Theory of [9]-, [12]-, and [18]Cycloparaphenylene: Carbon Nanohoop Structures, J. Am. Chem. Soc., 2008, 130, 17646–17647.
15. E. S. Hirst and R. Jasti, Bending Benzene: Syntheses of [n]Cycloparaphenylenes, J. Org. Chem., 2012, 77, 42.
16. J. Xia, J. W. Bacon and R. Jasti, Gram-scale synthesis and crystal structures of [8]- and [10]CPP, and the solid-state structure of C60@[10]CPP, Chem. Sci., 2012, 3, 3018–3021.
17. T. C. Lovell, C. E. Colwell, L. N. Zakharov and R. Jasti, Symmetry breaking and the turn-on fluorescence of small, highly strained carbon nanohoops, Chem. Sci., 2019, 10, 3786–3790.
18. H. Takaba, H. Omachi, Y. Yamamoto, J. Bouffard and K. Itami, Selective Synthesis of [12]Cycloparaphenylene, Angew. Chem., Int. Ed., 2009, 48, 6112–6116.
19. Y. Segawa, S. Miyamoto, H. Omachi, S. Matsuura, P. Šenel, T. Sasamori, N. Tokitoh and K. Itami, Concise synthesis and crystal structure of [12]cycloparaphenylene, Angew. Chem., Int. Ed., 2011, 50, 3244–3248.
20. E. Kayahara, L. Sun, H. Onishi, K. Suzuki, T. Fukushima, A. Sawada, H. Kaji and S. Yamago, Gram-Scale Syntheses and Conductivities of [10]Cycloparaphenylene and Its Tetraalkoxy Derivatives, J. Am. Chem. Soc., 2017, 139, 18480–18483.
21. T. Iwamoto, Y. Watanabe, Y. Sakamoto, T. Suzuki and S. Yamago, Selective and Random Syntheses of [n]Cycloparaphenylenes (n = 8–13) and Size Dependence of Their Electronic Properties, J. Am. Chem. Soc., 2011, 133, 8354–8361.
22. E. Kayahara, V. K. Patel and S. Yamago, Synthesis and Characterization of [5]Cycloparaphenylene, J. Am. Chem. Soc., 2014, 136, 2284–2287.
23. S. Yamago, Y. Watanabe and T. Iwamoto, Synthesis of [8]cycloparaphenylene from a square-shaped tetranuclear platinum complex, Angew. Chem., Int. Ed., 2010, 49, 757–759.
24. W. Zhang, A. Abdulkarim, F. E. Golling, H. J. Räder and K. Müllen, Cycloparaphenylenes and Their Catenanes: Complex Macrocycles Unveiled by Ion Mobility Mass Spectrometry, Angew. Chem., Int. Ed., 2017, 56, 2645–2648.
25. Z.-L. Qiu, D. Chen, Z. Deng, K.-S. Chu, Y.-Z. Tan and J. Zhu, Isolation of a carbon nanohoop with Möbius topology, Sci. China: Chem., 2021, 64, 1004–1008.
26. T. Iwamoto, Y. Watanabe, T. Sadahiro, T. Haino and S. Yamago, Size-Selective Encapsulation of C60 by [10]Cycloparaphenylene: Formation of the Shortest Fullerene-Peapod, Angew. Chem., Int. Ed., 2011, 50, 8342–8344.
27. H. Ueno, T. Nishihara, Y. Segawa and K. Itami, Cycloparaphenylene-Based Ionic Donor–Acceptor Supramolecule: Isolation and Characterization of Li + @C60⊂[10]CPP, Angew. Chem., Int. Ed., 2015, 54, 3707–3711.
28. O. A. Stasyuk, A. J. Stasyuk, M. Solà and A. A. Voityuk, Photoinduced electron transfer in host–guest complexes of double nanohoops, J. Nanostruct. Chem., 2022, 1–14.
29. T. Iwamoto, Y. Watanabe, H. Takaya, T. Haino, N. Yasuda and S. Yamago, Size- and Orientation-Selective Encapsulation of C70 by Cycloparaphenylenes, Chem. – Eur. J., 2013, 19, 14061–14068.
30. T. Iwamoto, Z. Slanina, N. Mizorogi, J. Guo, T. Akasaka, S. Nagase, H. Takaya, N. Yasuda, T. Kato and S. Yamago, Partial Charge Transfer in the Shortest Possible Metallofullerene Peapod, La@C82 ⊂ [11]Cycloparaphenylene, Chem. – Eur. J., 2014, 20, 14403–14409.
31. K. Ikemoto, K. Takahashi, T. Ozawa and H. Isobe, Akaike's Information Criterion for Stoichiometry Inference of Supramolecular Complexes, Angew. Chem., Int. Ed., 2023, 62, e202219059.
32. T. Matsuno, S. Terasaki, K. Kogashi, R. Katsuno and H. Isobe, A hybrid molecular peapod of sp2- and sp3-nanocarbons enabling ultrafast terahertz rotations, Nat. Commun., 2021, 12, 5062.
33. T. Matsuno, S. Kamata, S. Sato, A. Yokoyama, P. Sarkar and H. Isobe, Assembly, Thermodynamics, and Structure of a Two-Wheeled Composite of a Dumbbell-Shaped Molecule and Cylindrical Molecules with Different Edges, Angew. Chem., 2017, 129, 15216–15220.
34. H. Kwon and C. J. Bruns, All-hydrocarbon, all-conjugated cycloparaphenylene-polycyclic aromatic hydrocarbon host-guest complexes stabilized by CH−π interactions, Nano Res., 2022, 15, 5545–5555.
35. T. Matsuno, M. Fujita, K. Fukunaga, S. Sato and H. Isobe, Concyclic CH-π arrays for single-axis rotations of a bowl in a tube, Nat. Commun., 2018, 9, 3779.
36. T. Matsuno, K. Takahashi, K. Ikemoto and H. Isobe, Activation of Positive Cooperativity by Size-Mismatch Assembly via Inclination of Guests in a Single-Site Receptor, Chem. - Asian J., 2022, 17, e202200076.
37. S. Hashimoto, T. Iwamoto, D. Kurachi, E. Kayahara and S. Yamago, Shortest Double-Walled Carbon Nanotubes Composed of Cycloparaphenylenes, ChemPlusChem, 2017, 82, 1015–1020.
38. C. Zhao, F. Liu, L. Feng, M. Nie, Y. Lu, J. Zhang, C. Wang and T. Wang, Construction of a double-walled carbon nanoring, Nanoscale, 2021, 13, 4880–4886.
39. S. Fomine, M. G. Zolotukhin and P. Guadarrama, “Russian doll” complexes of [n]cycloparaphenylenes: a theoretical study, J. Mol. Model., 2012, 18, 4025–4032.
40. S. M. Bachrach and Z.-C. Zayat, “Planetary Orbit” Systems Composed of Cycloparaphenylenes, J. Org. Chem., 2016, 81, 4559–4565.
41. M. Solà, Forty years of Clar's aromatic π-sextet rule, Front. Chem., 2013, 1, 1.
42. S. Taubert, D. Sundholm and F. Pichierri, Magnetically induced currents in [n]Cycloparaphenylenes, n = 6-11, J. Org. Chem., 2010, 75, 5867–5874.
43. Y. Kuroda, Y. Sakamoto, T. Suzuki, E. Kayahara and S. Yamago, Tetracyclo(2,7-carbazole)s: Diatropicity and Paratropicity of Inner Regions of Nanohoops, J. Org. Chem., 2016, 81, 3356–3363.
44. A. Muñoz-Castro, Local and global aromaticity in a molecular carbon nanobelt: insights from magnetic response properties in neutral and charged species, Phys. Chem. Chem. Phys., 2018, 20, 3433–3437.
45. R. Lingas, N. D. Charistos and A. Muñoz-Castro, Aromaticity of ortho and meta 8-Cycloparaphenylene and Their Dications: Induced Magnetic Field Analysis with Localized and Delocalized Orbitals in Strained Nanohoops, ChemPhysChem, 2021, 22, 741–751.
46. D. Macleod-Carey and A. Muñoz-Castro, Enabling dual aromaticity in fused nanobelts: evaluation of the magnetic behavior of fused [10]CPP units, Phys. Chem. Chem. Phys., 2022, 24, 26701–26707.
47. E. Kayahara, T. Kouyama, T. Kato and S. Yamago, Synthesis and Characterization of [n]CPP (n = 5, 6, 8, 10, and 12) Radical Cation and Dications: Size-Dependent Absorption, Spin, and Charge Delocalization, J. Am. Chem. Soc., 2016, 138, 338–344.
48. N. Toriumi, A. Muranaka, E. Kayahara, S. Yamago and M. Uchiyama, In-Plane Aromaticity in Cycloparaphenylene Dications: A Magnetic Circular Dichroism and Theoretical Study, J. Am. Chem. Soc., 2015, 137, 82–85.
49. Y. Masumoto, N. Toriumi, A. Muranaka, E. Kayahara, S. Yamago and M. Uchiyama, Near-Infrared Fluorescence from In-Plane-Aromatic Cycloparaphenylene Dications, J. Phys. Chem. A, 2018, 122, 5162–5167.
50. E. Kayahara, T. Kouyama, T. Kato, H. Takaya, N. Yasuda and S. Yamago, Isolation and characterization of the cycloparaphenylene radical cation and dication, Angew. Chem., Int. Ed., 2013, 52, 13722–13726.
51. Z. Zhou, Z. Wei, T. A. Schaub, R. Jasti and M. A. Petrukhina, Structural deformation and host–guest properties of doubly-reduced cycloparaphenylenes, [n]CPPs2− (n = 6, 8, 10, and 12), Chem. Sci., 2020, 11, 9395–9401.
52. S. N. Spisak, Z. Wei, E. Darzi, R. Jasti and M. A. Petrukhina, Highly strained [6]cycloparaphenylene: crystallization of an unsolvated polymorph and the first mono- and dianions, Chem. Commun., 2018, 54, 7818–7821.
53. A. v Zabula, A. S. Filatov, J. Xia, R. Jasti and M. A. Petrukhina, Tightening of the Nanobelt upon Multielectron Reduction, Angew. Chem., Int. Ed., 2013, 52, 5033–5036.
54. R. Islas, T. Heine and G. Merino, The Induced Magnetic Field, Acc. Chem. Res., 2012, 45, 215–228.
55. G. Merino, T. Heine and G. Seifert, The Induced Magnetic Field in Cyclic Molecules, Chem. – Eur. J., 2004, 10, 4367–4371.
56. N. D. Charistos, A. G. Papadopoulos and M. P. Sigalas, Interpretation of electron delocalization in benzene, cyclobutadiene, and borazine based on visualization of individual molecular orbital contributions to the induced magnetic field., J. Phys. Chem. A, 2014, 118, 1113–1122.
57. N. D. Charistos, A. G. Papadopoulos, T. A. Nikopoulos, A. Muñoz-Castro and M. P. Sigalas, Canonical orbital contributions to the magnetic fields induced by global and local diatropic and paratropic ring currents, J. Comput. Chem., 2017, 38, 2594–2604.
58. A. G. Papadopoulos, N. D. Charistos and A. Muñoz-Castro, Magnetic Response of Aromatic Rings Under Rotation: Aromatic Shielding Cone of Benzene Upon Different Orientations of the Magnetic Field, ChemPhysChem, 2017, 18, 1499–1502.
59. N. Ozaki, H. Sakamoto, T. Nishihara, T. Fujimori, Y. Hijikata, R. Kimura, S. Irle and K. Itami, Electrically Activated Conductivity and White Light Emission of a Hydrocarbon Nanoring–Iodine Assembly, Angew. Chem., Int. Ed., 2017, 56, 11196–11202.
60. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, 2016.
61. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465.
62. Á. Vázquez-Mayagoitia, C. D. Sherrill, E. Aprà and B. G. Sumpter, An assessment of density functional methods for potential energy curves of nonbonded interactions: The XYG3 and B97-D approximations, J. Chem. Theory Comput., 2010, 6, 727–734.
63. T. Yumura, R. Miki, S. Fukuura and W. Yamamoto, Energetics of Hybrid Structures between Cycloparaphenylene and Carbon Nanotubes: A Dispersion-Corrected Density Functional Theory Study, J. Phys. Chem. C, 2020, 124, 17836–17847.
64. I. González-Veloso, J. Rodríguez-Otero and E. M. Cabaleiro-Lago, Carbon-nanorings ([10]CPP and [6]CPPA) as fullerene (C60 and C70) receptors: a comprehensive dispersion-corrected DFT study, Phys. Chem. Chem. Phys., 2016, 18, 31670–31679.
65. D. Josa, J. Rodríguez-Otero, E. M. Cabaleiro-Lago and M. Rellán-Piñeiro, Analysis of the performance of DFT-D, M05-2X and M06-2X functionals for studying π–π interactions, Chem. Phys. Lett., 2013, 557, 170–175.
66. D. Josa, J. R. Otero and E. M. Cabaleiro Lago, A DFT study of substituent effects in corannulene dimers, Phys. Chem. Chem. Phys., 2011, 13, 21139.
67. J. da Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
68. H. Sun and J. Autschbach, Electronic Energy Gaps for π-Conjugated Oligomers and Polymers Calculated with Density Functional Theory, J. Chem. Theory Comput., 2014, 10, 1035–1047.
69. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967.
70. ADF2019, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com.
71. J. M. del Campo, J. L. Gázquez, S. B. Trickey and A. Vela, Non-empirical improvement of PBE and its hybrid PBE0 for general description of molecular properties, J. Chem. Phys., 2012, 136, 104108.
72. A. M. Sarotti and S. C. Pellegrinet, Application of the multi-standard methodology for calculating 1H NMR chemical shifts, J. Org. Chem., 2012, 77, 6059–6065.
73. G. Schreckenbach and T. Ziegler, Calculation of NMR Shielding Tensors Using Gauge-Including Atomic Orbitals and Modern Density Functional Theory, J. Phys. Chem., 1995, 99, 606–611.
74. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
75. J. A. Bohmann, F. Weinhold and T. C. Farrar, Natural chemical shielding analysis of nuclear magnetic resonance shielding tensors from gauge-including atomic orbital calculations, J. Chem. Phys., 1997, 107, 1173–1184.
76. E. D. Glendening, C. R. Landis and F. Weinhold, NBO 6.0: Natural bond orbital analysis program, J. Comput. Chem., 2013, 34, 1429–1437.
77. N. D. Charistos, A. Muñoz-Castro and M. P. Sigalas, The pseudo-π model of the induced magnetic field: fast and accurate visualization of shielding and deshielding cones in planar conjugated hydrocarbons and spherical fullerenes, Phys. Chem. Chem. Phys., 2019, 21, 6150–6159.
78. M. Orozco-Ic, M. Dimitrova, J. Barroso, D. Sundholm and G. Merino, Magnetically Induced Ring-Current Strengths of Planar and Nonplanar Molecules: New Insights from the Pseudo-π Model, J. Phys. Chem. A, 2021, 125, 5753–5764.
79. P. W. Fowler and E. Steiner, Pseudo-π currents: rapid and accurate visualisation of ring currents in conjugated hydrocarbons, Chem. Phys. Lett., 2002, 364, 259–266.
80. W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38.
81. R. Lingas and N. Charistos, PyMAF, Laboratory of Quantum and Computational Chemistry, Aristotle University of Thessaloniki, 2023.
82. I. Mayer, Charge, bond order and valence in the AB initio SCF theory, Chem. Phys. Lett., 1983, 97, 270–274.
83. A. J. Bridgeman, G. Cavigliasso, L. R. Ireland and J. Rothery, The Mayer bond order as a tool in inorganic chemistry, J. Chem. Soc., Dalton Trans., 2001, 2095–2108.
84. P. Bultinck, R. Ponec and S. Van Damme, Multicenter bond indices as a new measure of aromaticity in polycyclic aromatic hydrocarbons, J. Phys. Org. Chem., 2005, 18, 706–718.
85. T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592.
86. P. Bultinck, M. Mandado and R. Mosquera, The pseudo-π method examined for the computation of multicenter aromaticity indices, J. Math. Chem., 2008, 43, 111–118.
87. N. Ramos-Berdullas, S. Radenković, P. Bultinck and M. Mandado, Aromaticity of Closed-Shell Charged Polybenzenoid Hydrocarbons, J. Phys. Chem. A, 2013, 117, 4679–4687.
88. I. Mayer and P. Salvador, Overlap populations, bond orders and valences for ‘fuzzy’ atoms, Chem. Phys. Lett., 2004, 383, 368–375.
89. R. Ayub, O. El Bakouri, J. R. Smith, K. Jorner and H. Ottosson, Triplet State Baird Aromaticity in Macrocycles: Scope, Limitations, and Complications, J. Phys. Chem. A, 2021, 125, 570–584.
90. G. Acke, S. Van Damme, R. W. A. Havenith and P. Bultinck, Interpreting the behavior of the NICSzz by resolving in orbitals, sign, and positions, J. Comput. Chem., 2018, 39, 511–519.
91. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. R. Schleyer, Nucleus-independent chemical shifts (NICS) as an aromaticity criterion, Chem. Rev., 2005, 105, 3842–3888.
92. E. Kleinpeter, S. Klod and A. Koch, Visualization of through space NMR shieldings of aromatic and anti-aromatic molecules and a simple means to compare and estimate aromaticity, THEOCHEM, 2007, 811, 45–60.
93. M. Orozco-Ic, N. D. Charistos, A. Muñoz-Castro, R. Islas, D. Sundholm and G. Merino, Core-electron contributions to the molecular magnetic response, Phys. Chem. Chem. Phys., 2022, 24, 12158–12166.
94. C. M. Widdifield and R. W. Schurko, Understanding chemical shielding tensors using group theory, MO analysis, and modern density-functional theory, Concepts Magn. Reson., Part A, 2009, 34A, 91–123.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp01994b

---