Photodissociation dynamics of tetrahydrofuran at 193 nm

Abstract

Tetrahydrofuran (THF), a cyclic ether with the chemical formula C₄H₈O, can be considered the simplest analog of the deoxyribose backbone component of deoxyribonucleic acid (DNA). As such, it provides a useful model for probing the photochemistry of such biomolecular motifs. We present a velocity-map imaging study into the ultraviolet dissociation of THF at a wavelength of 193 nm. Excitation to the S₁ state occurs via a 3s ← n transition involving a lone-pair electron on the oxygen atom, and has been shown by other authors to result in rapid ring opening via cleavage of one of the C–O bonds to form a ring-opened C₄H₈O diradical, followed by C–C bond cleavage over a longer timescale to form either OCH₂ + C₃H₆ products (Channel 1a), HOCH₂ + C₂H₅ products (Channel 1b), or OCH₂CH₂ + C₂H₄ products (Channel 2). The C₂H₄O products formed via Channel 2 are unstable on the timescale of our experiment and dissociate further to form CH₃ and CHO. We also observe a number of minor products resulting from H or H₂ loss from the primary photofragments. The speed distributions observed for all photofragments are broad, indicating excitation of a range of rotational and vibrational states of the products. The angular distributions of the photofragments show an interesting speed dependence: the slowest products have almost isotropic angular distributions, but the magnitude of the recoil anisotropy increases monotonically with photofragment speed. The fastest products exhibit highly anisotropic angular distributions, with the recoil anisotropy parameter β approaching its limiting value of −1 (−0.75 for Channel 1 and −0.5 for Channel 2). This behaviour is attributed to the range of timescales over which the diradical intermediate dissociates into the observed photofragments. Rapid dissociation leads to fast photofragments which retain the correlation between the transition dipole moment for the S₁ ← S₀ excitation (which lies perpendicular to the ring) and the photofragment velocities (which lie predominantly in the plane of the ring). Slow dissociation results in a high degree of energy redistribution into internal modes, slower photofragments, and loss of correlation between the photofragment velocities and the transition dipole. The higher barrier associated with dissociation via Channel 2 suggests somewhat longer lifetimes for the diradical intermediate and is consistent with a corresponding reduction in the maximum observed value for β.

---

1. Introduction

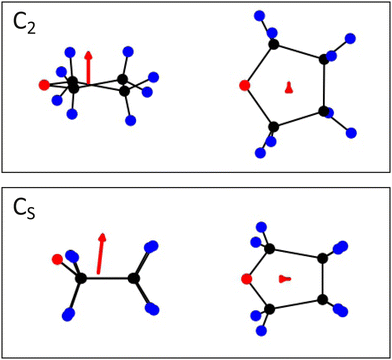
Extensive exposure of the human body to ultraviolet (UV) radiation can lead to damage of deoxyribonucleic acid (DNA), causing diseases such as skin cancer.^1–3 Probing the effect of radiation on the molecular structure of DNA is therefore of fundamental interest. Tetrahydrofuran (c-C₄H₈O), henceforth referred to as THF, is a cyclic either, which has been considered previously as a model compound for the DNA backbone constituent ribose.^4–10 THF also plays a vital role in polymerisation reactions^11,12 and is used as a polar solvent for organic synthesis. As a prototypical oxygen-containing heterocycle, investigations into the photostability and photofragmentation behaviour of THF are also of more general interest, and the molecule has previously been the subject of studies involving excitation at a variety of different wavelengths.^13,14

Several authors have reported gas-phase absorption spectra of THF.^15–18 The lowest energy (S₁ ← S₀) absorption band lies between 180 and 200 nm, and has been assigned to a 3s ← n transition involving one of the oxygen lone-pair electrons. The transition has been shown to form part of an s-type Rydberg series converging to the ground state of the ion at 9.41 eV.¹⁷ Giuliani and co-workers¹⁹ have probed the absorption spectrum in this region at high resolution, revealing separate but overlapping contributions to the band from the two near-degenerate ground-state conformers of THF, which have C₂ and C_S symmetry, respectively (see Fig. 5 for geometry-optimised structures of the two conformers). While the global energy minimum of ground-state THF is generally considered to correspond to the C_S conformer,^20–24 interconversion between the two near-degenerate conformers is almost barrierless via pseudorotation through a C₁ conformation.^23,25–27

When excited at the shorter wavelength of 160 nm, Röder et al.²⁸ assigned a 3d ← n transition followed by a 3d → 3p → 3s Rydberg cascade. The authors reported cuts through excited-state potential energy surfaces (PESs) of THF along the C–O, C_α–H, and C_α–C_β stretch coordinates. The S₁ state of THF is bound along both the C_α–H, and C_α–C_β coordinates. However, along the C–O stretching coordinate, the S₁ state is repulsive and changes its electronic character from Rydberg (3s) in the Franck–Condon region to valence (nπ*) at larger C–O separations, leading eventually to a conical intersection with the S₀ ground state along the ring-opening coordinate. In addition to direct dissociation on S₁, the conical intersection provides a non-adiabatic pathway for populating excited vibrational levels of the electronic ground state, from which fragmentation can also occur. A similar picture of S₁ ← S₀ excitation, C–O bond elongation, and internal conversion to the ground-state followed by fragmentation has also been observed in oxetane²⁹ and oxirane.³⁰ Asymmetric ring expansion leading to coupling of excited-state and ground-state surfaces has also been explored in other systems such as furan,^31,32 thiophene,^33,34 and tetrahydrothiophene.³⁵

The ring opening described above implies that THF dissociates in a stepwise manner following photoexcitation to the S₁ state. Fig. 1 summarises the main observed fragmentation pathways in THF following excitation at 193 nm. Ring opening forms the linear diradical C₄H₈O, which then dissociates along either the C_α–C_β (‘Channel 1a’) or the C_β–C_γ (‘Channel 2’) bond coordinate, leading to the product pairs C₃H₆ + OCH₂ and C₂H₄ + OCH₂CH₂, respectively.³⁶ It is interesting to note that Kramer³⁷ observed these same two channels by inducing decomposition of THF on the S₀ surface via infrared multiphoton dissociation. The C₃H₆ product of the first channel has the stable isomers propylene and cyclopropane. However, the diradical C₂H₄O product of the first channel, formed initially as the O–CH₂–CH₂ isomer, rapidly rearranges via a hydrogen-atom transfer to internally excited (CH₃–CHO)*, which decomposes into HCO and CH₃ on the sub-nanosecond timescale³⁸ in the absence of collisions to stabilise the excited intermediate. An intramolecular H atom migration can accompany the C_α–C_β cleavage (Channel 1b), leading to the products HO–CH₂ + CH₂CHCH₂.

Fig. 1 Reaction scheme for THF following 193 nm excitation. Absorption of a 193 nm photon leads to rapid cleavage of one of the C–O bonds to form the ring-opened diradical OCH₂CH₂CH₂CH₂. The diradical dissociates over a longer timescale via cleavage of either the C_α–C_β or C_β–C_γ bond to form C₃H₆ + OCH₂ (Channel 1a) and C₂H₄ + OCH₂CH₂ (Channel 2) products, respectively. An internal H-atom migration can accompany the C_α–C_β cleavage (Channel 1b). Several of the primary dissociation products undergo isomerisation and/or further dissociation, e.g. by loss of H or H₂. Shown beneath each chemical species is the respective ionisation energy and mass-to-charge ratio.

Lee³⁹ investigated the photofragmentation of THF following photoexcitation via the S₁ ← S₀ transition at 193.3 nm, the same wavelength employed in the present study. Based on an analysis of the photofragment time-of-flight (ToF) distributions, Lee determined branching ratios and (total) translational kinetic energy releases (TKER) for five different fragmentation channels. The three dissociation channels with significant branching ratios were those described above, leading to C₂H₄ + HCO + CH₃, C₃H₆ + OCH₂, and C₃H₅ + HOCH₂. The photofragment angular distributions were all reported to be nearly isotropic, which is somewhat surprising given that the fragmentations are believed to occur on the femtosecond timescale.^13,28 Lee offered two possible explanations for the lack of angular anisotropy: (i) that the non-planar structure of THF causes the fragmentation products to recoil at angles near to the magic angle⁴⁰ of 54.7° to the transition dipole; or (ii) that internal rotations within the diradical intermediate result in the dissociation products recoiling over a wide range of angles.

In the following, we present an experimental study into the photodissociation of THF at 193 nm in which we employ multi-mass velocity-map imaging to characterise the scattering distributions of the photofragments. We also report calculated transition dipole moments for the S₁ ← S₀ transition originating from the two possible ground-state conformers, and consider the relationship between these transition dipole moments, the angular dependence of the observed product scattering distributions, and the lifetime of the intermediate diradical C₄H₈O.

2. Methods

2.1 Experimental methods

The velocity-map imaging time-of-flight (ToF) mass spectrometer used in this work has been described in detail elsewhere.⁴¹ Briefly, helium (BOC, 99.9%) at a pressure of 1 bar was bubbled through liquid tetrahydrofuran (Sigma-Aldrich, ≥99.9%). The resulting gas mixture underwent supersonic expansion through a pulsed Solenoid Valve (Parker Hannifin, Series 9, 10 Hz) before being collimated by a 1.5 mm diameter skimmer and entering the interaction region, where the UV photolysis beam and VUV probe beam intersected the molecular beam at right angles.

The 193.3 nm (from hereon referred to as 193 nm) UV photolysis beam was generated by a Neweks PSX-100 ArF excimer laser (7 ns, ∼1.5 mJ pulses). A Rochon polarizer was used to polarise the photolysis beam linearly along a polarisation axis parallel to the detector plane (perpendicular to the time-of-flight axis). The pulse energy of the photolysis light at the entrance to the vacuum chamber after passing through the polariser and beam steering optics was measured to be between 0.1 and 0.6 mJ, and the beam was focused down to a diameter of around 5–10 microns at the interaction region. The estimated fluence is therefore in the range ∼1 × 10⁵ to 3 × 10⁶ mJ cm⁻².

After a delay of 20 ns, the neutral photofragments were ionized by the 118.2 nm (10.49 eV) vacuum-ultraviolet (VUV) probe beam, generated by frequency tripling the third harmonic of a Nd:YAG laser (Continuum Surelite I) in a phase-matched mixture of 298 mbar Argon (BOC, 99.9%) and 27 mbar Xenon (BOC, 99.9%).^42–45 The probe laser beam was linearly polarized along the time-of-flight axis (perpendicular to the imaging plane) to ensure that all anisotropy observed in the measured photofragment angular distributions results from the photolysis step. However, preliminary experiments performed with the probe laser polarised either parallel or perpendicular to the imaging plane revealed no differences in the recorded images.

The ionised photoproducts were accelerated towards the detector by the electric field maintained within the velocity-map imaging ion lens, which projects the three-dimensional scattering distribution for each ion mass-to-charge (m/z) ratio into a two-dimensional image on the detector plane.^46,47 The detector, consisting of a pair of microchannel plates (MCPs) coupled to a P47 phosphor screen, generates an optical signal on the phosphor for each incident ion. A Pixel Imaging Mass Spectrometry (PImMS2) camera^48–50 records an (x,y,t)-data point for each incident ion. The full multi-mass imaging data set was acquired over 80 000 pump–probe cycles.

In addition to the two-colour pump–probe signals, one-laser signals (pump only and probe only) were recorded. In the raw data sets the signal from a single ion generally extends over several adjacent pixels and time bins, so to improve the spatial and temporal resolution as well as to reduce the size of the data set, the signal from each ion was centroided to a single (x,y,t) point before further analysis. The one-laser signals were then subtracted from the pump–probe signals in order to obtain the true pump–probe signal. The resulting data set can then be integrated over the (x,y) coordinates to yield the product time-of-flight spectrum, and velocity-map images can be generated for each photofragment by integrating over the relevant range of arrival times. The photofragment scattering distributions are cylindrically symmetric about the photolysis laser polarisation axis, allowing us to Abel invert the images for each fragment ion using a Python version of the Basex software package.⁵¹ From the inverted images, we extracted radial and angular distributions and converted the radial distributions into kinetic energy distributions using a pixel-to-velocity calibration determined in previous measurements on the 355 nm photolysis of Cl₂.

2.2 Computational methods

The geometries of the C₂ and C_S ground-state conformers of THF were optimised in a B3LYP/aug-cc-pVQZ calculation using the Gaussian 09 software package.⁵² Transition dipole moments for the 3s ← n transition to the S₁ state were calculated for each conformer using EOM-CCSD/aug-cc-pVTZ.

3. Results

3.1 Time-of flight spectrum

Fig. 2 shows the mass-calibrated two-colour pump–probe ToF spectrum of THF and its photofragments following excitation at 193 nm and probe laser irradiation at 118 nm. The one-laser contributions have been subtracted from the two-colour signal, which leads to a negative peak in the ToF spectrum for the parent ion. This arises due to the depletion of neutral THF through dissociation by the pump laser, with the result that fewer intact molecules are available to be ionised by the probe laser in the pump–probe experiments than in the probe-only experiments. Note that because the parent ion velocites are essentially those of the neutral molecules in the molecular beam, the parent ions all arrive in a small spot at the centre of the detector (rather than being spread across the detector as in the case of fragment ions with non-zero kinetic energies) and often saturate the signal response of the microchannel plate to some extent. We therefore do not expect to observe a quantitative match between the intensity of this negative peak and the summed intensity of the fragment peaks.

Fig. 2 Background-subtracted time-of-flight mass spectrum for the 193 nm photolysis products of THF.

Based on the 10.49 eV photon energy of our probe laser and the ionisation energies given for the various molecular fragments in Fig. 1, we might expect to observe the following species from each of the three main dissociation channels:

1. Channel 1a: propene (m/z 42), cyclopropane (m/z 42), CH₂CHCH₂ (m/z 41), and CH₂CCH₂/CH₃CCH (m/z 40);

2. Channel 1b: HO–CH₂ (m/z 31) and CH₂CHCH₂ (m/z 41);

3. Channel 2: CH₃ (m/z 15), HCO(m/z 29), possibly CH₂CH₂ (m/z 28),and CHCH₂ (m/z 27).

Inspecting the time-of-flight spectrum in Fig. 2, we indeed see peaks at all of the predicted m/z values, indicating that we observe the same three major dissociation channels as reported by previous authors^37,39 and discussed in the Introduction. We do not see evidence in the ToF spectrum for cleavage of both C–O bonds as reported by SenGupta and co-workers,⁵³ although we note that the atomic oxygen formed in such a process would not be ionised by our probe laser and would therefore not be detected in our experiment.

3.2 Product speed and angular distributions

Our multi-mass velocity-map imaging detection system enables us to record scattering distributions for all of the reaction products appearing in the ToF spectrum. The measured velocity-map images are shown in Fig. 3. As explained in Section 2, Abel inversion of the images allows the speed and angular distributions to be determined for each fragment.

Fig. 3 Symmetrised velocity-map images for the observed photodissociation products of THF. The direction of linear polarisation of the 193 nm photolysis laser is indicated by the double-headed arrow in the first panel.

Inspection of the reaction scheme in Fig. 1 allows us to determine how the measured scattering distributions can best be used to probe the dynamics of the three dissociation channels. The most straightforward channel from this point of view is Channel 1b, which forms two momentum-matched products, HO–CH₂ and CH₂CHCH₂, neither of which undergo any further fragmentation or rearrangement. The HO–CH₂ product is uniquely assigned to m/z 31, and we can therefore use the corresponding image to determine the speed and angular distributions for the products of this channel. These are shown in Fig. 4(b).

Fig. 4 Speed distributions, P(v), and recoil anisotropy distributions, β(v), for the dissociation products of (a) Channel 1a, (b) Channel 1b, and (c) Channel 2. Speed and recoil anisotropy distributions are for the primary products indicated in red text, determined as explained in the text. The kinetic energy distributions determined in the present work are compared with the equivalent result from Lee,³⁹ and the maximum accessible kinetic energy is indicated by a dashed line.

The CH₂CHCH₂ product, appearing at m/z 41 in the ToF spectrum, is not unique to Channel 1b, since it is also formed as a secondary H-atom loss product in Channel 1a. The m/z 41 signal therefore contains contributions from both of these pathways.† However, as noted above, the component arising from Channel 1b is momentum matched with the HO–CH₂ product, allowing the components arising from the two channels to be disentangled: after appropriate correction for the branching ratios and ionisation efficiencies using data from Lee,³⁹ the momentum-matched distribution arising from Channel 1b can simply be subtracted from the total signal to leave the component arising from Channel 1a.

Moving now to Channel 1a, the O–CH₂ product is unique to this channel and its scattering distribution would provide all of the required information on the dynamics of this channel. Unfortunately, this scattering distribution is not available to us, since the ionisation energy of O–CH₂ lies above the 10.49 eV photon energy of our ionisation laser. Instead, we must consider the CH₂CH₂CH₂ product. The initially formed linear CH₂CH₂CH₂ primary product of C_α–C_β bond cleavage is unstable, rearranging on the femtosecond timescale^54,55 to either propene or cyclopropane.³⁷ The propene product of this rearrangement can undergo H₂ elimination to form CH₂CCH₂/CH₃CCH or loss of a single H atom to produce CH₂CHCH₂. The scattering distribution of the primary CH₂CH₂CH₂ product is unchanged by unimolecular rearrangement to propene or cyclopropane, so we do not lose any information in the isomerisation step. Additionally, the fact that linear momentum must be conserved during H or H₂ loss from propene, coupled with the much lighter mass of H/H₂ relative to the partner fragment, means that any kinetic energy released in the secondary dissociation step will almost all be carried away by the H or H₂ product, leaving the velocity distributions of the partner fragments unchanged to a very good approximation. As a result, summing the velocity distributions recorded for the m/z 40, 41, and 42 products of Channel 1a (noting that for the m/z 41 fragment we use the Channel 1a component described earlier), yields a very good approximation to the velocity distribution of the nascent primary CH₂CH₂CH₂ product. The speed and angular distributions determined using this approach are shown in Fig. 4(a).

Finally, we consider Channel 2. As noted earlier, the OCH₂CH₂ product (m/z 44) of this channel is known from previous work³⁸ to dissociate rapidly into CH₃ + HCO under the collision-free conditions of our experiment, consistent with the fact that we see virtually no signal at m/z 44. We therefore cannot use this product to learn about the primary dissociation step. Some of the partner fragment, CH₂CH₂, also dissociates further via H atom loss to give H + CHCH₂. However, as noted above, the recoil momentum imparted to the CHCH₂ product by the departing H atom is very small, and is expected to have an almost negligible effect on its velocity distribution. We can therefore sum the velocity distributions for the CH₂CH₂ and CHCH₂ products to give a good approximation to the velocity distribution of the nascent primary CH₂CH₂ product‡ The resulting speed and angular distributions associated with Channel 2 are shown in Fig. 4(c).

3.2.1 Channel 1a: THF → OCH₂ + C₃H₆. The velocity distribution for the products of Channel 1a (see Fig. 4(a) appear relatively broad, indicating that significant energy is released into translation and that a broad range of internal (rotational and vibrational) states are populated in the products. The recoil anisotropy parameter β(v) is close to zero for slow products with the highest degree of internal excitation, and decreases to a value of around −0.75 as the recoil velocity increases.

Previous time-of-flight measurements carried out by Lee³⁹ as a function of photolysis laser polarisation suggested that the average β parameter is close to zero, so our results do not agree with the conclusions drawn from these earlier measurements. The β(v) distributions measured in the present experiments lead to only a small asymmetry in the images. However, we have checked carefully that this anisotropy is real and is not caused by any artefacts of the experiment or the data processing. For example, we have made measurements on the same instrument of scattering distributions which by symmetry must be isotropic, and confirmed that they give rise to β values of zero across the full range of product velocities, as well as checking that we obtain β parameters in line with literature reports for processes such as the 355 nm photolysis of Cl₂. Having carried out these checks, and given that we are using VMI detection and can therefore clearly resolve β as a function of product recoil velocity, we believe our values are accurate, and that the discrepancy arises from the different velocity resolution achievable in our velocity-map imaging measurements and Lee's time-of-flight measurements. If we project our images along the x and y axes, equivalent to Lee's measurements with the photolysis laser linearly polarised parallel and perpendicular to the time-of-flight axis, there is a small but clear difference in the widths of the resulting distributions. The velocity-dependent anisotropy we measure is therefore easily resolved within the spatial resolution of our velocity-map images, but would be very difficult to resolve with the typical temporal resolution achievable in a time-of-flight measurement. This is consistent with the fact that while our β(v) distribution does not agree with that reported by Lee, our translational kinetic energy distribution for the products of Channel 1a is in excellent agreement.

Fig. 5 shows geometry-optimised structures for the C₂ and C_S conformers of ground-state THF, which we expect to be present at similar number densities within our molecular beam, together with the transition dipole moments (red arrows) associated with the S₁ ← S₀ transition in each conformer. For both conformers the transition dipole moment lies perpendicular to the plane of the ring. In the axial recoil limit, both the ring-opening step and the subsequent C–C bond cleavage occur in the molecular plane. We therefore expect the products to recoil in this same plane, perpendicular to the transition dipole moment, giving rise to a β parameter close to its limiting value of −1.

Fig. 5 Optimised structures and S₁ ← S₀ transition dipoles (red arrows) for the C₂ (top) and C_S (bottom) conformers of THF. For visualisation purposes the transition dipole moments have been elongated by factors of five and four for the C₂ and C_S conformers, respectively.

While the highest velocity products do have β parameters close to −1, we observe a strong dependence of β on the product recoil velocity. The slowest products have near-zero values, which decrease monotonically to a near-limiting value at the highest velocities. We ascribe this behaviour to the finite lifetime of the C₄H₈O diradical formed in the initial ring-opening step and to the distribution of internal energies with which the diradical is formed, noting from the discussion in Section 1 that dissociation can occur either directly on S₁ or following internal conversion to S₀. Following photoexcitation, the repulsive character of the S₁ surface leads to rapid C–O bond cleavage to form the diradical. When the ring-opened diradical dissociates on a timescale that is short relative to intramolecular vibrational relaxation and rotation, most of the available energy will be released into product translation. In this case the product recoil velocity is high and β approaches its limiting value determined by the perpendicular orientation of the transition dipole moment relative to the molecular plane, as described above. As the lifetime of the diradical increases, perhaps following internal conversion to S₁, the molecule has more time to undergo rotation and for energy to be redistributed into internal modes. This leads to a decrease both in the photofragment velocities and in the correlation between the transition dipole moment and the ejection direction of the photoproducts, explaining the reduction in β for slower fragments. The TKER distribution is consistent with this picture. The distribution peaks at low kinetic energies, indicating that a significant portion of the excess energy is partitioned into internal degrees of freedom in the photofragments. Taken together with the behaviour of β(v) described above, this is consistent wtih dissociation of the diradical over a relatively broad range of timescales.

3.2.2 Channel 1b: THF → HOCH₂ + CH₂CHCH₂. Formation of HOCH₂ + C₃H₅ products requires H-atom transfer to the oxygen atom, in addition to C–O and C–C bond cleavage. According to Lee,³⁹ this subchannel generally exhibits lower TKER when compared with the pathway forming C₃H₆ + H₂CO. This is entirely consistent with our own observations; the kinetic energy release distribution obtained from our velocity-map images is in excellent agreement with that reported by Lee, and peaks at significantly lower energies than that measured for Channel 1a. A plausible explanation for this behaviour is that internal H atom migration requires the C₄H₈O species to distort its geometry such that hydrogen and oxygen atoms are near each other, which becomes more likely at long C₄H₈O lifetimes following redistribution of energy into internal modes. The β(v) distribution shows almost identical behaviour to that measured for Channel 1a, with slow products exhibiting isotropic scattering and the fastest products having β values of around −0.75.

3.3 Channel 2: THF → OCH₂CH₂ + CH₂CH₂

The photofragment speed distribution for the products of Channel 2 is very similar to that observed earlier for the products of Channels 1a and 1b, comprising a broadly-peaked distribution extending out to maximum speeds of around 3000 m s⁻¹. As for the other channels, we can infer that the products are formed in a range of rotational and vibrational states. We also see similar behaviour for the velocity-dependence of the recoil anisotropy parameter β, which has values close to zero at low velocities (high internal excitation), but decreases monotonically to a value of around −0.5 at the highest velocities. We believe the explanation for this behaviour to be analogous to that for Channels 1a and 1b. Following the initial ring-opening step, dissociation of the diradical intermediates with the shortest lifetimes retains the highest degree of correlation between the transition dipole moment, which lies perpendicular to the plane of the ring, and the photofragment velocities, which lie in the plane of the ring. Dissociation on longer timescales degrades the correlation through rotational and vibrational motions prior to C–C bond cleavage, leading to a reduction in β for the slower products. The limiting value of β observed for Channel 2 of around −0.5 is significantly lower than the value of around −0.75 determined for Channels 1a and 1b. This perhaps implies a longer lifetime for C₄H₈O intermediates dissociating via Channel 2, which would be consistent with the higher barrier to dissociation for this channel reported by Scala et al.,¹³ and also with the lower branching ratio for Channel 2 relative to Channels 1a and 1b determined by Lee.³⁹ The velocity-averaged value for β of −0.23 is again in disagreement with the near-zero value determined by Lee.³⁹

The TKER distribution for the primary dissociation products of Channel 2 is again in excellent agreement with that reported by Lee.³⁹ The distribution peaks at around 0.15 eV and tails off by around 1 eV, intermediate between the behaviour for Channel 1a and Channel 1b, and well below the available energy of 2.30 eV. This is consistent with the lifetime arguments evoked above to explain the behaviour of β in the two channels. The longer lifetimes associated with dissociation via Channel 2 result in a greater degree of energy redistribution into internal modes, and therefore a smaller fraction of energy released into translation.

4. Conclusions

We have presented the results of a velocity-map imaging study into the 193 nm photodissociation of tetrahydrofuran. Excitation of THF at this wavelength leads to population of the S₁ state via an 3s ← n transition involving a lone-pair electron on the oxygen atom. The associated transition dipole lies perpendicular to the plane of the ring for both the C₂ and C_S conformers of THF. The S₁ state is repulsive along the C–O bond stretching coordinate, resulting in rapid bond scission to form a ring-opened diradical intermediate species. The diradical undergoes further dissociation over a broad range of timescales via cleavage of either the C_α–C_β bond to form OCH₂ + C₃H₆ or HOCH₂ + C₂H₅ products (denoted Channel 1a and Channel 1b, respectively) or cleavage of the C_β–C_γ bond to form OCH₂CH₂ + C₂H₄ (Channel 2). The C₃H₆ products of Channel 1a isomerise rapidly to cyclopropane and propene, the latter of which undergoes secondary decay via loss of H or H₂. The OCH₂CH₂ products of Channel 2 are also unstable on the timescale of our experiment, and dissociate to form CH₃ and CHO, while some of the CH₂CH₂ products decay via H loss to give CHCH₂.

The translational kinetic energy releases measured in the present work for all three channels are in excellent agreement with previous measurements by Lee.³⁹ However, Lee reported near-zero angular anisotropy for both channels, whereas we observe a recoil anisotropy parameter β that has near-zero values for products formed with low velocities, but decreases to around −0.75 for Channels 1a and 1b and −0.5 for Channel 2, respectively, for products formed with the highest recoil velocities. We attribute this behaviour to the extent of internal excitation of the C₄H₈O diradical intermediate and the range of lifetimes over which it survives prior to cleavage of a C–C bond. Diradicals which dissociate on a rapid timescale have the highest translational energies and retain the strongest correlation between the transition diople moment for the S₁ ← S₀ excitation and the recoil velocities of the photofragments. Since the transition dipole lies perpendicular to the plane of the ring and the recoil velocities of the photofragments lie preferentially in the plane of the ring, this results in negative β parameters which approach the limiting value of −1. In contrast, diradicals with longer lifetimes undergo both rotation and redistribution of energy into internal degrees of freedom prior to dissociation, both of which reduce both the magnitude of the photofragment velocities and their correlation with the transition dipole moment. The highest values of β observed for Channel 2 are significantly lower than those observed for Channels 1a and 1b, which is consistent with the higher barrier to dissociation via Channel 2 leading to dissociation on a slower timescale than via Channels 1a and 1b.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank the EPSRC for funding this work via Programme Grants EP/V026690/1 and EP/T021675/1.

References

1. B. Boudaïffa, P. Cloutier, D. Hunting, M. A. Huels and L. Sanche, Science, 2000, 287, 1658–1660.
2. B. Boudaïffa, P. Cloutier, D. Hunting, M. A. Huels and L. Sanche, Radiat. Res., 2002, 157, 227–234.
3. J. Cadet and T. Douki, Photochem. Photobiol. Sci., 2018, 17, 1816–1841.
4. S. Tonzani and C. H. Greene, J. Chem. Phys., 2006, 125, 094504.
5. C. J. Colyer, S. M. Bellm, B. Lohmann, G. F. Hanne, O. Al-Hagan, D. H. Madison and C. G. Ning, J. Chem. Phys., 2010, 133, 124302.
6. X. Ren, E. Wang, A. D. Skitnevskaya, A. B. Trofimov, K. Gokhberg and A. Dorn, Nat. Phys., 2018, 14, 1062–1066.
7. N. Y. Aouina and Z. E. A. Chaoui, Surf. Interface Anal., 2018, 50, 939–946.
8. W. Wolff, B. Rudek, L. A. Da Silva, G. Hilgers, E. C. Montenegro and M. G. Homem, J. Chem. Phys., 2019, 151, 064304.
9. H. J. Lüdde, M. Horbatsch and T. Kirchner, J. Phys. B: At., Mol. Opt. Phys., 2019, 52, 195203.
10. A. García-Abenza, A. I. Lozano, L. Álvarez, J. C. Oller, F. Blanco, P. Stokes, R. D. White, J. de Urquijo, P. Limão-Vieira, D. B. Jones, M. J. Brunger and G. García, Eur. Phys. J. D, 2021, 75, 303.
11. Y. Yagci and A. Ledwith, J. Polym. Sci. Part A Polym. Chem., 1988, 26, 1911–1918.
12. M. R. Rodrigues and M. G. Neumann, Macromol. Chem. Phys., 2001, 202, 2776–2782.
13. A. A. Scala, E. W. Diau, Z. H. Kim and A. H. Zewail, J. Chem. Phys., 1998, 108, 7933–7936.
14. T. J. Wasowicz, A. Kivimäki, M. Dampc, M. Coreno, M. De Simone and M. Zubek, Phys. Rev. A - At. Mol. Opt. Phys., 2011, 83, 033411.
15. B. L. W. Pickett, N. J. Hoeflich and T.-C. Liu, J. Am. Chem. Soc., 1951, 73, 4865–4869.
16. G. J. Hernandez, J. Chem. Phys., 1963, 38, 2233–2242.
17. J. Doucet, P. Sauvageau and C. Sandokfy, Chem. Phys. Lett., 1972, 17, 316–319.
18. L. J. Bremner, M. G. Curtis and I. C. Walker, J. Chem. Soc., Faraday Trans., 1991, 87, 1049–1055.
19. A. Giuliani, P. Limão-Vieira, D. Duflot, A. R. Milosavljevic, B. P. Marinkovic, S. V. Hoffmann, N. Mason, J. Delwiche and M. J. Hubin-Franskin, Eur. Phys. J. D, 2009, 51, 97–108.
20. B. Cadioli, E. Gallinella, C. Coulombeau, H. Jobic and G. Berthier, J. Phys. Chem., 1993, 97, 7844–7856.
21. A. H. Mamleev, L. N. Gunderova and R. V. Galeev, J. Struct. Chem., 2001, 42, 365–370.
22. D. G. Melnik, S. Gopalakrishnan, T. A. Miller and F. C. De Lucia, J. Chem. Phys., 2003, 118, 3589–3599.
23. V. M. Rayón and J. A. Sordo, J. Chem. Phys., 2005, 122, 204303–204311.
24. T. Yang, G. Su, C. Ning, J. Deng, F. Wang, S. Zhang, X. Ren and Y. Huang, J. Phys. Chem. A, 2007, 111, 4927–4933.
25. P. Duffy, J. A. Sordo and F. Wang, J. Chem. Phys., 2008, 128, 125102.
26. S. M. Park, Y. R. Lee, D. W. Kang, H. L. Kim and C. H. Kwon, Phys. Chem. Chem. Phys., 2017, 19, 30362–30369.
27. L. Paoloni, S. Rampino and V. Barone, J. Chem. Theory Comput., 2019, 15, 4280–4294.
28. A. Röder, A. B. Skov, A. E. Boguslavskiy, R. Lausten and A. Stolow, Phys. Chem. Chem. Phys., 2020, 22, 26241–26254.
29. S. H. Lee, J. Chem. Phys., 2009, 131, 224309.
30. E. Tapavicza, I. Tavernelli, U. Rothlisberger, C. Filippi and M. E. Casida, J. Chem. Phys., 2008, 129, 124108.
31. N. Gavrilov, S. Salzmann and C. M. Marian, Chem. Phys., 2008, 349, 269–277.
32. S. Oesterling, O. Schalk, T. Geng, R. D. Thomas, T. Hansson and R. De Vivie-Riedle, Phys. Chem. Chem. Phys., 2017, 19, 2025–2035.
33. M. Stenrup, Chem. Phys., 2012, 397, 18–25.
34. M. N. Ashfold, M. Bain, C. S. Hansen, R. A. Ingle, T. N. Karsili, B. Marchetti and D. Murdock, J. Phys. Chem. Lett., 2017, 8, 3440–3451.
35. N. Kotsina, S. L. Jackson, T. Malcomson, M. J. Paterson and D. Townsend, Phys. Chem. Chem. Phys., 2022, 24, 29423–29436.
36. B. C. Roquitte, J. Am. Chem. Soc., 1969, 91, 7664–7667.
37. J. Kramer, J. Phys. Chem., 1982, 86, 26–35.
38. S. W. Benson, J. Chem. Phys., 1964, 40, 105–111.
39. S. H. Lee, Phys. Chem. Chem. Phys., 2010, 12, 2655–2663.
40. C. H. Green and R. N. Zare, Ann. Rev. Phys. Chem., 1982, 33, 119–150.
41. W. S. Hopkins, M. L. Lipciuc, S. H. Gardiner and C. Vallance, J. Chem. Phys., 2011, 135, 034308.
42. A. H. Kung, J. F. Young and S. E. Harris, Appl. Phys. Lett., 1973, 22, 301–302.
43. A. H. Kung, J. F. Young and S. E. Harris, Appl. Phys. Lett., 1976, 28, 294.
44. N. P. Lockyer and J. C. Vickerman, Laser Chem., 1997, 17, 139–159.
45. J. M. Gray, J. Bossert, Y. Shyur, B. Saarel, T. C. Briles and H. J. Lewandowski, J. Chem. Phys., 2021, 154, 024201.
46. D. W. Chandler and P. L. Houston, J. Chem. Phys., 1987, 87, 1445–1447.
47. A. T. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484.
48. A. Nomerotski, M. Brouard, E. Campbell, A. Clark, J. Crooks, J. Fopma, J. J. John, A. J. Johnsen, C. Slater, R. Turchetta, C. Vallance, E. Wilman and W. H. Yuen, J. Instrum., 2010, 5, C07007.
49. E. S. Wilman, S. H. Gardiner, A. Nomerotski, R. Turchetta, M. Brouard and C. Vallance, Rev. Sci. Instrum., 2012, 83, 013304.
50. A. T. Clark, J. P. Crooks, I. Sedgwick, R. Turchetta, J. W. Lee, J. J. John, E. S. Wilman, L. Hill, E. Halford, C. S. Slater, B. Winter, W. H. Yuen, S. H. Gardiner, M. L. Lipciuc, M. Brouard, A. Nomerotski and C. Vallance, J. Phys. Chem. A, 2012, 116, 10897–10903.
51. V. Dribinski, A. Ossadtchi, V. A. Mandelshtam and H. Reisler, Rev. Sci. Instrum., 2002, 73, 2634–2642.
52. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, J. R. M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, M. C. X. Li, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, 2016.
53. S. SenGupta, H. P. Upadhyaya, A. Kumar, P. D. Naik and P. Bajaj, J. Chem. Phys., 2005, 122, 124309.
54. S. Pedersen, J. K. Herek and A. H. Zewail, Science, 1994, 266, 1359–1364.
55. C. Doubleday, J. Phys. Chem., 1996, 100, 3520–3526.

---

Footnotes

† We note that within the mass resolution of our experiment, there may also be some contributions to the ‘m/z 41’ signal from the higher velocity components of the m/z 40 and 42 signals. However, given the analysis we are about to describe, we do not believe that this is likely to introduce any significant error to the TKER and β(v) distributions reported for this channel, and does not change any of our conclusions.

‡ Interestingly, but not surprisingly, comparison of the velocity-map image fors the CHCH₂ and CH₂CH₂ products reveals more intensity in the centre of the image for the H-loss product. This implies that the slower-moving, more highly internally excited primary products are more likely to undergo H loss than the faster moving, less internally excited products.

---